Musculoskeletal model of trunk and hips for development of seated-posture-control neuroprosthesis

Abstract

The paralysis resulting from spinal cord injury severely limits voluntary seated-posture control and increases predisposition to a number of health risks. We developed and verified a musculoskeletal model of the hips and lumbar spine using published data. We then used the model to select the optimal muscles for—and evaluate the likely functional recovery benefit of—an 8-channel seated-posture-control neuroprosthesis based on functional electrical stimulation (FES). We found that the model-predicted optimal muscle set included the erector spinae, oblique abdominals, gluteus maximus, and iliopsoas. We mapped muscle excitations to seated trunk posture so that the required excitations at any posture could be approximated using a static map. Using the optimal muscle set, the model predicted a maximum stimulated range of motion of 49° flexion, 9° extension, and 16° lateral bend. In the nominal upright posture, the modeled user could hold almost 15 kg with arms at sides and elbows bent. We discuss in this article the practicality of using FES with the oblique abdominals. A seated-posture-control neuroprosthesis would increase the user’s bimanual work space and include several secondary benefits.

INTRODUCTION

The paralysis associated with spinal cord injury (SCI) severely limits mobility and function. The development of devices that use functional electrical stimulation (FES) for controlling bladder and bowel, walking, standing, and hand grasping has allowed many individuals to become independent and productive members of society, improving their quality of life. However, until recently, seated-posture-control systems using techniques other than bracing or harnessing have received relatively little attention [1].

Voluntary control of seated posture has significant clinical relevance. Affecting about 25 percent of the population with SCI each year [2], pressure ulcers are a primary cause of hospital admission and death due to septicemia and osteomyelitis [3–4]. The seated postures passively assumed by paralyzed individuals also lead to scoliosis, lordosis, kyphosis and extension of the cervical spine, and posterior tilt of the pelvis, which can compress internal organs [5]. Persons with SCI often suffer from neurogenic bowel, which, when confounded by a lack of postural support, causes difficulties with stool voiding. Additionally, two-handed reaching is extremely limited for wheelchair users with SCI confined to wheelchairs because of poor trunk stabilization. Improved seated posture, forward-leaning capability, and increased mobility from a seated-posture-control neuroprosthesis would decrease the risk of ulcer development, improve respiratory and other internal organ function, increase stool movement during toileting [6], and increase the bimanual work space.

Kukke and Triolo stimulated the spinal roots of the lumbar erector spinae at thoracic (T) 12 to lumbar (L) 1 or L1 to L2 and reported a more natural lumbar curvature, about a 7 cm increase in bimanual work space (forward or upward), and an ability to carry heavier loads during applied stimulation [7]. A 16-channel neuroprosthesis for standing after SCI is currently under active research and development [8–10]. This system involves erector spinae stimulation but otherwise has not been specifically optimized for seated-posture control.

Spine models have been widely used to study compressive and shear stresses on vertebral segments during varied posture such as lifting exercises [11–13] or spinal stability [14–19]. These models are mainly used to assess risk-prone postures or test theories about lower-back pain. While some models have attempted to maintain all degrees of freedom (DOFs) in the spine with intersegmental muscles or individual attachments on each vertebra [11,15–16,20], the spine may also be modeled as a flexible rod or a system of coupled or constrained joints [21]. The independent activation of different muscle fascicles in the trunk extensor muscles is controversial, so whole muscles may need to be modeled rather than individual excitable fascicles [22]. Wilkenfeld et al. demonstrated the feasibility of modeling the trunk with this technique, although this model excluded several potentially important muscles [23]. The musculoskeletal model we have developed is unique in that it determines muscle excitations required at hip and trunk muscles over the entire physiological range of joint angles and was specifically designed as a tool to develop a neuroprosthesis for seated-posture control.

We verified our musculoskeletal model with published data and used it to (1) determine the optimal muscle set for a seated-posture-control neuroprosthesis, assuming a reasonable number of channels, and (2) estimate the expected level of restored function for a person with SCI using these stimulation channels in order to evaluate the feasibility of such a system.

METHODS

Musculoskeletal Model

We described body segments, joints, and muscles mathematically with SIMM 4.1.1 (Software for Interactive Musculoskeletal Modeling; Musculographics, Inc; Santa Rosa, California). The trunk is based on the Wilkenfeld Trunk Model (WTM), a musculoskeletal model developed by Wilkenfeld et al. [23], and the lower limbs are based on the Delp Lower Extremity Model (DLEM) [24].

Body Segments

The model contains 16 segments: head and neck (to cervical [C] 7), 2 arms, thorax (T1–T12), 5 lumbar segments, pelvis-sacrum-coccyx, and 6 lower-limb segments. The lower limbs are used only for muscle attachment points and are assumed to be fixed to the seating surface. We used the same anthropometric data for segment dimensions and inertias as in the WTM.

Joints

The model has a 3-DOF joint at the lumbosacral joint. The other lumbar joints (T12–L1 to L4–L5) each have three constrained DOFs as in the WTM. That is, each lumbar joint angle is proportional to the lumbosacral joint angle according to representative ratios measured by White and Panjabi, thereby eliminating our need to independently control each lumbar segment with many muscle fascicles [25].

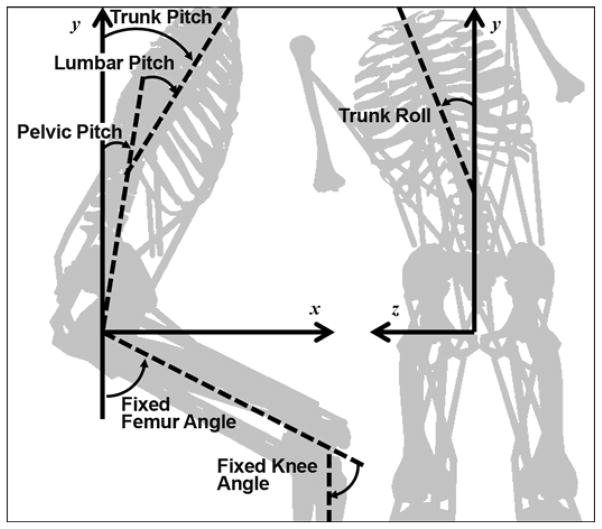
The hip joint is composed of two components: pelvic pitch (1 DOF) and femur angle. We assumed the femur and tibia to be fixed at given angles in the sagittal plane. We used the knee and patellar kinematics from the DLEM to determine the fixed locations of the tibia and patella with respect to the femur. We fixed the arms and head parallel to the long axis of the trunk. We considered movement at the iliosacral joint to be negligible because of the joint’s limited range of motion and high stiffness—an order of magnitude larger than spinal joints [25]. Thus, the model has a total of only four rotational DOFs, which we assumed to be frictionless. Figure 1 provides a schematic of joint angle definitions, including the fixed angles. Anterior pelvic pitch, lumbar flexion, right lateral bend, and counterclockwise (viewed from above) axial twist are considered positive.

Figure 1.

Schematic of joint angle definitions. While lumbar spine is also free to twist axially (yaw), muscle activations were constrained to prevent axial twist in this study. Trunk pitch (flexion) is defined as sum of pelvic and lumbar pitch.

Muscles

The musculoskeletal model uses a muscle model in which muscle force is a function of activation, muscle length, and pennation angle, scaled by the maximum force output of each specific muscle. Since we only used the model statically in this study, we ignored contraction velocity and activation dynamics. Similarly, the tendons were assumed to have reached equilibrium. Thus, activation and excitation are synonymous in this article and muscle length is only affected by change in fiber length. These steady state conditions are generally assumed when inverse dynamics are being performed, because many slow postural adjustments can be usefully viewed as quasi-static [23,26–28]. Furthermore, data on static muscle activations provide an estimate of the range of postures that can be maintained and the required muscle effort to do so, which could lead to further estimates for muscle stimulation patterns or the onset of fatigue.

The model has 15 muscles bilaterally, defined by single or multiple elements that total 36 muscle segments. Table 1 summarizes the muscle parameters used in the model. We took these parameters from the literature [29–30], previous models, or estimations. For modeling paralyzed muscles, we assumed that the maximal force that could be generated by electrical stimulation was half the nondisabled maximal force [23,26–28]. Each muscle uses a generic curve to describe the force-length relationship as in the DLEM. We removed individual muscle passive properties because the model uses joint-level passive properties (see “Passive Properties” section), encompassing all muscular and other tissue passive properties.

Table 1.

Summary of muscle parameters used in seated-posture-control neuroprosthesis model.

Muscle Segment	l0 (m)	lst (m)	&agr; (°)	PCSA (cm2)	f (N/cm2)	Fmax (N)
Erector Spinae	0.127 [1]	0.325 [1]	13.0 [1]	26.00 [2]	57.6	1,497.0
Latissimus Dorsi 1 (lateral)	0.328 [3]	0.111	0.0 [3]	2.00 [3]	57.6	115.2
Latissimus Dorsi 2 (medial)	0.321 [3]	0.142	0.0 [3]	2.10 [3]	57.6	121.0
Rectus Abdominis	0.280 [1]	0.076 [1]	0.0 [1]	6.80 [4]	22.0	149.6
External Obliques	0.129* [5]	0.029	0.0	6.85 [6]	22.0	150.7
Internal Obliques	0.091* [5]	0.031	0.0	5.68 [6]	22.0	125.0
Quadratus Lumborum	0.073 [1]	0.045 [1]	7.4 [1]	6.40 [4]	57.6	368.6
Gluteus Maximus 1 (lateral)	0.156†[7]	0.144‡[7]	5.0 [7]	15.01 [7]	32.0	480.4
Gluteus Maximus 2 (central)	0.162†[7]	0.146‡[7]	0.0 [7]	21.51 [7]	32.0	688.2
Gluteus Maximus 3 (medial)	0.158†[7]	0.167‡[7]	5.0 [7]	14.43 [7]	32.0	461.8
Adductor Magnus (posterior)	0.131 [7]	0.260 [7]	5.0 [7]	17.41 [7]	32.0	557.1
Semimembranosus	0.080 [7]	0.359 [7]	15.0 [7]	16.86 [7]	32.0	539.5
Semitendinosus	0.201 [7]	0.262 [7]	5.0 [7]	5.37 [7]	32.0	171.8
Biceps Femoris (long head)	0.109 [7]	0.341 [7]	0.0 [7]	11.74 [7]	32.0	375.7
Rectus Femoris	0.084 [7]	0.346 [7]	5.0 [7]	12.73 [7]	32.0	778.0
Sartorius	0.579 [7]	0.040 [7]	0.0 [7]	1.70 [7]	32.0	103.9
Iliacus	0.100 [7]	0.090	7.0 [7]	8.50 [7]	50.0	425.0
Psoas Major	0.137 [7]	0.183	8.0 [7]	14.70 [7]	50.0	735.0

^*Weighted average of segments [4].

^†+10%.

^‡+15%.

^[1]Delp SL, Suryanarayanan S, Murray WM, Uhlir J, Triolo RJ. Architecture of the rectus abdominis, quadratus lumborum, and erector spinae. J Biomech. 2001;34(3): 371–75. [PMID: 11182129]

DOI:10.1016/S0021-9290(00)00202-5

^[2]Marras WS, Jorgensen MJ, Granata KP, Wiand B. Female and male trunk geometry: Size and prediction of the spine loading trunk muscles derived from MRI. Clin Biomech (Bristol, Avon). 2001;16(1):38–46. [PMID: 11114442]

DOI:10.1016/S0268-0033(00)00046-2

^[3]Klein Breteler MD, Spoor CW, Van der Helm FC. Measuring muscle and joint geometry parameters of a shoulder for modeling purposes. J Biomech. 1999; 32(11):1191–97. [PMID: 10541069]

DOI:10.1016/S0021-9290(99)00122-0

^[4]Tracy MF, Gibson MJ, Szypryt EP, Rutherford A, Corlett EN. The geometry of the muscles of the lumbar spine determined by magnetic resonance imaging. Spine. 1989;14(2):186–93. [PMID: 2922639]

DOI:10.1097/00007632-198902000-00007

^[5]Gardner-Morse MG, Stokes IA. The effects of abdominal muscle coactivation on lumbar spine stability. Spine. 1998;23(1):86–91; discussion 91–92. [PMID: 9460158]

DOI:10.1097/00007632-199801010-00019

^[6]Yamaguchi GT, Sawa AG, Moran DW, Winters JM. A survey of human musculoskeletal actuator parameters. In: Winters JM, Woo SL, editors. Multiple muscle systems: Biomechanics and movement organization. New York (NY): Springer-Verlag; 1990. p. 717–78.

^[7]Delp SL, Loan JP, Hoy MG, Zajac FE, Topp EL, Rosen JM. An interactive graphics-based model of the lower extremity to study orthopaedic surgical procedures. IEEE Trans Biomed Eng. 1990;37(8):757–67. [PMID: 2210784]

DOI:10.1109/10.102791

α = pennation angle, f = specific force, F_max = maximum isometric force (nondisabled), l₀ = optimal fiber strength, l_st = tendon slack length, PCSA = physiological cross-sectional area.

We tuned the specific tension of the muscles such that maximal exertion moments agreed with data reported in the literature described later in the article. Specific tensions are within a physiologically valid range, between 22 and 100 N/cm² [21]. In addition, the specific trunk-extensor tension used agrees very well with the 50 to 65 N/cm² used by Granata and Marras [13] and the specific tension used for the psoas major is the same as that used by Hansen et al. [21].

Passive Properties

As just stated, we used lumped, joint-level passive properties for the model rather than individual muscle passive properties. Two reasons exist for this decision. First, the model appeared highly sensitive to individual muscle passive properties. In addition, persons with SCI may have spasticity or other changes in passive properties so the passive force length relationship in the DLEM may not apply for some muscles. Second, the muscle passive properties would not include additional passive properties arising from ligamentous structures and other soft tissues.

We estimated the joint-level passive properties at the hip from the work by Amankwah et al. as in the WTM [31]. This passive model uses a double exponential that depends on both knee and hip angles and has been determined for both nondisabled persons and persons with SCI. The model estimates the passive properties of the muscles, joints, and other tissues. The hip angle is the sum of the fixed femur angle and the pelvic pitch. The specific equations are shown as

$$\text{Normal}:T^{\text{hip}\text{passive}}=13\times exp(-0.87{\theta }_{\text{hip}}+0.51{\theta }_{\text{knee}})-6.3\times exp(1.3{\theta }_{\text{hip}}-0.65{\theta }_{\text{knee}})$$ (1)

and

$$\text{SCI}:T^{\text{hip}\text{passive}}=22\times exp(-1.4{\theta }_{\text{hip}}+0.16{\theta }_{\text{knee}})-0.83\times exp(2.9{\theta }_{\text{hip}}-1.3{\theta }_{\text{knee}}),$$ (2)

where T = joint torque (Newton meters) and θ = joint angle (radians).

We based passive properties of the spine on linear stiffness coefficients and a neutral zone at the lumbosacral joint. Passive properties can be neglected over small spinal ranges of motion: ±3.0° in flexion-extension, ±1.8° in lateral bend, and ±0.7° in axial twist at the lumbosacral joint [25]. Outside of this neutral zone, we modeled passive properties to vary linearly with the lumbosacral angle using stiffness coefficients reported by White and Panjabi: 1.28 N·m/° for extension, 1.0 N·m/° for flexion, 7.69 N·m/° for lateral bend, and 1.82 N·m/° for axial twist [25].

Dynamics

We created equations of motion from SIMM using the SIMM Dynamics Pipeline utility and SD/Fast (Parametric Technology Corporation; Needham, Massachusetts) to perform inverse dynamics. First, we computed the total required moments at each constrained and unconstrained joint to keep the model in static equilibrium. Next, we subtracted the passive joint torques from the total required torques at each unconstrained joint to find the required active joint torques. We then found the necessary muscle excitations, such that the product of muscle force generated at the current muscle length and the current muscle moment arm equaled the required active torque for the unconstrained joints, if feasible. For the constrained joints, we assumed that the constraint torques were satisfied by a combination of passive components (vertebral shape, ligaments, discs, etc.) at each vertebral joint.

Optimization

To find the necessary muscle excitations, we required an optimization routine to resolve the force redundancy problem. We implemented the objective function—the sum of squares of normalized muscle force (F/F_max), excitation bounds, and any excitation equality constraints—using the sequential quadratic nonlinear optimization software package SNOPT (Stanford Business Software, Inc; Palo Alto, California).

Geometric Tuning of Model

The model described here used 12 “wrap objects” in SIMM to simulate the action of bone, skin, and other soft tissues on the muscle paths. We determined the use of the wrap objects by muscle moment arm data found in the literature.

The moment arm of the erector spinae does not change significantly at all lumbar joints between neutral and 45° of trunk flexion except at the lumbosacral joint, where the moment arm decreases by about 10 percent [32]. We created wrap objects to achieve a similar relationship in the model; thus, we took into account the net action of all erector spinae muscle fascicles. The anatomical origins and insertions best approximate the moment arm in various postures for the other trunk muscles because experimental data were unavailable. However, in the nominal upright posture, the sagittal and coronal plane moment arms of the lumbar-crossing muscles were similar to those of a static imaging study in which the subject was in a supine position [33].

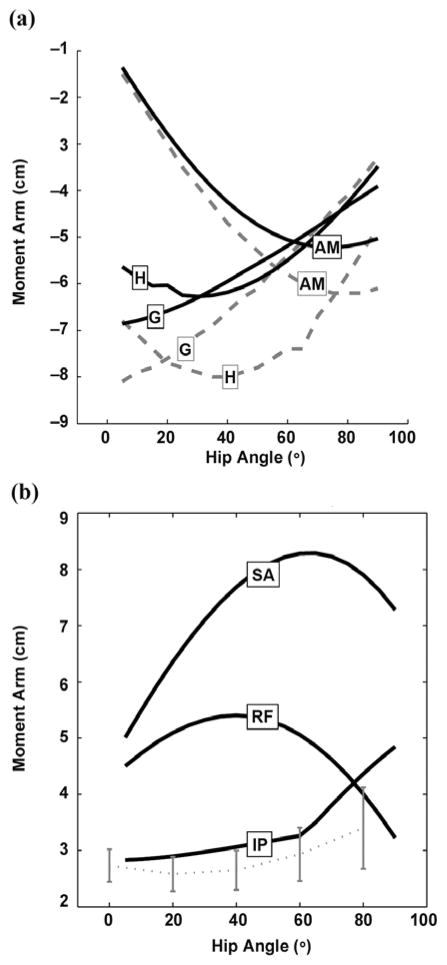
We compared the moment arms of the hip extensors with data reported in the literature. We found the moment arms of the gluteus maximus in the DLEM to be unacceptable for seated posture. Therefore, we used three wrap objects to create the path of the gluteus maximus segments bilaterally—one on the neck of the femur, one on the ischium, and one on the ilium—to simulate muscle wrapping over the other gluteals. Figure 2(a) illustrates the comparison between the hip extensor moment arms of the model and those reported by Nemeth and Ohlsén after adjustments to the DLEM [34]. We found the moment arms of the hamstrings to be underestimated relative to the Nemeth and Ohlsén study. However, in a study by Arnold et al. [35], the maximum moment arms of the semimembranosus and semitendinosus were 5.7 ± 0.6 cm and 7.1 ± 0.2 cm (mean ± standard deviation), respectively, which is significantly smaller than the maximum of 8.0 cm for all hamstrings reported by the Nemeth and Ohlsén study [34]. The moment arms of the iliopsoas compared reasonably well with experimental data (average of three specimens) from the Arnold et al. study (Figure 2(b)) [35]. We used a wrap object similar to one in the Arnold model to prevent the iliopsoas muscle path from intersecting the pelvis and femoral head. The rectus femoris and sartorius were not altered from the DLEM and have thus been previously verified.

Figure 2.

(a) Hip extensor moment arms. Solid lines = model, dashed lines = data published by Nemeth and Ohlsén. Source: Nemeth G, Ohlsén H. In vivo moment arm lengths for hip extensor muscles at different angles of hip flexion. J Biomech. 1985;18(2):129–40. [PMID: 3988782] DOI:10.1016/0021-9290(85)90005-3/. (b) Hip flexor moment arms. Solid lines = model, dashed line with error bars = data published (mean of 3 specimens ± 1 standard deviation) by Arnold et al. Source: Arnold AS, Salinas S, Asakawa DJ, Delp SL. Accuracy of muscle moment arms estimated from MRI-based musculoskeletal models of the lower extremity. Comput Aided Surg. 2000;5(2):108–19. [PMID: 10862133] DOI:10.3109/10929080009148877/. AM = adductor magnus, G = gluteus maximus, H = hamstrings average, IP = iliopsoas, RF = rectus femoris, SA = sartorius.

We used literature data concerning maximal voluntary contraction moments to find the joint angles at which the muscles are at their optimal lengths and to tune the specific force values. For the gluteus maximus, the tendon lengths had to be increased by 15 percent and the optimal fiber lengths by 10 percent such that the maximum moment generation occurred at the appropriate hip angle. We deemed this modification to the DLEM reasonable because the gluteus maximus segments have highly curved muscle paths. In order to achieve the appropriate moment arms, the model’s straight-line paths must exceed the length of a curved path. We adjusted the attachment and tendon length of the psoas major from the DLEM, which uses a fictional attachment point on the pelvis rather than a physiological origin on the lumbar spine. We simplified the psoas major into one line of action arising from the third lumbar segment, which we considered to be the average of all lines of action. We increased the tendon length to best match the joint angle-joint moment curve of the model to the corresponding experimental curve. Although the lines of action of the psoas major are known to cause extension about some lumbar joints, all fascicles cause flexion about the lumbosacral joint [36]. We also simplified the internal and external obliques into one line of action by computing the average direction of the segments in the Stokes and Gardner-Morse study [37] (weighted by PCSA) and comparing the lines of action in the coronal and sagittal planes visually with our model. Because of a lack of muscle parameters for the oblique muscles in the literature, we also approximated the optimal fiber lengths as the weighted average muscle lengths and calculated the tendon slack lengths, assuming that the optimal muscle lengths occurred in the neutral posture.

Kinetic Verification of Model

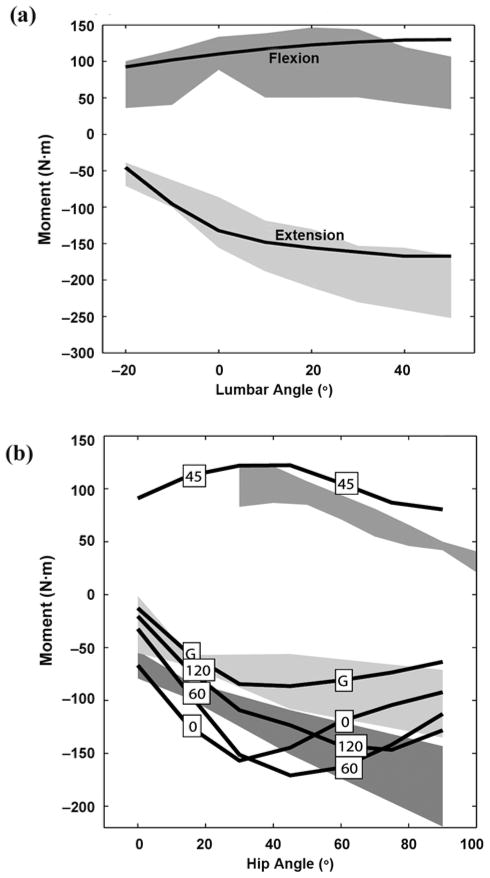
Figure 3(a) illustrates how the maximal active isometric lumbar extensor and flexor moments of the model compared with published data [38]. The maximum lumbar moment generation for the model closely matches published data with discrepancies beyond the error bars only for flexors at high flexion values beyond the range required for postural control. We found that each psoas major contributes 11.3, 16.1, and 30.1 N·m about the lumbosacral joint, in extended, erect, and flexed postures, respectively, compared with 13.6, 17.9, and 30.5 N·m as reported by Bogduk et al. [36].

Figure 3.

(a) Maximum isometric active lumbar moments at different postures. Shaded regions represent data published by Keller and Roy (mean ± 1 standard deviation [SD]). Source: Keller TS, Roy AL. Posture-dependent isometric trunk extension and flexion strength in normal male and female subjects. J Spinal Disord Tech. 2002;15(4):312–18. [PMID: 12177548]. (b) Maximum isometric active hip moments at different postures. Boxed numbers indicate knee angle (G = trial using only gluteus maximus as extensor, knee fully extended). Shaded regions represent published maximum voluntary contraction moment data (mean ± 1 SD): estimated flexion data from Inman et al. (upper) (source: Inman VT, Ralston HJ, Todd F, Lieberman JC. Human walking. Baltimore (MD): Williams and Wilkins; 1981); extension data from Waters et al. with sciatic nerve block; gluteus maximus only, knee extended (light gray, middle) and without block, knee flexed (dark gray, lower) (source: Waters RL, Perry J, McDaniels JM, House K. The relative strength of the hamstrings during hip extension. J Bone Joint Surg Am. 1974;56(8):1592–97. [PMID: 4434027]).

We found discrepancies in the literature regarding the hip extensors, particularly concerning the value of hip flexion at which the highest maximum extension moment occurs. Inman et al. reported that the highest maximal active isometric extension occurs about 70° of hip flexion when the knee is highly flexed [39]. This compares well with our model (Figure 3(b), knee at 120°). Waters et al. reported active extensor moments at 90° hip flexion that were unattainable by our model [40]. However, two of the eight subjects studied by Waters et al. exhibited peak maximal hip extension moment at 45° rather than 90°. Jensen et al. also showed that the hip extensors generate the most force around 40° to 45° [41]. The overall hip flexion moment compares well in shape with curves reported by Inman et al., although slightly higher in magnitude [39]. We found the muscles in the model generated ample feasible postures using nondisabled parameters in flexion and lateral bend.

Pelvic-Lumbar Rhythm

In the model, trunk and lumbar pitch are independent variables. However, during reaching or lifting activities, the pelvis and lumbar joints act in a stereotyped manner. For instance, in forward bending during standing, the spine plays a larger role in early flexion, whereas the pelvis plays a larger role in late flexion [14,42–43]. A study by Serber suggested that one ratio, 2.22 lumbar-to-hip movement, could be used for different seated postures [44]. We used this ratio to avoid the necessity for optimizing the joint movements. Note that Lee and Wong reported a ratio of 1.15 for forward bending during standing, so a lower ratio would be required to simulate standing conditions [42].

Cases Studied

We used initial inverse dynamic simulations and muscle excitation optimizations to verify the model structure as described previously and to determine the feasible seated-posture set for a nondisabled person. Subsequently, we ran 29 simulations with different muscle combinations to examine various sets of muscles, focusing on those that could be activated by 8 stimulation channels (Table 2). The minimum muscle set for a seated-posture-control neuroprosthesis must include a hip flexor, hip extensor, trunk flexor, and trunk extensor, bilaterally, and some means for lateral bend to resist perturbation and increase the user’s work space in all directions. The first five simulations used all 36 muscle segments available. Case 1 allowed for all segments to be activated individually, whereas cases 2 to 5 required the various elements of several muscles to be activated equally: the latissimus dorsi, gluteus maximus, hamstrings, posterior portion of the adductor magnus, and abdominals. The remaining simulations examined the effects of particular muscles on seated posture. We used simulation cases 7 to 12, 13 to 16, and 17 to 22 to determine the best lumbar flexors, hip flexors, and hip extensors, respectively. We used simulation cases 24 to 29 to analyze the benefit of adding an additional channel bilaterally.

Table 2.

Summary of cases for muscle selection analysis with results. Muscle segment activations subject to equality constraints are indicated by boxes spanning multiple segments (gray box = on, white box = off). Bold numbers indicate best 8-channel cases (posture maps shown in Figure 4). Bold lines indicate groups of simulation cases intended to determine best muscle set for given action.

Case No.*		Cases Studied Muscle Segments																		%†	Results Max Range (°)
		ES	L1	L2	QL	RA	EO	IO	G1	G2	G3	AM	SM	ST	BF	RF	SA	IL	PM		Flex	Ext	Lat
1	36																			100	51	22	19
2	30																			100	51	22	19
3	22																			90	51	22	18
4	20																			90	51	22	18
5	18																			81	51	22	17
6	16																			8	–4	22	4
7	8																			56	49	9	16
8	8																			63	49	9	16
9	8																			46	49	9	13
10	8																			49	49	9	14
11	8																			58	49	9	14
12	8																			52	49	9	14
13	8																			56	49	3	16
14	8																			36	49	–4	9
15	8																			32	49	–8	9
16	8																			39	49	–1	9
17	8																			62	47	9	16
18	8																			53	33	9	16
19	8																			44	24	9	16
20	8																			43	23	9	16
21	8																			29	14	9	15
22	8																			35	17	9	16
23	6																			42	49	9	13
24	10																			65	49	9	17
25	10																			67	49	9	17
26	10																			65	49	9	16
27	10																			68	50	9	17
28	10																			68	49	20	16
29	10																			63	49	9	16

^*No. = Required number of independent activations (number of stimulation channels).

^†% = Percentage of postures available with respect to complete muscle set (case 1).

AM = adductor magnus, BF = biceps femoris (long head), EO = external obliques, ES = erector spinae, Ext = extension, Flex = flexion, G1 = gluteus maximus 1 (lateral), G2 = gluteus maximus 2 (central), G3 = gluteus maximus 3 (medial), IL = iliacus, IO = internal obliques, L1 = latissimus dorsi 1 (lateral), L2 = latissimus dorsi 2 (medial), Lat = lateral bend, Max = maximum, PM = psoas major, QL = quadratus lumborum, RA = rectus abdominis, RF = rectus femoris, SA = sartorius, SM = semimembranosus, ST = semitendinosus.

For each case, the muscle excitations, muscle forces, required joint torques, and lumbar constraint torques were output from the simulation for an adequate range of trunk pitch and trunk roll in increments of 1° (a total of 1,701 postures per trial). Thus, we could analyze the excitations, forces, or constraint torques for each simulation case at each postural increment. We set the fixed femur and knee angle to 64° and constrained the muscle activations such that no axial twist (lumbar yaw) was allowed, as in the Wilkenfeld et al. study [23]. We mapped and plotted the excitation to trunk pitch and roll for the best-case muscle set.

External Loads

To estimate the resistance of the trunk to external loading, we applied a downward force at the hands to simulate a bimanual load-carrying task, with the humerus parallel to the long axis of the trunk and the elbows flexed 90°. Using the best-case muscle set, we ran simulations repeatedly with the external load incrementally increased by 1 N for each simulation until the available muscle forces were insufficient to hold a given posture. For each posture that was feasible with no external load, we recorded and plotted the maximum external load using this method.

RESULTS

For all simulations using the SCI-modified model, activation of the trunk extensor muscles was required for postures from 4° of extension through the full range of flexion. Hip extensor activation was required only for postures from 10° flexion through the full range of flexion. In other words, the trunk tended to fall into flexion from the neutral position while the pelvis tended to pitch posteriorly relative to the neutral position. We expected this result because persons with SCI generally adopt such a posture [5].

Muscle Selection

Table 2 summarizes results of the muscle selection process. A case number indicates the specific muscle set tested. Also indicated are the number of muscle stimulation channels that would be required (column labeled “No.”), the percentage of the tested postures that were feasible with the particular muscle set (column labeled “%”) relative to the complete muscle set, and the maximum trunk angles (flexion, extension, and lateral bend) that could be statically maintained by the particular muscle set. In cases where the activations of all of the elements of a muscle were constrained to be equal, a single box spans all the muscle elements.

Case 1 represents optimal performance, because all relevant muscles were included. This full muscle set allowed for 51° of flexion, 22° of extension, and 18° of lateral bend. Constraining the various gluteus maximus and latissimus muscle elements to have the same activation level (case 2) had no effect on the number of feasible seated postures or the range of trunk angles that could be maintained. Additionally constraining the various elements of the abdominals, hamstrings, and posterior portion of the adductor magnus to have equal activations (cases 3–5) showed decreasing performance, especially with the constrained activation of the abdominals. Case 6 tested whether the latissimus dorsi could be used to produce adequate trunk extension without the erector spinae. This was not successful, since only 8 percent of seated postures, including no flexed postures, were feasible.

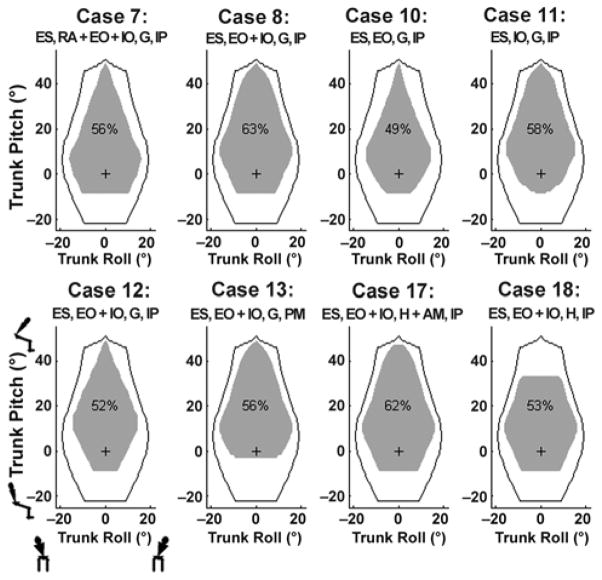
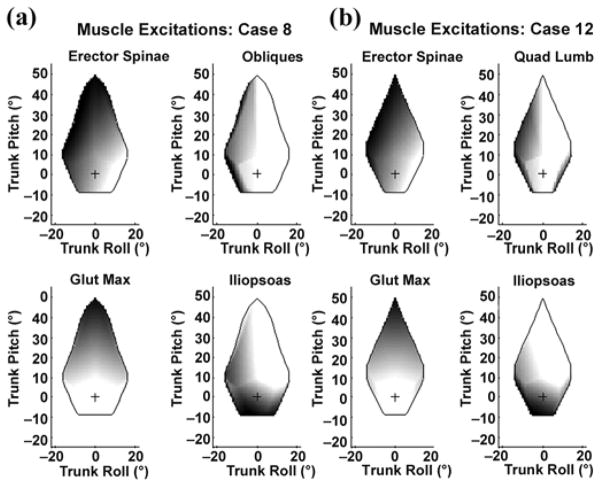
Cases 7 to 22 represent different 8-channel configurations, several of which had similar performance. Figure 4 illustrates the feasible posture regions for the best of these configurations (cases 7–8, 10–13, and 17–18) in terms of the feasible ranges of trunk roll and trunk pitch. The black boundary line indicates optimal performance (i.e., case 1), while the gray shaded area indicates the feasible range for each specific muscle set. Thus, we deemed case 8 to be the model-predicted optimal 8-channel muscle set: erector spinae, abdominal obliques (no rectus abdominis), gluteus maximus, and iliopsoas (all bilaterally). The 6-channel case (case 23) provided 42 percent of the possible postures, outperforming several of the nonideal 8-channel cases. Limited lateral bend relative to the best-case 8-channel muscle set was its greatest drawback.

Figure 4.

Feasible posture maps for best 8-channel configurations. Gray area: feasible postures using select muscles. Black boundary: feasible postures available using complete muscle set with spinal cord injury parameters. Small figures represent directions of posture movement. “+” = nominal posture, “%” = percentage of feasible postures within black boundary, AM = adductor magnus, EO = external oblique, ES = erector spinae, G = gluteus maximus, H = hamstrings, IO = internal oblique, IP = iliopsoas, PM = psoas major, RA = rectus abdominis.

We found the rectus femoris and latissimus dorsi to be the best additional channels, increasing the number of feasible postures relative to the model-predicted optimal 8-channel muscle set by 8 percent. The addition of the rectus femoris (case 28) provided substantially more extension range (11° at maximum) whereas the addition of the latissimus dorsi (case 27) provided additional lateral bend, especially in flexed positions. We found that the addition of the hamstrings (case 29) added no feasible postures. However, we did not model fatigue in this study, and introducing such redundant muscles would help reduce fatigue. As for hamstring benefit (determined by the percentage of feasible postures when the gluteus maximus was excluded), we found that the adductor magnus provided the most benefit, followed by the semi-membranosus, biceps femoris, and semitendinosus.

Excitation Mapping

We plotted the muscle activation levels needed for the range of feasible seated postures for the optimal 8-channel muscle set (case 8, right-side muscles) in Figure 5(a). The intensity of the shading indicates the magnitude of the required activation (with black representing 100% activation and white representing 0% activation). These right-sided muscles required increased activation for left-leaning postures as expected. In addition, the extensors (erector spinae and gluteus maximus) were clearly active during flexed postures, while the flexor (iliopsoas) was active in extended postures. These data could provide a lookup table for a seated-posture-control system, whereby if a subject was measured in a certain posture, the appropriate activations to maintain that posture could be applied.

Figure 5.

Excitation mapping plots for 4 channels (right-side) for (a) model-predicted optimal 8-channel system (case 8) and (b) proposed system (case 12). Black = 100% active, white = inactive, “+” = nominal posture, Glut Max = gluteus maximus, Quad Lumb = quadratus lumborum.

External Loading

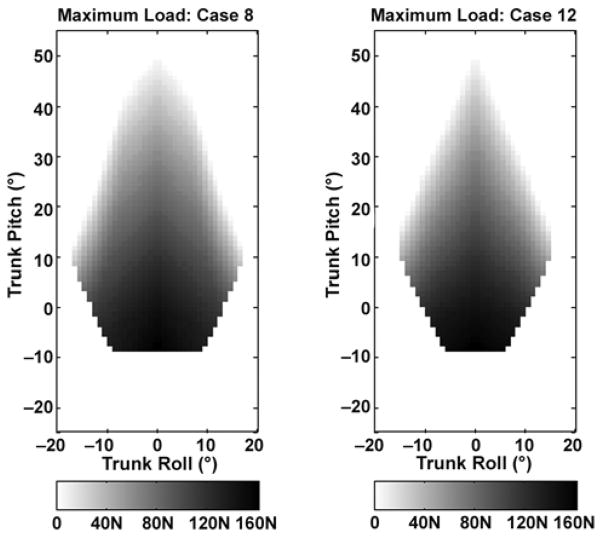
We plotted the maximum external loads applied to the model-predicted optimal 8-channel muscle set in Figure 6(a). The load is indicated by the intensity of the shading: white is 0 N and darker shades of gray reflect greater forces, as indicated by the scale below the plot. The maximum load across all postures was 162 N, which occurred at 9° extension. The maximum load at the nominal posture was 144 N. This finding implies that the activation of the model-predicted optimal muscles can account for the effects of body mass in the nominal position, plus an additional 14.7 kg held in the hands with elbows bent.

Figure 6.

Color bar indicates maximum external load that could be sustained (N). Force was applied downward at hands with arms held parallel to long axis of trunk and elbows at 90° simulating bimanual carrying task. (a) Model-predicted optimal 8-channel system (case 8) and (b) proposed system (case 12).

DISCUSSION

We developed a detailed musculoskeletal model that describes the mechanics of seated posture relevant to an individual with trunk and lower-limb muscle paralysis. We carefully adjusted several parameters of the model to match its characteristics to existing experimental data. We then performed a large number of inverse simulations to determine the ability of 29 different configurations of muscles to maintain a range of seated postures and resist external loads. The results of these simulations indicate that the stimulation of eight muscles (four muscles bilaterally) would allow stable seated postures over a wide range of trunk angles and that including additional muscles may have additional benefits, such as fatigue compensation or allowance of additional functions beyond seated-posture control. We also computed a mapping between a range of seated postures and the muscle activations needed to maintain these postures, specifying a static control algorithm that could be implemented in a future FES system.

Somewhat surprisingly, stimulating all the abdominals equally produced less feasible postures (especially in flexed positions) than stimulating the constrained obliques, considering the extra force generation available in the rectus abdominis. However, the obliques provide substantial lateral bend possibility in both flexed and extended positions. Requiring the muscle activations of the rectus abdominis to equal those of the obliques requires increased cocontraction of the erector spinae in flexed positions, limiting the number of feasible postures. Constraining these muscles in a ratio other than 1:1 could possibly improve performance [27].

While the model predicted which abdominal obliques provided the most postures, the abdominal muscles may not be practical for stimulation in the proposed FES system. From our experience, stimulation of the abdominals can be uncomfortable and cause breathing difficulty for the user because of increased intra-abdominal pressure (IAP) requiring extra effort from the diaphragm muscles. The abdominals could be stimulated temporarily to move from one posture to another, but continuous stimulation would be inadvisable. Therefore, we also investigated the best simulation case with no abdominal muscle use. Case 12, which used the quadratus lumborum in place of the abdominals, provided 52 percent of the total possible postures. Figures 5(b) and 6(b) show the excitations mapping and maximum external loads for case 12. No change occurred in the maximum load at the nominal posture, and the excitation patterns were similar to those in the model-predicted optimal muscle set (case 8).

Depending on the application, the best model-predicted additional channels were the latissimus dorsi for increased lateral bend/flexion range and the rectus femoris for increased hip extension range. The latissimus dorsi may also not be a very practical muscle to stimulate for trunk control, however, because it acts primarily on the arm. In our study, the arms were locked so the action was confined to occur at the trunk. Although not especially useful for this wheelchair seated-posture-control application (where the backrest prevents extended postures), stimulation of the rectus femoris could improve a user’s ability to transfer in and out of bed or stabilize the user when seated without a backrest. Stimulation of the quadratus lumborum in addition to the abdominal obliques provided similar results to using the latissimus dorsi with the abdominal obliques, except it provided more lateral bend in slightly flexed postures and less lateral bend in highly flexed postures.

The 8-channel seated-posture-control neuroprosthesis that we suggested in this article (FES of the erector spinae, quadratus lumborum or abdominal obliques, gluteus maximus, and iliopsoas, bilaterally) would significantly benefit its users by increasing the bimanual work space, contributing to a reduced incidence of pressure-ulcer development and allowing improved toileting and wheelchair propulsion. Users would also benefit from a more cosmetic and healthy seated posture that allows more normal internal organ function and respiration.

We built the musculoskeletal model used in this study making several assumptions, and therefore, some limitations exist. Fixation of the femurs allowed for only 1 DOF at the hip. Thus, left- and right-sided muscles had no independent effect on the movement produced at the hip. Also, since the femurs were fixed, balance was not a concern in the model. Furthermore, the action of hip flexors and extensors depends on what body part is fixed. For example, activation of the iliopsoas will cause flexion of the femurs if the trunk is fixed or flexion of the trunk if the femurs are fixed. Thus, a user of the proposed posture-control system would need to have his or her legs restrained to achieve the model-predicted results.

Our model used generic muscle parameters on the basis of highly variable cadaver and imaging data. We also simplified the muscle origins and insertions and lines of action. Some of the trunk muscles (e.g., obliques) are broad and insert on aponeuroses rather than bony landmarks. Thus, the function of muscles may not be exactly replicated. We assumed that paralyzed muscles can be activated to generate 50 percent of the normal muscle force, which assumes a well-conditioned muscle [45]. Electrode design, placement, muscle atrophy, and denervation affect the amount of fibers that can be excited in a muscle. Wilkenfeld et al. estimated that only 26 percent of the erector spinae bulk was actually activated in a specific FES system [23]. Additionally, while we attempted to tune and verify the model in numerous ways, the muscles have not been individually verified in all possible postures.

The model assumes that a fixed kinematical relationship in the movement of the lumbar spine exists and that the passive tissues can generate sufficient forces to maintain this kinematic constraint. In pitch and roll, we generally found the constraint torques to fall below the calculated passive torques at those joints according to the stiffness coefficients and neutral zone data from White and Panjabi [25]. Since no axial twist occurs in the model, the passive torques for yaw should be zero; however, the model did not demonstrate this. Coupling exists between lumbar roll and yaw, so if the spine is laterally bent or flexed, passive properties present may affect axial twisting [25].

We based the passive properties of the model on measurements of functional units of a cadaveric spine. The three-part linear passive model we used may be a large simplification of the actual passive properties present around the spine. Data from an in vivo study indicate that the passive properties of the lumbar spine in flexion and extension can each be divided into “three sections each having a distinctly different slope,” i.e., very low stiffness over the neutral zone, medium stiffness for small to medium lumbar angles outside of the neutral zone, and high passive properties closer to the limits of the range of motion [46]. We chose the passive model because stiffness coefficients were reported for each lumbar joint independently, so the passive properties of the lumbosacral joint could be applied individually. We did not include IAP in this model, although it may contribute 10 percent of the maximal voluntary lumbar extension torque [22]. It has a more important role, however, in reducing spinal compression (by up to 40%) [22]. This model does not examine the compressive forces in the spine, and axial loads in the trials studied were much smaller than those in heavy lifting tasks, so IAP unlikely played such a large role in our study.

The objective function of the optimization prevents coactivation by minimizing normalized force. Models of spinal stability have generally shown that when muscle exertions are small, coactivation of antagonist muscles is necessary to preserve stability [16–17]. Thus, we cannot consider the objective function physiological in postures close to neutral.

Finally, the results shown in this study are for a model with segment properties of an average male. By adjusting the muscle parameters accordingly, we could scale the model for individuals with different statures.

CONCLUSIONS

We developed a musculoskeletal model of the hips and lumbar spine to simulate seated posture in nondisabled persons and persons with SCI. We tuned and verified various muscle-tendon parameters using published data. We then performed inverse simulations with the model to evaluate a range of possible muscle configurations for a future FES system to restore seated-posture control. We found that a set of eight muscles (thoracic and lumbar erector spinae, abdominal obliques or quadratus lumborum, the gluteus maximus, and the iliopsoas, all bilaterally) produced a wide range of feasible seated postures, as well as substantial resistance to external loading. We further calculated the muscle activation patterns needed to hold the body in specified seated postures, providing the basic structure of a future FES controller for restoring seated posture. These results indicate that a seated-posture-control neuroprosthesis using four channels each for lumbar and hip control should be feasible. Such a system could increase the bimanual work space, reduce the development of pressure ulcers, and improve toileting and wheelchair propulsion. Users would also benefit from a more cosmetic and healthy seated posture that promotes more natural internal organ function and respiration.

Abbreviations

C

cervical

DLEM

Delp Lower Extremity Model

DOF

degree of freedom

FES

functional electrical stimulation

IAP

intra-abdominal pressure

L

lumbar

SCI

spinal cord injury

SIMM

Software for Interactive Musculoskeletal Modeling

T

thoracic

WTM

Wilkenfeld Trunk Model