MODULE COVER – A NEW APPROACH TO GENOTYPE-PHENOTYPE STUDIES¹

Abstract

Uncovering and interpreting phenotype/genotype relationships are among the most challenging open questions in disease studies. Set cover approaches are explicitly designed to provide a representative set for diverse disease cases and thus are valuable in studies of heterogeneous datasets. At the same time pathway-centric methods have emerged as key approaches that significantly empower studies of genotype-phenotype relationships. Combining the utility of set cover techniques with the power of network-centric approaches, we designed a novel approach that extends the concept of set cover to network modules cover. We developed two alternative methods to solve the module cover problem: (i) an integrated method that simultaneously determines network modules and optimizes the coverage of disease cases. (ii) a two-step method where we first determined a candidate set of network modules and subsequently selected modules that provided the best coverage of the disease cases. The integrated method showed superior performance in the context of our application. We demonstrated the utility of the module cover approach for the identification of groups ofrelated genes whose activity is perturbed in a coherent way by specific genomic alterations, allowing the interpretation of the heterogeneity of cancer cases.

1. Introduction

Complex diseases, such as cancer, are typically caused by a combination of genomic alterations, epigenetic and environmental factors, and different combinations of such factors may result in the same disease phenotype. In addition, signals that are associated with each individual genetic perturbation might be weak and difficult to separate from background noise. Collectively, these obstacles render the identification of subtle genotype-phenotype relationships extremely challenging.

Recently, pathway-centric methods have emerged as key approaches that empower studies on genotype-phenotype relationships. Such pathway-centric studies typically leverage large interaction networks inferred by high-throughput experiments. Projecting gene expression data on an interaction network, these approaches infer molecular activities on the level of biological pathways (subnetworks) rather than individual genes (1–5). Gene expression has been utilized to assess the activity of subnetworks (6), while genotypic data has lately been used to identify mutated subnetworks by exploring positions of mutated genes in interaction networks (7–9). An additional level of understanding of genotype-phenotype relationships can be obtained when both genotype and gene expression data are available. A recent study (10, 11) combined copy number alteration and gene expression data and applied a current flow approach to identify flow of information from potential genomic causes to differentially expressed disease genes.

Generally, pathway-centric approaches are based on the premise that different genetic perturbations often dys-regulate the same pathway, leading to the same disease phenotype. Therefore, the identification of such dys-regulated pathways is important for the understanding of a disease, potentially guiding drug development efforts. However, complex diseases are usually vaguely defined, and typically what can be seen as a spectrum of diseases is annotated as one disease. In such a heterogeneous set, individual disease cases may be characterized by various combinations of dys-regulated pathways.

Set cover approaches have been proven useful in the determination of disease markers in heterogeneous datasets (1, 2, 5, 11). In a set cover, a gene is considered to cover a disease sample if the gene is dys-regulated in the sample. The underlying assumption of the set cover approach is that each disease case has some dys-regulated (thus covering) genes but if the disease is heterogeneous, different cases will typically have different covering genes. In particular, a multi set cover approach aims to find a set of genes so that each disease case is represented (covered) by at least a certain number of differentially expressed genes while the total number of selected genes is minimized (11). However, current set cover approaches do not consider several important issues: (i) if two different disease cases are covered by two different sets of genes this does not necessarily means that they are caused by a dys-regulation of different pathways (ii) signals of associations from an individual gene to genetic alterations may be weak and noisy.

Combining the strength of the set cover approach with the power and stability of network-centric methods, we designed a new technique that extends the concept of set cover from single genes to network modules. In contrast to previous “connected network cover” approaches which strived to identify one connected subnetwork covering most disease cases (1, 2, 5), our approach allows us to identify multiple subnetworks (modules), so that each disease case is covered by a number of modules while the total “cost” of modules is minimized. In addition to network information, the definition of a module involves a similarity measure between pairs of genes that is based on eQTL association profiles. While modules can be comprised of singleton genes, the trade-off between module granularity and similarity of genes in the module is controlled by a cost function.

Given the above definition of similarity, the module cover approach can be used to find covering subnetworks such that genes in each module are jointly regulated by the same genetic alterations. The problem of detecting subnetworks that are influenced by common genetic alterations has been recently approached with a variant of the LASSO method (12) and Bayesian partition methods (13) with different objectives in mind. In particular, none of the approaches was designed to deal with data heterogeneity while our set cover modules capture the heterogeneity of samples where each module covers a different subset of samples. In addition, the LASSO based method, GFlasso, in its current implementation does not scale to large datasets while the Bayesian approach does not utilize network information.

To solve the module cover problem, we developed an integrated method that simultaneously determines network modules and optimizes the cover of disease cases. For comparison, we also implemented a two-step method where we first determined candidate network modules and subsequently selected a subset of modules that cover disease cases. While the performance of the integrated method is superior to the two-step method, the two-step approach still performed better than a naïve method that was based on a single gene cover.

We applied the module cover approach to discover modules associated with genomic alterations in cancer patients, utilizing genomic alteration and gene expression data. Representing each gene by its eQTL (expression Quantitative Trait Loci) association profile our algorithms harness profile similarities between genes and identify modules of genes with highly correlated eQTL profiles that collectively cover all disease cases.

We start by introducing a mathematical formalization of the module cover problem and subsequently describe our two algorithms: Integrated Module Cover and Two-Step Module Cover. Next, we introduce rigorous measures to compare the quality of the modules obtained by the two algorithms. Finally, we analyze the modules obtained by the Integrated Module Cover that was applied to Glioblastoma Multiforme (GBM) and ovarian cancer data. We conclude with a discussion of a broader spectrum of additional applications of the proposed approach.

2. Methods

2.1. Introduction of the Module Cover Problem

Here, we extended the concept of the minimum multi-set cover problem to a minimum multi-module cover problem. The classical minimum multi-set cover is formally defined as follows: Given a set of elements E = {e₁, e₂, …, e_n}, a family of subsets S = {E₁, E_2, …_, E_m|E_i ⊆ E} and a positive integer k, the goal is to select a subfamily of S so that each e_i is included at least k times. In our problem formulation, disease cases are the elements, and a subset of disease cases E_i corresponds to a gene where it is differentially expressed in those disease cases. More specifically, a gene g covers a disease case c (cover(c, g)=1) if the gene is differentially expressed in the given case, and cover(c, g) = 0 otherwise. To obtain the most prominent disease genes, we aim to select the smallest set of genes to cover all disease cases at least k times (11). Fig. 1A shows an example of a multi-set cover where disease cases are elements to be covered by selected genes. An edge between a gene and a case exists if the gene covers the case.

Figure 1. Set Cover vs. Module Cover.

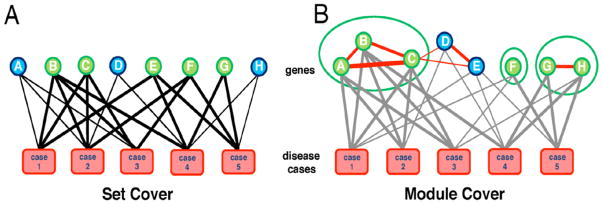
(A) In a classical set cover, an edge from a gene to a disease case exists if the gene is differentially expressed in the disease case (i.e. covering the case). Genes {B, C, E, F, G} are selected, and all cases are covered at least 3 times. (B) A module cover selects coherent modules. Red edges between genes represent the similarity between genes (e.g. based on the correlation coefficient of their eQTL profiles or gene expression patterns). In the example, modules {A, B, C}, {F}, {G, H} are selected, and all cases are covered at least 3 times.

In the module cover approach, we select modules (instead of single genes) to cover disease cases (Fig. 1B). To ensure that genes in a selected module are coherent, the ‘cost’ of modules was defined so that we preferentially assigns low cost to modules with genes that are close to each other in the network and are coherent according to a given similarity measure, such as correlation of expression or eQTL association profiles. In eQTL analysis, gene expression is considered as a quantitative phenotype and controlled by genotypic information. Utilizing matching gene expression and copy number variation, we determined eQTL profiles of each gene by computing significance levels of associations of each gene to genomic alterations (See Section 5.3 for the details).

Let sim(g1, g2) be the eQTL similarity of the two genes, which is computed based on the correlation of their eQTL profiles. We assume that 0 ≤ sim(g₁, g₂) ≤ 1. Let distance(g₁, g₂) be the shortest distance between the two genes in the interaction network. We first adjust the similarity by the distance as

$$\mathit{adjusted}\_\mathit{sim}(g_1,g_2)=\mathit{sim}{(g_1,g_2)}^{1+(\mathit{distance}(g1,g2)-1)/(\mathit{avg}\_\mathit{dist}-1)}$$ (1)

where avg_dist is the average distance between all pairs of genes in the network. Since our weight function adjusts the similarity value with interaction information we obtain higher weight if two genes have more similar eQTL profiles and are in close proximity in the network. We define the weight function as follows:

$$w(g_1,g_2)=\mathit{adjusted}\_\mathit{sim}(g_1,g_2)-\theta$$ (2)

where θ is a threshold parameter. The weight is positive (i.e. benefiting module cost) if the adjusted similarity is >θ. Consequently, we define the cost of a module M as

$$\mathit{Cost}(M)=\alpha +\mid M\mid -{\sum }_{x\in M}{\sum }_{y\in M,y\ne x}w(x,y)/(\mid M\mid -1)$$ (3)

where α is the module initializing cost when a new module is created. We include this initial module cost to minimize the number of selected modules. With a larger α, a smaller number of modules with larger average size will be obtained, since costs increase when a new module is created. The objective of the second term (i.e. the number of genes) is to minimize the total number of selected genes. Finally, we subtract the cost computed as the sum of average weights of genes in the module, ensuring coherence of modules since the cost of a module decreases as the weights(and similarities) between genes increase.

Our goal is to find a minimum cost set of modules that cover all disease cases at least k times where the depth of coverage is a user defined parameter. More specifically, we search for a module set S′ = {M₁, M₂, …, M_t} that minimizes Σ_Mi∈S′ Cost(Mi) with the constraint that Σ_Mi∈S′ Σ_g∈Mi cover(c,g) ≥ k for each disease case c. The minimum module cover problem is NP-hard as it is a generalization of the minimum set cover, which is known to be NP-hard. In the following two subsections, we describe two different heuristic algorithms: Integrated Module Cover and Two-Step Module Cover. In the integrated module cover algorithm, we discover modules on the fly while we select genes to cover disease cases. In the two-step module cover algorithm, we first cluster genes based on their similarity to obtain a candidate sets of modules and subsequently select a subset of modules to cover disease cases.

2.2. Integrated Module Cover

In this algorithm, we greedily select genes to cover disease cases and simultaneously create modules of ‘similar’ genes. In each iteration, we consider all unselected genes and compute the cost of adding each of those genes, assuming two ways to add a gene:

1. add the gene as a separate module: the cost of adding the gene is simply α + 1.

2. add the gene to an existing module: To maintain the coherence of a module, we first check if for the candidate gene g the average weight w(g, v) over all other genes in the module is positive. That is, we can add a gene g to a module M only if Σ_v∈M w(g,v) > 0. The increased cost resulting from adding gene g to module M is Cost(M+{g}) – Cost(M).

To find the best extension of the cover we proceed as follows: Let P(g) be the set of existing modules with a positive average edge weight with g as described in the case (2) The cost of adding a gene g is

$$IC(\text{g})=min(\alpha +1,{min}_{Mi\in P(g)}(\mathit{Cost}(M_i\text{U}\{g\})-\mathit{Cost}(M_i)))$$

Since we want to cover disease cases to the largest degree, we also account for the ‘benefit’ of adding genes. Considering the set of disease cases C′ that were covered less than k times by the end of the previous iteration we define the benefit by adding gene g as

$$\mathit{Benefit}(g)={\sum }_{c\in C^{\prime }}\mathit{cover}(c,g).$$

In each iteration, we greedily choose a gene with minimum IC (g)/Benefit (g). If the minimum cost of gene g is obtained adding gene g to an existing module M, the module is updated as M U{g}. Otherwise a new module {g} is created.

2.3. Two-Step Module Cover

In the Two-Step heuristic, we first find a candidate set of modules by clustering genes based on their similarity and interaction data. Subsequently, we apply a covering algorithm to select the best set of modules. Specifically, we used Markov Cluster Algorithm (MCL), an unsupervised clustering algorithm based on simulation of stochastic flow in a network (14). Note, that a predefined set of modules/pathways may be used instead as well. Given a network of interacting genes, we weight each edge by the corresponding similarity value and obtain a candidate set of modules {M₁, M₂, …, M_m} using MCL. We then select modules with coherent/similar genes, covering as many samples as possible. The cost of selecting a module M is given by (3), and we define the benefit of selecting a module as the total coverage

$$\mathit{Benefit}(M_i)={\sum }_{g\in Mi}{\sum }_{c\in C^{\prime }}\mathit{cover}(c,g)$$

Where, as before, C′ is the set of disease cases not covered k times by the end of the previous iteration. In each iteration, we greedily select a module with minimum Cost (M)/Benefit (M).

3. Results

We applied our module cover algorithms to two data sets: the first dataset includes the data for 158 Glioblastoma Multiforme patients (GBM) and 32 non-tumor control samples. The data was collected by the NCI-sponsored Glioma Molecular Diagnostic Initiative (GMDI), which includes matching mRNA expression and copy number variation data for each patient (http://rembrandt.nci.nih.gov/). The second dataset includes 489 Ovarian Cancer data samples from TCGA (The Cancer Genome Atlas). The technical details of data processing are described in the Materials section.

3.1. Analysis of Glioblastoma Multiforme Data from GMDI

First, we wanted to estimate which of the two methods provides a better heuristic in the context of our application. Since our goal was to selectmodules whose members are associated in a coherent way with genotypic changes, we evaluated the two methods based on significance, strength, and coherence of the association.

3.1.1. Comparison of the Module Cover approaches

We applied the integrated greedy module cover algorithm with k = 300 and α = 1, allowing 5 samples (3%) to be coveredless than k times to exclude outliers. We discuss the more detailed parameter selection in online Appendix Section 2. In particular, we found that the number of non-trivial modules (i.e. ≥ 3 genes) starts to level with k = 300, prompting us to choose this parameter value for our main analysis. We obtained 249 modules that contained a total of 513 genes including 41 non-singleton modules. The average distance between genes inside a module was 2.5.

For the two-step module cover, we applied MCL to the network of molecular interactions that have been weighted by correlating eQTL profiles of interacting genes. Using inflation parameter = 4 we obtained 3,401 candidate modules (see Appendix Table A1 and Figure A1 for details of parameter selection). The average size of the candidate modules was 3.21 and 2,677 modules were non-singleton. Subsequently, we greedily selected modules as described in Section 2.3. The two-step cover algorithm selected 801 genes in 454 modules. 233 modules (of which 171 modules are of size 2) were non-singleton. The average distance between genes inside a module was 1.1, indicating that the MCL cover provided more compact modules than the integrated module cover approach.

Testing which of the two approaches provided modules whose members were associated in a more coherent way with genotypic changes, we evaluated modules with respect to significance, strength and coherence of the association.

For each non-singleton module M, wefirst defined the significance of the association to each of tag loci as the average association significance of the genes in the module. Formally,

$$s_i(M)={\sum }_{g\in M}{s}_i(g)/\mid M\mid$$ (5)

where s_i(g) represents −log₁₀ p-value of the association provided by the linearlyregressi ng between expression values of gene g and copy number variation of i-th tag locus (see Section 5.1 for more details).

The upper panel of Fig. 2A shows such association significance profiles of the 10 largest modules. We found strong associations with tag-loci on chromosome 7 and 10. These chromosomes carry signature alterations of GBM, coinciding with the genomic locations of GBM related genes such as EGFR and PTEN. In the lower panel of Fig. 2A, we show association significance profiles of the 10 largest modules selected by the two-step algorithm. We observed that associations obtained by the two-step algorithm were weaker based on several different measures of quality introduced below.

Figure 2. Comparison of module covers approaches in GBMs.

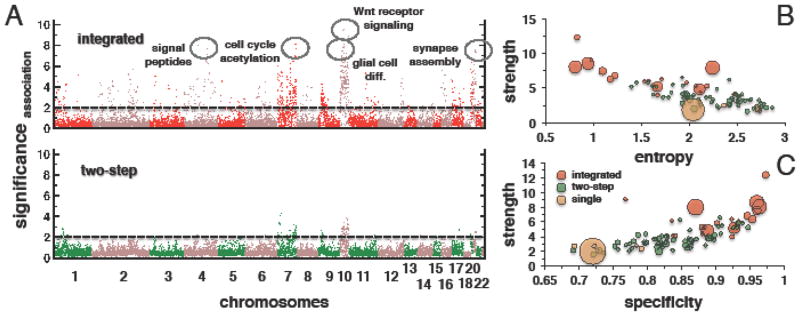
(A) Manhattan plots of module associations show average association significance for each tag-locus for the 10 largest modules we obtained with both methods. Modules obtained using the integrated method had more significant eQTL associations. In the upper panel, we also labeled associations that correspond to functionally coherent modules shown in Online Appendix Fig. A2. (B, C) Comparing the quality of modules, we observed that the Integrated method generated modules with higher strength, lower entropy and higher specificity Module size is indicated by the sizes of corresponding circles. The label “single” refers to modules we obtained using a set cover approach.

To compare the approaches more quantitatively, first note that the total cost of modules selected by the integrated and two-step algorithms was 744 and 1439.05, respectively (Appendix, Table A1). The total weights between genes in modules (the third term in cost function (3)) were 18.63 and −184.05, showing that the modules selected by the integrated algorithm were much more coherent compared to the modules obtained by two-step algorithm.

To further quantify the quality of modules in terms of their association to genomic alterations, we devised several measures: The strength of association significance of a module was defined as the maximum significance of the associations of the given module over all loci:

$$\mathrm{Strength}(M)={max}_i{s}_i(M).$$ (6)

We also computed the entropy of association profiles for each module. Since entropy measures the uncertainty of data, a good quality module (with only a few strong associations) is expected to have low entropy while entropy increases as data is more uniformly distributed. Formally, for each module M, we partitioned the range from 0 to strength (M) into 10 bins of equal sizes and assigned loci according to their significance. In each bin, we computed the percentage p_j of loci and defined the entropy as

$$\mathit{Entropy}(M)=-{\sum }_{j\in \mathit{bins}}{p}_j{log}_2{p}_j$$ (7)

For an association to be specific in a given module, only a few regulatory associations should have highly significant p-values while the remaining loci are expected to have insignificant p-values. Thus, we defined the specificity of a module M as the area of a cumulative histogram of association significance values. Specifically, we partitioned the range from 0 to strength (M) into 10 bins of equal sizesand defined c_j to be the cumulative percentage of j-th bin. Then the specificity is defined as:

$$\mathit{Specificity}(M)={\sum }_{j\in \mathit{bins}}{c}_j/\mid \mathit{bins}\mid$$ (8)

Similar to entropy, specificity quantifies the distinction between significant associations and the remainder of the loci. However specificity approaches 1 only if a small number of significant loci exist whereas theoretically entropy can be low in the case when there is a few insignificant and many significant loci.

We found that the integrated module cover outperformed the two-step module cover approach based on all three measures (as summarized in Online Appendix Table A1). The average strength of modules (size ≥ 3) selected by the integrated module cover algorithm was 6.4, significantly outscoring an average of 3.6 of modules obtained by the two-step module cover algorithm (P < 10⁻⁸, Wilcoxon test). Similarly, the average specificity for the integrated module cover was 0.9 while the average was 0.83 for the two-step cover (P < 10⁻⁴, Wilcoxon test). The average entropy of modules selected by the integrated algorithm and two-step cover were 1.6 and 2.2, respectively (P < 10⁻⁴, Wilcoxon test).

Fig. 2B, C presents a detailed comparison of the performance of the module cover approaches with respect to the mentioned measures. In addition, we included results obtained by the basic set cover algorithm labeled “single” in Figs. 2 B, C using the same parameter k = 300 and at most 5 outliers. In this case we defined the modules as the connected components of the subgraph spanned by the genes that were selected as the cover. We observed that modules of size ≥ 3 obtained by the integrated module cover approach were on average larger than modules found with the two-step approach. Specifically, modules identified by the integrated approach had significantly smaller entropy compared to modules obtained by the two-step approach (Fig. 2B, P < 10⁻⁶, Kolmogorov-Smirnov test). In addition, these modules showed significantly higher strength (Fig. 2C, P < 10⁻⁵, Kolmogorov-Smirnov test). However, the quality of modules obtained with both approaches was still superior to results of a single gene set cover, demonstrating general benefits of the module cover approach.

All alogrithms were implemented in Python and compute the solutions for the inputs of ~10,000 genes in a few minutes on NCBI linux machines.

3.1.2. Analysis of GBM data

We further analyzed modules provided by the integrated method. First, we determined enriched GO terms in modules using BINGO (15). Out of 21 modules with at least 3 genes, we found 14 modules having at least one GO term that they significantly enriched with (FDR < 0.05). In addition to modules enriched with typical cancer-related processes such as cell division, cell cycle, and immune response we also obtained more glioma-specific modules such as the WNT signaling pathway and glial cell differentiation. For example, only some subsets show dys-regulation of immune response or of WNT signaling while the cell cycle module is dys-regulated in almost all samples. Although our modules have been selected by using eQTL association profiles they allow us to recover GBM subtypes that previously were determined with expression profiles of single genes. Importantly, we observed that different modules were covering different sets of samples in a nonhierarchical (non-nested) way (Online Appendix, Fig. A2). This overlapping pattern of covering modules might explain why the number of GBM subtypes has been difficult to establish (16, 17).

3.1.3. Analysis of Ovarian Cancer Data

We also used the integrated module cover algorithm to analyze a set of 489 Ovarian Cancer samples from The Cancer Genome Atlas (TCGA). Applying the integrated module cover algorithm with k=70, α = 1, and 25 outliers, we selected 485 genes grouped in 235 modules including 54 non-singleton modules. As in the analysis of GBM data, we choose k for which the number of nontrivial modules starts to level. Out of 12 modules of size at least 5, 9 modules were enriched with at least one GO terms significantly (FDR < 0.05).

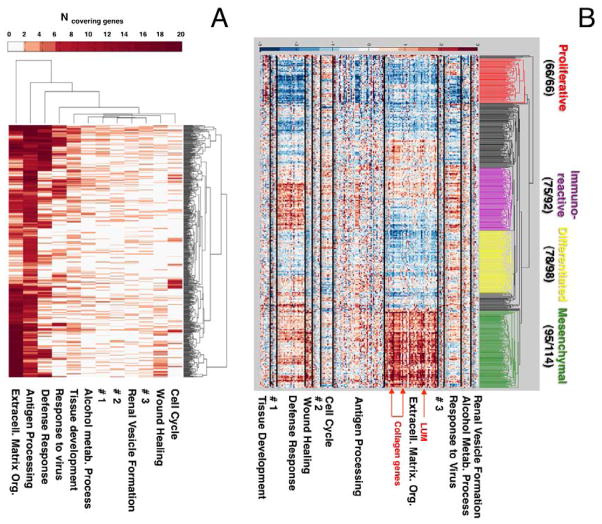
To visualize the coverage of disease cases by modules of size ≥5, we counted the number of genes covering each sample (Fig 3A). Similarly to GBMs, we found that different modules are covering different subsets of samples. Note that a gene may cover a sample when it is either significantly upregulated or downregulated. In Fig 3B, we investigated the expression patterns of individual genes in the modules. Performing hierarchical clustering of the genes based on expression level, we obtained clusters consistent with the existing classification of cancer subtypes (18), in which the gene expression profile of ~1,000 selected genes was used to define 4 disease subtypes. Using only 185 genes in the 12 largest modules from our module cover, we successfully recovered these 4 subtypes (Fig 3B) despite the fact that these genes have not been selected explicitly to classify expression based subtypes. In the TCGA analysis (18), the authors attempted to identify genes whose differential expression helped to define each disease subtype. However, we found that our module-based analysis often provided a more informative picture. For example, in (18) one subgroup of the collagen gene family was found to support the Mesenchymal subtype while another subgroup of this family as well as the LUM gene which binds collagen fibrils was associated to the Differential subtype. In contrast, our approach grouped all these genes into “extracellular matrix organization” module, also containing several matrix metalloproteinase (MMP) genes. We found that genes in this module had very similar expression and were overexpressed in the Mesenchymal subtype.

Figure 3. Modules in ovarian cancer obtained by the integrated module cover method.

(A) For each disease case (y-axis) we displayed in the heat map the number of genes in each module that covered the sample (B) Expression based clustering of the genes in the modules provided clusters consistent with the existing classification of cancer subtypes. Arrows indicate genes of the extracellular matrix module discussed in the text. The fraction of genes assigned to a given cluster in (18) is shown next to the cluster name.

4. Discussion

Uncovering modules that are associated with genomic alterations in a disease is a challenging task as well as an important step to understand complex diseases. To address this challenge we introduced a novel technique - module cover - that extends the concept of set cover to network modules. We provided a mathematical formalization of the problem and developed two heuristic solutions: the Integrated Module Cover approach, which greedily selects genes to cover disease cases while simultaneously detecting modules and a Two-Step approach that first detects modules and subsequently selects a cover. Using several quality measures, we established that the integrative approach outperformed the alternative two-step approach. However, both methods showed better performance than a naïve single gene based set cover approach. We also constructed modules utilizing gene expression rather than association profiles to define a similarity measure (data not shown). We observed that the modules obtained by the integrated approach based on gene expression showed lower association specificity/association strength than modules that were provided by eQTL profiles. However, expression based modules would be clearly preferred for uncovering expression patterns that occurs regardless of the association to genetic variations.

In general, the module cover approach is especially helpful in analyzing and classifying heterogeneous disease cases by exploring the way different combinations of dys-regulated of modules relate to a particular disease subcategory. Indeed, our analysis indicated that the gene set selected by module cover approach may be used for classification. Equally important, the selected module covers may help to interpret classifications that were obtained with other methods.

5. Materials

5.1 Data Treatment for Glioblastoma Multiforme Data from GMDI

Differentially Expressed Genes

Briefly, all samples were profiled using HG-U133 Plus 2.0 arrays that were normalized at the probe level with dChip (16, 19). Among probes representing each gene, we chose the probeset with the highest mean intensity in the tumor and control samples. We determined genes that are differentially expressed in each disease case compared to the non-tumor control cases with a Z-test. For a gene g and case c, we define cover(c, g) to be 1 if nominal p-value < 0.01 and 0 otherwise.

eQTL Profiles

To detect copy number alterations, samples were hybridized on the Genechip Human Mapping 100K arrays, and copy numbers were calculated using Affymetrix Copy Number Analysis Tool (CNAT 4). After probe-level normalization and summarization, calculated log2-tranformed ratios were used to estimate raw copy numbers. Using a Gaussian approach, raw SNP profiles were smoothed (> 500 kb window by default) and segmented with a Hidden Markov Model approach (20–22). We first performed local clustering, allowing us to obtain 911 tag loci (11). For each gene/tag-locus pair, we computed nominal p-values by linearly regressing gene expression and genomic alteration for all samples. We then define the eQTL significance profile for each gene, g, as Assoc (g) = {s₁(g), s₂(g), … s₉₁₁(g)}, where s_i(g) represents the −log₁₀ p-value of the association given by the linear regression between expression values of gene g and copy number variation of locus i. Using such profiles, we defined the similarity of two genes g₁ and g₂, sim(g₁, g₂), as Pearson’s correlation coefficient of Assoc (g₁) and Assoc (g₂).

Weights of Gene Pairs: We utilized human protein-protein interaction data from large-scale high-throughput screens (23–25) and several curated interaction databases (26–29), totaling 93,178 interactions among 11,691 genes. As a reliable source of experimentally confirmed protein-DNA interactions, we used 6,669 interactions between 2,822 transcription factors and structural genes from the TRED database (30). As for phosphorylation events between kinases and other proteins we found 5,462 interactions between 1,707 human proteins utilizing networKIN (31, 32) and phosphoELM database (33). Combining all interactions, the network contains 11,969 human proteins and 103,966 interactions. We computed the weights of each gene pairs using equation (1) with avg_distance = 3.6 and θ = 0.63, a threshold that corresponds to the top 1%ile of weights of any pairs.

5.2 Data Treatment for Ovarian Cancer Data from TCGA

We utilized the unified expression data compiled in (18) based on expression values from three different expression platforms. Since there is no control (non-cancer data) in this dataset, we defined that a gene covers a sample if its expression in this sample was in the extreme 3% of the expression distribution. We then narrowed down the set of genes to 1,889 genes by considering genes that covered at least 5% of the samples. As for copy number variations, we used level 4 data obtained with GISTIC (34) and selected 1,923 genes with copy number alterations (calls = ±2) in at least 5% of all samples. For each differentially expressed gene we used linear regression to compute associations of the expression of this gene with copy number variation of each of the 1,923 genes. We used p-values of these associations to compute association profiles as explained in 5.1. Edge weights in interaction graph were calculated as described in 5.1 with θ = 0.58, a threshold corresponding to the top 5% ile.