DiagTest3Grp: An R Package for Analyzing Diagnostic Tests with Three Ordinal Groups

Abstract

Medical researchers endeavor to identify potentially useful biomarkers to develop marker-based screening assays for disease diagnosis and prevention. Useful summary measures which properly evaluate the discriminative ability of diagnostic markers are critical for this purpose. Literature and existing software, for example, R packages nicely cover summary measures for diagnostic markers used for the binary case (e.g., healthy vs. diseased). An intermediate population at an early disease stage usually exists between the healthy and the fully diseased population in many disease processes. Supporting utilities for three-group diagnostic tests are highly desired and important for identifying patients at the early disease stage for timely treatments. However, application packages which provide summary measures for three ordinal groups are currently lacking. This paper focuses on two summary measures of diagnostic accuracy—volume under the receiver operating characteristic surface and the extended Youden index, with three diagnostic groups. We provide the R package DiagTest3Grp to estimate, under both parametric and nonparametric assumptions, the two summary measures and the associated variances, as well as the optimal cut-points for disease diagnosis. An omnibus test for multiple markers and a Wald test for two markers, on independent or paired samples, are incorporated to compare diagnostic accuracy across biomarkers. Sample size calculation under the normality assumption can be performed in the R package to design future diagnostic studies. A real world application evaluating the diagnostic accuracy of neuropsychological markers for Alzheimer’s disease is used to guide readers through step-by-step implementation of DiagTest3Grp to demonstrate its utility.

1. Introduction

In biomedical research, biomarkers reflecting different stages of diseases are usually measured. Those performed to aid patient diagnosis (e.g., healthy vs. diseased) or disease staging (e.g., early vs. full-blown disease) are called diagnostic tests/markers in diagnostic medicine. Well-known examples include the prostate-specific-antigen (PSA) testing for prostate cancer and mammography screening for breast cancer. The effectiveness of potential biomarkers in diagnosing diseases must be properly evaluated before their ultimate use as diagnostic tools.

For medical practitioners, the most crucial question about a potential diagnostic test is its diagnostic accuracy, i.e., the ability to correctly classify subjects into diagnostic groups (e.g. healthy vs. diseased in the binary case). While diagnostic groups are defined based on an established gold standard which operates without any information from the marker in question, the diagnostic marker is investigated as a potential proxy to the gold standard arising from concerns of time, cost, invasiveness etc. In diagnostic medicine, the diagnostic accuracy of a test centers on two measures: the sensitivity (i.e., the probability of a positive diagnostic test for a patient who truly has the disease) and the specificity (i.e., the probability of a negative diagnostic test for a subject who truly does not have the disease). These measures require a decision rule (or positivity threshold) for classifying the test results as either positive or negative. As an example, the BIRADS (Breast Imaging Reporting and Data System) scoring system is used in mammography to classify mammograms as normal, benign, probably benign, suspicious, or malignant. One positivity threshold is classifying probably benign, suspicious, and malignant findings as positive (and classifying normal and benign findings as negative). Another positivity threshold is classifying suspicious and malignant findings as positive. Each threshold leads to different estimates of sensitivity and specificity. Here, the second threshold would have higher specificity than the first but lower sensitivity. Also, note that trained mammographers with varying experience may use the scoring system differently.

Which decision threshold should be used to classify test results? How will the choice of a decision threshold affect comparisons between two diagnostic tests or between two clinicians? These are critical questions when computing sensitivity and specificity, yet the choice for the decision threshold is often arbitrary. The receiver operating characteristic (ROC) curve of a diagnostic test plots sensitivity (y-axis) against 1-specificity (x-axis) through all possible decision thresholds. In characterizing the accuracy of a diagnostic test, the ROC curve of the test provides all information about how the test performs than just a single estimate of the test’s sensitivity and specificity. Given a test’s ROC curve, a clinician can examine the trade-offs between sensitivity and specificity for various decision thresholds.

Diagnostic tests usually have different scales (continuous, semi-quantitative or categorical) and varying distributions, and are also subject to different medical costs. In search of the most accurate diagnostic test among multiple candidates, ROC curves are often the only valid method of comparison, regardless of the scales and the distributions of the tests. Summary measures of accuracy (Lusted 1971; Youden 1950; Swets 1988; Hand 2010) have been derived from the ROC curve to describe the inherent diagnostic accuracy of tests and are popularly employed in diagnostic medicine. The Youden index, defined as the maximum of (sensitivity+ specificity −1) over all possible decision thresholds is used to define sensitivity and specificity and the summary measure. The most popular summary measure of diagnostic accuracy is the area under the ROC curve (AUC). It ranges in value from 0.5 (classification by chance) to 1.0 (perfect discrimination). The AUC can be interpreted as the average sensitivity over all false-positive rates, the average specificity over all sensitivities, and the probability that, when presented with a randomly chosen subject with disease and a randomly chosen subject without disease, the results of a diagnostic test will be ranked in the correct order.

Whereas conventional statistical techniques, for instance, logistic regression can be used to evaluate the association between a diagnostic test and a binary outcome through the estimated odds ratio (and associated confidence interval and p value), statistical methods have been developed specifically for diagnostic medicine, focusing on the estimation and comparison of the accuracy of diagnostic tests (Swets and Pickett 1982; Zhou, Obuchowski, and McClish 2002; Pepe 2004). Often, a similar modeling framework is shared between conventional statistical techniques and the more specific methods to diagnostic medicine. For instance, Pepe (1997) derived ROC curves through a logistic modeling framework. Compared to conventional summary statistics such as odds ratios from logistic regression, the summary measures of diagnostic tests (e.g., the AUC and the Youden index) are scale-invariant. The same range of 0 to 1 for any diagnostic test makes it possible to compare multiple diagnostic tests on the same metric, which is especially appealing for clinicians. For the purpose of statistical comparison among potentially multi-modality biomarkers to select the best diagnostic tests, both parametric and nonparametric statistical tests on comparing summary measures of diagnostic accuracy have been well developed (Hanley and McNeil 1983; Wieand, Gail, James, and James 1989; DeLong, DeLong, and Clarke-Pearson 1988; Xiong et al. 2007). Standard analyses on the AUC and the Youden index have been implemented in R packages, for example, DiagnosisMed (Brasil 2010) and Epi (Carstensen, Plummer, Laara, and Hills 2012). Finally, the use of ROC curve and its summary measures also facilitate the identification of optimal decision thresholds (see Section 2.3) that can directly aid diagnostic decision in medical practice. ROC curve analysis has also been extended to other fields such as machine learning and data mining (Spackman 1989; Hand and Till 2001).

On the other hand, diagnostic decisions are not always binary. In fact, an early or intermediate disease stage usually exists in many complex disease processes when individuals transit from the healthy stage to the fully diseased stage. This transitional stage may represent an optimal treatment window before the disease is fully developed. The diagnostic accuracy of a potential test in classifying individuals into three groups (i.e., normal, early disease stage, fully developed disease stage) is described by a ROC surface over all possible decision thresholds (Xiong, van Belle, Miller, and Morris 2006, see also Section 2.1). To summarize a diagnostic test’s overall ability to simultaneously discriminate three diagnostic groups, the volume under the ROC surface (VUS), an extension of the AUC, has been proposed (Xiong et al. 2006; Ferri, Hernandez-Orallo, and Salido 2003). VUS serves as an overall summary measure integrating across all potential cut-points or thresholds. The optimal cut-points from the ROC surface can also be calculated for diagnosis, usually by minimizing the distance to the perfect classification coordinates. Both parametric and nonparametric inferences on the VUS have been developed (Xiong et al. 2006; Li and Zhou 2009; Inácio, Turkman, Nakas, and Alonzo 2011). Luo and Xiong (2012) recently generalized the Youden index to three ordinal diagnostic groups which provides another summary measure at an optimal pair of cut-points by maximizing the overall classification accuracy. Despite recent developments in the analysis of ROC surfaces, publically accessible computing packages are lacking. This paper addresses this very question by offering a new R package DiagTest3Grp, available from the Comprehensive R Archive Network at http://CRAN.R-project.org/package=DiagTest3Grp, for standard analysis on the ROC surface and the Youden index. We give necessary background on the ROC surface and its summary measures (i.e., VUS and the Youden index) in Section 2. In Section 3, we describe major functions in the R package. In Section 4, we present a step-by-step demonstration on the usage of the package through a comprehensive application assessing the diagnostic accuracy of real-world neuropsychological tests to diagnose individuals into very early and fully developed Alzheimer’s disease (AD).

2. Volume under the ROC surface and the Youden index

Denote the three ordered diagnostic groups in the order of increasing disease severity as D⁻ (healthy), D⁰ (transitional or mildly diseased) and D⁺ (diseased). Denote a diagnostic test by T, a random variable representing the test result of a subject. We assume that T is measured on a continuous scale and is monotonically and stochastically increasing with disease severity. The negated diagnostic test can be used if a monotonically decreasing trend exists. Let f_i and F_i, i = −, 0, +, be the probability density functions (PDF) and the cumulative distribution functions (CDF) of T in the three groups, respectively. Let G_i = 1 − F_i, i = −, 0, +. Based on two underlying cut-points t₋ and t₊ with t₋ < t₊, individuals can be grouped into the three ordinal groups: patients with T below t₋ will be assigned to D⁻; those with T above t₊ will be assigned to D⁺; the remaining will fall into D⁰. Let x and y be the probability of a randomly selected individual from D⁻ having a test result below t₋ and a randomly selected individual from D⁺ having a test result above t₊, respectively, i.e., x = Pr{T ≤ t₋|D⁻} = F₋ (t₋) and y = Pr{T ≥ t₊|D⁺} = G₊(t₊). Therefore, $t_{-}=F_{-}^{-1}(x)$ and $t_{+}=G_{+}^{-1}(y)$. Following the definitions of x and y, the probability that the test result of an individual randomly selected from D⁰ falls between the two cut-points can be expressed as,

$$z=Pr\{t_{-}<T<t_{+}\mid D^0\}=F_0(t_{+})-F_0(t_{-})=F_0(G_{+}^{-1}(y))-F_0(F_{-}^{-1}(x)).$$

z = z(x, y) constitutes a ROC surface in the three-dimensional space (x, y, z), 0 ≤ x, y, z ≤ 1. The coordinate (1, 1, 1) corresponds to a diagnostic test that perfectly classifies individuals into the three diagnosis groups. Two measures can be used to summarize the ROC surface over all possible choices of t₋ and t₊: the volume under the ROC surface (VUS) and the extended Youden index.

2.1. Volume under the ROC surface

The volume under the ROC surface (VUS) can be calculated as,

$$V_{00}=\int {\int }_{D_{00}}\{F_0(G_{+}^{-1}(y))-F_0(F_{-}^{-1}(x))\}\text{d}y\text{d}x$$ (1)

The integration domain is D₀₀ = {0 ≤ x ≤ 1, $D_{00}=\{0\le x\le 1,0\le y<G_{+}(F_{-}^{-1}(x))\}$. VUS represents the probability of correctly ranking a randomly selected triplet of diagnostic test results (U, V, W) from D⁻, D⁰ and D⁺, i.e., V₀₀ = Pr{U ≤ V ≤ W}. This interpretation gives rise to the nonparametric estimator of VUS by the empirical CDF method. A useless diagnostic test which randomly classifies individuals into the three groups has a VUS of 1=6 while a perfect diagnostic test has a VUS of 1. In clinical practice, a desirable requirement that a diagnostic marker produces a specificity at least p and a sensitivity at least q leads to the concept of partial VUS, denoted as V_pq, which can be calculated by integrating the ROC surface over the constrained domain $D_{pq}=\{p\le x\le 1,q\le y\le G_{+}(F_{-}^{-1}(x))\}$. For the partial VUS, a diagnostic test is useless if $V_{pq}=\frac{{(1-p)}^3}{6}-\frac{q^3}{6}-\frac{{(1-p)}^{2}q}{2}+\frac{(1-p)q}{2}$. The full VUS is a special case of the partial VUS under the p = q = 0 setting. The details on the estimation of VUS and partial VUS, as well as their associated variances under normality can be found in Xiong et al. (2006).

2.2. The extended Youden index

The Youden index (Youden 1950) in the binary case targets to maximize the combination of specificity and sensitivity (achieved at an optimal cut-point). The Youden index is optimal in the sense of maximizing the overall correctness of classification (Perkins and Schisterman 2006). Luo and Xiong (2012) extended the Youden index to three ordinal diagnostic groups,

$$J(t_{-},t_{+})=\frac{1}{2}(x+y+z-1)=\frac{1}{2}[F_{-}(t_{-})-F_0(t_{-})+F_0(t_{+})-F_{+}(t_{+})].$$ (2)

The optimal Youden index (abbreviated as Youden or J later) is achieved at an optimal pair of cut-points ( $t_{-}^{\ast },t_{+}^{\ast }$) which maximizes J(t₋, t₊). Youden has a practical range between 0 and 1, corresponding to a useless marker and a perfect marker, respectively. Parametric estimation on Youden can be estimated under normality assumptions while nonparametric estimation can be achieved by empirical CDF method and by kernel smoothing (see details in Luo and Xiong 2012).

As a simplified graphical visualization, Figure 1 plots three normal density curves representing the distribution of a diagnostic test in D⁻, D⁰ and D⁺, suggesting a unique pair of optimal cut-points ( $t_{-}^{\ast },t_{+}^{\ast }$). Geometrically, the lower optimal cut-point lies where the density curves of D⁻ and D⁰ intersect, whereas the upper optimal cut-point is at the intersection between f₀ and f₊, i.e., $f_{-}(t_{-}^{\ast })=f_0(t_{-}^{\ast })$ and $f_0(t_{+}^{\ast })=f_{+}(t_{+}^{\ast })$. The summation of the shaded areas graphically illustrates twice the Youden index evaluated at the optimal pair of cut-points. When multiple solutions exist, the global (local) maximum requires the second partial derivatives of J with respect to t₋ and t₊ be negative when evaluated at $t_{-}^{\ast }$ and $t_{+}^{\ast }$, i.e., $f_{-}^{\prime }(t_{-}^{\ast })<f_0^{\prime }(t_{-}^{\ast })$ and $f_0^{\prime }(t_{+}^{\ast })<f_{+}^{\prime }(t_{+}^{\ast })$ simultaneously.

Figure 1.

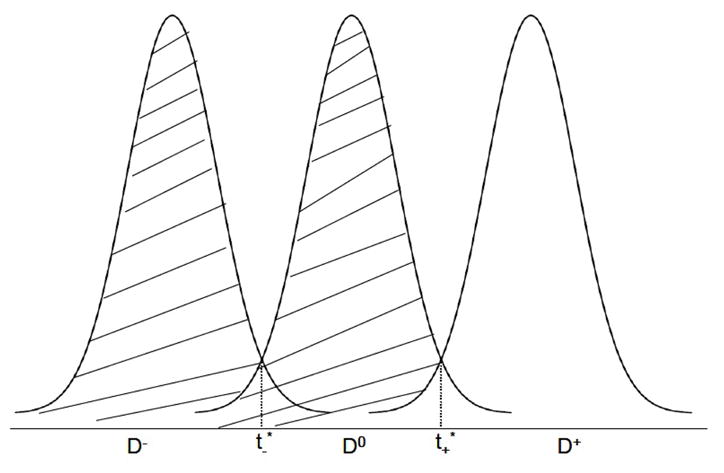
Graphical illustration of the extended Youden index and optimal cut-points under normal distributions.

2.3. Optimal cut-points for the ROC surface and the Youden index

As stated in Section 2.1, the ROC surface is the plot of the three correct classification probabilities (x, y, z) with z = z(x, y) in the 3-dimensional space. The vertex (1,1,1) therefore indicates the perfect classification point, whereas the equilateral-triangle plane x + y + z = 1 connecting the vertexes (1, 0, 0), (0, 1, 0) and (0, 0, 1) indicates diagnostic tests with no diagnostic ability. The optimal pair of cut-points ( $t_{-}^{\ast },t_{+}^{\ast }$) can thus be obtained as the pair that corresponds to the coordinate on the ROC surface with the shortest Euclidean distance to the vertex (1, 1, 1). The pair of optimal cut-points for Youden, however, is the pair which maximizes J in Equation (2). Closed-form expressions for the pair of optimal cut-points are available under normality assumptions, as well as under the Gamma distribution, though numerical optimization has to be implemented under nonparametric estimation (Luo and Xiong 2012). Generally, the pair of optimal cut-points leading to the maximum J differ from that of the ROC surface, with the exception of equality of the three correct classification probabilities: x = y = z, a simple generalization following Perkins and Schisterman (2006).

2.4. Comparison of diagnostic accuracy on multiple markers

Multiple diagnostic markers are usually compared on their diagnostic accuracy. Generally, analysis starts with an omnibus ANOVA (analysis of variance) type test to test the null hypothesis of overall equality among VUS or Youden estimates among all markers. If the null hypothesis is rejected, Wald tests can be subsequently used (in a pairwise manner and with multiple testing adjustment) to identify which pairs differ. We describe here the two tests for both VUS and Youden, assuming that markers are measured on either independent or paired samples.

Assume that we investigate Q diagnostic markers for their summary measure θ_q (referring to either VUS or Youden), q = 1, 2, · · ·, Q. The hypothesis for the omnibus ANOVA test is: H₀: θ₁ = · · · = θ_Q versus H_a: there exists at least a pair of markers with unequal θ’s. The test statistic constructed for the hypothesis is asymptotically χ² distributed with degrees of freedom Q − 1 (Xiong et al. 2007),

$${\chi }^2={\underset{\_}{\widehat{\theta }}}^{\top }{\mathbf{A}}^{\top }{(\mathbf{A}\widehat{\mathbf{\sum }}{\mathbf{A}}^{\top })}^{-1}\mathbf{A}\underset{\_}{\widehat{\theta }}$$ (3)

where A = (a_ij) is a contrast matrix of dimension Q − 1 by Q with a_ii = 1, a_{i, i+1} = − 1 and 0 elsewhere.

To compare two markers using the two-sided (one-sided) Wald test, H₀: θ_q1 − θ_q2 = θ₀ versus H_a: θq₁ − θ_q2 ≠ (or > or <) θ₀, for some θ₀ (usually 0), q_1, q₂ ∈ {1, 2, · · ·, Q}, q₁ ≠ q₂, we have the Z statistic,

$$Z=\frac{({\widehat{\theta }}_{q_1}-{\widehat{\theta }}_{q_2})-{\theta }_0}{\sqrt{\text{V}\widehat{\text{A}}\text{R}({\widehat{\theta }}_{q_1}-{\widehat{\theta }}_{q_2})}}.$$ (4)

For the χ² and the Z statistic, θ can be estimated following Section 2.1 and 2.2 though the covariance matrix Σ and VAR(θ̂_q1 − θ̂_q2) need more elaboration. Readers are referred to Xiong et al. (2007) for more details on the statistics and the variance/covariance estimation.

2.5. Sample size calculation

Sample size needs to be determined when planning a study to confirm the diagnostic ability of a marker or to compare between multiple markers. Sample size calculations vary greatly depending on research goals. Obuchowski (1998) provides a comprehensive review on various scenarios of sample size calculation for studies of diagnostic accuracy in the binary case. Literature on sample size calculation for three-group diagnostic tests is scarce. Here, we describe one method to plan the study such that a marker’s summary measure estimate (denoted as θ̂, representing either VUS or Youden) is estimated within a specified precision under normality assumptions (Xiong et al. 2006). As the asymptotic (1 − α) × 100% confidence interval (CI) is (θ̂ − z_α/2σ_θ̂, θ̂ + z_α/2σ_θ̂), assuming a margin of error Δ on the CI, we have Δ = z_α/2σ_θ̂ and ${\sigma }_{\widehat{\theta }}^2=\frac{{\mathrm{\Delta }}^2}{z_{\alpha /2}^2}$. Let λ_i, i = −,0, + be the population proportion of the three groups, i.e., ${\lambda }_i={lim}_{min(n_{-},n_0,n_{+})\to \infty }\frac{n_i}{{\sum }_{j=-,0,+}{n}_j}$, then $n_i=n_0\frac{{\lambda }_i}{{\lambda }_0}$, i = −, +. The asymptotic variance of θ̂ (both VUS and Youden) can be expressed as the product of $\frac{1}{n_0}$ and a function of other parameters. Denote this function of other parameters by M_θ. The sample size for D⁰ can be calculated as,

$$n_0=\frac{z_{\alpha /2}^2{M}_{\theta }}{{\mathrm{\Delta }}^2}.$$

M_θ for VUS has been provided in Xionget al. (2006, Equation F on page 1262). For Youden,

$$M_{\theta }={\sigma }_{-}^2\frac{{\lambda }_0}{{\lambda }_{-}}[{(\frac{\partial J}{\partial {\mu }_{-}})}^2+0.5{(\frac{\partial J}{\partial {\sigma }_{-}})}^2]+{\sigma }_0^2[{(\frac{\partial J}{\partial {\mu }_0})}^2+0.5{(\frac{\partial J}{\partial {\sigma }_0})}^2]+{\sigma }_{+}^2\frac{{\lambda }_0}{{\lambda }_{+}}[{(\frac{\partial J}{\partial {\mu }_{+}})}^2+0.5{(\frac{\partial J}{\partial {\sigma }_{+}})}^2].$$

The relevant partial derivatives can be readily found (Luo and Xiong 2012). The sample sizes for Dⁱ can be later calculated by $n_i=n_0\frac{{\lambda }_i}{{\lambda }_0}$, i = −, +.

Notice that both VUS and Youden have a range between 0 and 1. When an estimate approaches to the two extremes, the resulting CI will not achieve nominal coverage (Xiong et al. 2006, 2007). As a simple solution, we apply the Fisher’s Z transformation, ${\widehat{\theta }}^{\ast }=\frac{1}{2}log(\frac{1+\widehat{\theta }}{1-\widehat{\theta }})$ and derive the associated variance ${\sigma }_{{\widehat{\theta }}^{\ast }}^2=\frac{1}{{(1-{\widehat{\theta }}^2)}^2}{\sigma }_{\widehat{\theta }}^2$ (and CI). By placing the margin of error Δ on the resulting CI after the Fisher’s Z transformation, the sample size calculation can proceed,

$$n_0=\frac{z_{\alpha /2}^2{M}_{\theta }}{{\mathrm{\Delta }}^2}\frac{1}{{(1-{\widehat{\theta }}^2)}^2}.$$

3. The R package DiagTest3Grp

Constructed using the R (R Development Core Team 2012) statistical language, the package DiagTest3Grp provides a unified and user-friendly interface for diagnostic test analysis utilizing either VUS or Youden as a summary measure. A new S3 class object DiagTest3Grp has been defined. All statistical analysis topics of diagnostic tests as described in Section 2 are covered in the package, including point estimates of the two summary measures, variances/covariances estimation, finding optimal pair of cut-points and sample size calculation. Statistical tests among multiple markers and between two markers on both independent samples and paired samples are also provided.

3.1. Point estimate and confidence interval

A point estimate of either VUS or Youden summarizes a marker’s ability to discriminate diagnosis groups. The accompanying confidence interval quantifies the precision on the estimation. VUS() and Youden3Grp() are the wrapper functions for VUS and Youden analysis, respectively. Both return an object of S3 class DiagTest3Grp (see package manual for details). The generic print and plot methods are specifically designed for the DiagTest3Grp object to deliver important results to screen and to visualize data and results.

The basic usage of the two wrapper functions are provided with complete arguments as the following,

VUS(x, y, z, method = c(“Normal”, “NonPar”), p = 0, q = 0,alpha = 0.05,
 NBOOT = 100, subdivisions = 5000, lam.minus = 1/3, lam0 = 1/3,
 lam.plus = 1/3, typeIerror = 0.05, margin = 0.05, FisherZ = FALSE,
 optimalCut = TRUE, cut.seq = NULL, optimize = FALSE, …)
Youden3Grp(x, y, z, method = c(“Normal”, “TN”, “EMP”, “KS”, “KS-SJ”)
 randomStart.N = 1, optim.method = NULL, t.minus.start = NULL,
 t.plus.start = NULL, lam.minus = 1/3, lam0 = 1/3, lam.plus = 1/3,
 typeIerror = 0.05, margin = 0.05, NBOOT = 10, seed.seq = NULL,
 alpha = 0.05, FisherZ = FALSE, …)

The arguments x, y, z in the two functions take the measurements of a diagnostic marker in diagnosis group D⁻, D⁰ and D⁺, respectively, each in the format of a numeric vector. Based on the option specified for the method argument in both functions, either parametric estimates under normality assumptions (method = “Normal” in both functions) or nonparametric estimates can be delivered. Specification of method = “NonPar” in VUS() leads to the nonparametric VUS estimate, i.e., the empirical probability of correctly ranking a randomly selected triplet of a diagnostic test, each from a diagnostic group. Users can also carry out the partial VUS analysis satisfying a minimum specificity (p) and sensitivity (q) by changing the p, q argument from the default 0s. For Youden estimation, the method argument in Youden3Grp() can take one of the four options besides “Normal”:

• method = “TN”: this estimates the power parameter (λ) for use in Box-Cox transformations and implements either the log transformation (y = log(x)) or power transformations ( $y=\frac{y^{\lambda }-1}{\lambda }$) depending on whether the power parameter λ is estimated as zero or not. The transformed data is thereafter analyzed as in method = “Normal”;

• method = “EMP”: the empirical CDF method is used to estimate the CDFs in Equation (2);

• method = “KS”: the kernel density estimation technique is used to approximate the CDFs in Equation (2) with application of the normal reference rule for bandwidth specification,

  $$h_i=1.06n_i^{-0.2}min\{{\widehat{\sigma }}_i,\frac{{\mathit{IQR}}_i}{1.34}\},$$

  where IQR_i indicates the inter-quartile range of measurements in Dⁱ and σ_i indicates standard deviation, i = −, 0, +;

• method = “KS-SJ: the kernel density estimation is employed with the Sheather-Jones (SJ) plug-in method (Sheather and Jones 1991; Sheather 1992) for bandwidth selection. The SJ bandwidth is calculated by using the R package KernSmooth (Wand 2012).

Details on all the above can be found in Luo and Xiong (2012). The optimal pair of cut-points for diagnosis decision has been incorporated into the two wrapper functions. While Youden3Grp() returns associated optimal cut-points as an integral implementation, VUS() calls the function VUS.CutPoint() subsequently to find the solutions. The optimal cut-points for Youden have closed-form expressions under the “Normal” method but are obtained through optimization under other nonparametric methods. The R function optim() is adopted for the optimization with the application of a user-specified optimization algorithm therein (e.g., quasi-Newton algorithm L-BFG-B). Sample size calculation can be also provided from the two wrapper functions. In situations of a highly discriminative diagnostic test, Fisher’s Z transformation can be implemented with the option FisherZ = TRUE in both wrapper functions when the summary measure estimate, associated variance and CI (under both normal and non-normal methods) and sample size will be calculated in the logit scale through the Fisher’s Z transformation.

3.2. Statistical comparison on multiple markers

Statistical tests comparing either VUS or Youden of two markers or multiple markers measured on independent or paired samples are integrated into one function DiagTest3Grp.Test(). This function performs an omnibus test to compare multiple markers or a Wald test to compare between two markers if data on only two markers is provided. Taking advantage of the classic S3 class object htest (which is designed for classic statistical tests in R such as t test), the generic print method for htest produces a clean screen output. For users’ convenience, the package also supplies a useful function Pairwise.DiagTest3Grp.Test() which implements the two-marker test in a pairwise manner among multiple markers with multiple testing adjustment option. Ultimately, it provides a clear graphical visualization and outputs on all possible pairwise comparisons.

The basic usage of the two functions comparing multiple markers on the VUS or the Youden index are as the following with complete arguments,

DiagTest3Grp.Test(dat, paired = FALSE, type = c(“VUS”, “Youden”), p = 0,
 q = 0, mu = 0, conf.level = 0.95,
 alternative = c(“two.sided”, “less”, “greater”))
Pairwise.DiagTest3Grp.Test(dat, paired = FALSE, type = c(“VUS”, “Youden”),
 p = 0, q = 0, mu = 0, conf.level = 0.95,
 alternative = c(“two.sided”, “less”, “greater”),
 p.adjust.method = c(“none”, “holm”, “hochberg”, “hommel”, “bonferroni”,
  “BH”, “BY”, “fdr”), digits = 3)

In the above functions, data is input to the argument dat as a list if markers are each collected on independent subjects with the specification of paired = FALSE or as a data frame if the same set of subjects are measured with the option paired = TRUE. For the test on two markers, all the three alternative hypotheses can be implemented. The returned object is a htest object with one additional component named Sigma, storing the estimated covariance matrix. Users are referred to R help on htest and the multiple testing adjustment methods.

4. Using DiagTest3Grp

We illustrate the major steps involved in using DiagTest3Grp in this section. A real world dataset with fourteen neuropsychological markers for diagnosis of Alzheimer’s disease (AD) is used as an example. We first introduce the dataset and then choose a few markers to conduct a step-by-step demonstration of the package’s utilities. Finally, we analyze all the fourteen neuropsychological markers to evaluate and compare their abilities in diagnosing AD.

4.1. Example data

AD is the most common degenerative dementia affecting around 47% of the 85 and older population. Detecting the disease at a much earlier stage will enable timely treatment. Neuropsychological tests have been used to detect mild cognitive impairment (MCI) from normal aging and AD. The dataset includes individuals from the longitudinal cohort of Washington University Alzheimer’s Disease Research Center (ADRC). Disease severity of each individual in the cohort was staged by a global Clinical Dementia Rating (CDR) using published rules (Morris 1993). We followed Xiong et al. (2006) for data filtering where the same dataset was analyzed for VUS. See the paper for more details on subject filtering and marker description. To this end, we have fourteen neuropsychometric markers measured on 118 individuals of age 75 falling into three diagnostic categories: the non-demented/healthy group (D⁻, N = 45) with CDR = 0; the MCI group (D⁰, N = 44) with CDR = 0.5 and the AD group (D⁺, N = 29) with CDR = 1. The dataset exists in the R package as a data frame called AL, where the CDR group membership “group” is at the first column, followed by 14 columns of measurements of the markers (with some missing values).

4.2. Step-by-step demonstration

We first explore the data frame AL by examining the sample size and the mean of markers within the three diagnosis groups.

R> library(“DiagTest3Grp”)
R> data(“AL”)
R> group <- AL$group
R> table(group)
group
D− D0 D+
45 44 29
R> AL <- subset(AL, select = -group)
R> marker.name <- names(AL)
R> group.mean <- round(as.data.frame(sapply(1:ncol(AL), function(jj)
+  tapply(AL[, jj], group, mean, na.rm = TRUE))), 2)
R> names(group.mean) <- marker.name
R> group.mean
 FACTOR1 ktemp kpar kfront zpsy004 zpsy005 zpsy006 zinfo zbentc zbentd
D−  0.57 4.08 1.80 2.87 0.73 0.58 0.55 0.63 0.64 0.20
D0  −1.62 −0.99 −0.24 0.37 −0.86 −0.21 −0.40 −0.61 −0.82 −0.55
D+  −4.20 −5.86 −2.38 −2.68 −1.77 −1.21 −1.82 −2.30 −1.66 −1.77
 zboston zmentcon zworflu zassc
D−  0.59 0.46 0.73 0.74
D0  −0.50 −0.37 −0.25 −0.58
D+  −3.07 −1.72 −1.44 −1.50

The group means of all the fourteen markers are in a monotonically decreasing order from D⁻ to D⁺. Since our implementation assumes an monotonically increasing order, we therefore analyze the negated marker measurements.

R> AL <- -AL

Marker kfront is selected for the tutorial purpose. Its conformity to normality within each diagnosis group is examined before conducting VUS and Youden analysis.

R> kfront <- as.numeric(AL$kfront)
R> kfront.list <- split(kfront, group)
R> par(pty = “s”)
R> par(mfrow = c(1, 3))
R> for (i in 1:3) {
+  xx <- na.exclude(as.numeric(kfront.list[[i]]))
+  p0 <- shapiro.test(xx)$p.value
+  qqnorm(xx, main = paste(“kfront: p=”, round(p0, 3), sep = “”))
+  qqline(xx)
+  }

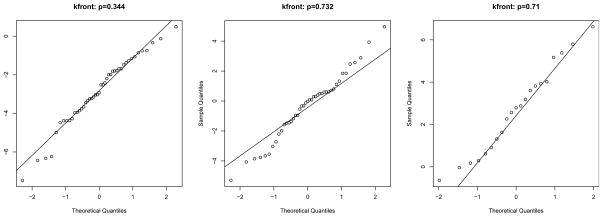
The QQ plots (Figure 2, from left to right are D⁻, D⁰ and D⁺) and Shapiro tests on normality (p value indicated in the plots) show that kfront basically follows a normal distribution in each diagnosis group. Therefore, VUS and Youden can be estimated under normality assumptions. VUS estimation on this marker based on the normal method (and the nonparametric method) can be obtained by preparing data inputs and calling the function VUS().

Figure 2.

QQ plots on the marker kfront by diagnostic groups.

R> xx <- kfront.list$“D−”
R> yy <- kfront.list$D0
R> zz <- kfront.list$“D+”
R> vus <- VUS(x = xx, y = yy, z = zz, method = “Normal”)
R> vus
The DiagTest3Grp summary measure:  VUS
Method used for VUS:Normal
Raw Data Summary:
  n     mu    sd
D− 45 −2.8657503 1.776514
D0 43 −0.3725226 2.212393
D+ 21 2.6817010 2.066669
VUS=0.6568, 95% CI=0.5491~0.7646
Best cut-points: lower=−1.6826, upper=0.9119
The group correct classification probabilities are:
  Sp   Sm   Se
0.7556 0.5581 0.7619
Sample Size to estimate VUS within specified margin of error=154

The print method defined for the DiagTest3Grp S3 object automatically comes into use to produce the above screen printout. The number of observations, sample mean and SD of each group are displayed. The VUS is estimated based on the normal method as 0.66 with 95% CI (0.55, 0.76). The derived optimal cut-points are (−1.68, 0.91). The resulting coordinate, i.e., classification probabilities of the three groups (Sp = 0.76, Sm = 0.56, Se = 0.76) are given as having the shortest squared distance to the perfect classification coordinate (1, 1, 1). To plan a future study to better estimate the diagnostic accuracy of kfront, a sample size of 154 will be needed for each group in order to estimate the VUS of the marker within a 5% margin of error.

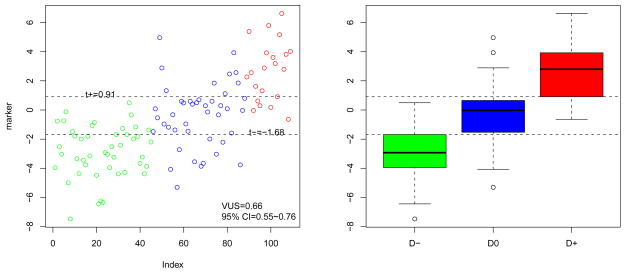
Utilizing the generic plot method, the data can be graphically summarized (see Figure 3) by a scatter plot and a boxplot, with observations from D⁻, D⁰ and D⁺ colored in green, blue and red, respectively. The estimated summary measure along with the CI is provided in the legend while the the optimal cut-points are labeled.

Figure 3.

Scatter plot and boxplot of the marker kfront (VUS and 95% CI in legend and the optimal cut-points indicated in dashed lines).

R> par(pty = “m”)
R> plot(vus)

Application of the nonparametric method leads to almost the same VUS estimate with a subtly different CI as shown below.

R> vus.nonpar <- VUS(x = xx, y = yy, z = zz, method = “NonPar”)
R> vus.nonpar
The DiagTest3Grp summary measure: VUS
Method used for VUS:NonPar
Raw Data Summary:
  n     mu    sd
D− 45 −2.8657503 1.776514
D0 43 −0.3725226 2.212393
D+ 21 2.6817010 2.066669
VUS=0.6565,95% CI=0.556~0.7708
Best cut-points: lower=−1.6826, upper=0.9119
The group correct classification probabilities are:
  Sp   Sm   Se
0.7556 0.5581 0.7619

When normality is violated, estimates from the normal method and the nonparametric method may deviate greatly. In such situations, we recommend the nonparametric method for VUS estimation, accompanied with the variance and CI derived from bootstrapping.

Taking the same data input, analysis on the Youden index can be easily completed by a simple call of Youden3Grp().

R> youden <- Youden3Grp(x = xx, y = yy, z = zz, method = “Normal”)
R> youden
The DiagTest3Grp summary measure: Youden
Method used for Youden:Normal
Raw Data Summary:
  n     mu    sd
D− 45 −2.8657503 1.776514
0 43 −0.3725226 2.212393
D+ 21 2.6817010 2.066669
Youden=0.4997,95% CI=0.4029~0.5964
Best cut-points: lower=−1.4195, upper=1.1048
The group correct classification probabilities are:
  Sp   Sm   Se
0.7922 0.4298 0.7773
Sample Size to estimate Youden within specified margin of error=115

The estimated Youden index under normality is 0.5. Its associated CI, correct classification probabilities corresponding to each group, optimal cut-points and sample size are printed (see above). The optimal cut-points from Youden analysis are not equivalent but quite close to the pair from previous VUS analysis. The sample size for a future study to estimate the Youden index of kfront within a margin of error of 5% is 115, slightly smaller than the sample size calculated for VUS. The other four methods for Youden estimation can be similarly implemented and thus are not demonstrated here. The four methods are potentially more robust to distribution assumptions and should be adopted when normality is in question. While the variance (and 95% CI) associated with the estimate of the Youden index is routinely returned from calling Youden3Grp(), the variances associated with the lower and upper optimal cut-points are not. They can be obtained by calling Youden3Grp.Variance.Normal() and Youden3Grp.Variance.Bootstrap() for the normality-based and the bootstrap-based variances and CIs, respectively. Below, we show how to obtain the variances.

R> var0 <- Youden3Grp.Variance.Normal(x = xx, y = yy, z = zz, alpha = 0.05)
R> round(c(lower.var = var0$var.t.minus, upper.var = var0$var.t.plus), 3)
lower.var upper.var
  0.063 0.102

Summarizing the above results of the VUS and Youden analysis, we conclude that kfront is a useful marker for AD diagnosis, since the 95% CI on the VUS has a lower limit of 0.55, higher than the VUS of a useless marker (1/6). The same conclusion can be drawn by comparing the Youden estimate to 0.

We leave the omnibus test to the complete analysis presented later and continue to demonstrate the functionality of statistical tests by comparing the VUS of kfront to that of zbentd and then to that of ktemp. Since the markers are measured on the same set of 118 subjects, we input the data to the function DiagTest3Grp.Test() as a data frame with the selected markers and set paired = TRUE in the function. The group membership must be placed at the first column followed by marker measurements.

R> new.AL <- data.frame(group = group, subset(AL,
+  select = c(kfront, zbentd)))
R> DiagTest3Grp.Test(dat = new.AL, paired = TRUE, type = “VUS”,
+  mu = 0, conf.level = 0.95, alternative = “two.sided”)
    normal-test
data: Test of new.AL on VUS
Z-stat = 4.451, mean = 0, sd = 1, p-value = 8.549e-06
alternative hypothesis: true diff in VUS is not equal to 0
95 percent confidence interval:
 0.1733938 0.4462536
sample estimates:
VUS of kfront VUS of zbentd
  0.6568242 0.3470005

The test results show that kfront exhibits greater discriminative power (p value = 8.549e − 06) compared with zbentd, as measured by the VUS (0.66 vs. 0.35) with the 95% CI on the difference in VUS estimates as (0.17, 0.45).

R> new.AL <- data.frame(group = group, subset(AL, select = c(kfront, ktemp)))
R> DiagTest3Grp.Test(dat = new.AL, paired = TRUE, type = “VUS”,
+  mu = 0, conf.level = 0.95, alternative = “two.sided”)
    normal-test
data: Test of new.AL on VUS
Z-stat = −1.6724, mean = 0, sd = 1, p-value = 0.09444
alternative hypothesis: true diff in VUS is not equal to 0
95 percent confidence interval:
 −0.20618129 0.01632036
sample estimates:
VUS of kfront VUS of ktemp
  0.6568242 0.7517546

Comparing kfront to ktemp above shows that ktemp has slightly higher VUS (= 0.75) than kfront though the difference is not statistically significant at the 5% level. In the above testings, we have hypothesized the true difference of 0 and implemented the two-sided alternative, however, the true difference can be changed to any value and one-sided alternatives can be tested.

For demonstration purpose, we now assume the markers are collected from independent subjects in the dataset. Notice that the data needs to be prepared in the format of a list where each component is a data frame with two columns: the group membership at the first column and the measurements of a marker at the second. Though less efficient by pretending independent samples, the test results still indicate a significant difference in VUS estimations between kfront and zbentd.

R> new.AL.list <- list()
R> new.AL.list[[1]] <- data.frame(group = group, subset(AL, select = kfront))
R> new.AL.list[[2]] <- data.frame(group = group, subset(AL, select = zbentd))
R> names(new.AL.list) <- c(“kfront”, “zbentd”)
R> DiagTest3Grp.Test(dat = new.AL.list, paired = FALSE, type = “VUS”,
+  p = 0, q = 0, conf.level = 0.95)
    normal-test
data: Test of new.AL on VUS
Z-stat = 3.9356, mean = 0, sd = 1, p-value = 8.298e-05
alternative hypothesis: true diff in VUS is not equal to 0
95 percent confidence interval:
 0.1555297 0.4641176
sample estimates:
VUS of kfront VUS of zbentd
  0.6568242 0.3470005

4.3. A complete demonstration

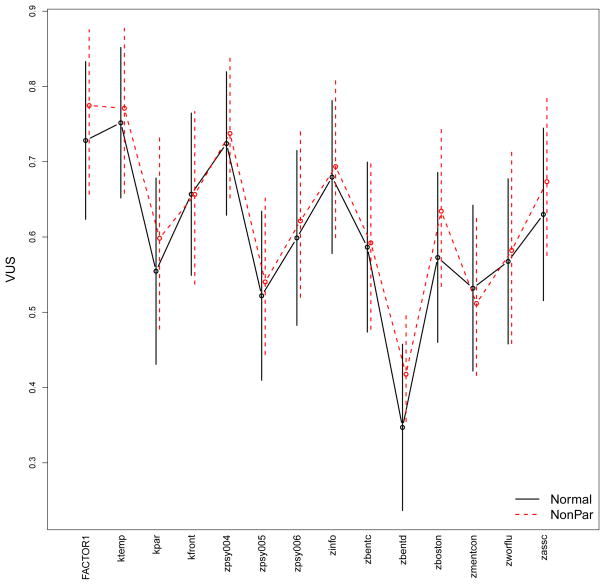
Now we analyze all the 14 markers in the AD dataset. In order to identify markers with the greatest diagnostic ability, we first estimate their VUS and the extended Youden index under all available methods with associated CIs, and plot the estimates and CIs for graphical comparison. For the estimation and graphical display purpose, we define an analysis function (the script AD.analysis.R is available in the supplemental files) for both VUS and Youden analysis. Using the analysis function (notice that the run time can be long), the following single-line command produces the VUS estimates and their 95% CIs from the normality-based and the nonparametric method on all the markers and displays the results in Figure 4. CIs for the nonparametric method are derived using 200 bootstrap samples.

Figure 4.

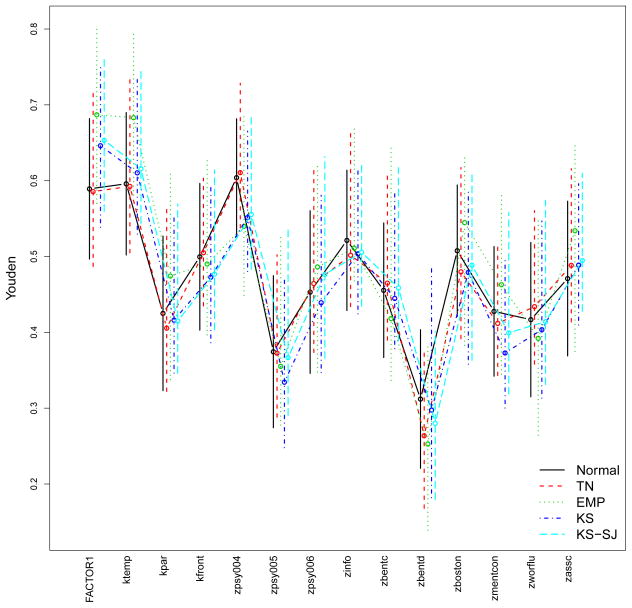
VUS estimates and 95% CIs under the normality assumptions (black solid lines) and the nonparametric method (red dashed line) for all the 14 markers.

R> all.vus <- AD.analysis(AL, type = “VUS”, NBOOT = 200)

The estimations based on the normality-based method reproduce the results displayed in Xiong et al. (2006, Table III). All the fourteen markers are useful to some extent since no CI spans across or below 1/6 (the VUS for a useless marker) with the exception of zbentd. Comparison between the results indicates that the two methods produce mostly similar VUS estimates. Based on averaged estimations from both methods, the most discriminative markers (almost indistinguishable) are global factor (FACTOR1), the temporal factor (ktemp) and logical memory (zpsy004) while the four weakest markers are visual retention-copy (zbentd), digital span forward (zpsy005) and mental control (zmentcon) and parietal factor (kpar).

Youden analysis can be similarly conducted using the same analysis function. The results are consistent with the VUS results on that all the markers are useful with their lower limits of the 95% CIs on the Youden estimates all above 0.

R> all.youden <- AD.analysis(AL, type = “Youden”, NBOOT = 200,
+  randomStart.N = 10)

For each marker, the estimated Youden indexes from various methods are very close, especially between the kernel methods (with two different options for bandwidth selection). The Youden index analysis results in similar but not identical rankings among the markers compared with the VUS analysis results.

An omnibus test among all the fourteen markers confirms that these markers are not equivalent in either VUS or Youden. Therefore, they have distinct levels of ability in discriminating AD patients.

R> new.AL <- data.frame(group = group, AL)
R> omni.vus <- DiagTest3Grp.Test(dat = new.AL, paired = TRUE, type = “VUS”,
+  p = 0, q = 0, mu = 0, conf.level = 0.95, alternative = “two.sided”)
R> omni.vus
    Chi-Sqaure test
data: Test of new.AL on VUS
Chi-square = 122.9344, df = 13, p-value < 2.2e-16
alternative hypothesis: true diff in VUS is not equal to 0
 percent confidence interval:
 NA NA
sample estimates:
 VUS of FACTOR1 VUS of ktemp VUS of kpar VUS of kfront VUS of zpsy004
   0.7282689    0.7517546 0.5545725    0.6568242   0.7241812
 VUS of zpsy005 VUS of zpsy006 VUS of zinfo VUS of zbentc VUS of zbentd
   0.5219222    0.5987500 0.6795676    0.5865334   0.3470005
 VUS of zboston VUS of zmentcon VUS of zworflu VUS of zassc
   0.5728167    0.5320187    0.5675800  0.6300100
R> new.AL <- data.frame(group = group, AL)
R> omni.youden <- DiagTest3Grp.Test(dat = new.AL, paired = TRUE,
+ type = “Youden”, p = 0, q = 0, mu = 0, conf.level = 0.95,
+ alternative = “two.sided”)
R> omni.youden
    Chi-Sqaure test
data:  Test of new.AL on Youden
Chi-square = 164.9056, df = 13, p-value < 2.2e-16
alternative hypothesis: true diff in Youden is not equal to 0
 percent confidence interval:
 NA NA
sample estimates:
 Youden of FACTOR1  Youden of ktemp Youden of kpar Youden of kfront
     0.5892511     0.5959572 0.4250516 0.4996535
 Youden of zpsy004 Youden of zpsy005 Youden of zpsy006 Youden of zinfo
     0.6040473     0.3744770 0.4531280 0.5213547
 Youden of zbentc Youden of zbentd Youden of zboston Youden of zmentcon
     0.4555184     0.3121202 0.5076940 0.4276617
 Youden of zworflu Youden of zassc
     0.4167880     0.4709709

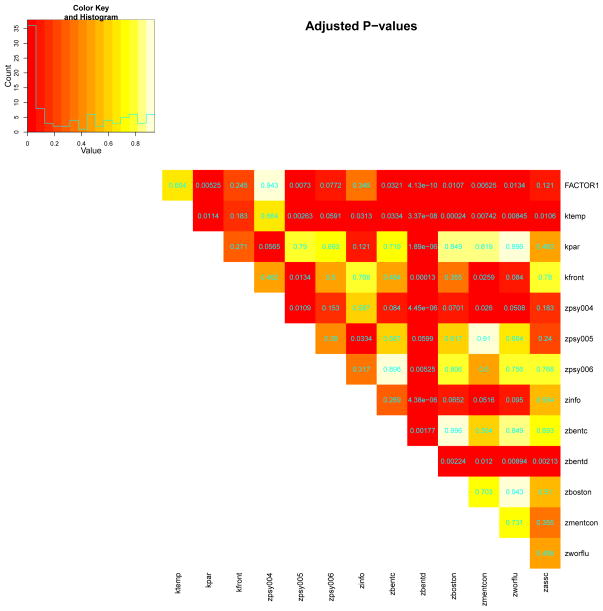
Further, we implement pairwise tests on the VUS estimates of the markers controlling for the false discovery rate to identify which specific pairs possess distinct diagnostic ability. An upper-triangular data frame is returned to exhibit the results (test statistics, raw p values and adjusted p values) on all the pairwise tests. Meanwhile, an upper-triangular heatmap is produced to visualize the adjusted p values (see Figure 6).

Figure 6.

Heatmap illustration on pairwise test p values among the 14 markers.

R> pairwise.vus <- Pairwise.DiagTest3Grp.Test(new.AL, paired = TRUE,
+  type = “VUS”, p = 0, q = 0, conf.level = 0.95, p.adjust.method = “fdr”)
R> print(pairwise.vus$print.matrix[1:18, 1:8], na = “”)
  MarkerID     Row ktemp   kpar kfront zpsy004 zpsy005 zpsy006
1 FACTOR1 Z-statistic −0.646  3.352 1.506 0.072 3.238  2.131
2          raw P 0.518 0.000802 0.132 0.943 0.00120 0.0331
3      adjusted P 0.664 0.00525 0.245 0.943 0.0073 0.0772
4   ktemp Z-statistic     2.995 1.672 0.648   3.6  2.278
5          raw P    0.00275 0.0944 0.517 0.000318 0.0227
6      adjusted P     0.0114 0.183 0.664 0.00263 0.0591
7   kpar Z-statistic        −1.434 −2.306  0.382 −0.589
8          raw P         0.152 0.0211  0.703  0.556
9      adjusted P         0.271 0.0565  0.79 0.693
10  kfront Z-statistic            −1.06  2.912 0.953
11          raw P            0.289 0.00359 0.341
12      adjusted P            0.462 0.0134  0.5
13 zpsy004 Z-statistic            3.022 1.777
14          raw P            0.00251 0.0756
15      adjusted P             0.0109 0.153
16 zpsy005 Z-statistic               −1.175
17          raw P                0.24
18      adjusted P                0.39

Based on the adjusted p values, the three best markers (FACTOR1, ktemp, zpsy004) are not statistically different from each other. However, they show much higher discriminative abilities than the bottom three markers in terms of VUS estimates. Particularly, zbentd is worse than almost all the other markers, especially than the top three markers. The differences between the top three markers and the other markers in between (e.g., zbentc, zboston, zworflu) are also statistically significant. The pairwise test results on the Youden index are very similar to the above results for VUS and therefore are omitted here.

Taken together, the VUS analysis and Youden index analysis provide consistent results on the AD dataset.

5. Summary

Diagnostic tests for three ordinal groups are important in biomedical practice but analysis software is lacking. We have introduced two useful summary measures (VUS and Youden) which can be adopted to evaluate the discriminative ability of a diagnostic test when there are three ordinal groups. We have described in details the R package DiagTest3Grp which implements important statistical inference (point estimate and CI, statistical test, sample size calculation) on diagnostic tests using either VUS or Youden in a unified interface. The utility of the package has been demonstrated using a real world AD dataset.

Alternatively, the classic proportional odds (PO) model can be employed to evaluate the importance of the markers based on odds ratio (OR) estimations, using the R packages MASS (function polr(), Venables and Ripley 2002) or rms (function lrm(), Harrell Jr. 2012) or ordinal (function clm(), Christensen 2012). The results from PO models may not be completely consistent with the results from VUS or Youden analysis due to distinct model frameworks and underlying assumptions. The VUS and Youden are estimated in the R package either under normality assumptions or nonparametrically. While the nonparametric approach assumes no specific distributional families, our normality-based parametric approach is restrictive to normally distributed data though it was found to be robust to slight deviations from normality (Luo and Xiong 2012, simulation results). When implementing PO mdoels, readers should be cautious about the underlying PO assumption and are referred to follow Harrell Jr. (2001, Chapter 14) for strategies of assessing the assumption. To the best of our knowledge, no formal mathematical and statistical connection has been established in the literature between the measures of diagnostic accuracy in diagnostic medicine and the traditional PO models when there are three diagnostic categories, although such a connection is available when the diagnosis is binary (Qin and Zhang 2003).

The R package DiagTest3Grp has the potential to help medical practitioners identify useful markers for early-stage disease detection and timely treatments when there are three diagnostic groups. The current version has its limitations. We are committed to continuous improvement of the package as research advances in this field, for example, by incorporating sample size calculation under various scenarios, nonparametric tests on VUS and Youden, and ROC surface analysis adjusting for covariates.

Figure 5.

Youden estimates and 95% CIs under the five approaches (see Section 3) for all the 14 markers.