Abstract
The fusion peptide (FP) of the human immunodeficiency virus (HIV) is part of the N-terminus of the viral envelope glycoprotein gp41 and is believed to play an important role in the viral entry process. To understand the immediate effect of this peptide on the cell membrane, we have studied the influence of the synthetic FP sequence FP23 on the mechanical properties of model lipid bilayers. For this purpose, giant unilamellar vesicles were prepared from the unsaturated lipid dioleoylphosphatidylcholine mixed in various molar ratios with FP23. The bending stiffness of the vesicles was measured with two different methods: fluctuation analysis and aspiration with micropipettes. The data obtained from both of these approaches show that the bending stiffness of the membrane decreases gradually with increasing concentration of the FP23 in the bilayer. Low concentrations of only a few mol% FP23 are sufficient to decrease the bending stiffness of the lipid bilayer by about a factor of 2. Finally, data obtained for the stretching elasticity modulus of the membrane suggest that the peptide insertion decreases the coupling between the two leaflets of the bilayer.
1. Introduction
The human immunodeficiency virus (HIV) uses ectodomain glycoproteins to dock with receptors on the T-cell membrane. Subsequently, it perturbs the target membrane forming a pore [1]. The glycoprotein gp41 of the HIV envelope is considered to be the main mediator of the viral entry process [2, 3]. gp41 is believed to induce crucial changes in the target membrane to facilitate fusion of the viral envelope with the target cell. Upon binding, it undergoes a conformational change that exposes a fusion peptide (FP) with a highly hydrophobic sequence. The first 23 amino acids of the N-terminal domain of gp41 constitute what is called the FP sequence FP23, which inserts into the target cell bilayer during viral entry [2]–[6]. The solubility of the synthetic peptide FP23 in chloroform and water is poor, but it dissolves well in hexafluorisopropanol (HiP). FP23 is reported to have a largely α-helical conformation in HiP and in phosphatidylglycerol–phosphatidylcholine membranes [7, 8]. Populations of both α-helical and β-sheet conformations have been observed for other membrane constructs, with β-sheet favored at higher peptide–lipid molar ratios and in membranes containing cholesterol [8]–[10]. On the other hand, FP23 is suggested to adopt an intermolecular β-sheet conformation when being part of the original gp41 trimer [8, 11]. It has even been proposed that conversion from α-helical to β-structure is a step in membrane fusion [12].
The FP23 sequence contains a large fraction of hydrophobic residues, which allow for secure anchoring in the target bilayer on insertion. FP23 is also positively charged because of arginine present in the peptide's C-terminus protruding at the membrane surface. The fusogenic effects of FP23 and its mutants were demonstrated on human erythrocytes [13, 14] and liposomes [15, 16].
As with any membrane fusion, the fusion of the HIV viral envelope and the target cell is supposed to have at least one highly curved intermediate state, which is responsible for the fusion energy barrier. On the other hand, bilayer curving is governed to a large extent by the membrane bending rigidity, which is a fine sensor for the effects of various inclusions in the membrane and molecules or ions present in the bilayer vicinity [17, 18]. Indeed, recent experiments on lipid bilayer stacks with x-ray diffuse scattering [19] reveal that the addition of small molar fractions of FP23 to the lipid bilayer significantly lowers the bending rigidity of the membrane, providing one possible mechanism for fusion mediation.
Unlike classical diffraction and scattering methods, which probe the elasticity of multilamellar stacks at a microscopic scale, giant unilamellar vesicles (GUVs) provide a more natural model system that ensures full hydration of the membrane, absence of any perturbations due to neighboring bilayers or a supporting substrate, and control over the membrane tension. In experiments with GUVs, the mechanical response of a single bilayer is revealed at a macroscopically averaged level. Being similar in size to actual living cells, GUVs provide a handy model to mimic the cell membrane at the cell-size scale and study the mechanical and rheological properties of bilayers as a function of membrane composition and environment [20]. Their size also allows for direct visualization of the membrane response to external factors (for example, electric fields [21, 22], hydrodynamic flows [23] and molecules inserting in the membrane [24]) with conventional light microscopy.
A number of methods have already been developed to study the elastic properties of lipid membranes in giant vesicles (see the overview in [25]). Fluctuation analysis (also referred to as flicker spectroscopy) is a well-established method for evaluating the bending rigidity of a lipid bilayer from stochastic analysis of the thermal undulations of a freely suspended membrane [26]–[29]. Micropipette aspiration is another common method for measuring the mechanical properties of lipid membranes [30]–[36]. It consists of analysing the response of the vesicle area to tensions induced by pressure applied with a micropipette. One advantage of this method is the possibility of obtaining the bending rigidity and the stretching elasticity of the particular vesicle membrane simultaneously in a single experiment. Yet another method is vesicle electrodeformation, which consists of analysing changes in the shape of the vesicle in response to an applied electric field [17, 37, 38].
In this paper, we report our results for the elastic properties of GUVs made of dioleoylphosphatidylcholine (DOPC) doped with FP23. Data were collected using two different methods—fluctuation analysis and micropipette aspiration. After introducing the experimental procedures, we show results for the electrophoretic mobility of vesicles containing FP23 and then present the softening of the membrane induced by FP23. In the analysis of the elastic properties of the examined membranes, we consider the effect of FP23 on the intermonolayer coupling in the bilayer. Finally, we discuss tests to fuse GUV couples.
2. Materials and methods
2.1. Preparation of giant unilamellar vesicles
The vesicles were prepared from DOPC (Avanti Polar Lipids Inc., Alabaster, AL), 4 mM stock solution in chloroform (Sigma Aldrich, Steinheim, Germany), mixed with FP23 (AVGIGALFLGFLGAAGSTMGARS, Peptide Synthesis Facility at the Pittsburgh Biotechnology Center, Pittsburgh, PA), 0.4 mM stock solution dissolved in HiP (Sigma–Aldrich). The GUVs were formed using the electroformation method [39] as follows. A solution prepared from the stocks mixed in certain ratios of lipid to peptide was dried out with nitrogen flow in a vial and then dissolved in a mixture of HiP and chloroform (5 : 1). The choice for this solvent composition was set by the limited miscibility of chloroform and HiP. The resulting solution was deposited on conducting glasses coated with indium tin oxide (ITO). The formed film was dried in vacuum for 2 h at 57 °C to remove traces of solvents. After that, the ITO glasses and a 2-mm-thick Teflon spacer were assembled into a chamber. The chamber was then filled with sugar solution and subjected to an ac electric field applied with an Agilent 33220A function generator (Agilent Technologies Deutschland GmbH, Böblingen, Germany). The exact composition of the sugar solution and the ac field parameters were set depending on the planned type of experiment. For the fluctuation analysis, a 10 mM solution of glucose (Sigma–Aldrich) was used with sine-shaped 10 Hz electric field of increasing strength (from 250 to 550 VRMS m−1 in 100 VRMS m−1 steps every 20 min). For the micropipette aspiration experiments, a 100 mM solution of sucrose (Sigma–Aldrich) was used, with the applied ac field being 10 Hz sine-shaped with 550 VRMS m−1 for 1 h. The two different protocols arise from trials to optimize the vesicle yield. In both cases, the electroformation was finished with a vesicle detachment stage (5 Hz, 550 VRMS m−1). For the aspiration experiment, the vesicles were subsequently diluted in a 110 mM solution of glucose. The choice for the solvents is justified later in the text. The exact osmolarities were measured with an Osmomat 030 cryoscopic osmometer (Gonotec, Berlin, Germany).
2.2. Preparation of large unilamellar vesicles
Large unilamellar vesicles (LUVs) were prepared from the same stocks as GUVs by depositing a certain amount of stock lipid/peptide solution into a vial, drying out the solvents, filling the vial with bidistilled water and shaking the vial for 15 min. After that, the obtained solution was extruded with a pneumatic extruder LiposoFast (Avestin Europe, Germany) successively through polycarbonate membranes from 400, to 200 and to 100 nm pore diameters to achieve homogeneous size distribution of the LUVs. The resulting average concentration of lipids was 73 nM, approximately corresponding to that in GUV solutions.
2.3. Fluctuation analysis experiments
For this type of experiment, GUVs were prepared with a 10 mM solution of glucose as both inner and outer media. This low concentration ensures osmotic stabilization and thus constant volume of the vesicle as assumed in the analysis procedure. Higher sugar concentrations were avoided to prevent gravity effects on fluctuation spectra [40]. In previous studies, such gravity effects were either neglected in the fluctuation analysis, minimized by choosing a certain subset of vesicles [41, 42], or taken into account by explicit shape calculations [29]. Note that for sugar concentrations in the 100–200 mM range, gravity has a significant effect on the fluctuation spectra for vesicles with radii larger than about 15 μm [29, 42]. The vesicles measured here were chosen large enough (10–50 μm in diameter) to ensure good optical resolution for the larger wavelengths. The vesicles exhibited visible fluctuations. Images over time were recorded with a fast digital camera (HG-100 K Redlake Inc., San Diego, CA) at 60 frames per second and an exposure time in the range of 100–150 μs. Approximately 5500 images for each measurement were collected under phase contrast with an Axiovert 135 upright optical microscope (Zeiss, Germany). The short exposure times allow capture of the higher modes of the fluctuations, preventing the image from being blurred by longer camera integration time [17, 43]. The image analysis was performed with in-house-developed software described in [17], which finds the contour of the vesicle on each image, carries out statistical analysis of the modal distribution and extracts the value for the bending rigidity and vesicle tension by means of fitting. Typical tensions of the vesicles in measurements accepted as successful are in the range of 0.5–50 nN m−1. All measurements were carried out at 25 °C.
2.4. Micropipette aspiration experiments
For this type of experiment, the GUVs were prepared with a 100 mM solution of sucrose as the inner medium and 110 mM solution of glucose as the outer medium. These solvent conditions were chosen in order to obtain reasonably good image contrast of the vesicle part aspirated into the pipette while preventing the vesicle from being too heavy to distort the axial symmetry of the part outside the pipette. Simultaneously, the sugar solutions ensured constant volume of the vesicle due to osmotic stabilization. The higher glucose (external) osmolarity guarantees volume-to-area ratios suitable for vesicle aspiration. The pipettes were pulled from glass capillaries (World Precision Instruments) with a pipettepuller (Sutter Instruments, Novato, CA) and polished with a microforge (Narishige, Tokyo, Japan). The inner pipette diameter varied in the range of 10–30 μm. Our experimental set up consists of two independently operational linear translational stages (M-531.DD and M-535.21; Physik Instrumente, Karlsruhe, Germany) with micromanipulators MP-225 (Sutter Instruments) rigged to an Axiovert 135 microscope with a 20× objective operated in phase-contrast mode. Single-pipette configuration was employed for elastic property measurements, while for the fusion tests, two pipettes were used. Images were recorded with a CCD camera (CS3960DCL; Toshiba Teli Corp., Tokyo, Japan) connected to a frame grabber (PCIe-1427; National Instruments, Austin, TX). The vesicle solution was deposited in a chamber of volume ~2 ml with a small opening to allow access for pipettes. After initial aspiration, first the vesicle was pre-stressed with a pressure of about 100 Pa to get rid of possible suboptical membrane folding and wrinkling defects [44]. Then the pressure was released to the initial value and the vesicle was subjected to a series of increasing pressures. To exclude errors caused by possible flickering of the membrane, several (usually 5) images were recorded for each pressure for further averaging during analysis. The waiting time between a pressure change and image acquisition was about 1 min, which for the soft membranes explored in this work was sufficient to establish equilibrium. The experimental time for scanning the full pressure range in the elasticity measurements was of the order of 1.5 h. Due to the small opening of the chamber, no substantial evaporation was observed during the experiment as judging from the constant vesicle volume. The whole setup was controlled with an in-house-developed LabVIEW-based software allowing for automatic scanning of the pressure range applied to both pipettes independently, and recording the corresponding images. The typical tension range explored in the micropipette aspiration experiments was from nearly 0 up to approximately 2 mN m−1. Higher pressures resulted in complete sucking of the vesicle into the pipette or vesicle budding. The images were analysed afterwards with in-house-developed software that detects and calculates the vesicle geometry as a function of the applied pressure and fits the area dilation versus tension plot with either logarithmic (for bending rigidity) or linear (for stretching elasticity) dependence [45, 46], with corrections outlined in [47]. More details of our implementation of the algorithm can be found in the supplementary material (available at stacks.iop.org/NJP/13/025004/mmedia). All measurements were carried out at 25 ° C.
2.5. ζ potential measurements
Electrophoretic mobilities at a temperature of 25 ° C were determined with a zetasizer (Zetasizer Nano ZS; Malvern Instruments, Worcestershire, UK) operating with a 4 mW HeNe laser (632.8 nm) and a temperature-control jacket for the cuvette. Each sample was degassed for 15 min prior to the measurement to remove air bubbles. The cuvette was sealed to avoid evaporation and left for 5 min to allow temperature equilibration. The samples (with volume 0.75 ml) were loaded into folded capillary ζ potential cells with integral gold electrodes. Three measurements consisting of 100 runs were carried out. The mobility μ was converted to ζ potential using the Helmholtz–Smoluchowski relation ζ = μη/∊∊0, where η is the solution viscosity, ∊ is the dielectric constant of water and ∊0 is the permittivity in vacuum. The measurement accuracy is about ±5 mV, as stated by the manufacturer. The data presented here were obtained on LUV solutions. Contrary to an earlier report [48], measurements carried out on GUVs showed poor reproducibility and larger errors and were thus discarded.
3. Results and discussion
3.1. Peptide incorporation
Because of the poor solubility of FP23 in chloroform-based solutions, we were concerned about the partitioning of the peptide in the membrane. In order to test whether the peptide incorporates into the vesicle membrane at all and how the incorporation depends on the amount of the peptide, we used ζ potential measurements. These are made possible by the fact that we use a zwitterionic lipid (DOPC) and the peptide has an arginine near the C-terminus. Upon FP23 insertion in the membrane, this positively charged amino acid at the tail of the peptide locates on the surface of the membrane. Thus, FP23 present in the membrane at various fractions is expected to influence the surface charge of the liposomes and therefore the measured ζ potential.
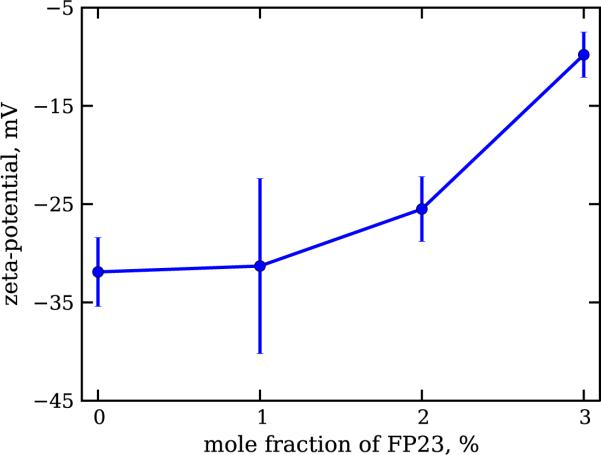
The results presented in figure 1 show that with increasing peptide concentration, the ζ potential grows, and so does the net positive charge of the vesicles used in the experiment. The data for each of the explored vesicle compositions were distributed in a single peak. This is an indication of the absence of FP23 aggregates in the water, which if present would produce a peak with positive ζ potential. Thus, our data suggest that on the bulk level, the peptide is indeed inserted into the membrane and not left in the solution, which is an expected result considering the high hydrophobicity of the peptide and the poor solubility in water.
Figure 1.
ζ potential in mV measured on LUV suspensions prepared from DOPC–FP23 mixtures. Error bars are standard deviations.
On the other hand, the resolution of the technique (a standard deviation of ±5 mV for a single measurement) did not allow us to identify whether the peptide is homogeneously distributed among all vesicles.
3.2. Bending rigidity
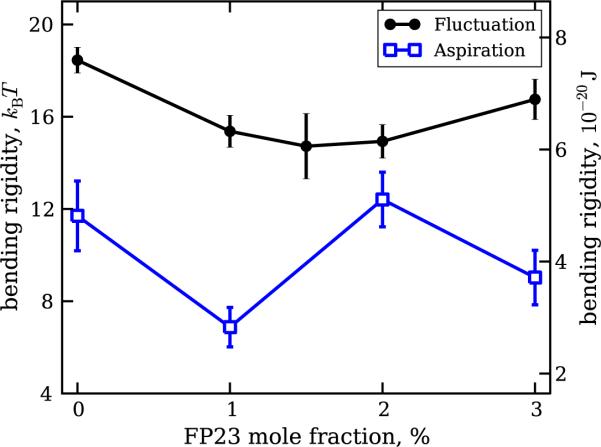
Bending rigidity measurements on a total of 278 vesicles were performed, with 176 of them studied with fluctuation analysis and the remaining 102 with micropipette aspiration. Examples of raw data collected with both techniques are provided in the supplementary material (see figures S2, S3 and S5 available at stacks.iop.org/NJP/13/025004/mmedia). The results for the dependence of the bending rigidity on the molar fraction of FP23 in the membrane are presented in figure 2, as measured with the two techniques.
Figure 2.
Bending rigidity of DOPC bilayers doped with various fractions of FP23 as measured by two experimental methods—fluctuation analysis (filled circles) and micropipette aspiration (open squares). The vesicles used for fluctuation analysis were in 10 mM glucose solutions, while those used for micropipette aspiration were prepared in a 100 mM sucrose solution and diluted in a 110 mM glucose solution. The data were averaged over measurements carried out on more than 20 vesicles per composition. The error bars represent standard errors. All experimentally obtained values are included (see text for details).
The data for pure DOPC obtained with fluctuation analysis are in good agreement with previously reported values [17, 49, 50] in the range of 7–10 × 10−20 J or 17–24 kBT, where kB is the Boltzmann constant and T is the temperature. The overall trend in the data indicates a decrease in the bending rigidity with increasing peptide concentration, supporting recently reported results [19]. However, it can be clearly seen that the two methods herein give different results. The origins of this difference are discussed below.
The sugar solutions used in these two methods are very different. While for the fluctuation analysis the vesicles were in a 10 mM glucose solution, the micropipette aspiration was performed on vesicles prepared in a 100 mM sucrose solution and diluted in a 110 mM glucose solution. The sugar type and concentration can have a drastic influence on the elastic properties of the lipid bilayer [51, 52]. As reported for stearoylphosphatidylcholine [51], sucrose at a concentration of 100 mM induces a decrease in the bending rigidity of the bilayer from 1.27 ± 0.07 × 10−19 J in the absence of sucrose to 0.75 ± 0.2 × 10−19 J in 100 mM sucrose solution (data for the effect of glucose were not reported in that work).
To test the effect of sugars in our system, we carried out a series of control aspiration experiments using 8 mM sucrose as the inner medium and 8 mM glucose as the outer medium. This posed a serious problem for image recognition because of the very faint contrast of the membrane, particularly inside the pipette due to strong reflection from the glass capillary. In fact, the automated procedure consistently failed to recognize the aspirated part of the vesicle. By performing manual measurements on recorded images, it was possible to measure 11 vesicles, with overall accuracy considerably lower than that of the automated procedure. The obtained average value for the bending rigidity was 22.8 kBT with standard error ±2.2kBT, which is about twice as much as the value measured for the case of 100 mM sucrose/110 mM glucose (11.7 kBT with standard error ±1.5kBT). This result qualitatively and quantitatively agrees with data on the sucrose effect on SOPC vesicles reported in [51]. Furthermore, the value obtained with micropipette aspiration for low sugar concentrations agrees reasonably with the one obtained with fluctuation analysis and with values for DOPC reported in [17, 49, 50]. The effect of sugars on the mechanical properties of the membrane is presumably due to their adsorption on the lipid bilayer, as suggested by earlier experimental data on the uptake of glucose by vesicle dispersions [53]. We cannot also exclude effects due to impurities in the sugars used here and in other studies. Let us also note that effects resulting from the use of lipids from different producers also cannot be excluded. Karatekin et al [54] have reported differences in the material properties of membranes prepared from lipids purchased from two different producers.
Another source of the discrepancy between the data obtained with micropipette aspiration and with fluctuation analysis may be attributed to the sugar asymmetry across the membrane in the micropipette aspiration experiments (sucrose inside and glucose outside) that may further affect the material properties of the membrane [55]. In addition, the difference between the results obtained with the two methods may also stem from limitations of the classical analysis procedure for the aspiration experiments [30], which was shown to give consistently lower bending rigidity values than the fluctuation analysis [47]. Similar differences were found for another mechanical method for measuring the membrane bending rigidity, namely vesicle electrodeformation [37], and were discussed in detail in [17].
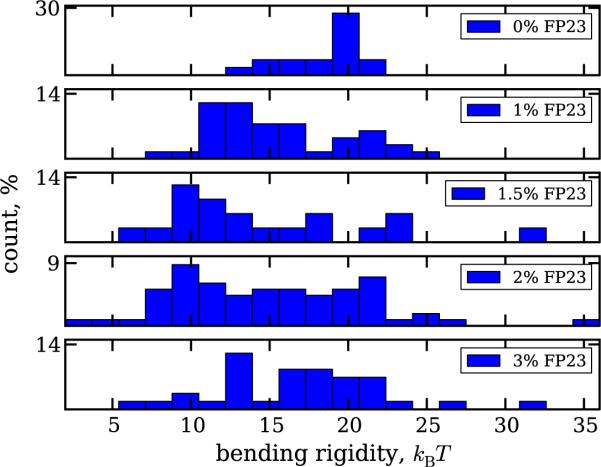
Another consistent problem faced in the analysis originates from heterogeneous distribution of the peptide among the different vesicles. The histograms of the bending rigidity values obtained with fluctuation analysis for various concentrations of FP23 are plotted in figure 3. The values corresponding to the peak in the distribution for pure DOPC appear in measurements on membranes with added FP23, suggesting the presence of peptide-free vesicles. The reason for such heterogeneity might be poor miscibility of the solvents for DOPC and FP23—chloroform and HiP, respectively. Adjusting the vesicle preparation procedure and the solvent ratio before the step of deposition on the ITO glasses (see section 2), we were able to achieve reasonable miscibility on the macroscopic level. However, microscopically, there is still the possibility of forming regions where FP23 was absent in the lipid bilayer, or where FP23 self-aggregated and came out of the bilayers. For some concentrations of the peptide, namely 1.5, 2 and 3%, we also observe deviations towards higher bending rigidity, which drive the average value up (see figure 2). These deviations could be due to multilamellarity of the vesicles.
Figure 3.
Histogram of the bending rigidity values obtained with fluctuation analysis. Values corresponding to pure DOPC membranes are observed also in the measurements on membranes with added FP23.
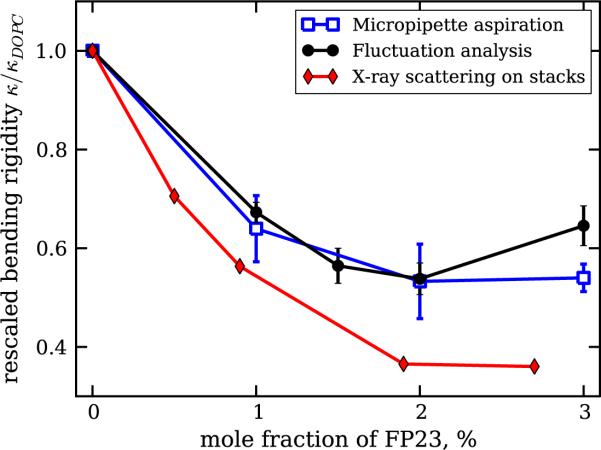
To be able to compare the results from the two methods with each other and with the results reported in [19], we performed the following steps. Firstly, to overcome the problem of heterogeneous distribution of the peptide among different vesicles, for the analysis of experiments with a nonzero fraction of FP23 obtained with the same method, we considered only vesicles with bending rigidity lower than that of pure DOPC including the standard error (see the supplementary material for details: available from stacks.iop.org/NJP/13/025004/mmedia). Secondly, we compared only relative changes in the bending rigidity as a function of the FP23 molar fraction in the sample, i.e. the data were rescaled by the value measured for pure DOPC membranes. The results are presented in figure 4 (see figure S6 in the supplementary material for the raw unrescaled data). The three methods, fluctuation analysis, micropipette aspiration and diffuse x-ray scattering from bilayer stacks, show reasonably good agreement, with the largest difference in the range of highest peptide concentration, where the measurements on GUVs show an insignificant increase in the bending rigidity. In addition, the experimental methods used in this work show slightly weaker softening of the bilayer as compared to the data reported in [19] when we consider the absolute values of the bending rigidity. For example, the values obtained for 2–3% FP23 from diffuse x-ray scattering are around 6–7kBT [19], while on GUVs we measure approximately 12kBT using fluctuation analysis (see figure S6 in the supplementary material). This small discrepancy is presumably because of the different lengthscales explored by the different techniques. However, the trend for the effect of the peptide on the membrane bending rigidity observed in both the systems, bilayer stacks and giant vesicles, is the same. Such a decrease in the bending rigidity is similar to that observed with co-surfactants [56] and theoretically expected for transmembrane inclusions (see e.g. [57]–[59]).
Figure 4.
Relative changes of the bending rigidity as a function of the concentration of FP23 in DOPC bilayers. Different datasets correspond to the results obtained with different methods: fluctuation analysis (filled circles), micropipette aspiration (open squares) and diffuse x-ray scattering from [19] (filled diamonds). The values obtained with the first two techniques are averaged over data where the values for pure DOPC have been filtered out, as described in the text.
3.3. Coupling of the bilayer leaflets
The micropipette aspiration technique allows us to simultaneously measure the bending rigidity κ and the stretching elasticity modulus K for a given vesicle. Unfortunately, K cannot be reliably measured for every vesicle, since often the vesicle is completely sucked into the pipette and lost before the tension regime governed by membrane stretching has been reached. It was possible to measure altogether 29 GUVs, on average 7 per peptide concentration, where both the bending rigidity and the stretching elasticity modulus could be evaluated for the same vesicle. The values of the stretching elasticity modulus K alone do not depend significantly on the concentration of FP23 (see supplementary material, figure S4, available from stacks.iop.org/NJP/13/025004/mmedia) and were found to be 124 mN m−1 with standard error ±18 mN m−1. For pure DOPC membranes, the stretching elasticity modulus was reported to be 265 ± 18 mN m−1 [49]; however, these measurements were carried out in sugar solutions at concentrations twice as high as the one here. Note that measurements at very low sugar concentration are not feasible because the low osmotic pressure will not ensure constant vesicle volume.
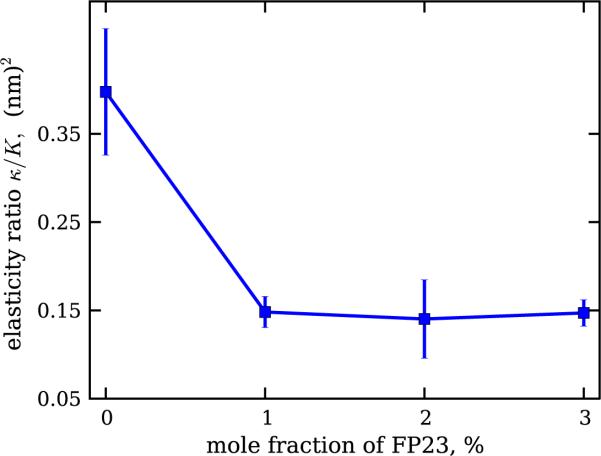
We considered the elasticity ratio κ/K, which shows the clustering behaviour exhibited in the distribution histograms of the bending rigidity in figure 3. After filtering out the contribution due to pure DOPC vesicles, one obtains the dependence shown in figure 5.
Figure 5.
Dependence of the ratio between the bending rigidity and the stretching elasticity modulus, κ/K, for DOPC membranes with increasing mole fraction of FP23. The inserted peptide reduces the elasticity ratio of the bilayer. The error bars represent standard errors.
The coupling between the two elasticity moduli, κ and K, is well established and has been theoretically considered [49, 60, 61] and experimentally explored for pure lipid bilayers [49]. The elasticity ratio κ/K scales quadratically with the hydrophobic thickness of the bilayer d following κ/K = βd2. The numerical constant β describes the coupling between the two bilayer leaflets. For completely bound leaflets, β = 1/12 [60], whereas for freely sliding monolayers, β = 1/48 [61]. A polymer brush model for the bilayer predicts the intermediate value β = 1/24 [49].
Using our results, we can estimate the value of the coupling constant β, provided that data for the membrane thickness d are available. For pure DOPC bilayers, d = 2.7 nm [62]. Thus, we obtain β ~ 1/18, which is between values for the polymer brush model and for completely bound monolayers. Experiments based on x-ray scattering show only a slight thinning of DOPC bilayers containing FP23. For a peptide molar fraction of 6%, the bilayer thinning was estimated to be about 0.4 nm [63]. Thus, for the highest FP23 fraction measured here, the membrane thickness is minimum d = 2.3 nm. Taking this estimate and the measured value of elasticity ratio in the presence of the peptide ~0.14 nm2, we obtain the monolayer coupling constant β ~ 1/38. This finding suggests that the peptide significantly reduces the interleaflet interaction, shifting it towards β values characteristic for freely sliding monolayers. On the molecular level, this result could be understood if one considers the peptide as an obstacle (or a molecular spring) in the hydrophobic core of the bilayer, which effectively pushes the two monolayers apart. Indeed, the peptide length, whether in α-helical or β-strand conformation, can slightly overspan the bilayer thickness, as demonstrated in simulations [64] and NMR studies [65]. In any conformation, the peptide is longer than the monolayer thickness and is typically located in the membrane at a specific tilt angle with respect to the membrane plane. Simulations [64, 66] and experiments [67, 68] have provided estimates for the tilt angle of the helical FP, and FTIR experiments have shown that a β-sheet FP can also be tilted [69]. The peptide tilting in the bilayer core might be relevant for the intermonolayer coupling in the membrane effectively sliding in between the two monolayers. A recent study of one of the authors shows that in DOPC, FP23 is located near the centre of the hydrocarbon interior of each monolayer, not at the centre of the bilayer. This is consistent with a tilted peptide that is not transmembrane. We are tempted to speculate that the weakening of the interaction between the bilayer leaflets as reported here is energetically favorable for reaching the intermediate fusion state in which gp41 is involved.
3.4. Vesicle fusion
A number of studies report on the fusogenic activity of the FP23-peptide on membranes [14]–[16], [70]–[73]. To probe this behaviour on giant vesicles, we brought two GUVs into close contact while holding them with micropipettes. In this experimental configuration, it is possible to independently set the tensions of the two membranes to facilitate fusion [74, 75]. The applied tensions were in the range of 0–0.7 mN m−1. Higher tensions in the range of significant membrane stretching could not be explored, as discussed in the previous section. Fusion between GUVs was not observed, even if we kept the vesicles in contact for 2 h. The vesicles were also not observed to adhere after moving them away from each other.
Compared to LUVs, which have been used in fusion assays with FP23 [16, 70, 71], giant vesicles have practically zero membrane curvature. LUVs have a two orders of magnitude greater curvature. High curvature is known to promote fusion [76], but it may not be the sole factor. Peptide-mediated fusion has been reported on less curved membranes compared to those of cells and cell ghosts [14, 72, 73]. Thus, other prerequisites, mainly specific membrane composition, may be required. For example, the presence of phosphatidylethanolamine in the bilayer was found necessary for the HIV-1 gp41 peptide to induce membrane fusion [77]. Also reported is the necessity of Ca2+ and Mg2+ ions to be present in order that successful fusion events in the presence of FP23 occur [70].
4. Conclusion
Our studies on giant vesicles show that the HIV-1 FP lowers the bending rigidity of freely suspended lipid bilayers made of DOPC. These results support earlier studies collected on lipid membrane stacks [19], suggesting coherence of the behaviour of the DOPC–FP23 system on different lengthscales. Quite a strong decrease in the bending rigidity is observed already at very low concentrations of the peptide, with some sort of saturation at higher peptide content. The well-known fusion enhancement attributed to FP23 was not observed in our experiments with GUVs. Previous studies report FP23-mediated fusion on phosphatidylethanolamine-containing LUVs, which have much higher curvature compared to GUVs. We do not observe fusion in DOPC giant vesicles doped with the peptide even at the moderate tensions applied. This outcome emphasizes the importance of membrane curvature and composition in fusion. Finally, our experimental data for the ratio of the bending rigidity to the stretching elasticity modulus suggest that the insertion of FP23 into the membrane changes the coupling between the leaflets of the bilayer considerably. This novel result and the exhibited behaviour may be relevant for the exact mechanism of action of the HIV FP upon viral fusion with the target membrane.
Supplementary Material
Acknowledgments
We thank the editors of this issue for the invitation to submit this article. We also thank N Bezlyepkina for support and numerous tips on handling giant vesicles. RD acknowledges R Lipowsky and T Weikl for insightful discussions about theoretical models about the effect of inclusions on the membrane bending rigidity.
Footnotes
Online supplementary data available from stacks.iop.org/NJP/13/025004/mmedia
References
- [1].Hernandez LD, Hoffman LR, Wolfsberg TG, White JM. Virus–cell and cell–cell fusion. Annu. Rev. Cell Dev. Biol. 1996;12:627–61. doi: 10.1146/annurev.cellbio.12.1.627. [DOI] [PubMed] [Google Scholar]
- [2].Wyatt R, Sodroski J. The HIV-1 envelope glycoproteins: fusogens, antigens and immunogens. Science. 1998;280:1884–8. doi: 10.1126/science.280.5371.1884. [DOI] [PubMed] [Google Scholar]
- [3].Mobley PW, Pilpa R, Brown C, Waring AJ, Gordon LM. Membrane-perturbing domains of HIV type 1 glycoprotein 41. AIDS Res. Human Retroviruses. 2001;17:311–27. doi: 10.1089/08892220150503681. [DOI] [PubMed] [Google Scholar]
- [4].Weissenhorn W, Dessen A, Harrison SC, Skehel JJ, Wiley DC. Atomic structure of the ectodomain from HIV-1 gp41. Nature. 1997;387:426–30. doi: 10.1038/387426a0. [DOI] [PubMed] [Google Scholar]
- [5].Weissenhorn W, Dessen A, Calder LJ, Harrison SC, Skehel JJ, Wiley DC. Structural basis for membrane fusion by enveloped viruses. Mol. Membr. Biol. 1999;16:3–9. doi: 10.1080/096876899294706. [DOI] [PubMed] [Google Scholar]
- [6].Eckert DM, Kim PS. Mechanisms of viral membrane fusion and its inhibition. Annu. Rev. Biochem. 2001;70:777–810. doi: 10.1146/annurev.biochem.70.1.777. [DOI] [PubMed] [Google Scholar]
- [7].Gordon LM, Mobley PW, Pilpa R, Sherman MA, Waring AJ. Conformational mapping of the N-terminal peptide of HIV-1 gp41 in membrane environments using 13c-enhanced Fourier transform infrared spectroscopy. Biochim. Biophys. Acta. 2002;1559:96–120. doi: 10.1016/s0005-2736(01)00443-6. [DOI] [PubMed] [Google Scholar]
- [8].Zheng Z, Yang R, Bodner ML, Weliky DP. Conformational flexibility and strand arrangements of the membrane-associated HIV fusion peptide trimer probed by solid-state NMR spectroscopy. Biochemistry. 2006;45:12960–75. doi: 10.1021/bi0615902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Yang J, Parkanzky PD, Bodner ML, Duskin CA, Weliky DP. Application of redor subtraction for filtered mas observation of labeled backbone carbons of membrane-bound fusion peptides. J. Magn. Reson. 2002;159:101–10. doi: 10.1016/s1090-7807(02)00033-2. [DOI] [PubMed] [Google Scholar]
- [10].Wasniewski CM, Parkanzky PD, Bodner ML, Weliky DP. Solid-state nuclear magnetic resonance studies of HIV and influenza fusion peptide orientations in membrane bilayers using stacked glass plate samples. Chem. Phys. Lipids. 2004;132:89–100. doi: 10.1016/j.chemphyslip.2004.09.008. [DOI] [PubMed] [Google Scholar]
- [11].Sackett K, Wexler-Cohen Y, Shai Y. Characterization of the HIV N-terminal fusion peptide-containing region in context of key gp41 fusion conformations. J. Biol. Chem. 2006;281:21755–62. doi: 10.1074/jbc.M603135200. [DOI] [PubMed] [Google Scholar]
- [12].Epand RM, Epand RF. Modulation of membrane curvature by peptides. Biopolymers. 2000;55:358–63. doi: 10.1002/1097-0282(2000)55:5<358::AID-BIP1009>3.0.CO;2-8. [DOI] [PubMed] [Google Scholar]
- [13].Gordon LM, Curtain CC, Zhong YC, Kirkpatrick A, Mobley PW, Waring AJ. The amino-terminal peptide of HIV-1 glycoprotein 41 interacts with human erythrocyte membranes: peptide conformation, orientation and aggregation. Biochim. Biophys. Acta. 1992;1139:257–74. doi: 10.1016/0925-4439(92)90099-9. [DOI] [PubMed] [Google Scholar]
- [14].Mobley PW, Lee H-F, Curtain CC, Kirkpatrick A, Waring AJ, Gordon LM. The amino-terminal peptide of HIV-1 glycoprotein 41 fuses human erythrocytes. Biochim. Biophys. Acta. 1995;1271:304–14. doi: 10.1016/0925-4439(95)00048-9. [DOI] [PubMed] [Google Scholar]
- [15].Slepushkin VA, Andreev SM, Sidorova MV, Melikyan GB, Grigoriev VB, Chumakov VM, Grinfeldt AE, Manukyan RA, Karamov EV. Investigation of human immunodeficiency virus fusion peptides. analysis of interrelations between their structure and function. Aids Res. Hum. Retroviruses. 1992;8:9–18. doi: 10.1089/aid.1992.8.9. [DOI] [PubMed] [Google Scholar]
- [16].Peisajovich SG, Epand RF, Pritsker M, Shai Y, Epand RM. The polar region consecutive to the hiv fusion peptide participates in membrane fusion. Biochemistry. 2000;39:1826–33. doi: 10.1021/bi991887i. [DOI] [PubMed] [Google Scholar]
- [17].Gracià RS, Bezlyepkina N, Knorr RL, Lipowsky R, Dimova R. Effect of cholesterol on the rigidity of saturated and unsaturated membranes: fluctuation and electrodeformation analysis of giant vesicles. Soft Matter. 2010;6:1472–82. [Google Scholar]
- [18].Klasczyk B, Knecht V, Lipowsky R, Dimova R. Interactions of alkali metal chlorides with phosphatidylcholine vesicles. Langmuir. 2010;26:18951–8. doi: 10.1021/la103631y. [DOI] [PubMed] [Google Scholar]
- [19].Tristram-Nagle S, Nagle JF. HIV-1 fusion peptide decreases bending energy and promotes curved fusion intermediates. Biophys. J. 2007;93:2048–55. doi: 10.1529/biophysj.107.109181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Dimova R, Aranda S, Bezlyepkina N, Nikolov V, Riske KA, Lipowsky R. A practical guide to giant vesicles probing the membrane nanoregime via optical microscopy. J. Phys.: Condens. Matter. 2006;18:S1151–76. doi: 10.1088/0953-8984/18/28/S04. [DOI] [PubMed] [Google Scholar]
- [21].Dimova R, Riske KA, Aranda S, Bezlyepkina N, Knorr RL, Lipowsky R. Giant vesicles in electric fields. Soft Matter. 2007;3:817–27. doi: 10.1039/b703580b. [DOI] [PubMed] [Google Scholar]
- [22].Dimova R, Bezlyepkina N, Jordo MD, Knorr RL, Riske KA, Staykova M, Vlahovska PM, Yamamoto T, Yang P, Lipowsky R. Vesicles in electric fields: some novel aspects of membrane behavior. Soft Matter. 2009;5:3201–12. [Google Scholar]
- [23].Abkarian M, Viallat A. Vesicles and red blood cells in shear flow. Soft Matter. 2008;4:653–7. doi: 10.1039/b716612e. [DOI] [PubMed] [Google Scholar]
- [24].Stavans J. Instabilities of membranes with anchored polymers. Physica. 2002;A 306:368–75. [Google Scholar]
- [25].Marsh D. Elastic curvature constants of lipid monolayers and bilayers. Chem. Phys. Lipids. 2006;144:146–59. doi: 10.1016/j.chemphyslip.2006.08.004. [DOI] [PubMed] [Google Scholar]
- [26].Brochard F, Lennon JF. Frequency spectrum of the flicker phenomenon in erythrocytes. J. Physique. 1975;36:1035–47. [Google Scholar]
- [27].Servuss RM, Harbich V, Helfrich W. Measurement of the curvature-elastic modulus of egg lecithin bilayers. Biochim. Biophys. Acta. 1976;436:900–3. doi: 10.1016/0005-2736(76)90422-3. [DOI] [PubMed] [Google Scholar]
- [28].Duwe HP, Kaes J, Sackmann E. Bending elastic moduli of lipid bilayers: modulation by solutes. J. Physique. 1990;51:945–61. [Google Scholar]
- [29].Henriksen JR, Ipsen JH. Thermal undulations of quasi-spherical vesicles stabilized by gravity. Eur. Phys. J. 2002;E 9:365–74. doi: 10.1140/epje/i2002-10091-3. [DOI] [PubMed] [Google Scholar]
- [30].Evans E, Rawicz W. Entropy-driven tension and bending elasticity in condensed-fluid membranes. Phys. Rev. Lett. 1990;64:2094–7. doi: 10.1103/PhysRevLett.64.2094. [DOI] [PubMed] [Google Scholar]
- [31].Hochmuth RM. Micropipette aspiration of living cells. J. Biomech. 2000;33:15–22. doi: 10.1016/s0021-9290(99)00175-x. [DOI] [PubMed] [Google Scholar]
- [32].Olbrich K, Rawicz W, Needham D, Evans E. Water permeability and mechanical strength of polyunsaturated lipid bilayers. Biophys. J. 2000;79:321–7. doi: 10.1016/S0006-3495(00)76294-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Fournier J-B, Ajdari A, Peliti L. Effective-area elasticity and tension of micromanipulated membranes. Phys. Rev. Lett. 2001;86:4970–3. doi: 10.1103/PhysRevLett.86.4970. [DOI] [PubMed] [Google Scholar]
- [34].Manneville J-B, Bassereau P, Ramaswamy S, Prost J. Active membrane fluctuations studied by micropipet aspiration. Phys. Rev. 2001;E 64:021908. doi: 10.1103/PhysRevE.64.021908. [DOI] [PubMed] [Google Scholar]
- [35].Bermúdez H, Hammer DA, Discher DE. Effect of bilayer thickness on membrane bending rigidity. Langmuir. 2004;20:540–3. doi: 10.1021/la035497f. [DOI] [PubMed] [Google Scholar]
- [36].Heinrich V, Rawicz W. Automated, high-resolution micropipet aspiration reveals new insight into the physical properties of fluid membranes. Langmuir. 2005;21:1962–71. doi: 10.1021/la047801q. [DOI] [PubMed] [Google Scholar]
- [37].Kummrow M, Helfrich W. Deformation of giant lipid vesicles by electric fields. Phys. Rev. 1991;A 44:8356. doi: 10.1103/physreva.44.8356. [DOI] [PubMed] [Google Scholar]
- [38].Niggemann G, Kummrow M, Helfrich W. The bending rigidity of phosphatidylcholine bilayers: Dependences on experimental method, sample cell sealing and temperature. J. Physique. 1995;II 5:413–25. [Google Scholar]
- [39].Angelova MI, Dimitrov DS. Liposome electroformation. Faraday Discuss. Chem. Soc. 1986;81:303–11. [Google Scholar]
- [40].Dobereiner HG, Evans E, Kraus M, Seifert U, Wortis M. Mapping vesicle shapes into the phase diagram: a comparison of experiment and theory. Phys. Rev. 1997;E 55:4458–74. [Google Scholar]
- [41].Pécréaux J, Döbereiner H-G, Prost J, Joanny J-F, Bassereau P. Refined contour analysis of giant unilamellar vesicles. Eur. Phys. J. 2004;E 13:277–90. doi: 10.1140/epje/i2004-10001-9. [DOI] [PubMed] [Google Scholar]
- [42].Nikolov V, Lipowsky R, Dimova R. Behavior of giant vesicles with anchored DNA molecules. Biophys. J. 2007;92:4356–68. doi: 10.1529/biophysj.106.100032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Faucon JF, Mitov MD, Meleard P, Bivas I, Bothorel P. Bending elasticity and thermal fluctuations of lipid-membranes-theoretical and experimental requirements. J. Physique. 1986;50:2389–414. [Google Scholar]
- [44].Vitkova V, Genova J, Bivas I. Permeability and the hidden area of lipid bilayers. Eur. Biophys. J. Biophys. Lett. 2004;33:706–14. doi: 10.1007/s00249-004-0415-2. [DOI] [PubMed] [Google Scholar]
- [45].Helfrich W, Servuss RM. Undulations, steric interaction and cohesion of fluid membranes. Nuovo Cimento. 1984;D 3:137–51. [Google Scholar]
- [46].Evans E, Rawicz W. Elasticity of `fuzzy' biomembranes. Phys. Rev. Lett. 1997;79:2379–82. [Google Scholar]
- [47].Henriksen JR, Ipsen JH. Measurement of membrane elasticity by micro-pipette aspiration. Eur. Phys. J. 2004;E 14:149–67. doi: 10.1140/epje/i2003-10146-y. [DOI] [PubMed] [Google Scholar]
- [48].Carvalho K, Ramos L, Roy C, Picart C. Giant unilamellar vesicles containing phosphatidylinositol(4,5)bisphosphate: characterization and functionality. Biophys. J. 2008;95:4348–60. doi: 10.1529/biophysj.107.126912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49].Rawicz W, Olbrich KC, McIntosh T, Needham D, Evans E. Effect of chain length and unsaturation on elasticity of lipid bilayers. Biophys. J. 2000;79:328–39. doi: 10.1016/S0006-3495(00)76295-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50].Pan J, Tristram-Nagle S, Kucerka N, Nagle JF. Temperature dependence of structure, bending rigidity, and bilayer interactions of dioleoylphosphatidylcholine bilayers. Biophys. J. 2008;94:117–24. doi: 10.1529/biophysj.107.115691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51].Vitkova V, Genova J, Mitov MD, Bivas I. Sugars in the aqueous phase change the mechanical properties of lipid mono- and bilayers. Mol. Cryst. Liq. Cryst. 2006;449:95–106. [Google Scholar]
- [52].Genova J, Zheliaskova A, Mitov MD. The influence of sucrose on the elasticity of SOPC lipid membrane studied by the analysis of thermally induced shape fluctuations. Colloids Surf. 2006;A 282–283:420–2. [Google Scholar]
- [53].Bummer PM, Zografi G. The association of d-glucose with unilamellar phospholipid-vesicles. Biophys. Chem. 1988;30:173–83. doi: 10.1016/0301-4622(88)85014-2. [DOI] [PubMed] [Google Scholar]
- [54].Karatekin E, Sandre O, Guitouni H, Borghi N, Puech PH, Brochard-Wyart F. Cascades of transient pores in giant vesicles: line tension and transport. Biophys. J. 2003;84:1734–49. doi: 10.1016/S0006-3495(03)74981-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [55].Dobereiner HG, Selchow O, Lipowsky R. Spontaneous curvature of fluid vesicles induced by trans-bilayer sugar asymmetry. Eur. Biophys. J. Biophys. Lett. 1999;28:174–8. [Google Scholar]
- [56].Israelachvili J. Intermolecular and Surface Forces. Academic; London: 1992. [Google Scholar]
- [57].Leibler S. Curvature instability in membranes. J. Physique. 1986;47:507–16. [Google Scholar]
- [58].Fournier JB. Nontopological saddle-splay and curvature instabilities from anisotropic membrane inclusions. Phys. Rev. Lett. 1996;76:4436–9. doi: 10.1103/PhysRevLett.76.4436. [DOI] [PubMed] [Google Scholar]
- [59].Bivas I, Meleard P. Bending elasticity and bending fluctuations of lipid bilayer containing an additive. Phys. Rev. 2003;E 67:012901. doi: 10.1103/PhysRevE.67.012901. [DOI] [PubMed] [Google Scholar]
- [60].Evans EA. Bending resistance and chemically induced moments in membrane bilayers. Biophys. J. 1974;14:923–31. doi: 10.1016/S0006-3495(74)85959-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [61].Goetz R, Gompper G, Lipowsky R. Mobility and elasticity of self-assembled membranes. Phys. Rev. Lett. 1999;82:221–4. [Google Scholar]
- [62].Kučerka N, Nagle JF, Sachs JN, Feller SE, Pencer J, Jackson A, Katsaras J. Lipid bilayer structure determined by the simultaneous analysis of neutron and x-ray scattering data. Biophys. J. 2008;95:2356–67. doi: 10.1529/biophysj.108.132662. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [63].Tristram-Nagle S, Chan R, Kooijman E, Uppamoochikkal P, Qiang W, Weliky DP, Nagle JF. HIV fusion peptide penetrates, disorders and softens T-cell membrane mimics. J. Mol. Biol. 2010;402:139–53. doi: 10.1016/j.jmb.2010.07.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [64].Maddox MW, Longo ML. Conformational partitioning of the fusion peptide of HIV-1 gp41 and its structural analogs in bilayer membranes. Biophys. J. 2002;83:3088–96. doi: 10.1016/S0006-3495(02)75313-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [65].Qiang W, Bodner ML, Weliky DP. Solid-state NMR spectroscopy of human immunodeficiency virus fusion peptides associated with host-cell-like membranes: 2D correlation spectra and distance measurements support a fully extended conformation and models for specific antiparallel strand registries. J. Am. Chem. Soc. 2008;130:5459–71. doi: 10.1021/ja077302m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [66].Kamath S, Wong TC. Membrane structure of the human immunodeficiency virus gp41 fusion domain by molecular dynamics simulation. Biophys. J. 2002;83:135–43. doi: 10.1016/S0006-3495(02)75155-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [67].Bradshaw JP, Darkes MJM, Harroun TA, Katsaras J, Epand RM. Oblique membrane insertion of viral fusion peptide probed by neutron diffractions. Biochemistry. 2000;39:6581–5. doi: 10.1021/bi000224u. [DOI] [PubMed] [Google Scholar]
- [68].Brasseur R, Vandenbranden M, Cornet B, Burny A, Ruysschaert JM. Orientation into the lipid bilayer of an asymmetric amphipathic helical peptide located at the N-terminus of viral fusion proteins. Biochim. Biophys. Acta. 1990;1029:267–73. doi: 10.1016/0005-2736(90)90163-i. [DOI] [PubMed] [Google Scholar]
- [69].Castano S, Desbat B. Structure and orientation study of fusion peptide FP23 of gp41 from HIV-1 alone or inserted into various lipid membrane models (mono-, bi- and multibi-layers) by FT-IR spectroscopies and Brewster angle microscopy. Biochim. Biophys. Acta. 2005;1715:81–95. doi: 10.1016/j.bbamem.2005.07.008. [DOI] [PubMed] [Google Scholar]
- [70].Nieva JL, Nir S, Muga A, Goni FM, Wilschut J. Interaction of the HIV-1 fusion peptide with phospholipid vesicles: different structural requirements for fusion and leakage. Biochemistry. 1994;33:3201–9. doi: 10.1021/bi00177a009. [DOI] [PubMed] [Google Scholar]
- [71].Pereira FB, Goi FM, Nieva J. Liposome destabilization induced by the HIV-1 fusion peptide effect of a single amino acid substitution. FEBS Lett. 1995;362:243–6. doi: 10.1016/0014-5793(95)00257-a. [DOI] [PubMed] [Google Scholar]
- [72].Gerber D, Pritsker M, Gunther-Ausborn S, Johnson B, Blumenthal R, Shai Y. Inhibition of HIV-1 envelope glycoprotein-mediated cell fusion by a dl-amino acid-containing fusion peptide. J. Biol. Chem. 2004;279:48224–30. doi: 10.1074/jbc.M403436200. [DOI] [PubMed] [Google Scholar]
- [73].Quintana FJ, Gerber D, Kent SC, Cohen IR, Shai Y. HIV-1 fusion peptide targets the TCR and inhibits antigen-specific T-cell activation. J. Clin. Investigation. 2005;115:2149–58. doi: 10.1172/JCI23956. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [74].Shillcock JC, Lipowsky R. Tension-induced fusion of bilayer membranes and vesicles. Nat. Mater. 2005;4:225–8. doi: 10.1038/nmat1333. [DOI] [PubMed] [Google Scholar]
- [75].Grafmuller A, Shillcock J, Lipowsky R. Pathway of membrane fusion with two tension-dependent energy barriers. Phys. Rev. Lett. 2007;98:2181011–4. doi: 10.1103/PhysRevLett.98.218101. [DOI] [PubMed] [Google Scholar]
- [76].Talbot WA, Zheng LX, Lentz BR. Acyl chain unsaturation and vesicle curvature alter outer leaflet packing and promote poly(ethylene glycol)-mediated membrane fusion. Biochemistry. 1997;36:5827–36. doi: 10.1021/bi962437i. [DOI] [PubMed] [Google Scholar]
- [77].Martin I, Defrise-Quertain F, Decroly E, Vandenbranden M, Brasseur R, Ruysschaert J-M. Orientation and structure of the NH2-terminal HIV-1 gp41 peptide in fused and aggregated liposomes. Biochim. Biophys. Acta. 1993;1145:124–33. doi: 10.1016/0005-2736(93)90389-h. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.