Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2013 Mar 13;3:1435. doi: 10.1038/srep01435

Indirect reciprocity is sensitive to costs of information transfer

Shinsuke Suzuki 1,2,a, Hiromichi Kimura 3
PMCID: PMC3595703  PMID: 23486389

Abstract

How natural selection can promote cooperative or altruistic behavior is a fundamental question in biological and social sciences. One of the persuasive mechanisms is "indirect reciprocity," working through reputation: cooperative behavior can prevail because the behavior builds the donor's good reputation and then s/he receives some reciprocal benefits from someone else in the community. However, an important piece missed in the previous studies is that the reputation-building process requires substantial cognitive abilities such as communication skills, potentially causing a loss of biological fitness. Here, by mathematical analyses and individual-based computer simulations, we show that natural selection never favors indirect reciprocal cooperation in the presence of the cost of reputation building, regardless of the cost-to-benefit ratio of cooperation or moral assessment rules (social norms). Our results highlight the importance of considering the cost of high-level cognitive abilities in studies of the evolution of humans' and animals' social behavior.

Cooperative interactions among genetically unrelated individuals are a fundamental aspect of human society. However, cooperation accrues a cost, c, to the donor of the cooperation while conferring a benefit, b, to another individual (b > c > 0). What mechanism enables the evolution of this costly behavior, i.e., cooperation? This issue has been of considerable concern in both social and biological sciences1,2,3,4,5,6.

One of the proposed mechanisms for the evolution of cooperation is "indirect reciprocity" working through reputation7,8,9,10,11. That is, cooperative behavior can prevail because the behavior builds the donor's good reputation and then he or she receives some reciprocal benefits from someone else in the community. For example, if an individual A helps B, another individual C observes the cooperation; C builds and spreads A's good reputation, and then another individual D helps A by referring to A's reputation. This account is quite powerful because this does not require kinship, a spatial (group)-structure, or repeated interactions among individuals to explain the emergence of cooperation.

It is important to note that the indirect reciprocity account relies on individuals' substantial cognitive abilities for reputation processing (e.g., communication skills, capacity for judgment based on social norms). High-level intelligence has been thought to be very costly in terms of biological fitness12,13. In other words, natural selection does not favor the evolution of intelligence unless excessive benefit is present. Although the concept of indirect reciprocity is based on humans' high-level intelligence, which potentially causes a loss of biological fitness, to our knowledge no study has investigated the effect of the cost of reputation processing on the evolution of indirect reciprocity.

In this study, we examine the evolution of indirect reciprocity in light of the cost of reputation building (spreading). By mathematical analyses and individual-based computer simulations, we demonstrate that the slight cost of reputation building completely destroys indirect reciprocal cooperation regardless of the cost-to-benefit ratio of cooperation or moral assessment rules (social norms).

Results

Let's consider a population comprising an infinite number of individuals. Each individual in the population has a reputation, either good or bad. For each round t = 1, 2… in a generation, each individual randomly finds an opponent and plays a one-shot prisoner's dilemma game. In this game, two individuals in a pair simultaneously choose to either “cooperate” or “defect”. Cooperation confers a benefit, b, to the recipient while accruing a cost, c, to the donor (b > c > 0). In contrast, defection yields nothing to either person. Moreover, each individual's behavior in the game is witnessed by an observer who decides whether to build and spread the donor's reputation at a cost cR (> 0). Finally, at the end of the generation, each individual leaves offspring depending on his/her fitness defined as the total payoff during the generation (i.e., natural selection). Higher fitness implies a higher probability that the individual can leave more offspring.

How does an observer build the donor's reputation? In other words, what behavior of the donor is interpreted as good or bad? We assume that an observer build the donor's reputation based on the donor's own reputation and behavior and the opponent's reputation14, and that all individuals in the population share the same moral assessment rule9,14,15,16 (see Methods). Furthermore, each individual's reputation at the initial round is assumed to be good.

In the present study, as in the previous studies9,15,17, we assume that each individual makes decisions in the prisoner's dilemma game based on the opponent's reputation. Such a decision-making rule, called a behavioral strategy, is denoted by a two-dimensional vector, p = (pB, pG), where pBand pG 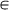Inline graphic [0,1] indicate the probability that the individual cooperates when his/her opponent's reputation is bad and good, respectively. In addition, each individual in the role of the observer decides whether to build and spread the reputation of the donor. By q Inline graphic [0,1], we denote the probability that the individual builds the donor's reputation. That is, each individual's strategy is defined as a pair of p and q, indicated by (p, q).

Let Gt(p, q) be the fraction of individuals among (p, q) strategists whose reputation is good at round t, and let x(p, q) be the probability density of (p, q) strategists over the population. Then, the average payoff of (p*, q*) strategists at round t is:

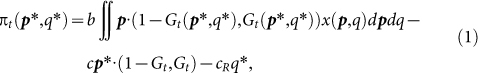graphic file with name srep01435-m1.jpg

where 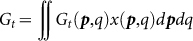Inline graphic denotes the fraction of individuals whose reputation is good in the whole population. The first term of equation (1) represents the benefit of cooperation multiplied by the probability that the focal (p*, q*) strategist is cooperated with by other individuals; the second term denotes the cost of cooperation multiplied by the probability that s/he cooperates, and the third term is the cost of reputation building multiplied by the probability that s/he builds the donor's reputation when s/he is in a role of an observer.

Since we can show that the reputation dynamics, Gt(p*, q*), depends on p*, but not on q*, for any moral assessment rules11,14 (see Methods), Gt(p*, q*) in equation (1) can be replaced by Gt(p*), that is:

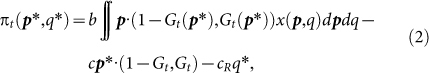graphic file with name srep01435-m2.jpg

Given that in equation (2) only the third term depends on q*, we can rewrite equation (2) as follows:

graphic file with name srep01435-m13.jpg

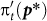where Inline graphic indicates the payoff in the prisoner's dilemma game, which depends on p* but not q*, and cRq* denotes the cost of reputation building, which depends on q* but not p*.

Equation (3) indicates that, given a value of p, individuals with q = 0 always get the highest payoff in each round, regardless of the cost-to-benefit ratio of cooperation (c/b), the amount of the cost of reputation building (cR > 0), or the moral assessment rules (update rule of Gt(p, q)). This means individuals with q = 0 always get the highest fitness, sum of the payoffs, for any p. In other words, natural selection always favors individuals who never build and spread a reputation (i.e., q = 0) for any behavioral strategies, p. Note that this statement is also true when we assume more general behavioral strategies, that is, when individuals make decisions based not only on the opponent's reputation but also on their own reputation (see Methods)14,18. In summary, we show that, in the presence of the cost of reputation building, natural selection results in a society where no individual builds a reputation and thus indirect reciprocity never works.

To further explore the effect of the cost of reputation building in more complicated situations, we constructed an individual-based computer simulation model. Let us consider a population of n individuals. As in the seminal work on indirect reciprocity7, each player has a reputation score, s, that ranges from −5 to 5. At the beginning of each generation, which comprises m x n consecutive rounds, scores are reset to zero.

In each round, three individuals are chosen randomly from the population: one is a potential donor of help, another is a potential recipient of the help, and the third is an observer. A potential donor decides to either give help (cooperation) or to refuse help (defection). Cooperation confers a benefit, b, to the recipient while accruing a cost, c, to the donor (b > c > 0). Defection yields nothing to either person. Note that we assume that, with the probability ε (0 < ε ≪ 1), an individual who intends to cooperate fails to cooperate because of, for example, a lack of resources or a mistake, called an implementation error9,16,19. After this, the observer decides whether or not to update and spread the donor's reputation score (i.e., reputation building) with a cost cR > 0.

As in the analytical model, we assume all individuals in the population share the same moral assessment rule (social norm). We consider the following three rules. One is the simple, called SCORING7, in which the reputation score increases by one unit if a potential donor cooperates; it decreases by one unit if s/he defects. That is, cooperation and defection are judged as good and bad, respectively. Another rule is MILD (or sometimes called STANDING)11,16,20: the score increases if a donor defects against a bad individual (s < 0) or cooperates; it decreases otherwise. This rule incorporates the concept of justified defection7,11 and has been known to stabilize the indirect reciprocal cooperation9,16,18,20. The third rule is STERM (or sometimes called KANDORI)9,11,21: the score increases if a donor cooperates with a good individual (s > = 0) or defects against a bad individual; it decreases otherwise. This includes not only the concept of justified defection but also unjustified cooperation (i.e., cooperation with a bad individual is regarded as bad)11.

A donor's behavioral strategy is given by a number, k (k = −5 to 6): an individual with this strategy, k, cooperates if the score of the recipient is at least k. In other words, a high reputation score of an individual often implies a higher probability that others will cooperate with the individual. An observer's strategy is depicted by a number, 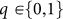Inline graphic: an individual with q = 1 (0) does (does not) update and spread the donor's reputation score based on the moral assessment rule. That is, each individual's heritable traits are k and q.

At the end of each generation, each individual leaves offspring depending on his/her fitness (i.e., natural selection). The fitness value is defined as the total payoff received during the generation (m × n rounds). Higher fitness implies a higher probability that the individual can leave offspring. We use the "binary tournament selection" procedure, a genetic algorithm, to select individuals22. In addition, mutation is introduced: with the small probability μ, each individual's strategy k and q changes to another value randomly.

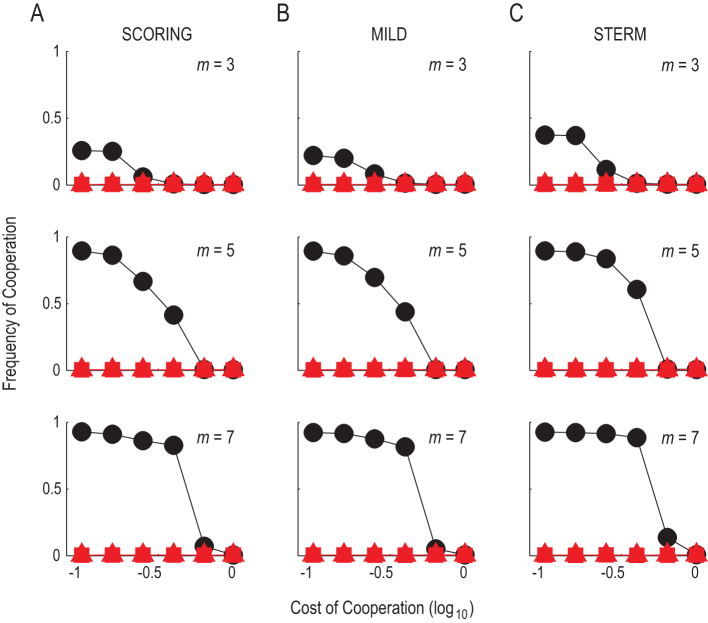
Consistent with the previous studies7,8, we find that, in the absence of cost of reputation building, the frequency of cooperation increases with the decrease in the cost-to-benefit ratio of cooperation and the increase in the number of rounds in a generation (see the black points in Fig. 1). This tendency is common to all the three moral assessment rules (compare the panels A vs. B vs. C in Fig. 1). This indicates that the evolution of indirect reciprocal cooperation becomes easy as the net benefit of cooperation and the number of interactions among individuals increase.

Figure 1. Effect of cost of reputation building, cR, on the evolution of cooperation.

Figure 1

Open in a new tab

Black points indicate the case without the cost of reputation building; red represents the case with the cost (triangles: cR = 0.1; squares: cR = 0.01; these symbols overlap). The frequency of cooperation at the 1,000th generation is plotted as a function of cost of cooperation, c (benefit of cooperation, b, is fixed at 1; population size n = 200; probability of implementation error ε = 0.05; mutation rate μ = 0.01; an individual's strategy at the first generation is determined randomly). Each point denotes the values averaged over 200 computer simulation runs. (A) Individuals use the moral assessment rule, SCORING. Top row: the average number of rounds for each individual in a generation, m, is 3; Middle row: m = 5; Bottom row: m = 7. (B) MILD. (C) STERM.

However, the presence of the cost of reputation building completely destroys indirect reciprocal cooperation regardless of the cost-to-benefit ratio of cooperation or moral assessment rules (see the red points in Fig. 1). Even when the amount of cost of reputation building is only 1% of the benefit of cooperation, the evolution of cooperation is impossible (red squares in Fig. 1). We also examined another case in which the reputation of a donor is built by the recipient instead of a third person/observer. That is, the recipient decides to or not to incur a cost of building the reputation of the donor. We confirm that, consistent with the original case, introducing the cost of reputation building makes it the evolution of indirect reciprocal cooperation impossible (see Suppl. Fig. S1).

We also investigated a situation in which an observer who does not build the donor's reputation can lose his/her own good reputation. In other words, individuals who do not incur a cost of reputation building can be judged as bad. We assume that, at each round, in addition to a donor, a recipient and an observer, one individual is selected as an observer of the observer, who we call a “second-order observer.” S/he decides whether or not to update and spread the observer's reputation score with a cost cR' > 0. A second-order observer's strategy is depicted by a number, 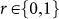Inline graphic: an individual with r = 1 (0) does (does not) build the observer's reputation. When a second-order observer's strategy is r = 1, the (first-order) observer's reputation score increases by one unit if s/he builds the donor's reputation; it decreases by one unit otherwise. The results of the computer simulation show that, consistent with the original case, natural selection never leads to indirectly reciprocal cooperation regardless of the cost-to-benefit ratio of cooperation or moral assessment rules (see the red points in Suppl. Fig. S2), except for the unrealistic case without the cost of reputation building for second-order observers (i.e., cR′ = 0; see the black points in Suppl. Fig. S2). This is because individuals building a reputation as a second-order observer (i.e., r = 1) are exploited by individuals with r = 0 for the cost, cR′ (see Suppl. Fig. S3).

These results together demonstrate that, as predicted by the analytical models, the evolution of cooperation based on indirect reciprocity is extremely vulnerable to the cost of reputation building in a complicated situation (e.g., a reputation score is 11-scale but not binary23).

Discussion

We have examined the effect of the cost of reputation building on the evolution of cooperation through indirect reciprocity. By analytical investigation and individual-based computer simulations, we have shown that the slight cost of reputation building completely destroys indirect reciprocal cooperation regardless of the cost-to-benefit ratio of cooperation or moral assessment rules.

In a broad sense, our results are closely related to the second-order free rider problem24,25, which asks "who incurs a cost to preserve social systems for the maintenance of cooperation?". A typical example is the evolution of altruistic punishment, which asks26,27,28 "who bears a cost of the punishment of defectors?". Imagine that there are three types of individuals: free riders (defectors), altruistic punishers (cooperators who punish free riders) and cooperators who do not punish, and that there is a cost to administering punishment. In this situation, although altruistic punishers punish free riders with a cost, cooperators never bear the cost. In other words, cooperators can "take a free ride" on punishers' punishment of free riders, the so-called second-order free ride. Natural selection therefore favors cooperators and leads to the extinction of altruistic punishers, and then, after the extinction of the punishers, defectors finally dominate the population of cooperators.

In a context of indirect reciprocity, it has been demonstrated that cooperation can evolve through indirect reciprocity given an appropriate reputation system7,11. However, little attention has been paid to the issue of who covers the costs of maintaining the reputation system. As shown in the present study, in the presence of the cost, the reputation system is no longer sustainable and thus indirect reciprocal cooperation vanishes. The present results shed light on the possibility that the second-order free rider problem is inherent in various contexts other than altruistic punishment.

One caveat to our conclusion is that other mechanisms may support the evolution of cognitive abilities to build reputations and thus indirect reciprocity. One candidate is multilevel (group) selection29,30,31. Suppose that individuals of a population are subdivided into groups and interact within these groups, and that individuals who build reputations are concentrated together within the same groups. Then, groups of individuals who build reputations can achieve high-level indirectly reciprocal cooperation and thus, despite the cost of reputation building, outperform the other groups of individuals who do not build reputations. Consistent with this conjecture, it has been demonstrated that, in the absence of costs of reputation building, multilevel selection supports the evolution of a moral assessment rule under which indirectly reciprocal cooperation is evolutionarily stable21.

Another candidate is network reciprocity5,32,33. In a typical setting considered in studies of network reciprocity, individuals of a population occupy the vertices of a graph and the edges determine who interacts with whom. That is, each individual plays a game only with her neighbors and mimics the most successful neighbor's strategy. In this setting, individuals who build reputations can form a cluster in which indirect reciprocity is established, and thus might be able to prevail in the population.

Moreover, it might be possible that building reputations is beneficial enough to overcome the cost in situations that differ from those considered in our study. Indeed it has been mathematically shown that, when individuals engage in several games, an evolutionary outcome of a single game cannot be predicted without assessing the structures of the other games34. How these mechanisms complement indirect reciprocity in the presence of the cost of reputation building will require further investigation.

Further, it is worth noting that indirectly reciprocal cooperation does not necessarily rely only on reputation building. For example, if the population is small enough, each individual can judge others' goodness by direct observation, instead of the indirect observation via reputation. Moreover, experimental studies on humans and rats demonstrated another type of indirect reciprocity: an individual is more likely to help anonymous others when s/he received help in previous interactions, compared with when s/he did not35,36,37. This type of reciprocity, called upstream indirect reciprocity, seems to be driven by a feeling of gratitude rather than reputation building. However, to date, few studies have provided theoretical explanations of the evolutionary origin of upstream indirect reciprocity38,39,40.

Humans' sociality is supported by their sophisticated cognitive abilities, e.g., language skills, which are biologically costly12,13. Despite the importance of the cost of intelligence in human evolution, little is known about the effects of this cost on the evolution of cooperation (but see references41,42). This study is, to our knowledge, the first to assess the relationship between the cost of high intelligence and the evolution of indirect reciprocal cooperation, highlighting the importance of considering the costs of high-level cognitive abilities in studies of the evolution of humans' and animals' social behavior.

Methods

Reputation dynamics in the basic analytical model

Here we show that the dynamics of the fraction of individuals among (p, q) strategists who have a good reputation, Gt(p, q), depends on p, but not on q.

We can consider various ways to update reputations, called moral assessment rules7,11,14,18. One way is that cooperation (defection) is simply regarded as good (bad) irrespective of the donor's or the opponent's reputation. Another way is to introduce the concept of justified defection: defection against a bad opponent is judged as good. Moreover, one might judge cooperation with a bad opponent as bad, which is the concept of unjustified cooperation. Taking these possibilities together, we assume that individuals in a community share the same moral assessment rule and they judge a donor's goodness based on the donor's own reputation and behavior and the opponent's reputation.

A moral assessment rule is then represented by an eight-dimensional vector, R = (RBDB, RBDG, RBCB, RBCG, RGDB, RGDG, RGCB, RGCG). The subscript letters indicate, from the left to the right, the donor's reputation, the donor's behavior and the opponent's reputation, respectively, and R Inline graphic [0, 1] denotes the probability that the donor's behavior is judged as good in each of the eight situations. For example, (0,0,1,1,0,0,1,1) indicates IMAGE SCORING43 in which cooperation (defection) is simply regarded as good (bad). Further, R*DB = 1 is consistent with the concept of justified defection, and R*CB = 0 reflects the concept of unjustified cooperation (* is a wild card).

At round t, consider the probabilities that: (1) a bad (p, q) strategist defects against a bad opponent, (1 − Gt(p, q)) (1 − pB) (1 − Gt); (2) a bad (p, q) strategist defects against a good opponent, (1 − Gt(p, q)) (1 − pG) Gt; (3) a bad (p, q) strategist cooperates with a bad opponent, (1 − Gt(p, q)) pB (1 − Gt); (4) a bad (p, q) strategist cooperates with a good opponent, (1 − Gt(p, q)) pG Gt; (5) a good (p, q) strategist defects against a bad opponent, Gt(p, q) (1 − pB) (1 − Gt); (6) a good (p, q) strategist defects against a good opponent, Gt(p, q) (1 − pG) Gt; (7) a good (p, q) strategist cooperates with a bad opponent, Gt(p, q) pB (1 − Gt); and (8) a good (p, q) strategist cooperates with a good opponent, Gt(p, q) pG Gt. These probabilities are represented by a vector, S. Since each component of S is a function of Gt(p, q) and p, we rewrite S as S[Gt(p, q), p].

Recall that the reputation of an individual is updated only when the observer decides to build that individual's reputation, the probability of which is 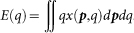Inline graphic. Hence, the fraction of individuals among (p*, q*) strategists whose reputation is good at round t+1 can be written as:

graphic file with name srep01435-m3.jpg

Given equation (4) and G1(p, q) = 1 for any (p, q), we can see that Gt+1(p*, q*) depends on p* but not q* for any moral assessment rules.

In conclusion, the fraction of individuals among (p, q) strategists who has a good reputation at round t is determined by p but not by q.

Extended analytical model

Here we assume that each individual makes decisions based not only on the opponent's reputation but also on his/her own reputation. In this case, a behavioral strategy is denoted by a four-dimensional vector, p = (pBB, pBG, pGB, pGG), where the left subscript letter denotes the focal individual's own reputation, the right denotes the opponent's reputation, and p represents the probability that s/he cooperates given his/her own reputation and that of the opponent.

Here, the average payoff of (p*, q*) strategists at round t can be calculated as:

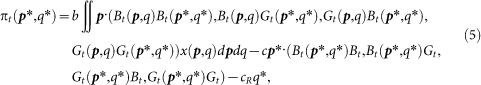graphic file with name srep01435-m4.jpg

where Bt = 1 − Gt denotes the fraction of individuals who have a bad reputation. In the same way as that in the basic model, we can show that the reputation dynamics Gt(p*, q*) depend on p* but not on q*. Hence, we can show that, given a value of p, individuals with q = 0 always get the highest payoff in each round, regardless of the cost-to-benefit ratio of cooperation (c/b), the amount of the cost of reputation building (cR > 0), or moral assessment rules. In other words, natural selection always favors individuals who never build and spread a reputation, and thus indirect reciprocity never works.

Author Contributions

S.S. and H.K. designed and performed the research; S.S. wrote the paper.

Supplementary Material

Supplementary Information

Supplementary Figures

srep01435-s1.pdf (620KB, pdf)

Acknowledgments

This research was partially supported by the Ministry of Education, Culture, Sports, Science and Technology and a Grant-in-Aid for JSPS Fellows, 2011–2013, #232648.

References

  1. Wedekind C. & Milinski M. Cooperation through image scoring in humans. Science 288, 850–852 (2000). [DOI] [PubMed] [Google Scholar]
  2. Milinski M., Semmann D., Bakker T. C. & Krambeck H. J. Cooperation through indirect reciprocity: image scoring or standing strategy? Proc Biol Sci 268, 2495–2501 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Axelrod R. & Hamilton W. D. The evolution of cooperation. Science 211, 1390–1396 (1981). [DOI] [PubMed] [Google Scholar]
  4. Fehr E. & Fischbacher U. The nature of human altruism. Nature 425, 785–791 (2003). [DOI] [PubMed] [Google Scholar]
  5. Nowak M. A. Five rules for the evolution of cooperation. Science 314, 1560–1563 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Suzuki S., Niki K., Fujisaki S. & Akiyama E. Neural basis of conditional cooperation. Social Cognitive and Affective Neuroscience 6, 338–347 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Nowak M. A. & Sigmund K. Evolution of indirect reciprocity. Nature 437, 1291–1298 (2005). [DOI] [PubMed] [Google Scholar]
  8. Nowak M. A. & Sigmund K. Evolution of indirect reciprocity by image scoring. Nature 393, 573–577 (1998). [DOI] [PubMed] [Google Scholar]
  9. Ohtsuki H. & Iwasa Y. Global analyses of evolutionary dynamics and exhaustive search for social norms that maintain cooperation by reputation. J Theor Biol 244, 518–531 (2007). [DOI] [PubMed] [Google Scholar]
  10. Suzuki S. & Akiyama E. Evolution of indirect reciprocity in groups of various sizes and comparison with direct reciprocity. J Theor Biol 245, 539–552 (2007). [DOI] [PubMed] [Google Scholar]
  11. Sigmund K. Moral assessment in indirect reciprocity. J Theor Biol 299, 25–30 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Brosnan S. F., Salwiczek L. & Bshary R. The interplay of cognition and cooperation. Philosophical Transactions of the Royal Society B: Biological Sciences 365, 2699–2710 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. McNally L., Brown S. P. & Jackson A. L. Cooperation and the evolution of intelligence. Proceedings of the Royal Society B: Biological Sciences 279, 3027–3034 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Ohtsuki H. & Iwasa Y. How should we define goodness?--reputation dynamics in indirect reciprocity. J Theor Biol 231, 107–120 (2004). [DOI] [PubMed] [Google Scholar]
  15. Takahashi N. & Mashima R. The importance of subjectivity in perceptual errors on the emergence of indirect reciprocity. J Theor Biol 243, 418–436 (2006). [DOI] [PubMed] [Google Scholar]
  16. Panchanathan K. & Boyd R. A tale of two defectors: the importance of standing for evolution of indirect reciprocity. J Theor Biol 224, 115–126 (2003). [DOI] [PubMed] [Google Scholar]
  17. Brandt H. & Sigmund K. The good, the bad and the discriminator--errors in direct and indirect reciprocity. J Theor Biol 239, 183–194 (2006). [DOI] [PubMed] [Google Scholar]
  18. Brandt H. & Sigmund K. The logic of reprobation: assessment and action rules for indirect reciprocation. J Theor Biol 231, 475–486 (2004). [DOI] [PubMed] [Google Scholar]
  19. Fishman M. A. Indirect reciprocity among imperfect individuals. J Theor Biol 225, 285–292 (2003). [DOI] [PubMed] [Google Scholar]
  20. Leimar O. & Hammerstein P. Evolution of cooperation through indirect reciprocity. Proc Biol Sci 268, 745–753 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Pacheco J. M., Santos F. C. & Chalub F. A. C. C. Stern-judging: A simple, successful norm which promotes cooperation under indirect reciprocity. PLoS Comput Biol 2, e178 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Suzuki S. & Akiyama E. Reputation and the evolution of cooperation in sizable groups. Proc Biol Sci 272, 1373–1377 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Tanabe S., Suzuki H. & Masuda N. Indirect reciprocity with trinary reputations. J Theor Biol 317C, 338–347 (2012). [DOI] [PubMed] [Google Scholar]
  24. Fehr E. Human behaviour: don't lose your reputation. Nature 432, 449–450 (2004). [DOI] [PubMed] [Google Scholar]
  25. Panchanathan K. & Boyd R. Indirect reciprocity can stabilize cooperation without the second-order free rider problem. Nature 432, 499–502 (2004). [DOI] [PubMed] [Google Scholar]
  26. Boyd R., Gintis H., Bowles S. & Richerson P. J. The evolution of altruistic punishment. Proc Natl Acad Sci USA 100, 3531–3535 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Hauert C., Traulsen A., Brandt H., Nowak M. A. & Sigmund K. Via freedom to coercion: the emergence of costly punishment. Science 316, 1905–1907 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Nakamaru M. & Iwasa Y. The coevolution of altruism and punishment: role of the selfish punisher. J Theor Biol 240, 475–488 (2006). [DOI] [PubMed] [Google Scholar]
  29. Traulsen A. & Nowak M. A. Evolution of cooperation by multilevel selection. Proc Natl Acad Sci USA 103, 10952–10955 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Boyd R. & Richerson P. J. Group beneficial norms can spread rapidly in a structured population. J Theor Biol 215, 287–296 (2002). [DOI] [PubMed] [Google Scholar]
  31. Bowles S., Choi J.-K. & Hopfensitz A. The co-evolution of individual behaviors and social institutions. J Theor Biol 223, 135–147 (2003). [DOI] [PubMed] [Google Scholar]
  32. Ohtsuki H., Hauert C., Lieberman E. & Nowak M. A. A simple rule for the evolution of cooperation on graphs and social networks. Nature 441, 502–505 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Santos F. C., Pacheco J. M. & Lenaerts T. Evolutionary dynamics of social dilemmas in structured heterogeneous populations. Proc Natl Acad Sci USA 103, 3490–3494 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Hashimoto K. Unpredictability induced by unfocused games in evolutionary game dynamics. J Theor Biol 241, 669–675 (2006). [DOI] [PubMed] [Google Scholar]
  35. Greiner B. & Vittoria Levati M. Indirect reciprocity in cyclical networks. Journal of Economic Psychology 26, 711–731 (2005). [Google Scholar]
  36. Stanca L. Measuring indirect reciprocity: Whose back do we scratch? Journal of Economic Psychology 30, 190–202 (2009). [Google Scholar]
  37. Rutte C. & Taborsky M. Generalized reciprocity in rats. Plos Biol 5, e196 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Pfeiffer T., Rutte C., Killingback T., Taborsky M. & Bonhoeffer S. Evolution of cooperation by generalized reciprocity. Proc Biol Sci 272, 1115–1120 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Nowak M. A. & Roch S. Upstream reciprocity and the evolution of gratitude. Proc Biol Sci 274, 605–609 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Iwagami A. & Masuda N. Upstream reciprocity in heterogeneous networks. J Theor Biol 265, 297–305 (2010). [DOI] [PubMed] [Google Scholar]
  41. Binmore K. & Samuelson L. Evolutionary stability in repeated games played by finite automata. Journal of Economic Theory (1992). [Google Scholar]
  42. Imhof L., Fudenberg D. & Nowak M. Evolutionary cycles of cooperation and defection. Proc Natl Acad Sci USA 102, 10797 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Nowak M. & Sigmund K. The dynamics of indirect reciprocity. J Theor Biol 194, 561–574 (1998). [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Figures

srep01435-s1.pdf (620KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES