Breaking the Diffraction Barrier Using Fluorescence Emission Difference Microscopy

Abstract

We propose a novel physical mechanism for breaking the diffraction barrier in the far field. Termed fluorescence emission difference microscopy (FED), our approach is based on the intensity difference between two differently acquired images. When fluorescence saturation is applied, the resolving ability of FED can be further enhanced. A detailed theoretical analysis and a series of simulation tests are performed. The validity of FED in practical use is demonstrated by experiments on fluorescent nanoparticles and biological cells in which a spatial resolution of <λ/4 is achieved. Featuring the potential to realize a high imaging speed, this approach may be widely applied in nanoscale investigations.

Because of diffraction in the imaging system, the lateral resolution of conventional optical microscopes was limited to about half the illumination wavelength until the past two decades¹. Since the 1990s, several methods of breaking the diffraction limit have been proposed, including stochastic optical reconstruction microscopy (STORM)², photoactivated localization microscopy (PALM)³, stimulated emission depletion microscopy (STED)⁴, structured illumination microscopy (SIM)⁵,⁶, digital image processing⁷,⁸, and total-internal-reflection microscopy based on a nanostructured substrate⁹. Among them, STORM, PALM, STED, and SIM are the most widely applied. They have all been demonstrated to achieve super-resolution in the far field¹⁰,¹¹,¹²,¹³, but each still has limitations. STORM and PALM have long been hampered by limited imaging speed. In their imaging process, thousands of frames must be acquired, so reconstructing the super-resolution image takes a long time. Although the imaging speed of STORM was recently improved to ~3 s per image¹⁴,¹⁵, it is still too low for live-cell investigation. Moreover, the localization accuracy of these two methods is sharply limited when imaging rotation-impaired fluorophores of unknown random orientation, which restricts the attainable resolution¹⁶. By applying a second beam to spatially narrow the potential fluorescence through stimulated emission, STED can realize super-resolution imaging at a relatively high speed. However, the fluorescent dyes available for STED microscopy are still limited because both the excitation and emission spectra have to be matched with the given excitation and depletion wavelength. SIM can also be used to break the diffraction barrier. By periodically patterning the excitation light, it shifts the high-frequency information from the sample into a lower-frequency detection range. However, because the periodicity of the illumination pattern is limited by diffraction, SIM can extend the resolution only by a factor of 2⁵. In addition, SIM requires an expensive setup to realize video-rate imaging speeds in practice. Although the resolution of SIM can be further improved in the case of saturated fluorescence, the so-called SSIM¹⁰,¹⁷ is also costly and difficult to conduct. Moreover, the fluorescence in SSIM easily becomes photobleached and will cause phototoxicity owing to the sample's long-duration exposure to the high-power-density illumination beam. Hence, a continuing effort is needed to develop new techniques that further exploit the potential of optical microscopy for super-resolution imaging.

Subtractive imaging¹⁸,¹⁹ can provide new possibilities for improving the spatial resolution. In this method, the spatial resolution is enhanced by the subtraction of confocal signals taken at different pinhole sizes. However, the signal-to-noise ratio (SNR) is relatively low. The reason is that the confocal signals taken at different pinhole sizes are excited by the same illumination beam. As a result, after subtraction, the signals used to construct the final super-resolution image are those emitted at the periphery of the excitation spot. However, the real effective signals, which are emitted at the center of the excitation spot, have been subtracted during the process. Recently, another full-field microscope based on image subtraction has been proposed which can improve the axial resolution while maintaining the lateral one²⁰. Unfortunately, its resolution enhancement can be achieved only in the near field.

Here, we propose a novel imaging method, fluorescence emission difference microscopy (FED), that provides a new way to perform investigations at the nanoscale. Two differently modulated beams are used to illuminate the sample, thus realizing two scanning images. After subtraction, the resulting difference image features super-resolution together with a comparatively high SNR.

Results

In FED, two different scanning images must be processed. One is the conventional confocal image acquired when the sample is illuminated by a solid excitation pattern; the other, the negative confocal image, is obtained when the sample is illuminated by a doughnut-shaped excitation pattern that can be generated by modulating the illumination beam with a vortex 0–2 phase plate. Both images are detected by the same pinhole, which works as a spatial filter. The final super-resolution FED image is constructed by intensity subtraction of these two images,

where 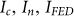are the normalized intensity distributions of the confocal, negative confocal, and FED images, respectively, and is the subtractive factor. Some negative intensity values will inevitably appear in the difference image after subtraction. We simply exclude these negative intensities from the image to improve the imaging quality²¹.

In the processing of the confocal image, the point-spread function (PSF) can be calculated as²²

where 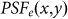denotes the PSF for the objective lens used to excite the fluorescence, which is shown in Fig. 1(a), and 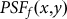denotes the PSF for the objective lens evaluated at the fluorescence wavelength. Further, is the transmission function of the pinhole. Figure 1(c) shows the resulting 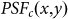calculated by Eq. 2. Being modulated by a vortex 0–2 phase plate, the PSF for the excitation pattern is doughnut-shaped, as shown in Fig. 1(b). After convolution with 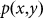, the PSF for negative confocal imaging, 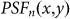, also forms a doughnut shape, as shown in Fig. 1(d). By subtracting from 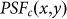using Eq. 1, the FED PSF, 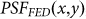, is obtained, as shown in Fig. 1(e).

Figure 1. Illustration of FED theory.

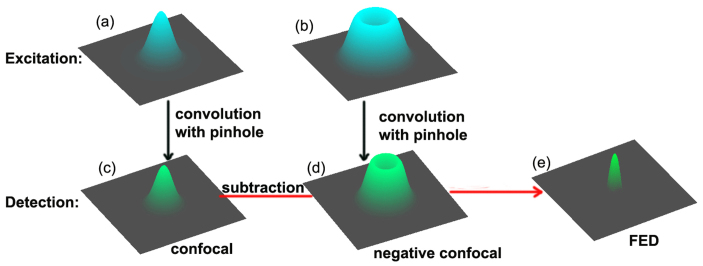
(a) PSF of confocal excitation pattern. (b) PSF of negative excitation pattern. (c) PSF for confocal imaging. (d) PSF for negative confocal imaging. (e) PSF of FED image.

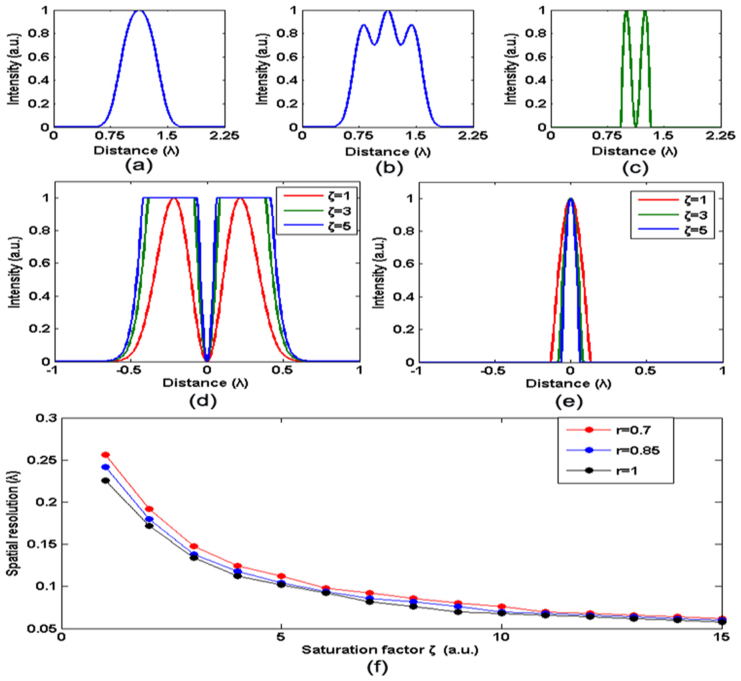
To demonstrate the resolving ability of FED, we assume that two fluorescent particles are separated by a distance of λ/4 and calculate the corresponding FED image by simulation. Here, is the wavelength of the illumination beam. The normalized line intensity profiles of the corresponding confocal, negative confocal, and FED images are shown in Fig. 2(a), (b), and (c), respectively. As expected, the confocal line intensity profile features only one peak, which indicates a failure to resolve these two particles. In contrast, in the FED image, we can clearly distinguish two intensity peaks in the line profile. This result theoretically demonstrates that a spatial resolution of <λ/4, which is far beyond the diffraction barrier, can be realized by FED.

Figure 2. Simulated FED imaging.

Normalized line intensity profiles of the (a) confocal, (b) negative confocal, and (c) FED images for two nanoparticles separated by λ/4. Line profiles of PSF for (d) negative confocal and (e) FED imaging under different saturation factors: 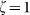(red curve), 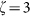(green curve), and 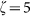(blue curve). (f) Attainable resolution of FED, in units of illumination beam wavelength, as a function of the saturation factor under different subtractive factors: r = 0.7 (red curve), r = 0.85 (blue curve), and r = 1 (black curve). All the simulated results are presented with an objective lens of NA = 1.4.

The resolving ability of FED can be further improved when the fluorescence saturation is considered. According to the theory of fluorescence, on average, each fluorophore molecule can emit at most one photon per lifetime ¹⁰. Hence, when it is illuminated by beam intensities above the threshold 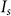, its fluorescence emission will become saturated and respond nonlinearly to the excitation intensity²³. In our saturated FED approach, only negative confocal imaging is performed in the fluorescence saturated condition. Confocal imaging is still conducted in the non-saturated case. Thus, the PSF for negative confocal microscopy should be rewritten as

Here, 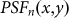denotes the PSF for negative confocal microscopy in the non-saturated case, and is the saturation factor, which is defined as 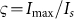, where 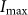is the peak intensity of the excitation beam; 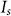is the threshold intensity. Further, the resulting PSF for the saturated FED can be expressed as

Line profiles of the PSFs for negative confocal and FED imaging under different saturation factors are shown in Fig. 2(d) and (e), respectively. When 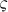increases, the FWHM of the intensity profile in the FED image decreases. Therefore, better resolution can be obtained when the fluorescence emission in negative confocal imaging is saturated by a high-intensity illumination beam.

The attainable resolution of FED can be estimated by calculating the FED intensity distribution of two closely placed fluorescent nanoparticles and using the Rayleigh criterion²⁴ to evaluate whether the two intensity peaks can be distinguished. Figure 2(f) and the data in Supplementary Table S1 show the spatial resolutions of FED under several conditions. Note that the value of the subtractive factor will also affect the performance of FED. A higher could suppress more noise, but at the same time, it may also introduce artifacts into the image. Hence, the value of should be set to maintain a balance between the achievable resolution and the appearance of negative intensities¹⁹. In practice, after obtaining the corresponding confocal and negative confocal image, we simply tune the value of in the range between 0.7 and 1 (this is an empirical range) to achieve the highest-quality difference image.

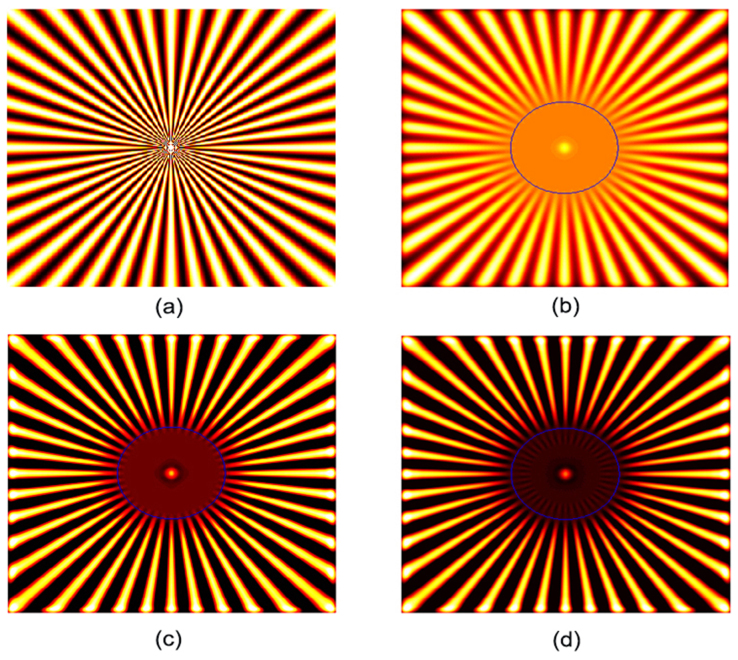
Note that the resolution estimation method proposed above corresponds best to sparse samples. The resolving ability of FED will deteriorate slightly when imaging high-density samples such as some realistic biological cells. To estimate the attainable spatial resolution in such cases, we performed a simulation test on a spoke-like sample²⁵. This sample is widely used because the resolution of an imaging technique can be assessed very simply by measuring the radius of a circle delimiting the ‘unresolved’ central area and the ‘resolved’ peripheral area in the corresponding image. The results shown in Fig. 3 illustrate that while the features inside the region indicated by the blue circle cannot be discerned in the confocal image, some features inside the same region can be distinguished in the FED image, which indicates enhanced resolution. Moreover, as expected, for saturated FED, further details inside the blue circle were clearly resolved. Hence, FED is feasible for the nanoscopy of those high-density samples as well.

Figure 3. Simulated results for test sample.

(a) Test sample. Region size: 8 μm by 8 μm, pixel size: 20 nm. (b) Confocal image. (c) FED image with subtractive factor r = 0.7. (d) Saturated FED image with subtractive factor r = 0.7 (ζ = 2).

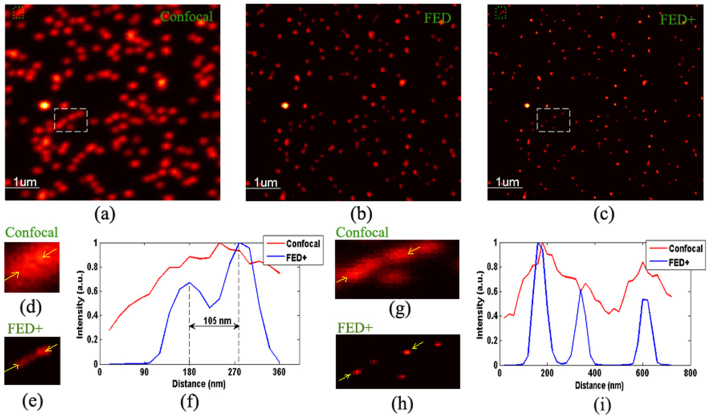
The performance of FED in practice was tested by imaging fluorescent nanoparticles (100 nm, yellow-green FluoSpheres, Molecular Probes). The illumination beams were provided by pulsed laser diodes at a wavelength of 488 nm. The confocal and FED images are shown in Fig. 4(a) and (b), respectively. Using the Richardson–Lucy algorithm to perform deconvolution of the FED image, we obtain the FED+ image, as shown in Fig. 4(c). Fig. 4(d) and (e) are magnified views of the regions indicated by green boxes in Fig. 4(a) and (c), respectively. The intensity profile along the line indicated by yellow arrows in Fig. 4(d) clearly shows that two nanoparticles separated by a distance of 105 nm can be distinguished, which implies that a resolving ability of ~λ/4.6 has been achieved. However, the same two nanoparticles appear together in the confocal image. Hence, the resolution is substantially enhanced by FED. A comparison of Fig. 4(g) and (h), which are magnified views of the data indicated by white boxes in Fig. 4(a) and (c), respectively, further demonstrates the superior resolving power of FED over confocal microscopy. Figure 4(i) shows that three intensity peaks were clearly resolved by FED, but these three peaks overlapped in the confocal image and cannot be distinguished.

Figure 4. Fluorescent nanoparticle imaging by FED.

(a) Confocal image. (b) FED image with subtractive factor r = 0.75. (c) FED+ image. (d) Magnified view of data indicated by green box in (a). (e) Magnified view of data indicated by green box in (c). (f) Normalized intensity profiles along lines indicated by yellow arrows in (d) and (e). (g) Magnified view of data indicated by white box in (a). (h) Magnified view of data indicated by white box in (c). (i) Normalized intensity profiles along line indicated by yellow arrows in (g) and (h).

In addition to better resolution, the FED image also features a higher SNR. This can be explained by the process of FED imaging. The PSF for the confocal image is solid, whereas that for the negative confocal image is doughnut-shaped (hollow). Hence, when the FED image is generated, those fluorescence signals emitted at the periphery of the excitation pattern, which can be considered noise, were subtracted, improving the SNR. After deconvolution using the Richardson–Lucy algorithm, the SNR of the FED images can be slightly improved even further, as shown in Fig. 4.

Next, we show the imaging results of biological cells labelled with green fluorescent protein (GFP). Two different regions of a sample of Human Embryonic Kidney 293 (HEK293) cells were used in the imaging. The HEK293 cells that were stably expressed with GFP-LC3 throughout the cytoplasm were grown on sterile glass coverslips and fixed with 4% formaldehyde. The illumination beams were also provided by pulsed laser diodes at a wavelength of 488 nm. The resulting confocal and FED images are shown in Fig. 5. By comparing the FED images with their confocal counterparts, we demonstrate a considerable improvement in resolution and SNR when these biological samples were imaged by FED. Many features that correspond to real structures in the sample that were completely hidden under confocal observation were disclosed by FED imaging.

Figure 5. Experimental results of biological cells imaged by FED.

(a) Confocal image of region 1 in HEK293. (b) Confocal image of region 2 in HEK293. (c) FED image of region 1 in HEK293 with subtractive factor r = 0.95. (d) FED image of region 2 in HEK293 with subtractive factor r = 0.9.

Discussion

In our experiment, the sample was scanned laterally by a nano-positioning stage. However, spatial scanning can also be performed by a resonant mirror because the required dwell time per pixel in FED can be relatively short. In that case, a video rate imaging speed can be achieved; this is ample for live-cell investigation. Moreover, a high scanning speed enables a much smaller dwell time per pixel in FED compared with SSIM, which greatly reduces the possibility of photobleaching and phototoxicity.

In this paper, the confocal and negative confocal images are subtracted frame by frame while the experiment is performed. More specifically, the fluorescent sample is first scanned continuously by the solid illumination pattern to obtain the confocal image. Next, the illumination beam is modulated to form a doughnut-shaped pattern and scans the sample continuously again to obtain the negative confocal image. During this process, an image mismatch may arise owing to sample drift. As a result, the positions of the scanning points in the two images are not strictly the same, which affects the quality of the resulting image. This problem may be solved by using a point-by-point subtraction scheme. After detecting the fluorescence excited by the solid illumination pattern at a scanning point, the illumination beam is modulated to form the doughnut-shaped pattern, which excites fluorescence at the same scanning point. Then, the illumination pattern is converted back to the solid one and moved to the next scanning point. In this scheme, the time interval between the confocal and negative confocal detection on the same pixel is equal to the scanning dwell time. As discussed above, when scanning is performed by the resonant mirror, the dwell time on each pixel can be very short (~0.3 μs). Hence, the sample drift during this period can be considered negligible.

The blinking of the fluorescence may affect the quality of the FED image because it will cause a single molecule to emit fluorescence of different intensities in the confocal scanning and negative confocal scanning. The situation is most serious when the sample is scanned by a high-speed resonant mirror and the point-by-point subtraction scheme is implemented. In that case, the time interval between the confocal and negative confocal imaging on the same pixel will be comparable to the fluorescence fluctuation period. Hence, for video rate scanning, it is preferable to choose fluorescent dyes that blink slowly.

In summary, the novel nanoscopy FED was proposed. On the basis of the intensity differences between two differently acquired images, FED can achieve a resolution of <λ/4 in the far field, which is well beyond the conventional diffraction barrier. Moreover, its resolving ability can be further improved when the fluorescence emission of the sample in negative confocal imaging is saturated. We believe this method can be widely applied in nanoscale investigations.

Methods

Calculations of the PSF in FED

According to the theory of FED, its PSF can be calculated as

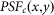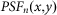where and denote the PSFs for confocal and negative confocal imaging, respectively, and represents the subtractive factor.

The PSF for confocal microscopy, , is given by

where 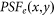denotes the PSF for the objective lens used to excite the fluorescence. In other words, it is the normalized intensity distribution of the excitation pattern on the sample. 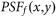denotes the PSF for the objective lens evaluated at the fluorescence wavelength, and p(x,y) is the transmission function of the pinhole. For simplicity, we ignore the wavelength difference between the excitation and fluorescence beams and assume an infinitely small pinhole. Hence, 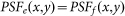, and . Then the PSF for confocal microscopy can be written as

Similarly, the PSF for negative confocal imaging can be calculated as

where is the normalized intensity distribution of the hollow excitation pattern on the sample.

The electric field distribution on the sample can be calculated using the generalized Debye integral as

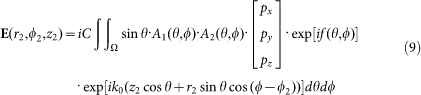where 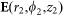is the electric field vector at (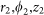) expressed in cylindrical coordinates whose origin is located at the ideal focal point of the objective lens, 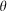is the angle between the ray direction and the optical axis, 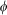is the azimuthal angle, C is the normalized constant, 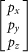is a matrix unit vector about the polarization of the incident beam, 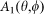is the amplitude function of the incident light, 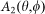denotes the wavefront aberration function of the objective lens, and 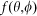is the phase modulation function for the incident beam. In the confocal case, 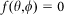, whereas in the negative confocal case, where the illumination beam is phase-modulated by a vortex 0–2 phase plate, .

Finally, the PSF for FED can be calculated using Eqs. (5), (7), (8), and (9).

Estimation of the attainable resolution of FED

In this paper, the resolution is defined as the smallest distance at which two fluorescent nanoparticles can be distinguished. To estimate this, we assume that two nanoparticles are placed close to each other on the X axis separated by a distance of 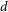and are imaged by FED. In this case, the intensity distribution of the corresponding confocal image, , will be

Here, 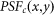denotes the PSF for confocal imaging.

Similarly, the intensity distribution of the corresponding negative confocal image, 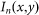, can be written as

where 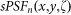denotes the PSF for negative confocal imaging under different saturation factors. Note that in the non-saturated case, can also be written as .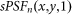

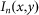Then, the intensity distribution of the resulting FED image, , can be obtained by subtracting from .

We use the Rayleigh criterion to evaluate whether the two intensity peaks in can be distinguished. According to the Rayleigh criterion, two peaks can be resolved when the minimum intensity between them is less than 73.5% of the peak intensity. In FED, when the distance 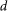between the two nanoparticles decreases, the two intensity peaks in 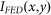will move closer together, and the minimum intensity between them will surely increase. When the minimum intensity value exceeds the Rayleigh threshold, these two peaks can no longer be distinguished. Hence, the attainable resolution of FED can be determined.

In the simulation, we changed the value of 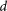continuously in 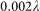steps and calculated the resulting 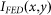. Changing the values of and will also affect the attainable resolution. Here, we simulated the conditions when r = 0.7, r = 0.85, and r = 1, and the value of changes from 1 to 15 with a resolution of 1.

Imaging setup

Supplementary Fig. S1 shows the setup of our FED system. Two differently modulated beams, beam1 and beam2, which have the same wavelength of 488 nm, are used as the illumination beams. In the first half-period of the imaging time T, only beam1 works, whereas in the second half-period, beam1 is switched off, and only beam2 works. The modulation frequency is set to twice the imaging speed. When beam1 is present, a polarizer (polar1) is used to convert it into a linearly polarized beam. After being reflected by a mirror and passing through a polarization beam splitter (B. Halle GmbH, Berlin, Germany), beam1 is reflected by a dichroic mirror (Di02-R488-25 × 36, Semrock) and circularly polarized by a quarter-wave plate. Then, beam1 is focused onto the sample through an objective lens (HCX PL APO 100×/1.40–0.7 Oil, Leica Microsystems, Germany) and forms a solid focal spot. The fluorescence excited by beam1 is collected by the same objective lens and passes through the dichroic mirror to separate it from beam1. Next, the fluorescence beam is further cleaned up by a bandpass filter (FF03-525/50-25, Semrock) before being focused into a multimode optical fiber (M31L02, Thorlabs), which serves as a confocal pinhole. The fiber is attached to an avalanche photodiode (SPCM-AQR-16-FC, PerkinElmer) which detects the intensity of the fluorescence beam. The detected fluorescence data are processed by a counting module (PicoHarp 300, PicoQuant GmbH, Germany) and saved to a PC. The sample is spatially scanned by a nano-positioning stage (P-734.2, Physik Instrumente GmbH & Co., Germany). In this way, the confocal image is obtained. In the beam2 case, a vortex 0–2π phase plate (VPP-A1, RPC Photonics, USA) is inserted into the optical path. As a result, after passing through the objective lens, beam2 forms a doughnut-shaped hollow focal spot on the sample, realizing negative confocal imaging. The resulting fluorescence is detected as in the beam1 case. Before imaging, calibration is necessary to ensure that both beam1 and beam2 illuminate the same position on the sample. The acquired data are processed and analysed by software we developed (Supplementary Fig. S2).

Calibration of the FED system

A calibration that produces both the solid and doughnut-shaped light patterns at the same point on the sample is essential before imaging to ensure the quality of the resulting FED images. In this paper, calibration is achieved by imaging a single fluorescent nanoparticle. After obtaining the corresponding confocal and negative confocal images (Supplementary Fig. 3), we fitted their intensity distributions with a Gaussian function, thus determining the central coordinates of these two illumination patterns. By determining the difference between these two central coordinates, we can easily estimate the lateral displacement between the illumination beams and adjust it by tuning the position and orientation of the reflecting mirror in the setup.

It is obviously much simpler to calibrate the FED setup than a STED system because in STED, calibration can be done only by imaging metal nanoparticles, so several optical elements in the imaging system, such as the bandpass filter and dichroic mirror, have to be removed or replaced during calibration. For FED, no optical elements need to be changed.

Author Contributions

C.K., X.H. and X.L. conceived and designed the study. S.L. and X.H. performed the theoretical studies and simulations. C.K., Z.G. and J.G. performed the experiments. W.L. prepared the biological samples. C.K., S.L. and Y.W. analysed the data. S.L., C.K., X.H. and H.L. wrote the manuscript. All authors discussed the conceptual and practical implications of the method at all stages.

Supplementary Material

Supplementary Information

supplementary file