Image Charge Method for Reaction Fields in a Hybrid Ion-Channel Model

Abstract

A multiple-image method is proposed to approximate the reaction-field potential of a source charge inside a finite length cylinder due to the electric polarization of the surrounding membrane and bulk water. When applied to a hybrid ion-channel model, this method allows a fast and accurate treatment of the electrostatic interactions of protein with membrane and solvent. To treat the channel/membrane interface boundary conditions of the electric potential, an optimization approach is used to derive image charges by fitting the reaction-field potential expressed in terms of cylindric harmonics. Meanwhile, additional image charges are introduced to satisfy the boundary conditions at the planar membrane interfaces. In the end, we convert the electrostatic interaction problem in a complex inhomogeneous system of ion channel/membrane/water into one in a homogeneous free space embedded with discrete charges (the source charge and image charges). The accuracy of this method is then validated numerically in calculating the solvation self-energy of a point charge.

1 Introduction

Biological ion channels, which play a central role in controlling the appropriate electrostatic properties across the cell membrane [10, 14], are of interest in many areas of research such as neuroscience, cell biology, and biomedical science. To study the structural and functional properties of ion channels by dynamics simulations at the atomic scale, it is important to develop fast and accurate computational models [20, 30, 33] for treating long-ranged electrostatic interactions, in particular, to reflect the influence of the solvent and membrane.

Models employing explicit lipid and solvent molecules are impractical in many cases for large simulation systems. Implicit continuum methods (the Poisson-Boltzmann theory) provide a reasonable approximation of the electrostatic polarization effect of solvent on the structures and interactions of biomolecules in solution. For instance, the approaches [17, 19, 32, 34] based on the generalized Born theory are widely adopted in practical simulations. Hybrid explicit/implicit solvent models [28, 38] have attracted great attention for molecular simulations in aqueous solutions, which seek to take advantage of both the accuracy of explicit all-atom approaches [7, 9, 26] and the reduced cost of implicit ones [11, 15, 25, 35]. Typically, the hybrid models truncate the target system by a fixed volume which includes the solute and some explicit solvent molecules, and treat the outside solvent as a continuum medium. The benefits of such a treatment are several-fold. The primary benefit over explicit methods is the greatly reduced system size with only a small number of explicit solvent molecules to be simulated. Second, the artificial periodicity associated with most of explicit methods is avoided. Further, as the number of explicit waters is flexible, the dielectric boundary can be selected as of a regular shape, and thus analytical-based algorithms [3, 4, 36, 39] can be developed to speed up the calculations.

In the presence of a membrane, such as in the simulation of a protein ion channel embedded in a membrane lipid bilayer, however, it is challenging to develop analytical-based algorithms for the hybrid model due to the dielectric inhomogeneity of the medium. As schematically shown in Fig. 1, a hybrid ion-channel model uses a cylindrical cavity as the explicit region, which includes the protein, ions, waters, and a portion of membrane. Outside the cavity, the membrane and bulk water are separated by two parallel planes, and characterized by dielectric permittivities ε_m and ε_w, respectively. The exact solution of this model is very difficult, and a fast and accurate approximation has to be developed. It is with this purpose in mind, we will present in this paper an image charge method to calculate the reaction field for a point charge within a finite length cylindrical cavity. Our novel technique converts the potential problem in an inhomogeneous system to that in a homogeneous system with a cluster of point charges, which in turn can be handled by techniques such as Fast Multipole Methods (FMMs) [5, 13, 24, 41] for achieving linear-scaling computational cost.

Figure 1.

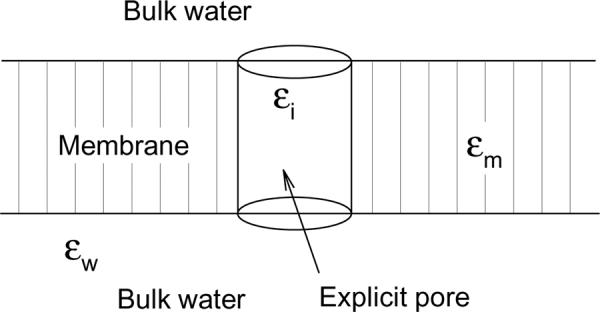
Schematic illustration of an ion-channel model. The molecules inside the cylindrical pore are treated explicitly at the atomic scale, while outside the pore the membrane and water are treated as homogeneous media, characterized by dielectric constants ε_m and ε_w, respectively.

Image methods, which represent the reaction field of a point charge due to the surrounding medium by some image charges, have been widely studied in the potential theory for various shapes of dielectric or conducting materials [23, 31]. In molecular simulations, the single image methods of Friedman [12], and Abagyan and Totrov [1] are often employed with spherical cavities. More accurate methods include the multiple image methods [4, 8, 21, 39], developed recently by representing the exact line image [22, 27, 42] by discrete charges using numerical quadratures. However, the analytical derivation for image approximation in a cylinder remains an open problem. In this paper, multiple images for the case of a finite cylindrical cavity are constructed by solving an optimization problem. Specifically, the charge strengths and locations of the images are obtained by minimizing the error of the reaction-field potentials between the exact solution and the image-based representation. This approach is an extension of the least-square image charge method for a three-layer sphere model [29], though it is more complex for the cylinder case as the locations of image charges are unknown, and thus the optimization problem becomes nonlinear.

The organization of this paper is as follows. For an infinite cylinder, the exact series solution in terms of cylindrical harmonics was recently derived [6]. We start with an overview of this solution in Section 2. In Section 3, we develop a method to approximate the exact solution by image point charges, and then extend it to solve the hybrid ion-channel model. In Section 4, numerical tests are performed to show the accuracy of image charge approximations. In Section 5, concluding remarks are made.

2 Cylindrical harmonic expansion

Let us first consider a point charge, q, located at position r_s inside an infinite cylinder of radius a, surrounded by a continuum dielectric. The cylindrical surface Γ separates the space into two regions Ω_i and Ω_m, characterized by dielectric permittivities ε_i and ε_m, respectively. The electrostatic potential Φ for the system satisfies the Poisson equation, which can be written in the cylindrical coordinate system r = (ρ, φ,z) as:

$$\frac{{\partial }^2\Phi }{\partial {\rho }^2}+\frac{1}{\rho }\frac{\partial \Phi }{\partial \rho }+\frac{1}{{\rho }^2}\frac{{\partial }^2\Phi }{\partial {\phi }^2}+\frac{{\partial }^2\Phi }{\partial z^2}=-\frac{4\pi q}{{\epsilon }_{\mathrm{i}}}\delta (\mathbf{r}-{\mathbf{r}}_s),$$ (2.1)

and boundary conditions at the interface Γ from the continuities of the potential and the normal component of the dielectric displacement:

$${\Phi }_{\mathrm{i}}={\Phi }_{\mathrm{m}},\text{and}{\epsilon }_{\mathrm{i}}\frac{\partial {\Phi }_{\mathrm{i}}}{\partial \rho }={\epsilon }_{\mathrm{m}}\frac{\partial {\Phi }_{\mathrm{m}}}{\partial \rho },\text{for}\rho =a.$$ (2.2)

The potential Φ_i inside the cylinder can be rewritten as a sum of a Coulombic contribution Φ_coul(r) = q/ε_i|r−r_s| and a reaction potential Φ_rf which is a harmonic function. The Coulombic potential can be expanded in terms of cylindrical harmonics [18], for ρ > ρ_s,

$${\Phi }_{\text{coul}}\left(\mathbf{r}\right)={\int }_0^{\infty }\mathit{dk}\cos k(z-z_s)\sum _{m=0}^{\infty }\frac{(4-2{\delta }_{m0})q}{\pi {\epsilon }_{\mathrm{i}}}{I}_m\left(k{\rho }_s\right)K_m\left(k\rho \right)\cos m(\phi -{\phi }_s),$$ (2.3)

where δ_m0 is the Kronecker delta function, I_m and K_m are the modified Bessel functions of the first and second kind [2]. Also, because the reaction potential Φ_rf and the potential in region Ω_m, Φ_m, satisfy a Laplace equation, their solutions can be written as series of cylindrical harmonics,

$${\Phi }_{\text{rf}}\left(\mathbf{r}\right)={\int }_0^{\infty }\mathit{dk}\cos k(z-z_s)\sum _{m=0}^{\infty }{A}_m\left(k\right)I_m\left(k\rho \right)\cos m(\phi -{\phi }_s),$$ (2.4a)

$${\Phi }_{\text{m}}\left(\mathbf{r}\right)={\int }_0^{\infty }\mathit{dk}\cos k(z-z_s)\sum _{m=0}^{\infty }{B}_m\left(k\right)K_m\left(k\rho \right)\cos m(\phi -{\phi }_s),$$ (2.4b)

respectively, where A_m(k) and B_m(k) are unknowns to be determined by the boundary conditions. By using the orthogonality of the cylindrical harmonics, the boundary conditions (2.2) lead us to a linear system of two equations for each order m,

$$c_m{I}_m\left(k{\rho }_s\right)K_m\left(\mathit{ka}\right)+A_m\left(k\right)I_m\left(\mathit{ka}\right)=B_m\left(k\right)K_m\left(\mathit{ka}\right),$$ (2.5a)

$$c_m{I}_m\left(k{\rho }_s\right)K_m^{\prime }\left(\mathit{ka}\right)+A_m\left(k\right)I_m^{\prime }\left(\mathit{ka}\right)=\frac{1}{\epsilon }{B}_m\left(k\right)K_m^{\prime }\left(\mathit{ka}\right),$$ (2.5b)

where ε=ε_i/ε_m and c_m=(4−2δ_m0)q/πε_i are constants. Solving these linear systems yields

$$A_m\left(k\right)=\frac{(\epsilon -1)c_m{I}_m\left(k{\rho }_s\right)K_m\left(\mathit{ka}\right)K_m^{\prime }\left(\mathit{ka}\right)}{I_m\left(\mathit{ka}\right)K_m^{\prime }\left(\mathit{ka}\right)-\epsilon K_m\left(\mathrm{ka})I_m^{\prime }\right(\mathit{ka})},$$ (2.6a)

$$B_m\left(k\right)=\epsilon c_m{I}_m\left(k{\rho }_s\right)\frac{I_m^{\prime }\left(\mathit{ka}\right)K_m\left(\mathit{ka}\right)-I_m\left(\mathit{ka}\right)K_m^{\prime }\left(\mathit{ka}\right)}{I_m\left(\mathrm{ka})K_m^{\prime }\right(\mathit{ka})-\epsilon K_m(\mathit{ka}\left)I_m^{\prime }\right(\mathit{ka})},$$ (2.6b)

and the corresponding reaction field inside the cylinder reads [6]

$${\Phi }_{\mathrm{rf}}\left(\mathbf{r}\right)={\int }_0^{\infty }\mathit{dk}\cos k(z-z_s)\sum _{m=0}^{\infty }\cos m(\phi -{\phi }_s)\frac{(\epsilon -1)c_m{I}_m\left(k{\rho }_s\right)K_m\left(\mathit{ka}\right)K_m^{\prime }\left(\mathit{ka}\right)}{I_m\left(\mathit{ka}\right)K_m^{\prime }\left(\mathit{ka}\right)-\epsilon K_m\left(\mathit{ka}\right)I_m^{\prime }\left(\mathit{ka}\right)}{I}_m\left(k\rho \right).$$ (2.7)

3 Image charge methods

3.1 Multiple-image representation for the infinite cylinder

The image charge method is a promising way to speed up the calculation of electrostatic interactions in dielectric or conducting objects, in comparison with directly truncating the exact series solution. For spherical geometries, numerical evidence [4] illustrated that the pairwise sum of the image method is dozens of times faster than the direct series expansion method for the same level of accuracy. The exact solution for the cylindrical geometry is even more expensive because Eq. (2.7) includes not only an infinite series, but also an infinite domain integral. The so-called image charge method is to find some image point charges outside the cylinder such that their electrostatic contributions approximate the exact reaction field Φ_rf(r),

$${\Phi }_{\mathrm{rf}}^{\text{img}}\left(\mathbf{r}\right)=\frac{q}{{\epsilon }_{\mathrm{i}}}\sum _{m=1}^M\frac{f_m}{\mid \mathbf{r}-{\mathbf{x}}_m\mid },\text{for}\mathbf{r}\in {\Omega }_{\mathrm{i}},$$ (3.1)

where unknown f_m and x_m are the strength and location of the m-th image charge. Once we obtain these unknowns for each source charge located at r_s, the potential can be calculated by a pairwise sum of Coulombic interactions, which becomes feasible to take advantage of fast techniques [21], such as FMMs [5, 13, 41].

We compute the locations and charge strengths by minimizing the following sum of the squares of the errors of the approximate reaction field using the images

$$E^2=\min \sum _{n=1}^N{\left[{\Phi }_{\mathrm{rf}}^{\text{img}}\left({\mathbf{r}}_n\right)-{\Phi }_{\mathrm{rf}}\left({\mathbf{r}}_n\right)\right]}^2,$$ (3.2)

where r_n is the location of the n-th monitoring point. The minimization problem is nonlinear and most optimization algorithms can only find a local minimum, and thus it is necessary to give suitable initial values for iterations (the results with fewer monitoring points are used to estimate the initial data). Naturally, we can search the minimum on the plane z=z_s as the reaction potential has only one extremum along the z-axis, and thus the m-th image location can be defined by x_m = (ρ_m, φ_s+φ_m,z_s). Each image is represented by three unknowns, f_m, ρ_m and φ_m, which depend only on the radius, ρ_s, of the source charge.

A program based on Mathematica 7 is developed to calculate the locations and strengths of images for a given set of dielectric parameters, in which the “FindMinimum” subroutine [37] is used to solve the minimization problem. In order to show the feasibility and the performance of the code, we consider the case of ε_i=1 and ε_m=2. Here ε_i=1 represents a vacuum phase inside the cylinder, which is usually used as the dielectric constant of the explicit region. A relative small ε_m is selected to represent the dielectric constant of the membrane, such that the model can be used to study ion channels in the future. In all the calculations, we take N=640 monitoring points uniformly distributed in four circular disks inside the cylinder. To show the results, we take M=4, and due to the symmetry of the reaction field, the four charges can be denoted as (f_m, ρ_m, φ_m)=(f₁, ρ₁, ±φ₁) and (f₂, ρ₂, ±φ₂). So we have 6 unknowns for the minimization problem. It should be noted that the strengths, and azimuths of the images only depend on the ratio, p=ρ_s/a, and the radial coordinates of the images are linear functions of a. The six minimized unknowns are further fitted by fifth order polynomials of variable p. These polynomials are expressed in the matrix form as

$$\left(\begin{array}{c}\hfill f_1\hfill \\ \hfill {\rho }_1∕a\hfill \\ \hfill {\phi }_1\hfill \\ \hfill f_2\hfill \\ \hfill {\rho }_2∕a\hfill \\ \hfill {\phi }_2\hfill \end{array}\right)=\left(\begin{array}{cccccc}\hfill 0.1312\hfill & \hfill -0.1977\hfill & \hfill 0.1109\hfill & \hfill -0.0051\hfill & \hfill -0.00779\hfill & \hfill -0.1513\hfill \\ \hfill -0.2686\hfill & \hfill 0.3460\hfill & \hfill -0.1735\hfill & \hfill -0.1624\hfill & \hfill -0.2040\hfill & \hfill 1.4747\hfill \\ \hfill 0.3395\hfill & \hfill -0.7958\hfill & \hfill 0.5599\hfill & \hfill -0.2468\hfill & \hfill -0.6227\hfill & \hfill 0.7850\hfill \\ \hfill -0.2220\hfill & \hfill 0.3788\hfill & \hfill -0.2358\hfill & \hfill 0.0762\hfill & \hfill 0.0742\hfill & \hfill -0.1512\hfill \\ \hfill 3.1136\hfill & \hfill -5.5166\hfill & \hfill 3.5964\hfill & \hfill -1.1565\hfill & \hfill 0.2990\hfill & \hfill 1.4730\hfill \\ \hfill -0.7020\hfill & \hfill 1.5219\hfill & \hfill -1.0178\hfill & \hfill 0.3509\hfill & \hfill -0.6686\hfill & \hfill 2.3567\hfill \end{array}\right)\left(\begin{array}{c}\hfill p^5\hfill \\ \hfill p^4\hfill \\ \hfill p^3\hfill \\ \hfill p^2\hfill \\ \hfill p\hfill \\ \hfill 1\hfill \end{array}\right).$$ (3.3)

Fig. 2 illustrates the relative L₂ errors

$$E_{\text{rel}}=\sqrt{\sum _{n=1}^N{\left[{\Phi }_{\mathrm{rf}}^{\text{img}}\left({\mathbf{r}}_n\right)-{\Phi }_{\mathrm{rf}}\left({\mathbf{r}}_n\right)\right]}^2∕\sum _{n=1}^N{\Phi }_{\mathrm{rf}}{\left({\mathbf{r}}_n\right)}^2},$$ (3.4)

of both the original minimized data and the fitted data. The error curve shows that the polynomial fitting is in agreement with the minimized data. Overall, the relative errors to the cylindrical expansion solution are less than 2%, demonstrating the high accuracy of the multiple-image method using only 4 images. It is also evident that the method of images is less accurate for a source at the cylindrical axis than near the interface, while the opposite is observed for the image method in a sphere [4]. This difference can be explained as follows. When the source is at the center of the cylinder, the image can be considered as a plane integral where the integrand is symmetric in φ, and thus many points are required to accurately discretize this integral. However, as the source approaches the surface, the surface can be approximated as a wall for which only one image will represent the reaction field exactly.

Figure 2.

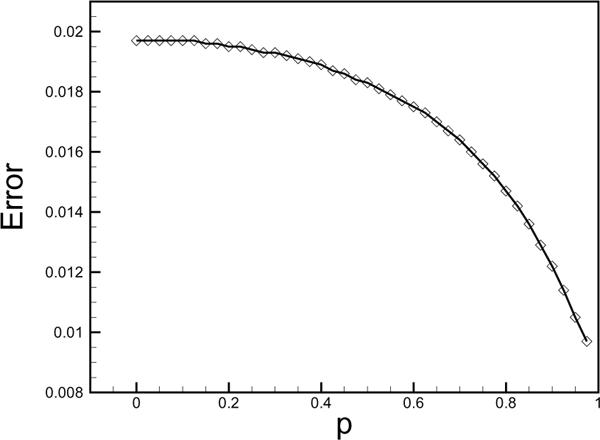
Relative L₂ errors (3.4) of the approximate reaction field of the infinite cylinder with four image charges as a function of p = ρ_s/a. The diamonds represent the minimization results and the solid lines are results with the fifth order polynomial fittings.

It should be stressed that, the fitted polynomials are independent of the cylindrical radius, and therefore they can be readily used for any other cylindrical geometry. But they do depend on the dielectric ratio ε_m/ε_i. For each ratio, new polynomials have to be regenerated. The Mathematica program is available (upon request) for generating such polynomials.

3.2 Multiple images for the ion-channel model

For the infinite cylinder, we have represented the reaction field (due to the source charge at r_s) by four image charges,

$${\Phi }_{\mathrm{rf}}^{\text{img}}\left(\mathbf{r}\right)=\frac{q}{{\epsilon }_{\mathrm{i}}}\sum _{m=1}^M\frac{f_m}{\mid \mathbf{r}-{\mathbf{x}}_m\mid },$$ (3.5)

where M=4 and x_m=(ρ_m,φ_s+φ_m,z_s), and ρ_m and φ_m are functions of p=ρ_s/a, given by Eq. (3.3).

We extend this result to solve the ion-channel model illustrated in Fig. 1. In this model, the explicit region, composed of embedded biomolecules, some water molecules, ions, and a portion of membrane, is a finite cylinder surrounded on the side by the rest of membrane. Beyond the cylindrical cavity and membrane is the bulk water. These three regions are characterized by dielectric constants ε_i, ε_m, and ε_w, respectively.

Suppose the two infinite boundaries of the bulk water are the parallel planes z =0 and z=b with b being their distance, and the origin is located on the bottom plane. We assume the medium between the two planes is homogeneous with dielectric ε_i, namely, we assume that ε_m =ε_i. Then for a source charge q at r_s =(x_s,y_s,z_s) with 0 < z_s < b, the reaction potential due to the two boundary planes can be described by a sum of infinite images [40]:

$${\Phi }_{\mathrm{rf}}^{\text{planes}}\left(\mathbf{r}\right)=\frac{q}{{\epsilon }_{\mathrm{i}}}\sum _{l=-\infty }^{\infty }\frac{(1-{\delta }_{l0}){\gamma }^{\mid l\mid }}{\mid \mathbf{r}-{\mathbf{x}}^{\left(l\right)}\mid },\text{for}0<z<b,$$ (3.6)

where

$${\mathbf{x}}^{\left(l\right)}=\left(x_s,y_s,{(-1)}^l\left(z_s-\frac{b}{2}\right)+\left(l+\frac{1}{2}\right)b\right),\text{and}\gamma =\frac{{\epsilon }_{\mathrm{i}}-{\epsilon }_{\mathrm{w}}}{{\epsilon }_{\mathrm{i}}+{\epsilon }_{\mathrm{w}}}.$$

Outside the two planes, a simple calculation with the boundary conditions (2.2) gives the electric potential,

$${\Phi }_{\mathrm{w}}^{\text{planes}}\left(\mathbf{r}\right)=\{\begin{array}{c}\frac{2q}{{\epsilon }_{\mathrm{i}}+{\epsilon }_{\mathrm{w}}}\sum _{l=0}^{\infty }\frac{{\gamma }^l}{\mid \mathbf{r}-{\mathbf{x}}^{(l+1)}\mid },\text{for}z\le 0,\hfill \\ \frac{2q}{{\epsilon }_{\mathrm{i}}+{\epsilon }_{\mathrm{w}}}\sum _{l=0}^{\infty }\frac{{\gamma }^{-l}}{\mid \mathbf{r}-{\mathbf{x}}^{(-l-1)}\mid },\text{for}z\ge b,\hfill \end{array}\phantom{\}}$$ (3.7)

which is an infinite sum of images in the opposite half space.

In practice, the infinite summation needs to be truncated at a finite term l =L, so an estimate of the truncation error of Eq. (3.6) is necessary. We consider the self energy of a point q inside the domain between the two planes, V(r_s)=qΦ_rf(r_s)/2, then the error can be expressed as

$$E_L\left({\mathbf{r}}_s\right)=\frac{q^2}{2{\epsilon }_{\mathrm{i}}}\sum _{l=L+1}^{\infty }\frac{{\gamma }^l}{\mid {(-1)}^l(z_s-\frac{b}{2})+(l+\frac{1}{2})b-z_s\mid }+\frac{{\gamma }^l}{\mid {(-1)}^l(z_s-\frac{b}{2})-(l-\frac{1}{2})b-z_s\mid }.$$ (3.8)

Thus, when L=2N, the error can be rewritten as

$$E_{2N}\left({\mathbf{r}}_s\right)=\frac{q^2}{2{\epsilon }_{\mathrm{i}}}\sum _{n=N}^{\infty }{\gamma }^{2n+1}\left[\frac{1}{(2n+2)b-2z_s}+\frac{1}{2nb+2z_s}+\frac{2\gamma }{(2n+2)b}\right].$$

Clearly, each term in the above sum is negative for z_s ∊[0,b], and the maximum error is reached at two ends z_s=0 and b, given by

$$\underset{z_s\in [0,b]}{\overset{\max }{}}\mid E_{2N}\left({\mathbf{r}}_s\right)\mid =-\frac{q^2}{2{\epsilon }_{\mathrm{i}}}\sum _{n=N}^{\infty }{\gamma }^{2n+1}\frac{2(1+\gamma )n+1}{n(2n+2)b}.$$ (3.9)

Similarly, we have

$$E_{2N+1}\left({\mathbf{r}}_s\right)=\frac{q^2}{2{\epsilon }_{\mathrm{i}}}\sum _{n=N}^{\infty }{\gamma }^{2n+2}\left[\frac{\gamma }{(2n+4)b-2z_s}+\frac{\gamma }{(2n+2)b+2z_s}+\frac{2}{(2n+2)b}\right],$$

in which, each term is positive. The maximum error is obtained at z_s=b/2, which yields

$$\underset{z_s\in [0,b]}{\overset{\max }{}}\mid E_{2N+1}\left({\mathbf{r}}_s\right)\mid =-\frac{q^2}{2{\epsilon }_{\mathrm{i}}}\sum _{n=N}^{\infty }{\gamma }^{2n+2}\frac{2(1+\gamma )n+(3+2\gamma )}{(n+1)(2n+3)b}.$$ (3.10)

As γ≈−1, the convergence rate of the infinite series is on order 1/N².

Now, we can obtain the image representation of the ion-channel model by combining the cylindrical images (3.5) and the planar images (3.6). Suppose the origin is the intersection between the bottom plane and the cylindrical axis. Obviously, the source charge and the M image charges are bounded by the two membrane boundaries. For convenience, denote the position of the source by r_s =x₀ =(ρ₀,φ_s+φ₀,z_s) and let f₀ =1. The total reaction field due to the source charge inside the cylinder can be expressed by

$${\Phi }_{\mathrm{rf}}\left(\mathbf{r}\right)\approx \frac{q}{{\epsilon }_i}\sum _{l=-\infty }^{\infty }\sum _{m=0}^M\frac{(1-{\delta }_{l0}{\delta }_{m0}){\gamma }^{\mid l\mid }{f}_m}{\mid \mathbf{r}-{\mathbf{x}}_m^{\left(l\right)}\mid },$$ (3.11)

where

$${\mathbf{x}}_m^{\left(l\right)}=\left({\rho }_m,{\phi }_s+{\phi }_m,{(-1)}^l(z_m-b∕2)+(l+1∕2)b\right).$$

The major assumption of using Eq. (3.6) to construct images of the ion-channel model is the homogeneity of the medium between the two planes by disregarding the dielectric difference between the membrane and the interior of the cylinder, which is reasonable because both ε_i and ε_m are very small in comparison to the water dielectric, ε_w, roughly, the error is bounded by |ε_i–ε_m|/ε_w. As the boundary condition on the cylindrical surface remains correct when using the formula (3.11), the inhomogeneity only introduces an error in satisfying the planar boundary condition. However, the region of interest is the explicit pore, and we use ε_i as the dielectric of the region between the two planes. It turns out that the formula (3.11) represents a reaction potential which precisely matches the boundary conditions on the surface of the explicit pore-the region of interest. The mathematical error analysis would be a difficult issue, therefore we will demonstrate the error performance by numerical experiments.

4 Numerical results

The image solution (3.11) for the ion-channel model is tested by calculating the self energy V(r_s)=qΦ_rf(r_s)/2 of a unit point charge located within a finite cylinder. The cylinder is of radius 4Å, and height 12Å. In the calculations, we set the source charge at (x,0,z) where x takes two values, 0 and 2Å, and z varies from 2 to 10Å. To compare the results, the Poisson-Boltzmann equation is numerically solved by a 3D finite difference (FD) method in [16] with grid size h=0.5Å.

The infinite sum in Eq. (3.11) is truncated at l≤L=±15, say, the images with $z_m^{\left(l\right)}\langle 180\mathrm{Å}$ are all included, and therefore, it is accurate enough to approximate the infinite sum. Figs. 3(a) and (b) give the comparative results between the image-based and finite difference self energies for the case of ε_m=2. It can be seen from Fig. 3(b) that the relative errors are all less than 1.1%. As is known, Eq. (3.6) is only an approximation by assuming the region between two planes is homogeneous. The main reason for this high accuracy is because the membrane permittivity is close to 1 of the explicit region in comparison to the water dielectric constant, and the boundary conditions on the two ends of the cylinder are precisely satisfied. To see the accuracy of the formula (3.11) for higher membrane dielectrics, the image-based and FD solutions are also calculated for ε_m=4 for which the fitted polynomials of image parameters are given in Appendix A. The self-energy results and the relative errors are again plotted in Figs. 3(c) and (d). It is seen that the maximum error is 2.3% relative to the FD solution. This result is not surprising as the dielectric ratio of membrane and water is doubled, the error is expected to increase. In order to investigate the error performance of the self energy near the boundary, Fig. 4 plots the results for the charges located at 1 Å distance to the bottom plane. The average error is below 1%, while for charges close to the radial boundary the error increases to 1.5%, which shows the method of images is accurate for charges close to the planar boundary.

Figure 3.

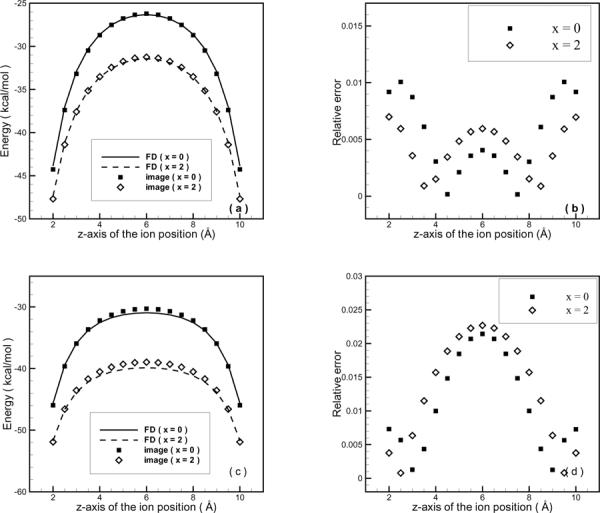
Self energy of a unit charge located at (x,0,z) within the ion channel. The membrane dielectric takes (a)(b) ε_m = 2, and (c)(d) ε_m = 4.

Figure 4.

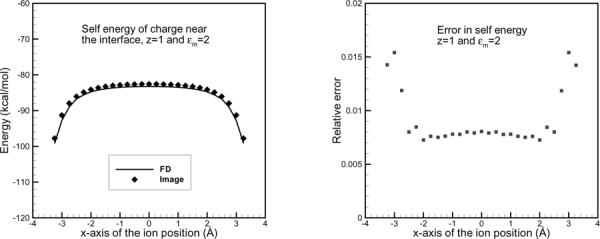
Self energy of a unit charge located at (x,0,1) near the interface between the cylinder and water for x varying from −3.5 to 3.5 Å. The membrane dielectric takes ε_m = 2.

One natural concern with fast calculation of the reaction field is the correct truncation terms l ≤ L for the infinite sum of Eq. (3.11), for which we expect to take the smallest L for a desired accuracy. In Fig. 5, we have calculated the maximum relative errors of the sampling points by comparing with the FD solutions, where the source charge is on the cylindrical axis (0,0,z) for z varying from 2 to 10Å. The membrane dielectrics take two values ε_m=2 and 4. The results indicate that when ε_m=2 the error rapidly converges to a level of 1% in comparison to the reference solution if using an odd L, while the error when using even number of terms remains about 0.7% larger than the odd case with the increase of L. This differential converging behavior does not agree with the error analysis shown in Eqs. (3.8) and (3.10). However, noticing that the reference solutions are also numerically obtained, and it could be an error cancelation between the finite difference solver and the method of images for odd L. As E_2N+1(r_s) and E_2N(r_s) are opposite in sign, the error cancelation for odd images implies an error accumulation for even ones. This saw-like error phenomenon also appears in the case of ε_m =4, whereas, the errors keep about 2.3% because of the higher dielectric ratio between membrane and water.

Figure 5.

Maximum relative error of the self energy vs. different truncation terms. The membrane dielectric takes ε_m = 2 and 4. The unit charge is located at the cylindrical axis. The error takes the maximum of the relative error for z varying from 2 to 10Å.

For the purpose of comparison, we also perform the calculations for the following two limiting cases: i) the conductor limit of the water dielectric (∊_w→∞) with the membrane dielectric ε_m=2, for which the infinite images for planes are exact; and ii) the finite cylinder immersed in the bulk water (both the membrane and water dielectrics are set to 80). The position of the source charge varies along the cylindrical axis. Fig. 6 displays the results of these two cases. We see the image result agrees well with the finite difference result for a large ε_w, which is theoretically exact in the conductor limit. As is shown, due to the high dielectric property of the solvent, the conductor limit is a good approximation to the reaction potential. For the second case with a large ε_m, the image approximation breaks down with the maximum error being 1.73 kcal/mol (4.77% in relative error), which highlights the proper treatment of membrane environment is essential in the ion-channel model.

Figure 6.

Two limiting cases. (a) ε_w = ∞, where the result with ε_w = 80 is also plotted; (b) the finite cylinder immersed in the bulk solvent, say, ε_m = ε_w = 80.

5 Concluding remarks

In conclusion, we have developed a multiple-image method to approximate the reaction field due to a point charge in a hybrid ion-channel model, which uses a cylindrical cavity of a finite height as the explicit region and everything outside as a continuum characterized by two dielectric constants. The main challenge for simulation of an ion channel is that the simulation system is made up of not only protein itself, but also the lipid bilayer, water and ions, and thus computer resources are usually limited to treat such an inhomogeneous system. The implicit approaches based on the Poisson-Boltzmann theory can treat this system more efficiently, but are still very slow for dynamics simulations. The image charge approximation can successfully treat an inhomogeneous system by representing the polarization effects with multiple image charges, leading to a homogeneous system with the source charges and their corresponding images, thus many existing fast algorithms can be used to accelerate the pairwise Coulombic interactions.

Many issues remain to be addressed, such as how to take into account of ionic effects in solution, and to assess the performance in force calculations. The incorporation of the developed method into practical molecular simulations is currently under way.

Appendix

A Fitting polynomials for membrane dielectric=4

For membrane dielectric ε_m = 4, the fitting polynomials are given by

$$\left(\begin{array}{c}\hfill f_1\hfill \\ \hfill {\rho }_1∕a\hfill \\ \hfill {\phi }_1\hfill \\ \hfill f_2\hfill \\ \hfill {\rho }_2∕a\hfill \\ \hfill {\phi }_2\hfill \end{array}\right)=\left(\begin{array}{cccccc}\hfill 0.3371\hfill & \hfill -0.5880\hfill & \hfill 0.3648\hfill & \hfill -0.0659\hfill & \hfill -0.1458\hfill & \hfill -0.2253\hfill \\ \hfill -0.3646\hfill & \hfill 0.5433\hfill & \hfill -0.2995\hfill & \hfill -0.1423\hfill & \hfill -0.1569\hfill & \hfill 1.4262\hfill \\ \hfill 0.3021\hfill & \hfill -0.7001\hfill & \hfill 0.4723\hfill & \hfill -0.1665\hfill & \hfill -0.6774\hfill & \hfill 0.7851\hfill \\ \hfill -0.4614\hfill & \hfill 0.8616\hfill & \hfill -0.5648\hfill & \hfill 0.1828\hfill & \hfill 0.1392\hfill & \hfill -0.2248\hfill \\ \hfill 6.8556\hfill & \hfill -13.350\hfill & \hfill 9.2180\hfill & \hfill -2.8621\hfill & \hfill 0.4275\hfill & \hfill 1.4206\hfill \\ \hfill -0.2925\hfill & \hfill 1.3146\hfill & \hfill -1.2073\hfill & \hfill 0.4113\hfill & \hfill -0.7401\hfill & \hfill 2.3572\hfill \end{array}\right)\left(\begin{array}{c}\hfill p^5\hfill \\ \hfill p^4\hfill \\ \hfill p^3\hfill \\ \hfill p^2\hfill \\ \hfill p\hfill \\ \hfill 1\hfill \end{array}\right).$$ (A.1)

B Images for force calculations

In this Appendix, we consider how to find force images. The expression based on minimizing the reaction potential error could be simply used. However, more accurate image approximation can be derived by minimizing the force error. For a test point charge of unit strength at field point r, its force, due to the source charge q, is expressed as

$$\mathbf{F}\left(\mathbf{r}\right)=-\nabla \left[{\Phi }_{\text{coul}}\right(\mathbf{r})+{\Phi }_{\mathrm{rf}}(\mathbf{r}\left)\right].$$ (B.1)

Similar to the setting of free energy calculations, we solve the following minimization problem by comparing the forces along the radial and axial directions,

$$\text{Err}\left(\{f_m,{\mathbf{x}}_m\}{\mid }_{m=1}^M\right)=\min \sum _{n=1}^N{\left[\frac{\partial }{\partial \rho }{\Phi }_{\mathrm{rf}}^{\text{img}}\left({\mathbf{r}}_n\right)-\frac{\partial }{\partial \rho }{\Phi }_{\mathrm{rf}}\left({\mathbf{r}}_n\right)\right]}^2+{\left[\frac{\partial }{\partial z}{\Phi }_{\mathrm{rf}}^{\text{img}}\left({\mathbf{r}}_n\right)-\frac{\partial }{\partial z}{\Phi }_{\mathrm{rf}}\left({\mathbf{r}}_n\right)\right]}^2.$$ (B.2)

Again, for the case of four images, we suppose the four charges have parameters (f_m, ρ_m, φ_m) = (f₁, ρ₁, ± φ₁) and (f₂, ρ₂, ± φ₂), i.e., we have 6 unknowns. These polynomial fitting functions read

$$\left(\begin{array}{c}\hfill f_1\hfill \\ \hfill {\rho }_1∕a\hfill \\ \hfill {\phi }_1\hfill \\ \hfill f_2\hfill \\ \hfill {\rho }_2∕a\hfill \\ \hfill {\phi }_2\hfill \end{array}\right)=\left(\begin{array}{cccccc}\hfill -0.0516\hfill & \hfill 0.2440\hfill & \hfill -0.2253\hfill & \hfill -0.0232\hfill & \hfill 0.1151\hfill & \hfill -0.2422\hfill \\ \hfill 0.2865\hfill & \hfill -0.8883\hfill & \hfill 0.6610\hfill & \hfill 0.0144\hfill & \hfill -0.9196\hfill & \hfill 1.8518\hfill \\ \hfill 1.0179\hfill & \hfill -1.9966\hfill & \hfill 1.2305\hfill & \hfill -0.1078\hfill & \hfill -0.9082\hfill & \hfill 0.7850\hfill \\ \hfill -0.7017\hfill & \hfill 1.0028\hfill & \hfill -0.1342\hfill & \hfill 0.0108\hfill & \hfill 0.1189\hfill & \hfill -0.2422\hfill \\ \hfill 3.4815\hfill & \hfill -5.7516\hfill & \hfill 2.6601\hfill & \hfill -0.6269\hfill & \hfill 0.9935\hfill & \hfill 1.8508\hfill \\ \hfill -0.1743\hfill & \hfill 0.1207\hfill & \hfill 0.3758\hfill & \hfill -0.1107\hfill & \hfill -0.9412\hfill & \hfill 2.3565\hfill \end{array}\right)\left(\begin{array}{c}\hfill p^5\hfill \\ \hfill p^4\hfill \\ \hfill p^3\hfill \\ \hfill p^2\hfill \\ \hfill p\hfill \\ \hfill 1\hfill \end{array}\right).$$ (B.3)