Accessing long-lived nuclear singlet states between chemically equivalent spins without breaking symmetry

Abstract

Long-lived nuclear spin states could greatly enhance the applicability of hyperpolarized nuclear magnetic resonance. Using singlet states between inequivalent spin pairs has been shown to extend the signal lifetime by more than an order of magnitude compared to the spin lattice relaxation time (T₁), but they have to be prevented from evolving into other states. In the most interesting case the singlet is between chemically equivalent spins, as it can then be inherently an eigenstate. However this presents major challenges in the conversion from bulk magnetization to singlet. In the only case demonstrated so far, a reversible chemical reaction to break symmetry was required. Here we present a pulse sequence technique that interconverts between singlet spin order and bulk magnetization without breaking the symmetry of the spin system. This technique is independent of field strength and is applicable to a broad range of molecules.

Hyperpolarization methods to greatly exceed the thermal nuclear spin magnetization have attracted considerable attention, particularly to broaden applications of magnetic resonance imaging past hydrogen in water^1–5. The first studies used ³He or ¹²⁹Xe (refs 6–8), but methods to hyperpolarize hydrogen, carbon or nitrogen in small molecules are much more generally applicable^1–3. The fundamental challenge has been that the nuclear spin-lattice relaxation time T₁ is generally short in solution or tissue (seconds to a minute for most carbon spins), so the large magnetization often disappears too rapidly to monitor meaningful biological dynamics. Fifty years of pulse sequence development has been spectacularly successful in selectively controlling the effects of spin interactions such as chemical shifts or scalar couplings, but spin lattice relaxation is fundamentally different: relaxation occurs owing to fluctuating fields at multiples of the resonance frequency, far too rapid for pulse sequence manipulation⁹. For this reason, inherently long-lived nuclear spin states have drawn considerable attention^10–17, starting with the pioneering work of Levitt and co-workers^{12,13,16,18–23}, which has shown the singlet state lifetime for ¹⁵N₂O to be as long as 30 min (ref. 16). This paper presents a new approach (Fig. 1) which accesses such states in symmetric spin systems, and should be applicable to a wide range of interesting molecular targets.

Figure 1. The M2S-S2M pulse sequence, all pulses are resonant with the ¹³C Larmor frequency.

a, Magnetization to singlet spin order (M2S) sequence, the first part is equivalent to a CPMG sequence with each echo pulse composed of a [90₀180₉₀90₀]_ϕ composite pulse unit with an overall phase increment ϕ = [0022…]. The interpulse delay $\tau ∕2=1∕\left(4\sqrt{{(J_{\mathrm{CC}}+J_{\mathrm{HH}})}^2+{(J_{\mathrm{CH}}-J_{\mathrm{CH}}^{\prime })}^2}\right)$ is determined to be around 2.46 ms. The CPMG sequence is followed by another 90° pulse with a 90° phase shift compared with the first 90°. Then a second multiple echo sequence with half as many pulses (n₂ ≅ n₁/2) is preceded by a 1/(4J_cc) delay. Inset, Structure of DEO–¹³C₂, dissolved in DMSO-d6 (stars indicate ¹³C atoms). The concentration of DEO–¹³C₂ is around 2 M. b, Complete M2S-S2M sequence. A gradient is added right after the M2S sequence to suppress the single-quantum coherence generated by M2S, a variable waiting time τ_r is followed by another 90° pulse and a gradient to suppress recovered I_Z magnetization during τ_r. Then the time-reversed M2S (S2M) converts the singlet state population back to magnetization. A final 90° pulse tips down the bulk magnetization for detection.

In general the lifetime extensions stem from preparing spins in a state that has symmetry-forbidden dipolar transitions, such as the two-spin singlet state $S\equiv (\alpha \beta -\beta \alpha )∕\sqrt{2}$, which is disconnected from the triplet states (T₁ ≡ αα, T₋₁ ≡ ββ, $T_0\equiv (\alpha \beta +\beta \alpha )∕\sqrt{2}$). The basic challenge is that same symmetry property that reduces relaxation in such disconnected states also makes it difficult to load population into them, or later convert this population to observable magnetization for detection. The initial solution was to create singlets between chemically inequivalent spins, making all of the energy levels accessible by frequency-selective pulse sequences at high field^12,13,19. However, the singlet is not an eigenstate at high field; it is preserved using spin locking sequences or by rapid translation to very low magnetic field²⁴. Unfortunately both continuous irradiation and rapid field shuttling create serious challenges for in vivo imaging applications. A recent paper took a very different approach, exploring singlets between chemically equivalent spins which by symmetry have the same resonance frequency. Here the challenge of accessing the disconnected state was solved by reversible chemical transformation¹⁰. The singlet is essentially an eigenstate at any field without concurrent irradiation, which avoids the problems associated with systems containing inequivalent spins, but the required chemical transformation imposes limitations in itself.

We show here that it is possible to transfer population in and out of chemically equivalent singlet states at high field, using only radiofrequency pulses to make the transfer. This requires scalar couplings from the singlet spins to other spins in the molecule that break the magnetic equivalence, but is far more general than any previous approach. This looks at first glance as if it violates symmetry, but the basic trick is straightforward. As an example, consider an AA′XX′ 4-spin system which has only two pairs of chemical equivalent spins (for example ¹³C₂ and ¹H₂); a simple example system would be the linear molecule diacetylene, H–¹²C ≡ ¹³C–¹³C ≡ ¹²C–H, because ¹²C has no nuclear spin. The ¹³C and H pairs are symmetric around the same inversion centre. The state |SS〉 = |(αβ − βα)_C(αβ − βα)_H〉/2, which we call here `singlet–singlet', has no dipole-allowed transitions to other states. However, unlike the singlet in a two-spin system, this state is not isolated by symmetry from all other states; it has the same overall inversion symmetry as the `triplet–triplet' |T₀T₀〉 = |(αβ + βα)_C(αβ + βα)_H〉/2, which does have dipole-allowed transitions. With the right combinations of scalar couplings (which diacetylene has, as discussed below) the singlet–singlet can essentially be an eigenstate, so it is preserved without irradiation. However, simple pulse sequences can migrate population between the singlet–singlet and triplet–triplet states. Thus, it is possible to store population in disconnected states for an extended period, yet recall the spins when desired.

More precisely, the basis functions of this AA′XX′ spin system can be categorized into symmetric and antisymmetric groups with respect to spin exchange parity^25–27. Within the symmetric part of the resulting Hamiltonian, there is a two-level subspace composed of the singlet–singlet and triplet–triplet states:

$$\underset{\langle \mathrm{SS}\mid }{\langle T_0{T}_0\mid }\left(\begin{array}{cc}\hfill \mid T_0{T}_0\rangle \hfill & \hfill \mid \mathit{SS}\rangle \hfill \\ \hfill \frac{1}{2}(J_{\mathrm{CC}}+J_{\mathrm{HH}})\hfill & \hfill -\frac{1}{2}(J_{\mathrm{CH}}-{J_{\mathrm{CH}}}^{\prime })\hfill \\ \hfill -\frac{1}{2}(J_{\mathrm{CH}}-{J_{\mathrm{CH}}}^{\prime })\hfill & \hfill -\frac{1}{2}(J_{\mathrm{CC}}+J_{\mathrm{HH}})\hfill \end{array}\right)$$ (1)

(plus a term proportional to the identity matrix, which does not affect the evolution). There are no secular off-diagonal elements connecting either of the two states to other states. From equation (1), if the difference between the diagonal elements (the sum of the homonuclear scalar couplings) is much larger than the off-diagonal elements (the difference between the heteronuclear couplings), the SS and T₀T₀ states will closely resemble the exact energy eigenstates; however, even very small off-diagonal elements provide a handle to interconvert the two states. This is readily understood by analogy with a well-known problem, irradiation of a single spin 1/2 in a strong B₀ field along $\widehat{z}$ by a much weaker B₁ field along $\widehat{x}$. The full Hamiltonian in that case is:

$$H=\underset{\langle \alpha \mid }{\langle \beta \mid }\left(\begin{array}{cc}\hfill \mid \beta \rangle \hfill & \hfill \mid \alpha \rangle \hfill \\ \hfill \frac{1}{2}\gamma B_0\hfill & \hfill \frac{1}{2}\gamma B_1\hfill \\ \hfill -\frac{1}{2}\gamma B_1\hfill & \hfill -\frac{1}{2}\gamma B_0\hfill \end{array}\right)$$ (2)

where α and β are the eigenstates of I_z. If B₁ is constant (first panel of Fig. 2a) the equilibrium magnetization vector $M_0\widehat{z}$ precesses a maximum of 2tan⁻¹(B₁/B₀) away from its initial position at time $\tau =\pi ∕\left(\gamma B_{\mathrm{eff}}\right)=\pi ∕\left(\gamma \sqrt{B_0^2+B_1^2}\right)$, and further irradiation brings the magnetization back towards its initial value. However, if the phase of B₁ is reversed whenever the magnetization reaches the maximum excursion (equivalent to resonant, square wave irradiation) the magnetization can be moved arbitrarily far away; the number of full cycles required to generate a complete inversion is n ≈ π/(2tan⁻¹(B₁/B₀)). As an aside, we note that this square-wave excitation solution is exact; the more common experimental case (resonant sinusoidal excitation) requires the rotating wave approximation and induces a frequency shift²⁸.

Figure 2. Analogy between population inversion in a single spin 1/2 two-level system and population inversion in the singlet-singlet and triplet-triplet two-level system.

a, Irradiation of single spin 1/2 by a continuous square wave pulse with constant field strength B₁, which is much smaller than the main field B₀, shows that an arbitrarily small B₁ field can flip spins if the field is modulated (change of spin state is illustrated by the change of magnetization vector which starts as the blue arrow and changes into red, green and at last purple arrow at indicated time). As discussed in the text, conversion between the singlet-singlet and triplet-triplet states works in exactly this same way, with the `square wave' replaced by selective 180° pulses on one of the two types of spins. b, Population interconversion between singlet-singlet (black) and triplet-triplet (red) states in a pseudo CC′HH′ 4-spin system. The following scalar couplings were assumed: J_CC = 153 Hz, J_CH = 52 Hz, J′_CH = 6.4 and J_HH = 0 Hz. An interpulse delay of 3.12 ms is calculated according to $\tau =1∕\left(2\sqrt{{(J_{\mathrm{CC}}+J_{\mathrm{HH}})}^2+{(J_{\mathrm{CH}}-J_{\mathrm{CH}}^{\prime })}^2}\right)$.

Inspection of equations (1) and (2) shows that the homonuclear and heteronuclear couplings in the singlet–singlet/triplet–triplet system play the same roles as the B₀ and B₁ fields respectively in the spin-1/2 system. However, in an interaction representation, the sign of the operators associated with the heteronuclear couplings can be reversed by 180° pulses resonant with either ¹³C or ¹H. Thus a train of 180° pulses separated by delays that permit accumulation of state mixing can interconvert SS and T₀T₀ (Fig. 2b). The `resonance condition' which maximizes the effect is then

$$\tau =1∕\left(2\sqrt{{(J_{\mathrm{CC}}+J_{\mathrm{HH}})}^2+{(J_{\mathrm{CH}}+J_{\mathrm{CH}}^{\prime })}^2}\right)$$

and the number of 180° pulses needed to invert the population is:

$$n\approx \pi ∕(2\times \text{arctan}((J_{\mathrm{CH}}-J_{\mathrm{CH}}^{\prime })∕(J_{\mathrm{CC}}+J_{\mathrm{HH}})\left)\right)$$ (3)

The counterpart of this two-level system in the antisymmetric state group is comprised of states `singlet–triplet' and `triplet–singlet', which are defined as:

$$\mid {\mathit{ST}}_0\rangle =\frac{1}{2}\mid {(\alpha \beta -\beta \alpha )}_{\mathrm{C}}{(\alpha \beta +\beta \alpha )}_{\mathrm{H}}\rangle$$

$$\mid T_{0}S\rangle =\frac{1}{2}\mid {(\alpha \beta +\beta \alpha )}_{\mathrm{C}}{(\alpha \beta -\beta \alpha )}_{\mathrm{H}}\rangle$$

In the limit J_CC ⪢ J_HH, which is the common limit, the resonance condition is the same for this transition (the precise resonance condition is $\tau =1∕\left(2\sqrt{{(J_{\mathrm{CC}}-J_{\mathrm{HH}})}^2+{(J_{\mathrm{CH}}-J_{\mathrm{CH}}^{\prime })}^2}\right)$). The 180° pulse sequence is very similar to the `Magnetization to Singlet–Singlet to Magnetization (M2S–S2M)' sequence introduced recently^14,16 for interconversion between slightly chemically inequivalent spins, except that here chemical equivalence is preserved and magnetic equivalence is broken by means of scalar couplings.

The approach is easy to generalize to larger spin systems, as we demonstrate experimentally on diethyl oxalate–¹³C₂ (DEO–¹³C₂, (${\mathrm{CH}}_3{\mathrm{CH}}_2^{13}{\mathrm{CO}}_2$)₂, Fig. 1a, inset). Considering only the methylene protons, this is an ${\mathrm{AA}}^{\prime }{\mathrm{X}}_2{\mathrm{X}}_2^{\prime }$ system, and there are eight similar two-level systems that connect the carbon singlet state to the central triplet state. For instance, states

$$\mid S\left(\alpha \alpha \right)S\rangle =\frac{1}{2}\mid {(\alpha \beta -\beta \alpha )}_{\mathrm{C}}{\left(\alpha \alpha \right)}_{\mathrm{H}1}{(\alpha \beta -\beta \alpha )}_{\mathrm{H}2}\rangle$$

$$\mid T_0\left(\alpha \alpha \right)T_0\rangle =\frac{1}{2}\mid {(\alpha \beta +\beta \alpha )}_{\mathrm{C}}{\left(\alpha \alpha \right)}_{\mathrm{H}1}{(\alpha \beta +\beta \alpha )}_{\mathrm{H}2}\rangle$$

constitute one such two-level subspace, where `H1' and `H2' denote two pairs of ¹H spins and each pair are symmetric around the inversion centre.

The density operator transformation induced by the M2S–S2M sequence in the AA′XX′ spin system (assuming J_CC ⪢ J_CH, $J_{\mathrm{CH}}^{\prime }$; J_HH = 0) is outlined below and the extension to systems including more pairs of chemically equivalent spins such as ${\mathrm{AA}}^{\prime }{\mathrm{X}}_2{\mathrm{X}}_2^{\prime }$ can be easily made. Written in the symmetry-adapted basis set (αα ≡ T₁, ββ ≡ T₋, $(\alpha \beta +\beta \alpha )∕\sqrt{2}\equiv T_0$, $(\alpha \beta -\beta \alpha )∕\sqrt{2}\equiv S$), with the first two spins being ¹³C, the equilibrium magnetization for carbon is proportional to

$$\begin{array}{cc}\hfill {\rho }_0& \propto I_z\cong \mid T_1{T}_1\rangle \langle T_1{T}_1\mid +\mid T_1{T}_0\rangle \langle T_1{T}_0\mid +\mid T_{1}S\rangle \langle T_{1}S\mid \hfill \\ \hfill & +\mid T_1{T}_{-1}\rangle \langle T_1{T}_{-1}\mid -\mid T_{-1}{T}_1\rangle \langle T_{-1}{T}_1\mid -\mid T_{-1}{T}_0\rangle \langle T_{-1}{T}_0\mid \hfill \\ \hfill & -\mid T_{-1}S\rangle \langle T_{-1}S\mid -\mid T_{-1}{T}_{-1}\rangle \langle T_{-1}{T}_{-1}\mid \hfill \end{array}$$

All pulses in Fig. 1 are resonant with ¹³C. The first 90°_Y pulse converts the I_Z magnetization into single quantum coherences (coherences that go through interconversion are in the second bracket in equation (4)):

$$\begin{array}{c}\hfill {\rho }_1\cong \frac{\sqrt{2}}{2}(\mid T_1{T}_1\rangle \langle T_0{T}_1\mid +\mid T_0{T}_1\rangle \langle T_{-1}{T}_1\mid +\mid T_1{T}_{-1}\rangle \langle T_0{T}_{-1}\mid \hfill \\ \hfill +\mid T_0{T}_{-1}\rangle \langle T_{-1}{T}_{-1}\mid )+\frac{\sqrt{2}}{2}(\mid T_1{T}_0\rangle \langle T_0{T}_0\mid +\mid T_{1}S\rangle \langle T_{0}S\mid \hfill \\ \hfill +\mid T_0{T}_0\rangle \langle T_{-1}{T}_0\mid +\mid T_{0}S\rangle \langle T_{-1}S\mid )+c.c\hfill \end{array}$$ (4)

where c.c are the complex conjugates of coherences above. The subsequent multiple echo pulses generate a 180° rotation within the SS/T₀T₀ and ST₀/T₀S two-level systems, giving rise to the following coherences

$$\begin{array}{cc}\hfill {\rho }_2& \cong \frac{\sqrt{2}}{2}(\mid T_1{T}_1\rangle \langle T_0{T}_1\mid +\mid T_0{T}_1\rangle \langle T_{-1}{T}_1\mid +\mid T_1{T}_{-1}\rangle \langle T_0{T}_{-1}\mid \hfill \\ \hfill & +\mid T_0{T}_{-1}\rangle \langle T_{-1}{T}_{-1}\mid )+i\frac{\sqrt{2}}{2}(\mid T_1{T}_0\rangle \langle \mathit{SS}\mid +\mid T_{1}S\rangle \langle {\mathit{ST}}_0\mid \hfill \\ \hfill & +\mid \mathit{SS}\rangle \langle T_{-1}{T}_0\mid +\mid {\mathit{ST}}_0\rangle \langle T_{-1}S\mid )+c.c\hfill \end{array}$$ (5)

Notice that coherences that involve states such as |T₀T₁〉 and |T₀T₋₁〉 (the first bracket in equation (5)) are not perturbed by the multiple echo sequence, so they are left out in the following derivation. The subsequent 90°_X exchanges the coherences within the ¹³C₂ triplet state manifold (highlighted using the tilde):

$${\rho }_3\cong \mid {\tilde{T}}_0{T}_0\rangle \langle \mathit{SS}\mid +\mid {\tilde{T}}_{0}S\rangle \langle {\mathit{ST}}_0\mid +\mid \mathit{SS}\rangle \langle {\tilde{T}}_0{T}_0\mid +\mid {\mathit{ST}}_0\rangle \langle {\tilde{T}}_{0}S\mid$$

A waiting period of 1/(4J_CC) is used to generate a phase shift of the coherence within the SS/T₀T₀ and ST₀/T₀S two-level systems before another multiple 180°_X sequence, which finally converts the coherence into a population difference within the SS/T₀T₀ and ST₀/T₀S two-level systems. As this conversion can be perceived as a 90° rotation in these two-level systems, it requires half as many 180°_X pulses as the first multiple echo sequence (n/2 in equation (3)). Accordingly, the ultimate density matrix after the M2S sequence is:

$${\rho }_4\cong \mid T_0{T}_0\rangle \langle T_0{T}_0\mid -\mid \mathit{SS}\rangle \langle \mathit{SS}\mid +\mid T_{0}S\rangle \langle T_{0}S\mid -\mid {\mathit{ST}}_0\rangle \langle {\mathit{ST}}_0\mid$$

Population evolution after the M2S sequence considering this CC′HH′ 4-spin system is depicted in Supplementary Fig. S1. After the middle delay for relaxation (τ_r in Fig. 1b), we need to chronologically reverse the M2S sequence to convert the population difference back to M_Z magnetization. An extra 90°_X tips down the magnetization for signal detection. The pulse sequence in Fig. 1b has several minor modifications to improve the practical performance. First, to avoid distortions from unperturbed single-quantum coherences after the first multiple 180° pulse train, a spoiler gradient is added right after the M2S sequence to dephase these coherences. Second, to compensate for flip angle inaccuracy with this large number of pulses, composite pulses (90°_X 180°_Y 90°_X)_ϕ with overall phase increment ϕ = [0,0,2,2] (ref. 29) are used instead of hard pulses 180°_X. Finally, for studies on thermally polarized samples, an extra 90_Y pulse and a G_Z gradient are also added immediately before the S2M sequence to suppress any recovered I_Z magnetization (Fig. 1b). The 90_Y – G_Z combination has no effect on the singlet state population whereas it does perturb the triplet state population, which goes through extremely fast equilibration (2–3 s in DEO–¹³C₂) within the triplet manifold.

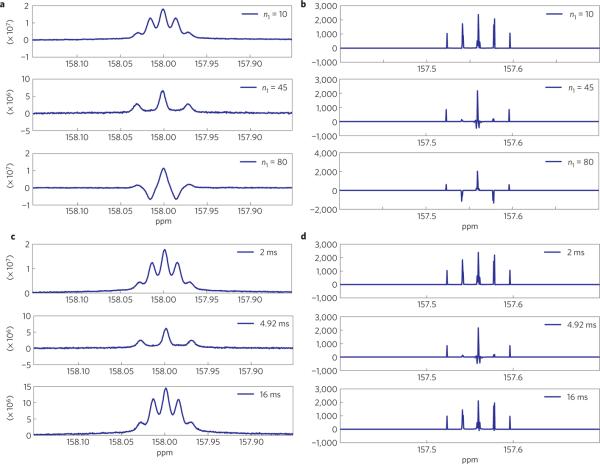
Figure 3 compares 360 MHz (8.45 T) NMR spectra after the initial part of the M2S sequence (essentially a CPMG sequence) against those simulated with the SPINACH simulation package^30–33, which uses Bloch–Redfield–Wangsness^34,35 relaxation theory. These spectra correlate with density matrix transformations from ρ₁ to ρ₂ outlined in equations (4) and (5). Interconversion within the SS/T₀T₀ and ST₀/T₀S two-level systems only occurs when the interpulse delay permits a resonance effect with the two-level state mixing. This effect manifests itself in the spectra (for example Fig. 3b), where inversion of the two side peaks demonstrates interconversion between coherences involving a triplet and those involving a singlet. The consistent results from experiments and simulation show that an interpulse delay of 4.92 ms induces the most efficient exchange between the carbon singlet and triplet manifolds, which corresponds in the simulation to J_CC = 101.6 Hz and J_CH = 3.4 Hz between each carbon and the adjacent methylene protons. The maximum conversion is reached when the two middle side peaks are completely suppressed (for example, middle row of Fig. 3b). This requires 45 180° pulses, which is not surprising given the large J_CC/J_CH ratio. Accordingly, the second multiple echo pulse train requires 22 180° pulses. Figure 4 shows the signal decay after the complete M2S–S2M sequence detailed in Fig. 1b. Slow singlet order decay is observed in both simulation (Fig. 4a) and experiment (Fig. 4b) after the initial fast triplet signal decay (this fast decay observed to be about 1.8 s is omitted in Fig. 4). For the experiment, the best single exponential fit produces a time constant T_S of around 50.6 s, which is about twice as long as the measured T₁ (22.2 s) of the carbonyl ¹³C spin, whereas in simulation the fitted T_S of 110.2 s is about six times T₁ (17 s given a 40 ps correlation time). This predicted longer lifetime is not unexpected for several reasons (for example, dipole–dipole (DD) interactions from remote methyl protons are disregarded in the simulation; the solvent is not degassed).

Figure 3. Single scan ¹³C spectra of DEO-¹³C₂ acquired after the CPMG part of the M2S sequence.

a,b, Consistent pertubation in ¹³C spectra in experiment (a) and simulation (b) after the CPMG sequence with the same interpulse delay (4.92 ms) and with various numbers of echo pulses (n₁); maximum conversion in the singlet-triplet subspace occurs after 45 echo pulses, middle row of b, which is the spectrum after a perfect conversion from carbon triplet to singlet (see the text). c,d, Consistent pertubation in ¹³C spectra in experiment (c) and simulation (d) after the CPMG sequence with the same number of echo pulses (n₁ = 45) and various interpulse delays (τ = 2, 4.92 or 16 ms). Minimum perturbation can be observed with 2 or 16 ms interpulse delays.

Figure 4. DEO ¹³C signal from the M2S-τ_r-S2M sequence decays as a function of the waiting time τ_r.

a–c, Signal intensity is normalized against the full thermal polarized magnetization in all cases (simulation at thermal condition (a), experiment at thermal condition (b) and natural logarithm of DNP-hyperpolarized signal (c)), all estimations include a 95% confidence interval. In a, a rotational correlation time of 40 ps is assumed, corresponding to a T₁ of 17 s in a 360 MHz B₀ field. The singlet signal decays with a lifetime T_S of 116.8±7.4 s. In b, T₁ of ¹³C₂-DEO is measured to be 22.2±0.6 s in a Bruker 360 MHz magnet, the sample is dissolved with DMSO-d6. The singlet signal decays with a lifetime T_S of 50.6±2.1 s. In c, the hyperpolarized singlet signal is acquired in a 7 T (300 MHz) Bruker MRI scanner and plotted on a semilog scale. A T_S of 41.4±3.2 s is obtained compared with a T₁ of 23±0.6 s.

To prove that lifetime extension does not depend on the polarization level we also conducted the analogous experiment with hyperpolarized initial states, this time using a 7 T animal imager with about 1 ppm linewidth (Fig. 4c). These data show that the presented technique does not require high homogeneity, and can readily be adapted to experiments using hyperpolarization for applications such as in vivo magnetic resonance imaging (MRI).

The lifetime extension in the examined molecule is modest, but this is clear evidence that the proposed pulse sequence successfully stores bulk magnetization in the singlet spin order, which has extended lifetime compared with T₁. The residual relaxation of the singlet state is complicated and depends on the structure of the multi-spin system^36–39. For instance, states that are linear combinations or products of localized singlet states (for example `singlet–singlet' in a 4-spin system) are likely to be long-lived³⁸. Yet in DEO–¹³C₂, states such as |S(αα)S〉 accessed by the current sequence are not entirely immune from DD relaxation, because of strong dipole couplings between protons in the same methylene group. Residual relaxation can be further reduced by deuteration of the methyl groups, suppressing remote DD interaction from methyl protons. Relaxation due to interaction with unpaired electron spins is also worthy of consideration, such as in the context of hyperpolarization experiments where organic radicals are used. Also as pointed out in the literature, oxalates tend to chelate transitional metal ions⁴⁰. Relaxation caused by paramagnetic species has been generally described by assuming randomly fluctuating fields generated by the paramagnetic species at the nuclear sites^9,41. Its relaxation effects on the singlet state between chemically inequivalent spins have been discussed^23,42 and a strong correlation between the random fields at the two nuclear sites reduces the relaxation enhancement on the singlet state lifetime compared with that on T₁. The same argument is most likely valid in the case with chemically equivalent spins. Noticeably, ethylenediamine tetraacetate and ascorbate⁴³ have been proven to reduce relaxation due to paramagnetic agents by forming stronger chelates or by reacting with superoxide species.

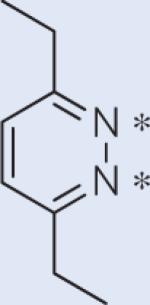
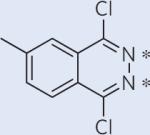
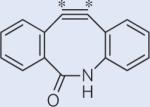
The general method presented here can be undoubtedly applied to a broad range of molecules; a few examples are shown in Table 1. For symmetric spin systems with modest scalar couplings, this technique works at any field strength; it can also be applied to slightly unsymmetric systems at moderate field strengths. Significant lifetime extension is also appealing for ¹⁵N spin pairs, where, in favourable cases T₁ can be a couple of minutes. We also included two cyclooctyne derivatives (the second and last in Table 1), which can go through a strain-promoted azide–alkyne reaction. Developed by Bertozzi et al.⁴⁴, these molecules can be used for specific labelling of biomolecules and potentially for in vivo molecular imaging. We get similar improvements for gemdifluoro compounds, which are often biologically compatible; for example, for 2,2-difluorosuccinic acid we predict a singlet state about ten times T₁ at 8.45 T. However, we should note that our theoretical predictions are most credible for rigid structures, and a formal procedure including a Boltzmann average over all relevant geometries would be essential for flexible molecules.

Table 1.

Examples of molecules that have isolated ¹³C or ¹⁵N spin pairs and ideal scalar couplings that permit application of the current pulse sequence technique.

Ts/T1	B0 =8.45 T	B0 =3 T	JCC(NN)/JCH(NH), JNN/Δω
	4.8	14.5	3.8
	3.6	8.9	28
	7.2	9.1	6
	–	12*	4.3*
	–	16†	5.4, 29†

The singlet state lifetime (T_s) versus spin-lattice relaxation time (T₁) ratios (T_s/T₁) as well as J_CC(NN)/J_CH(NH), J_CC(NN)/Δω ratios (J_CH(NH) is the biggest heteronuclear coupling) are predicted at field strengths of 8.45 and 3 T unless noted otherwise. Time constants are derived from the inverse of matrix elements of the incoherent relaxation superoperator. Relaxation due to coherent oscillation is disregarded here, as it is quenched by dominant scalar couplings across the singlet spin pair.

^*The two ¹⁵N spins have an estimated chemical shift difference (Δω) of 3 ppm. The T_s/T₁ ratio is therefore estimated at a field strength of 0.5 T, which leads to a J_NN/δω ratio around 4.3.

^†A chemical shift difference of around 2 ppm is estimated between the ¹³C₂ spin pair. Estimations of lifetime extension are made at field strength of 1.5 T, where J_CC/J_CH≅29 and J_CC/Δω≅5.4.

Our demonstration of the M2S–S2M pulse sequence accomplishes interconversion between magnetization and singlet state population in chemically equivalent spin pairs without requiring symmetry breaking. This can be applied to other symmetric (and for that matter slightly asymmetric) spin systems. Essentially this will work for any symmetric molecule containing two directly bonded ¹³C or ¹⁵N atoms, without protons directly attached to these atoms. Furthermore, the J-coupling between the fluorine atoms in a CF₂ group will virtually always exceed J-couplings to other atoms. It is important to point out that singlet states are not guaranteed to be particularly long lived, depending on the specific molecular geometry; however, many such cases have been verified both experimentally and theoretically. Thus, singlet states at chemically equivalent sites may significantly aid the development of novel contrast agents for application using hyperpolarization techniques.

Methods

Sample preparation and experimental set-up for thermal polarized spectra

DEO–¹³C₂ (Isotec) was dissolved in undegassed dimethyl sulphoxide (DMSO)-d6 at a 2 M concentration. All spectra using thermal polarization were acquired on a Bruker 360 MHz (~8.45 T) magnet with a 5 mm 1H and X broadband probe. A single scan was acquired for each spectrum. Fractional uncertainty due to spectrum noise was consistent and determined to be no more than one thousandth of the lowest signal (last point in Fig. 4b), therefore it is not shown in Fig. 4. The same is true for the hyperpolarized spectra described below.

Sample preparation and experimental set-up for hyperpolarized spectra

Studies combined with hyperpolarization were performed on a 7 T Bruker Biospect small animal MRI scanner. The samples contained 4 μl DEO–¹³C₂ (Isotec), 1 μl DMSO (Sigma-Aldrich), and 15 mM Finland Radical (GE Healthcare). Hyperpolarization was achieved using a Hypersense hyperpolarizer (Oxford Instruments Molecular Biotools). The polarization time constant was 1,600 s. After 1 h of polarization the dissolution of the sample was performed with 3 ml of DMSO at 140°C, resulting in a solution of 0.8 mM hyperpolarized DEO. 50 μl of the hyperpolarized DEO (40 nmol DEO) were placed inside a lab-built solenoid coil. In a separate experiment, the liquid state polarization of the hyperpolarized DEO, 40 s after dissolution, was measured to be 3,300 times greater than thermal polarization. The 40 s delay between dissolution and acquisition allowed time for transferring the sample from the Hypersense to the scanner, placing the hyperpolarized DEO inside the coil, and beginning the scan. For experiments reporting retrieved singlet polarization as a function of singlet decay time, the following formula was used:

$$S_{\text{Hyperpolarized,singlet}}∕S_{\text{Thermal}}=3,300\times \frac{\sin (5°)}{\sin (90°)}\times \frac{S\left(\text{MSM}\right)}{S(5°-\text{acquire})}$$

where S(MSM) was the signal after the MSM pulse sequence, and S(5° – acquire) was the signal from a 5° -acquire pulse sequence that was performed immediately (100 ms) before the MSM sequence. To determine the relaxation rate of the singlet state, a line was least-squares fitted to ln(S_{Hyperpolarized,singlet}/S_Thermal) as a function of waiting time, τ_r.

Simulation method

Prediction of chemical structure and all nuclear parameters (chemical shielding, scalar coupling, and so on.) was conducted with Gaussian 09 (ref. 45). Geometry optimization was conducted with DFT method, specifically with the B3LYP/6–31+G* hybrid functional and basis set combination; single point energy calculations with `GIAO' and `SPINSPIN' key words were performed with B3LYP/aug-cc-pVTZ (refs 46–50). The predicted properties were used in SPINACH (ref. 30) to predict primary interactions such as DD, chemical shielding anisotropy and cross correlations thereof. From there, the relaxation profiles of DEO–¹³C₂ due to perturbing fields were simulated with semi-classical relaxation theory assuming a 40 ps isotropic rotational correlation time.