A Bayesian Multiple Imputation Method for Handling Longitudinal Pesticide Data with Values below the Limit of Detection

Abstract

Environmental and biomedical research often produces data below the limit of detection (LOD), or left-censored data. Imputing explicit values for values < LOD in a multivariate setting, such as with longitudinal data, is difficult using a likelihood-based approach. A Bayesian multiple imputation (MI) method is introduced to handle left-censored multivariate data. A Gibbs sampler, which uses an iterative process, is employed to simulate the target multivariate distribution within a Bayesian framework. Following convergence, multiple plausible data sets are generated for analysis by standard statistical methods outside of a Bayesian framework. With explicit imputed values available variables can be analyzed as outcomes or predictors. We illustrate a practical application using longitudinal data from the Community Participatory Approach to Measuring Farmworker Pesticide Exposure (PACE3) study to evaluate the association between urinary acephate concentrations (indicating pesticide exposure) and self-reported potential pesticide poisoning symptoms. Additionally, a simulation study is used to evaluate the sampling property of the estimators for distributional parameters as well as regression coefficients estimated with the generalized estimating equation (GEE) approach. Results demonstrated that the Bayesian MI estimates performed well in most settings, and we recommend the use of this valid and feasible approach to analyze multivariate data with values < LOD.

Introduction

Environmental and biomedical research often produces data below the limit of detection (LOD) due to constraints of measurement methods. Such data are referred to as left-censored data or non-detections. These data are informative but incomplete in the sense that the true values are greater than zero but less than the LOD. A variety of methods have been proposed to utilize the information provided by the non-detections without any knowledge of their explicit values. The majority of methods are especially well suited to analyze the left-censored data as the outcomes of interest (for example, Helsel 2005a; Helsel 2005b; Chu et al. 2008; Fu and Wang 2011). In situations where the left-censored data (e.g., analytes) are exposures or predictor variables researchers can use Theil-Sen estimator for simple linear regression when both the outcome and the predictor are left-censored (Akritas 1995) or rely on the categorization of the left-censored data based on the LODs followed by analysis of the detected values alone. However, to adequately determine the nature of the relationship between analyte(s) and the outcome of interest in more complex models, the explicit values of non-detections are needed. This leads to more and more researchers to opt for imputation of values below the LOD.

Whereas researchers have historically used simple substitution methods (e.g., LOD, LOD/2 or $\text{LOD}/\sqrt{2}$) to generate explicit values for non-detections, today more statistically sound approaches are available (Hopke et al. 2001; Groves et al. 2002; Gelman et al. 2004; Lockwood and Schervish 2005). Such approaches include Bayesian methods and multiple imputation (MI). The Bayesian methods usually involve imputing left-censored data using a data augmentation (DA) technique and draw inferences such as estimation of summary statistics or regression coefficients based on prediction with a Bayesian framework. These procedures have been applied to several studies such as examinations of chemicals in water resources (Lockwood et al. 2004; Francis et al. 2009; Francis et al. 2010), and road site contaminations (Fridley and Dixon 2007). Although highly valuable and increasingly popular, currently, widespread use of the Bayesian analysis completely within the Bayesian network by ordinary researchers is impeded by the need for extensive specialized training in Bayesian theory as well as computational techniques, especially when the modeling of the data is complex.

The MI approach provides a compelling alternative for addressing the issue of left-censoring. This approach creates a small number of multiply imputed data sets, typically five to ten. Each complete data set is analyzed and the results are combined to account for the uncertainty embedded in the imputed values (Little and Rubin 2002). Results obtained using an MI approach, like those obtained from the Bayesian methods, accommodate left-censored data while at the same time retaining good statistical properties for the parameter estimates. MI methods offer a relatively straightforward, yet rigorous, way of analyzing complicated scientific questions, while involving significantly less programming effort. Once the complete data sets are generated, most analyses can be performed with readily available standard statistical techniques and software packages (e.g., SAS). Specifically, distribution-based MI methods have been applied to left-censored data in both univariate (Baccarelli et al. 2005; Huybrechts et al. 2002; Lubin et al. 2004) and bivariate settings (Chen et al. 2011). These methods of MI first obtain estimates of the distribution parameters using a likelihood-based approach. Then the values below the LOD are imputed multiple times based on the parameter estimates to create multiple complete data sets.

The extension of a distribution-based MI method to cope with left-censored data in a multivariate setting confronts a significant practical barrier: the estimation of parameters for a left-censored multivariate distribution involves the implementation of the expectation-maximization (EM) algorithm, which can be extremely complex, computationally intensive, and time consuming (Dempster, Laird and Rubin 1977). This drawback severely hinders its application to high dimensional multivariate data in practice. This paper demonstrates how a longitudinal pesticide concentration data set with values below the LOD can be imputed using a frequently used tool in Bayesian methodology called the Gibbs sampler (Gelfand et al. 1990), and subsequently analyzed with MI method. That is, following the creation of multiply imputed data sets, all statistical inferences will be based on theory well established for MI methods, outside of the Bayesian framework. We note that the built-in procedures for MI in most commercial statistical packages assume that the data are missing at random (MAR), an assumption that is violated for left-censored data. Thus, a customized program based on SAS IML (Cary, NC) is used to implement this Bayesian MI method. This SAS macro is available from the authors upon request.

Furthermore, many non-human environmental data have large sample sizes, commonly in the magnitude of thousands. Human studies frequently have comparatively fewer observations which impose additional constraints on the efficiency of parameter estimates in the presence of left-censoring. Therefore, we conduct a simulation study to evaluate the influence of various degrees of left-censoring and a range of small to moderate sample sizes on the parameter estimates obtained from the Bayesian MI method. Robustness of the approach is also investigated.

Methods

In this section, we detail the necessary steps to perform Bayesian MI. We first introduce notations for a left-censored multivariate setting. For clarity we use bolded letters to represent vectors and matrices and non-bolded for individual random variables. Consider p variables Z = {Z_j, j = 1, …, p}. These variables represent not only multivariate data that arise from repeated measures over time (e.g., collection of the same analyte over time in a longitudinal study), but also multivariate data that emerge from the simultaneous evaluation of multiple discrete analytes in a cross-sectional study. Let Z_ij denote the jth observation on subject i for i = 1, …, n; j = 1, …, p. To simplify notation, a row vector Z_i is used to denote the p multivariate measures on subject i. We assume that Z_i’s are independently and identically distributed as multivariate normal. We further assume that each variable Z_j is subject to left-censoring with fixed and known LOD, denoted as L_j, j = 1, …, p. With such left-censored data, the values below the LODs are neither completely missing nor completely observed. This type of incomplete data is referred to as coarsened data (Heitjan and Rubin 1990). In the situation where LODs are fixed and known, the coarsening mechanism can be considered as coarsening at random (CAR), and therefore appropriate to ignore the randomness in the coarsening process for Bayesian and likelihood inferences (Heitjan and Rubin 1991).

Next we describe a multivariate MI of left-censored data using Gibbs sampler (Hopke et al. 2001). Gibbs sampler is a type of Markov Chain Monte Carlo (MCMC) method that aims to simulate direct draws from a target distribution using iterative algorithms. The most attractive feature of Gibbs sampler is that it only requires draws from univariate conditional distributions at each step. Values simulated from successive iterations form a Markov chain (or Gibbs sequence). The Gibbs sequence converges to the target multivariate distribution through a large number of iterations of sequential sampling from the univariate conditional distributions. The conditional distributions involved in the Gibbs sampler for the multivariate normal subject to left-censoring are described below.

Let ${\sigma }_j^2$ and β_j,k represent the residual variance and regression coefficients (including an intercept) for the regression of Z_j on the remaining variables {Z_k, k ≠ j}. For ease of exposition, we use vector notations L = {L_j, j = 1, …, p} and β_j = {β_j,k, j = 1, …, p; k = 0, 1, …, p and k ≠ j} for the derivations below. In addition, let X_j be the design matrix for the regression equation. The multiple linear regression equation defines the likelihood function of Z_j to be a univariate normal:

$$f(Z_j\mid {\sigma }_j^2,{𝛃}_j,{\mathit{X}}_j,\mathit{L})~N({\mathit{X}}_j{𝛃}_j,{\sigma }_j^2).$$ (1)

We choose Jeffery’s prior as the prior distribution for ${\sigma }_j^2$ and β_j. Namely,

$$f({\sigma }_j^2,{𝛃}_j)\propto 1/{\sigma }_j^2.$$ (2)

Equations (1) and (2) collectively define the joint posterior distribution for ${\sigma }_j^2$ and β_j, that is, $f({\sigma }_j^2,{𝛃}_j\mid \mathit{Z},\mathit{L})$. We note that $f({\sigma }_j^2,{𝛃}_j\mid \mathit{Z},\mathit{L})$, can be factored into the product of the posterior for ${\sigma }_j^2$ and the conditional posterior for ${𝛃}_j\mid {\sigma }_j^2$:

$$f({\sigma }_j^2,{𝛃}_j\mid \mathit{Z},\mathit{L})=f({\sigma }_j^2\mid \mathit{Z},\mathit{L})\times f({𝛃}_j\mid {\sigma }_j^2,\mathit{Z},\mathit{L}),$$ (3)

where ${\sigma }_j^2\mid \mathit{Z},\mathit{L}$ follows an inverse χ² distribution and ${𝛃}_j\mid {\sigma }_j^2,\mathit{Z},\mathit{L}$ is distributed as a multivariate normal (see details later). Random draws from the posterior predictive distribution for Z_j can be achieved by alternating draws based on equations (3) and (1) and used for imputing values below the LOD.

The Gibbs sampler is carried out as follows based on these conditional distributions. At iteration t = 0, data are initialized by assigning arbitrary starting values to values below the LOD. It is arbitrary in the sense that the Gibbs sequence will converge to a stationary distribution that is independent of the choice of the starting values. A practical choice of the starting values for observations below the LOD can be random draws from a normal distribution based on the mean and variance of the detected values. At iteration t +1, for j = 1, …, p, all p variables are cycled through sequentially with the following steps.

• Step 1: regress $Z_j^{(t)}$ on { $Z_k^{(t+1)}$, k < j} and { $Z_k^{(t)}$, k > j} to obtain estimates for residual variance, ${\widehat{\sigma }}_j^{2(t+1)}$, and regression coefficients, ${\widehat{𝛃}}_j^{(t+1)}$. Note that in this regression equation, the values below the LOD for {Z₁, …, Z_j−1}have been updated with random draws from their respective posterior predictive distributions (see step 4); while the values below the LOD for {Z_j+1, …, Z_p} are still values from the previous iteration t. Thus, the design matrix ${\mathit{X}}_j^{(t+1)}$ needs to be constructed accordingly.

• Step 2: draw a random observation ${\stackrel{\sim }{\sigma }}_j^{2(t+1)}$ from the marginal posterior for ${\sigma }_j^2$,

  $${\stackrel{\sim }{\sigma }}_j^{2(t+1)}~f\left({\sigma }_j^2|\mathit{Z}=\left\{Z_k^{(t+1)},k<j;Z_k^{(t)},k\ge j\right\},\mathit{L}\right),$$

  which is an inverse χ² distribution with n − p degree of freedom and scale parameter ${\widehat{\sigma }}_j^{2(t+1)}$.

• Step 3: draw a random observation ${\stackrel{\sim }{𝛃}}_j^{(t+1)}$ from the conditional posterior for ${𝛃}_j\mid {\sigma }_j^2$,

  $${\stackrel{\sim }{𝛃}}_j^{(t+1)}~f\left({𝛃}_j|{\sigma }_j^2={\stackrel{\sim }{\sigma }}_j^{2(t+1)},\mathit{Z}=\left\{Z_k^{(t+1)},k<j;Z_k^{(t)},k\ge j\right\},\mathit{L}\right),$$

  which is a multivariate normal with mean ${\widehat{𝛃}}_j^{(t+1)}$, and variance-covariance matrix ${\stackrel{\sim }{\sigma }}_j^{2(t+1)}{\left({\mathit{X}}_j^{{(t+1)}^{\prime }}{\mathit{X}}_j^{(t+1)}\right)}^{-1}$.

• Step 4: impute values below the LOD for Z_j with independent random draws from its posterior predictive distribution. This is accomplished via random draws based on equation (1), that is,

  $$Z_j^{(t+1)}~f\left(Z_j\mid {\sigma }_j^2={\stackrel{\sim }{\sigma }}_j^{2(t+1)},{𝛃}_j={\stackrel{\sim }{𝛃}}_j^{(t+1)},{\mathit{X}}_j={\mathit{X}}_j^{(t+1)},\mathit{L}\right),$$

  from a univariate normal with mean ${\mathit{X}}_j^{(t+1)}{\stackrel{\sim }{𝛃}}_j^{(t+1)}$, and variance ${\stackrel{\sim }{\sigma }}_j^{2(t+1)}$, subject to the constraint that the imputed values $Z_j^{(t+1)}$ are less than L_j. The values above the LOD remain unchanged throughout the iterations.

To summarize the process described above, two basic steps are involved in a Gibbs sampler at each iteration: a posterior step (P step) and an imputation step (I step). During the P step (steps 1–3) the parameter values are updated from the posterior distributions based on the data from the previous iterations and previous steps within the current iteration, while during the I step (step 4) the coarsened data are imputed from the posterior predictive distributions based on the current parameter values. Data that are completely missing can also be imputed without additional burdens if they are considered as MAR. With the completion of one iteration one set of values are simulated for the left-censored multivariate distribution. Eventually, the Gibbs sequence will approximate the target multivariate distribution through a sufficiently large number of iterations.

In practice, convergence diagnostics need to be conducted carefully before any inferences can be drawn. Graphical evaluations such as trace plots and autocorrelation function (ACF) plots, time series statistics such as potential scale reduction factors (PSRF), as well as formal statistical tests are available to test the stationarity of the Gibbs sampler (Geweke 1992; Raftery and Lewis 1992; Gelman et al. 2004). After the Gibbs sampler is deemed convergent to the target distribution, multiply imputed data sets can be output from the Gibbs sequence, usually from near the end of the sequence. Since sample draws from adjacent iterations are correlated in a Gibbs sequence, thinning is commonly performed by keeping only every kth draw to reduce sample autocorrelations. There is no deterministic rule for the choice of k. It is largely dependent upon how quickly the simulated draws are moving around the parameter space (Gilks et al. 1996). Alternatively, several Gibbs sequences can be run independently to create multiply imputed data sets. Analyses using standard statistical techniques can be performed on each imputed data set and results can be combined for valid statistical inferences.

A Case Study of Longitudinal Acephate Data across Four Different Periods in the Agricultural Season

The Data

This research is motivated by the longitudinal data collected from the Community Participatory Approach to Measuring Farmworker Pesticide Exposure (PACE3) study. In this longitudinal study, urinary pesticide concentrations were measured across four time periods in the 2007 agricultural season from a total of 287 farmworkers (Arcury et al. 2009). This demonstration focuses on concentrations of the urinary analyte for acephate (APE), an organophosphorus (OP) pesticide widely used to treat tobacco (Southern and Sorenson 2008). In each period, study participants also responded to interviewer-administered questionnaires to assess immediate symptoms indicative of potential pesticide poisoning including nausea, burning nose or throat, rash, vomiting, dizziness, headache, red or burning eyes, blurred vision, and/or weak or heavy arms in the last 3 days (Reigart and Roberts 1999). The presence of any of the nine symptoms was our primary health outcome in this analysis.

Since the emphasis of the paper is on the handling of the values below the LOD, observations with missing APE values were excluded. Furthermore, farmworkers involved in activities such as topping, harvesting, or curing pesticide-treated tobacco were almost definitely exposed to APE. Thus, we also excluded observations from farmworkers with an APE measurement < LOD who did not top, harvest, or barn tobacco during the corresponding period, to avoid imputing a positive value for a true zero. The final sample comprised 234 farmworkers and 553 data points across the four time periods. Specifically, 54 (23.1%), 72 (30.8%), 77 (32.9%), 31 (13.2%) individuals contributed 1, 2, 3, and 4 observations to the data analyses.

Preliminary examination of the data suggested that a lognormal distribution appeared a reasonable assumption for the APE concentrations. Consequently, all analyses were conducted on the log scale. This included the log transformation of the LOD. Little to heavy left-censoring for the APE analyte was observed in different periods, with values below the LOD ranging from 4% in period 1 to 47% in period 4 (Table 1).

Table 1.

Degree of left-censoring of APE data (frequencies and percentages)

	Period 1	Period 2	Period 3	Period 4
≤LOD	3 (4.3)	22 (20.2)	28 (14.0)	82 (46.9)
>LOD	66 (95.7)	87 (79.8)	172 (86.0)	93 (53.1)
Total	69	109	200	175

Monitoring Convergence

We employed the Bayesian MI method described above to simulate the multivariate distribution of interest. We ran five independent sequences of Gibbs sampler. For each sequence we used 5000 iterations and a burn-in sample of 1000 (the first 1000 iterations) was discarded to reduce the influence of the starting values on the convergence of the Gibbs sequence. Convergence was first visually assessed using trace plots and ACF plots. A trace plot for a parameter is a plot of sample draws from its posterior distribution against the iteration indices. All the trace plots indicate that the mixing of the Gibbs sequences were quite good. There were some fluctuations around the center of the sequences and no obvious patterns were present (details not shown). An ACF plot for a parameter is a graphic display of the serial correlations between adjacent sample draws (autocorrelation) as a function of the time lag. All autocorrelations appeared to decay toward 0 as the lag increased. On the whole, the autocorrelations were all very weak by lag 50 with most autocorrelations being close to 0 (details not shown). We also computed PSRF for each parameter on the basis of between- and within-sequence variances of the five parallel sequences. For our log APE data all PSRFs are close to 1 (less than 1.01), indicating good mixing of all the sequences. In summary, both visual and quantitative analyses provide no evidence against the convergence of the Gibbs sampler in the analyses of the four repeated measures on log APE concentrations.

Analysis using multiply imputed data sets

We output the data set from the last iteration for each of the five independent sequences to approximate independent draws from the target multivariate distribution. Normal quantile-quantile (Q-Q) plots were used to examine the overall distribution of the observed (> LOD) and the imputed (≤ LOD) log APE concentrations in different time periods. Figure 1 displays the Q-Q plot for each time period with values from the five imputed data sets overlaid in the same panel. A horizontal reference line valued at log LOD was drawn to separate the observed data values (> LOD and common to all imputed data sets) and the imputed data values (≤ LOD and vary from data set to data set). The plots indicate greater variability in the imputed values near the tail of the distribution (extreme values); otherwise, the imputed values overlapped substantially across different imputations. Furthermore, a slanting reference line was drawn using Bayesian MI estimates (described below) of the mean as intercept and standard deviation as slope. Overall, both the observed and the imputed values tend to fall on the reference line except for period 2. This suggests that there might be a slight deviation from normality for period 2. We therefore examined simultaneous 95% confidence band (CB) for the Q-Q plot for each of the five imputed data set for each period (Doksum 1974). The reference lines are contained in the CBs for all five imputed data sets for periods 1 and 4; while the reference lines cross the CBs in the area right below the log (LOD) for period 3 and in the area close to the middle of the distribution for period 2 for all five imputed data sets. However, as a whole, the log transformed data conform reasonably well to the estimated multivariate normal distribution.

Figure 1.

Normal Quantile-Quantile plots of observed and imputed log APE in different periods

We estimated the distributional parameters using the multiply imputed data sets. Summary statistics including geometric means, geometric standard deviations (SD), and pairwise correlations were produced using data from each individual imputed data set and the results were combined to yield valid point estimates (Table 2). The APE concentration, represented by geometric means, reveals a significant seasonal pattern (p < 0.0001) with the lowest in period 4 (0.05 ng/mL) and the highest in period 3 (0.66 ng/mL). The APE concentration is most variable in period 4 and least variable in period 1 with estimated geometric SDs of 45.35 and 4.60, respectively. In general, the correlations between the repeated measures are not very strong in this study, with the weakest being close to 0 for periods 1 and 3 and the strongest being around 0.4 for periods 3 and 4.

Table 2.

Geometric means ± geometric standard deviations (GSD) for APE concentrations in different periods and odds ratios (95% confidence intervals) for every unit increase in log APE for predicting pesticide poisoning symptoms using Bayesian MI and some ad hoc methods

	Bayesian MI	Impute log (LOD)	Impute log (LOD)/2	Exclusion of non-detections
Period 1: geometric mean± GSD	0.47±4.60	0.48±4.42	0.52±3.90	0.55±3.92
Period 2: geometric mean± GSD	0.44±11.49	0.57±7.13	0.83±4.08	1.27±3.49
Period 3: geometric mean± GSD	0.66±9.12	0.76±6.80	0.99±4.48	1.34±4.04
Period 4: geometric mean± GSD	0.05±45.35	0.17±10.08	0.40±5.18	0.95±6.52
OR (95% CI)	1.08 (0.97–1.20)	1.09 (0.97–1.23)	1.09 (0.94–1.26)	1.04 (0.88–1.23)

Next we fit logistic regression models to investigate the association of APE concentrations with the presence of potential pesticide poisoning symptoms. About 43%, 52%, 42%, and 44% of the farmworkers experienced at least one of the nine symptoms in periods 1, 2, 3, and 4, respectively. A generalized estimating equation (GEE) approach was used to account for the correlation among the repeated measures within each imputed data set. The results were combined using SAS PROC MIANALYZE to obtain valid point estimates and standard errors that incorporate both between- and within-imputation variability. The explanatory variables in the model included log APE, time, and their interaction effect. No significant time, log APE, and time by log APE interaction effects were found. On average, with one unit increase of log APE, the odds of reporting any symptoms increased by 8%. The odds ratio (OR) and the associated 95% confidence interval (CI) are 1.08 (0.97–1.20), p =0.15.

Finally, we repeated the above analyses using some ad hoc approaches, specifically, simple substitution for non-detections using the log (LOD) and log (LOD)/2, as well as exclusion of non-detections completely in the analyses. Distributional parameter estimates from these methods are substantially different from those based on the Bayesian MI method. Compared to the Bayesian MI estimates, all three ad hoc methods yielded elevated estimates for the mean APE concentrations and reduced estimates for the variability in different time periods (Table 2). These phenomena agree with what has been previously reported in the literature (Helsel 2005b). The estimated correlation among the repeated measures for the ad hoc strategies varied in terms of magnitude and direction (i.e., positive or negative) in contrast to the Bayesian MI estimates for the correlations. As for the OR estimates, the two simple substitution approaches yielded a somewhat similar effect of log APE on the presence of any symptoms with wider CIs (OR 1.09, 95% CI: 0.97–1.23, p = 0.16 and OR 1.09, 95% CI: 0.94–1.26, p = 0.23, respectively); while the exclusion of non-detections yielded a slightly weaker effect of log APE (OR 1.04, 95% CI: 0.88–1.23, p=0.66).

Simulation Study

We conducted a simulation study to assess the effect of various degrees of left-censoring and different sample sizes on the performance of the Bayesian MI method. We examine the sampling property of the Bayesian MI estimators for the distributional parameters of the multivariate left-censored data as well as for the regression coefficients when the left-censored data are used as predictors in a longitudinal binary outcome setting that is similar to our case study. Situations where the assumption about the underling distribution deviates from the truth are also investigated. Each MI estimate was obtained from five multiply imputed data sets. All simulation results were based on 5000 replicates of parameter estimates.

The Estimation of Distributional Parameters

For simplicity, we considered a trivariate normal distribution with an equal variance of one for z₁, z₂, and $z_3({\sigma }_1^2={\sigma }_2^2={\sigma }_3^2=1)$. The pairwise correlations were set as ρ₁₂ = ρ₂₃ = 0.4 and ρ₁₃ =0.2. This mimics a correlation structure that might occur in a longitudinal study where the observations taken at adjacent time points have stronger correlations whereas the observations taken at distant time points have weaker correlations. Without loss of generality, we assume that the mean of z₁(μ₁) is zero. The means of z₂(μ₂) and z₃(μ₃), together with LOD, were chosen so that the marginal distributions of z₁, z₂, and z₃ are subject to different levels of left-censoring. Additionally, we examined four different sample sizes (n = 50,100,200 and 400) that occur commonly in environmental studies involving human subjects.

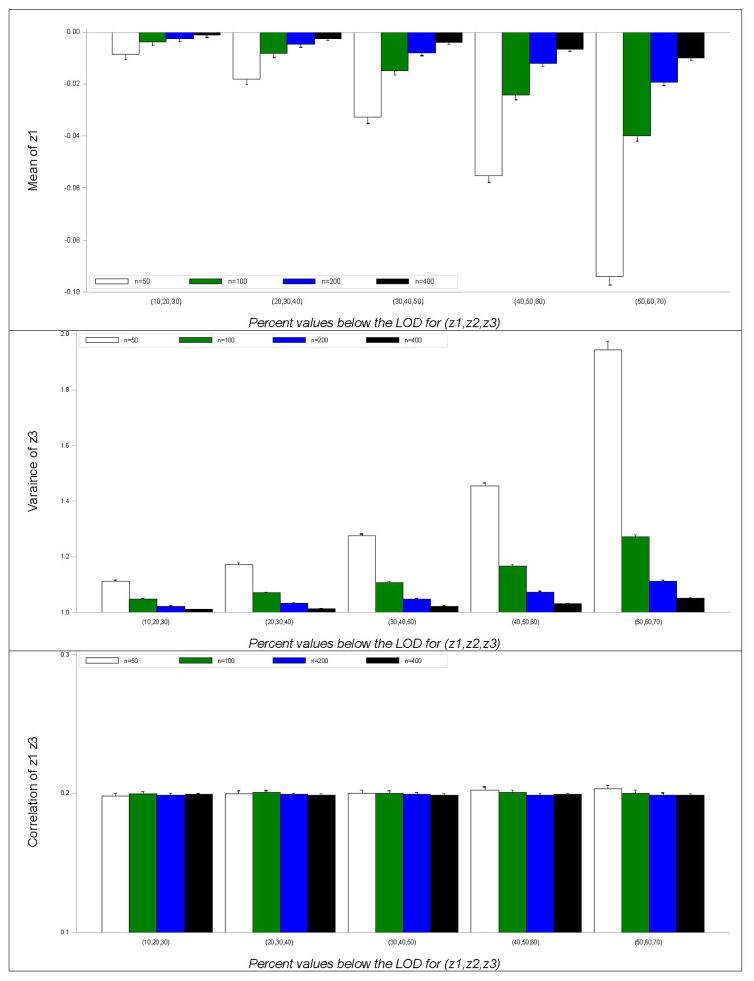
For brevity, only the simulation results for the Bayesian estimates of μ₁, ${\sigma }_3^2$, and ρ₁₃ were summarized in Figure 2, with error bars representing the standard error (SE) of each estimate. As expected, the variability of an estimate (as indicated by SE) decreases as the sample size grows larger and increases as the degree of left-censoring becomes heavier. Overall, the bias in the mean estimates diminishes as the sample size increases. Results indicate that for a fixed degree of left-censoring, a doubling of sample size leads to a roughly 50% reduction in the bias of the mean estimates. This effect is especially notable in the situation of heavy left-censoring. The results for the variance estimates exhibit similar patterns. For example, ${\sigma }_3^2$ was overestimated by 94.5%, 27.2%, 11.3%, and 4.9% at sample size of 50, 100, 200, and 400, respectively, when 70% of z₃ was below the LOD. Further, the increase in the degree of left-censoring exacerbates the estimation bias in the means and variances. For instance, ${\sigma }_1^2$ was only overestimated by 3.5% with a sample size of 50 and 10% of z₁ below the LOD; while that bias accelerated to 28.4% with the same sample size but 50% of z₁ below the LOD. Strikingly, the correlation estimates perform remarkably well under either small sample size and/or heavy degree of left-censoring. The bias was minimal across all the simulation settings carried out in this study, ranging from 0.1% to 1.5%.

Figure 2.

Bayesian multiple imputation estimates for μ₁, ${\sigma }_3^2$, and ρ₁₃

Note: The true values for μ₁, ${\sigma }_3^2$, and ρ₁₃ are 0, 1, and 0.2, respectively.

The Estimation of Regression Coefficients

In this portion of the simulation study we aim to provide a preliminary comparison for the Bayesian MI, the distribution-based MI, and the simple substitution methods when left-censored data are used to predict a longitudinal binary outcome as in our case study. We first simulated a bivariate normal distribution for the time-varying predictor x = (x₁, x₂). Next we simulated a bivariate binary outcome y based on the assumed relationship logit(y_ij) = β₀ + β₁time_ij + β₂x_ij, i = 1, …, n, j =1,2. Then various degrees of left-censoring were imposed on (x₁, x₂). Logistic regression models were fit using a GEE approach with the left-censored data substituted by the LOD, or multiply imputed using distribution-based MI or Bayesian MI methods. Bias and mean square error (MSE) were calculated for the estimates of the regression coefficients. The relative efficiency (RE) of the distribution-based MI and Bayesian MI methods compared to the simple substitution method is defined as the ratios of the corresponding MSEs. Nominal coverage for 95% CIs and average width of CIs were also computed. We set β₂ = 0.1 in this study. This corresponds to an OR of 1.1, similar to the effect size observed in our case study.

Table 3 compares the estimates of β₂ obtained from the three different methods under various scenarios. By and large, the bias under both the distribution-based MI and the Bayesian MI methods is comparable to each other and is consistently smaller compared to the simple substitution method. When the amount of left-censoring is < 30%, the bias is nearly negligible even with a sample size of 50 under the two MI methods. In general, the bias increases for all three methods as the degree of left-censoring increases. However, the simple substitution method suffers more in comparison with the two MI methods. The bias can be as high as 70–90% for the simple substitution method, in contrast to 30–35% for the two MI methods. Elevated left-censoring leads to broader average CI width for all three methods. However, the two MI methods yield noticeably narrower CIs than the simple substitution method. In the presence of a large amount of left-censoring, the nominal CI coverage for the simple substitution method constantly dips below 95%, while it remains well above 95% for the two MI methods. Moreover, the REs for the two MI methods rise substantially as the left-censoring becomes heavier, indicating a significant improvement in the performance of the two MI estimates compared to the simple substitution estimate. When about a half of the data is below the LOD, the two MI methods can be 4–5 times as efficient as the simple substitution method.

Table 3.

Bias, coverage, average width of 95% confidence interval (CI), and means square error (MSE) for the regression coefficient estimate for x under the correct assumption that the underlying distribution for x is bivariate normal

		Simple substitution of LOD			Distribution-based MI			Bayesian MI
sample size	% <LOD (x1, x2)	bias	CI coverage	CI width	bias	CI coverage	CI width	bias	CI coverage	CI width	MSEs	MSEs/MSEd	MSEs/MSEb
50	(10,20)	0.0157	94.42	0.88	0.0021	95.10	0.80	0.0004	95.34	0.79	0.06	1.32	1.37
	(20,30)	0.0227	94.62	0.97	−0.0031	96.34	0.82	−0.0057	96.42	0.81	0.07	1.66	1.76
	(30,40)	0.0327	94.32	1.08	−0.0079	97.42	0.85	−0.0118	97.62	0.83	0.09	2.17	2.38
	(40,50)	0.0457	94.12	1.23	−0.0144	98.20	0.89	−0.0203	98.40	0.85	0.12	3.01	3.46
	(50,60)	0.0624	94.00	1.43	−0.0204	99.00	0.93	−0.0272	98.98	0.87	0.16	4.43	5.31
	(60,70)	0.0905	93.76	1.73	.*	. *	. *	−0.0362	99.34	0.89	0.27	. *	9.72
200	(10,20)	0.0140	94.80	0.44	0.0004	95.60	0.39	−0.0002	95.48	0.39	0.01	1.35	1.36
	(20,30)	0.0218	94.64	0.48	−0.0032	96.34	0.40	−0.0043	96.52	0.40	0.02	1.69	1.73
	(30,40)	0.0304	94.54	0.54	−0.0078	97.10	0.41	−0.0093	97.24	0.41	0.02	2.22	2.27
	(40,50)	0.0405	94.38	0.60	−0.0140	97.86	0.43	−0.0153	97.58	0.43	0.03	2.96	3.08
	(50,60)	0.0523	94.12	0.70	−0.0216	98.02	0.45	−0.0234	98.02	0.44	0.04	4.07	4.22
	(60,70)	0.0673	94.18	0.83	−0.0307	98.62	0.47	−0.0335	98.66	0.46	0.05	6.15	6.43

Note: The true regression coefficient for x is 0.1. MSE_s is the MSE for the estimate based on simple substitution of LOD; MSE_s/MSE_d is the relative efficiency of distribution-based MI and simple substitution methods; MSE_s/MSE_b is the relative efficiency of Bayesian MI and simple substitution methods. The correct underlying distributional assumption for x is bivariate normal.

^*The results are not presented due to convergence problems in the estimation process when sample size is small and the degree of left-censoring is high.

Finally, we investigated the estimation of the regression coefficients in situations where the assumed underlying distribution for x = (x₁, x₂) is bivariate lognormal while the true underlying distribution is bivariate gamma. In each simulation we generated data from bivariate gamma and incurred different levels of left-censoring. Subsequent analyses were then conducted on the log scale. Non-detections were substituted using log (LOD) or multiply imputed by the MI methods under the incorrect assumption that log (x) followed a bivariate normal. A bivariate binary outcome y is simulated with the assumed relationship logit(y_ij) = β₀ + β₁time_ij + β₂ log(x_ij), i = 1, …, n, j =1,2. Table 4 shows that an erroneous assumption for the underlying distribution resulted in wider CIs for each simulation scenario, indicating greater variability in the estimation process compared to the situation where the assumed underlying distribution is correct. However, the magnitude of bias and RE are in general comparable to what we observed in Table 3.

Table 4.

Bias, coverage, average width of 95% confidence interval (CI), and means square error (MSE) for the regression coefficient estimate for log(x) under the incorrect assumption that the underlying distribution for x is bivariate lognormal

		Simple substitution of LOD			Distribution-based MI			Bayesian MI
sample size	% <LOD (x1, x2)	bias	CI coverage	CI width	bias	CI coverage	CI width	bias	CI coverage	CI width	MSEs	MSEs/MSEd	MSEs/MSEb
50	(10,20)	0.0175	94.64	1.21	0.0045	95.54	1.09	0.0026	95.86	1.08	0.11	1.32	1.35
	(20,30)	0.0281	94.94	1.39	0.0016	96.48	1.17	−0.0003	96.66	1.15	0.14	1.64	1.73
	(30,40)	0.0418	94.78	1.61	−0.0030	97.84	1.25	−0.0066	98.02	1.22	0.19	2.15	2.34
	(40,50)	0.0577	94.96	1.90	−0.0066	98.32	1.36	−0.0119	98.64	1.30	0.27	2.94	3.35
	(50,60)	0.0772	94.84	2.29	−0.0139	99.32	1.49	−0.0195	99.32	1.39	0.41	4.42	5.31
	(60,70)	0.0973	94.50	2.86	.*	.*	.*	0.0332	99.58	1.47	0.68	.*	9.01
200	(10,20)	0.0196	95.24	0.60	0.0040	95.72	0.54	0.0055	95.98	0.54	0.02	1.39	1.36
	(20,30)	0.0309	94.82	0.69	0.0035	96.44	0.57	0.0037	96.56	0.57	0.03	1.76	1.70
	(30,40)	0.0433	94.44	0.80	0.0008	97.56	0.62	0.0011	97.36	0.61	0.05	2.29	2.28
	(40,50)	0.0575	94.28	0.94	−0.0033	98.32	0.66	−0.0045	98.04	0.65	0.06	3.11	3.13
	(50,60)	0.0749	94.36	1.12	−0.0109	99.02	0.72	−0.0106	98.42	0.70	0.09	4.38	4.54
	(60,70)	0.0972	94.54	1.39	−0.0209	99.26	0.78	−0.0204	99.10	0.77	0.14	6.68	6.98

Note: The correct underlying distributional assumption for x is bivariate gamma. The true regression coefficient for log(x) is 0.1. MSE_s is the MSE for the estimate based on simple substitution of LOD; MSE_s/MSE_d is the relative efficiency of distribution-based MI and simple substitution methods; MSE_s/MSE_b is the relative efficiency of Bayesian MI and simple substitution methods.

^*The results are not presented due to convergence problems in the estimation process when sample size is small and the degree of left-censoring is high.

Discussions

Several issues posed analytical challenges in the PACE3 study. There are more than two repeated measures of left-censored pesticide concentration data. The percentages of observations below the LOD were fairly high, an average of 25% across the four time periods. Our primary aim was to assess the relationship between pesticide concentrations as a predictor and immediate health outcomes. The Bayesian MI method permitted analyses of such data without having to resort to a complex EM algorithm used by likelihood-based approaches or sophisticated setup of Bayesian models in a full Bayesian approach. It thereby allows the ordinary researchers to interact with the left-censored data with considerably more flexibility. An additional benefit of the proposed method is that it can accommodate different LOD values. Different LODs frequently occur, for example, when analyte values are obtained from different batches in the same or multiple labs, or when different discrete analytes are being studied. This artificial difference in analytical precision (higher or lower LODs) would have a strong impact on the statistical analyses if the simple substitution methods were used, or data were dichotomized based on the LODs. Bayesian MI methods take into account different LODs in the algorithm and resolves this issue with ease.

In our case study, we selected only APE to illustrate the capability of the Bayesian MI method to deal with complex multivariate data. However, one pesticide metabolite may not accurately capture the comprehensive pesticide exposure that a farmworker has experienced. More than 10 pesticide metabolites were measured at each time point in PACE3 study (Arcury et al. 2010). To investigate in greater detail the association between pesticide metabolites and health outcomes, it might be of interest to calculate a summary measure to reflect the cumulative exposure originating from a group of metabolites. For example, total molar concentrations of different metabolites can be computed with the imputed data. Similarly, toxicities of different substances can be combined by summing the measured concentration of each substance multiplied by its toxic equivalent weighting factor (Helsel 2010). All these in-depth analyses are now possible but beyond the scope of this paper.

Of note, more extensive research is needed to have a comprehensive understanding of the Bayesian MI method. First, for our longitudinal APE data we only employed the source of information from the four time points in the imputation process. It is conceivable that other sources of information that might be related to APE concentrations can be incorporated into the imputation process. These sources of information may include both time-varying (e.g., weeks spent performing agricultural work) and time invariant variables (e.g., genetic variation in PON1). The effect of this added source of information on the performance of the Bayesian method has not been studied. Second, we used the normal distribution as the basis for running Gibbs sampler. This is often a reasonable assumption because a large number of the environmental exposures and biomarkers follow a normal distribution after log transformation. However, it is also quite common that the upper tail distribution of an analyte is not as long as expected under a lognormal with the same first and second moments. In our simulation study, we selected a gamma distribution that has many similarities with a lognormal distribution to provide a preliminary assessment on this issue. Results in a simple bivariate setting support that the distribution-based and Bayesian MI methods are reasonably robust to the potential deviation from the assumed underlying distribution. More extensive research is necessary to evaluate the robustness in multivariate settings, complicated by the possible misspecifications of variance-covariance structures in GEE. Furthermore, departure from normality can also occur when some values below the LOD are actually true zeros. This demands some modifications of the Gibbs sampler to impute non-detections on the basis of a mixture distribution such as zero-inflated lognormal. Future work is needed to explore this area of research further.

In conclusion, our simulation results indicated that, except for the robustness of the correlation coefficients, the degree of left-censoring could impact negatively the estimation of the distributional parameters as well as the regression coefficients associated with the left-censored analyte when it is used as a predictor in models. The effect was definitely detrimental when the sample size was small, characterized by large bias and wide CIs. However, the imputed values and the observed measurable values together yielded consistent estimates for the assumed underlying distribution when the sample size was large enough to offset the influence of left-censoring. The REs compared to the simple substitution method signify substantial benefit in the estimation process. Thus, the Bayesian MI method is valid and feasible for handling left-censored multivariate data, and we encourage the application of this method in future research.