Abstract
Background
Accurate evaluation of glomerular filtration rates (GFRs) is of critical importance in clinical practice. A previous study showed that models based on artificial neural networks (ANNs) could achieve a better performance than traditional equations. However, large-sample cross-sectional surveys have not resolved questions about ANN performance.
Methods
A total of 1,180 patients that had chronic kidney disease (CKD) were enrolled in the development data set, the internal validation data set and the external validation data set. Additional 222 patients that were admitted to two independent institutions were externally validated. Several ANNs were constructed and finally a Back Propagation network optimized by a genetic algorithm (GABP network) was chosen as a superior model, which included six input variables; i.e., serum creatinine, serum urea nitrogen, age, height, weight and gender, and estimated GFR as the one output variable. Performance was then compared with the Cockcroft-Gault equation, the MDRD equations and the CKD-EPI equation.
Results
In the external validation data set, Bland-Altman analysis demonstrated that the precision of the six-variable GABP network was the highest among all of the estimation models; i.e., 46.7 ml/min/1.73 m2 vs. a range from 71.3 to 101.7 ml/min/1.73 m2, allowing improvement in accuracy (15% accuracy, 49.0%; 30% accuracy, 75.1%; 50% accuracy, 90.5% [P<0.001 for all]) and CKD stage classification (misclassification rate of CKD stage, 32.4% vs. a range from 47.3% to 53.3% [P<0.001 for all]). Furthermore, in the additional external validation data set, precision and accuracy were improved by the six-variable GABP network.
Conclusions
A new ANN model (the six-variable GABP network) for CKD patients was developed that could provide a simple, more accurate and reliable means for the estimation of GFR and stage of CKD than traditional equations. Further validations are needed to assess the ability of the ANN model in diverse populations.
Introduction
Chronic kidney disease (CKD) is a major public health problem worldwide [1]. The Center for Disease Control in the USA declared that the prevalence of CKD was 26 million in the United States [2] and the number of patients with CKD in China was estimated to be about 119.5 million [3]. CKD is a serious threat to health and quality of life [4]. The number of patients that accepted maintenance renal replacement therapy in the United States increased from 281,000 in 2000 to 547,000 in 2010 to 571,000 in 2011 [5]. Currently, over 270,000 chronic hemodialysis patients were registered in the Chinese Renal Data System [6].
Accurate evaluation of glomerular filtration rates (GFRs) is of critical importance in clinical practice and research [7]. Although inulin clearance and renal radionuclide excretion rates are the gold standards to determine GFRs, they cannot be used widely because of inconvenience and high cost. Therefore, serum creatinine (SC)-based estimating equations for GFR were developed. The National Kidney Foundation - Kidney Disease Outcomes Quality Initiative Working Group recommended that the Cockcroft-Gault equation [8] and the Modification of Diet in Renal Disease (MDRD) equations [9] could be used to calculate the GFRs of adults [10]. In order to improve the accuracy of estimation, the MDRD researchers in 2006 used a more accurate isotope dilution mass spectrometry to measure the SC level, and they developed re-expressed MDRD formulas [11]. Furthermore, the studies were extended to 8,254 cases. The newly estimated GFR (eGFR) formula of the Chronic Kidney Disease Epidemiology Collaboration (CKD-EPI) equation was revised [12]. However, the correct CKD stage classification rates of the Cockcroft-Gault and MDRD formulas were only 64% and 62%, suggesting that the traditional SC-based equations remain relatively imprecise in the estimation of GFR [13] due to SC and the non-GFR determinants introducing significant errors when calculating the GFR [14]. Such imprecision can potentially result in misclassification of the CKD stage, which leads to both incorrect diagnosis and treatment for individuals and bias in estimating the prevalence of CKD in the general population [15]. Finding a more accurate method for estimating GFR is an urgent problem that needs to be solved.
Recently, Inker et al. developed a new estimating equation based on cystatin C in combination with creatinine and found that the combined equation performed better than equations based on either marker alone [13]. These results indicated that the combination of novel filtration markers, such as cystatin C and SC, into the GFR estimating formula may be a key factor for improving the accuracy of estimation. However, the incremental cost of introducing the new marker should be considered.
The traditional GFR estimation equations were all developed by the linear regression method. A large number of samples, a priori knowledge, and specific limits such as absence of multi-collinearity between independent variables were necessary during the development of the equations. With the development of modern mathematics and information technology, artificial neural networks (ANNs) are one of the methods of mathematical modeling that has been widely applied in the field of engineering prediction. An ANN has been applied in the field of medicine and biology as well, such as cardiac output [16] and in other physiological measurements [17]–[18]. A specifically trained three-layer ANN can infinitely approximate any linear or nonlinear function with precision [19]-[20]. Traditionally, the Back Propagation (BP) networks are widely used, though they have inherent defects [21]. More complicated ANN models have been recently published with greater descriptions of the construction of the models and software sharing [22]–[23]. A genetic algorithm, a random search algorithm enlightened from biological natural selection and genetic mechanisms, can be applied to optimize BP networks [24] for better performance.
In a previous study, we found that the Radial Basis Function network was superior to the traditional equations at estimating GFR [25]. In the large-sample cross-sectional survey reported here, we assessed the performance of a BP network optimized by a genetic algorithm (GABP network) for the estimation of GFR, which had similar features to the Radial Basis Function network.
Methods
Patients
Chronic kidney disease was defined and staged according to the National Kidney Foundation - Kidney Disease Outcomes Quality Initiative clinical practice guidelines [10]. Patients with acute kidney function deterioration, clinical edema, skeletal muscle atrophy, pleural effusion or ascites, malnutrition, amputation, heart failure or ketoacidosis were excluded from the study. Patients that were younger than 18 years were excluded. Patients that were taking cimetidine or trimethoprim were excluded as well. No subject was being treated with dialysis at the time of the study.
Measurement
The GFR was measured by the method of technetium-99 m diethylenetriaminepentaacetic acid (99 mTc-DTPA) renal dynamic imaging (modified Gate's method) was used as the standard GFR (sGFR) [24]-[25]. A Millennium TMMPR SPECT with a General Electric Medical System was used to measure 99 mTc-DTPA renal dynamic imaging as previously described [26]. There was good agreement between 99 mTc-DTPA renal imaging and plasma clearance of 51 chromium ethylenediamine tetraacetic acid [27]. An enzymatic method was used to measure SC. Values of SC in the development data set, the internal validation data set and the external validation data set were all traceable to the National Institute of Standards and Technology creatinine standard reference material (SRM 967). Data on gender, age, height, and weight were recorded at the same time.
Study design
From January 2005 through December 2009, 831 patients with CKD in the third affiliated hospital of Sun Yat-sen University, China, were enrolled, of which 562 patients were randomly selected as the development data set and the remaining 269 patients constituted the internal validation data set. From January 2010 through December 2010, 349 patients in the same hospital were included in the external validation data set. An additional 222 patients were admitted to two independent institutions in other Chinese cities for external validation (Table 1 and Table S1). Stages 1 and 2, as well as stages 4 and 5 were combined for convenience. The study protocol was approved by the institutional review board at the Third Affiliated Hospital of Sun Yat-sen University and written informed consent was obtained before the study.
Table 1. Patient characteristic.
| Characteristic | Development and Internal Validation (N = 831) | External Validation (n = 349) | Additional External Validation (n = 222) |
| Causes of CKD, N (%) | |||
| Primary glomerular disease | 255(30.7) | 71(20.3) | 71(32.0) |
| Diabetic nephropathy | 205(24.0) | 147(42.1) | 48(21.6) |
| Hypertension | 115(13.8) | 44(12.6) | 45(20.3) |
| Chronic tubulointerstitial disease | 81(9.7) | 30(8.6) | 16(7.2) |
| Polycystic kidney disease | 27(3.2) | 8(2.3) | 2(0.9) |
| Lupus nephritis | 13(1.6) | 5(1.4) | 5(2.3) |
| Other causes or causes unknown | 135(16.2) | 44(12.6) | 35(15.8) |
| Distribution of CKD stages, N (%) | ‡ | * | |
| CKD 1 | 62(7.5) | 32(9.2) | 39(17.6) |
| CKD 2 | 167(20.1) | 75(21.5) | 63(28.4) |
| CKD 3 | 310(37.3) | 140(40.1) | 73(32.9) |
| CKD 4 | 195(23.5) | 80(22.9) | 32(14.4) |
| CKD 5 | 97(11.7) | 22(6.3) | 15(6.8) |
| Age, mean (s.d.) in years | 53(17) | 58(15)* | 57(17)† |
| Male / Female (%) | 63.4/36.6 | 60.2/39.8 | 54.1/45.9‡ |
| Weight, mean (s.d.), kg | 61(11) | 62(12) | 62(10) |
| Height, mean (s.d.), cm | 163(8) | 162(8) | 164(7) |
| BMI, mean (s.d.), kg/m2 | 23(3) | 23(4)‡ | 23(3) |
| BSA, mean (s.d.), m2 | 1.65(0.17) | 1.66(0.18) | 1.67(0.15) |
| Serum albumin, mean (s.d.), g/dL | 3.8(0.7) | 3.8(0.6) | 3.9(0.7)‡ |
| Serum urea nitrogen, mean (s.d.), mg/dL | 37(24) | 36(26) | 30(23)* |
| Serum creatinine, mean (s.d.), mg/dL | 3.0(2.7) | 2.5(2.3)† | 2.8(3.4) |
| sGFR, mean (s.d.), ml/min/1.73 m2 | 45 (27) | 49 (27)‡ | 60(32)* |
:P<0.001 compared with the combined development and internal validation data sets.
:P<0.01 compared with the combined development and internal validation data sets.
:P<0.05 compared with the combined development and internal validation data sets.
Abbreviations: CKD, chronic kidney disease; BMI, body mass index; BSA, body-surface area; sGFR, standard glomerular filtration rate.
Independent variables taken into account included albumin (Alb), serum urea nitrogen (SUN), SC, age, height, weight and gender, and the only dependent variable was estimated GFR. Gender as a binary variable was transformed with dumb variable encoding; e.g., male equaled 1 and female equaled 0. As the range of each variable from the raw data was not the same, and it would affect construction of the ANN, each variable was normalized into the same range. The maximum and minimum values of normalization are shown in Table S2, and all minimum values were set to be not less than 0 considering the practical significance of the data.
Modeling with the ANN
A three-layer BP network was constructed using commercial software (Matlab software version 2011b, The Mathworks, Boston MA, USA). The neurons of the input layer included all independent variables as the input variables of the network, and the neuron of the output layer was the dependent variable; i.e., eGFR, as the output variable of the network. Each neuron of the hidden layer took the S function as an exciting function, and several networks were constructed with different numbers of neurons in the hidden layer (1 to 13). Each BP network was initialized randomly and then trained by learning the rule of back propagation with the development data set, and was validated with the internal validation data set to achieve a superior topology. Performance was defined as mean square error of the internal validation data set. A set of thresholds and weights could be specified after training, and then the output of the network was calculated by the weighted summation of each neuron to approximate sGFR.
To achieve better performance of the ANN, initialization of the weights and thresholds of the BP network was optimized by the Genetic algorithm (GABP network). All weights and thresholds of one network were encoded as a chromosome, and then evolved from one generation to another, including the progression of mutation and crossing. When a network could achieve better performance in the internal validation data set, the initial weights and thresholds were selected for the next generation. Finally, superior initial weights and thresholds were achieved, and then applied in the initialization of the network.
To facilitate clinical use, we used a mean impact value analysis [28] to select variables from the seven input variables of the GABP network gradually and, in turn, excluded Alb, gender, height, SUN, weight and age. We then established the appropriate GABP network with different input variables. The six-variable (including SC, age, weight, SUN, height and gender) GABP network with a topology of 6-2-1 (named the GABP6 network) was the optimal model in the internal validation data set. Explanations of the network are listed in Tables S3, S4, S5, S6, S7, S8, S9, S10, S11, S12, S13, S14, S15 and Figure S1. Detailed performances in the internal validation data set are presented in Tables S16 and S17, and Figures S2 and S3.
Calculations
The GFR was estimated by using the following equations:
- Cockcroft-Gault-equation (CG) [8]:
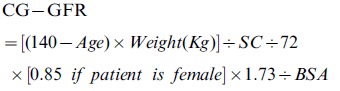
- Six-variable MDRD equation (MDRD1) [9]:

- Four-variable MDRD equation (MDRD4) [9]:

-
CKD-EPI equation (CKD-EPI) [12]:
κ = 0.7(Female)or 0.9(Male);
α = −0.329 (Female and SC≤0.7 mg/dl), α = −1.209(Female and SC>0.7 mg/dl);
α = −0.411(Male and SC≤0.9 mg/dl), α = −1.209(Male and SC>0.9 mg/dl)
Statistical analysis
Quantitative data were expressed as mean ± SD or as median. The difference between eGFR and standard GFR (sGFR) was defined as eGFR minus sGFR. Accuracy was defined as the percentage of estimated GFR not deviating more than 15, 30, and 50% from the sGFR. The precision was defined as the width between the 95% limits of agreement. A prior acceptable tolerance for the precision was defined 60 ml/min/1.73 m2 [29]. The difference between eGFR and sGFR was regressed against the average of eGFR and sGFR. The bias for eGFR was expressed as the slope of the regression line against the X-axis. The trend of accuracy for eGFR was expressed as the intercept of the regression line against the Y-axis. Independent samples t-test was used to compare the quantitative variables between two data sets. Wilcoxon Mann-Whitney test and Pearson's chi-squared test were used to compare the difference and accuracy between two data sets. Wilcoxon signed rank test and McNemar test were used to compare the difference and accuracy within data set. ANCOVA tests were used to compare first the slopes, and then the intercepts of the regression line. All statistics were performed using SPSS software (version 11.0 SPSS, Chicago IL, USA) and Medcalc for Windows (version 9.3.9.0 Medcalc software, Mariekerke, Belgium).
Results
Patients
The clinical characteristics of the development data set (n = 562), internal validation data set (n = 269) external validation data set (n = 349) and the additional external validation data set (n = 222) are shown in Table 1 and Table S1. In the development data set, the mean sGFR was 46.1 ml/min/1.73 m2 (SD, 27.0 ml/min/1.73 m2) and ranged from 3.3 ml/min/1.73 m2 to 130.1 ml/min/1.73 m2. The external validation data set had a similar mean sGFR, gender, weight, height, body surface area (BSA) and mean SUN level with the development and internal validation data sets but differed in the distribution of CKD stages, age, body mass index (BMI), and mean Alb and SC levels.
Performance of the estimation models in the external validation data set
Bland-Altman analysis demonstrated that the precision of the six-variable GABP network was the highest among all of the estimation models (46.7 ml/min/1.73 m2 vs. a range from 71.3 ml/min/1.73 m2 to 101.7 ml/min/1.73 m2). Therefore, we chose eGFR calculated by the six-variable GABP network as the reference against which all comparisons between estimation models were made. Both the slope and the intercept of the regression line of the six-variable GABP network were improved (slope, −0.15 ml/min/1.73 m2 vs. a range from 0.34 ml/min/1.73 m2 to 0.53 [P<0.001 for all]; intercept, 5.88 vs. a range from −14.79 to −21.54 [P<0.01 for all]; Table 2, Figure 1). The accuracies within 15%, 30% and 50% of the six-variable GABP network were all the greatest (P<0.001 for all), and the median percent of the absolute difference was least (15.61 ml/min/1.73 m2 vs. a range from 26.00 ml/min/1.73 m2 to 36.21 ml/min/1.73 m2, P<0.001 for all; Table 3).
Table 2. Overall performance of agreement between eGFR and sGFR in the external validation data set.
| Precision (ml/min/1.73 m2) | Slope of regression line with the X-axisa (95% CI) | Intercepts of regression line with the Y-axisa (95% CI) | |
| CG equation | 92.8 | 0.46(0.40,0.52)* | −19.83(−23.40,−16.26)† |
| MDRD1 equation | 90.3 | 0.46(0.40,0.51)* | −19.44(−22.85,−16.02)* |
| MDRD4 equation | 101.7 | 0.53(0.47,0.59)* | −21.54(−25.11,−17.64)* |
| CKD-EPI equation | 71.3 | 0.34(0.29,0.39)* | −14.79(−17.78,−11.80)† |
| GABP6 network | 46.7 | −0.15(−0.20,−0.10) | 5.88(3.20,8.55) |
Abbreviations: eGFR, estimated glomerular filtration rate; sGFR, standard glomerular filtration; CG, Cockcroft-Gault; MDRD, Modification of Diet in Renal Disease; CKD-EPI, Chronic Kidney Disease Epidemiology Collaboration; GABP, BP network with genetic algorithm
a:The difference between eGFR and sGFR was regressed against the average of eGFR and sGFR. X-axis represented the average of eGFR and sGFR. Y-axis represented the difference between eGFR and sGFR. eGFR, estimated glomerular filtration rate; sGFR, standard glomerular filtration rate.
:P<0.001 compared with GABP6 network-GFR.
:P<0.01 compared with GABP6 network-GFR.
:P<0.05 compared with GABP6 network-GFR.
Figure 1. Bland–Altman plot of eGFR and sGFR (ml/min/1.73 m2) in the external validation data set.
Solid blue line represents the mean of difference between methods; dashed brown lines represent 95% limits of agreement of the mean of difference between methods; solid red line represents the regression line of difference between methods against average of methods; dotted green lines represent 95% confidence intervals for the regression line, and dashed purple lines represent 95% limits of agreement of the regression line. A, B, C, D and E represent for the results of GFR estimated by the Cockcroft-Gault equation, the six variable MDRD equation, the four variable MDRD equation, the CKD-EPI equation and the six variable GABP network, respectively. Abbreviations: eGFR, estimated glomerular filtration rate; sGFR, standard glomerular filtration; CG, Cockcroft-Gault equation; MDRD: Modification of Diet in Renal Disease; CKD-EPI: Chronic Kidney Disease Epidemiology Collaboration; GABP: BP network with genetic algorithm.
Table 3. Overall performance of difference and accuracy between eGFR and sGFR in the external validation data set.
| Median of difference (25%, 75% Percentile) | Median % Absolute difference (25%, 75% Percentile) | Accuracy within | |||
| 15% | 30% | 50% | |||
| CG equation | −1.23(9.96,12.25) | 26.00(13.03,47.55)* | 29.2* | 55.0* | 77.6* |
| MDRD1 equation | −0.70(−10.16,15.22) | 31.71(13.75,52.25)* | 26.3* | 46.7* | 72.2* |
| MDRD4 equation | 1.18(−9.48,16.38)‡ | 32.21(14.08,54.45)* | 26.9* | 46.1* | 70.7* |
| CKD-EPI equation | −0.12(−9.95,13.51)† | 30.74(12.57,50.90)* | 26.9* | 49.6* | 73.9* |
| GABP6 network | −0.26(−8.54,5.73) | 15.61(8.44,29.87) | 49.0 | 75.1 | 90.5 |
:P<0.001 compared with GABP6 network-GFR.
:P<0.01 compared with GABP6 network-GFR.
:P<0.05 compared with GABP6 network-GFR.
Abbreviations: eGFR, estimated glomerular filtration rate; sGFR, standard glomerular filtration; CG: Cockcroft-Gault; MDRD: Modification of Diet in Renal Disease; CKD-EPI: Chronic Kidney Disease Epidemiology Collaboration; GABP: BP network with genetic algorithm
The performance of the six-variable GABP network in various stages of CKD was analyzed. The median of the difference of the six-variable GABP network was less than the traditional equations in CKD stages 1–2 and CKD stages 4–5 (P<0.001 for all), as was the absolute difference in CKD stages 1–2 and CKD stage 3 (P<0.001 for all). Accuracy within 30% and 50% of the six-variable GABP network in CKD stages 1–2 and CKD stage 3 were the greatest (P<0.001 for all). There was also improvement in accuracy within 15% of the six-variable GABP network in CKD stages 1–2 (P<0.001 for all). All estimation models showed the same variation trend for performances from CKD stage 1 to CKD stage 5; that is, performance of one specific CKD stage became worse with the progression of CKD stage. This is due to sGFR becoming smaller during the progression of CKD stages, and therefore the relative error becoming greater. Detailed performances are listed in Table S18. We also evaluated misclassification of CKD by various estimation models. Misclassification for the diagnosis of moderate renal failure (GFR <60 ml/min/1.73 m2) as well as severe renal failure (GFR <15 ml/min/1.73 m2) were improved (P<0.01 for all) by the means of the six-variable GABP network (8.2% and 7.4%), as compared with those of the traditional equations (ranging from 12.6% to 13.2% and from 12.6% to 17.5%; Table 4). The six-variable GABP network improved the CKD stage misclassification rate (32.4% vs. a range from 47.3% to 53.3%, P<0.001 for all). In CKD stage 1 classified by various estimation models, the correct classification ratio of CKD stage 1 of the six-variable GABP network was significantly higher than for all traditional equations (90.9% vs. a range from 36.2% to 42.4%, P<0.01 for all). There were also some improvements in the correct classification ratios of the six-variable GABP network in CKD stage 2, CKD stage 4 as well as CKD stage 5, but without statistical significance (Table S19).
Table 4. CKD Misclassification in the external validation data set.
| Misclassification rate for the diagnosis of | CKD stage misclassification rate | ||
| sGFR <60 ml/min/1.73 m2 | sGFR <15 ml/min/1.73 m2 | ||
| CG equation | 12.6† | 12.6† | 47.3* |
| MDRD1 equation | 12.6† | 17.2* | 52.4* |
| MDRD4 equation | 13.2† | 17.5* | 51.9* |
| CKD-EPI equation | 12.9† | 17.5* | 53.3* |
| GABP6 network | 8.3 | 7.4 | 32.4 |
:P<0.001 compared with GABP6 network-GFR.
:P<0.01 compared with GABP6 network-GFR.
:P<0.05 compared with GABP6 network-GFR.
Abbreviations: sGFR, standard glomerular filtration rate; CG, Cockcroft-Gault; MDRD, Modification of Diet in Renal Disease; CKD-EPI, Chronic Kidney Disease Epidemiology Collaboration; GABP, BP network with genetic algorithm; CKD, chronic kidney disease
Performance of the estimation models in the additional external validation data set
Bland-Altman analysis demonstrated that the precision of the six-variable GABP network was the highest among all of the estimation models (62.4 ml/min/1.73 m2 vs. a range from 68.0 ml/min/1.73 m2 to 73.5 ml/min/1.73 m2). The intercept of the regression line of the six-variable GABP network was improved (4.91 vs. a range from −16.07 to −18.05, P<0.01 for all). However, the slope of the regression line of the six-variable GABP network was the worst (−0.27 vs. a range from 0.18 to 0.24, P<0.001 for all; Table 5 and Figure S4), as was bias (median difference, −8.84 ml/min/1.73 m2vs. a range from −4.60 ml/min/1.73 m2 to −6.56 ml/min/1.73 m2; P<0.05 for all). The accuracies within 30% and 50% of the six-variable GABP network were all the greatest, and the median percent of the absolute difference was the least (20.75 ml/min/1.73 m2 vs. a range from 21.52 ml/min/1.73 m2 to 23.57 ml/min/1.73 m2, P<0.05 for all; Table 6). The misclassification rate for the diagnosis of severe renal failure (GFR <15 ml/min/1.73 m2) was also improved (11.3% vs. a range from 16.7% to 17.1%, P<0.01 for all) with the six-variable GABP network (Table 7).
Table 5. Overall performance of agreement between eGFR and sGFR in the additional external validation data set.
| Precision (ml/min/1.73 m2) | Slope of regression line with the X-axisa (95% CI) | Intercepts of regression line with the Y-axisa (95% CI) | |
| CG equation | 72.5 | 0.21(0.15,0.28)* | −17.99(−22.29,−13.69)† |
| MDRD1 equation | 68.0 | 0.20(0.14,0.26)* | −16.16(−20.23,−12.09)* |
| MDRD4 equation | 73.5 | 0.24(0.18,0.30)* | −18.05(−22.28,−13.83)* |
| CKD-EPI equation | 68.4 | 0.18(0.12,0.25)* | −16.07(−20.24,−11.91)† |
| GABP6 network | 62.4 | −0.27(−0.34,−0.20) | 4.91(0.76,9.06) |
Abbreviations: eGFR, estimated glomerular filtration rate; sGFR, standard glomerular filtration rate; CG, Cockcroft-Gault; MDRD, Modification of Diet in Renal Disease; CKD-EPI, Chronic Kidney Disease Epidemiology Collaboration; GABP, BP network with genetic algorithm
a:The difference between eGFR and sGFR was regressed against the average of eGFR and sGFR. X-axis represented the average of eGFR and sGFR. Y-axis represented the difference between eGFR and sGFR.
:P<0.001 compared with GABP6 network-GFR.
:P<0.01 compared with GABP6 network-GFR.
:P<0.05 compared with GABP6 network-GFR.
Table 6. Overall performance of difference and accuracy between eGFR and sGFR in the additional external validation data set.
| Median of difference (25%, 75% Percentile) | Median % Absolute difference (25%, 75% Percentile) | Accuracy within | |||
| 15% | 30% | 50% | |||
| CG equation | −6.56(−16.85,3.42)‡ | 23.57(10.49,43.11)† | 34.6 | 61.2 | 80.8† |
| MDRD1 equation | −4.60(−15.38,5.14)* | 21.52(9.78,44.38)‡ | 39.2 | 63.3 | 78.3* |
| MDRD4 equation | −4.92(−15.02,5.10)* | 23.26(8.94,46.84)† | 34.2 | 60.4 | 76.7* |
| CKD-EPI equation | −5.71(−16.47,4.48)* | 23.52(8.82,47.21)† | 35.8 | 60.0* | 77.1* |
| GABP6 network | −8.44(−19.57,0.22) | 20.75(11.19,34.18) | 34.6 | 67.5 | 88.8 |
Abbreviations: eGFR, estimated glomerular filtration rate; sGFR, standard glomerular filtration; CG: Cockcroft-Gault; MDRD: Modification of Diet in Renal Disease; CKD-EPI: Chronic Kidney Disease Epidemiology Collaboration; GABP: BP network with genetic algorithm
:P<0.001 compared with GABP6 network-GFR.
:P<0.01 compared with GABP6 network-GFR.
:P<0.05 compared with GABP6 network-GFR.
Table 7. CKD Misclassification in the additional external validation data set.
| Misclassification rate for the diagnosis of | CKD stage misclassification rate | ||
| sGFR <60 ml/min/1.73 m2 | sGFR <15 ml/min/1.73 m2 | ||
| CG equation | 9.0 | 16.7† | 47.7 |
| MDRD1 equation | 10.4 | 16.7† | 49.5 |
| MDRD4 equation | 10.4 | 17.1* | 51.4‡ |
| CKD-EPI equation | 10.4 | 17.1* | 53.6† |
| GABP6 network | 9.5 | 11.3 | 42.3 |
Abbreviations: CG, Cockcroft-Gault; MDRD, Modification of Diet in Renal Disease; CKD-EPI, Chronic Kidney Disease Epidemiology Collaboration; GABP, BP network with genetic algorithm; CKD, chronic kidney disease
:P<0.001 compared with GABP6 network-GFR.
:P<0.01 compared with GABP6 network-GFR.
:P<0.05 compared with GABP6 network-GFR.
According to the comprehensive information from the internal validation data set and both external validation data sets, the six-variable GABP network was selected as the optimal estimation model for patients with CKD. In order to show the model and facilitate external validations, a table based on the Excel software (File S1) was developed for convenience.
Discussion
The GFR is defined as the number of milliliters of plasma per unit time from kidney filtration and is a direct indicator of glomerular filtration function. GFR is the basis of CKD definition and staging and it affects evaluation of evolution, prognosis and follow-up [7]. With a worsening baseline of renal function, patients seem to have a greater probability of progressing to a worse CKD stage in the next year [30]. Early detection and diagnosis are important means of effective prevention and treatment of CKD and its associated complications. Accurate evaluation of GFR is essential for CKD patients. Using this new ANN model (the six-variable GABP network, with a topology of 6-2-1), better precision and accuracy were achieved, which resulted in more accurate classification of severe renal failure (GFR <15 ml/min/1.73 m2). This will be of great help to physicians in making proper decisions for patients with CKD, thereby avoiding unnecessary diagnostic and therapeutic interventions. The previous finding [25] that the ANN was superior to the traditional equation in GFR estimation was supported as well by data. In conjunction with other studies [31]–[34], it indicated that the method of ANN may have an advantage in solving clinical problems.
In the field of medical data processing, the traditional statistical regression method takes the ‘law of large numbers’ as the theoretical basis, with some assumptions and prior knowledge. An equation is developed by collecting large amounts of data to fit the general law of the population. This equation is very dependent on the samples collected, which are supposed to have the same distribution as the population, so a decline in accuracy would happen when applied to the other population. In addition, the regression methods can only fit limited functional forms. Multicollinearity and interactions between independent variables also limit the application of regression methods. However, ANN, as a common method of machine learning, is widely applied in the fields of not only science and engineering but also medicine with its own advantages such as nonlinear mapping and robustness. This method does not require any a priori knowledge of the data. Multicollinearity and interaction is no longer a limitation of the application of this method. Even if the sample size is small, the law of population can still be learned from the sample with limited accuracy.
There were limitations in this study. First, SC in the MDRD equations [9] was measured by using the picric acid method. In the CKD-EPI equation [12] and the development data set, the internal validation data set and the external validation data set of our models, SC was determined by the enzymatic method traceable to isotope dilution-mass spectrometry. In the additional external validation data set of our models, SC levels were measured by the enzymatic method. The Cockcroft-Gault-equation [8] was developed long ago, and the methods of SC measurement are not available now. The difference in calibration of SC assays introduces error in the comparison between different GFR estimation models and subgroups [35]. Second, different estimation models used different ways to measure sGFR, which was also a source of system bias. Both the MDRD equations [9] and the CKD-EPI equation [12] used urinary clearances of 125I-iothalamate as the sGFR. In the Cockcroft-Gault equation [8], the method of sGFR measurement used the means of two 24-hour urine creatinine clearances. In this study, according to other studies [29], [36], sGFR was measured by the 99mTc-DTPA renal dynamic imaging method. It is likely that differences in the results of our study and others were partly due to the use of different methods. Third, the sample contained only Chinese CKD patients. Further validations in separate studies with different races/ethnicities of CKD patients are needed to confirm the advantages of this ANN. Fourth, an ANN model is a ‘black box’, and cannot be expressed by a single mathematical equation. As a result, physicians are reluctant to accept the ANN's interpretation of data. In order to facilitate the application on a daily bedside basis, a simple table based on Excel software (File S1) was developed.
Conclusions
A new ANN model (the six-variable GABP network) for CKD patients was developed and can provide a simple, more accurate and reliable means for the estimation of GFR and stage of CKD than traditional equations. Further validations are needed to assess the ability of ANN model in diverse populations.
Supporting Information
Topology of artificial neural network.
(DOC)
Bland–Altman plot of eGFR and sGFR (ml/min/1.73 m2) in the internal validation data set. Solid blue line represents the mean of difference between methods; dashed brown lines represent 95% limits of agreement of the mean of difference between methods; solid red line represents the regression line of difference between methods against average of methods; dotted green lines represent 95% confidence intervals for the regression line, and dashed purple lines represent 95% limits of agreement of the regression line. A, B, C, D, E and F represent for the results of GFR estimated by GABP-7 network, GABP-6 network, GABP-5 network, GABP-4 network, GABP-3 network and GABP-2 network, respectively.
(DOC)
Bland–Altman plot of eGFR and sGFR (ml/min/1.73 m2) in the internal validation data set. Solid blue line represents the mean of difference between methods; dashed brown lines represent 95% limits of agreement of the mean of difference between methods; solid red line represents the regression line of difference between methods against average of methods; dotted green lines represent 95% confidence intervals for the regression line, and dashed purple lines represent 95% limits of agreement of the regression line. G represent for the results of GFR estimated by GABP-1 network.
(DOC)
Bland–Altman plot of eGFR and sGFR (ml/min/1.73 m2) in the additional external validation data set. Dotted blue line represents the mean of difference between methods; dashed brown lines represent 95% limits of agreement of the mean of difference between methods; solid red line represents the regression line of difference between methods against average of methods. A, B, C, D and E represent for the results of GFR estimated by the Cockcroft-Gault-equation, the six variable MDRD equation, the four variable MDRD equation, the CKD-EPI equation and the six variable GABP network, respectively.
(DOC)
Detailed characteristic in different subgroup of patients.
(DOC)
Maximum and minimum values of normalization of raw data.
(DOC)
Performance of GABP network with different topology.
(DOC)
MIV analysis based on GABP network with a topology of 7-11-1.
(DOC)
Performance of GABP network with 6 input variables.
(DOC)
MIV analysis based on GABP network with a topology of 6-2-1.
(DOC)
Performance of GABP network with 5 input variables.
(DOC)
MIV analysis based on GABP network with a topology of 5-4-1.
(DOC)
Performance of GABP network with 4 input variables.
(DOC)
MIV analysis based on GABP network with a topology of 4-2-1.
(DOC)
Performance of GABP network with 3 input variables.
(DOC)
MIV analysis based on GABP network with a topology of 3-4-1.
(DOC)
Performance of GABP network with 2 input variables.
(DOC)
MIV analysis based on GABP network with a topology of 2-3-1.
(DOC)
Performance of GABP network with 1 input variable.
(DOC)
Overall performance of agreement between eGFR and sGFR in GABP networks with different input variables in the internal validation data set.
(DOC)
Overall performance of difference and accuracy between eGFR and sGFR in GABP networks with different number of input variables in the internal validation data set.
(DOC)
Performances between eGFR and sGFR in different stages of CKD in the external validation data set.
(DOC)
Classification the CKD stage by the estimation models in different stages of CKD.
(DOC)
An Excel table based on the six-variable GABP network to estimate GFR.
(XLS)
Acknowledgments
Thanks to the patients for their good cooperation.
We would also like to thank Dr. David Cushley from International Science Editing, Clare, Ireland for assistance with the English version of the manuscript.
Funding Statement
Project 81070612 supported by National Natural Science Foundation of China. This work was also supported by the China Postdoctoral Science Foundation (Grant No. 201104335), Guangdong Science and Technology Plan (Grant No. 2011B031800084), the Fundamental Research Funds for the Central Universities (Grant No. 11ykpy38) and the National Key Technology Research and Development Program of the Ministry of Science and Technology of China (Grant No. 2011BAI10B00). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Levey AS, Coresh J (2012) Chronic kidney disease. Lancet 379: 165–80. [DOI] [PubMed] [Google Scholar]
- 2. Crews DC, Plantinga LC, Miller ER 3rd, Saran R, Hedgeman E, et al. (2010) Prevalence of chronic kidney disease in persons with undiagnosed or prehypertension in the United States. Hypertension 55: 1102–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Zhang L, Wang F, Wang L, Wang W, Liu B, et al. (2012) Prevalence of chronic kidney disease in China: a cross-sectional survey. Lancet 379: 815–22. [DOI] [PubMed] [Google Scholar]
- 4. Chronic Kidney Disease Prognosis Consortium (2010) Matsushita K, van der Velde M, Astor BC, Woodward M, et al. (2010) Association of estimated glomerular filtration rate and albuminuria with all-cause and cardiovascular mortality in general population cohorts: a collaborative meta-analysis. Lancet 375: 2073–81. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Collins AJ, Foley RN, Chavers B, Gilbertson D, Herzog C, et al. (2012) United States Renal Data System 2011 Annual Data Report: Atlas of chronic kidney disease & end-stage renal disease in the United States. Am J Kidney Dis59: e1–420. [DOI] [PubMed] [Google Scholar]
- 6. Xie F, Zhang D, Wu J, Zhang Y, Yang Q, et al. (2012) Design and implementation of the first nationwide, web-based Chinese Renal Data System (CNRDS). BMC Med Inform Decis Mak 12: 11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Stevens LA, Coresh J, Greene T, Levey AS (2006) Assessing kidney function--measured and estimated glomerular filtration rate. N Engl J Med 354: 2473–83. [DOI] [PubMed] [Google Scholar]
- 8. Cockcroft DW, Gault MH (1976) Prediction of creatinine clearance from serum creatinine. Nephron 16: 31–41. [DOI] [PubMed] [Google Scholar]
- 9. Levey AS, Bosch JP, Lewis JB, Greene T, Rogers N, et al. (1999) A more accurate method to estimate glomerular filtration rate from serum creatinine: a new prediction equation. Modification of Diet in Renal Disease Study Group. Ann Intern Med 130: 461–70. [DOI] [PubMed] [Google Scholar]
- 10. National Kidney Foundation (2002) K/DOQI clinical practice guidelines for chronic kidney disease: evaluation, classification, and stratification. Am J Kidney Dis 39: S1–266. [PubMed] [Google Scholar]
- 11. Levey AS, Coresh J, Greene T, Stevens LA, Zhang YL, et al. (2006) Using standardized serum creatinine values in the modification of diet in renal disease study equation for estimating glomerular filtration rate. Ann Intern Med 145: 247–54. [DOI] [PubMed] [Google Scholar]
- 12. Levey AS, Stevens LA, Schmid CH, Zhang YL, Castro AF 3rd, et al. (2009) A New Equation to Estimate Glomerular Filtration Rate. Ann Intern Med 150: 604–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Inker LA, Schmid CH, Tighiouart H, Eckfeldt JH, Feldman HI, et al. (2012) Estimating glomerular filtration rate from serum creatinine and cystatin C. N Engl J Med 367: 20–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Botev R, Mallié JP, Wetzels JF, Couchoud C, Schück O (2011) The clinician and estimation of glomerular filtration rate by creatinine-based formulas: current limitations and quo vadis. Clin J Am Soc Nephrol 6: 937–50. [DOI] [PubMed] [Google Scholar]
- 15. Matsushita K, Mahmoodi BK, Woodward M, Emberson JR, Jafar TH, et al. (2012) Comparison of risk prediction using the CKD-EPI equation and the MDRD study equation for estimated glomerular filtration rate. JAMA 307: 1941–51. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Young J, Macke CJ, Tsoukalas LH (2012) Short-term acoustic forecasting via artificial neural networks for neonatal intensive care units. J Acoust Soc Am 132: 3234–9. [DOI] [PubMed] [Google Scholar]
- 17. Emoto T, Abeyratne UR, Chen Y, Kawata I, Akutagawa M, et al. (2012) Artificial neural networks for breathing and snoring episode detection in sleep sounds. Physiol Meas 33: 1675–89. [DOI] [PubMed] [Google Scholar]
- 18. Hu K, Wan JQ, Ma YW, Wang Y, Huang MZ (2012) A fuzzy neural network model for monitoring A2/O process using on-line monitoring parameters. J Environ Sci Health A Tox Hazard Subst Environ Eng 47: 744–54. [DOI] [PubMed] [Google Scholar]
- 19. Das A, Ben-Menachem T, Cooper GS, Chak A, Sivak MV Jr, et al. (2003) Prediction of outcome in acute lower-gastrointestinal haemorrhage based on an artificial neural network: internal and external validation of a predictive model. Lance 362: 1261–6. [DOI] [PubMed] [Google Scholar]
- 20. Goldfarb-Rumyantzev AS, Pappas L (2002) Prediction of renal insufficiency in Pima Indians with nephropathy of type 2 diabetes mellitus. Am J Kidney Dis 40: 252–64. [DOI] [PubMed] [Google Scholar]
- 21.Hagan MT, Demuth HB, Beale MH (1996) Neural Network Design. Pws Pub. Co .
- 22. Magosso E, Cuppini C, Ursino M (2012) A neural network model of ventriloquism effect and aftereffect. PLoS One 7: e42503. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Seguritan V, Alves N Jr, Arnoult M, Raymond A, Lorimer D, et al. (2012) Artificial neural networks trained to detect viral and phage structural proteins. PLoS Comput Biol 8: e1002657. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Tong DL, Schierz AC (2011) Hybrid genetic algorithm-neural network: feature extraction for unpreprocessed microarray data. Artif Intell Med 53: 47–56. [DOI] [PubMed] [Google Scholar]
- 25. Liu Xun, Wu Xiaoming, Li Lingshan, Lou Tanqi (2010) Application of radial basis function neural network to estimate glomerular filtration rate in Chinese patients with chronic kidney disease. ICCASM 15: 332–5. [Google Scholar]
- 26. Liu X, Lv L, Wang C, Shi CG, Cheng CL, et al. (2012) Comparison of prediction equations to estimate glomerular filtration rate in Chinese patients with chronic kidney disease. Intern Med J 42: e59–67. [DOI] [PubMed] [Google Scholar]
- 27. Carlsen O (2004) The gamma camera as an absolute measurement device: determination of glomerular filtration rate in 99mTc-DTPA renography using a dual head gamma camera. Nucl Med Commun 25: 1021–9. [DOI] [PubMed] [Google Scholar]
- 28. Shi H, Lu Y, Du J, Du W, Ye X, et al. (2012) Application of Back Propagation Artificial Neural Network on Genetic Variants in Adiponectin ADIPOQ, Peroxisome Proliferator-Activated Receptor-γ, and Retinoid X Receptor-α Genes and Type 2 Diabetes Risk in a Chinese Han Population. Diabetes Technol Ther 14: 293–300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Du X, Hu B, Jiang L, Wan X, Fan L, et al. (2011) Implication of CKD-EPI equation to estimate glomerular filtration rate in Chinese patients with chronic kidney disease. Ren Fail 33: 859–65. [DOI] [PubMed] [Google Scholar]
- 30. Liu Xun, Lv Linsheng, Ling Li, Lou Tanqi (2012) A Markov model study on the hierarchical prognosis and risk factors in patients with chronic kidney disease. ICCSEE 2: 334–8. [Google Scholar]
- 31. Gaweda AE, Jacobs AA, Aronoff GR, Brier ME (2008) Model predictive control of erythropoietin administration in the anemia of ESRD. Am J Kidney Dis 51: 71–9. [DOI] [PubMed] [Google Scholar]
- 32. Baxt WG, Skora J (1996) Prospective validation of artificial neural network trained to identify acute myocardial infarction. Lancet 347: 12–5. [DOI] [PubMed] [Google Scholar]
- 33. Dybowski R, Weller P, Chang R, Gant V (1996) Prediction of outcome in critically ill patients using artificial neural network synthesised by genetic algorithm. Lancet 347: 1146–50. [DOI] [PubMed] [Google Scholar]
- 34. Guh JY, Yang CY, Yang JM, Chen LM, Lai YH (1998) Prediction of equilibrated postdialysis BUN by an artificial neural network in high-efficiency hemodialysis. Am J Kidney Dis 31: 638–46. [DOI] [PubMed] [Google Scholar]
- 35. Vickery S, Stevens PE, Dalton RN, van Lente F, Lamb EJ (2006) Does the ID-MS traceable MDRD equation work and is it suitable for use with compensated Jaffe and enzymatic creatinine assays? Nephrol Dial Transplant 21: 2439–45. [DOI] [PubMed] [Google Scholar]
- 36. DU X, Liu L, Hu B, Wang F, Wan X, et al. (2012) Is the Chronic Kidney Disease Epidemiology Collaboration four-level race equation better than the cystatin C equation? Nephrology (Carlton) 17: 407–14. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Topology of artificial neural network.
(DOC)
Bland–Altman plot of eGFR and sGFR (ml/min/1.73 m2) in the internal validation data set. Solid blue line represents the mean of difference between methods; dashed brown lines represent 95% limits of agreement of the mean of difference between methods; solid red line represents the regression line of difference between methods against average of methods; dotted green lines represent 95% confidence intervals for the regression line, and dashed purple lines represent 95% limits of agreement of the regression line. A, B, C, D, E and F represent for the results of GFR estimated by GABP-7 network, GABP-6 network, GABP-5 network, GABP-4 network, GABP-3 network and GABP-2 network, respectively.
(DOC)
Bland–Altman plot of eGFR and sGFR (ml/min/1.73 m2) in the internal validation data set. Solid blue line represents the mean of difference between methods; dashed brown lines represent 95% limits of agreement of the mean of difference between methods; solid red line represents the regression line of difference between methods against average of methods; dotted green lines represent 95% confidence intervals for the regression line, and dashed purple lines represent 95% limits of agreement of the regression line. G represent for the results of GFR estimated by GABP-1 network.
(DOC)
Bland–Altman plot of eGFR and sGFR (ml/min/1.73 m2) in the additional external validation data set. Dotted blue line represents the mean of difference between methods; dashed brown lines represent 95% limits of agreement of the mean of difference between methods; solid red line represents the regression line of difference between methods against average of methods. A, B, C, D and E represent for the results of GFR estimated by the Cockcroft-Gault-equation, the six variable MDRD equation, the four variable MDRD equation, the CKD-EPI equation and the six variable GABP network, respectively.
(DOC)
Detailed characteristic in different subgroup of patients.
(DOC)
Maximum and minimum values of normalization of raw data.
(DOC)
Performance of GABP network with different topology.
(DOC)
MIV analysis based on GABP network with a topology of 7-11-1.
(DOC)
Performance of GABP network with 6 input variables.
(DOC)
MIV analysis based on GABP network with a topology of 6-2-1.
(DOC)
Performance of GABP network with 5 input variables.
(DOC)
MIV analysis based on GABP network with a topology of 5-4-1.
(DOC)
Performance of GABP network with 4 input variables.
(DOC)
MIV analysis based on GABP network with a topology of 4-2-1.
(DOC)
Performance of GABP network with 3 input variables.
(DOC)
MIV analysis based on GABP network with a topology of 3-4-1.
(DOC)
Performance of GABP network with 2 input variables.
(DOC)
MIV analysis based on GABP network with a topology of 2-3-1.
(DOC)
Performance of GABP network with 1 input variable.
(DOC)
Overall performance of agreement between eGFR and sGFR in GABP networks with different input variables in the internal validation data set.
(DOC)
Overall performance of difference and accuracy between eGFR and sGFR in GABP networks with different number of input variables in the internal validation data set.
(DOC)
Performances between eGFR and sGFR in different stages of CKD in the external validation data set.
(DOC)
Classification the CKD stage by the estimation models in different stages of CKD.
(DOC)
An Excel table based on the six-variable GABP network to estimate GFR.
(XLS)



