Modeling the Generation of Output by the Cerebellar Nuclei

Abstract

Functional aspects of network integration in the cerebellar cortex have been studied experimentally and modeled in much detail ever since the early work by theoreticians such as Marr, Albus and Braitenberg more than 40 years ago. In contrast, much less is known about cerebellar processing at the output stage, namely in the cerebellar nuclei (CN). Here, input from Purkinje cells converges to control CN neuron spiking via GABAergic inhibition, before the output from the CN reaches cerebellar targets such as the brainstem and the motor thalamus. In this article we review modeling studies that address how the CN may integrate cerebellar cortical inputs, and what kind of signals may be transmitted. Specific hypotheses in the literature contrast rate coding and temporal coding of information in the spiking output from the CN. One popular hypothesis states that postinhibitory rebound spiking may be an important mechanism by which Purkinje cell inhibition is turned into CN output spiking, but this hypothesis remains controversial. Rate coding clearly does take place, but in what way it may be augmented by temporal codes remains to be more clearly established. Several candidate mechanisms distinct from rebound spiking are discussed, such as the significance of spike time correlations between Purkinje cell pools to determine CN spike timing, irregularity of Purkinje cell spiking as a determinant of CN firing rate, and shared brief pauses between Purkinje cell pools that may trigger individual CN spikes precisely.

1. Introduction

Many experimental and theoretical studies have addressed the question how neuronal activity is processed in cerebellar cortex, but there is still no unified view about the computational role of the cerebellum as a whole. One of the main reasons for this lack of understanding of cerebellar function is that we still know very little about the processing of incoming signals and the generation of output by the cerebellar nuclei (CN). This is an important topic, as almost the entire output from the cerebellar cortex through Purkinje cell (PC) axons ends as GABAergic inhibition in the CN (Figure 1), with an additional small specialized component going to the vestibular nuclei. Thus, cerebellar function cannot be determined without considering processing at the level of CN, where inputs from PCs are integrated with signals from the excitatory mossy fibers and climbing fibers that also drive cerebellar cortical processing (Figure 1).

Figure 1.

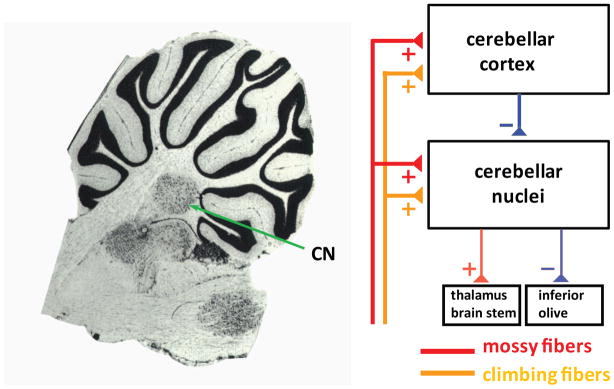
Cerebellar circuit diagram. The left panel shows a sagittal section of the rat cerebellum at the level of the lateral nucleus (diagram adapted from Paxinos and Watson, The Rat Brain in Stereotaxic Coordinates, Academic Press, 2006). The right panel shows a simplified circuit diagram of the cerebellum, highlighting the central position of the cerebellar nuclei (CN) in processing cerebellar cortical Purkinje cell inhibition before the final output leaves the cerebellum.

Neural coding can be broadly categorized as rate based, where the number or rate of spikes in a particular time window is the carrier of information, or as temporal coding, where information is represented by the timing of individual spikes or bursts of spikes. Both temporal and rate coding have been observed to take place in the cerebellum and are likely to serve important functions (De Zeeuw, et al., 2011; Walter & Khodakhah, 2009). With respect to rate coding, linear response mechanisms of CN neurons can sum the combination of input rates from PCs, which themselves can exhibit a linear spike rate code of external events such as smooth eye movements (Medina & Lisberger, 2009). Potentially important mechanisms serving temporal coding are given by synchronized PC complex spiking, and by the ability of CN neurons to fire rebound spike bursts following strong inhibition (De Zeeuw, et al., 2011). In this review, we summarize the existing field of modeling studies by others and by ourselves that have tried to elucidate how CN neurons could use different forms of neural coding to transmit signals from the cerebellar cortex to the rest of the brain. Moreover, we relate these results to the involvement of the CN in simple computational tasks, and we discuss computer simulations of pathological responses in CN neurons that are associated with motor dysfunction.

2. Simple models of CN neurons and temporal coding

A central question of simulation studies that have included computational models of CN neurons has been how the cerebellum could use temporal coding to generate appropriately timed output signals. A simple behavioral paradigm that requires the generation of such a well-timed output signal by the cerebellar circuitry is delay eye-blink conditioning. When an animal is trained during eye-blink conditioning, a conditioned stimulus (CS, such as a tone) is paired repeatedly with an unconditioned stimulus (US, for example periorbital electrical stimulation). In delay conditioning, the CS and US co-terminate, and the onset of the US follows the CS onset by an inter-stimulus interval (ISI), which is typically between 100 ms and 1 s. The animal then learns to respond to presentations of the CS alone with eye-blink conditioned responses (CRs) that are timed adaptively so that the peak of the CR occurs at the time of the US presentations during training.

Several lines of evidence indicate an involvement of the CN in the execution of these timed responses. Electrical stimulation of the interpositus nucleus can elicit eye-blinks, and interpositus neurons show an increase in activity that precedes and resembles eye-blink CRs (McCormick & Thompson, 1984). Based on these experimental results, computational studies of cerebellum-dependent eye-blink conditioning have assumed that the output of CN neurons predicts the amplitude and timing of conditioned eye-blink responses (Medina, Garcia, Nores, Taylor, & Mauk, 2000; Wetmore, Mukamel, & Schnitzer, 2008). An example of such a computational study is the cerebellar network model by Medina et al. (2000). In the model by Medina and collaborators, the neural network model of cerebellar cortex by Buonomano and Mauk (1994) has been extended to include six CN neurons that provide the output from the model, generating spike responses with temporal profiles that replicate experimentally measured eye-blink responses. Each of these CN neuron models receives inhibitory input from 15 PCs and excitatory input from 100 mossy fibers; the CN neurons are implemented as leaky integrate-and-fire models and provide a simple readout mechanism for the combined excitatory and inhibitory input. The Medina model generates appropriately timed responses based on long-term depression (LTD) at parallel fiber – PC synapses that are active at the same time as the US, and it suppresses responses at incorrect times based on long-term potentiation (LTP) at these synapses when they are activated without a coincident US. Moreover, LTP at mossy fiber – CN neuron synapses is included to be able to replicate the short-latency responses that are observed after lesions to the cerebellar cortex.

Apart from adjusting synaptic parameters based on available electrophysiological data, the Medina model does not make any specific assumptions about the physiological characteristics of the different cerebellar neurons. A hallmark behavior of CN neurons is the generation of rebound spike responses at the offset of inhibitory synaptic inputs and hyperpolarizing current injections (Figure 2). The rebound responses that follow hyperpolarizing current injections are well characterized, and they are formed by varying combinations of fast rebound spike bursts, and prolonged periods of accelerated spiking (Llinas & Muhlethaler, 1988; Sangrey & Jaeger, 2010) (Figure 2). Rebound responses can also follow strong bursts of inhibitory synaptic inputs, but these have been studied to a lesser extent and their relevance for cerebellum dependent behaviors and their contribution to cerebellar computation and neural coding are unresolved questions (Alvina, Walter, Kohn, Ellis-Davies, & Khodakhah, 2008; Bengtsson, Ekerot, & Jorntell, 2011a; Tadayonnejad, et al., 2010; Tadayonnejad, Mehaffey, Anderson, & Turner, 2009).

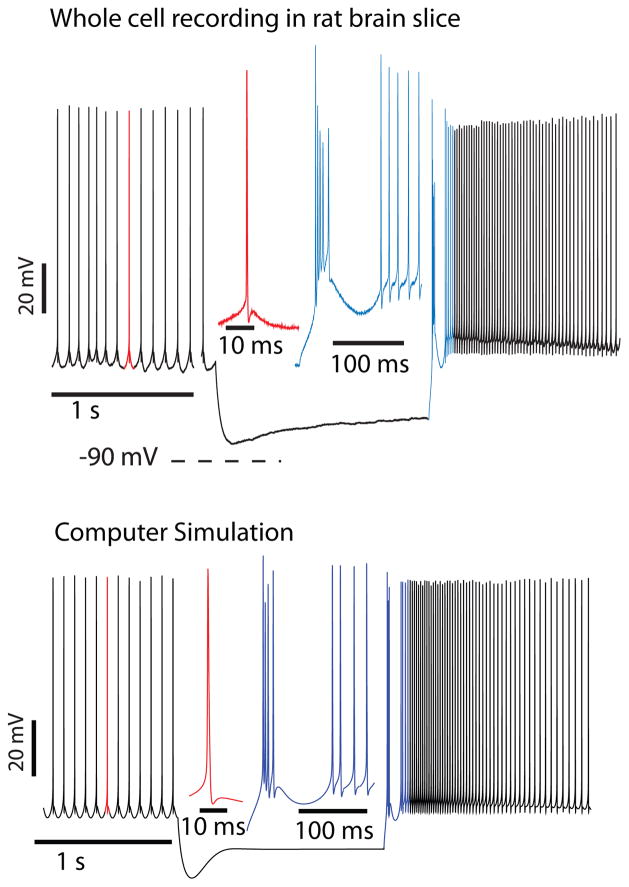
Figure 2.

Rebound response in CN neurons (adapted from Steuber et. al., 2011). Top panel: Response of a CN neuron in a brain slice recording to a 1.5 s current injection of −150 pA. Two clear components of the strong rebound response can be discriminated: a fast spike burst, and a prolonged period of spike rate acceleration. Bottom Panel: The computer model can reproduce these rebound components through the activation of T-type calcium current for the fast rebound burst and persistent sodium current for the slow rebound period. These currents are de-inactivated during the period of hyperpolarization, and the depth and duration of hyperpolarization determine the intensity of each rebound component (see Steuber et al, 2011 for details).

Rebound bursts are a prime candidate mechanism for temporal coding in that they create a well-timed spike burst following a specific input event. In their computational study of cerebellar learning, Wetmore and colleagues (2008) suggest that the rebound spike responses that can follow inhibitory input to CN neurons are crucial for the recall of memories and the generation of appropriately timed output from the cerebellar circuitry. According to their “lock-and-key” hypothesis, the induction of LTD and LTP at parallel fiber – PC synapses is necessary, but not sufficient, to generate a desired cerebellar output. In addition, cerebellar cortical synaptic plasticity has to result in temporal patterns of PC activity that can elicit rebound responses in CN neurons (Figure 2). Rebounds will only be triggered by temporal input spike patterns that comprise an increase followed by a decrease in the PC spike rate. Thus, Wetmore et al. consider these temporal spike patterns a “key”, and the temporal filtering properties of CN neurons that determine whether or not a rebound response occurs a “lock”. They demonstrate the potential contribution of rebound responses to retrieving correct and suppressing unwanted memories using three different conductance-based models of CN neurons with different degrees of complexity. Their Model 1 has a single compartment with a leak conductance and a low-voltage activated (LVA, T-type) calcium conductance. When this model is presented with a temporal pattern of PC input often assumed to result from standard delay conditioning, that is increased PC spiking early during the CS followed by decreased PC spiking late during the CS (but see Steuber, et al., 2007), the resulting de-inactivation of the T-type calcium channels together with the decreased inhibitory input late during the CS leads to T-type calcium spike rebounds just prior to the time of the US onset during training. However, when a backward conditioning paradigm is simulated so that the onsets of the short US and longer CS coincide, the resulting biphasic PC activity provides an early decrease in inhibition followed by a late increase in inhibition to the CN neuron, and no rebound responses are observed. Wetmore and collaborators then add other components to their simple model to study how the T-type rebounds could be translated into output from the CN. Their Model 2 is a modification of Model 1 that includes a high-voltage activated (HVA) calcium conductance, and their Model 3 is a two-compartmental model comprised of weakly coupled somatic and dendritic compartments, with additional SK-type calcium dependent potassium conductances in both compartments, and fast sodium and delayed rectifier potassium conductances in the somatic compartment. Both models receive synaptic inputs with Poisson statistics and generate non-deterministic all-or-none rebound responses; these are HVA calcium spikes in Model 2 and sodium spike bursts in Model 3. In both models, the curve describing the probability of rebound responses as a function of the CS – US ISI resembles the dependence of the reliability of conditioned eye-blink responses on the CS – US ISI in eye-blink conditioning experiments in rabbits, with diminished response probabilities for ISIs < 100 ms, and no responses for backward conditioning with negative ISIs.

A more general functional role for rebound responses in CN neurons has been suggested by Kistler and colleagues (Kistler & De Zeeuw, 2003; Kistler & Van Hemmen, 1999; Kistler, van Hemmen, & De Zeeuw, 2000). Kistler and collaborators model CN neurons by adapting a single-compartmental conductance-based model of a thalamo-cortical relay neuron (McCormick & Huguenard, 1992); their adaptations include a two-fold reduction in model size and changes to the T-type calcium conductance and hyperpolarization-activated cyclic nucleotide-gated (HCN) conductance. In their model, post-inhibitory rebounds translate inhibitory PC inputs into a delayed excitatory CN output, with a delay of approximately 100 ms that is independent of the strength or temporal synchronization of the simulated PC input (but see Steuber, Schultheiss, Silver, De Schutter, & Jaeger, 2011). This feature of the CN neuron response is then incorporated into simulations of a cerebellar network using spike response models, and it is shown that, under some specific assumptions about cerebellar anatomy and physiology, the rebound responses in the CN can contribute to the generation of reverberatory loops and form the basis of the storage and recall of spatio-temporal activity patterns.

3. Rebound responses in morphologically realistic CN neuron models

The previous section has described two computational studies that have implicated rebound responses in CN neurons in temporal coding in the cerebellum and assume that they contribute an essential mechanism to cerebellar function. However, the conditions required for the generation of robust rebound responses in CN neurons in vivo are under active debate (Alvina, et al., 2008; Bengtsson, et al., 2011a; Tadayonnejad, et al., 2010; Tadayonnejad, et al., 2009). In cerebellar slices, rebound responses can be elicited more effectively by stimulation of PC inputs than by injection of a hyperpolarizing current into the soma that results in the same level of somatic hyperpolarization as elicited synaptically (Aizenman & Linden, 1999). Given that T-type LVA calcium channels are present at particularly high densities in CN neuron dendrites (Gauck, Thomann, Jaeger, & Borst, 2001; Pugh & Raman, 2006), this suggests that rebound responses are mediated to some extent by dendritic T-type channels. However, a further enhancement of rebounds by mGluR activation when synapses are stimulated electrically has also been observed (Zheng & Raman, 2011). A recent modeling study by the authors used a morphologically realistic model of a CN neuron to explore how different conductance densities of T-type calcium channels and other voltage-gated ion channels can shape the heterogeneous pattern of rebound responses observed in in vitro recordings (Steuber, et al., 2011). The model is based on a morphological reconstruction of a CN neuron with a large soma (diameter 22 μm, Steuber et al., 2004) and has a total membrane capacitance of 203 pF when measured with somatic current injection, which is in good agreement with the capacitance of glutamatergic projection neurons in the CN (Uusisaari, Obata, & Knopfel, 2007). The 517 compartments of the model are divided into four groups: soma, axon, proximal dendritic and distal dendritic, with a specific set of ion channels for each of these divisions. Whole cell slice recordings from 129 CN neurons (including recordings from Gauck & Jaeger, 2000) were used as a target for model behavior during tuning of the active conductances. Eight Hodgkin-Huxley type ion channels are distributed differentially over the different regions of the model: a fast sodium current (NaF), a mixture of fast Kv3 (fKdr) and slow Kv2 (sKdr) delayed rectifiers, which together form a TEA sensitive Kdr current, an SK-type calcium-gated potassium current, an HCN current, an HVA calcium current, a Cav3.1 type LVA calcium (CaT) current and a persistent sodium (NaP) current. Moreover, the model contains a tonic non-specific cation (TNC) current that provides inward current to drive membrane repolarization during spikes, resulting in rhythmic pacemaking activity in the absence of synaptic input (Raman, Gustafson, & Padgett, 2000). The SK current is activated purely by intracellular calcium, which is modelled as an exponentially decaying pool with inflow from the HVA, but not the LVA, calcium current. The selective coupling of SK current to HVA calcium current was an early prediction of the model that has been verified by an independent experimental study (Alvina, et al., 2008).

The model was tuned to replicate characteristics of excitatory projection neurons that were present in the recordings and have been reported previously (Uusisaari, et al., 2007), such as spontaneous activity and a spike waveform with a narrow width and discernible fast and slow after-hyperpolarizations (AHPs) that are separated by an after-depolarization (ADP). In the model, this ADP results from a push-pull interaction between soma and dendrites. During the action potential, current flows from the soma into the dendrites, followed by a large current flowing back into the soma that generates the ADP. Thus, the model predicts that removal or reduction of the size of the dendrites for example in dissociated neurons should remove or greatly reduce the ADP. Another modeling prediction is that the intrinsic currents during the inter-spike interval (ISI) are much smaller than the synaptic currents, resulting in a temporal spike pattern and firing rate that are very sensitive to modulation by synaptic input.

In the recordings that were used as a target for model tuning, hyperpolarizing current injections were followed by heterogeneous rebound spike responses comprising different extents of fast rebound bursts and slower and prolonged increases in spike rate (Steuber, et al., 2011) (Figure 2). A similar heterogeneity of rebound responses has been described elsewhere (Engbers, et al., 2011; Molineux, et al., 2006; Molineux, et al., 2008; Tadayonnejad, et al., 2010), although the slow and prolonged responses have not been studied in as much detail as the fast rebound bursts. The range of rebound responses that were observed experimentally could be reproduced in the model by adjusting the conductance densities of the CaT, HCN and NaP currents (Figure 2). As expected from the faster activation and inactivation kinetics of the CaT conductance compared to the NaP conductance, the fast rebound bursts in the model are mostly driven by the CaT current, while the slow and prolonged rebound responses can be attributed to the NaP current (Llinas & Muhlethaler, 1988; Sangrey & Jaeger, 2010). However, the effects of the different rebound conductances are interdependent, and in particular the predicted contribution of the HCN current is complex, given that high HCN conductance densities result in decreased hyperpolarizations and therefore diminished de-inactivation of the NaP and CaT conductances. When the reduction of the NaP and CaT conductance de-inactivation by the HCN current is eliminated by replacing the hyperpolarizing current injection with transient voltage clamp pulses to −90 mV, the main effects of the HCN current are a decrease in latency of the fast rebound burst, and the elimination of a pause between the fast rebound bursts and the prolonged rebound period. The effect of the HCN current in response to hyperpolarizing current injections depends on the duration of the current injection, with long current injections resulting in rebound latencies that are governed by the extent of activation of HCN conductance, and short current injections leading to rebound latencies that are determined by the depth of the preceding hyperpolarization. As a consequence, increasing the level of hyperpolarizing current decreases the rebound latency for long current injections (≥ 250 ms), while increasing the rebound latency for short current injections (≤ 125 ms). The predicted modulation of rebound latencies by inhibitory input is different from the study by Kistler and collaborators, where constant rebound delays in response to variable inhibitory stimuli form the basis of spatio-temporal pattern learning (Kistler & De Zeeuw, 2003; Kistler & Van Hemmen, 1999; Kistler, et al., 2000)

Although rebound responses at the offset of hyperpolarizing current injections are a hallmark behavior of CN neurons, the ability of CN neurons to generate rebound responses in vivo, and the conditions that favor rebound responses in vivo, have not been clearly established (Alvina, et al., 2008; Bengtsson, et al., 2011a; Tadayonnejad, et al., 2010; Tadayonnejad, et al., 2009). Rebound responses in vivo may be impeded by shunting due to the increase in membrane conductance by background synaptic input (Destexhe, Rudolph, & Pare, 2003; Stern, Jaeger, & Wilson, 1998), and synaptic inhibition from PCs can only lead to hyperpolarizations down to the chloride reversal potential (E_Cl), which may not be enough to result in sufficient de-inactivation of the CaT and NaP conductances and activation of the HCN conductance. To explore the conditions required for the expression of rebounds in response to bursts of inhibitory synaptic inputs, simulations were performed for a range of synaptic background rates and different values of E_Cl. These simulations show that the rebound responses in the model are robust against shunting by background synaptic input, but that the value of E_Cl has to be −75 mV or lower for inhibitory synaptic input to be able to trigger rebound responses. However, the predicted dependence of rebound responses on the value of E_Cl is based on the half-inactivation voltages of the CaT and NaP conductance and the half-activation voltage of the HCN conductance, which are set to −80 mV in the model. These values are variable and can be modulated (Jagodic, et al., 2007; Pape, 1996), and small changes to these parameters are expected to have a strong effect on the expression of rebound responses in vivo.

Recent recordings of CN neurons in slices have shown that hyperpolarizations down to −72 mV make small proportions of the CaT and HCN conductances available, and that they are sufficient to generate reliable rebound responses (Engbers, et al., 2011). These experimental results are complemented by simulations of two-compartmental models of CN neurons with a soma compartment that contains NaF, Kdr and HCN conductances and a dendrite compartment with CaT and slow potassium conductances. The results of these simulations agree with the prediction of the multi-compartmental model that the HCN current mediates a hyperpolarization-induced reduction in the rebound latency for sufficiently long hyperpolarizations. Moreover, they predict that the HCN current increases the precision of the timing of the first rebound spike, and that the HCN and CaT currents act synergistically to increase the rate of fast rebound bursts (Engbers, et al., 2011). Notably, the half-inactivation voltages of the CaT conductance and the half-activation voltage of the HCN conductance in the model by Engbers et al. (2011) are set to −64 mV and −92 mV, respectively, and are therefore quite different from the values in the model by Steuber et al. (2011). Clearly, an understanding of synaptic integration and rebound responses in CN neurons would benefit from a more thorough characterization of intrinsic conductances at physiological temperature. In general, it is important to realize that a computational model is always work in progress, presenting a working hypothesis that reflects current knowledge as well as currently missing data, and that it needs to be updated continuously as new experimental data become available. In fact, there is now a family of CN neuron models that are derived from the original implementation of the morphologically realistic CN neuron model (Steuber, et al., 2011), different versions have been implemented in the GENESIS (Bower & Beeman, 1997) and NEURON (Hines & Carnevale, 1997) simulators, and a six-compartmental version of the model has been developed with the goal of using this model for network simulations (unpublished). The original GENESIS version (Steuber, et al., 2011) and the NEURON version of the model (Luthman, et al., 2011) are available through the Model DB repository (senselab.med.yale.edu/modeldb/, accession numbers 136175 and 144523, respectively).

A CN rebound in vivo would depend on strong PC input transients to a given CN neuron followed by a pause in PC activity that allows a rebound to develop. One candidate mechanism for such input patterns is given by the climbing fiber activation of PCs, which occurs synchronously with millisecond precision across parasagittal bands of cerebellar cortex (Bengtsson, Ekerot, & Jorntell, 2011b; Blenkinsop & Lang, 2011; Hoebeek, Witter, Ruigrok, & De Zeeuw, 2010; Ozden, Sullivan, Lee, & Wang, 2009; Schultz, Kitamura, Post-Uiterweer, Krupic, & Hausser, 2009; Welsh, Lang, Suglhara, & Llinas, 1995). The ensuing synchronous complex spikes that are usually followed by PC spike pauses (Davie, Clark, & Hausser, 2008; Sato, Miura, Fushiki, & Kawasaki, 1992) are likely to converge onto CN neurons, which receive input from parasagittal bands of PCs (Apps & Garwicz, 2000; Garwicz & Ekerot, 1994). Different mechanisms of generating patterns of PC activation and pauses converging onto CN neurons that not depend on CF inputs are also plausible, however. PC simple spike trains have been found to be comprised of patterns of regular activity that are interspersed by pauses (Shin, et al., 2007). Moreover, computer simulations and experiments have shown that the duration of simple spike pauses can be modulated by synaptic plasticity at parallel fiber synapses (Steuber, et al., 2007), and the timing and duration of these pauses, when shared by populations of PCs, could determine the timing and duration of rebound responses in CN neurons (De Schutter & Steuber, 2009). In addition to the potential temporal code that is based on the timing of pauses in PC activity and the resulting CN rebounds, information could also be carried by the rate of spikes in the rebound burst, given that the rate of PC simple spikes before a pause will determine the depth of CN hyperpolarization and thus regulate the strength of rebound current activation (De Schutter & Steuber, 2009). This would constitute a form of rate coding within rebound bursts, which could operate in parallel to the more common forms of rate coding proposed to underlie cerebellar function that are reviewed below.

4. CN spike rate and spike time precision as a function of input rates and input correlations

A large number of studies have shown that PC spike rates are modulated by sensory stimuli as well as during movement, and such rate modulation has been deemed sufficient to encode information transmission to the CN (Walter & Khodakhah, 2006, 2009). Using the detailed compartmental CN model described above, it can indeed be confirmed that the biophysics of a CN neuron capable of strong rebounds equally supports a rate code, such that increases in excitatory mossy fiber input rate or decreases in inhibitory PC input rates are translated into smooth increases of CN spike rates (Steuber, et al., 2011). Moreover, increasing the rate of PC inhibition shifts the curves of CN output rate against mossy fiber input rate to the right and performs a purely additive operation on the excitatory input. Although many types of neural computations require multiplicative rather than additive operations (for review, see Silver, 2010), additive operations have also been implicated in cerebellar functions such as vestibulo-ocular reflex adaptation (Medina & Lisberger, 2009).

Dynamic clamp studies undertaken in the lab of one of the authors (Gauck & Jaeger, 2000; Gauck & Jaeger, 2003) demonstrate, however, that CN firing rates are not only determined by the rate of PC and mossy fiber inputs, but strongly depend on the amount of synchronization present in the population of inputs. In these studies, CN neurons in brain slice recordings were subjected to controlled excitatory and inhibitory input patterns which were applied as synaptic conductances through the recording pipette as dynamic clamp stimuli. Dynamic clamping is a real-time feedback technique (Robinson & Kawai, 1993; Sharp, Oneil, Abbott, & Marder, 1993), in which the synaptic input current equation I_syn = G_ex (V_m − E_ex) + G_in (V_m − E_in) is updated at a rate of at least 10 KHz, and synaptic current (I_syn) is injected into the recorded neuron as a function of excitatory (G_ex) and inhibitory (G_in) conductances and their driving forces. These experiments showed that application of random independent inputs through a population of 400 synapses results in much lower CN spike rates than the application of highly correlated PC input patterns converging on a CN neuron with the same total number of synaptic input events per second. Therefore, synchronization of PCs presents a powerful signal that can control CN output. Such synchronization may for example be achieved through aligned short pauses or regular spike patterns as described above, but many other network mechanisms based on the architecture of cerebellar cortical connections or mossy fiber input correlations could also result in PC synchronization. Interestingly, our dynamic clamp studies also showed that the strong NMDA component of the excitatory input that is found in CN neurons (Anchisi, Scelfo, & Tempia, 2001) creates a smoothing function such that the precise temporal structure of the excitatory input is much less effective in determining CN spiking than the temporal structure of the inhibitory PC input. Therefore, the NMDA conductance in CN neurons may enable a predominant control of CN processing by the fine temporal structure of PC inputs. More recently, the estimates for the number of PCs converging onto a single CN neuron have been revised downwards to 50, but nevertheless, synchronization within this smaller than previously envisioned input population still plays a large role in controlling CN spike rates, as well as generating the potential for a synchrony based temporal code (Person & Raman, 2012).

Besides rebound timing and rate coding, another possible code is given by synchronization of CN output spikes that would be decoded by the postsynaptic targets of the CN. While such coding is entirely speculative for the cerebellum, several theories of cerebral cortical function depend on precise spike times aligned in pulse packets to support synfire chains (Abeles, Hayon, & Lehmann, 2004; Aertsen, Diesmann, & Gewaltig, 1996) or polychronization (Izhikevich, 2006; Izhikevich & Edelman, 2008; Izhikevich & Hoppensteadt, 2009). The dynamic clamp studies cited above also examined the degree of spike time precision that CN neurons are capable of, given their potential unreliability through current noise and stochastic channel properties. Again, it was found that the degree of synchronicity of the PC inputs was key to determining the precision of spike timing in the CN. For high degrees of PC input synchrony, up to 60% of CN spikes were precisely timed within a 1 ms window when the same synaptic conductance pattern was applied multiple times. While a candidate function for such precision in the CN output awaits a better understanding of postsynaptic processing of CN inputs by its target brain areas such as the red nucleus or the motor thalamus, these findings demonstrate that the cerebellum could in principle partake in pulse packet communication schemes. In our dynamic clamp studies synchronicity was controlled by precisely aligned PC input spike times; however, in principle any mechanism that leads to pronounced fast depolarizing transients in input conductance to a CN neuron will create a precise trigger time for an individual spike.

A limitation of dynamic clamping is given by the application of all synaptic currents at the soma of the recorded cell, which clearly does not correspond to the distributed dendritic input patterns in vivo. Computer simulations of the detailed compartmental model (Steuber, et al., 2011) were used in a bootstrapping fashion to examine the potential effects of focalizing all input at the soma as in dynamic clamping (Lin & Jaeger, 2011). The same conductances as applied in the original dynamic clamp study (Gauck & Jaeger, 2000) were applied to the model, with the addition of a band-limited white noise current delivered to the soma, which faithfully reproduced the voltage noise and spike time variability seen in CN slice recordings. The model did indeed very closely replicate the spike patterns induced by dynamic clamp input to CN neurons in slices when all synapses were applied to the soma, thus further validating the accuracy of the model. Then in a second step the same pattern of synaptic inputs was distributed over all dendrites to examine the consequences of distributed input currents. Somewhat surprisingly, the differences in output spike patterns were very small, leading to almost identical output rates and spike precision indices, which validates the results obtained with dynamic clamping for more natural distributed input patterns. This finding can be understood by considering the relatively electrotonically compact structure of CN neurons with sparsely branched dendrites that do not exceed one length constant in general.

5. Short-term depression as a mechanism to decode input irregularity

In addition to being modulated by the rate and synchrony of PC inhibition, the CN neuron spike rate can also be affected by the degree of irregularity of the PC input spike trains. Several experimental results suggest that the regularity of PC spiking is important for cerebellar information processing and motor control. For example, the extent and duration of regular patterns in PC spike trains can be increased by sensory stimulation (Shin et al., 2007). Moreover, irregular PC activity has been associated with cerebellar pathologies. In tottering mice, a natural mutation in the Cacna1a gene that encodes the α_1A subunit of P/Q-type calcium channels leads to an increased irregularity of PC spiking (Hoebeek, et al., 2005; Walter, Alvina, Womack, Chevez, & Khodakhah, 2006). Although the amplitude modulation of the PC spike rate during optokinetic stimulation in these mutant mice is indistinguishable from that in healthy wild-type mice, they suffer from impaired motor behavior and abnormal optokinetic reflexes (OKRs). The motor deficits can be rescued by the application of regular electrical stimulation patterns, which suggests a causal link between the irregular PC activity and the impaired motor control (Hoebeek, et al., 2005).

The effect of irregular PC input on the spike output of CN neurons has been investigated in a recent modeling study conducted in the group of one of the authors (Luthman, et al., 2011). Luthman and colleagues modified the multi-compartmental CN model from Steuber et al. (2011) by including short-term depression (STD) at PC – CN neuron synapses (Pedroarena & Schwarz, 2003; Shin, et al., 2007; Telgkamp & Raman, 2002), and presented their model with artificial inhibitory input trains with varying degrees of regularity and with spike trains recorded in vivo from tottering and wild-type mice. Their simulations predict that an increased irregularity of the inhibitory PC input results in an increased output spike rate in the CN neuron. The mechanism of this encoding of input irregularity as output spike rate depends on the number of PC converging onto a single CN neuron. When the CN neuron receives input from several unsynchronized PCs, the irregularity driven spike rate acceleration is mediated by STD and based on a reduction of inhibitory synaptic conductance in response to irregular input, which implements low-pass filtering of high-frequency components of the input spike trains. Only for an unrealistic convergence ratio of one, or for completely synchronized inhibitory input, the input irregularity based output rate acceleration is independent of STD. Interestingly, the spike rates of CN neurons in anaesthetized tottering mice are also increased compared to their wild-type littermates (Hoebeek, Khosrovani, Witter, & De Zeeuw, 2008), although these data should be confirmed by recordings from awake behaving animals. Altogether, these results suggest that the impaired motor control in tottering mice may be caused by an increased CN neuron spike rate that results from the disrupted regularity in the PC activity, and that this causal link depends on STD at the PC – CN neuron synapses.

Other computational function of STD at this synapse should be an interesting subject for future research. STD at other synapses has been implicated in many different computations such as gain modulation (Rothman, Cathala, Steuber, & Silver, 2009), coincidence detection (Tsodyks & Markram, 1997), the generation of phase shifts (Chance, Nelson, & Abbott, 1998; Fortune & Rose, 2000; Varela, et al., 1997) balancing inhibitory and excitatory inputs (Galarreta & Hestrin, 1998) and the detection of relative rather than absolute changes in input rate (Abbott, Varela, Kamal, & Nelson, 1997).

6. Conclusions

The present review has summarized a number of modeling studies that have explored a range of rate codes and temporal codes that could be used by CN neurons to transmit information from the cerebellar cortex to the rest of the brain. These modeling studies have employed different approaches, using models at different levels of complexity and with different amounts of biological detail. In general, the choice of model should be determined by the research question that is being addressed, and by the available physiological data (Herz, Gollisch, Machens, & Jaeger, 2006). In the absence of reliable data on ion channel kinetics, and if the spike generation is not affected by complex interactions between ion channels, it is often appropriate to use simple spiking models such as integrate-and fire models, with the added advantage that these models are much less computationally intensive and in their simplest form amenable to mathematical analysis. If the goal is to study how spike patterns are modulated by complex interactions between different voltage and calcium gated conductances, or if such interactions are expected to affect the spike output and therefore influence neuronal information processing, it is necessary to use conductance-based models with Hodgkin-Huxley or Markov models of ion channels. Thus, modeling studies that have investigated the generation of rebound responses in CN neurons have used conductance-based models. Moreover, multi-compartmental conductance based models are required to understand many phenomena such as differences in responses to dendritic and somatic input, and push-pull interactions between soma and dendrites. If a morphological reconstruction of a neuron is available, it is usually better to use a morphologically realistic model, as such a model can have realistic local input resistances, and therefore realistic local ion channel conductance densities. However, sometimes limited computational resources require the use of reduced models for network simulations.

At present, there are several important unresolved questions regarding information transmission through and processing by the CN that require additional experimental and computational studies. More anatomical work is needed to characterize the afferent, efferent and, in particular, intrinsic circuitry of the CN (Uusisaari & De Schutter, 2011; Uusisaari & Knopfel, 2012). More electrophysiological data will be required to elucidate the effect of different input pathways to CN neurons, and how these inputs interact. For example, very little is currently known about responses of CN neurons to input from climbing fiber collaterals. Moreover, although some progress has been made, the differences between different types of CN neurons will need to be characterized in much more detail (Uusisaari & De Schutter, 2011; Uusisaari & Knopfel, 2012), and computer simulations will be required to understand the interaction of different types of neurons in the CN network.