Performance Characteristics of a Positron Projection Imager For Mouse Whole-body Imaging

Abstract

Introduction

We describe a prototype positron projection imager (PPI) for visualizing the whole-body biodistribution of positron-emitting compounds in mouse-size animals. The final version of the PPI will be integrated into the MONICA portable dual-gamma camera system to allow the user to interchangeably image either single photon or positron-emitting compounds in a shared software and hardware environment.

Methods

A mouse is placed in the mid-plane between two identical, opposed, pixelated LYSO arrays separated by 21.8-cm and in time coincidence. An image of the distribution of positron decays in the animal is formed on this mid-plane by coincidence events that fall within a small cone angle to the perpendicular to the two detectors and within a user-specified energy window. We measured the imaging performance of this device with phantoms and in tests performed in mice injected with various compounds labeled with positron-emitting isotopes.

Results

Representative performance measurements yielded the following results (energy window 250–650 keV, cone angle 3.5-degrees): resolution in the image mid-plane, 1.66-mm (FWHM), resolution ±1.5-cm above and below the image plane, 2.2-mm (FWHM), sensitivity: 0.237-cps/kBq (8.76-cps/μCi) ¹⁸F (0.024% absolute). Energy resolution was 15.9% with a linear-count-rate operating range of 0–14.8 MBq (0–400 μCi) and a corrected sensitivity variation across the field-of-view of <3%. Whole-body distributions of [¹⁸F] FDG and [¹⁸F] fluoride were well visualized in mice of typical size.

Conclusion

Performance measurements and field studies indicate that the PPI is well suited to whole-body positron projection imaging of mice. When integrated into the MONICA gamma camera system, the PPI may be particularly useful early in the drug development cycle where, like MONICA, basic whole-body biodistribution data can direct future development of the agent under study and where logistical factors (e.g., available imaging space, non-portability, and cost) may be limitations.

INTRODUCTION

Small animal imaging has become commonplace in biomedical research and very high performance PET, SPECT, CT, MRI, US and optical imaging systems (and combinations of these systems) have been, and continue to be, developed. These systems typically offer state-of-the-art performance and are designed to maximize the functional capabilities available to the user within each technology. However, certain experimental questions can potentially be answered with simpler, more limited and less expensive devices when the goal is not to determine the exact quantitative biodistribution of a putative diagnostic or therapeutic agent but rather to determine if the tracer meets minimal biodistribution requirements that support further development of the compound. For example, our laboratory commonly performs whole-body single photon projection imaging in mice with MONICA [1], a compact, portable dual-gamma camera system developed in our laboratory, as a precursor to further development of tumor-directed single photon radiotracers in humans. A similar need exists for efficiently imaging positron-emitting compounds.

With this reasoning in mind, we constructed a positron projection imager (PPI) for performing whole-body coincidence projection imaging of mice with the intent of integrating a final version into MONICA. In this configuration, the PPI and MONICA would share much of the same hardware and software (since both are projection imagers) and, because of comparable imaging performance and physical proximity, might offer additional experimental opportunities to the user, for example, sequential, single photon and positron imaging studies in the same animal. In this report, we characterize the PPI with phantom measurements and mouse imaging studies.

MATERIALS AND METHODS

System Overview and Data Processing

Image Formation

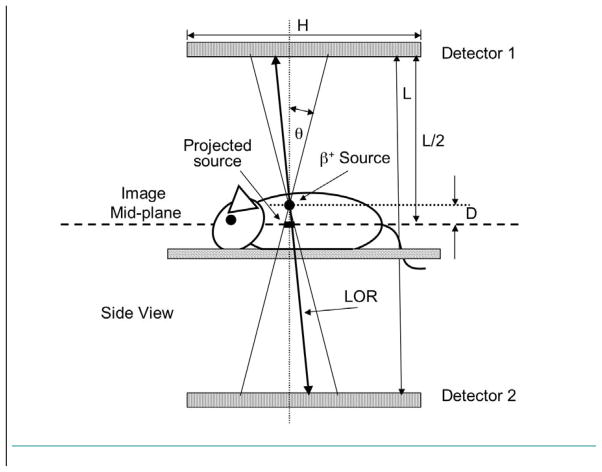
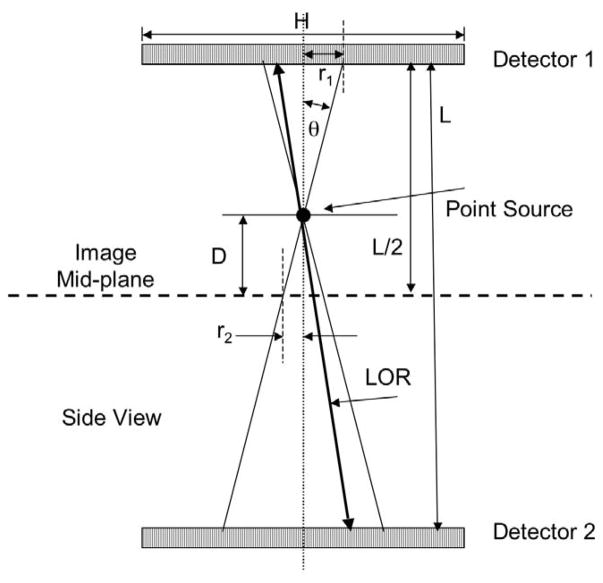
Image formation with the PPI is illustrated in Figure 1. The object to be imaged is centered in the image plane halfway between two, exactly opposed, pixelated “flat panel” scintillation detectors in time coincidence. When a line-of-response (LOR) between a pair of crystals in the detectors is activated by a valid coincident event along that LOR, the point of intersection of that LOR and the image plane is incremented by one count. The ensemble of all such intersections from all LORs falling within a small, fixed angle θ to the vertical between the detector pair forms a projection image of the activity distribution on the image plane.

Figure 1.

Image formation with the positron projection imager. The point of intersection of an activated line-of-response (LOR) with the image mid-plane is incremented by one count if the LOR lies within a small user-selected cone angle (θ) and energy window. The ensemble of all such events within cone angle θ forms a projection image of the positron annihilation distribution in the animal on the image plane. Sources above and below the image plane are “blurred” (see Appendix) depending on the distance (D) from the image mid-plane and resolution is ultimately set by animal thickness (2D_max = T). The angle θ has been greatly exaggerated for clarity in Figure 1 and the pictured objects are not to scale.

Spatial resolution (R), absolute sensitivity (S) and the fraction of the field-of-view (F) over which sensitivity is constant are given for the PPI by the following (small angle approximation) equations derived in the Appendix:

$$\text{R}={[{(2\text{D}(tan\theta )/\surd 2)}^2+{({\text{R}}_{int})}^2]}^{1/2}$$ (1)

$$\text{S}={\alpha }^2{\epsilon }^2{(tan\theta )}^2/4$$ (2)

$$\text{F}=[1-(\text{L}/\text{H})(1+(2\text{D}/\text{L}))tan\theta ][1-(\text{L}/\text{W})(1+(2\text{D}/\text{L}))tan\theta ]$$ (3)

Here, D is the vertical distance to a source located above or below the mid-plane, θ is the cone angle shown in Figure 1 and R_int is resolution (FWHM) in the image mid-plane (where D = 0) that reflects the intrinsic imaging behavior of the detector modules. The factor α is the fraction of annihilation photons that interact in a detector, ε is the fraction of absorbed photons that meet a user-specified absorbed energy condition, L is the face-to-face separation between detectors and H and W are the edge dimensions of the (identical) detector crystal arrays. These equations indicate that once the PPI detectors are designed, that is, H, W, R_int and α are fixed, spatial resolution is ultimately set by the ventral-dorsal thickness, T, of the animal (2D_max = T) and sensitivity is determined by cone angle and energy window. Thus, we explore the consequences of variations in ε, θ and D_max. The uniformity fraction, F, depends on detector separation that, in turn, depends on the count rate capability of the data acquisition system. For reasons described later, detector separation was fixed at 21.8-cm for this study.

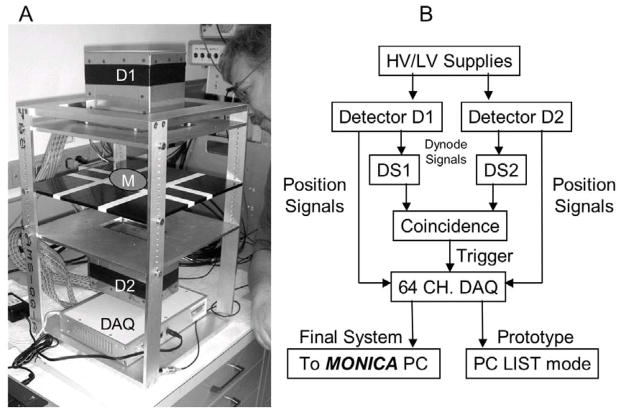
The prototype PPI is pictured in Figure 2A. The PPI system diagram in Figure 2B shows the data pathway to MONICA that will ultimately allow hardware and software common to both applications to be shared. In the present study, the “LIST” mode data pathway shown for the “prototype” in Figure 2B was used in all experiments. Unformatted list mode acquisition allows different versions of an image to be created from the same list mode data set, thereby minimizing the number of data collections required to study many parameter variations.

Figure 2.

(A) PPI prototype showing detectors 1 and 2 (D1 and D2) above and below the image plane (slightly above the striped black plate), the data acquisition system (DAQ) and the position occupied by the mouse during imaging (M); (B) PPI system diagram. In its final form, the PPI will be connected to the MONICA PC enabling use of the same acquisition, analysis and display options available for single photon imaging.

Detector Modules and Data Acquisition

Each of the two opposed detector modules is comprised of an array of 26 × 59 individual LYSO:Ce (lutetium yttrium oxyorthosilicate:cerium, Omega Piezo, State College, PA) crystal pixels 1.5-mm square × 12-mm deep (1.6-mm pitch) surrounded on five sides by opaque reflector and optically coupled to two side-by-side Hamamatsu H8500C position-sensitive photomultiplier tubes (PSPMTs, Hamamatsu, Japan) through a 3.5-mm thick optical window. Signal processing boards are attached to the rear of each PSPMT to complete the detector module. The 64 anode pads of each tube are combined by resistive division to yield eight row and eight column position signals for each event for a total of 32 position signals per detector module. The 64 amplified position signals from both detectors are acquired (digitized) by a 64-channel data acquisition system (DAQ, Adaptive I/O Technologies, Blacksburg, VA) triggered by summed dynode signals from each PSPMT pair (DS1 and DS2 in Figure 2B) that are in time coincidence (10 ns coincidence window). The DAQ then transmits these coincidence event position data and other information to a PC for pre-processing into list mode format and storage on the PC. Subsequently, images are created from these list mode files by re-processing these data using different energy window and cone angle settings.

Data Pre-processing

Data sent from the DAQ to the PC consist of the 64 digitized row and column position signals that locate the pair of coincident scintillation events in the two detectors, the output of a coincidence rate meter at that moment and a high resolution time stamp for the event. Transformation of these data to list mode format consists of the following steps for each scintillation event pair: (1) compute the raw x,y position of the scintillation event in each detector using a 16 × 8 signal centroid algorithm and assign each event to the crystal at that location, N_i, where i is the detector number (1 or 2) and N is the crystal number where the event occurred in that detector (N = 1 to 1534), (2), sum the raw x,y signals for each detector and multiply each sum by the appropriate gain scaling factor, g(N₁) or g(N₂), to obtain an estimate of the “true” absorbed photon energy (E₁ and E₂) at each location and (3), create a low resolution time stamp (TS, msec) from the high resolution time stamp (ns) that is more appropriate for biological timing. As these calculations are completed, a list mode entry of the form (N₁, N₂, E₁, E₂, TS) is created for each coincidence event and written to disk. Approximately every two seconds (more frequently at high event rates), a second type of list mode entry is formed that consists of the total coincidence rate, C, the time stamp TS and a digital ID code that uniquely identifies this type of event, i.e. (ID, C, TS), and is also written to disk. The association of a scintillation event with a scintillation crystal number and the gain correction factors needed to compensate for gain variations from crystal to crystal are determined during detector calibration as described in a later section.

Data Post-processing

These list mode data sets can be subsequently manipulated to yield mid-plane images for different values of energy window and cone angle for data collections representing different source distributions. To do so, each event in the list mode data set is examined and if the absorbed photon energy of both scintillation events in the pair falls within the selected energy window, the event is accepted. If not, the event is skipped and the next event examined. If the event is accepted, it is next tested against the required cone angle. The cone angle is the angle between the line joining crystals N₁ and N₂ and the vertical to the detectors. The crystal numbers N₁ and N₂ are associated with the exact physical position in space of each crystal because of the known mechanical dimensions of the detectors and the detector separation. If the absolute x,y positions of the interacting crystals in the plane of each detector are X₁, Y₁ and X₂, Y₂, the cone angle, θ, is given by:

$$\theta ={tan}^{-1}({[{(\text{X}1-\text{X}2)}^2+{(\text{Y}1-\text{Y}2)}^2]}^{1/2}/\text{L}).$$ (4)

If θ is less than or equal to the required cone angle, the event is accepted and the position of the event in the mid-plane (m) is calculated as:

$${\text{X}}_{\text{m}}=[{\text{X}}_1+{\text{X}}_2]/2\text{and}{\text{Y}}_{\text{m}}=[{\text{Y}}_1+{\text{Y}}_2]/2.$$ (5)

For an accepted event, the accumulating mid-plane image (51 × 117 pixels) is incremented by one count at this location. If the cone angle does not meet the required angle condition the event is skipped and the next list mode entry is examined. After all list mode events have been considered, an image of the object is formed on the mid-plane that meets the required energy and cone angle conditions.

The procedure just described converts a list mode file into a single image and is thus appropriate for representing a static activity distribution in the animal. If the activity distribution is changing over time, a sequence of these images is required. To obtain a sequence of images each with duration T, the time stamp information is used to locate the first event for a frame (at TS₁) and then sort the subsequent event data into a single image until the last event for that frame is detected (at TS₂, where TS₂ = T + TS₁). When the last event is detected, sorting begins again with the next event to create the next image and so on until the list file is exhausted.

Finally, these images are corrected approximately for pulse pileup and ADC dead time by applying the count rate linearity correction described later. In order to make this correction, the average total coincidence count rate is determined from the list mode entries between times TS₁ and TS₂. This value is then inserted into the appropriate correction equation and all pixels in the corresponding image multiplied by this calculated correction factor. The result is an image or image sequence corrected approximately for count rate losses due to pileup and dead time effects.

Detector Calibration and Corrections

Five calibration/correction procedures are required for the PPI to perform properly.

Pedestals

Analog-to-digital converter (ADC) pedestal values (small, constant voltage offsets at the inputs to all ADC channels) are automatically measured for each of the 32 signal channels in each detector module from a short (less than one minute) data collection using triggers generated internally to the DAQ. These new pedestal values are stored and used to correct all ADC values (by subtraction) in all subsequent data collection until changed in the next pedestal acquisition.

Crystal Identification

Crystal regions-of-interest (ROIs) are determined automatically by irradiating both detectors with a custom-made ⁶⁸Ge field flood source (half-life = 270.8 days, 6.5-cm × 12-cm active area, 7.4 MBq (0.2 mCi) on delivery, Eckert and Ziegler, Valencia, CA) and identifying the location of each of the individual 26 × 59 crystals (each appearing as a point in the raw, unprocessed images). A small region around each point is automatically identified and all events falling into this region are assigned to the (known) position of the crystal center at this location. This process removes any spatial non-linearity in event positioning since the location of these centers is precisely known by virtue of exact mechanical fabrication of the arrays. These regions are contiguous and collectively cover the entire field of view (FOV) of each detector module.

Gain Calibration

Spatial variations in apparent gain (energy) across the FOV of each detector are removed by first collecting energy spectra for each individual crystal using the ⁶⁸Ge field-flood source centered in the mid-plane of the FOV. The location of the maximum counts in each spectrum (center of the 511 keV photopeak) is identified and this region is fit with a Gaussian function to estimate the photopeak location. A scale factor is then determined for each crystal that scales the photopeak location of that crystal along the energy axis to the same channel number. These scale factors are stored as a lookup table for each detector and used to correct subsequent events to the same apparent gain so that only coincidence events within a single energy window (set by the user) will be included in the projection image.

Geometric Sensitivity Correction

The projected area of the acceptance cone onto the detector faces decreases as the cone crosses the edges of the detector arrays. As a result, sensitivity around the edges of the FOV decreases relative to the central rectangular region. To compensate for this geometrical effect, a ⁶⁸Ge field-flood projection image (250–650 keV energy window) is acquired for each cone angle that might be used in a “real” data collection (2, 3.5 and 5-degrees in the present work). Each of these acquisitions is sufficiently long that the relative standard deviation of counts at each point in the flood image is less than 2%. The mean counts/pixel (M) in this image is determined and a scale factor (A) calculated for each image point using the relation A_i = M/C_i where C_i is the counts in image pixel “i”. This scale factor is determined for every image point in the projection image and stored in the form of an image. Every image point “i” in a subsequently collected image is multiplied by A_i resulting in an image acquired with apparently uniform geometric sensitivity.

Count-Rate Linearity Correction

As activity increases in the FOV, count rate departs increasingly from linearity due to pulse pileup and ADC dead time. It is possible in principle to correct exactly for this effect by knowing the instantaneous (nearly equal) singles rates on the detectors. The present DAQ does not output these singles data but does yield the total instantaneous coincidence count rate. Under these conditions, a multiplicative linearity correction, G, can be derived that has the form: G = 1/(1 – Cτ) where C is the instantaneous total coincidence count rate and τ is an experimentally determined constant (described below). All image points in a projection image created when the total coincidence rate is C are multiplied by this correction factor G.

The magnitude of the parameter τ depends not only on the pulse integration period and ADC dead time, but also on the size, shape, location and distribution of activity in the object. As a result, the magnitude of the correction factor G also depends on these variables. In order to obtain an estimate of a realistic value of τ, a 30 cc syringe was filled to 25 cc (a mass and size similar to a typical mouse) with 18.5 MBq (500 μCi) of ¹⁸F in uniform solution and centered in the FOV. Data were acquired for 1200 minutes to allow the total coincidence count rate on the detector pair to decrease by a large factor. Total coincidence rate was then plotted as function of activity in the FOV. This curve was found to be comprised of two distinct parts, a semi-linear region at low to modest activities and a region at higher activities that departed abruptly from linearity due to saturation of the USB bus between DAQ and PC.

At very low activities in the FOV, the relationship between total coincidence count rate and activity (A) is linear and this region of the curve was fit with a straight line, S(A), to determine ideal behavior over a wide activity range. The function G was then fit to the ratio function S(A)/C(A) (which measures the deviation of count rate from the ideal linear behavior), up to the point of abrupt departure from linearity, by allowing τ to vary to obtain the best match. This value of τ was then used to correct subsequent count rate data for count rate losses. Values for sensitivity and count-rate linearity reported in the Results section were determined using this correction.

The accuracy of this correction is specific to this particular calibration object and its location in the FOV. The correction could thus be less accurate at high rates when applied to different objects located elsewhere in the FOV. Whole-body imaging with the PPI, however, is restricted to mice. For mice, body mass variations are small (typically of the order of 28 g ± 20%), even “organ-specific” tracer distributions include significant whole-body (or background) activity, the animal must be centerd in the FOV to visualize the whole-body and administered activities are often well within the range which yields count-rate linearity. As a result, corrected count rates for mice are relatively insensitive to any correction errors and the correction method is adequate for mouse studies. We note, however, that additional data channels will be provided in the final version of the PPI that will allow the singles count rate in each detector to be recorded along with the other position signal and timing information. These data will allow exact, object and position independent correction for count rate losses and also for random coincidences (below).

Random Coincidence Correction

Data transmitted from the DAQ to the PC does not contain the information needed to make a computed correction for random coincidences. However, a special experimental arrangement of the prototype electronics allowed the random coincidence rate to be estimated from measured singles rates on the detectors during the 30 cc syringe ¹⁸F count rate linearity experiment described above. It was found that at the highest singles rate with approximately 18.5 MBq (500 μCi) in the FOV, the calculated random coincidence rate did not exceed 5.5% of the total coincidence rate. Since activity levels in typical PPI studies will be substantially less than this amount, and the random coincidence rate much less, the presence of random coincidences was ignored.

Imaging Performance

Imaging performance was evaluated with sources, phantoms and animal studies after all corrections (described above) were implemented.

Spatial Resolution

Spatial resolution was determined by imaging a ²²Na point source (0.3-mm diameter) at different locations offset from the image mid-plane and measuring the apparent width (FWHM) of a profile across this source in the mid-plane image. In addition, these resolution results were fit with the functional form shown in Equation 1 allowing the parameter “R_int” to vary for best fit. Intrinsic resolution in the image mid-plane was taken as the best-fit value for each of three cone angles (2, 3.5 and 5-degrees).

Sensitivity and Count-Rate Linearity

The list-mode count rate versus activity data acquired in the 30 cc ¹⁸F syringe experiment described above were processed for three different cone angles: 2, 3.5 and 5-degrees and for three different energy windows: 100–650, 250–650 and 400–650 keV. The slope (cps/kBq) of the fit to the corrected count rate versus activity curve for each combination is the sensitivity of the PPI for that combination. Sensitivity was also calculated with Equation 2 using α = 0.64 and ε = 0.93, 0.77 and 0.63 for energy windows of 100, 250 and 400 to 650 keV, respectively. These values for ε where obtained by curve fitting the measured sensitivity versus cone angle results with the functional form shown in Equation 2 (all with r > 0.99) and are similar to independent estimates of ε obtained from a detailed computer simulation of the PPI. The value of α was calculated analytically assuming a 511 keV linear-attenuation coefficient for LYSO of 0.86/cm [2].

As described above, pulse pileup and ADC dead time are the dominant forms of data loss in the semi-linear counting rate regime. As activity in the FOV increases, however, a point is reached where coincidence count rate abruptly flattens out as the USB bus between DAQ and PC saturates. Beyond this point, PPI data cannot be corrected for nonlinearity so this point represents the upper FOV activity bound for the system. In the present case, this upper bound is about 14.8 MBq (400 μCi) of ¹⁸F when the detectors are separated by 21.8-cm. If the detectors were brought closer together, the gamma ray flux onto each detector would increase and this maximum activity bound would decrease below 14.8 MB (400 μCi). However, a “safety” factor of about two times typical study activities (< 7.4 MBq (200 μCi)) is recommended for actual mouse imaging studies. Moving the detectors closer together would reduce this upper activity bound and encroach on this safety range. Thus, we report results only for this one detector separation although the mechanical device for holding the detectors apart allows smaller (but not larger) separations (Figure 2).

Uniformity Fraction

The fraction of the FOV over which geometric sensitivity is constant increases with decreasing detector separation and decreases with increasing cone angle as shown in Equation 3. To verify this purely geometric effect, data were acquired for an extended period from the uniform ⁶⁸Ge field flood phantom and used to create projection images of the FOV for cone angles of 2, 3.5 and 5-degrees. These images were formed, however, without applying the correction for the geometric variation in sensitivity. These images were analyzed by plotting profiles along the central X and Y axes and noting where these centrally flat profiles declined abruptly near both edges of the FOV due to cone angle truncation. The area of the central rectangular region within which counts were constant (within 3% of the mean counts in the central region) was calculated from these measurements and compared to the total detector area to estimate this uniformity fraction “F” for each cone angle.

¹⁷⁶Lutetium Background

The crystals in the PPI detectors contain 2.6% by weight of ¹⁷⁶Lu, a naturally occurring radioactive isotope of Lutetium, that causes an inherent coincidence background count rate in the PPI when no sources are present. In order to assess the magnitude of this background (for a detector separation of 21.8-cm), a 1200-minute data collection was performed with no sources in the FOV and these data formatted into three projection images, each with a different energy window (100–650, 250–650 and 400–650 keV). The count rate within the whole FOV and the counts/pixel due to this background for each energy window were determined from these images and compared to typical count rates observed in actual studies for these same windows.

Energy Resolution

The detectors were exposed to the ⁶⁸Ge field-flood source described above. A coincidence energy spectrum was created for each crystal in a detector and these spectra added together point-wise to yield a single representative spectrum for that detector. The FWHM of the 511 keV photopeak of this spectrum was taken as the energy resolution of that detector. These values were nearly identical for both detectors and only a single value is reported.

Timing Resolution

A coincidence event occurs when the summed dynode signals from each detector module occur within 10 ns of each other. In order to determine the intrinsic timing resolution of this system, the summed dynode outputs from the two detectors were fed to the two start-stop inputs of a time-to-digital converter. The FWHM of the resulting Gaussian-like frequency distribution function of arrival time differences was taken as the intrinsic timing resolution of the system. This arrangement was calibrated in the time domain by inserting a known time delay into one of the signal inputs and noting the displacement of the frequency distribution function along the time axis. The magnitude of this displacement (in ns) was then used to scale the FWHM of the Gaussian to absolute time.

Mouse Imaging Studies

Like MONICA, the PPI is intended to produce high quality mouse whole-body projection images under commonly encountered experimental conditions (i.e., with typical tracer doses, typical animal sizes, etc). To explore this range of conditions, two studies were performed, an [¹⁸F ]fluoride bone scan and an [¹⁸F] FDG study in two mice of typical size (31 and 25 g, respectively). By virtue of high bone uptake, low soft tissue uptake, arrangement and small transverse dimensions of the skeletal bones, the fluoride images provide a useful qualitative way to visualize image resolution when the biological signal-to-noise level in the body is very high. In contrast, the distribution of FDG is substantially more diffuse with higher concentrations only in several organs (e.g., the heart). The FDG image, therefore, provides an opportunity to assess image quality when the biological signal-to-noise level in the body is relatively low.

Both animals were injected awake with ~ 7.4 MBq (200 μCi) of [¹⁸F] fluoride and ~ 3.7 MBq (100 μCi) of [¹⁸F] FDG, respectively, and allowed free movement during the uptake period (two hours for fluoride, one hour for FDG). These amounts were chosen such that after uptake and excretion reasonable amounts of ¹⁸F would remain within the body (~1.85 MBq (50 μCi), fluoride); ~1.85 MBq (50 μCi), FDG). Both animals were sacrificed just prior to imaging to eliminate the possibility of movement during data collection. With the animals centered in the FOV and in the image mid-plane, image data were acquired for 45 minutes. This extended imaging period was purposefully chosen to minimize statistical “noise” in the images so that spatial resolution differences between images with different cone angles would be more readily detectable. Following collection, these data were formatted into mid-plane projection images with cone angles of 2, 3.5 and 5-degrees (energy window 250–650 keV) and compared to ascertain the practical effects of cone angle differences on image “quality” for low and high biological contrast studies.

RESULTS

Spatial Resolution

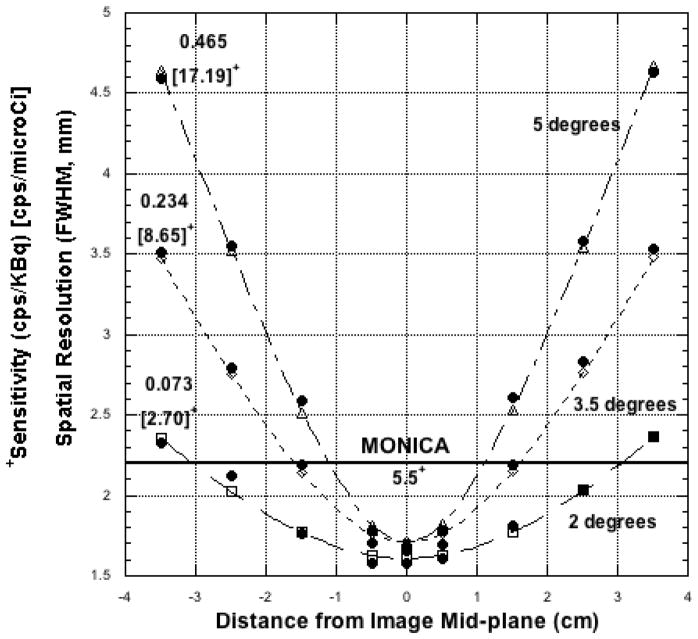
Spatial Resolution measured with the ²²Na point source is plotted against source position above, below and on the image mid-plane in Figure 3 for three different cone angles. The fitted curves to these data (all with r > 0.99) use the functional form shown in Equation 1. Intrinsic (image plane) resolution for each of the three fits is listed in Table 1. Measured and calculated FWHM spatial resolution values are compared in Table 1 for selected (identical) source positions 15-mm above and below the image plane, a distances range that corresponds roughly to the ventral-dorsal thickness of a typical mouse (≤ 3-cm). For comparison purposes, the resolution of the MONICA gamma cameras one centimeter away from the collimator surface is 2.2-mm (FWHM) at 140 keV with a 20% energy window (i.e., ±10%).

Figure 3.

Spatial resolution vs. distance above, below and on the PPI image mid-plane for three different cone angles and an energy window of 250–650 keV. Sensitivities for each angle are also noted. For a cone angle of 3.5 degrees and mice less than 2D_max = 3-cm thick, PPI spatial resolution will be at least as good as single photon imaging with MONICA and sensitivity higher. Curve fits use the functional form shown in Equation 1 (see text).

Table 1.

Cone Angle^*

	2°	3.5°	5°
Image Mid-plane Spatial Resolution (FWHM - mm)	1.61	1.71	1.71
Resolution (mm) at ± 15 mm above, below image plane	1.8 (1.8)	2.2 (2.2)	2.6 (2.5)
Sensitivity cps/kBq– 18F	0.0730 (0.0740)	0.234 (0.227)	0.465 (0.468)
Uniformity Fraction (dimensionless)	0.75 (0.76)	0.58 (0.58)	0.43 (0.48)
Total FOV 176Lu Background Count Rate (cps) field- flood corrected	1.3	4.0	7.6

^*Energy window: 250–650 keV, all entries. Measured values are without parentheses, calculated values are with parentheses. Calculated values for Resolution and Uniformity Fraction where obtained from Equations 1 and 3, respectively. Calculated values for Sensitivity were obtained from Equation 2 with α= 0.64 and ε= 0.77.

Sensitivity and Count Rate Linearity

Sensitivity of the PPI (slope of the straight line fit to the corrected count rate versus ¹⁸F activity plot) is listed in Table 2 for three energy windows and three cone angles. Measured sensitivity values for three cone angles and an energy window of 250–650 keV are compared (Table 1) to sensitivity values calculated from Equation 2. For comparison purposes, the MONICA gamma cameras have a sensitivity of 0.149-cps/kBq (5.5-cps/μCi) at 140 keV with a ±10% energy window.

Table 2.

Sensitivity - cps/kBq (cps/μCi)

Cone Angle	2°	3.5°	5°
Energy Window
100–650 keV	0.105 (3.89)	0.337 (12.5)	0.673 (24.9)
250–650 keV	0.073 (2.70)	0.234 (8.65)	0.465 (17.2)
400–650 keV	0.049 (1.82)	0.158 (5.85)	0.314 (11.6)

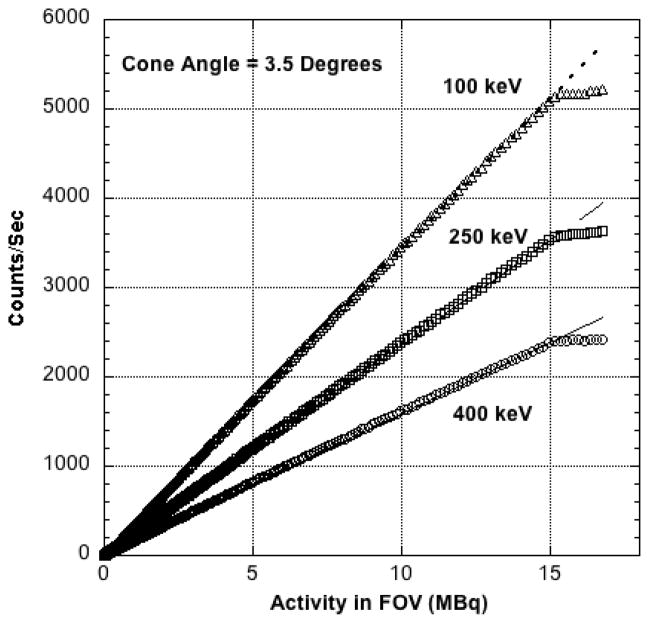
Corrected coincidence count rate is plotted against ¹⁸F activity in the FOV in Figure 4 for three different energy windows. These curves depart abruptly from linearity at approximately 14.8 MBq (400 μCi) in the FOV, the upper limit of activity that can be imaged with the PPI. All three curves exhibit the same activity cutoff since the total count rate, not the count rate in each energy window, determines the cutoff value.

Figure 4.

Corrected count rate vs. activity in the FOV for three different energy windows and the same cone angle. The source was a cylinder (2-cm diameter × 7.5-cm length) containing a uniform solution of ¹⁸F centered in the FOV. Numerical values assigned to each curve are the lower energy window settings. The upper level setting was fixed at 650 keV. Correction fails at approximately 14.8 MBq (400 μCi) of ¹⁸F in the field of view.

Energy Resolution

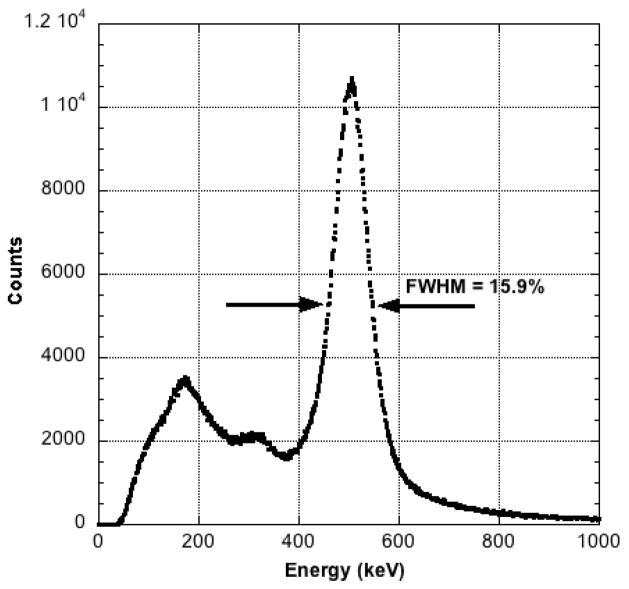
The gain-corrected, summed coincidence ⁶⁸Ge energy spectrum for one detector is shown in Figure 5. The FWHM of the Gaussian portion of this plot is 15.9%, a value identical to that obtained for the second detector.

Figure 5.

Point-wise summed ⁶⁸Ge composite coincidence energy spectrum for one detector after gain correction for each LYSO crystal pixel.

Timing Resolution

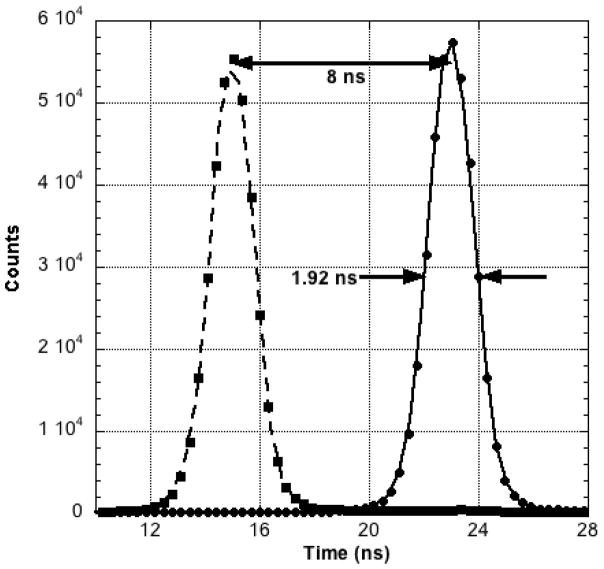
The frequency distribution of trigger-pulse-arrival time differences is shown in Figure 6. The FWHM of the two Gaussian-like distributions is 1.92 ns. The second peak was purposefully generated by inserting a known (8 ns) time delay into one of the summed dynode signal lines. The observed displacement of the second peak along the time axis allows the FWHM curve width to be calibrated in nanoseconds.

Figure 6.

Frequency distribution of trigger start-stop pulse arrival time differences for the PPI. Second peak was created by inserting a known time delay (8 ns) into one of the signal lines and using the observed shift along the time axis to convert the FWHM curve width to absolute units (nanoseconds).

¹⁷⁶Lu Background and Uniformity Fraction

The total background-coincidence count rate from ¹⁷⁶Lu and estimates of the uniformity fraction (F) are listed in Table 1 for three different cone angles and an energy window of 250–650 keV. As expected, the background coincidence rate increases with increasing cone angle but is negligible for all three angles compared to anticipated count rates from “real” objects. It would be expected that these rates would be higher for an energy window of 100–650 keV and lower for a window of 400–650 keV. Values for the uniformity fraction calculated from Equation 3 are in good agreement (Table 1) with the experimental measurements of “F”.

Mouse Imaging Studies

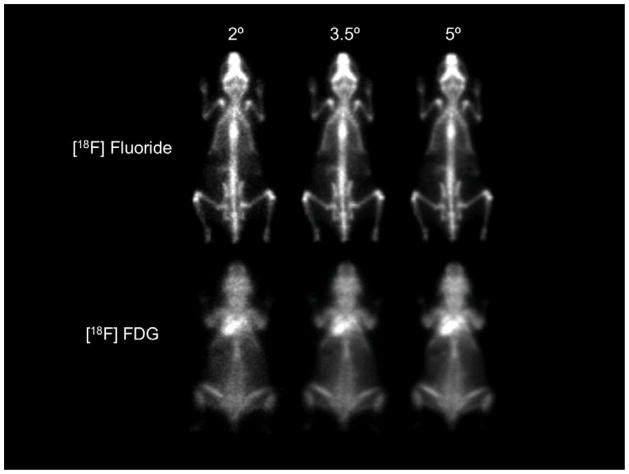
Mouse [¹⁸F] fluoride and [¹⁸F] FDG images are shown in Figure 7 for three different cone angles. According to Equation 1, spatial resolution degrades with increasing cone angle and careful inspection of these images shows this trend. The sensitivity difference with cone angle predicted by Equation 2 is not readily evident since each of these demonstration images were acquired for 45 minutes (to reveal resolution differences), a time interval long enough that all three images appear almost equally “smooth”. In a “real” imaging study of typically shorter duration, the user might be required to choose a large cone angle that increases sensitivity in order to decrease statistical noise. Should this be necessary, the images in Figures 7 suggest that adequate spatial resolution is preserved even for the largest cone angle (5-degrees), thereby allowing the user to take potential advantage of a six-fold sensitivity increase compared to a 2-degree cone angle acquisition (Table 2).

Figure 7.

PPI whole-body images of the distribution of [¹⁸F] fluoride (31-g animal) and [¹⁸F] FDG (25-g animal) for three different cone angles and an energy window of 250–650 keV. Both animals were sacrificed at the end of the uptake periods to eliminate movement during imaging. Each animal was imaged for 45 minutes to suppress image noise, contained approximately 1.85 MBq (50 μCi) of ¹⁸F at the start of imaging and was injected awake and free to move about during the uptake periods. These images suggest that a cone angle of 3.5 degrees is a reasonable tradeoff between resolution and sensitivity.

The mouse images shown in Figure 7 suggest that the PPI can differentiate between labeled structures in close proximity to one another in high biologic contrast studies (e.g., distinguish between femur and tibia at the knee joint between these bones) and identify organs in lower contrast studies, for example, the myocardium in the FDG study. In this latter case, the image of the myocardium is overlaid by FDG accumulated in the animal’s dorsal muscles and brown fat during the free-roaming uptake period.

DISCUSSION

Results obtained in the present work suggest that the PPI detector design, electronics and geometry create an effective positron projection imaging system. For an energy window of 250–650 keV, spatial resolution of the PPI (≤ 2.2-mm FWHM) when imaging a typical ~3-cm thick mouse is comparable to MONICA (2.2-mm FWHM, energy window of 140 keV ± 10%, 1-cm from the MONICA collimator). Similarly, PPI sensitivity (<0.235-cps/kBq (8.7-cps/μCi) for cone angles less than 3.5-degrees is comparable to MONICA (0.149-cps/kBq (5.5-cps/μCi)). The intrinsic properties of the PPI detectors that contribute to this performance also meet modern standards (15.9% energy resolution, 1.92 ns timing resolution). Finally, Equations 1–3 accurately describe the major performance properties of the PPI, implying that knowledge of a few first-order physical processes (i.e. photon attenuation by LYSO at 511 keV, etc.) and the system geometry are sufficient to predict system behavior under different circumstances.

The principal disadvantage of whole-body projection imaging systems, like the PPI or collimated gamma cameras like MONICA, is low sensitivity. Projections images are formed by only accepting radiation traveling near the perpendicular to the PPI detectors or along the axes of the parallel collimator holes of MONICA and rejecting radiation from all other directions. This process is inherently inefficient and sensitivities for these kinds of devices are typically very much lower than some other kinds of small animal whole-body imaging systems, e.g. a small animal PET scanner with cylindrical detector geometry and large axial field-of-view. In addition, projection imaging systems collapse the third or depth dimensions onto a plane and thus lose any information about the distribution of activity in depth. Both of these disadvantages conspire to limit the application of projection systems in the field.

Nonetheless, projection imaging of small animals offers a number of practical advantages in certain experimental settings. For example, our laboratory uses mouse tumor xenograft models to evaluate newly developed, single-photon-labeled tumor-seeking compounds [3]. Here, tumor xenografts implanted on the animal’s flank are seen by the MONICA gamma cameras in relief away from other labeled body structures in the anterior or posterior projections. As a result, estimates of total tumor activity can be gotten simply by placing a region-of-interest over the tumor and, after small corrections for tumor background and attenuation, multiplying the tumor count rate by a known calibration factor that relates count rate to total tumor radioactivity. In this setting, collapse of the third dimension onto a plane by the PPI (or MONICA) is acceptable since surrounding radioactivity that might confound this measurement is made minimal by the experimental design and total tumor activity can be calculated with reasonable accuracy.

Under such conditions, static or dynamic whole-body imaging studies can be carried out with the additional advantages of an “open” architecture that simplifies access to the animal for injection and maintenance during imaging as well as immediate analysis of images without image reconstruction. Projection imaging also lends itself to display of a “persistence” image throughout the imaging process that provides useful QC information, (e.g., the success of tracer injection, position of the animal in the FOV, etc.). When integrated with the MONICA system, the PPI will share other useful MONICA features such as portability and the ability to operate the PPI and view the persistence image remotely through a wireless laptop connection. While these advantages individually may be of modest value, together they significantly increase efficiency when large number of animals must be imaged (often the case in biodistribution studies) and these data analyzed. The potentially lower cost and operational simplicity of projection imaging systems are also attractive features.

From the user’s point of view, there will be no practical distinction between MONICA and PPI projection imaging studies and all data acquisition, display and analysis features available with MONICA for single photon images will be available for positron images. This similarity between the PPI and MONICA systems in fields of view and performance suggests that this combination might be useful when attempting temporally sequential single photon and positron projection imaging studies (in that order) in the same animal, since both systems will be proximate to one another and to common support devices (e.g., anesthesia equipment). Development of a mechanically registered animal bed compatible with both MONICA and the PPI is straightforward and spatial registration should be straightforward as well. If the single photon compound emits photons of typically lower energy, thin Pb shielding can be placed over both PPI detectors to reduce or eliminate the single photon background on each detector without significantly affecting PPI performance (unpublished results). If this approach proves feasible, potentially useful and complementary imaging studies could be performed to investigate paired phenomena in a variety of mouse models, for example, comparison of [¹⁸F] FDG and [¹¹¹In] Panitumumab uptake in the same tumor xenograft at nearly the same time.

Projection imaging has been used extensively and recently in other specialty imaging devices, notably in positron emission mammography [4, 5] and many of the details [6] of this methodology, including the use of iterative reconstruction methods to estimate lesion depth [7] have been worked out in this context. The PPI, too, can be configured as a limited angle tomograph as described by Zhang, et al. [8] by bringing the detectors close together and nearly touching the mouse in between. This approach allows imaging of animals injected with very small amounts of activity since geometric sensitivity is very high due to the small detector separation. Other novel devices [9, 10] have also been reported that capitalize on the advantages of projection-like limited angle imaging.

The PPI could also be used to image in vitro longitudinal whole body tissue sections of mice or other large area mouse (or human) tissue samples containing positron-emitting compounds. Here, the detectors would be placed very close together (< 1-cm) so that F would be near unity, an allowable arrangement since activity in a thin whole body section would necessarily be much lower than in an entire mouse (or organ) and the upper activity bound for linear operation would not be exceeded. In this mode, the lower level discriminator would be set near 400 keV to greatly reduce the effect of the ¹⁷⁶Lu coincidence background [11].

The PPI could thus be used in several modes simply by changing the detector separation: as a whole-body mouse projection imager with the detectors relatively far apart (10s of-cm), as an in vitro tissue section projection imager with the detectors very close together (a fraction of a centimeter) and as a limited angle tomograph (detectors separated by several centimeters). This combination of applications and the potentially reduced cost of PPI-like devices may, where experimental conditions permit, provide the user with a viable alternative to small animal tomographs of conventional cylindrical design.

APPENDIX

The equations that describe spatial resolution (R), sensitivity (S) and the fractional area of constant sensitivity response (F) for the PPI are derived below. The variables described in the derivations are defined in Figures A1 and A2. These equations are derived assuming the validity of small angle approximations in the solid angle calculations, that the detectors are continuous rather than arrays of discrete crystals and, with the exception of the uniformity fraction, that the lateral dimensions of the detector arrays are large compared to the lateral dimensions of the objects being imaged.

Figure A1.

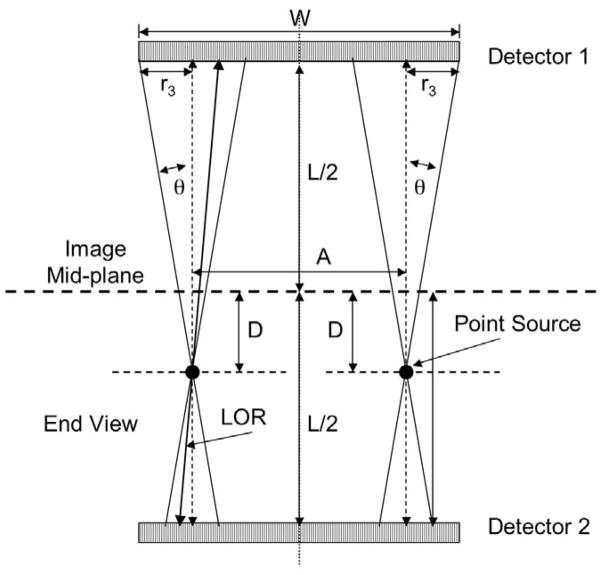
Definition of the geometric variables affecting the performance of the positron projection imager. Only lines-of-response (LORs) falling within the small, user-selected cone angle θ contribute counts to the mid-plane image. The FWHM of the projected spot size 2r₂ increases (resolution degrades) as the distance from the mid-plane increases but sensitivity remains constant.

Figure A2.

Definition of geometric variables affecting calculation of the uniformity fraction, F. If the two sources shown in the Figure are moved further outwards, the two projected cones (with radius r₃) will no longer fall entirely within the boundaries of the detector and sensitivity will decline. The length A is thus the greatest width that still contains these cones and sources within A will be “seen” with constant geometric sensitivity.

Spatial Resolution

If a point source of positron emitter is placed a distance D above the image plane, two coaxial cones with half angle θ are created with a common apex that project circular regions onto both detector faces (Figure A1). The width of this projected point source onto the image plane (2r₂) is a measure of the geometric “blurring” of this source by the system. The FWHM of this spot can be approximated as twice that radius that creates a circle with half the area of the circle πr₂² since half the lines-of-response within cone angle θ will penetrate this smaller circle. This radius is r₂/√2 and the FWHM is twice this value or 2r₂/√2. The radius r₂ is given by D tan (θ) so that the geometric FWHM resolution, R_geo, is given by:

$${\text{R}}_{\text{geo}}=2{\text{r}}_2/\surd 2=2\text{D}tan(\theta )/\surd 2$$ (a)

According to this equation, the geometric FWHM of the projected spot is zero when the source point lies on the image plane (D=0). The actual FWHM resolution for a point source on the image plane, however, will not be zero but must instead have some finite value. This value will be determined by the design and behavior of the detector arrays and will depend on factors such as crystal cross-sectional size, etc., This intrinsic FWHM resolution of the system, R_int, is not easily determined from first principles so we have measured this parameter experimentally by imaging a point source on the image plane for three different cone angles and determining R_int from the Gaussian-like profiles across this source. These measured values are listed in Table 1.

The overall FWHM resolution of the system for arbitrary D and θ can now be calculated by combining the geometric and intrinsic resolutions by quadrature:

$$\text{R}(\text{D},\theta )={[{{\text{R}}_{\text{geo}}}^2+{{\text{R}}_{int}}^2]}^{1/2}$$ (b)

Substituting equation (a) into this expression gives:

$$\text{R}(\text{D},\theta )={[{(2\text{D}tan(\theta )/\surd 2)}^2+{{\text{R}}_{int}}^2]}^{1/2}$$ (c)

According to Eqn. (c), a point source is increasingly “out of focus” (seen with poorer resolution) as distance above or below the image plane increases and as cone angle increases. It is thus important that “thin” (in the vertical direction) objects be imaged with the PPI so that sources from all depths in the animal are seen with roughly the same (and highest) resolution. Note that spatial resolution is independent of detector separation.

Sensitivity

The geometric sensitivity, S_geo, of the PPI, the fraction of annihilation gamma rays emitted from the point source shown in Figure A1 that fall onto the detectors, is the ratio of the projected cone area πr₁² to the total spherical area surrounding the point:

$${\text{S}}_{\text{geo}}=\pi {{\text{r}}_1}^2/4\pi {((\text{L}/2)-\text{D})}^2$$ (d)

The radius r₁ is also equal to ((L/2)-D) tan (θ) so that the expression for S_geo becomes:

$${\text{S}}_{\text{geo}}=\pi {((\text{L}/2)-\text{D})}^{2}tan{(\theta )}^2/4\pi {((\text{L}/2)-\text{D})}^2$$

$${\text{S}}_{\text{geo}}=tan{(\theta )}^2/4$$ (e)

Of this fraction, only a portion will interact in the detectors and only a fraction of these will meet the absorbed energy condition, that is, be inside the energy window set by the user. If the fraction that interact in a detector is α and the fraction of those that meet the energy condition is ε, then the probability that an annihilation event in the acceptance cone will contribute to the image is the square of the product of these two variables, α²ε². The square is required since the annihilation photons must meet the absorption and energy deposition requirements in both detectors at the same time. The overall sensitivity of the PPI is the product of the geometric sensitivity and these absorption/acceptance probabilities:

$$\text{S}={\alpha }^2{\epsilon }^2{\text{S}}_{\text{geo}}={\alpha }^2{\epsilon }^{2}tan{(\theta )}^2/4$$ (f)

According to Eqn. (f), the sensitivity of the PPI depends only on the acceptance angle θ and the interaction and energy deposition probabilities. Conversely, sensitivity is independent of detector separation and the source distance above or below the image plane.

Uniformity Fraction

If a point source is moved laterally across the field-of-view of the PPI with cone angle θ, a source position will be reached where one edge of a cone just touches the edge of the field-of-view of the detectors as shown for the left and right point sources in Figure A2.

For all source positions between these two extremes (within the length A), sensitivity will be constant since the cones falling on each detector are completely within the detector boundaries. However, for source positions just beyond these points, only a portion of the projected circles will fall on each detector and apparent sensitivity will decline.

In the general case of point sources off the image mid-plane, e.g. the point sources shown in Figure A2, the sizes of the projected circles on the two detectors are different with the largest projected circle (upper detector in Figure A2) affecting the uniformity fraction near the detector boundaries. If the width of a detector array is W, the length along W for which the cones are contained within W is W – 2r₃. Similarly, if the height of a detector is H, the length along H for which the cones are contained within H is H – 2r₃. Thus, the area of the detector within which sensitivity is uniform is the product of these two lengths:

$$\text{uniformity}\text{area}=(\text{H}-2{\text{r}}_3)(\text{W}-2{\text{r}}_3)$$ (g)

Inspection of Figure A2 shows that r₃ = ((L/2) +D) tan (θ). Making this substitution in Eqn. (g) gives:

$$\text{uniformity}\text{area}=\text{HW}(1-(\text{L}/\text{H})(1+(2\text{D}/\text{L}))tan(\theta ))(1-(\text{L}/\text{W})(1+(2\text{D}/\text{L}))tan(\theta ))$$ (h)

The uniformity fraction for a point source above, below or on the image plane, F, is the ratio of this area to the total detector area, HW, so the uniformity fraction is:

$$\text{F}(\text{D},\theta )=(1-(\text{L}/\text{H})(1+(2\text{D}/\text{L}))tan(\theta ))(1-(\text{L}/\text{W})(1+2\text{D}/\text{L})tan(\theta ))$$ (i)

If D_max is the location of the maximum anterior and posterior surfaces of the animal above and below the image mid-plane, then 2D_max = T, the anterior to posterior thickness of the animal. In this case, Eqn. (f) becomes:

$$\text{F}(\text{D},\theta )=(1-(\text{L}/\text{H})(1+(\text{T}/\text{L}))tan(\theta ))(1-(\text{L}/\text{W})(1+(\text{T}/\text{L}))tan(\theta ))$$

According to Eqn. (i), the fraction of the field of view over which sensitivity is constant can be increased by increasing the height and width of the detector arrays relative to detector separation, L. The uniformity fraction can also be increased by imaging animals whose “thickness”, T, is small relative to detector separation and by reducing the cone angle.

By way of example, for point sources in the mid-plane of the PPI (T = 0), a 3.5 degree cone angle and a detector separation of 218 mm, the effective values of H (94.3 mm) and W (41.5 mm) are H = 81 mm and W = 28.2 mm and the calculated uniformity fraction for the image mid-plane is approximately 0.58 or 58% of the total detector area, a value identical to the measured value (Table 1). A similar calculation for a mouse-size animal (T = 30 mm) yields a uniformity fraction of 0.53 or 53% of the total field of view.

While sensitivity begins to decrease for objects larger than the reduced values of H and W, these reduced values are generally sufficient to “see” nearly an entire mouse. Thus, the correction described in the text to compensate for the decline in sensitivity around the edges of the field-of-view has relatively little practical impact in most circumstances.