Characterizing Inter-Compartmental Water Exchange in Myelinated Tissue using Relaxation Exchange Spectroscopy

Abstract

Purpose

To investigate inter-compartmental water exchange in two model myelinated tissues ex vivo using relaxation exchange spectroscopy (REXSY).

Methods

Building upon a previously developed theoretical framework, a three-compartment (myelin, intra-axonal, and extra-axonal water) model of the inversion-recovery prepared REXSY signal was applied in excised rat optic nerve and frog sciatic nerve samples to estimate the water residence time constants in myelin (τ_myelin).

Results

In the rat optic nerve samples, τ_myelin = 138 ± 15 ms (mean ± standard deviation) was estimated. In sciatic nerve, which possesses thicker myelin sheaths than optic nerve, a much longer τ_myelin = 2046 ± 140 ms was observed.

Conclusions

Consistent with previous studies in rat spinal cord, the extrapolation of exchange rates in optic nerve to in vivo conditions indicates that τ_myelin < 100 ms. This suggests that there is a significant effect of inter-compartmental water exchange on the transverse relaxation of water protons in white matter. The much longer τ_myelin values in sciatic nerve supports the postulate that the inter-compartmental water exchange rate is mediated by myelin thickness. Together, these findings point to the potential for MRI methods to probe variations in myelin thickness in white matter.

INTRODUCTION

The transverse relaxation of water protons in nerve and white matter is multiexponential and typically characterized by two or three signal components: (i) a short transverse relaxation time constant (T₂) component arising predominantly from water between myelin bilayers (i.e., myelin water) and (ii) one or two longer-T₂ components arising predominantly from water within and between axons (i.e., nonmyelin water) (1–3). The fractional contribution of the short-T₂ water signal to the total signal is known as the myelin water fraction (MWF). Previous work has demonstrated that the MWF reports on myelin content (4, 5); however, it is also sensitive to the rate of inter-compartmental water exchange, which has been predicted to vary as a function of axon diameter and myelin thickness (6, 7). Thus, the exact relationship between MWF and myelin volume fraction, and, more generally, between the spectrum of water proton T₂s (T₂ spectrum) and neuronal microstructure remains undefined.

Previous attempts to characterize inter-compartmental water exchange in myelinated tissues used two-dimensional (2D) magnetization transfer (MT)–T₂ measurements (8–10). The resulting data were fitted to a four-pool model (myelin and nonmyelin water and two associated macromolecular (MM) proton pools) that included exchange between the water pools and between the water and MM pools. Such studies are challenging because of the large number of free and covarying parameters, particularly when MT and water exchange rates are of similar magnitude. Therefore, it is not surprising that these studies resulted in widely varied estimates of the mean water residence in myelin (τ_myelin)—160 to 310 ms ex vivo at bore temperature (8, 9) and 280 to 780 ms in vivo (10).

A potentially more direct approach to measuring inter-compartmental water exchange is through relaxation exchange spectroscopy (REXSY) (11, 12). With REXSY, the presence of inter-compartmental water exchange during a mixing period is directly observed as off-diagonal components in a 2D T₂–T₂ relaxation spectrum; and the evolution of these off-diagonal peaks is sensitive to the rate of inter-compartmental water exchange. Thus, it is possible to estimate exchange rates by acquiring 2D REXSY data over a range of mixing times, although this results in a long, 3D experiment. In cases where apparent T₁ differences exist between water pools, a more expedient method (IR-REXSY) uses an inversion-recovery (IR) magnetization preparation to reduce the acquisition from three to two dimensions (13). To date, REXSY-based methods have been used to study water dynamics in porous media (14–17), model chemical systems (11, 13), and hydrated elastin (18), but not yet intact tissues. In this study, relaxation exchange spectroscopy was applied to the study of inter-compartmental water exchange in freshly excised rat optic nerves and frog sciatic nerves, two model myelinated tissues with different mean myelin sheath thickness. Because these studies were performed in freshly excised samples, the more expedient IR-REXSY approach was employed.

THEORY

A detailed description of relaxation exchange spectroscopy methods, including IR-REXSY has been published previously (13). Here, the IR-REXSY method is briefly summarized. The IR-REXSY sequence (Fig. 1) involves an IR preparation period of duration t_I designed to approximately null of the longitudinal magnetization of one signal T₂-component; an excitation and pre-storage delay of duration t_E1; a storage period of duration t_M to allow mixing of water between compartments; and a readout out using a Carr-Purcell-Meiboom-Gill (CPMG) measurement (19, 20). The sequence is repeated over a range of t_M values, resulting in 2D experiment—number of CPMG echoes (NE) × number of t_M values (NM). Note that the phase-cycled excitation between the IR and storage periods subtracts the magnetization from acquisitions stored on the ±z-axis during the mixing period and is employed to ensure that the signal acquired during the CPMG readout arises solely from spins that are excited by the first π/2 pulse. Therefore, any growth in the magnitude of the IR-suppressed signal component during the mixing period is directly attributable to exchange with the non-suppressed component(s).

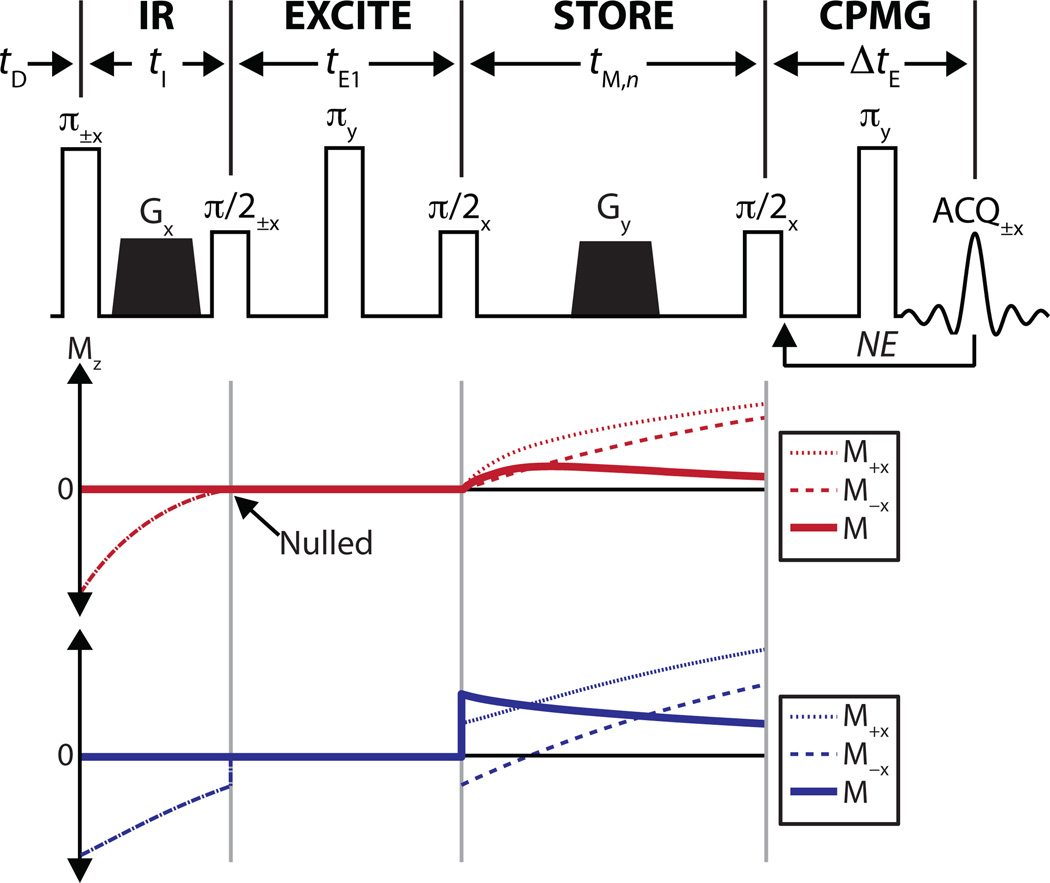
Fig. 1.

(Top) Pulse sequence diagram for the IR-REXSY sequence. To quantify exchange, a CPMG measurement is performed over a range of t_M,n (n = 1 to NM) values with all other timings fixed. Legend: t_D = predelay, t_I = inversion time, t_E1 = delay prior to the mixing period, t_M,n = n^th mixing time, Δt_E = echo spacing of CPMG measurement, NE = number of CPMG echoes, NM = number of mixing times, ACQ = acquisition, and G_x,y = crusher gradients applied along x or y directions. The phase each RF pulse and acquisition across the two-step phase cycle is given as a subscript (a single value is given for pulses of constant phase). (Bottom) Simulated M_z for a two-component system undergoing exchange. In these simulations, t_I has been chosen to null one of the two components. Shown are the M_z for the 1^st (M₊) and 2^nd step (M₋) of the phase cycle along with the final magnetization (M = M₊−M₋). Note the initial increase in the magnitude of the nulled component during the mixing period, which can be directly attributed to exchange with the other component.

To quantitatively analyze NMR data from multiple exchanging compartments, consider N exchanging water compartments defined by unique equilibrium magnetizations M_0,i(i = 1 to N), longitudinal and transverse relaxation rate constants R_1,i and R_2,i (or time constants T_1,i and T_2,i), and inter-compartmental exchange rate constants k_ij. Note that k_ij represents the rate constant of exchange from compartment i to compartment j (j = 1 to N, j ≠ i), and under the principle of detailed balance, k_ijM_0,i = k_jiM_0,j. If the compartments are assumed to be well-mixed at all times (see Discussion), the Bloch-McConnell (21) equations can be solved to provide a signal equation for a given pulse sequence during free precession. For a CPMG measurement acquired at equilibrium with a perfect 90° excitation, the signal equation is

$$S_{\text{CPMG}}(t_{\mathrm{E},m})={\mathbf{1}}_{1\times N}\text{exp}\left({\mathbf{L}}_2{t}_{\mathrm{E},m}\right){\mathbf{M}}_0,$$ [1]

where t_E,m(m = 1 to NE) is the echo time, 1_1×N is 1 × N vector of ones, M₀ is a N × 1 column vector of compartmental equilibrium magnetizations, and L₂ is a N × N matrix defined as

$${\mathbf{L}}_2=\left(\begin{array}{ccc}-R_{2,1}-{\displaystyle {\sum }_{i\ne 1}{k}_{1i}}& \square & k_{N1}\\ ⋮& \ddots & ⋮\\ k_{1N}& \cdots & -R_{2,N}-{\displaystyle {\sum }_{i\ne N}{k}_{Ni}}\end{array}\right).$$ [2]

Reducing the matrix exponential in Eq. [1] by expanding L₂ in terms of its eigenvalues and eigenvectors yields

$$S_{\text{CPMG}}(t_{\mathrm{E},m})={\mathbf{1}}_{1\times N}\mathbf{U}\left(\begin{array}{ccc}\text{exp}\left(-{\lambda }_1{t}_{\mathrm{E},m}\right)& \square & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & \text{exp}\left(-{\lambda }_N{t}_{\mathrm{E},m}\right)\end{array}\right){\mathbf{U}}^{-1}{\mathbf{M}}_0,$$ [3]

where λ_i is the i^th eigenvalue of L₂ and U is a matrix whose columns are the corresponding eigenvectors.

From this equation, it can be seen that the magnetization from each pool, and thus also the total signal, evolves as a sum of N exponentials terms with observed transverse relaxation time constants T_2obs, where T_2obs,i = −1/λ_i. Given a sampling of S_CPMG(t_E,m) with sufficient signal-to-noise ratio (SNR) over a suitable number/range of t_E values, it is possible to estimate these T_2obs,i terms and corresponding signal component amplitudes P_CPMG,i using a numerical inverse Laplace transform (ILT) algorithm (e.g., (22, 23)). Factoring Eq. [3] with respect to each exponential term, one can obtain a relationship between model parameters (in M₀ and L₂) and these observed signal component amplitudes

$${\mathbf{P}}_{\text{CPMG}}=\left({\mathbf{U}}^{-1}{\mathbf{M}}_0\right)○{\left({\mathbf{1}}_{1\times N}\mathbf{U}\right)}^{\mathrm{T}}.$$ [4]

Here P_CPMG is a N × 1 vector of component amplitudes (P_CPMG,i) derived from the ILT of S_CPMG(t_E,m), ○ represents the element-wise (or Hadamard) matrix multiplication operation, and ^T represents the matrix transpose operation.

From a similar approach, the signal equation for the IR-REXSY sequence is

$$S_{\mathit{\text{IREX}}}(t_{\mathrm{E},m},t_{\mathrm{M},n})={21}_{1\times N}\text{exp}\left({\mathbf{L}}_2{t}_{\mathrm{E},m}\right)\text{exp}\left({\mathbf{L}}_1{t}_{\mathrm{M},n}\right)\text{exp}\left({\mathbf{L}}_2{t}_{\mathrm{E}1}\right)\left[2{\text{exp}(\mathbf{L}}_1{t}_{\mathrm{I}}{)\mathbf{M}}_0-{\mathbf{M}}_0\right],$$ [5]

where t_E,m is defined as above, t_M,n(n = 1 to NM) is the mixing time, t_E1 is the pre-storage echo time, and L₁ is defined similarly to L₂ (Eq. [2]) except with compartment longitudinal relaxation rate constants (R_1,i) in place of the transverse relaxation rate constants (R_2,i). Note that this signal equation assumes the previously mentioned two-part phase cycle, which subtracts the magnetization from acquisitions stored on the ±z-axis (the factor of 2 in Eq. [5] accounts for this, see Fig. 1 for details). Again, the matrix exponential terms dependent on t_E can be expanded and then the equation can be factored with respect to the resulting apparent transverse relaxation rate terms, resulting in

$${\mathbf{P}}_{\text{IREX}}(t_{\mathrm{M},n})=2\{\left({\mathbf{U}}^{-1}\text{exp}\left({\mathbf{L}}_1{t}_{\mathrm{M},n}\right)\text{exp}\left({\mathbf{L}}_2{t}_{\mathrm{E}1}\right)\left[2\text{exp}\left({\mathbf{L}}_1{t}_{\mathrm{I}}\right){\mathbf{M}}_0-{\mathbf{M}}_0\right]\right)\}○{\left[{\mathbf{1}}_{1\times N}\mathbf{U}\right]}^{\mathrm{T}},$$ [6]

where P_IREX(t_M,n) is N × 1 vector of component amplitudes derived from the 1D ILT of S_IREX(t_M,t_E) with respect to t_E at each t_M value. In other words, it describes the evolution of the apparent component amplitudes with respect to t_M.

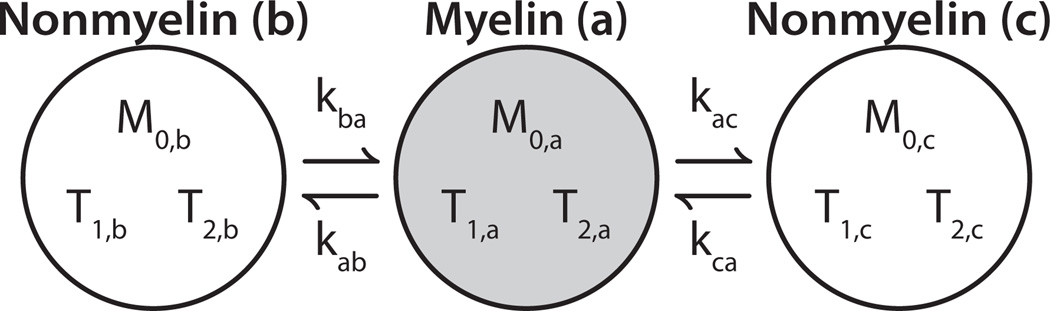
In the context of myelinated tissues, the microstructures of both sciatic and optic nerve suggest the need for a three-compartment model of water: water in-between myelin bilayers (myelin water), water in the axoplasm (intra-axonal), and water in outside of myelinated axons (extra-axonal). Sciatic nerve NMR relaxometry has long been known to exhibit three distinct T₂ components (1), which current literature assigns to myelin, extra-axonal, and intra-axonal water in order of increasing relaxation time (24–26). The interpretation of a shorter T₂ of extra-axonal compared with intra-axonal water, which may be counter-intuitive, is based on observations of water diffusion (24) and contrast-agent effects (25, 26) on the water T₂ spectrum of nerve, and is likely due to the abundance of collagen in peripheral nerve, as noted by Peled et al. (23). In contrast, most previous studies of white matter (3–6, 26) and optic nerve (8, 26, 27) have identified two T₂ components, although at least one study has identified three T₂ components in optic nerve (28). Consequently, the present study uses a three-compartment model for sciatic nerve and investigates both two- and three-compartment models for optic nerve. To simplify the three-compartment models, it is assumed that no exchange occurs directly between intra- and extra-axonal water. That is, water must traverse the myelin sheath to travel between the intra- and extra-axonal spaces. For the analysis herein, we arbitrarily label each of the three nerve water compartments as i □ [a, b, c], where ‘a’, ‘b’ and ‘c’ represent signal from components in order of increasing T₂. As summarized in Fig. 2, this results in a model with 11 independent parameters: three equilibrium magnetizations (M_0,a/b/c), three each longitudinal and transverse relaxation time constants (T_1,a/b/c and T_2,a/b/c), and two exchange rate constants (k_ab and k_ac).

Fig. 2.

Three-compartment model of optic and sciatic nerve. The three compartments are labeled ‘a’, ‘b’, and ‘c’ in order of increasing T₂. The short-T₂ component (gray circle) represents myelin water, while the other two components (white circles) represent nonmyelin water (intra- and extra-axonal water). Because water must traverse the myelin sheath to pass between intra- and extra-axonal spaces, exchange between the nonmyelin compartments in neglected. Under the condition of equilibrium (i.e., compartment sizes are constant), this results in model defined by 11 independent parameters: three equilibrium magnetizations (M_0,a/b/c), three transverse relaxation times (T_2,a/b/c), three longitudinal relaxation times (T_1,a/b/c), and two exchange rate constants (k_ab and k_ac).

METHODS

Sample Preparation

Adult male rats (Sprague-Dawley) and African clawed frogs (Xenopus laevis) were used for all studies in accordance with protocols approved by the Institutional Animal Care and Use Committee of Vanderbilt University. Rats (n = 5, 432 ± 64 grams) were euthanized via CO₂ inhalation. Following euthanasia, both optic nerves were excised from the optic chiasm to the skull (≈1 cm segments), cleaned of attached blood and soft tissue, and immersed in phosphate buffered saline (PBS; Mediatech Inc., Herdon, VA) at room temperature until NMR was performed. Frogs (n = 4, 143 ± 22 grams) were euthanized by immersion in a 10 g/L bath of tricaine methanesulfonate (Finquel^®; Argent, Redmond, WA) for 20–30 minutes. Following euthanasia, a 1–2 cm segment of sciatic nerve were excised from one hindlimb, cleaned of attached blood and soft tissue, and immersed in amphibian Ringer’s solution (Fisher Scientific, Rochester, NY) at room temperature until NMR was performed.

Prior to each NMR session, the nerve sample was patted dry to remove extraneous fluid, placed in a 5-mm NMR tube, and bathed in perfluorcarbon solution (Fomblin^®; Solvay Solexis, Thorofare, NJ) to prevent tissue drying without contributing proton signal. NMR measurements were immediately performed as described in the following section. The total time from euthanasia until the end of the NMR experiments was approximately two hours. To test for relevant changes in tissue microanatomy during this period, CPMG measurements (see below) were made at the beginning and end of each NMR session.

Following NMR, one optic and one sciatic nerve sample were processed for light microscopy. To do so, samples were fixed by immersion in 0.5% paraformaldehyde/4% glutaraldehyde in buffer (0.1 M phosphate buffer for rat optic nerve and Amphibian Ringer’s solution for frog sciatic nerve), post-fixed in osmium tetroxide, and embedded in Epon. From these blocks, sections (1 µm thick) were cut, stained with toluidine blue, and evaluated by light microscopy on an Olympus BX41 microscope equipped with an Optronics Microfire digital camera. Fields at 40× and 100× were photographed for sciatic and optic nerve, respectively. Axon diameters and myelin sheath thicknesses were manually measured in these sections as described previously (6).

Data Acquisition

NMR measurements were performed on freshly excised nerve samples at bore temperature (≈20°C). Sciatic nerve samples were scanned on a 4.7-T (200 MHz), 31-cm bore Varian/Agilent (Santa Clara, CA) Direct Drive MRI system, while the smaller optic nerve samples were scanned on a 9.4-T (400 MHz), 16-cm bore (same console type). An in-house-built loop-gap resonator (29) was used for RF transmission and reception at both field strengths. One sciatic nerve and three optic nerve samples were scanned at both field strengths to test for a systemic difference between systems.

Data were collected with CPMG [S_CPMG(t_E,m), m = 1 to NE] and IR-REXSY [S_IREX(t_E,m, t_M,n), m = 1 to NE, n = 1 to NM] pulse sequences. All measurements used NE = 1024 and an echo spacing (Δt_E) of 1 ms. The predelay (t_D) was set long enough to ensure magnetization had returned to equilibrium [8/12 s (optic/sciatic nerve, IR-REXSY) or 15 s (CPMG)], and 4 to 16 excitations were averaged to ensure adequate SNR. Because IR-REXSY model does not require perfect myelin water signal nulling and a short study time was needed to accommodate the fresh tissue samples, t_I was quickly set to approximately null the myelin water T₂ component as measured from IR-CPMG acquisitions over a few t_I values. Using this t_I value and a t_E1 = 2 ms, IR-REXSY data were collected NM = 16 or 20 t_M values logarithmically spaced between 10–15 ms and 2 s. For all experiments, the RF pulses were carefully calibrated by pulse width adjustment, resulting in ≈ 10 µs and ≈ 20 µs durations for 90° and 180° hard pulses, respectively.

Data Analysis

All data were processed using MATLAB (The Mathworks, Natick, MA). The first five echoes of each measurement were discarded to avoid previously observed signal components with T₂ ≈ 1 ms (30), and echoes beyond t_E = 350 ms for optic nerve and t_E = 800 ms for sciatic nerve (≈ 4× the longest respective nerve T₂ components) were discarded to minimize the impact of Rician noise (31) as the decay approached the noise floor, which was especially important in analyzing the lower-SNR IR-REXSY data. In order to utilize Eqs. [4] and [6], which relate the T₂ spectral component amplitudes and mean T₂s to intrinsic model parameters, both S_CPMG and S_IREX signals were transformed from the echo-time domain to the T₂ domain. In general, this is an ill-posed transformation, but was made more robust by defining a fixed number of signal components (two or three) and defining each component as a Gaussian shape in a logarithmically spaced T₂ domain. This method has been previously described by Stanisz et al. (27) and, compared to more general approaches (23), has the benefit of producing a specified number of signals components with well-defined integrated amplitudes in the presence of spectral overlap. For comparison, T₂ spectra were also computed from S_CPMG data using a non-negative least-squares algorithm (22) with minimum curvature regularization (23) (NNLS-MC) that was adjusted by the generalized cross-validation method (32). This more general approach fits echo magnitudes to decaying exponential functions across a wide range of time constants and does not make any assumptions about the number of spectral peaks.

The multiple Gaussian-component fitting was performed using a separable least-squares approach (33), which utilized standard nonlinear regression of the two or three component mean T₂ values and a constant offset interleaved with an linear regression step to estimate the corresponding component amplitudes. For the S_CPMG fitting, no constraints were applied to the fitted parameters. For the S_IREX fitting, component mean T₂ values for a given sample were constrained to be equal across the different mixing times and to be within ±20% of the mean T₂ values fitted from S_CPMG from the same sample. Also, for S_IREX fitting, the amplitude of the myelin water component was allowed to be positive or negative (since IR-preparation did not exactly null this signal component), while the longer T₂ signal components were constrained to be non-negative in amplitude. The standard deviations (SDs) of the residuals to the fits of S_CPMG and S_IREX over the last 50 echo times were used as estimates of the added noise to each signal.

The estimated T₂ component amplitudes fitted from S_CPMG and S_IREX provided values for P_CPMG and P_IREX, respectively, while the mean component T₂s from the CPMG measurement provided values for T_2obs. In theory, these values can be simultaneously fitted with Eq. [4], Eq. [6], and the negative reciprocal eigenvalues of L₂ to provide estimates of the 11 independent model parameters (M_0,a/b/c, T_1,a/b/c, T_2,a/b/c, k_ab, and k_ac); however, such a fitting is computational demanding. Therefore, starting with P_CPMG and T_2obs as estimates of intrinsic compartmental model parameters M₀ and T₂, the remaining five model parameters (T_1,a/b/c, k_ab, and k_ac) were estimated by fitting P_IREX with Eq. [6] by nonlinear regression. The resulting estimates of k_ab and k_ac were then used in Eqs. [2] and [4] to provide updated estimates of M₀ and T₂ by a secondary nonlinear regression step. This process was repeated until all parameters converged to a stable solution. To ensure that a global minimum was found, the whole process was repeated 50 times with randomly varied initial estimates of T_1,a/b/c, k_ab, and k_ac. Finally, the myelin water lifetime, defined as the reciprocal of the sum of the rate constants of water moving out of compartment a, was computed as τ_myelin = (k_ab +k_ac )⁻¹.

Given the complexity of the model and analysis, a Monte Carlo approach was used to evaluate propagation of error from measured echo amplitudes to fitted model parameters. Fitted S_CPMG and S_IREX signals from typical optic and sciatic nerve samples were used as noiseless synthetic data. Added to these data were randomly generated zero-mean Gaussian noise data with SDs as determined from the fit residuals (above) from the sample with the lowest SNR (for the each nerve type). These noisy synthetic signals were then used to estimate model parameters as described above. The process was repeated with 500 independent noise realizations to estimate the uncertainty in P_IREX data and each fitted model parameter.

RESULTS

In all cases, the equilibrium S_CPMG from optic nerve samples were better fitted (p < 0.05) with three Gaussian-shaped components than with two, as determined by the relative change in the χ² fit statistics tested against an F-distribution (34). Thus, optic nerve, like sciatic nerve, was analyzed in terms of a three-compartment model. For all sciatic nerve samples and all optic nerve samples studied at 9.4 T, the S_CPMG signals before and after the IR-REXSY acquisitions showed little change in the fitted T₂s (mean/max absolute change of 5/16.6% across all samples and components), indicating stable T₂ relaxation characteristics throughout the S_IREX acquisition. Two of the three optic nerve measurements at 4.7 T showed substantial changes (mean/max absolute change of 27.4/57.1%) and, therefore, were not included in subsequent analysis.

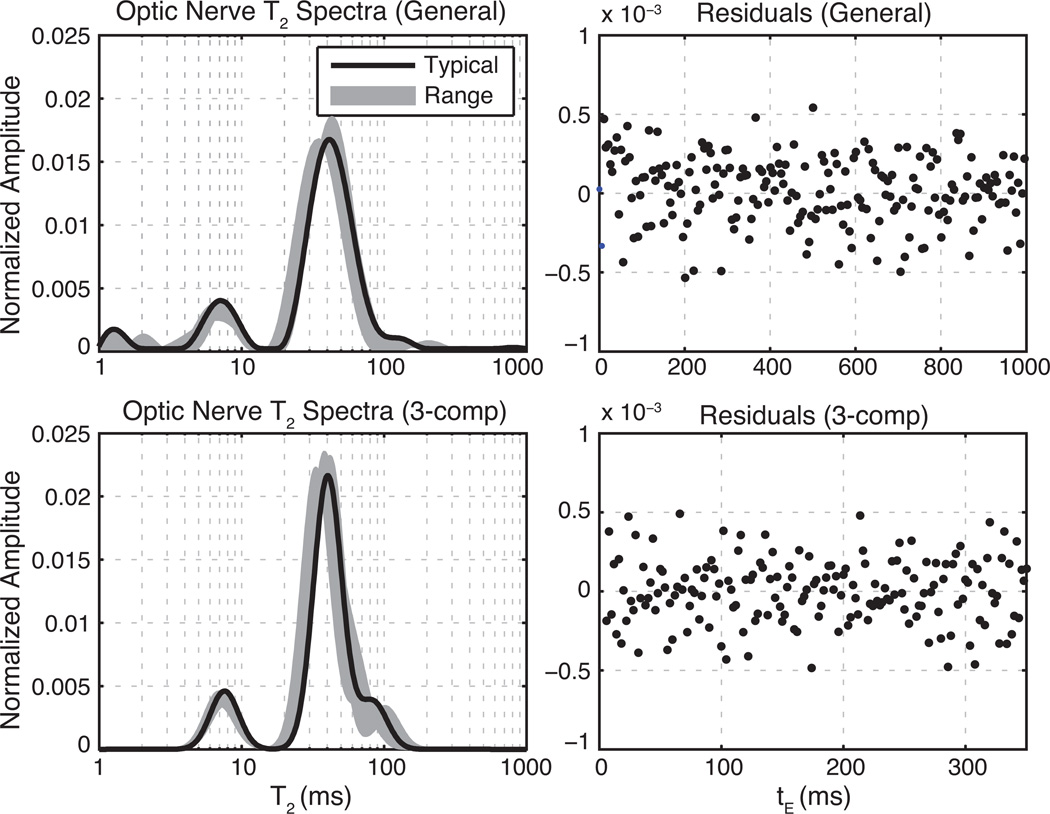
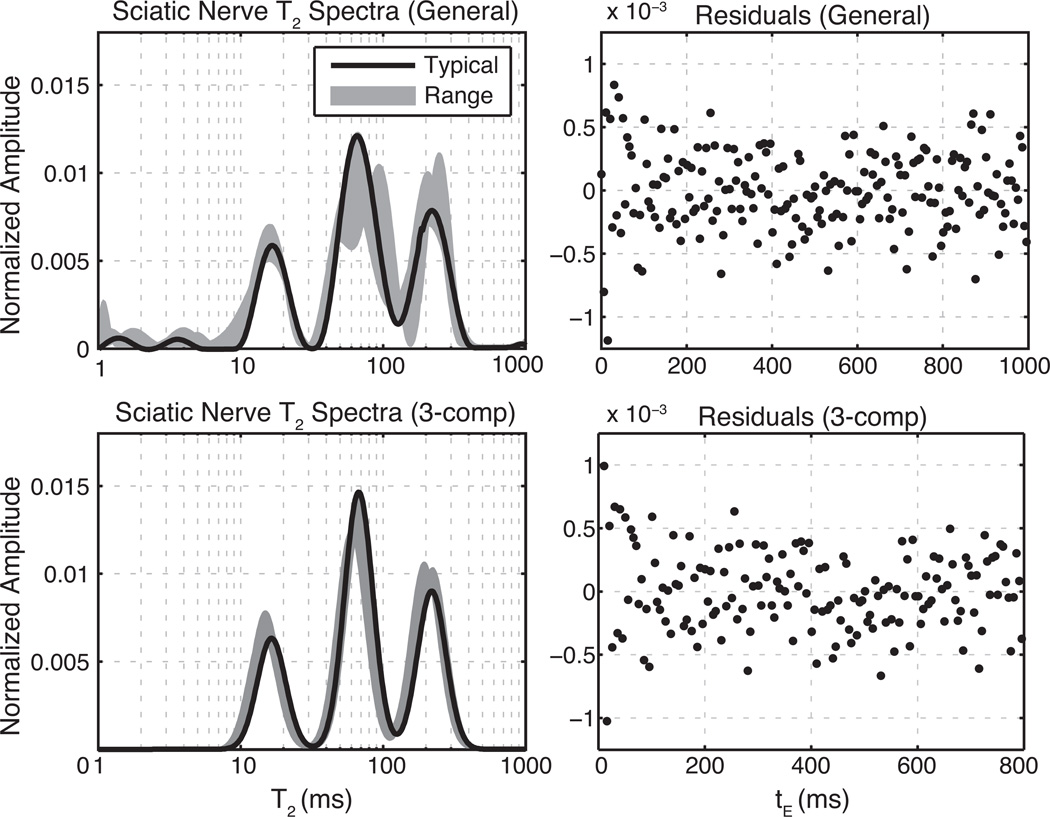
Representative equilibrium T₂ spectra (left) and corresponding residuals of the T₂ spectral fit (right) are shown for optic and sciatic nerve samples in Figs. 3 and 4 respectively. The top panels of each figure show T₂ spectra and fit residuals resulting from the fitting of all equilibrium CPMG echoes using the NNLS-MC method. The lower panels show similar results from the fit of equilibrium CPMG data over the restricted t_E domain (6–350 ms for optic nerve, 6–800 ms for sciatic nerve) with three Gaussian-shaped T₂ components. For both nerve types, the Gaussian component fits replicate the NNLS-MC well within the T₂ domains of 5–200 ms (optic) and 5–400 ms (sciatic), while avoiding extraneous signals outside these domains. The fitted spectra also agree well with previous studies of transverse relaxation in optic (8, 26, 27) and sciatic (26, 35–37) nerves ex vivo. The residuals (normalized to the first echo amplitude) show little structure, particularly near the end of the echo-train, which supports their use for characterizing the added noise as described above. The mean square fit error was 15% larger on average (across samples) for the Gaussian-component fitting over the reduced t_E domain compared with the NNLS-MC fitting over the full t_E domain. These poorer fits result from not fully accounting for the extraneous signals, particularly in the very short T₂ domain. Table 1 summarizes the fitted component amplitudes and mean T₂s as well as range of SNRs (defined as the maximum echo magnitude divided by the SD of the added noise).

Fig. 3.

Equilibrium T₂ spectra of optic nerve at 9.4 T. Left panels show fitted T₂ spectra and right panels show residuals from a typical sample fit normalized to the maximum echo amplitude. Top panels show results of fitting the full echo train with only non-negative and minimum curvature constraints. The bottom panels show the results of fitting the truncated echo train with three Gaussian-shaped T₂ components. For clarity, only every 5^th residual is plotted in the upper right frame.

Fig. 4.

Equilibrium T₂ spectra of sciatic nerve at 4.7 T. Left panels show fitted T₂ spectra and right panels show residuals from a typical sample fit normalized to the maximum echo amplitude. Top panels show results of fitting the full echo train with only non-negative and minimum curvature constraints. The bottom panels show the results of fitting the truncated echo train with three Gaussian-shaped T₂ components. For clarity, only every 5^th residual is plotted in the upper and lower right frames.

Table 1.

T₂ spectral characteristics from equilibrium CPMG measurements of sciatic and optic nerve. All sciatic nerve samples were scanned at 4.7 T, and all optic nerve samples were scanned at 9.4 T. Values of signal component fractions (P_CPMG,i) and mean observed T₂s (T_2obs,i) are given as the mean ± SD across samples. The three signal components are labeled i ∈[a, b, c] in order of increasing observed T₂, with the short-T₂ component (‘a’) representing myelin water.

	Optic Nerve (n = 5)	Sciatic Nerve (n = 4)
PCPMG,a (%)	13.6 ± 1.9	22.9 ± 2.5
PCPMG,b (%)	71.3 ± 4.7	44.3 ± 3.0
PCPMG,c (%)	15.1 ± 5.3	32.8 ± 1.8
T2obs,a(ms)	7.2 ± 0.2	15.6 ± 1.0
T2obs,b(ms)	36.6 ± 2.5	65.6 ± 4.3
T2obs,c(ms)	79.9 ± 13	212 ± 11
SNR1	2960-6830	3120–11000

¹SNR of the S_CPMG signal. variation within a given nerve type is due to variation in sample size.

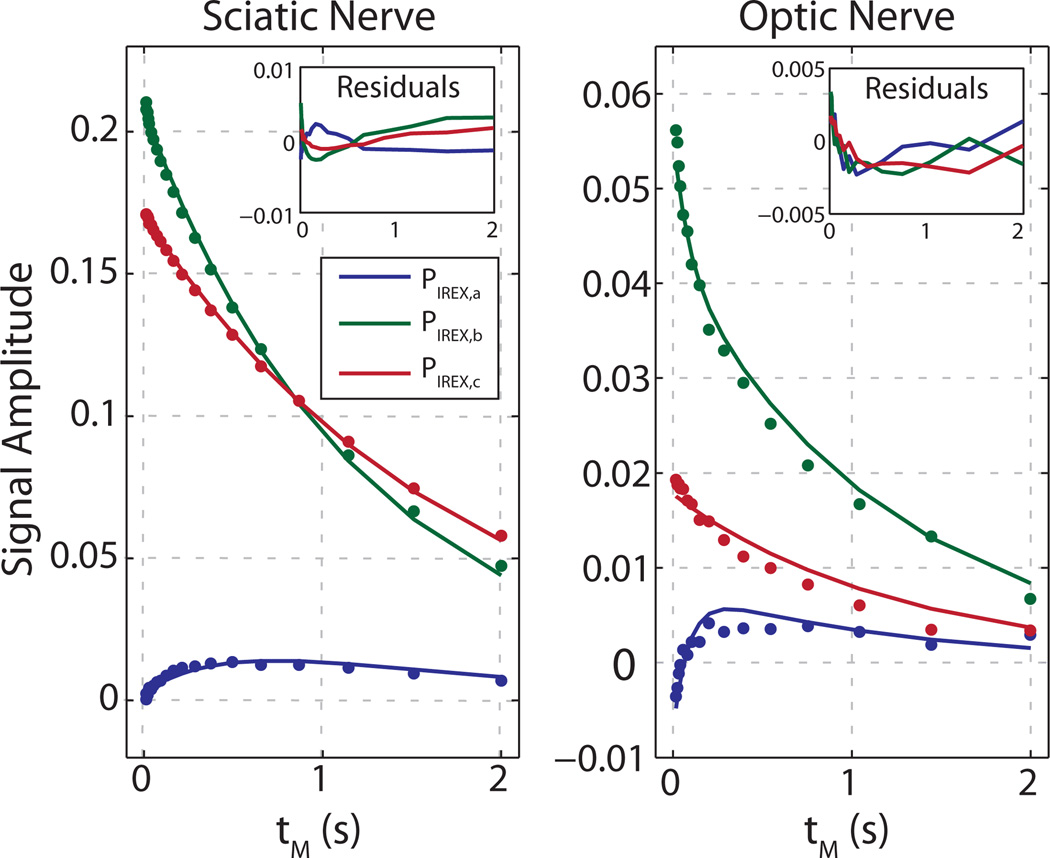
The IR-REXSY data are summarized in Fig. 5 and Table 2. Figure 5 shows representative P_IREX data and model-predicted curves for each of the three T₂ components for both sciatic nerve (left) and optic nerve (right). For both cases, the Monte Carlo estimated error bars are not visible because they are smaller than the size of the data marker. Table 2 summarizes the mean fitted model parameters for both nerve types. Also shown is the inter-sample SD and the Monte-Carlo estimated SD for each fitted parameter. The Monte Carlo estimates demonstrate that the effect of the propagation of error on each fitted parameter (computed with the worst-case noise level for each nerve type) is similar in magnitude to the inter-sample SD. Thus we can conclude that the SNR obtained for the current experiments was sufficient to fit all model parameters, subject to the limitations of the model (see Discussion). In particular, Fig. 5 also shows that residuals to the fits were structured with amplitudes on order of a few percent of the P_IREX signals, which demonstrates small systematic misfits of the data and model. Not apparent from in this figure, although more apparent in Tables 1 and 2, is the somewhat larger inter-sample variance in fitted amplitudes of the two longer T₂ components for optic nerve compared to sciatic nerve. This likely reflects the inherent difficulty for T₂ relaxometry to distinguish intra- and extra-axonal water in optic nerve. Thus, while the relationship between the three model compartments and micro-anatomy is well supported for sciatic nerve, distinguishing the contributions of intra- and extra-axonal environments to the observed signal components in optic nerve should be made more cautiously.

Fig. 5.

Sample IR-REXSY data (P_IREX) from sciatic nerve (left) and optic nerve (right). In both cases, error bars, as determined by Monte Carlo simulation for the worst case SNR across respective samples, are smaller than the data marker size.

Table 2.

Fitted three-compartment model values from IR-REXSY measurements in optic and sciatic nerve. All sciatic nerve samples were scanned at 4.7 T, and all optic nerve samples were scanned at 9.4 T. Values are given as the mean ± SD across samples (SD across Monte Carlo trials). For both optic and sciatic nerves, the Monte Carlo trials were generated using an SNR equal to the lowest SNR observed across samples. The three signal components are labeled i ∈[a, b, c] in order of increasing observed T₂, with the short-T₂ component (‘a’) representing myelin water.

	Optic Nerve (n = 5)	Sciatic Nerve (n = 4)
M0,a (%)	15.5 ± 2.2 (0.3)	23.3 ± 2.5 (0.1)
M0,b (%)	69.3 ± 4.4 (6.2)	43.9 ± 3.0 (0.1)
M0,c (%)	14.9 ± 5.1 (6.5)	32.7 ± 1.7 (0.2)
T2,a (ms)	7.6 ± 0.2 (0.3)	15.7 ± 1.0 (0.1)
T2,b (ms)	38.6 ± 2.7 (1.3)	66.5 ± 4.3 (0.3)
T2,c (ms)	81.8 ± 11 (6.9)	215 ± 11 (1.2)
T1,a (ms)	547 ± 54 (48)	651 ± 19 (0.8)
T1,b (ms)	1730 ± 203 (64)	1517 ± 101 (5.8)
T1,c (ms)	1558 ± 86 (150)	1960 ± 107 (23)
kab (s−1)	6.7 ± 1.9 (0.6)	0.39 ± 0.01 (0.03)
kac (s−1)	0.6 ± 1.2 (3.7)	0.10 ± 0.02 (0.03)
τmyelin (ms)	138 ± 15 (30)	2046 ± 140 (24)
SNR1	310–814	2409–5508

¹SNR of the S_IREX signal. SNR variation within a given nerve type is due to variation in sample size.

For the individual sciatic and optic nerves studied at both B₀ fields, shorter T₂s and a longer T₁s were observed at 9.4 T compared to at 4.7 T, but the fitted exchange rates were similar, as expected: τ_myelin = 153/139 ms (optic nerve) and 2250/2210 ms (sciatic) at 4.7/9.4T, indicating no systematic difference in evaluating the samples at different B₀ fields.

DISCUSSION

Recent ex vivo (6) and in vivo (7) studies of transverse relaxation in rat spinal cord revealed a substantial variation in MWF between different white matter tracts with similar myelin content. Computational models derived from light microscopy sections (7) indicated that differing rates of inter-compartmental water exchange between these tracts might explain the observed variation in MWF. Water exchange was predicted to be faster in tracts with smaller axons and thinner myelin sheaths compared to tracts with larger axons and thicker myelin sheaths. More recently, in vivo studies of human brain have postulated a similar mechanism may be responsible for variations in observed water T₂ spectra in various white matter tracts (38). In these previous studies, the effect of water exchange was inferred or suspected indirectly by the experimental observations of transverse relaxation. Here, a more direct experimental approach based on relaxation exchange spectroscopy (13) is used to observe and quantify inter-compartmental water exchange in freshly excised sciatic and optic nerves.

Qualitatively, Fig. 5 demonstrates water exchanging into myelin from nonmyelin regions in sciatic and optic nerve as a function of mixing time. Note that, because of the phase-cycle employed, only water exchange during the mixing period can cause the myelin water signal magnitude to increase. To better appreciate the much faster exchange rate in the optic compared to sciatic nerves, note that the myelin water signal in the optic nerve initially increases by ≈10% of the total water signal at the minimum mixing time (that is, the total longitudinal magnetization remaining after the IR preparation) before decreasing due to longitudinal relaxation. In contrast, the sciatic nerve myelin signal increases to only a few percent of the total water signal at the minimum mixing time, suggesting a much slower initial rise due to exchange.

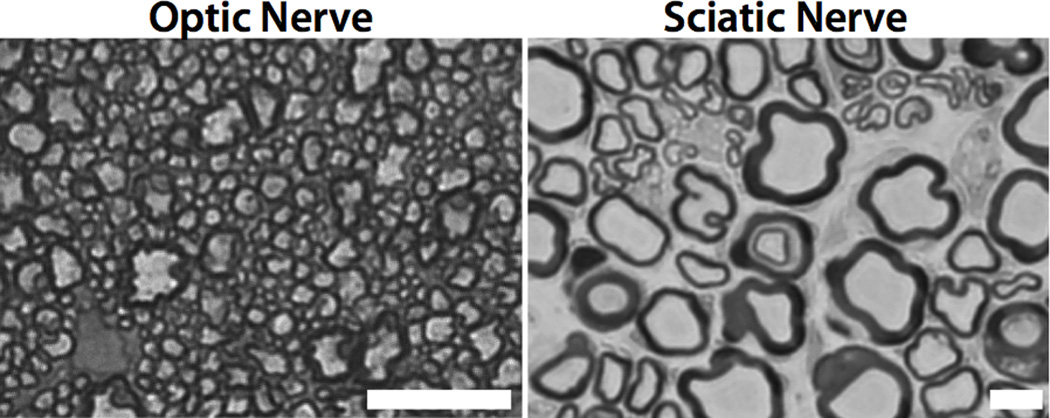
Quantitatively, the fitted results in Table 2 reveal a myelin water lifetime for sciatic nerve that is ≈15× greater than that of optic nerve, which we postulate is primarily due to its characteristically thicker myelin sheaths. Area-weighted mean myelin sheath thicknesses, as measured manually from the light micrographs in Fig. 6 (6, 7), were ≈0.3 and ≈1.7 µm for optic and sciatic nerve, respectively. If exchange is limited by the boundary permeability between the myelin and nonmyelin compartments, then the myelin water lifetime is proportional to the ratio of the myelin volume to the inter-compartmental boundary surface area, which is proportional to myelin thickness. In this case, we would expect lifetimes in sciatic nerve to be ≈5.6× longer than in optic nerve. Alternatively, if exchange is limited by the permeability of each lipid bilayer comprising the myelin, which is akin to saying that exchange is limited by the radial diffusion coefficient of water in the myelin, then one might crudely expect myelin water lifetime to vary with the square of the myelin thickness (mean squared displacement being proportional to time). In this case, we would expect lifetimes in sciatic nerve to be ≈32× longer than in optic nerve. Note that a single time constant is insufficient to characterize water exchange in the case of diffusion-limited exchange; therefore, the models derived from the Bloch-McConnell equations, which assume well-mixed compartments, do not fully describe water exchange under these conditions.

Fig. 6.

Representative light micrograph images from optic and sciatic nerve. The white scale bar = 10 µm in both frames.

In the case of diffusion-limited exchange, one can alternatively consider the water between each bilayer as an individual, well-mixed compartment using a formalism similar to that described in the Theory section. In round numbers (estimated from (39)), these water compartments are 3 nm (optic nerve) or 4 nm (sciatic nerve) thick, separated by 5 nm thick permeable barriers (lipid bilayers) with permeability to water of P_lipid. As above, the exchange rate constant of water out of each compartment can be computed as the permeability times the surface-area to volume ratio. Defining all compartments for a given myelin sheath be full of water at time t = 0, and ignoring water moving into the myelin, then the total amount of water remaining in the myelin as a function of time is characterized by an equation similar to Eq. [1] without the relaxation terms. Solutions with P_lipid = 2.9 µm/ms yield an apparent τ_myelin = 132 ms and 2150 ms, respectively, for total myelin sheath thicknesses matching the optic (0.3 µm) and sciatic nerve (1.7µm), respectively. These results are roughly consistent with the mean fitted values of τ_myelin = 138 ms and 2046 ms, as measured by IR-REXSY, suggesting that the difference in their relative sizes is due to differences in myelin thickness between optic and sciatic nerves. Of course the actual P_lipid of the membranes that make up myelin is not known, but P_lipid = 2.9 µm/ms is consistent with, and even on the low end of, previously reported water permeability in biological membranes (40).

The mean value of τ_myelin = 138 ms in optic nerve reported here is similar to the τ_myelin =161 ms reported by a previous ex vivo optic nerve study by Stanisz et al. (8), although approximately two-fold shorter than τ_myelin = 310 ms reported by Bjarnason et al. (9) in bovine white matter ex vivo at 24 °C. The Bjarnason study also found approximately 2× decrease in τ_myelin by increasing the temperature of the ex vivo sample to 37 °C. Applying the same factor to the present ex vivo data, we predict τ_myelin ≈ 70 ms in optic nerve at 37 °C. This value is in the range of apparent myelin water lifetimes (43–150 ms) in vivo in rat spinal cord predicted by Harkins et al. (7), although still somewhat long considering that the smallest mean myelin thickness in the spinal cord study was 0.43 µm compared with 0.3 µm for the optic nerves studied here. Likewise, the value of P_lipid = 2.9 µm/ms (above) is somewhat lower than the range of values predicted from the same rat spinal cord study. One interpretation of the discrepancy between the water exchange rates predicted by Harkins et al. and the present study is that exchange is faster in vivo due to more than a temperature dependent increase in the rate of water diffusion. Finally, while there are no previously published values of myelin water lifetimes in peripheral nerve with which to compare the present observations, the measured τ_myelin ≈ 2 s is in agreement with a previous assertion that water exchange is very slow in peripheral nerve (37).

In terms of the effect of water exchange on MWF measurements, the data presented here show ≈13% underestimation of MWF in optic nerve at room temperature (compare P_CPMG,a in Table 1 to M_0,a in Table 2). Again, extrapolating to the in vivo case is an open question, but using the aforementioned factor of 2× in exchange rates and model parameters for optic nerve in Table 2, one can calculate a MWF underestimation of ≈25% for optic nerve in vivo. This value is shy of the ≈50% predicted by Harkins et al. for the dorsal cortical spinal tract in rats, but still substantial compared to other studies that have indicated no effect of water exchange on measured MWF. Also, at lower B₀ (compared to the 9.4 T used for the optic nerve studies here) T₂s will be longer and relatively more affected by water exchange. While one might see underestimation of MWF as a shortcoming of myelin water imaging based on multi-exponential transverse relaxation, it also means that the water T₂ spectrum of white matter contains microstructural information related to myelin thickness.

Another potential implication of relatively short myelin water lifetimes is on microstructural inference from diffusion weighted imaging (DWI). Most quantitative models of water diffusion in white matter (see the recent summary by Panagiotaki et al. (41)) treat intra-axonal water as fully restricted over typical diffusion-times (10–50 ms) and neglect the presence of myelin all together. At least two such models have demonstrated the ability of DWI with varied gradient strengths and diffusion times to measure axon diameters (42, 43). The present findings raise the question of how these models are affected by inter-compartmental water exchange, and whether appropriate DWI studies might also be sensitive to myelin thickness.

Although the relative exchange lifetimes fitted from sciatic and optic nerve were consistent with their different microanatomies, and the Monte Carlo analysis indicated that the data were acquired with sufficient SNR to fit the model parameters, several limitations of the model used herein need to be addressed. As shown in Fig. 5, some systematic differences were observed between the model and the measured P_IREX signals, indicating that the model is not fully describing the data. Likely causes for these deviation include (i) inappropriate compartment-component model assignments (i.e., the compartmental model of transverse relaxation in myelinated tissue), (ii) the treatment of certain model parameters as discrete, rather than continuous distributions (as was done for the T₂ spectral fitting), and (iii) magnetization transfer (MT) between water and MM protons within each anatomical compartment. Ultimately, the results and conclusions presented here are meaningful only in the context of the model used, so we consider below the potential model shortcomings in more detail.

Regarding point (i), because the inversion of exponentially decaying data to a spectrum of T₂ component amplitudes is generally ill posed, some assumptions about the model are required for any meaningful interpretation of the data. Although compartmental modeling of the ¹H NMR signal in myelinated tissue is an ongoing area of research, the compartment-component relationships used here were based upon a sizeable body of literature (3–6, 24–26) and represents the most well supported explanation of multi-exponential transverse relaxation in myelinated tissues. Regarding point (ii), previous work (7) found that incorporating microanatomical heterogeneity into a model of water diffusion and relaxation in WM provided better fits to experimental observations than did a Bloch-McConnell model based on three discrete compartments. Such an approach to IR-REXSY analysis would be computationally demanding, but might also better describe experimental data, particularly in cases where tissues with similar mean axon dimensions but widely different distribution of sizes were being compared. In the present case, the microstructural differences between optic and sciatic nerve are stark enough that the inclusion of microscopic heterogeneity is unlikely to change the conclusion that water exchange is much faster in optic nerve than sciatic nerve, although it might affect the absolute values of fitted model parameters.

Finally, with regards to point (iii), the model used here considers only magnetization from water, although it is well known that there is a significant MT effect between water and MM protons in myelinated tissues (8, 9, 37). In fact, inverting longitudinal magnetization of water protons while leaving MM magnetization near equilibrium results in a distinctly bi-exponential relaxation of the water longitudinal magnetization, which is the basis for some quantitative magnetization transfer imaging methods (44). Without a priori knowledge of MM proton T₂ and lineshape, the relative contribution of saturation and rotation effects of RF pulses on the MM longitudinal magnetization (M_z,MM) is unclear. If we assume pure saturation, the high power 90°–180°–90° pulses in the ‘EXCITE’ period (see Fig. 1) will drive the MM longitudinal magnetization toward, but not below, zero (M_z,MM ≥ 0). If, however, we assume pure rotation, the MM magnetization will be rotated into the transverse by the first 90° pulse in the ‘EXCITE’ period and then filtered out because t_E1 >> T_2,MM. Combining these effects, one can assume that M_z,MM ≥ 0 at the beginning of the IR-REXSY mixing period. At the same time, because the myelin water nulls at a shorter t_I that the other signal components, the longitudinal magnetization of the nonmyelin water pools will be < 0 at the onset of the mixing period. Thus, exchange between myelin water and MM protons during the mixing period will either be small (if M_z,MM ≈ 0 when M_{z,MyelinWater} ≈ 0) or will tend to compete with exchange between myelin water and nonmyelin water compartments (if M_z,MM > 0 when M_{z,NonmyelinWater} < 0), resulting in only overestimations of τ_myelin. Thus, we reason that MT effects on the IR-REXSY studies here should be small and are unlikely to explain the relatively large differences in τ_myelin found in optic nerve compared to sciatic nerve.

CONCLUSIONS

Relaxation exchange spectroscopy was used to provide novel and direct observations of inter-compartmental water exchange in freshly excised rat optic nerve and frog sciatic nerve samples. In the optic nerve samples, the measured τ_myelin values were similar to those from a previous report in bovine optic nerve ex vivo, but significantly shorter than others reported from cerebral white matter. Extrapolation of the present results to in vivo temperatures supports previous reports that inter-compartmental water significantly alters water proton transverse relaxation in white matter. In sciatic nerve, the measured τ_myelin values were much longer, consistent with the interpretation τ_myelin is largely dictated by the myelin sheath thickness. These findings offer the potential for the development of novel MRI methods for characterizing myelin thickness.