Making Medicare Advantage a Middle-Class Program

Abstract

This paper studies the role of Medicare's premium policy in sorting beneficiaries between traditional Medicare (TM) and managed care plans in the Medicare Advantage (MA) program. Beneficiaries vary in their demand for care. TM fully accommodates demand but creates a moral hazard inefficiency. MA rations care but disregards some elements of the demand. We describe an efficient assignment of beneficiaries to these two options, and argue that efficiency requires an MA program oriented to serve the large middle part of the distribution of demand: the “middle class.” Current Medicare policy of a “single premium” for MA plans cannot achieve efficient sorting. We characterize the demand-based premium policy that can implement the efficient assignment of enrollees to plans. If only a single premium is feasible, the second-best policy involves too many of the low-demand individuals in MA and a too low level of services relative to the first best. We identify approaches to using premium policy to revitalize MA and improve the efficiency of Medicare.

1. Introduction

Beneficiaries in Medicare, the federal health insurance program for the elderly and disabled, have for some time chosen between two major options: traditional Medicare (TM) and a set of private health insurance plans, including managed care plans, offered under Medicare Part C. Presently, only about 27% of beneficiaries elect a Part C plan. The objectives of Part C, since 2003 known as Medicare Advantage (MA),¹ are to expand health insurance options for beneficiaries while taking advantage of economies of managed care to save money for Medicare. Achieving these dual objectives requires that Medicare pay an MA plan less than what beneficiaries would cost Medicare in TM but more than cost for the beneficiaries in MA, leaving some savings to share with beneficiaries in the form of lower premiums/better coverage in MA to attract them to an MA plan. Research and policy have focused on the “risk adjustment” of Medicare payments to pay more for the sick and less for the healthy joining the MA plans.² In spite of improvements in risk adjustment technology and many other policy reforms, Part C has yet, however, to save Medicare money (McGuire, Newhouse and Sinaiko, 2011). As part of the Affordable Care Act (ACA), Medicare payments to MA plans are being cut, and, based on experience, plan and beneficiary exit will follow;³ but, based on the same experience, these cuts are unlikely to move the MA program into the black for Medicare.⁴

We argue that a major contributor to the chronically poor performance of Part C is the inefficient sorting of beneficiaries between MA and TM caused by Medicare’s premium policy. In this paper, we shift analytic focus away from plan payment and risk adjustment and to the premiums and the incentives faced by heterogeneous beneficiaries when they elect MA or TM. To address normative questions around beneficiary choice between MA and TM, we propose a formulation of which beneficiaries should be in MA and in TM. Somewhat surprisingly, in light of the policy attention to Medicare and the Part C program, the Medicare policy literature says little about what socially efficient sorting looks like. The fundamental answer to who should be in MA underlies the title of the paper. We argue that MA should, from the standpoint of social welfare, draw beneficiaries from the thick central part of the distribution of preferences for health care, and in this sense make MA a “middle class” program.

Our approach is based on the observation that beneficiaries vary in their demand for health care for many reasons. Most attention has been directed to the heterogeneity related to “health status” and the risk adjustment technology designed to deal with it (Pope et al., 2004). Health status-based risk adjustment explains a small share (10% or less) of the individual variation in health care spending, partly because health status is difficult to measure and predict. Another reason, and one that we call attention to here, is that factors other than health status – income, education, “taste” more generally⁵ – also influence demand for health care, and therefore choice of plan.

From the standpoint of the beneficiary, anticipated demand for health care, together with the premiums for TM and MA, determine the best plan option. Premiums for TM are described below, and depend on the circumstances of the beneficiary. MA plans choose the premium beneficiaries pay (subject to Medicare regulation), and this premium is the same for all beneficiaries. There is a fundamental problem with this approach. Generally, efficient pricing of health insurance options requires beneficiaries be charged their incremental cost in the various options. Thus, at least some price discrimination according to incremental cost can improve efficiency. Furthermore, any single premium for MA cannot sort beneficiaries between MA and TM. We argue that some form of premium discrimination by non-health status factors affecting demand is necessary to rescue MA from its chronically poor performance. After our analysis, we discuss some ways to change premium policy in TM as well as MA to better achieve Medicare objectives and economic efficiency.

2. Traditional Medicare and Medicare Advantage

2.1 Program Descriptions

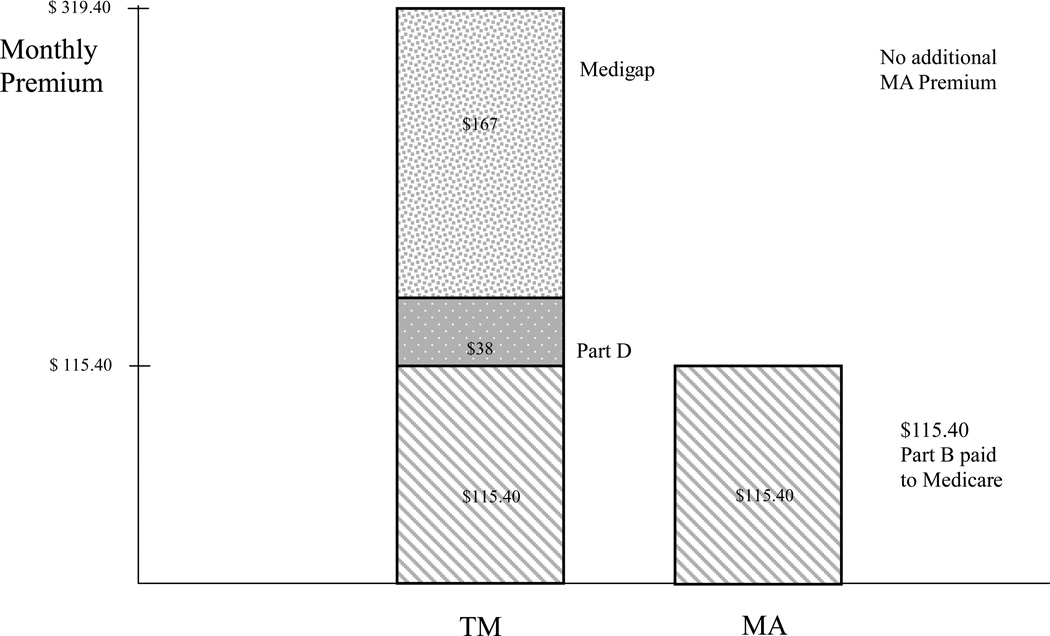
At age 65, most Americans become eligible for Medicare.⁶ If beneficiaries do not elect an MA plan, they are automatically enrolled in Part A of Medicare at no cost to them.⁷ Part A is financed largely by a payroll tax shared by employees and employers (Kaiser Family Foundation, (KFF) 2008). Part A covers inpatient hospital services, some post-hospital stays in nursing facilities and home health care, and hospice care, but requires considerable beneficiary cost sharing. The most significant beneficiary cost sharing is the deductible ($1,132 for 2011) per hospital episode (“benefit period”). Beneficiaries may also enroll in Part B, which covers doctors’ visits, other ambulatory services and some drugs administered in physician offices. The standard Part B premium for 2011, which applies to new enrollees, is $115.40 per month. Many enrollees pay only $96.40 per month because of hold-harmless provisions applying to social security payments from which the Part B premium is deducted (CMS, 2010). Very few (3%) of beneficiaries pay a higher premium because of high individual or family income, and some (17%) have premiums all or partly covered by Medicaid.⁸ Part B premiums cover only about 25 percent of Medicare's cost of Part B, the balance being paid for by general revenues (Kaiser Family Foundation, 2008). The vast majority of beneficiaries in TM enroll in Part B. Beneficiary cost sharing in Part B includes an annual deductible of $162 in 2011 and a 20 percent coinsurance on Medicare allowed charges. Since 2006, beneficiaries may also join a Part D plan covering prescription drug costs. Part D plans receive about 75 percent of their federal revenue from general revenues, are offered by private insurers, and vary in coverage. Part D premiums are set by a bidding procedure, the average premium for a stand-alone drug plan (taken as part of TM) was $38/month in 2011 (MedPAC, 2011b, Section 10). Low-income beneficiaries receive a premium subsidy (and lower cost sharing). Beneficiaries with Part A, and the optional Parts B and D, are considered to be in “traditional Medicare.”

Most beneficiaries in TM avoid cost sharing in Parts A and B with medigap or some other supplemental coverage. Medicaid pays cost sharing for eligible low-income beneficiaries. Some employers buy wrap-around coverage for retirees. Finally, most beneficiaries in neither of these groups buy medigap policies to cover some or all of the cost sharing. The average monthly premium for the most popular medigap policy (Plan F) was $167 in 2009 (MedPAC, 2011a). Given the pervasiveness of supplemental coverage, we think of TM as traditional health insurance with low cost sharing, with a premium for beneficiaries equal to the Part B premium plus what they pay for Part D and supplemental coverage.

Virtually all hospitals and practicing physicians accept Medicare payment, giving beneficiaries wide choice of providers. Medicare and its regional intermediaries make broad coverage decisions but do not interfere with (aka “manage”) physician and patient choice of treatment. Health care in TM has been criticized as being uncoordinated and costly (Newhouse, 2002). TM contends with cost issues primarily by using its monopsony power to pay physicians and hospitals roughly 20–30 percent less than private plans on average (MedPAC, 2008).⁹

The Medicare Modernization Act of 2003 (MMA) created MA to replace the short-lived Medicare+Choice version of Part C. MA plans are private, must cover all Part A and B benefits, and may supplement these benefits by reduced cost sharing or coverage for additional services not part of TM, such as vision or dental care (Gold, 2008).¹⁰ MA plans may or may not include drug coverage. Those that do are referred to as MA-PD (i.e., “Prescription Drug”) plans. In total, 11 million beneficiaries, or 24% of all, were enrolled in an MA plan in 2010 (KFF, 2010a).

The MMA created new plan types within MA and the higher payments mandated in the legislation awakened dormant plan types established earlier. We distinguish between what we consider to be bona fide managed care plans and others. We regard Health Maintenance Organizations (HMOs), the oldest and largest plan type, and the mostly tightly managed, along with Local Preferred Provider (PPOs) and the small number of Provider-Sponsored Organizations (PSOs) as managed care. The other plan types, notably the Regional PPOs and Private Fee-for-Service (PFFS) plans, are not in this category.¹¹ Our model of MA plan behavior laid out below applies to managed care plans only; 78 percent of Medicare beneficiaries in MA were in bona fide managed care plans in 2010.¹² Coverage in MA managed care plans is more comprehensive than in TM, with smaller (or no) deductibles, less cost sharing, and some coverage of additional services. Beneficiaries in MA plans cannot purchase medigap coverage.

Beneficiaries in MA plans must pay the Part B premium (which goes to Medicare).¹³ MA plans can charge a premium above this. Many plans, however, are “zero premium” plans, meaning they charge nothing above the Part B premium. A small percentage of plans reduce the beneficiary Part B premium obligation. More than half of beneficiaries in HMO plans pay zero premium. Most beneficiaries are in MA-PD plans. The average monthly premium for an MA-PD plan (across all plan types) was $51 per month, unweighted by enrollment (KFF (2010b)).

Medicare payments to plans are based on a Medicare “benchmark” rate set for each county and the plan's “bid.” The benchmark is based on the maximum of the CMS estimate of Medicare costs for a typical beneficiary in Parts A and B, a minimum or “floor” payment, and the past payment rate for the county trended forward at national average Medicare cost growth rates. In the past several years, benchmarks have generally exceeded expected FFS costs in a county (GAO, 2011). For 2011, benchmarks were frozen at 2010 levels. Beginning in 2012, the ACA phases in a new formula by which the benchmark is a percentage of the estimated FFS spending based on a county’s level of spending relative to other counties. For counties in the lowest spending quartile the new formula pays 115% of the benchmark, and this ranges down to 95% of the benchmark for the highest quartile counties (GAO, 2011). In most counties, these changes are expected to reduce Medicare payments (Afendulis et al., 2011).

A plan's bid is supposed to be the plan's estimate of what regular benefits from Part A and B would cost the plan for a beneficiary of average health status. If a plan bids above the benchmark, the plan is paid the benchmark. If the bid falls below the benchmark, Medicare pays the bid plus 75% of the difference between the bid and the benchmark. The idea is that Medicare gets 25% of any “savings” (difference between benchmark and bid) and the plan must use the balance of the difference to reduce beneficiary premiums or provide additional coverage and benefits. In 2010, the average plan bid was 98% of the benchmark, but HMO forms were the only plan type with an average below the benchmark (94%) (GAO, 2011). All others were greater than 100% of the benchmark. As a final step in figuring plan payments, Medicare then applies the CMS-HCC risk adjustment formula reflecting the measured health status of actual enrollees.

Figure 1 summarizes the typical 2011 monthly premium costs for a Medicare beneficiary in TM and MA. The beneficiary would pay the Part B premium to Medicare in either case. She buys a Part D free-standing drug plan for $38/month and a medigap plan for $167. If the beneficiary were to join a typical “zero-premium MA-PD plan, she pays nothing per month over Part B.

Figure 1.

2011 Monthly Premiums for Beneficiary in “Typical” Situation in TM and MA

2.2 Previous Research

A large literature in public finance is concerned with the public provision of private goods. Health care is a private good financed collectively for reasons, among others, related to equity. In Besley and Coate (1991), rich and poor consumers demand a good that could be provided by government with an equal consumption requirement, or left to the market.¹⁴ Some redistribution to the poor can be achieved by providing a base level to everyone financed collectively by progressive taxes, and letting the rich opt out to the private system. Within a health care context, researchers study resource allocation in public systems, and how a private sector fringe affects public costs and efficiency (Barros and Siciliani, 2012). Grassi and Ma (2008) analyze the interaction between a budget-constrained public health care system that allocates by rationing and a private sector that accommodates demand but may set prices. Consumers differ according to wealth and cost. The analogy to our paper is that our MA plan has an equal consumption feature, and the consumer has the option of choosing a TM plan that accommodates heterogeneity. In our analysis of Medicare, however, the alternative system, TM, is also publicly financed and subject to regulation.

A focus on the premiums paid by beneficiaries recalls Rothschild and Stiglitz (1976) who recognized the premium as a powerful selection device. In a Medicare context, the emphasis in the literature has been on skimping on services as a tool for selection.¹⁵ Other papers stress that plan choice of benefits and premiums can serve beneficiary heterogeneity, as well as being a device for selection.¹⁶ The idea, as expressed by Pizer, Frakt and Feldman (2003), is that “Beneficiaries who highly value certain benefits can search for a plan that offers those benefits and pay the marginal premium that corresponds to their choice.” One can imagine Medicare risk-adjusted plan payments as a voucher, with plan-set premiums sorting beneficiaries by tastes for additional services.¹⁷ However, as shown in Bundorf et al. (2009) and Glazer and McGuire (2011), except in special circumstances, a single premium for each plan does not sort beneficiaries efficiently among plans.¹⁸

Bundorf et al. (2009) show, in their theoretical analysis, that any uniform price for health plans will generally not lead patients to efficiently sort themselves across plans. They also estimate the efficiency loss due to this inefficient pricing in the context of a small group market in California. Glazer and McGuire (2011) model managed competition with demand heterogeneity to consider plan payment and enrollee premium policies in relation to efficiency and fairness. Specifically, this paper studies how to implement a “Silver” and “Gold” health plan efficiently and fairly in a managed competition context. The assumption shared with these two papers and the current one is that demand for health services and health insurance is driven by both tastes and need. The current paper introduces demand heterogeneity in the context of Medicare, with beneficiaries faced with a choice between TM and MA. This specific application allows us to demonstrate the fundamental inefficiencies in current Medicare policy, and to identify new approaches to address these inefficiencies.

3. Utility and Willingness to Pay for MA and TM

Beneficiaries are heterogeneous in their demand for health care. A beneficiary’s valuation of the quantity of health care, x, is positively related to a preference parameter, θ. Specifically, we assume that a beneficiary characterized by θ values health care at V(x, θ), with V_x > 0, V_xx < 0, V_xxx ≤ 0, V_θ > 0, V_xθ > 0, and as a normalization, we assume V_θθ = 0.¹⁹ We also assume that θ ∈ θ |θ̱, θ̄|, F(θ) is the distribution function and f(θ) is the density function of θ. We assume that f(θ) has full support over the interval |θ̱, θ̄|. Quantity x is measured in dollars so the cost of x is 1. Efficient x for beneficiary θ is x*(θ), the solution to V_x(x*,θ) = 1.

In order to focus on heterogeneity in demand from sources other than health status, we interpret θ as representing elements affecting demand for health care that the MA plan does not or cannot accommodate. Such elements could include income, education, and other dimensions affecting taste, so long as these elements are not recognized and responded to by the plan. In our model, individuals differ only in θ, implying that demand varies only because of taste parameters. We make this assumption because we regard the clinicians in the managed care MA plan as trained and interested in gearing treatment to health status (more resources go to a patient with greater need), but not in accommodating differences in “taste” for health care. The “equal consumption” assumption about MA plans refers to heterogeneity with respect to taste.

The economic literature on managed care is concerned with rationing in the presence of heterogeneity in demand, which is most often associated with health status differences.²⁰ Rationing can avoid moral hazard problems and improve efficiency, but an equal consumption feature of rationing creates inefficiency by homogenizing services to those with heterogeneous preferences. Essentially, this paper is about how to use the efficiency gains MA plans can create to best advantage among Medicare beneficiaries with heterogeneous preferences for health care. We now describe more specifically our models of MA and TM.

In MA there are no copayments. Since (by assumption) individuals differ only on dimensions not accommodated by the MA plan, quantity in MA is the same for everyone in the plan at x^MA. Willingness to pay (or utility measured in dollars) for MA is simply:

$${\mathrm{U}}^{\text{MA}}({\mathrm{x}}^{\text{MA}},\mathrm{\theta })=\mathrm{V}({\mathrm{x}}^{\text{MA}},\mathrm{\theta })$$ (1)

U^MA is positive for every value of θ and, given our normalization on V_θθ, for a given x^MA, it increases with θ at a constant rate.

We assume, in contrast to MA, TM does accommodate beneficiary demand due to heterogeneity in θ. In TM, beneficiaries pay a copayment 0 < c < 1 for each unit of x, and choose quantity to maximize utility by setting the marginal valuation of x equal to c:

$${\mathrm{V}}_{\mathrm{x}}(\mathrm{x},\mathrm{\theta })=\mathrm{c}$$ (2)

We define x^TM(θ) to be the solution to (2) above. Note that our assumption that V_xθ > 0 implies that consumers with higher θ demand more care in TM. Willingness to pay for TM is then:

$${\mathrm{U}}^{\text{TM}}(\mathrm{\theta })=\mathrm{V}({\mathrm{x}}^{\text{TM}}(\mathrm{\theta }),\mathrm{\theta })-{\text{cx}}^{\text{TM}}(\mathrm{\theta })$$ (3)

This is also everywhere positive, increasing in θ at an increasing rate.²¹ Intuitively, this is because as demand shifts out, quantity increases (unlike in MA) and consumer surplus goes up approximately quadratically with quantity demanded.

Throughout the analysis we will focus on the case where x^MA is located in the interior; by “interior” we mean that the level of care provided under managed care is higher than the level of care consumed by the lowest type, θ̱, under TM and lower than the efficient level of care for the highest type, θ̄, individual:

Assumption 1: x^TM (θ̱) < x^MA < x* (θ̄)

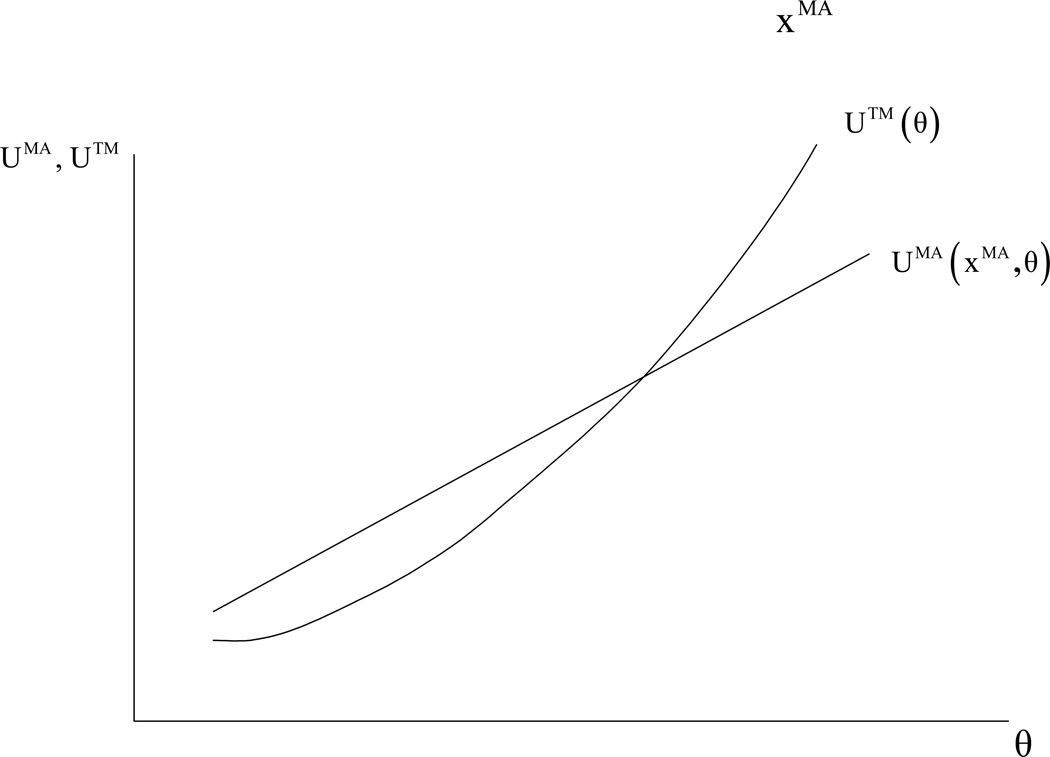
Figure 2 depicts the two functions U^TM(θ) and U^MA(x^MA, θ) for an arbitrary level of x^MA that satisfies Assumption 1.

Figure 2.

Utility in TM and MA for a Fixed Level of

Efficiency involves both the level of managed care, x^MA, and the sorting of beneficiaries between MA and TM, given the efficient x^MA. We conduct our analysis in several steps. In Section 4 we take x^MA as given and study how to efficiently divide consumers between MA and TM. In Section 5 we keep the assumption that x^MA is fixed and characterize a premium policy to implement the efficient sorting. We show that, for any level of x^MA, a single premium cannot implement the efficient sorting whereas a premium policy with two levels of premium that depends on θ, can implement the efficient sorting. In Section 6 we allow the regulator to choose x^MA and analyze the first-best and second-best levels of managed care (x^MA) depending on whether the regulator can condition premiums on θ (the first-best case) or it can use only a single premium (the second-best case).

4. Efficient Sorting

We consider how to efficiently divide consumers between MA and TM for a given x^MA. We establish (Proposition 1) that the optimal division of consumers between MA and TM is characterized by consumers in a single range of θ in MA with the others in TM. We will first present our result formally and then discuss the interpretation. Maximizing social welfare (efficiency) requires dividing beneficiaries into the two insurance types based on social welfare defined as utility less cost.²²

Given an x^MA, welfare in MA as a function of θ is given by:

$${\mathrm{W}}^{\text{MA}}({\mathrm{x}}^{\text{MA}},\mathrm{\theta })=\mathrm{V}({\mathrm{x}}^{\text{MA}},\mathrm{\theta })-{\mathrm{x}}^{\text{MA}}$$ (4)

And welfare in TM is given by:

$${\mathrm{W}}^{\text{TM}}(\mathrm{\theta })=\mathrm{V}({\mathrm{x}}^{\text{TM}}(\mathrm{\theta }),\mathrm{\theta })-{\mathrm{x}}^{\text{TM}}(\mathrm{\theta })$$ (5)

Proposition 1: For every x^MA there exists θ₁ and θ₂ with θ₁ < θ₂ such that W^TM (θ_i) = W^MA (x^MA, θ_i) for i = 1, 2, W^TM (θ) < W^MA (x^MA, θ) if θ₁ < θ < θ₂ and W^TM (θ) > W^MA (x^MA, θ) otherwise.

Proposition 1 says that the efficient division of beneficiaries can be expressed in terms of two cutoff values θ₁ and θ₂. All individuals below θ₁ and all individuals above θ₂ should be TM. Beneficiaries between θ₁ and θ₂ should be in MA.²³ (Proofs of all results in this paper are contained in the Appendix.)²⁴

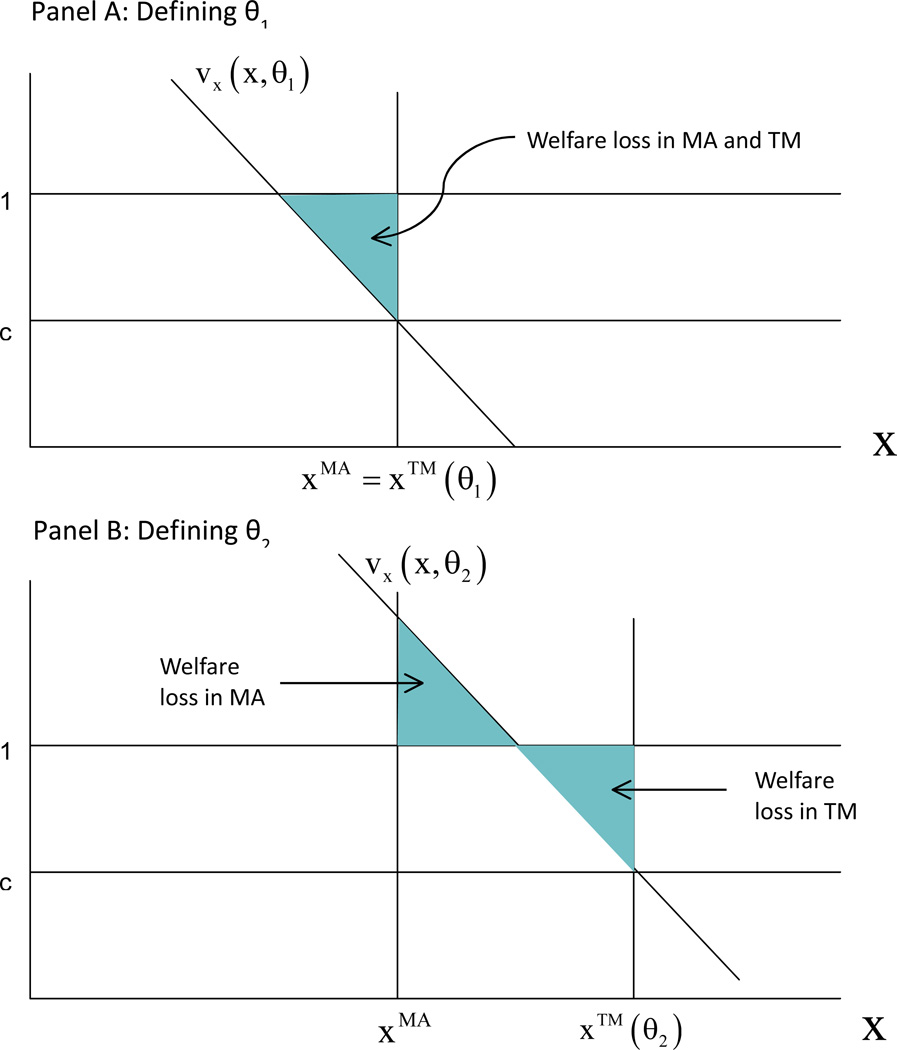
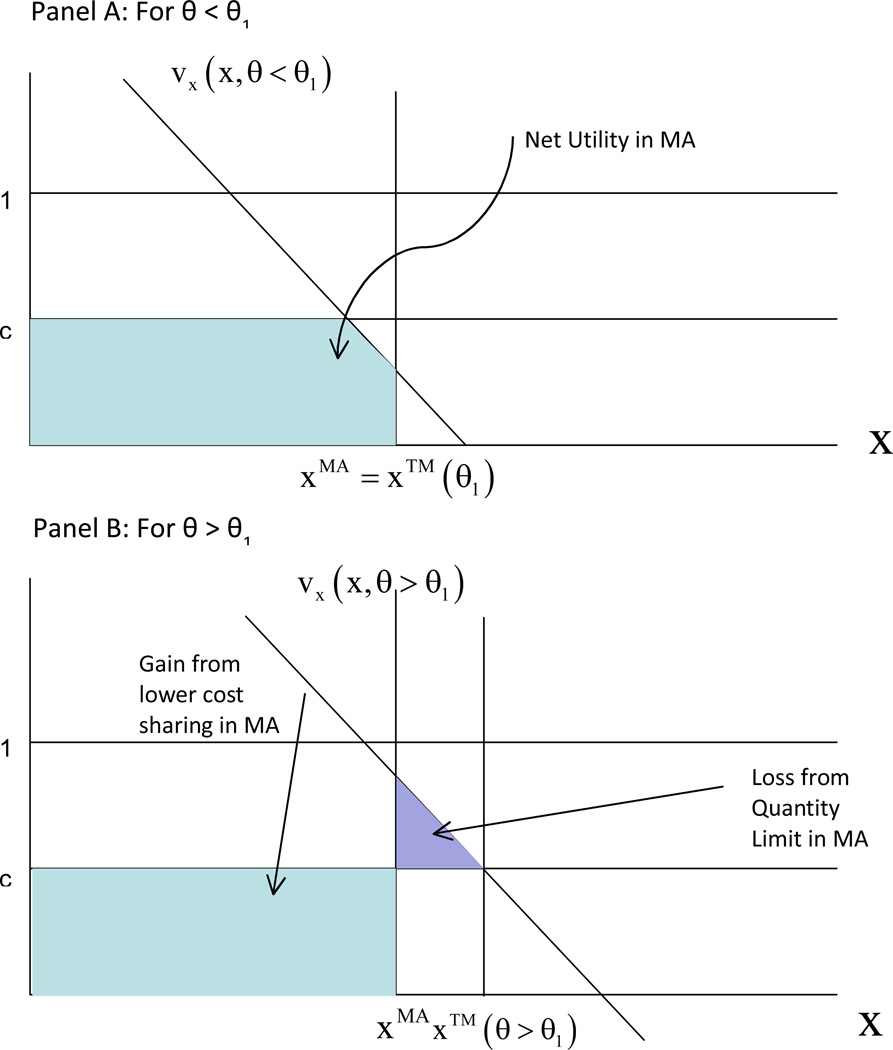
For the person on the boundary between TM and MA, the social net benefits (welfare) in MA and TM are equalized. Figure 3, Panel A shows demand for type θ₁, defining the lower boundary of those who should be in MA. For this beneficiary, consumption in TM, x^TM just equals the given x^MA. Obviously, social welfare in MA and TM for this beneficiary must be the same in both MA and TM. Depicted in terms of the welfare loss against the first best level of care for this beneficiary, the shaded triangle welfare loss must be the same when x^MA = x^TM. For any θ lower than θ₁, the beneficiary is still “over consuming” in both systems, but since x^TM for a θ less than θ₁ would be less than x^MA, the welfare loss in TM would be less than in MA. Thus, for any demand to the left of θ₁, the beneficiary belongs in TM. For θ just greater than θ₁, the welfare loss in MA is strictly less than the loss in TM. To see this, imagine shifting the demand shown in Panel A slightly to the right. The higher θ type is over consuming, but since x^MA < x^TM, the welfare loss due to over consumption is less in MA.

Figure 3.

The Socially Efficient θ Cutoffs

Panel B of Figure 3 shows demand for beneficiary θ₂, defining the upper boundary of efficient assignment into MA. For the given x^MA, there is a second level of demand in TM for which the welfare loss is the same as it would be if the beneficiary were in MA, the θ for which the two shaded triangles in Panel B, the welfare loss in MA and the welfare loss in TM, are equal. The loss from “under consumption” in MA for type θ₂ just equals the loss from over consumption in TM. As θ increases beyond θ₂, the loss from over-consumption in TM goes up by less (and, in fact, could even go down) than the increase in the welfare loss in MA. Thus, anyone with θ > θ₂ belongs in TM. A similar argument applies in the opposite case as θ decreases below θ₂. These beneficiaries belong in MA.

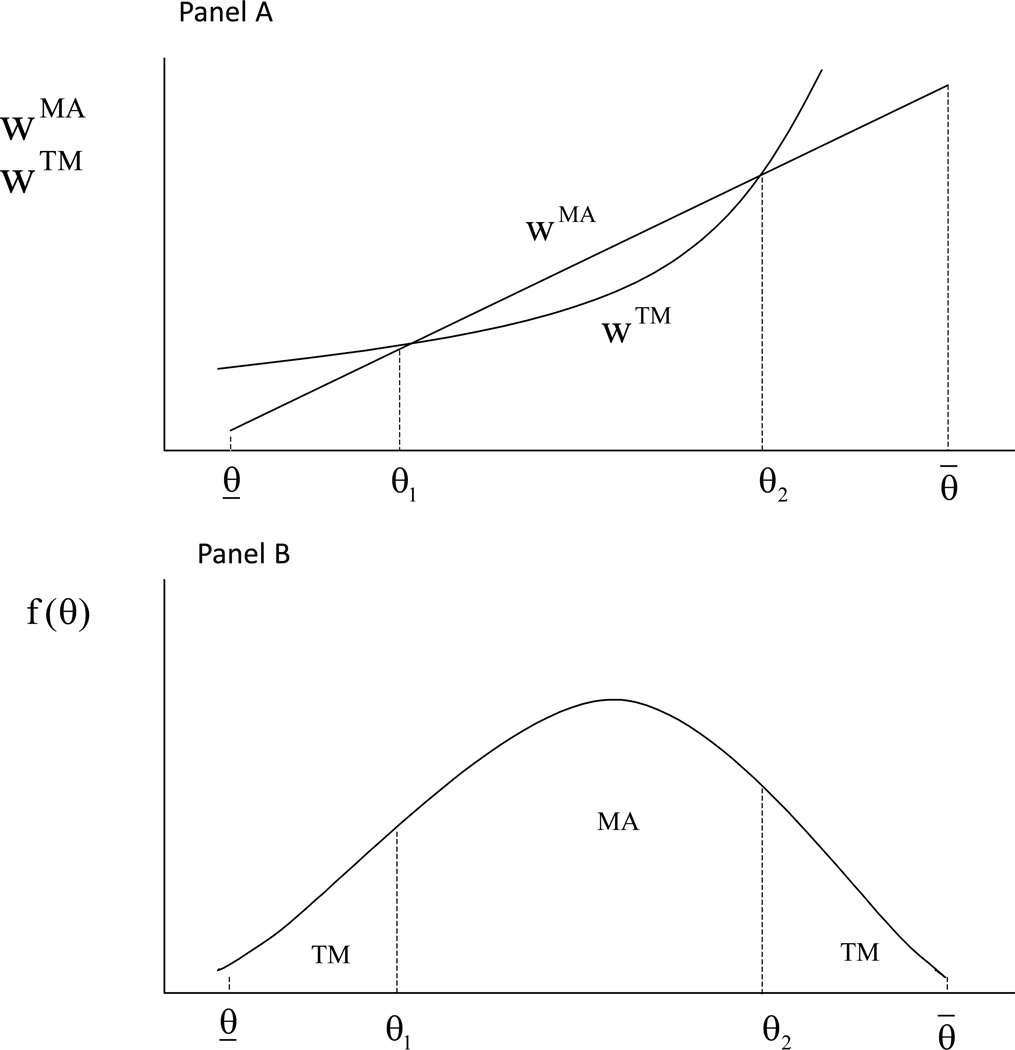
Figure 4 depicts the cutoffs in terms of welfare and the distribution of demand for care. As shown in Panel A, for a fixed level of x^MA welfare in MA increases as a constant rate, whereas welfare in TM is concave. Panel B depicts a plausible distribution of θ among beneficiaries, with the bulk of the population falling in the “middle class” in terms of demand.

Figure 4.

Optimal Division Between MA and TM for Fixed x^MA

The single range of θ result in Proposition 1 is due to fundamental properties of demand. Only one MA plan offers the same level of care for everyone serving a population with heterogeneous tastes. The offered care is just right for a certain type of consumer but as more and more people are included in the MA plan, on either side of the distribution of tastes, the fit becomes worse and worse. Indeed, the welfare loss from being in the MA plan goes up approximately quadratically as less well-suited consumers are included. It is this rapidly increasing welfare loss with more inclusion on either side of the “right” θ that puts a bound on each side of the efficient range of θ in MA.

Our single-range result is robust to reasonable modifications of our assumptions about underlying demand. Our main requirement is that the quadratic property of loss as the taste parameter, θ, moves in either direction from the MA plan is just right for, eventually dominates the MA-TM comparison. One could alter our assumptions and assume the loss from moral hazard in TM goes up more than proportionately with θ, but responsiveness proportional to the square of θ seem implausible.

5. Implementation of Efficient Sorting

We now consider the premium policy required to implement the optimal division of beneficiaries between MA and TM, for a given x^MA.

Beneficiaries sort themselves between MA and TM based on their willingness to pay for each alternative and the relative premiums. The difference in willingness to pay for MA and TM, which we refer to as ΔU, is a function of θ:

$$\mathrm{\Delta }\mathrm{U}({\mathrm{x}}^{\text{MA}},\mathrm{\theta })=\mathrm{V}({\mathrm{x}}^{\text{MA}},\mathrm{\theta })-\left(\mathrm{V}\right({\mathrm{x}}^{\text{TM}}(\mathrm{\theta }),\mathrm{\theta })-{\text{cx}}^{\text{TM}}(\mathrm{\theta }))$$ (6)

Beneficiaries compare this difference to the difference in premiums between the two options and choose the option with the highest net benefit.

The following Lemma regarding ΔU is central to our results about premium policies and beneficiary sorting.

Lemma 1: The beneficiary whose utility in MA exceeds TM by the maximum amount is θ₁ (as given by Proposition 1), the marginal beneficiary defining the lower bound of the types who are more efficiently served in MA.

In other words, the beneficiary for whom social welfare is equal in MA and TM defining the low end of the θ distribution belonging in MA is the beneficiary for whom the difference in utility (before any premiums) is the maximum between the two options. The advantage of TM in comparison to MA is the beneficiary’s ability to choose quantity. For one type of beneficiary, that defining θ₁, this advantage counts for nothing – the beneficiary would choose x^MA in any case. MA absolves the beneficiary of cost sharing, and thus for this beneficiary the utility advantage of MA is cx^MA. The point of Lemma 1 is that this is as good as it gets: cx^MA is the maximum any beneficiary gains from being in MA. Figure 5 shows why (with proof in Appendix). For a beneficiary with θ < θ₁, the gain from MA is less since some of the services are valued at less than c. For a beneficiary with θ > θ₁, there is a cost sharing gain of cx^MA but then a deduction because of the services lost with a value greater than c to the beneficiary. Thus, as θ moves away from θ₁ in either direction, the gain from MA is falling.

Figure 5.

Net Utility in MA

The unusual relationship between the private and social rankings of the alternatives poses a challenge for premium policy and sorting. Choice is based on utility and efficiency is governed by social welfare. The challenge is this: of the beneficiaries with the same net private utility in MA (those just to the left and right of θ₁), some (those to the left of θ₁) should be directed into TM, and some others (those to the right of θ₁) should be directed into MA. As we will show, no single premium can achieve this desired sorting. It should be emphasized that the result presented in Lemma 1 is quite general as it follows only from our assumptions about the shape of the individual’s utility function, V(x, θ), which are conventional, and on the way the level of service is determined in MA and in TM.

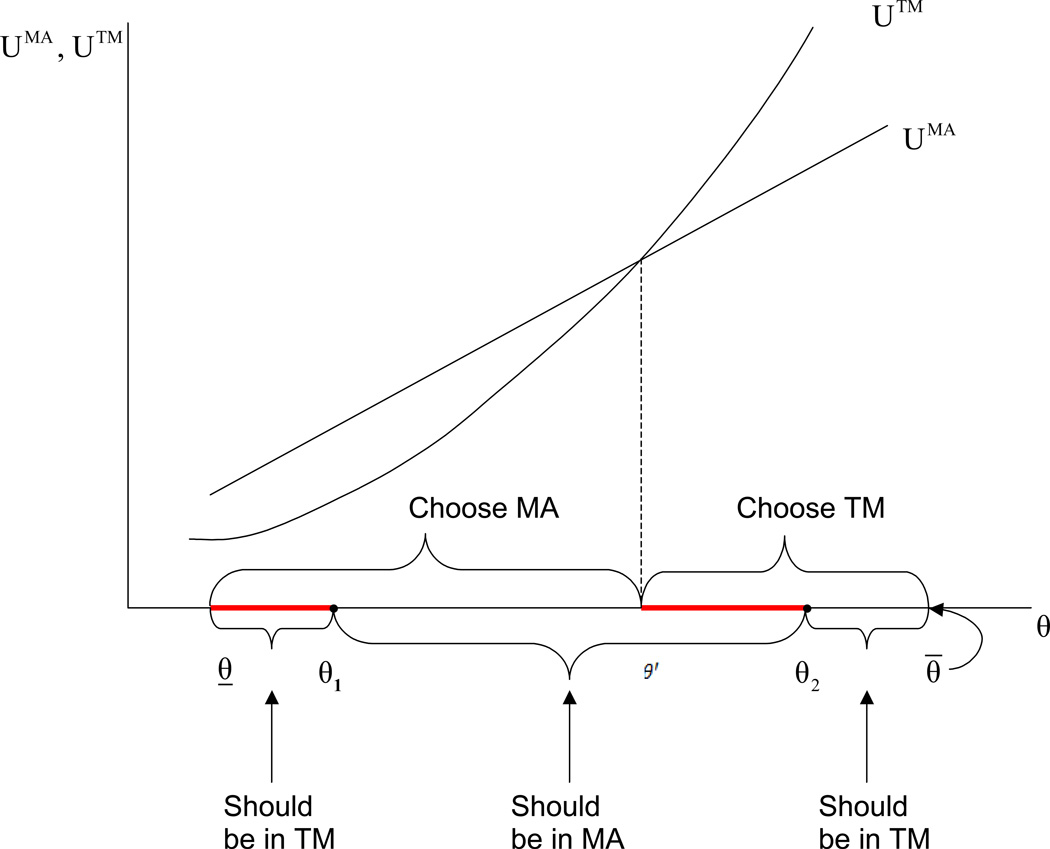
By Lemma 1 we know that for all θ > θ₁, U^TM(θ) increases at a rate faster than U^MA(x^MA, θ) and, hence, there exists a θ’ > θ₁ such that U^TM is equal to U^MA at θ’. In general, θ’ can be either smaller or larger than θ₂ depending on the level of the copayment c. In our analysis, hereafter, we focus on the relevant case where c is not too large and hence, U^TM intersects U^MA at a θ less than θ₂. This situation is depicted in Figure 6 if there were no premiums for either alternative. The bolded (red) regions of the θ-axis flag the discrepancy between the beneficiaries who should be in MA and those who via utility maximization choose MA.

Figure 6.

Comparing Efficient and Utility Max Sorting

We consider now how the ranges of sorting can be affected by premium policy. Let y(θ) denote the premium paid by an individual of type θ if she joins TM (without loss of generality we normalize the premium in MA to zero). We allow for y(θ) to be either positive or negative. Premiums paid to TM are like a tax and do not affect services received by a beneficiary in TM. With a premium the net utility of type θ joining the MA plan is, therefore, ΔU(x^MA, θ) + y(θ).

A premium schedule y(θ) implements the efficient sorting (assignment) if, given x^MA, ΔU(x^MA, θ) + y(θ) ≥ 0, for all θ, θ₁ ≤ θ ≤ θ₂, and ΔU(x^MA, θ) + y(θ) < 0 otherwise. That is, a premium schedule implements the efficient sorting if, given that schedule, all individuals of type θ, θ₁ ≤ θ ≤ θ₂ prefer MA over TM, and all other individuals prefer TM over MA.

5.1 Failure of Any Single Premium

The following proposition follows directly from Lemma 1:

Proposition 2: A single premium cannot implement the efficient sorting.

The proof is based on the following logic. According to Lemma 1, the premium beneficiary θ₁ pays for TM should make him indifferent between TM and MA so that beneficiaries with lower values of θ will not be willing to pay this premium and (efficiently) stay in TM. However, given Lemma 1, if type θ₁ is just indifferent between MA and TM, then all other beneficiaries strictly prefer TM over MA and they will all choose TM, which is obviously not what the first best calls for.²⁵

With the premium for MA set at zero, as we raise the single premium for TM, the first beneficiary willing to join MA is at θ₁, but then, as the premium is raised further, MA attracts beneficiaries on both sides of θ₁; those on the right who we want in MA, and those on the left we do not. Lemma 1 identifies the severe handicap constraining the MA program based on a single premium policy. Any (single) premium attracting enrollment to MA brings in beneficiaries who would be more efficiently served in TM.

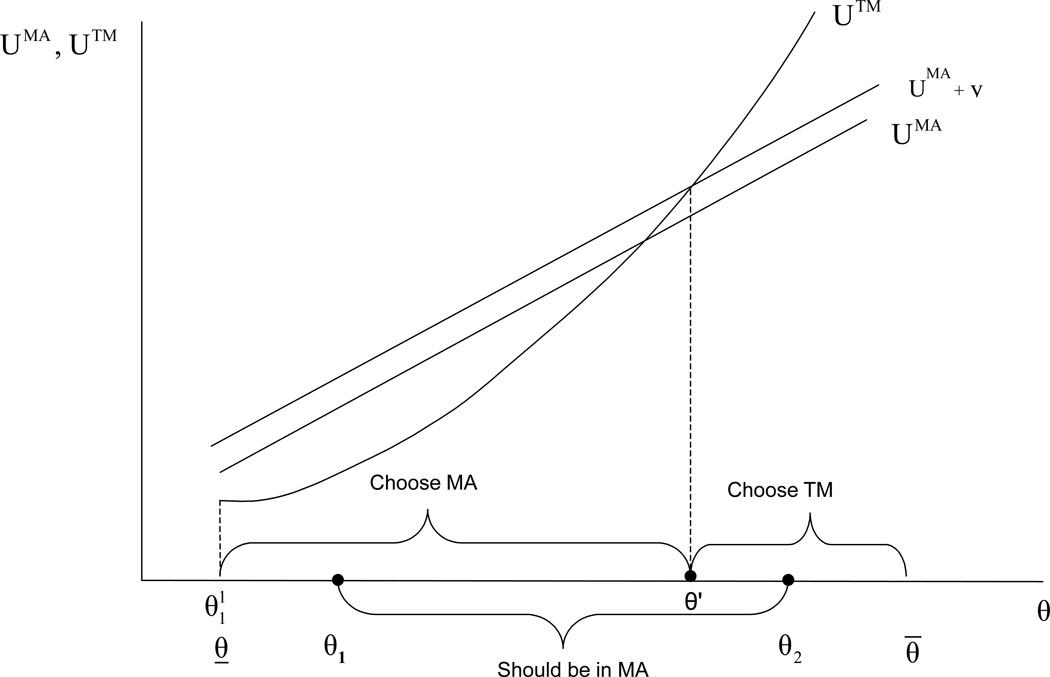
Figure 7 shows the effect of a positive single premium for TM, shifting upward the net utility in MA. The positive premium moves some beneficiaries who should be in MA from TM (those just to the right of the θ’ in Figure 6), initially improving efficiency. Beneficiaries to the left of θ₁ continue to make the wrong choice. Eventually, further increases in the single premium for TM will lead to inefficient choices in the range above θ₂ as well. There is no way to manipulate the single premium (positive or negative) to attain the efficient sorting.

Figure 7.

Sorting with a Single Premium

5.2 Implementing Efficient Sorting Requires Two Premiums

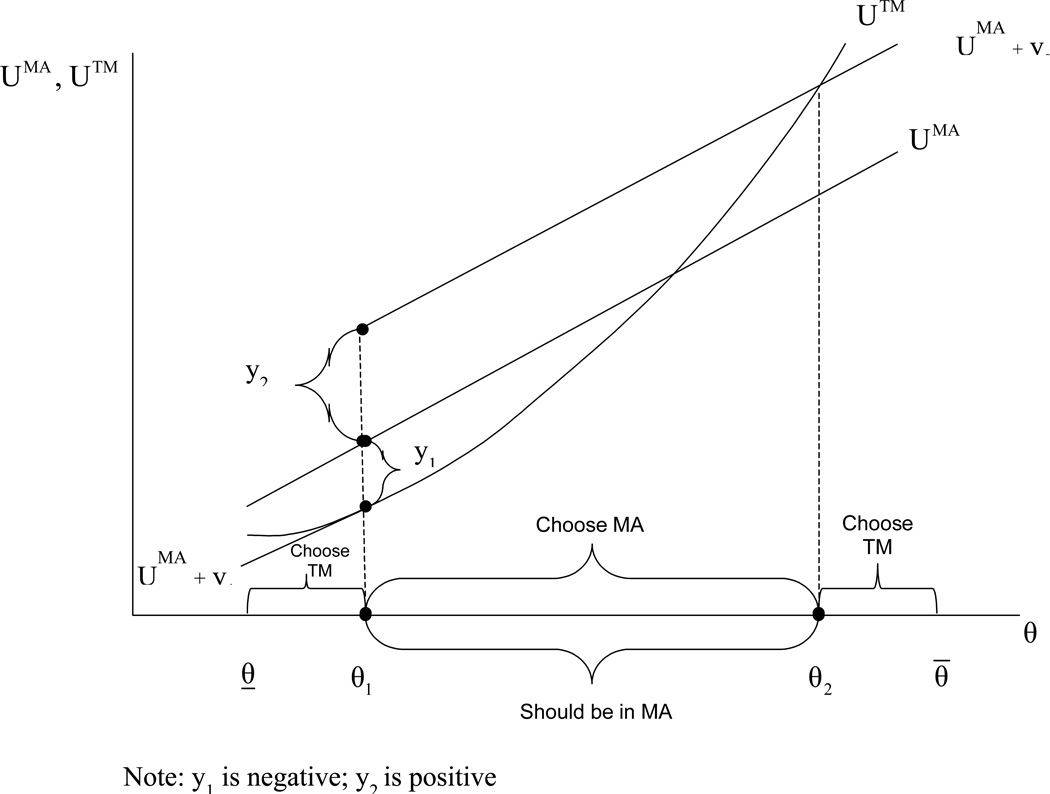
From Proposition 2 we know that at least two premium levels are necessary to implement the efficient sorting. In Proposition 3 we describe how premiums need to depend on θ to lead to an efficient division between MA and TM. The premium policy uses two premium levels y₁ and y₂, where y₁(y₂) is the level of premium that would make type θ₁(θ₂) just indifferent between MA and TM. The premium y₁(y₂) is paid by all individuals of type θ < θ₁ (θ ≥ θ₁) if they choose to be in TM.

Proposition 3: Let x^MA be given, let y₁ = −cx^MA, and let

$${\mathrm{y}}_2=\mathrm{V}({\mathrm{\theta }}_2,{\mathrm{x}}^{\text{TM}}({\mathrm{\theta }}_2\left)\right)-\mathrm{V}({\mathrm{\theta }}_2,{\mathrm{x}}^{\text{MA}})-{\text{cx}}^{\text{TM}}\left({\mathrm{\theta }}_2\right)$$ (7)

The premium policy: y(θ) = y₁ if θ < θ₁, and y₂ if θ ≥ θ₁, implements the efficient sorting.

Figure 8 illustrates the two-level premium policy. (See Appendix for a formal proof.) Beneficiaries below θ₁ would pay the negative premium y₁ = −cx^MA (be subsidized) to join TM; this subsidy is large enough to keep all beneficiaries in this range in TM. Everyone else pays a positive premium for TM, calculated so as to make the beneficiary at the upper end of the efficient range just indifferent between the two options. This premium, y₂, is high enough to keep all the beneficiaries between θ₁ and θ₂ in MA, but is not enough for the very high-demand types, those with θ < θ₂, and they go to TM (where they belong).

Figure 8.

Efficient Sorting with Two Premiums

Note: y₁ is negative; y₂ is positive

There are obviously other premium policies that would also sort beneficiaries efficiently (for example, the subsidy for TM need not be equal to y₁ for all the beneficiaries below θ₁, but the (y₁, y₂)-policy we describe is the simplest – the only two-premium policy that does the job.

5.3 Second-Best Sorting Using a Single Premium

The two-premium policy described in Proposition 3 relies on the regulator using θ as a basis for premiums. Such a policy may not be feasible as the factors behind θ, e.g., education, attitudes towards health and health care, are not easily observable by the regulator and even if observable, cannot be used as a basis for a premium policy. If θ cannot be used to set premiums, the regulator must pick just one premium to sort beneficiaries, and we know from Proposition 2 that the socially efficient sorting cannot be implemented. The question then becomes what is the optimal (second-best) single premium to sort beneficiaries between MA and TM?

When the regulator chooses a single premium for TM, y, and the level of care is x^MA, two distinct possibilities arise. The first is when the premium is positive and, hence, there exists a single cutoff θ’ such that all individuals with θ < θ’ choose MA and all individuals with θ ≥ θ’ prefer TM. The second is when the premium for TM is sufficiently negative, so that there are two cutoffs θ₁’ and θ₂’ with θ̱ ≤ θ₁’ < θ₂’ ≤ θ̄, such that all individuals with θ₁’ ≤ θ ≤ θ₂’ choose MA and all other individuals choose TM. In the first case the cutoff θ’ is given by −ΔU(x^MA, θ’) = y. In the second case the two cutoffs are given by −ΔU(x^MA, θ_i’) = y, for i = 1,2.

The first case is of more practical significance, since Medicare’s single premium policy leads to a positive premium for TM, when the medigap and Part D premiums are factored into the picture. This is the case we select for analysis. How should consumers be divided between MA and TM in this case? We characterize the second-best sorting in Proposition 4.

Proposition 4: Assume that x^MA is given and let θ’ denote the second-best efficient cutoff given that a positive premium is implemented for TM (i.e., y > 0). Then, θ’ = θ₂ where θ₂ is the first-best cutoff given by Proposition 1.

The second-best policy must accept that the low-demand beneficiaries (with the lowest willingness to pay for TM) will be in MA. With x^MA given, the tradeoff on the upper end of the distribution of demand is unaltered from the first-best case, the same cutoff, θ₂, will be the target of the TM premium. Thus, the single-premium (given an x^MA) is y₂ from Proposition 3.

6. Efficient Level of Care

Now suppose that Medicare can set the level of x^MA by altering the level of its payments to plans.²⁶ How should x^MA be set if Medicare’s objective is to maximize social welfare? We will first consider the first-best where we assume that Medicare can implement efficient sorting by using a premium policy such as the one discussed in Proposition 3. We next restrict Medicare to use a single premium and, hence, the best it can achieve is a second-best sorting as described in Proposition 4.

6.1 The First-Best Level of Managed Care

Suppose that Medicare can implement efficient sorting as given by Proposition 1. We can then express social welfare as the sum of three integrals, and the efficient outcome is given by the solution to the following problem:

$${\text{Max}}_{({\mathrm{\theta }}_1,{\mathrm{\theta }}_2,{\mathrm{x}}^{\text{MA}})}{\displaystyle {\int }_{\mathrm{\theta ̱}}^{{\mathrm{\theta }}_1}}\left(\mathrm{V}\right({\mathrm{x}}^{\text{TM}}(\mathrm{\theta }),\mathrm{\theta })-{\mathrm{x}}^{\text{TM}}(\mathrm{\theta }))\mathrm{f}(\mathrm{\theta })\mathrm{d}\mathrm{\theta }+{\displaystyle {\int }_{{\mathrm{\theta }}_1}^{{\mathrm{\theta }}_2}}\left(\mathrm{V}\right({\mathrm{x}}^{\text{MA}},\mathrm{\theta })-{\mathrm{x}}^{\text{MA}})\mathrm{f}(\mathrm{\theta })\mathrm{d}\mathrm{\theta }+{\displaystyle {\int }_{{\mathrm{\theta }}_2}^{\mathrm{\theta ̄}}}(\mathrm{V}({\mathrm{x}}^{\text{TM}}(\mathrm{\theta }),\mathrm{\theta })-{\mathrm{x}}^{\text{TM}}(\mathrm{\theta }))\mathrm{f}(\mathrm{\theta })\mathrm{d}\mathrm{\theta }$$ (8)

Three first-order conditions (FOC) define the solution, (θ₁*, θ₂*, x*), to (8). Consider the FOC with respect to x^MA describing the x* best for the beneficiaries in MA:

$${\displaystyle {\int }_{{\mathrm{\theta }}_1^{*}}^{{\mathrm{\theta }}_2^{*}}}\left({\mathrm{V}}_{\mathrm{x}}\right({\mathrm{x}}^{*},\mathrm{\theta })-1)\mathrm{f}(\mathrm{\theta })\mathrm{d}\mathrm{\theta }=0$$ (9)

Condition (9) is a public good-like condition stating that at x*, the sum of the marginal valuations of x less marginal cost, weighted by the frequency of θ in MA, equals zero. x* is the efficient care for just one value of θ (the value that solves V_x(x*, θ) =1)), but the efficient sorting puts beneficiaries with θ in a range above and below this value into MA (because of the overconsumption for all beneficiaries in TM). The compromise on x* reflects the relative frequency among beneficiaries between the θ₁* and θ₂* cutoffs.

The FOCs describing the optimal cutoffs between MA and TM are characterized in Proposition 1 and the two panels of Figure 3 when x^MA is chosen optimally at x*. The same modification could be made to Panels A and B of Figure 4, adding stars to depict θ₁* and θ₂* to indicate that x^MA is chosen optimally. There is a welfare gain in MA for a range of beneficiaries to avoiding the over-consumption in TM. The value of x* maximizes this gain. One consideration in this choice is the frequency of θ among the population of beneficiaries. With a plausible distribution of θ, maximizing social welfare implies setting the level of services in MA to serve the large bulk of the population.²⁷

6.2 The Second-Best Level of Care with a Single Premium

Suppose now that y > 0 and the premium implements a single cutoff.

Proposition 5: When a single premium is implemented, the (second-best) efficient level of care is lower than the first-best level of care.

When the single premium is positive there is a single cutoff and beneficiaries with a low θ are in MA, whereas in a first best these low-demand types would be in TM. This will lower the efficient x^MA, implying that the second-best high-end cutoff will fall below θ₂. Thus, in this case, services in MA will be lower than in the first best and too few higher θ beneficiaries will be in MA.

7. Discussion

Part C of Medicare has been a disappointment for more than 25 years. Our paper identifies one fundamental reason for this. Policies governing the premiums for MA plans and TM lead to inefficient distribution of beneficiaries between the options. Although our model does not generate quantitative conclusions, the character of the optimal equilibrium is so different from what we see in practice that we are confident that the welfare losses associated with current policy are large. Enrollment in MA has vacillated between 10 and 27% in the past 15 years, and is likely to be driven down from its recent highs with cuts in plan payments set in the ACA. Each MA plan sets its own “single premium.” Premiums for TM are highly subsidized and also do not vary according to demand-related factors.

We argue that MA should be directed to serve the large middle part of the distribution of demand for health care – what we refer to as the “middle class.” Instead, current premium policies encourage MA plans tend to attract beneficiaries with lower demand, both for reasons of better health status and for non-health status factors.²⁸

Increasing pressure on public budgets mean two things for Medicare Advantage (MA): first, it is even more important for Medicare to achieve the savings potential of managed care plans; second, in one form or another, beneficiary premiums (rather than tax-supported payments) will play a larger role in financing Medicare, both on the TM and the MA side. Premium policy will inevitably be reformulated for financing reasons, yielding an opportunity to get more and more of the right beneficiaries in improved MA plans.

A comprehensive discussion of restructuring Medicare policy towards MA requires consideration of issues not addressed in this paper, including: the cost-effectiveness and quality of care in MA plans compared to TM; the desirable forms of MA plans; the level of the benchmark payment and bidding; the role medigap and employer plans; regional differences in patterns of care; the “choice architecture” for MA plans and the setup of the default option; the broader (spillover) effects of Medicare MA policy on health financing systems; and equity-distributional concerns in terms of rich-poor, healthy-sick and young-old.

While noting these concerns, we point out here two practical implications of our analysis of premiums and beneficiary sorting. First, our main message is that the premium for joining TM should be higher for higher-demand beneficiaries. Socially, there is more to be gained by keeping these high-demand types in MA. Currently, the Part B premium is mildly income-related, but the beneficiary pays the same premium whether they join an MA plan or stay in TM. We recommend that the income-related portion of the Part B premium be waived if the beneficiary elects MA. This step would introduce a simple version of a two-level premium based on income and may open important options for further differentiating premiums down the road. In the future, as more is asked of beneficiaries in terms of premium, widening the premium differences by income will work towards the premium discrimination called for in our analysis.

Second, the structure is also in place to create options attractive to low-demand beneficiaries. Low income/asset Medicare beneficiaries qualify for special premium and cost sharing subsidies through state Medicaid programs. These expensive “dual eligible” would likely benefit most from coordination of care in MA, but face no premiums at all. Furthermore, their cost sharing in TM is paid by Medicaid, biasing their choice toward TM. Translating some of the subsidy for this group into income support if these beneficiaries choose economical Medicaid managed care plans would could make beneficiaries better off, improve sorting, and reduce public health care spending.

More broadly, our analysis implies that Medicare should take a direct hand in setting premiums for MA plans. Although it would represent a big change for Medicare, there is nothing radical about a sponsor setting premiums for plan options. Virtually all large private employers do this, setting the price employees pay for any health plans offered through employment. Employers recognize their interest in affecting incentives employees face in deciding about plans. Like private employers, Medicare should take charge of the premium paid by beneficiaries to join health plans, and set those premiums in order to forward Medicare objectives.

Our model is not well-suited to a making a comprehensive estimate of the welfare effects of a more efficient premium policy. There would, however, be an immediate impact on Medicare costs of moving more beneficiaries into MA plans. A doubling of MA enrollment (to, say, 50%) would move about 25% of Medicare costs into managed care – at a 10% saving over TM, health costs would fall about 2.5%, corresponding to over $13billion in the $565 billion (in 2011) Medicare program. Recent research finds that the MA program affects practice style in TM and commercial populations, leading to additional savings (Baicker et al., 2012).

The more important beneficial effect, however, of revitalizing MA in Medicare comes in the longer term. Medicare is evolving to a system in which there are more than two types of plans. In addition to TM and MA, practice groups can now organize into Accountable Care Organizations (ACOs) and accept payment from Medicare with some prospective features. No premium-side policies work along with this provider-side payment reform. Efficient premium policy should complement new provider payment policies in Medicare, not continue to sort beneficiaries inefficiently among plan options.

Pursuit of efficiency in health insurance when serving a heterogeneous population runs up against concerns for fairness. Health care policy in the U.S. leaves much more room for gradations in health insurance (e.g., the Bronze-to-Platinum range in the ACA) than in most other countries. Nonetheless, targeting MA plans to groups across the range of socioeconomic status raises fundamental positive and normative questions about serving taste heterogeneity in health insurance, and about the role and fairness of collective methods of finance.

Our analysis leaves a number of questions unanswered. Incorporation of an explicit analysis of MA plan behavior should be high on the agenda. Within a population of heterogeneous beneficiaries, many MA plans setting different levels of services will better serve diverse tastes than a single MA product.

In this paper we abstract from heterogeneity in health status and issues related to risk adjustment and MA plan resource allocation according to health need also need incorporation. MA plans obviously do respond to some dimensions of beneficiary heterogeneity. This form of heterogeneity has been recognized in the literature, and raises a different set of issues than our concern in this paper. A comprehensive analysis would include consideration of heterogeneity which plans respond to in resource allocation (e.g., health status), and heterogeneity which plans do not (e.g., income-related tastes). One could ask our question: who should be in MA along dimensions of health status as well as taste for health care. With new data becoming available on what goes on inside the black box of managed care plans, empirical patterns of care in MA and TM, and how they respond to these factors can be assessed empirically. This can be a basis for theory development and policy application.

Appendix

Proof of Proposition 1:

We define the difference between social welfare in MA and social welfare in TM to be:

$$\mathrm{\Delta }\mathrm{W}({\mathrm{x}}^{\text{MA}},\mathrm{\theta })={\mathrm{W}}^{\text{MA}}({\mathrm{x}}^{\text{MA}},\mathrm{\theta })-{\mathrm{W}}^{\text{TM}}(\mathrm{\theta })$$

The change in ΔW as θ changes is given by (recall that V_θθ = 0):

$$\mathrm{d}\mathrm{\Delta }\mathrm{W}({\mathrm{x}}^{\text{MA}},\mathrm{\theta }/\mathrm{d}\mathrm{\theta }={\mathrm{V}}_{\mathrm{\theta }}({\mathrm{x}}^{\text{MA}},\mathrm{\theta })-{\mathrm{V}}_{\mathrm{\theta }}({\mathrm{x}}^{\text{TM}}(\mathrm{\theta }),\mathrm{\theta })-[{\mathrm{V}}_{\mathrm{x}}({\mathrm{x}}^{\text{TM}}(\mathrm{\theta }),\mathrm{\theta })-1]{\text{dx}}^{\text{TM}}/\mathrm{d}\mathrm{\theta })={\mathrm{V}}_{\mathrm{\theta }}({\mathrm{x}}^{\text{MA}},\mathrm{\theta })-{\mathrm{V}}_{\mathrm{\theta }}({\mathrm{x}}^{\text{TM}}(\mathrm{\theta }),\mathrm{\theta })+[{\mathrm{V}}_{\mathrm{x}}({\mathrm{x}}^{\text{TM}}(\mathrm{\theta }),\mathrm{\theta })-1][\frac{{\mathrm{V}}_{\mathrm{\theta }\mathrm{x}}({\mathrm{x}}^{\text{TM}}(\mathrm{\theta }),\mathrm{\theta })}{{\mathrm{V}}_{\text{xx}}({\mathrm{x}}^{\text{TM}}(\mathrm{\theta }),\mathrm{\theta })}]$$

The second equality follows from our definition of x^TM (θ).

The curvature of the ΔW is given by:

$$\frac{\mathrm{d}2\mathrm{\Delta }\mathrm{W}({\mathrm{x}}^{\text{MA}},\mathrm{\theta })}{\mathrm{d}{\mathrm{\theta }}^2}=\frac{{\text{dx}}^{\text{TM}}}{\mathrm{d}\mathrm{\theta }}[-{\mathrm{V}}_{\mathrm{\theta }\mathrm{x}}+({\mathrm{V}}_{\mathrm{x}}-1)(2\frac{{\mathrm{V}}_{\mathrm{\theta }\text{xx}}}{{\mathrm{V}}_{\text{xx}}}-\frac{{\mathrm{V}}_{\text{xxx}}{\mathrm{V}}_{\mathrm{\theta }\mathrm{x}}}{{({\mathrm{V}}_{\text{xx}})}^2}\left)\right]<0$$

The inequality follows from the fact that

$${\mathrm{V}}_{\mathrm{\theta }\mathrm{\theta }}=0,{\mathrm{V}}_{\mathrm{\theta }\mathrm{x}}>0,\frac{{\text{dx}}^{\text{TM}}}{\mathrm{d}\mathrm{\theta }}>0,{\mathrm{V}}_{\text{xx}}<0,{\mathrm{V}}_{\text{xxx}}\le 0,{\mathrm{V}}_{\mathrm{x}}({\mathrm{x}}^{\text{TM}}(\mathrm{\theta }),\mathrm{\theta })<1,$$

V_θθx = 0 and V_θxx = V_xxθ by our assumption that V_θθ = 0.

Given X^MA there exists a θ, call it θ^MA, for which, x^MA is socially efficient, that is V_x(x^MA, θ^MA) = 1 and, hence, ΔW(x^MA, θ1) = 0. Furthermore, there exists another θ < θ^MA, call it θ₁ for which x^MA = x^TM (θ₁) and, hence, ΔW(x^MA, θ₁) = 0. By the concavity of ΔW, we know, therefore, that there exists at most one more θ, call it θ₂, such that θ₂ > θ^MA and ΔW(x^MA, θ₂) = 0.

Proof of Lemma 1:

Using the envelope theorem one can see that:

$$\frac{\mathrm{d}\mathrm{\Delta }\mathrm{U}}{\mathrm{d}\mathrm{\theta }}={\mathrm{V}}_{\mathrm{\theta }}({\mathrm{x}}^{\text{MA}},\mathrm{\theta })-{\mathrm{V}}_{\mathrm{\theta }}({\mathrm{x}}^{\text{TM}}(\mathrm{\theta }),\mathrm{\theta })$$

We know that at θ₁, x^TM (θ₁) = x^MA, and thus at θ₁,ΔU/dθ = 0. Furthermore, by the linearity of U^MA and the convexity of U^TM we know that ΔU is convex with respect to θ. Thus, ΔU is maximized at θ₁.

Proof of Proposition 2:

Assume a single premium y for TM. For the premium to implement the efficient sorting it must be that −y + ΔU(x^MA, 0) ≤ 0 for all θ< θ₁ and −y + ΔU(x^MA, 0) ≥ 0 for θ > θ₁. However, since with θ̱ < θ₁ θ̄ and ΔU(x^MA, θ₁) is maximized at θ₁, the two conditions above cannot be met simultaneously.

Proof of Proposition 3:

Since y₁ = −cx^MA = ΔU(x^MA,θ₁) > ΔU(x^MA,θ) for all θ < θ₁, all individuals with θ < θ₁ will prefer TM over MA. Since ΔU(x^MA,θ) is decreasing with θ, for all θ > θ₁ and since y₂ = −ΔU(x^MA,θ₂), it must be that ΔU(x^MA,θ) + y₂ > 0 for all θ, θ₁ < θ < θ₁ and ΔU(x^MA,θ) + y₂ < 0 for all θ > θ₁.

Proof of Proposition 4:

When y = 0 there is a single cutoff to the left of θ₂. By increasing the premium the single cutoff moves towards θ₂ and welfare is increased. Once the cutoff reaches θ₂, welfare will be decreased if the premium is further increased. (See Figure 7.)

Proof of Proposition 5:

When y > 0, and there is a single cutoff between MA and TM, the second-best outcome is given by:

$${\text{Max}}_{({\mathrm{\theta }}^1,\mathrm{x})}{\displaystyle {\int }_{\mathrm{\theta ̱}}^{{\mathrm{\theta }}^1}}\left(\mathrm{V}\right(\mathrm{x},\mathrm{\theta })-\mathrm{x})\mathrm{f}(\mathrm{\theta })+{\displaystyle {\int }_{{\mathrm{\theta }}^1}^{\mathrm{\theta ̄}}}\left(\mathrm{V}\right({\mathrm{x}}^{\text{TM}}(\mathrm{\theta }),\mathrm{\theta })-{\mathrm{x}}^{\text{TM}}(\mathrm{\theta }))\mathrm{f}(\mathrm{\theta })\mathrm{d}\mathrm{\theta }$$ (10)

The first-order condition implies:

$$\mathrm{V}(\mathrm{x}\text{'},\mathrm{\theta }\text{'})-\mathrm{x}\text{'}=\mathrm{V}\left({\mathrm{x}}^{\text{TM}}\right(\mathrm{\theta }\text{'}),\mathrm{\theta }\text{'})-{\mathrm{x}}^{\text{TM}}(\mathrm{\theta }\text{'}),$$ (11)

and:

$${\displaystyle {\int }_{\mathrm{\theta ̱}}^{\mathrm{\theta }\text{'}}}\left({\mathrm{V}}_{\mathrm{x}}\right(\mathrm{x}\text{'},\mathrm{\theta })-1)\mathrm{f}(\mathrm{\theta })\mathrm{d}\mathrm{\theta }=0$$ (12)

Condition (11) is similar to the result obtained in Proposition 4, namely that θ’ = θ₂. Using the fact that θ’ = θ₂ and θ < θ₁, where θ₁ is the first-best lower cutoff, (12) implies:

$${\displaystyle {\int }_{{\mathrm{\theta }}_1}^{{\mathrm{\theta }}_2}}\left({\mathrm{V}}_{\mathrm{x}}\right(\mathrm{x}\text{'},\mathrm{\theta })-1)\mathrm{f}(\mathrm{\theta })\mathrm{d}\mathrm{\theta }>0$$

Thus, when the cutoffs can be chosen efficiently (i.e., at the first-best), welfare at x’ is increasing in x. Thus, x* > x’.