Transtibial amputee joint motion has increased attractor divergence during walking compared to non-amputee gait

Abstract

The amputation and subsequent prosthetic rehabilitation of a lower leg affects gait. Dynamical systems theory would predict the use of a prosthetic device should alter the functional attractor dynamics to which the system self-organizes. Therefore, the purpose of this study was to compare the largest Lyapunov exponent (a nonlinear tool for assessing attractor dynamics) for amputee gait compared to healthy non-amputee individuals. Fourteen unilateral, transtibial amputees and fourteen healthy, non-amputee individuals ambulated on a treadmill at preferred, self-selected walking speed. Our results showed that the sound hip (p=0.013), sound knee (p=0.05), and prosthetic ankle (p=0.023) have significantly greater largest Lyapunov exponents than healthy non-amputees. Furthermore, the prosthetic ankle has a significantly greater (p=0.0.17) largest Lyapunov exponent than the sound leg ankle. These findings indicate attractor states for amputee gait with increased divergence. The increased attractor divergence seems to coincide with decreased ability for motor control between the natural rhythms of the individual and those of the prosthetic device. Future work should consider the impact of different prostheses and rehabilitation on the attractor dynamics.

Introduction

The goal of lower limb prosthetic rehabilitation is to restore the individual’s function back to pre-amputation levels. While current prostheses permit walking, running, and other gait tasks, gait is hardly restored to a healthy level. Individuals with lower limb prostheses ambulate with impaired walking balance; nearly 53% of such individuals report falling in the previous year.²⁵ In addition, the metabolic cost of walking is elevated as much as 135% as compared to healthy non-amputee gait.³⁹

The amputation of a leg has traditionally been viewed as primarily affecting the musculoskeletal system and peripheral nervous system.²² Yet, the impact on the central nervous system’s control over limb movement resulting from changes to the mechanical properties of a leg in non-amputees has been reported.^{10, 12, 17, 28, 33} The result is a drastic alteration to the individual’s morphology. From a theoretical perspective, the dynamical systems theory of motor control would suggest an altered movement pattern which is a new solution that arises from this change in morphology (and biomechanics).^{15, 35} Thus, the development of coordinative structures and functionally preferred behavioral patterns, or attractor states using dynamical systems theory phraseology, should be expected to be altered as the self-organization of the modified sub-systems is affected.^{13, 40} An attractor is the region within state space to which all points sufficiently close are drawn towards, thus acting as a multi-dimensional representation of a point’s previous and future occurrences.^{26, 43}

The notion that amputation and subsequent prosthetic rehabilitation affects the functionally preferred attractor seems to be supported by our previous work that found the largest Lyapunov exponent (lLya) to be strongly related to patient prosthesis preference.⁴³ The lLya is a measure of the divergence of an attractor, or the variation within the attractor.^{14, 19, 23, 29, 42} Variation, in this case, refers to the time dependent variance between the trajectories within the attractor; referred to more commonly under the umbrella term of structure of variability. In mathematics, this concept is referred to as the stability of the attractor. In clinically based research, we distinctly avoid the use of the term stability to avoid confusion with the more common meaning associated with balance as these are markedly different. In gait, these time dependent variations manifest as stride-to-stride fluctuations. Recently, Wurdeman et al.⁴³ investigated transtibial amputees who walked with two different prostheses. Following walking trials with both prostheses, subjects were asked to mark their preference between the prostheses on a continuous visual analog scale. The preference was then found to be strongly correlated to the difference in the lLya between prostheses at the prosthetic ankle representing the stride-to-stride fluctuations in the joint’s motion. Subjects displayed an affinity towards a decreased lLya, or decreased attractor divergence.⁴³

Therefore, the purpose of this study was to expand on the study of Wurdeman et al.⁴³ and determine the underlying alterations in the movement patterns or attractor states due to amputation of the lower leg. By understanding these changes, it may be possible to improve prosthetic prescription criteria and rehabilitation techniques by targeting an aspect of amputee gait previously discounted. Furthermore, it is important to establish the “typical” attractor divergence for amputee gait compared to healthy non-amputee gait to better understand whether the attractor has too little or too much divergence. Some divergence is considered optimal as it allows for the flexible and adaptive motor system behavior seen in healthy non-amputees.¹³ On the other hand, too little divergence reflects a rigid, “robotic” system,³⁶ while too much or excessive divergence is also not desired as the attractor is less bounded and could potentially switch to a different functional attractor or behavioral state.³⁶ Based on previous work that found amputees preferred a prosthesis that permitted decreased attractor divergence of the prosthetic ankle,⁴³ it was hypothesized that amputees would have greater lLya values for joint angles during walking compared to healthy non-amputees. More specifically, it was expected to identify this difference at the prosthetic ankle compared to healthy non-amputees since this has been shown to be strongly related to prosthesis preference. It was hypothesized that the prosthetic leg would display greater lLya values compared to the sound leg. Finally, we expand on the previous work of Wurdeman et al.⁴³ by examining the embedding dimension and time lag of the resulting movement attractor at the ankle, knee, and hip for amputee gait.

Methods

Participants

Fourteen individuals with unilateral, transtibial amputation and fourteen healthy, non-amputee individuals were recruited for participation in this study (Table 1). All subjects provided informed consent approved by the University Medical Center Institutional Review Board. Inclusion criteria for individuals with amputation were: 1) unilateral, transtibial amputation, 2) ability to ambulate non-stop for three minutes without an assistive device (other than prosthesis), 3) have had an amputation for at least one year (median time since amputation: 3.5 yrs, range: 1-27 yrs), and 4) have had current prosthesis for greater than 30 days to assure fully acclimated. Healthy, non-amputee subjects were required to be able to ambulate without stopping for three minutes. Exclusion criteria for all subjects included: 1) any existing ulcers on lower extremities, and 2) presence of any neuromuscular or musculoskeletal conditions (beyond amputation and diabetes for amputees) that may affect gait.

Table 1.

Wurdeman

	Age (yrs)	Height (cm)	Mass (kg)	Self-selected speed (m/s)	Residual limb length (cm)	Cause of amputation	Prescribed prosthetic foot type
Amputee	48.2 (14.8)	179.6 (5.9)	91.9 (21.4)	0.85 (0.41)	17.8 (4.7)	8 trauma, 5 vascular/diabetes, 1 osteosarcoma	14 ESAR
Control	51.6 (11.4)	174.3 (7.0)	82.5 (12.8)	1.01 (0.20)	---	---	---
p-value	0.508	0.039	0.170	0.193	---	---	---

Experimental Procedures

Subjects walked for three minutes non-stop on a treadmill at their preferred self-selected speed (Table 1). Preferred self-selected walking speed was chosen in order to enhance the translation of our results to real world applications. Speeds other than a subject-preferred have been reported to increase metabolic cost and decrease comfort.¹⁶ Furthermore, walking speed has been shown to affect the lLya.^{5, 9, 11} This is in strict accordance with dynamical systems theory where a change in parameters will lead to a different movement solution. Thus, by studying subjects under a preferred self-selected walking speed, it is possible to quantify the dynamics under which the system has truly chosen to self-organize.

Subjects wore a secure fitting uniform during all trials. Twenty-seven retroreflective markers were affixed to anatomical landmarks of the pelvis and lower extremities to permit three-dimensional joint angle calculations.⁴¹ Markers were affixed bilaterally at: 1) anterior superior iliac spine, 2) posterior superior iliac spine, 3) greater trochanter, 4) mid lateral thigh, 5) lower front thigh, 6) lateral knee joint space, 7) tibial tubercle, 8) lower lateral shank, 9) lateral malleolus, 10) top of second metatarsal phalangeal joint, 11) posterior heel aspect, 12) lateral head of fifth metatarsal phalangeal joint, and 13) lateral calcaneus and a single marker on the sacrum. For amputee subjects, markers on the prosthetic limb were placed in analogous locations as the sound limb. The three-dimensional motion of the markers was recorded with a 12 camera motion capture system sampling at 60 samples/second (Motion Analysis Corp., Santa Rosa, CA, USA). Lower limb joint angle flexion/extension time series for the duration of the three minute walking trial were calculated from raw marker position data using custom Matlab software (Matlab 2010, Mathworks Inc., Concord, MA, USA). Sagittal plane joint angles were then used for calculations.

Data Analysis

The lLya was used to quantify the attractor divergence. The lLya has been described in great detail elsewhere,^{2, 3, 5, 6, 8, 23, 29, 42, 43} but is briefly reviewed here. The lLya measures the exponential divergence of trajectories within the state space reconstructed attractor (Figure 1).^{6, 8, 29, 42} The state space attractor reconstruction involves using a time delay (τ) to create M copies of the original time series (M is the embedding dimension). After determining the proper delay and embedding dimension, the reconstructed state space vector can be obtained (Eq. 1).

$$y\left(t\right)=[x\left(t\right),x(t+\tau ),x(t+2\tau ),\dots ,x(t+(M-1)\tau )]$$ (1)

Figure 1.

(A) The motion of a joint over multiple strides is recorded to produce the time series In this case, nearly five strides are shown. For this study, analysis was performed on 104 strides. (B) The embedding dimension is calculated from the False Nearest Neighbors algorithm, detailing the number of time delay copies that are required to accurately represent the attractor. This example shows an embedding dimension of 3 (original plus 2 copies). The time delay (τ) is determined through the Average Mutual Information algorithm. Thus, it is possible to see the original time series (solid), the first delayed copy (dashed line), and the second delayed copy (dotted line). (C) Each of the time series (original plus copies) are plotted against each to provide the state space reconstructed attractor. the above pictured is an example of the ankle angle time series embedded into 3 dimensions for viewing purposes. Actually dimensionality however, may exceed this and is typically around 5 for gait dynamics in healthy individuals. (D) Inset from (C) showing calculation of the largest Lyapunov exponent. A point along a fiduciary trajectory and its true nearest neighbor are selected and the Euclidean distance between these points is calculated (d_t; upper right). These points are then followed along their respective trajectories a certain number of time points (n), followed by distance recalculation (d_t’). The log₂ of the ratio of these distances is calculated and then normalized to the time that the points traversed through the trajectory to yield the Lyapunov exponent.

The time delay (τ) is calculated through the average mutual information algorithm.¹ The average mutual information algorithm will calculate the probability that information within the time series of the delayed copies is different.^{1, 18} This is found by testing each potential time delay and calculating the probability; the proper delay is determined when the probability reaches the first local minimum. In this manner, the delay is the time at which the original series and copies are maximally independent.²² The result is that signals that are typically more repetitive have increased time delays as points are more dependent on previous points in the signal.²² On the other hand, a time series that was representative of a purely random signal would have a time delay of 1 as each point is completely independent of the previous and has no effect on the next. But, it should be noted that time delay in experimental settings will also be influenced by sampling frequency (e.g. a signal sampled at 120 Hz results in 2 points for every 1 point in a signal sampled at 60 Hz). Thus, caution should be used when comparing time delays across studies.

The embedding dimension, M, is calculated from the false nearest neighbors procedure.^{1, 18, 35} This procedure creates multiple time delayed copies of the original series and then calculates the percentage of “false nearest neighbors”. A “false nearest neighbor” is a point that in lower dimensions is relatively close in terms of a small Euclidean distance, but the unfolding of the attractor into a larger dimension results in the spatial separation between the points growing to where they are no longer relatively close in the state space.^{1, 43} The determination of the embedding dimension details how many state variables are necessary to accurately describe the uniqueness of each point.¹ It is similar to time delay in that signals that are more repetitive will have lower dimensionality, whereas a truly random signal will have an infinite number of state variables required to uniquely describe each point.¹ Thus, signals with greater time delays and embedding dimensions are approaching random signals with less organization.

Once each time series has been properly embedded into its reconstructed state space, the lLya can be measured as the average divergence of neighboring trajectories within the attractor. This is done by selecting a point along a single fiduciary trajectory and allowing this point to propagate through the attractor.^{8, 42, 43} As the point propagates through the attractor, neighboring points are selected and the Euclidean distance (d_t) between the reference point and neighboring point is calculated.⁴² These points are then propagated through the attractor a certain amount of time (k) and the distance between the points is then recalculated (d_t’).⁴² The local convergence/divergence rate (Z) at that instant is then calculated as:

$$Z=\left({\log }_2(d_{t^{\prime }}∕d_t)\right)∕k$$ (2)

where k is equal to the number of time points (n) to propagate before replacing the nearest neighbor divided by the sampling frequency to allow proper time normalization. The long time average of the running sum of the Z values is then calculated, at which point the nearest neighbor is replaced with a new point that is a closer neighbor and the process of propagation and distance calculation is repeated.^{42, 43} This continues until the reference point has moved through the entire time series, at which point the long time average of the Z values is the lLya.⁴² Input parameters required were set at n equal to 3,⁴³ max angle of 0.3 radians (maximum angle from reference trajectory to replacement neighbor ^{42, 43}), minimum scale length of 0.0001 (minimum distance to selection of new nearest neighbor ^{42, 43}), and maximum scale length of 0.1 times the maximum length of the attractor (maximum distance to selection of new nearest neighbor^{42, 43}). These parameters when used on known signals of similar data length (~8200 points) as the current study trials produce the following results: sine wave = 0 bits/s, Lorenz equations = 1.96 bits/s, and white noise = 32.77 bits/s.

In order to compare the attractor divergence between amputees and non-amputees, the reconstructed attractors should contain similar number of trajectories.⁶ This is controlled by cropping all walking trials to an equal number of strides.^{6, 23} Thus, all time series were cropped to the minimum number of strides that any individual was able to attain in the three minute walking trial which equated to 104 strides. Subject group demographics were compared through independent t-tests. Differences in the attractor’s lLya, embedding dimension, and time delay for the lower limb joint motions between amputee’s sound leg and healthy, non-amputee right legs and between amputee’s prosthetic leg and healthy, non-amputee right legs were tested through independent t-tests. The attractor’s lLya, embedding dimension, and time delay for the amputees’ prosthetic leg and sound leg were compared through dependent t-tests. Significance was set at 0.05.

Results

Our amputee subjects and healthy non-amputee controls were similar for age, weight, and their self-selected speeds (Table 1). The amputee group’s average height was slightly taller than the control group (p=0.039).

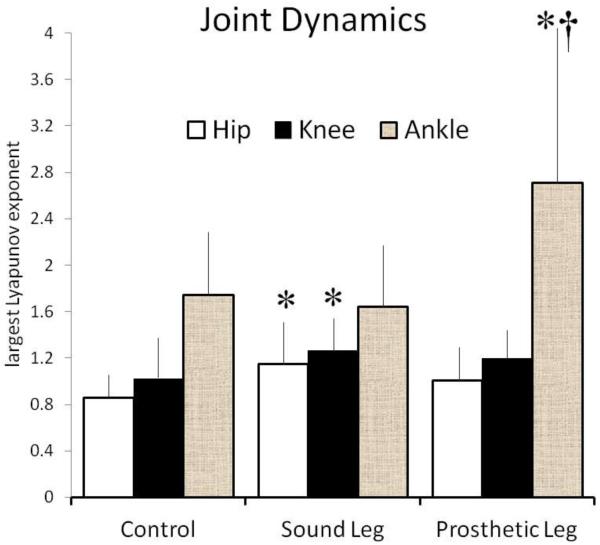
The lLya for the sound leg hip (p=0.013) and knee (p=0.050) were significantly greater than the healthy, non-amputees (Table 2; Figure 2). The lLya for the prosthetic leg ankle was significantly greater than the healthy, non-amputees (p=0.023) and the sound leg ankle (p=0.017). The lLya of the sound leg ankle (p=0.639), prosthetic leg hip (p=0.113), and prosthetic leg knee (p=0.128) were not different from healthy, non-amputees. The lLya between the sound and prosthetic leg’s hip (p=0.179) and knee (p=0.397) were also not different (Figure 3).

Table 2.

Wurdeman

		Control	Sound Leg	Prosthetic Leg
ILya	Hip	0.85 ± 0.19	1.15 ± 0.37*	1.01 ± 0.29
	Knee	1.02 ± 0.34	1.27 ± 0.28*	1.20 ± 0.24
	Ankle	1.74 ± 0.53	1.65 ± 0.54	2.71 ± 1.34*†
M	Hip	5.64 ± 0.63	5.36 ± 0.74	5.64 ± 0.63
	Knee	5.71 ± 0.83	6.21 ± 0.89	6.57 ± 1.02*
	Ankle	6.57 ± 1.02	6.93 ± 0.92	6.29 ± 0.83 †
τ	Hip	20.00 ± 3.44	21.64 ± 3.84	21.64 ± 5.09
	Knee	17.29 ± 5.84	19.00 ± 9.64	18.29 ± 6.82
	Ankle	15.86 ± 5.50	14.07 ± 4.10	15.14 ± 3.39

Figure 2.

Exemplary reconstructed attractors for ankle motion of an amputee and healthy control. The prosthetic ankle motion (A) has greater attractor divergence than the sound ankle (B) and a healthy non-amputee ankle (C). Notice, however, the Lyapunov exponent quantifies attractor divergence but is not largely affected by the overall shape of the attractor.

Figure 3.

The attractor state for unilateral, transtibial amputee gait at the prosthetic ankle, as well as sound leg hip and knee, has greater divergence. The difference at the prosthetic ankle was a large magnitude and should be considered a functional problem. These differences may explain the large number of falls recorded in amputees. Units: bits/s *Sig. vs. healthy, non-amputee controls (p<0.05) †Sig. vs. sound leg (p<0.05)

The embedding dimensions and time delays for the reconstructed attractors were statistically similar for nearly all comparisons. The embedding dimensions used to reconstruct the prosthetic leg ankle attractors were slightly less compared to the sound ankle (p=0.045; Table 2). The embedding dimensions for the hip and knee were not different between the sound and prosthetic legs (p=0.165 and 0.096, respectively). The embedding dimensions for the prosthetic leg knee was greater than the control knee (p=0.021). The embedding dimensions for the prosthetic leg ankle (p=0.422) and hip (p=1.000), as well as the sound leg ankle (p=0.338), knee (p=0.136), and hip (p=0.284), were not different from the control group. The time delays used to reconstruct the attractors for the prosthetic leg ankle (p=0.421), knee (p=0.794) and hip (p=1.000) were not different from the sound leg. The prosthetic leg ankle (p=0.683), knee (p=0.680), and hip (p=0.327), as well as the sound leg ankle (p=0.339), knee (p=0.574), and hip (p=0.244), were not different from the control leg.

Discussion

Individuals with unilateral, transtibial amputation ambulate with altered dynamics. The lLya was larger (greater attractor divergence) for the motion of the sound leg hip and knee and the prosthetic leg ankle compared to the healthy, non-amputees. Furthermore, the lLya for the prosthetic ankle was significantly greater than the sound leg ankle. The attractors for the sound leg ankle required more state dimensions to fully describe the system compared to the prosthetic leg ankle motion. The prosthetic leg knee also required more state dimensions to describe the movement compared to healthy controls. The larger divergence and differing embedding dimensions for the functionally preferred attractor states found in unilateral, transtibial amputee gait reflect an altered motor control schema.

From the dynamical systems theoretical framework, we expected an altered attractor state due to the significant change in morphology and biology.^{13, 15} But, the question that should be considered is whether these altered functional attractors are a failure of the system to optimize to movements similar as healthy, non-amputees. In the case of an individual with an amputation but no other major co-morbidities, it is possible the central nervous system is largely intact and fully capable of performing. Kurz et al.²⁰ demonstrated that in fact a healthy central nervous system under altered mechanics leads to altered dynamics. They had subjects ambulate with increased propulsive force which led to a systematic change. Thus, the altered functional attractor of the amputee gait would seem to be an optimized solution based on the altered mechanics as well as changes to the amputee’s neurological system. The problem is that this optimized solution is different from the solution converged upon by healthy, non-amputees, thus may be associated with the poor gait outcomes in this group.

Rather, the differences found in the nonlinear dynamics of individuals with unilateral, transtibial amputation highlight the change from the optimal state of the healthy non-amputees. Specifically, based on the recently proposed theory of optimal movement variability, the healthy non-amputee individual has a complex variance within the functional attractor.^{36, 37} The term “optimal” used in optimal movement variability should be considered different from the “optimization” principle associated with dynamical systems theory. In the case of optimal movement variability, “optimal” refers to the high degree of flexibility and adaptability afforded to the movement pattern for healthy, non-amputee individuals.³⁶ The concept of “optimization” associated with dynamical systems theory describes the reduction in degrees of freedom of the motor system based on the constraints on the system.^{13, 15, 38, 40} However, this “optimization” only explains how the neuromuscular system is able to manage the high number of degrees of freedom. In an altered but healthy system, such as an amputee, it does not account for whether the “optimization” will be the state that leads to the most clinically functional movement where clinical function can be seen to encompass maintaining walking balance, reduced metabolic cost, transitioning between different gaits (and safely stopping), etc. Thus, from dynamical systems theory we expected an altered attractor state at one or more of the joints, but based on the theory of optimal movement variability we must conclude that the attractor state that is being utilized in amputee gait is not what should be considered the optimal for these individuals to safely and efficiently ambulate. ^{13, 36, 40}

We predicted that the prosthetic ankle in particular would have an altered attractor state with increased divergence. This was based on our previous work that showed an affinity towards the prosthesis that allowed them to settle into an attractor state with decreased attractor divergence.⁴³ Consistent with the theory of optimal movement variability,³⁶ then they would already have greater attractor divergence than what the central nervous system would know to be optimal. Thus, we assumed that these individuals are ambulating with an attractor at the prosthetic ankle that has increased divergence within its structure. Calculation of the lLya confirmed our assumptions.

It was unexpected, however, to see increased attractor divergence in the sound leg hip and knee joints (Table 2). Prosthesis use is known to cause compensatory changes in the sound leg.^{30, 32} However, the lack of difference between the hip and knee for the prosthetic and sound legs combined with the influence of the prosthetic ankle on amputee perception ⁴³ seems at this point to indicate the major functional impairment is the change at the prosthetic ankle. Further work is needed to determine the implications of the altered attractors for the sound leg hip and knee movement, possibly through protocols of incline and decline walking which require increased hip and knee activity.

Differences in the embedding dimensions at the prosthetic leg knee and ankle further demonstrate existing differences in the functionally preferred attractor states. However, the results from the embedding dimensions are less clear. Specifically, although the prosthetic leg knee motion had increased dimensionality compared to the control leg, it was the sound leg knee motion’s attractor that contained increased divergence compared to the control leg knee. Furthermore, the prosthetic leg ankle attractors had decreased dimensionality compared to the sound leg ankle attractors, yet the opposite was found for the lLya. Thus, it seems that altered attractor divergence may not simply be the result of altered embedding dimension. Regardless, altered embedding dimensions further confirm altered attractor dynamics in amputee gait.

At this time, we are only aware of one other study that compared the lLya in individuals with limb loss and healthy non-amputees. Lamoth et al.²² compared eight unilateral, transfemoral amputees to healthy, non-amputee controls. They found increased attractor divergence when walking for the amputee group. This is consistent with our findings. However, they measured the attractor state for the anterior-posterior and medial-lateral signals from dual axis accelerometers placed at the hips.²² Furthermore, they examined gait for individuals with transfemoral level amputation. As a result, it is difficult to compare our findings with theirs beyond a qualitative level, noting the increased lLya values measured in individuals with lower limb loss.

Finally, while our group has examined the attractor divergence with lLya in the past,^{7, 18,20, 21, 27, 29} we have previously utilized commercially available software (CDA)³⁴ for analysis of attractor divergence to promote replication of our work. CDA³⁴ utilizes the Wolf et al.⁴² algorithm, however, it does not account for sampling frequency (see Equation 2). We have overcome this limitation imposed by CDA by now utilizing a custom Matlab program (Matlab 2010, Mathworks Inc., Concord, MA, USA) that includes a correction with normalizing to time due to sampling frequency. The correction hinders direct comparison to previously reported values of lLya that were not calculated in time constrained units (e.g. bits/s) as provided by Wolf et al.⁴² There are additional limitations to consider for this study. First, the amputee participants walked with several different prostheses. This method was chosen for the most “real-world” representation of amputee gait. While placing all individuals in the same type of prosthesis would have controlled for prosthesis type, it could have resulted in individuals walking with a less than appropriate prosthesis that would likely not be prescribed, losing the “real-world” applicability and likely further affecting the functional attractor states. Future work can begin to look at the effects of prosthesis types on the lLya of joint motions. This, however, will need to be done cautiously as it should not be expected that one type of prosthesis will result in similar lLya when worn on two different individuals since the attractor represents the cooperation of the prosthetic system and the biological system. Another potential limitation to consider is the difference in residual limb length. Our cohort had a range of 10 - 28.5 cm from the residual limb distal end to the patella tendon. This would seemingly affect the functional attractor state that the prosthetic ankle settled into based on the difference in morphology and mechanical lever arm allowed to contribute motion to the prosthetic ankle.

In conclusion, we note that individuals with unilateral, transtibial amputation typically ambulate with increased divergence within the functional attractors at the sound leg hip and knee and in particular the prosthetic ankle. The inability to settle into an attractor state similar to healthy non-amputees may be the reason that nearly 52% of amputees report falling within the previous year, and 75% of those individuals report multiple falls.²⁵ A positive note to these findings is that from a dynamical systems theory perspective we would expect a change in the mechanics of the system would result in a new attractor state. For an amputee, this can easily be done by simply switching the prosthesis, which has been shown to be able to immediately impact the attractor.⁴³ Furthermore, the implementation of therapy and a rehabilitation program may also be able to affect the movement to optimally settle at a different attractor state.³⁷ Future work is needed to determine the efficacy of rehabilitation programs on improving the attractor dynamics in amputee gait as well as the potential for quantifying attractor divergence to determine a better prosthesis.