Multi-Scale Continuum Modeling of Biological Processes

Abstract

This article provides a brief review of multi-scale modeling at the molecular to cellular scale, with new results for heart muscle cells. A finite element-based simulation package (SMOL) was used to investigate the signaling transduction at molecular and sub-cellular scales (http://mccammon.ucsd.edu/smol/, http://FETK.org) by numerical solution of time-dependent Smoluchowski equations and a reaction-diffusion system. At the molecular scale, SMOL has yielded experimentally-validated estimates of the diffusion-limited association rates for the binding of acetylcholine to mouse acetylcholinesterase using crystallographic structural data. The predicted rate constants exhibit increasingly delayed steady-state times with increasing ionic strength and demonstrate the role of an enzyme’s electrostatic potential in influencing ligand binding. At the sub-cellular scale, an extension of SMOL solves a non-linear, reaction-diffusion system describing Ca²⁺ ligand buffering and diffusion in experimentally-derived rodent ventricular myocyte geometries. Results reveal the important role for mobile and stationary Ca²⁺ buffers, including Ca²⁺ indicator dye. We found that the alterations in Ca²⁺-binding and dissociation rates of troponin C (TnC) and total TnC concentration modulate subcellular Ca²⁺ signals. Model predicts that reduced off-rate in whole troponin complex (TnC, TnI, TnT) versus reconstructed thin filaments (Tn, Tm, actin) alters cytosolic Ca²⁺ dynamics under control conditions or in disease-linked TnC mutations. The ultimate goal of these studies is to develop scalable methods and theories for integration of molecular-scale information into simulations of cellular-scale systems.

1. Introduction

Diffusion of enzymes and ions plays an important role in a variety of biological processes and has been studied extensively using various biophysical, biochemical, and computational approaches. Computational models of diffusion have been widely used in both discrete [1] and continuum methods [2]. Discrete methods describe the stochastic trajectories of individual particles and include methods like Monte Carlo [3], Brownian dynamics [4], and Langevin dynamics [5]. Continuum approaches model particle diffusion by the evolution of continuous probability distributions and include the Smolochowski and Fokker-Planck formalisms. Relative to discrete methods, continuum approaches provide an inexpensive alternative to the modeling of individual Brownian particles.

In our previous work, we applied adaptive finite element methods to solve the time-dependent Smoluchowski equation on a single enzyme molecule (mouse acetylcholinesterase, mAChE) or clusters of mAChEs [6–8]. We observed both steady-state and time-dependent diffusive particle distributions on the diffusion domain and calculated the rate association coefficient for acetylcholine (ACh) diffusive particles. Including the electrostatic field determined by solution of the Poisson-Boltzmann equation allowed us to examine the role of electrostatics in guiding diffusive particles to the active center. This study resulted in the SMOL software package, which facilitates the finite-element solution of steady-state and time-dependent Smoluchowski equations for molecular species.

Recently, the SMOL package was generalized to model signaling transduction processes on the sub-cellular level and specifically the role of calcium (Ca²⁺) diffusion and binding to mobile and stationary buffers during the cardiac excitation-contraction cycle [9–11]. Previous approaches employed a systems biology approach, in which components of the myocyte are represented by simple geometries [12–14]. In recent years, advancements in the electron microscopy community have enabled the 3-dimensional (3-D) structure determination of cells and sub-cellular organelles across a wide range of spatial scales [15]. Simulations utilizing experimentally-derived structures offer a degree of realism that cannot be easily captured with reduced representations.

The extended simulation tool SMOL represents progress toward unifying molecular-level and cellular level dynamics via the solution of partial differential equations on 3-D tetrahedral meshes representative of realistic systems. In this article, we summarize capabilities of SMOL in modeling molecular-level and cellular level events, provide new data for myocyte cellular modeling, and discuss potential further applications and extensions of the SMOL multi-scale modeling tool.

2. Methods and software

2.1 Time-Dependent Smoluchowski Equation

The starting point for solving the time-dependent SMOL equation is based on the steady-state Smoluchowski equation solver described by Song et al. [16–17]. The original time-dependent Smoluchowski equation has the form of a continuity equation,

$$\frac{du(\overrightarrow{R};t)}{dt}=-\overrightarrow{\nabla }•\overrightarrow{j}(\overrightarrow{R};t)$$ (1)

where the particle flux j⃗(R⃗; t) is defined as

$$\begin{array}{l}\overrightarrow{j}(\overrightarrow{R};t)=D(\overrightarrow{R})[\overrightarrow{\nabla }u(\overrightarrow{R};t)+\beta \overrightarrow{\nabla }W(\overrightarrow{R})u(\overrightarrow{R};t)]\\ =D(\overrightarrow{R})e^{-\beta W(\overrightarrow{R})}\nabla e^{\beta W(\overrightarrow{R})}u(\overrightarrow{R};t)\end{array}$$ (2)

Here u(R⃗; t) is the distribution function of the ensemble of Brownian particles, D(R⃗) is the diffusion coefficient, β = 1/k_B T is the inverse Boltzmann energy, k_B is the Boltzmann constant, T is the temperature, and W(R⃗) is the potential of mean force (PMF) for a diffusing particle due to solvent-mediated interactions with the target molecule. For simplicity, D(R⃗) is assumed constant. The two terms contributing to the flux have clear physical meanings. The first is due to free diffusion processes, as quantified by Fick’s first law. The second contribution is due to the drift velocity, ∇W(r)/γ, induced by the systematic forces, ∇W(r) and friction quantified by the friction constant γ. The relation between diffusion coefficient D(R⃗) and friction constant γ is given by Stokes-Einstein equation: Dβγ =1.

The diffusion-determined reaction rate constant during the simulation time can be obtained from the flux j⃗(R⃗; t) by integration over the active site boundary (Γ), i.e.

$$k_{on}(t)=u_{\mathit{bulk}}^{-1}\underset{\mathrm{\Gamma }}{\int }n(\overrightarrow{R})·j(\overrightarrow{R};t)dS$$ (3)

where u_bulk is bulk concentration at the outer boundary; n(R⃗) is the surface normal [6]. The variation of reaction rates with ionic strength is often interpreted via the Debye-Huckel limiting law [18–19].

For molecular simulations, the long-range contributions to the PMF are electrostatic in nature and thus may be estimated by solving the Poisson-Boltzmann equation. Typical approaches consider the positions of atoms from high-resolution X-ray crystal structures available in the Protein Data Bank (http://www.rcsb.org) and their corresponding partial charges, as well as the dielectric constant of the surrounding solvent. For sub-cellular systems, we assume that the electrostatic potential arising from the cell membrane is screened beyond the characteristic Debye length, which is less than 1.0 nm at physiological ionic strengths. As such, the W(R) term defined in (2) may be neglected and one arrives at Fick’s law of diffusion [6].

2.2 Reaction-Diffusion Equations

In this section, we derive a model which describes the diffusive transport of Ca²⁺ in the presence of stationary and mobile Ca²⁺ buffers. Assuming mass action kinetics and Fickian diffusion [20], we can write the transport equations,

$$\frac{\partial {[{Ca}^{2+}]}_i}{\partial t}=D_{Ca}{\nabla }^2{[{Ca}^{2+}]}_i-\sum _{m=1}^{m_{max}}{R}_{B_m}-\sum _{s=1}^{s_{max}}{R}_{B_s}+J_{{Ca}_{\mathit{flux}}}$$ (4)

$$\frac{\partial [Ca{B}_m]}{\partial t}=D_{{\mathit{CaB}}_m}{\nabla }^2[{\mathit{CaB}}_m]+R_{B_m}$$ (5)

$$\frac{\partial [{\mathit{CaB}}_s]}{\partial t}=R_{B_s}$$ (6)

$$R_{B_m}=k_{on}^m([B_m]-[{\mathit{CaB}}_m]){[{Ca}^{2+}]}_i-k_{\mathit{off}}^m[{\mathit{CaB}}_m]$$ (7)

$$R_{B_s}=k_{on}^s([B_s]-[{\mathit{CaB}}_s]){[{Ca}^{2+}]}_i-k_{\mathit{off}}^s[{\mathit{CaB}}_s]$$ (8)

where [Ca²⁺]_i is intracellular Ca²⁺ concentration, $k_{on}^i$ and $k_{\mathit{off}}^i$ are the association and dissociation buffer rate constants, [B_s] is the concentration of stationary buffer, [B_m] is the concentration of mobile buffer, D_Ca and D_CaBm are the diffusion constants for free Ca²⁺ and Ca²⁺-bound to mobile buffer, and J_Caflux is the total Ca²⁺ flux via the cell membrane.

2.3 Numerical Algorithms, Software and Meshing Tools

In 3-D finite element methods, the geometry is discretized into polyhedrons, over which the local solution to the partial differential equations may be estimated. This process is usually referred to as mesh generation [21–22]. Although different types of meshes may be generated depending on the numerical solvers to be employed, we restrict ourselves to triangular (surface) and tetrahedral (volumetric) mesh generation as commonly used in biomedical simulation (http://fetk.org/codes/gamer/index.html). Of particular interest are 3-D scalar volumes obtained by imaging techniques such as the 3-D electron tomography (cellular level) and X-ray crystal structures (molecular level).

The time-dependent Smoluchowski equation and nonlinear reaction-diffusion system were solved by a finite difference method in time and finite element method in space using our SMOL software tool. The SMOL program utilizes libraries from the finite element tool kit (FEtK, http://FETK.org), which previously has been used in several molecular level studies [6–8], [23–25]. To extend SMOL to sub-cellular simulations, the reaction terms due to buffering were decoupled from the diffusion and flux boundary conditions defined in (4–8). Simulation results were visualized using OpenDX and GMV mesh viewers, while post-processing and data analyses were implemented by customized Python, MATLAB 2008b (The MathWorks, Natick, MA) scripts and Xmgrace software [26].

3. Results and discussion

3.1 Continuum Diffusion on Molecular Level

This section demonstrates SMOL’s proficiency in the numerical modeling of diffusion-limited binding kinetics of single enzyme molecule (in this particular case, mouse acetylcholinesterase, mAChE) under various ionic strength conditions [6], [19]. Acetylcholinesterase is an enzyme that hydrolyzes ACh during neuron signaling. Under physiological conditions, the experimentally suggested association rate constant (k_on) is ~10¹² M⁻¹min⁻¹, which is close to the diffusion limit. Therefore, it is not easy to accurately measure k_on. By numerically solving the Poisson-Boltzmann and time-dependent Smoluchowski equations, we calculated k_on under the influence of a molecular electrostatic field. The tetrahedral mashes in this numerical experiment were obtained from the inflated van der Waals-based accessibility data for the mAChE monomer and tetramers using the level-set boundary interior exterior-mesher, (Fig. 1) [6].

Figure 1.

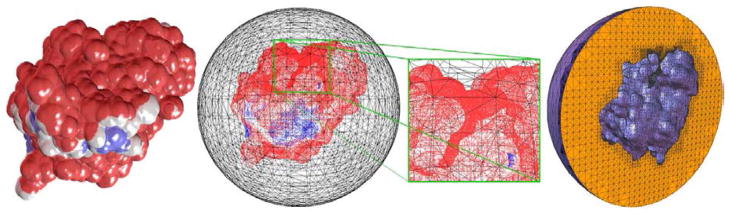
Left to right mAChE monomer; the molecular surface and outer sphere; magnification of the active site gorge; the tetrahedral mesh of the internal volume between the molecular surface and the outer sphere.

The steady-state k_on value (t > 10 μs) for a charged ligand in a 0.0 M ionic strength solution was estimated to be 9.56*10¹¹M⁻¹min⁻¹, which is consistent with the experimentally suggested value of 9.8±0.6*10¹¹M⁻¹min⁻¹ [18], and the predicted value from the time-independent solution of the Smoluchowski equation [16]. Our model studies also indicate that mAChE association rate was rapidly attenuated by increasing ionic strength (ranging in this numerical experiment from 0.0 to 0.67 M), which supports the idea of electrostatically-guided molecular diffusion [6]. We concluded that accurate estimation of the electrostatic potential and of the time to reach steady-state are important factors in modeling the activity of enzymes and buffers in cellular volumes.

To further test the SMOL solver, recently we also applied it to study the drug molecular diffusion in wild-type neuraminidase and its mutants [27]. We observed quantitatively consistent trends compared with experimental measurements, although the predictions were an order of magnitude higher than experiment. This indicates that the finite size of the drug molecule, as well the conformational changes of the active site of the target protein, may be significant. These attributes are neglected in the current SMOL tool. To overcome this limitation, we are developing a new multi-scale algorithm to couple the SMOL continuum formulation with particle-based Brownian dynamics. The simulation of explicit particles naturally accommodates finite-size and conformational effects that may influence association rate constants. These studies also establish the foundation for integrating molecular-scale information into cellular-scale systems such as Ca²⁺ signaling transduction in cardiac myocytes [9–11].

3.2 Continuum Diffusion on Sub-Cellular Level

In cardiac muscle cells, calcium (Ca²⁺) is best known for its role in contraction activation [28]. A remarkable amount of quantitative data on cardiac cell structure, ion-transporting protein function and distribution, and intracellular Ca²⁺ dynamics has become available [15], [28–30]. Alterations in myocyte ultra-structure and in protein function and distribution are now recognized to be the primary mechanisms of cardiac dysfunction in a diverse range of common pathologies including cardiac arrhythmias and hypertrophy [28].

3.2.1 Cardiomyocyte ionic model with realistic t-tubule geometry

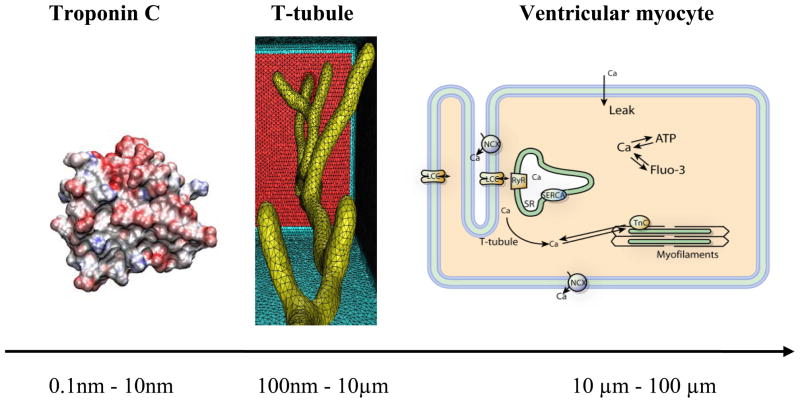
In this paper, we used our published computational model with realistic transverse-axial t-tubule geometry and experimentally suggested ion-transporting protein distributions, to analyze several important spatial and temporal features of Ca²⁺ signaling, buffering and diffusion in rat ventricular myocytes [11]. We considered a small compartment containing a single t-tubule and its surrounding half-sarcomeres (Fig. 2 middle panel). The t-tubule diameter varied from 0.19 μm to 0.469 μm and the t-tubule depth was 5.645 μm. The surrounding half-sarcomeres were modeled as a rectangular-shaped box of 2 μm ×2 μm in the plane of external sarcolemma and 5.96 μm in depth. Because the original t-tubule model did not include the realistic cell surface, one of the box faces (top red surface in Fig. 2) was assumed to be the external cell membrane [11]. To generate the high-fidelity and quality tetrahedral meshes for 3-D t-tubular system we used GAMer [22].

Figure 2.

Left panel Troponin C monomer. Middle panel: Geometric model of single t-tubule and surrounding half-sarcomeres extracted from 2-photon microscopy images in mice [15]. Right panel: Schematic drawing of Ca²⁺ entrance and extrusion via the cell membrane and Ca²⁺ buffering and diffusion inside the cell. L-type Ca²⁺ channel (LCC), Na⁺/Ca²⁺ exchanger (NCX), membrane Ca²⁺ leak (Leak), ryanodine receptor (RyR), sarcoplasmic reticulum (SR), SR Ca²⁺ pump (SERCA), troponin C (TnC), adenosine triphosphate (ATP), fluorescent indicator (Fluo-3). Bottom: Scale bar showing the relative lengths of TnC macro-molecule, t-tubule and myocyte.

The overall scheme of the ionic model is shown in Fig. 2 (right panel). In the present study we examined Ca²⁺ diffusion in rat cells that were treated with ryanodine and thapsigargin to eliminate the release and uptake of Ca²⁺ by the sarcoplasmic reticulum (e.g. Ca²⁺ fluxes via the ryanodine receptors and the SR Ca²⁺ pumps blocked), [11]. At rest, Ca²⁺ influx via Ca²⁺ leak was adjusted to match Ca²⁺ efflux via NCX thus no net movement across the cell membrane would occur. The depolarization of the sarcolemma activates L-type Ca²⁺ channels. The subsequent influx of Ca²⁺ increases the intracellular Ca²⁺ concentration ([Ca²⁺]_i). Free Ca²⁺ diffuse and react throughout the cytoplasm. The equations describing Ca²⁺ fluxes via the t-tubule and surface membrane (J_Caflux = J_Ca + J _NCX + J_M–leak, J_Ca - LCC Ca²⁺ influx-; J _NCX - NCX Ca²⁺ flux; J_M–leak - membrane Ca²⁺ leak) were the same as in Cheng et al. (see also APPENDIX). The generalized SMOL package was used to solve the nonlinear reaction-diffusion system defined in (4–8) [11]. Unless specified otherwise in the Figures’ legends or in the text, all initial conditions and values of the parameters that are not included in the present paper correspond to those used in Cheng et al. [11].

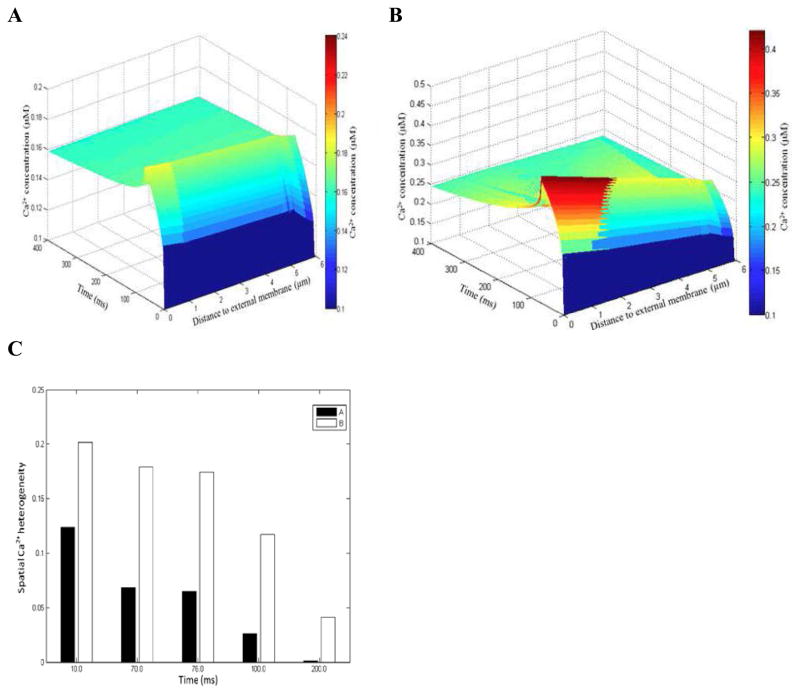
In agreement with experiment [31], the model predicts that spatially uniform Ca²⁺ transients can be achieved with 100 μM Fluo-3 when total Ca²⁺ flux (J_Caflux) was heterogeneously distributed along the sarcolemma (Fig. 3). Figure 3 also shows that strongly non-uniform Ca²⁺ signals are predicted in the absence of fluorescent indicator. The surface plots in Fig. 3 were computed from Cheng et al. line-scan images (Fig. 4F and Fig. 6F in Cheng et al., [11]). To delineate further the suggested spatial differences in [Ca²⁺]_i (see Fig 3A–B), we introduced a quantity called ‘spatial Ca²⁺ heterogeneity’ (SCH). The SCH is defined to be the difference of the maximal and minimal [Ca²⁺]_i values, normalized by the maximal value at given reference point along the scanning line in given moment t_j of interest. High SCH suggests non-uniform [Ca²⁺]_i distribution and SCH of zero indicates spatially uniform [Ca²⁺]_i distribution. The histogram in Fig. 3C shows that in the absence of dye SCH(10ms) increased by 1.64 folds, SCH(70ms) by 2.63 folds, SCH(76ms) by 2.68 folds, SCH(100ms) by 4.46 folds, and SCH(200ms) by 28.65 folds.

Figure 3.

Ca²⁺ signals in the presence (panel A) and absence of dye (panel B). Estimated SCH with 100 μM Fluo-3 and zero Fluo-3 (panel C). In panels A–B the line-scan was positioned at 200nm from the surface of the t-tubule. Featured spots along the scanning line: 17 μm, 3.09 μm, 5.45 μm. Moments t_j of interest: 10ms - L-type Ca²⁺ current peak (t_ICa–peak); 70 ms - duration of L-type Ca²⁺ current (t_ICa–max); 76 ms - [Ca²⁺]_i peak (t_{[Ca²⁺]i–peak}); 100ms and 200ms – relaxation times for [Ca²⁺]_i (t_100ms, t_200ms).

Figure 4.

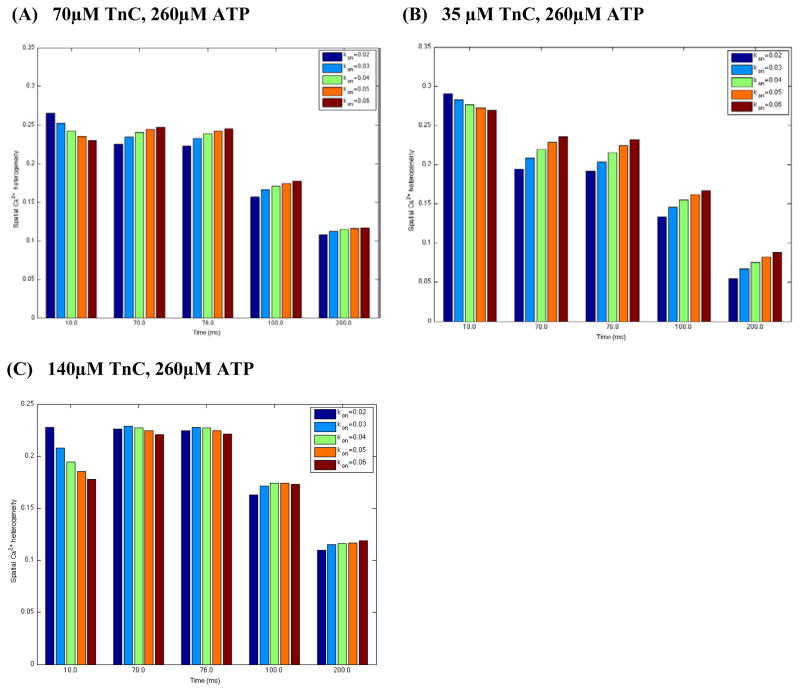
Figure 4A–C. Estimated spatial Ca²⁺ heterogeneity index with respect to ±25% and ±50% changes in control Ca²⁺ on-rate for TnC ( $k_{on}^{\mathit{CaTn}}=0.04\mu {\text{M}}^{-1}{\text{ms}}^{-1}$, assuming basic $k_{\mathit{off}}^{\mathit{CaTn}}$ value of 0.04/ms unchanged) in the absence of dye. In panels A–C Ca²⁺ flux was heterogeneously distributed, line-scan positioned at 200nm away from the t-tubule membrane, and the featured spots along the scan line were chosen to be the same as in Fig. 3.

In this particular model, the effects of exogenous and endogenous Ca²⁺ buffers (Fluo-3, ATP, troponin C) were considered. The buffer Ca²⁺ dissociation constants ( $K_D^{\mathit{CaFluo}}=0.739\mu \text{M},K_D^{\mathit{CaATP}}=200\mu \text{M},K_D^{\mathit{CaTn}}=1\mu \text{M}$) and on-rate constants ( $k_{on}^{\mathit{CaFluo}}=0.23\mu {\text{M}}^{-1}{\text{ms}}^{-1},k_{on}^{\mathit{CaATP}}=0.225\mu {\text{M}}^{-1}{\text{ms}}^{-1},k_{on}^{\mathit{CaTn}}=0.04\mu {\text{M}}^{-1}{\text{ms}}^{-1}$) used here are average values measured in different cardiac species under physiological conditions [9–11]. Theoretical estimates of $k_{on}^{\mathit{CaTn}},k_{on}^{\mathit{CaATP}}$ or $k_{on}^{\mathit{CaFluo}}$ rates in the literature, however, are lacking. Moreover, the Ca²⁺-binding buffer constants for several other important buffers regulating cardiac cell cycle (including calmodulin, myosin, TnC high-affinity sites, ADP) are controversial or unknown [12], [28]. Thus, in the event that the association rate (k_on) is unknown, we assume a typical near-diffusion-limited on-rate value of 0.125 μM⁻¹ms⁻¹ [12]. Hence, the computational estimation of these kinetic parameters presents an exciting opportunity to leverage our advanced molecular-level tools.

Two classes of Ca²⁺ binding sites have been identified on cardiac TnC subunit (Fig. 2 left panel); one low-affinity Ca²⁺-specific site on the amino end of TnC (N-domain) and two high-affinity Ca²⁺/Mg²⁺ binding sites on the carboxy end of TnC (C-domain) [28, 32]. The high affinity Ca²⁺/Mg²⁺ sites are saturated at resting [Ca²⁺]_i (~100 nM). Therefore, in our model only the low-affinity Ca²⁺-specific site was included since large and rapid changes in the Ca²⁺ occupancy of these sites can occur during the Ca²⁺ transient [32]. We assume also that TnC is immobile because it is attached to the thin filament [28]. Little is known, however, how alterations in TnC on- and off-rates in the whole Tn compex (TnC, TnI, TnT) modulate the spatial and temporal features of the Ca²⁺ signaling, buffering and diffusion in rats. Therefore our goal here was to examine these effects from a modeling perspective. In this study we used published experimental measurements for $k_{on}^{\mathit{CaTn}}$ and $k_{\mathit{off}}^{\mathit{CaTn}}$ because currently at the molecular scale we do not have yet theoretical estimates as for mAChE monomer on-rate [6].

3.2.1.1 Effects of changes in Ca²⁺ on-rate to TnC in whole Tn complex on local Ca²⁺ signals

Recently, a study has clarified the role of a specific, disease-associated mutation of the TnC regulatory domain in altered Ca²⁺ binding, signal transmission and myocyte contractile dysfunction in rats [33]. Lim and collaborators, by combining targeted expression/integration of recombinant mutant TnC in cardiomyocytes and in vitro functional analysis, found a decrease in myofilament Ca²⁺-sensitivity and Ca²⁺ binding affinity. It is difficult, however, to derive an understanding from Lim’s et al. studies how changes in the Ca²⁺ on-rate for TnC ( $k_{on}^{\mathit{CaTnC}}$) modulate spatial Ca²⁺ distribution in rats. Our studies imply here that in the absence of dye with 70μM TnC (see Fig. 4A), inflated $k_{on}^{\mathit{CaTn}}$ values tend to decrease SCH within the initial 10 ms of simulation, during which the calcium concentration ([Ca²⁺]_i) is low. SCH however increases at the total [Ca²⁺]_i beyond 10 ms.

Measurements have demonstrated also that the total TnC concentration ([TnC]_tot) can range from 30 μM to 150 μM [28, 32]. With this in mind, we computed SCH decreasing or increasing [TnC]_tot. Figures 4A–C show that at t_{ICa –peak} (10ms) 35 μM [TnC]_tot enhanced SCH while 140 μM [TnC]_tot tend to decrease SCH as predicted with 70 μM[TnC]_tot. Interestingly, with $k_{on}^{\mathit{CaTn}}$ ranging from 0.02 to 0.06 μM⁻¹ms⁻¹: (1) beyond 10 ms [Ca²⁺]_i was more uniformly distributed with 35 μM [TnC]_tot than was predicted for 70 μM[TnC]_tot; (2) 140 μM[TnC]_tot also decreased SCH(70 μM [TnC]_tot) at t_{ICa – max}, t_{[Ca²⁺ ]i –peak} and t_100ms while at 200ms SCH remined almost unchanged. Additional model findings are that with 35 μM [TnC]_tot SCH increased at the total [Ca²⁺]_i beyond 10 ms (Fig. 4B) while the changes in $k_{on}^{\mathit{CaTn}}$ slightly affected the predicted SCH (70ms, 76 ms, 100ms, 200ms) when control [TnC]_tot increased two-fold (Fig. 4C). Taken together, our numerical work and analyses suggest that the disease-linked changes in $k_{on}^{\mathit{CaTn}}$ (respectively in $K_D^{\mathit{CaTn}}=k_{\mathit{off}}^{\mathit{CaTn}}/k_{on}^{\mathit{CaTn}}$) and the alterations in [TnC]_tot level at low free [Ca²⁺]_i (SR activity disabled) alter the effective diffusion coefficient for free ( ${\text{Ca}}^{2+}(D_{Ca}^{\mathit{eff}})$) [8, 9]. The changes in $D_{Ca}^{\mathit{eff}}$ will affect local flow rates of membrane Ca²⁺ transporters and local Ca²⁺ trigger fluxes (d[Ca²⁺]_i/dt) controlling SR Ca²⁺-release, and ultimately the normal myocyte function [33].

3.2.1.2 Effects of changes in Ca²⁺ off-rate to TnC in whole Tn complex on local Ca²⁺ signals

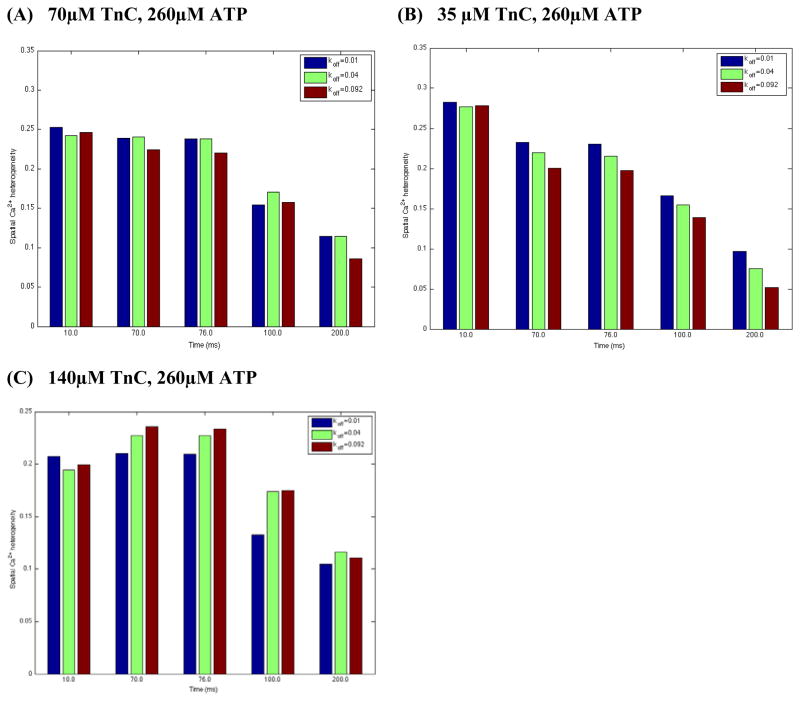
Kreutziger and colleagues introduced site-directed mutations in the N-terminus of rat TnC (L48Q TnC, I61Q TnC) that altered the control Ca²⁺ off-rate value [34]. Using stopped-flow spectroscopy they measured Ca²⁺ dissociation rates from whole troponin complex containing recombinant WT TnI and WT TnT and either WT TnC, L48Q TnC, or I61Q TnC (in the paper Ca²⁺ off-rates are denoted as $k_{\mathit{off}}^{\mathit{CaTn}},k_{\mathit{off}(L48Q)}^{\mathit{CaTn}}$ or $k_{\mathit{off}(I61Q)}^{\mathit{CaTn}}$, respectively). These experiments demonstrated that the mutations in TnC altered the basic $k_{\mathit{off}}^{\mathit{CaTn}}$ value, reducing it by 75% for L48Q TnC and increasing it by 3.2-fold for I61Q TnC. It is difficult, however, to derive an understanding from these studies how these site-directed mutations in TnC (e.g. altered $k_{\mathit{off}}^{\mathit{CaTn}},K_D^{\mathit{CaTn}}$ and $D_{Ca}^{\mathit{eff}}$) modulate the cytosolic Ca²⁺ dynamics that ultimately will affect the normal cell function. Here, we used our 3-D reaction-diffusion model to investigate this. Figure 5A shows that with 70 μM [TnC]_tot: (1) the both alterations in $k_{\mathit{off}}^{\mathit{CaTn}}$ enhanced SCH at t_{ICa – peak} (10ms); (2) at t_{ICa –max} (70ms), t_{[Ca²⁺]i–peak} (76ms) and t_200ms inflated $k_{\mathit{off}(I61Q)}^{\mathit{CaTn}}$ decreased SCH while no visible differences in SCH were found when the control $k_{\mathit{off}}^{\mathit{CaTn}}$ was reduced by 75% (L48Q Tn mutation); (3) at 100 ms the both alterations in $k_{\mathit{off}}^{\mathit{CaTn}}$ decreased SCH.

Figure 5.

Figure 5A–C. Estimated spatial Ca²⁺ heterogeneity index with respect to 75% decrease and 2.3-fold increase in WT Tn off-rate ( $k_{\mathit{off}}^{\mathit{CaTn}}=0.04/\text{ms}$, assuming basic $k_{on}^{\mathit{CaTn}}$ value of 0.04 μM⁻¹ms⁻¹ unchanged) in the absence of dye. L48Q Tn mutation - $k_{\mathit{off}(L48Q)}^{\mathit{CaTn}}=0.01/\text{ms}$. I61Q Tn mutation - $k_{\mathit{off}(I61Q)}^{\mathit{CaTn}}=0.092/\text{ms}$. In these sets of simulations the line-scan was positioned at 200nm away from the surface of the t-tubule, Ca²⁺ flux was heterogeneously distributed and the reference points were chosen to be the same as in Fig. 3.

The model also predicts that at t_ICa–peak the decrease in control TnC buffer capacity to 35 μM increased SCH while 140 μM [TnC]_tot decreased SCH for all TnC variants (Fig. 5A–C). In addition, Fig. 5B demonstrates that with 35 μM [TnC]_tot SCH decreased at the total [Ca²⁺]_i beyond 10 ms. The predicted changes in SCH beyond 10 ms with 140 μM[TnC]_tot are shown in Figure 5C. This set of simulations demonstrates that: (1) at 70ms and 76ms inflated $k_{\mathit{off}(I61Q)}^{\mathit{CaTn}}$ increased SCH while [Ca²⁺]_i was more uniformly distributed when $k_{\mathit{off}}^{\mathit{CaTn}}$ decreased (L48Q Tn mutation); (2) at 100 ms no visible differences in SCH were found when $k_{\mathit{off}}^{\mathit{CaTn}}$ was increased 2.3-fold (I61Q Tn mutation) while 75% drop in the basic $k_{\mathit{off}}^{\mathit{CaTn}}$ (L48Q Tn mutation) decreased SCH notably; (3) at 200 ms the both alterations in $k_{\mathit{off}}^{\mathit{CaTn}}$ tended to decrease the SCH. In summary, our results demonstrate that the mutation-linked changes in $k_{\mathit{off}}^{\mathit{CaTn}}$ (in $K_D^{\mathit{CaTn}}$ respectively) and the variations in [TnC]_tot levels alter control $D_{Ca}^{\mathit{eff}}$, thereby altering the local sarcolemmal fluxes, SR Ca²⁺ trigger fluxes and local [Ca²⁺]_i inside the cell with SR disabled. The model demonstrates also that the alterations in $k_{\mathit{off}}^{\mathit{CaTn}}$ may affect quite differently local Ca²⁺ distributions ([Ca²⁺]_i and d[Ca²⁺]_i/dt) with respect to those when control $k_{on}^{\mathit{CaTn}}$ is varied (compare Fig. 4 and Fig. 5).

In Kreutziger’s et al. experiment, $k_{\mathit{off}}^{\mathit{CaTn}}$ was determined for each $\text{Tn}(k_{\mathit{off}}^{\mathit{CaTn}}=0.0297/\text{ms};k_{\mathit{off}(L48Q)}^{\mathit{CaTn}}=0.0073/\text{ms};k_{\mathit{off}(I61Q)}^{\mathit{CaTn}}=0.067/\text{ms})$ by fitting fluorescence data (at 15°C) with exponential curves [34]. We then calculated SCH replacing the model $k_{\mathit{off}}^{\mathit{CaTn}}$ values (0.01/ms L48Q Tn, 0.04/ms WT Tn, 0.092/ms I61Q Tn) with the experimentally measured values. Yet only minor effects in predicted SCH were found with 70 μM[TnC]_tot (compare Fig. 5A and Fig. 6A).

Figure 6.

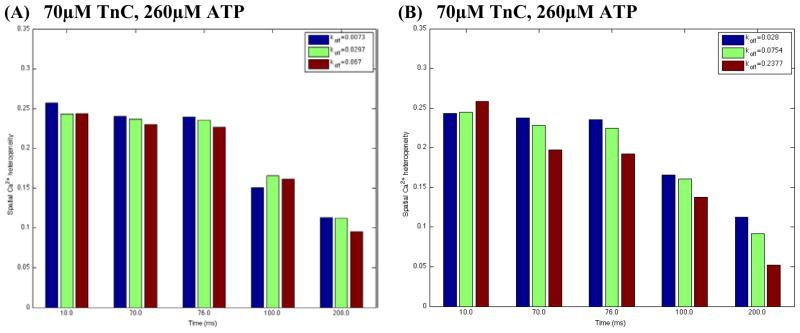
Estimated spatial Ca²⁺ heterogeneity index for all TnC variants in whole Tn complex (panel A) and reconstructed thin filaments (panel B) in the absence of dye. Panel A: $k_{\mathit{off}}^{\mathit{CaTn}}=0.0297/\text{ms},k_{\mathit{off}(L48Q)}^{\mathit{CaTn}}=0.0073/\text{ms},k_{\mathit{off}(I61Q)}^{\mathit{CaTn}}=0.067/\text{ms}$. Panel B: $k_{\mathit{off}}^{\mathit{CaTn}(TF)}=0.0754/\text{ms},k_{\mathit{off}(L48Q)}^{\mathit{CaTn}(TF)}=0.028/\text{ms},k_{\mathit{off}(I61Q)}^{\mathit{CaTn}(TF)}=0.2377/\text{ms}$. In this set of simulations: $k_{on}^{\mathit{CaTn}}$value was 0.04 μM⁻¹ms⁻¹; Ca²⁺ flux was heterogeneously distributed; the line-scan positioned at 200nm from the surface of the t-tubule; reference points along the scaned line were chosen to be the same as in Fig. 3.

3.2.1.3 Effects of changes in Ca²⁺ off-rate to TnC in reconstructed thin filaments on local Ca²⁺ signals

Recently, Kreutziger’s et al. measured also the off-rates in reconstructed thin filaments with WT or mutant whole TnC, WT Tm, and WT actin (in the paper these Ca²⁺ off-rates are denoted as $k_{\mathit{off}}^{\mathit{CaTn}(TF)},k_{\mathit{off}(L48Q)}^{\mathit{CaTn}(TF)}$, or $k_{\mathit{off}(I61Q)}^{\mathit{CaTn}(TF)}$, respectively), [34]. They found 2.2–3.4-fold increase in off-rates for all TnC variants vs. isolated whole Tn-complex. The relative effect of the mutations in TnC remained almost the same as for whole Tn, such that $k_{\mathit{off}}^{\mathit{CaTn}(TF)}$ was reduced by 63% for L48Q (vs. 75% in isolated Tn-complex) and increased by 3.2-fold for I61Q Tn in the thin filaments. It remains unclear, however, whether the changes in off-rates in reconstructed thin filaments would have a different effect on Ca²⁺ dynamics relative to those predicted with the isolated whole Tn-complex. Our numerical results demonstrate that with 70 μM[TnC]_tot visible differences in the calculated SCH-s compared to those in isolated whole Tn-complex were found. At I_Ca peak (10 ms) ~2.5-fold increase in WT variant had little or no effect on SCH, ~3.85 fold increase in L48Q variant decreased SCH while ~3.55 fold increase in I61Q variant increased SCH (Fig. 6A vs. Fig. 6B).

Figures 5–6 also show that at the moment of I_Ca closing (70ms) and at [Ca²⁺]_i peak (76ms) SCH decreased for WT and I61Q variants vs. the whole Tn-complex. Model also predicts that: (1) at $t_{100ms}\text{SCH}(k_{\mathit{off}}^{\mathit{CaTn}})~\text{SCH}(k_{\mathit{off}}^{\mathit{CaTn}(TF)}),\text{SCH}(k_{\mathit{off}(L48Q)}^{\mathit{CaTn}})<\text{SCH}(k_{\mathit{off}(L48Q)}^{\mathit{CaTn}(TF)})$ and $\text{SCH}(k_{\mathit{off}(I61Q)}^{\mathit{CaTn}})>\text{SCH}(k_{\mathit{off}(I61Q)}^{\mathit{CaTn}(TF)})$; (2) at $t_{200ms}\text{SCH}(k_{\mathit{off}}^{\mathit{CaTn}})>\text{SCH}(k_{\mathit{off}}^{\mathit{CaTn}(TF)}),\text{SCH}(k_{\mathit{off}(L48Q)}^{\mathit{CaTn}})~\text{SCH}(k_{\mathit{off}(L48Q)}^{\mathit{CaTn}(TF)})$ and $\text{SCH}(k_{\mathit{off}(I61Q)}^{\mathit{CaTn}})>\text{SCH}(k_{\mathit{off}(I61Q)}^{\mathit{CaTn}(TF)})$. These findings suggest that the use of whole Tn off-rates vs. reconstructed thin filaments off-rates into cardiac cellular and sub-cellular models may alter the predicted control and disease-linked Ca²⁺ transporter rates, Ca²⁺ trigger fluxes for SR release and local Ca²⁺ signals.

In summary, our studies provide a foundation for a more comprehensive understanding of signaling transduction at molecular and sub-cellular scales. Our studies also illustrate the importance of improved experimental measurements of Ca²⁺ buffering kinetics and of complementary theoretical estimates of Ca²⁺ buffer reaction rates. Together, this will lead to a better understanding of Ca²⁺ signaling in heart under normal or pathological conditions.

4. Conclusions

In this paper, we applied the SMOL package to molecular-level reaction kinetics of ACh and cellular-level Ca²⁺ dynamics. Our data demonstrate that a continuum-based description of ion diffusion, the Smoluchowski equation, captures molecular-level details impacting reaction rates. This suggests that alternative descriptions of electrodynamics, such as the Poisson-Nernst-Planck equation, could further improve our estimates. These data also demonstrate progress toward sub-cellular modeling of heart, in which buffering dynamics are handled at a molecular level. Future applications of SMOL will feature spatially coupled 3-D structural and functional models of ventricular cardiac myocytes with (1) realistic sub-cellular anatomical structures, such as Ca²⁺-signaling micro-domains and cell organelles; (2) sarcoplasmic reticulum fluxes via ryanodine receptors (RyR) and the SERCA pump; and (3) spatial and temporal scales spanning from single channel ion fluxes to tension development in actin and myosin filaments. These developments would facilitate modeling excitation-contraction coupling influenced by mutations, phosphorylation, and alterations in protein expression. Other molecular-level approaches that could further benefit excitation-contraction modeling include analysis of nucleotide-activated conformational dynamics [35], kinase activity [36], channel gating [37] and structure-based drug design [38]. In concert, these approaches constitute a prototypical workflow for patient-specific modeling and therapies.

APPENDIX

Equations describing total Ca²⁺ flux (J_Caflux), L-type Ca²⁺ current (J_Ca), Na⁺/Ca²⁺ exchanger flux (J _NCX), and Ca²⁺ leak current (J_M–leak) throughout the t-tubule and external membrane:

$$J_{{Ca}_{\mathit{flux}}}=J_{Ca}+J_{\mathit{NCX}}+J_{M-\mathit{leak}}$$ (9)

$$I_{Ca}(t)=I_{{Ca}_o}f(t)$$ (10)

$$f(t)=\{\begin{array}{ll}1.14380t\hfill & 0<t<t_a\hfill \\ 1.73189+5.11444e^{-\frac{t}{30.31164}}\hfill & t_a\le t<t_b\hfill \\ 0\hfill & t\ge t_b\hfill \end{array}$$ (11)

$$I_{\mathit{NCX}}=g_{\mathit{NCX}}\frac{e^{\eta VF/RT}{[{Na}^{+}]}_i^3{[{Ca}^{2+}]}_e-e^{(\eta -1)VF/RT}{[{Na}^{+}]}_e^3{[{Ca}^{2+}]}_i}{(k_{m,Na}^3+{[{Na}^{+}]}_e^3)(k_{m,Ca}+{[{Ca}^{2+}]}_e)(1+k_{\mathit{sat}}{e}^{(\eta -1)VF/RT})}$$ (12)

$$I_{M-\mathit{leak}}=g_{M_{\_}\mathit{leak}}({[{Ca}^{2+}]}_e-{[{Ca}^{2+}]}_i)$$ (13)

Flux parameter values were estimated or taken from the literature (see Table 1). In this study, the Ca²⁺ leak is not actually a particular “leak protein”. The Ca²⁺ leak was included and adjusted so that at rest Ca²⁺ influx via Ca²⁺ leak to match Ca²⁺ efflux via NCX thus no net movement across the cell membrane to occur.

Table 1.

Membrane calcium fluxes parameters

Symbol	Definition	Value	Ref.
L-type Ca2+ current
ICao	Constant	1	[9]
ta	Constant	4 ms	[40]
tb	Constant	70 ms	[40]
Na+/Ca2+ exchange current
[Na+]e	Extracellular Na+ concentration	140 mM	[28]
[Na+]i	Resting Na+ concentration	10 mM	[28]
gNCX	Pump rate of NCX	38.5 μM ms−1	[41]
η	Voltage dependence of NCX control	0.35	[41]
km,Na	Na+ half saturation of NCX	87.5 mM	[41]
km,Ca	Ca2+ half saturation of NCX	1380 μM	[41]
ksat	Low potential saturation factor of NCX	0.1	[41]
Membrane Ca2+leak
gM_ leak	Conductance	3.4e-6 μM mV−1ms−1	Estimated

In the model, each current density (I_i) was converted to Ca²⁺ flux (J_i) by using the experimentally suggested surface to volume ratio ( $\frac{C_m}{V_{\mathit{cell}}}~8.8\text{pF}/\text{pL}$) in adult rat ventricular myocytes [39]:

$$J_i=\left(\frac{1}{2F}\frac{C_m}{V_{\mathit{cell}}}\right)I_i$$ (14)

The voltage-clamp protocol (holding potential –50mV, electric pulse of 10mV for 70ms) and whole-cell L-type Ca²⁺ current were derived from Zahradnikova et al. data with the blocked SR activity [40].