A Unifying Mathematical Framework for Genetic Robustness, Environmental Robustness, Network Robustness and their Tradeoff on Phenotype Robustness in Biological Networks Part II: Ecological Networks

Abstract

In ecological networks, network robustness should be large enough to confer intrinsic robustness for tolerating intrinsic parameter fluctuations, as well as environmental robustness for resisting environmental disturbances, so that the phenotype stability of ecological networks can be maintained, thus guaranteeing phenotype robustness. However, it is difficult to analyze the network robustness of ecological systems because they are complex nonlinear partial differential stochastic systems. This paper develops a unifying mathematical framework for investigating the principles of both robust stabilization and environmental disturbance sensitivity in ecological networks. We found that the phenotype robustness criterion for ecological networks is that if intrinsic robustness + environmental robustness ≦ network robustness, then the phenotype robustness can be maintained in spite of intrinsic parameter fluctuations and environmental disturbances. These results in robust ecological networks are similar to that in robust gene regulatory networks and evolutionary networks even they have different spatial-time scales.

Introduction

In the last two decades, robust stabilization and noise filtering theories have been developed by control engineers in order to improve the reliability and performance of control systems. In previous papers,^1–3 the network robustness and network sensitivity of gene regulatory networks and evolutionary networks have been discussed from a nonlinear, stochastic systems point of view. In these nonlinear biological networks, many local stable equilibrium points (phenotypes) exist. It has been found that if a network can confer enough intrinsic robustness to tolerate intrinsic parameter fluctuations, to buffer genetic mutations and resist environmental disturbances in gene regulatory networks or evolutionary networks, then the existing phenotype of these networks can be maintained despite intrinsic parameter fluctuations, genetic mutations and environmental disturbances. In most ecosystems, phenotype changes of ecological networks caused by losses of biodiversity may come from habitat destruction, alien species introduction, climate change, and pollution.^4,5 Phenotype changes are likely to reduce not only the number of species but also the complexity of the ecological network and the function of the ecosystem. To maintain a pre-existing phenotype, the ecological networks, like food webs, should be more robust to bear random or selective removal of species in the trophic links. In this study, results will be extended from gene regulatory networks and evolutionary networks at the molecular level to ecological networks on a large scale, while considering the compartment effect of habitats.

Darwin used the metaphor of a ‘tangled bank’ to describe the complex interactions between species. All interactions between species can be visualized as ecological networks in which species are linked together, either directly or indirectly, through intermediate species.⁶ Ecological networks, although complex, have well-defined patterns that both illuminate the ecological mechanisms underlying them and promise a better understanding of the relationship between complex and ecological stability.^7,8 Ecological research has widely demonstrated that community fragility is far from being understood. It is commonly accepted that community fragility and persistence are related to the way in which ecological communities are structured, specifically to the distribution of trophic links throughout the community.^8,9 Nevertheless, both the scarcity of high-quality data and lack of methods suitable for a detailed analysis of the complexity of ecological networks result in the lack of a unified picture of community fragility and persistence.¹⁰ In recent years, some topological features, the so-called “small world” behavior and “scale-free” distributions of links have been applied to ecological networks for examining ecosystem stability against different types of species loss.⁸ Although ecological networks are generally not small-world, scale-free networks, this topology is consistent with patterns found within those classes of networks.¹¹ In general, increasing biodiversity increases the likelihood that an ecosystem will have, first, species that will respond differently under variable environmental conditions and perturbations, and second, functional redundancy; that is, species that are capable of functionally replacing extinct species. The higher levels of biodiversity present in a non-fragmented food web might support several ecosystem functions that a fragmented food web would not manage.¹² High biodiversity also reduces the probability of secondary extinctions.¹³ An analysis considering interaction strengths among species would be very useful in confirming whether highly connected species play a stabilizing role in ecosystems, but early studies provide little or no information on the strength of trophic links because identifying strength of trophic links is difficult. Recently, some analyses based on predator-to-prey interactions propose that body size ratio can predict trophic strength. The larger the ratio, the stronger the interaction,^14,15 which can link the food web to the relationship between body size and numerical abundance for ecological network analysis.¹⁶ As we know, ecological networks can be very robust against random removals of species, but can be extremely fragile when selective attacks are used.^5,17 These further models involving species removal according to criteria other than the most-connected species would help establish a more global view of the effects of human-driven disturbances.¹² In this study, nonlinear stochastic partial differential systems will be employed to describe ecological networks under intrinsic perturbations and environmental disturbances. The robust stabilization problem of large-scale ecological networks will be discussed with consideration of the compartment effect of habitat. Robust stabilization (persistence) and environmental sensitivity (community fragility) will be investigated from a systematic perspective. The finite difference scheme will be employed to treat the species diffusion operation for easy estimation of network sensitivity and network robustness of ecological networks in a habitat.

To measure the network sensitivity of an ecological network relies on solving a Hamilton Jacobin integral inequality (HJII)-constrained optimization problem. Based on the HJII, we could find that if the network robustness can confer intrinsic robustness to tolerate intrinsic parameter fluctuations and environmental robustness to resist the environmental disturbances simultaneously, then the phenotype of ecological network could be maintained in spite of intrinsic parameter fluctuations and environmental disturbances. The framework of phenotype robustness criterion in an ecological network is similar to that of the gene regulatory network and evolutionary network at the molecular level. Moreover, the tradeoff between network robustness, intrinsic robustness and environmental robustness are also found to be the same at different biological levels from gene regulatory networks and evolutionary networks to ecological networks.

However, it is still very difficult to solve HJII for phenotype robustness criterion in order to discuss the tradeoff between network robustness, intrinsic robustness and environmental robustness in ecological networks. In this study, the global linearization technique,¹ finite difference scheme and spatial state space method^18–20 are employed to transform the HJII-constrained optimization problem for network sensitivity to an equivalent linear matrix inequalities (LMIs)-constrained optimization problem, which can be easily solved with the help of LMI toolbox in Matlab.²¹ Then the phenotype robustness criterion of the ecological system can be discussed from the local linearized system point of view. If the eigenvalues of local linearized ecological systems are in the farther left hand complex domain (more stable), then the ecological network will have more network robustness. Finally, to verify the existence of phenotype robustness criterion and to estimate the network sensitivity of a nonlinear stochastic partial differential ecosystem, an in silico example is given to illustrate the tradeoff between the network robustness, intrinsic robustness and environmental robustness in an ecological network.

Tradeoff between Intrinsic Robustness, Environmental Robustness and Network Robustness in Ecological Biology

Examples of robust biological systems are found on many scales, from biological genetic networks to ecological networks. In previous papers,^1–3,22 we have discussed the robust stabilization problem of gene regulatory networks and evolutionary networks at the molecular level. In this section, the robust stabilization problem of a large-scale ecological network will be discussed with consideration of the compartment effect of habitat.

Consider the following ecological network in the spatial domain:^8–10,23

$$\begin{array}{ll}dx\left(y,t\right)=\hfill & \left(N\left(x\left(y,t\right)\right)+v\left(y,t\right)+\kappa \left(\tilde{x}\left(y,t\right)\right){\nabla }^{2}x\left(y,t\right)\right)dt\hfill \\ \hfill & +\sum _{i=1}^L\mathrm{\Delta }{N}_i\left(x\left(y,t\right)\right)d{w}_i\left(y,t\right),\hfill \\ y\in U\hfill & \hfill \end{array}$$ (1)

where the network state x(y,t) = [x₁(y,t), x₂(y,t), … x_n(y,t)] denotes the number of different species or population; y = [y₁,y₂]^T ∈ R² denotes the location of two-dimensional spatial domain in habitat U; N(x(y,t)) denotes the interactions among these species; $\sum _{i=1}^L\mathrm{\Delta }{N}_i\left(x\left(y,t\right)\right)d{w}_i\left(y,t\right)$ denotes the intrinsic perturbations due to stochastic parameter fluctuations from L random sources, for example, the species loss and the change of species richness from direct trophic links; v(y,t) denotes the environmental disturbance, for example, the invasion of new species and the change of species richness from indirect trophic links due to pollution; the habitat U denotes the total multi-species interaction domain, ie, the living area of interacting species, and the diffusion operator is denoted as diffusive spatial dispersal in the two-dimensional spatial domain of habitat U as follows:

$${\nabla }^{2}x\left(y,t\right)=\frac{{\partial }^{2}x\left(y,t\right)}{\partial y_1^2}+\frac{{\partial }^{2}x\left(y,t\right)}{\partial y_2^2},y=\left[\begin{array}{c}{y}_1\\ y_2\end{array}\right]\in U$$

Then we want to discuss the robust stabilization problem of the nonlinear stochastic partial differential ecological system in (1). Suppose the origin is shifted to the equilibrium point (phenotype) of interest, then (1) is modified as follows:^18,24

$$\begin{array}{ll}d\tilde{x}(y,t)=\hfill & (N(\tilde{x}(y,t))+v(y,t)\hfill \\ \hfill & +\kappa (\tilde{x}(y,t)){\nabla }^2\tilde{x}(y,t)dt\hfill \\ \hfill & +\sum _{i=1}^L\mathrm{\Delta }{N}_i(\tilde{x}(y,t))d{w}_i(y,t),\hfill \\ y\in U\hfill & \hfill \end{array}$$ (2)

In general, it is still very difficult to estimate the network sensitivity of nonlinear stochastic partial differential ecological networks in (2) to environmental disturbances directly. We will estimate its upper bound, ie, its network sensitivity level, and then decrease this upper bound to approach the network sensitivity indirectly. In this situation, the environmental disturbance sensitivity level for the nonlinear stochastic partial differential ecological network in (1) is to consider the total multi-species interaction domain U as follows:

$$\begin{array}{l}\frac{E{\int }_U{\int }_0^{\infty }{\tilde{x}}^T\left(y,t\right)\tilde{x}\left(y,t\right)dtdy}{E{\int }_U{\int }_0^{\infty }{v}^T\left(y,t\right)v\left(y,t\right)dtdy}\le {\rho }^2\\ or\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}E{\int }_U{\int }_0^{\infty }{\tilde{x}}^T\left(y,t\right)\tilde{x}\left(y,t\right)dtdy\le {\rho }^2\\ E{\int }_U{\int }_0^{\infty }{v}^T\left(y,t\right)v\left(y,t\right)dtdy\end{array}$$ (3)

in the case x̃(y, 0) = 0. The physical meaning in (3) is that the total effect of environmental disturbances on the phenotype in the spatial-temporal domain is smaller than the disturbance sensitivity level ρ. If the intrinsic parameter fluctuations and extrinsic disturbances are non-random, then the expectation E(•) in (3) could be neglected.

Remark 1: (a) Given the ecological network structure (or the trophic links of food webs), the stochastic processes $\sum _{i=1}^L\mathrm{\Delta }{N}_i\left(\tilde{x}\left(y,t\right)\right){\mathit{dw}}_i\left(y,t\right)$ and v(y,t) are used to represent the effects of the intrinsic perturbations and extrinsic invasions on species richness, respectively, ie, strength changes of trophic links in the food web and loss or gain of particular species in the ecological network. To represent the selective changes in species richness, we can take it as a special case by simply setting the unselected elements in the random vector variables dw_i(y,t) and v(y,t) with different mean and zero variances to represent the random strong or weak perturbations of invasion on trophic links. (b) If the initial condition x̃(y, 0) ≠ 0, then the network sensitivity level in (3) should be modified as:

$$\begin{array}{l}E{\int }_U{\int }_0^{\infty }{\tilde{x}}^T\left(y,t\right)\tilde{x}\left(y,t\right)dtdy\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\le EV\left(\tilde{x}\left(y,0\right)\right)+{\rho }^{2}E{\int }_U{\int }_0^{\infty }{v}^T\left(y,t\right)v\left(y,t\right)dtdy\end{array}$$ (4)

for some Lyapunov positive function V(•) > 0.

According to the spatial-temporal environmental disturbance sensitivity in (3), we get the following phenotype robustness (community stability) criterion for the ecological system in (1).

Proposition 1: If the following HJII holds for some positive definite function V (x̃(y, t)) > 0

$${\int }_U\left[\begin{array}{l}{\left(\frac{\partial V\left(\tilde{x}\left(y,t\right)\right)}{\partial \tilde{x}\left(y,t\right)}\right)}^T\left(N\left(\tilde{x}\left(y,t\right)\right)+\kappa \left(\tilde{x}\left(y,t\right)\right){\nabla }^2\tilde{x}\left(y,t\right)\right)+\frac{1}{2}\sum _{i=1}^L\mathrm{\Delta }{N}_i^T\left(\tilde{x}\left(y,t\right)\right)\frac{{\partial }^{2}V\left(\tilde{x}\left(y,t\right)\right)}{\partial {\tilde{x}}^2\left(y,t\right)}\mathrm{\Delta }{N}_i\left(\tilde{x}\left(y,t\right)\right)\hfill \\ +\frac{1}{4{\rho }^2}{\left(\frac{\partial V\left(\tilde{x}\left(y,t\right)\right)}{\partial \tilde{x}\left(y,t\right)}\right)}^T\left(\frac{\partial V\left(\tilde{x}\left(y,t\right)\right)}{\partial \tilde{x}\left(y,t\right)}\right)+{\tilde{x}}^T\left(y,t\right)\tilde{x}\left(y,t\right)\hfill \end{array}\right]dy\le 0$$ (5)

then the intrinsic parameter fluctuations $\sum _{i=1}^L\mathrm{\Delta }{N}_i\left(x\left(y,t\right)\right){\mathit{dw}}_i\left(y,t\right)$ in the nonlinear stochastic partial differential ecological network in (1) can be tolerated, which means the phenotype of the ecological network will be still robustly stable under intrinsic parameter fluctuations, and the effect of environmental disturbance v(y,t) on the network state x(y,t) can also be attenuated below a network sensitivity level ρ in (3). In other words, phenotype robustness (community stability) of the nonlinear stochastic partial differential ecological network is maintained under these intrinsic parameter fluctuations and environmental disturbances if HJII in (5) has a positive solution V (x̃(y,t)). The proof of Proposition 1 is included in Appendix A.

Remark 2: (i) If the following HJI holds for all points of y in habitat U

$$\begin{array}{l}{\left(\frac{\partial V\left(\tilde{x}\left(y,t\right)\right)}{\partial \tilde{x}\left(y,t\right)}\right)}^T\left(N\left(\tilde{x}\left(y,t\right)\right)+\kappa \left(\tilde{x}\left(y,t\right)\right){\nabla }^2\tilde{x}\left(y,t\right)\right)+\frac{1}{2}\sum _{i=1}^L\mathrm{\Delta }{N}_i^T\left(\tilde{x}\left(y,t\right)\right)\frac{{\partial }^{2}V\left(\tilde{x}\left(y,t\right)\right)}{\partial {\tilde{x}}^2\left(y,t\right)}\mathrm{\Delta }{N}_i\left(\tilde{x}\left(y,t\right)\right)\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+\frac{1}{4{\rho }^2}{\left(\frac{\partial V\left(\tilde{x}\left(y,t\right)\right)}{\partial \tilde{x}\left(y,t\right)}\right)}^T\left(\frac{\partial V\left(\tilde{x}\left(y,t\right)\right)}{\partial \tilde{x}\left(y,t\right)}\right)+{\tilde{x}}^T\left(y,t\right)\tilde{x}\left(y,t\right)\le 0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall y\in U\end{array}$$ (6)

then the phenotype robustness criterion in (5) also holds and the phenotype of the nonlinear stochastic ecological network in (1) is robust. However, the HJI is more conservative than HJII in (5) because it needs to hold for every y ∈ U. (ii) If the diffusion operator ∇²x̃(y, t) is neglected in the nonlinear stochastic ecological system in (1), then the phenotype robustness criterion of HJII in (5) can be reduced to a simplified phenotype robustness criterion of a conventional biological network in systems biology without consideration of compartment.¹

The network sensitivity ρ₀ of nonlinear stochastic ecological networks can be obtained by solving the following constrained optimization:

$$\begin{array}{l}{\rho }_o=\text{min}\hspace{0.17em}\rho \\ \text{subject}\hspace{0.17em}\text{to}\hspace{0.17em}\text{HJII}\hspace{0.17em}\text{in}\hspace{0.17em}\left(5\right)\end{array}$$ (7)

According to the above network sensitivity ρ₀, the phenotype robustness (community stability) criterion in (5) for the nonlinear stochastic ecological network in habitat U can be modified as the following equivalent criterion:

$$\begin{array}{c}\underset{\text{int}\mathit{rinsic}\hspace{0.17em}\mathit{robustness}}{\underbrace{\frac{1}{2}\sum _{i=1}^L{\int }_U\mathrm{\Delta }{N}_i^T\left(\tilde{x}\left(y,t\right)\right)\frac{{\partial }^{2}V\left(\tilde{x}\left(y,t\right)\right)}{\partial {\tilde{x}}^2\left(y,t\right)}\mathrm{\Delta }{N}_i\left(\tilde{x}\left(y,t\right)\right)dy+}}\underset{\mathit{environmental}\hspace{0.17em}\mathit{robustness}}{\underbrace{\frac{1}{4{\rho }_0^2}{\int }_U{\left(\frac{\partial V\left(\tilde{x}\left(y,t\right)\right)}{\partial \tilde{x}\left(y,t\right)}\right)}^T\left(\frac{\partial V\left(\tilde{x}\left(y,t\right)\right)}{\partial \tilde{x}\left(y,t\right)}\right)+{\tilde{x}}^T\left(y,t\right)\tilde{x}\left(y,t\right)dy}}\\ \underset{\mathit{network}\hspace{0.17em}\mathit{robustness}}{\underbrace{\le -{\int }_U{\left(\frac{\partial V\left(\tilde{x}\left(y,t\right)\right)}{\partial \tilde{x}\left(y,t\right)}\right)}^T\left(N\left(\tilde{x}\left(y,t\right)\right)+\kappa \left(\tilde{x}\left(y,t\right)\right){\nabla }^2\tilde{x}\left(y,t\right)\right)dy}}\end{array}$$ (8)

where the first term and the second term denote the effect of intrinsic parameter fluctuations and environmental disturbances on the network stability of ecological networks in the total habitat U from the covariant point of view, respectively. It can be seen from the phenotype robustness criterion in (8) that if the network robustness of nonlinear stochastic ecological networks can confer simultaneously intrinsic robustness for tolerating spatio-temporal intrinsic parameter fluctuations and environmental robustness for resisting spatio-temporal environmental disturbances in habitat U, then the phenotype of the nonlinear stochastic ecological network (community stability) is maintained. In other words, the species of the ecological system still persists at the stable equilibrium point in the phenotypic landscape despite intrinsic parameter fluctuations and environmental disturbances in habitat U. If the diffusion operator ∇²x̃(y, t) of the nonlinear stochastic system is neglected in (1), then the integration around the spatial domain of the habitat U can be neglected, and the phenotype robustness criterion in (8) is reduced to a simplifier form without integration over U.

To maintain proper functions of an ecosystem that can produce enough foods or services for species, enough network robustness should be ensured for the ecological network in face of intrinsic parameter fluctuations, such as changes of species from trophic links, and environmental disturbances, such as the invasion of new species or pollution from human activities. In order to increase the network robustness on the right-hand side of (8) so as to ensure robust community stability of the ecological system in habitat U, negative feedback and negative (inward) diffusion are appealing.^12,17 Further, a power law distribution of interactions among species with small-world behavior and fast responses to environmental changes is also a favored network structure for an ecological network to efficiently examine the robust ecosystem stability against different types of species and the network sensitivity in response to environmental disturbances.⁸ Species redundancy is useful for decreasing intrinsic parameter fluctuations to maintain the community stability of ecological networks.²⁵ In general, increasing biodiversity will increase network robustness of an ecosystem against different types of species loss under variable environmental conditions and disturbances.⁸ Functional redundancy, meaning species being capable of functionally replacing extinct species, is useful for buffering the intrinsic parameter fluctuations and can therefore increase the intrinsic robustness of ecological networks.

If the ecological network in (1) does not have enough network robustness to guarantee the phenotype robustness criterion in (8), the community stability of ecological system cannot be maintained. In this situation, in order to maintain the phenotype at x_e, some regulation control is needed to improve the network robustness of the ecological network as follows:

$$d\tilde{x}\left(y,t\right)=\left(N\left(\tilde{x}\left(y,t\right)\right)+K\left(\tilde{x}\left(y,t\right)\right)+v\left(y,t\right)+\kappa \left(\tilde{x}\left(y,t\right)\right){\nabla }^2\tilde{x}\left(y,t\right)\right)dt+\sum _{i=1}^L\mathrm{\Delta }{N}_i\left(\tilde{x}\left(y,t\right)\right)d{w}_i\left(y,t\right),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}y\in U$$ (9)

where u(y, t) = K (x̃(y, t)) denotes the state feedback control design for improving network robustness of the ecological network. We suppose that the perturbation of K (x̃(y, t)) can be neglected. After introducing state feedback control, the phenotype robustness criterion in (8) should be modified as:

$$\begin{array}{c}\underset{\text{int}\mathit{rinsic}\hspace{0.17em}\mathit{robustness}}{\underbrace{\frac{1}{2}\sum _{i=1}^L{\int }_U\mathrm{\Delta }{N}_i^T\left(\tilde{x}\left(y,t\right)\right)\frac{{\partial }^{2}V\left(\tilde{x}\left(y,t\right)\right)}{\partial {\tilde{x}}^2\left(y,t\right)}\mathrm{\Delta }{N}_i\left(\tilde{x}\left(y,t\right)\right)dy+}}\underset{\mathit{environmental}\hspace{0.17em}\mathit{robustness}}{\underbrace{\frac{1}{4{\rho }_0^2}{\int }_U{\left(\frac{\partial V\left(\tilde{x}\left(y,t\right)\right)}{\partial \tilde{x}\left(y,t\right)}\right)}^T\left(\frac{\partial V\left(\tilde{x}\left(y,t\right)\right)}{\partial \tilde{x}\left(y,t\right)}\right)+{\tilde{x}}^T\left(y,t\right)\tilde{x}\left(y,t\right)dy}}\\ \le \underset{\mathit{network}\hspace{0.17em}\mathit{robustness}}{\underbrace{-{\int }_U{\left(\frac{\partial V\left(\tilde{x}\left(y,t\right)\right)}{\partial \tilde{x}\left(y,t\right)}\right)}^T\left(N\left(\tilde{x}\left(y,t\right)\right)+K\left(\tilde{x}\left(y,t\right)\right)+\kappa \left(\tilde{x}\left(y,t\right)\right){\nabla }^2\tilde{x}\left(y,t\right)\right)dy}}\end{array}$$ (10)

That is, the robust ecological network design in (9) functions to specify the state feedback control u(y, t) = K (x̃(y, t)) in order to make network robustness in the right-hand side of (10) as large a value as possible. This will help to override the intrinsic robustness and environmental robustness of the ecological network.

In general, it is not easy to solve HJII in (5) or (8) for the phenotype robustness criterion of the nonlinear stochastic ecological network in (1). The nonlinear stochastic ecological network in (1) can be represented by the interpolation of local linearized systems according to the global linearization method as follows:

$$\begin{array}{l}d\tilde{x}\left(y,t\right)\\ =\sum _{i=1}^M{\alpha }_i\left(\tilde{x}\left(y,t\right)\right)\left\{\begin{array}{l}\left[N_i\tilde{x}\left(y,t\right)+v\left(y,t\right)+{\kappa }_i{\nabla }^2\tilde{x}\left(y,t\right)\right]dt\hfill \\ +\sum _{j=1}^L\mathrm{\Delta }{N}_{ji}\tilde{x}\left(y,t\right)d{w}_j\left(y,t\right)\hfill \end{array}\right\}\end{array}$$ (11)

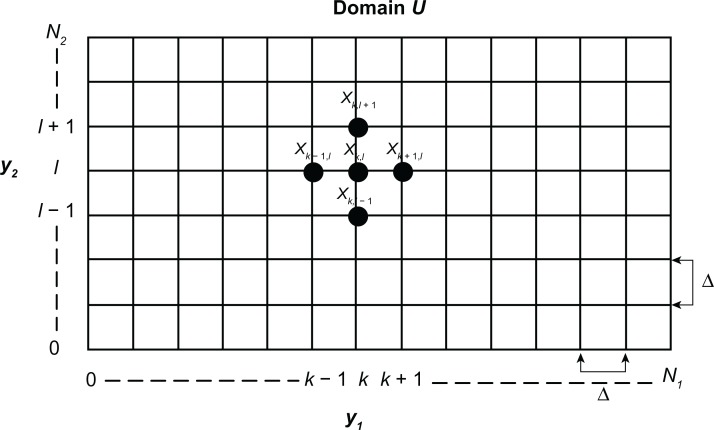
where the interpolation bases α_i (x̃(y, t)) satisfies 0 ≤ α_i (x̃(t)) ≤ 1 and $\sum _{i=1}^M{\alpha }_i\left(\tilde{x}\left(t\right)\right)=1$. However, even with the global linearization model in (11), it is still not easy to get a simple phenotype robustness criterion for the estimation of network sensitivity or network robustness of the nonlinear stochastic ecological system due to the differential diffusion operator ∇²x̃(y, t). In this situation, the finite difference scheme is employed to approximate the partial differential diffusion operator ∇²x̃(y, t) in (11) for investigating the network robustness criterion of the nonlinear stochastic ecological network. Consider a typical mesh of spatial domain of ecological system as shown in Figure 1.

Figure 1.

Finite difference grids of a two-dimensional space y = [y₁,y₂] with the uniform grid space Δ on the spatial domain of habitat U in an ecological system.

The state x(y,t) is represented by x_k,l (t) ∈ Rⁿ at the grid node y_k,l (y₁ = kΔ, y₂ = lΔ, where k = 1, … N₁ and l = 1, … N₂, ie, x(y,t) |_y=yk,l ≡ x_k,l(t) and Δ denotes the grid space. At the grid point y_k,l, the central difference approximation for the partial differential operator can be written as follows:¹⁸

$$\begin{array}{l}{\kappa }_i{\nabla }^{2}x\left(y,t\right)\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\cong {\kappa }_i\frac{x_{k+1,l}\left(t\right)+x_{k-1,l}\left(t\right)-2x_{k,l}\left(t\right)}{{\mathrm{\Delta }}^2}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+{\kappa }_i\frac{x_{k,l+1}\left(t\right)+x_{k,l-1}\left(t\right)-2x_{k,l}\left(t\right)}{{\mathrm{\Delta }}^2}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}={\kappa }_i\frac{1}{{\mathrm{\Delta }}^2}\left[\begin{array}{l}{x}_{k+1,l}\left(t\right)+x_{k-1,l}\left(t\right)+x_{k,l+1}\left(t\right)\hfill \\ +x_{k,l-1}\left(t\right)-4x_{k,l}\left(t\right)\hfill \end{array}\right]\\ \triangleq {\kappa }_i{T}_{k,l}{x}_{k,l}\left(t\right)\end{array}$$ (12)

where T_k,l denotes the difference operator at the grid point y_k,l. If the grid points in the spatial domain of habitat U are dense enough, then the approximation error between the differential operator ∇² and the difference operator T_k,l in the above will be small enough.

Remark 3: The local truncation errors O_k,l (Δ) = κ_i∇²x̃ (y_k,l, t) – κ_iT_k,lx_k,l(t) that depend on the size of grid space Δ can be omitted. If the grid node points in a spatial domain are dense enough, then the truncation error will be small enough.²⁶ Because, in ecological community, the finite difference approach may capture enough realistic aspects of the ecological system for investigation, we will neglect the local truncation errors in the following network robustness analysis.

Following this, according to the finite difference approximation in (12), the nonlinear stochastic partial differential ecological network in (11) can be represented by the following stochastic finite difference ecological system:

$$\begin{array}{l}d{\tilde{x}}_{k,l}\left(y,t\right)=\sum _{i=1}^M{\alpha }_i\left(\tilde{x}\left(y,t\right)\right)\left[\begin{array}{l}{N}_i{\tilde{x}}_{k,l}\left(t\right)dt+{\kappa }_i{T}_{k,l}{\tilde{x}}_{k,l}\left(t\right)dt\hfill \\ +\sum _{j=1}^L\mathrm{\Delta }{N}_{ji}{\tilde{x}}_{k,l}\left(t\right)d{w}_{j,k,l}\left(t\right)\hfill \end{array}\right]\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+v_{k,l}\left(t\right)dt\end{array}$$ (13)

To simplify the representation of stochastic finite difference ecological system in (13), we definite a spatial state vector x̃(t) for collecting the state variable x̃_k,l (t) at all grid nodes in Figure 1. For the Dirichlet boundary condition,¹⁸ the values of x̃_k,l (t) 0 at the boundary are fixed; for example, x̃_k.l (t) 0 on ∂U, we have x̃_k,l(t) = 0 at k = 0, N₁ + 1 or l = 0, N₂ + 1. Therefore, the spatial state vector x̃(t) ∈ R^nN for state variables of an ecological system at all grid notes is defined as follows:^18,19

$$\tilde{x}\left(t\right)={\left[\begin{array}{l}{\tilde{x}}_{11}^T\left(t\right),\dots ,{\tilde{x}}_{k1}^T\left(t\right),\dots ,{\tilde{x}}_{N_{1}1}^T\left(t\right),\dots ,{\tilde{x}}_{k1}^T\left(t\right),\\ \dots ,{\tilde{x}}_{1N_2}^T\left(t\right),\dots ,{\tilde{x}}_{k{N}_2}^T\left(t\right),\dots ,{\tilde{x}}_{N_1{N}_2}^T\left(t\right)\end{array}\right]}^T$$

where N = N₁ × N₂. Note that n is the dimension of the vector x_k,l(t) for each grid node and N = N₁ × N₂ is the total number of grid nodes. For example, if N₁ = 2 and N₂ = 2, then we have $\tilde{x}\left(t\right)={\left[{\tilde{x}}_{11}^T\left(t\right),{\tilde{x}}_{12}^T\left(t\right),{\tilde{x}}_{21}^T\left(t\right),{\tilde{x}}_{22}^T\left(t\right)\right]}^T\in R^{4n}$. In order to simplify the index of the node x̃_k,l (t) ∈ R in the spatial state vector x̃(t) ∈ R^nN, we use the symbol x̃_j(t) ∈ Rⁿ to replace x̃_k,l (t) ∈ Rⁿ. Note that the index j is from 1 to N, ie, x̃₁(t) = x̃_1,1(t) = x̃₂(t) = x̃_2,1(t), ..., x̃_j (t) = x̃_k,l (t), ..., x̃_N (t) = x̃_{N1, N2} (t), where j = (l – 1) N₁ + k in the above spatial state vector. In other words, the above spatial state vector for all grid notes in habitat U is represented by the following form:^18,20

$$\tilde{x}\left(t\right)={\left[{\tilde{x}}_1^T\left(t\right),{\tilde{x}}_2^T\left(t\right),\dots ,{\tilde{x}}_j^T\left(t\right),\dots ,{\tilde{x}}_N^T\left(t\right)\right]}^T$$

ie, x̃(t) denotes the spatial state vector of all state variables of ecological systems at all grid nodes in habitat U. According to the above analysis, the stochastic finite difference ecological system in (13) can be represented with only one index as follows:

$$\begin{array}{ll}d{\tilde{x}}_j\left(y,t\right)=\hfill & \sum _{i=1}^M{\alpha }_i\left(\tilde{x}\left(y,t\right)\right)\left[\begin{array}{l}{N}_i{\tilde{x}}_j\left(t\right)dt+{\kappa }_i{T}_j{\tilde{x}}_j\left(t\right)dt\\ +\sum _{n=1}^L\mathrm{\Delta }{N}_{ni}{\tilde{x}}_j\left(t\right)d{w}_{n,j}\left(t\right)\end{array}\right]\hfill \\ \hfill & +v_j\left(t\right)dt\hfill \end{array}$$ (14)

where v_j (t) = v_k,l (t), dw_n,j (t) = dw_n,k,l (t), with j = (l – 1) N₁ + k and

$$\begin{array}{l}{T}_j\tilde{x}\left(t\right)=\frac{1}{{\mathrm{\Delta }}^2}\left[\begin{array}{ccccccccccccccccc}{0}_n& \cdots & 0_n& I_n& 0_n& \cdots & 0_n& I_n& -4I_n& I_n& 0_n& \cdots & 0_n& I_n& 0_n& \cdots & 0_n\end{array}\right]\tilde{x}\left(t\right)\\ \mathit{Position}\to \begin{array}{ccccccc}1& j-N_i& j-1& j& j+1& j+N_1& N_1{N}_2\end{array}\end{array}$$

Let us denote α_i(x̃(t)) = diag[α_i(x̃(t)), ..., α_i(x̃_N(t))]. Some properties of α_i(x̃(t)) can then be obtained by the following lemma.

Lemma 1:²⁰

Using the properties of Kronecker product, we have the following properties:

1. $\begin{array}{ll}{\alpha }_i\left(\tilde{x}\left(t\right)\right)\otimes N_i\hfill & =\left({\alpha }_i\left(\tilde{x}\left(t\right)\right)\otimes I_n\right)\left(I_n\otimes N_i\right)\hfill \\ \hfill & =\left(I_n\otimes N_i\right)\left({\alpha }_i\left(\tilde{x}\left(t\right)\right)\otimes I_n\right)\in R^{nN\times nN}\hfill \end{array}$where N_i ∈ R^n×n.

2. $\begin{array}{l}\left({\alpha }_i\left(\tilde{x}\left(t\right)\right)\otimes I_n\right)\left({\alpha }_j\left(\widehat{x}\left(t\right)\right)\otimes I_n\right)\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=\left({\alpha }_i\left(\tilde{x}\left(t\right)\right){\alpha }_j\left(\widehat{x}\left(t\right)\right)\otimes I_n\right)\in R^{nN\otimes nN}.\end{array}$

3. $\begin{array}{l}\sum _{i=1}^M{\alpha }_i\left(\tilde{x}\left(t\right)\right)=I_N,\hspace{0.17em}\hspace{0.17em}\sum _{i=1}^M\left({\alpha }_i\left(\tilde{x}\left(t\right)\right)\otimes I_n\right)=I_{nN}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{and\hspace{0.17em}}\sum _{i=1}^M\sum _{j=1}^M\left({\alpha }_i\left(\tilde{x}\left(t\right)\right){\alpha }_j\left(\widehat{x}\left(t\right)\right)\otimes I_n\right)=I_{nN}.\end{array}$

Proof: The properties (1) and (2) are the fundamental properties for Kronecker product, and property (3) can be proven via $\sum _{i=1}^M{\alpha }_i\left(\tilde{x}\left(t\right)\right)=1$ for j = 1,2, ..., N.

By using the Kronecker product in Lemma 1, the stochastic finite difference ecological systems in (14) at all grid points in habitat U can be integrated as the following stochastic spatial space system:

$$\begin{array}{l}d\tilde{x}\left(t\right)\\ =\sum _{i=1}^M\left\{{\alpha }_i\left(\tilde{x}\left(t\right)\right)\otimes N_i+\left[{\alpha }_i\left(\tilde{x}\left(t\right)\right)\otimes {\kappa }_i\right]T\right\}\tilde{x}\left(t\right)dt\\ +\left({\alpha }_i\left(\tilde{x}\left(t\right)\right)\otimes \sum _{j=1}^L{N}_{ji}\right)\tilde{x}\left(t\right)\circ d{w}_j\left(t\right)+v\left(t\right)\\ =\sum _{i=1}^M{\overline{\alpha }}_i\left(\tilde{x}\left(t\right)\right)\left\{\begin{array}{l}\left[I_N\otimes N_i\right]\tilde{x}\left(t\right)dt+\left[I_N\otimes {\kappa }_i\right]T\tilde{x}\left(t\right)dt\\ +\left(I_N\otimes \sum _{j=1}^L{N}_{ji}\right)\tilde{x}\left(t\right)\circ d{w}_j\left(t\right)\end{array}\right\}\\ +v\left(t\right)\end{array}$$ (15)

where ᾱ_i(x̄(t)) ≜ α_i(x̄(t)) ⊗ I_n, dw_j (t) ≜ [J^T dw_j1 (t), ..., J^T dw_jN (t)] with J ≜ [111 ... 1] ∈ Rⁿ, ie, all the elements in J are equal to 1. The spatial state vector x̃(t) represents x̃ (y, t) at all grid points on the spatial domain of habitat U in Figure 1. The corresponding matrices are defined as $T\triangleq {\left[T_1^T,\dots ,T_N^T\right]}^T\in R^{nN\times nN},v\left(t\right)={\left[v_1\left(t\right)\dots v_N\left(t\right)\right]}^T\in R^{nN}$. The physical meaning of the stochastic spatial space system in (15) is that the globally linearized ecological systems at all grid points of spatial domain U can be represented by a spatial vector dynamic equation. According to the stochastic spatial space system in (15), the disturbance sensitivity in (3) can be modified as

$$\frac{E{\int }_0^{\infty }{\tilde{x}}^T\left(t\right)\tilde{x}\left(t\right)dt}{E{\int }_0^{\infty }{v}^T\left(t\right)v\left(t\right)dt}\le {\rho }^2$$ (16)

Then, based on the stochastic spatial space dynamic equation of ecological system in (15), we get the following phenotype robustness (community stability) criterion for ecological systems.

Proposition 2: If the following phenotype robustness (community stability) criterion holds with a common positive solution P > 0,

$$\underset{\mathit{Position}\to 1}{T_j\tilde{x}\left(t\right)=\frac{1}{{\mathrm{\Delta }}^2}[0_n}\cdots 0_n\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\underset{j-N_1}{I_n\hspace{0.17em}\hspace{0.17em}{0}_n}\cdots 0_n\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\underset{j-1}{I_n}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\underset{j}{-4I_n}\hspace{0.17em}\hspace{0.17em}\underset{j+1}{I_n\hspace{0.17em}\hspace{0.17em}{0}_n}\cdots 0_n\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\underset{j+N_1}{I_n\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{0}_n}\cdots \underset{N_1{N}_2}{0_n]\tilde{x}\left(t\right)}$$ (17)

then the intrinsic parameter fluctuations of ecological system can be tolerated and the effect of environmental disturbances can be attenuated to a sensitivity level ρ. In other words, the phenotype of ecological system (community stability) could be maintained under these intrinsic parameter fluctuations and environmental disturbances. For the proof for this proposition, please see Appendix B.

Similarly, the network sensitivity ρ₀ of the ecological network can be obtained by solving the following constrained optimization:

$$\begin{array}{l}{\rho }_0=\underset{P>0}{\text{min}}\hspace{0.17em}\rho \\ \text{subject}\hspace{0.17em}\text{to}\hspace{0.17em}\left(17\right)\end{array}$$ (18)

Therefore, after replacing ρ in (17) with the above network sensitivity ρ₀, the phenotype robustness (community stability) criterion of ecological network in (17) could be modified as the following form:

$$\begin{array}{l}\underset{\mathit{local}\hspace{0.17em}\text{int}\mathit{rinsic}\hspace{0.17em}\mathit{robustness}}{\underbrace{{\left(I_N\otimes \sum _{j=1}^L{N}_{ji}\right)}^{T}P\left(I_N\otimes \sum _{j=1}^L{N}_{ji}\right)+}}\underset{\mathit{local}\hspace{0.17em}\mathit{environmental}\hspace{0.17em}\mathit{robustness}}{\underbrace{\frac{1}{{\rho }_0^2}PP+I_N}}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\le \underset{\mathit{local}\hspace{0.17em}\mathit{network}\hspace{0.17em}\mathit{robustness}}{\underbrace{-\left\{P\left(\left[I_N\otimes N_i\right]+\left[I_N\otimes {\kappa }_i\right]T\right)+{\left(\left[I_N\otimes N_i\right]+\left[I_N\otimes {\kappa }_i\right]T\right)}^{T}P\right\}}},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}i=1,\dots ,M\end{array}$$ (19)

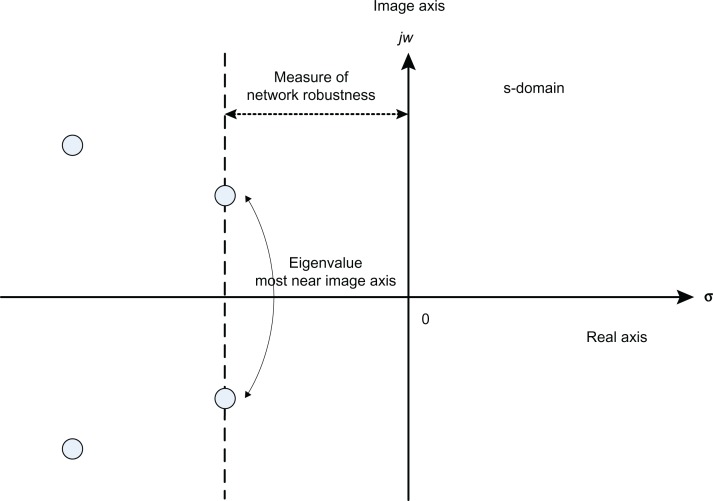
It is seen that if each local linearized ecological partial differential system has enough local network robustness to confer local intrinsic robustness and local environmental robustness, then the phenotype of nonlinear stochastic partial differential ecological systems is robust under intrinsic parameter fluctuations and environmental disturbances. The tradeoff between local intrinsic robustness and local environmental robustness can be seen from (19). If the eigenvalues of each local system matrix [I_N ⊗ N_i] + [I_N ⊗ κ_i]T are in the far left-hand plane of Figure 2, then the ecological network has more network robustness to tolerate intrinsic parameter fluctuations and to resist environmental disturbances, so as to maintain community stability in an uncertain habitat and changing environment.

Figure 2.

The smaller distance between the locations of eigenvalues of [I_N ⊗ N_i] + [I_N ⊗ κ_i]T and the image axis can be taken as the measure of network robustness for the local linear stochastic gene networks in (20). Therefore, the local linear stochastic gene networks become more robust while the eigenvalues are located in the far left-hand side of image axis.

State feedback control to improve the network robustness of ecological networks in (9) can also be approximated by the global linearization and finite difference scheme as follows:

$$\begin{array}{l}d\tilde{x}\left(t\right)\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=\sum _{i=1}^M{\overline{\alpha }}_i\left(\tilde{x}\left(t\right)\right)\left\{\begin{array}{l}\left[I_N\otimes N_i\right]\tilde{x}\left(t\right)dt+\left[I_N\otimes K_i\right]\tilde{x}\left(t\right)dt\hfill \\ +\left[I_N\otimes {\kappa }_i\right]T\tilde{x}\left(t\right)dt+\left(I_N\otimes \sum _{j=1}^L{N}_{ji}\right)\hfill \\ \tilde{x}\left(t\right)\circ d{w}_j\left(t\right)\hfill \end{array}\right\}\\ +v\left(t\right)\end{array}$$ (20)

where K_i, i = 1, …, M denote the local control gains via the global linearization of K (x̃(y, t)), ie, $K\left(\tilde{x}\left(y,t\right)\right)=\sum _{i=1}^M\alpha \left(\tilde{x}\left(y,t\right)\right)K_i\tilde{x}\left(y,t\right)$. In this situation, the phenotype robustness criterion in (19) should be modified as follows:

$$\begin{array}{l}\underset{\mathit{local}\hspace{0.17em}\text{int}\mathit{rinsic}\hspace{0.17em}\mathit{robustness}}{\underbrace{{\left(I_N\otimes \sum _{j=1}^L{N}_{ji}\right)}^{T}P\left(I_N\otimes \sum _{j=1}^L{N}_{ji}\right)+}}\underset{\mathit{local}\hspace{0.17em}\mathit{environmental}\hspace{0.17em}\mathit{robustness}}{\underbrace{\frac{1}{{\rho }_0^2}PP+I_N}}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\le \underset{\mathit{local}\hspace{0.17em}\mathit{network}\hspace{0.17em}\mathit{robustness}}{\underbrace{-\left\{P\left(\left[I_N\otimes N_i\right]+\left[I_N\otimes K_i\right]+\left[I_N\otimes {\kappa }_i\right]T\right)+{\left(\left[I_N\otimes N_i\right]+\left[I_N\otimes K_i\right]+\left[I_N\otimes {\kappa }_i\right]T\right)}^{T}P\right\}}},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}i=1,\dots ,M\end{array}$$ (21)

Then, the robust ecological network design must specify an adequate K_i, i = 1, …, M, so that the local network robustness on the right-hand side of (21) should be large enough to provide enough local intrinsic robustness to tolerate local intrinsic parameter fluctuations, and enough local environmental robustness for resisting local environmental disturbances. Obviously, if the local feedback control gains K_i need to be specified so that the eigenvalues of [I_N ⊗ N_i]+[I_N ⊗ K_i] + [I_N ⊗ κ_i]T are in the farther left hand complex domain (more stable), then the ecological network will have more network robustness to confer intrinsic environmental robustness, which makes sense from the modern system control design point of view.^1,27–30

Computer Simulation

In the real world, most phenomena are governed by partial differential equations such as population dynamics in ecology, chemical dispersion in chemistry and heat flow or wave propagation in physics.^31,32 In this section, a simple ecological example for nonlinear stochastic partial differential system is given to illustrate and to confirm the phenotype robustness criterion of the ecological network. This mono-species population system is used to describe the dynamical interaction between the native species and the environmental disturbances in a two-dimensional spatial domain.²³ The individual’s spatial dispersal in the field of ecological biology can be seen as the heat transfer or fluid diffusion in physics. Suppose the mono-species population system with stochastic intrinsic fluctuation and environmental disturbance could be formulated as follows:²⁰

$$\begin{array}{l}dx\left(y,t\right)=\left(\left(-2\times {10}^{-12}\left(x{\left(y,t\right)}^4+1092x{\left(y,t\right)}^3+447174x{\left(y,t\right)}^2\right)-0.0042x\left(y,t\right)\right)+0.1v\left(y,t\right)+\kappa {\nabla }^{2}x\left(y,t\right)\right)dt\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+\left({10}^{-12}\left(x{\left(y,t\right)}^4+1092x{\left(y,t\right)}^3+447174x{\left(y,t\right)}^2+81385668x\left(y,t\right)\right)+0.002x\left(y,t\right)\right)dw\left(y,t\right)\\ y\in U=\left[0,1\right]\times \left[\begin{array}{cc}0,& 0.5\end{array}\right]\end{array}$$ (22)

where x(y,t), which is a function of two-dimensional space y = [y₁,y₂] and time t, is the concentration of native species in the spatial domain. κ is the species diffusion coefficient. The grid space Δ of the finite difference scheme is chosen as 0.125 so that there are N = 7 × 3 = 21 grid points. Note that the origin of the ecological system in this example has been shifted to the desired steady state. The concentration of initial distribution of the native species is given as x(y, 0) = 100×e^{−10|0.5–y₁|−0.6738 – 30×|0.5–2y₂|} The Dirichlet boundary conditions are used to restrict the concentration to be zero at the boundary, ie, x ([0,  0], t) = 0, x ([0,  0.5], t) = 0, x ([1,  0], t) = 0 and x ([1,  0.5], t)= 0.

The spatial-time profiles of the nonlinear partial differential system is approximated by global linearization scheme with vertices M = 3. The parameters in the globally linearized PDE system (11) are obtained as N₁ = −0.00412256, N₂ = −0.0042616 and N₃ = −0.0045441; ΔN₁ = 0.00206, N₂ = 0.00213 and N₃ = 0.00227. Using the finite difference scheme, we can construct a spatial state-space model as (15). Following the proposed procedure in earlier section, the network sensitivity ρ₀ = 1.01 could be obtained easily by solving the constrained optimization problem in (18). For simulation, we assume the environmental disturbance is v(y, t) = 10 sin (0.2t)e^{−0.001t– 0.1y₁}. From the simulation results, the proposed phenotype robustness (community stability) of the nonlinear stochastic partial differential ecological network is maintained by efficiently attenuating the intrinsic fluctuations and environmental disturbances. From the Monte Carlo simulation with 100 runs, the attenuation performance in (16) could be computed as follows:

$$\frac{E{\int }_0^{150}{x}^T\left(t\right)x\left(dt\right)}{E{\int }_0^{150}{v}^T\left(t\right)v\left(t\right)dt}\approx {0.29}^2<{1.01}^2$$ (23)

with the variance 0.062. This conservative result is due to the conservative nature of the global linearization in (11) and the solving inequalities in (17). Therefore, the simulation example has shown the existence of the proposed phenotype robustness criterion for the nonlinear partial differential system from the practical verification. In a real ecosystem, the effects of environmental disturbances on the phenotype of an ecological network could be efficiently attenuated if the network robustness could satisfy its phenotype robustness criterion in (8) or (19).

Discussion

There are many examples of robust biological systems found at many scales, from biochemical networks to ecological networks. At each scale, robustness may reflect the properties of individual elements or, alternatively, the dynamic feedback between interacting elements. For example, the expression of some metabolic functions may be robust in the face of temperature changes, because an enzyme maintains its shape and specificity across a range of temperatures or because an interconnected network of reactions sustains the supply of product, even when some enzymes fail. A genome may be robust because it encodes proofreading and repair systems that reduce replication errors or because it gets organized such that many mutations have little effect on its phenotype. An ecosystem might be robust if it resists the extinction of some keystone species or, if extinction does occur, because surviving species can compensate over physiological, demographic, or evolutionary time scales.^33,34

Ecological networks may pose a challenge when one considers severe changes such as the addition or removal of species.¹⁷ By topological approaches (without population dynamics), it is seen that the network will appear ‘species deletion unstable’.³⁵ ie, the network quickly breaks into many disconnected subnetworks when the most connected species are successively removed from the network. Dynamical models of species removals also show that the more polyphagous the predators, the less the effect caused by removing one of its prey species.³⁵ Thus, whether simple or highly connected model food webs are robust to the loss of species depends entirely on whether one looks at top predators or plant species.³⁶ By contrast, when disasters ruin species randomly, these networks will be more robust, showing both little fragmentation and few secondary extinctions.^5,7,12 But a lack of integrated concepts about how an ecological network can maintain its phenotype robustness under random or selective changes and how to evaluate the network sensitivity still exists. This study has developed a unifying mathematical framework for investigating the principles of both robust stabilization and environmental disturbance sensitivity in ecological networks from a systematic perspective.

From the gene regulatory network to the ecological network, it can be seen that, for different scales of biological systems, their phenotype robustness criteria according to their global linearization models can be demonstrated within a unifying mathematical framework, even when the partial differential diffusion operator is considered in the ecological network. From the systems theory perspective, the phenotype robustness of nonlinear stochastic gene networks in systems, evolutionary¹ and ecological biology needs to obey a similar phenotype robustness criterion, ie, “intrinsic robustness + genetic robustness + environmental robustness ≤ network robustness”. This means that network robustness needs to be strong enough to tolerate either heritable perturbations (genetic variations) or non-heritable perturbations (ie, random molecular fluctuations and environmental disturbances) so that the phenotype of biological networks can be maintained in systems, evolutionary and ecological biology using a similar mathematical framework.

In general, random genetic variations, phenotype perturbations and heterogeneity are neither desired nor deliberate outcomes of systems, evolutionary and ecological biology. However, heterogeneity and diversity form the very basis of evolutionary biology, not only within genetically diverse populations but also within the same allele or genome. Thus, random genetic variations, environmental disturbances and phenotypic perturbations are inherent features of biological systems and networks. Random perturbative biological networks may contain more connected and interconnected systems, which may provide multifunctionality of the biological network. This multifunctionality may result in increased robustness and a capacity to cope with diverse challenges. However, multifunctionality also increases the complexity and variations of the biological network, which may increase adaptive potential. Thus, behind the façade of perfection and optimality of systems, evolutionary and ecological biology lies the messy biology that originates from the genetic variations and environmental disturbances in evolution. There exists the tradeoff among intrinsic robustness, genetic robustness, environmental robustness and network robustness in the phenotype robustness of stochastic biological networks. That is, if intrinsic robustness + genetic robustness + environmental robustness ≤ network robustness, then the phenotype of the biological network is maintained. This sheds light on the mechanisms that govern the exploitation and toleration of the messiness of biological networks in systems, evolutionary and ecological biology, from a systematic perspective. Obviously, network robustness needs to be strong enough to tolerate either heritable perturbations (genetic variations) or non-heritable perturbations (random molecular fluctuations and environmental disturbances) so that the phenotype can be maintained in biological networks at different levels.

For gene regulatory networks, evolutionary networks¹ and ecological networks, two favored strategies can improve phenotype robustness in the network evolutionary process. One is to improve network robustness to provide enough intrinsic robustness for tolerating intrinsic parameter fluctuations, genetic robustness for buffering genetic variations and environmental robustness for resisting environmental disturbances, so that phenotype robustness of these biological networks at different scales can be maintained under these uncertain perturbations and environmental disturbances. Negative feedback is a mechanism that can improve network robustness (ie, it can make right-hand sides of (8), (19) larger) and is favored by natural selection in biological networks at different levels in the network evolutionary process. Another strategy is to reduce the effect of intrinsic parameter fluctuations, genetic variations and environmental disturbances on different biological networks (ie, it can make the left-side of (8), (19) smaller). Redundancies and repairs are the mechanisms of this strategy and are favored by natural selection in evolution. This is the reason why there are so many different redundancies from duplicated genes in gene regulatory networks, redundant pathways in biochemical networks and species redundancies in ecological systems.

From the phenotype criteria of the ecological network in (8) and (19), if the network robustness in the right-hand side is fixed, it is seen that if the intrinsic robustness becomes large to tolerate more intrinsic parameter fluctuations in the first term, it will lead to the decrease of environmental robustness or the increase of the network sensitivity ρ₀ in the second term. For example, large intrinsic robustness of ecological network could lead to large network sensitivity to environmental disturbances. On the contrary, an ecological network with more environmental robustness or less network sensitivity ρ₀ will lead to less intrinsic robustness, to tolerate less intrinsic parameter fluctuations for maintaining community stability. By comparing these phenotype robustness criteria and the tradeoff between network robustness, intrinsic robustness and environmental robustness in ecological networks with those in gene regulatory networks and evolutionary networks, we can find a unifying framework for genetic robustness, environmental robustness, network robustness and their tradeoff on the phenotype robustness in different levels of biological networks.

Conclusion

This paper presents a unifying mathematical framework to describe stochastic ecological networks under intrinsic parameter fluctuations and environmental disturbances. Then, according to the unifying stochastic biological systems, the phenotype robustness criteria of ecological networks are also investigated from the robust stabilization and network sensitivity perspective. It is found that if the phenotype criterion “intrinsic robustness + environmental robustness ≤ network robustness” is guaranteed, ie, network robustness can confer intrinsic robustness for tolerating intrinsic parameter fluctuations and environmental robustness for resisting the environmental disturbances, then the phenotype will be robust in ecological networks. Using the global linearization method and finite difference scheme to estimate network robustness, based on spatial state space system, we found that if the network robustness of each local linearized ecological network is greater than the total sum of intrinsic robustness and environmental robustness of each local linear ecological network, then the phenotype of the ecological network is also maintained, despite intrinsic parameter fluctuations and environmental disturbances. We also found that the phenotype robustness criterion and the tradeoff among network robustness, intrinsic robustness and environmental robustness are similar for different scales of biological networks, from gene regulatory networks and evolutionary networks to ecological networks. Finally, if the network structure is given, by taking into account different strengths of trophic links, or the removal of species in trophic links, the phenotype robustness criterion may also be employed in food webs to discuss the network robustness with random or selective removal of species in the trophic links.

Supplementary Data: Appendix

Before the proofs of these propositions, the following lemma is useful and should be given beforehand

Lemma A: For any vector a and b, then we get

$$a^{T}b=2\left(\frac{a^T}{2\rho }\right)\left(\rho b\right)\le \frac{1}{4{\rho }^2}{a}^{T}a+{\rho }^2{b}^{T}b,\hspace{0.17em}\text{for}\hspace{0.17em}\text{any}\hspace{0.17em}\rho \hspace{0.17em}>0$$

Appendix A: Proof of Proposition 1

For the nonlinear stochastic ecological network in (2), with the Lyapunov function V (x̄(y, t)) > 0 and V (x̄(y, t)) = 0, we have the following result by Ito formula,³⁰,³⁷

$$\begin{array}{l}E{\int }_U{\int }_0^{\infty }{\tilde{x}}^T\left(y,t\right)\tilde{x}\left(y,t\right)dtdy=E{\int }_U\left[v\left(\tilde{x}\left(y,0\right)\right)-V\left(\tilde{x}\left(y,\infty \right)\right)+{\int }_0^{\infty }\left({\tilde{x}}^T\left(y,t\right)\tilde{x}\left(y,t\right)+\frac{dV\left(\tilde{x}\left(y,t\right)\right)}{dt}\right)dt\right]dy\\ \le E{\int }_{U}V\left(\tilde{x}\left(y,0\right)\right)dy+E{\int }_U{\int }_0^{\infty }\left(\begin{array}{l}{\tilde{x}}^T\left(y,t\right)\tilde{x}\left(y,t\right)+{\left(\frac{\partial V\left(\tilde{x}\left(y,t\right)\right)}{\partial \tilde{x}\left(y,t\right)}\right)}^T\left(N\left(\tilde{x}\left(y,t\right)\right)+v\left(y,t\right)+\kappa \left(\tilde{x}\left(y,t\right)\right){\nabla }^2\tilde{x}\left(y,t\right)\right)\hfill \\ +\frac{1}{2}\sum _{i=1}^L\mathrm{\Delta }{N}_i^T\left(\tilde{x}\left(y,t\right)\right)\frac{{\partial }^{2}V\left(\tilde{x}\left(y,t\right)\right)}{\partial {\tilde{x}}^2\left(y,t\right)}\mathrm{\Delta }{N}_i\left(\tilde{x}\left(y,t\right)\right)\hfill \end{array}\right)dtdy\end{array}$$ (A1)

By the fact x̃(y, 0) = 0 and V (x̄ (y, 0) = 0, then we get

$$\begin{array}{l}E{\int }_U{\int }_0^{\infty }{\tilde{x}}^T\left(y,t\right)\tilde{x}\left(y,t\right)dtdy\\ \le E{\int }_U{\int }_0^{\infty }\left(\begin{array}{l}{\tilde{x}}^T\left(y,t\right)\tilde{x}\left(y,t\right)+{\left(\frac{\partial V\left(\tilde{x}\left(y,t\right)\right)}{\partial \tilde{x}\left(y,t\right)}\right)}^T\left(N\left(\tilde{x}\left(y,t\right)\right)+v\left(y,t\right)+\kappa \left(\tilde{x}\left(y,t\right)\right){\nabla }^2\tilde{x}\left(y,t\right)\right)\hfill \\ +\frac{1}{2}\sum _{i=1}^L\mathrm{\Delta }{N}_i^T\left(\tilde{x}\left(y,t\right)\right)\frac{{\partial }^{2}V\left(\tilde{x}\left(y,t\right)\right)}{\partial {\tilde{x}}^2\left(y,t\right)}\mathrm{\Delta }{N}_i\left(\tilde{x}\left(y,t\right)\right)\hfill \end{array}\right)dtdy\end{array}$$ (A2)

By Lemma A, then we get

$${\left(\frac{\partial V\left(\tilde{x}\left(y,t\right)\right)}{\partial \tilde{x}\left(y,t\right)}\right)}^{T}v\left(y,t\right)\le \frac{1}{4{\rho }^2}{\left(\frac{\partial V\left(\tilde{x}\left(y,t\right)\right)}{\partial \tilde{x}\left(y,t\right)}\right)}^T\left(\frac{\partial V\left(\tilde{x}\left(y,t\right)\right)}{\partial \tilde{x}\left(y,t\right)}\right)+{\rho }^2{v}^T\left(y,t\right)v\left(y,t\right)$$ (A3)

Substituting (A3) into (A2), we get

$$\begin{array}{l}E{\int }_U{\int }_0^{\infty }{\tilde{x}}^T\left(y,t\right)\tilde{x}\left(y,t\right)dtdy\\ \le E{\int }_0^{\infty }{\int }_U\left(\begin{array}{l}{\tilde{x}}^T\left(y,t\right)\tilde{x}\left(y,t\right)+{\left(\frac{\partial V\left(\tilde{x}\left(y,t\right)\right)}{\partial \tilde{x}\left(y,t\right)}\right)}^T\left(N\left(\tilde{x}\left(y,t\right)\right)+\kappa \left(\tilde{x}\left(y,t\right)\right){\nabla }^2\tilde{x}\left(y,t\right)\right)\hfill \\ +\frac{1}{2}\sum _{i=1}^L\mathrm{\Delta }{N}_i^T\left(\tilde{x}\left(y,t\right)\right)\frac{{\partial }^{2}V\left(\tilde{x}\left(y,t\right)\right)}{\partial {\tilde{x}}^2\left(y,t\right)}\mathrm{\Delta }{N}_i\left(\tilde{x}\left(y,t\right)\right)\hfill \\ +\frac{1}{4{\rho }^2}{\left(\frac{\partial V\left(\tilde{x}\left(y,t\right)\right)}{\partial \tilde{x}\left(y,t\right)}\right)}^T\left(\frac{\partial V\left(\tilde{x}\left(y,t\right)\right)}{\partial \tilde{x}\left(y,t\right)}\right)+{\rho }^2{v}^T\left(y,t\right)v\left(y,t\right)\hfill \end{array}\right)dydt\end{array}$$ (A4)

If the HJII in (5) holds, then (A4) is reduced to the following inequality

$$E{\int }_U{\int }_0^{\infty }{\tilde{x}}^T\left(y,t\right)\tilde{x}\left(y,t\right)dtdy\le E{\rho }^2{\int }_0^{\infty }{\int }_U\left(v^T\left(y,t\right)v\left(y,t\right)\right)dydt$$

which is Equation (3) with the sensitivity level ρ. If V (x̃(y, 0)) ≠ 0, then the above inequality should be modified as (4). Q.E.D.

Appendix B: Proof of Proposition 2

For the stochastic spatial space system in (15) with x̃(0) = 0 and v(t) ≠ 0, by the Ito formula,³⁰,³⁷ we get

$$\begin{array}{c}E{\int }_0^{\infty }{\tilde{x}}^T\left(t\right)\tilde{x}\left(t\right)dt=E\left[{\tilde{x}}^T\left(0\right)P\tilde{x}\left(0\right)-{\tilde{x}}^T\left(t\right)P\tilde{x}\left(t\right)+{\int }_0^{\infty }\left({\tilde{x}}^T\left(t\right)\tilde{x}\left(t\right)+\frac{d}{dt}{\tilde{x}}^T\left(t\right)P\tilde{x}\left(t\right)\right)dt\right]\\ \le E{\tilde{x}}^T\left(0\right)P\tilde{x}\left(0\right)+E{\int }_0^{\infty }\left(\begin{array}{l}{\tilde{x}}^T\left(t\right)\tilde{x}\left(t\right)dt+d{\tilde{x}}^{T}P\tilde{x}\left(t\right)+{\tilde{x}}^T\left(t\right)Pd\tilde{x}\left(t\right)\hfill \\ +\frac{1}{2}{\tilde{x}}^T\left(t\right){\left(I_N\otimes \sum _{j=1}^L{N}_{ji}\right)}^T\frac{{\partial }^2\left({\tilde{x}}^T\left(t\right)P\tilde{x}\left(t\right)\right)}{\partial {\tilde{x}}^2\left(t\right)}\left(I_N\otimes \sum _{i=1}^L{N}_{ji}\right)\tilde{x}\left(t\right)\hfill \end{array}\right)dt\end{array}$$ (B1)

By the fact that x̃(0) = 0 and (15), we get

$$\begin{array}{l}E{\int }_0^{\infty }{\tilde{x}}^T\left(t\right)\tilde{x}\left(t\right)dt\\ \le E{\int }_0^{\infty }\left({\tilde{x}}^T\left(t\right)\tilde{x}\left(t\right)+\sum _{i=1}^M{\overline{\alpha }}_i\left(\tilde{x}\left(t\right)\right)\left(\begin{array}{l}{\tilde{x}}^T\left(t\right)\left({\left(\left[I_N\otimes N_i\right]+\left[I_N\otimes {\kappa }_i\right]T\right)}^{T}P+P\left(\left[I_N\otimes N_i\right]+\left[I_N\otimes {\kappa }_i\right]T\right)\right)\tilde{x}\left(t\right)\hfill \\ +{\tilde{x}}^T\left(t\right){\left(I_N\otimes \sum _{j=1}^L{N}_{ji}\right)}^{T}P\left(I_N\otimes \sum _{j=1}^L{N}_{ji}\right)\tilde{x}\left(t\right)+v^T\left(t\right)P\tilde{x}\left(t\right)+{\tilde{x}}^T\left(t\right)Pv\left(t\right)\hfill \end{array}\right)\right)dt\end{array}$$ (B2)

By Lemma A, we get

$$v^T\left(t\right)P\tilde{x}\left(t\right)+{\tilde{x}}^T\left(t\right)Pv\left(t\right)\le \frac{1}{{\rho }^2}{\tilde{x}}^T\left(t\right)PP\tilde{x}\left(t\right)+{\rho }^2{v}^T\left(t\right)v\left(t\right)$$ (B3)

From (B3) and (B2), we get

$$\begin{array}{l}E{\int }_0^{\infty }{\tilde{x}}^T\left(t\right)\tilde{x}\left(t\right)dt\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\le E{\int }_0^{\infty }\sum _{i=1}^M{\overline{\alpha }}_i\left(\tilde{x}\left(t\right)\right){\tilde{x}}^T\left(t\right)\left(\begin{array}{l}\left({\left(\left[I_N\otimes N_i\right]+\left[I_N\otimes {\kappa }_i\right]T\right)}^{T}P+P\left(\left[I_N\otimes N_i\right]+\left[I_N\otimes {\kappa }_i\right]T\right)\right)\hfill \\ +{\left(I_N\otimes \sum _{j=1}^L{N}_{ji}\right)}^{T}P\left(I_N\otimes \sum _{i=1}^L{N}_{ji}\right)+I_N+\frac{1}{{\rho }^2}PP\hfill \end{array}\right)\tilde{x}\left(t\right)dt\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+E{\rho }^2{\int }_0^{\infty }{v}^T\left(t\right)v\left(t\right)dt\end{array}$$ (B4)

By the (17), we get

$$E{\int }_0^{\infty }{\tilde{x}}^T\left(t\right)\tilde{x}\left(t\right)dt\le E{\rho }^2{\int }_0^{\infty }{v}^T\left(t\right)v\left(t\right)dt$$

which is the inequality in (16) with the sensitivity level ρ.

Q.E.D.