A Unifying Mathematical Framework for Genetic Robustness, Environmental Robustness, Network Robustness and their Trade-offs on Phenotype Robustness in Biological Networks. Part III: Synthetic Gene Networks in Synthetic Biology

Abstract

Robust stabilization and environmental disturbance attenuation are ubiquitous systematic properties that are observed in biological systems at many different levels. The underlying principles for robust stabilization and environmental disturbance attenuation are universal to both complex biological systems and sophisticated engineering systems. In many biological networks, network robustness should be large enough to confer: intrinsic robustness for tolerating intrinsic parameter fluctuations; genetic robustness for buffering genetic variations; and environmental robustness for resisting environmental disturbances. Network robustness is needed so phenotype stability of biological network can be maintained, guaranteeing phenotype robustness. Synthetic biology is foreseen to have important applications in biotechnology and medicine; it is expected to contribute significantly to a better understanding of functioning of complex biological systems. This paper presents a unifying mathematical framework for investigating the principles of both robust stabilization and environmental disturbance attenuation for synthetic gene networks in synthetic biology. Further, from the unifying mathematical framework, we found that the phenotype robustness criterion for synthetic gene networks is the following: if intrinsic robustness + genetic robustness + environmental robustness ≦ network robustness, then the phenotype robustness can be maintained in spite of intrinsic parameter fluctuations, genetic variations, and environmental disturbances. Therefore, the trade-offs between intrinsic robustness, genetic robustness, environmental robustness, and network robustness in synthetic biology can also be investigated through corresponding phenotype robustness criteria from the systematic point of view. Finally, a robust synthetic design that involves network evolution algorithms with desired behavior under intrinsic parameter fluctuations, genetic variations, and environmental disturbances, is also proposed, together with a simulation example.

Introduction

Synthetic biology is the design and construction of biological devices and systems for useful purposes.¹ Such purposes include a focus on finding how the synthetic gene or man-made DNA works in a living cell, how to use the genetic engineering to build new biological systems, and rebuilding natural systems as platforms to benefit human society. Real physical and biological systems inherently suffer from intrinsic perturbations and external disturbances. In the last two decades, robust stabilization and noise-filtering theories have been developed by control engineers both in order to achieve the robust stability needed for tolerating intrinsic perturbations and in order to obtain the ability to noise filter against external disturbance; these would in turn improve the reliability and performance of control systems.^2–6 Their applications are also extended from control systems^2–5 to signal processing systems,⁶ communication systems,⁷ and biological systems.^8,9 Since both engineered systems and biological systems need robust stabilization and noise-filtering abilities to tolerate intrinsic perturbations and resist external disturbances (or noises) so as to maintain their desired function or performance, there should exist some common schemes for robust stabilization and disturbance attenuation for these two kinds of systems. In previous studies,^10,11 network robustness, genetic robustness, intrinsic robustness, and environmental robustness—and their trade-off on phenotype robustness—have been discussed in gene regulatory networks, evolutionary networks, and ecological networks. Since synthetic biology combines engineering methodology and biological technology in order to design artificial biological systems in host cells—which suffer from intrinsic parameter fluctuations, genetic mutations, and environmental disturbances in vivo—the network robustness and phenotype robustness criteria of synthetic biology are to be discussed in this study.

In general, there are several methods that have been proposed to design or construct a gene circuit for synthetic biology; these involve (1) DNA modification, (2) transcription regulation, (3) post-transcriptional regulation, and (4) post-translational regulation.¹² The goal is to create biological modules that can perform several different basic functions, including the design and engineering of new biological functions and systems by BioBrick-assembled gene circuits, which have been widely used in synthetic biology.^13,14 These gene circuits are reengineered with different promoters, ribosome binding sites (RBS), protein or RNA regions, and transcriptional terminators. Despite recent efforts targeting engineering at the genome level, most synthetic biology constructs are engineered at the level of genetic circuits encoded on plasmids, from a very simple device like a repressilator¹⁵ to the more complicated devices like a counter¹⁶ or a switch.^12,17 This relatively new field has provided insights into the mechanisms of natural gene networks,¹⁸ engineered multicellular pattern formations,¹⁹ bacterial photography,²⁰ tumor-target bacterial,²¹ feed-forward network-based concentration sensors,²² robust and tunable oscillators,²³ genetic networks that count,¹⁶ genetic sequential logic circuit such as Push-on Push-off switch,¹⁷ and the more complicated synchronous toggle switch.¹² Furthermore, entire metabolic pathways have been engineered on the genome level to produce an anti-malaria compound,²⁴ biofuels from plant biomass,^25,26 lycopene through automated genome engineering and accelerated evolution,²⁷ and a synthetic chromosome²⁸ translated into a host bacterium.²⁹

However, a wide variety of loss-of-function mutations or genetic variations are observed in BioBrick-assembled genetic circuits, including point mutations, inversions, and deletions.¹³ One problem with engineered genetic circuits in synthetic biology is their robust stability under genetic variations and environmental disturbances.³⁰ Therefore, how to design a robust synthetic gene network that can tolerate genetic variations due to point mutations, inversions or deletions, resist environmental disturbances, and also function properly in a host cell, is an important topic of synthetic biology.^13,31–39 In systems biology, a core mechanism has been found showing that there exists an interplay between system disorder and robustness of gene networks.⁴⁰ Additionally, in the evolutionary process there exists some interplay in evolutionary gene networks between the ability to evolve and network robustness.⁴¹ According to our previous studies, we have found that there exists a unifying mathematical framework in systems, evolutionary, and ecological networks.^10,11,41 Here, we would like to propose a robust gene network design which can ensure the specified network function (phenotype robustness) according to our previous works to see if there still exists a similar mathematical framework in synthetic biology. This design also provides an insight into how to design a robust synthetic gene network based on phenotype robustness criteria. In synthetic biology, it does not matter whether gene circuits are simple devices such as a repressilator or complicated devices such as a toggle switch, the dynamics of these biological systems are represented by ordinary differential equations (ODEs) and thus can be analyzed using our proposed phenotype robustness theory from the system perspective.

Recently, Kuepter et al⁴² have developed an approach based on semi-definite programming that identifies a consistent steady state for polynomial equations and inequality constraints this allows one to certify the feasible and infeasible regions of parameter space. In synthetic biology, ‘feasible region’ means the parameter set for a desired steady state in a synthetic gene network; the design of synthetic gene networks is difficult because of the uncertainties in molecular concentrations and parameter values. Batt and his colleague⁴³ provide an approach to develop efficient algorithms for solving robustness analyses and tuning problems. This approach was implemented in a publicly available tool RoVerGeNe; its practical applicability has been demonstrated on a synthetic transcriptional cascade in E. coli. to search for parameter sets that satisfied some given properties. More recently, a robust synthetic biology design with environmental disturbances was developed according to stochastic game theory from the minimax perspective.⁴⁴ Furthermore, in order to achieve a desired behavior in spite of genetic variations, environmental disturbances, and functional variations in the host cell, four system design specifications were given beforehand by users⁴⁵ so that designers could engineer an artificial robust gene network to meet these design specifications. This robust synthetic gene network design problem could be considered as robust stabilization around the desired behavior under intrinsic parameter variations, genetic variations, and environmental disturbances. In general, it is still difficult to specify a set of feasible kinetic parameters in a nonlinear synthetic gene network that is designed to achieve a desired behavior under intrinsic parameter fluctuations, genetic variations, and environmental disturbances. Based on the global linearization technique for interpolating several local linearized systems to approximate a nonlinear synthetic gene network,⁴⁶ a systematic method is proposed to efficiently select a set of appropriate design parameters for a synthetic gene network that satisfies the design specifications needed to tolerate intrinsic parameter fluctuations and genetic variations, efficiently filter environmental disturbances, and most importantly, achieve the desired steady state.

In general, synthetic biologists always had to select a set of design parameters using conventional trial-and-error methods to achieve the desired behavior of a synthetic gene network. However, when the scale of a synthetic gene network becomes large and the desired behavior becomes complex, how to select a set of adequate design parameters becomes an important topic for synthetic biology. Natural genetic circuits have evolved and have been optimized for their functions by means of natural selection, while at the same time being robust enough to handle genetic variation and environmental changes. Can we use the same principle to select an adequate parameter set for engineering a synthetic gene circuit? Genetic algorithm (GA) based design methods have been employed to mimic natural selection in the evolution process and to select adequate kinetic parameters for designing robust genetic oscillators with prescribed amplitude, period, and phase, under genetic variations and environmental disturbances.⁴⁷ GA is a stochastic optimization algorithm, which was inspired by the mechanisms of natural selection and evolution genetics⁴⁸ to optimally track a desired target. The proposed GA based design method can search for design parameters from feasible ranges to achieve fitness maximization, which is equivalent to the optimal robust tracking of a desired oscillation behavior under the effect of intrinsic and extrinsic perturbations on the host cell. The robust tracking problem is equivalent to the robust stabilization problem for the desired oscillatory behavior, whose tracking error is inversely proportional to the fitness function of synthetic oscillator to the oscillation, ie, the minimum tracking error is equivalent to the maximum fitness function. Therefore, a GA based design method is to efficiently search for an adequate set of design kinetic parameters in order to maximize the fitness function and achieve the optimal (minimum error) tracking of the desired oscillation behavior, which is done by mimicking natural selection in the evolutionary process.⁴⁷

Based on previous studies,^10,11 the framework of phenotype robustness criteria has been constructed for systems, evolutionary, and ecological biology. We found that if network robustness can confer intrinsic robustness for tolerating intrinsic parameter fluctuations, genetic robustness for buffering genetic variations and environmental robustness for resisting environmental stimuli, then the phenotypes of these biological networks will be maintained under intrinsic parameter fluctuations, genetic variations, and environmental stimuli. Moreover, the trade-off between intrinsic robustness, genetic robustness, environmental robustness, and network robustness can be revealed by the phenotype robustness criteria for biological networks at different levels from gene regulatory networks, evolutionary networks, and ecological networks. In the following sections, intrinsic robustness, genetic robustness, environmental robustness, network robustness, and their trade-off on phenotype robustness in systems, evolutionary, and ecological networks are to be extended to synthetic biology in sequence.

Trade-off between Genetic Robustness, Environmental Robustness and Network Robustness in Synthetic Biology

Network robustness analysis of synthetic gene network

Synthetic biology can be seen as the application of engineering to biological molecular systems, with a particular purpose. By transformative innovation, it is possible to build living machines from off-the-shelf chemical parts using similar strategies to what electrical engineers employ to design computer chips.^15,18,19 The ultimate goal of synthetic biology is to design and construct biological systems with desired behaviors.^8,49 Drawing upon the automated synthesis of DNA molecules and their assembly into genes and microbial genomes, it is predictable for the more efficient redesign of natural biological systems as well as the construction of functional “genetic circuit” and metabolic pathways for practical purposes.^16,20–29 Synthetic biology is foreseen to have important applications in biotechnology and medicine, as well as in revolutionizing how we conceptualize and approach the engineering of biological systems.³³ However, although the construction of gene regulatory networks has demonstrated the feasibility of synthetic biology,^13,30–34 the design of gene networks is still a difficult problem and the most newly designed gene networks cannot function properly.¹⁵ These design failures are due mainly to both intrinsic perturbations—such as intrinsic parameter fluctuations due to random molecular fluctuations (gene expression noise), genetic variations due to mutation, splicing, evolution from the fast metagenesis of host cell (E. coli and yeast in general)—and environmental disturbances such as changing extra-cellular environments.³³ Therefore, how to design a robust synthetic gene network that can tolerate intrinsic perturbations, resist environmental disturbances, and also function properly in a host cell is an important topic of synthetic biology.^33,38

For gene network design in synthetic biology, we first architect a gene circuit system for some functions, then specify the gene components and synthesize these gene components into a gene circuit, and finally send the engineered gene network into the host cell E. coli or yeast to function. However, due to random molecular fluctuations (or gene expression noises), the synthetic gene circuit suffers from Brownian (Weiner) molecular fluctuations. Owing to genetic mutations from the fast metagenesis of the host cell, the synthetic gene network also suffers from the Poisson genetic variations. Many examples of synthetic gene circuits losing function over evolutionary time are illustrated by studies of microchemostate-evolved strains containing a cell-density regulation circuit that lose function in less than 100 hours.¹³ The evolutionary stability of whole synthetic gene circuits is therefore an emergent property of the context of its biological parts. The evolutionary stability of synthetic gene networks will be an increasingly significant issue as these synthetic gene networks become more complex and need to be functional over longer periods of time.¹³ Finally, because of interactions with the cellular context in its host cell and changes in extra-cellular environments, the synthetic gene circuit suffers from environmental disturbances. In this situation, the dynamic behavior of a synthetic gene network with n genes in the host cell can be described by the following nonlinear stochastic system:^45,50

$$\begin{array}{l}\mathit{dx}(t)=(\mathit{Nf}(x(t))+v(t))\mathit{dt}+\sum _{i=1}^{L_1}\mathrm{\Delta }{N}_i{g}_i(x(t))P(t-t_i)\mathit{dt}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+\sum _{j=1}^{L_2}\delta N_j{h}_j(x(t))d{W}_j(t)\end{array}$$ (1)

where the state vector x(t) = [ x₁(t), …, x_n(t)]^T denotes the concentrations of proteins in the synthetic gene network. N denotes the corresponding stoichiometric matrix of the n-gene synthetic network. f(x(t)) denotes the nonlinear interaction vector. δN_j, j = 1, … L₂ denotes the fluctuation matrices due to L₂ independent random noise sources, such as random molecular fluctuations (or gene expression noises), and the elements of δN_j denote the standard deviations of the corresponding parameter fluctuations due to the jth Wiener molecular fluctuations W_j(t). h_j(x(t)) denotes the effect of the jth random noise source on the synthetic gene network. ΔN_i, i = 1, … L₁ denote the parameter variations due to the ith Poisson genetic variation P(t − t_i) occurred at t = t_i with intensity λ in the synthetic gene network engineered in the host cell with fast cell division. g_i(x(t)) denotes the effect of the ith Poisson genetic variation on the synthetic gene network. v(t) denotes the vector of environmental disturbances. The stochastic system of a synthetic gene network in (1) is employed to mimic the realistic dynamic behaviors of a population of synthetic gene networks consisting of n genes in the host cells, operating under random intrinsic parameter fluctuations due to random molecular fluctuations, random genetic variations due to mutations, and environmental disturbances due to changes in the cellular context. For example, the population of synthetic gene networks consist of a nominal (mean) synthetic gene network dx(t) = (Nf(x(t)) + v(t))dt and other synthetic gene networks with random genetic variation and parameter fluctuation $\sum _{i=1}^{L_1}\mathrm{\Delta }{N}_i{g}_i(x(t))P(t-t_i)+\sum _{j=1}^{L_2}\delta N_j{h}_j(x(t))n_j(t)$. Therefore, besides intrinsic parameter fluctuations,^45,50 in this study we also consider the heritable Poisson genetic variations in the synthetic gene network due to the fast cell division of host cell.

The design purpose of the synthetic gene network in (1) is to specify the kinetic parameters in the stoichiometric matrix N within a feasible region (ie, N∈[N₁,N₂] so that (i) the stochastic intrinsic perturbations $\sum _{i=1}^{L_1}\mathrm{\Delta }{N}_i{g}_i(x(t))P(t-t_i)$—due to genetic variations—and $\sum _{j=1}^{L_2}\delta N_j{h}_j(x(t))d{W}_j(t)$—due to intrinsic parameter fluctuations—can be tolerated by the synthetic gene network, (ii) the desired behavior x_d can be obtained, ie, x(t)→x_d as t→∞, and (iii) the following disturbance filtering (attenuation) level ρ can be achieved:

$$\frac{E{\int }_0^{\infty }{(x(t)-x_d)}^{T}Q(x(t)-x_d)\mathit{dt}}{E{\int }_0^{\infty }v{(t)}^{T}v(t)\mathit{dt}}\le {\rho }^2$$ (2)

for all possible environmental disturbances v(t), where Q ≥ 0 is a symmetric weighting matrix and ρ < 1 is a disturbance filtering level prescribed by the synthetic biologist beforehand. In other words, the effect of environmental disturbances v(t) on the regulation error x(t) − x_d should be less than the disturbance filtering level ρ, from the average energy perspective. In this situation, the synthetic gene network can efficiently attenuate the effect of environmental disturbances on the regulation of network state x(t) to the desired behavior x_d. There may be a trade-off between the disturbance filtering level ρ and the feasible parameter design range; ie, a small ρ with a strict specification of disturbance filtering may lead to a small feasible range of N. According to the design specifications (i)–(iii) of the stochastic synthetic gene network in (1), the design goal is to choose some kinetic parameters and decay rates in the stoichiometric matrix N from the biologically feasible parameter range [N₁,N₂] so that the desired steady state x_d can be achieved, the stochastic variations $\sum _{i=1}^{L_1}\mathrm{\Delta }{N}_i{g}_i(x(t))P(t-t_i)$ and $\sum _{j=1}^{L_2}\delta N_j{h}_j(x(t))d{W}_j(t)$ can be robustly tolerated (stabilized), and the prescribed disturbance filtering level ρ on environmental disturbances v(t) in (2) can be attained.

In order to achieve the desired steady state x_d, for convenience of design the origin of the nonlinear stochastic synthetic system in (1) should be shifted to x_d. In such a situation, if the shifted nonlinear stochastic synthetic system is robustly stabilized at the origin, then the robust stability of the desired steady state x_d will be equivalently achieved. This will simplify the design procedure of the synthetic gene network. Let us denote x̃(t) = x(t) − x_d ; we then get the following shifted stochastic system:

$$\begin{array}{l}d\tilde{x}(t)=(\mathit{Nf}(\tilde{x}(t))+v(t))\mathit{dt}+\sum _{i=1}^{L_1}\mathrm{\Delta }{N}_i{g}_i(\tilde{x}(t))P(t-t_i)\mathit{dt}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+\sum _{j=1}^{L_2}\delta N_j{h}_j(\tilde{x}(t))d{W}_j(t)\end{array}$$ (3)

ie, the origin x̃(t) ≡ 0 of the stochastic synthetic biological system in (3) is at the desired steady state x_d of the original stochastic synthetic biological system in (1), ie, the regulation problem of the nonlinear stochastic synthetic gene network in (1) to the desired state x_d is transformed to the stabilization problem of the shifted stochastic gene network to x̃(t) ≡ 0 in (3). For the stochastic synthetic biological system in (3), if we specify N∈[N₁,N₂] such that the origin x̃(t) ≡ 0 can be robustly stabilized to tolerate the stochastic intrinsic perturbations $\sum _{i=1}^{L_1}\mathrm{\Delta }{N}_i{g}_i(\tilde{x}(t))P(t-t_i)$ and $\sum _{j=1}^{L_2}\delta N_j{h}_j(\tilde{x}(t)){\mathit{dW}}_j(t)$, and the system can efficiently attenuate the effect of environmental disturbances v(t) to the following prescribed disturbance filtering level ρ (ie, H∞ filtering level):^50,51

$$\begin{array}{l}\frac{E{\int }_0^{\infty }{\tilde{x}}^T(t)Q\tilde{x}(t)\mathit{dt}}{E{\int }_0^{\infty }{v}^T(t)v(t)\mathit{dt}}\le {\rho }^2\\ \text{or}\hspace{0.17em}E{\int }_0^{\infty }{\tilde{x}}^T(t)Q\tilde{x}(t)\mathit{dt}\le \hspace{0.17em}{\rho }^{2}E{\int }_0^{\infty }{v}^T(t)v(t)\mathit{dt}\end{array}$$ (4)

then we get the following robust synthetic gene network results.

Proposition 1

If some design kinetic parameters and decay rates in the stoichiometric matrix N∈[N₁,N₂] are chosen for a synthetic gene network, such that the following phenotype robustness criterion has a positive solution V(x̃(t)) > 0 with V(0) = 0:

$$\begin{array}{l}{\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}(t)}\right)}^T\mathit{Nf}(\tilde{x}(t))+{\tilde{x}}^T(t)Q\tilde{x}(t)\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+\frac{1}{4{\rho }^2}{\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}(t)}\right)}^T\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}(t)}\right)\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+\frac{1}{2}\sum _{j=1}^{L_2}{h}_j^T(\tilde{x}(t))\delta N_j^T\frac{{\partial }^{2}V(\tilde{x}(t))}{\partial {\tilde{x}}^2(t)}\delta N_j{h}_j(\tilde{x}(t))\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+\frac{1}{2}{\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}(t)}\right)}^T\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}(t)}\right)\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+\frac{1}{2}\sum _{j=1}^{L_1}{g}_j^T(\tilde{x}(t))\mathrm{\Delta }{N}_j^T\frac{{\partial }^{2}V(\tilde{x}(t))}{\partial {\tilde{x}}^2(t)}\mathrm{\Delta }{N}_j{g}_j(\tilde{x}(t))\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+\sum _{i=1}^{L_1}\left(V\left(\tilde{x}(t)+\mathrm{\Delta }{N}_i(\tilde{x}(t)\right)\right)-V(\tilde{x}(t))\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}-{\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}(t)}\right)}^T\mathrm{\Delta }{N}_i(\tilde{x}(t)))\lambda \le 0\end{array}$$ (5)

then (a) the stochastic synthetic gene network in (3) can achieve both robust stabilization (phenotype robustness) at the origin x̃(t) ≡ 0 in order to tolerate intrinsic perturbations, genetic variations, and to achieve the prescribed disturbance filtering level ρ on environmental disturbances, ie, the design specifications (i) and (iii) are all satisfied; and (b), if the stochastic synthetic gene network is free of environmental disturbances, ie, v(t) = 0, then the shifted synthetic gene network in (3) will asymptotically converge to x̃(t) ≡ 0 or x(t)→ x_d stochastically or equivalently, and the original stochastic synthetic gene network in (1) will asymptotically converge to the desired steady state x_d stochastically; ie, the design specification (ii) is achieved.

Proof

For the complete proof, see Appendix A. By considering the case of the corresponding uncertainty, the phenotype robustness criterion of the synthetic gene network in (5) can also be rewritten as follows:

$$\begin{array}{l}\underset{\text{int}\mathit{rinsic}\hspace{0.17em}\mathit{robustness}}{\underbrace{\frac{1}{2}\sum _{j=1}^{L_2}{h}_j^T(\tilde{x}(t))\delta N_j^T\frac{{\partial }^{2}V(\tilde{x}(t))}{\partial {\tilde{x}}^2(t)}\delta N_j{h}_j(\tilde{x}(t))}}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+\underset{\mathit{genetic}\hspace{0.17em}\mathit{robustness}}{\underbrace{\left(\begin{array}{l}\frac{1}{2}{\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}(t)}\right)}^T\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}(t)}\right)\hfill \\ +\frac{1}{2}\sum _{j=1}^{L_1}{g}_j^T(\tilde{x}(t))\mathrm{\Delta }{N}_j^T\frac{{\partial }^{2}V(\tilde{x}(t))}{\partial {\tilde{x}}^2(t)}\mathrm{\Delta }{N}_j{g}_j(\tilde{x}(t))\hfill \\ \sum _{i=1}^{L_1}\left(\begin{array}{l}V(\tilde{x}(t)+\mathrm{\Delta }{N}_i(\tilde{x}(t)))-V(\tilde{x}(t))\\ -{\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}(t)}\right)}^T\mathrm{\Delta }{N}_i(\tilde{x}(t))\end{array}\right)\lambda \hfill \end{array}\right)}}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+\underset{\mathit{environmental}\hspace{0.17em}\mathit{robustness}}{\underbrace{\frac{1}{4{\rho }^2}{\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}(t)}\right)}^T\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}(t)}\right)+{\tilde{x}}^T(t)Q\tilde{x}(t)}}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\le -\underset{\mathit{Network}\hspace{0.17em}\mathit{robustness}}{\underbrace{{\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}(t)}\right)}^T\mathit{Nf}(\tilde{x}(t))}}\end{array}$$ (6)

where the network robustness denotes the ability of the synthetic gene network to tolerate the intrinsic molecular noise, genetic variation, and environmental disturbance, so that the phenotype of the network is still maintained in spite of these network uncertainties. From the phenotype robustness criterion of the synthetic gene network in (6), it can be seen that the effect of heritable genetic variations on the phenotype robustness is much larger than non-heritable intrinsic parameter fluctuations. Therefore, network robustness needs to confer more genetic robustness than intrinsic robustness. If we can specify design parameters in the stoichiometric matrix N so that network robustness of the synthetic gene network is large enough to provide intrinsic and genetic robustness to tolerate intrinsic parameter fluctuations and genetic variations, respectively, as well as environmental robustness to resist environmental disturbances, then the phenotype of the synthetic gene network will be robustly stabilized around the desired steady state x_d.

Remarks

Previous robust synthetic designs^45,50,51 considered only random molecular fluctuations. In Proposition 1, both random molecular fluctuations and discontinuous genetic variations from generation to generation are considered in the design procedure of a synthetic gene network that is intended to mimic the real synthetic gene network in the host cell. This is because yeast and E. coli are always selected as host cells in synthetic biology and their fast cell division always leads to genetic variations of synthetic gene circuits.

In general, it is very difficult to specify the stoichiometric matrix N∈[N₁,N₂] to solve HJI in (5) or (6) for V(x̃(t)) > 0 using a systematic method. Therefore, the global linearization method is employed to treat the robust design problem of nonlinear stochastic synthetic gene networks. Suppose the nonlinear stochastic synthetic gene network in (3) could be approximated by the following globally linearized synthetic gene network:

$$\begin{array}{ll}d\tilde{x}(t)=& \sum _{i=1}^M{\alpha }_i(\tilde{x}(t))\\ & [\left(N{A}_i\tilde{x}(t)+v(t)\right)\mathit{dt}+\sum _{j=1}^{L_1}\mathrm{\Delta }{N}_j{G}_{\mathit{ij}}\tilde{x}(t)P\left(t-t_j\right)\mathit{dt}\\ & +\sum _{j=1}^{L_2}\delta N_j{H}_{\mathit{ij}}\tilde{x}(t)d{W}_{\mathit{ij}}(t)]\end{array}$$ (7)

where all the global linearizations are bounded by the following polytope consisting of M vertices:

$$\left[\begin{array}{c}\frac{\partial f(\tilde{x}(t))}{\partial \tilde{x}(t)}\\ ⋮\\ \frac{\partial g_j(\tilde{x}(t))}{\partial \tilde{x}(t)}\\ ⋮\\ \frac{\partial h_j(\tilde{x}(t))}{\partial \tilde{x}(t)}\end{array}\right]\in C_o\left(\left[\begin{array}{c}{A}_1\\ ⋮\\ G_{j1}\\ ⋮\\ H_{j1}\end{array}\right]\left[\begin{array}{c}{A}_2\\ ⋮\\ G_{j2}\\ ⋮\\ H_{j2}\end{array}\right]\left[\begin{array}{c}{A}_M\\ ⋮\\ G_{\mathit{jM}}\\ ⋮\\ H_{\mathit{jM}}\end{array}\right]\right),\forall \tilde{x}(t)$$ (8)

where C_o denotes the convex hull of polytope with M vertices; ie, the nonlinear stochastic synthetic gene network in (3) could be interpolated by M local linearized synthetic gene networks at M vertices as (7). In (7), the interpolation functions α_i (x̃(t)),i = 1 … M are with the properties 0 ≤ α_i (x̃(t)) ≤ 1 and $\sum _{i=1}^M{\alpha }_i(\tilde{x}(t))=1$, ie, the trajectory of nonlinear stochastic synthetic gene network in (3) could be represented by the interpolated synthetic gene network in (7), which is the convex combination of M linearized gene networks at M vertices in (8).

Proposition 2

Assume that some design kinetic parameters and decay rates in the stoichiometric matrix N∈[N₁,N₂] are chosen such that the following M Riccati-like inequalities have a common symmetric positive definite solution P > 0:

$$\begin{array}{l}\mathit{PN}{A}_i+A_i^T{N}^{T}P+\mathit{PP}+\sum _{j=1}^{L_1}{G}_{\mathit{ji}}^T\mathrm{\Delta }{N}_j^T\mathrm{\Delta }{N}_j{G}_{\mathit{ji}}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+\sum _{j=1}^{L_1}\lambda G_{\mathit{ji}}^T\mathrm{\Delta }{N}_j^{T}P\mathrm{\Delta }{N}_j{G}_{\mathit{ji}}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+\sum _{j=1}^{L_2}{H}_{\mathit{ji}}^T\delta N_j^{T}P\delta N_j{H}_{\mathit{ji}}+\frac{1}{{\rho }^2}P{P}^T+Q\le 0,\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}i=1,2,\dots ,M\end{array}$$ (9)

then there are two results: (a) The phenotype robustness of the nonlinear synthetic gene network in (3) or (7) is maintained under intrinsic parameter fluctuations and genetic variations (ie, the synthetic gene network is robustly stable at x_d) and achieves a prescribed disturbance filtering level ρ on environmental disturbance [ie, the design specifications (i) and (iii) are also satisfied]; and (b) if the synthetic gene network is free of environmental disturbance, ie, v(t) = 0, then the synthetic gene network in (3) will asymptotically converge to x̃(t) = 0 stochastically, or, equivalently, the original synthetic gene network in (1) will asymptotically converge to the desired steady state x_d stochastically (ie, the design specification (ii) is achieved). For a complete proof consult Appendix B.

Remarks

The disturbance filtering level ρ in the synthetic gene network could be taken as the evolution level of the synthetic gene network to environmental disturbances. Therefore, in order to maintain the phenotype of the synthetic gene network under intrinsic parameter fluctuations, genetic variations, and environmental disturbances, it is appealing to minimize the disturbance filtering level ρ so as to attenuate the effect of environmental disturbance in the design procedure, ie, specifying design parameters in the stoichiometric matrix N∈[N₁,N₂] to solve the following constrained optimization problem:

$$\begin{array}{l}{\rho }_o=\underset{N\in [N_1,N_2]}{\text{min}}\rho \\ \text{subject}\hspace{0.17em}\text{to}\hspace{0.17em}(9)\end{array}$$ (10)

The optimal filtering level (ie, network sensitivity) ρ₀ of the synthetic gene network can also be taken as the network evolvability of the synthetic gene network under intrinsic parameter fluctuations, genetic variations, and environmental disturbances. From the network evolvability ρ₀ = 1/f₀, where f₀ is the network fitness of the synthetic gene network, the phenotype robustness criterion in (9) can be modified as:

$$\underset{\text{int}\mathit{rinsic}\hspace{0.17em}\mathit{robustness}}{\underbrace{\sum _{j=1}^{L_2}{H}_{\mathit{ji}}^T\delta N_j^{T}P\delta N_j{H}_{\mathit{ji}}}}+\underset{\mathit{genetic}\hspace{0.17em}\mathit{robustness}}{\underbrace{\mathit{PP}+\sum _{j=1}^{L_1}{G}_{\mathit{ji}}^T\mathrm{\Delta }{N}_j^T\mathrm{\Delta }{N}_j{G}_{\mathit{ji}}+\sum _{j=1}^{L_1}\lambda G_{\mathit{ji}}^T\mathrm{\Delta }{N}_j^{T}P\mathrm{\Delta }{N}_j{G}_{\mathit{ji}}}}+\underset{\mathit{environmental}\hspace{0.17em}\mathit{robustness}}{\underbrace{\frac{1}{{\rho }_0^2}{P}^{T}P+Q}}\le \underset{\mathit{network}\hspace{0.17em}\mathit{robustness}}{\underbrace{-{(\mathit{PN}{A}_i+A_i^{T}N}^{T}P}}$$ (11)

i = 1,2, … M, ie, in every local linearized synthetic gene network, if the network robustness can confer intrinsic robustness, genetic robustness, and environmental robustness, then the phenotype of the synthetic gene network can be maintained despite intrinsic parameter fluctuations, genetic variations, and environmental disturbances. In general, if the eigenvalues of NA_i for local synthetic gene networks in (7) contain a more negative real part (ie, the right hand side of (11) is larger), then the synthetic gene network has more network robustness on the right hand side of (11) to confer intrinsic robustness, genetic robustness, and environmental robustness that guarantees the phenotype robustness criterion in (11).

Robust Synthetic Gene Network Design via Network Evolution

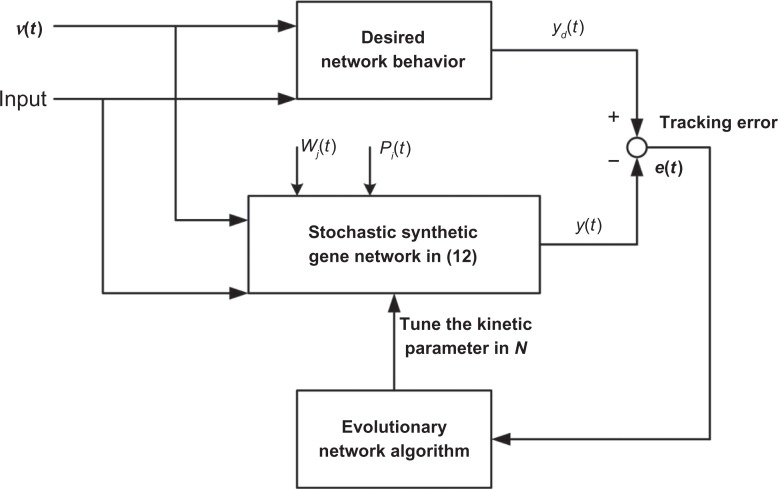
In the above robust synthetic gene network design, we need to select a set of design parameters in the stoichiometric matrix N∈[N₁,N₂] to solve the constrained optimization problem in (10). However, how to solve the constrained optimization problem in (10) so as to select adequate biological components, or designing parameters for achieving the design specifications of a nonlinear stochastic synthetic gene network, is not generally a straightforward task. In light of natural selection of traits best suited for environmental changes being an important mechanism in evolution,⁵² the question of whether a similar strategy can be adapted for gene network design arises. Inspired by biological evolution such as mutation, crossover, recombination, and selection, the evolutionary algorithm is a population-based methodology meant to solve optimization problems.⁵² In recent years, evolutionary systems biology focuses on links between evolution and function, that is, network evolution plays an important role between genotype and phenotype for developing methods to reconstruct and compare transcriptional regulatory networks.^{47,48,53–57} Hence, an evolutionary network algorithm can be employed in tuning the kinetic parameters with respect to component characteristic, in order to maximize the fitness function under intrinsic and extrinsic perturbations in the cellular context.^47,48 In order to mimic the naturally occurring biological systems in the evolutionary process, the fitness function is selected to be inversely proportional to the tracking errors between the synthetic gene network and the desired behaviors (see Fig. 1); this is done so that the evolutionary kinetic parameters of a synthetic biological network can achieve optimal tracking via the maximization of fitness, together with all speed to mimic the evolutionary process of a gene network. If the adaptations of kinetic parameters of a synthetic gene network are reflected by the proposed network evolution algorithm to achieve optimal fitness, the evolutionary gene network will both optimally track the desired biological function in spite of intrinsic parameter fluctuations, genetic variations, and environmental disturbances, and it will behave more robustly inside a host cell.

Figure 1.

The block diagram of the proposed optimal tracking scheme for a synthetic gene network via network evolution algorithm.

Notes:y_d(t) and y(t) denote the desired and actual output of synthetic gene network, W_j(t) and P_i(t) denote the Wiener process and the Poisson point process of random molecular fluctuations and genetic mutations, respectively.

Consider using the nonlinear stochastic gene network in (1) to describe a synthetic gene network in the host cell as follows:

$$\begin{array}{l}\mathit{dx}(t)=\left(\mathit{Nf}(x(t))+v(t)\right)\mathit{dt}+\sum _{i=1}^{L_1}\mathrm{\Delta }{N}_i{g}_i(x(t))P(t-t_i)\mathit{dt}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+\sum _{j=1}^{L_2}\delta N_j{h}_j(x(t))d{W}_j(t)\\ \hspace{0.17em}y(t)=\mathit{Cx}(t)\end{array}$$ (12)

where y(t) denotes the output vector. For example, we are only interested in the last gene output, then y(t) = x_n(t) and c = [00 … 001]. In real biological networks, the gene network in (12) could evolve adaptively with kinetic parameters in N by natural selection through mutations (or genetic variations), so that y(t) can robustly achieve some desired behavior y_d(t) in spite of intrinsic parameter fluctuations, genetic variations, and environmental disturbances (see Fig. 1). In the network evolution design method, we mimic the evolutionary biological network to adapt the kinetic parameters in N for the synthetic genetic network in (12). This is done via an evolutionary network algorithm under a fitness function, both so that the synthetic gene network can achieve a desired behavior, and intrinsic parameter fluctuations, genetic variations, and environmental disturbances in vivo can be tolerated.

Let us denote tracking errors between the output of a synthetic gene network and the output of some desired systems of interest as follows (see Fig. 1):

$$e(t)=y_d(t)-y(t)$$ (13)

where y_d(t) denotes the output of some desired systems, eg, a desired XOR logic circuit. Then our design purpose is to tune design parameters in the stoichiometric matrix N∈[N₁,N₂] using network evolution algorithm so that the nonlinear stochastic gene network in (12) can achieve the following optimal tracking:

$$\underset{N\in [N_1,N_2]}{\text{min}}E{\int }_0^{t_p}{e}^T(t)e(t)\mathit{dt}$$ (14)

where t_p denotes the time needed to be trained in the adaptive tracking. Since the evolutionary tracking ability of gene networks within synthetic microbes will be an increasingly significant issue as these gene networks become more complex and need to be functional over a long period of time, t_p has to be large enough that synthetic gene networks can perform long-term functions under intrinsic parameter fluctuations, genetic variations, and environmental disturbances. If the above mean square tracking error can be minimized for the nonlinear stochastic synthetic gene network with intrinsic parameter fluctuations, genetic variations, and environmental disturbances, the robust synthetic gene network design can be achieved under stochastic intrinsic parameter fluctuations, genetic variations, and environmental disturbances in vivo so that the synthetic gene network can track a desired behavior more reliably in the host cells. Therefore, general principles are needed for engineering evolutionary synthetic gene networks that will optimize robust tracking over time.

In general, it is not easy to directly solve the constrained optimization tracking problem in (14) by using the conventional optimal method and tuning the design parameters in the stoichiometric matrix N∈[N₁,N₂] for the nonlinear stochastic synthetic gene network in (12). According to evolutionary systems biology algorithms, to mimic the parametric tuning of a biological network for the purposes of achieving a desired function via natural selection, an artificial network evolution algorithm has been developed; this network mimics the real natural selection scheme for tuning the design parameters in the stoichiometric matrix N∈[N₁,N₂] to achieve the optimal tracking design of the synthetic gene network in (14), only with a faster speed than real natural selection.⁴⁸ Evolution algorithms⁴⁸ are the result of an effort to model adaptation phenomena in natural and artificial systems. These evolution algorithms will be modified to tune the kinetic parameters of the nonlinear stochastic gene network in (12) that is the so-called network evolution algorithm, in order to rapidly evolve to a desired output behavior via a fitness function. In the nonlinear stochastic synthetic gene network in (12), let us denote the tracking mean square error in (14) as:

$$J(N)=E{\int }_0^{t_p}{e}^T(t)e(t)\mathit{dt}$$ (15)

and define the fitness function as:^58–60

$$F(N)=\frac{1}{J(N)}$$ (16)

That is, a small mean square tracking error would imply a large fitness and vice versa. If we adapt the kinetic parameters (chromosomes) in the stoichiometric matrix N∈[N₁,N₂] by network evolution algorithms to minimize J in (15) or (16), then we can achieve the maximization of fitness function in (16) for the synthetic gene network in (12) to meet the natural selection in evolution.

Therefore, the robust synthetic gene network design with desired output behavior y_d(t) in Figure 1 is equivalent to solving the following fitness maximization problem by network evolution algorithms:^47,48

$$F\left(N^{*}\right)=\underset{N\in [N_1,N_2]}{\text{min}}F\left(N\right)$$ (17)

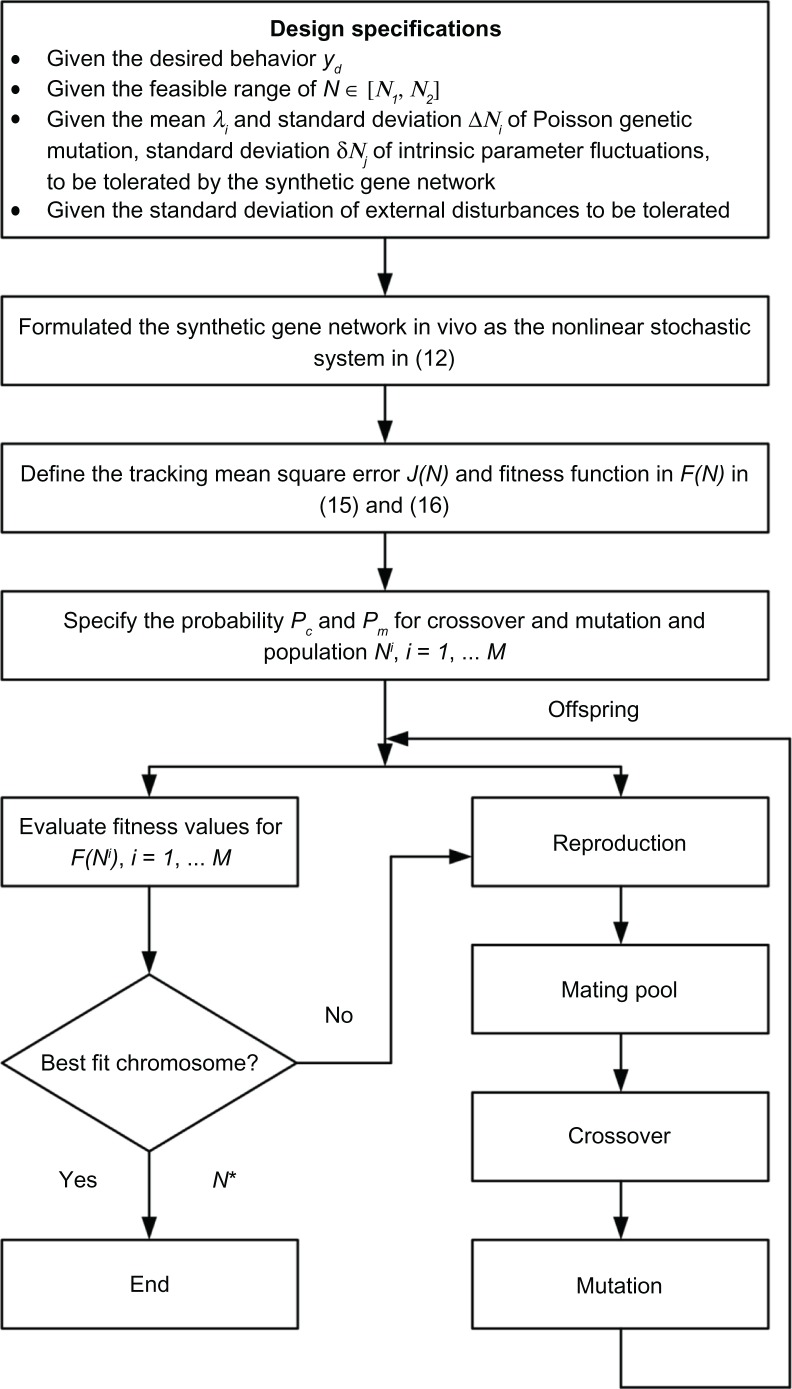
The network evolution algorithm is employed to solve the above fitness maximization problem via genetic operators such as selection, crossover, and mutation, and to mimic natural selection in the evolutionary process for tuning the kinetic parameters in the stoichiometric matrix N∈[N₁,N₂] of a synthetic gene network to solve the optimization problem in (17). This is done so as to achieve robust optimal tracking of the desired behavior. A simple network evolution algorithm is proposed for robust synthetic gene network design as follows (see Fig. 2):⁴⁸ Step (1), start with the design specifications such as the mean value λ and standard deviations ΔN_i of Poisson genetic variations, the standard deviations δN_j of intrinsic parameter fluctuations and the standard deviation σ_v of environmental disturbances v(t) in (12), which are to be tolerated by synthetic gene networks in the host cells; Step (2), take the design specifications in Step (1) and model the synthetic gene network as a nonlinear stochastic synthetic gene network in (12), then specify the desired output y_d and define the tracking error e(t) = y_d(t) − y(t) and fitness function F(N) in (16); Step (3), specify the probabilities P_c and P_m for crossover and mutation in the network evolution algorithm, respectively, and the population Nⁱ,i = 1,2, … M with size M; Step (4), randomly generate a population of candidate chromosomes; Step (5), evaluate the fitness F(Nⁱ) for each candidate solution Nⁱ∈[N₁,N₂] in the population to find the best fit N^* for achieving the best fitness F(N^*); Step (6), if the search goal is achieved, or an allowable generation is attained, then stop. Otherwise, continue to the next step; Step (7), replace the current population with a new population by applying selection, crossover, and mutation operations to the current population and go to Step (5).

Figure 2.

The flow chart of network evolution algorithm for solving the best fit N^* of synthetic gene network design from the maximization problem of the fitness function in (17).

Remark

Unlike natural selection, the above intelligent network evolution algorithm can be incorporated with an elitist strategy to enhance the convergence of network evolution algorithms. This strategy copies the best chromosomes from the old population into the next population so as to prevent losing the best solutions in succeeding iterations. It has been shown that the elitist strategy can improve the performance of network evolution algorithm.

The proposed network evolution algorithm is a powerful search algorithm for kinetic parameter selection in synthetic gene network design procedures involving natural genetics. The algorithm evaluates many points in the parameter space of the stoichiometric matrix N∈[N₁,N₂] (genotype space) for the best fitness F(N^*), so as to achieve a robust synthetic gene network design with a desired behavior in vivo. A similar genetic algorithm (GA) based design algorithm has also been developed for synthetic genetic oscillators with prescribed amplitude, period, and phase.⁴⁷ GA is also a search algorithm that mimics natural selection in an evolutionary process but with chromosomes in binary bits. When the number of kinetic parameters to be designed becomes large, the length of binary chromosomes also becomes large, thus increasing the difficulty in searching the best fit design parameters for complex synthetic gene networks.

Robust Synthetic Gene Network Design via Library-Based Network Evolution

Many standard parts (devices) have recently been constructed for BioBrick,^50,51 from which some adequate parts will be selected by synthetic biologists to be physically assembled into a multi-component synthetic gene network. In order to completely implement a transcription unit in a synthetic gene network, one needs the promoter, ribosome binding site (RBS), protein coding region, and a terminator, which can be obtained from the BioBrick. Therefore, several promoter libraries and promoter-RBS libraries have been constructed for the design of synthetic gene networks according to the kinetic activities of promoters and protein expression abilities of promoter-RBS, respectively. In other words, if we select only an adequate set of promoter devices or promoter-RBS devices from the corresponding libraries, then we could engineer a robust synthetic gene network with a desired behavior.^50,51

Let us denote promoter libraries and promoter-RBS libraries as Lib_i, i = 1, … m. In this situation, the robust design of the synthetic gene network via network evolutionary algorithm in Proposition 2 can be changed to the following library-based evolutionary search algorithm (for robust synthetic gene network design), by selecting a set of promoter devices or a set of promoter-RBS devices from the corresponding libraries.

Proposition 3

Assume we select a set of promoter devices or a set of promoter-RBS devices from the corresponding libraries, ie, N∈ Lib_i, i = 1,2, … m, such that the Riccati-like inequalities in (9) have a positive definite solution; then (a) the phenotype robustness of nonlinear synthetic gene network in (3) is both maintained under intrinsic parameter fluctuations and genetic variations, and a prescribed disturbance filtering level ρ on environmental disturbances can also be achieved; and (b), the synthetic gene network in (3) will asymptotically converge to x̃ (t) = 0 or x(t)→x_d stochastically if the environmental disturbance disappears.

Similarly, the optimal disturbance filtering (network sensitivity) design of synthetic gene network in (10) can be changed by the library-based evolutionary search method, as follows:

$$\begin{array}{l}{\rho }_o=\underset{N\in {\mathit{Lib}}_i,i=1,2,\dots ,m}{\text{min}}\rho \\ \text{subject}\hspace{0.17em}\text{to}\hspace{0.17em}(9)\end{array}$$ (18)

When the number of promoter devices or promoter-RBS devices of libraries becomes very large, it is not easy to select an adequate set of promoter devices or promoter-RBS devices from the corresponding promoter libraries or promoter-RBS libraries. In this situation, the library-based network evolution algorithm can be used to search a set of promoter devices or a set of promoter-RBS devices from the corresponding libraries, in order to let the synthetic gene network achieve a desired behavior. Therefore, selecting corresponding design parameters from the feasible range of the stoichiometric matrix N∈[N₁,N₂] in (17) for the fitness maximization should be changed to selecting a set of promoter devices or promoter-RBS devices from their corresponding libraries as follows:

$$F\left(N^{*}\right)=\underset{N\in \mathit{Li}{b}_i,i=1,2,\dots ,m}{\text{min}}F\left(N\right)$$ (19)

where the fitness function is defined as the inverse of the total tracking error in (16). That is, the network evolution of the synthetic gene network selects only some devices from libraries Lib_i, i = 1,2, … m so as to achieve the optimal tracking of the desired output behavior y_d(t) in Figure 1. In other words, the synthetic network evolves only within the promoter libraries or promoter-RBS libraries through an evolution algorithm that maximizes the fitness function in (19) and achieves the optimal tracking of desired output behavior y_d(t).

Computer Simulation Example

Here, an in silico design example is introduced to both verify the robust synthetic gene network design and to confirm the robust stabilization and disturbance attenuation performance by the network evolution algorithm, using the GA searching method. Although the synthetic gene circuits may be either simple devices or more complex ones, their dynamic profiles in vivo can be represented by nonlinear stochastic ODEs, which are suitable for the proposed systematic design method. In this example, we want to synthesize a cascade loop of transcriptional inhibitions built in E. coli,^45,61 which is called the repressilator.¹⁵ The synthetic gene network is represented in Figure 3. In this synthetic gene network, the expression dynamics of three repressor proteins (TetR, LacI, CI) and one fluorescent protein (EYFP) are determined by the regulation occurring among four genes (tetR, lacI, cI, and eyfp, respectively).⁴³ The protein CI inhibits gene eyfp and gene tetR, TetR inhibits gene lacI, and LacI inhibits gene cI. The fluorescence, due to the protein EYFP, is the measured output of the system.¹⁵ The dynamic equations of synthetic gene network in Figure 3 are given as follows:^43,45

$$\left[\begin{array}{c}{\dot{x}}_{\mathit{tetR}}\\ {\dot{x}}_{\mathit{lacI}}\\ {\dot{x}}_{\mathit{cI}}\\ {\dot{x}}_{\mathit{eyfp}}\end{array}\right]=\left[\begin{array}{c}{\kappa }_{\mathit{tetR},0}+{\kappa }_{\mathit{tetR}}{r}_{\mathit{tetR}}(x_{\mathit{cI}})-{\gamma }_{\mathit{tetR}}{x}_{\mathit{tetR}}\\ {\kappa }_{\mathit{lacI},0}+{\kappa }_{\mathit{lacI}}{r}_{\mathit{lacI}}(x_{\mathit{tetR}})-{\gamma }_{\mathit{lacI}}{x}_{\mathit{lacI}}\\ {\kappa }_{\mathit{cI},0}+{\kappa }_{\mathit{cI}}{r}_{\mathit{cI}}(x_{\mathit{lacI}})-{\gamma }_{\mathit{cI}}{x}_{\mathit{cI}}\\ {\kappa }_{\mathit{eyfp},0}+{\kappa }_{\mathit{eyfp}}{r}_{\mathit{eyfp}}(x_{\mathit{cI}})-{\gamma }_{\mathit{eyfp}}{x}_{\mathit{eyfp}}\end{array}\right]$$ (20)

where the nominal generating ratios of the corresponding proteins are:

$${\kappa }_{\mathit{tetR},0}=150,{\kappa }_{\mathit{lacI},0}=587,{\kappa }_{\mathit{cI},0}=210,{\kappa }_{\mathit{eyfp},0}=3487;$$ (21)

the biological allowable ranges of the kinetic parameters are:

$$\begin{array}{l}{\kappa }_{\mathit{tetR}}\in [50,5000],{\kappa }_{\mathit{lacI}}\in [70,7000],\\ {\kappa }_{\mathit{cI}}\in [75,8000],{\kappa }_{\mathit{eyfp}}\in [30,30000];\end{array}$$ (22)

and the biological allowable ranges of the decay rates are:

$$\begin{array}{l}{\gamma }_{\mathit{tetR}}\in [0.2,\hspace{0.17em}\hspace{0.17em}4.8],\hspace{0.17em}\hspace{0.17em}{\gamma }_{\mathit{lacI}}\in [0.02,\hspace{0.17em}\hspace{0.17em}0.14],\\ {\gamma }_{\mathit{cI}}\in [0.6,\hspace{0.17em}\hspace{0.17em}0.8],{\gamma }_{\mathit{eyfp}}\in [0.1,\hspace{0.17em}\hspace{0.17em}1]\end{array}$$ (23)

which need to be specified according to some design specifications. Furthermore, r_tetR(x), r_lacI(x), r_cI(x), and r_eyfp(x) are the Hill functions for repressors. The Hill function is a decreasing S-shaped curve, which can be described in the form r_i(x) = β/(1+(x/K_i)ⁿ) with β = 1, n = 2, K_i = 1000, i = tetR, lacI, cI, eyfp.⁶²

Figure 3.

Synthetic transcriptional cascade loop in silico design example.

Notes: TetR represses lacI, LacI represses cI and CI represses eyfp and tetR. The fluorescent protein EYFP is the output.

In reality the gene network in the host cell (ie, E. coli) not only suffers from intrinsic parameter fluctuations, but also from external disturbances. According to the stochastic gene network in (1), the stochastic gene network in (20), which is affected by random parameter fluctuation sources and external noises, can be represented by following nonlinear stochastic system:

$$\begin{array}{cc}d\left[\begin{array}{c}{x}_{\mathit{tetR}}\\ x_{\mathit{lacI}}\\ x_{\mathit{cI}}\\ x_{\mathit{eyfp}}\end{array}\right]& =\left(\left[\begin{array}{c}{\kappa }_{\mathit{tetR},0}+{\kappa }_{\mathit{tetR}}{r}_{\mathit{tetR}}(x_{\mathit{cI}})-{\gamma }_{\mathit{tetR}}{x}_{\mathit{tetR}}\\ {\kappa }_{\mathit{lacI},0}+{\kappa }_{\mathit{lacI}}{r}_{\mathit{lacI}}(x_{\mathit{tetR}})-{\gamma }_{\mathit{lacI}}{x}_{\mathit{lacI}}\\ {\kappa }_{\mathit{cI},0}+{\kappa }_{\mathit{cI}}{r}_{\mathit{cI}}(x_{\mathit{lacI}})-{\gamma }_{\mathit{cI}}{x}_{\mathit{cI}}\\ {\kappa }_{\mathit{eyfp},0}+{\kappa }_{\mathit{eyfp}}{r}_{\mathit{eyfp}}(x_{\mathit{cI}})-{\gamma }_{\mathit{eyfp}}{x}_{\mathit{eyfp}}\end{array}\right]+\left[\begin{array}{c}{v}_1\\ v_2\\ v_3\\ v_4\end{array}\right]\right)\mathit{dt}\\ & +\left(\left[\begin{array}{c}\delta {\kappa }_{\mathit{tetR},0}+\delta {\kappa }_{\mathit{tetR}}{r}_{\mathit{tetR}}(x_{\mathit{cI}})-\delta {\gamma }_{\mathit{tetR}}{x}_{\mathit{tetR}}\\ \delta {\kappa }_{\mathit{lacI},0}+\delta {\kappa }_{\mathit{lacI}}{r}_{\mathit{lacI}}(x_{\mathit{tetR}})-\delta {\gamma }_{\mathit{lacI}}{x}_{\mathit{lacI}}\\ \delta {\kappa }_{\mathit{cI},0}+\delta {\kappa }_{\mathit{cI}}{r}_{\mathit{cI}}(x_{\mathit{lacI}})-\delta {\gamma }_{\mathit{cI}}{x}_{\mathit{cI}}\\ \delta {\kappa }_{\mathit{eyfp},0}+\delta {\kappa }_{\mathit{eyfp}}{r}_{\mathit{eyfp}}(x_{\mathit{cI}})-\delta {\gamma }_{\mathit{eyfp}}{x}_{\mathit{eyfp}}\end{array}\right]\right)d\omega (t)\end{array}$$ (24)

The robust synthetic gene network requires designing the parameters κ_i and γ_i in the stoichiometric matrix N within biological allowable range, ie, N∈[N₁,N₂], so as to meet the following specifications (where N = [κ_tetR   κ_lacI   κ_cI   κ_eyfp   γ_tetR   γ_lacI   κ_cI   κ_eyfp]^T in this example):

1. The standard deviations of intrinsic parameter fluctuations and external noises to be tolerated are given as:

   $$\begin{array}{l}\left[\begin{array}{c}\delta {\kappa }_{\mathit{tetR},0}\\ \delta {\kappa }_{\mathit{lacI},0}\\ \delta {\kappa }_{\mathit{cI},0}\\ \delta {\kappa }_{\mathit{eyfp},0}\end{array}\right]=\left[\begin{array}{c}30\\ 50\\ 30\\ 50\end{array}\right],\left[\begin{array}{c}\delta {\kappa }_{\mathit{tetR}}\\ \delta {\kappa }_{\mathit{lacI}}\\ \delta {\kappa }_{\mathit{cI}}\\ \delta {\kappa }_{\mathit{eyfp}}\end{array}\right]=\left[\begin{array}{l}50\hfill \\ 200\hfill \\ 50\hfill \\ 200\hfill \end{array}\right],\\ \left[\begin{array}{c}\delta {\gamma }_{\mathit{tetR}}\\ \delta {\gamma }_{\mathit{lacI}}\\ \delta {\kappa }_{\mathit{cI}}\\ \delta {\kappa }_{\mathit{eyfp}}\end{array}\right]=\left[\begin{array}{c}0.3\\ 0.3\\ 0.3\\ 0.3\end{array}\right],\left[\begin{array}{c}{v}_1\\ v_2\\ v_3\\ v_4\end{array}\right]=\left[\begin{array}{l}10n_1\hfill \\ 1000n_2\hfill \\ 10n_3\hfill \\ 1000n_4\hfill \end{array}\right]\end{array}$$ (25)

   where n_i, i = 1, …, 4 are independent Gaussian white noises with unit variance.
2. The desired steady state x_d is given by:⁴³

   $$x_d=\left[\begin{array}{c}{x}_{\mathit{tetR},d}\\ x_{\mathit{lacI},d}\\ x_{\mathit{cI},d}\\ x_{\mathit{eyfp},d}\end{array}\right]=\left[\begin{array}{l}1000\hfill \\ 30000\hfill \\ 300\hfill \\ 30000\hfill \end{array}\right]$$ (26)

3. The prescribed disturbance filtering (attenuation) level of external disturbances is specified by ρ = 0.3.

Based on the design procedure, we first shift the desired steady state of the synthetic gene system to x_d the origin, then perform the global linearization in (8) to obtain A_i and H_ji for i = 1, …, 3, j = 1, …, 4, and finally solve inequalities in (9) via network evolution for fine tuning parameters. The allowable range [N₁,N₂] of the stoichiometric matrix N has been obtained by the parameter-range specification in (22) and (23). Following the proposed network evolution algorithm in the earlier section, the prescribed disturbance filtering level ρ could be easily obtained by solving Riccati-like inequalities in (9); this is done via a network evolution algorithm⁴⁸ for fine tuning parameters from the allowable range [N₁,N₂] of the stoichiometric matrix N. Using the GA searching method,⁴⁷ we can find a positive definite matrix P with the prescribed disturbance filtering level ρ = 0.3 of inequalities in (9), as long as the design kinetic parameters (κ_i) and decay rates (γ_i) of the synthetic gene network are specified within the following ranges:

$$\begin{array}{l}{\kappa }_{\mathit{tetR}}\in [891,4159],{\kappa }_{\mathit{lacI}}\in [1248,5822],\\ {\kappa }_{\mathit{cI}}\in [1422,6652],{\kappa }_{\mathit{eyfp}}\in [5124,24906];\\ {\gamma }_{\mathit{tetR}}\in [0.97,4.03],{\gamma }_{\mathit{lacI}}\in [0.04,0.08],\\ {\gamma }_{\mathit{cI}}\in [0.65,0.75],{\gamma }_{\mathit{eyfp}}\in [0.27,83];\end{array}$$ (27)

then the three design specifications (i)—(iii) are satisfied, ie, if we select κ_i and γ_I within the ranges in (27), the designed synthetic gene network can tolerate the parameter fluctuations with standard deviations specified in (25) and the external noises could be attenuated below the prescribed disturbance filtering level ρ = 0.3.

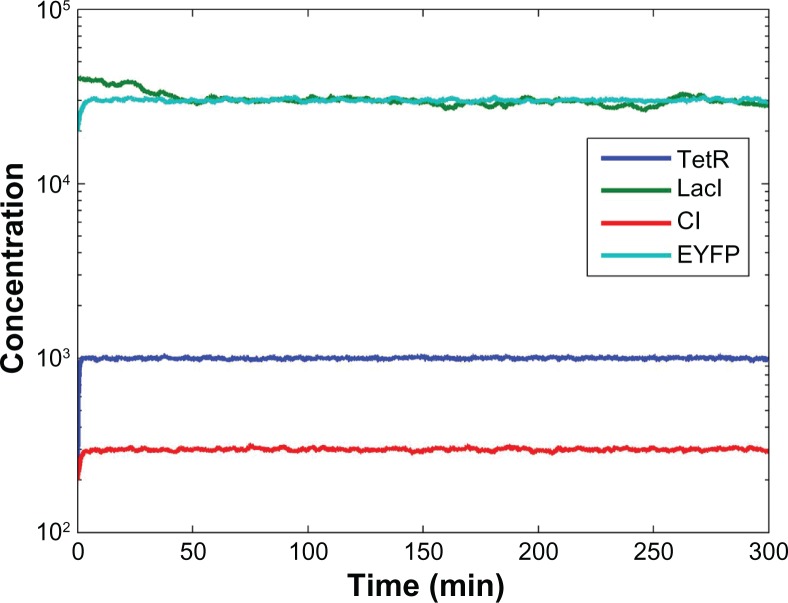
In order to confirm the performance of the proposed robust synthetic gene network, we design the synthetic gene network with a set of kinetic parameters (κ_i) and decay rates (γ_i) selected in the ranges given in (27); this is one so as to see if they can achieve the desired steady state in spite of intrinsic parameter fluctuations and external disturbances. Let us choose the following design parameters from the ranges given in (27):

$$\left[\begin{array}{c}{\kappa }_{\mathit{tetR}}\\ {\kappa }_{\mathit{lacI}}\\ {\kappa }_{\mathit{cI}}\\ {\kappa }_{\mathit{eyfp}}\end{array}\right]=\left[\begin{array}{l}2000\hfill \\ 2000\hfill \\ 2000\hfill \\ 15000\hfill \end{array}\right],\left[\begin{array}{c}{\gamma }_{\mathit{tetR}}\\ {\gamma }_{\mathit{lacI}}\\ {\gamma }_{\mathit{cI}}\\ {\gamma }_{\mathit{eyfp}}\end{array}\right]=\left[\begin{array}{l}1.98\hfill \\ 0.05\hfill \\ 0.7\hfill \\ 0.57\hfill \end{array}\right]$$ (28)

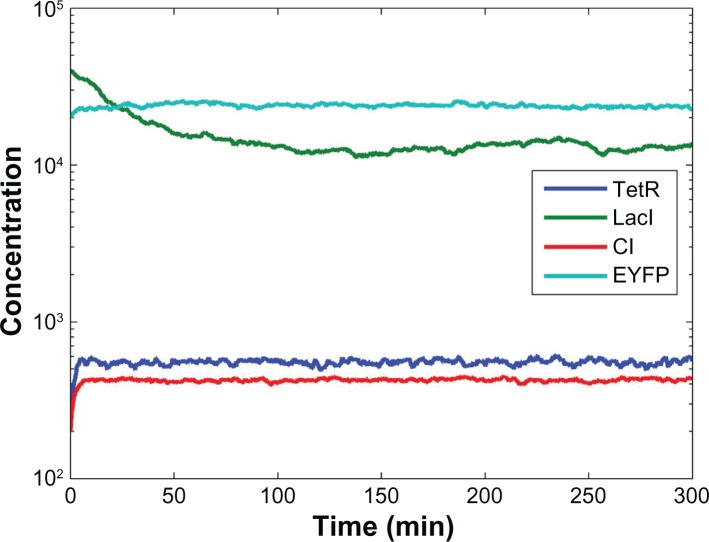
In Figure 4, by choosing design parameters in (28) which are within the specified range in (27), the desired steady states (x_d) in (26) can be achieved under intrinsic parameter fluctuations and external disturbances by the proposed robust synthetic gene network design method. In contrast, in Figure 5, if the design parameters are outside the specified range in (27), ie, (κ_tetR, κ_lacI, κ_cI, κ_eyfp) = (150, 100, 500, 1500) and (γ_tetR, γ_lacI, γ_cI, γ_eyfp) = (0.5, 0.05, 0.5, 0.2), the synthetic gene network suffers from more fluctuations and the expression cannot be guaranteed to achieve the desired steady state (x_d) in (26) under the influence from intrinsic parameter fluctuations and external disturbances in the host cell. From the Monte Carlo simulation with 500 runs, the disturbance filtering level of external disturbances in (4), which should be bounded by the prescribed disturbance filtering level ρ = 0.3, is estimated as:

$$\frac{E{\int }_0^{1000}{\tilde{x}}^{T}Q\tilde{x}\mathit{dt}}{E{\int }_0^{1000}{v}^T\mathit{vdt}}={0.2874}^2<{0.3}^2$$ (29)

Figure 4.

Within the specified parameter range in (27), by choosing the design parameters κ_i and γ_i given in (28), it is seen that, when under the influence of intrinsic parameter fluctuations and external disturbances in the host cell, the synthetic gene network has enough robust stability and noise filtering ability to achieve the desired steady state x_d described in (26).

Figure 5.

As evidence to the contrary, if the design parameters are outside the specified range in (27), eg, with (κ_tetR, κ_lacI, κ_cI, κ_eyfp) = (150, 100, 500, 1500) and (γ_tetR, γ_lacI, γ_cI, γ_eyfp) = (0.5, 0.05, 0.5, 0.2), the expression of the synthetic gene network shows that it suffers from more fluctuations and that, when under the influence of intrinsic parameter fluctuations and external disturbances in the host cell, the expression cannot be guaranteed to achieve the desired steady state x_d described in (26).

Clearly, the prescribed disturbance filtering level is achieved by the proposed method. In the simulation results, it is obvious that the synthetic gene network applying the proposed design method has both the robust stability to tolerate intrinsic parameter fluctuations and the filtering ability needed to attenuate the external disturbances and achieve the desired steady states. In practical application, if the synthetic gene network has enough robust stability and filtering ability, then the gene network could work with proper functions under intrinsic fluctuations and external molecular noises on the host cell. Furthermore, according to the network evolution algorithm, the design ranges of kinetic parameters and decay rates can easily be solved by fine tuning parameters; this fine tuning can be done via GA-based searching methods in design procedures found in Matlab’s LMI Toolbox. Using the proposed design procedure, the synthetic gene network can be guaranteed to meet the three design specifications (i)–(iii) with enough robust stability and noise filtering to achieve the desired steady state (ie, to maintain the proper network function). Here, the primary goal is to confirm that GA-based search methods in the design procedure can be used to efficiently find the suitable system parameters needed for synthetic gene circuit design. Based on the proposed design procedure, the robust synthetic gene circuit can function properly to achieve some steady state (x_d) under intrinsic parameter fluctuations and with prescribed disturbance filtering level (ρ) of external disturbances; this can be recognized from our simulation results.

Discussion

The simulation example in (24) consists of a negative circuit made from the sequence inhibitions of three repressor genes and a fluorescent output; it is designed to reveal the gene expression state in vivo. In general, negative feedback can reduce noises and improve stability,⁶³ but it can also generate oscillations with a long time delay.^15,64 In this example, the kinetic parameters κ_i and decay rates γ_i chosen from the feasible ranges in (27) can satisfy the three design specifications (i)–(iii). To modify the kinetic parameter κ_i (ie, binding affinity), popular recombination technology can be used to insert strong or weak TF binding sites—or simply delete TF binding sites—in the promoter region of a regulated gene.^65,66 To change the decay rate γ_i, shortening the 3′ polyadenylate tail by deadenylation or removal of 3′ polyadenylate tail can facilitate the decay rate γ_i⁶⁷ Therefore, the decay rate can be easily changed by shortening or elongating the gene’s 3′ polyadenylate tail. Specification (ii) delivers the desired steady state x_d to validate the robust regulation of synthetic gene network. To tolerate the effects of uncertainties, specifications (i) provides the prescribed standard deviations of intrinsic parameter fluctuations and the external noises to be tolerated in vivo; specification (iii) provides the prescribed disturbance filtering level ρ required to guarantee the stability robustness and filtering ability of the synthetic gene network.

The study and design of gene networks has become a hot topic in systems and synthetic biology. At the nano-scale, a gene regulatory network inherently experiences random intrinsic parameter fluctuations, genetic variations, and environmental disturbances. A nascent field, synthetic biology, has recently been anticipated to have important applications in biotechnology and medicine and to contribute significantly to better understanding of the functioning of complex biological systems. At present, the development of a gene network under some prescribed design specifications is still difficult; most newly created gene networks are non-functional due to intrinsic parameter fluctuations, genetic variations, and environmental disturbances. How to design a robust synthetic gene network with desired behavior under some specified (or allowable) intrinsic parameter fluctuations, genetic variations, and environmental disturbances in vivo is an important issue for robust synthetic gene networks. This is also the most important feature of a biological network—to maintain its phenotype in the face of genetic variations and changing environmental conditions in the evolutionary process.

To achieve this consistency, biological networks strike a balance between robustness and evolvability, ie, between resisting and allowing changes in their own internal states. In a series of studies,^10,11 we have developed a single unifying mathematical framework for encompassing such diverse examples of stochastic biological networks to discuss intrinsic robustness, genetic robustness, environmental robustness, and network robustness, as well as their trade-off in systems, synthetic, ecological, and evolutionary biology. According to our analyses, the phenotype robustness criteria of stochastic biological networks in systems, synthetic, ecological, and evolutionary biology have a similar mathematical framework. The biological networks in systems, synthetic, ecological, and evolutionary biology can be modeled as nonlinear stochastic systems with intrinsic parameter fluctuations, genetic variations, and environmental disturbances. In these systems intrinsic parameter fluctuations are described by the Wiener (Brownian) process, environmental disturbances are described by the Gaussian white noise, and genetic variations are described by the Poisson point process. Therefore, the interplay of network robustness, intrinsic robustness, genetic robustness, and environmental robustness can be analyzed by the nonlinear stochastic system theory. This interplay can also therefore be analyzed by linear stochastic system theory to get more insight into the network robustness mechanism, when the global linearization technique is employed in interpolating several local linear stochastic systems so as to approximate the nonlinear stochastic system.

From the system theory perspective, the phenotype robustness of nonlinear stochastic gene networks in synthetic biology needs to obey a similar phenotype robustness criterion, ie, “intrinsic robustness + genetic robustness + environmental robustness ≤ network robustness”, which means network robustness needs to be strong enough to tolerate either heritable perturbations (genetic variations) or non-heritable perturbations (ie, random molecular fluctuations and environmental disturbances). This robustness is needed so that the phenotype of gene networks can be maintained in systems, synthetic, and evolutionary biology with a similar mathematical framework. The phenotype robustness of the stochastic gene network is completely consistent with the idea of canalization of development and inheritance of acquired characters reported in previous studies.⁶⁸ According to these phenotype robustness criteria, the correlation among intrinsic robustness, genetic robustness, environmental robustness, and network robustness by recent genomic experiments in yeast—ie, genes conferring similar intrinsic, genetic, and environmental robustness to maintain phenotypic robustness—can be rationally explained from the systematic perspective.⁶⁹ In other words, if the network robustness of gene network is large enough, genetic perturbations or environmental disturbances can then be taken over respectively or simultaneously to maintain the functional phenotype in systems, synthetic, and evolutionary biology.

Rather than desirable features of biological networks, genetic, environmental, and phenotypic random variations are inevitably noisy processes in systems, synthetic and, evolutionary biology.^40,70 These stochastic processes arise from the complexity and evolutionary process of biological gene networks. However, there is evidence of high fidelity and minimal noise, including the proof editing of DNA replication and protein translation, in systems and evolutionary biology. Enzymes have evolved toward high specificity. Gene expression is regulated by elaborate mechanisms; random variations seem to have been minimized in systems, synthetic, and evolutionary biology. For instance, gene regulatory networks within bacterial operons may have evolved to minimize genetic and phenotypic noises and infidelity. However, chemo-physical constraints on the specificity and fidelity of biological networks are costly so that there is a trade-off between the benefits of fidelity and its cost. Therefore, if biological networks want to retain enough network robustness to confer intrinsic robustness for tolerating intrinsic parameter fluctuations, genetic robustness for buffering genetic variations, and environmental robustness for resisting environmental disturbances, much effort has to be taken and a high cost must be paid.

In general, it is very difficult to solve the HJI in (5) for the phenotype robustness criterion in synthetic gene networks. With the global linearization technique, the HJI problem for robust stabilization of nonlinear stochastic biological networks is reduced to solving an equivalent set of Riccati-like inequalities in (9), looking for the robust stabilization of each local linearized synthetic gene network. We also found that if the network robustness of each local linearized synthetic gene network can take on the local intrinsic robustness, genetic robustness, and environmental robustness of each local linearized synthetic gene network, then the phenotype of the nonlinear stochastic synthetic gene network could also be maintained. Furthermore, from the robust linear system theory point of view, the global linearization method can be used to solve the robust design problem of nonlinear synthetic gene networks, according to the phenotypic robustness criterion in (11).

In synthetic biology, all biological devices have their own system characteristics chosen within their biological allowable range. Thus, to find decisions that satisfy given design constraints and that meet a specific goal at its optimal value (from a huge search space), genetic algorithms (GA) are used to manipulate the problem of searching many parameters simultaneously. A GA has several advantages. It can quickly scan a vast solution set. The GA works by its own internal rules, which means that it doesn’t have to know any rules of the problem; this is very useful for complex or loosely defined optimization problems. Due to the parallelism that allows them to implicitly evaluate many schemas at once, GAs are particularly well-suited to solving optimal problems where the space of all potential solutions is truly huge, primarily because they can produce multiple, equally good solutions, for the same optimal problem. However, GAs also have some drawbacks. Although GAs find solutions through evolution, this is their biggest disadvantage. Evolution is inductive and thus it evolves away from bad circumstances which may cause a species to evolve into an evolutionary dead end. Therefore, GAs run the risk of finding a suboptimal solution. If the optimal disturbance filtering design problem of the nonlinear stochastic synthetic gene network is convex, GAs will not be the best method to find the optimal solution. However, in practice, GAs are undoubtedly the best choice for (a) quickly finding kinetic parameters and decay rates in the stoichiometric matrix N (from the biologically feasible parameter range [N₁,N₂]) and (b) ensuring the prescribed disturbance filtering level ρ is achieved. In the near future, we hope the synthetic biology industry can reach the stage of mass production for biological devices as the proposed robust synthetic gene network design is suited for the customization and simplification of synthetic gene network design.

Conclusion

In this study, based on the nonlinear stochastic synthetic gene network in vivo, we developed a phenotype robustness criterion for synthetic gene networks; we also proposed a robust synthetic gene network design, using network evolution algorithm, to find out adequate system parameters within feasible ranges for the gene circuit design. Because gene circuit design is similar to electronic chip design, some intrinsic parameter fluctuations (eg, genetic mutations) and external disturbances (eg, molecular noises) may cause the synthetic gene circuits to lose function after a single life-time or a number of generations. Based on our previous studies, similar phenotype robustness criterion is also found in synthetic gene networks. Thus, we also proposed a library-based search method using Genetic Algorithms; this method was used to choose suitable biological devices for use in gene circuit designs that ensure functional performance, in spite of adverse effects from random parameter fluctuations, genetic mutations, and external noises.

This series of studies (Part I to Part III) presents a unifying mathematical framework that describes different levels of stochastic biological networks under intrinsic parameter fluctuations, genetic variations, and environmental disturbances. According to the unifying stochastic biological systems, the phenotype robustness criteria of biological networks in systems, synthetic, ecological, and evolutionary biology are also investigated from the robust stabilization and disturbance sensitivity perspective. It was found that if intrinsic robustness + genetic robustness + environmental robustness ≤ network robustness (ie, network robustness can confer intrinsic robustness for tolerating intrinsic parameter fluctuations, genetic robustness for buffering genetic variations, and environmental robustness for resisting the environmental disturbances), then the phenotype will be robust in biological networks at different levels of systems, synthetic, ecological, or evolutionary biology. Using the global linearization method, we also found that if the network robustness of each local linearized system is greater than the total sum of intrinsic robustness, genetic robustness, and environmental robustness of each local linear system, then the phenotype of the biological network is also maintained, regardless of intrinsic parameter fluctuations, genetic variations, and environmental disturbances. Furthermore, network evolution algorithms are also introduced to mimic genetic evolution under natural selection, to search for adequate design parameters from feasible parameter regions, and to select a set of adequate devices from promoter libraries or promoter-RBS libraries for the purpose of engineering robust synthetic gene network; by robust we mean those networks which can perform reliably under intrinsic parameter fluctuations, genetic variations, and environmental disturbances, in vivo, for a long time. The network evolution-based design method may have significant potential for application in the synthetic design of biological networks when synthetic gene networks become more complex.

Supplementary Data: Appendix

Before the proofs of these propositions, the following lemma is useful and should be given beforehand

Lemma A: For any vector a and b, then we get

$$a^{T}b=2\left(\frac{a^T}{2\rho }\right)(\rho b)\le \frac{1}{4{\rho }^2}{a}^{T}a+{\rho }^2{b}^{T}b,\text{for}\hspace{0.17em}\text{any}\hspace{0.17em}\rho >0.$$

Appendix A: Proof of Proposition 1

Consider the stochastic synthetic gene network in (3) with x̃(0) = 0 and v(t) ≠ 0. Based on Wiener process in intrinsic parameter fluctuations and Poisson point process in genetic variations, we get

$$\begin{array}{l}E{\int }_0^{\infty }{\tilde{x}}^T(t)Q\tilde{x}(t)\mathit{dt}=E\left[V\left(\tilde{x}(0)\right)-V\left(\tilde{x}(t_p)\right)+{\int }_0^{\infty }\left({\tilde{x}}^T(t)Q\tilde{x}(t)+\frac{d}{\mathit{dt}}V\left(\tilde{x}(t)\right)\right)\mathit{dt}\right]\\ \le V(\tilde{x}(0))+E{\int }_0^{\infty }\left(\begin{array}{l}{\tilde{x}}^T(t)Q\tilde{x}(t)+{\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}(t)}\right)}^T\left(\mathit{Nf}(\tilde{x}(t))+v(t)+\sum _{i=1}^{L_1}\mathrm{\Delta }{N}_i{g}_i(\tilde{x}(t))P(t-t_i)+\sum _{j=1}^{L_2}\mathrm{\Delta }{N}_j{h}_j(\tilde{x}(t))d{W}_j(t)\right)\hfill \\ +\sum _{i=1}^L\left(V(\tilde{x}(t)+\mathrm{\Delta }{N}_i(\tilde{x}(t)))-V(\tilde{x}(t))-{\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}(t)}\right)}^T\mathrm{\Delta }{N}_i{g}_i(\tilde{x}(t))\right)\lambda \hfill \\ +\sum _{j=1}^{L_2}\left(h_j^T(\tilde{x}(t))\delta N_j^T\left(\frac{{\partial }^{2}V(\tilde{x}(t))}{\partial {\tilde{x}}^2(t)}\right)\delta N_j{h}_j(\tilde{x}(t))\right)\hfill \end{array}\right)\mathit{dt}\end{array}$$ (A1)

By Lemma A

$${\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}(t)}\right)}^{T}v(t)\le \frac{1}{4{\rho }^2}{\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}(t)}\right)}^T\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}(t)}\right)+{\rho }^2{v}^T(t)v(t)$$ (A2)

$${\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}(t)}\right)}^T\left(\sum _{i=1}^{L_1}\mathrm{\Delta }{N}_i{g}_i(\tilde{x}(t))P(t-t_i)\right)\le \frac{1}{2}{\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}(t)}\right)}^T\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}(t)}\right)+\frac{1}{2}\sum _{i=1}^{L_1}{g}_i^T(\tilde{x}(t))\mathrm{\Delta }{N}_i^T\mathrm{\Delta }{N}_i{g}_i(\tilde{x}(t))$$ (A3)

Substituting (A2) and (A3) into (A1), with V(0) = 0 and EP(t − t_i)dt = Edw_j(t) = 0, we get

$$\begin{array}{l}E{\int }_0^{\infty }{\tilde{x}}^T(t)Q\tilde{x}(t)\mathit{dt}\\ \le V(\tilde{x}(0))+E{\int }_0^{\infty }\left(\begin{array}{l}{\tilde{x}}^T(t)Q\tilde{x}(t)+{\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}(t)}\right)}^T\mathit{Nf}(\tilde{x}(t))+\frac{1}{2}{\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}(t)}\right)}^T\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}(t)}\right)+\frac{1}{2}\sum _{i=1}^{L_1}{g}_i^T(\tilde{x}(t))\mathrm{\Delta }{N}_i^T\mathrm{\Delta }{N}_i{g}_i(\tilde{x}(t))\hfill \\ +\sum _{i=1}^{L_1}\left(V(\tilde{x}(t)+\mathrm{\Delta }{N}_i(\tilde{x}(t)))-V(\tilde{x}(t))-{\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}(t)}\right)}^T\mathrm{\Delta }{N}_i(\tilde{x}(t))\right)\lambda \hfill \\ +\sum _{j=1}^{L_2}\left(h_j^T(\tilde{x}(t))\delta N_j^T\left(\frac{{\partial }^{2}V(\tilde{x}(t))}{\partial {\tilde{x}}^2(t)}\right)\delta N_j{h}_j(\tilde{x}(t))\right)+\frac{1}{4{\rho }^2}{\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}(t)}\right)}^T\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}(t)}\right)+{\rho }^2{v}^T(t)v(t)\hfill \end{array}\right)\mathit{dt}\end{array}$$ (A4)

By the phenotype robustness criterion in (5), we get

$$E{\int }_0^{\infty }{\tilde{x}}^T(t)Q\tilde{x}(t)\mathit{dt}\le E{\rho }^2{\int }_0^{\infty }{v}^T(t)v(t)\mathit{dt}$$ (A5)

which is the inequality in (4) with the filtering level ρ.

Appendix B: Proof of Proposition 2

Consider the global linearized synthetic gene network in (7) with x̃(0) = 0 and v(t) ≠ 0. By the Wiener process and Poisson point process, we get the following result

$$\begin{array}{l}E{\int }_0^{\infty }{\tilde{x}}^T(t)Q\tilde{x}(t)\mathit{dt}=\text{E}\left[{\tilde{x}}^T(0)P\tilde{x}(0)-{\tilde{x}}^T(\infty )P\tilde{x}(\infty )+{\int }_0^{\infty }\left({\tilde{x}}^T(t)Q\tilde{x}(t)+\frac{d}{\mathit{dt}}{\tilde{x}}^T(t)P\tilde{x}(t)\right)\mathit{dt}\right]\\ \le E{\tilde{x}}^T(0)P\tilde{x}(0)\\ +E{\int }_0^{\infty }\left({\tilde{x}}^T(t)Q\tilde{x}(t)+\sum _{i=1}^M{\alpha }_i(\tilde{x}(t))\left(\begin{array}{l}{\left[N{A}_i\tilde{x}(t)+v(t)+\sum _{j=1}^{L_1}\mathrm{\Delta }{N}_j{G}_{\mathit{ij}}\tilde{x}(t)P(t-t_i)+\sum _{j=1}^{L_2}\delta N_j{H}_{\mathit{ji}}\tilde{x}(t)d{W}_j(t)\right]}^{T}P\tilde{x}(t)\hfill \\ +{\tilde{x}}^T(t)P\left[N{A}_i\tilde{x}(t)+v(t)+\sum _{j=1}^{L_1}\mathrm{\Delta }{N}_j{G}_{ij}\tilde{x}(t)P(t-t_i)+\sum _{j=1}^{L_2}\delta N_j{H}_{\mathit{ji}}\tilde{x}(t)d{W}_j(t)\right]\hfill \\ \begin{array}{l}+\frac{1}{2}\sum _{j=1}^{L_1}{\tilde{x}}^T(t)G_{\mathit{ij}}^T\mathrm{\Delta }{N}_j^T\frac{{\partial }^2{\tilde{x}}^T(t)P\tilde{x}(t)}{\partial {\tilde{x}}^2(t)}\mathrm{\Delta }{N}_j{G}_{\mathit{ij}}\tilde{x}(t)\lambda \\ +\frac{1}{2}\sum _{j=1}^{L_2}{\tilde{x}}^T(t)H_{\mathit{ji}}^T\delta N_j^T\frac{{\partial }^2{\tilde{x}}^T(t)P\tilde{x}(t)}{\partial {\tilde{x}}^2(t)}\delta N_j{H}_{\mathit{ji}}\tilde{x}(t)\end{array}\hfill \end{array}\right)\right)\mathit{dt}\end{array}$$ (B1)

By the fact EP(t − t_i) = Edw_j (t) = 0, x̃(0) = 0 and

$$v^T(t)P\tilde{x}(t)+{\tilde{x}}^T(t)\mathit{Pv}(t)\le \frac{1}{{\rho }^2}{\tilde{x}}^T(t)\mathit{PP}\tilde{x}(t)+{\rho }^2{v}^T(t)v(t)$$ (B2)

$$\begin{array}{c}{\tilde{x}}^T(t)P\left(\sum _{j=1}^{L_1}\mathrm{\Delta }{N}_j{G}_{\mathit{ij}}\tilde{x}(t)P(t-t_i)\right)+{\left(\sum _{j=1}^{L_1}\mathrm{\Delta }{N}_j{G}_{\mathit{ij}}\tilde{x}(t)P(t-t_i)\right)}^T\\ P\tilde{x}(t)\le {\tilde{x}}^T(t)\mathit{PP}\tilde{x}(t)+{\tilde{x}}^T(t)\sum _{j=1}^{L_1}{G}_{\mathit{ij}}^T\mathrm{\Delta }{N}_j^T\mathrm{\Delta }{N}_j{G}_{\mathit{ij}}\tilde{x}(t)\end{array}$$ (B3)

we get

$$\begin{array}{l}E{\int }_0^{\infty }{\tilde{x}}^T(t)Q\tilde{x}(t)\mathit{dt}\\ \le E{\int }_0^{\infty }\sum _{i=1}^M{\alpha }_i(\tilde{x}(t))\left({\tilde{x}}^T(t)\left[\begin{array}{l}{A}_i^T{N}^{T}P+{\mathit{PNA}}_i+\mathit{PP}+\sum _{j=1}^{L_1}{G}_{\mathit{ij}}^T\mathrm{\Delta }{N}_j^T\mathrm{\Delta }{N}_j{G}_{\mathit{ij}}+\sum _{j=1}^{L_1}{G}_{\mathit{ij}}^T\mathrm{\Delta }{N}_j^{T}P\mathrm{\Delta }{N}_j{G}_{\mathit{ij}}\lambda \\ +\sum _{j=1}^{L_2}{H}_{\mathit{ji}}^T\delta N_j^{T}P\delta N_j{H}_{\mathit{ji}}+\frac{1}{{\rho }^2}\mathit{PP}+Q\end{array}\right]\tilde{x}(t)+{\rho }^2{v}^T(t)v(t)\right)\mathit{dt}\end{array}$$ (B4)

By the Riccati-like inequalities in (9), we get

$$E{\int }_0^{\infty }{\tilde{x}}^T(t)Q\tilde{x}(t)\mathit{dt}\le E{\rho }^2{\int }_0^{\infty }{v}^T(t)v(t)\mathit{dt}$$ (B5)

which is the inequality in (4) with the filtering level ρ.