Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2013 Nov 1.
Published in final edited form as: J Mech Behav Biomed Mater. 2012 Jun 20;15:199–207. doi: 10.1016/j.jmbbm.2012.06.008

Multilayer material properties of aorta determined from nanoindentation tests

Ali Hemmasizadeh a, Michael Autieri b, Kurosh Darvish a,*
PMCID: PMC3597096  NIHMSID: NIHMS419376  PMID: 23123343

Abstract

In a wide range of biomechanical modeling of aorta from traumatic injury to stent grafts, the arterial wall has been considered as a single homogeneous layer vessel, ignoring the fact that arteries are composed of distinct anatomical layers with different mechanical characteristics. In this study, using a custom-made nanoindentation technique, changes in the mechanical properties of porcine thoracic aorta wall in the radial direction were characterized using a quasi-linear viscoelastic model. Two layers of equal thickness were mechanically distinguishable in descending aorta based on the radial variations in the instantaneous Young's modulus E and reduced relaxation function G(t). Overall, comparison of E and G∞ of the outer half (70.27 ± 2.47 kPa and 0.35 ± 0.01) versus the inner half (60.32 ± 1.65 kPa and 0.33 ± 0.01) revealed that the outer half was stiffer and showed less relaxation. The results were used to explain local mechanisms of deformation, force transmission, tear propagation and failure in arteries.

Keywords: Nanoindentation, Aorta, Viscoelasticity, Multilayer properties

1. Introduction

Arterial mechanical properties have received increasing attention in the past few decades due to their vast effect on predicting cardiovascular diseases and injuries. On one side of this effort, researchers investigated the mechanobiological behavior of healthy and diseased arteries in the physiological range to obtain better characterization of cardiovascular diseases such as atherosclerosis, which afflicts about 795,000 Americans every year (Roger et al., 2011), and on the other side they developed mathematical models to predict large deformations and injuries such as Traumatic Aortic Rupture (TAR), which is one of the leading causes of fatality in motor vehicle crashes (Richens et al., 2003). For this purpose diverse methodologies have been utilized, among them are static and dynamic uniaxial and biaxial tests (Mohan and Melvin, 1983; Bass et al., 2001), inflation tests (Schulze Bauer et al., 2002), and indentation tests (Ebenstein and Pruitt, 2004).

In most of the previous studies the arterial wall was considered as a single homogeneous layer vessel ignoring the fact that arteries are composed of three anatomically distinct layers. Tunica intima is the innermost layer consisting of a single layer of endothelial cells that line the lumen. In healthy young human this layer is very thin and does not have a significant contribution to the wall mechanical behavior but its thickness and stiffness generally increases with age (Holzapfel and Gasser, 2000). Such changes in intima with age have not been observed in animals. Tunica media is the middle layer consisting mainly of elastin lamellae, collagen, and smooth muscle cells (SMC). Elastin lamellae and the interlamellar elastin fibers form a cage-like structure that surrounds the SMC (O'Connell et al., 2008). Media is responsible for the elastic recoil that maintains blood pressure during diastole. Tunica adventitia is the outermost layer consisting of mostly longitudinally running collagen fibers, thin elastic fibers, and fibroblasts. The adventitia's main mechanical function is to prevent excessive dilatation and permanent deformation (Fung, 1996).

The mechanical characteristics of separated arterial layers have been studied by a few investigators. In these studies, two or three layers were distinguished based on histological investigations and the layers were separated mechanically by cutting along the anatomical boundaries. Holzapfel et al. (2005) investigated three layers of human coronary arteries with nonatherosclerotic intimal thickening using cyclic quasi-static uniaxial tension tests superimposed on 5% pre-stretch and found significantly different anisotropic mechanical properties for these layers. The reported ratios of adventitia, media and intima thicknesses to total wall thickness were 0.4, 0.36, and 0.27 respectively. Based on their average experimental results, Young's modulus in the low loading domain (at which the noncollagenous matrix material is mainly active) was lower for media compared to adventitia (approximately 20 kPa versus 200 kPa). Teng et al. (2009) quantified the ultimate strength of human atherosclerotic carotid arteries by direct mechanical testing of media and adventitia. They identified the adventitia and media visually with equal thickness and found that adventitia was stiffer than media. In the axial direction, the adventitia ultimate strength (1996±867 kPa) was significantly higher than media (519 ± 720 kPa) while their stretch ratios at failure (1.54±0.23 and 1.40 ± 0.18 respectively) were not significantly different.

Most test methods used for characterizing the mechanical properties of arteries are dealing with the macroscopic properties of vessels. Recently nanoindentation techniques have been used to describe the local material properties of various tissues including bone (Rho et al., 1997), teeth (Habelitz et al., 2002), cartilage (Pierce et al., 2010) and vascular tissues (Ebenstein and Pruitt, 2004; Matsumoto et al., 2004; Levental et al., 2010). Ebenstein and Pruitt (2004) used conospherical tips for nanoindentation of internal surface of porcine aorta. They applied a trapezoidal load control profile and calculated the reduced modulus in the range of 700–800 kPa based on the method of Oliver and Pharr (1992) which considered an elastic material in unloading. Matsumoto et al. (2004) developed a scanning micro indentation setup, a scaled-up version of the atomic force microscope (AFM), and determined Young's modulus distribution of the lamellar unit (separated media) of porcine aorta in the axial and circumferential directions in the range of 50–180 kPa where the lower and higher values corresponded to the smooth muscle-rich layer (SML) and elastic lamina (EL) respectively. They reported no significant difference between the sections with different directions.

In this study, using a custom-made nanoindentation technique, local changes of the mechanical properties of porcine thoracic aorta wall in the axial direction were characterized. The results are summarized as a multilayer viscoelastic material model which can be used to investigate local mechanisms of aorta deformation, force transmission, tear propagation and failure.

2. Materials and methods

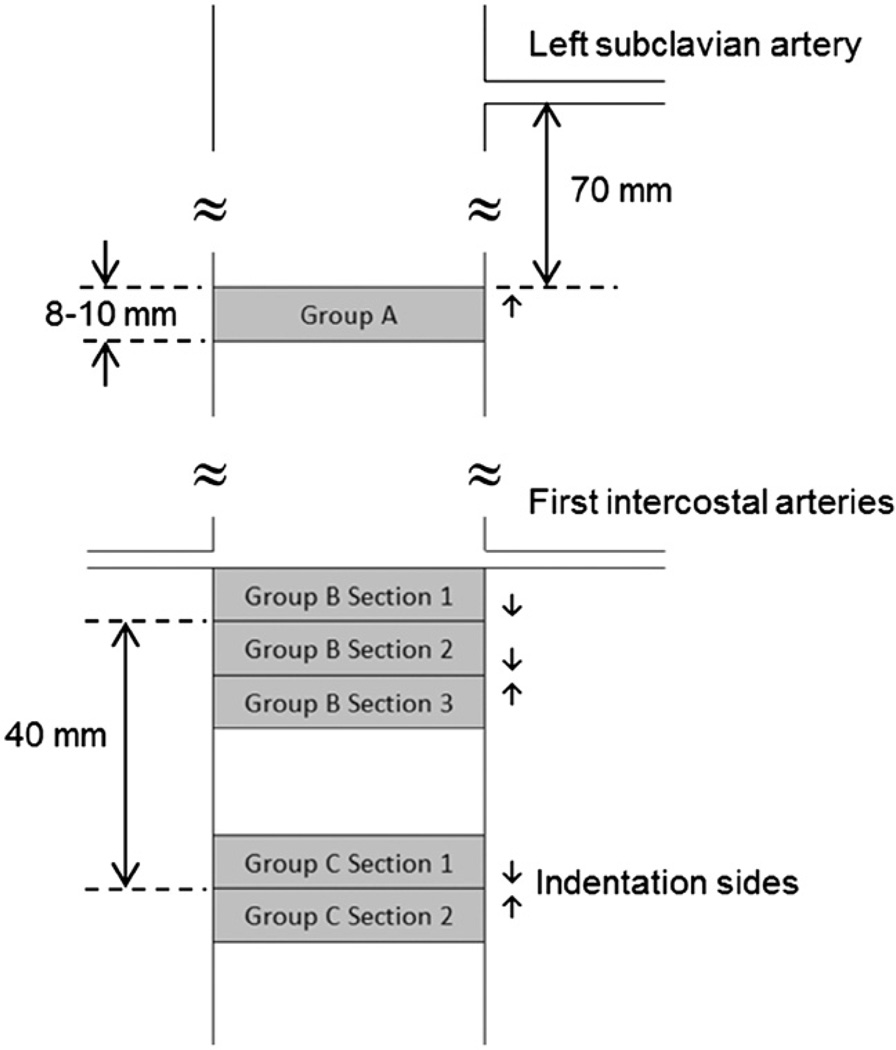
Twelve fresh porcine aorta specimens were obtained from a local slaughterhouse (Hatfield Quality Meats, Hatfield, PA). Each specimen was submerged in physiologic Phosphate Buffered Solution (PBS) immediately post-mortem and stored in an ice filled cooler while transported to the Laboratory. Specimens were cleaned from the surrounding tissues and 39 cylindrical samples were excised from the three locations. Group A (n=5) were extracted 70 mm inferior to the left subclavian artery (Fig. 1). Group B (n=20 at three sections) were extracted inferior to the first intercostal arteries and Group C (n=14 at two sections) at 40 mm inferior to Group B. Group A was extracted from five aortas and Groups B and C from the remaining seven aortas. To achieve straight edges in fresh tissues, a cylindrical polyethylene foam (McMaster-carr Catalog no. 93295K35, 15.87 mm diameter) was inserted in aorta and 8–10 mm long cylinders with diameter between 15 and 20 mm were cut using a razor blade.

Fig. 1.

Fig. 1

Open in a new tab

Schematic of locations of 3 different groups of aorta samples. Arrows show the sides where indentation tests were conducted.

A custom-made test setup was designed to perform nanoindentation tests (Fig. 2), consisting of a Z-axis nano-positioner with resolution of 0.2 nm and 100 µm range of motion (Nano-Z100, MCL,WI) combined with a horizontal piezo micro-positioner (M-663.4 PX, PI, MA). A conical indenter (XPT, Agilent Technologies, CA, 55° tip angle, 10 µm tip rounding radius) was attached to a force transducer (Aurora Scientific, Ontario, Canada, Model 406A) with resolution of 0.1 µN. The setup was equipped with a horizontally positioned 300x Stereo Microscope (Olympus SZX7) for contact visualization and the whole setup was mounted on an active vibration isolation table (TMC 63–533 Peabody, MA).

Fig. 2.

Fig. 2

Open in a new tab

The nanoindentation test setup.

Soft tissues' material properties are sensitive to hydration (Solanes et al., 2004). Preliminary results showed that force and consequently elastic modulus of aorta increased when the tissue dried. Therefore, to avoid dehydration, ring-shaped samples were placed in a 15 mm height aluminum container and were immersed in PBS to their top surface. Since the density of aorta is more than PBS, samples stayed stationary and no adhesive was used. As the indenter tip was lowered to make contact with the sample top surface, it first became in contact with a thin layer of PBS and resulted in a small tensile load due to the liquid surface tension. The tip was lowered further to the point when the tensile load started to decrease, which was considered to be the initial point of contact with the tissue (Cao et al., 2005).

The indentation tests were performed in the longitudinal direction at various points along the thickness of aorta (Fig. 3). The indentation site was chosen at 90° counterclockwise with respect to intercostal arteries to minimize the variability due to circumferential location. For each sample, the indenter tip was aligned to the outermost layer of aorta and the first point of indentation was 100 µm inward from this point. Successive indentation tests were performed toward the innermost layer with distances of 100 µm or 200 µm between points. The average wall thickness was 1.76 ± 0.05 µm and depending on local wall thickness 6–13 points were tested on each sample. The distance of the indentation points from the innermost layer was normalized (r) based on the wall thickness, where r=0 represented the innermost layer and r=1 the outmost layer. Samples were moved upward toward the indenter with a ramp and hold displacement with 40 µm indentation depth, 10 ms ramp time and 30 s hold time. The force and displacement data were collected at 5 kHz. In total, 318 points were tested and analyzed. All indentation tests were conducted in less than 8 h post-mortem.

Fig. 3.

Fig. 3

Open in a new tab

Conical tip used for nanoindentation in the longitudinal direction along aorta wall thickness.

3. Formulations and calibration

The mechanical behavior of the vessel in axial indentation was characterized assuming the material to be locally homogeneous, isotropic and linearly viscoelastic. The force history of the indenter in loading P(t) was written in terms of the indentation depth h(t) using a quasi-linear viscoelastic (QLV) model (Fung, 1996):

P(t)=∫0tG(t−τ)∂Pe(h)∂h∂h∂τdτ (1)

in which Pe(h) is the instantaneous elastic force that can generally be a nonlinear function of h. G(t) is the reduced relaxation function which was assumed to be a Prony series:

G(t)=G∞+∑i=14Gi exp (βit) (2)

in which Gi and βi represent the relaxation amplitudes and decay rates respectively. According to the ramp and relaxation times, four decay rates were chosen to capture the decays that occurred during the tests (β1 = 0.1, β2=1, β3 = 10, and β4=100s−1). Pe was selected based on the total elastic load necessary to cause a penetration h for a conical indenter which can be written as (Sneddon, 1965)

Pe=2E cot(β)π(1−v2)h2 (3)

where β is the cone angle with respect to the horizontal axis (β=62.5°), E is the instantaneous Young's modulus, and v is the Poisson's ratio which was assumed to be 0.5 (incompressible) for fresh aorta due to its high water content.

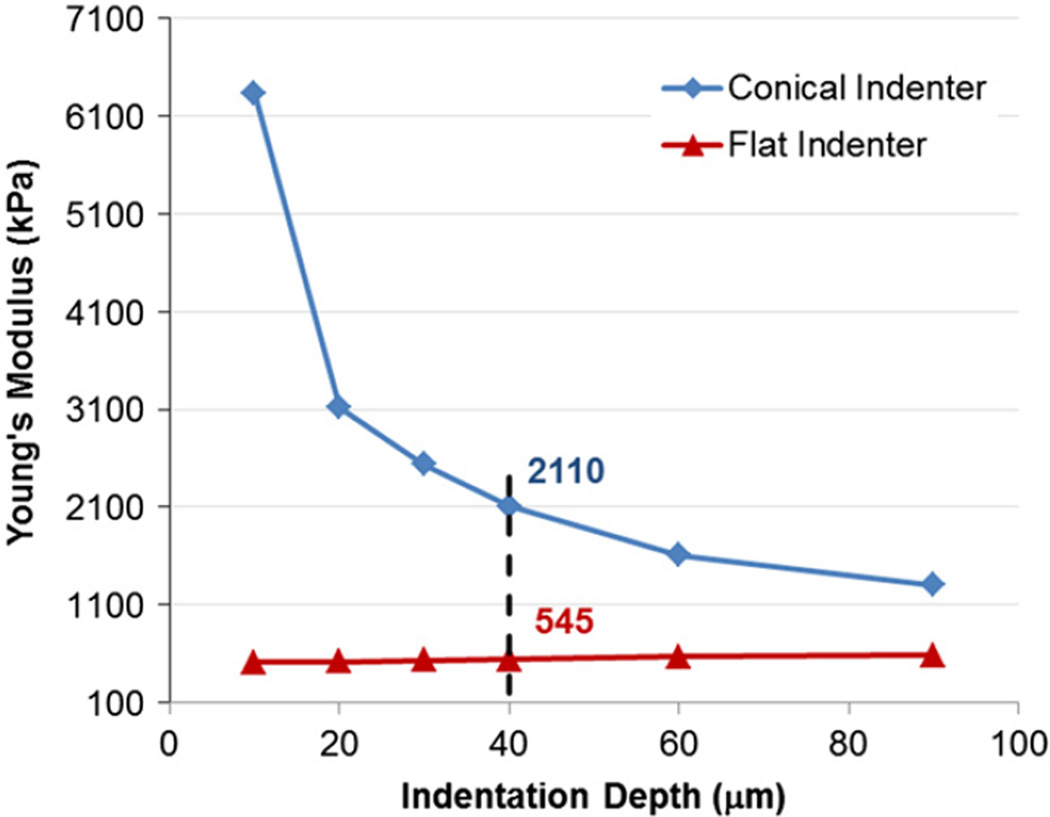
The nanoindentation test setup was calibrated using a cylindrical homogeneous extra soft isotropic viscoelastic polyurethane specimen with Durometer grade 7A (McMaster-Carr Catalog no. 20125K61, 12.7 mm diameter) as a substitute for aortic tissue. The material properties of the calibration specimen were determined using a flat ruby indenter (1 mm diameter) and axial compression experiments of the whole specimen. Both tests resulted in instantaneous Young's moduli of approximately 500 kPa which is in agreement with the reported data for Duromoeter 7A rubber (Qi et al., 2003) and is close to the elastic moduli of aorta (Holzapfel et al., 2005). Based on the comparison between conical and flat indenter results, a correction factor α was defined as the ratio of experimental (conical) to theoretical (flat) instantaneous Young's moduli. α was shown to be a function of the penetration depth h (Fig. 4). For the test conditions used in this study, it was found that α(h=40 µm)≈4. The relaxation behaviors for both indenters were determined to be the same and independent of the penetration depth (G∞ =0.123±0.002, G1 =0.016±0.002, G2 = 0.086 ± 0.001, G3 = 0.144±0.005, and G4 = 0.630 ± 0.006). It was therefore concluded that α is independent of time and only affects the instantaneous response Pe. α can be attributed to the non-ideal tip geometry, imperfections in contact surfaces, and the nonlinearity of system compliance among other factors (Fischer-Cripps, 2011).

Fig. 4.

Fig. 4

Open in a new tab

Experimental Young's moduli of the calibration specimen using conical and flat indenters show that for h=40 µm, the correction factor α for is approximately 4.

Results

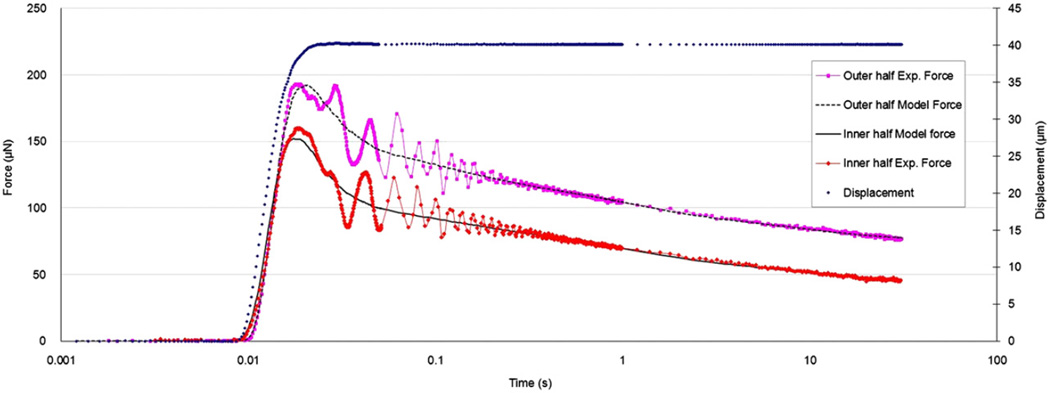
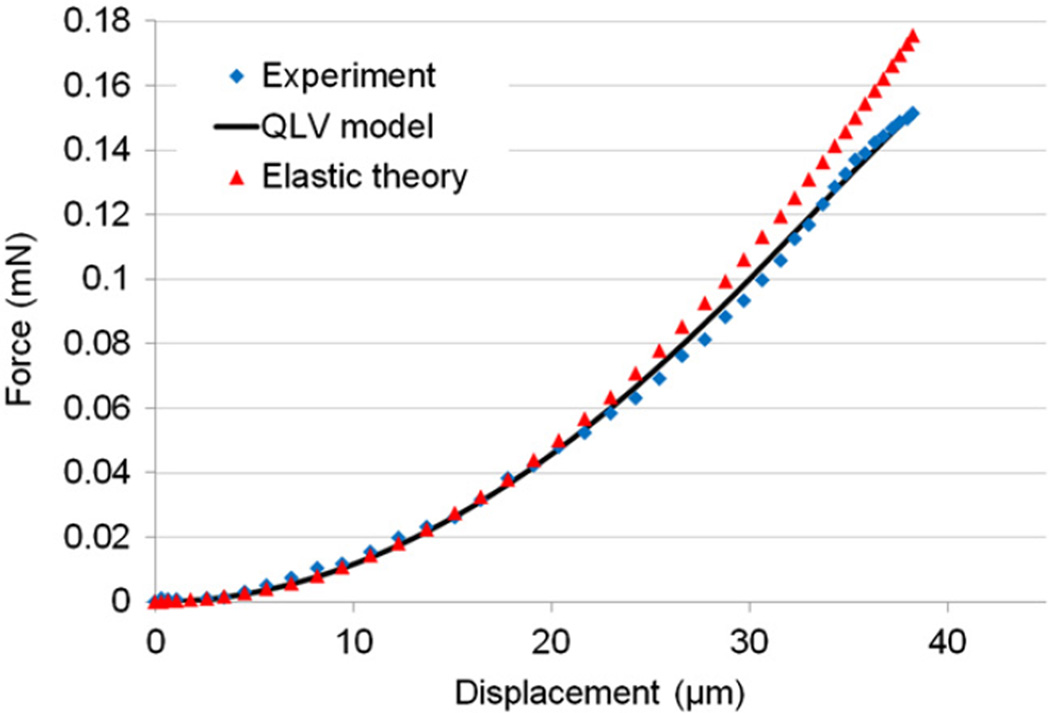
From nanoindentation tests, the viscoelastic material properties (Eqs. (2) and (3)) were obtained by fitting the model to experimental force history curves using a direct integration technique for the viscoelastic response to a general input (Simo and Hughes, 1998) and the method of least squares. The relaxation data was resampled (0–0.05 s at 5 kHz, 0.05–1 s at 250 Hz, 1–30 s at 5 Hz) to give approximately equal weights to different time scales. Representative curve fit results for the inner half of wall thickness (0<r≤0.5) and the outer half (0.50<r≤1.0) are shown in Fig. 5 which shows the experimental forces including the peak forces were matched adequately (overall R2 values of 0.9 or greater were achieved). The transient vibration observed in the response was due to sample natural frequency (dependent on sample geometry and material properties) which did not affect the viscoelastic characterization. A representative force-displacement curve (corresponding to the ramp region) is shown in Fig. 6 which demonstrates good agreement between the QLV model and the experimental data. This figure also verifies the quadratic form of the elastic function (Eq. (3)) and that the effect of relaxation was negligible for small displacements due to the short applied ramp time.

Fig. 5.

Fig. 5

Open in a new tab

Force and displacement history curves from typical indentation tests in the inner and outer halves of the aorta thickness.

Fig. 6.

Fig. 6

Open in a new tab

Representative indentation force-displacement curves for the elastic theory, experimental data and QLV model.

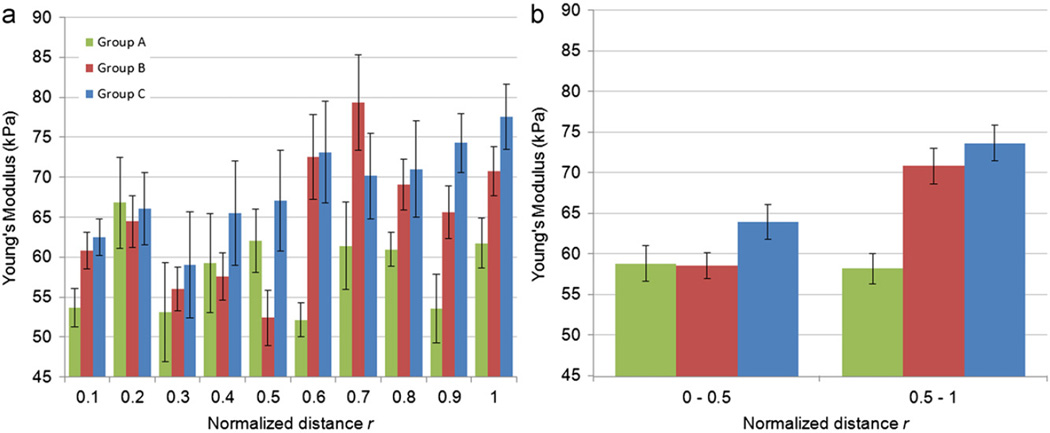
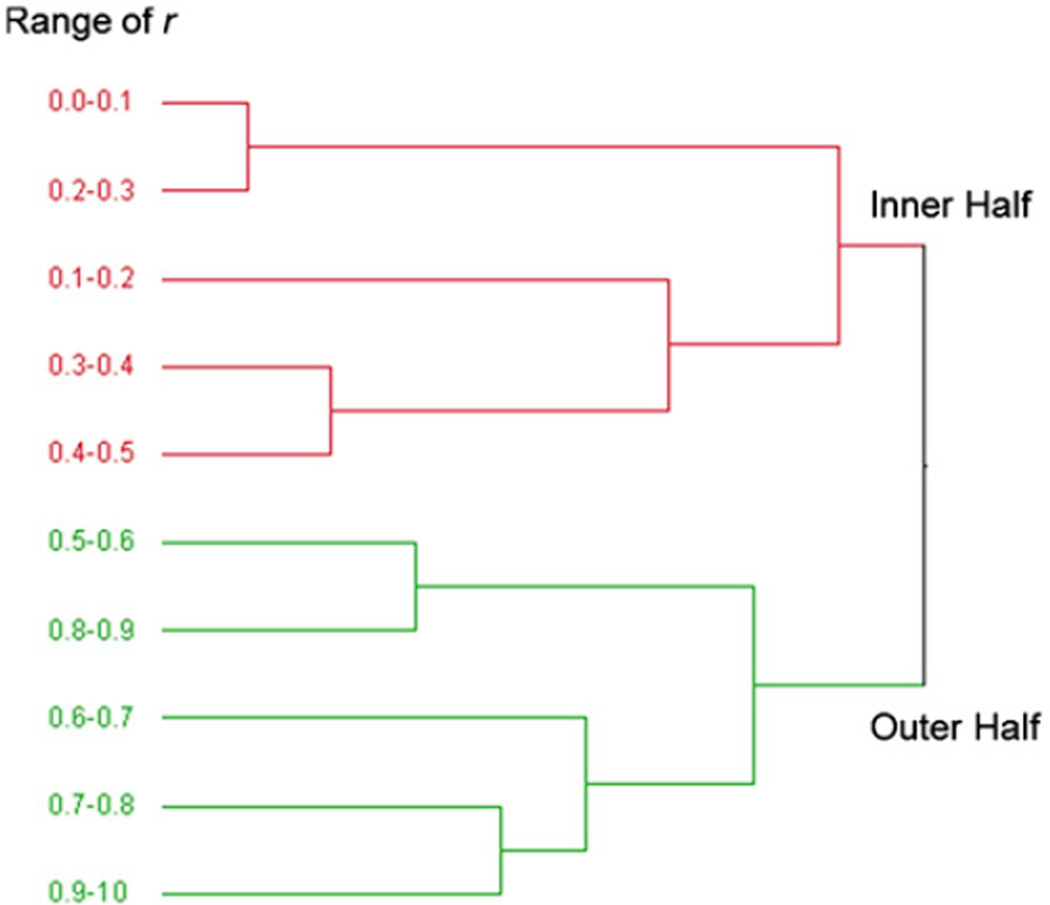
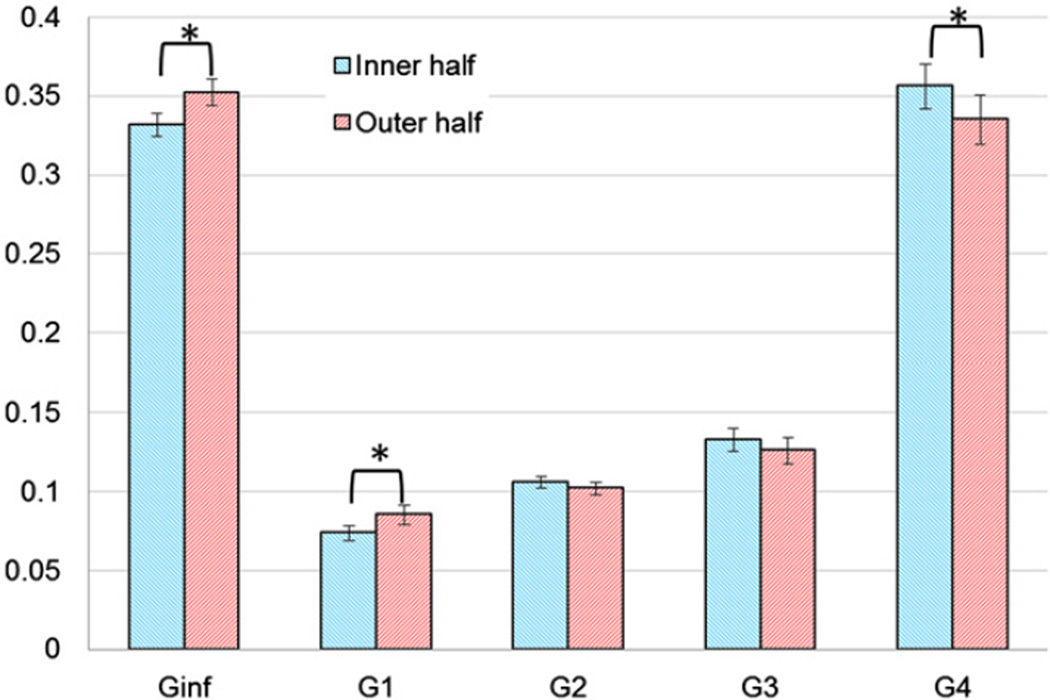
To achieve a better understanding of the trend of distribution of the material properties within the aorta wall, the results of Groups A, B, and C were divided into 10 regions based on r. The variation of E with respect to r is shown in Fig. 7a which demonstrates that the outer half was generally stiffer than the inner half. The grouping of material properties into inner and outer halves (Fig. 7b) was verified by applying hierarchical cluster analysis (JMP SAS, Version 8, Cary, NC) in which the regions data were combined in several steps into clusters whose values were closer to each other relative to those of other clusters based on Ward's minimum variance. At each step, the two clusters that had the smallest distance were combined into a single cluster and this process was continued until one cluster remained containing all the data. Fig. 8 shows that the 10 regions were combined in such a way that finally two clusters were distinguishable where one contained the inner half of the wall thickness and the other contained the outer half. Additionally, paired t-test was conducted between E in the inner half and outer half of all samples (Table 1) which confirmed a significant difference (p <0.001) between these regions. This difference was more pronounced below the first intercostal arteries, i.e., Groups B and C (p=0.0015 and p=0.0006 respectively) and was negligible in Group A taken near the arch (Fig. 7b). Therefore, it can be concluded that r=0.5 acted as a cut-off for the inhomogeneity of E in the radial direction. Paired t-tests on Gi showed that G∞ and G1 were significantly higher in the outer half region and G4 was significantly lower (Fig. 9). This means that the outer half was generally more elastic than the inner half.

Fig. 7.

Fig. 7

Open in a new tab

(a) Distribution of E in 10 regions along the aorta wall thickness. (b) Average values of E for inner and outer halves.

Fig. 8.

Fig. 8

Open in a new tab

The dendrogram results of E from applying hierarchical cluster analysis. The results show that 10 regions of r used in this study were combined in several steps and at the end, two regions were distinguishable with one containing the inner half of the wall thickness (r=0.0–0.5) and the other the outer half (r=0.5–1.0).

Table 1.

Average values of E and Gi for inner half and outer half regions and their standard errors and p values for paired two-tail t-tests.

E G∞ G1 G2 G3 G4
Inner half 60.32±1.65 0.33±0.01 0.07±0.01 0.11±0.01 0.13±0.01 0.36±0.01
Outer half 70.27±2.47 0.35±0.01 0.09±0.01 0.10±0.01 0.13±0.01 0.34±0.02
p-value 0.001 0.006 0.043 0.353 0.247 0.032
Open in a new tab

Fig. 9.

Fig. 9

Open in a new tab

Relaxation amplitudes of the inner and outer halves of wall thickness.

Comparison of section 2 of Groups B and C with paired t-test was used to evaluate the heterogeneity of material properties due to 40 mm longitudinal distance. The results (Table 2) showed that E was significantly higher (p=0.03) in Group C but Gi were not significantly different. In other words, the material was heterogeneous with respect to E but homogeneous with respect to G(t) in the longitudinal direction.

Table 2.

Average values of E and Gi in two sections that are 40 mm apart and their standard errors and p values for paired two-tail t-test.

E G∞ G1 G2 G3 G4
Group B Section 2 64.60±4.76 0.35±0.02 0.12±0.02 0.10±0.01 0.13±0.02 0.29±0.03
Group C Section 2 69.32±3.40 0.36±0.02 0.12±0.02 0.12±0.01 0.17±0.02 0.23±0.03
p-value 0.03 0.28 0.38 0.04 0.14 0.13
Open in a new tab

5. Discussion

An indentation technique was developed to study local variability of the viscoelastic behavior of aorta wall with respect to the radial distance. The test setup enabled reaching 40 µm spatial resolution and 10 regions were characterized on the aorta wall thickness. It was determined that below the first intercostal arteries, two larger regions with equal thickness were mechanically distinguishable with significantly different values of instantaneous Young's modulus (E) and reduced relaxation function (G(t)) whereas near the arch region the mechanical properties were less variable. The thicknesses of media and adventitia layers are reported to be almost the same (Holzapfel and Gasser, 2000; Teng et al., 2009) and for the young specimens used in this study, it was expected that the intima layer was significantly thinner that the other two layers (Holzapfel and Gasser, 2000). Therefore, it may be concluded that the inner and outer halves of aorta approximately coincide with the media and adventitia layers respectively.

Characterization of the material behavior was based on the QLV theory applied to the force data obtained during loading in a displacement-control setup. The force time histories (Fig. 5) and force-displacement curves (Fig. 6) verified the applicability of the QLV model (Eqs. (1)–(3)). In elastic and elastic-plastic materials, often the unloading force-displacement curve in a force-control setup is used for material characterization to eliminate the effect of friction during loading (e.g., Oliver and Pharr, 1992). However, in viscoelastic materials, due to creep (delay in displacement response), the unloading force-displacement curve would overestimate the material stiffness. This may explain the relatively high values of Young's modulus (700–800 kPa) determined by Ebenstein and Pruitt (2004) for porcine aorta.

The obtained instantaneous Young's moduli for the inner half are consistent with the range of 50–180 kPa reported by Matsumoto et al. (2004) for porcine aorta media layer where the lower value corresponded to the SML and the higher value corresponded to the EL. Due to the release of residual stress in dissected tissue, these layers form hills (EL) and valleys (SML) with less than10 µm difference in height. The ratio of the thickness of EL and SML was determined to be 6/22. In this study, with 40 µm indentation depth, both of these layers were compressed and the larger area of SML may justify why the inner half apparent modulus (60.32 ± 1.65) was closer to the lower limit.

The results of this study for the steady state Young's modulus (E∞ = G∞ E) showed that the outer half layer (E∞ =24.6 ± 1.1 kPa) was 24% stiffer than the inner half (E∞ =19.9±0.8 kPa) which is significantly smaller than the differences reported in Holzapfel et al. (2005). The steady state Young's moduli of the toe region inHolzapfel et al. (2005) were approximately 20 kPa and 200 kPa for media and adventitia respectively. Considering that Holzapfel et al. (2005) applied 5% prestretch before pulling the separated media and adventitia layers to failure, it may be concluded that the initial prestretch, that represents the tissue in vivo residual stress, had a significant effect on the collagen-rich adventitia layer stiffness but had negligible effect on the media layer stiffness. This may be attributed to the undulated geometry of collagen fibers in the stress-free state (Holzapfel et al., 2005).

The viscoelastic behavior of aortic tissue was characterized by the values of relaxation amplitudes Gi. In particular, G∞ showed that the steady state Young's modulus was on average 34% of the instantaneous Young's modulus. G∞, G1, and G4 for inner half and outer half were significantly different from each other, which implied that aorta wall long-term and short-term damping mechanisms were also inhomogeneous (Fig. 9). Overall, the outer layer showed less damping, which may be attributed to the layers infrastructure. The damping mechanism in media, in addition to the movement of interstitial fluid within the solid phase cage-like microstructure, can be attributed to smooth muscle cells (SMC) that constitute about 24% of this layer (O'Connell et al., 2008). SMC in non-active state, without the presence of a vasoconstrictor, show significant viscoelasticity (Fung, 1996). Therefore, lack of SMC in adventitia makes it effectively more elastic.

The knowledge of the material properties of aortic wall is fundamental to the understanding of aorta failure mechanisms and how a local tear propagates through the aortic wall. Many instances of partial aortic rupture occur (about 10–20%) in which the outermost layer of aorta does not rupture and the chance of survival of the patient is significantly increased (Fattori et al., 1996). Considering aorta as a pressure vessel, the inner layers are exposed to higher stress levels than the outer layers (Lai et al., 2010). Mohan and Melvin (1983) showed that the failure of aorta is strain based with approximately 50% and 60% ultimate strain for quasi-static and dynamic (80 s−1 strain rate) stretch tests respectively. Moreover, Holzapfel et al. (2005) reported that the ultimate stretches are similar for separated aorta tissue layers. The results of this study revealed that, in descending aorta, the inner layer is more compliant than the outer one. Therefore, it can be concluded that, based on only pressure loading, the inner layer would sustain higher strains and would be more vulnerable to failure. In other words, failure in aorta would propagate from inner layers toward the outer layers. This conclusion is in agreement with several previous experimental studies on blunt carotid injuries by Cogbill et al. (1994), Fabian et al. (1996), Punjabi et al. (1997), Cohuet et al. (2001), and the tensile experiments on aorta byTeng et al. (2009).

Various studies showed that TAR happens at the isthmus region of aortic arch (Fattori et al., 1996; Richens et al., 2003; Amabile et al., 2004). The results of this study showed that in Group A (which is near the arch) the outer half was more compliant compared to Groups B and C (below the arch region) and its mechanical properties were similar to the inner half. This would generally (e.g., in pressure loading) result in higher strains in this region and increase in the risk of failure. Therefore, it could be concluded that the outer layers failure containment capacity near the arch region was less than the descending aorta that could partially explain the high occurrence of TAR in the isthmus region.

Surface detection is a challenge in nanoindentation of soft materials and the changes in the adhesion force curve are generally used to determine the point of contact (Cao et al., 2005; Kaufman, 2009; Ebenstein, 2011). In this study, the adhesion force between the PBS layer and the indenter tip was maximum 6 µN tension and the initial decrease in this force (after about 1–2 µm displacement) was considered as the point of contact which is in agreement with Cao et al. (2005). This force was much smaller than the maximum indentation force (about 170 µN) and was considered negligible in the analysis.

It should be noted that Eq. (3) used for the elastic solution of conical indenters is derived for infinitesimal deformations and assumes the material to be locally isotropic and homogeneous. In terms of homogeneity, this study is limited by the resolution of the indentation site (40 µm). This resolution, however, was sufficient to achieve the conclusions regarding the material properties of inner and outer halves in the radial direction. While the material properties of human arteries, with elastin lamellae and collagen fibers running generally in the circumferential direction, have shown to be anisotropic (e.g., Holzapfel et al., 2005), many studies that were conducted on young and healthy animal and human specimens show that the material is effectively isotropic (Mohan and Melvin, 1983; Lally et al., 2004; Matsumoto et al., 2004; Vande Geest et al., 2004; Virues Delgadillo et al., 2010). Particularly,Matsumoto et al. (2004) reported no significant difference in Young's modulus of excised porcine aorta samples in longitudinal and transverse directions measured by AFM and Virues Delgadillo et al. (2010) biaxial tests of fresh porcine aortas showed that the difference in the mechanical behavior of these two directions below the stretch ratio of 1.5 is small. The comparison of experimental force-displacement curves with the theoretical model (Fig. 6) demonstrated that the application of Eq. (3) in the present study was valid. At higher indentation depths the experimental force is slightly less than the theoretical values, which is due to viscoelastic relaxation that occurred during the 10 ms ramp time. This relatively small ramp time made the calculated elastic Young's modulus to be closer to the true instantaneous Young's modulus of the material (Fung, 1996) which requires a step change in displacement. However, this ramp time resulted in transient vibration after the peak force due to the sample inertia. It was confirmed that the frequency of this vibration (approximately 60 Hz) coincided with the first natural frequency of samples in the longitudinal direction (Gladwell and Tahbildar, 1972). It was assumed that the effect of this transient vibration was negligible in the conclusions of this study as the viscoelastic model passes approximately through the local average forces (Fig. 5). Although, aorta in vivo is in tension, it should be noted that Eq. (3) implies that the material behavior is the same in tension and compression as long as the deformations are small.

Conclusions

Using a custom-made nanoindentation technique, changes in the mechanical properties of porcine thoracic aorta wall in the radial direction were characterized using a quasi-linear viscoelastic model. Two layers of equal thickness were mechanically distinguishable based on the radial variations in the instantaneous Young's modulus E and the reduced relaxation function G(t). Overall, comparison of E and G∞ of the outer half versus the inner half revealed that the outer half was stiffer and showed less relaxation. These layers may approximately correspond to media and adventitia in the specimens. The results partly explained why tissue mechanical failure starts from inner layers and showed that the outer layers failure containment capacity was less in the arch region.

Acknowledgment

Authors appreciate the guidance of Dr. Farrokh Darvish on the cluster analysis used in the study and Mr. Soroush Assari for his help in improving and assembling the test setup. The support for this work was provided partially by the NHLBI under Grant nos. K25 HL086512-03 and R21 HL088159-02.

Nomenclature

α

Correction factor for conical indenter

βi

Decay rates

v

Poisson’s ratio

E

Instantaneous Young’s modulus

Gi

Relaxation amplitudes

h

Penetration depth

P(t)

Indentation force history

Pe

Instantaneous elastic force

r

Normalized radial distance

REFERENCES

  1. Amabile P, Collart F, Gariboldi V, Rollet G, Bartoli JM, Piquet P. Surgical versus endovascular treatment of traumatic thoracic aortic rupture. Journal of Vascular Surgery. 2004;40:873–879. doi: 10.1016/j.jvs.2004.08.053. [DOI] [PubMed] [Google Scholar]
  2. Bass CR, Darvish K, Bush B, Crandall JR, Srinivasan SC, Tribble C, Fiser S, Tourret L, Evans JC, Patrie J, Wang C. Material properties for modeling traumatic aortic rupture. Stapp Car Crash Journal. 2001;45:143–160. doi: 10.4271/2001-22-0006. [DOI] [PubMed] [Google Scholar]
  3. Cao Y, Yang D, Soboyejoy W. Nanoindentation method for determining the initial contact and adhesion characteristics of soft polydimethylsiloxane. Journal of Materials Research. 2005;20:2004–2011. [Google Scholar]
  4. Cogbill TH, Moore EE, Meissner M. The spectrum of blunt injury to the carotid artery: a multicenter perspective. The Journal of Trauma. 37:473–479. doi: 10.1097/00005373-199409000-00024. [DOI] [PubMed] [Google Scholar]
  5. Cohuet G, Challande P, Osborne-Pellegrin M, Arribas SM, Dominiczak A, Louis H, Laurent S, Lacolley P. Mechanical strength of the isolated carotid artery in SHR. Hypertension. 2001;38:1167–1171. doi: 10.1161/hy1101.095995. [DOI] [PubMed] [Google Scholar]
  6. Ebenstein DM. Nano-JKR force curve method overcomes challenges of surface detection and adhesion for nanoindentation of a compliant polymer in air and water. Journal of Materials Research. 2011;26:1026–1035. [Google Scholar]
  7. Ebenstein DM, Pruitt LA. Nanoindentation of soft hydrated materials for application to vascular tissues. Journal of Biomedical Materials Research. 2004;69A:222–232. doi: 10.1002/jbm.a.20096. [DOI] [PubMed] [Google Scholar]
  8. Fabian TC, Patton JH, Croce MA, Minard G, Kudsk KA, Pritchard FE. Blunt carotid artery injury: importance of early diagnosis and anticoagulant therapy. Annals of Surgery. 1996;223:513–525. doi: 10.1097/00000658-199605000-00007. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Fattori R, Celletti F, Bertaccini P, Galli R, Pacini D, Pierangeli A, Gavelli G. Delayed surgery of traumatic aortic rupture. Circulation. 1996;94:2865–2870. doi: 10.1161/01.cir.94.11.2865. [DOI] [PubMed] [Google Scholar]
  10. Fischer-Cripps AC. Nanoindentation. 3rd ed. Springer; 2011. [Google Scholar]
  11. Fung YC. Biomechanics Mechanical Properties of Living Tissues. Springer; 1996. [Google Scholar]
  12. Gladwell GML, Tahbildar UC. Finite element analysis of the axisymmetric vibrations of cylinders. Journal of Sound and Vibration. 1972;22(2):143–157. [Google Scholar]
  13. Habelitz S, Marshall GW, Jr, Balooch M, Marshall SJ. Nanoindentation and storage of teeth. Journal of Biomechanics. 2002;35:995–998. doi: 10.1016/s0021-9290(02)00039-8. [DOI] [PubMed] [Google Scholar]
  14. Holzapfel GA, Gasser TC. A new constitutive framework for arterial wall mechanics and a comparative study of material models. Journal of Elasticity. 2000;61:1–48. [Google Scholar]
  15. Holzapfel GA, Sommer G, Gasser CT, Regitnig P. Determination of layer-specific mechanical properties of human coronary arteries with nonatherosclerotic intimal thickening and related constitutive modeling. American Journal of Physiology—Heart and Circulatory Physiology. 2005;289:H2048–H2058. doi: 10.1152/ajpheart.00934.2004. [DOI] [PubMed] [Google Scholar]
  16. Kaufman JD. Surface detection errors cause overestimation of the modulus in nanoindentation on soft materials. Journal of the Mechanical Behavior of Biomedical Materials. 2009;2:312–317. doi: 10.1016/j.jmbbm.2008.08.004. [DOI] [PubMed] [Google Scholar]
  17. Lai WM, Rubin D, Krempl E. Introduction to Continuum Mechanics. 4th ed. Elsevier; 2010. [Google Scholar]
  18. Lally C, Reid AJ, Prendergast PJ. Elastic behavior of porcine coronary artery tissue under uniaxial and equibiaxial tension. Annals of Biomedical Engineering. 2004;32:1355–1364. doi: 10.1114/b:abme.0000042224.23927.ce. [DOI] [PubMed] [Google Scholar]
  19. Levental I, Levental KR, Klein EA, Assoian R, Miller RT, Wells RG, Janmey PA. A simple indentation device for measuring micrometer-scale tissue stiffness. Journal of Physics: Condensed Matter. 2010;22:194120–194128. doi: 10.1088/0953-8984/22/19/194120. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Matsumoto T, Goto T, Furukawa T, Sato M. Residual stress and strain in the lamellar unit of the porcine aorta: experiment and analysis. Journal of Biomechanics. 2004;37:807–815. doi: 10.1016/j.jbiomech.2003.08.014. [DOI] [PubMed] [Google Scholar]
  21. Mohan D, Melvin JW. Failure properties of passive human aortic tissue. I-uniaxial tension tests. Journal of Biomechanics. 1983;16:31–37. doi: 10.1016/0021-9290(83)90044-1. [DOI] [PubMed] [Google Scholar]
  22. O'Connell MK, Murthy S, Phan S, Xu C, Buchanan J, Spilker R, Dalman RL, Zarins CK, Denk W, Taylor CA. The three-dimensional micro- and nanostructure of the aortic medial lamellar unit measured using 3D confocal and electron microscopy imaging. Matrix Biology. 2008;27:171–181. doi: 10.1016/j.matbio.2007.10.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Oliver WC, Pharr GM. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. Journal of Materials Research. 1992;7:1564–1583. [Google Scholar]
  24. Pierce DM, Trobin W, Raya JG, Trattnig S, Bischof H, Glaser C, Holzapfel GA. DT-MRI based computation of collagen fiber deformation in human articular cartilage: a feasibility study. Annals of Biomedical Engineering. 2010;38:2447–2463. doi: 10.1007/s10439-010-9990-9. [DOI] [PubMed] [Google Scholar]
  25. Punjabi AP, Plaisier BR, Haug RH, Malangoni MA. Diagnosis and management of blunt carotid artery injury in oral and maxillofacial surgery. Journal of Oral and Maxillofa-cial Surgery. 1997;55:1388–1395. doi: 10.1016/s0278-2391(97)90634-0. [DOI] [PubMed] [Google Scholar]
  26. Qi HJ, Joyce K, Boyce MC. Durometer hardness and the stress-strain behavior of elastomeric materials. Rubber Chemistry and Technology. 2003;72:419–435. [Google Scholar]
  27. Rho J-Y, Tsui TT, Pharr GM. Elastic properties of human cortical and trabecular lamellar bone measured by nanoindentation. Biomaterials. 1997;18:1325–1330. doi: 10.1016/s0142-9612(97)00073-2. [DOI] [PubMed] [Google Scholar]
  28. Richens D, Kotidis K, Neale M, Oakley C, Fails A. Rupture of the aorta following road traffic accidents in the United Kingdom 1992–1999. The results of the co-operative crash injury study. European Journal of Cardio-Thoracic Surgery. 2003;23:143–148. doi: 10.1016/s1010-7940(02)00720-0. [DOI] [PubMed] [Google Scholar]
  29. Roger VR, Go AS, Lloyd-Jones DM, Adams RJ. Heart disease and stroke statistics-2011 update: a report from the American Heart Association. Circulation. 123:e18–e209. doi: 10.1161/CIR.0b013e3182009701. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Schulze Bauer CA, Regitnig P, Holzapfel GA. Mechanics of the human femoral adventitia including the high-pressure response. American Journal of Physiology Heart and Circulatory Physiology. 2002;282:H2427–H2440. doi: 10.1152/ajpheart.00397.2001. [DOI] [PubMed] [Google Scholar]
  31. Simo JC, Hughes TJR. Computational Inelasticity first ed. Springer; 1998. [Google Scholar]
  32. Sneddon IN. The relation between load and penetration in the axisymmetric boussinesq problem for a punch of arbitrary profile. International Journal of Engineering Science. 1965;3:47–57. [Google Scholar]
  33. Solanes N, Rigol M, Castella M, Khabiri E, Ramirez J, Segales J, Roque M, Agusti E, Perez-Villa F, Roig E, Pomar JL, Sanz SG, Heras M. Cryopreservation alters antigenicity of allografts in a porcine model of transplant vasculopathy. Transplantation Proceedings. 2004;36:3288–3294. doi: 10.1016/j.transproceed.2004.10.053. [DOI] [PubMed] [Google Scholar]
  34. Teng Z, Tang D, Zheng J, Woodard PK, Hoffman AH. An experimental study on the ultimate strength of the adventitia and media of human atherosclerotic carotid arteries in circumferential and axial directions. Journal of Biomechanics. 2009;42:2535–2539. doi: 10.1016/j.jbiomech.2009.07.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Vande Geest JP, Sacks MS, Vorp DA. Age dependency of the biaxial biomechanical behavior of human abdominal aorta. Journal of Biomechanical Engineering. 2004;126:815–822. doi: 10.1115/1.1824121. [DOI] [PubMed] [Google Scholar]
  36. Virues Delgadillo JO, Delorme S, El-Ayoubi R, Diraddo R, Hatzikirakos SG. Effect of freezing on the biaxial mechanical properties of arterial samples. Journal of Biomedical Science and Engineering. 2010;3:645–652. [Google Scholar]

RESOURCES