Combined arterial spin labeling and diffusion-weighted imaging for noninvasive estimation of capillary volume fraction and permeability-surface product in the human brain

Abstract

A number of two-compartment models have been developed for the analysis of arterial spin labeling (ASL) data, from which both cerebral blood flow (CBF) and capillary permeability-surface product (PS) can be estimated. To derive values of PS, the volume fraction of the ASL signal arising from the intravascular space (v_bw) must be known a priori. We examined the use of diffusion-weighted imaging (DWI) and subsequent analysis using the intravoxel incoherent motion model to determine v_bw in the human brain. These data were then used in a two-compartment ASL model to estimate PS. Imaging was performed in 10 healthy adult subjects, and repeated in five subjects to test reproducibility. In gray matter (excluding large arteries), mean voxel-wise v_bw was 2.3±0.2 mL blood/100 g tissue (all subjects mean±s.d.), and CBF and PS were 44±5 and 108±2 mL per 100 g per minute, respectively. After spatial smoothing using a 6-mm full width at half maximum Gaussian kernel, the coefficient of repeatability of CBF, v_bw and PS were 8 mL per 100 g per minute, 0.4 mL blood/100 g tissue, and 13 mL per 100 g per minute, respectively. Our results show that the combined use of ASL and DWI can provide a new, noninvasive methodology for estimating v_bw and PS directly, with reproducibility that is sufficient for clinical use.

Introduction

Arterial spin labeling (ASL) is a noninvasive technique, which can be used to measure cerebral blood flow (CBF), by magnetically labeling water molecules in the arterial blood supply.^{1, 2} In contrast to perfusion measurements acquired using either gadolinium bolus tracking approaches, such as dynamic susceptibility contrast magnetic resonance imaging (DSC-MRI), or PET (positron emission tomography), ASL utilizes a purely endogenous tracer (blood water molecules), and as such is well suited for repeated measurements in longitudinal studies, or in patients where exogenous contrast agents can be problematic (such as renal pathologies or pediatrics).

Early ASL models assumed that magnetically labeled water molecules act as a freely diffusible tracer.¹ However, both radiolabeling³ and magnetic resonance^{4, 5, 6} experiments have demonstrated that this is not the case, particularly in the central nervous system, where the blood–brain barrier (BBB) reduces water permeability by an order of magnitude compared with systemic circulation. A number of ‘two-compartment' ASL models have been developed to account for this,^{5, 6} in which the permeability-surface product (PS) of the capillary wall is included as a fitted parameter when analyzing data acquired at multiple inflow times. These models provide a means to obtain localized measurements of water permeability, which could provide a surrogate index of the integrity of the BBB throughout the brain. This is a potentially clinically useful biomarker, as the permeability of the BBB can be altered in brain tumors and in neurodegenerative diseases such as multiple sclerosis.

To derive PS values from two-compartment ASL models, the fraction of the ASL signal that arises from intravascular ‘blood–water' and extravascular ‘tissue–water' compartments must be known (v_bw and v_ex, respectively). Because local values of v_bw are usually not known a priori, rather than deriving a value of PS from a two-compartment model, only the ratio of PS/v_bw can be obtained (see Model Fitting). Following this, a number of previous studies⁵ have assumed a fixed, global value for v_bw to estimate voxel-wise values of PS in the brain. However, PS values obtained using this method are prone to errors introduced by both regional variations in v_bw, as well as dynamic changes brought about by neuronal activation. Furthermore, v_bw itself is a clinically useful biomarker in pathologies such as brain tumors, in which tumor-induced neoangiogenesis may lead to localized changes in the microvascular volume fraction. In such cases assumed values of v_bw, based on measurements made in healthy tissue, are likely to be incorrect, which will lead to inaccuracies in estimates of PS. Therefore, significant advantages can be gained from decoupling the PS and v_bw parameters in a two-compartment analysis of ASL data.

Traditionally, v_bw measurements have been made using MR-based methods combined with exogenous contrast agents, or non-MR-based techniques such as computed tomography, single photon emission computed tomography, and PET. However, as these techniques are all invasive, they are not well suited for intrasubject longitudinal studies or pediatric patients. Alternatively, a number of noninvasive spin labeling approaches for measuring arterial cerebral blood volume (aCBV) have been developed over recent years, such as the VASO (vascular space occupancy) technique,⁷ which has been extended to provide quantification of aCBV in units of mL blood/100 mL parenchyma.^{8, 9} However, as shown by Donahue et al, the VASO technique predominantly measures vasculature at the precapillary level.

Here, we introduce an alternative, noninvasive methodology for incorporating measured values of v_bw into a two-compartment ASL model, using data derived from diffusion-weighted imaging (DWI). This method utilizes an adapted version of the intravoxel incoherent motion (IVIM) model, introduced by Le Bihan et al,^{10, 11, 12} which states that two diffusing species give rise to the observed signal during in vivo DWI. These are the incoherent flow of blood–water in the randomly orientated microvascular network (referred to as microcirculation driven pseudo-diffusion), and molecular, thermally driven diffusion of water molecules in the extravascular space. Provided a suitable range of b values are applied (including a number of measurements at low b values, <∼200 s/mm²), a deviation from mono-exponential signal attenuation with increasing b value will be observed. By fitting measured data to the IVIM model (see Model Fitting), the volume fraction of water molecules contributing to the microvascular pseudo-diffusion signal can be estimated. This parameter will be sensitive to changes in the local capillary density, and therefore provides important information when modeling kinetic ASL data using a two-compartment model.

The combined use of ASL and the IVIM model has previously been suggested.^{13, 14} However, in these studies diffusion-weighting gradients were applied to the ASL signal itself, to separate the fast flowing (vascular) and slow (tissue) contributions. Although promising, the applied diffusion gradients spoil a considerable portion of the ASL signal using these techniques, and the eddy-currents induced at higher b values significantly increase the temporal fluctuations in the raw data. As ASL suffers from intrinsically low SNR (signal-to-noise ratio), analysis is therefore limited to large ROIs, which constitutes a limitation when localized values of PS and v_bw are required. Also, although physiologically sensible values of PS have been measured,¹⁵ assumed rather than measured values of v_bw were used in the analysis, which may not be physiologically accurate, particularly in pathologies.

The purpose of this study was to demonstrate a new methodology for localized, ASL-derived measurement of PS, which incorporates measured values of v_bw in the analysis, utilizes pulse sequences that are widely clinically available, and does not further attenuate the low-SNR ASL signal. Both multi-inversion-time pulsed-ASL and multi-b value DWI measurements were obtained in 10 healthy adult subjects (and repeated in five subjects for the assessment of reproducibility), and voxel-wise values of v_bw, derived from an IVIM analysis of the DWI data, were substituted into a two-compartment ASL model to measure local values of both CBF and PS. Previously, the majority of two-compartment ASL studies have reported results from whole-gray matter ROIs. However, there is evidence to suggest that the analysis of ASL data based on large ROIs may suffer from inaccuracies due to a wide distribution of bolus transit times, and averaging of kinetic ASL data over such a large region should be avoided.¹⁶ Furthermore, the advantage gained from incorporating local, measured values of v_bw would be lost if such large ROIs were used. We therefore performed our analysis on a voxel-by-voxel basis, and performed analysis on both raw data, and spatially smoothed data, to increase the effective region of interest beyond the single voxel level. Spatial smoothing also helps to correct for subject motion and imperfections in coregistration of DWI and ASL data.

Materials and methods

Magnetic Resonance Experiments

All experiments were performed on a 1.5-T Siemens Magnetom Avanto scanner (Siemens, Erlangen, Germany), equipped with 40 mT/m gradients and a 12-channel head receive coil. Ten healthy subjects (age 22 to 32 years, mean age 27 years, four females), who provided informed written consent in accordance with the guidelines and approval of the institutional ethical review board, were scanned, and all data were acquired in the brain, using the protocols described below. Imaging was repeated in five of the subjects, ∼30 minutes after the initial scan, without repositioning inside the magnet, to test intrasubject reproducibility.

Diffusion-Weighted Imaging Protocol

Diffusion-weighted imaging data were acquired using a diffusion-sensitized axial 2D single shot spin-echo sequence (with echo planar imaging (EPI) readout), with the following imaging parameters: TR/TE=3,800/120 milliseconds, field of view=230 mm, matrix size=64 × 64, 20 contiguous slices with 5 mm thickness, NSA (number of averages)=3. Diffusion sensitizing gradients were applied in three orthogonal directions with b values of 0, 20, 40, 80, 120, 160, 200, 300, 500, and 1000 s/mm². In-plane resolution was 3.6 × 3.6 mm², and total acquisition time was 11 minutes. As it has been shown that partial volume effects between cerebrospinal fluid (CSF) and tissue will contribute to the biexponential behavior observed in DWI of the brain,¹⁷ all DWI acquisitions were performed with CSF suppression (prior inversion pulse, TI=2,200 milliseconds).

Arterial Spin Labeling protocol

Arterial spin labeling data were acquired using a flow-sensitive alternating inversion recovery (FAIR) pulsed-ASL sequence, with 3D single shot gradient and spin echo (GRASE) data acquisition,¹⁸ with the following imaging parameters: TR=3.0 seconds, TE=31.6 milliseconds, and NSA=8. The field of view and resolution were identical to the diffusion-weighted scan, and measurements were made at 12 inflow times (TI), ranging from 0.2 to 2.4 seconds in 0.2-second intervals, with total scan time=9.6 minutes. Arterial spin labeling measurements were made twice, once with background suppression of static tissue,¹⁸ and once without (for quantification of voxel-wise T₁ and M₀ values, see Preprocessing). The use of background suppression allowed the scanner gain to be increased by a factor of 10 to maximize the signal from the inflowing blood.

Preprocessing

All DWI data were corrected for eddy-current distortions using FSL (FMRIB's Software Library, Oxford University, www.fmrib.ox.ac.uk/fsl), and the mean of the signal intensity values from the three diffusion encoding directions was used for analysis. Signal intensity values from the multi-TI non-background suppressed ASL acquisition were used to fit a T₁ inversion recovery curve in each voxel, to obtain maps of T₁ and M₀. The T₁ maps from each subject were then used to register all DWI and ASL raw data to the MNI template (Montreal Neurological Institute), using an affine 12-parameter model provided by the FLIRT algorithm in FSL.¹⁹ Intravoxel incoherent motion and ASL model fitting was then performed on the raw, registered data (see Model Fitting). Voxel-wise analysis of fitted parameters was performed on unsmoothed data, as well as spatially smoothed data after application of Gaussian kernels of 2, 4, and 6 mm full width at half maximum (FWHM).

Model Fitting

All postprocessing and analysis was performed using Matlab (MathWorks, Natick, MA, USA).

Intravoxel Incoherent Motion Model Fitting

The original IVIM model stated that the relationship between signal intensity, S, and the applied diffusion-weighting (b value) is given by:

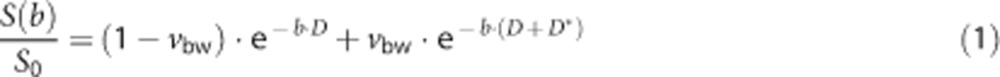where S₀ is the signal intensity with no diffusion-weighting (i.e., b=0), D is the diffusion coefficient of water molecules in the tissue, D* is the pseudo-diffusion coefficient of water molecules in randomly orientated microvasculature, and v_bw is the fraction of the total DWI signal that arises from this compartment. Since its introduction, a number of issues have arisen regarding the validity of the assumptions in the original IVIM model. Using ¹⁹F NMR detectable perfluorocarbons as a blood substitute, Neil and Ackerman²⁰ demonstrated that the diffusion-weighted signal arising from just the intravascular compartment was itself biexponential. Henkelman et al²¹ went on to suggest a more complex approach based on a hierarchical, self-similar network of blood vessels, to explain the biexponential intravascular behavior. However, estimates of perfusion in the rat brain using this model were an order of magnitude lower than literature values, and Duong and Kim²² later demonstrated that the intravascular biexponential behavior is likely to result from separate arterial and venous components. In this work, it was shown that the pseudo-diffusion coefficient of arterial blood was ∼80 times higher than that of venous blood, as, partly due to its pulsatile and more turbulent nature, arterial blood is significantly more attenuated by diffusion gradients. Therefore, in experiments where both intravascular and extravascular water contribute to the DWI signal, it is likely that the contribution to the fast pseudo-diffusion component will be dominated by water molecules on the arterial side of the vascular network, extending down to the capillary level (in which, although flow is slower, the vasculature is more randomly orientated, and therefore spins lose their phase memory in the period during which the measurement is sensitive to motion, and contribute to the IVIM effect).

A further limitation of the original IVIM model was demonstrated by Lemke et al,²³ in which it was shown that, because equation (1) does not account for the different relaxation times of tissue and blood, values of v_bw will vary as a function of TE. As transverse relaxation times in tissue are generally shorter than that of blood, when TE is not accounted for, blood volume fractions will be overestimated. Furthermore, as an inversion pulse was applied at the start of our DWI sequence, differences in longitudinal magnetization relaxation times of blood and tissue should also be accounted for. Therefore, a modified IVIM equation, similar to the one presented in reference²³ but adapted to include the effect of our prior inversion pulse, was used:

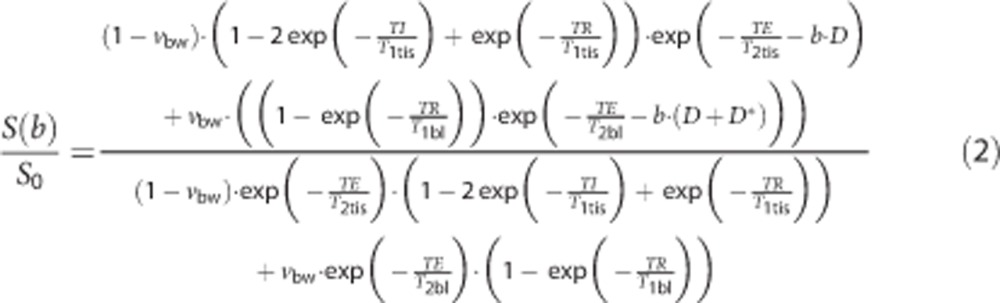where T_1tis, T_1bl, and T_2tis, T_2bl are the longitudinal and transverse relaxation times of tissue and blood, respectively. The T₁ maps acquired in each subject were used to provide values of T_1tis, and values of T_1bl=1.3 seconds, T_2bl=290 milliseconds, and T_2tis=92 milliseconds were assumed.^{24, 25} Equation (2) was fit to the measured DWI signal intensity values using an iterative Nelder–Mead nonlinear least squares algorithm, with v_bw, D, and D* as fitted parameters (Figure 1). Starting values of D, D*, and v_bw were automatically generated in each voxel by performing a prior dual-linear fit to the log transformed data.²⁶ Note Equation (2) assumes that intravascular blood–water, which was initially inverted at time t=0, is replaced by fresh inflowing blood with fully relaxed longitudinal magnetization at t=TI. We used a long TI in our experiments, ensuring this assumption is valid for blood contained within the arterioles and capillaries (the approximate range of capillary arrival times in the healthy adult brain is in the region of 839<TI<1,064 milliseconds⁹).

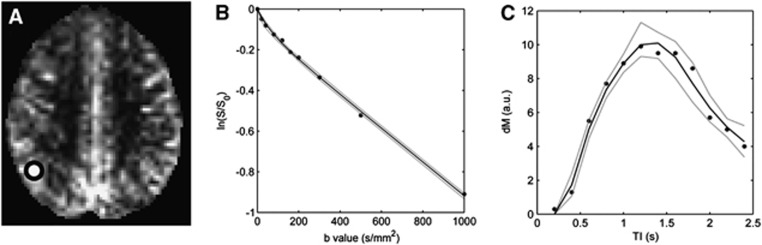
Figure 1.

Example of model fitting in a single voxel. (A) dM map in one subject, shown here at TI=1.8 seconds, after registration to MNI (Montreal Neurological Institute) standard space. The white circle shows the approximate location of the voxel (enlarged for clarity). Plots of the intravoxel incoherent motion (IVIM) (B) and arterial spin labeling (ASL) (C) data from this voxel. Filled circles=measured data, solid black lines=fitted data, gray dashed lines=95% confidence interval from wild bootstrap analysis (see Results section).

Arterial Spin Labeling Model Fitting

As the aim of this study was to investigate microvasculature, we attempted to segment voxels in which the ASL signal arises predominantly from large arteries (see Data Segmentation). However, signal from smaller arteries and arterioles will remain after segmentation, and therefore a model that describes the passage of the labeled bolus through both small arteries and the capillary bed is needed. The four-phase single capillary stepwise model⁴ is suitable for this. This methodology models the contribution to the total ASL signal, dM(t) (the difference in signal intensity between control and labeled acquisitions) from labeled water in arterial (dM_a(t)), capillary (dM_c(t)), and tissue (dM_t(t)) compartments. The contributions are calculated over four phases, with respect to the temporal position of the labeled slab of water as it travels from the tag region to the capillary bed. The details of the equations governing the four phases are given below, and all parameters used in the model are defined in Table 1.⁴

Table 1. Definition of parameters in the ASL modela.

Symbol	Definition	Units
CBF	Cerebral blood flow	mL blood per minute per 100 mL tissue
tA	Bolus arrival time in voxel of interest	seconds
τ	Bolus duration	seconds
tex	Bolus transit time through the arteries and arterioles in a voxel, before reaching capillary bed	seconds
Tex	Tex=tA+tex	seconds
α	Labeling efficiency (α=1)
λ	Brain–blood partition coefficient for water (λ=0.9)	mL blood/mL tissue
M0a	Equilibrium magnetization of arterial blood	Magnetic moment/mL blood
PS	Permeability-surface product	mL water per minute per 100 mL tissue
R1b	Longitudinal relaxation rate of water in blood (R1b=1/1.3)	per second
R1e	Longitudinal relaxation rate of water in extravascular space	per second

ASL, arterial spin labeling.

^aWhere a fixed value has been used, the value is given in parenthesis next to the parameter definition.

Transit phase (0<t≤t_A):

Arterial phase (t_A<t≤T_ex):

(Note the min() function returns the smaller of its two arguments.)

Arterial–capillary transitional phase (T_ex<t≤T_ex+τ):

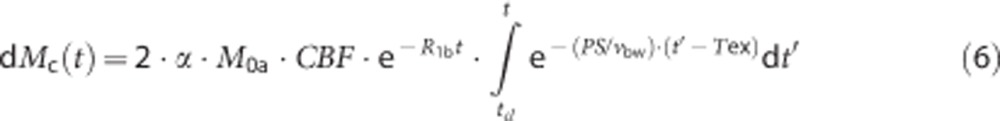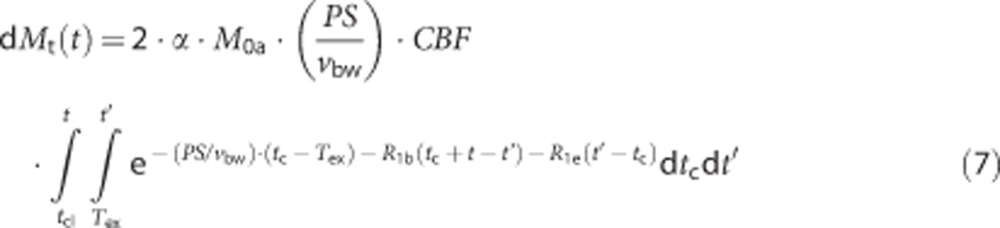where t_cl=max(T_ex, t−τ)=T_ex

Capillary phase (t>T_ex+τ): Here dM_a(t)=0, and equations (6) and (7) further describe dM_c(t) and dM_t(t), respectively, with t_cl=max(T_ex, t−τ)=t−τ.

To estimate the equilibrium longitudinal magnetization of blood (M_0a), a voxel containing only CSF was identified in each subject, and, similar to the method described in reference,²⁷ an estimate of M_0a was made using the fitted value of M₀ in the CSF (see Preprocessing), and assuming a proton density ratio of blood to that of CSF of 0.72.²⁸ The fitted parameters in the four-phase model were then t_A, CBF, t_ex, PS, and τ. Before fitting the two-compartment model, the single-compartment Buxton model²⁹ was fit in each voxel, to provide starting guesses for t_A, CBF, and τ. The starting guesses of PS and t_ex were 150 mL per 100 g per minute and 0.5 seconds, respectively. Values of all fixed parameters used in our analysis are given in Table 1. An iterative Nelder–Mead nonlinear least squares algorithm was used for model fitting (see Figure 1). Note the ratio of PS/v_bw would usually be modeled as a single parameter, rather than PS itself. However, in our analysis, measured values of v_bw, derived from the IVIM analysis, were used.

Data Segmentation

As mentioned previously, we attempted to segment voxels that contained large arteries, before analysis. We were unable to use previously published techniques, such as QUASAR,³⁰ to eliminate macro-vascular ASL signal during acquisition, as these involve the application of bipolar crusher gradients, which are incompatible with the GRASE readout module.³¹ Instead, we first identified a voxel that was primarily filled with blood: this was chosen by automatically selecting the voxel with the greatest peak in dM(t). The variation of dM(t) as a function of TI within this voxel was chosen as a rough estimation of the ‘global' AIF (arterial input function). Note, the AIF determined using this technique will suffer from inaccuracies due to the low resolution of our data and local bolus dispersion; it will however suffice here as it is simply used to facilitate the segmentation process. The approximate range of capillary arrival times (T_ex) in the healthy adult brain is in the region of 839<TI<1,064 milliseconds,⁹ and the dM(t) time series for TI<T_ex should represent the passage of labeled blood at the precapillary level, and will not be influenced by bolus exchange with surrounding tissue. Therefore, for our segmentation process we set T_ex=800 milliseconds, and integrated the area under the dM(t) curve between 0<t<T_ex in each voxel. We then normalized to the area under the global AIF curve over the same time period, to estimate local values of relative arterial volume fraction (rV_a), i.e.,

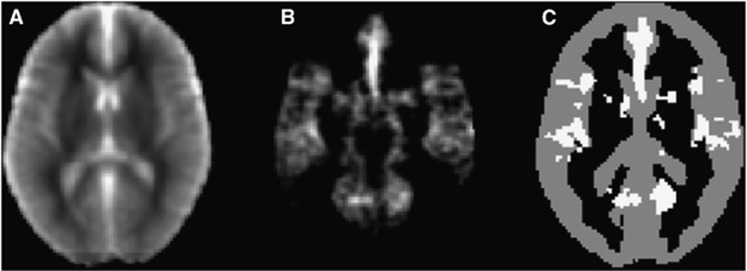
A minimum threshold value of rV_a=0.15 was chosen to identify voxels that predominantly contain large arteries. This was based on visual assessment of rV_a threshold values that most clearly delineate easily identifiable large arteries, such as the middle/anterior cerebral arteries, from the surrounding tissue (see Figure 2). Voxels with an rV_a value above 0.15 were excluded, which ensures that measurements are not corrupted by voxels containing predominantly large arteries rather than microvasculature.

Figure 2.

Overview of the segmentation process. (A) T₁ map, produced using data from the multi-TI non-selective, non-background suppressed arterial spin labeling (ASL) data. (B) Relative arterial volume fraction (rV_a) map at the same location. (C) Data from the T₁ and rV_a map were used to segment the gray matter (gray voxels), while excluding regions that are likely to contain large arteries (white voxels). All data are shown after registration to MNI (Montreal Neurological Institute) standard space.

Because the difference between the control and label ASL acquisition (dM) is very small (typically of the order 1% to 2% without background suppression³⁰), the inherent low SNR of ASL data can lead to large uncertainties in modeled parameters, particularly in two-compartment models.³² As white matter regions suffer from both intrinsically low perfusion and long transit delays, which further reduces the SNR of the ASL signal, additional segmentation was applied to restrict our analysis to gray matter regions. T₁ maps were used to segment the gray matter regions using the Fast module within FSL (Figure 2).

Error Analysis

Monte Carlo simulations were conducted to assess the accuracy and precision of fitted PS and v_bw values. Synthetic ASL and DWI data were generated using the two-compartment ASL model (equations 3, 4, 5, 6, 7) and the extended IVIM model (equation (2)), using typical human gray matter tissue parameters (Table 2). Based on SNR levels measured in the experimental data (Table 2), appropriate levels of random noise (Gaussian for ASL, Rician for DWI) were then added to the synthetic data. This process was repeated to produce 1,000 sets of synthetic raw data, sampled at the same TI/b values acquired in the experimental protocol. The IVIM and ASL model fitting was performed for each synthetic data set, to generate 1,000 samples of all fitted parameters. The mean values of the samples of each fitted parameter were used to determine accuracy, and the standard deviation was used to determine precision. The above process was repeated for input PS values between 80 and 300 mL per 100 g per minute, and input v_bw values between 2 and 6 mL/100 g tissue, chosen to extend beyond the typical values observed in healthy human GM, and cover elevated values which may be encountered in pathology (see Discussion). A one-way analysis of variance followed by a post hoc Tukey–Kramer analysis, with a significance level of P<0.05, was used to test differences between group means in the Monte Carlo simulations.

Table 2. Typical ASL and DWI parameters in human brain gray matter at 1.5 T, used in the Monte Carlo simulations.

Parameter	Description	Value
ASL parameters
SNR	Signal-to-noise ratio of dM data	10a
T1b	T1 of water in blood	1.3 secondsb
T1e	T1 of water in gray matter	1.1 secondsc
α	Inversion efficiency	1.0
λ	Blood:brain partition coefficient	0.9
tA	Bolus arrival time	0.37 secondsa
tex	Bolus transit time (from tA to arrival in capillaries)	0.61 secondsd
τ	Bolus duration	0.74 secondsa
CBF	Cerebral blood flow	44 mL per 100 g per minutea
vbw	Blood volume in voxel	2 mL/100 g tissuee
PS	Permeability-surface product	80–300 mL per 100 g per minute
DWI parameters
SNR	Signal-to-noise ratio of S0 data	120a
D	Diffusion coefficient of tissue water	1.0 × 10−3 mm2/sf
D*	Pseudo-diffusion coefficient of vascular water	1.0 × 10−2 mm2/sf
vbw	Blood volume in voxel	2–6 mL per 100 g per minute

ASL, arterial spin labeling; DWI, diffusion-weighted imaging.

^aMean gray matter values from experimental data measured in 10 subjects.

^bData from Buxton et al.²⁹

^cData from Steinhoff et al.⁴⁰

^dDerived from value of t_A and data in Donahue et al.⁹

^eData from Zhon et al.⁶

^fData from Pekar et al.²⁶

Reproducibility Analysis

To assess intrasubject reproducibility, fitted parameters were analyzed from the test–retest data collected in five of the subjects, after registration into standard space. The within-subject standard deviation (SD_w) was calculated on a voxel-wise basis, using the following formula:³³

where θ₁–θ₂ is the difference in the parameter of interest (i.e., θ=CBF,PS,v_bw) between scans one and two, and N=number of subjects. The coefficient of repeatability (COR) for each fitted parameter was defined as the 95% confidence interval for repeated measurements,³³ given by: COR=1.96 × SD_w. This defines the largest difference between measurements that is likely to be due to measurement error. The repeatability index was defined as RI (%)=100 × COR/mean (i.e., large values of RI indicate that the 95% confidence interval in a voxel is large compared with the mean value, and hence reproducibility is poor). Analysis was first performed without spatial smoothing, and repeated after applying a Gaussian kernel of 2, 4, and 6 mm FWHM to the fitted parameters.

Results

Model Sensitivity and Error Analysis

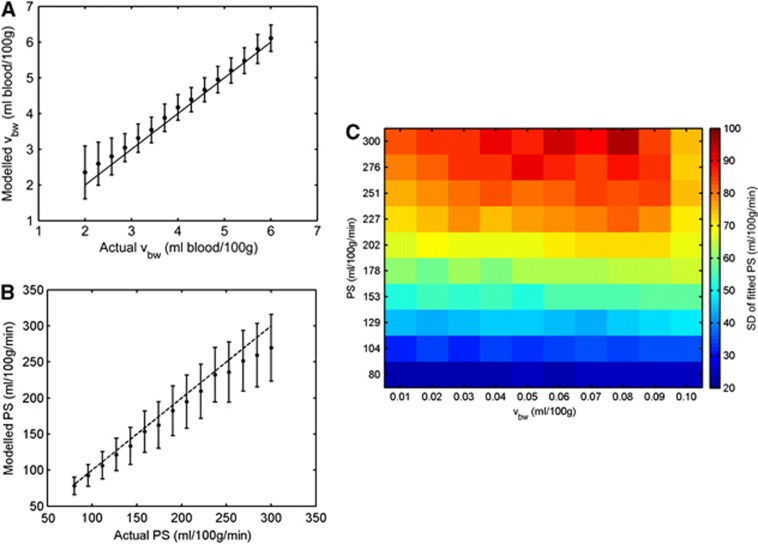
Figure 3 shows the mean fitted values of v_bw and PS derived from the Monte Carlo simulations, plotted against the input value used to generate the data. For v_bw>3 mL blood/100 g tissue, fitted values showed a very small positive bias. However, below this, the bias increased with decreasing values of v_bw, with the mean fitted value being overestimated by 19% at v_bw=2 mL blood/100 g tissue. Precision also decreased at lower values of v_bw, with the COV (coefficient of variation) in fitted values of v_bw increasing from 14% at v_bw=6 mL blood/100 g tissue, to 60% at v_bw=2 mL blood/100 g tissue.

Figure 3.

(A) Mean fitted value of v_bw (vascular volume fraction) as a function of input v_bw value from the diffusion-weighted imaging (DWI) Monte Carlo simulations, at signal-to-noise ratio (SNR)=120. (B) Variation of mean fitted permeability-surface product (PS) as a function of input PS value from the arterial spin labeling (ASL) Monte Carlo simulations, at SNR=10, with v_bw=2 mL blood/100 g tissue (mean value from in vivo data). In both plots, filled circles represent the mean fitted value after 1,000 iterations, and error bars represent s.d. The dashed lines represent input value=fitted value. (C) 2D precision plot of fitted PS values. Color indicates SD of the fitted PS value over 1,000 Monte Carlo simulations, as a function of both input v_bw value (horizontal axis) and input PS value (vertical axis). Typical parameters found in human gray matter at 1.5 T were used to generate all synthetic data (Table 2). The color reproduction of this figure is available on the Journal of Cerebral Blood Flow and Metabolism journal online.

The mean fitted value of PS was also sensitive to changes in the input value, but showed an increasing negative bias as PS increased, with fitted values being underestimated by 10% at the maximum input PS value of 300 mL per 100 g per minute. The COV of fitted PS values increased from 31% at PS=80 mL per 100 g per minute, to 34% at PS=300 mL per 100 g per minute.

Experimental Data

An example of IVIM and ASL model fitting in one voxel is shown in Figure 1. A wild bootstrap technique³⁴ was used to estimate the uncertainty on the fitted values in this example; after initial model fitting, the polarity of the residuals at each data point was either unperturbed or inverted with a 50% probability. New data sets were created by adding the adjusted residuals to the fitted data, after which model fitting was repeated. This process was repeated over 5,000 iterations, after which the distribution of fitted parameters was used to estimate uncertainty. In the example shown in Figure 1, the (2.5 percentile,<mean>,97.5 percentile) values of the IVIM fitted parameters were: v_bw=(4.4,<6.0>,7.5) mL blood/100 g tissue, D=(0.80,<0.83>,8.6) × 10⁻³ mm²/s, and D*=(10.0,<19.1>,50.0) × 10⁻³ mm²/s. The corresponding uncertainty estimates on the ASL fitted parameters were: t_A=(0.28,<0.32>,0.35) seconds, CBF=(85.9,<88.0>,102.5) mL per 100 g per minute, PS=(87.5,<133.9>,164.5) mL per 100 g per minute, τ=(0.89,<1.25>,1.51) seconds, and T_ex=(0.75,<1.08>,1.31) seconds.

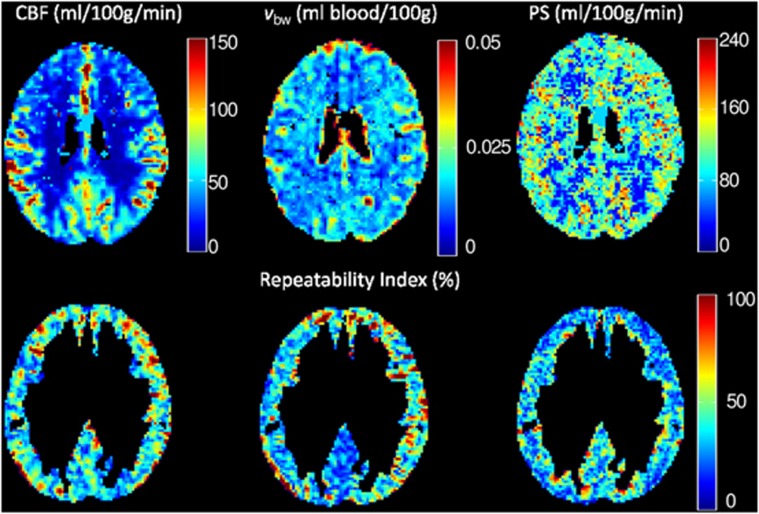
Example maps of CBF, v_bw, and PS from one representative subject are shown in Figure 4, along with voxel-wise values of RI at the same location. After coregistration into standard space and segmentation of the white matter and large arteries, the mean value of CBF, v_bw, and PS in the gray matter across all subjects was 44±5 mL per 100 g per minute, 2.3±0.2 mL blood/100 g tissue, and 108±2 mL per 100 g per minute, respectively. For comparison, the mean gray matter CBF in all subjects obtained using the single-compartment Buxton general kinetic model²⁹ was 48±6 mL per 100 g per minute. Data from the Monte Carlo simulations suggest that statistically significant changes in these mean fitted values could be observed for an underlying change in PS beyond the range 96<PS_mean(108)<143 mL per 100 g per minute, and v_bw beyond the range 2.0<v_bw,mean(2.3)<2.6 mL blood/100 g tissue (P<0.05).

Figure 4.

(Top row) Maps of fitted cerebral blood flow (CBF) (left), blood volume fraction (v_bw) (middle), and permeability-surface product (PS) (right) in a representative subject, before segmentation and spatial smoothing. (Bottom row) Voxel-wise repeatability index (RI) across five subjects in the same slice, after segmentation of white matter and large arteries.

Mean voxel-wise values of SD_w and RI, for unsmoothed and smoothed data, are given in Table 3. Without spatial smoothing, poor intrasubject reproducibility was observed, with COR values of 29 mL per 100 g per minute, 1.6 mL/100 g tissue, and 80 mL per 100 g per minute for CBF, v_bw, and PS, respectively. However, spatial smoothing improved reproducibility considerably, with COR values for CBF, v_bw, and PS of 8 mL per 100 g per minute, 0.4 mL/100 g tissue, and 13 mL per 100 g per minute, respectively, when a 6-mm FWHM Gaussian kernel was applied.

Table 3. Within-subject standard deviation (SD_w) and repeatability index (RI) for fitted values of cerebral blood flow (CBF), microvascular volume fraction (v _bw), and permeability-surface product (PS).

	CBF (mL per 100 g per minute)		vbw (mL blood/100 g tissue)		PS (mL per 100 g per minute)
FWHM (mm)	SDw	RI (%)	SDw	RI (%)	SDw	RI (%)
0	22.6	62.2	1.17	65.2	31.7	70.8
2	17.4	47.9	0.85	51.2	17.0	38.7
4	13.0	32.5	0.60	35.7	10.7	22.4
6	10.3	24.7	0.46	27.3	7.9	15.9

FWHM, full width at half maximum.

All values represent mean value per voxel, in the gray matter, after registration into standard space.

Discussion

The mean CBF in the gray matter in our subjects is slightly lower than previously reported values.³⁵ However, our values were calculated after the segmentation of large arteries, and are therefore not contaminated by high signal from labeled blood in large vessels, which is destined to perfuse tissue in more distal regions. Furthermore, most previous ASL-based CBF measurements have used a single-compartment model. It has been shown that this tends to overestimate the true value of CBF, by ∼17% in human gray matter at 1.5 T,⁵ although in our case, analysis with the single-compartment Buxton model produced CBF values which were ∼9% higher.

Our mean rV_a maps (Figure 2) are visually similar to the arterial blood volume maps produced using the QUASAR method,³⁰ and it would appear that our methodology provides an effective means of identifying and segmenting large feeding arteries in the brain. This could be beneficial when it is not possible to apply bipolar crusher gradients during the ASL acquisition protocol.

The expected value of v_bw in healthy gray matter is difficult to predict without a comprehensive understanding of the source of the fast diffusing signal in DWI data. The mean, total CBV in human gray matter in subjects aged ∼30 years has been measured as 5.2 mL blood/100 g tissue.³⁶ As mentioned earlier, the IVIM effect arises predominantly from blood in the arterial/capillary compartments of the vascular network. Arterial blood has been shown to contribute ∼30% of total CBV,²² which would suggest an expected v_bw value in the region of 1.6 mL blood/100 g tissue in our subjects. However, this neglects the contributions from blood in the capillary bed, and is therefore likely to represent the lower limit on the expected v_bw value. Also, as our mean measured value of v_bw was 2.3 mL blood/100 g, and our Monte Carlo simulations show that modeled v_bw values at this level will be overestimated by ∼18%, the corrected mean v_bw value in our subjects is∼1.9 mL blood/100 g tissue, which shows good agreement with expected v_bw values in healthy GM.

When measured values of v_bw are used to obtain PS values from the two-compartment ASL model, estimated values also show good agreement with previous studies: our mean PS was 108 mL per 100 g per minute; previously reported values in healthy human gray matter range from 80 to 169 mL per 100 g per minute.⁶ After accounting for the known bias in fitted PS values, our PS data remain within the range of previously reported values, suggesting that physiologically sensible estimates of PS in the gray matter can be obtained using a combined DWI/ASL methodology. However, it should be noted that because IVIM-derived v_bw values are likely to represent the sum of the arteriole and capillary volume fractions, the v_bw value will be an overestimate of the compartment size involved in the extravasation of labeled water in the ASL model, which may lead to an underestimation of PS. Nonetheless, v_bw will be sensitive to an underlying change in capillary volume fraction, and as such it should be possible to decouple local changes in v_bw and PS using our methodology.

If the combined IVIM-ASL methodology is to be clinically useful, it is important to quantify the precision and reproducibility of the technique, and to assess whether it would be sensitive to pathologically induced changes. For instance, in pathologies such as brain tumors, which induce angiogenesis and increase BBB permeability, we would expect increases in v_bw by a factor of ∼3,³⁷ and increases in PS by up to a factor of ∼20.³⁸ Our sensitivity analysis suggests that underlying changes in PS and v_bw of this magnitude would lead to significant changes in the corresponding fitted values from the two-compartment ASL and IVIM models. However, it should be noted that in pathologies, a wider range of ASL and DWI parameters may change in parallel, which would be difficult to model accurately using simulated data. Also, our Monte Carlo simulations represent the ‘best-case scenario', in which the model used to generate the data is the same as that used to fit the data.

The COR values in our experimental data define the largest difference between measurements that is likely to be caused by the combined effect of model fitting and measurement error (patient movement, eddy-currents, etc). Without spatial smoothing, our COR values suggests that within-subject voxel-wise reproducibility of PS and v_bw measurements is inadequate for clinical use. However, given the low SNR of ASL data, registration inaccuracies (see below), and subject motion between scans, this is perhaps not surprising. The improved reproducibility at increased levels of spatial smoothing suggests that measurement of v_bw and PS with a reasonable reproducibility would be possible, at the cost of slightly reduced spatial resolution. However, as the majority of previous ASL-derived PS measurements have been performed using large, often whole-gray matter ROIs, our methodology offers an alternative approach, providing PS measurements on a more localized scale.

Study Limitations

A limitation of two-compartment ASL models is that they are typically two orders of magnitude less sensitive to changes in PS than CBF,³² which, combined with the typically low SNR of ASL data, makes PS a difficult parameter to fit. Our ASL protocol was designed to counteract this as far as possible. For instance, we employed a 3D GRASE pulse sequence for data acquisition, rather than 2D EPI sequences as used in previous two-compartment ASL studies.^{5, 6} This has the advantage that the entire imaging volume is acquired at a single TI time, and 3D acquisition has an inherently higher SNR than 2D multislice (it has been shown that the 3D GRASE technique yields a 2.8-fold increase in SNR compared with 2D EPI at the same nominal resolution¹⁸). This is improved further by our use of background suppression of the static tissue signal, which has not been applied in previous two-compartment studies. Because the signal differences between the label and control experiments are of the order of a few percent, scanner gain adjustment is usually ineffective for extracting the labeled blood signal. However, when background suppression is applied, scanner gain can be increased (in our case by a factor of 10), to improve the dynamic range of the labeled blood signal without risking saturation from the static tissue signal. The noise added to the labeled bolus signal from instabilities in the static tissue will also be reduced. However, despite these SNR gains, the point spread function in the second phase encoding direction (inferior–superior in our case) is very different compared with the EPI sequence used for DWI acquisition, therefore differences in image distortion and point spread function between the 3D GRASE and 2D EPI sequences may lead to inaccuracies when coregistering raw data into standard space. More advanced registration algorithms (unwarping with field maps, nonlinear normalization, etc) may reduce this source of error. However, a previous study has compared CBF values acquired in healthy humans using our GRASE sequence with those obtained in the same subjects, using identical parameters and a 2D EPI readout,¹⁸ and found no significant difference in CBF.

A further limitation is that, because a multislice DWI acquisition was used, each slice will have a slightly different TI following the initial inversion pulse, which will compromise the accuracy of v_bw values obtained using equation (2) in some slices. We used interleaved slices to reduce the effect of a systematic bias in v_bw as a function of slice position in the stack; however, variations in TI may have led to inaccuracies in modeled v_bw values in some locations. Furthermore, as subjects were not repositioned between scans, it should be noted that the COR values quoted here represent within-session reproducibility rather than between session reproducibility. Lastly, while our segmentation process appears to be effective at excluding large arterial signals, it will not exclude small arterial/arteriole signals. The Bayesian model presented in³⁹ may help with this, and is an area that warrants further investigation.

Given the significant changes in v_bw and PS that neurological pathologies, such as brain tumors, can induce as a result of angiogenesis and disruption to the BBB, the data shown in Table 3 suggest that pathologically induced changes should exceed the COR of the technique, and the methodology should be adequate for clinical use. Furthermore, we have demonstrated this technique at 1.5 T; given the potential for increased SNR at higher field strengths, further improvements to both the precision and spatial resolution of the technique could be realized once ASL becomes generally clinically available at 3 T and beyond.

In conclusion, we present a new, noninvasive methodology for MR-derived measurement of PS in the human brain, which incorporates IVIM-derived estimates of v_bw into a two-compartment ASL model. The additional v_bw measurements can be made using standard DWI protocols that are widely clinically available, and provide a mechanism by which fitted values of PS would not be corrupted by pathologically induced changes in v_bw. By measuring PS, CBF, and v_bw directly using noninvasive MRI techniques such as this, a ‘suite' of biomarkers become available, which in the future could be used to characterize pathologies and treatment response, and will be particularly well suited for repeated measurements in longitudinal studies, or for use in pediatric patients.

The authors declare no conflict of interest.