Abstract
The basal ganglia is a brain region critically involved in reinforcement learning and motor control. Synaptic plasticity in the striatum of the basal ganglia is a cellular mechanism implicated in learning and neuronal information processing. Therefore, understanding how different spatio-temporal patterns of synaptic input select for different types of plasticity is key to understanding learning mechanisms. In striatal medium spiny projection neurons (MSPN), both long term potentiation (LTP) and long term depression (LTD) require an elevation in intracellular calcium concentration; however, it is unknown how the post-synaptic neuron discriminates between different patterns of calcium influx. Using computer modeling, we investigate the hypothesis that temporal pattern of stimulation can select for either endocannabinoid production (for LTD) or protein kinase C (PKC) activation (for LTP) in striatal MSPNs. We implement a stochastic model of the post-synaptic signaling pathways in a dendrite with one or more diffusionally coupled spines. The model is validated by comparison to experiments measuring endocannabinoid-dependent depolarization induced suppression of inhibition. Using the validated model, simulations demonstrate that theta burst stimulation, which produces LTP, increases the activation of PKC as compared to 20 Hz stimulation, which produces LTD. The model prediction that PKC activation is required for theta burst LTP is confirmed experimentally. Using the ratio of PKC to endocannabinoid production as an index of plasticity direction, model simulations demonstrate that LTP exhibits spine level spatial specificity, whereas LTD is more diffuse. These results suggest that spatio-temporal control of striatal information processing employs these Gq coupled pathways.
Author Summary
Change in the strength of connections between brain cells in the basal ganglia is a mechanism implicated in learning and information processing. Learning to associate a sensory input or motor action with reward likely causes certain patterns of input to strengthen connections, a phenomenon known as long term potentiation (LTP), and other patterns of input to weaken those connections, known as long term depression (LTD). Both LTP and LTD require elevations in calcium, and a critical question is whether different patterns of input cause different patterns of calcium dynamics or activate different downstream molecules. To address this issue we develop a spatial, computational model of the signaling pathways in a dendrite with multiple spines. Model simulations show that stimulation patterns that produce LTP experimentally activate more protein kinase C than stimulation patterns that produce LTD. We experimentally confirm the model prediction that protein kinase C is required for LTP. The model also predicts that protein kinase C exhibits spatial specificity while endocanabinoids do not.
Introduction
The striatum is a brain structure involved in motor control [1], reward learning [2], and addiction [3]. Medium spiny projection neurons (MSPN) are the principal neurons of the striatum [4], and their activity shapes motor behavior through control of activity in downstream structures such as the globus pallidus [4]. Striatal processing of converging cortical glutamatergic inputs is not static, but instead is modulated by synaptic plasticity which depends on nigral dopaminergic inputs [5] and intrinsic cholinergic inputs [6], [7]. Not only is synaptic plasticity a mechanism used for storage of motor memories and adaptive changes in behavior [8], but alterations in synaptic plasticity during or after withdrawal from chronic alcohol or drug use may contribute to relapse behavior [9], [10]. Therefore, understanding the control of synaptic plasticity will illuminate mechanisms underlying reward learning, addiction and motor control in the striatum.
Synaptic plasticity can either potentiate or depress synaptic strength depending on spatio-temporal pattern of activation. For example, in spike timing dependent plasticity [11]–[14], the direction of plasticity depends on whether the post-synaptic action potential precedes or follows pre-synaptic glutamate release. Another type of temporal sensitivity to pre-synaptic stimulation frequency has been observed in the hippocampus [15] and is attributed to calcium activated signaling pathways: high frequency stimulation preferentially activates calcium-calmodulin dependent protein kinase type II (CaMKII), whereas low frequency only activates calcineurin [16]. In contrast to the hippocampus, endocannabinoid production is required for striatal long term depression (LTD) [7], whereas protein kinase C (PKC) has been implicated in striatal long term potentiation (LTP) [17]. Curiously, both PKC and endocannabinoids require diacylglycerol and calcium elevation [18], though the source of calcium entry may be different for the two phenomena as L type calcium channels are required for LTD [19] and NMDA receptors are required for LTP [20]. An unresolved question is whether the two calcium permeable channels are coupled to distinct signaling pathway molecules [21], or whether different calcium dynamics, as produced by different stimulation patterns, can lead to activation of different signaling pathways, as has been shown in striatal cholinergic neurons [22].
Previous modeling studies have investigated how temporal pattern selects for LTP versus LTD. In one striatal model [23], a small calcium elevation yielded dephosphorylation of the glutamate receptor GluA1 subunit on S845 (LTD), whereas a large calcium elevation produced phosphorylation of GluA1 on S845 (LTP). Other striatal models focused on activation of protein kinase A and its phorphorylation of DARPP-32 [24]–[26]. None of these studies investigated the role of endocannabinoids, which are critical for LTD in the striatum, nor the spatial specificity of diverse signaling pathways. Thus, in this study we employ a computational model of Gq coupled pathways to investigate how temporal pattern of calcium and Gαq activation selects for either endocannabinoids (and LTD) or PKC (and LTP). We compare simulation of a recently developed theta-burst stimulation paradigm that produces LTP in striatal brain slice in normal magnesium solutions [27] with simulation of an LTD protocol to facilitate investigating how temporal pattern controls the direction of plasticity.
Methods
Signaling Network
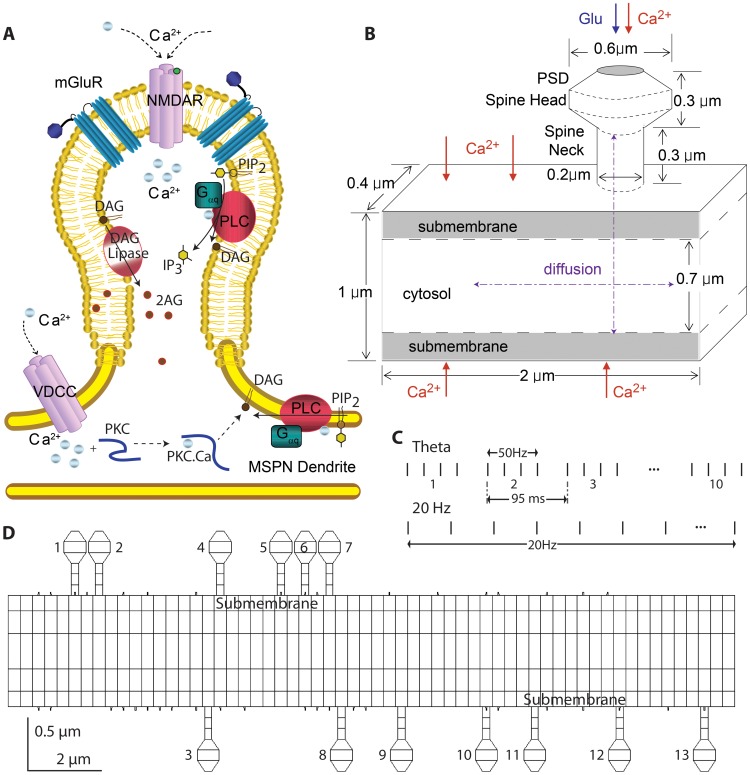
The modeled biochemical signaling network contains calcium activated molecules as well as Gq coupled pathways (Fig. 1A, Table 1), both of which are essential for LTP [28], LTD [19] and depolarization induced suppression of inhibition (DSI) [29]. Glutamate bound metabotropic glutamate receptors (mGluR) act as an enzyme and produce GαqGTP from the inactive Gαβγ heterotrimeric G protein. Phospholipase Cβ is activated by binding to calcium, and its activity is enhanced by binding to GαqGTP [30]–[32]. Phospholipase Cβ produces both inositol triphosphate and diacylglycerol from phosphoinositol bisphosphate [33]. The diacylglycerol can bind to either the calcium bound form of diacylglycerol lipase, which produces the endocannabinoid 2-arachidonoylglycerol (2AG) [34], [35], or the calcium bound form of PKC [18], [36] to produce activated PKC. Other calcium binding proteins in the model include calbindin, calmodulin [37], [38], and both a high affinity and low affinity plasma membrane calcium pump [39], [40] in order to regulate the calcium concentration.
Figure 1. Morphology and signaling pathways in the model.
(A) Glutamate binds to metabotropic glutamate receptors (mGluR), which activate the Gq subtype of G protein. Calcium, in the absence or presence of activated GαqGTP, binds to and activates phospholipase C (PLC), which produces diacylglycerol (DAG) and inositol trisphosphate (IP3). Diacylglycerol lipase (DAGL) converts diacylglycerol to 2-arachidonyl glycerol (2AG), an endocannabinoid implicated in both LTD and DSI. Alternatively, calcium and then DAG bind to protein kinase C (PKC), forming the activated form, implicated in LTP. (B) For most simulations, the morphology consists of a single spine and a 2 µm length of dendrite. Calcium influx into the postsynaptic density (PSD) represents influx through both NMDA receptors and voltage dependent calcium channels in the spine, and calcium influx into the dendrite represents voltage dependent calcium channels. Glutamate or DHPG (a metabotropic receptor glutamate agonist) is provided to the PSD. (C) Stimulation patterns used for theta burst and 20 Hz stimulation. A single train is illustrated for both stimulation patterns. (D) Several simulations used a 20 µm long dendrite with 12 spines. Reactions and initial conditions are the same as for the smaller morphology. Spine numbering is used for Fig. 9 and 10.
Table 1. Reactions and rate constants of signaling pathways in the model.
| Reaction | kf | kb | kcat | Description |
Ca+PMCA⇔PMCA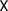 Ca⇒PMCA+CaExt Ca⇒PMCA+CaExt
|
0.05 | 7 | 3.5 | Calcium pump |
Ca+NCX⇔NCX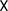 Ca⇒NCX+CaExt Ca⇒NCX+CaExt
|
0.0168 | 11.2 | 5.6 | Calcium exchanger |
CaExt+Leak⇔CaExt
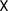 Leak⇒Ca+Leak Leak⇒Ca+Leak |
0.0015 | 1.1 | 1.1 | Calcium leak |
Ca+calbindin⇔calbindin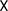 Ca Ca |
0.028 | 19.6 | Calcium buffer | |
Cam+2Ca⇔CamC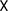 Ca2 Ca2
|
0.006 | 9.1 | Calmodulin C site 1st | |
CamC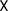 Ca2+2Ca⇔Cam Ca2+2Ca⇔Cam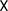 Ca4 Ca4
|
0.1 | 1000 | Calmodulin N site 2nd | |
Cam+2Ca⇔CamN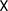 Ca2 Ca2
|
0.1 | 1000 | Calmodulin N site 1st | |
CamN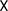 Ca2+2Ca⇔Cam Ca2+2Ca⇔Cam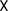 Ca4 Ca4
|
0.006 | 9.1 | Calmodulin C site 2nd | |
| Glu⇔GluInact | 2 | 2.0E-05 | mGluR agonist uptake | |
Glu+mGluR⇔Glu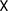 mGluR mGluR |
0.0001 | 10 | mGluR agonist binding | |
Glu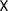 mGluR⇔Glu mGluR⇔Glu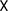 mGluRdesens mGluRdesens |
0.25 | 0.001 | mGluR desensitization | |
Glu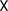 mGluR+Gαβγ⇔Glu mGluR+Gαβγ⇔Glu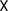 mGluR mGluR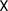 Gαβγ⇔Glu Gαβγ⇔Glu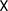 mGluR+GαGTP mGluR+GαGTP |
0.015 | 7.2 | 0.5 | G protein activation |
PLC+Ca⇔PLC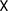 Ca Ca |
0.02 | 120 | PLC binds calcium 1st | |
PLC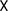 Ca+GαGTP⇔PLC Ca+GαGTP⇔PLC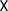 Ca Ca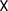 GαGTP GαGTP |
0.1 | 10 | PLC binds GαGTP 2nd | |
PLC+GαGTP⇔PLC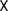 GαGTP GαGTP |
0.01 | 12 | PLC binds GαGTP 1st | |
PLC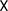 GαGTP+Ca⇔PLC GαGTP+Ca⇔PLC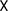 Ca Ca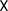 GαGTP GαGTP |
0.08 | 40 | PLC binds calcium 2nd | |
PLC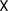 Ca+PIP2⇔PLC Ca+PIP2⇔PLC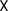 Ca Ca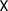 PIP2⇒PLC PIP2⇒PLC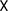 Ca Ca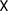 DAG+IP3 DAG+IP3
|
0.006 | 10 | 25 | Production of DAG, step 1 |
PLC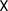 Ca Ca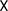 DAG⇔PLC DAG⇔PLC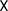 Ca+DAG Ca+DAG |
200 | Production of DAG, step 2 | ||
PLC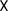 Ca Ca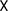 GαGTP+PIP2⇔PLC GαGTP+PIP2⇔PLC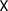 Ca Ca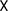 GαGTP GαGTP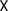 PIP2⇒PLC PIP2⇒PLC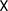 Ca Ca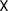 GαGTP GαGTP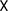 DAG+IP3 DAG+IP3
|
0.015 | 75 | 250 | Production of DAG, step 1 |
PLC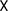 Ca Ca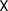 GαGTP GαGTP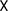 DAG⇔PLC DAG⇔PLC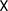 Ca Ca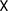 GαGTP+DAG GαGTP+DAG |
1000 | Production of DAG, step 2 | ||
| IP3⇔IP3deg | 10 | Degradation of IP3 | ||
IP3deg+PIKin⇔IP3deg PIKin⇒PIP2+PIKin PIKin⇒PIP2+PIKin |
0.002 | 1 | 1 | PIP2 regeneration by PI kinase |
PLC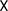 GαGTP⇒PLC+GαGDP GαGTP⇒PLC+GαGDP |
30 | GAP activity of PLC | ||
PLC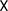 Ca Ca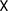 GαGTP⇒PLC GαGTP⇒PLC Ca+GαGDP Ca+GαGDP |
30 | GAP activity of PLC | ||
| GαGTP⇒GαGDP | 1 | Hydrolysis of GαGTP | ||
| GαGDP⇒Gαβγ | 10 | Regeneration of G protein | ||
Ca+DAGL⇔Ca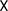 DAGL DAGL |
0.125 | 50 | Calcium activate DAG Lipase | |
DAG+Ca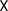 DAGL⇔DAG DAGL⇔DAG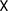 Ca Ca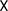 DAGL⇒Ca DAGL⇒Ca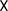 DAGL+2AG DAGL+2AG |
0.0025 | 1.5 | 1 | 2AG production |
| 2AG⇔2AGdeg | 5 | 2AG degradation | ||
DAG+DagK⇔DagK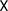 DAG⇒PA DAG⇒PA |
0.0007 | 40 | 10 | DAG inactivation by DAG kinase |
Inactive PKC+Ca⇔PKC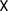 Ca Ca |
0.02 | 50 | PKC binds calcium | |
PKC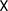 Ca+Dag⇔active PKC Ca+Dag⇔active PKC |
1.5E-05 | 0.15 | PKC binds DAG |
Units are nM−1s−1 for 2nd order reactions and s−1 for 1st order reactions.
The initial concentration and distribution of molecules are indicated in Table 2. Membrane bound molecules include the metabotropic glutamate receptors, G proteins, phospholipase C [41], phosphoinositol bisphosphate, diacylglycerol, diacylglycerol lipase [42], and both plasma membrane pumps [39], [40]. Diffusible molecules (Table 3) include calcium, calbindin, calmodulin, and 2AG. Diffusion constants were estimated as previously [26], using a cytosolic viscosity of 4.1 for small molecules and 8.7 for proteins such as calmodulin [43], [44].
Table 2. Initial concentrations of molecule species in the simulation.
| Molecule | General Cytosol (nM) |
| Ca | 51 |
| CaExt | 2015100 |
| Calbindin | 153290 |
Calbindin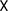 Ca Ca |
7648 |
| Cam | 7940 |
CamC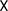 Ca2 Ca2
|
60 |
CamN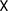 Ca2 Ca2
|
60 |
| GluInact | 1019100 |
| Inactive PKC | 15000 |
Molecules not listed have initial concentrations of 0. General cytosol means that molecules populated the entire morphology.
Molecules initialized in the dendrite submembrane are specified in picoMoles per m2 (picoSD).
NCX was present only in the spine neck and was excluded from spine head.
Table 3. Diffusion constants for diffusible molecules in the model.
| Molecule Name | Diffusion Constant (µm2/sec) |
| Glu | 100 |
| GluInact | 100 |
| Ca | 174.3 |
| CaExt | 174.3 |
| Calbindin | 9.3 |
Calbindin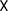 Ca Ca |
9.3 |
| Cam | 11 |
CamC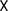 Ca2 Ca2
|
11 |
CamN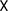 Ca2 Ca2
|
11 |
Cam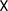 Ca4 Ca4
|
11 |
| IP3 | 10.6 |
| IP3deg | 10.6 |
| Inactive PKC | 14 |
PKC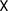 Ca Ca |
14 |
| 2AG | 88.6 |
| 2AGdeg | 88.6 |
Molecules not listed do not diffuse; thus, their diffusion constants are zero.
Morphology
The biochemical network was simulated in a 2 µm long segment of dendrite (1 µm wide by 0.6 µm depth) with one spine (Fig. 1B). The dendrite was subdivided into multiple compartments of size 0.14×0.14×0.4 µm in order to simulate 2-D diffusion. Both layers of dendritic subvolumes on the edge were considered as the submembrane region for placement of membrane bound molecules. A single spine was subdivided into a spine head (0.6 µm diameter), a neck (0.2 µm diameter and 0.3 µm long) and a post-synaptic density (PSD), which were further subdivided into 0.1 µm cylindrical slices, to simulate 1-D diffusion. For the purpose of investigating spatial specificity, the biochemical network was simulated in a 20 µm long dendrite with spines randomly placed with a density of 0.8 spines/µm (Fig. 1D).
Stimulation
Depolarization induced suppression of inhibition (DSI) is a short lasting decrease in the strength of inhibitory synaptic input, and is produced experimentally by depolarizing the post-synaptic neuron without stimulating pre-synaptic fibers [29]. This depolarization causes influx of calcium through voltage gated calcium channels but does not activate synaptic channels. Thus, for simulation of DSI, we inject calcium both in the spine and the dendrite, both of which are locations of voltage gated calcium channels. The amount of calcium injection is adjusted to produce a calcium elevation consistent with published measurements [45]; thus the quantity of injected calcium decreases over time for 1s and 5s depolarizations to approximate the voltage and calcium dependent inactivation of channels.
For synaptic plasticity simulations, two different patterns of stimuli are used. Theta burst stimulation, which produces LTP [27], consists of 4 pulses per burst, 10 bursts per train (Fig. 1C) and 10 trains total. Pulses within the burst are provided at 50 Hz, bursts occur at ∼10.5 Hz (95 ms from the first pulse in one burst to the first pulse in the next burst), and trains are spaced 15 seconds apart. 20 Hz stimulation, which produces 2AG dependent LTD [46], consists of 20 trains of 20 pulses at 20 Hz, with 9 sec between trains. For both theta burst and 20 Hz stimulation, a total of 400 calcium pulses is provided. In addition to the calcium influx, ligand for the metabotropic glutamate receptors is released with every calcium pulse.
Simulation Environment
The signaling pathways activated by calcium and mGluR stimulation in striatal medium spiny neurons are implemented using a well-validated, efficient, mesoscopic stochastic reaction-diffusion algorithm, NeuroRD [47]. The numerical method is a spatial extension [48] of Gillespie's tau leap algorithm [49]. A stochastic approach is required when molecule species have very low copy numbers [50], which in our simulations is partly due to the small size of the spine and submembrane domains. All simulations use a time step of 2.5 µs, and the simulations are repeated 3 times using different random number seeds, analogous to repeated experimental trials. Simulation output is processed using NRDPost (to calculate average concentration for defined regions in the morphology) and VNRD (for visualization). Graphs show concentration (calculated by dividing the number of molecules by Avogadro's number and the appropriate volume) instead of molecule number to control for different subvolume sizes. The simulation and output processing software and the files used for the model simulations are freely available from the author's website (http://krasnow.gmu.edu/CENlab/) and modelDB (http://senselab.med.yale.edu/ModelDB/).
Experiments
All animal handling and procedures were in accordance with the National Institutes of Health animal welfare guidelines and were approved by the George Mason University IACUC committee. Male C57BL/6 mice (2–5 months) were anesthetized with isoflurane and decapitated. Brains were quickly extracted and placed in oxygenated ice-cold slicing solution (in mM: KCL 2.8, Dextrose 10, NaHCO3 26.2, NaH2PO4 1.25, CaCl2 0.5, Mg2SO4 7, Sucrose 210). Hemicoronal slices from both hemispheres were cut 350 µm thick using a vibratome (Leica VT 1000S). Slices were immediately placed in an incubation chamber containing artificial cerebrospinal fluid (aCSF) (in mM: NaCl 126, NaH2PO4 1.25, KCl 2.8,CaCl2 2, Mg2SO4 1, NaHCO3 26.2, Dextrose 11) for 30 minutes at 33°C, then removed to room temperature (21–24°C) for at least 90 more minutes before use.
Two hemislices were transferred to a submersion recording chamber (Warner Instruments) gravity-perfused with oxygenated aCSF (30–32°C) containing 50 µM picrotoxin. Pipettes were pulled from borosilicate glass on a laser pipette puller (Sutter P-2000) and filled with aCSF (resistance ∼4 MΩ). Field population spikes (PopSpikes) were recorded from brain slices using an intracellular electrometer IE-251A (Warner Instruments) and 4-pole Bessel filter (Warner Instruments), sampled at 20 kHz and processed using a PCI-6251 and LabView (National Instruments). PopSpikes were measured using extracellular stimulation of white matter at a rate of 0.05 Hz through a bipolar electrode before and after the induction protocol. Stimulation intensity was adjusted to produce 40–60% of the peak pop-spike amplitude on an input-output curve. Baseline data was collected for at least 10 minutes to ensure response stability prior to induction. Chelerythrine was obtained from LC Laboratories, and applied at least 20 min prior to induction.
Results
Validation of Model using DSI
We developed a reaction-diffusion model of the post synaptic signaling pathways in striatal medium spiny projection neurons underlying PKC activation and 2AG production (Fig. 1A,B and Tables 1–3) to investigate whether temporal pattern of synaptic input selects for direction of plasticity. To validate the model, we first performed simulations of depolarization induced suppression of inhibition (DSI), which is a type of short-term plasticity that is induced by postsynaptic depolarization. Similar to 20 Hz LTD, DSI depends on retrograde transmission of the endocannabinoid 2AG, which is produced in response to calcium elevation. Experiments show that Gq coupled receptor activation facilitates 2AG –dependent DSI in response to 100 ms or 1 s depolarization, but not in response to 5 s depolarization. The proposed explanation of this result is that 2AG –dependent DSI is already saturated by the large amount of calcium due to a 5 s depolarization [29], [42]. Thus, we validate our model by comparing the enhancement in 2AG production produced by mGluR agonists with the enhancement in DSI produced by mGluR agonists.
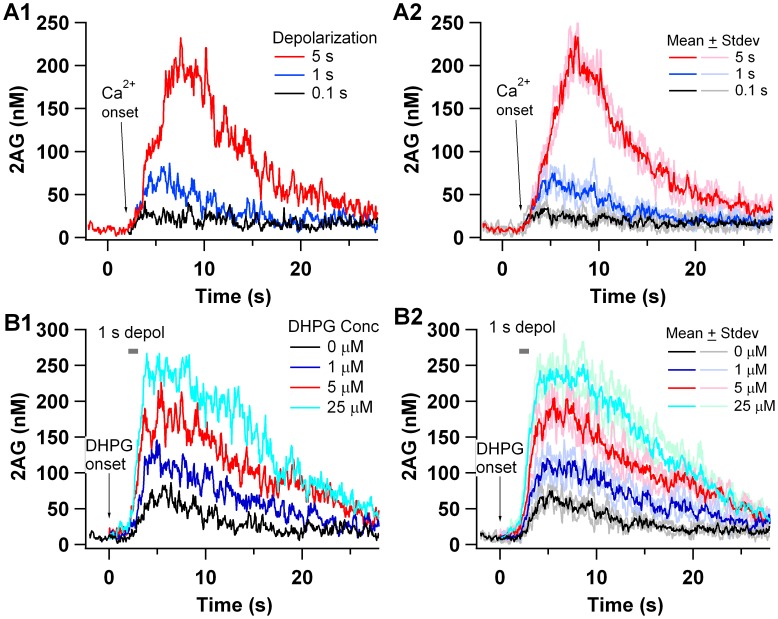
In the model, the quantity of 2AG produced depends on both the duration of calcium influx (Fig. 2A1,2) and the concentration of DHPG (Fig. 2B1,2). The small 2AG in response to 100 ms depolarization alone (Fig. 2A1,2) is consistent with the experimentally observed absence of DSI with the same condition [42]. In contrast, the 5 s depolarization is sufficient to produce a robust 2AG response, consistent with the DSI response observed experimentally. The effect of mGluR facilitation of 2AG production is illustrated in Fig. 2B1,2 for a 1 sec depolarization. The application of the mGluR agonist dihydroxyphenylglycine (DHPG) 2 sec prior to the onset of depolarization facilitates the production of 2AG in a concentration dependent manner. Fig. 2A2 and 2B2 show the response averaged over 3 independent trials (random seeds) and the standard deviation of the response, whereas Fig. 2A1 and 2B1 show single trials. Note that the fluctuations are much greater for single trials as compared to the mean responses. The calcium concentration corresponding to the 100 ms, 1 s and 5 s depolarization is illustrated in Fig S1.
Figure 2. 2AG in response to depolarization is facilitated by mGluR activation.
(A) 2AG in response to depolarization (calcium influx) alone. 2AG increases with duration of calcium influx, but minimal 2AG is detectable with a 0.1 sec depolarization. (B) 2AG in response to depolarization together with mGluR stimulation. DHPG is applied at 0 sec and depolarization starts at 2 sec. Increased mGluR stimulation increases quantity of 2AG production. A1 and B1 show results of a single trial, while A2 and B2 show the average and standard deviation of 3 independent trials (random seeds).
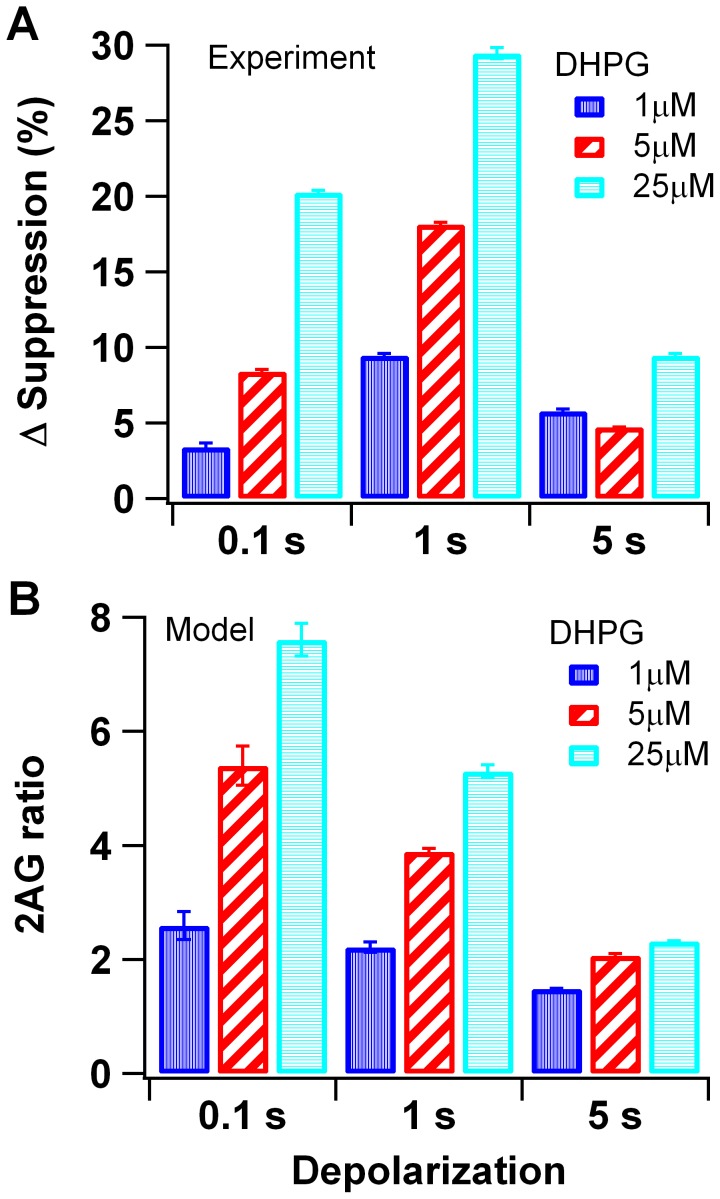
We compared simulations with DSI experiments evaluating the role of DHPG by calculating the mean 2AG in the presence of DHPG and then normalizing by dividing by mean 2AG produced in the absence of DHPG. This normalization is similar to that employed experimentally, in which the amount of suppression following DHPG is expressed as a change from that produced without DHPG. Our results show that the effect of DHPG depends on the duration of the calcium injection, similar to that observed for experiments. An increase in DHPG increases the amount of 2AG (Fig. 3B) and DSI (Fig. 3A) for both 100 ms and 1 s depolarizations (calcium injection); however, DHPG has very little effect on the 5 sec depolarization, for both experiments and simulations. This result is robust to variation in parameters (Fig S2A).
Figure 3. DHPG concentration-dependent enhancement of DSI and 2AG production.
(A) Experimental results replotted from Uchigashima et al. J. Neurosci. 2007. The enhancement of suppression was calculated as the change in the magnitude of DSI with DHPG application relative to the suppression without DHPG. (B) Simulation results. Mean and standard error calculated from 3 simulations repeated with different random number seeds. The enhancement of 2AG production is calculated as the ratio of mean 2AG in response to DHPG+calcium divided by 2AG in response to calcium alone. Simulations show that endocannabinoid production in the model is strongly facilitated when calcium influx into the spine and Gq coupled receptor activation are combined. This result matches experimental data in which DSI experiments show that depolarization synergizes with Gq coupled receptor activation.
The critical enzymes for 2AG production are phospholipase C (PLC) and diacylglycerol (DAG) lipase, both of which function as coincidence detectors (see Fig. 4). PLC produces DAG when activated by calcium binding, but the activity of the calcium bound PLC is markedly increased by GαqGTP binding [30], [31], [51]. The DAG produced by PLC is converted to 2AG by DAG lipase [34], [35], but the rate of this conversion is enhanced by calcium elevation. Accordingly in the model, DAG is produced from PLC even in the absence of Gq coupled (mGluR) receptor activation (black traces of Fig S3B–D), but the quantity of DAG is enhanced by the GαqGTP produced by mGluR activation (Fig S3A). The increased DAG production is translated into increased 2AG for 100 ms and 1 s, but not for 5 sec stimulation due to saturation of DAG lipase (Fig S3F); i.e., even for low DHPG concentrations, nearly the entire 1.7 µM of DAG lipase is bound to DAG. This suggests that the additional DAG produced during the 5 s stimulation could be activating other downstream targets, such as PKC.
Figure 4. Simplified schematic of signaling pathways demonstrating the three coincidence detection molecules (red): PLC, DAG lipase and PKC, and that DAG lipase and PKC compete for calcium (purple arrows) and DAG (blue arrows).
PKC Activation with DSI
Previous research has shown that interactions between molecule pathways is important in control of synaptic plasticity [46]. PKC was included in the model simulations above because it is a target of DAG [18] and the competition between PKC and DAG lipase for DAG (Fig. 4) could influence 2AG production. In addition, if stimulation were to activate PKC, then other post-synaptic targets could be phosphorylated, such as ionic channels to alter neuronal activity patterns in response to depolarization [52], [53]. Therefore, we examined PKC activity during the same calcium plus DHPG conditions as above.
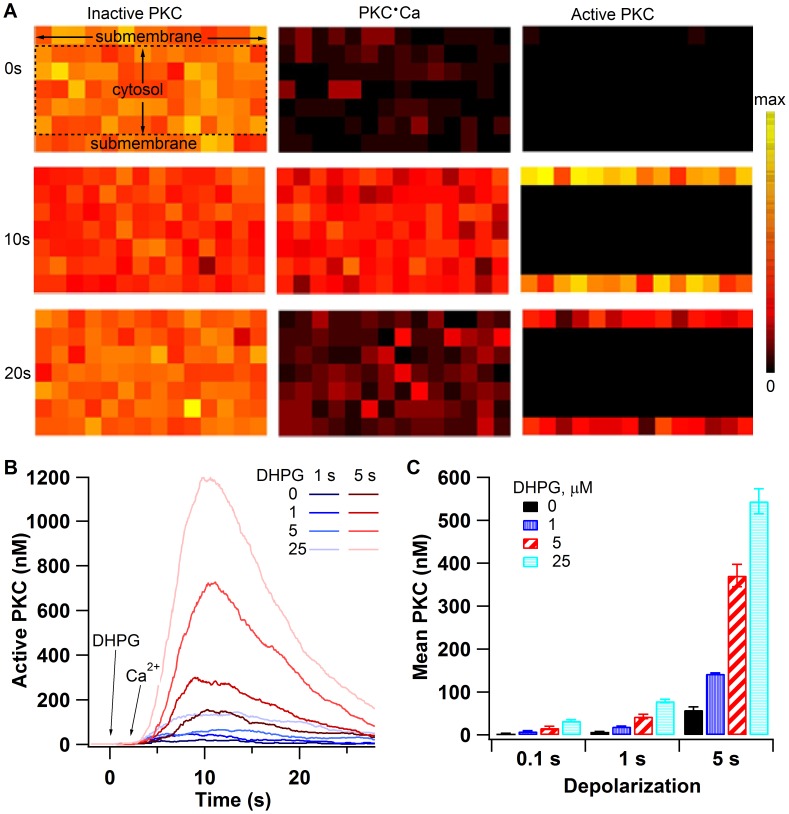
PKC activity is strongly dependent on both calcium and DHPG. Fig. 5A shows that PKC translocates to the membrane with a time frame similar to experiments [18], due to the membrane location of DAG. Fig. 5B, C show that the 100 ms depolarization does not produce sufficient calcium for PKC activation, and the 1 sec depolarization requires a large DHPG concentration to activate PKC. Even with the 5 s depolarization, PKC activity is greatly enhanced by DHPG. PKC activation is slower than 2AG production (compare figures 2A2, 2B2 with 5B), and this slow activation of PKC indicates that the kinetics of PKC activation and 2AG production (produced by interactions between calcium and activation of mGluR) are very different. This suggests that differences in magnitude and rate of response of PKC and 2AG to various stimulation paradigms may determine whether LTP or LTD occurs.
Figure 5. PKC activated by DSI stimulation requires a long depolarization duration or strong mGluR activation.
(A) PKC translocates to the membrane via passive diffusion coupled with binding to the membrane phospholipid DAG. Left column shows inactive PKC, middle column shows calcium bound PKC, and right column shows active (DAG-bound) PKC. Three different time points are shown in response to 25 µM DHPG and 5 s calcium, corresponding to pre-stimulation (0s), near the peak of PKC activity (10s) and as PKC is decreasing in activity (20s). The color scale indicates number of molecules per subvolume, from minimum (black: 25, 0 and 0) to maximum (yellow: 114, 34 and 30) for inactive, Ca bound, and active PKC, respectively. Delineation of cytosol and submembrane indicated on the upper left panel applies to all panels. (B) Time course of PKC activation. After 1 s depolarization, DHPG enhanced PKC activation is relatively small. After 5 s depolarization, DHPG markedly enhances PKC activation, showing no saturation over the spectrum of conditions evaluated. (C) Effect of calcium influx and DHPG on mean PKC activation. Error bars indicate ± 1 standard error.
Temporal Pattern Selects for PKC versus 2AG
In the striatum, three pre-synaptic stimulation patterns have been employed in normal magnesium solutions: 100 Hz and 20 Hz stimulation typically produce long term synaptic depression in striatal brain slices [46], [54], whereas a recently developed theta burst stimulation paradigm produces LTP [27]. For all of these induction paradigms, glutamate released by cortico-striatal terminals activates Gq coupled mGluRs while NMDA receptors and voltage-gated calcium channels increase intracellular calcium during both LTP and LTD [46]; thus, our simulations address whether temporal pattern of mGluR stimulation or calcium elevation can select for LTD versus LTP.
The effect of temporal stimulation pattern was simulated using 20 Hz stimulation as the LTD induction paradigm, because the pathway leading to production of 2AG is better characterized, and theta burst as the LTP induction paradigm, since it is effective in normal Mg++. 20 Hz stimulation consisted of 20 pulses at 20 Hz; this train of pulses was repeated 20 times with a 10 sec interval for a total of 400 pulses. Theta burst stimulation comprised 4 pulses at 50 Hz (one burst) repeated 10 times at the theta frequency of 10.5 Hz. This train of bursts was repeated 10 times with a 15 sec interval for a total of 400 pulses. Each pulse (independent of the train) consisted of a 3 ms calcium influx [55] and release of mGluR ligand. We use these two stimulation paradigms to determine whether temporal pattern can select for PKC versus 2AG.
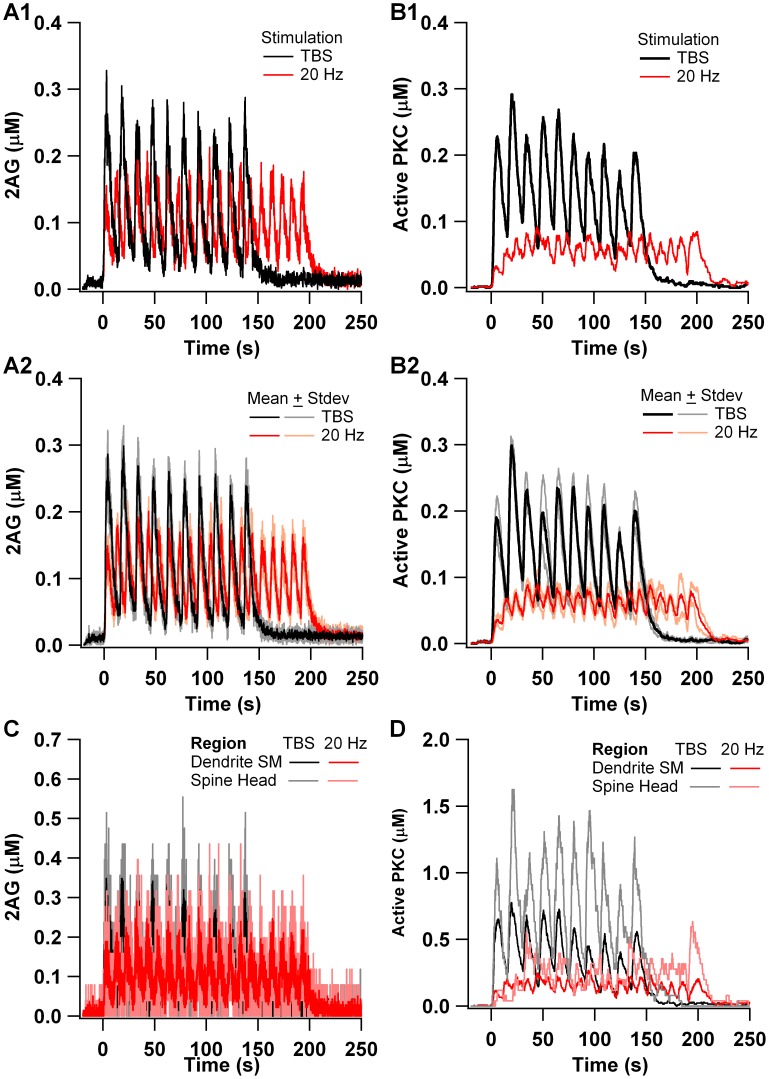
The two stimulation patterns produced different activation of signaling molecules. The total production of 2AG is similar for both 20 Hz and theta burst (Fig. 6A1,2), though peaks are slightly higher for theta burst, and the duration of elevated 2AG is slightly higher for 20 Hz. In contrast, the activation of PKC is considerably greater for theta burst (Fig. 6B1,2). Though the duration of PKC activation is similar to that for 2AG, theta burst produces peak PKC activity more than four times greater than 20 Hz. This observation holds when evaluating either dendrite submembrane, or spine head molecule quantity (Fig. 6C,D), though the active PKC in the spine head is considerably greater than that in the dendrite. Fig. 7A summarizes these results and shows that the quantity of 2AG is similar for both 20 Hz and theta burst, but that the quantity of active PKC is more than two fold greater for theta burst as compared to 20 Hz. This result is robust to variation in several parameters (Fig. 7B, Fig S2B), and suggests that LTP occurs with theta burst stimulation due to PKC activity dominating the effect of 2AG, as opposed to a lack of 2AG production with theta burst stimulation. This leads to the prediction that PKC is required for theta burst LTP, and that the magnitude of the ratio of activated PKC to level of 2AG determines whether LTP or LTD is produced.
Figure 6. Activation of PKC, but not 2AG, is greater with theta burst than with 20 Hz stimulation.
(A) 2AG production for theta burst and 20 Hz stimulation. (B) Active PKC for theta burst and 20 Hz stimulation. A1 and B1 show results of a single trial, and A2 and B2 show the average and standard deviation of 3 independent trials (random seeds). (C) and (D) show that little gradient develops between spine head and dendritic submembrane region. For PKC, this is due to translocation of PKC to the membrane in addition to the spine head. For 2AG, this is due to the diffusibility of 2AG.
Figure 7. Summary of active PKC and 2AG production in response to theta burst and 20 Hz stimulation.
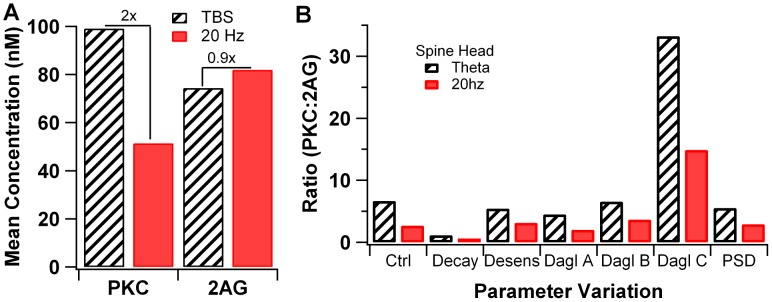
(A) PKC is greater for theta burst stimulation than for 20 Hz stimulation, but 2AG is similar. Thus, the ratio of PKC to 2AG is greater for theta burst stimulation than for 20 Hz stimulation. (B) The enhanced ratio of PKC to 2AG for theta burst stimulation is observed for several different parameter variations. Decay: 2AG decay rate is 50% of control; Desens: mGluR desensitization is 50% of control; Dagl A: affinity of Dag Lipase for calcium is 50% of control; Dagl B: affinity of Dag Lipase for calcium is 200% of control; Dagl C: the affinity of Dag Lipase for Dag is 50% of control; PSD: molecules located in the spine head are added to PSD region. Additional parameter variations are illustrated in Fig S2B.
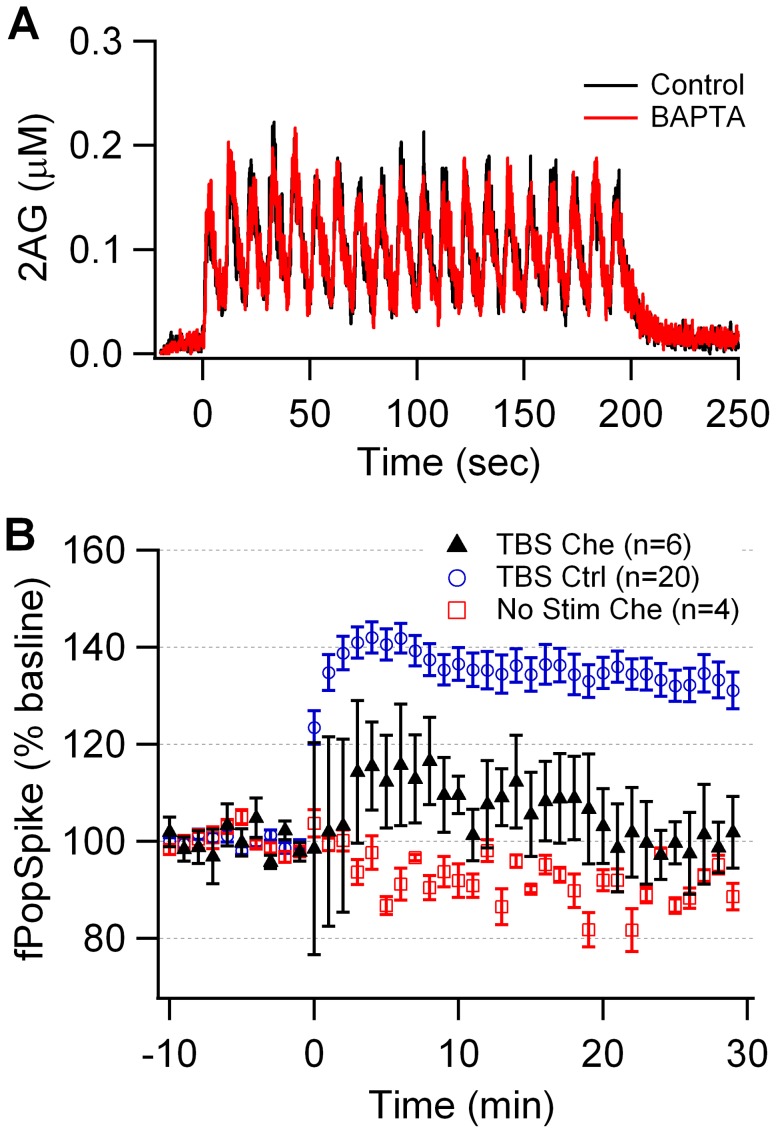
The model was validated further both by an additional simulation and by performing an additional experiment. Previous experiments demonstrated that 10 µM of the calcium buffer BAPTA does not block 2AG dependent LTD [46]; thus, simulations of the 20 Hz stimulation were repeated in the presence of 10 µM BAPTA. Figure 8A shows that 2AG in the presence of BAPTA is similar to the control, confirming that BAPTA does not block LTD in the model. Furthermore, we experimentally tested the model prediction that PKC is required for theta burst LTP in striatal coronal brain slices by recording the field population spike in response to white matter stimulation in normal Mg++. We induced LTP using the same theta burst stimulation protocol as used in the model, in the presence and absence of the PKC inhibitor chelerythrine. Fig. 8B shows that theta burst stimulation produces LTP which has a peak amplitude of 140% and which remains above 130% for more than 30 min. In the presence of chelerythrine, the peak LTP amplitude never reaches 120% and has decayed to baseline within 10 min. This effect is not due to non-specific effects as bath application of chelerythrine in the absence of stimulation produces no change in population spike amplitude, similar to the non-stimulated condition without chelerythrine (not shown). At 30 min after induction, these three groups are significantly different (SAS GLM, F = 27.0, P<0.0001, n = 30), with the theta burst control significantly greater than the two chelerythrine groups (P = 0.001, post-hoc Tukey). These results confirm the role of PKC in theta burst induction of LTP.
Figure 8. Validation of the model.
(A) 2AG production is not altered by 10 µM BAPTA included in the simulation, which is consistent with the observation that 10 µM BAPTA does not block 20 Hz LTD. (B) The PKC inhibitor chelerythrine (Che) blocks LTP induced by theta burst stimulation (TBS) but does not produce a non-specific decay in the field population spike in striatal slices.
Spatial Specificity
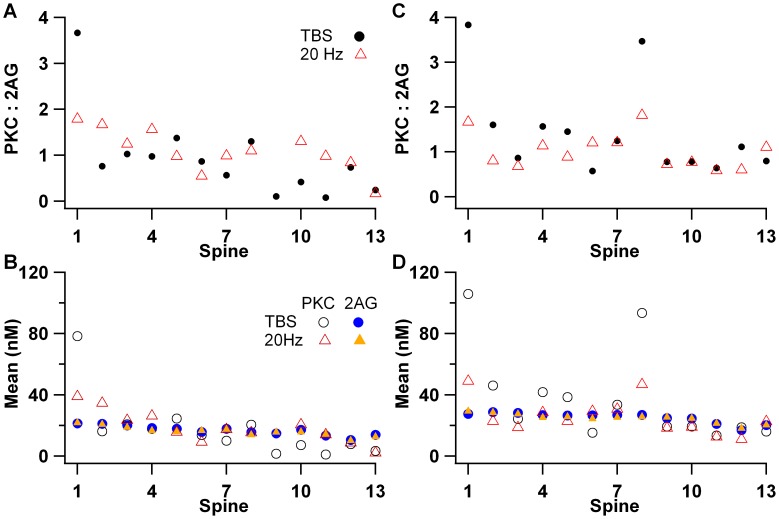
Using this validated model, we performed simulations in a larger dendrite with multiple spines (Fig. 1D) in order to investigate the spatial specificity of PKC and 2AG. In particular we asked whether induction of plasticity at a single spine will be associated with plasticity (of the same or different direction) at neighboring spines. We stimulated with either theta burst or 20 Hz applied to a single spine to represent glutamatergic activation of the synaptic channels in that spine, and simultaneously stimulated the dendrite with calcium injection to represent calcium influx through voltage dependent channels in response to depolarization. As with simulations in the smaller morphology, the number of glutamate and calcium molecules did not differ between 20 Hz and theta burst stimulation. Simulations with the smaller morphology suggested that the ratio of PKC to 2AG might predict the direction of plasticity, with a large ratio (greater than 2) producing LTP and smaller ratio (closer to 1) producing LTD. Thus, we evaluated the ratio of PKC to 2AG for each spine in the larger morphology.
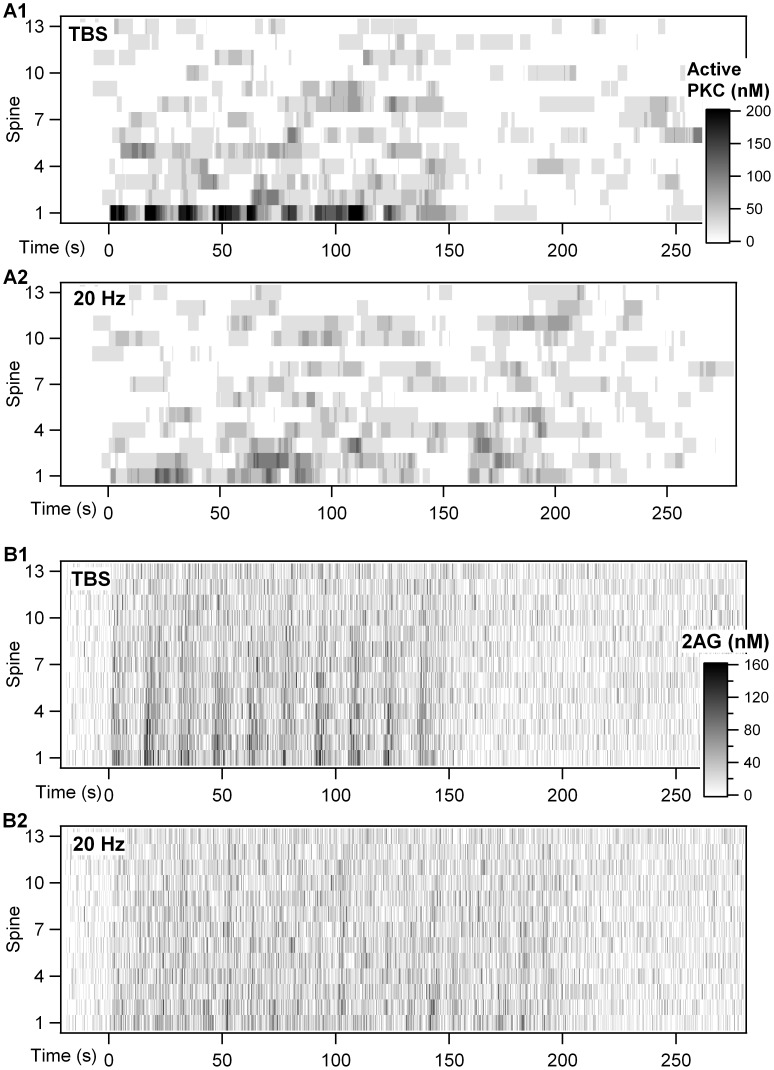
Fig. 9 shows the time course of PKC and 2AG in the spines of the larger morphology. PKC activation is quite evident for theta burst stimulation (Fig. 9A1), but only in the stimulated spine 1. The PKC activation in response to 20 Hz is much smaller (Fig. 9A2), and the difference between stimulated and non-stimulated spines is correspondingly smaller. In contrast, 2AG is elevated in response to either theta burst stimulation (Fig. 9B1) or 20 Hz (Fig. 9B2), and this elevation extends to several nearby spines. These results are summarized in Fig. 10A, which shows the ratio of mean PKC to mean 2AG for each spine. In response to theta burst, this ratio is significantly greater than 2 for the stimulated spine, but closer to 1 for all non-stimulated spines. This suggests that only the stimulated spine will undergo LTP. In contrast, for 20 Hz, none of the stimulated spines has a ratio greater than 2, and most of the spines have similar ratios. The same pattern of results was observed when the mean values of molecule quantities were evaluated instead of the ratio (Fig. 10B). This suggests that even adjacent spines will undergo LTD and, within a small length of dendritic branch, LTD does not exhibit spatial specificity. To further investigate spatial specificity and spine interactions, simulations were repeated with calcium and mGluR agonist input to two spatially separated spines (1 and 8). Fig. 10C shows a similar degree of spatial specificity when two spines are stimulated. None of the non-stimulated spines exhibit an elevation in the PKC∶2AG ratio for theta burst, and 20 Hz does not produce an elevated ratio for any of the spines. The non-specific increase in PKC activity and 2AG (e.g. in un-stimulated spines 8–13) is very small (Fig. 10D versus 10B). Overall, these results suggest that LTP will occur in response to theta burst stimulation in stimulated spines only, whereas LTD can occur in neighboring un-stimulated spines in response to both theta burst and 20 Hz stimulation.
Figure 9. Spatial specificity of 2AG and PKC in a 20 µm long dendrite with 13 spines (see fig. 1 for morphology).
In the simulation, spine 1 is stimulated with calcium and glutamate at time 0. (A) The gray scale shows how active PKC changes over time (x axis) for each spine (y axis). (A1) PKC is activated mostly in the stimulated spine with theta burst stimulation. (A2) Very little PKC is activated even in the stimulated spine for 20 Hz stimulation. (B) The gray scale shows how 2AG changes over time (x axis) for each spine (y axis). 2AG elevation is slightly larger for stimulated than non-stimulated spines, both for theta burst stimulation (B1) and 20 Hz stimulation (B2).
Figure 10. Summary of spatial specificity in 20 µm dendrite with 13 spines (see fig. 1 ).
(A) Ratio of active PKC to 2AG versus spine for both theta burst stimulation (TBS) and 20 Hz stimulation. The ratio is much higher in stimulated spine 1 for TBS, then decreases slightly with distance from the non-stimulated spine. (B) Mean value of active PKC or 2AG exhibits a similar pattern as the ratio. PKC is much greater for the stimulated spine 1, especially for TBS, and PKC activity is close to basal for the four spines furthest from the stimulation. In contrast, 2AG decreases slightly with distance from stimulated spine, independent of stimulation pattern. (C,D) When spines 1 and 8 are stimulated with TBS, the ratio of PKC to 2AG (C), as well as mean PKC activity itself (D), is much higher for the stimulated spines as compared to non-stimulated spines. Mean PKC activity in the non-stimulated spines is slightly higher, but spatial specificity is still strong. Mean 2AG is similar regardless of one or two spines being stimulated.
Discussion
We developed a quantitative model of Gq coupled signaling pathways in striatal spiny projection neurons in order to investigate information processing mechanisms. Model simulations evaluated endocannabinoid production and PKC activation in response to synaptic stimulation paradigms that produce long-term depression and long-term potentiation. The model was validated by reproducing experimental results of a 2AG-dependent phenomenon: depolarization induced suppression of inhibition. Our results showed that theta burst stimulation produces much more PKC than does 20 Hz stimulation but similar amounts of 2AG, suggesting that theta burst induces LTP because the effect of PKC dominates that of 2AG. The model prediction was tested experimentally by demonstrating that theta burst LTP was blocked by inhibitors of PKC. Using the validated model, simulations of a dendrite with multiple spines revealed that PKC exhibits a spatial gradient in response to theta burst stimulation, whereas 2AG does not exhibit a spatial gradient. This suggests that LTP will exhibit more spatial specificity than LTD, which is consistent with theoretical studies showing that stability requires LTD to be more prevalent then LTP [56].
The validation of the model using DSI is qualitative rather than quantitative, in that mGluR agonists facilitate 1s more than 0.1s depolarizations experimentally, but 0.1s is facilitated more in the model. A likely source of the discrepancy is that response properties of the CB1 receptors on the pre-synaptic terminals produce a non-linear response to the 2AG increments, e.g. with a sigmoid with the steepest response for the 2AG increments produced by 1s depolarization. Adding signaling pathways of the pre-synaptic terminal in order to produce a quantitative agreement is beyond the scope of the current research. Another possibility is that the calcium influx for the different depolarizations are not accurate, in large part because calcium imaging under DSI stimulation has not been reported. The 2AG ratios are influenced by the 2AG response to calcium alone, thus a larger calcium influx for 100 ms could produce smaller ratios for this condition. Producing a quantitative agreement in DSI must await additional research on the calcium dynamics underlying this phenomenon.
Our results demonstrate that signaling molecules can discriminate temporal dynamics, nonetheless, spatial localization can still play a role in selecting the direction of plasticity. For example, NMDA receptors may be coupled to PKC whereas CaV1.3 may be coupled to endocannabinoid production. Even though both calcium sources are located in the spine head [21], anchoring proteins [57] that colocalize proteins into multi-protein complexes may emphasize the importance of calcium nano-domains. These effects would only enhance the discrimination of temporal patterns observed in this study.
Due to the difficulty in measuring single spine responses in slice, spatial specificity of LTP has not been tested in the striatum, and thus this simulation result remains a prediction. On the other hand, the spatial specificity of LTD has been evaluated [58]. These experiments measured the response of a single neuron to two independent populations of pre-synaptic fibers and revealed that LTD requires both pre-synaptic activity as well as activation of CB1 cannabinoid receptors. This suggests that the increase in 2AG in spines near the stimulated spine does not necessarily result in LTD; rather, activation of inputs on these neighboring spines also would be required. The distance over which neighboring spines show increased 2AG was not determined in our simulations. Our simulation morphology was restricted to a 20 micron long dendrite, thus the lack of spatial specificity in our model is limited to this small spatial scale, in which the dendritic calcium elevation exhibits no gradient. In spiny projection neurons, somatic action potentials do not propagate into the entire dendritic tree [59], thus the calcium influx into tertiary branches is controlled by synaptic input [60], and gradients of signaling molecules are likely. To evaluate spatial specificity of signaling pathways in tertiary branches of a spiny projection neuron, the model requires more accurate simulation of the synaptically driven calcium influx.
Post-synaptic depolarization can induce suppression of both inhibition (DSI) and excitation (DSE) [42]. DSI involves GABAergic synapses located on the dendrites or spine shafts, whereas DSE involves glutamatergic synapses located on spine heads. Experimentally, DSE is less sensitive and requires a greater mGluR agonist concentration than does DSI [42]. Several mechanisms underlying this observation have been proposed. Measurements of the location of DAG Lipase, mGluR, and PLC suggest that the lower DSE sensitivity is not due to a lower concentration of 2AG producing enzymes in the spine head [42]. Another possibility, that the 2AG producing enzymes are less active in the spine head, is not supported by our simulations showing no gradient of 2AG between spine and dendrite (results not shown). Thus, our model supports the alternative that lower sensitivity of DSE is due to lower expression of CB1 receptors on cortico-striatal terminals as compared to inhibitory neuron terminals [42].
The biochemical pathways leading to production of PKC with subsequent LTP and 2AG with subsequent LTD share several elements. Our simulations show an interesting pattern of competition between and coincidence detection by these elements (Fig. 4). The role of NMDA receptors in coincidence detection is generally accepted [61], but other intracellular signaling molecules have coincidence detection properties. PLC is one such molecule included in our model. PLC requires calcium for activation, but GαqGTP synergistically enhances DAG production [30]–[32]. Other molecules in the model also act as coincidence detectors: DAG lipase and PKC require both DAG and calcium though in different ways. DAG lipase requires DAG as a substrate, but calcium enhances its activity [34], [35]. In contrast, PKC requires DAG binding after calcium, and thus exhibits sensitivity to temporal pattern [18]. The time course of DAG and calcium are longer than glutamate and action potentials, respectively; thus the coincidence detection of PLC, DAG lipase and PKC likely operates on much longer time scales than that of NMDA receptors.
Activation of Gq coupled pathways is not restricted to mGluR5 receptors as m1 muscarinic acetylcholine receptors also are coupled to the Gq subtype of G protein [62] and facilitate 2AG production in the striatum [63]. Other than the immediate peri-synaptic region, the distribution of m1 receptors in the spine is similar to that of mGluR5 [42]. Therefore, including an explicit m1 receptor population in the model is unlikely to change the simulation results. On the other hand, during reward learning activation of m1 receptors is likely to have a different temporal pattern than activation of mGluR5 receptors [64], [65]. Consequently, to simulate synaptic activation patterns similar to learning, it would be necessary to de-activate Gq coupled pathways in response to the pauses in acetylcholine neurons observed in response to reward [66].
Not only acetylcholine [7], [67], but also dopamine [5], [68] is involved in striatal synaptic plasticity. These are less likely to be critical determinants in the spatial specificity of LTP versus LTD given the diffuse nature of dopamine and acetylcholine innervation [69]. Nonetheless, to thoroughly understand the signaling pathways underlying learning, it is critical to include the Gs/cAMP/PKA pathways that are activated by dopamine neurons [70] (or A2A receptors) in response to reward or expectation of reward [66]. PKA can influence plasticity by direct phosphorylation of AMPA GluA1 receptors [71], DARPP-32 [72], and other molecules. In addition, both PKA and PKC can lead to activation of ERK1/2 [73], which has been implicated in striatal dependent learning tasks [74], and which is activated in response to the overly strong rewards of drugs of abuse [75]. More relevant to the present study, PKA phosphorylation of RGS proteins, which accelerate the hydrolysis of GαqGTP, may inhibit the production of 2AG in response to theta burst stimulation [46]. Integrating the present model with existing computational models of Gs/cAMP/PKA pathways will shed insight on signaling molecule control of synaptic plasticity and information processing.
Supporting Information
Calcium concentration resulting from the stimulation for DSI simulation. (A) 100 ms depolarization (B) 1s depolarization, (C) 5s depolarization. In all cases onset is at 2 sec. Red traces show calcium in the spine head, black traces show calcium in the dendrite. The blue bar represents the stimulation time. Though mean values are similar, fluctuations in the spine head are much greater due to the smaller volume.
(PNG)
Results are robust to variation in parameters for both DSI and synaptic plasticity stimuli. (A) Robustness of DSI. The enhancement in 2AG by mGluR activation is quantified as the slope of the 2AG increase versus mGluR concentration for each depolarization duration. 12 parameter variations are illustrated along with the default parameters and experiment results. (B) Additional parameter variations demonstrate the robustness of the enhanced ratio of PKC to 2AG for theta burst as compared to 20 Hz. For both (A) and (B), the following parameter variations were used: Decay: 2AG decay rate is 50% of control; LowGap: decreased rate of GαqGTP hydrolysis; PSD: molecules located in the spine head are added to PSD region. SpinePLC/SpPLC: redistributed PLC, PIP2 and mGluR into spine to make local concentration the same as in dendrite submembrane; SpineDgl/SpDgl: increased PLC, PIP2, mGluR and DAG lipase into spine to make local concentration the same as in dendrite submembrane; Desens 0.5: mGluR desensitization is 50% of control; Desens 0.2: mGluR desensitization is 20% of control; Desens 4×: mGluR desensitization is 400% of control, and also G protein is ∼3× of control; Dagl A: affinity of Dag Lipase for calcium is 50% of control; Dagl B: affinity of Dag Lipase for calcium is 200% of control; Dagl C: the affinity of Dag Lipase for Dag is 50% of control; Dagl D: the affinity of Dag Lipase for Dag is 200% of control.
(PNG)
DAG production is enhanced by GαqGTP, but high values of DAG saturate DAG Lipase. (A) GαqGTP increases linearly with mGluR activation (at t = 0s), with no effect of calcium (at t = 2s). (B–D) DAG production is enhanced by GαqGTP for all durations of depolarization. (E–F) The increased DAG production is translated into increased 2AG for 1s depolarization (E), but less so for 5 s depolarization since DAG saturates the DAG lipase (i.e., the DAG bound DAG lipase approaches the total 1.7µM of DAG lipase) with low concentrations of DHPG (F).
(PNG)
Funding Statement
This work was supported by ONR grant MURI N00014-10-1-0198 and through the joint NIH-NSF CRCNS program through NIAAA grant RO1AA-16022. Publication of this article was funded in part by the George Mason University Libraries Open Access Publishing Fund. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Dunnett SB, Lelos M (2010) Behavioral analysis of motor and non-motor symptoms in rodent models of Parkinson's disease. Prog Brain Res 184: 35–51 S0079-6123(10)84003-8 [pii];10.1016/S0079-6123(10)84003-8 [doi]. [DOI] [PubMed] [Google Scholar]
- 2. Yin HH, Ostlund SB, Knowlton BJ, Balleine BW (2005) The role of the dorsomedial striatum in instrumental conditioning. Eur J Neurosci 22: 513–523. [DOI] [PubMed] [Google Scholar]
- 3. Gerdeman GL, Partridge JG, Lupica CR, Lovinger DM (2003) It could be habit forming: drugs of abuse and striatal synaptic plasticity. Trends Neurosci 26: 184–192. [DOI] [PubMed] [Google Scholar]
- 4. Smith AD, Bolam JP (1990) The neural network of the basal ganglia as revealed by the study of synaptic connections of identified neurones. Trends Neurosci 13: 259–265. [DOI] [PubMed] [Google Scholar]
- 5. Reynolds JN, Wickens JR (2002) Dopamine-dependent plasticity of corticostriatal synapses. Neural Netw 15: 507–521. [DOI] [PubMed] [Google Scholar]
- 6. Calabresi P, Centonze D, Gubellini P, Bernardi G (1999) Activation of M1-like muscarinic receptors is required for the induction of corticostriatal LTP. Neuropharmacology 38: 323–326. [DOI] [PubMed] [Google Scholar]
- 7. Wang Z, Kai L, Day M, Ronesi J, Yin HH, et al. (2006) Dopaminergic control of corticostriatal long-term synaptic depression in medium spiny neurons is mediated by cholinergic interneurons. Neuron 50: 443–452. [DOI] [PubMed] [Google Scholar]
- 8. Yin HH, Mulcare SP, Hilario MR, Clouse E, Holloway T, et al. (2009) Dynamic reorganization of striatal circuits during the acquisition and consolidation of a skill. Nat Neurosci 12: 333–341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Shen H, Moussawi K, Zhou W, Toda S, Kalivas PW (2011) Heroin relapse requires long-term potentiation-like plasticity mediated by NMDA2b-containing receptors. Proc Natl Acad Sci U S A 108: 19407–19412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Kasanetz F, Deroche-Gamonet V, Berson N, Balado E, Lafourcade M, et al. (2010) Transition to addiction is associated with a persistent impairment in synaptic plasticity. Science 328: 1709–1712. [DOI] [PubMed] [Google Scholar]
- 11. Fino E, Glowinski J, Venance L (2005) Bidirectional activity-dependent plasticity at corticostriatal synapses. J Neurosci 25: 11279–11287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Pawlak V, Kerr JN (2008) Dopamine receptor activation is required for corticostriatal spike-timing-dependent plasticity. J Neurosci 28: 2435–2446. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Shen W, Flajolet M, Greengard P, Surmeier DJ (2008) Dichotomous dopaminergic control of striatal synaptic plasticity. Science 321: 848–851. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Shindou T, Ochi-Shindou M, Wickens JR (2011) A Ca(2+) threshold for induction of spike-timing-dependent depression in the mouse striatum. J Neurosci 31: 13015–13022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Dudek SM, Bear MF (1993) Bidirectional long-term modification of synaptic effectiveness in the adult and immature hippocampus. J Neurosci 13: 2910–2918. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Castellani GC, Quinlan EM, Bersani F, Cooper LN, Shouval HZ (2005) A model of bidirectional synaptic plasticity: from signaling network to channel conductance. Learn Mem 12: 423–432. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Gubellini P, Centonze D, Tropepi D, Bernardi G, Calabresi P (2004) Induction of corticostriatal LTP by 3-nitropropionic acid requires the activation of mGluR1/PKC pathway. Neuropharmacology 46: 761–769. [DOI] [PubMed] [Google Scholar]
- 18. Oancea E, Meyer T (1998) Protein kinase C as a molecular machine for decoding calcium and diacylglycerol signals. Cell 95: 307–318. [DOI] [PubMed] [Google Scholar]
- 19. Kreitzer AC, Malenka RC (2005) Dopamine modulation of state-dependent endocannabinoid release and long-term depression in the striatum. J Neurosci 25: 10537–10545. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Calabresi P, Pisani A, Mercuri NB, Bernardi G (1992) Long-term Potentiation in the Striatum is Unmasked by Removing the Voltage-dependent Magnesium Block of NMDA Receptor Channels. Eur J Neurosci 4: 929–935. [DOI] [PubMed] [Google Scholar]
- 21. Olson PA, Tkatch T, Hernandez-Lopez S, Ulrich S, Ilijic E, et al. (2005) G-protein-coupled receptor modulation of striatal CaV1.3 L-type Ca2+ channels is dependent on a Shank-binding domain. J Neurosci 25: 1050–1062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Goldberg JA, Teagarden MA, Foehring RC, Wilson CJ (2009) Nonequilibrium calcium dynamics regulate the autonomous firing pattern of rat striatal cholinergic interneurons. J Neurosci 29: 8396–8407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Nakano T, Doi T, Yoshimoto J, Doya K (2010) A kinetic model of dopamine- and calcium-dependent striatal synaptic plasticity. PLoS Comput Biol 6: e1000670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Fernandez E, Schiappa R, Girault JA, Le Novere N (2006) DARPP-32 is a robust integrator of dopamine and glutamate signals. PLoS Comput Biol 2: e176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Lindskog M, Kim M, Wikstrom MA, Blackwell KT, Kotaleski JH (2006) Transient calcium and dopamine increase PKA activity and DARPP-32 phosphorylation. PLoS Comput Biol 2: e119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Oliveira RF, Kim M, Blackwell KT (2012) Subcellular Location of PKA Controls Striatal Plasticity: Stochastic Simulations in Spiny Dendrites. PLoS Comput Biol 8: e1002383 10.1371/journal.pcbi.1002383 [doi];PCOMPBIOL-D-11-01087 [pii]. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Hawes S, Blackwell KT (2012) Theta-burst LTP in dorsal striatum [Abstract:79.05]. In 2011 Neuroscience Meeting Planner, Nov 12–16 2011, Washington, DC, United States. Available: http://www.abstractsonline.com/plan/start.aspx?mkey=8334BE29-8911-4991-8C31-32B32DD5E6C8.
- 28. Gubellini P, Saulle E, Centonze D, Costa C, Tropepi D, et al. (2003) Corticostriatal LTP requires combined mGluR1 and mGluR5 activation. Neuropharmacology 44: 8–16. [DOI] [PubMed] [Google Scholar]
- 29. Narushima M, Uchigashima M, Hashimoto K, Watanabe M, Kano M (2006) Depolarization-induced suppression of inhibition mediated by endocannabinoids at synapses from fast-spiking interneurons to medium spiny neurons in the striatum. Eur J Neurosci 24: 2246–2252. [DOI] [PubMed] [Google Scholar]
- 30. Smrcka AV, Hepler JR, Brown KO, Sternweis PC (1991) Regulation of polyphosphoinositide-specific phospholipase C activity by purified Gq. Science 251: 804–807. [DOI] [PubMed] [Google Scholar]
- 31. Taylor SJ, Chae HZ, Rhee SG, Exton JH (1991) Activation of the beta 1 isozyme of phospholipase C by alpha subunits of the Gq class of G proteins. Nature 350: 516–518 10.1038/350516a0 [doi]. [DOI] [PubMed] [Google Scholar]
- 32. Blank JL, Ross AH, Exton JH (1991) Purification and characterization of two G-proteins that activate the beta 1 isozyme of phosphoinositide-specific phospholipase C. Identification as members of the Gq class. J Biol Chem 266: 18206–18216. [PubMed] [Google Scholar]
- 33. Biddlecome GH, Berstein G, Ross EM (1996) Regulation of phospholipase C-β1 by Gq and m1 muscarinic cholinergic receptor. J Biol Chem 271: 7999–8007. [DOI] [PubMed] [Google Scholar]
- 34. Bisogno T, Howell F, Williams G, Minassi A, Cascio MG, et al. (2003) Cloning of the first sn1-DAG lipases points to the spatial and temporal regulation of endocannabinoid signaling in the brain. J Cell Biol 163: 463–468 10.1083/jcb.200305129 [doi];jcb.200305129 [pii]. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Rosenberger TA, Farooqui AA, Horrocks LA (2007) Bovine brain diacylglycerol lipase: substrate specificity and activation by cyclic AMP-dependent protein kinase. Lipids 42: 187–195 10.1007/s11745-007-3019-7 [doi]. [DOI] [PubMed] [Google Scholar]
- 36. Hellgren Kotaleski J, Lester DS, Blackwell KT (2002) Subcellular interactions between parallel fibre and climbing fibre signals in Purkinje cells predict sensitivity of classical conditioning to interstimulus interval. Integrative Physiological and Behavioral Science 37: 265–292. [DOI] [PubMed] [Google Scholar]
- 37. Putkey JA, Kleerekoper Q, Gaertner TR, Waxham MN (2003) A new role for IQ motif proteins in regulating calmodulin function. J Biol Chem 278: 49667–49670. [DOI] [PubMed] [Google Scholar]
- 38. Gaertner TR, Putkey JA, Waxham MN (2004) RC3/Neurogranin and Ca2+/calmodulin-dependent protein kinase II produce opposing effects on the affinity of calmodulin for calcium. J Biol Chem 279: 39374–39382. [DOI] [PubMed] [Google Scholar]
- 39. Lorincz A, Rozsa B, Katona G, Vizi ES, Tamas G (2007) Differential distribution of NCX1 contributes to spine-dendrite compartmentalization in CA1 pyramidal cells. Proc Natl Acad Sci U S A 104: 1033–1038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Majewska A, Brown E, Ross J, Yuste R (2000) Mechanisms of calcium decay kinetics in hippocampal spines: role of spine calcium pumps and calcium diffusion through the spine neck in biochemical compartmentalization. J Neurosci 20: 1722–1734. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Fukaya M, Uchigashima M, Nomura S, Hasegawa Y, Kikuchi H, et al. (2008) Predominant expression of phospholipase Cbeta1 in telencephalic principal neurons and cerebellar interneurons, and its close association with related signaling molecules in somatodendritic neuronal elements. Eur J Neurosci 28: 1744–1759 EJN6495 [pii];10.1111/j.1460-9568.2008.06495.x [doi]. [DOI] [PubMed] [Google Scholar]
- 42. Uchigashima M, Narushima M, Fukaya M, Katona I, Kano M, et al. (2007) Subcellular arrangement of molecules for 2-arachidonoyl-glycerol-mediated retrograde signaling and its physiological contribution to synaptic modulation in the striatum. J Neurosci 27: 3663–3676 27/14/3663 [pii];10.1523/JNEUROSCI.0448-07.2007 [doi]. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Swaminathan R, Hoang CP, Verkman AS (1997) Photobleaching recovery and anisotropy decay of green fluorescent protein GFP-S65T in solution and cells: cytoplasmic viscosity probed by green fluorescent protein translational and rotational diffusion. Biophys J 72: 1900–1907 S0006-3495(97)78835-0 [pii];10.1016/S0006-3495(97)78835-0 [doi]. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Khan S, Zou Y, Amjad A, Gardezi A, Smith CL, et al. (2011) Sequestration of CaMKII in dendritic spines in silico. J Comput Neurosci 31: 581–594 10.1007/s10827-011-0323-2 [doi]. [DOI] [PubMed] [Google Scholar]
- 45. Regehr WG, Tank DW (1992) Calcium concentration dynamics produced by synaptic activation of CA1 hippocampal pyramidal cells. J Neuroscience 12:4202–4223: 4202–4223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46. Lerner TN, Kreitzer AC (2012) RGS4 Is Required for Dopaminergic Control of Striatal LTD and Susceptibility to Parkinsonian Motor Deficits. Neuron 73: 347–359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47. Oliveira RF, Terrin A, Di Benedetto G, Cannon RC, Koh W, et al. (2010) The role of type 4 phosphodiesterases in generating microdomains of cAMP: large scale stochastic simulations. PLoS One 5: e11725. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48. Blackwell KT (2006) An efficient stochastic diffusion algorithm for modeling second messengers in dendrites and spines. J Neurosci Methods 157: 142–153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. Gillespie DT (2001) Approximating accelerated stochastic simulation of chemically reacting systems. J Chemical Physics 115: 1716–1733. [Google Scholar]
- 50. Liu Z, Pu Y, Li F, Shaffer CA, Hoops S, et al. (2012) Hybrid modeling and simulation of stochastic effects on progression through the eukaryotic cell cycle. J Chem Phys 136: 034105 10.1063/1.3677190 [doi]. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51. Rack M, Xhonneux-Cremers B, Schraermeyer U, Stieve H (1994) On the Ca2+ dependence of insitol-phospholid-specific phospholipase C of micovillar photoreceptors from sepia officinalis. Exp Eye Res 58: 659–664. [DOI] [PubMed] [Google Scholar]
- 52. Hoffman DA, Johnston D (1998) Downregulation of transient K+ channels in dendrites of hippocampal CA1 Pyramidal neurons by activation of PKA and PKC. Journal of Neuroscience 18: 3521–3528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53. Perez-Burgos A, Perez-Rosello T, Salgado H, Flores-Barrera E, Prieto GA, et al. (2008) Muscarinic M(1) modulation of N and L types of calcium channels is mediated by protein kinase C in neostriatal neurons. Neuroscience 155: 1079–1097 S0306-4522(08)00975-5 [pii];10.1016/j.neuroscience.2008.06.047 [doi]. [DOI] [PubMed] [Google Scholar]
- 54. Ronesi J, Lovinger DM (2005) Induction of striatal long-term synaptic depression by moderate frequency activation of cortical afferents in rat. J Physiol 562: 245–256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55. Sabatini BL, Oertner TG, Svoboda K (2002) The life cycle of Ca(2+) ions in dendritic spines. Neuron 33: 439–452. [DOI] [PubMed] [Google Scholar]
- 56. Song S, Miller KD, Abbott LF (2000) Competitive Hebbian learning through spike-timing-dependent synaptic plasticity. Nat Neurosci 3: 919–926. [DOI] [PubMed] [Google Scholar]
- 57. Brooks IM, Tavalin SJ (2011) Ca2+/calmodulin-dependent protein kinase II inhibitors disrupt AKAP79-dependent PKC signaling to GluA1 AMPA receptors. J Biol Chem 286: 6697–6706. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58. Singla S, Kreitzer AC, Malenka RC (2007) Mechanisms for synapse specificity during striatal long-term depression. J Neurosci 27: 5260–5264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59. Day M, Wokosin D, Plotkin JL, Tian X, Surmeier DJ (2008) Differential excitability and modulation of striatal medium spiny neuron dendrites. J Neurosci 28: 11603–11614 28/45/11603 [pii];10.1523/JNEUROSCI.1840-08.2008 [doi]. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60. Plotkin JL, Day M, Surmeier DJ (2011) Synaptically driven state transitions in distal dendrites of striatal spiny neurons. Nat Neurosci 14: 881–888. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61. Yuste R, Majewska A, Cash S, Denk W (1999) Mechanisms of calcium influx into hippocampal spine: heterogeniety among spines, coincidence detection by NMDA receptors, and optical quantal analysis. Journal of Neuroscience 19: 1976–1987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62. Wess J, Eglen RM, Gautam D (2007) Muscarinic acetylcholine receptors: mutant mice provide new insights for drug development. Nat Rev Drug Discov 6: 721–733 nrd2379 [pii];10.1038/nrd2379 [doi]. [DOI] [PubMed] [Google Scholar]
- 63. Narushima M, Uchigashima M, Fukaya M, Matsui M, Manabe T, et al. (2007) Tonic enhancement of endocannabinoid-mediated retrograde suppression of inhibition by cholinergic interneuron activity in the striatum. J Neurosci 27: 496–506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64. Goldberg JA, Reynolds JN (2011) Spontaneous firing and evoked pauses in the tonically active cholinergic interneurons of the striatum. Neuroscience 198: 27–43 S0306-4522(11)01025-6 [pii];10.1016/j.neuroscience.2011.08.067 [doi]. [DOI] [PubMed] [Google Scholar]
- 65. Roesch MR, Bryden DW (2011) Impact of size and delay on neural activity in the rat limbic corticostriatal system. Front Neurosci 5: 130 10.3389/fnins.2011.00130 [doi]. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66. Morris G, Arkadir D, Nevet A, Vaadia E, Bergman H (2004) Coincident but distinct messages of midbrain dopamine and striatal tonically active neurons. Neuron 43: 133–143. [DOI] [PubMed] [Google Scholar]
- 67. Calabresi P, Centonze D, Gubellini P, Pisani A, Bernardi G (1998) Blockade of M2-like muscarinic receptors enhances long-term potentiation at corticostriatal synapses. Eur J Neurosci 10: 3020–3023. [DOI] [PubMed] [Google Scholar]
- 68. Centonze D, Picconi B, Gubellini P, Bernardi G, Calabresi P (2001) Dopaminergic control of synaptic plasticity in the dorsal striatum. European J Neuroscience 13: 1071–1077. [DOI] [PubMed] [Google Scholar]
- 69. Arbuthnott GW, Wickens J (2007) Space, time and dopamine. Trends Neurosci 30: 62–69. [DOI] [PubMed] [Google Scholar]
- 70. Calabresi P, Gubellini P, Centonze D, Picconi B, Bernardi G, et al. (2000) Dopamine and cAMP-regulated phosphoprotein 32 kDa controls both striatal long-term depression and long-term potentiation, opposing forms of synaptic plasticity. J Neuroscience 20: 8443–8451. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71. Wolf ME, Mangiavacchi S, Sun X (2003) Mechanisms by which dopamine receptors may influence synaptic plasticity. Ann N Y Acad Sci 1003: 241–249. [DOI] [PubMed] [Google Scholar]
- 72. Hemmings HC Jr, Nairn AC, Greengard P (1984) DARPP-32, a dopamine- and adenosine 3′:5′-monophosphate-regulated neuronal phosphoprotein. II. Comparison of the kinetics of phosphorylation of DARPP-32 and phosphatase inhibitor 1. J Biol Chem 259: 14491–14497. [PubMed] [Google Scholar]
- 73. Bouschet T, Perez V, Fernandez C, Bockaert J, Eychene A, et al. (2003) Stimulation of the ERK pathway by GTP-loaded Rap1 requires the concomitant activation of Ras, protein kinase C, and protein kinase A in neuronal cells. J Biol Chem 278: 4778–4785 10.1074/jbc.M204652200 [doi];M204652200 [pii]. [DOI] [PubMed] [Google Scholar]
- 74. Shiflett MW, Balleine BW (2011) Contributions of ERK signaling in the striatum to instrumental learning and performance. Behav Brain Res 218: 240–247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75. Lu L, Koya E, Zhai H, Hope BT, Shaham Y (2006) Role of ERK in cocaine addiction. Trends Neurosci 29: 695–703. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Calcium concentration resulting from the stimulation for DSI simulation. (A) 100 ms depolarization (B) 1s depolarization, (C) 5s depolarization. In all cases onset is at 2 sec. Red traces show calcium in the spine head, black traces show calcium in the dendrite. The blue bar represents the stimulation time. Though mean values are similar, fluctuations in the spine head are much greater due to the smaller volume.
(PNG)
Results are robust to variation in parameters for both DSI and synaptic plasticity stimuli. (A) Robustness of DSI. The enhancement in 2AG by mGluR activation is quantified as the slope of the 2AG increase versus mGluR concentration for each depolarization duration. 12 parameter variations are illustrated along with the default parameters and experiment results. (B) Additional parameter variations demonstrate the robustness of the enhanced ratio of PKC to 2AG for theta burst as compared to 20 Hz. For both (A) and (B), the following parameter variations were used: Decay: 2AG decay rate is 50% of control; LowGap: decreased rate of GαqGTP hydrolysis; PSD: molecules located in the spine head are added to PSD region. SpinePLC/SpPLC: redistributed PLC, PIP2 and mGluR into spine to make local concentration the same as in dendrite submembrane; SpineDgl/SpDgl: increased PLC, PIP2, mGluR and DAG lipase into spine to make local concentration the same as in dendrite submembrane; Desens 0.5: mGluR desensitization is 50% of control; Desens 0.2: mGluR desensitization is 20% of control; Desens 4×: mGluR desensitization is 400% of control, and also G protein is ∼3× of control; Dagl A: affinity of Dag Lipase for calcium is 50% of control; Dagl B: affinity of Dag Lipase for calcium is 200% of control; Dagl C: the affinity of Dag Lipase for Dag is 50% of control; Dagl D: the affinity of Dag Lipase for Dag is 200% of control.
(PNG)
DAG production is enhanced by GαqGTP, but high values of DAG saturate DAG Lipase. (A) GαqGTP increases linearly with mGluR activation (at t = 0s), with no effect of calcium (at t = 2s). (B–D) DAG production is enhanced by GαqGTP for all durations of depolarization. (E–F) The increased DAG production is translated into increased 2AG for 1s depolarization (E), but less so for 5 s depolarization since DAG saturates the DAG lipase (i.e., the DAG bound DAG lipase approaches the total 1.7µM of DAG lipase) with low concentrations of DHPG (F).
(PNG)