Evaluating the accuracy of SHAPE-directed RNA secondary structure predictions

Abstract

Recent advances in RNA structure determination include using data from high-throughput probing experiments to improve thermodynamic prediction accuracy. We evaluate the extent and nature of improvements in data-directed predictions for a diverse set of 16S/18S ribosomal sequences using a stochastic model of experimental SHAPE data. The average accuracy for 1000 data-directed predictions always improves over the original minimum free energy (MFE) structure. However, the amount of improvement varies with the sequence, exhibiting a correlation with MFE accuracy. Further analysis of this correlation shows that accurate MFE base pairs are typically preserved in a data-directed prediction, whereas inaccurate ones are not. Thus, the positive predictive value of common base pairs is consistently higher than the directed prediction accuracy. Finally, we confirm sequence dependencies in the directability of thermodynamic predictions and investigate the potential for greater accuracy improvements in the worst performing test sequence.

INTRODUCTION

RNA structure predictions have been advancing molecular biology research for decades (1,2), in conjunction with ongoing work (3–5) to improve prediction accuracy. Comparative methods (6,7) are the current gold standard for secondary structure determination, but a suitable set of homologous sequences is too often not available. Hence, thermodynamic optimization remains the most widely used approach to predicting RNA base pairings (8,9).

Thermodynamic optimization methods calculate an optimal structure for an RNA sequence according to the current objective function. Two of the best known prediction programs implementing this approach are UNAfold (10) and RNAfold (11). At their core, each takes an RNA sequence as input, and outputs a secondary structure, which has minimum free energy (MFE), according to the nearest neighbor thermodynamic model (NNTM) (12). Despite the significant utility of these RNA secondary structure predictions to molecular biologists, a crucial caveat has always been the ‘fundamental ill-conditioning of the folding problem’ (13).

One way to understand this issue is through the explosion of suboptimal structures (14); there are an exponential number of distinct structures (15), and even of more abstract ‘shapes’ (16), within a small range of the computed optimum. Equivalently, small perturbations in the NNTM objective function can result in significant changes in the optimal structure (17,18). Either way, this ill-conditioning is one of the reasons why thermodynamic optimization methods are often insufficient on their own (19–22) to predict native base pairings accurately.

Nonetheless, NNTM prediction accuracies can be improved significantly by incorporating auxiliary information (13). For example (22,23), additional criteria can be imposed on the optimization, such as enforcing single-strandedness in regions of high chemical reactivity or prohibiting base pairs between distant nucleotides. In optimization parlance, these are ‘hard’ constraints, as they must necessarily be satisfied in the predicted structure(s).

In contrast, ‘soft’ constraints direct the optimization towards greater accuracy by modifying the reward/penalty structure of the objective function. A notable example of this is the increasing prevalence of SHAPE-directed RNA secondary structure predictions (24–27), including an entire HIV-1 genome (28). These predictions use data from high-throughput chemical probing experiments commonly known as SHAPE (29), for ‘selective 2′-hydroxyl acylation analyzed by primer extension’, as soft constraints on the thermodynamic optimization. Although SHAPE-directed prediction accuracies above 95% have been achieved for large ribosomal RNA sequences (25), such marked improvements have not been universally observed (30).

This discrepancy indicates a need to understand better the extent and nature of improvements in directed prediction accuracy. The problem is that, unlike hard constraints, soft constraints interact with the massive NNTM objective function in ways which are difficult to analyse directly. We address this challenge using a stochastic model of SHAPE data to investigate the accuracy of data-directed predictions for a diverse set of 16S/18S ribosomal sequences.

We find that incorporating this auxiliary data into the thermodynamic optimization as soft constraints consistently improves the directed prediction accuracy over the original MFE structure. However, the extent of the improvement is sequence dependent and roughly correlated with MFE accuracy. Notably, the data-directed predictions for more than 1/3 of our ribosomal test sequences do not achieve the high accuracy of the other 10 sequences—which are at the level of previous experimental studies (25).

Investigating the nature of the correlation between data-directed and MFE prediction accuracies, we find that accurate MFE base pairs are typically preserved in a data-directed prediction, whereas inaccurate ones are not. Thus, if the similarity between the two structures is especially low or high, this provides information about the correlated accuracies of the MFE and data-directed predictions. Furthermore, we show that the positive predictive value (PPV) of the common base pairs is high, even for sequences where the prediction accuracy is not.

Finally, we illustrate clear sequence dependencies in the directability of thermodynamic optimization. Our results show that soft constraints based on SHAPE data are not always sufficient to overcome limitations (19–22) in the NNTM approximation to RNA folding. However, we also give a proof-of-concept demonstration that auxiliary data which more clearly distinguishes between the presence and absence of base pairs can modify the NNTM sufficiently to consistently achieve high prediction accuracy.

MATERIALS AND METHODS

MFE and SHAPE-directed predictions

For the purposes of thermodynamic optimization, an RNA secondary structure is defined to be a set of base pairs without pseudoknots. Two consecutive base pairs form a stack, and consecutive stacks create a helix. Unpaired nucleotides belong to a single-stranded loop substructure.

Each stack and loop is assigned a thermodynamic value under the NNTM, and the free energy change of the entire secondary structure is approximated by summing over these substructure values. RNA molecules fold to minimize free energy, and an optimal MFE structure according to the NNTM can be computed efficiently using dynamic programming.

As a model of RNA base pairing, the NNTM is known to be more accurate for shorter sequences, including domains within longer ones (19,22). It is also well-known that the quality of the thermodynamic approximation has significant sequence dependencies. In particular, prediction accuracies can vary widely even for sequences that fold into essentially the same secondary structure (20,21).

To improve thermodynamic prediction accuracy, SHAPE data can be incorporated into the optimization as soft constraints. Details of the experimental method are summarized in (31). For our purposes, it suffices to know that SHAPE interrogates conformational flexibility at single nucleotide resolution. Low values are strongly correlated with base pairing—as well as other stabilizing interactions (32,33).

This auxiliary information is used to modify the reward/penalty structure of the thermodynamic objective function. More specifically, the standard practice (25), implemented in the RNAstructure prediction program (34), is to convert the SHAPE value for nucleotide i into a pseudo-free energy term according to the equation:

(1)

using slope m = 2.6 kcal/mol and intercept b = −0.8 kcal/mol as parameters. The NNTM is then modified by adding the ΔG_SHAPE(i) term to the free energy change of each base pairing stack involving nucleotide i. Our work assesses the extent and nature of accuracy improvements in such SHAPE-directed predictions using simulated data.

Modeling SHAPE data

We give a probabilistic method for simulating SHAPE data for sequences with known secondary structures. Our stochastic model is based on experimental data (Weeks, personal communication) for two Escherichia coli ribosomal sequences, 16S rRNA with 1542 nt and 23S rRNA with 2904 nt. Nucleotides without data were removed, leaving a total of 4187 nucleotides in the experimental data set.

We considered three different divisions of this data set for our model. Nucleotides were classified into the categories given below according to the comparative secondary structures (35) for the two E. coli sequences. All variation in values within a subdivision was treated as random. We modeled this uncertainty with empirical probability density functions obtained by maximum likelihood fitting using the Statistics Toolbox in MATLAB R2010b. In order of increasing complexity, the models and their subdivision are as follows:

Unary model

No division of the SHAPE data set; one probability distribution fit to all values.

Binary model

Data set is divided into paired and unpaired nucleotides with different probability functions.

Ternary model

Paired nucleotides are further subdivided into stacked or helix-end pairs. The three distinct probability density functions are shown in Figure 1.

Figure 1.

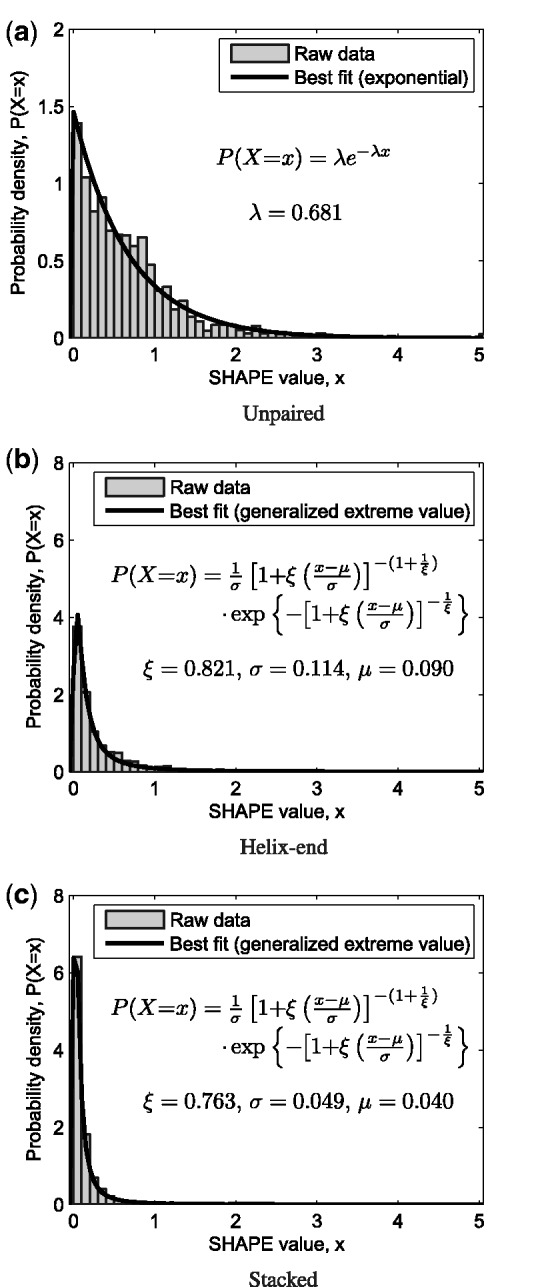
Ternary model distinguishing (a) unpaired, (b) helix-end and (c) stacked nucleotides. Maximum likelihood probability density functions fit to the experimental data set are given. SHAPE data for E. coli 16S and 23S ribosomal sequences are shown in normalized histograms. Vertical scale on the two paired distributions is four times that of the unpaired.

The first is our null model. The second reflects that SHAPE chemistry measures conformational flexibility with clear differences between paired and unpaired nucleotides on average. The third distinguishes ‘stacked’ base pairs (which are bracketed by two other base pairs within the same helix) from ‘helix-end’ pairs (which are adjacent to unpaired nucleotides or to a base pair from a different helix). This resembles the approach in (36), and ultimately is the chosen model.

As described further in the Results section, the appropriate granularity of the model was evaluated in two ways. First, we verified with MATLAB that each subdivision generates two new probability functions with statistically significant differences. Second, each model was used to simulate SHAPE data for the E. coli ribosomal 16S sequence by the method described next. The improvement in prediction accuracy for 1000 trials using values generated under the ternary model, but not the other two, was consistent with the experimental data (25).

Simulating SHAPE-directed predictions

Our study is based on a diverse set of 16S/18S ribosomal sequences with secondary structures available through the Comparative RNA Web (CRW) site (35). The 16 test sequences represent a variety of organisms over a wide range of lengths and MFE prediction accuracies. Additional details are provided in Supplementary Table S1.

For simplicity, we refer to the pseudoknot-free comparative structure from the CRW site as the native base pairings. For our purposes, any nucleotides involved in stabilizing interactions, such as pseudoknots or base triples, belonging to the tertiary or quarternary RNA structure were treated as unpaired. However, known non-canonical base pairs were classified in the same manner as the Watson–Crick and wobble base pairs.

Given a sequence and its native structure, each nucleotide was assigned to the appropriate category (distinguishing unpaired from paired, subdivided into stacked or helix-end) for the current model. The corresponding probability density functions were then used to generate a random value from the appropriate distribution for each nucleotide. This produced a single simulated SHAPE data set for the given sequence. Unless otherwise specified, 1000 trials were run for each sequence.

To minimize simulation run times, secondary structures were predicted using GTfold (37), a parallelized multi-core thermodynamic optimization program. Like UNAfold (10) and RNAfold (11), GTfold implements the standard Turner NNTM energy model (22,23). Like RNAstructure (34), GTfold provides integrated support for SHAPE-directed predictions. When comparing prediction results across programs, it is well understood [see for instance (37) or http://rna.urmc.rochester.edu/GUI/html/Introduction.html (26 October 2012, date last accessed)] that small implementation differences can result in noticeable differences in predicted optimum structures.

Unless otherwise specified, Equation 1 as implemented in GTfold uses the default parameters (m = 2.6, b = −0.8). Default options were used, and there were no additional constraints on the thermodynamic optimization other than the simulated SHAPE data.

When the thermodynamic optimization is modified by soft constraints from simulated SHAPE data, we refer to the resulting optimal base pairings as the data-directed or simply directed secondary structure. When discussing the average data-directed prediction accuracy for 1000 trials, we will usually refer simply to the directed accuracy.

Prediction accuracy and structure similarity

The accuracy of predicted MFE and data-directed secondary structures was determined against the native base pairings. As seen in Table 1, using the experimental SHAPE data as soft constraints improves the prediction significantly.

Table 1.

Data-directed prediction accuracy for E. coli 16S rRNA

Prediction details	Accuracy, %	Proportion
Undirected MFE, GTfold	41.1	–
Undirected MFE, RNAstructure	34.6	–
Experimental SHAPE data, GTfold	76.4	–
Experimental SHAPE data, RNAstructure	72.8	–
Simulated data, no division	20.94 (mean)	0.00
Simulated data, paired/unpaired	69.03 (mean)	0.10
Simulated data, stacked/helix-end/unpaired	74.35 (mean)	0.37

Data-directed predictions were computed with GTfold; accuracy is averaged for 1000 trials for each model. Proportion (above 76.4 threshold) is the fraction of simulated data with prediction accuracy at least as good as the GTfold SHAPE-directed one.

The numbers are lower than previously reported (25) because we used a simpler method for calculating accuracy. In this work, only a base pair (i, j) occurring in both the native and a predicted structure was counted as a true positive (TP). In particular, ‘slipped’ base pairs (22,38) are not considered correctly predicted. Base pairs in the predicted but not native structure were classified as false positives (FP), whereas false negative (FN) base pairs occur in the native but not predicted structure.

Predicted structures were scored for both PPV, the fraction of true positives in the predicted structure, and sensitivity, the fraction of true positives in the native structure. When comparing RNA secondary structures, the Matthews correlation coefficient can be approximated by the arithmetic mean of the PPV and sensitivity (6). Hence, the overall prediction accuracy was evaluated as the average of these two values:

(2)

For comparison purposes, Table 1 also lists the accuracy for the same computation performed with RNAstructure (34). The highest accuracy (96.2% by our measure) reported earlier in (25) required expert curation of the RNAstructure prediction to account for factors such as local refolding. Without manual adjustment, we considered 70% to be a reasonable threshold for high prediction accuracy under our measure.

Finally, the accuracy measurement given above is symmetric in the choice of reference (native) and object (predicted) structure. Hence, we used the same symmetric measure when comparing two predicted structures, and we define the similarity of two secondary structures as the accuracy of one with reference to the other.

RESULTS AND DISCUSSION

Choice of simulation model

The appropriate level of granularity for our stochastic model was determined by two criteria. To begin, we confirmed that each subdivision of the experimental data set is necessary to distinguish nucleotides with different SHAPE behavior. We then verified that the ternary model was sufficient to recapitulate the improvement in prediction accuracy for E. coli 16S rRNA using experimental SHAPE data.

Each subdivision of the experimental SHAPE data set yields probability distributions with statistically significant differences. The two-sample Kolmogorov–Smirnov test rejected the hypothesis that the paired and unpaired nucleotides had the same distribution (P = 2.03 × 10⁻¹⁹⁹, 5% significance). Likewise, the hypothesis that the stacked and helix-end nucleotides had the same distribution was rejected (P = 1.08 × 10⁻⁴⁰, 5% significance). This justifies distinguishing at least the unpaired, stacked and helix-end nucleotides with different distributions in any stochastic model of SHAPE data.

Next, we computed the directed prediction accuracies for E. coli 16S rRNA for 1000 simulations under each model. As shown in Table 1, the directed (i.e. the average data-directed prediction) accuracy decreased using the null model. Although the directed accuracy increased under the binary model, only 10% of the predictions were at least as good as the one using experimental data. However, when stacked and helix-end nucleotides are distinguished, the accuracy improvement with experimental data is no longer an outlier. Hence, the ternary model is sufficient to simulate SHAPE data, and all further results were produced using this model.

Data-directed predictions vary in accuracy

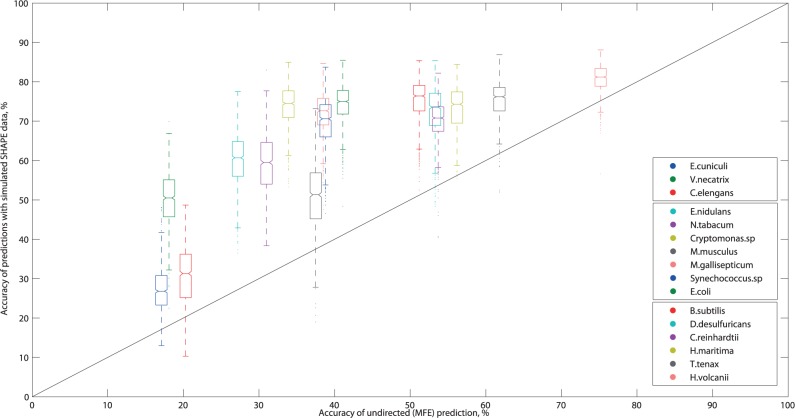
Using the stacked/helix-end/unpaired model, we investigated the effect of soft constraints on prediction accuracy for 1000 trials for each of our 16 test sequences. In general, the directed accuracy improved over the MFE prediction for each 16S/18S ribosomal RNA sequence; as seen in Figure 2, all boxes lie above the diagonal line. However, our results indicate that the high accuracy and significant improvement seen in the E. coli data-directed predictions, from 41.1% to 74.35% on average, is not always achieved.

Figure 2.

Boxplots of data-directed prediction accuracy versus accuracy of the undirected (MFE) prediction. In each box, the midline marks the median accuracy for 1000 predictions, and notches show the 95% confidence interval of the median. Non-overlapping notches indicate the medians are different at 5% significance. The box boundaries mark the 25th and 75th percentiles, and the whisker length shows predictions within 1.5 times the inter-quartile range. Outliers are marked as individual points. The line x = y represents no improvement over the undirected prediction. Points above this line are predictions where the addition of simulated SHAPE data has improved prediction quality. The legend is ordered after increasing MFE accuracy.

By the 70% accuracy threshold, our test sequences group into three categories. When the MFE accuracy is moderate-to-high (over 50%, e.g. for Haloferax volcanii), the directed accuracy is consistently above 70%. When the MFE accuracy is particularly low (under 25%, e.g. for Encephalitozoon cuniculi), the directed accuracy is consistently well below 70%. In between (e.g. for E. coli), the behavior is variable, with four of the sequences performing well but three significantly less so.

These results indicate a rough correlation between MFE and directed accuracy. However, they also demonstrate that the ‘directability’ of the NNTM optimization, like MFE predictions, has some critical sequence dependencies. Both points are addressed in more detail in subsequent sections.

In terms of improving thermodynamic predictions through soft constraints, all but one of the middle group of seven sequences exhibited significant gains over their MFE accuracy. In contrast, the six sequences with moderate-to-high MFE accuracy had average improvements well below +30%. This suggests that attaining high accuracy requires additional information and/or expert curation, even for sequences with good data-directed predictions.

Finally, all sequences including E. coli exhibited a range of accuracies, with the amount of variation broadly but inversely correlated with the average. This raises some questions for further study. On the one hand, SHAPE data have been reported to be ‘highly reproducible’ across several independent replicants (29), with standard deviations on the order of 0.1 normalized SHAPE unit or less. On the other, MFE predictions can be sensitive even to small perturbations in the thermodynamic parameters (17,18). Hence, further analysis is needed to reconcile these results.

Taken together, our simulation results address the extent of improvements in SHAPE-directed prediction accuracy. Foremost, 3 of 16 test sequences (E. cuniculi, Caenorhabditis elegans, Mus musculus) have a directed accuracy well below 60% and an average improvement over MFE below 15%. From this, we conclude that directed predictions are a complex interplay between RNA sequence, auxiliary data and thermodynamic optimization which do not always result in high accuracy or large improvements. Although this conclusion remains to be confirmed by experiment, it is in full agreement with other results investigating the limitations of SHAPE data (30).

Data-directed predictions preserve accurate MFE pairs

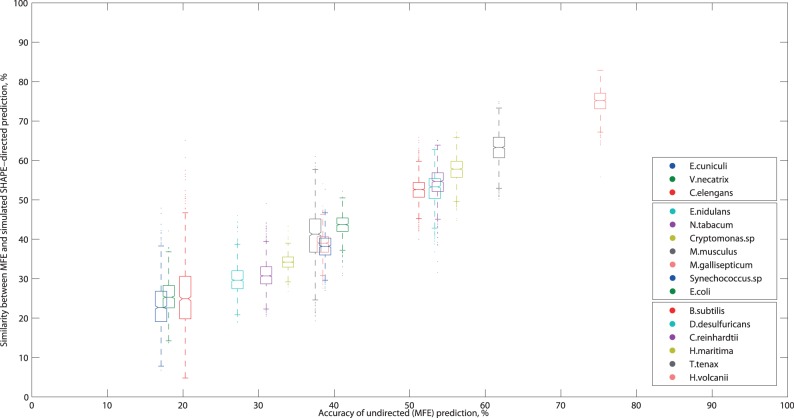
Having demonstrated variability in the extent of accuracy improvements, we investigate their nature, namely the rough correlation observed in Figure 2. Our hypothesis was that MFE base pairs which are accurately predicted tend to remain optimal in a directed prediction whereas incorrect ones do not.

Indeed, Figure 3 shows a surprisingly strong correlation between the similarity of each directed prediction to the MFE and the MFE accuracy. From this, we conclude that if the former is especially low or high, then the latter is likely to fall outside the typical range (30–60%). In these cases, our previous results indicate that the data-directed prediction accuracy is likely to also be correspondingly low or high.

Figure 3.

Boxplots of similarity between the undirected (MFE) and a data-direction prediction versus MFE accuracy. In each box, the midline marks the median accuracy for 1000 predictions, and notches show the 95% confidence interval of the median. Non-overlapping notches indicate the medians are different at 5% significance. The box boundaries mark the 25th and 75th percentiles, and the whisker length shows predictions within 1.5 times the inter-quartile range. Outliers are marked as individual points. The legend is ordered after increasing MFE accuracy.

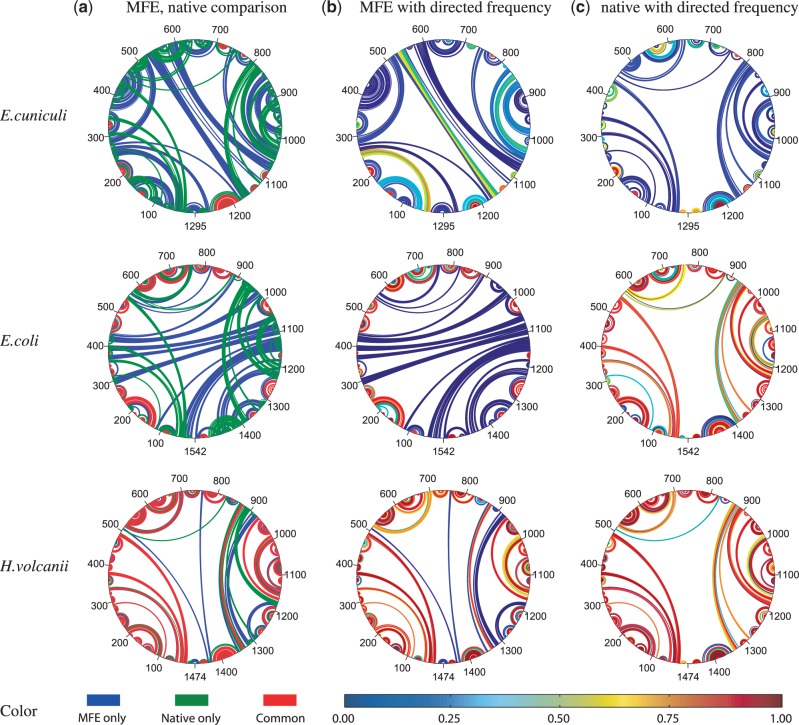
This is highlighted in Figure 4c, for E. cuniculi and H. volcanii, the test sequences with the lowest and highest MFE accuracies (below 20% and above 70%), respectively. As expected, the directed prediction accuracy for these sequences is very low/high, as seen by the predominantly blue/red native base pairings annotated with directed frequency in Figure 4c.

Figure 4.

Circular arcplots of E. cuniculi, E. coli and H. volcanii 16S secondary structures. Sequence is drawn as a circle, and each arc denotes a base pair. Column (a) shows an overlay of MFE (blue) and native (green) structures with common base pairs in red. Column (b) shows the MFE structure with base pairs annotated by the fraction of data-directed structures also containing that pair, as indicated by the color bar at the bottom. Column (c) show the native structure likewise annotated.

Further analysis at the base pair level for these sequences and for E. coli confirmed our initial hypothesis, and provides a means of identifying sets of base pairs with high PPV. We found that the majority of MFE base pairs exhibited one of two behaviors: either occurring in nearly all directed predictions or in close to none of them. Moreover, the former were generally correctly predicted, whereas the latter were not.

As seen in Figure 4b, almost all MFE base pairs are colored either orange/red or aqua/blue, according to their frequency in the directed structures. Those occuring at high frequency are correctly predicted in the MFE structure [red in column (b) correlates with red in column (a)]. Conversely, MFE pairs occuring at low frequency in directed structures tend to be incorrectly predicted [blue in column (b) correlates with blue in column (a)]. Similar patterns were observed for all 16 test sequences. Hence, the accuracy of directed structures is correlated with the accuracy of the undirected MFE prediction.

This correlation is clearly not perfect, however, as indicated by the high frequency with which E. coli native base pairs occur in the directed structures [red in column (c) middle]. However, it does suggest using auxiliary data to identify MFE pairings with high PPV—independent of the data-directed prediction accuracy.

For our test sequences, the PPV of the MFE structure M has a broad range from 0.165 to 0.726 with a median of only 0.3785. However, these values improve dramatically for base pairs, which are common to both M and a single data-directed structure D.

For each test sequence, we computed the PPV of the subset 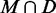, that is the fraction of true positives, for each of the 1000 directed structures. As given in Table 2, these values are high overall, with averages ranging from 0.532 to 0.909 with a median of 0.871. Likewise, the average PPV of the remaining MFE base pairs 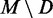is low, ranging from 0.245 down to 0.026 with a median of 0.079. Finally, these values are remarkably stable for 1000 trials. Hence, MFE base pairs that are preserved in a directed structure are significantly more likely to be accurately predicted than those that are not preserved. Thus, any base pairs common to both the MFE and a SHAPE-directed structure should have high PPV.

Table 2.

PPV of MFE base pairs

Organism	PPV (M)	PPV	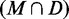PPV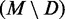
E. cuniculi	0.165	0.532 ± 0.143	0.065 ± 0.026
Vairimorpha necatrix	0.177	0.648 ± 0.100	0.026 ± 0.016
C. elegans	0.186	0.609 ± 0.152	0.059 ± 0.039
Emericella nidulans	0.267	0.770 ± 0.076	0.062 ± 0.026
Nicotiana tabacum	0.303	0.862 ± 0.077	0.063 ± 0.029
Cryptomonas.sp	0.333	0.909 ± 0.032	0.044 ± 0.020
M. musculus	0.381	0.751 ± 0.080	0.130 ± 0.051
Mycoplasma gallisepticum	0.377	0.872 ± 0.037	0.077 ± 0.030
Synechococcus.sp	0.380	0.887 ± 0.046	0.081 ± 0.033
E. coli	0.399	0.875 ± 0.038	0.055 ± 0.028
Bacillus subtilis	0.500	0.880 ± 0.039	0.102 ± 0.036
Desulfovibrio desulfuricans	0.517	0.885 ± 0.034	0.136 ± 0.050
Chlamydomonas reinhardtii	0.526	0.874 ± 0.032	0.133 ± 0.051
Thermotoga maritima	0.541	0.868 ± 0.034	0.125 ± 0.044
Thermoproteus tenax	0.589	0.870 ± 0.029	0.150 ± 0.053
H. volcanii	0.726	0.903 ± 0.017	0.245 ± 0.064

PPV(M) is the number of native base pairs in the MFE structure M. For each directed prediction D, the PPV of the set of common base pairs 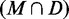and the set of remaining MFE base pairs 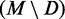was computed. Values are the mean for 1000 trials ± standard deviation.

Another method for improving confidence in thermodynamic predictions uses base pair probabilities computed from the partition function (39) or by stochastic sampling (40). It is known (38) that high probability MFE base pairs also have a significantly increased PPV. We confirmed that base pairs in 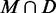are not simply the high probability ones. This was true particularly for sequences with low MFE accuracy, when a SHAPE-directed prediction may also be less accurate (See Supplementary Table S2 for details).

Directability of NNTM optimization

The purpose of soft constraints is to direct the optimization towards a more accurate solution. However, like the undirected MFE prediction, the ability of auxiliary data to improve thermodynamic prediction accuracy has sequence dependencies. We illustrate the differences in NNTM directability by parameterizing the slope m and intercept b in Equation 1 against three test sequences: E. cuniculi, E. coli and H. volcanii.

The default parameters (m = 2.6, b = −0.8) were chosen by identifying a ‘sweet spot’ maximizing both sensitivity and PPV of E. coli 23S rRNA using experimental SHAPE data (25). Under the same procedure using a random simulated data set, Figure 5 shows the parameterization space for each of our three 16S sequences.

Figure 5.

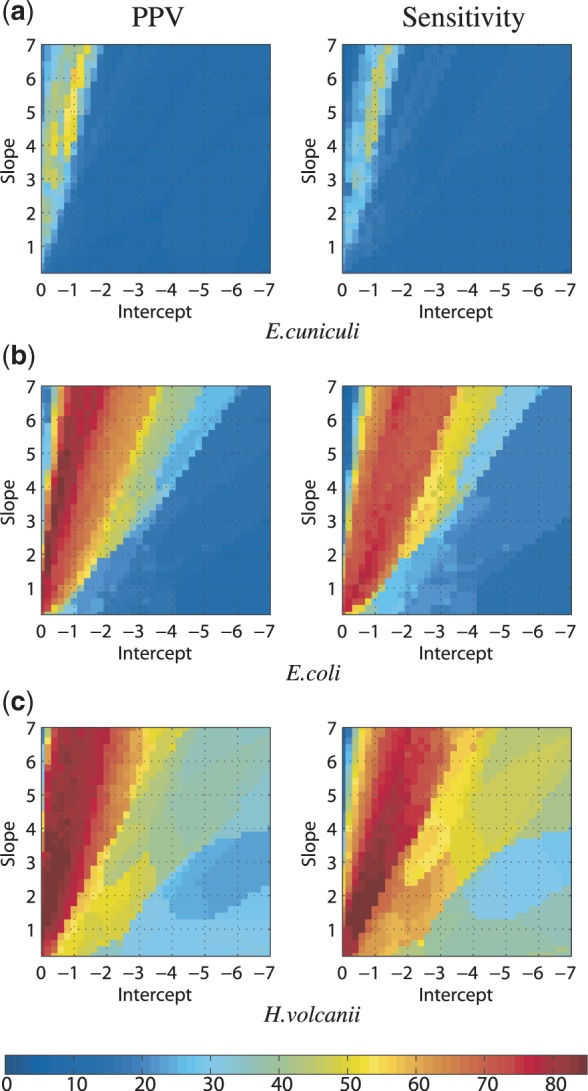
Variation in PPV and sensitivity as a function of the Equation 1 parameters for a random simulated SHAPE data set for (a) E. cuniculi, (b) E. coli and (c) H. volcanii 16S rRNA. The color bar indicates percentage measurements for PPV and sensitivity.

Our results for E. coli 16S recapitulate the 23S experimental ones. Namely, there is a large optimal region with a maximum PPV of 86.2% when m = 3.2, b = −0.4 and a maximum sensitivity of 78.8% when m = 1.2, b = −0.6. The average of these values (m = 2.2, b = −0.5) is close to the default parameters.

The situation with E. cuniculi is markedly different. The optimal region is small, and the maximum obtainable PPV is 58% and sensitivity is 47.5%, when m = 6.2, b = −1.0 and m = 4.2, b = −1.0, respectively. Repeating the process with other randomly chosen data sets did not qualitatively change the outcome (data not shown). We conclude that no choice of Equation 1 parameters would improve the E. cuniculi directed predictions to the level of E. coli.

In contrast, the optimal region for H. volcanii is larger than E. coli and contains more high sensitivity/PPV combinations of parameters. What is especially striking is the gradual degradation in accuracy as the parameters are varied away from optimal. Hence, the NNTM is a good model for the base pairing of H. volcanii, a reasonable one for E. coli, as it can be directed to high accuracy predictions using SHAPE data, and a poor one for E. cuniculi.

In view of this unsatisfactory situation with E. cuniculi, we further explored its directability. As a conceptual exercise, we increased the separation between the unpaired and two paired probability distributions in our ternary model. (Recall that all three distributions have a peak at low values.) The original unpaired distribution P_orig was modified to be a convex combination with a normal distribution P_norm of higher mean;

(3)

where 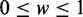and P_w(x) denotes the new probability of SHAPE value x. The normal distribution used had a mean of 3.51 and standard deviation of 1.78 obtained by hypothesizing a 6-fold increase in reagent reactivity for a Gaussian model of SHAPE chemistry kinetics (41).

Under this modified model, as the normal component of the unpaired distribution increased to 80%, the directed prediction accuracy for E. cuniculi increased above 70%. (see Supplementary Figure S1.) In fact, when the normal component is 100% of the unpaired distribution, then 15 of 16 of our chosen sequences have a directed prediction accuracy at least this high (see Supplementary Table S3).

These ‘proof-of-concept’ results indicate that, even for sequences like E. cuniculi whose base pairing are not modeled well by the NNTM, auxiliary information has significant potential for improving prediction accuracy. However, a critical factor in directing the thermodynamic optimization towards the native base pairings may be the strength of the ‘unpaired’ signal.

Conclusions and future directions

We introduced a stochastic model for experimental SHAPE data, and evaluated data-directed RNA secondary structure prediction accuracy for a diverse set of 16S/18S ribosomal sequences. Using this auxiliary data as soft contraints consistently improved thermodynamic optimization accuracy. However, there was significant variation in the average data-directed prediction accuracy between sequences, correlated with the undirected (MFE) accuracy. Thus, although many of our test sequences achieved the high accuracy reported for experimental SHAPE-directed predictions, this level of accuracy was by no means universally attained.

When accuracy cannot be evaluated by direct comparison with a known structure, our results still yield helpful insights. In particular, the similarity between the undirected and a data-directed prediction is highly correlated with the MFE accuracy, which in turn is roughly correlated with the data-directed prediction accuracy. Hence, if the similarity is particularly low (below 30%), it is likely that the directed prediction accuracy is correspondingly low—as illustrated by the E. cuniculi example. Even in these cases, though, the PPV of base pairs common to both the MFE and a directed prediction should be much higher.

The lack of directability for the E. cuniculi predictions suggests several potential directions for further investigation. For instance, no systematic study of more than three sequences has yet been done on the effects of varying the slope and intercept parameters for the current implementation of soft constraints. It would be interesting to analyse more completely this variable aspect of thermodynamic optimization and to characterize its sequence dependencies. Furthermore, although the current method of soft constraints works well in many circumstances, it is not the only one (27). Hence, it is possible that alternative methods of incorporating SHAPE data into secondary structure predictions may address this issue in the future.

Finally, these results demonstrate the importance of statistically reproducible results in SHAPE-directed secondary structure predictions. An alternative method for simulating SHAPE reactivities, particularly when a known secondary structure is not available, would use a structural alignment to map nucleotides back to a related sequence with an experimental data set. In a small, exploratory investigation of this approach, we found that it generated similar results to the stochastic model presented here, and hence should be investigated further in the future.

AVAILABILITY

Further information including the computational tools developed for this study is available online via the website http://users-birc.au.dk/zs/SHAPEsimulations/.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online: Supplementary Tables 1–3 and Supplementary Figure 1.

FUNDING

The National Institutes of Health [NIGMS R01 GM083621 to C.E.H.]; Danish Council for Strategic Research [#09-061856 to J.K.]; Burroughs Wellcome Fund [CASI #1005094 to C.E.H.]; Aarhus University Research Foundation [#4-56125-437150 to Z.S.]. Funding for open access charge: The National Institutes of Health [NIGMS R01 GM083621 to C.E.H.].

Conflict of interest statement. None declared.