Skip to main content
PMC home page
Journal of Digital Imaging logoLink to Journal of Digital Imaging
. 2012 Jul 26;26(2):344–352. doi: 10.1007/s10278-012-9510-6

UMMPerfusion: an Open Source Software Tool Towards Quantitative MRI Perfusion Analysis in Clinical Routine

Frank G Zöllner 1,✉, Gerald Weisser 2, Marcel Reich 1,2, Sven Kaiser 1,2, Stefan O Schoenberg 2, Steven P Sourbron 3, Lothar R Schad 1
PMCID: PMC3597952  PMID: 22832894

Abstract

To develop a generic Open Source MRI perfusion analysis tool for quantitative parameter mapping to be used in a clinical workflow and methods for quality management of perfusion data. We implemented a classic, pixel-by-pixel deconvolution approach to quantify T1-weighted contrast-enhanced dynamic MR imaging (DCE-MRI) perfusion data as an OsiriX plug-in. It features parallel computing capabilities and an automated reporting scheme for quality management. Furthermore, by our implementation design, it could be easily extendable to other perfusion algorithms. Obtained results are saved as DICOM objects and directly added to the patient study. The plug-in was evaluated on ten MR perfusion data sets of the prostate and a calibration data set by comparing obtained parametric maps (plasma flow, volume of distribution, and mean transit time) to a widely used reference implementation in IDL. For all data, parametric maps could be calculated and the plug-in worked correctly and stable. On average, a deviation of 0.032 ± 0.02 ml/100 ml/min for the plasma flow, 0.004 ± 0.0007 ml/100 ml for the volume of distribution, and 0.037 ± 0.03 s for the mean transit time between our implementation and a reference implementation was observed. By using computer hardware with eight CPU cores, calculation time could be reduced by a factor of 2.5. We developed successfully an Open Source OsiriX plug-in for T1-DCE-MRI perfusion analysis in a routine quality managed clinical environment. Using model-free deconvolution, it allows for perfusion analysis in various clinical applications. By our plug-in, information about measured physiological processes can be obtained and transferred into clinical practice.

Keywords: Algorithms, Perfusion, Image processing, Computer-assisted, Magnetic resonance imaging

Background

Magnetic resonance perfusion imaging has become an important tool for functional assessment in various applications, like tumor diagnostics and therapy, stroke, (cardio-) vascular diseases, or functional assessment of organs [1–4]. Currently, contrast-enhanced dynamic MR imaging (DCE-MRI) is the method of choice to measure perfusion non-invasively and without radiation exposure. Various approaches were proposed to assess hemodynamic parameters (e.g., blood flow, blood volume, and mean transit times) as well as permeability–surface area product or interstitial volume by dynamic MRI [5–10]. Added value of perfusion imaging has been reported, e.g., for kidney [3, 11] or heart disease [12]. In prostate cancer perfusion imaging has developed as one part of a multi-parametric approach to stage cancer [13–16].

However, so far MR perfusion imaging remained a research tool and was not broadly introduced in the clinical domain [17, 18]. One problem is the lack of standardization in technical aspects which have to be considered for successful quantitative evaluation, including sequence and contrast agent dose optimization [19], correct selection of the arterial input function [20], or correction for motion artifacts [21, 22].

The second problem is a lack of tools that allow a direct integration into the diagnostic workflow in radiology. Research tools that allow calculations of hemodynamic parameters are developed often as offline solutions and the clinician has to transfer the large image data sets to a separate workstation for analysis [3, 23–27]. Furthermore, to include the results in the clinical workflow they have to be transferred back into the diagnostic system. However, results obtained from most research software are stored in various formats that could not easily be converted to DICOM objects to be stored in picture archive and communication systems (PACS) [23]. Certainly, the aforementioned procedure is feasible in the research context investigating small patient groups; however, in daily practice this becomes cumbersome.

Commercial software solutions for perfusion imaging exist. They allow (partial) integration into the clinical environment, especially if provided by the vendors of the MR scanners. However, such software is expensive which prevents ubiquitous usage, i.e., only few licenses or dedicated workstations are usually purchased. Even more, available commercial software solutions are often dedicated to a single application, i.e., heart, brain, or prostate perfusion [15, 27, 28] which does not allow for easy extension and adaption beyond the intended usage in the clinical situation [29].

Here, we present our results of the development of an Open Source OsiriX plug-in for the analysis of magnetic resonance perfusion imaging that allows for integration into the radiological and clinical workflow. We implemented a classic, pixel-by-pixel deconvolution approach to quantify T1-weighted DCE-MRI perfusion data thereby, providing a generic approach to be used with various clinical applications. Furthermore, we established a test suite that allows for automatically testing of the correctness of the obtained results to a given reference implementation and reporting tools to enable quality management with perfusion analysis.

Materials and Methods

Data Sets

Clinical Data

To test our plug-in, we applied it retrospectively to ten MR perfusion data sets of the prostate. Patients were selected randomly without any prior knowledge about the acquired data. All patient information was anonymized before processing.

All data were acquired on a 3 T scanner (Tim Trio, Siemens Medical Healthcare, Erlangen, Germany) using a 32 elements spine matrix array and a six channel surface body coil. The data sets were acquired by a standardized protocol using a 2D inversion-recovery TurboFlash sequence with parameters TR/TE/TI/FA = 193 ms/1.05 ms/72 ms/12°, matrix size of 108 × 192 reconstructed to 288 × 384, FOV = 29 × 39 cm2, in-plane resolution after reconstruction of 1 × 1 mm2, six 6-mm thick slices, 150 time points with temporal resolution of 3.4 s. A bolus of 0.1 mmol/kg body weight of gadolinium chelate (Dotarem®, Guerbet, Roissy CdG Cedex, France) at 2.5 ml/s was injected with a power injector (Medrad Inc., Pittsburgh, PA, USA) followed by a saline flush of 40 ml.

Calibration Data Set

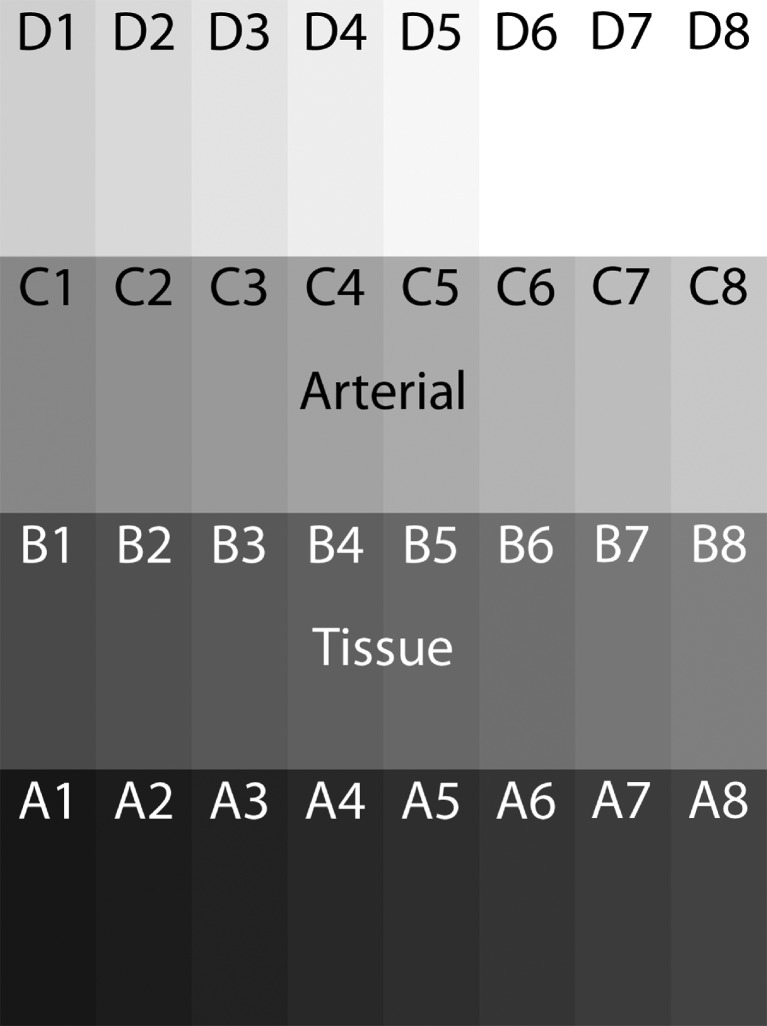
Each calibration data set was generated out of our 4D perfusion data sets. Therefore, 32 voxel time intensity courses were selected: 16 voxel were taken from a region of interest (ROI) in an artery, i.e., forming the arterial input function (AIF; C1–D8 in Fig. 1), and 16 voxels were taken from prostate tissue (A1–B8, see Fig. 1). In total ten calibration data sets were generated.

Fig. 1.

Fig. 1

Open in a new tab

Calibration data set of size of 32 pixels. Sixteen pixels were taken from an artery (C1–D8) and 16 pixels from the prostate (A1–B8) to obtain intensity values. Color coding of the pixel is for visualization purpose only

Data Analysis Algorithm

The core algorithm for data analysis was translated into C from an IDL implementation that is embedded in the software Platform for Medical Imaging research (PMI) [24]. The PMI algorithm is optimized for robustness, precision, and calculation time, and presented to the user as "Fast Deconvolution". For applications where high accuracy is less important, it offers a suitable alternative to more accurate, but slower and less robust algorithms for model-free deconvolution on the pixel level [30]. Calculating the perfusion parameters by deconvolution is given in the Appendix.

The implemented “Fast Deconvolution” algorithm in PMI is a modified version of the highly successful truncated singular value decomposition (TSVD) algorithm with a fixed regularization parameter, as first proposed for dynamic susceptibility contrast MRI (DSC-MRI) by Ostergaard et al. [31]. Four different modifications were implemented:

  1. A preprocessing step is included that resamples the data to a fixed temporal resolution in case they are acquired in a triggered mode that produces non-uniform temporal sampling (e.g., in the heart, or with breathing-triggered acquisitions).

  2. Since the algorithm in Ostergaard et al. [31] was developed for T2*-weighted DSC-MRI, the conversion of signal to concentration is modified for use in T1-weighted DCE-MRI.

  3. For calculating the convolution product the Volterra formula [32] is used, which corrects an error in the original formula for discretization with linear interpolation proposed in Ostergaard et al. [31].

  4. Since the algorithm is designed generic to be applicable in different applications, the extracted parameters are plasma flow and volume of distribution rather than blood flow and blood volume. The latter interpretation is only justifiable for intravascular tracers, which is the context of Ostergaard et al. [31]. The interpretation in terms of plasma values is more general and applies to extravasating tracers as well.

The algorithm consists of four consecutive steps: signal conversion, data resampling, deconvolution, and parameterization.

To calculate the tracer concentrations C(t) from the DCE-MRI signals S(t) and for the sake of robustness on the pixel level, signal conversion is performed assuming a linear relation between S and C. First, the baseline signal S0 is calculated by averaging the first n time points of S(t). Two alternative formulae for signal conversion are implemented: "Signal Enhancement" is defined as C(t) = a(S(t) − S0); it is the most robust option and is preferred for sufficiently homogeneous MRI coils; "Relative Signal Enhancement" is defined as C(t) = b(S(t) − S0)/S0, and should be used when sufficient uniformity of the coils cannot be guaranteed. Further it is assumed that the slopes "a" and "b" are tissue-independent, so that they cancel out when comparing arterial- and tissue curves, and can be set to 1.

To obtain results in terms of plasma flow and volume, the arterial input function is divided by 1-Hct, where Hct is the hematocrit of the patient, a user-defined parameter. A default value of Hct = 0.45 is set for cases when the actual hematocrit is unknown (see Fig. 2). For intravascular tracers, the plasma flow and volume of distribution produced by the algorithm can be divided by 1-Hct again to retrieve the blood flow—and volume. The latter parameters will then be independent of the value chosen for Hct.

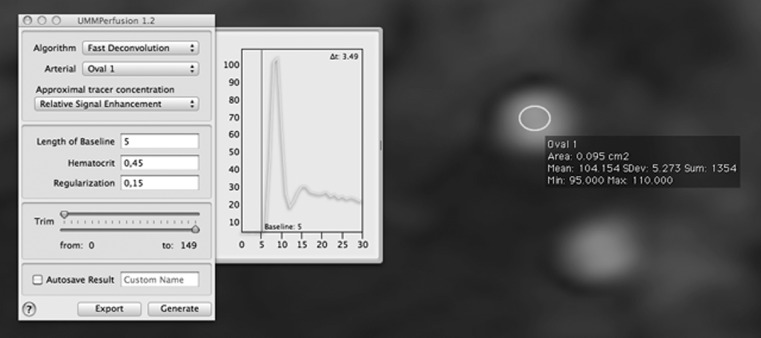
Fig. 2.

Fig. 2

Open in a new tab

Graphical user interface of the perfusion plug-in. The arterial input function (green curve) selected by the user is shown in display window. The plot is updated in real-time when the user changes the corresponding ROI in the image. Also the current setting of the baseline (red line) is depicted

After signal conversion, if the data has temporal non-uniform sampling the concentration time curve is resampled by linear interpolation to a uniform grid with spacing Δt equal to the smallest time-interval in the series.

OsiriX Dicom Viewer

OsiriX is an Open Source image processing software dedicated to DICOM images produced by various imaging modalities such as MRI, CT, or PET and ultrasound [33, 34]. As it is fully compliant with the DICOM standard for image communication and image file formats, OsiriX is able to communicate with any PACS or imaging modality by the DICOM communication protocol. It provides support to view and multi-dimensional imaging data [35]. Furthermore, it provides a plug-in interface to expand the capabilities of the OsiriX software [36]. Thereby, one can take advantage of the communication and viewing functionality provided by the main OsiriX software but also one is flexible to implement own algorithms and to access the image data. Currently, about 45,000 active user of this software were reported [37]. In this study, OsiriX version 3.7.1 and 3.8.1 as well as the FDA-approved version OsiriXPro 2.0 (aycan Medical Systems, LLC, Rochester, NY, USA) were utilized.

Plug-in Implementation

Our OsiriX plug-in was implemented using Objective-C and C++. The latter was mainly used for the internal image data structures used with the SVD algorithm, since these could be processed significantly faster than the corresponding native Objective-C constructs [38].

Since the deconvolution operation can be performed independently for each pixel [30], the calculations can be processed in parallel. The operating system platform (MacOS X) provides native support for parallel processing [39]; therefore, we incorporated support for multi-core/threaded processing to speed-up the calculation. Thereby, the plug-in automatically detects if multiple central processing units (CPUs) are available and distributes the calculations. In our implementation, the single cross sections of a data set are distributed to the available CPUs.

The plug-in architecture is designed such that other perfusion analysis algorithms could be integrated with the user interface. Each possible algorithm is wrapped into a separate class (Algorithm), the class UMMPAlgorithm provides an interface to our plug-in. Figure 2 depicts the user interface of the perfusion plug-in.

Calculated parametric maps can be saved as DICOM series with the current study for archiving or further tasks.

Quality Management

Besides the implementation of the deconvolution algorithm, a second goal of this work was to establish means to ensure a quality management during analysis of the perfusion data. Several pitfalls exist that can invalidate the results of a perfusion analysis [19]. The most obvious is an inappropriate choice of the AIF [20]. Commonly, the AIF is selected by drawing a small ROI into an artery supplying the tissue under investigation. In our plug-in implementation, the AIF (mean curve of all pixels within the ROI) is plotted online so that errors made while choosing an inadequate AIF are reduced (see Fig. 2). It is updated real-time if the user modifies the ROI used for the AIF measurement.

A second important aspect is defining a correct range of baseline time points for signal normalization and signal conversion into tracer concentration, respectively. The baseline selection is visualized in the display window where the AIF is plotted and can be adjusted manually. Furthermore, the total number of volumes (time points) to be processed can be adjusted by trimming the time series. This is potentially useful if, e.g., the MR sequence does not reach the steady state within the first acquired volume; such data can be discarded not to hamper the perfusion estimation.

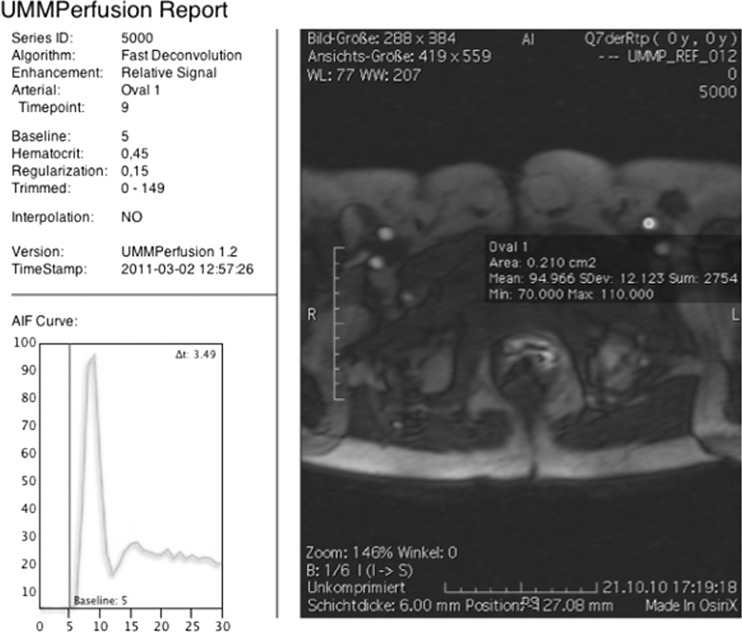
To be able to (later) follow-up steps taken to calculate perfusion parameters, a report sheet was implemented. It depicts the AIF time intensity curve, its corresponding ROI including slice position and time point, and the number of baseline elements as well as the type of signal normalization selected. The report is automatically added as DICOM object to the current study to be archived together with the patient record in a PACS system. Also all resulting perfusion parametric maps can be automatically saved with a prefix defined by the clinical user. To allow image fusion between the saved parametric maps and the original image data the corresponding frame of reference is preserved.

Evaluation

Evaluation of our software was performed by comparing the results of the perfusion plug-in to a reference software implementation of the TSVD algorithm (PMI 0.4, written in IDL 6.0, ITT VIS, Boulder, CO, USA) [24] that has been used and evaluated in several studies, e.g., to the artificial data sets. All parameter settings were kept the same for all calculations. To make sure that the ROIs were the same within the two programs, the coordinates of the ROI were noted during drawing of ROIs within PMI and transformed into the coordinate space of OsiriX. Thereby, exact locations of the ROIs could be maintained. The results of the two programs were compared by calculating the mean difference between the corresponding parametric maps. A two-sample t test was employed to test if these differences are significant. Thereby, a p value less than 0.05 was assumed as significant different.

In addition, results obtained by PMI were saved and bundled with the calibration data to form a test suite. The whole evaluation procedure was automated, so that it could be repeated at any time, e.g., when extending the plug-in.

We also processed the ten MRI prostate perfusion data sets to test the stability of our plug-in. Furthermore, we were interested in the processing time of our implementation to see the effect of the implemented support for parallel processing. Therefore, we used two computers with typical hardware settings at our radiology department: a MacPro with 2 × 2.8 GHz Quad-Core Intel Xeon 5400 and 12 GB memory, and an iMac with 3 GHz Intel Core 2 Duo E7600 and 4 GB, respectively. Measured processing times only include the calculation of the perfusion maps, i.e., the time measurement started after the user clicked the ‘generate’ button.

Results

For all data sets parametric maps of plasma flow, volume of distribution, and mean transit time were calculated without problems.

Comparing the calibration data between our implementation and the reference implementation in PMI, on average a deviation of 0.032 (±0.02) ml/100 ml/min for the plasma flow, 0.004 (±0.0007) ml/100 ml for the volume of distribution, and 0.037 (±0.03) s for the mean transit time was observed. Differences were not significant for all three parameters (plasma flow: p = 0.9997, volume of distribution: p = 1.000, mean transit time: p = 0.9952).

Average processing time using two CPUs was 49.5 (±1.7) s for computing the parametric maps, using eight CPUs, 19.5 (±0.5) s, respectively. An increase in processing speed of 2.5-fold was achieved using a multiprocessing unit.

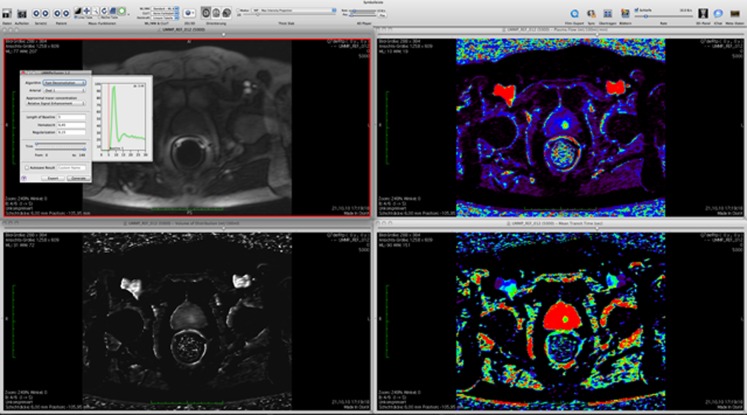
Figure 3 depicts the results obtained for analyzing a prostate perfusion data set, as an example. In addition to the primary viewing window containing the 4D perfusion data set, three viewer instances are automatically generated each showing one of the obtained parametric maps (plasma flow, volume of distribution, mean transit time). Color coding of the parametric maps is arbitrary. It can be adjusted by the reader using the built-in color maps provided by OsiriX. Moreover, a fusion of the parametric maps with the high-resolution anatomical MR images was available with one mouse click. Three-dimensional resampling of the parametric maps, already provided by OsiriX, allowed for the adaption to MR images with different slice orientations (cf. Fig. 4).

Fig. 3.

Fig. 3

Open in a new tab

Visualization of perfusion analysis results by our plug-in using. Top left the original data set (3D + time), top right plasma flow, lower left volume of distribution, lower right mean transit time. Data originates from a prostate MR exam

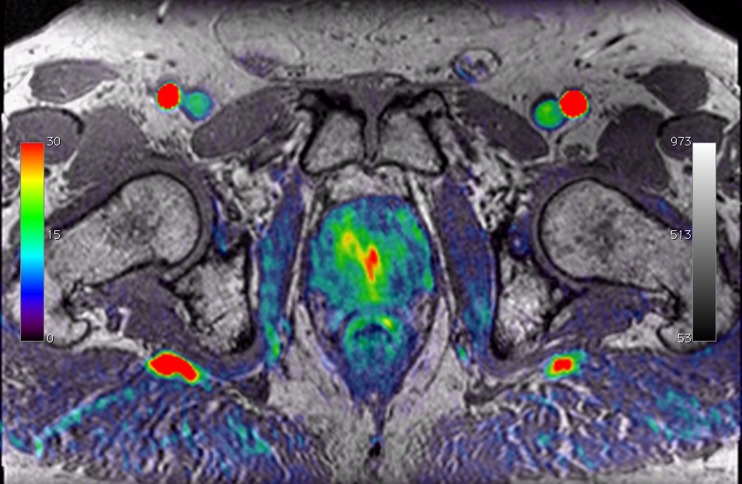
Fig. 4.

Fig. 4

Open in a new tab

Illustration of image fusion of a plasma flow map calculated by our plug-in to a high-resolution T1-weighted MRI of the same patient data set. The T1-weighted image is given in grayscale, the plasma flow map in a rainbow colormap

Figure 5 depicts the report that is automatically generated and stored in the DICOM database during the calculation of the perfusion parameters by our plug-in. It depicts the parameters of the algorithm like regularization or the length of the baseline, the type and position of the ROI drawn to select the AIF by a screen shot, and finally, the time intensity curve of the AIF generated from the aforementioned ROI. If temporal resampling by linear interpolation was used during the calculations it is noted in the report, too.

Fig. 5.

Fig. 5

Open in a new tab

Report generated during perfusion analysis. It shows location and shape of the arterial input function and parameter settings like the chosen regularization for the perfusion calculation

Discussion

We developed successfully a perfusion analysis plug-in for the Open Source DICOM workstation OsiriX. It provides quantitative pixel-by-pixel analysis of T1-weighted DCE-MRI data and fast computation by using parallel processing. Calculated parametric maps are saved directly to the OsiriX DICOM data base, allowing for transferring data easily to a PACS or other workstations. A report that records all parameter settings of the perfusion analysis is automatically generated and saved with the patient record, too. Thereby, our plug-in provides quality management for perfusion analysis. While implementing the plug-in, an interface to easily extent the plug-in, e.g., to incorporate other perfusion calculations, was created.

We selected OsiriX as platform since it is already used in several clinical applications, ranging from reading multimodal images to spine surgery or aortic stent graft planning [34, 37, 40, 41]. In addition, a plug-in interface allows extending the OsiriX software and numerous plug-ins already exist [36]. Furthermore, as Open Source software, OsiriX provides vendor neutral processing and cost-efficient reading of images [37] including image fusion and multimodal reading. Therefore, it was a reasonable step to implement the TSVD approach into this system.

The implementation of the plug-in was tested using artificially constructed data similar to Kosior et al. [23]; however, we did not simulate the perfusion data but obtained them from real-world data. Setting up a small matrix of only 32 pixels compared to a matrix of 50 by 50 as Kosior et al. allows for fast and easy assessment of the calculated results. Even a manual step by step verification of the TSVD algorithm is feasible.

Results showed only very small differences between our implementation and the reference PMI. These differences were not significant (p > 0.05) and might be due to the iterative numerical calculation scheme of the TSVD algorithm. Results on perfusion MRI in prostate reported standard deviations for the plasma flow of up to 39.7 ml/100 ml/min, for the volume of distribution of 2.7 ml/100 ml, and mean transit times variation of up to 9.6 s [2]. With respect to these variations, probably mostly due physiological variations in the patients, the differences in the second decimal place between the two implementations are acceptable. We conclude that our implementation is technically correct.

Besides integrating perfusion analysis into the radiological workflow itself, also the time needed to compute results is an important aspect, especially if used in a clinical setting [16]. In our implementation, parallel data processing is supported, allowing utilizing hardware advantages like multiple CPUs to reduce calculation time. Certainly, calculation times are heavily dependent on the size of the data set and the utilized hardware. Thus, our results (ca. 1 min for iMac, 30 s for an eight-core MacPro) could be seen as orientation. We think that a processing time of less than 30 s is acceptable for the use in clinical routine.

The developed plug-in was evaluated on MRI of prostate. Software already exists for this purpose, also including DICOM communication [15, 28]. However, these applications cover a whole multi-spectral approach to prostate cancer diagnosis, rather than only perfusion analysis. Our aim was not to build specific software for prostate cancer diagnostics, but a plug-in to perform perfusion analysis in general, not limited to a single clinical application. Nevertheless, in conjunction with other OsiriX plug-ins (i.e., ADC, T2 mapping) [36], a multi-spectral analysis and diagnostic of prostate cancer is possible, too, without the need for separate, dedicated software.

In contrast to most reported tools for perfusion analysis [23, 25, 28], our software provides means for basic quality management. Thereby, it is possible to track and identify errors made during the initial analysis easily at a later time. This might probably reduce the propagation of wrong results within the clinical workflow and therefore, in the end, prevent false diagnosis or decisions in treatment of patients. Moreover, a risk analysis and quality management plan as well as a handbook for the use of the software was authored (available at http://www.opossumm.de/). These efforts strongly support a possible in-house certification according to the Medical Devices Directive of the European Union for the use of the software in clinical routine. Thereby, the software module can be used in a clinical environment without additional costs and with minimal efforts.

So far, we implemented in our plug-in a deconvolution method to analyze perfusion data. Our rational was that this algorithm is generic (i.e., model-free approach) and robust. This is reflected by numerous studies using deconvolution-based perfusion analysis for diagnostic of diseases in the brain [9, 42], the heart [43, 44], the lungs [45, 46], the breast [47], the kidneys [48], and the prostate [14]. This technique is not limited to MRI and was also applied to CT perfusion data [49, 50]. In principle, the only prerequisite for using deconvolution analysis in all these applications is a bolus tracking experiment.

However, more dedicated physiological models can provide not only perfusion-related parameters (blood flow, blood volume, and mean transit time) but also additional, tissue-specific parameters like permeability or filtration. This is desirable, i.e., when studying brain barrier leakage [51], tumors [52], or kidney filtration [4, 11, 18]. Such tasks can be performed when applying compartment models [6, 19]. Future research will be directed towards implementing a one- and two-compartment model as reported in the literature [5, 6, 8].

Our plug-in is limited to calculating the perfusion from T1-weighted DCE-MRI data. However, we implemented an interface within the plug-in to allow for extensions or to integrate other computations of the perfusion. Since the only difference in calculating perfusion parameters from T1- and T2*-weighted dynamic MRI is the signal to concentration conversion [30], such an extension will be easily to implement in a future version of our plug-in. Also, when using the plug-in for perfusion analysis of moving organs like the heart or the kidneys, motion artifacts have to be corrected for independently, using image registration [21] or breathing, triggering, or navigation techniques during image acquisition [22, 53].

Another aspect of deploying such a plug-in into a clinical routine is its usability. We currently roll out the tool at our radiology department (about 70 diagnostic OsiriX workstations) and thus, only little information about usability issues is yet available. However, initial feedback was positive, stating an easy usage of the tool and only few minutes for learning how to use the plug-in. A more detailed analysis of usability aspects is currently investigated.

The plug-in is licensed under a BSD type license and is available at http://www.opossumm.de/projects/ummperfusion/files. The website also provides access to a source code repository and documentation. We further plan to list our plug-in with the OsiriX website to reach a broader audience of possible users or developers.

Conclusion

We successfully developed an Open Source plug-in for perfusion analysis. The plug-in is integrated in the DICOM workstation OsiriX, therefore, providing integration in a clinical environment. We envision that by our plug-in approach, an important tool was created to bring further perfusion analysis into the clinical practice.

Acknowledgments

We kindly acknowledge the financial support from Heinrich-Vetter-Stiftung.

Appendix

Truncated Singular Value decomposition for Perfusion Analysis

For the tracer kinetic analysis, we modified the deconvolution approach proposed by Ostergaard et al. [31]. This is based on the basic relation for residue detection in linear and stationary systems, which relates the tissue concentrations to the concentrations in the arterial plasma by a convolution:

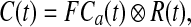graphic file with name M1.gif 1

with C(t) the measured tissue concentration, Ca(t) the arterial plasma concentrations, R(t) the tissue residue function, and F is the plasma flow. The relation is discretized assuming linear interpolation between measured points, using the Volterra formula in [32]. This produces a matrix equation

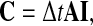graphic file with name M2.gif 2

where A is an n × n matrix with n is the number of time points, depending on the values of Ca only. The singular value decomposition

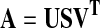graphic file with name M3.gif 3

is calculated, all singular values S below a given cut-off λ are set to zero, and the pseudo-inverse

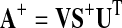graphic file with name M4.gif 4

is calculated. The impulse response Ik for each pixel k is then calculated by

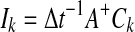graphic file with name M5.gif 5

The value of the regularization parameter λ is fixed in this algorithm. The software sets a default value of 0.15 max (S), but allows the user to select a different value if required. A more detailed discussion of selecting the regularization parameter can be found in [30, 54]. To parameterize the results, the plasma flow Fk of each pixel k is calculated as

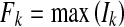graphic file with name M6.gif 6

Using the central-volume theorem and the definition of the residue function we can also determine the volume of distribution as the area under the impulse response

graphic file with name M7.gif 7

and the mean transit time

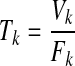graphic file with name M8.gif 8

Footnotes

Frank G. Zöllner and Gerald Weisser contributed equally to this study.

References

  • 1.Thng CH, Koh TS, Collins DJ, Koh DM. Perfusion magnetic resonance imaging of the liver. World J Gastroenterol. 2010;16:1598–1609. doi: 10.3748/wjg.v16.i13.1598. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 2.Scherr MK, Seitz M, Muller-Lisse UG, Ingrisch M, Reiser MF, Muller-Lisse UL. MR-perfusion (MRP) and diffusion-weighted imaging (DWI) in prostate cancer: quantitative and model-based gadobenate dimeglumine MRP parameters in detection of prostate cancer. Eur J Radiol. 2010;76:359–366. doi: 10.1016/j.ejrad.2010.04.023. [DOI] [PubMed] [Google Scholar]
  • 3.Attenberger UI, et al. Comprehensive MR evaluation of renal disease: added clinical value of quantified renal perfusion values over single MR angiography. J Magn Reson Imaging. 2010;31:125–133. doi: 10.1002/jmri.21994. [DOI] [PubMed] [Google Scholar]
  • 4.Bokacheva L, Rusinek H, Zhang JL, Lee VS. Assessment of renal function with dynamic contrast-enhanced MR imaging. Magn Reson Imaging Clin N Am. 2008;16:597–611. doi: 10.1016/j.mric.2008.07.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5.Sourbron S. Compartmental modelling for magnetic resonance renography. Z Med Phys. 2010;20:101–114. doi: 10.1016/j.zemedi.2009.10.010. [DOI] [PubMed] [Google Scholar]
  • 6.Sourbron SP, Buckley DL. Tracer kinetic modelling in MRI: estimating perfusion and capillary permeability. Phys Med Biol. 2012;57:R1–R33. doi: 10.1088/0031-9155/57/2/R1. [DOI] [PubMed] [Google Scholar]
  • 7.Thompson G, Mills SJ, Stivaros SM, Jackson A. Imaging of brain tumors: perfusion/permeability. Neuroimaging Clin N Am. 2010;20:337–353. doi: 10.1016/j.nic.2010.04.008. [DOI] [PubMed] [Google Scholar]
  • 8.Tofts PS, et al. Estimating kinetic parameters from dynamic contrast-enhanced T(1)-weighted MRI of a diffusable tracer: standardized quantities and symbols. J Magn Reson Imaging. 1999;10:223–232. doi: 10.1002/(SICI)1522-2586(199909)10:3<223::AID-JMRI2>3.0.CO;2-S. [DOI] [PubMed] [Google Scholar]
  • 9.Ostergaard L. Principles of cerebral perfusion imaging by bolus tracking. J Magn Reson Imaging. 2005;22:710–717. doi: 10.1002/jmri.20460. [DOI] [PubMed] [Google Scholar]
  • 10.Buckley DL, Shurrab AAE, Cheung CM, Jones AP, Mamtora H, Kalra PA. Measurement of single kidney function using dynamic contrast-enhanced MRI: comparison of two models in human subjects. J Magn Reson Imaging. 2006;24:1117–1123. doi: 10.1002/jmri.20699. [DOI] [PubMed] [Google Scholar]
  • 11.Attenberger U, et al.: Clinical Value of MR-Based Quantification of Renal Perfusion Parameters with a Separable Two-Compartment Model. Proceedings 16th Scientific Meeting, International Society for Magnetic Resonance in Medicine, Toronto:3680, 2008
  • 12.Miller WL, Hodge DO, Tointon SK, Rodeheffer RJ, Nelson SM, Gibbons RJ. Relationship of myocardial perfusion imaging findings to outcome of patients with heart failure and suspected ischemic heart disease. Am Heart J. 2004;147:714–720. doi: 10.1016/j.ahj.2003.10.045. [DOI] [PubMed] [Google Scholar]
  • 13.Futterer JJ, et al. Prostate cancer: local staging at 3-T endorectal MR imaging–early experience. Radiology. 2006;238:184–191. doi: 10.1148/radiol.2381041832. [DOI] [PubMed] [Google Scholar]
  • 14.Futterer JJ, et al. Prostate cancer localization with dynamic contrast-enhanced MR imaging and proton MR spectroscopic imaging. Radiology. 2006;241:449–458. doi: 10.1148/radiol.2412051866. [DOI] [PubMed] [Google Scholar]
  • 15.Litjens GJS, Vos PC, Barentsz JO, Karssemeijer N, Huisman HJ. Automatic computer aided detection of abnormalities in multi-parametric prostate MRI. Orlando: SPIE; 2011. [Google Scholar]
  • 16.Weidner AM, et al. Value of multiparametric prostate MRI of the peripheral zone. Z Med Phys. 2011;21:198–205. doi: 10.1016/j.zemedi.2010.12.004. [DOI] [PubMed] [Google Scholar]
  • 17.Sorensen AG. Perfusion MR imaging: moving forward. Radiology. 2008;249:416–417. doi: 10.1148/radiol.2492081429. [DOI] [PubMed] [Google Scholar]
  • 18.Grenier N, et al. Measurement of glomerular filtration rate with magnetic resonance imaging: principles, limitations, and expectations. Semin Nucl Med. 2008;38:47–55. doi: 10.1053/j.semnuclmed.2007.09.004. [DOI] [PubMed] [Google Scholar]
  • 19.Sourbron S. Technical aspects of MR perfusion. Eur J Radiol. 2010;76:304–313. doi: 10.1016/j.ejrad.2010.02.017. [DOI] [PubMed] [Google Scholar]
  • 20.Cutajar M, Mendichovszky IA, Tofts PS, Gordon I. The importance of AIF ROI selection in DCE-MRI renography: reproducibility and variability of renal perfusion and filtration. Eur J Radiol. 2010;74:e154–e160. doi: 10.1016/j.ejrad.2009.05.041. [DOI] [PubMed] [Google Scholar]
  • 21.Zöllner FG, et al. Assessment of 3D DCE-MRI of the kidneys using non-rigid image registration and segmentation of voxel time courses. Comput Med Imaging Graph. 2009;33:171–181. doi: 10.1016/j.compmedimag.2008.11.004. [DOI] [PubMed] [Google Scholar]
  • 22.Lietzmann F, Zöllner FG, Michaely HJ, Schad LR. Untersuchung von selbstnavigierenden MR-Sequenzen für die Perfusionsbildgebung der Nieren. Z Med Phys. 2010;20:124–133. doi: 10.1016/j.zemedi.2010.02.001. [DOI] [PubMed] [Google Scholar]
  • 23.Kosior JC, Frayne R. PerfTool: a software platform for investigating bolus-tracking perfusion imaging quantification strategies. J Magn Reson Imaging. 2007;25:653–659. doi: 10.1002/jmri.20843. [DOI] [PubMed] [Google Scholar]
  • 24.Sourbron S, Biffar A, Ingrisch M, Fierens Y, Luypaert R. PMI: platform for research in medical imaging. Magn Reson Mater Phy. 2009;22:539. [Google Scholar]
  • 25.Wittsack HJ, Ritzl A, Modder U. User friendly analysis of MR investigations of the cerebral perfusion: Windows(R)-based image processing. Rofo. 2002;174:742–746. doi: 10.1055/s-2002-32216. [DOI] [PubMed] [Google Scholar]
  • 26.Ferl GZ. DATforDCEMRI: an R package for deconvolution analysis and visualization of DCE-MRI data. J Stat Softw. 2011;44:1–18. [Google Scholar]
  • 27.Whitcher B, Schmid VJ. Quantitative analysis of dynamic contrast-enhanced and diffusion-weighted magnetic resonance imaging for oncology in R. J Stat Softw. 2011;44:1–29. [Google Scholar]
  • 28.Puech P, Betrouni N, Makni N, Dewalle AS, Villers A, Lemaitre L. Computer-assisted diagnosis of prostate cancer using DCE-MRI data: design, implementation and preliminary results. Int J Comput Assist Radiol Surg. 2009;4:1–10. doi: 10.1007/s11548-008-0261-2. [DOI] [PubMed] [Google Scholar]
  • 29.Caban JJ, Joshi A, Nagy P. Rapid development of medical imaging tools with open-source libraries. J Digit Imaging. 2007;20(Suppl 1):83–93. doi: 10.1007/s10278-007-9062-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 30.Sourbron S, Dujardin M, Makkat S, Luypaert R. Pixel-by-pixel deconvolution of bolus-tracking data: optimization and implementation. Phys Med Biol. 2007;52:429–447. doi: 10.1088/0031-9155/52/2/009. [DOI] [PubMed] [Google Scholar]
  • 31.Østergaard L, Weisskoff RM, Chesler DA, Gyldensted C, Rosen BR. High resolution measurement of cerebral blood flow using intravascular tracer bolus passages. Part I: mathematical approach and statistical analysis. Magn Reson Med. 1996;36:715–725. doi: 10.1002/mrm.1910360510. [DOI] [PubMed] [Google Scholar]
  • 32.Sourbron S, Luypaert R, Morhard D, Seelos K, Reiser M, Peller M. Deconvolution of bolus-tracking data: a comparison of discretization methods. Phys Med Biol. 2007;52:6761–6778. doi: 10.1088/0031-9155/52/22/014. [DOI] [PubMed] [Google Scholar]
  • 33.Rosset A, Spadola L, Ratib O. OsiriX: an open-source software for navigating in multidimensional DICOM images. J Digit Imaging. 2004;17:205–216. doi: 10.1007/s10278-004-1014-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 34.Jalbert F, Paoli JR. Osirix: free and open-source software for medical imagery. Rev Stomatol Chir. 2008;109:53–55. doi: 10.1016/j.stomax.2007.07.007. [DOI] [PubMed] [Google Scholar]
  • 35.Rosset A, Spadola L, Pysher L, Ratib O. Informatics in radiology (infoRAD)—navigating the fifth dimension: innovative interface for multidimensional multimodality image navigation. Radiographics. 2006;26:299–308. doi: 10.1148/rg.261055066. [DOI] [PubMed] [Google Scholar]
  • 36.OsiriX Plugins. Available at http://www.osirix-viewer.com/Plugins.html. Accessed 24 Jan 2011
  • 37.Ratib O, Rosset A, Heuberger J. Open Source software and social networks: disruptive alternatives for medical imaging. Eur J Radiol. 2011;78:259–265. doi: 10.1016/j.ejrad.2010.05.004. [DOI] [PubMed] [Google Scholar]
  • 38.Vetter S: Optimising an OsiriX Plug-in for Perfusion Analysis of MR Images Applied University Mannheim, Faculty of Computer Science, Bachelor of Science, Bachelor’s Thesis (24.9.2010 2010)
  • 39.Apple Inc.: Introducing Blocks and Grand Central Dispatch, http://developer.apple.com/library/mac/#featuredarticles/BlocksGCD/index.html: Apple Inc., 2010
  • 40.Weidenhagen R, Meirnarakis G, Jauch KW, Becker CR, Kopp R. OsiriX. An open-source solution for planning aorta stent grafts. Gefässchirurgie. 2008;13:278–290. doi: 10.1007/s00772-008-0608-6. [DOI] [Google Scholar]
  • 41.Yamauchi T, et al. Efficacy and reliability of highly functional open source DICOM software (OsiriX) in spine surgery. J Clin Neurosci. 2010;17:756–759. doi: 10.1016/j.jocn.2009.09.037. [DOI] [PubMed] [Google Scholar]
  • 42.Calamante F, Gadian DG, Connelly A. Quantification of perfusion using bolus tracking magnetic resonance imaging in stroke: assumptions, limitations, and potential implications for clinical use. Stroke. 2002;33:1146–1151. doi: 10.1161/01.STR.0000014208.05597.33. [DOI] [PubMed] [Google Scholar]
  • 43.Jerosch-Herold M, Seethamraju RT, Swingen CM, Wilke NM, Stillman AE. Analysis of myocardial perfusion MRI. J Magn Reson Imaging. 2004;19:758–770. doi: 10.1002/jmri.20065. [DOI] [PubMed] [Google Scholar]
  • 44.Ali B, Hsiao E, Di Carli MF. Combined anatomic and perfusion imaging of the heart. Curr Cardiol Rep. 2010;12:90–97. doi: 10.1007/s11886-009-0081-1. [DOI] [PubMed] [Google Scholar]
  • 45.Ohno Y, et al. Primary pulmonary hypertension: 3D dynamic perfusion MRI for quantitative analysis of regional pulmonary perfusion. AJR Am J Roentgenol. 2007;188:48–56. doi: 10.2214/AJR.05.0135. [DOI] [PubMed] [Google Scholar]
  • 46.Zöllner FG, Zahn K, Schaible T, Schoenberg SO, Schad LR, Neff KW: Quantitative pulmonary perfusion imaging at 3.0 T of 2-year-old children after congenital diaphragmatic hernia repair: initial results. Eur Radiol, 2012. doi:10.1007/s00330-012-2528-9 [DOI] [PubMed]
  • 47.Makkat S, Luypaert R, Sourbron S, Stadnik T, De Mey J. Quantification of perfusion and permeability in breast tumors with a deconvolution-based analysis of second-bolus T1-DCE data. J Magn Reson Imaging. 2007;25:1159–1167. doi: 10.1002/jmri.20937. [DOI] [PubMed] [Google Scholar]
  • 48.Aumann S, et al. Quantification of renal perfusion using an intravascular contrast agent (part 1): results in a canine model. Magn Reson Med. 2003;49:276–287. doi: 10.1002/mrm.10380. [DOI] [PubMed] [Google Scholar]
  • 49.Eastwood JD, et al. CT perfusion scanning with deconvolution analysis: pilot study in patients with acute middle cerebral artery stroke. Radiology. 2002;222:227–236. doi: 10.1148/radiol.2221010471. [DOI] [PubMed] [Google Scholar]
  • 50.Bisdas S, et al. A comparison of tumour perfusion assessed by deconvolution-based analysis of dynamic contrast-enhanced CT and MR imaging in patients with squamous cell carcinoma of the upper aerodigestive tract. Eur Radiol. 2008;18:843–850. doi: 10.1007/s00330-007-0827-3. [DOI] [PubMed] [Google Scholar]
  • 51.Sourbron S, Ingrisch M, Siefert A, Reiser M, Herrmann K. Quantification of cerebral blood flow, cerebral blood volume, and blood–brain-barrier leakage with DCE-MRI. Magn Reson Med. 2009;62:205–217. doi: 10.1002/mrm.22005. [DOI] [PubMed] [Google Scholar]
  • 52.Padhani AR. Dynamic contrast-enhanced MRI in clinical oncology: current status and future directions. J Magn Reson Imaging. 2002;16:407–422. doi: 10.1002/jmri.10176. [DOI] [PubMed] [Google Scholar]
  • 53.Lietzmann F, Zöllner FG, Attenberger UI, Haneder S, Michaely HJ, Schad LR. DCE-MRI of the human kidney using BLADE: a feasibility study in healthy volunteers. J Magn Reson Imaging. 2011;35:868–874. doi: 10.1002/jmri.23509. [DOI] [PubMed] [Google Scholar]
  • 54.Hansen PC. Rank-Deficient and Discrete Ill-Posed Problems: Numerical Aspects of Linear Inversion. Philadelphia: SIAM; 1998. [Google Scholar]

Articles from Journal of Digital Imaging are provided here courtesy of Springer

RESOURCES