An Effective Dental Shape Extraction Algorithm Using Contour Information and Matching by Mahalanobis Distance

Abstract

Human identification using dental radiographs is important in biometrics. Dental radiographs are mainly helpful for individual and mass disaster identification. In the 2004 tsunami, dental records were proven as the primary identifier of victims. So, this work aims to produce an automatic person identification system with shape extraction and matching techniques. For shape extraction, the available information is edge details, structural content, salient points derived from contours and surfaces, and statistical moments. Out of all these features, tooth contour information is a suitable choice here because it can provide better matching. This proposed method consists of four stages. The first step is preprocessing. The second one involves integral intensity projection for segmenting upper jaw, lower jaw, and individual tooth separately. Using connected component labeling, shape extraction was done in the third stage. The outputs obtained from the previous stage for some misaligned images are not satisfactory. So, it is improved by fast connected component labeling. The fourth stage is calculating Mahalanobis distance measure as a means of matching dental records. The matching distance observed for this method is comparatively better when it is compared with the semi-automatic contour extraction method which is our earlier work.

Introduction

Forensic odontology is the application of dentistry in legal proceedings deriving from any evidence that pertains to teeth. Teeth are the hardest tissues in the human body and they play key roles in forensic medicine. It can withstand decomposition, heat degradation, water immersion, and desiccation. Automating the postmortem identification of deceased individuals based on dental characteristics is receiving increased attention especially with the large number of victims encountered in mass disasters. An automated dental identification system compares the teeth present in multiple digitized dental records in order to access their similarity. A survey report states that during the 2004 tsunami in Thailand, around 75 % of person identification was done by dental images only. So, it proves that dental radiographs can be useful for individual identification and also mass disaster identification. There are several approaches for dental radiograph segmentation. Iterative thresholding technique is used to segment both pulp and teeth [1]. Anil K. Jain and Hong Chen dedicated a concept of semi-automatic contour extraction method for shape extraction and pattern matching [2]. The shortcomings in their approach are if the image is too blurred, their algorithm is not applicable and slight angle deviation in the ante-mortem and postmortem images may not be handled with this approach. Morphological corner detection algorithm and Gaussian mask are used to extract the shape of tooth contour in [3]. But Gaussian method does not show satisfying results for all the images. Said et al. [4] offered a mathematical morphology approach, which used a series of morphology filtering operations to improve the segmentation, and then analyzed the connected components to obtain the desired region of interest. Paper [5] explains three different fusion approaches for the matching algorithms to get better matching between ante- and post-mortem images. Human identification using the shape and appearance of the tooth is explained in [6]. Multiresolution wavelet-Fourier descriptors are used to classify the teeth sequence in multislice computed tomography images as proposed in [7]. Morphological filters like top hat and bottom filters are used for tooth segmentation [8]. Based on analyses of tooth anatomy and tooth growth direction, a dental radiograph segmentation algorithm was developed in [9]. A concept of finding missing tooth using classification and numbering was done in [10]. Dental segmentation using tooth anatomy was explained in [11], but it is not the suitable one for individual matching. Automatic tooth segmentation using active contours without edges using directional snake was explained in [12]. In this approach, the tooth shape obtained using directional snake does not suit some of the images. Person matching using dental works was experimented in [13]. But extracting dental work alone may not be sufficient for better matching. In addition with the tooth contour, dental work may also be considered.

Proposed Methodology

The pipeline of this method is shown in Fig. 1. This paper work is organized as four sections. The first section is the preprocessing to produce uniform illumination in the dental input images. In the second section, radiograph segmentation is done with the integral intensity projection logic. The third section is contour extraction using connected component labeling and improved by fast connected component labeling. Finding Mahalanobis distance measure is the fourth section

Fig. 1.

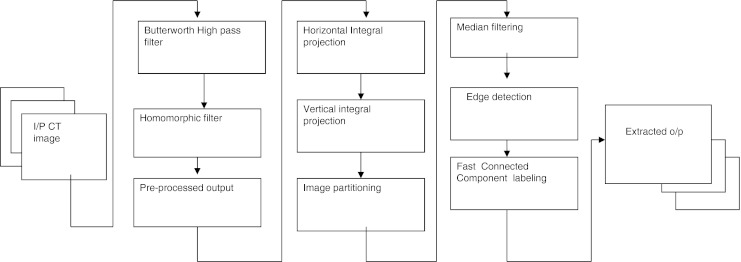
Pipeline of the proposed methodology

Preprocessing

Image preprocessing is needed as a first section here because dental radiographs will always suffer from noise, low contrast, and uneven exposure. To overcome this problem, a section of frequency domain filters, i.e., Butterworth filter, followed by homomorphic filters, is used. This procedure is almost uniformly good for most of the images. Homomorphic filters are widely used in image processing for compensating the effect of non-uniform illumination in an image. The preprocessing stage consists of two steps. In the first step, the input image is subjected to Butterworth high-pass filter. In the second step, it is processed with homomorphic filter to get uniform illumination of the image.

1. Butterworth Filter

Butterworth high-pass filter is used to provide uniform sensitivity to all the frequencies. The transfer function of Butterworth filter is defined as:

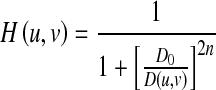1

Where n is the order of the filter. Here, order 2 is considered for better performance.

1. Homomorphic Filter

In homomorphic filters, an image function I(x, y) may be characterized by the multiplicative combination of an illumination component i(x, y) and a reflectance component r(x, y).

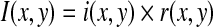2

Since teeth, pulp, and gums in a dental radiograph should each have similar reflectivity [1], a homomorphic filtering method to suppress the uneven illumination effect while preserving the intensity discrepancies among all the components in the radiograph is used here. For a given dental radiograph image I(x, y), by taking first the Fourier transform of the logarithm of image function the sum of its low-frequency illumination component and high-frequency reflectance component are obtained as:

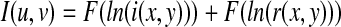3

By applying a Gaussian low-pass filter, its detailed components are removed and illumination distribution is retained.

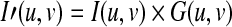4

Where,

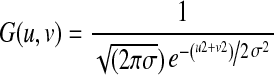5

The inverse transform I′ help us to obtain the spatial domain equivalent for the filtered homomorphic view of illumination

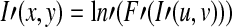6

Integral Intensity Projection

Since the intensity of teeth differ from the gap between the upper and the lower jaw, the separation between each tooth can be carried out by obtaining the integral intensity projection in two ways, horizontally and also vertically. Summing of intensities along the horizontal direction will provide the gap valley; whereas, summing of intensities along the vertical direction will segment the individual tooth separately [1]. Consider proj(y) is the accumulative intensity of pixels in each row of the image function f(x, y), (0 ≤ × ≤ w − 1) and (0 ≤ × ≤ h − 1), then the series {proj(y₀), proj(y₁),……..proj(y_H − 1)} forms a graph of integral intensity. Mathematically, the projection function is defined as:

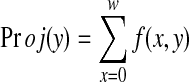7

Since the teeth usually have a higher gray level intensity than the jaws and other tissues in the radiographs due to their higher tissue density, the gap between the upper and lower teeth will form a valley in the y-axis projection histogram, which is called as the gap valley [2]. After finding the gap valley, the vertical line is drawn by obtaining integral intensity. Horizontal integral projection followed by vertical integral projection is applied to separate each individual tooth. The horizontal integral projection separates the upper jaw from the lower jaw, while the vertical integral projection separates each individual tooth.

Shape Extraction

Here, shape extraction is done in two ways. One way is using connected component labeling and then it is further improved by fast connected component algorithm.

1. Connected Component Labeling

The partitioned image from the previous stage is subjected through median filter to remove some unwanted information even after preprocessing and then edge map is created using canny operator [6]. Then, it is convolved with the following proposed mask to trace the shape of the desired dental pattern. The mask elements are selected so as to get the desired connected components.

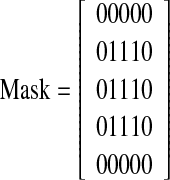8

Connected component labeling is grouping of pixels with the same class label into regions. Here, 8-connectivity is used to trace the boundary of the teeth.

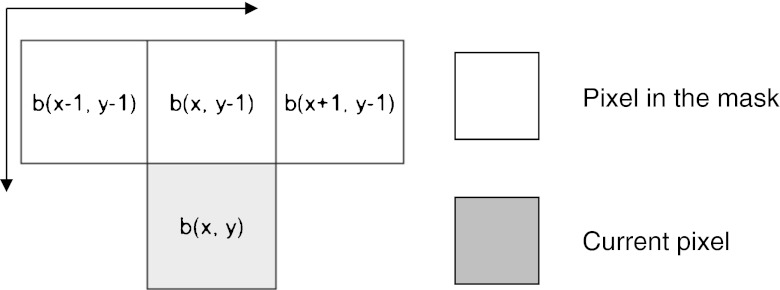
1. Fast Connected Component Algorithm

The conventional two-scan connected component algorithms complete labeling in three phases: a first scanning phase, an analysis phase, and a relabeling phase. In the first phase, a provisional label is assigned to each object pixel and their label equivalences are stored. In analysis phase, label equivalences are solved. In the third phase, final label to each object pixel is assigned. Whereas, this algorithm resolves the label equivalences immediately whenever they are found during the first scan, all label equivalences are resolved at the completion of the first scan; thus, the second scan can start immediately [14]. In other words, resolving label equivalences is combined into the first scanning phase. The computation time of this algorithm is computationally efficient than the conventional connected component labeling. The pixels are processed in the raster scan direction. Each row is considered as a contiguous foreground pixel block and contiguous background pixel blocks. The background pixel block is processed first and the first pixel in the foreground pixel block is scanned. Since this pixel is followed by a background pixel, then it is labeled as a background pixel. Then the other pixels in the foreground pixel block are scanned next. Since these pixels are followed by the foreground pixel, it is labeled as a foreground pixel. So during the first scan, all the foreground pixels are classified into two classes. Class I consists of pixels which follows foreground pixels and class II consists of pixels which follows background pixels. Since the decision is made with the pixel b(x − 1, y), this pixel can be left out from the mask. Thus, the mask for 8-connectivity is reduced to three pixels only, without the b(x − 1, y) pixel. Since in the first scan itself, labeling and solving label equivalences are done, this algorithm seems to be a better choice here. The mask chosen is shown in Fig. 2.

Fig. 2.

Mask used in the fast connected component labeling

Mahalanobis Distance

The distance measure for finding the similarity is of critical importance here. A well-known distance measure which takes into account the covariance matrix is the Mahalanobis distance. It can also be defined as the dissimilarity measure between two random vectors. When comparing with Euclidean distance, this distance measure takes into account the correlations of the dataset and is scale invariant. The Mahalanobis distance is given by

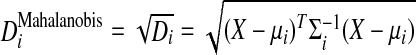9

Where 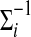represents the inverse of the covariance matrix class {I}. The Mahalanobis distance is therefore a weighted Euclidean distance where the weight is determined by the range of variability of the sample points, expressed by the covariance matrix.

Results and Discussion

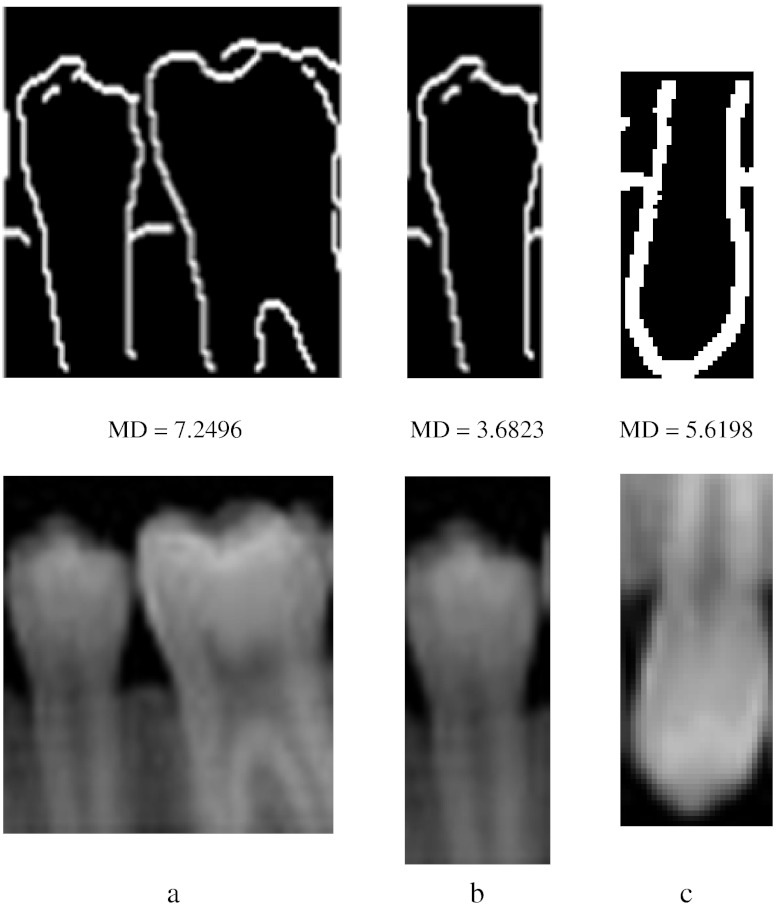
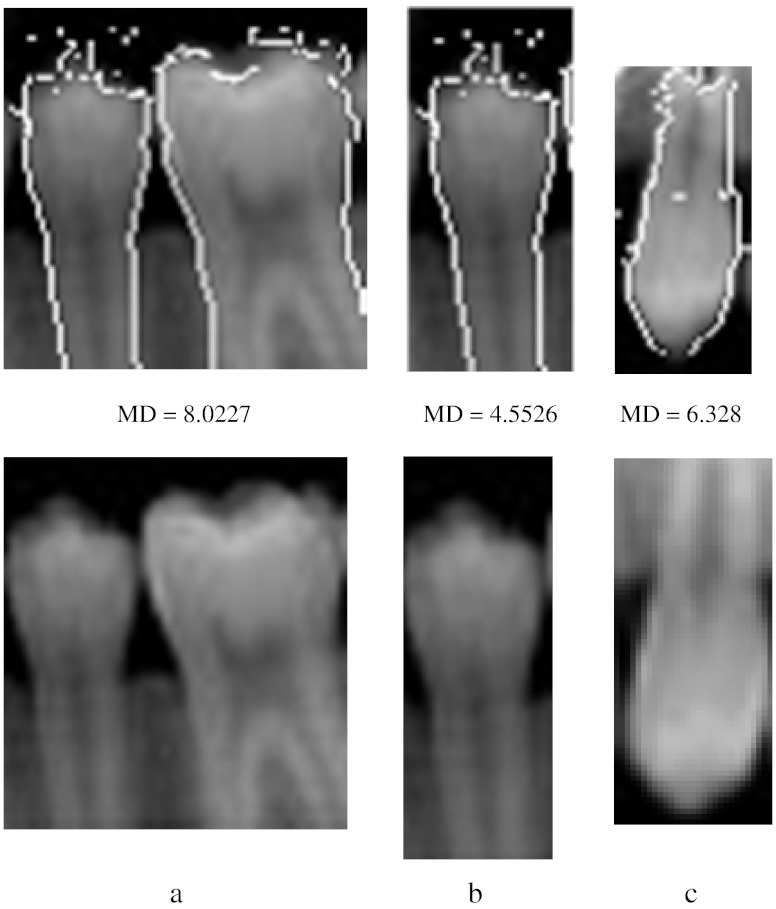
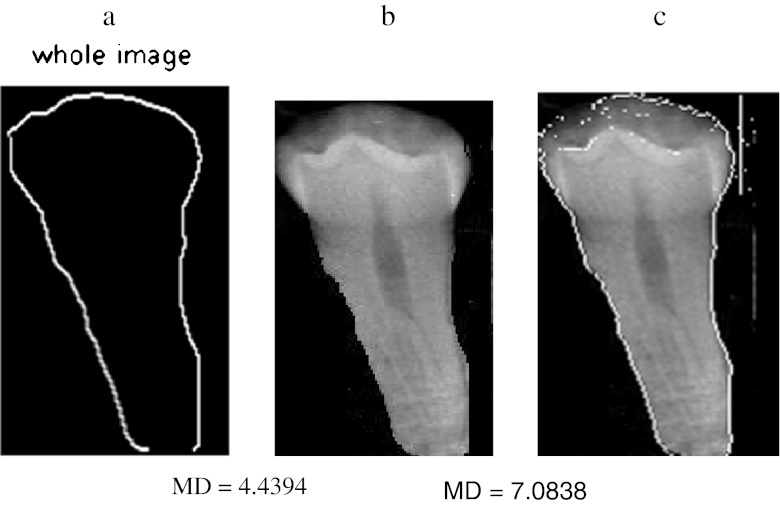
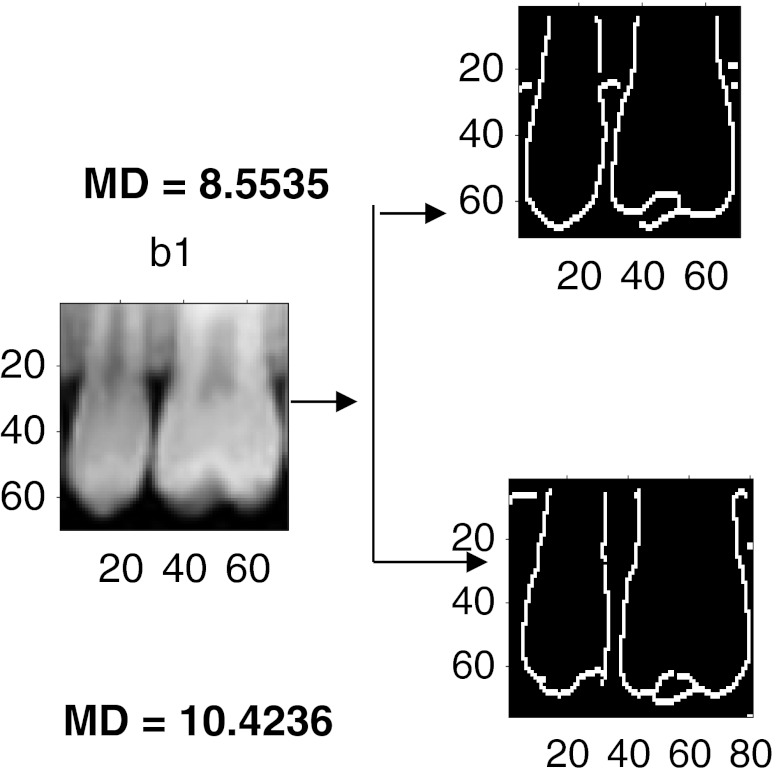
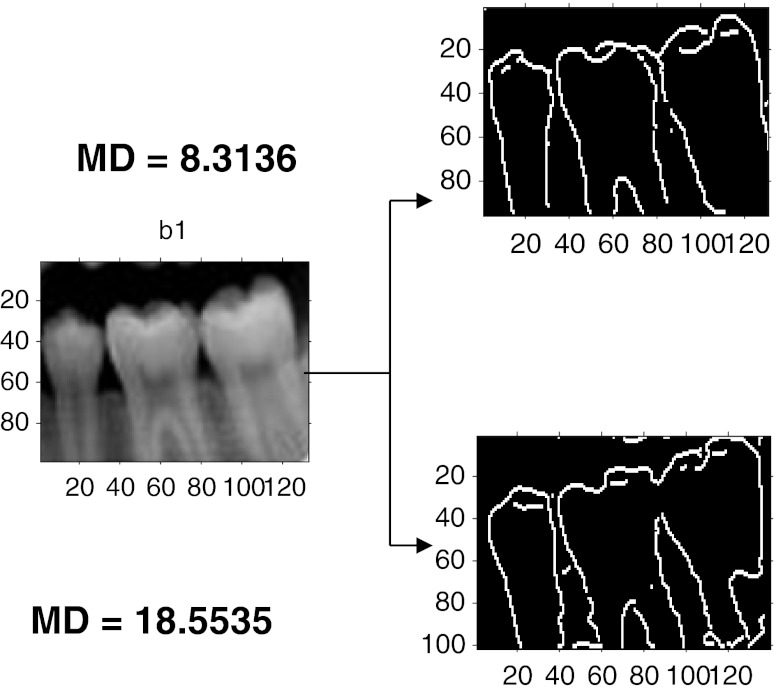
The algorithm is developed in Matlab-R10b and it is tested with the database of approximately 50 images. The sample input images taken for analysis are dent 19 of size (159, 160), dent 24 of size (74, 98), occ9 of size (135, 166), occ10 of size (546, 409), tooth 4 of size (171, 98), and occ1 of size (109, 83). The preprocessing algorithm of our proposed method produces better results for almost all the dental images including some partially occluded images. The following are the results shown for the preprocessing step. Figure 3a shows some of the sample input images. Figure 3b shows that the outputs obtained preserve all the edges of the image and it seems better than the morphological operations that were shown in our earlier work. Moreover, it is justified by the similarity measures like average difference, structural content, normalized absolute error, normalized cross-correlation, etc. [15]. The test images taken were tabulated in Table 1. In the table, the first column before homomorphic filtering refers to the output obtained with morphological operations. The second column refers to the output with homomorphic filter. From the table, it is clear that the similarity measures like average difference and normalized cross-correlation seems to be better even though the error is marginally higher. The similarity measures are obtained for several images and similar concept was observed for all. So, it proves that homomorphic filter is chosen as a preferable choice for preprocessing here. To partition the given input image, initially observe the horizontal projection to obtain the gap valley. It is observed that the integral projection of actual input image seemed to have a little difference from the preprocessed image. Figure 4 shows the horizontal and vertical integral intensity projection of the pre processed image “a” of Fig. 3b. The colored dots on the top peak and the bottom peak values refer to the maximum and minimum intensity valley helps to easily trace the gap between the teeth. It is observed by the peak value detection logic. The upper jaw and the lower jaw can be separated or cropped by knowing the intensity projections. Similarly, the horizontal and vertical projections of the upper jaw are obtained. Using the integral intensity projections, the upper jaw is partitioned as shown in Fig. 5a and b. Similarly, the lower jaw alone can be cropped and then partitioned which may produce better results than comparing as a whole image for matching dental radiographs for person identification application. For the partitioned image, an edge map is created using canny operator and it is median filtered, then convolved with the proposed mask to get the thick boundary as shown in Fig. 6a and b. The sharpness of the boundary can be adjusted by the proper selection of mask elements. Using connected component labeling, the pulp region which may also be picked up as an edge in Fig. 6b can be removed as shown here in Fig. 7a–c. The algorithm is tested for several other images also. It holds good for most of the images. Another sample image dent 11 of size (98, 74) was taken and is shown in Fig. 8a–c are the Butterworth and homomorphic filtered outputs. The horizontal and vertical integral projections of the preprocessed outputs are obtained. Thus, the image is partitioned. The corresponding outputs of connected component labeling are shown in Fig. 9a–d. The algorithm produces satisfied results for certain childhood age images like Fig. 10a–d. The tooth contours of some images like Figs. 11a and 12a are not extracted by the connected component labeling. So, using fast connected component labeling approach was tried and the results obtained are shown in Figs. 11b, c and 12b, c. However, it fails to suit to certain severely occluded images as in Fig. 13. The results obtained using this technique is compared with the semi-automatic contour extraction output. For person identification while matching [8, 9] post mortem and ante-mortem images, better results may be expected by comparing a single tooth or a jaw instead of matching the whole image. The results shown in Fig. 14a–c are obtained for the input image 1 using this method and it is compared with their corresponding input image. The Mahalanobis distance is noted for each case. Figure 15a–c are the results of semi-automatic contour extraction method which was shown in our previous work [3]. For evaluation purpose, Mahalanobis distance is obtained for both these outputs by matching it with the original image. Figure 16b is another sample image tooth 4 of size (171, 98). Figure 16c is the contour extracted by semi-automatic extraction method. Figure 16a is the result obtained by connected component analysis. The results obtained are evaluated with the percentage of similarity measure and listed in Table 2. In the table, MD refers to Mahalanobis distance and it is clear that better matching (i.e.,) good percentage of similarity is achieved for the proposed method only rather than the semi-automatic method. The distance measure can further be improved by matching original image with the affine-transformed connected component output. Thus, person identification can be done by matching the whole image or a part of the image with the database image. A perfect matching can be achieved for the one with lesser matching distance. The matching results obtained for two sample cases are shown in Figs. 17 and 18. In Fig. 17, the upper one with matching distance of 8.5535 is the genuine image rather than the bottom one. In the same way, the upper image with Mahalanobis distance of 8.3136 is the genuine image in Fig. 18. While matching the connected component equivalent of the dent 18 image with itself, the matching distance is observed to be zero gives perfect matching. Whereas the same with dent 25 image gives the matching distance of 2.315 is an impostor.

Fig. 3.

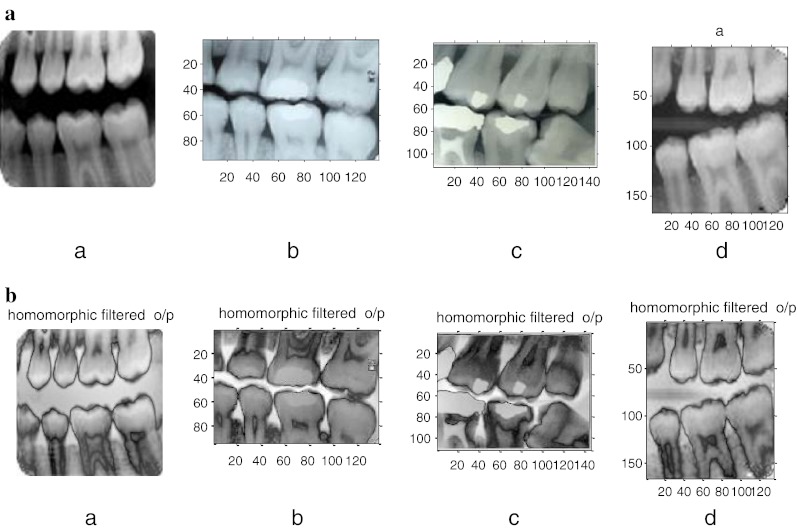
a Sample images taken. b Corresponding preprocessed outputs for a

Table 1.

Quality factor table

Quality factor table for image 1 (dent 17)
Quality factor	Before homomorphic filtering	After homomorphic filtering
Average difference	−0.0021	−170.8499
Structural content	0.7726	0.1983
Normalized absolute error	0.3122	1.3080
Normalized cross-correlation	1.0969	2.2131

Fig. 4.

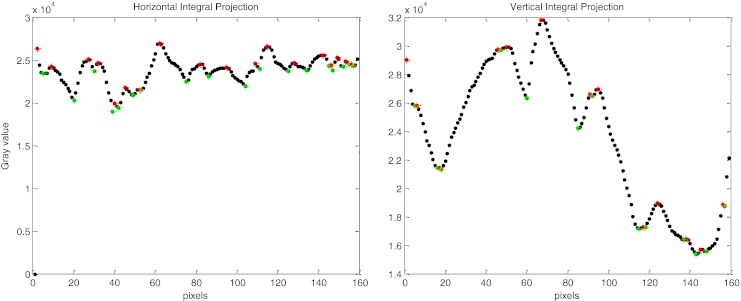
Horizontal and vertical integral intensity projection of the preprocessed image 1 (i.e.) a in Fig. 3b

Fig. 5.

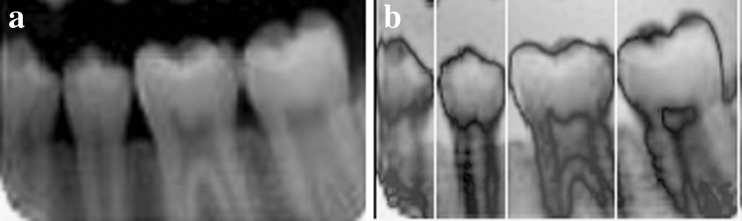
a, b Partitioned lower jaw and its segmented output

Fig. 6.

a, b Edge map and corresponding connected component output

Fig. 7.

Connected component output after convolving with the proposed mask. a Segmented upper jaw, b segmented lower jaw, c segmented single lower tooth

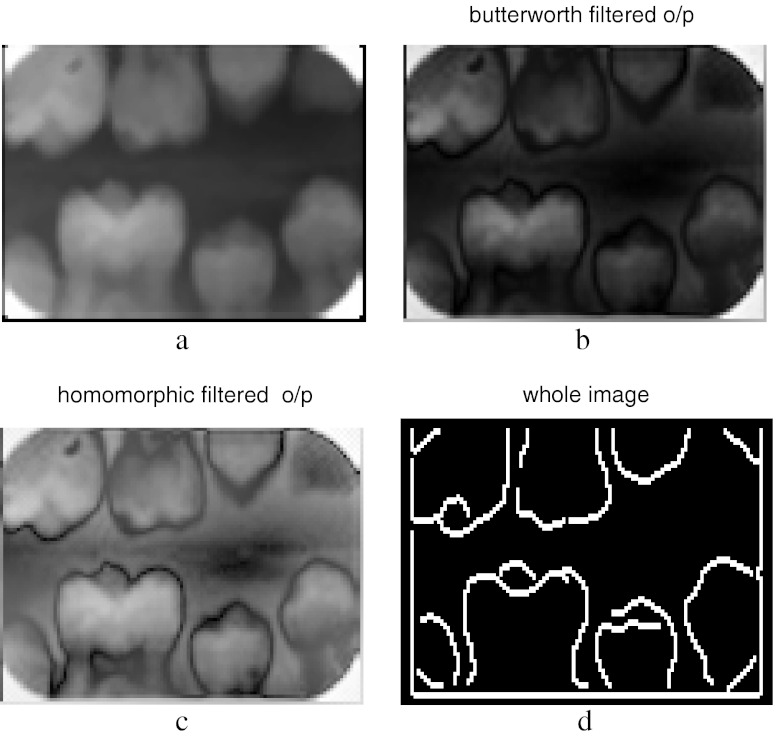
Fig. 8.

Input image 2 and its preprocessed outputs. a Original image, b Butterworth filtered, c homomorphic filtered

Fig. 9.

a Edge map, b segmented upper jaw, c segmented lower jaw, d single lower tooth

Fig. 10.

Results obtained for the childhood age image. a Input image 3, b Butterworth filtered, c homomorphic filtered, d connected component output

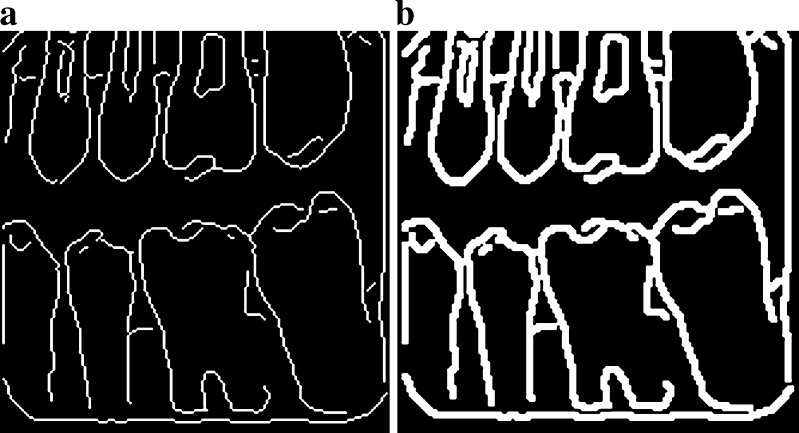
Fig. 11.

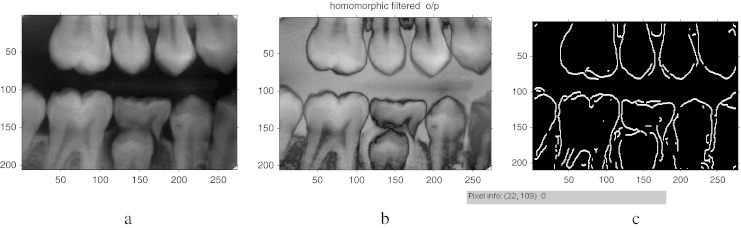
a Input image 4, b homomorphic filtered output, c fast connected component output

Fig. 12.

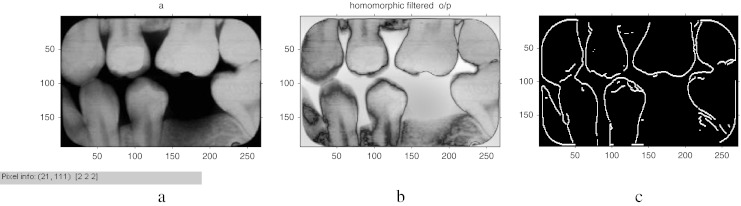
a Input image 5, b homomorphic filtered output, c fast connected component output

Fig. 13.

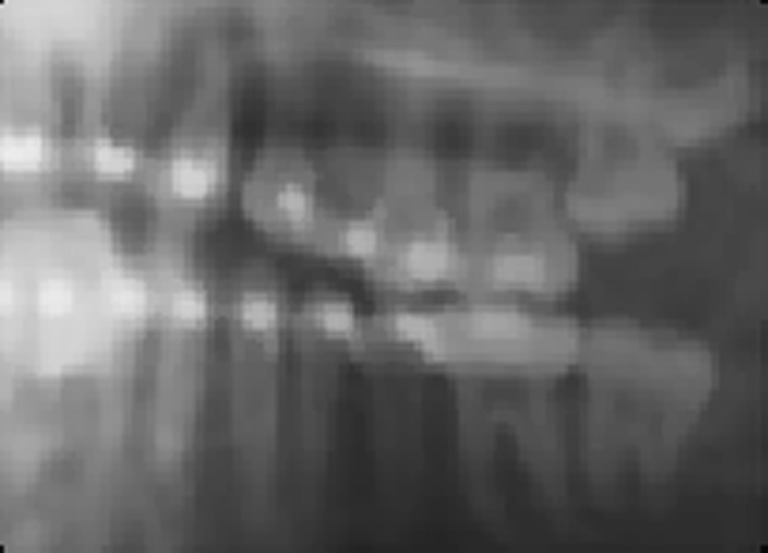
Failure case

Fig. 14.

Output of connected component labeling method with Mahalanobis distance for the sample images; a tooth 8 image, b tooth 10 image, c tooth 21 image

Fig. 15.

Output of semi-automatic contour method with Mahalanobis distance for the sample images, a tooth 8 image, b tooth 10 image, c tooth 21 image

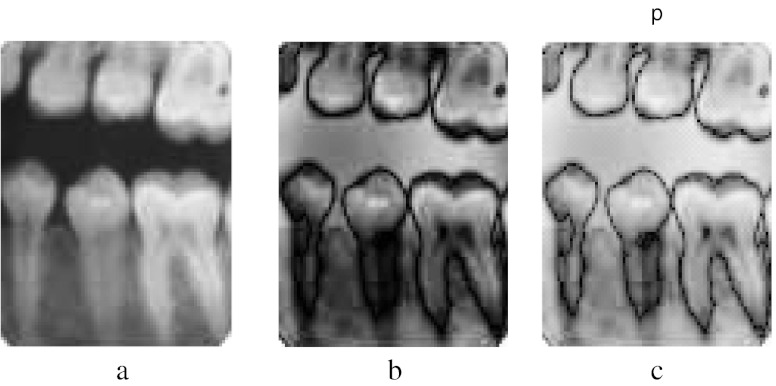
Fig. 16.

Mahalanobis distance measure for sample image tooth 4. a Connected component output, b original image, c output of semi-automatic method

Table 2.

Comparative table of Mahalanobis distance

Sample images	Connected component analysis output			Semi automatic contour extraction output
	MD	% of similarity	CT (s)	MD	% of similarity	CT (s)
Tooth 4	4.43	95.56	11.95	7.08	92.92	12.44
Tooth 8	7.24	92.75	11.95	8.02	91.98	12.44
Tooth 10	3.68	96.38	11.95	4.55	95.45	12.44
Tooth 21	5.61	94.38	11.95	6.32	93.67	12.44

Fig. 17.

Matching distance calculation for a sample image dent 18 with dent 25 and dent 18

Fig. 18.

Matching distance calculation for a sample image dent 2 with dent 2 and dent 36

Conclusion

In this paper, a simple tooth shape extraction algorithm and a matching technique for person identification is presented. This will be helpful for forensic dentistry to identify the missing persons in some critical mass disaster situations. After analysis, it is observed that this algorithm proved to be automatic, less complex, and produces satisfying results. This work involves four sections. It includes preprocessing, integral intensity projection, segmentation by connected component labeling, improved by fast connected component labeling, and finally matching dental records by Mahalanobis distance calculation. The proposed pre-processing technique is uniformly holds good for almost all the images. From the observed Table 1, it is clear that the details in the image are maintained better after doing homomorphic filter rather than with morphological filter operation. Connected component labeling technique provides satisfied results for most of the images as shown, but it fails for some of the misaligned dental patterns. Hence, these results are improved by fast connected component labeling technique and the results obtained are satisfied. Finally, for matching purpose, Mahalanobis distance measure is used. From Table 2, it is observed that good percentage of similarity is obtained by shape extraction using connected component labeling only. This algorithm fails to hold good for the dental pattern which is not perfectly aligned with the vertical strips (i.e.) if it is occluded. So this can be enhanced further by projecting curved lines by using angle and distance approach.