Abstract
Background
Most phase II clinical trials utilize a single primary endpoint to determine the promise of a regimen for future study. However, many disorders manifest themselves in complex ways. For example, migraine headaches can cause pain, auras, photophobia, and emesis. Investigators may believe a drug is effective at reducing migraine pain and the severity of emesis during an attack. Nevertheless, they could still be interested in proceeding with development of the drug if it is effective against only one of these symptoms. Such a study would be a candidate for a clinical trial with co-primary endpoints.
Purpose
The purpose of the article is to provide a method for designing a 2-stage clinical trial with dichotomous co-primary endpoints of efficacy that has the ability to detect activity on either response measure with high probability when the drug is active on one or both measures, while at the same time rejecting the drug with high probability when there is little activity on both dimensions. The design enables early closure for futility and is flexible with regard to attained accrual.
Methods
The design is proposed in the context of cancer clinical trials where tumor response is used to assess a drug's ability to kill tumor cells and progression-free survival (PFS) status after a certain period is used to evaluate the drug's ability to stabilize tumor growth. Both endpoints are assumed to be distributed as binomial random variables, and uninteresting probabilities of success are determined from historical controls. Given the necessity of accrual flexibility, exhaustive searching algorithms to find optimum designs do not seem feasible at this time. Instead, critical values are determined for realized sample sizes using specific procedures. Then accrual windows are found to achieve a design's desired level of significance, probability of early termination (PET), and power.
Results
The design is illustrated with a clinical trial that examined bevacizumab in patients with recurrent endometrial cancer. This study was negative by tumor response but positive by 6-month PFS. The procedure was compared to modified procedures in the literature, indicating that the method is competitive.
Limitations
Although the procedure allows investigators to construct designs with desired levels of significance and power, the PET under the null is smaller than single endpoint studies.
Conclusions
The impact of adding an additional endpoint on the sample size is often minimal, but the study gains sensitivity to activity on another dimension of treatment response. The operating characteristics are fairly robust to the level of association between the two endpoints. Software is available for implementing the methods.
Keywords: Binomial distribution, multinomial distribution, correlated primary endpoints, cytotoxic, cytostatic, two-stage design
1. Introduction
Phase II studies evolved over time to simultaneously manage several goals of a clinical trial while maintaining their modest sample size. Initially, they were simple, single stage studies, designed to distinguish between the null and alternative hypotheses (e.g. H0 : πr ≤ πr0 versus H1 : πr ≥ πr1 where πr is the true probability of response) with α level of significance and power (1 – β). However, it is considered unethical to treat a full sample of patients with an inactive agent in settings involving life threatening diseases such as cancer. Instead, it is more desirable to examine the drug's possible futility at an earlier time in the trial. Gehan 1 proposed a method to meet this goal in 1961, which rejected the drug as being ineffective if there were no observed responses in the first sample. Otherwise, the trial proceeded to a second stage for additional evaluation. A general design that allows multistage testing for arbitrary values of πr0 and πr1 was provided by Fleming in 1982.2 Simon then proposed a 2-stage design that had either optimal or minimax properties. 3 His solution was extended with flexible designs that allowed for deviations from the targeted sample sizes, which clarified the conduct of many nationally run phase II studies. 4, 5
In addition to incorporating flexible, interim futility analyses, several authors proposed utilizing more than one primary endpoint. Treatment toxicities are of particular interest to investigators. Bryant and Day 6 as well as Conaway and Petroni 7 explicitly use the number of patients who have severe adverse events in their decision rules for recommending further study.
Some authors refined response to therapy into three ordered classes such as not effective, mildly effective, and very effective. In the arena of oncology, patient responses can be classified as progressive disease, stable disease, and tumor response so that therapies capable of reducing the proportion with progressive disease or increasing the proportion with tumor responses are of interest. 8 Other authors differentiate complete tumor response from partial responses and study the impact of employing both of these positive outcomes to trial characteristics. 9-11
Another approach examined in the literature is the utilization of two (or more) fundamentally different measures of treatment efficacy. 12, 13 Examples of co-primary efficacy endpoints include the severity of angina pectoris and shortness of breath for studies involving coronary artery disease, severity of pain and the degree of photophobia in migraine headache studies, and auditory hallucinations and delusions in studies of schizophrenia. Unlike the gradation of a univariate response into separate categories, these designs consider the multivariate nature of response to treatment which is complicated by variable associations and study objectives. The current paper provides investigators with a method for obtaining a flexible, 2-stage trial design with an interim futility rule where interest is focused on detecting activity on either (or both) of two primary response variables.
2 Methodology
For ease of exposition, our methodology will be developed in the context of phase II cancer clinical trials. In this setting, many drugs have been evaluated with tumor response, which has a specific definition that loosely translates into a reduction in the tumor size (or reduction in overall volume of disease).14 The probability of response will be designated with πr. Another variable of interest in phase II oncology is the probability a patient survives without experiencing a progression of disease for a specified period of time (say 6 months or 2 years, depending on the aggressiveness of the disease). We will use 6 months as a matter of convenience and denote this binomial variable as “6-month progression-free survival (PFS)” or “at risk for PFS at 6 months.” The probability of this event will be designated with πs. Tumor response is a variable that is capable of detecting agents that are effective at selectively killing tumor cells (cytotoxic) whereas 6-month PFS is capable of detecting agents that can stabilize disease but are not necessarily effective at cell kill (cytostatic).
The null hypothesis is formulated as follows: H0 : πr ≤ πr0, and πs ≤ πs0, where πr0 and πs0 are specified values (obtained from historical data) that are believed to be uninteresting or comparable to the current standard of care. The alternative hypothesis is the complement of this null parameter space. Commonly the area of the parameter space where high statistical power is desired can be written as follows: H1 : πr ≥ πr1 = πr0 + Δr or πs ≥ πs1 = πs0 + Δs where Δr and Δs are the (minimal) clinically significant improvements in the proportion responding and with 6-month PFS, respectively.
2.1 Relationships between Critical Values and the Design's Operating Characteristics
Before a testing procedure can be constructed and characterized, consideration should be given to the joint distribution of the number of patients who respond or have 6-month PFS. The parameters of this distribution are described by Table 1.
Table 1.
| PFS>6Mo. | ||||
|---|---|---|---|---|
| Yes | No | |||
| Response | Yes | π 11 | π 12 | π r |
| No | π 21 | π 22 | π 2+ | |
| π s | π +2 | |||
Similarly, the number of patients who have the qualities of interest in this particular trial are described by Table 2 where n(k) is the sample size for stage k = 1,2 of the trial, Xr(k) is the number of patients who have an objective response in stage k, and Xs(k) is the number of patients at-risk for PFS at 6 months. It can be shown that the joint distribution of Xij(k), where i = 1,2 and j = 1,2, is multinomial with the corresponding parameters listed in Table 1 under the restrictions π22 = 1 – π11 – π12 – π21 and X22(k) = n(k) – X11(k) – X12(k) – X21(k). The probability mass function of this distribution can be written as follows:
| (1) |
Table 2.
| PFS>6Mo. | ||||
|---|---|---|---|---|
| Yes | No | |||
| Response | Yes | X11(k) | X12(k) | Xr(k) |
| No | X21(k) | X22(k) | X2+(k) | |
| Xs(k) | X+2(k) | n(k) | ||
The null hypothesis will be accepted at Stage 1 if Xr(1) ≤ Cr(1) and Xs(1) ≤ Cs(1) or at Stage 2 if Xr ≤ Cr and Xs ≤ Cs where Cr(1) and Cs(1) are the Stage 1 critical values for the number of patients who have a response and the number at-risk for PFS at 6 months, respectively, Xr = Xr(1) + Xr(2), Xs = Xs(1) + Xs(2), and Cr and Cs are the critical values at the end of Stage 2. Note that the following relationships hold in general:
| (2) |
| (3) |
| (4) |
To determine the probability of accepting the null hypothesis after a particular stage using (1), it is helpful to define a probability mass function and a cumulative distribution function in terms of n(k), Xs(k), and Xr(k) :
| (5) |
| (6) |
The probability of early termination (PET), which is the probability of accepting the null hypothesis after the first stage can be calculated simply with the cumulative distribution function and using the first stage parameters, i.e.,
| (7) |
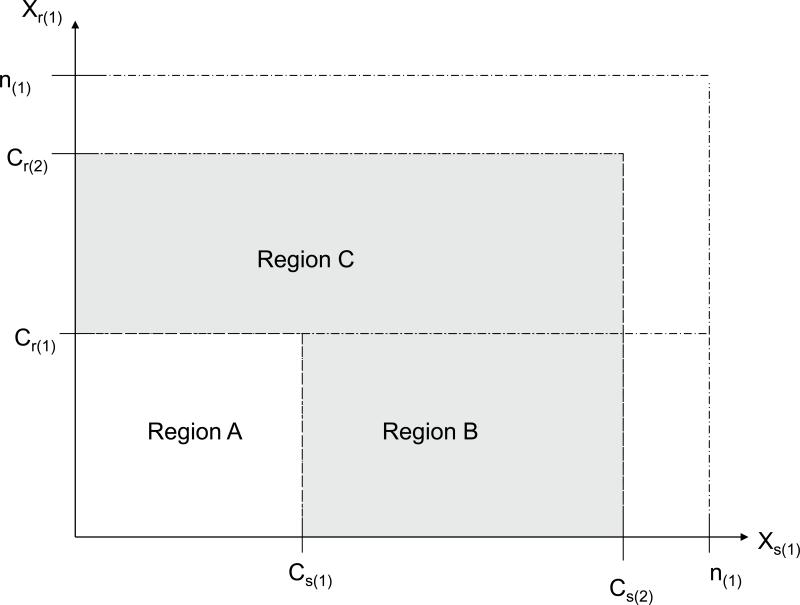
where n(1) is the first stage sample size. In order for the null hypothesis to be accepted after the second stage, it is required that the outcome after the first stage not lie within the acceptance region (i.e. Xr(1) ≤ Cr(1) and Xs(1) ≤ Cs(1)) but the outcome in the second stage lie within its acceptance region (i.e. Xr ≤ Cr and Xs ≤ Cs). In order for this condition to be true, it is required that the following condition hold: Xr(1) > Cr(1) or Xs(1) > Cs(1), and simultaneously that Xr(1) ≤ Cr and Xs(1) ≤ Cs for the first stage outcome. Using Figure 1, this region corresponds to the union of Region B and Region C (Note that it is possible for Cs and Cr to be greater than n(1)).
Figure 1.
The sample space for Xr(1) and Xs(1), divided into several important regions. Region A is the set of outcomes that lead the trial into early termination. Regions B and C are areas that allow the trial to proceed to Stage 2 but do not necessary lead to rejection of the null hypothesis. The complement of would ultimately lead to rejection of the null hypothesis (this is expected to be rare and the set may be empty).
To calculate the probability that the null hypothesis is accepted in the second stage, it is important to note that Xr – Xr(1) and Xs – Xs(1) are marginal totals equal to Xr(2) and Xs(2) whose cells have a multinomial distribution with the parameters listed in Table 1 with a sample size of n(2). Xs ≤ Cs if and only if Xs – Xs(1) ≤ Cs – Xs(1) and Xr ≤ Cr if and only if Xr – Xr(1) ≤ Cr – Xr(1). It follows that the probability of accepting the null hypothesis in Stage 2 is calculated as:
| (8) |
where is Region B union Region C and n = n(1) + n(2). The total probability of accepting the null hypothesis is the sum of the probabilities of accepting the null hypothesis in each stage. That is, P(Accept H0) = PET + P (Accept H0 in Stage 2), and the power of the study is simply the probability of rejecting H0 :
| (9) |
2.2 The Search for Designs with Desirable Operating Characteristics
There are a myriad of critical values and sample sizes to choose from. Even with the help of a computer, the task can be overwhelming and time consuming. To help narrow the range of possibilities, it is helpful to focus on essential qualities. Important features include a high probability of early termination (PET) under the null, low power under the null, and high power under the alternative. As stated previously, this design is motivated by an interest in detecting agents that are active either cytostatically or cytotoxically. More generally, this design is useful for trials where the investigators want to detect true activity on either endpoint with high probability, and activity on either endpoint is sufficient reason to conduct more study. Therefore, useful designs are ones that have a low probability of accepting the null hypothesis when either πr = πr0 + Δr or πs = πs0 + Δs. There are three design parameters that are believed to be of particular interest:
where α is the probability of a type I error. βr is the probability of a type II error when the agent is clinically active by cytotoxic mechanisms but is not capable of stabilizing the disease for long periods, and βs is the probability of a type II error when the regimen is clinically active through cytostatic mechanisms (produces significant stabilization of disease) but does not significantly reduce tumor burden. Generally speaking, all of these quantities are ideally kept small to varying degrees, based on the needs of the study. For a particular set of critical boundaries, Cs(1), Cr(1), Cs, and Cr, the following quantities can be found:
where “PET” stands for the probability of early termination and “TPRT” stands for the total probability of rejecting the treatment in a manner similar to Chen and Ng.4
There are many ways to obtain sample sizes and critical values that achieve a study with the desired levels of α, βr, and βs.
2.3 Optimal and Minimax Designs
Exhaustive searching algorithms can be developed first to find the set of designs that meet the specified requirements of the investigator such as α ≤ 0.10, βr ≤ 0.10, and βs ≤ 0.10. To achieve this goal, all designs with 15 ≤ n ≤ 100 (for practical reasons) and, say, 5 ≤ n(1) ≤ n – 1, can be examined with particular attention paid to PETHo, TPRTHo, TPRTHr, and TPRTHs. To find the optimal design among all designs meeting the investigator's specifications, the design associated with the minimal value of E[Nt] under the null would be selected where:
| (10) |
where Nt is the total sample size, which is a random variable equal to n(1) with probability PETH0 and n = n(1) + n(2) otherwise. The minimax design would be a design (with specifications) associated with the smallest n, called min {n}. If several designs existed with n = min {n}, then the one that minimizes equation (10) would be utilized.
2.4 Flexible Optimal and Flexible Minimax Designs
Flexible optimal designs, developed in a manner similar to Chen and Ng 4, would provide designs where accrual windows are allowed such as nL ≤ N(1) ≤ nU and NL ≤ N ≤ NU where N(1) and N are the first stage and total sample sizes, respectively. The size of these windows are usually 8 patients wide (e.g. decision rules could be provided when 21 ≤ N(1) 28 and 50 ≤ N ≤ 57). N(1) and N are random variables with realized values equal to n(1) and n , respectively. Assuming a uniform accrual distribution (e.g. P(N(1) = n(1)) = 1/8 for nL ≤ n(1) ≤ nU and P(N(1) = n(1), N = n) = 1/64), these designs can be characterized by mean values of α, βr, and βs over all possible accrual combinations (typically 8×8=64 possibilities). Alternatively, the design can be characterized by the more conservative values of max {α}, max {βr}, and max {βs}. Then a searching algorithm can be developed in a manner similar to the “rigid” designs as discussed above. The practical application of these ideas is challenging since the total number of designs is very large, making the feasibility of an exhaustive searching algorithm questionable.
2.5 A Green-Dalberg Searching Algorithm
Green and Dalberg 5 proposed a simple, flexible design for clinical trials that utilize a single, dichotomous primary endpoint. Their design tests a one-sided alternative hypothesis against the null hypothesis (stating the drug is inactive) at the 2% level of significance after the first stage. If they are able to reject the alternative hypothesis in favor of the null, they declare the drug to be unworthy at the interim analysis. Otherwise, they continue to the second stage and test the study agent's activity with classical techniques.
We propose a similar method for the interim futility rule for the bivariate design, testing the alternative hypotheses at levels of significance equal to one half the desired values of βr and βs. More specifically, we propose using the critical values Cr(1) and Cs(1), that maximize PETHo from among all designs that limit PETHr ≤ βr / 2 and PETHs ≤ βs / 2 for a particular, realized first stage sample size n(1). For purposes of efficiency, these values are calculated under the assumption that Xr(1) is independent of Xs(1).
Interim Decision Rule
If either Xs(1) > Cs(1) or Xr(1) > Cr(1) after the first stage and medical judgment indicates, then the study will open to a second stage of accrual to further evaluate the activity of the drug.
If the design proceeds to a second stage, an eventual sample size of n patients will be realized. We propose several methods (with available software) for determining the critical values at the final stage, Cr and Cs. The first method utilized in clinical trials (called the minimum C method) found Cr and Cs such that the following cost function was minimized:
| (11) |
These decision rules tend to yield satisfactory designs if α ≈ βr ≈ βs is desired. Of course, there are often other constellations of the design parameters of interest to investigators. For example, some researchers prefer designs with α ≤ 0.05 with βr ≈ βs ≈ 0.20. To help achieve designs with characteristics such as these, an “alpha restricted method” is offered. This method searches for a Cr and Cs that minimizes the quantity, max {TPRTHr, TPRTHs}, among all designs where TPRTHo ≥ 1 – α, assuming that Xr(i) is independent of Xs(i), i = 1,2.
Second Stage Decision Rule
If either Xs > Cs or Xr > Cr after the second stage (and clinical judgment indicates), then the regimen will be deemed clinically interesting and worthy of further investigation (in a phase III study).
These decision rules may not yield a design with the desired operating characteristics for the particular sample sizes obtained in the clinical trial, n(1) n, but a design that follows these procedures will yield unambiguous decision criteria when n(1) and n deviate from the targeted values, say and n*. Additionally, if n(1) and n are close to and n*, then the realized operating characteristics should not be substantially different from the planned study characteristics.
2.6 Searching for Flexible Designs that Obtain the Planned α, βr, and βs
The first step in obtaining a flexible design is the tabulation of Cr(1), Cs(1), Cr, and Cs along with the design's operating characteristics for all values of n such that 25 ≤ n ≤ 100 (or some other suitable range) and 15 ≤ n(1) ≤ n – 10 (the thinking behind using n – 10 as an upper bound for n(1) lies in a desire to accrue as least 10 patients in the second stage).
The next step is to characterize the flexible designs by the minimum values of N(1) and N, (i.e. by nL and NL) where nL ≤ N(1) ≤ nU, NL ≤ N ≤ NU, nU = nL + 7, and NU = NL +7. The characterization can be done with mean values of PETHo, TPRTHo, TPRTHr, and TPRTHs. Alternatively, they can be characterized by the min {PETHo}, min{TPRTHo}, max {TPRTHr}, and max {TPRTHs} over all 64 possible accrual combinations.
A common design criterion is to require the average PETHo or the min {PETHo} to be at least some minimal value such as 50% or 60%, so the subsequent step is to find the smallest nL where this criterion is satisfied. Given a fixed first stage sample size, the final step is to find the smallest value of NL so that the average (or maximum values) of TPRTHr and TPRTHs are ≤ βr and βs, respectively.
Once the design is found under the assumption of independence, it is characterized under different degrees of association. Investigation has shown that PETHo tends to be moderately dependent on the level of association between the two endpoints whereas TPRTHr and TPRTHs tend to be fairly robust against this nuisance parameter. Also, it can be shown that both PETHo and TPRTHo are higher for positive association of the two endpoints (the anticipated relationship) than for independence. This is an important characteristic since it assures that assuming independence of the two endpoints is conservative in the sense that this assumption yields an upper bound on type 1 error and a lower bound on PETHo assuming that violations of this assumption are always in the direction of positive association of the two endpoints.
3. Illustration of Study Design for GOG 0229E
3.1 Study Design
The first study that utilized the proposed methods was a protocol called GOG 0229E, which investigated the effects of bevacizumab on patients with recurrent or persistent endometrial cancer. Like many cancer patients in the phase II setting, these patients are characterized by a disease that is often rapidly progressing and refractory to additional chemotherapy. The values for design parameters of GOG 0229E (πr0 and πs0) were obtained from the results of a series of prior protocols in GOG 0129 and GOG 0229. See Table 1 in the published results of this study by Aghajanian et al. for further details.15 The patients enrolled into GOG 0229E were expected to behave similarly to those eligible in the historical studies if the agent was not clinically active.
Based on the historical data, the null hypothesis was formulated as follows: H0 : πr ≤ 0.10 and πs ≤ 0.15. With Δr = 0.20 and Δs = 0.20 considered clinically significant, the alternative region of interest is specified with H1 : πr ≥ 0.30 or πs ≥ 0.35. A design was found using the “Minimum C method” along with using average values of PETHo, TPRTHo, TPRTHr and TPRTHs. The actual accrual window for GOG 0229E was only 5 patients wide (in contrast the currently used designs that are 8 patients wide). A similar design can be obtained with the available software by specifying a minimal PETHo = 0.45, α ≤ 0.10, and max {βr, πs} ≤ 0.08 (i.e. power at least 92%). The targeted accrual for the first stage was set to 19 eligible and evaluable patients. The cumulative targeted accrual for the second stage was set to 42 patients. Critical values for each stage are provided in the Table 3:
Table 3.
| Stage 1 | Stage 2 (Cr, Cs) n | |||||
|---|---|---|---|---|---|---|
| n (1) | (Cr(1), Cs(1)) | 40 | 41 | 42 | 43 | 44 |
| 17 | (2,2) | (7,9) | (7,9) | (7,10) | (7,10) | (8,10) |
| 18 | (2,2) | (7,9) | (7,9) | (7,10) | (8,10) | (8,10) |
| 19 | (2,3) | (7,9) | (7,9) | (7,10) | (8,10) | (8,10) |
| 20 | (2,3) | (7,9) | (7,9) | (7,10) | (8,10) | (8,10) |
| 21 | (2,3) | (7,9) | (7,9) | (7,10) | (8,10) | (8,10) |
The operating characteristics of these designs are provided below using the usual definition of power. The reason for requiring the minimum (average) power to be at least 92% was from a desire to keep the minimum power over all possible accrual combinations to about 90%. Additionally, the power of the study drops (modestly) when the association between the two endpoints increases. To assess the operating characteristics when the two primary endpoints are not independent, the probability calculations were done with the assumption that the joint probability was π11 = 0.90·min {πr, πs}, which usually carries a fairly high degree of association (e.g. odds ratios ranging from 22.1 to 126 at the various hypotheses). As can be seen from this example in Table 4, the power of the study is not highly dependent on the level of association between response and PFS at 6 months.
Table 4.
| Value of π11 | π r | π s | Power (%) | PET(%) |
|---|---|---|---|---|
| πr · πs | 0.10 | 0.15 | 9.0 | 41.3 |
| 0.30 | 0.15 | 93.4 | 2.8 | |
| 0.10 | 0.35 | 92.2 | 2.7 | |
| 0.30 | 0.35 | 99.5 | 0.2 | |
| 0.90min{πr ,πs} | 0.10 | 0.15 | 7.2 | 52.5 |
| 0.30 | 0.15 | 91.8 | 4.7 | |
| 0.10 | 0.35 | 91.4 | 3.7 | |
| 0.30 | 0.35 | 96.1 | 1.8 |
The average PETHo is 41.3% under independence and 52.5% under high association. The design had PETHr and PETHs equal to 2.8 and 2.7% respectively under independence, and it had PETHr and PETHs equal to 4.7 and 3.7% under high association.
3.2 Study Results
Results of the study are published by Aghajanian et al. and reproduced here for illustrative purposes.15, 16 The study had an unusually high accrual rate for this population with many institutions enrolling patients in the last week before study closure. The first stage of the study enrolled 23 patients with 2 being excluded for not meeting eligibility criteria leaving 21 eligible and evaluable patients. Of these, one patient responded and 5 were at-risk for PFS at 6 months. Based on Table 3 (Cr(1) = 2 and Cs(1) = 3) with evidence of good tolerability, a decision was made to open the study to the second stage.
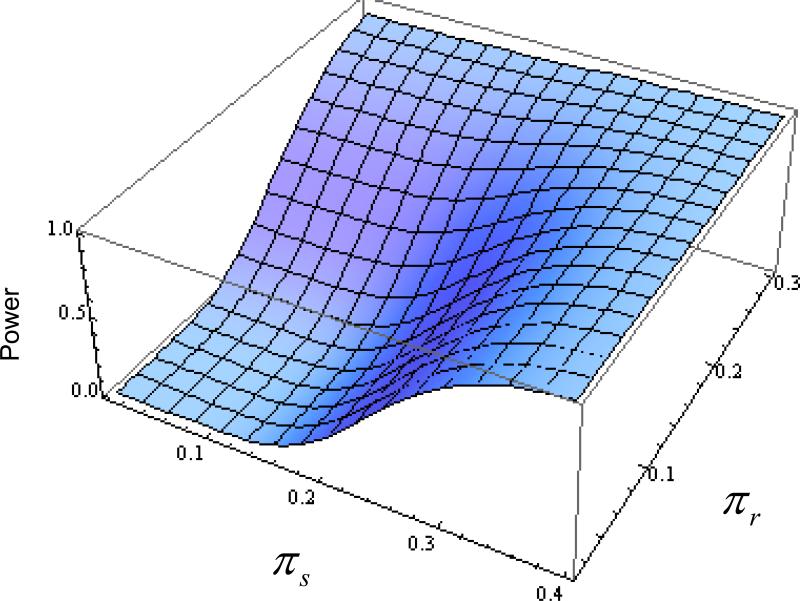
Stage 2 accrued 33 additional patients with 2 exclusions based on eligibility criteria, leaving a cumulative accrual of 52 patients. This sample size fell outside the targeted window, so a specific rejection boundary had to be calculated for this particular accrual. Using the methodology listed above with the first stage accrual, the second stage critical boundary was easily adjusted to reflect the larger cohort (Cr = 9 and Cs = 12). The larger sample size provided more information to reduce the error probabilities (e.g. α = 0.066, βr = 0.039, and βs = 0.058 under independence, and α = 0.053, βr = 0.047, and βs = 0.066 under high association). Figure 2 provides a power surface for the realized sample size. Note that the power of the test is small (i.e. ≤ 0.10) over the entire region of the null hypothesis but becomes large (i.e. power is at least 90%) as either πr → 0.30 or πs → 0.35.
Figure 2.
Power surface of the realized sample size for GOG 0229E, which had sample sizes of 21 and 31 patients in Stage 1 and Stage 2, respectively. The calculated power was done under the assumption of independence. Utilizing the interim decision rules and cost function to determine the rejection boundaries, the size of the test is 6.6% and power approximately 95% under the specified alternative hypotheses. The power of the procedure is 85% when the response rate is 25%.
The observed number of patients with responses or who were at-risk for PFS at 6 months was 7 (13.5%) and 21 (40.4%), respectively. Since Xs = 21 > 12 = Cs, the agent was deemed active and warrants further investigation.15, 16 The regimen's response rate was close to the null value of 10% and was insufficient (on its own merits) to open the study to the second stage or declare it worthy of further investigation.
4 Comparisons with Other Procedures
4.1 Alternative Procedures
To compare the methods presented in this paper to simple modifications of existing procedures, an adjusted Simon's procedure was examined. Simon's procedure can be adjusted for a bivariate design by providing the algorithm ½ the intended probability of a type I error (alpha). For example, if the desired overall probability of a type I error in a bivariate design is 10%, then the user would enter 0.05 for alpha into the program. This method approximately limits the overall study's statistical size of the bivariate procedure to approximately alpha. It should be noted, however, that the study's size is not guaranteed to be strictly less than alpha as suggested by a Bonferroni correction since an interim analysis using two variables for proceeding onto Stage 2 can substantially increase the probability of proceeding to Stage 2. In spite of this problem, the rule works fairly well in practice. The intended probability of a type II error (beta) was not adjusted since the investigator is expected to be interested in detecting activity on either scale with the desired level of power (1-beta). When the null probabilities for both scales are equal with the same levels of clinical significance (i.e. Δr = Δs), Simon's modified procedure can be used to obtain the required sample sizes (Stage 1 and 2) and the rejection boundaries for each measure of interest. It is important to remember that typical output characterizing Simon's method cannot be used to characterize a bivariate design. For example, the PET for Simon's design is listed as 71.7% when πr = 0.05, α = 0.05, β = 0.10, and Δr = 0.15. Yet, under independence, the PET is reduced to 0.7172 = 0.514 (see Table 5 on the first row). Instead, programs utilizing the joint distribution are needed to calculate the operating characteristics.
Table 5.
Operating Characteristics for Three Methods: Simon's Adjusted Design (or a Modified Simon-Schultz Procedure), A Flexible Bivariate-Binomial Method Evaluated at Simon's Sample Sizes, and an Optimal Bivariate-Binomial Method.
| Method | πr0 (%) | πs0 (%) | n 1 | n | PET (%) | E[Nt | H0] | Size (%) | Power Hr (%) | Power Hs (%) |
|---|---|---|---|---|---|---|---|---|---|
| Simona | 5 | 5 | 21 | 41 | 51 | 30.7 | 9.3 | 91.4 | 91.4 |
| Flx-Biv | 51 | 30.7 | 9.3 | 91.4 | 91.4 | ||||
| Opt-Biv | 21 | 40 | 51 | 30.2 | 8.6 | 90.6 | 90.6 | ||
| Simona | 10 | 10 | 21 | 66 | 42 | 47.1 | 10.4 | 92.5 | 92.5 |
| Flx-Biv | 42 | 47.1 | 7.9 | 92.4 | 89.8 | ||||
| Opt-Biv | 27 | 57 | 52 | 41.5 | 9.5 | 90.7 | 90.7 | ||
| Simona | 20 | 20 | 37 | 83 | 47 | 61.4 | 9.9 | 91.5 | 91.5 |
| Flx-Biv | 47 | 61.4 | 9.9 | 91.5 | 91.5 | ||||
| Opt-Biv | 37 | 78 | 47 | 58.7 | 9.2 | 90.0 | 90.0 | ||
| Simona | 30 | 30 | 39 | 100 | 38 | 76.7 | 9.6 | 91.9 | 91.9 |
| Flx-Biv | 38 | 76.7 | 9.6 | 91.9 | 91.9 | ||||
| Opt-Biv | 49 | 91 | 52 | 69.4 | 9.4 | 90.0 | 90.0 | ||
| Simona | 70 | 70 | 25 | 79 | 43 | 55.5 | 10.3 | 92.5 | 92.5 |
| Flx-Biv | 43 | 55.5 | 8.3 | 92.3 | 89.9 | ||||
| Opt-Biv | 34 | 68 | 54 | 49.8 | 9.8 | 90.6 | 90.6 | ||
| Simona | 80 | 80 | 19 | 42 | 58 | 28.6 | 9.7 | 91.6 | 91.6 |
| Flx-Biv | 42 | 32.4 | 7.2 | 85.2 | 92.2 | ||||
| Opt-Biv | 18 | 43 | 53 | 29.7 | 8.8 | 91.7 | 91.7 | ||
| Simonbc | 5 | 10 | 21 | 66 | 22 | 56.1 | 10.0 | 98.2 | 94.3 |
| Flx-Biv | 26 | 54.2 | 9.9 | 96.8 | 95.3 | ||||
| Opt-Biv | 28 | 46 | 58 | 35.5 | 9.9 | 90.8 | 90.1 | ||
| Simonb | 10 | 15 | 30 | 82 | 13 | 75.2 | 8.7 | 96.9 | 95.0 |
| Flx-Biv | 46 | 58.1 | 9.5 | 93.0 | 93.6 | ||||
| Opt-Biv | 37 | 61 | 58 | 47.2 | 9.3 | 90.6 | 90.3 | ||
| Simonb | 10 | 25 | 37 | 99 | 7 | 94.6 | 9.5 | 98.8 | 94.9 |
| Flx-Biv | 48 | 69.4 | 9.3 | 96.3 | 93.1 | ||||
| Opt-Biv | 38 | 74 | 54 | 54.5 | 9.5 | 90.2 | 90.4 |
Note that Δr = Δs = 0.15, α = β = 0.10
Procedure utilized the modified Simon procedure as defined above.
Procedure utilized the modified Simon-Schultz method.
The Simon-Schultz method recommended always proceeding to the second stage. In this case, we required at least 1 response before proceeding to the second stage.
For cases where the null probabilities are not the same or the interval for clinical significance is different (i.e. Δr ≠ Δs), then a two-step procedure using univariate methods can be used. For example Simon's procedure was used to examine the sample size requirements on both scales, and the scale requiring the larger total sample size was used to determine the study's interim and final sample size as well as the rejection boundaries for this more demanding parameter (in our examples this was usually πs). However, it was not appropriate to use the same rejection boundaries for both measures of efficacy. In this case, another procedure by Schultz was used to find the rejection boundaries for the other scale (e.g. response) conditioned on the interim and final sample sizes. 17 Again, a value of ½ the intended alpha was provided to the algorithm without modification to beta. This procedure is referred to as the modified Simon-Schultz method.
Simon's optimal procedure determined the sample size in two of the cases examined per parameter setting. Since the procedures proposed in this manuscript are flexible with regard to study accrual, the rejection boundaries for this method (labeled “Flx-Biv”) were characterized at these accrual combinations. Five features were inspected under the assumption of independent clinical outcomes: PET, the expected sample size under the null hypothesis (E[Nt | H0]), the realized size of the test, and the realized statistical power under two alternative hypotheses (Hr and Hs).
Finally, a so-called “optimal” procedure was examined (labeled “Opt-Biv”) which utilized the procedures of this manuscript to find the smallest E[Nt | H0] subject to the desired statistical size and power. These designs were characterized by the same 5 features as described above.
4.2 Results
For the designs where Δr = Δs = 0.15, α = 0.10, Simon's adjusted procedure was quite competitive with the Flx-Biv procedure evaluated at Simon's sample sizes (when πr0 = πs0). Often both procedures yielded identical rejection boundaries. For the case where πr0 = πs0 = 10%, the size of Simon's procedure was slightly greater than 10%, so its power was slightly greater than the Flexible Procedure in this case (especially under Hs). All of the procedures controlled the probability of a type I error fairly closely. Simon's procedure slightly exceeded the targeted power of 90% in many cases, which may be considered an attractive feature since power drops slightly when response is correlated with the PFS outcome. The modified Simon-Schultz method performed poorly on several points. It had a low PET and power higher than the desired level (90%). This made the expected sample size under the null hypothesis considerably larger than the Bivariate procedures.
When examining the expected sample size under the null, the Optimal procedure seemed to perform the best. The only exception was when πr0 = 80% and πs0 = 80%, but the expected sample sizes were quite close in this case.
For the designs where Δr = Δs = 0.20, α = 0.05, and β = 0.20, Table 6 shows that Simon's procedure often equaled or outperformed the Flexible method by the expected sample sizes. Some of these comparisons may be considered “unfair” since the actual size of Simon's procedure occasionally was greater than 5%. Although Simon often beat the Flexible method by PET and E[Nt | H0], the Flexible method often had superior statistical size and power. For the case where πr0 = πs0 = 70%, the two procedures had identical operating characteristics. The Simon-Schultz method suffered from the same deficiencies as above, leading to designs with poor operating characteristics.
Table 6.
Operating Characteristics for Three Methods: Simon's Adjusted Design (or a Modified Simon-Schultz Procedure), A Flexible Bivariate-Binomial Method Evaluated at Simon's Sample Sizes, and an Optimal Bivariate-Binomial Method.
| Method | πr0 (%) | πs0 (%) | n 1 | n | PET (%) | E[Nt | H0] | Size (%) | Power Hr (%) | Power Hs (%) |
|---|---|---|---|---|---|---|---|---|---|
| Simona | 5 | 5 | 8 | 23 | 44 | 16.4 | 4.6 | 83.1 | 83.1 |
| Flx-Biv | 44 | 16.4 | 4.6 | 83.1 | 83.1 | ||||
| Opt-Biv | 7 | 23 | 48 | 15.2 | 4.4 | 81.1 | 81.1 | ||
| Simona | 10 | 10 | 10 | 38 | 54 | 22.8 | 5.0 | 84.0 | 84.0 |
| Flx-Biv | 26 | 30.8 | 3.9 | 84.3 | 88.2 | ||||
| Opt-Biv | 11 | 30 | 49 | 20.8 | 4.6 | 80.6 | 80.6 | ||
| Simona | 20 | 20 | 13 | 55 | 56 | 31.4 | 5.5 | 83.7 | 83.7 |
| Flx-Biv | 37 | 39.3 | 4.7 | 87.0 | 86.9 | ||||
| Opt-Biv | 17 | 45 | 57 | 28.9 | 4.2 | 81.0 | 81.0 | ||
| Simona | 30 | 30 | 17 | 65 | 60 | 36.2 | 4.7 | 83.2 | 83.2 |
| Flx-Biv | 46 | 42.8 | 4.1 | 86.2 | 85.5 | ||||
| Opt-Biv | 18 | 50 | 52 | 33.3 | 4.3 | 80.0 | 80.0 | ||
| Simona | 50 | 50 | 18 | 57 | 58 | 34.5 | 5.0 | 82.9 | 82.9 |
| Flx-Biv | 45 | 39.4 | 4.2 | 82.3 | 84.3 | ||||
| Opt-Biv | 20 | 51 | 56 | 33.6 | 4.2 | 80.2 | 80.2 | ||
| Simona | 70 | 70 | 12 | 35 | 55 | 22.2 | 4.6 | 82.9 | 82.9 |
| Flx-Biv | 55 | 22.2 | 4.6 | 82.9 | 82.9 | ||||
| Opt-Biv | 12 | 35 | 55 | 22.2 | 4.6 | 82.9 | 82.9 | ||
| Simonbc | 10 | 15 | 12 | 45 | 21 | 38.1 | 3.9 | 90.4 | 88.0 |
| Flx-Biv | 48 | 29.0 | 3.5 | 86.7 | 83.9 | ||||
| Opt-Biv | 17 | 35 | 58 | 24.6 | 4.4 | 84.7 | 80.8 | ||
| Simonb | 40 | 50 | 16 | 61 | 8 | 57.6 | 5.1 | 89.9 | 88.2 |
| Flx-Biv | 43 | 41.7 | 4.5 | 84.8 | 85.2 | ||||
| Opt-Biv | 20 | 54 | 57 | 34.8 | 4.2 | 81.2 | 80.1 | ||
| Simonb | 50 | 65 | 18 | 57 | 21 | 48.9 | 4.5 | 87.3 | 92.5 |
| Flx-Biv | 49 | 37.9 | 4.1 | 83.8 | 90.7 | ||||
| Opt-Biv | 19 | 47 | 57 | 30.9 | 4.7 | 83.0 | 80.0 |
Note that Δr = Δs = 0.20, α = 0.05 β = 0.02
Procedure utilized the modified Simon procedure as defined above.
Procedure utilized the modified Simon-Schultz method.
The Simon-Schultz method recommended always proceeding to the second stage. In this case, we required at least 1 response before proceeding to the second stage.
The Optimal procedure was superior to the other procedures (by expected sample sizes and having design parameters closer to the desired levels) in all of the settings examined except for the case where πr0 = πs0 = 0.70; in this case, all of the designs had identical operating characteristics.
5 Discussion
5.1 General Points
The proposed method discussed here has been utilized in a number of phase II trials by the Gynecologic Oncology Group (GOG). During the development of GOG 0229E, there were discussions about the cytotoxic attributes of bevacizumab and suggestions of replacing 6-month PFS with response. This seemed appropriate since a sufficient number of responses were seen in a phase II ovarian cancer study to justify further study.18 However, some investigators were hesitant about its degree of cytotoxic activity (with a 21% observed response rate) and the sensitivity of the trial to detect activity through other mechanisms (e.g. 40% of patients were 6-month PFS).18 It is worth noting that if the study replaced the primary endpoint with only response, the conclusions about the agent in this population would have been negative. At the same time, requiring study suspension to allow official data maturation by 6-month PFS can be difficult if initial results indicate an extraordinary response rate. A nice solution to these problems is to incorporate both outcomes into the design as a co-primary endpoint study. The probability of a type I error can be controlled without causing undue costs to statistical power or sample size requirements. For example, using Simon's optimal design with α = β = 0.08 (these values were selected since they are similar to finalized design in GOG 0229E) and πr0 = 0.10 versus πr1 = 0.30 requires 13 patients in the first stage and 40 patients cumulatively. Likewise, a design with α = β = 0.08 and πs0 = 0.15 versus πs1 = 0.35 requires 20 patients in the first stage and 41 patients cumulatively. Again, these sample sizes are comparable to the settled design for GOG 0229E (n(1) = 19 and n = 42). In this case, the cost of adding another primary was minimal. Yet, the gain was the assurance of trial sensitivity to two mechanisms of drug activity. Additionally, prospective use of two important endpoints reduces the risk of post-hoc analyses of endpoints (perhaps to the point of exploratory analyses) where the authors cannot legitimately claim knowledge of the true probability of a type I error. Unfortunate instances such as this can lead to skepticism of truly useful drugs, acceptance of useless drugs into phase III studies, or another phase II study (i.e. the realization that the initial phase II results are uninterpretable).
An important characteristic of the proposed design (as well as the one proposed by Yu) is its robustness against the degree of association between the co-primary endpoints and, moreover, the conservative quality of the assumption of independence of the two endpoints, as indicated at the end of section 2.6.12 This feature is important because the level of association likely changes in significant ways from one study to the next. Therefore, designing a study (with a method that is not robust) based on a particular level of association is unlikely to yield reliable conclusions.
Unfortunately, there is a degree of dependence with regard to the PET. In the illustrations provided here, the PET varied from about 43% to 54%. These values are also less than typically seen with Simon's univariate designs. Perhaps this is an unavoidable cost from using two variables. If the drug is rejected correctly by one measure, there is still a chance of incorrectly proceeding according to the other measure. This leads to more trials that complete the second stage with truly inactive agents. In this regard, the trials are a bit less efficient than single endpoint trials even if the overall risk of recommending an inactive drug remains the same.
5.2 Differences with Other Works
Lin, Allred, and Andrews 13 developed a procedure that utilizes the primary endpoint at the interim analysis, then uses both endpoints at the end of the trial. This is an important distinction. Our procedures use both endpoints at both stages of the trial since we were equally interested in either efficacy measure. The methods of Lu, Jin, and Lamborn 9 can potentially be applied to the problem discussed here if all (or at least most) patients who respond are at-risk for PFS at 6 months. The applicability depends on the duration of response in most people. Data within the GOG indicated that patients with short term responses were not exceedingly rare, so this category of patients was preferably modeled. Lin and Chen 10 transformed bivariate information (complete responses and partial responses) into a univariate scale, utilizing a weighted linear combination with greater weight given to complete responses. Since these characteristics are mutually exclusive, and because we were equally interested in activity on either scale, we did not examine this approach in great detail. We believe there is no reason why the methods of Bryant and Day 6 could not be applied to problems of efficacy by substituting patients who experience non-toxic reactions with patients who have beneficial response. However, their decision criteria would require activity on both endpoints before declaring the drug active. There are cases where such decision criteria are required (for example by the FDA in drugs being marketed for activity against migraines), but this was not required for our purposes. For similar reasons, the methods of Yu et al. 12 and Conaway and Petroni 7 were not interesting to us. Many of the methods provided here follow an unpublished technical report by Sill and Yothers. 19
5.3 Comparison of Methods
First, the PET was exceptionally low for the Simon-Schultz procedure, making the utilization of an interim analysis almost unworthy of incorporation into the design (7% for the case where πr0 = 0.10 and πs0 = 0.25 in Table 5). This low PET resulted mostly from Schultz's procedure. Because the univariate procedures (especially Simon) expect a higher percentage of the trials to be erroneously stopped early under the alternative hypothesis, they are designed to have more “generous” thresholds in the second stage. When this normally univariate procedure is tied into a bivariate procedure, the higher than expected probability of proceeding to a second stage results in higher than expected power. These designs are therefore systematically overpowered. Therefore, this procedure is not recommended for the design of bivariate studies.
Simon's procedure provides a formidable competitor to the Flexible procedure (Flx-Biv) in the case where πr0 = πs0 and Δr = Δs. However, this method requires fairly strong assumptions that may not apply to many clinical questions. In addition, if the targeted sample size is not met in either stage, the method does not offer any remedial recommendations. Finally, if a sponsor can attain a sample size to such a rigorous requirement, then they will generally do better by applying an Optimal Bivariate-Binomial (Opt-Biv) procedure.
5.4 Future Work
The flexibility of the design has been questioned by several statisticians in the field as a clever procedure to enable investigators to test the null hypothesis multiple times in an attempt to obtain significant results. Although abuse of the method in this way is possible as it is with Chen and Ng's method 4, the procedure should only be used by organizations that have relatively imprecise control over study accrual, and the decision rules should only be applied once at each stage. For organizations that have precise control over study accrual, a rigid design should be used. They should use a method such as that provided by the “Optimum” procedure described in Section 4. Also, we are looking into developing an exhaustive algorithm that finds the optimal or minimax designs for bivariate rigid designs.
The approach of finding solutions to the flexible and optimum or minimax designs within the set of designs derived by the minimum C method was provided by Bill Brady. We are considering work on making this software more user-friendly.
Acknowledgments
The authors would like to thank Bill Brady at Roswell Park Cancer Institute and the GOG for his thoughts, insights, and work on these designs using SAS macros. Research for the first author was supported in part by the National Cancer Institute grant to the Gynecologic Oncology Group Statistical and Data Center (CA37517).
References
- 1.Gehan EA. The determination of the number of patients required in a preliminary and a follow-up trial of a new chemotherapeutic agent. J Chronic Dis. 1961;13:346–53. doi: 10.1016/0021-9681(61)90060-1. [DOI] [PubMed] [Google Scholar]
- 2.Fleming TR. One-sample multiple testing procedure for phase II clinical trials. Biometrics. 1982;38:143–51. [PubMed] [Google Scholar]
- 3.Simon R. Optimal two-stage designs for phase II clinical trials. Control Clin Trials. 1989;10:1–10. doi: 10.1016/0197-2456(89)90015-9. [DOI] [PubMed] [Google Scholar]
- 4.Chen TT, Ng TH. Optimal flexible designs in phase II clinical trials. Stat Med. 1998;17:2301–12. doi: 10.1002/(sici)1097-0258(19981030)17:20<2301::aid-sim927>3.0.co;2-x. [DOI] [PubMed] [Google Scholar]
- 5.Green SJ, Dahlberg S. Planned versus attained design in phase II clinical trials. Stat Med. 1992;11:853–62. doi: 10.1002/sim.4780110703. [DOI] [PubMed] [Google Scholar]
- 6.Bryant J, Day R. Incorporating toxicity considerations into the design of two-stage phase II clinical trials. Biometrics. 1995;51:1372–83. [PubMed] [Google Scholar]
- 7.Conaway MR, Petroni GR. Bivariate sequential designs for phase II trials. Biometrics. 1995;51:656–64. [PubMed] [Google Scholar]
- 8.Zee B, Melnychuk D, Dancey J, Eisenhauer E. Multinomial phase II cancer trials incorporating response and early progression. J Biopharm Stat. 1999;9:351–63. doi: 10.1081/BIP-100101181. [DOI] [PubMed] [Google Scholar]
- 9.Lu Y, Jin H, Lamborn KR. A design of phase II cancer trials using total and complete response endpoints. Stat Med. 2005;24:3155–70. doi: 10.1002/sim.2188. [DOI] [PubMed] [Google Scholar]
- 10.Lin SP, Chen TT. Optimal two-stage designs for phase ii clinical trials with differentiation of complete and partial responses. Communications in Statistics - Theory and Methods. 2000;29:923–40. [Google Scholar]
- 11.Panageas KS, Smith A, Gonen M, Chapman PB. An optimal two-stage phase II design utilizing complete and partial response information separately. Control Clin Trials. 2002;23:367–79. doi: 10.1016/s0197-2456(02)00217-9. [DOI] [PubMed] [Google Scholar]
- 12.Yu J, Kepner JL, Iyer R. Exact tests using two correlated binomial variables in contemporary cancer clinical trials. Biom J. 2009;51:899–914. doi: 10.1002/bimj.200900082. [DOI] [PubMed] [Google Scholar]
- 13.Lin X, Allred R, Andrews G. A two-stage phase II trial design utilizing both primary and secondary endpoints. Pharm Stat. 2008;7:88–92. doi: 10.1002/pst.255. [DOI] [PubMed] [Google Scholar]
- 14.Therasse P, Arbuck SG, Eisenhauer EA, et al. New guidelines to evaluate the response to treatment in solid tumors. European Organization for Research and Treatment of Cancer, National Cancer Institute of the United States, National Cancer Institute of Canada. J Natl Cancer Inst. 2000;92:205–16. doi: 10.1093/jnci/92.3.205. [DOI] [PubMed] [Google Scholar]
- 15.Aghajanian C, Sill MW, Darcy KM, et al. Phase II Trial of Bevacizumab in Recurrent or Persistent Endometrial Cancer: A Gynecologic Oncology Group Study. J Clin Oncol. 2011;29:2259–65. doi: 10.1200/JCO.2010.32.6397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Aghajanian C, Sill M, Darcy K, et al. Abstract (ASCO#5531): A phase II evaluation of bevacizumab in the treatment of recurrent or persistent endometrial cancer: a Gynecologic Oncology Group (GOG) study. J Clin Oncol. 2009;27:284s. doi: 10.1200/JCO.2010.32.6397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Schultz JR, Nichol FR, Elfring GL, Weed SD. Multiple-stage procedures for drug screening. Biometrics. 1973;29:293–300. [PubMed] [Google Scholar]
- 18.Burger RA, Sill MW, Monk BJ, Greer BE, Sorosky JI. Phase II trial of bevacizumab in persistent or recurrent epithelial ovarian cancer or primary peritoneal cancer: a Gynecologic Oncology Group Study. J Clin Oncol. 2007;25:5165–71. doi: 10.1200/JCO.2007.11.5345. [DOI] [PubMed] [Google Scholar]
- 19.Sill MW, Yothers G. Technical Report. State University of New York at Buffalo; Buffalo: 2006. A method for utilizing bivariate efficacy outcome measures to screen agents for activity in 2-stage phase II clinical trials. [Google Scholar]