Differential electronic detector to monitor apoptosis using dielectrophoresis-induced translation of flowing cells (dielectrophoresis cytometry)

Abstract

The instrument described here is an all-electronic dielectrophoresis (DEP) cytometer sensitive to changes in polarizability of single cells. The important novel feature of this work is the differential electrode array that allows independent detection and actuation of single cells within a short section ($\sim 300\hspace{0.17em}\mu \mathrm{m}$) of the microfluidic channel. DEP actuation modifies the altitude of the cells flowing between two altitude detection sites in proportion to cell polarizability; changes in altitude smaller than 0.25 μm can be detected electronically. Analysis of individual experimental signatures allows us to make a simple connection between the Clausius-Mossotti factor (CMF) and the amount of vertical cell deflection during actuation. This results in an all-electronic, label-free differential detector that monitors changes in physiological properties of the living cells and can be fully automated and miniaturized in order to be used in various online and offline probes and point-of-care medical applications. High sensitivity of the DEP cytometer facilitates observations of delicate changes in cell polarization that occur at the onset of apoptosis. We illustrate the application of this concept on a population of Chinese hamster ovary (CHO) cells that were followed in their rapid transition from a healthy viable to an early apoptotic state. DEP cytometer viability estimates closely match an Annexin V assay (an early apoptosis marker) on the same population of cells.

INTRODUCTION

Changes in cell physiology are known to result in changes in dielectric properties of the cell.^{1, 2} This is exploited in a number of techniques that make use of dielectrophoresis (DEP)—the migration of a particle towards or away from the region of the maximum electric field. Descriptions of numerous ways in which cells can be characterized, sorted, separated, isolated, or manipulated according to their dielectric properties can be found in recent reviews.^{3, 4} DEP can be successfully used to: separate viable from non-viable yeast cells^{5, 6} and do it on a continuous basis using innovative configurations;⁷ separate cells of different type in blood analysis;⁸ characterize human red blood cells based on their health⁹ or based on blood type;¹⁰ separate cancerous cells from the healthy ones;¹¹ identify different types of cultured tumor cells;¹² study stem cells.^{1, 13, 14, 15} It is also used to probe and study the biophysical properties of the cells and their components and quantify their electric properties.¹⁶ Recent studies confirm that subtle changes in electrical properties of the cytoplasm play a critical role in cell physiology and behavior, for example, in multi-drug resistant (MDR) leukemic¹⁷ and breast cancer cells.¹⁸

The analysis of single cells is fundamental to understanding the important processes that underlie the workings of healthy cells and their normal growth and development, as well as in recognizing and tracking down how these processes become disrupted, potentially leading to adverse conditions and disease.^{19, 20, 21} Unfortunately, due to heterogeneity of biological cells present even in genetically identical populations, pinpointing these processes is not easy. Cells exhibit great similarities, both in morphology and physiology, and therefore require different preparation procedures and specific markers to reveal important individual variations.^{22, 23, 24} To quantify the extent of variation between individual cells in a given population, it is necessary to analyse thousands or even tens of thousands of single cells. This daunting task has been made easier with the advance of novel techniques involving microfluidics which allows efficient delivery of individual cells and high throughput;²⁵ the difficulty of finding the adequate specific markers is still a major hindrance.²⁶ DEP-based techniques present a way around these obstacles and are increasingly often used as a label-free method for sensitive discrimination between cells. For example, heterogeneous bioparticles can be filtered, focused, sorted, and trapped using 3D DEP forces.²⁷ More recent studies promote applications such as isolation and enrichment of viable cancer cells from blood²⁸ or discrimination between stages of multipotent cell differentiation.²⁹

An all-electronic analysis of single cells involving DEP actuation would offer additional ability of miniaturization and high level of integration. Electronic detection of cells began in earnest with Coulter counter³⁰ and has been extended to RF microfluidic configurations (Refs. ^{31, 32, 33} and references therein). However, studies that employ electronic techniques for simultaneous sensing and actuation^{33, 34, 35} often do not show high enough sensitivity to allow measurements of subtle changes in dielectric properties.

In this article, we describe in detail a novel system for characterizing cells by DEP actuation in between two altitude detection sites. Numerical simulation of the apparatus, matched to experimental conditions and performed for the model system of polystyrene spheres (PSS), is used to provide a verification of the method and calibration. Our specific setup allows us to relate a simple physical quantity, such as the change in altitude of cells during their flow through the microfluidic channel, to the Clausius-Mossotti factor, the quantity directly related to the polarizability of cells. Experimental results that we collected in studies of mammalian cells indicate that the instrument described here is sensitive to subtle changes in cellular physiology and thereby allows label-free DEP detection of physiologically relevant cellular properties in an all-electronic manner. One of the most important physiological changes in the cell are those associated with programmed cell death, or apoptosis; if the signals that trigger and arrest it can be identified, it may be possible to very efficiently regulate processes associated with both cell death and survival.³⁶ As an illustration and application of our method, we observe the onset of apoptosis in Chinese hamster ovary (CHO) cells actuated with DEP potentials at a frequency of 6 MHz.

Background

It is possible to explore the electric properties of cells because any biological cell, regardless of its origin or type, is densely packed with ions and charged or polar molecules, distributed throughout the cell and often compartmentalized within membrane-bound cellular organelles.³⁷ The presence of an externally applied electric field will induce individual free charges to move and orient and perturb the bound charges within the cell.⁴ In addition, a viable cell is an out-of-equilibrium system that communicates with its environment and controls the membrane transport of its electrolytes via ATP-activated membrane-bound proteins (known as ionic channels); capacitance and conductivity of cell membrane are both affected by ATP-dependent changes in influx and efflux of ions.^{16, 38, 39} Therefore, changes in metabolic or physiological state of the cell lead to changes in polarizability of the cell, which, in turn, directly influence the response of the cell to the surrounding electric field.⁴⁰

A way to macroscopically register the presence of a cell in a volume of a fluid permeated by an electric field is to measure a change in capacitance of this volume, $\Delta C$, as the cell flows through it and momentarily displaces the liquid. Amplitude of the electronic signature produced by the cell is directly proportional to the change in capacitance, $S\propto \Delta C$. A detailed description of the microwave interferometric approach that we use to capacitively detect single cells and obtain their electronic signatures is provided in our previously published work^{41, 42} and will not be repeated here. However, in previously published work,² the detection and actuation were closely coupled. Changes in polarizability could be detected but were very difficult to quantify. This work addresses that shortcoming by separating the detection and actuation. With the approach described here we are able to quantify smaller changes in individual polarizability of cells than in our previous design. This additional sensitivity allows us to detect subtle changes in cell physiological properties, such as the transition from healthy viable to early apoptotic cells.

As shown previously,⁴¹ the change in capacitance of the detector-electrode pair is

$$\Delta C=3{\epsilon }_{m}VRe\left\{K_{\mathit{C}\mathit{M}}\right\}\frac{E_{\mathit{r}\mathit{m}\mathit{s}}^2}{U_{\mathit{r}\mathit{m}\mathit{s}}^2},$$ (1)

where ${\epsilon }_m$ is the (real) dielectric permittivity of the fluid medium, V is the volume of the cell, E_rms and U_rms are the root-mean-squared values of the magnitude of the applied electric field and the voltage applied to the electrodes, respectively, and K_CM represents the Clausius-Mossotti factor, generally a complex quantity of the form

$$K_{\mathit{C}\mathit{M}}=\frac{{\tilde{\epsilon }}_p-{\tilde{\epsilon }}_m}{{\tilde{\epsilon }}_p+2{\tilde{\epsilon }}_m}.$$ (2)

The Clausius-Mossotti factor (CMF) expresses the cell polarizability per unit volume relative to that of the surrounding medium at a given (angular) field frequency ω. The frequency dependence comes in through the complex dielectric permittivities of the cell and the medium, ${\tilde{\epsilon }}_i$, where i = p, m:

$${\tilde{\epsilon }}_i={\epsilon }_i^{\prime }-j{\epsilon }_i^{″}-\frac{j}{\omega }{\sigma }_i,$$ (3)

which represent the ability of the material to polarize ${\epsilon }_i^{\prime }$, but also account for the losses associated with different polarization mechanisms. (In the above, j is the imaginary unit.) Specifically, these losses may result from the viscosity hindering rotation of dipoles ${\epsilon }_i^{″}$, or from the finite time required to build up charges on the membranes (${\sigma }_i$). At the frequencies considered in this work, as will be explained shortly, it is safe to assume that ${\sigma }_i\gg \omega {\epsilon }_i^{″}$, and consequently we can neglect the term $j{\epsilon }_i^{″}$. In addition, we omit the prime symbol on the real part of dielectric permittivity in the rest of the paper (${\epsilon }_i^{\prime }\to {\epsilon }_i$).

Cell actuation is effected using the DEP force.^{42, 43} In a non-uniform electric field, the cell is subject to a force directed along the field gradient, expressed as

$${\mathbf{F}}_{\mathit{D}\mathit{E}\mathit{P}}=\frac{3}{2}{\epsilon }_{m}VRe\left\{K_{\mathit{C}\mathit{M}}\right\}\nabla (E_{\mathit{r}\mathit{m}\mathit{s}}^2).$$ (4)

The DEP force is directly related to the polarizability of a cell in a given medium and can be oriented with or against the field gradient (pDEP or nDEP) depending on the sign of $Re\left\{K_{\mathit{C}\mathit{M}}\right\}$. In addition, DEP force depends, in general, on both conductive and dielectric properties of the suspending medium and the particle (cell), but the relative importance of these properties is highly dependent on frequency, as explained in detail in Ref. 4.

The essence of our method is in using an electronic detection that allows us to observe and quantify individual variations between the cells belonging to the same population. To this end, we use a coplanar differential electrode array, fabricated at the bottom of the microfluidic channel. Altitudes of cells are detected using a gigahertz frequency field as the cells flow above the array, first at the entrance to the electrode region and again at the exit. This generates an electronic signature, S. In between these two detection regions, cells are actuated by a megahertz frequency field, resulting in change in cell altitude. This modulates the amplitude of the signature S, as shown in Fig. 1.

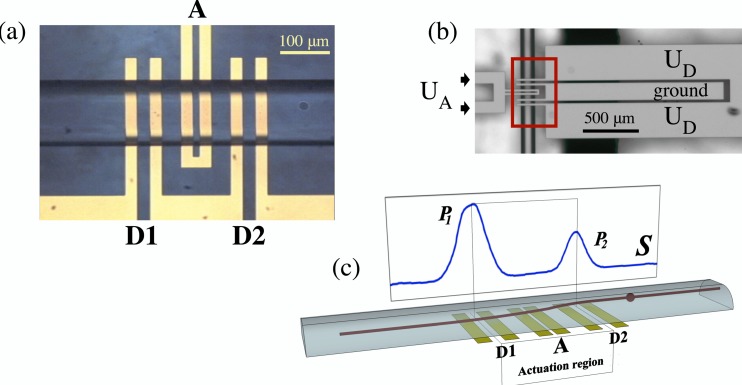
Figure 1.

(a) Micrograph of the electrode array viewed from the top of the channel (with a CHO cell exiting the analysis volume, flowing left to right). Each electrode in the array is 25 μm wide, but the spacing between them varies: between the two central actuation electrodes, the gap is 15 μm; between the electrodes of the detection sets D1 and D2, it is 25 μm; finally, the spacing between the actuation set A and the two detection sets D1 and D2 is 35 μm on each side. (b) Zoomed-out (and rotated by 90°) view of the microelectrode array from the channel bottom shows the configuration of the electrode pads and the way in which the electrodes are connected and energized. Outlined by the rectangle is the approximate area depicted in the previous micrograph. (c) Schematic representation of a side view of the channel displays a trajectory of a small sphere flowing through the microfluidic channel and actuated by an nDEP force using a megahertz signal applied to the central electrodes in the actuation region. Corresponding electronic signature, S, shown in the background and obtained by capacitive detection at 1.29 GHz by electrodes D1 and D2, is an experimental signature produced by a PSS actuated by a DEP force at 0.1 MHz. Peaks P1 and P2 are produced when the sphere is situated directly above the gap centers at D1 and D2, which are 210 μm apart.

Through the ratio $E_{\mathit{r}\mathit{m}\mathit{s}}^2/U_{\mathit{r}\mathit{m}\mathit{s}}^2$, the amplitude of the electronic detection signature, S, depends on the spatial configuration of the (non-uniform) electric field, and therefore on the altitude of the cell measured from the coplanar electrode array. Thus, any modulation of the detection signature can be related to a simple physical variable, such as the amount of vertical cell translation during actuation. In addition, S is proportional to the size of the cell and its polarizability within a given suspension medium. Both of these factors can be offset by normalizing the signature S to its average amplitude. Note that, since $E_{\mathit{r}\mathit{m}\mathit{s}}\propto U_{\mathit{r}\mathit{m}\mathit{s}}$, the voltage applied to the electrodes, $U_{\mathit{r}\mathit{m}\mathit{s}}$, scales out of the Eq. 1 and has no influence on the magnitude of S.

Unlike the change in capacitance and the electronic signature, the DEP force strongly depends on the amplitude of the electric field, as can be observed from Eq. 4. This allows us to detect cells at one frequency and simultaneously actuate them at another while keeping the two events clearly separate. As part of our design, the detection electrodes are energized by an intentionally low voltage (upper limit $\sim 300\hspace{0.17em}\text{mV}$); this ensures negligible DEP actuation at gigahertz frequency without any significant effect on detection signal-to-noise ratio.^{42, 44} By contrast, the actuation electrodes are energized with voltage amplitude at least 10 times higher. The resulting DEP force in the megahertz region prevails by two orders of magnitude and effectively accounts for the entire particle displacement due to actuation.

MATERIALS AND METHODS

Experimental setup

The differential coplanar electrode array that allows us to probe the dielectric properties of biological cells by independently detecting and actuating the cells is shown in Fig. 1a. It is fabricated on the bottom of the channel by sputtering a 180 nm thick gold layer on a 20 nm titanium adhesion layer (Micronit Microfluidics BV, Enschede, Netherlands). As can be seen from the micrograph, the array extends completely across the channel width and consists of the actuation set (A) flanked by the two altitude detection sets (D1 and D2). Each microelectrode is 25 μm wide, but the spacing between them varies—see Fig. 1.

Electrodes of the altitude detection pair extend into wider electrode pads, shown in full in the rotated, zoomed-out view in Fig. 1b. The function of the pads is to provide a contact for the electrode wires extending from the microwave resonator, and in this way couple the microfluidic channel to the resonator—see our related work⁴¹ for details. Outer electrodes of the sets D1 and D2 are energized using a 1.29 GHz signal, whose amplitude is $U_D$; inner electrodes are grounds. Through a separate connection, actuation electrodes A are energized by a megahertz region signal whose amplitude is $U_A$, with $U_A\gg U_D$, as explained previously.

Cells are pumped in a liquid suspension through the microfluidic channel in a Poiseuille flow with a parabolic velocity profile. Coplanar electrodes generate non-uniform electric fields in the volume directly above. As shown previously,⁴¹ by making the flow path long enough prior to cells entering the electrode region we ensure that 90% of cells enter the electrode region at altitudes within 3 to 4 μm of one another. The actuation process can be monitored, through the signature S, by keeping track of the changes in altitude before and after the cell enters the actuation region: (1) initially, a cell is detected as soon as it enters the electrode region, resulting in a signature amplitude $P_1$; (2) as it continues on its path over the electrodes, it is subjected to a DEP force in the region of the actuation electrodes; (3) as a result of the actuation, the cell enters the second detection region at a different altitude, and produces a signature amplitude $P_2\ne P_1$.

The aim is to modify the total electronic signature produced by the cell in a way that corresponds to the properties and composition of that particular cell. When the actuation electrodes A are energized at low frequency 0.1–20 MHz, whose amplitude, $U_A$, is typically greater than $1\hspace{0.17em}{\mathrm{V}}_{\text{pp}}$, the resulting electric field exerts a significant DEP force on the cell. Depending on whether this force acts with or against the field gradient, the cell will be attracted or repelled to the actuation electrodes in proportion to the polarizability (determined, in this case, primarily by conductivity) of the cell in the particular medium. This will result in a change of cell altitude as it exits the actuation region, and a corresponding difference in signal amplitude at the second high frequency detection point, D2.

The signature shown in the schematic representation of the microfluidic channel in Fig. 1 is, in fact, an experimental signature produced by a 10 μm–diameter polystyrene sphere (PSS), a model dielectric particle that we use in our studies (${\epsilon }_p=2.5{\epsilon }_0$, and ${\sigma }_p<{10}^{-14}\mathrm{S}/\mathrm{m}$,⁴⁵). PSS of this size will experience only nDEP⁴⁵ and will be deflected away from the electrodes (towards the region of a weaker electric field), resulting in a diminished amplitude ($P_2<P_1$) on exit from the electrode region.

To quantify the changes in signature, S, it is useful to introduce a “force index”

$$\varphi =\frac{P_2-P_1}{P_1+P_2},$$ (5)

which represents a ratio of the difference and the sum of signature amplitudes (peaks) before and after cell actuation. As discussed earlier, normalizing the peak amplitudes to the peak sum allows us to relate the change in electronic signature to the amount of vertical translation during cell actuation (cell-size independent). Positive or negative ϕ is associated with pDEP or nDEP, respectively; $\varphi =0$ corresponds to no actuation. Magnitude of ϕ is related to the strength of the DEP force that caused the altitude change, and a linear correlation between the two exists for small values of force ${\mathbf{F}}_{\mathit{D}\mathit{E}\mathit{P}}$. For a very large force, ϕ tends to ±1 (large pDEP and amplitude $P_2\gg P_1$, or large nDEP and amplitude $P_1\gg P_2$).

Theoretically, for a large population of cells with a range of different polarizabilities, values of ϕ are expected to follow a sigmoid function that saturates at the two extreme values. In practice, however, neither of these limits is ever reached: the lower limit ($\varphi =-1$) is unattainable due to the limits of equipment sensitivity and signal-to-noise issues, while the higher limit ($\varphi =+1$) lies beyond the cutoff imposed by how close the attracted cells can approach the electrodes. These issues will be discussed further in the section on data analysis.

Cell culture

Chinese Hamster ovary (CHO) cells expressing a human-llama chimeric antibody (EG2) for epidermal growth factor receptor (EGFR) were used in this work. The cell line (CHODG44-EG2-hFc/clone 1A7) was provided by Yves Durocher of the NRC, Canada (Bell et al., 2010). The cells were cultured in a 3 l glass bench-top bioreactor (Applikon, Foster City, CA) with the following set-points maintained throughout: 37 °C, 40% ${\text{dO}}_2$, 7.2 pH, and 200 rpm. The cells were grown in BioGro-CHO serum-free medium (BioGro Technologies, Winnipeg, MB) supplemented with 0.5 g/l yeast extract (BD, Sparks, MD), 1 mM glutamine (Sigma, St. Louis, MO), and 4 mM GlutaMax I (Invitrogen, Grand Island, NY). Samples for cell density and viability monitoring were taken every 24 h in the first part and for the first 3 days and then every 6 h for the next 24 h in the second part of the experiment.

RESULTS

Simulations of signatures and trajectories

To relate experimental results to the theoretical model, we performed finite element simulations for our setup using COMSOL Multiphysics^®. (Details of the simulation algorithm are provided in earlier work.^{42, 46}) Symmetry of the problem allows these simulations to be performed in two dimensions, in the vertical plane along the center of the 40 μm high, 120 μm wide microfluidic channel. Cells were assumed to be spherical particles, with cell altitude defined as the distance from the channel floor to the cell center of mass. As with the apparatus and the method, there are two aspects to the simulations: detection and actuation.

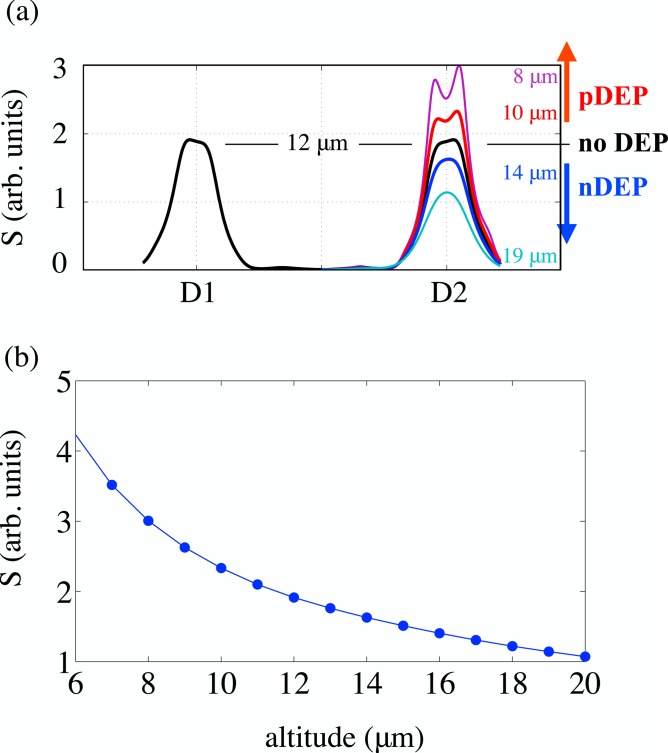
To simulate detection, we simulate possible experimental signatures; to this end, it is adequate to simulate the ratio $E_{\mathit{r}\mathit{m}\mathit{s}}^2/U_{\mathit{r}\mathit{m}\mathit{s}}^2$ for different altitudes of the cell. Fig. 2a shows the signature profiles of a particle (cell) at constant altitude for 1 μm increments in altitude between 5 and 19 μm. Fig. 2b illustrates how peak amplitudes change with altitude, with discrete points collected from the signal amplitude, and the curve connecting them obtained via spline interpolation. Note that it is possible to resolve two peaks (corresponding to the inner edges of the detection electrodes) for lower altitudes (12 μm or less); in these cases, the peak amplitude plotted in Fig. 2b is the higher of the two. Simulated force index values can be easily obtained using the interpolation curve in Fig. 2b.

Figure 2.

(a) Simulated detection signatures for 1 μm nDEP-induced increments in altitude. Figure indicates the expected signature profiles for different types of actuation. (b) Change of peak amplitude with altitude. Points obtained from simulation are connected with a spline interpolation curve.

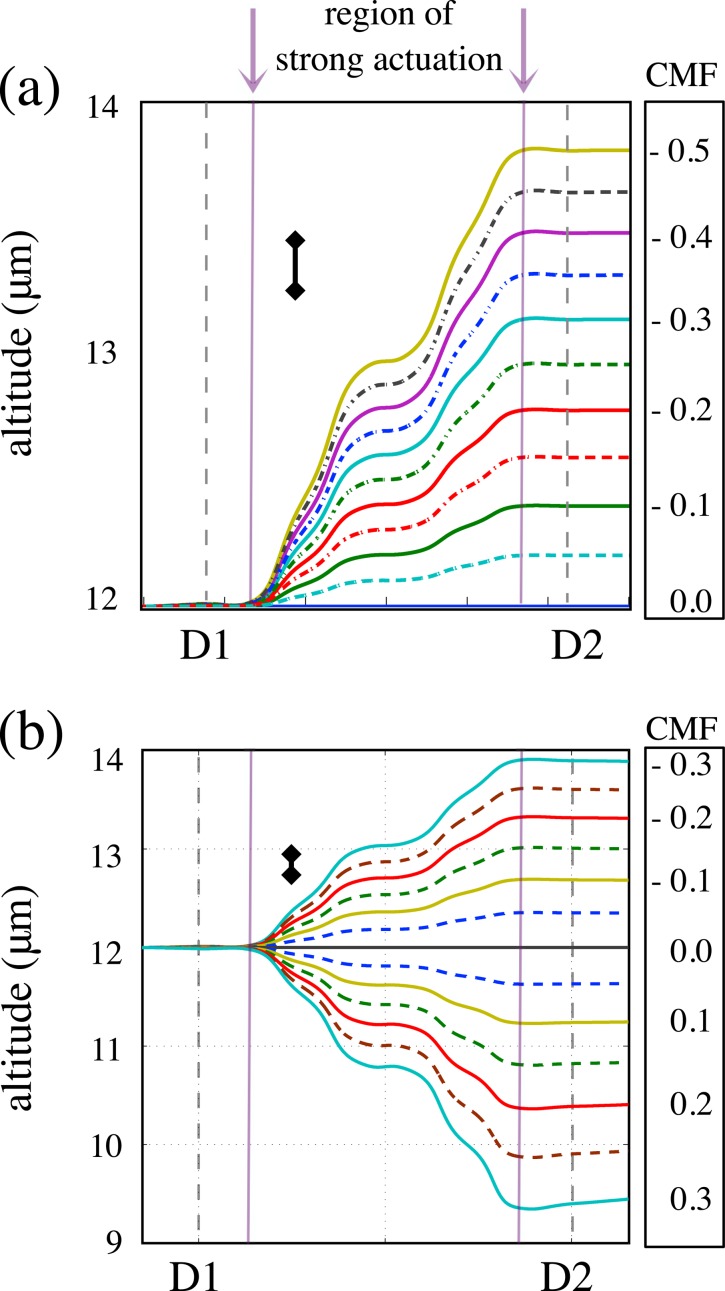
Simulations of cell actuation employ numerical solutions of the equations of motion resulting from a simple physical model⁴² in which the only forces acting on the cell are apparent gravity, hydrodynamic lift, DEP force, and fluid drag. This yields the trajectories of the cells when a DEP force is applied in the actuation region. As reported in Ref. 42, finite element simulations based on this model show that the DEP force component perpendicular to the channel floor is dominant to the extent that all of the other forces can be neglected. This is certainly true within the 150 μm-wide central region of strong actuation (indicated in Figs. 3a, 3b). An exception applies in the 30 μm-interval between the exit from the region of strong actuation and the second detection site, D2, where the DEP force is comparable to apparent gravity and lift, resulting in a slight change in altitude evident in Figs. 3a, 3b. At our experimental flow rates (at least $1500\hspace{0.17em}\mu \mathrm{m}/\mathrm{s}$), cells cover this distance in 0.02 s or less; for a CHO cell settling rate of about $5\hspace{0.17em}\mu \mathrm{m}/\mathrm{s}$, this translates into a change in altitude of less than 0.1 μm, which is not large enough to be observable by our apparatus and influence the force index significantly. PSS, which are smaller than CHO cells, settle at an even slower rate—about $2\hspace{0.17em}\mu \mathrm{m}/\mathrm{s}$, resulting in an even smaller altitude “adjustment,” as evident from comparison of Figs. 3a, 3b. Even though we do include the full set of forces in our simulations and account for the altitude adjustment, the rest of our discussion proceeds as if the vertical DEP force were the only one acting on the cells.

Figure 3.

(a) Trajectories for nDEP actuated 10 μm-diameter PSS for equally spaced steps in CMF in the interval [−0.5, 0]; assumed $U_A=4\hspace{0.17em}{\mathrm{V}}_{\text{pp}}$; (b) trajectories simulated for 13 μm-diameter CHO cells for CMF in the interval [−0.3, 0.3]; assumed $U_A=8\hspace{0.17em}{\mathrm{V}}_{\text{pp}}$. Note the difference in vertical scale on the two plots. Inset bars drawn next to the trajectories on both plots represent the relative sizes of the smallest change in altitude observable with our apparatus; in both cases, it is about 0.25 μm. A slight change in altitude, expected as the cell exits the region of strong actuation and begins to return to equilibrium position, is not large enough to be observable by our apparatus.

Examples of trajectories, simulated for values of CMF in steps of 0.05, are represented in Fig. 3 for a 10 μm-diameter PSS, as well as for a 13 μm-diameter CHO cell. The actuation force on the PSS was calculated using $U_{\mathit{r}\mathit{m}\mathit{s}}=4\sqrt{2} {\mathrm{V}}_{\text{pp}}$ with values of $Re\left\{K_{\mathit{C}\mathit{M}}\right\}$ in the interval [–0.5, 0], and for CHO cells, using $U_{\mathit{r}\mathit{m}\mathit{s}}=8\sqrt{2} {\mathrm{V}}_{\text{pp}}$, with $Re\left\{K_{\mathit{C}\mathit{M}}\right\}$ in the interval [–0.3, 0.3]. These simulations clearly show that if the experimental measurements are sensitive to changes in altitude of about a quarter of a micron, a difference in CMF of approximately 0.05 will be observable. We address this issue in Sec. 3B.

Apparatus sensitivity

For the PSS trajectories (a), this estimate was obtained from sensitivity evaluations described in Sec. 4—see Fig. 4; for the CHO cell trajectories, it was obtained from the width of the distribution of the force index values obtained for the control set of unactuated cells—see Fig. 6a.

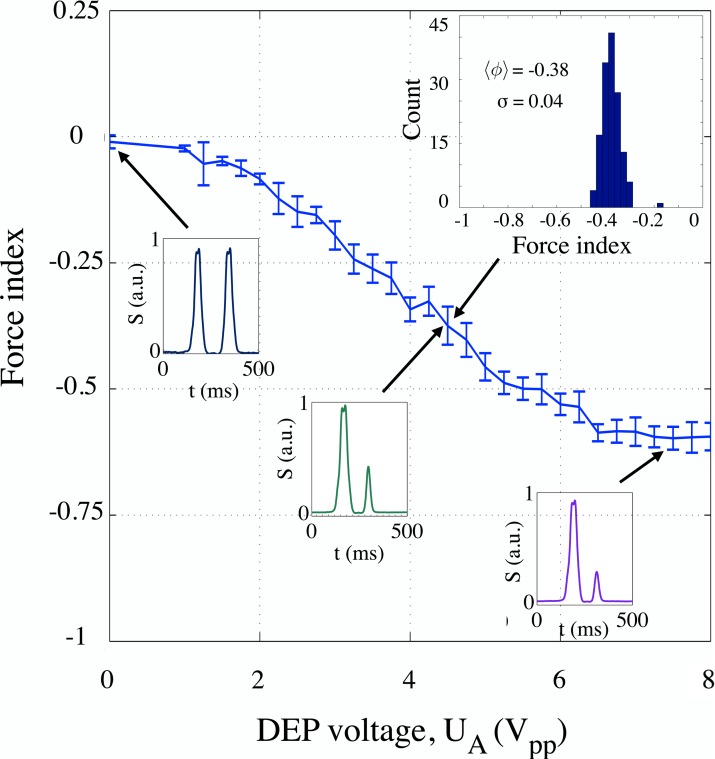
Figure 4.

Mean force index values for PSS populations actuated at 1 MHz by signals of amplitudes 0 to $8 {\mathrm{V}}_{\text{pp}}$, in steps of $0.25 {\mathrm{V}}_{\text{pp}}$. Inset shows an example of the force index histogram for $U_A=4.5 {\mathrm{V}}_{\text{pp}}$ with the mean force index and standard deviation as indicated. Examples of individual signatures produced by PSS entering the analysis volume at about the same altitude are provided for different actuation voltages, U_A (values of 0, 4.5 and $7.5 {\mathrm{V}}_{\text{pp}}$, as indicated by arrows). The response has a linear characteristic for signal amplitudes between about 2 and $6 {\mathrm{V}}_{\text{pp}}$; the change in voltage of about $0.25 {\mathrm{V}}_{\text{pp}}$ results in an observable change in force index of about 0.025. This allows us to use the force index to estimate the actuation and the corresponding expected change in polarizability.

Figure 6.

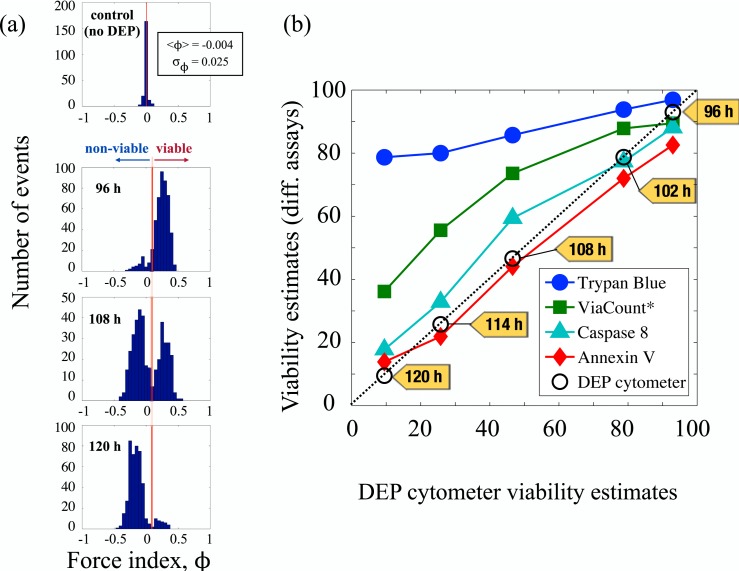
Detection of early stage apoptosis. (a) After the culture was maintained for 96 h through growth and stable phase, histograms of the force index values obtained from a sample population of CHO cells suspended in a medium of conductivity ${\sigma }_m=0.17\hspace{0.17em}\mathrm{S}/\mathrm{m}$ and actuated using a 6 MHz signal with an amplitude of $8 {\mathrm{V}}_{\text{pp}}$ show an incipient subpopulation of early apoptotic cells. Within the next 12 h, more than half of all cells show changes in dielectric properties indicating early apoptosis. After another 12 h, changes are evident in almost entire population. (b) The figure shows viability estimates of different assays plotted against the viability estimates provided by DEP cytometry, and indicates clearly the strong correlation between the DEP cytometer and the Annexin V assay. Note: ViaCount assay uses a proprietary mix of two DNA binding dyes to detect viable, apoptotic and dead cells.

To evaluate the sensitivity of our apparatus, we collected signatures produced by a population of model particles, 10 μm-diameter PSS (Polybead–Polystyrene 10.0 Micron Microspheres, Polysciences, Inc.), as the voltage amplitude of a 1 MHz DEP signal increased from 0 to $8\hspace{0.17em}{\mathrm{V}}_{\text{pp}}$, in steps of $0.25\hspace{0.17em}{\mathrm{V}}_{\text{pp}}$. Increasing the applied voltage resulted in increasing the nDEP force on PSS. Corresponding force index steadily decreased from zero and saturated at approximately –0.6. The results are plotted in Fig. 4.

Individual points on the plot represent the mean force index (averaged over the corresponding population with, on the average, a 100 particles per population) extracted for each $0.25\hspace{0.17em}{\mathrm{V}}_{\text{pp}}$ step. The response is fairly linear for voltages between 2 and $6\hspace{0.17em}{\mathrm{V}}_{\text{pp}}$, indicating that, for a low strength DEP force, the force index can be used to extrapolate the magnitude of cell actuation. From the plot in Fig. 4, we can also conclude that, in the region of linear response, change in voltage of about $0.25\hspace{0.17em}{\mathrm{V}}_{\text{pp}}$ corresponds to an observable change in force index of 0.025, resulting from about 0.1 to 0.25 μm deflection.

Within the region of linear response, a small change in DEP force would produce the same corresponding change in deflection regardless of whether differences in actuation are effected by differences in CMF at a constant voltage amplitude U_rms (the case of cells whose dielectric properties are changing), or by differences in U_rms at a constant CMF (the situation encountered in our PSS example). Therefore, these two situations would result in the same corresponding change in force index, ϕ. In general, relative change in the DEP force (neglecting the variations in volume, as PSS are uniform in size to a high degree) can be written as

$$(|\delta {\mathbf{F}}_{\mathit{D}\mathit{E}\mathit{P}})|){\hspace{0.17em}}^2={(\delta Re\{K_{\mathit{C}\mathit{M}}\})}^2+{(2\delta U_{\mathit{r}\mathit{m}\mathit{s}})}^2,$$ (6)

which leads to the conclusion that

$$\left|\delta Re\right\{K_{\mathit{C}\mathit{M}}\}{|}_U\approx 2|\delta U_{\mathit{r}\mathit{m}\mathit{s}}{|}_{\mathit{C}\mathit{M}\mathit{F}}.$$ (7)

As explained before (cf. Fig. 4), in the region of linear response, the smallest observable change in force index (0.025) is achieved for a change in voltage of $0.25\hspace{0.17em}{\mathrm{V}}_{\text{pp}}$. For a midpoint of the linear response region ($4\hspace{0.17em}{\mathrm{V}}_{\text{pp}})$, this translates into the relative change in voltage of ($0.25\hspace{0.17em}{\mathrm{V}}_{\text{pp}}/4\hspace{0.17em}{\mathrm{V}}_{\text{pp}}$), or about 6%, which, according to Eq. 7, corresponds to a relative change in CMF of about 12%.

Detection of dielectric changes at the onset of apoptosis

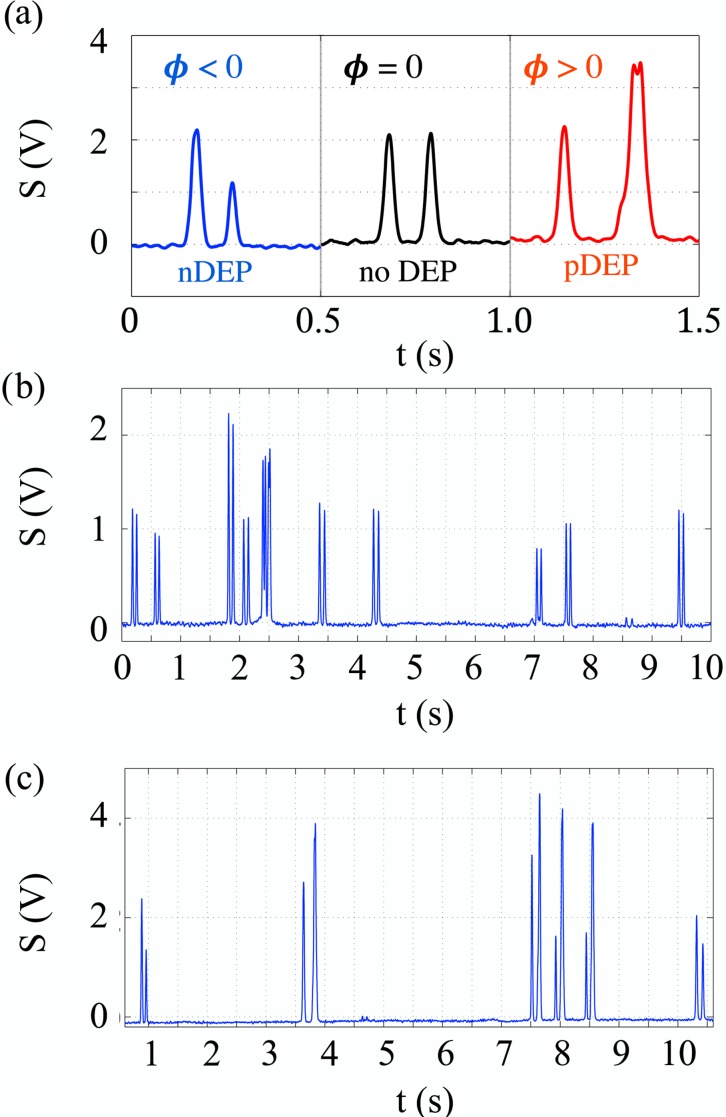
Finally, we illustrate the use of our device on the batch culture of CHO cells suspended in a medium of conductivity ${\sigma }_m=0.17\hspace{0.17em}\mathrm{S}/\mathrm{m}$. Experimental signatures depicted in Fig. 5a were taken from a set of typical signals produced by CHO cells during the experiment, but chosen for cells of similar sizes and entering the actuation region with similar velocities. Hence, an almost identical initial peak, $P_1$, was produced by all three at the first detection site, D1. The actuation region determines how the signature evolves. Without a DEP force, the cell remains at the same altitude as it flows above the second set of detection electrodes, resulting in a second peak that is practically identical in amplitude and width to the initial one. In contrast, a CHO cell experiencing a pDEP or nDEP force will be deflected downwards or upwards from its original path; in either case, its velocity will change as it enters different fluid layers (Poiseuille flow). A cell that is attracted to the actuation electrodes (pDEP) will slow down, and therefore take longer to both reach the second detection area and pass over it: the resulting electronic signature reveals a wider second peak that is also delayed compared to the control (no DEP) signature. Conversely, the electronic signature of a cell repelled from the actuation electrodes (nDEP) and moving into faster fluid layers will exhibit a narrower second peak that occurs earlier than that of the control signature. The idea to use DEP force to alter the position of the particle is not entirely new, having been previously developed by Pethig, Gascoyne, and Markx who used nDEP in flow fractionation applications.^{47, 48} The novel approach here, rather than trying to merely separate the particles in order to elute them at different altitudes and different times, uses both nDEP and pDEP force to modulate the signature amplitude in a way that uniquely reflects the physiological state of the cell and creates an electronic stamp.

Figure 5.

Experimental signatures of CHO cells. (a) Signatures produced by cells entering the actuation region at about the same altitudes and with similar velocities, but actuated in a different way depending on the frequency of the applied signal. Examples were deliberately chosen from measurements performed at lower flow rates to allow characteristic features to be clearly observable. This allows, for example, the cell actuated by the pDEP to approach the electrodes close enough for the double peak to be resolvable at the second detection site; this feature disappears at higher flow rates as hydrodynamic focusing forces the flow to higher altitudes. Note also that evenly matched entrance peak amplitudes of these signatures become distinctly modified due to the DEP actuation in between detections. (b) Sample signatures produced by unactuated CHO cells (no DEP applied) at flow rates of 5 nl/s and cell density 0.5 × 10⁶ cells/ml; (c) Signatures for a similar flow rate produced by actuated CHO cells. Both nDEP and pDEP signatures can be observed.

Two of the three signatures in Fig. 5a document the CHO cell response at different frequencies: 0.1 MHz (nDEP, $\varphi <0$) and 6 MHz (pDEP, $\varphi >0$); the remaining one corresponds to a neutral situation with no DEP applied ($\varphi =0$). Sweeping the entire frequency region from 0.1 to 6 MHz provides the CMF spectrum. Low flow rate examples in Fig. 5a, produced by similarly sized cells, were provided to illustrate the shape of the signatures and their agreement with profiles obtained through simulations. Our typical experimental flow rates are actually higher (5–10 nl/s); some samples of experimental signatures are shown in Figs. 5b, 5c. From our study of a population of about 3000 cells, a crossover frequency between nDEP and pDEP for healthy viable cells is at ≈0.5 MHz. By contrast, nonviable cells experience only nDEP through this entire frequency region. This suggests that measurements at the 6 MHz frequency could be used to monitor CHO cells over a period of time and predict the onset of programmed cell death or apoptosis.

Figure 6 refers to one such experiment on CHO cells involved in a bioprocess. A CHO batch culture was maintained in a bench-top bioreactor for 120 h through growth, stationary, and declining phase;⁴⁹ during that time, samples were collected every 24 h, and the dielectric response of the cells was measured by actuating cells at 6 MHz. Figure 6a shows the changes in distribution of force index values, taking part during the final 24 h of the experiment. The pronounced bimodal distributions indicate the presence of at least two different populations of cells: one with $\varphi >0$, the other with $\varphi <0$. The negative ϕ population (“non-viable cells”), begins to emerge at about 96 h from the bioreactor seeding. Within 12 h, it starts to take over, and within the next 12 h it almost completely dominates. Note that the mean force index for the population of the unactuated cells (control group) remains very close to 0, demonstrating clearly that the changes in dielectric properties are only observable at megahertz frequencies.

DISCUSSION

To confirm that the observed changes are related to physiological changes in the cell, in addition to DEP cytometer measurements, cells were monitored during the same 120 h using four standard biological assays. These were trypan blue exclusion test, and three different fluorescent cytometry assays: ViaCount, Annexin V, and caspase 8 (Millipore—Guava EasyCyte HT Base System). Within the final 24 h period (96–120 h from the time of bioreactor seeding), decline in cell viability was noted by all assays. However, since they follow different events in cell physiology, it is typical that the assays disagree on the rate at which the viability declines. Trypan blue selectively colours non-viable cells, but can only enter the cells whose membrane is ruptured (lysed). Thus, trypan blue can only identify necrotic cells, which represent one of the final stages in a cell death process.³⁸ It is possible for a cell viability to be compromised even though the cell membrane is intact. ViaCount and Caspase 8 assays are both fluorescence flow cytometry assays which bind, respectively, to DNA and caspase 8 protein. Caspase 8 is known to appear inside the cytoplasm in the early stages of cell death. ViaCount assay uses a proprietary mix of two DNA binding dyes—one membrane-permeant and the other membrane-impermeant—to detect viable, apoptotic and dead cells. The membrane-permeant dye is able to get inside the cell before trypan blue molecules do, which accounts for the sequence order in Fig. 6b. However, one of the earliest events associated with changes in cell viability is the loss of asymmetry of the cell lipid membrane and the appearance of the phosphatidyl serine (PS) head group in the outer leaflet of the lipid bilayer. This event is regarded in the literature as the onset of apoptosis and is customarily detected by fluorescence when protein Annexin V selectively binds to PS heads.⁵⁰ From the table and plot shown in Fig. 6b, it is obvious that the DEP cytometer viability estimates closely follow those of Annexin V assay. Since binding of Annexin V protein to the membrane indicates one of the earliest stages in apoptosis, we conclude that the DEP cytometer is sensitive to changes in dielectric properties of the cell associated with this event.

Two earlier studies followed apoptosis by treating cells with different chemicals and subsequently monitoring morphological changes using SEM observations⁵¹ and fluorescent cytometry (FACS) measurements.⁵² In both cases, DEP profiling was performed by tracking the changes in DEP in the crossover frequency range. The combined information from these observations and measurements of cell size was used to clearly associate the onset of apoptosis with the dielectric alterations of the membrane and to determine effective capacitance of the plasma membrane of the cell. These results highlight the advantage of DEP profiling techniques which monitor the cell's intrinsic dielectric properties and allow unlabeled cells to be studied. In addition, the study by Wang et al.⁵¹ found that alterations in dielectric characteristics of the cell appear to be very sensitive measurements of the cell “dielectric phenotype,” and that DEP changes were detected even before the PS externalization, as observed by Annexin V assay. Furthermore, Wang et al.⁵¹ suggest the possibility of distinguishing between apoptotic and necrotic cells.

Our contribution is to follow the onset of apoptosis in a bioprocess. Like the previous two studies, we find that the DEP changes precede caspase activation and correlate with Annexin V results. Our method allows us to monitor changes in single cell polarizability and, in this way, is particularly promising in terms of identifying emerging subpopulations of apoptotic cells. In addition, our detection and actuation system is completely electronic (and therefore accommodating miniaturization and integration) and produces a quantifiable analog measurement of the physiological state of each individual cell. This enables us to rapidly and reliably, and without the use of markers or additional preparation, determine the viability of the samples.

One final remark: note that, due to the nature of our technique, high throughput is not critical here. To obtain histograms shown in Fig. 6, it is enough to analyze 500–1000 cells. Therefore, even at a low throughput rate of 1 event per second, it would take only 10–15 min to determine the fraction of cells involved in early apoptosis in a given dilute sample. In comparison, a standard fluorescent flow cytometer assay for detection of early apoptosis, Annexin V, requires between 2 and 10 thousand cells (in dilutions of 10⁶ cells/ml, concentration that is required by our apparatus), which then have to be incubated for at least 15 min before the measurements can be made. This further emphasizes that the strength of our method is in its sensitivity and the ability to quantify changes in the electronic signature produced by single cells.

CONCLUSION

A differential electrode array that permits independent detection and actuation of single cells within a short section ($\sim 300\hspace{0.17em}\mu \mathrm{m}$) of the microfluidic channel allows detection of subtle changes to the dielectric character of cells. Polarizability of each individual cell varies with its biological properties and physiological state. The DEP force on the cell is directly related to cell polarizability in a given medium; cell actuation that results from it can be measured very sensitively to allow the inherent properties of the cell to be used as a marker of its physiological state.

We presented in this work a novel method for independent detection and actuation of biological cells which allows us to use a differential detection of altitudes to electronically monitor changes in the physiological properties of the cells. The differential electrode array design presented in this work separates the regions of detection and actuation and in this way enables us to sense smaller changes in cell polarizability than were previously possible. Because the electric fields are applied only momentarily and with a low amplitude, the method is non-invasive and leaves the cells available for further culturing and observations. High sensitivity of the apparatus allows us to use a relatively small number of cells (on the order of 1000s) to determine the fraction of cells involved in apoptosis. Last but not least, an all-electronic approach allows miniaturization and automated analysis, making a DEP cytometer a particularly suitable candidate for a number of low-cost applications in biomedical research and health care.