Quantitative multicolor subdiffraction imaging of bacterial protein ultrastructures in 3D

Abstract

We demonstrate quantitative multicolor 3D subdiffraction imaging of the structural arrangement of fluorescent protein fusions in living Caulobacter crescentus bacteria. Given single-molecule localization precisions of 20–40 nm, a flexible locally-weighted image registration algorithm is critical to accurately combine the super-resolution data with <10 nm error. Simple surface-relief dielectric phase masks implement a double-helix response at two wavelengths to distinguish two different fluorescent labels and to quantitatively and precisely localize them relative to each other in 3D.

The nanoscale architecture of living cells is beginning to be explored beyond the diffraction limit (super-resolution) by fluorescence microscopy, and simple methods for precise, multicolor three-dimensional (3D) imaging over a large depth of field are essential. Single-molecule localization microscopy with subdiffraction resolution relies on the ability to control the emitter density in any imaging frame and to sequentially and precisely determine the single-molecule positions^1–3. To achieve super-resolution imaging, the images of single molecules in subsequent frames are fit with mathematical functions to determine positions, and the list of fitted positions is then used to produce a reconstruction of the specimen with significantly improved spatial resolution. To extract the full three-dimensional information from the specimen, it is clear that the single molecules need to be precisely localized in all three dimensions, x, y, and z. Unfortunately, the point-spread function (PSF) of a conventional wide-field microscope contains little information about the axial z position of a single emitter, such that, for a single PSF axial section, the localization precision in the z dimension remains poor (depth of focus ~ 500 nm), while PSF fitting in the transverse x and y dimensions can localize single molecules with high precision (standard deviation σ in the 10–40 nm range with conventional labels providing sufficient photons)⁴. Complex dual-objective schemes using interferometry along the z axis can provide high z precision^{5, 6}. A simpler solution to provide the necessary z position information involves altering the PSF of the optical imaging system in a such a way that the recorded image of a single molecule changes measurably as a function of its z position, for example by adding astigmatism⁷, by multiplane imaging^{8, 9}, and by manipulating the phases of the fluorescent light emission in the Fourier domain to produce a rotating PSF¹⁰. Among the last group, the double-helix point-spread function (DH-PSF)^11–13 is particularly useful, because it allows 3D localization of single-molecule emitters over a large axial depth of field (~1.5–2 μm in current implementations) and has a more uniform localization precision throughout that range compared to other approaches^{14, 15}.

The DH-PSF is generated by inserting an optical phase mask in the conjugate plane of the exit pupil of the objective. In the early implementations, this was achieved with a programmable phase-only reflective liquid crystal spatial light modulator (SLM) placed in the Fourier plane of the 4f optical processing section^{12, 13}. While there are numerous advantages to being able to manipulate the phases of the fluorescent light field through the programmability of an SLM¹⁶, the currently available high resolution SLMs are only able to phase-shift light of a single polarization. This results in either the loss of roughly half of the usable photons for 3D single-molecule imaging or requires more complex optical configurations¹⁷. Recently, however, phase modulation was achieved by replacing the SLM with a transmissive surface-relief phase mask made by grayscale photolithography which makes the optical setup much simpler and modulates phase for both polarizations¹⁸. Here we utilize improved surface-relief phase masks with eight phase-levels made by a sequence of photolithography steps. We demonstrate a simple and efficient phase mask-based DH-PSF microscope that, combined with a spectrally sensitive detection scheme and appropriate image registration algorithms, enables quantitative multicolor, 3D super-resolution microscopy over a large depth-of-field.

To demonstrate the capabilities of the two-color DH-PSF microscope, we address the challenge of super-resolution imaging of protein superstructures in live bacterial cells, specifically genetically expressed fluorescent protein fusions to PopZ^{19, 20} and CreS²¹ proteins in the dimorphic bacterium Caulobacter crescentus. For these experiments, the time scale of imaging has to be sufficiently fast to avoid blurring of the images due to changes in the structure of interest. Thus, we concentrated on quasi-static structures produced by a polar anchor and a cytoskeletal protein which did not change appreciably on the ~10 minute time scale of imaging, a small fraction of the 140–160 min cell cycle under our conditions. To enable active experimental control over the emitter concentrations, we employ blinkable and photoactivatable fluorescent protein fusions to eYFP²² and PAmCherry1²³, respectively, to image intracellular proteins. In addition, we provide contextual information by imaging the bacterial cell surface with the PAINT scheme using the Nile Red dye^{13, 24}.

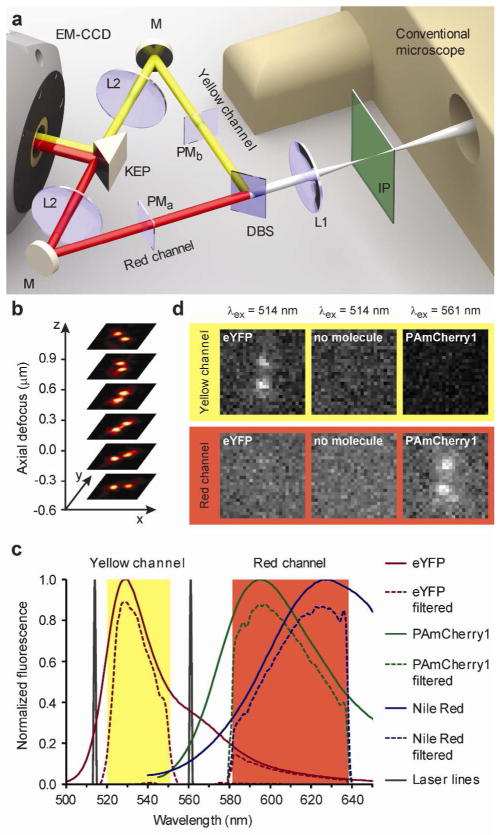
The arrangement of the detection optics for the dual-channel DH-PSF microscope is shown in Figure 1a. The inverted wide-field epifluorescence microscope requires no modification, and the conventional image is formed at the first image plane, where the camera is usually placed for 2D imaging. To produce the DH-PSF in two detection channels, termed red and yellow, the optical system is simply augmented with a dichroic beamsplitter and two 4f optical processing sections containing two lenses, L1 and L2, before two images are allowed to form on the EMCCD camera. The first 4f-lens produces a Fourier transform of the light field from the first image plane at the position of the phase masks. These transmissive dielectric phase masks modulate the phases of the resulting light fields in the spatial frequency domain (Supplementary Figure 1). The second 4f-lenses generate another Fourier transform to give the final real images on the EMCCD camera. After this manipulation, each single emitter appears with a characteristic DH-PSF image that is composed of two spots on the detector, instead of a single Airy spot. These two spots revolve around each other for different z positions of the single emitter, thereby tracing out a double-helix (Figure 1b). The angular orientation of the line connecting the two spots reports on the z position of the molecule and the midpoint between the two spots reports on the x, y position. In this way, the DH-PSF precisely reports positional information of each single molecule in all three dimensions, simultaneously over a large depth-of-field^{11, 12}.

Figure 1.

Multicolor imaging with DH-PSF phase masks. a Schematic of the multicolor DH-PSF microscope. The conventional wide-field inverted fluorescence microscope is at the right with the conventional image plane IP. The dichroic mirror DM splits the emission into two spectrally distinct optical paths for proper phase modulation by two different phase masks PM_a and PM_b. Lenses L1 and L2 in each path form a 4f optical processing system, with the phase masks located one focal length away from the first lens L1 and from the second lens L2. The knife edge prism KEP directs both paths onto two adjacent regions of the same EMCCD. b For a single emitter, the DH-PSF microscope generates two focused spots on the detector, which revolve around each other as a function of z position of the emitter. c Raw and filtered emission spectra of fluorescent labels used in this work. The various filters in the optical system create two spectrally distinct detection channels. d Even bright localizations (~4000 detected photons) of eYFP and PAmCherry1 do not produce a detectable signal in the spatially corresponding region of the opposing channel. Also shown are the background levels for 514 nm excitation, when no molecules are present (middle column).

The genetically expressed eYFP and PAmCherry1 fluorescent proteins employed here have very different emission spectra (Figure 1c) and by choosing a standard dichroic beamsplitter with a transition at 560 nm and a suitable set of emission filters, we are able to provide two spectrally isolated detection windows and still capture a substantial fraction of the emitted photons from each fluorescent label (Supporting Information). The nearly complete spectral separation results in an undetectable level of cross-talk between the two channels and unambiguous fluorophore identification (Figure 1d). To maximize throughput, each channel has a different phase mask matched to the central wavelength of the corresponding fluorophore (Supporting Information).

With spectral separation at 560 nm, the third single-molecule emitter, the Nile Red dye, cannot be distinguished spectrally from the PAmCherry1 fluorescence. Therefore, we imaged the intracellular fluorescent proteins (eYFP and PAmCherry1) with interleaved 514 nm and 561 nm laser excitation and then subsequently imaged the cell boundary with Nile Red, similar to the previously described SPRAIPAINT scheme¹³. First, we photobleached the population of PAmCherry1 emitters through repeated activation and imaging intervals, and then added a small amount of Nile Red solution to the imaging buffer around the cells; turn-on of individual Nile Red molecules upon binding enabled super-resolution imaging. Excitation at 561 nm then continued without the activation laser which ensured that only emission from Nile Red was collected.

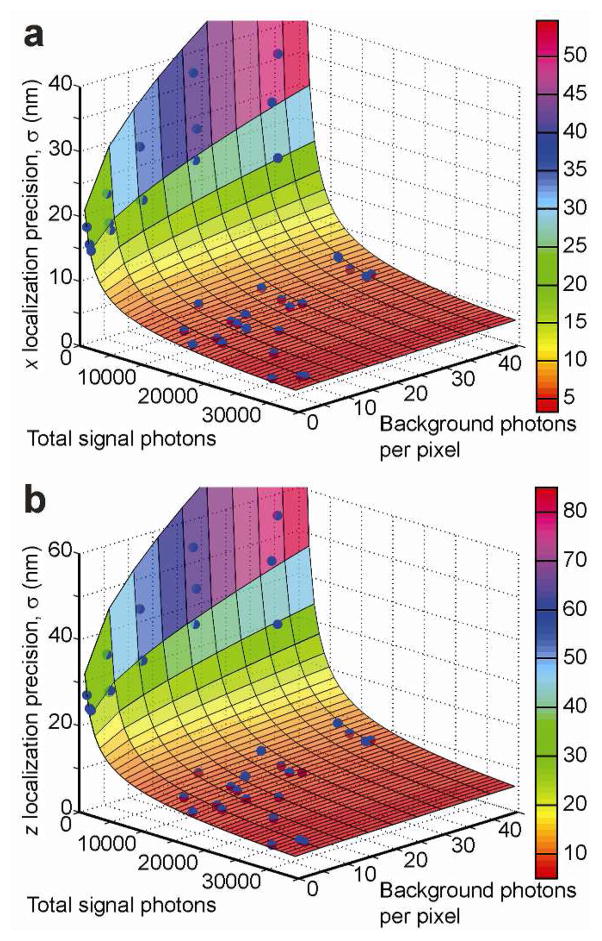
Of fundamental importance for every type of single-molecule localization microscopy is the localization precision (standard deviation σ of localizations) that the instrument can deliver for a given level of integrated signal photon counts and background photon counts. These two observables vary substantially for the numerous fluorescent proteins and organic dyes available for single-molecule imaging, as well as for different imaging conditions (i.e. cell type, filter sets, excitation laser intensity, frame exposure times, etc.). For this reason, we performed localization precision measurements by repeatedly localizing a stationary bead with different signal-to-background ratios (Supporting Information). Figure 2ab show the experimentally determined localization precisions in the transverse x dimension (x and y dimensions are roughly equivalent), as well as in the axial z dimension for a wide range of imaging conditions. We can model these data satisfactorily with the following equation based on a statistical model of the fitting process²⁵,

Figure 2.

3D Localization Precision. Dependence of the experimentally obtained localization precision on the measured signal and background levels in a the transverse (shown is x) dimension and b the axial (z) dimension. Also shown are the best-fit surfaces based on the model of Equation 1. The residual errors of the fit are bounded by the 15% error margin in all dimensions.

$${\sigma }_i^2=(1/N_{\mathit{Signal}})\left[a_i+4a_i{b}_i{\mathit{SBR}}^{-1}+a_i\sqrt{\frac{2b_i}{\mathit{SBR}+4b_i}}\right],$$

where SBR is N_Signal/N_Background, N_Signal is the total signal photons above background, N_Background is the number of background photons per pixel, and the constant coefficients a_i and b_i are fit to match measured fluorescent bead data for dimensions i = x y z,,, respectively (Figure 2cd and Supplementary Table 1). Our DH-PSF calibrations (Supporting Information) further show that the localization precision is constant over the measured z range. This model therefore allows us to estimate the localization precision of an arbitrary single-molecule fit simply from its signal and background values. For example, during live-cell imaging of the fluorescent proteins eYFP and PAmCherry1, we typically detect 500–5000 signal photons/frame and 7–30 background photons/pixel/50 ms frame. Using Equation 1, this produces localization precisions in the range of 10–46 nm, 10–49 nm, and 16–71 nm, in x, y, and z, respectively. Thus the localization precision can vary substantially over the whole field-of-view due to the non-uniform intensity distribution of the illumination laser beam.

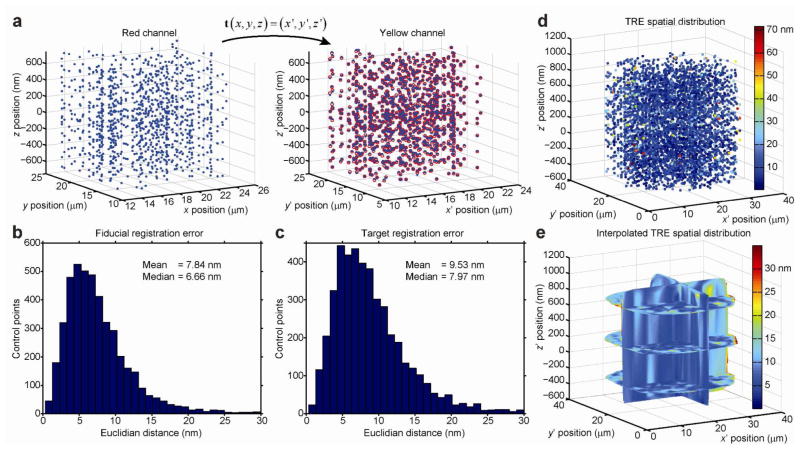
Having measured the localization precision of the DH-PSF microscope for 3D single-molecule imaging, we next quantified the error associated with the computational registration of the localization data between the two color channels during post-processing. Due to the a priori unknown aberrations present in the two spectral channels, we assume that the single molecules detected in each channel are localized in two differently distorted 3D coordinate systems (Supplementary Figure 3ab and 4ab). To quantitatively register and overlay the two datasets in space (image fusion), we evaluated a mapping function that accurately transforms points from one 3D image domain (the red channel) to the other 3D image domain (the yellow channel), as illustrated in Figure 3a. To obtain these points, we imaged single bright fluorescent beads with a peak emission wavelength at λ= 560 nm (Molecular Probes, 540/560 carboxylate-modified FluoSpheres, 100 nm diameter) that are simultaneously visible in both detection channels and can be localized in each channel to a very high precision using double-Gaussian fitting of the DH-PSF images (Supporting Information). By repeatedly scanning the position of beads throughout the entire 3D field-of-view (~30×30×1.5 μm), we assembled a large set (N = 4544) of corresponding control point pairs to finely calibrate the spatial differences in the DH-PSF optical response function at many locations in the two image domains. We imaged each bead position 7–8 times, which allowed us to estimate position for each bead with a measured standard error of the mean (s.e.m.). Averaged over all bead positions, the average s.e.m. values are 1.34, 1.39, and 1.84 nm in the reflected channel and 1.18, 1.22, and 1.55 nm in the transmitted channel in x, y, and z, respectively. We used this large set of control point pairs to optimize the parameters of a locally-weighted quadratic mapping function (Supporting Information).

Figure 3.

Quantitative image registration in 3D. a A set of beads are simultaneously localized with high precision in both channels producing a set of control point pairs (blue dots). Shown are zoomed-in volumes at the center of the 3D fields-of-view. The mapping function t (x) transforms measured coordinates in the red channel to coordinates in the yellow channel (red circles), x → (x′). b The fiducial registration error (FRE) is the Euclidian distance between the transformed and measured coordinates of corresponding control points. c The target registration error (TRE) is computed by iteratively removing a given control point pair and then computing t (x)_n–1 based on the remaining n-1 control point pairs. The removed control point is subsequently transformed with t (x)_n–1 and the Euclidian distance between the transformed and n-1 measured coordinates of that control points is determined. d The spatial distribution of the TRE (a more conservative measure than the FRE) represents an upper bound of the performance of t (x). e To estimate the TRE at any arbitrary location in the 3D image domain, we interpolated the TRE spatial distribution between the respective (x′, y′, z ′) coordinates of the control points with a natural neighbor algorithm. From the spatial distribution of the interpolated TRE, it is evident that there is more variation in the x and y dimensions than in. Because the axial z dimension is sampled much more densely than the transverse dimensions, this highlights the dependency of t (x) on the local density of control points (Supporting Information). (The axial z dimension is sampled much more densely than the transverse dimensions.

An accurately quantified mapping function defined over the entire 3D field of view is essential for any wide-field high-resolution microscopy method that relies on computational registration and fusion of image data during postprocessing. Sampling the image domains with a large set of control points makes it possible to fully assess the performance of different mapping functions. In general, the performance of any image transformation function is best quantified at the locations of the control points by the fiducial registration error (FRE) and in the spaces between the control points by the target registration error (TRE).^{26, 27} Using our entire set of control points and using a locally-weighted 3D quadratic transformation function, we achieved an FRE of 7.84 nm and a TRE of 9.53 nm when averaged over the entire 3D field-of-view (Figure 3bc). Furthermore, the spatial distribution of the TRE showed uniformly small values in the interior of the image domain and increased slightly only at the edges of the field-of-view (Figure 3de). The major factors contributing to non-zero registration errors are discussed in more detail in the Supporting Information.

A flexible locally-weighted mapping function is capable of compensating differential aberrations between the two channels over a large range of spatial frequencies and is particularly appropriate to use when the various aberrations of the optical system have not been fully quantified. Given that for our set of control points the local Gaussian weights have an average range of 〈σ_i〉 ~ 634 nm (Supplementary Figure 2d), our locally-weighted quadratic mapping function is flexible enough to account for even small-scale image distortions that occur over length scales as small as ~600 nm and it can identify regions in the field of view where data collection might not be reliable (Supplementary Movie 1).

Importantly, global mapping functions may not be flexible enough to accurately register high-resolution single-molecule localization data. Global mapping functions have the advantage that they can be estimated from only a few corresponding control point pairs, but, while the FRE estimated from such a small set can be quite satisfactory (~5 nm)²⁸, the registration error throughout the rest of the image domain reflected in the TRE will likely be much larger, especially for 3D applications. We found that the performance of a single polynomial mapping function applied globally to the entire image domain was highly variable and extremely dependent on the 3D locations of the utilized control points (Supplementary Figure 2ef), thus our locally-weighted map is superior.

The 3D locally-weighted image registration procedure makes image registration errors smaller than the localization precision of our single-molecule localization data. Specifically, the total photons detected from fluorescent proteins typically yield a localization precision of ~30 nm, which is about a factor of 3 larger than the obtained registration errors. If we express the error in distance measurement between two single molecules as ${\sigma }_{\mathit{dist}}=\sqrt{{\sigma }_{\mathit{loc},1}^2+{\sigma }_{\mathit{loc},2}^2+{\sigma }_{\mathit{reg}}^2}\approx \sqrt{{\sigma }_{\mathit{loc}}^2+{\sigma }_{\mathit{loc}}^2+{\left({\sigma }_{\mathit{loc}}/3\right)}^2}$, then it follows that σ_dist is increased by only $\left(\sqrt{2.11}-\sqrt{2}\right)/\sqrt{2}\approx 3\%$ by the presence of the image registration error σ_reg. It is important to note that in single-molecule localization experiments with brighter labels that are able to localize emitters to a precision of <10 nm and that rely on image registration^{29, 30}, the image registration error, unless it is further reduced (e.g., by strategies discussed in Supplementary Information), may likely represent a limiting factor in co-localization accuracy.

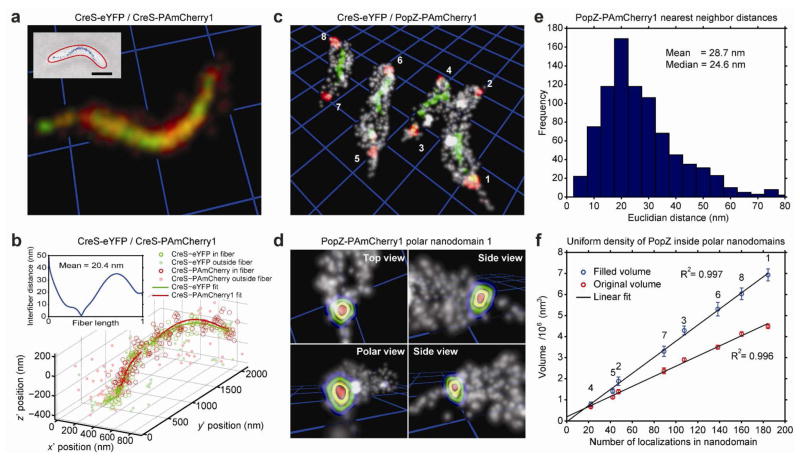
To demonstrate the quality of the image registration procedure, we imaged a Caulobacter strain expressing CreS-eYFP and CreS-PAmCherry1 (JP431) simultaneously (Supporting Information). CreS is an intermediate filament-like fiber that is essential for the characteristic crescent shape of the Caulobacter cell^{21, 31}. For CreS-eYFP, we obtained a median localization precision of (σ_x, σ_y, σ_z) = (30.3, 31.9, 46.8) nm and for CreS-PAmCherry1, we obtained (σ_x, σ_y, σ_z) = (28.0, 29.1, 43.1) nm. After image registration, the two fibers overlapped well visually as judged from the rendered 3D reconstructions (Figure 4a and Supplementary Movie 2). To quantify the quality of overlap, we fit two parameterized helical curves to the eYFP and PAmCherry1 single-molecule localizations separately (Supporting Information). Even in the presence of stochastic sampling of the fiber (which might skew the parametric fits in 3D space), we achieved very good agreement between the eYFP and PAmCherry1 estimates for the 3D CreS fiber structure (Figure 4b). Similar values for the average separation between eYFP and PAmCherry1 fits were found for other fibers as well (34 ± 14 nm, mean ± s. d, n = 8 fibers).

Figure 4.

Two-color super-resolution imaging in live Caulobacter cells. a The fully characterized mapping function produces high-quality 3D overlap of CreS-eYFP (green) and CreS-PAmCherry1 (red) labels that are incorporated into the same CreS fiber (fiber 3, Supplementary Figure 3) in a live JP431 Caulobacter cell (inset). Single-molecule localizations are visualized as Gaussian spheres of width σ equal to the average localization precision. Yellow/orange volumes mark regions of mixing between eYFP and PAmCherry1 localizations. Brightness and contrast of the image are adjusted to emphasize the high density of molecules attached to the fiber, rather than isolated single molecules. Gridline spacing (blue) and scale bar is 1 μm. For an animated sweep through this volume, see Supplementary Movie 2. b Parametric helical fits to CreS-eYFP (green) and CreS-PAmCherry1 (red) localizations of fiber 2. Empty circles denote localizations within 3.5w of the calculated radial distributions and filled circles denote cytosolic localizations that were not included in the fit (Supporting Information). The histogram inset shows the shortest Euclidian distances between the two helical fits over the normalized length of the CreS-PAmCherry1 fiber. c Multicolor 3D reconstruction of the CreS-eYFP fiber (green), PAmCherry1-PopZ polar nanodomains (red), and the Caulobacter cell surface (gray) in strain JP432. Gridline spacing (blue) is 1 μm. For an animated sweep through this volume, see Supplementary Movie 3. d PopZ nanodomain 1 fills a large portion of the polar space (perspective rendering; contours delineate increasing PAmCherry1-PopZ probability density enclosed within the nearby surface PAINT localizations in gray, see also Supplementary Movie 4). e Measured nearest neighbor distances between individual PAmCherry1-PopZ localizations within polar nanodomains 1–8 indicate fairly dense sampling. f Estimated volumes of the indicated PopZ nanodomains before and after filling unsampled spaces in the interior of the clustered PAmCherry1-PopZ localizations. Error bars are ± 1 s.d. (Supporting Information). Both the filled and unfilled volumes correlate linearly with the measured number of PAmCherry1-PopZ localizations.

We further analyzed the cell-to-cell variability of the CreS fiber and its interaction with the different fluorescent protein fusions. Using the best-fit curves to eight individual fibers, we measured the radial distributions of the single-molecule localizations relative to the curve and used them to estimate the apparent Gaussian widths of these CreS fibers (Supporting Information). For CreS-eYFP we obtained w_CreS–eYFP = 40 ± 5 nm (mean ± S.D) and for CreS-PAmCherry1 we obtained w_{CreS–PAmCherry1} = 50 ± 8 nm (Supplementary Figure 3cd). These widths are consistent with our prior CreS-eYFP result of 39 nm, where a Gaussian fit of a 1D line profile drawn through a 2D projection image was used¹³. Given the fact that the localization precisions for both labels are approximately the same under our experimental conditions, the discrepancy between the CreS-eYFP and CreS-PAmCherry1 estimates may point to an alteration in the binding affinity to the fiber structure due to the different fluorescent protein labels. Indeed, more cytoplasmic localizations were observed for the PAmCherry1 fusion.

It has been previously shown that C-terminal CreS-GFP fusions localize to the ventral side of the crescent cell only if they are expressed at very low concentrations on top of native CreS background²¹. The expression levels in our experiments, tuned to collect a sufficient number of single-molecule localizations, are high enough to cause the CreS fiber to detach from the cell membrane. Presumably, once the membrane anchoring points are lost, the free CreS-fibers start to curl up into a more curved morphology, suggesting that the native stretched out morphology of CreS is under tension³¹. The helical fits to our data (collected 120 minutes after the start of induction) show that there are noticeable variations in pitch and radius along the detached CreS fibers in addition to variations in handedness between individual CreS fibers (Supplementary Figure 3ed). These detailed measurements of the morphologies of the doubly-labeled CreS fibers conclusively demonstrate the capability of the DH-PSF microscope, as well as the accuracy of our multicolor 3D image registration algorithm.

Next, we imaged a strain of Caulobacter (JP432) that simultaneously expressed CreS-eYFP and PAmCherry1-PopZ and we assembled quantitative two-color 3D reconstructions of these localizations in the context of the cell surface (Figure 4c and Supplementary Movie 3). As before, we observed detached CreS fibers in these cells after expressing the CreS-eYFP fusion (green). The PAmCherry1-labeled PopZ proteins (red), however, exhibited their native localization pattern: PopZ is thought to form a polymeric meshwork-like structure at the cell poles that is fine enough to exclude large ribosomes from the polar space and these ribosome-exclusion zones can be observed in electron micrographs³². Our data show that rather than forming a shell that lines the polar tips of the cells, PopZ forms a solid “plug” that fills a large portion of the polar space. Thus, in our direct 3D images of PAmCherry1-PopZ, the observed morphologies and positioning of these nanodomains relative to the PAINTed cell surface are consistent with the shapes of the ribosome-exclusion zones (Figure 4d and Supplementary Movie 4).

For the 4 cells shown in Figure 4c, we observed between 20 and 185 PAmCherry1-PopZ localizations in the polar nanodomains and only very few (<50) diffuse cytosolic localizations using exposure times of 50 ms. Due to the propensity of the PAmCherry1-PopZ fusions to localize to the cell poles and the small available volume of this region, these localizations are much denser than e.g. the CreS-eYFP fusions in the same cells. The mean Euclidian nearest neighbor distance between labeled PopZ proteins within the polar endcaps of these four cells peaks at ~20 nm (Figure 4e). These higher densities allow us to additionally estimate the volume of the PopZ nanodomains without the need to express a high concentration of labeled proteins in addition to the native PopZ background (Figure 4f and Supporting Information). Given the previously reported cell cycle-dependent accumulation of PopZ at the poles^{19, 20, 32}, we observe, as expected, a sizable distribution in PopZ nanodomain volumes, when imaging an unsynchronized population of cells. Strikingly, we observe a linear correlation between the PopZ volumes and the numbers of observed PopZ-PAmCherry1 localizations suggesting a constant density of labels among the four cells independent of the expression level in a given cell (Figure 4f). We would not expect to see such clear linear correlations, if the relative PAmCherry1-PopZ and wild-type PopZ expression levels fluctuated excessively between cells. If we assume, on the other hand, that the detected PAmCherry1-PopZ molecules faithfully report on the overall PopZ concentration (the imaging conditions are the same for all four cells), then our data further suggest that the PopZ volume density is constant, which could arise from an underlying PopZ ultrastructure that is invariant from cell to cell. This conclusion is indeed corroborated by previous results obtained with electron microscopy showing that the sizes of the ribosome exclusion zones correlate with the overall PopZ expression levels³². Here, our 3D super-resolution single-molecule data allows us to directly quantify this correlation.

This study conclusively demonstrates the capabilities of the phase mask-based dual-channel DH-PSF microscope to produce quantitative multicolor 3D super-resolution images in living cells with only a simple modification of a standard microscope. Combined with a comprehensive registration algorithm, the method yields both visual and quantitative co-localization between eYFP- and PAmCherry1-labeled CreS and PopZ, as well as the PAINTed cell surface. Biologically relevant parameters are extracted from the resulting images: For the CreS fibers, we determined the intracellular locations, the 3D curvatures, and the widths. For the PopZ nanodomains, we determined the intracellular locations, the shapes, and observed a constant volume density. The dual channel DH-PSF detection scheme (Figure 1a) can be implemented with minor modification to existing 2D super-resolution microscopes and can readily be used with additional fluorophores to simultaneously image three or even four spectrally distinguishable labels^33–35. Thus, the dual-channel phase mask-based DH-PSF microscope and the accompanying image registration and analysis framework can now provide the basis for further super-resolution studies of the 3D topology of intracellular protein architecture and organization, foreseeably in a wide variety of cell types.