Abstract
Two experiments are reported concerning the perception of ground extent in order to discover whether prior reports of anisotropy between frontal extents and extents in depth were consistent across different measures (visual matching and pantomime walking) and test environments (outdoor environments and virtual environments). In Experiment 1 it was found that depth extents of up to 7 m are indeed perceptually compressed relative to frontal extents in an outdoor environment, and that perceptual matching provided more precise estimates than did pantomime walking. In Experiment 2, similar anisotropies were found using similar tasks in a similar (but virtual) environment. In both experiments pantomime walking measures seemed to additionally compress the range of responses. Experiment 3 supported the hypothesis that range compression in walking measures of perceived distance might be due to proactive interference (memory contamination). It is concluded that walking measures are calibrated for perceived egocentric distance, but that pantomime walking measures may suffer range compression. Depth extents along the ground are perceptually compressed relative to frontal ground extents in a manner consistent with the angular scale expansion hypothesis.
Keywords: Spatial perception, path integration, distance perception, leaky integration, angular scale expansion
Systematic perceptual biases are commonly observed in studies of spatial perception. For example, perceived surface orientation relative to horizontal is exaggerated both for large distal surfaces such as hills (Hajnal, Abdul-Malak & Durgin, 2011; Kammann, 1967; Li & Durgin, 2009, 2010; Proffitt, Bhalla, Gossweiler & Midget, 1995; Ross, 1974) and for small surfaces within reach (Durgin, Li & Hajnal, 2010; Li & Durgin, 2011). Similarly, vertical extents are perceptually exaggerated relative to horizontal extents both for extents formed by large outdoor objects (Chapanis & Mankin, 1967; Higashiyama, 1996; Yang, Dixon & Proffitt, 1999) and for simple 2D lines (Avery & Day, 1969; Fick, 1851; Finger & Spelt, 1947; Kunnapas 1955, 1957; Thompson & Schiffman, 1974). In addition, many studies have found that extents in depth along the ground appear perceptually compressed relative to frontal ground extents (Foley, Ribeiro & Da Silva, 2004; Kudoh 2005; Levin & Haber, 1993; Loomis et al., 1992; Loomis & Philbeck, 1999; Toye 1986; Wagner 1985). Perceptual comparisons between vertical extents and depth extents along the ground show even more extreme biases (Li, Phillips & Durgin, 2011; Higashiyama & Ueyama, 1988).
The angular expansion hypothesis
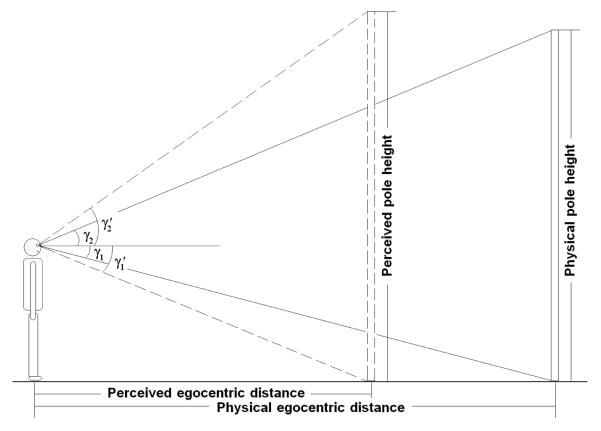
However, whereas some of the phenomena described above could be interpreted in terms of depth compression along the line of sight (a failure of depth perception), Durgin and Li (2011; Li, Phillips & Durgin, 2011) have proposed a quantitative functional account for all of these phenomena in terms of angular biases affecting the evaluation of the geometry of action space. We will call this exaggerated angular coding idea, the angular expansion hypothesis. The proposed functional account is that angular variables are so important that coding them on an expanded scale might be used as a method for reducing error due to additive noise variance in transmission within the brain. In particular, Durgin and Li noted that biases in estimates of egocentric ground extent (egocentric distance underestimation) were quantitatively consistent with newly measured biases (overestimation) in the perceived angular declination of gaze (see Durgin, Leonard-Solis, Masters, Schmelz & Li, 2012). Li et al. showed that new and existing data (Higashiyama & Ueyama, 1988) concerning the perceptual comparison of egocentric extents and vertical extents could be perfectly fit by a parameter-free model based on these previously-measured errors in perceived gaze declination. The geometry of the situation is shown in Figure 1. In addition, Li and Durgin (2009) had already shown that these biases in perceived declination of gaze were implicated in the perception of hills. That is, when looking down a hill, depth compression along the line of sight should predict the hill would look less steep, but hills are overestimated from the top as well. Biases in perceived gaze declination (measured in the absence of hills, Durgin & Li, 2011) can quantitatively explain downhill perception data in combination with bias in the perception of optical slant (Li & Durgin, 2009, 2010).
Figure 1.
Illustration of how a misperception in angular gaze declination can account for empirical matches between perceived egocentric distance and vertical extent (Li et al., 2011). Angular gaze declination (and elevation) is exaggerated with a gain of 1.5 (Durgin & Li, 2011). Egocentric matches to vertical extents are highly biased (Higashiyama & Euyama, 1988) in a manner that is perfectly predicted by this 1.5 gain (Li et al., 2011).
Angular variables are extremely useful sources of information about distance along the ground, and they are relatively easy for the visual system to estimate with precision. Wallach and O’Leary (1982) regarded gaze declination as a learned distance cue and showed that altering perceived gaze declination with prisms had the predicted effect on perceived size of an object on the ground (this distance effect is not to be confused with the effects of eye-height scaling – Wraga, 1999). Similarly Ooi, Wu and He (2001) showed that aftereffects on perceived elevation of gaze affected egocentric walking performance, and Messing and Durgin (2005) showed that shifting the visible horizon by 1.5° in a virtual environment produced predicted quantitative effects on both explicit egocentric distance estimation and egocentric walking measures.
Note that the main perceptual error (egocentric distance underestimation) implied by the angular expansion hypothesis should not be detectable by action measures such as egocentric walking under normal circumstances because locomotor behavior is calibrated by experience (Durgin, Fox & Kim, 2003; Durgin, Hajnal, Li, Tonge & Stigliani, 2010; Durgin, Pelah, et al., 2005; Rieser et al., 1995). That is, if people walk accurately to egocentric targets, it may be that they can accurately update their (biased) angular position with respect to a target (i.e., accurately predict changes in perceived angular direction to the target) based on experience even though they perceive its location according to a biased angular metric. Prism adaptation studies show action can become accurate, even when perception is not, by means of changes in proprioception rather than in vision (e.g., Harris, 1963). Although Loomis and Philbeck (2008) have argued against a calibration account of walking performance, they did so with respect to theories of non-linear compression of perceived distance (e.g., Gilinsky, 1951). The angular expansion hypothesis, however, supposes that perceived egocentric distance in locomotor space is approximately linearly compressed so that linear calibration would be effective.
The angular expansion hypothesis has been successfully applied to findings regarding the perception of egocentric extents, vertical extents and slant whereas other theories tend to have a more limited scope (see Li & Durgin, 2012a). In the present paper we will show how the angular expansion hypothesis can be applied to an anisotropy of perceived extents on the ground plane. It has been shown using a variety of techniques (e.g. magnitude estimation, perceptual matching, ratio estimation, walking measures) that the perceived length of ground extents in depth is substantially compressed relative to perceived frontal distances (Foley, Ribeiro & Da Silva, 2004; Kudoh 2005; Levin & Haber, 1993; Li et al., 2011; Loomis et al., 1992; Loomis & Philbeck, 1999; Toye 1986; Wagner 1985).
Li and Durgin (2012a, see also Li et al., 2011) suggested that there were actually two forms of distance anisotropies. One, associated with shape tasks such as the aspect ratio task developed by Loomis et al. (1992), is quite a large anisotropy that seems to be related to the misperception of local optical slant (Li & Durgin, 2010, 2012a; Loomis & Philbeck, 1999; Loomis et al., 2002). This form of anisotropy can also be related to the compressive distance functions observed for small exocentric extents, and typically exceeds 1.5 to 1. In the present work we seek to better characterize a second form of anisotropy which the angular expansion hypothesis attributes to the linear compression of perceived egocentric distance associated with errors in perceived gaze declination (Durgin & Li, 2011). This anisotropy was demonstrated, for example between frontal extents and egocentric distances (Li et al., 2011), but may also apply to large exocentric extents. The magnitude of this anisotropy was typically around 1.3 to 1.
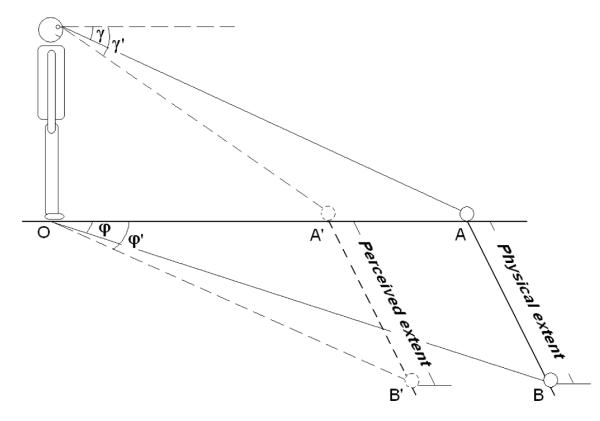
Li et al.’s (2011) findings can be understood by the angular expansion hypothesis using the diagram illustrated in Figure 2. The angular expansion hypothesis supposes that the location of target A is misperceived to be A’ because the perceived gaze declination to target A (i.e. γ’) is exaggerated by about 1.5 times relative to its physical gaze declination γ (Durgin & Li, 2011). That is, the perceived egocentric distance OA’ is foreshortened relative to its physical distance OA. Note that if the azimuthal (horizontal) gaze angle to target B (i.e. φ) were perceived accurately, the model should predict that frontal distances would be scaled similarly to egocentric distances, and no anisotropy would be observed. In order to fit the observed anisotropy, φ’ must also be exaggerated (i.e. φ’>φ) so that the perceived frontal extent A’B’ is largely the same as its physical extent AB. In this way, the perceived frontal extent could preserve its perceived size (show good constancy) but the perceived ratio between the frontal and the egocentric extent would be exaggerated. Based on the matching data of Li et al., the observed expansion gain of φ’ was about 1.2. That is, when participants were asked to match their distance from point A to the magnitude of the extent between point A and point B, they should set the perceived angular distance between A and B to 45° (and indeed a few subjects mentioned using this strategy in post-experimental interviews), but the mean matched angle was instead 37.5° (even for those who mentioned the 45° strategy).
Figure 2.
Diagram depicting a possible angular expansion model of the foreshortening in perceived egocentric extent relative to the perceived frontal extent (i.e. the finding of Li et al., 2011). The depicted configuration ABO lies on a horizontal ground plane.
Action measures of distance
It has been shown that naïve participants can walk to a previewed target location without vision pretty accurately up to 20 m (e.g. Loomis et al., 1992; Rieser, Ashmead, Talor, and Youngquist, 1990; Thomson, 1983). Although this seems contradictory to the assumption that perceived gaze angles are exaggerated and that perceived egocentric distances are foreshortened, as we have mentioned above, there is no actual contradiction because action can be calibrated to visual experience (Harris, 1963; Held & Freedman, 1965; Li & Durgin, 2012b; Rieser et al., 1995). Thus, accurate action does not necessarily guarantee veridical perception. Similarly, in the debate about whether the Ebbinghaus circles illusion affects grasping, the key issue is not whether grasping is calibrated or not (it clearly must be), but whether grasping differs across illusion conditions, and thus whether or not perception-for-action is immune to the Ebbinghaus illusion (Franz & Gegenfurtner, 2008: Milner & Goodale, 1995). In fact, in the present case, distance anisotropy between frontal extents and depth extents along the ground has been seen in walking measures in several labs.
Loomis et al. (1992) asked participants to walk to two targets that defined a frontal extent in quick succession. While the walking response to the first target was pretty accurate, the walked interval between the two targets overshot the physical extent. The fact that the egocentric distance is walked accurately and the frontal distance is overshot is consistent with the idea that the perceived egocentric distance was compressed relative to the perceived frontal distance, and that walking is calibrated to egocentric distance (because those are the distances that, by definition, we walk). Note that we will assume in our exposition that egocentric distance is underperceived both because that is what the angular scale expansion hypothesis implies (see Figure 1), and because essentially all studies of explicit egocentric distance judgments show that verbal estimates of egocentric distance underestimate it. Note that the compression of distance implied by both these kinds of evidence is fairly constant (about 70% to 80% of physical distance).
Philbeck, O’Leary and Lew (2004) developed a pantomime walking paradigm to assess perceived extents on the ground. Participants were asked to preview an exocentric extent and then pace off the length of the extent without vision from the initial viewing position. Note that pantomime walking involves actual locomotor travel, but not toward the target location. It was shown by Philbeck et al. that frontal extents are also overshot in pantomime walking, which has been replicated by others (Geuss, Stefanucci, Creem-Regehr and Thompson, in press; Kudoh 2005). This, again, suggests that walked egocentric distance (i.e., walked distance in a pantomime walking task) is perceptually compressed relative to the perceived frontal extent, which is also consistent with the prediction of the angular expansion hypothesis in conjunction with the calibration hypothesis (i.e., people think they are walking less far than they actually walk).
Although the pantomime walking task (used by Philbeck et al., 2004) and the visually directed walking task (used by Loomis et al., 1992) showed similar trends (i.e. overshoot) in response to a frontal extent, it must be emphasized that the two action tasks might be very different kinds of responses as the differences between the name “pantomime walking” and the name “visual directed walking” suggest. In the visually directed walking task, participants may continuously update their location in relation to the previewed target(s) during walking and continuously estimate the remaining distance (or angular relation) between their updated position and the target(s). However, this self-updating strategy can’t be used in the same way for the pantomime walking task because the target, by definition, is not in the direction of the walking.
Conflicting evidence
If pantomime walking is indeed similar to visual matching, we should expect similar distance anisotropy in both the walking and matching tasks. However, whereas visual matching tasks showed dramatic anisotropy (Loomis et al., 1992; Loomis and Philbeck, 1999), the results of pantomime walking studies are much more variable. For example, Philbeck et al. (2004) found no anisotropy overall but reported evidence of anisotropy for the longest extent (3.5 m) they tested. Kudoh (2005) found anisotropy using a walking task but he asked participants to walk along different directions in response to depth and frontal extents respectively, so that there was a confound in his measure (Philbeck et al., 2004). Geuss et al. (in press) found the expected anisotropy in a virtual environment but no anisotropy in the real world; however they used an indoor environment where distances might be estimated relative to the size of the room itself. Because Li et al. (2011) had found identical depth/frontal anisotropies in virtual and real outdoor environments using the egocentric/frontal matching tasks (Figures 1 and 2), we sought to do a similar test for evidence of the expected anisotropy in an outdoor environment.
Overview of studies
In Experiment 1 of the present paper we sought to use both perceptual matching tasks and pantomime walking tasks with the same kinds of outdoor distances. The range of distances used was somewhat larger than previous studies, but largely comparable. To anticipate, we found evidence of a similar anisotropy with both kinds of task.
In Experiment 2 we conducted a similar experiment in a virtual outdoor scene and obtained similar results with the exception that all walked distances were shorter, as would be expected in virtual environments.
Because our walking measures tended to show a compressed range of response relative to matching tasks in both Experiments 1 and 2, we sought in Experiment 3 to better characterize response compression in walking measures. We found that pantomime walking tends to show range compression effects, which may explain why previous studies with pantomime walking have led to conflicting results.
In the General Discussion we will consider whether the angular expansion hypothesis provides a reasonable account of the data.
Experiment 1. Walking and matching in an outdoor environment
In Experiment 1, we sought to investigate the expected exocentric distance anisotropy using both pantomime walking and visual matching paradigms. To make the visual matching paradigm comparable to the procedure of the pantomime walking, we used a new matching paradigm, in which participants were required to adjust an egocentric distance to match the exocentric extent. This seemed roughly parallel to the task of walking an egocentric extent to match an exocentric extent.
Method
The experimental procedures reported in this paper were approved by the local research ethics committee.
Participants
Sixteen Swarthmore undergraduates (7 female) participated in this experiment for payment. All had normal or corrected to normal visual acuity.
Environment and materials
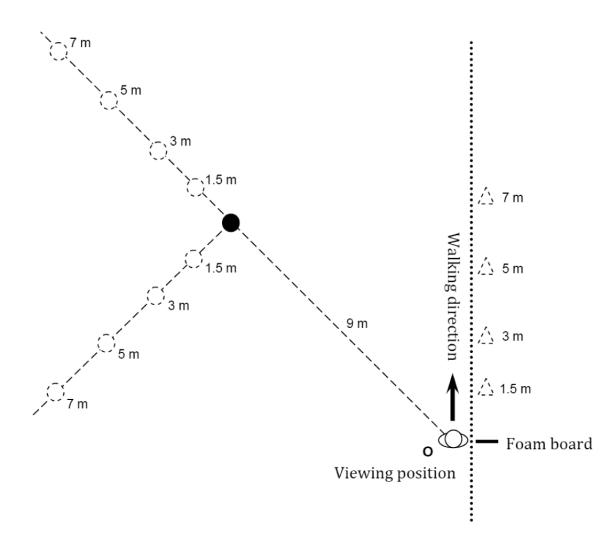
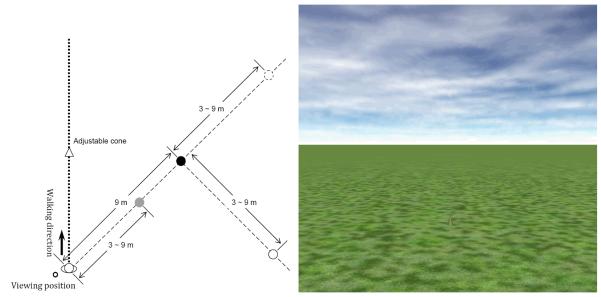
The experiment was conducted in an outdoor grass field (about 40 m × 50 m), surrounded by trees, buildings and a parking lot. A guide wire (more than 50 m long) was stretched across one side of the field between two trees (Figure 3, dotted line) about a meter above the ground. Participants in the walking tasks held on by a segment of PVC pipe, 15 cm long, 2.5 cm in diameter, that could slide along the guide wire. A location 10 m from the middle of the guide wire was marked as the observation/starting point, and was marked by a vertical foam board used, in conjunction with a laser range finder, for measurement of travelled and set distances.
Figure 3.
Diagram depicting the setup in Experiment 1 (top view). The dotted line represents a stretched guide wire for the pantomime walking task. The circles represent the possible positions of cones defining the exocentric extent. The triangles represent the positions of target cones defining egocentric extents.
Exocentric extents were marked, on each trial with two orange sport cones (23 cm tall, 13 cm in base diameter), with one cone (Figure 3, black circle) being fixed at 9 m away from the viewing position and about 45° to the left of the guide wire. The other cone was either along the line of sight to the fixed cone or to the left of it (Figure 3, dashed circles). The positions were marked in advance with labels (stuck into the ground) that could not be seen by participants. Four positions along the guide wire (Figure 3, dashed triangles) were used for the egocentric distance walking task.
Design
All participants did all three types of task in the same order to avoid allowing the perceptual matching task to influence the pantomime walking task: Each participant first did two trials of egocentric distance walking to become familiar with using the guide wire and with blindfolded walking. The first trial was a practice trial with the target distance varied across participants. The target distance of the second egocentric walking trial was fixed to 4 m. Participants then did 8 trials of pantomime walking in which each of four exocentric ground extents (1.5, 3, 5, 7 m) were tested in each of the two extent orientations (frontal and in depth). These eight trials were presented in random order. After the pantomime walking task, each participant then did eight trials of visual matching, seeing the same extents in a new random order. Finally, each participant did four trials of egocentric walking (1.5, 3, 5, 7 m) in random order to provide a baseline of their walking performance.
Procedure
In the egocentric walking task, the target cone was put in position about 25 cm to the right of the guide wire while the participant was looking in a different direction. The participants then stood at the viewing position holding a tube that could slide along the guide wire in their right hand and with a blindfold resting on their forehead. They viewed the target cone freely (usually for only a few seconds), and, when they felt ready, they closed their eyes, pulled down the blindfold with their left hand, and walked along the guide wire until they felt they were right next to the cone. The experimenter then went to the participant’s position and measured the walked distance with a laser range finder. The participants were asked to walk back to the viewing position with eyes still closed. No feedback regarding their performance was ever given to the participants. Back at the starting position, participants were allowed to pull up the blindfold and open eyes, but they were asked to face the opposite direction while the experimenter changed the target position.
The pantomime walking to represent an exocentric distance was similar to that of the egocentric walking task except that the targets were two cones at the left direction relative to the walking guide wire (Figure 3, circles). After an initial viewing, participants were asked to walk along the guide wire with eyes closed until they felt their walked distance matched the distance between the two target cones. No feedback regarding their performance was given. They were then required to face in the opposite direction while the experimenter repositioned the targets.
In both walking tasks, the participants were encouraged to walk confidently and to use a normal walking speed. Participants were told that during blind walking people tend to walk slower than they usually do, and that they should avoid walking slowly. If the participants walked slowly in the practice trial, they were reminded by the experimenter to walk faster.
In the visual matching task, a third cone was placed along the walking guide wire (25 cm to the left of the line so that it was directly in front of the participants). Participants stood at the viewing position and directed the experimenter to move the cone closer or farther until they felt their distance to the third cone matched the distance between the two cones at their left. The participants then turned around while the experimenter measured the distance from the third cone to the viewing position and repositioned the two cones marking the exocentric extent. Then, the participants turned back to look at the cones and a new trial began. In half the trials, the apparent initial egocentric distance between the third cone and the participant was obviously larger than the exocentric extent; in the other half the trials the initial egocentric distance to the third cone was obviously shorter.
Results
We will consider the results with respect to three kinds of question. First we will characterize the overall trends in order to see if there is evidence of the frontal/depth anisotropy for ground extents in each task. Second we will consider whether the quality of data from each task is similar or different to the others. Finally, we will consider whether the different tasks seem to indicate different underlying representations or simply different response characteristics.
Overall trends with regard to anisotropy
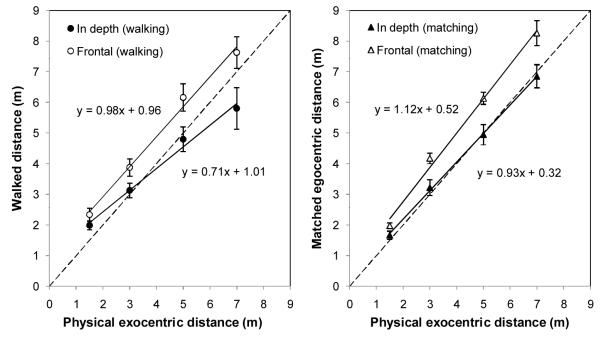
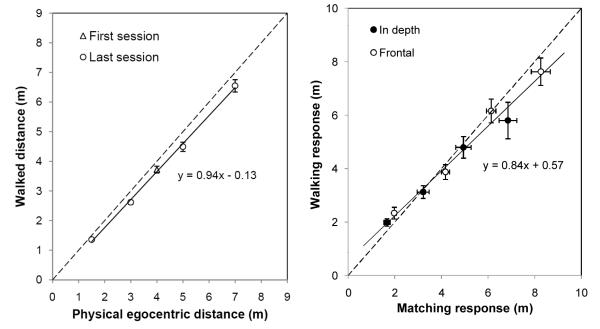
The results of the exocentric distance pantomime walking and of visual matching task are shown in Figure 4. Consistent with the expected frontal/depth anisotropy, the walked distance in response to the frontal extents tended to overshoot the physical extent in all extent conditions. In contrast, the walked distance for the exocentric depth extent only tended to overshoot short physical extents but it undershot long physical extents. The matching data are similar in that the matched distance to the frontal extent was longer than the physical extent in all tested conditions while the matched distance to the depth extent was very close to accurate.
Figure 4.
Performance of the exocentric distance pantomime walking task (left) and performance of the visual matching task (right). Standard errors are shown.
A two way repeated-measures ANOVA (4 Exocentric Distances × 2 Extent Orientations) of the walking data showed not only a reliable effect of Distance, F(3, 45) = 68.3, p < 0.0001, but also a reliable effect of extent orientation, F(1, 15) = 56.6, p < 0.0001, and a reliable interaction between distance and orientation, F(3, 45) = 6.37, p < 0.01, consistent with the different slopes of the two Orientations. The same analysis applied to the matching data also showed a significant effect of Exocentric Distance, F(3, 45) = 262.7, p < 0.0001; a significant effect of Extent Orientation, F(1, 15) = 36.6, p < 0.0001; and an interaction between Distance and Orientation, F(3, 45) = 2.96, p < 0.05. But how should performance be compared across the two tasks?
Consider the depth extent data first. By hypothesis, large exocentric depth extents could be coded as the difference between two egocentric distances. This means that walking measures should be well calibrated for depth extents and that perceptual matching using egocentric extents should be largely unbiased. Indeed, for walking and matching measures, the best fitting regression lines both seem to represent the depth extents with some accuracy, but the gain (regression slope) of the pantomime walking measure is only 0.71, whereas the gain of the perceptual matching measure is 0.93. It seems unlikely that these differing gains reflect different underlying perceptual gains, but it is as if the estimates of the pantomime walking measure to exocentric depth extents are compressed toward the mean response (see Petzschner & Glasauer, 2011)
Consider now the data regarding frontal extents. Here we expected to see anisotropy both for perceptual matching (extending Li et al., 2011) and for walking, and indeed we do. That is, the frontal data are clearly higher than the exocentric depth data for both measures. But the slope of the regression line for the frontal data in the walking measure is nearly 1, whereas that for the perceptual matching measure is 1.12. Given the comparison of depth intervals above, it is reasonable to assume that the walking measure is also compressed relative to the perceptual experience, and this is why the slope is (accidentally) close to 1, even though the actual estimates are all higher than that for the depth interval.
Properties of the measures
Although the egocentric walking task does not bear on the anisotropy, it does bear on the evaluation of pantomime walking as a measure. The left panel of Figure 5 shows the averaged performance of all 16 participants in the egocentric distance walking task. Walking performance was fairly accurate, which replicates previous studies (e.g. Loomis et al., 1992), and it was stable between pretest and posttest. Most significant, from our perspective, is that the variability in performance of egocentric walking is obviously tiny compared to that of pantomime walking. This is consistent with the supposition that egocentric walking can take advantage of spatial updating processes while pantomime walking is more dependent on cognitive processes.
Figure 5.
Left: Mean walking performance in the egocentric-distance walking task. The line is the best linear fit. Right: Comparison of the pantomime walking responses and the corresponding matching responses in Experiment 1. The best fitting line across all the data is shown. Standard errors of the means are shown.
For each target distance (and extent orientation, when relevant) we computed the coefficient of variation (CoV: SD divided by the mean). The average CoV for egocentric distance walking was 0.13, whereas that for pantomime walking was 0.33, which is substantially higher. The CoV for the matching task was intermediate. A t-test comparing CoVs across all eight stimulus items found that the matching task was reliably less variable than pantomime walking, t(7) = 2.91, p = . 0228. Moreover, for perceptual matching, CoVs were higher in the depth orientation (0.28) than in the frontal orientation (0.17), t(3) = 3.77, p = .0327, which is consistent with the idea that the estimation of depth intervals is more complex than the estimation of frontal intervals. In contrast, CoVs for pantomime walking, though numerically lower for frontal extents (0.31) than for depth extents (0.35), were not reliably different for the two orientations, t(3) < 1, presumably because the inter-subject variability was more extreme for this measure. Finally, the CoVs for egocentric distance (visually directed walking) were not reliably lower than those for perceptual matching for frontal extents, t(3) = 2.11, p = .1259, but they were reliably lower than the CoVs for perceptual matching for depth extents, t(3) = 5.67, p = .0109. Overall, the pantomime walking data were more variable than the matching task data and also showed some of the range compression associated with certain kinds of path integration tasks (e.g. Petzschner & Glasauer, 2011).
Do the measures tap different perceptual representations?
Although the evidence reviewed above suggests clear distance anisotropy in both the walking and the matching tasks, it might still be asked whether it is the same anisotropy in both cases. We therefore considered the ratio between the response to the frontal extent and the response to the depth extent as a function of extent length and task. A 4 × 2 (Extent Length × Measure) repeated-measures ANOVA on these ratios showed no reliable effect of Measure, F(1, 15) < 0.001, p = 0.98. There was also no reliable effect of Extent Length, F(3, 45) = 1.93, p = 0.14, (though the anisotropy appears somewhat weaker for the very shortest length), and no reliable interaction between Extent Length and Measure, F(3, 45) = 2.08, p = 0.12. This suggests that the magnitude of the anisotropy found with the walking and matching tasks are consistent with one another and probably reflect the same perceptual experience. The overall average ratio was 1.30.
The right panel of Figure 5 illustrates the relationship between the two measures for each of the eight tested extents by plotting the mean walking response as a function of the mean matching response for each stimulus. A single best-fit line through all the data show that, overall, the walking data have a gain of 0.84 relative to the matching data. This is consistent with the idea that the two measures are sensitive to the same anisotropy, but have different output gains – which may be due to range compression in the pantomime walking measure.
Discussion
As we reviewed above, several investigators have reported evidence from walking tasks that suggest that frontal intervals appear larger than their corresponding depth extents. Here we have used a pantomime walking task as well as an egocentric distance matching task to test whether such an anisotropy would be found in an outdoor environment. The results showed the same amount of anisotropy for both measures. The anisotropy in the matching task is similar to the one observed by Li et al. (2011) using an egocentric matching task in which the participants set their egocentric distance from one end of a frontal extent to match the length of the frontal extent.
Although a number of investigators have used visual matching tasks for small configurations (e.g., Loomis et al., 1992; Philbeck et al., 2004) and found large anisotropies that were contrasted with egocentric walking tasks, we developed a visual matching paradigm that was more consistent with a pantomime walking paradigm (both paradigms involve matching a large exocentric extent with an egocentric extent). Whereas the classic aspect ratio task (Loomis et al., 1992) may be primarily affected by distortions in perceived optical slant (Li and Durgin, 2010, 2012a) or perceived shape (Loomis et al., 2002), the egocentric distance matching paradigm used in the present study requires explicit matches between two fairly large intervals in different parts of space, and is more likely related to distortions in the perceived direction of gaze. The fact that a small, but consistent distance anisotropy was observed in the egocentric distance-matching paradigm suggests that the exocentric distance anisotropy is a robust phenomenon – at least in an outdoor field.
The overshooting of the frontal extents by pantomime walking is consistent with the finding that the perceived egocentric distance is compressed relative to the perceived frontal extent (Li et al., 2011). The overshoot of the 1.5 m depth extent replicated Philbeck et al.’s (2004) finding, and is consistent with Kudoh’s observations of anisotropy. Because the walking direction was fixed, the present anisotropy cannot be attributed to walking direction (Philbeck et al., 2004). Moreover, the present walking data cannot simply be attributed to Philbeck et al.’s proposal that overshoot occurred only as a result of adaptation to walking. By using a larger range of distances and novel perceptual matching task, the present data help to support the notion that there are real anisotropies between frontal extents and depth extents even when the judgments can’t be reduced to shape judgments
Experiment 2. Walking and matching in a virtual environment
Geuss et al. (in press) reported no anisotropy in an indoor walking task similar to the pantomime walking task of Experiment 1, but they did find an anisotropy in an experiment using virtual reality. They proposed that this meant that although depth extents were compressed in VR, frontal extents were not. This would be rather surprising, if true, because although size-distance-invariance has been routinely disputed in the literature, a complete dissociation would be unusual. That is, frontal extents, insofar as they are perceived as nearer, ought to seem smaller in the same proportion. Moreover, the idea that frontal intervals in VR are uncompressed is difficult to square with the exact replication reported by Li et al. (2011) of their egocentric L-shaped matching task in VR and in an outdoor environment. They found that perceptual matches in VR and in an outdoor environment were not different, consistent with the idea that the scaling of virtual space was isomorphic across dimensions.
If frontal extents are compressed in VR by about 75%, for example, then based on Experiment 1, we should predict that pantomime walking of frontal extents might appear to be surprisingly accurate simply because pantomime walking exaggerated frontal extents by 1.3 in Experiment 1, so the two errors might roughly cancel out. Conversely, pantomime walking of depth extents in VR should no longer be properly calibrated because of VR compression. Nonetheless, we should predict that the relative perceived distances would be just as they were observed in our outdoor study.
Method
Participants
Twenty-five Swarthmore undergraduates participated in this experiment for payment. All had normal or corrected to normal visual acuity. None had participated in Experiment 1.
Design
As in the outdoor experiment, pantomime walking was employed as one measure and perceptual matching to an egocentric interval was used as a second measure in VR. This time, three types of ground extent (egocentric, exocentric frontal, and exocentric depth) were used as the visual stimuli in both the pantomime walking and the visual matching tasks. Seven extent lengths were used for the three types of extent, but for each task type (e.g., pantomime walking) each participant only received each of the seven lengths once (in one of the 3 types of layout), and thus only contributed 7 trials for each measure to the 21 trial types tested across participants for each measure. In the walking task, participants were required to pace out the same distance as the presented extent. In the matching task, participants were asked to adjust an egocentric distance (by moving a virtual cone) to match the presented extent.
The order of trial types is schematically illustrated in Figure 6. To provide a baseline of visually-directed walking performance, each participant did 4 trials of egocentric walking to targets presented in the physical environment (a hallway), with 2 trials (3.5 and 8.5 m) at the very beginning and 2 trials (7.5 and 4.5 m) at the very end of the walking session. After the 2 initial visually-directed walking trails, each participant did 7 trials of pantomime walking in the virtual environment in 3 blocks which represented (in counterbalanced order) the three types of extent to be matched: Within each block, the same extent presentation (egocentric, frontal or in depth) was shown. Following the walking trials, each participant did 7 matching trials (Mx in Figure 6) based on the same trial structure as for pantomime walking. The order of the extent presentation was counterbalanced across participants for both the walking and the matching tasks. Because there were 7 extent lengths for each extent presentation condition (i.e. total 21 different visual stimuli), each participant were shown only one third of the possible stimuli. The visual stimuli were randomly selected and were presented in random order for each participant with the criterion that every three successive participants got the whole set of stimuli.
Figure 6.

Task sequence used in Experiment 2. Each block represents one trial. Rx represents egocentric walking trials to targets in the real environment. Wx represents the walking trials in the virtual environment. Mx represents matching trials in the virtual environment. Different gray colors represent different extent presentations (i.e. egocentric, exocentric frontal, and exocentric depth). The order of the various extent types was counterbalanced across participants.
Apparatus
The physical environment for the experiment was a long hallway with a guide wire along one side as in the outdoor experiment. Participants stood in the hallway (3 m × 22 m) and wore an xSight HMD (Sensics, Inc.) that has a factory calibrated horizontal field of view of 126° (90° per eye, with 54° binocular overlap) and a vertical field of view of 44°. The optics of the xSight are free of pincushion distortion present in most immersive HMDs. A Hiball 3000 tracker was used to update the orientation and position of the HMD. The virtual scenes were rendered by a two-computer cluster using Vizard (V.4, Worldviz, LLC) at a 60 Hz frame rate. A radio mouse was used by the participants to adjust the position of the movable cone.
Displays
The main experiment was conducted in a virtual environment simulating an outdoor open field covered with realistic grass texture as shown in Figure 7 right (see also, Li et al., 2011). The targets were small orange cones like the one used in the real environment in Experiment 1.
Figure 7.
Overview of the setup in Experiment 2 (left). The dotted line represents the walking direction along the guide wire, which was aligned with the direction of the physical hallway where the experiment was conducted. An image of the virtual environment (right) used in Experiment 2. Note that participants had a panoramic, 44° × 126° field of view, not a small view like this.
In the egocentric extent presentation, an orange cone was presented 45° to the right of the participant’s walking direction (Figure 7 left, gray circle). In the frontal extent presentation, two orange cones were presented to the right of the participant’s walking direction, with one cone fixed at 45° and 9 m from the viewing position as in Experiment 1 (Figure 7 left, black circle) and another cone to the right of the fixed cone (Figure 7 left, open circle). In the exocentric depth extent presentation, two orange cones were presented at 45° to the right of the participant’s walking direction, with one cone fixed at 9 m from the viewing position (Figure 7 left, black circle) and another cone behind the fixed cone (Figure 7 left, dashed circle). In the visual matching task, a purple cone (with the same size as the orange cones) was presented at the walking direction (Figure 7 left, triangle). The position of the purple cone could be moved along the walking direction by the participants using a radio mouse. All that was visible was the field and the cones.
Procedure
In the initial (actual hallway) egocentric walking task, participants were shown a real sport cone (as in Experiment 1) on the ground of the hallway and were asked to walk to its position while blindfolded. The cone was removed after the participants started to walk. No feedback regarding their walking performance was ever given to the participants. In the VR walking task, participants wore the HMD and were presented with virtual cone(s). They signaled the experimenter when ready to walk. The experimenter pressed a key on a radio keyboard to turn off the virtual scenes and record the head-tracked starting position of the participants. In the meantime, the participants closed their eyes, held a small segment of PVC pipe that slid along the guide wire and started to walk. They stopped when they felt the walked distance matched the length of the extent shown to them. The experimenter pressed another key on the keyboard to record the ending position. The participants were then led back to the starting position while the virtual scenes were still turned off. After participants were in position, the experimenter turned on the virtual scenes with a new extent stimulus and a new trial began. In the matching task, participants used a radio mouse to control the movable (purple) cone until they felt their egocentric distance to the movable cone matched the extent presented to them.
Results
Distance underestimation in VR
The results of the egocentric distance walking task are shown in Figure 8. Open symbols represent the walking responses to the real world target and the solid circles represent the walking responses to the virtual target. It is clear that the walking responses at the beginning of the walking task (i.e. open circles) are collinear with the walking responses at the end of the walking task (i.e. open triangles), which suggests that there was no status change in the walking response during the experiment. There was some undershoot in the walking response to the real target, with a walking gain of 0.91. However, the walking responses to the virtual targets substantially underestimated the actual simulated egocentric distance, with a walking gain of 0.71. These data suggest that the perceived egocentric distance in the present VR is compressed by about 78% (i.e. 0.71/0.91) relative to the perceived egocentric distance in the real environment.
Figure 8.
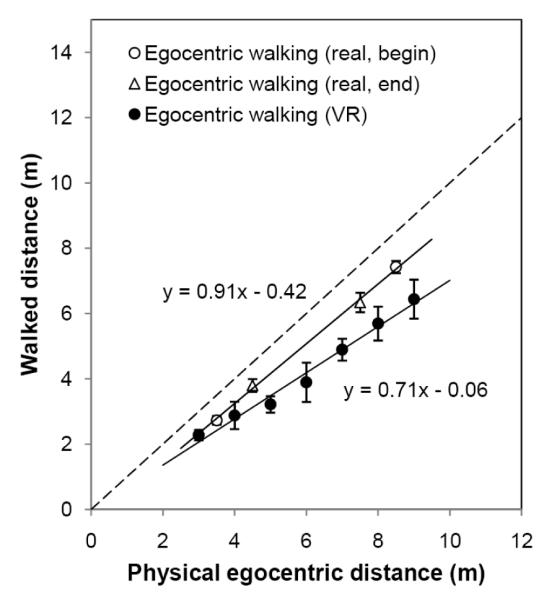
The mean walking responses to the egocentric extent. Open symbols represent responses to physical targets and solid symbols represent responses to virtual target. Standard errors are shown.
Evidence of anisotropy in VR
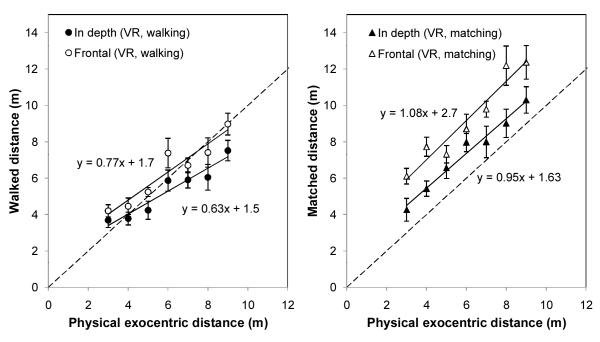
The results of the walking and matching responses to the exocentric extents in the virtual environment are shown in Figure 9. Both the walking and the matching responses to the exocentric depth extent (solid circles and triangles) are systematically less than that to the frontal extents (open circles and triangles). A mixed-effects model of the complete data set with subject as a random effect revealed that the mean response to the depth extent is smaller than the mean response to the frontal extent (95% CI: 0.13 to 0.67 m, t = 2.94, p < 0.01).
Figure 9.
The walking responses (left) and matching responses (right) to exocentric extents presented in the virtual environment. Standard errors are shown.
The smaller responses to the depth extents indicate distance anisotropy. To estimate the anisotropy, we computed the ratio between the response to the frontal extent and the response to the depth extent as a function of extent and task. The ratios in the matching task were not systematically different. In this Experiment the mean ratio overall was 1.23, which is quite similar to the 1.30 ratio found in Experiment 1 in the outdoor environment.
Discussion
Geuss et al. (in press) reported that pantomime walking responses to a frontal extent are fairly close to the simulated extents in VR, whereas pantomime walking responses to depth extents were foreshortened. They concluded that the perceived frontal distance in VR is unaffected by VR size compression, but the data they reported were entirely consistent with the alternative hypothesis suggested by the large literature showing that depth extents are seen as compressed relative to frontal extents. Experiment 2 replicated the main findings of Geuss et al., but provides evidence for the alternative interpretation. Compared to the walking responses for frontal extents in the outdoor environment of Experiment 1, which systematically overshot the actual simulated extents, the relatively accurate walking response to frontal extents in VR suggests the perceived frontal extent in VR is also compressed relative to the perceived frontal extent in the real environment.
Given the mass of evidence of anisotropy between frontal extents and extents in depth from both explicit verbal estimation and now visual matching, the fact that in both Experiment 1 and Experiment 2 we found similarities between pantomime walking and explicit visual matching is most parsimoniously interpreted by understanding that pantomime walking tends to be guided by the same underlying representation as perceptual matching. To avoid contamination of the walking measure by the perceptual matching measure, we always did the perceptual matching task second. Although it is possible that performance of the walking task influenced the visual matching task, the visual matching data are already consistent with other studies (e.g., Li et al., 2011) where pantomime walking was not used and are also consistent with explicit verbal estimation data (e.g., Foley et al., 2004; Wagner, 1985).
Experiment 3: A closer look at pantomime walking
In the present paper it has been necessary to distinguish between pantomime walking (walking out a distance – without visual feedback – so as to represent a previewed distance) and visually-directed walking (walking – without visual feedback – to a previewed target location). In Experiment 1 it was observed that pantomime walking responses were much more variable than visually-directed walking. Indeed, not only was walking more variable than perceptual matching, but it also provided a more compressed response range (as seen in the right panel of Figure 5).
Lappe, Jenkin and Harris (2007) have noted a similar problem with pantomime walking. They argued that path integration during walking is biased because of a leaky integrator. This argument was based on two patterns of data. First, when participants were asked to walk out a distance as a response (i.e., pantomime walking), Lappe et al. found that the responses under such circumstances tended to compress far distances. Conversely if walking was used as the initial stimulus and some other measure was used to assess the integrated distance, they found that this measure tended to be set too short. This posed a puzzle: Were participants overestimating their travel distance (as suggested by the first result) or underestimating their travel distance (as suggested by the second result)? Lappe et al. proposed that a leaky integrator model could account for both these results because integration proceeded differently in the two types of tasks. They proposed that if the magnitude to be produced were given first, then participants would subtract their progress from the total magnitude, but that the integrator would also leak away the (large) magnitude faster at each step.
Petzschner and Glasauer (2011) have proposed a general Bayesian model for response range compression in tasks of this sort. They found that when using path integration with optic flow alone, reproduced distances tended to overestimate short distances and underestimate long distances. In essence, response-range compression, which is what we seemed to observe with pantomime walking tasks in Experiments 1 and 2, might be a generalized form of memory contamination, which can be expressed in Bayesian terms as effects of memory from prior trials on the Bayesian prior.
In order to test the memory contamination theory against the leaky integration theory as a way of characterizing pantomime walking performance, the following reasoning was applied: If the presented interval and the response interval were both pantomime walking (rather than forcing a translation between visual distance and locomotor distance), then leaky integration theory should predict that the second interval would always undershoot the first. This is because not only is the first walking interval subject to underestimation due to leaky integration, but the second interval would then start with that already-low magnitude and proceed to drain it off even more quickly by further leaky integration. In contrast, if the memory contamination account were correct, then the distribution of responses should accurately represent the mean distance (presumably in logarithmic space), but should be symmetrically compressed with shorter distances being overwalked in about the same proportion that longer distances are underwalked. Durgin, Akagi, Gallistel and Haiken (2008) used a distance reproduction task to measure variability in walking performance when the same interval (up to 100 m) was attempted to be produced over and over again (up to 50 times). Because the same interval was used on every trial in each session, there should be no effect of proactive interference. Indeed Durgin et al. reported no evidence of bias such as a leaky integration mechanism should predict.
Many participants engaged in pantomime walking report the use of step counting strategies (e.g., Geuss et al., in press, reported that their participants engaged in step counting). Such a strategy, which seems to be a form of explicit distance estimation, would trivialize the current task because human step lengths are highly stable patterns and their use will lead to higher precision than normal path integration (Durgin et al., 2008; Durgin, Reed & Tigue, 2007). For this reason, participants in the present study were told not to count steps and were also required to store an alphanumeric memory load during the task so that it would be difficult to count steps. In the absence of step counting, memory contamination (proactive interference) predicts response compression such that shorter presented distances would be overwalked and longer presented distances would be underwalked at the time of response.
Method
Participants
Twenty-two Swarthmore undergraduates participated in Experiment 3 for payment. None of them had participated in Experiment 1 and 2. Twelve participants were randomly assigned to the Return condition and ten to the Reproduce condition.
Design and materials
The experiment was conducted in a large field house. In the Reproduce condition, two long guide wires (like the guide wires in Experiments 1 and 2) were set up perpendicular to each other, as shown in the right panel of Figure 10. In the Return condition, a single guide wire was used and a location marker (a stout PVC tube about 1.2 m tall mounted on a sturdy platform) was positioned close the starting position as a salient spatial reference point that was haptically previewed (touched) before each trial. The initial task for all participants was to walk along the guide wire while blindfolded until they were told to stop by the experimenter. They were then to walk the same amount of distance again without feedback. Participants in the Return condition were simply asked to return to the starting position (the marking pole), whereas those in the Reproduce condition switched guide wires and walked along a direction that was perpendicular to their first walking path.
Figure 10.
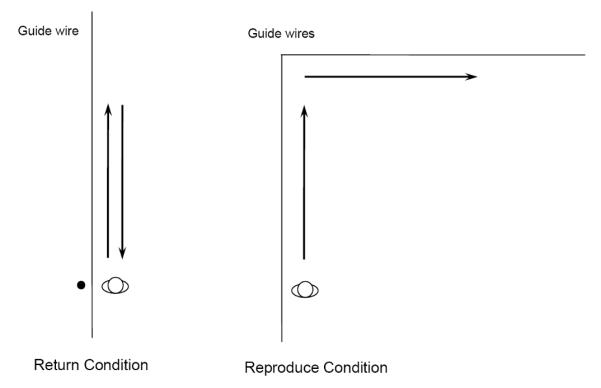
Diagram depicting the setup in Experiment 3 (top view). The lines represent the guide wire, along which the participants walked. The black circle represents a pole at the starting position of the return condition.
Distances walked were measured using a laser range finder. The starting position in the Reproduce condition was planned so that the interval ended at the second guide wire, and participants were led on a long, disorienting roundabout path between trials in both conditions so that they could not easily get feedback about their performance or information about the upcoming trial. Each participant was given 2 practice trials (7 m and 28 m in random order), followed by 7 test trials (5, 7, 10, 14, 20, 28, 40 m in random order). To prevent participants from using step-counting, an alphanumeric cognitive load (8 alternating letters and digits) was used.
Procedure
In the Return condition, participants started from a position that was very close to the PVC pole, which they saw at the beginning of the experiment. Once they were wearing the blindfold, they were required to touch the pole at the beginning of each trial. Before the participants started to walk, the experimenter read an alphanumeric list to them and asked them to keep it in mind during the walk. Then, when they were ready, they started to walk along the guide wire. When they had traveled the desired distance, they were stopped by the experimenter and were asked to report back the alphanumeric list. Then they were asked to turn around and try to return to the starting position (i.e. the pole). During the return trip, no cognitive load was used. When they felt they had reached the pole, they stopped. Their distance to the pole was recorded and then they were led back to the starting position (still blindfolded) by the experimenter in an irregular course (walking far away from the guide wire to avoid providing feedback about their walking performance on the previous trial).
The procedure of the Reproduce condition was similar except that the starting position of each trial was changed according to the target distance of that trial, so that the intersection of the two guide wires represented the target distance. As they reached the intersection, they were stopped by the experimenter and were asked to switch to the second guide wire, which was used in reproducing the distance.
Results
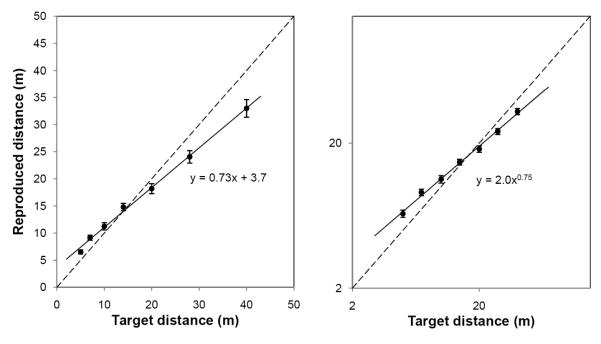
A two way repeated-measures ANOVA (2 Tasks: Return vs. Reproduction × 7 Distances) found no reliable difference between the Return and Reproduce conditions, F(1,20) = 0.94, p = 0.344 and no interaction between Task and Distance, F(1, 20) = 1.47, p = 0.239. There was, of course, a reliable effect of target distance, F(1, 20) = 368.5, p < 0.0001. Figure 11 shows the mean reproduced distances, plotted as a function of the target distance, collapsed across both conditions. The left plot shows the data in linear space (which appears similar to the patterns reported by Lappe et al., 2007, as consistent with leaky integration), while the right plot shows the data in logarithmic space. The main feature of the data shown in Figure 11 is that the reproduced distances were too long for short extents and too short for long extents, as predicted by proactive interference. In the logarithmic plot, the power function fit has an exponent of 0.75. Moreover, the logarithmic plot strongly illustrates that the magnitudes of distance being produced are compressed symmetrically about the logarithmic center of the range of distances used. This pattern of finding strongly supports the proactive interference interpretation of response compression in pantomime walking.
Figure 11.
The reproduced distance as a function of the target distance in Experiment 3. The data are collapsed across walking directions because these did not differ. The same data are plotted in both linear space (left) and logarithmic space (right). Best fitting lines in each space are shown. Standard errors are shown.
As a further test of the proactive interference hypothesis, it might be anticipated that the target distance on the previous trial predicted the ratio between the walked distance and the target distance on each current trial. That is, overshoot or undershoot on trial N might be predicted by the target distance on trial N-1. A mixed effects model of the ratio between produced and presented distance on trial N with presented distance on trials N and N-1 as predictors was tested, with random error terms for subjects as well as random slopes for each predictor showed that there was indeed a reliable effect of the prior trial on the relative response on the current trial, t(14) = 2.62, p = .0204.
Discussion
In Experiments 1 and 2, response compression was observed in the walking task relative to the perceptual matching task. Overall, walking had a gain of about 0.84 relative to perceptual matching in Experiment 1. In Experiment 3, response compression was present even when the walking task was simply to repeat the distance just walked. Whereas Lappe et al. (2007) observed a similar form of response compression for pantomime walking, they modeled this by leaky integration. An alternative interpretation is that the present function was caused by proactive interference: The memory of the just-presented target distance on each trial was contaminated by the memory of prior trials.
Could it be that the use of an alphanumeric memory load produced the proactive interference? After all, the use of an alphanumeric cognitive load is not typical in walking experiments. The memory load was used to mitigate concerns that participants would count steps. This was done because step counting would obviate the need for spatial updating and path integration (Durgin et al., 2008). Although the use of an additional memory burden may, in theory, have exacerbated the problem of proactive interference, the response compression observed for pantomime walking in Experiment 1 is quite similar to that in the present experiment. Since there was no added memory burden in Experiment 1, it is evident that the present results cannot be due entirely to the cognitive load employed here. Indeed, the data of Experiment 3 are quite similar to the patterns of over- and under-shoot observed by Lappe et al. (2007), and those of Petzschner and Glasauer (2011) who employed no additional memory burden in their path integration tasks.
Whereas visually-directed walking can be easily related to normal actions associated with daily life (walking to an intended location), pantomime walking appears to be harder to identify with a specific action in daily life. Walking so as to represent an extent without intending to actually traverse the to-be-represented extent is not a common activity for humans or other animals. Automatic updating during visually-guided action may be experienced in terms of angular variables (e.g., angular or gaze declination) representing target location as an egocentric direction rather than, or in addition to an overall distance, but such variables only apply to the extents we actually traverse. Although humans can estimate walked extents with some precision, it seems that, at the very least, their productions of walked distances in experiments with multiple trials of different lengths may tend to show range compression due to proactive interference across trials. This is sufficient to explain the differences between perceptual matching responses and walking responses in Experiment 1.
General Discussion
The present study was primarily concerned with an anisotropy in the perception of ground extents. Based on visual matching, pantomime walking, and verbal report tasks from several labs suggesting anisotropy, we tested whether relatively large exocentric depth extents along the ground were perceptually compressed relative to frontal ground extents. Li et al. (2011) had observed such a pattern of data for large egocentric extents using a novel perceptual matching task in which observers adjusted their egocentric distance from one experimenter until it appeared equal to the frontally observed interval between that experimenter and a second experimenter. Participants set the egocentric distance too far, consistent with the compression of depth intervals relative to frontal intervals. In that study, the same pattern of anisotropy was found in an outdoor environment and in a simulated outdoor environment in VR. In the present study we utilized an oblique pantomime walking measure previously employed by several other labs, in combination with a novel perceptual matching measure in which an oblique egocentric interval was adjusted to match exocentric frontal and depth extents along the ground. Both measures detected the expected anisotropy, though the walking measure showed additional evidence of range compression. The anisotropy was similar in the outdoor environment and in VR.
Extending the angular expansion hypothesis
The angular expansion hypothesis is based on evidence that two angular variables, optical slant and the gaze declination, are perceptually exaggerated in the range most relevant in action space (Durgin and Li, 2011; Durgin et al., 2010; Li and Durgin, 2009, 2010, 2012a; Li et al., 2011). One direct consequence of this angular expansion is that perceived ground distance in depth should be underestimated, which is consistent with verbal estimation of perceived distance (e.g. Foley et al., 2004; Kelly, Loomis and Beall, 2004).
Modeling exocentric depth extents is slightly more complicated. Empirical evidence suggests that whereas perceived gaze declination (i.e. gaze angle in the sagittal plane) is nearly a linear function (with a gain of 1.5) of actual gaze declination in the range between 0° to 50° (Durgin and Li, 2011), perceived optical slant is a function of both actual optical slant and viewing distance (Li and Durgin, 2010). When viewing distance is held constant, perceived optical slant approximates a linear function of actual optical slant (also with a gain of 1.5). In near space, the bias function of perceived optical slant is very similar to that of gaze declination, so that a horizontal surface would still seem flat even though perceived distances in depth are compressed. However, as distance increases the bias function of the two angular variables separates. Thus, the perceived ground distance determined by perceived optical slant alone would be different from that estimated by perceived gaze declination alone.
Li and Durgin (2012a) suggested that this dual feature of the angular expansion hypothesis made it possible to explain the qualitative difference between perceived egocentric and perceived exocentric distance when the magnitude of the exocentric extents are much smaller than their egocentric distances. It is generally agreed that perceived egocentric distance is a nearly linear function of physical distance but that perceived exocentric distance in depth is increasingly compressed with physical distance (see Loomis and Philbeck, 2008 for a recent review). Li and Durgin suggested that this is because perceived egocentric distance may mainly depend on perceived gaze declination (which is independent of viewing distance) while perceived exocentric distance may depend primarily on the perceived optical slant (which increases as a logarithmic function of viewing distance). However, Li and Durgin further suggested that when the exocentric extent is large, such as in distance bisection tasks, even exocentric distance estimation may depend more on perceived gaze angle.
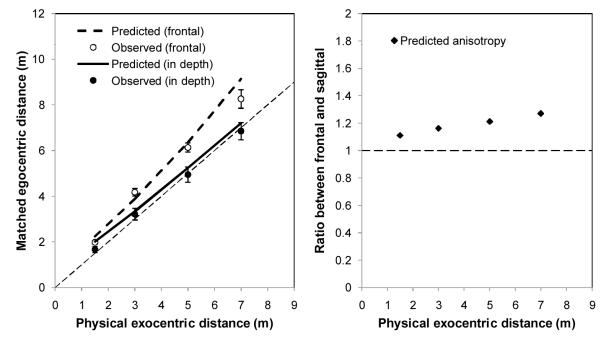
In Experiment 1, the exocentric extents were from 1.5 m to 7 m, which represents a larger range than that used by Loomis et al. (1992, 1 to 3 m) and by Philbeck et al. (2004, 1 to 3.5 m). Although a complete model of exocentric depth extent should take into account both perceived optical slant and perceived gaze declination (by assigning different weights to them), the 7 m extent approaches the range of distance bisection tasks which tend not to show compressive functions (e.g., Purdy & Gibson, 1955). A model of exocentric extent perception that considers only biases in perceived gaze declination is presented in Appendix A. The predictions of the model are shown for Experiment 1 in Figure 12.
Figure 12.
Model predictions and data for the egocentric distance-matching task of Experiment 1. In the left panel, the solid line represents the angular expansion hypothesis prediction for exocentric depth extent matching based on Equation 2 of Appendix A, which has no free parameters; the relevant observed data are the solid circles. The dashed line represents the prediction of the model for frontal extents; the single unknown parameter in this model has been set based on the results of Li et al., (2011); the relevant observed data are the open circles. In the right panel, the predicted anisotropy (ratio between perceived frontal and depth extents) for each exocentric distance is shown.
The prediction shown in the left panel of Figure 12 depends on assuming an azimuthal gain of 1.2 (in perceived azimuthal angular extent), as measured by Li et al. (2011). The predicted data closely match the observed results in the matching task. In fact the only point that does not seem to fit well is the one most similar to the perceptual 45° actually measured by Li et al. It is possible that the structure of the current experimental scene (see Figure 3) provided participants with evidence that the farthest extent was less than 45° to the left, leading to the slight compression in the observed pattern of results for this longest extent.
The right panel of Figure 12 shows that the anisotropy between frontal and sagittal extents viewed at the 9 m distance used in this experiment is predicted to be smallest for small extents. For the 1.5 m extent, which was the primary focus of the investigations of Philbeck et al. (2004), for example, the gaze-based angular scale expansion model predicts only a 10% anisotropy, which may have been difficult to detect using pantomime walking measures. Note, in contrast, that if an L-shape configuration (1.5 m × 1.5 m) were placed on the ground 9 m away, and the direct comparison of the frontal and depth legs were requested, participants might tend to switch to a judgment based on estimating the optical slant (Li & Durgin, 2012a). Under such conditions, the predicted anisotropy based on the angular expansion equations derived by Li and Durgin (2010) would be at least 1.75 (Li & Durgin, 2012a), which is similar to what Loomis et al. (1992) and Philbeck et al. (2004) observed for such stimulus configurations.
Conclusions
The present results are consistent with four main conclusions:
Large depth extents show perceptual compression relative to frontal extents that can be modeled based on the gaze angle exaggeration of the angular expansion hypothesis – which is distinct from the more dramatic anisotropies observed for small exocentric intervals.
Pantomime walking measures showed less sensitivity than perceptual matching measures and show range compression effects that can be attributed to proactive memory interference.
Spatial anisotropies observed in VR are similar or identical to those observed in an outdoor environment. The anisotropy observed by Geuss et al. (in press) in VR appears to be the same as the ones observed here in the outdoor environment and predicted by the anisotropies observed by Li et al. (2011) in outdoor environments (and in VR). Relative to outdoor environments, frontal extents appear to be compressed in VR in the same proportion as are depth extents. Real indoor environments may provide additional scaling cues.
Visually-directed walking performance to egocentric locations was much less variable than was pantomime walking of similar exocentric extents. Studies that use walked distance as a measure of perception should be cautious when comparing the results of pantomime walking (or other forms of path integration) with visually-directed walking. Much as there are multiple sources of information for the perception of visual extent, there are multiple sources of information available for visually directed walking and not all of these can be used for pantomime walking.
Acknowledgments
This research was supported by Award Number R15 EY021026 to FHD from the National Eye Institute. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Eye Institute or the National Institutes of Health. This work was also supported by a Howard Hughes Medical Institute grant to Swarthmore College. Experiment 3 was conducted as a senior thesis by the second author and was presented at the annual meeting of the Vision Sciences Society in 2009. Thanks to Christyn Chambers and Swarthmore Athletics for the use of the Lamb-Miller Field House.
Appendix A.
Consider the perception of the exocentric depth extent in Figure A1. If the gaze declinations to the two endpoints are γ1 and γ2, the corresponding perceived gaze declinations are γ1’ and γ2’, and the average eye height of the participants is H, then the distance of the exocentric extent, D, can be expressed as:
| (1) |
Assuming the perceived variables preserve the same geometric relationship, perceived eye height is accurate, and the perceived gaze angle is 1.5 times the physical gaze angle (Durgin & Li, 2011), this becomes:
| (2) |
Equation 2, a model with no free parameters, can thus be used to model the perceived exocentric sagittal extent. It is based on the assumption that the perceived gaze declination is exaggerated by a gain of 1.5, which has been observed in several studies using different techniques (Durgin and Li, 2011; Li and Durgin, 2009; Li et al., 2011). The fit of this model to the exocentric depth extent matches is shown in left panel of Figure 12 (solid line) in the main text.
To model the perceived frontal extent, we need one additional parameter. That is, we need to assume the perceived azimuthal gaze angle is also exaggerated with some unknown gain. There is evidence supporting this assumption (e.g. Foley, 1965; Foley et al., 2004; Higashiyama, 1992; Li et al., 2011). As discussed in the Introduction, Li et al. (2011) had participants match their egocentric distance to an experimenter to a frontal distance between the same experimenter and a second experimenter (the egocentric-L matching task). The participants set the egocentric distance substantially longer to make it perceptually match the frontal distance. This result implied that to match a perceived 45° azimuthal gaze angle, the participants set the physical azimuthal gaze angle less than 45°. On average, the azimuth angle set by the participants was about 37.5°, which suggests that the azimuthal gaze gain is about 1.2. Li et al. varied the sizes of their frontal extents, but because the task was always to find the equidistance point, their data may not generalize to other frontal extent estimation tasks that cannot be reduced to estimating a 45° angle. In Experiment 1, the frontal extents represented a range of azimuthal angles from 9.5° to 38°. Does an azimuthal gain of 1.2 fit the data?
As illustrated in Figure 2 in the main text, if the physical and the perceived gaze declinations to the near end of frontal extent are γ and γ’, the physical and perceived azimuthal gaze angle are φ and φ’, and the average eye height of the participants is H, then the frontal distance, D, can be expressed as:
| (3) |
Assuming the perceived variables preserve the same geometric relationship, the perceived eye height is accurate, the perceived gaze declination gain is 1.5 (Durgin & Li, 2011), and the perceived azimuth gaze gain is 1.2 (Li et al., 2011) leads to the predictive model, equation 4 with no remaining free parameters:
| (4) |
Plugging in an average eye-height of 1.6 m, leads to the prediction shown as the dashed line in Figure 12, left.
Figure A1.
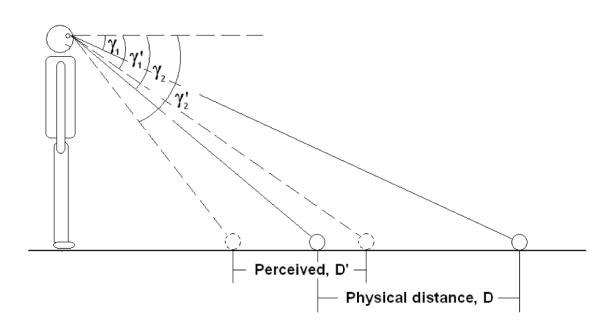
Diagram depicting a perceived exocentric ground distance in depth based solely on perceived gaze angles to the endpoints of the extent. Since perceived gaze is exaggerated with a constant gain of 1.5, the perceived exocentric distance would be foreshortened.
References
- Avery GC, Day RH. Basis of the horizontal-vertical illusion. Journal of Experimental Psychology. 1969;81:376–380. doi: 10.1037/h0027737. [DOI] [PubMed] [Google Scholar]
- Chapanis A, Mankin DA. The vertical-horizontal illusion in a visually-rich environment. Perception & Psychophysics. 1967;2:249–255. [Google Scholar]
- Durgin FH, Akagi M, Gallistel CR, Haiken W. The precision of locomotor odometry in humans. Experimental Brain Research. 2008;193:429–436. doi: 10.1007/s00221-008-1640-1. DOI 10.1007/s00221-008-1640-1. [DOI] [PubMed] [Google Scholar]
- Durgin FH, Fox LF, Kim DH. Not letting the left leg know what the right leg is doing: limb-specific locomotor adaptation to sensory-cue conflict. Psychological Science. 2003;14:567–572. doi: 10.1046/j.0956-7976.2003.psci_1466.x. [DOI] [PubMed] [Google Scholar]
- Durgin FH, Hajnal A, Li Z, Tonge N, Stigliani A. Palm boards are not action measures: An alternative to the two-systems theory of geographical slant perception. Acta Psychologica. 2010;134:182–197. doi: 10.1016/j.actpsy.2010.01.009. [DOI] [PubMed] [Google Scholar]
- Durgin FH, Leonard-Solis K, Masters O, Schmelz B, Li Z. Expert performance by athletes in the verbal estimation of spatial extents does not alter their perceptual metric of space. iPerception. 2012;3:357–367. doi: 10.1068/i0498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Durgin FH, Li Z. Perceptual scale expansion: an efficient angular coding strategy for locomotor space. Attention, Perception, & Psychophysics. 2011;73:1856–1870. doi: 10.3758/s13414-011-0143-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Durgin FH, Li Z, Hajnal A. Slant perception in near space is categorically biased: Evidence for a vertical tendency. Attention, Perception, & Psychophysics. 2010;72:1875–1889. doi: 10.3758/APP.72.7.1875. [DOI] [PubMed] [Google Scholar]
- Durgin FH, Pelah A, Fox LF, Lewis J, Kane R, Walley KA. Self-motion perception during locomotor recalibration: more than meets the eye. Journal of Experimental Psychology: Human Perception and Performance. 2005;31:398–419. doi: 10.1037/0096-1523.31.3.398. [DOI] [PubMed] [Google Scholar]
- Durgin FH, Reed C, Tigue C. Step frequency and perceived self-motion. ACM Transactions on Applied Perception. 2007;4(1):1–23. Article 5. [Google Scholar]
- Fick A. De errore quodam optico asymmetrica bulbi effecto. J. A. Kochin; Marburg: 1851. [Google Scholar]
- Finger FW, Spelt DK. The illustration of the horizontal -vertical illusion. Journal of Experimental Psychology. 1947;37:243–250. doi: 10.1037/h0055605. [DOI] [PubMed] [Google Scholar]
- Foley JM. Visual space: a scale of perceived relative direction. Proceedings of the annual convention of the American Psychological Association. 1965;1:49–50. [Google Scholar]
- Foley JM, Ribeiro-Filho NP, Da Silva JA. Visual perception of extent and the geometry of visual space. Vision Research. 2004;44:147–156. doi: 10.1016/j.visres.2003.09.004. [DOI] [PubMed] [Google Scholar]
- Franz VH, Gegenfurtner KR. Grasping visual illusions: Consistent data and no dissociation. Cognitive Neuropsychology. 2008;25:920–950. doi: 10.1080/02643290701862449. [DOI] [PubMed] [Google Scholar]
- Geuss MN, Stefanucci JK, Creem-Regehr SH, Thompson WB. Effect of viewing plane on perceived distances in real and virtual environments. Journal of Experimental Psychology: Human Perception and Performance. doi: 10.1037/a0027524. (in press) [DOI] [PubMed] [Google Scholar]
- Hajnal A, Abdul-Malak DT, Durgin FH. The perceptual experience of slope by foot and by finger. Journal of Experimental Psychology, Human Perception and Performance. 2011;37:709–719. doi: 10.1037/a0019950. [DOI] [PubMed] [Google Scholar]
- Harris CS. Adaptation to displaced vision: Visual, motor, or proprioceptive change? Science. 1963;1140:812–813. doi: 10.1126/science.140.3568.812. [DOI] [PubMed] [Google Scholar]
- Held R, Freedman SJ. Plasticity in human sensorimotor control. Science. 1965;142:455–462. doi: 10.1126/science.142.3591.455. [DOI] [PubMed] [Google Scholar]
- Higashiyama A. Anisotropic perception of visual angle: implications for the horizontal-vertical illusion, overconstancy of size, and the moon illusion. Perception & Psychophysics. 1992;51:218–230. doi: 10.3758/bf03212248. [DOI] [PubMed] [Google Scholar]
- Higashiyama A. Horizontal and vertical distance perception: The discorded-orientation theory. Perception & Psychophysics. 1996;58:259–270. doi: 10.3758/bf03211879. [DOI] [PubMed] [Google Scholar]
- Higashiyama A, Ueyama E. The perception of vertical and horizontal distances in outdoor settings. Perception & Psychophysics. 1988;44:151–156. doi: 10.3758/bf03208707. [DOI] [PubMed] [Google Scholar]
- Kammann R. Overestimation of vertical distance and slope and its role in moon illusion. Perception & Psychophysics. 1967;2:585–589. [Google Scholar]
- Kelly JW, Loomis JM, Beall AC. Judgments of exocentric direction in large-scale space. Perception. 2004;33:443–454. doi: 10.1068/p5218. [DOI] [PubMed] [Google Scholar]
- Kudoh N. Dissociation between visual perception of allocentric distance and visually directed walking of its extent. Perception. 2005;34:1399–1416. doi: 10.1068/p5444. [DOI] [PubMed] [Google Scholar]
- Kunnapas TM. An analysis of the “vertical-horizontal illusion”. Journal of Experimental Psychology. 1955;49:134–139. [PubMed] [Google Scholar]
- Kunnapas TM. The vertical-horizontal illusion and the visual field. Journal of Experimental Psychology. 1957;53:405–407. [PubMed] [Google Scholar]
- Lappe M, Jenkin M, Harris LR. Travel distance estimation from visual motion by leaky path integration. Experimental Brain Research. 2007;180:35–48. doi: 10.1007/s00221-006-0835-6. [DOI] [PubMed] [Google Scholar]
- Levin CA, Haber RN. Visual angle as a determinant of perceived interobject distance. Perception and Psychophysics. 1993;54:250–259. doi: 10.3758/bf03211761. [DOI] [PubMed] [Google Scholar]
- Li Z, Durgin FH. Downhill slopes look shallower from the edge. Journal of Vision. 2009;9(11):1–15. doi: 10.1167/9.11.6. Art. 6. doi:10.1167/9.11.6. [DOI] [PubMed] [Google Scholar]
- Li Z, Durgin FH. Perceived slant of binocularly viewed large scale surfaces: A common model from explicit and implicit measures. Journal of Vision. 2010;10(14):1–16. doi: 10.1167/10.14.13. Art. 13. doi:10.1167/10.14.13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Z, Durgin FH. Design, data and theory regarding a digital hand inclinometer: a portable device for studying slant perception. Behavior Research Methods. 2011;43:363–371. doi: 10.3758/s13428-010-0047-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Z, Durgin FH. A comparison of two theories of perceived distance on the ground plane: The angular expansion hypothesis and the intrinsic bias hypothesis. iPerception. 2012a;5:368–583. doi: 10.1068/i0505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Z, Durgin FH. Manual matching of perceived surface orientation is affected by arm posture: evidence of calibration between proprioception and visual experience in near space. Experimental Brain Research. 2012b;216:299–309. doi: 10.1007/s00221-011-2934-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Z, Phillips J, Durgin FH. The underestimation of egocentric distance: evidence from frontal matching tasks. Attention, Perception, & Psychophysics. 2011;73:2205–2217. doi: 10.3758/s13414-011-0170-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loomis JM, Da Silva JA, Fujita N, Fukusima SS. Visual space perception and visually directed action. Journal of Experimental Psychology: Human Perception and Performance. 1992;18:906–921. doi: 10.1037//0096-1523.18.4.906. [DOI] [PubMed] [Google Scholar]
- Loomis JM, Philbeck JW. Is the anisotropy of perceived 3-D shape invariant across scale? Perception & Psychophysics. 1999;61:397–402. doi: 10.3758/bf03211961. [DOI] [PubMed] [Google Scholar]
- Loomis JM, Philbeck JW. Measuring spatial perception with spatial updating and action. In: Klatztky RL, Behrmann M, McWhinney B, editors. Egospace and Action. Taylor and Francis; New York: 2008. pp. 1–44. [Google Scholar]
- Loomis JM, Philbeck JW, Zahorik P. Dissociation between location and shape in visual space. Journal of Experimental Psychology: Human Perception and Performance. 2002;28:1202–1212. [PMC free article] [PubMed] [Google Scholar]
- Messing RM, Durgin FH. Distance perception and the visual horizon in head-mounted displays. ACM: Transactions on Applied Perception. 2005;2:234–250. [Google Scholar]
- Milner AD, Goodale MA. The visual brain in action. Oxford University Press; Oxford: 1995. [Google Scholar]
- Ooi TL, Wu B, He ZJ. Distance determined by the angular declination below the horizon. Nature. 2001;414:197–200. doi: 10.1038/35102562. [DOI] [PubMed] [Google Scholar]
- Petzschner FH, Glasauer S. Iterative Bayesian estimation as an explanation for range and regression effects: A study on human path integration. The Journal of Neuroscience. 2011;31:17220–17229. doi: 10.1523/JNEUROSCI.2028-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Philbeck JW, O’Leary S, Lew ALB. Large errors, but no depth compression, in walked indications of exocentric extent. Perception & Psychophysics. 2004;66:377–391. doi: 10.3758/bf03194886. [DOI] [PubMed] [Google Scholar]
- Proffitt DR, Bhalla M, Gossweiler R, Midgett J. Perceiving geographical slant. Psychonomic Bulletin & Review. 1995;2:409–428. doi: 10.3758/BF03210980. [DOI] [PubMed] [Google Scholar]
- Purdy J, Gibson EJ. Distance judgment by the method of fractionation. Journal of Experimental Psychology. 1955;50:374–380. doi: 10.1037/h0043157. [DOI] [PubMed] [Google Scholar]
- Rieser JJ, Ashmead DH, Talor CR, Youngquist GA. Visual perception and the guidance of locomotion without vision to previously seen targets. Perception. 1990;19:675–689. doi: 10.1068/p190675. [DOI] [PubMed] [Google Scholar]
- Rieser JJ, Pick HL, Jr., Ashmead D, Garing A. Calibration of human locomotion and models of perceptual-motor organization. Journal of Experimental Psychology: Human Perception and Performance. 1995;21:480–497. doi: 10.1037//0096-1523.21.3.480. [DOI] [PubMed] [Google Scholar]
- Ross HE. Behaviour and perception in strange environments. Allen & Unwin; London: 1974. [Google Scholar]
- Thomson JA. Is continuous visual monitoring necessary in visually guided locomotion? Journal of Experimental Psychology: Human Perception and Performance. 1983;9:427–443. doi: 10.1037//0096-1523.9.3.427. [DOI] [PubMed] [Google Scholar]
- Thompson JG, Schiffman HR. The influence of figure size and orientation on the magnitude of the horizontal-vertical illusion. Acta Psychologica. 1974;38:413–420. doi: 10.1016/0001-6918(74)90045-6. [DOI] [PubMed] [Google Scholar]
- Toye RC. The effect of viewing position on the perceived layout of scenes. Perception and Psychophysics. 1986;40:85–92. doi: 10.3758/bf03208187. [DOI] [PubMed] [Google Scholar]
- Yang TL, Dixon MW, Proffitt DR. Seeing big things: Overestimation of heights is greater for real objects than for objects in pictures. Perception. 1999;28:445–467. doi: 10.1068/p2854. doi:10.1068/p2854. [DOI] [PubMed] [Google Scholar]
- Wagner M. The metric of visual space. Perception and Psychophysics. 1985;38:483–495. doi: 10.3758/bf03207058. [DOI] [PubMed] [Google Scholar]
- Wagner M. The geometries of visual space. Lawrence Erlbaum; New Jersey: 2006. [Google Scholar]
- Wallach H, O’Leary A. Slope of regard as a distance cue. Perception & Psychophysics. 1982;31:145–148. doi: 10.3758/bf03206214. [DOI] [PubMed] [Google Scholar]
- Wraga M. The role of eye height in perceiving affordances and object dimensions. Perception, & Psychophysics. 1999;61:490–507. doi: 10.3758/bf03211968. [DOI] [PubMed] [Google Scholar]