Protein Secondary Structure Determination by Constrained Single-Particle Cryo-Electron Tomography

SUMMARY

Cryo-electron microscopy (cryo-EM) is a powerful technique for 3D structure determination of protein complexes by averaging information from individual molecular images. The resolutions that can be achieved with single-particle cryo-EM are frequently limited by inaccuracies in assigning molecular orientations based solely on 2D projection images. Tomographic data collection schemes, however, provide powerful constraints that can be used to more accurately determine molecular orientations necessary for 3D reconstruction. Here, we propose “constrained single-particle tomography” as a general strategy for 3D structure determination in cryo-EM. A key component of our approach is the effective use of images recorded in tilt series to extract high-resolution information and correct for the contrast transfer function. By incorporating geometric constraints into the refinement to improve orientational accuracy of images, we reduce model bias and overrefinement artifacts and demonstrate that protein structures can be determined at resolutions of ~8 Å starting from low-dose tomographic tilt series.

INTRODUCTION

Emerging methods in single-particle cryo-electron microscopy (cryo-EM) allow structure determination of macromolecular complexes spanning a wide range of sizes and shapes, at resolutions as high as ~3 Å for proteins in highly symmetric assemblies (Jonić et al., 2008; Orlova and Saibil, 2011; Chang et al., 2012; Milne et al., 2012). The principle for structure determination consists in computationally combining 2D projection images from a large number of structurally identical particles into a 3D density map. The standard protocol for single-particle reconstruction entails an initial model building phase followed by a refinement phase (Frank, 2006). The goal of model building is to provide a faithful representation of the complex of interest at low resolution that correctly represents the projection data, has the correct handedness, and where heterogeneity within the sample has been dealt with properly. In the refinement phase, the goal is to improve the resolution of the initial model(s) by gradually improving the accuracy of orientation determination of each particle projection.

Although initial models can be obtained from single projection views of each molecule using angular reconstitution methods (Van Heel et al., 1997), the use of pairs or series of projections of the same molecule at different tilt angles have had greater success achieving this goal because the additional geometric information can be used to resolve ambiguities in assigning orientations to noisy 2D projection images. Examples of this include the random conical tilt and orthogonal tilt reconstruction approaches (Radermacher et al., 1987; Luigi Bellon et al., 1998;Leschziner and Nogales, 2006; Sander et al., 2010) and cryo-electron tomography (cryo-ET) combined with subvolume averaging (Bartesaghi and Subramaniam, 2009; Hrabe et al., 2011). The resolutions obtained with these methods, however, are limited to ~20 Å for most applications, partly due to the inferior quality of tilted images, inaccuracies in the determination of tilt-geometry parameters, lack of standardized contrast transfer function (CTF) correction procedures, and the detrimental effects of missing data in the intermediate subvolume reconstructions.

Conversely, once a reliable initial model has been obtained using one of the above methods, the use of single projection views of each molecule in conjunction with projection matching procedures has been very successful in refining those models to higher resolution, because the increased contrast and quality of untilted projections allows for more accurate determination of particle orientations (Penczek et al., 1994; Ludtke et al., 1999; van Heel et al., 2000; Frank, 2006; Grigorieff, 2007). In some favorable scenarios, these techniques can achieve atomic resolutions as is the case of large and highly symmetrical entities such as icosahedral viruses (Grigorieff and Harrison, 2011). In general, however, a number of factors can limit the resolutions achieved by this strategy, including model-bias effects (Shaikh et al., 2003), overrefinement (Stewart and Grigorieff, 2004; Scheres and Chen, 2012), and inaccuracy of orientation determination (Henderson et al., 2011). Each of these problems derive, in part, from the low-contrast inherent to cryo-EM images and are particularly detrimental for structural analysis of complexes that are small and display low symmetry.

We propose a hybrid strategy, constrained single-particle tomography (CSPT), that combines the advantages of cryo-ET and subvolume averaging with those of traditional single-particle reconstruction and projection matching refinement. Its key components are (1) the effective manipulation of images from tomographic tilt series to successfully extract high-resolution information and correct for the CTF, (2) the incorporation of geometric information provided by tomography into the refinement of image alignments, and (3) improved accuracy of orientation determination by minimizing the effects of model bias and overrefinement associated with working with low-dose tilted projections. In this work, we describe and validate the proposed method demonstrating its application to experimentally derived data of GroEL.

RESULTS

Conceptual Foundation and Strategy to Test Performance

The first step in our approach involves obtaining tilt series to generate tomograms, followed by subtomogram averaging to get an ab initio model at resolutions in the range of ~20–30 Å. We then substitute the 3D representation of each subtomogram with a collection of corresponding 2D projection images extracted from the raw tilt series. After assigning each image a defocus value and the alignments used to produce the initial reconstruction by subtomogram averaging, we perform simultaneous CTF correction and reconstruction using traditional single-particle reconstruction methods. Particle orientations and parameters of the tilt geometry are then refined using a constrained projection-matching refinement procedure that takes advantage of the geometry imposed by tomography.

We first demonstrate that the improved alignment parameters that are derived by constrained refinement minimize model-bias effects and lead to higher resolution using synthetic data derived from a known crystallographic structure (RNA polymerase II-TFIIB). We then apply the technique to experimentally derived data of GroEL and demonstrate that constrained refinement can increase the accuracy of orientation determination and minimize the effects of overfitting caused by the low dose and quality of tilted projections, attaining resolutions comparable to those obtained by traditional single-particle cryo-EM, a significant improvement over conventional subvolume averaging.

CTF-Corrected Subvolume Averaging by Merging of Projection Sets

To overcome the loss in information that arises in the alignment of tilt series, generation of tomograms, classification, alignment, and averaging of subvolumes, we begin by substituting the 3D representation of each subvolume with a collection of corresponding 2D projections extracted from the raw tilt series. We then assign to each image the orientations and shifts used to produce the initial reconstruction by subvolume averaging so that a traditional single-particle reconstruction may be obtained. Strategies for “merging of reconstructions through merging of projection sets into a common coordinate frame” (Frank, 2006) have been used before, both for reconstruction methods that use tilt pairs (Penczek et al., 1994) and tilt series (Walz et al., 1997) of projections. We extend these ideas in two fundamental ways: we propose a strategy for full CTF correction, and we improve the reconstructions by weighting the contribution of individual projections and by refining image alignments using sets of projections instead of subvolumes.

To obtain a CTF-corrected reconstruction, we first assign a defocus value to each particle projection and then use a Fourier-based simultaneous CTF correction and reconstruction strategy (Grigorieff, 2007). We overcome the difficulty of estimating the defocus of tilted and very low-contrast particle projections by first calculating the defocus at the untilted plane for each tilt series and then applying a correction according to the height of each particle with respect to this plane. Under parallel illumination conditions and using automatic defocus and stage displacement adjustments during tomographic data collection, tilt series can be assumed to be approximately eucentric. Periodogram averaging strategies using tiles from regions with similar defocus throughout the tilt series can then be used to estimate the defocus at the untilted plane (Fernández et al., 2006). Using the 3D information provided by tomography on the location of each particle within the tomogram, we derive an expression for the defocus value of each particle projection:

$$\mathrm{f}=F_0=Z\cos \left(\theta \right)+X\sin \left(\theta \right),$$

where F₀ is the defocus at the untilted plane, z the height of the particle with respect to the untilted plane, x its abscissa measured from the tilt-axis location, and θ is the tilt angle (Figure S1 available online).

We also use information about the contribution of each particle projection to the reconstruction to identify whether some parts of the tomographic data are better quality than others, and to improve the reconstruction by downweighting the contribution of lower quality images. Compared to subvolume averaging, this approach provides a much finer control over what portions of the raw data are used for the reconstruction, resulting in a more effective use of the tomographic data. Moreover, the fact that we can manipulate individual particle projections, allows us to independently refine their alignment parameters providing an additional level of refinement to further improve the reconstruction.

Projection-Matching Refinement of Images Extracted from Tilt Series

In traditional single-particle analysis, projection matching is the most commonly used procedure to refine particle orientations with the goal of improving the resolution of the initial model. This method produces for every image I_i=1:N in a data set, the three Euler angles (φ_i, θ_i, ψ_i) and the two translations that minimize a measure of dissimilarity, d, defined between I_i and reprojections of a model R:

$$\underset{{\phi }_i,{\theta }_i,{\psi }_i}{\text{argmin}}\sum _{i=1}^{N}d\left(l_i,R{\mid }_{{\phi }_i,{\theta }_i,{\psi }_i}\right),$$ (1)

where R|_φi, θ_i, ψ_i represents a reprojection of the model at the orientation given by the corresponding Euler angles, and to simplify the notation, we have omitted the image translations because they can be readily obtained using the cross-correlation theorem. Throughout this work we use the phase residual as defined in (Grigorieff, 2007) as the measure of dissimilarity. The solution to Equation (1) are the 5N alignment parameters that are assigned to all particle projections (three angles and two shifts for each of the N images), so that a refined reconstruction can be obtained.

Compared to images used in traditional single-particle cryo-EM, particle projections extracted from the tilt series have lower contrast (due to the dose fractionation needed to prevent radiation damage) and also lower quality (because they include tilted projections). This, combined with the large number of unknown parameters in Equation (1), can lead to heavy underdetermination of the projection-matching problem resulting in overfitting and failure of the orientation assignment procedure. One way to address this problem is to reduce the number of unknowns involved in Equation (1), which can be accomplished in several ways. One solution is to only refine a subset of the 5N parameters, for example, by keeping the 3N orientations provided by subvolume averaging fixed, and refining only the remaining 2N translational shifts. The resolution achieved using this strategy, however, will be limited by the accuracy of the orientation assignment procedure used in subvolume averaging which is obviously insufficient for high-resolution structure determination. A second solution is to first group raw images into homogeneous class averages and assign orientations to class averages instead of particle projections, effectively reducing the number of unknowns by a factor proportional to the average number of images per class (Ludtke et al., 1999; van Heel et al., 2000;Frank, 2006). The success of this strategy depends on the accuracy of alignment and classification of raw images in 2D, which, in turn, is limited by the poor contrast and low quality of tomographic images. Here, we propose and implement a third and more effective way to reduce the effective number of unknowns involved in the solution of Equation (1), which takes advantage of the geometric constraints imposed by the tomographic imaging system, and is not subject to the limitations of the previous two strategies.

Geometric Constraints Imposed by Tomography between Tilted Exposures

In cryo-ET, images in a tilt series are spatially related by the parameters of the tilt geometry. These relationships can be uniquely characterized by determining the orientation of the tilt axis in each micrograph and the associated tilt angle (we ignore the translational parameters that define the location of the tilt axis for the same reasons we omitted the x,y translations in the previous section). “Alignment of tilt series” is the term used in cryo-ET to refer to the determination of these constraints, usually done using either fiducial-based or marker-free techniques (Frank, 2004). Once determined, constraints between images in a tilt series are imposed by constructing the tomogram, which effectively fixes the relative orientation and position of projections in 3D with respect to each other.

Alignment of a tilt series containing M micrographs requires the determination of 2M constraints (two orientations per micrograph) before a tomogram can be built. If P subvolumes representing individual particles are then extracted from the tomogram and subjected to subvolume averaging to determine their relative orientations in 3D, an additional 3P orientations must be determined (three Euler angles per single-particle), giving a combined total of 2M + 3P unknowns. Processing the same tilt series using our strategy for reconstruction that uses individual particle projections, will produce a total of N = MP projection images, and refinement of such data set using the projection-matching strategy defined by Equation (1) will require the determination of 3MP orientations. The enforcement of geometric constraints implicit in cryo-ET and subvolume averaging procedures, thus effectively reduces the number of unknown orientations from 3MP down to 2M + 3P. For typical data collection conditions (see Experimental Procedures), this amounts to a significant reduction of roughly two orders of magnitude in the number of unknowns.

The reduced set of unknowns can be mapped into the higher dimensional set of orientations through the geometric transformation, $g:{\mathbb{R}}^{2M+3P}\to {\mathbb{R}}^{3MP}$, by composing the pairs of rotations that define the tilt geometry with the orientation assigned to each single-particle in 3D (Walz et al., 1997):

$$[{\phi }_i,{\theta }_i,{\psi }_i]=g\left({\alpha }_{\mathcal{M}\left(i\right)},{\beta }_{\mathcal{M}\left(i\right)},{\Phi }_{\mathcal{P}\left(i\right)},{ϴ}_{\mathcal{P}\left(i\right)},{\Psi }_{\mathcal{P}\left(i\right)}\right),$$ (2)

where φ_i, θ_i, ψ_i are the projection orientations as defined in Equation (1), ${\alpha }_{\mathcal{M}\left(i\right)}$ and ${\beta }_{\mathcal{M}\left(i\right)}$ are the tilt-axis angle and tilt angle associated to micrograph $\mathcal{M}\left(i\right)$, and ${\Phi }_{\mathcal{P}\left(i\right)},{ϴ}_{\mathcal{P}\left(i\right)},{\Psi }_{\mathcal{P}\left(i\right)}$, represent the three Euler angles associated to single-particle $\mathcal{P}\left(i\right)$. The index functions $\mathcal{M}\left(i\right):\{1\cdots N\}\to \{1\cdots M\}$ and $\mathcal{P}\left(i\right):\{1\cdots N\}\to \{1\cdots P\}$ indicate the micrograph and particle identities associated to image I_i, that is, I_i is the projection of single-particle $\mathcal{P}\left(i\right)$ extracted from micrograph $\mathcal{M}\left(i\right)$. Equation (2) will be used to derive the projection matching refinement procedure that takes advantage of the geometric constraints imposed by tomography.

Refinement of Particle Orientations Using Constrained Projection Matching

In traditional single-particle analysis where a single projection view of each particle is available, summands in Equation (1) can be optimized independently of each other because image orientations are uncorrelated. When multiple tilted projections of each particle are available, however, they will be related by the geometric constraints of the tilt scheme causing the corresponding summands in Equation (1) to be coupled as well. Once the geometric constraints ${\alpha }_{\mathcal{M}\left(i\right)}$, ${\beta }_{\mathcal{M}\left(i\right)}$ have been determined by aligning the tilt series, we can use the transformation g introduced in Equation (2) to mathematically express the objective function for constrained refinement of particle orientations:

$$\underset{{\Phi }_p,{ϴ}_p,{\Psi }_p}{\text{argmin}}\sum _{p=1}^P\sum _{i\mid \mathcal{P}\left(i\right)=p}d\left(l_i,R{\mid }_{g\left({\alpha }_{\mathcal{M}\left(i\right)},{\beta }_{\mathcal{M}\left(i\right),{\Phi }_p,{ϴ}_p,{\Psi }_p}\right)}\right).$$ (3)

The overall sum in Equation (3) is identical to the one in Equation (1), only that it has been rearranged into P groups (one per particle, first summation), each having M terms (one per micrograph, second summation). The other important change compared to Equation (1) is the domain in which the minimization is carried out, which is now the one given by the particle orientations Φ_p, Θ_p, Ψ_p with dimension 3P, instead of the one given by the particle-projection orientations φ_i, θ_i, ψ_i used in Equation (1) which had dimension 3MP.

The refinement of each particle’s orientation Φ_p, Θ_p, Ψ_p is governed by the cumulative contribution of dissimilarity from all its tilted projections (second summation in Equation [3]). This has several implications and advantages, both with respect to subvolume averaging and traditional single-particle projection matching. Compared to subvolume averaging, there is no need to deal with the missing wedge because we are strictly using the raw data measured along 2D planes and all operations take the CTF of each projection into account. We can also control the contribution of each particle projection to the objective function, for example, by downweighting the dissimilarity values of higher tilt images that are of lower quality and may adversely affect the accuracy of particle alignment. Compared to unconstrained projection matching, averaging the contribution from several particle projections covering a range of tilt angles and defocus values, adds robustness to the orientation assignment procedure making it less prone to model bias and overfitting effects caused by working with low-dose images extracted from the tilt series.

Data-Driven Refinement of Geometric Constraints Imposed by Tomography

The success of the refinement procedure introduced above is contingent on the assumption that the geometric constraints can be determined with sufficiently high accuracy. Several factors can adversely affect the accuracy of tilt axis and tilt angles determination in cryo-ET, for example, inaccuracies in measuring the positions of gold markers, not having enough fiducials, choice of alignment model being fit, absence of strong features throughout the tilt series in the case of marker-free strategies, and sequential alignment and error accumulation. Enforcement of inaccurate constraints in the refinement procedure may actually degrade the performance of the orientation assignment routine eventually leading to loss of resolution in the final reconstruction.

To overcome this limitation, we refine the initial value of the geometric constraints obtained by aligning the tilt series, using the image information present in the cutout projections. This is achieved by minimizing the projection matching objective function now with respect to the geometric constraints α_m, β_m:

$$\underset{{\alpha }_m,{\beta }_m}{\text{argmin}}\sum _{m=1}^M\sum _{i\mid \mathcal{M}\left(i\right)=m}d\left(l_{i}R{\mid }_{g\left({\alpha }_m,{\beta }_m,{\Phi }_{\mathcal{P}\left(i\right)},{ϴ}_{\mathcal{P}\left(i\right)},{\Psi }_{\mathcal{P}\left(i\right)}\right)}\right).$$ (4)

As before, the overall sum is identical to the one in Equation (1) only that it has been rearranged into M groups now (one per micrograph, first summation), each having P terms (one per particle, second summation). The domain in which the minimization is carried out is now given by the geometric constraints α_m, β_m which has a dimension of 2M.

Refinement of the tilt-axis angle and tilt angle for each micrograph is based on the average contribution of dissimilarity from all particle projections present in that micrograph (second summation in Equation (4)). This has interesting implications because it is the equivalent of doing marker-free alignment of tilt series using exclusively the signal from the particles. It also has the additional benefit of not being sensitive to the fact that gold fiducials are present in the data because the refinement uses only the cutout particle projections that do not include gold.

Constrained Single-Particle Tomography

Having introduced all the necessary foundational components, we now present the overall strategy for structure determination of single-particles using CSPT:

1. Align tilt series, construct tomograms, and select particles in 3D.

2. Perform subvolume averaging to produce an ab initio model at low resolution.

3. Extract corresponding particle projections from raw tilt series and assign orientations and defocus values to every image.

4. Simultaneous CTF correction and reconstruction using Fourier-based approach.

5. Iterate until convergence:

   1. Refine particle orientations [Φ_p, Θ_p, Ψ_p] keeping constraints fixed, Equation (3).
   2. Refine constraints [α_m, β_m] keeping particle orientations fixed, Equation (4).
   3. Update reconstruction using refined set of alignments and use as reference for next iteration.

A key feature of CSPT is the combination of particle orientation refinement and refinement of geometric constraints within the same iterative loop (steps 5a and 5b). This guarantees that improvements in the determination of geometric constraints will lead to better determination of particle orientations and vice versa, overcoming the sequential nature of the conventional strategy adopted in subvolume averaging, where constraints are determined only once by aligning the tilt series and then left unchanged throughout refinement.

The total number of unknown orientations that have to be determined in CSPT is 2M + 3P, significantly lower than the 3MP required in traditional or unconstrained projection matching. Minimization of the combined objective function is done using a block-coordinate-descent method and the Powell minimizer (Powell, 1962). If we arrange all particle-projections extracted from a tilt series into a 2D matrix, where each row represents projections extracted from the same micrograph and each column all tilted projections of a given particle, the block-coordinate descent strategy alternates between the optimization of column-wise (Equation 3) and row-wise (Equation 4) averages of the dissimilarity computed between each particle-projection and the current 3D model (Figure 1).

Figure 1. Conceptual Foundation of Constrained Single-Particle Tomography Refinement.

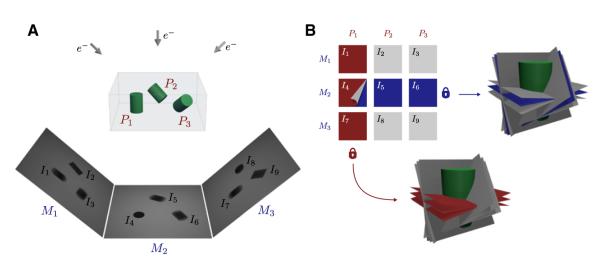
Imaging single-particles using cryo-ET imposes geometric constraints between particle projections that can be enforced in the refinement of image orientations.

(A) Imaging P_i=1:3 single-particles using a series of tilted projections produces a set of micrographs M_i=1:3, each at a different tilt angle. Individual particle projections I_i=1:9 are then extracted and subjected to refinement to determine their relative orientations in 3D.

(B) Particle projections can be arranged into a 2D matrix where each column represents projections of the same single-particle P_i, and each row represents projections extracted from the same micrograph M_i. Constrained refinement of particle orientations guarantees that the angular relationship between projections of the same single-particle does not change during refinement (red lock). Likewise, refinement of parameters of the tilt geometry guarantees their coplanarity constraint throughout the refinement procedure (blue lock).

Evaluation of CSPT Using RNA Polymerase II-TFIIB Complex as a Test Case

To evaluate the performance of the proposed refinement strategy, we first used a phantom data set where particle orientations produced by the refinement algorithm can be compared with the correct values that are known precisely at the beginning of the experiment. We selected the RNA Polymerase II-TFIIB complex (Liu et al., 2010) as an example, which is an asymmetric, 500 kDa complex. Using the atomic model, we simulated a single-particle data set by placing multiple copies of the complex in 3D, each in a random orientation. We then generated tomographic tilt series from each mock specimen covering a ±60 degree range using two degree increments. Images in the tilt series were subjected to random in-plane rotations to simulate changes in the orientation of the tilt axis. To simulate errors in the goniometer readings, we added a random perturbation to the true tilt angle values using a uniform distribution of ±1 degree width. A total of 1,220 particle projections were extracted from four tilt series (each containing five particles and 61 micrographs), keeping track of the geometric relationships provided by the tilt geometry.

We compared the performance of CSPT against traditional or unconstrained projection matching as a function of image contrast, and in terms of the reference used for refinement to study the effects of model bias. Contrast changes were simulated by adding increasing amounts of noise to each particle projection (we used 11 conditions ranging from the noiseless option SNR = ∞, down to SNR = 0.01 to mimic actual experimental conditions). Model-bias effects were studied by using different starting models for refinement. Using the same set of particle projections, multiple initial references were obtained by changing the orientations assigned to each image and computing the corresponding Fourier-based reconstructions. Starting from the ground-truth orientations, we added perturbations drawn from uniform distributions with increasing interval sizes (0° to ± 30°) to simulate initial models at progressively lower resolutions (11 conditions including the no perturbation option were used). For each of the combined 121 conditions, we ran 20 iterations of traditional projection matching and our constrained approach. To eliminate the influence of the number of particles in the quality of the reconstructions and in the measurements of resolution, we performed all reconstructions using the noiseless particle projections and used the noisy projections exclusively to derive their orientations using both refinement strategies. To compare the performance between the two strategies, we looked at Fourier shell correlation (FSC) plots and the variance alignment error (VAE), which measures the mismatch between alignments produced by the refinement procedure and the “ground-truth” values (Figures S2 and S3). To make the VAE insensitive to rigid body rotations, we define it as the average Frobenius norm of the difference between the rotation matrix assigned to each image and the mean rotation of all images.

Constrained refinement consistently outperforms traditional projection matching both in terms of resolution and in terms of accuracy of orientation assignment, showing the benefits of using the geometric constraints provided by the tilt geometry in the refinement strategy. The gains in resolution obtained by constrained refinement get progressively better the lower the image contrast, indicating the increased usefulness of geometric constraints in low-contrast conditions. The invariance of resolution with respect to the dimension that encodes perturbations to the initial model shows the reduced effects of model bias of the constrained approach. Consistently, plots of errors in orientation assignment show a similar behavior, with the constrained approach doing a better job at recovering the ground-truth orientations, especially at the weakest contrast settings, and exhibiting improved robustness to model bias.

CSPT Applied to Low-Dose Tilt Series of GroEL

To test the performance of the proposed procedure with experimentally obtained data, we used tilt series of GroEL for which high-resolution structures are available both from X-ray crystallography and traditional single-particle cryo-EM. Tilt series were acquired under low-dose conditions using ~2 e⁻/Ų per exposure (~105 e⁻Ų total dose) and aligned using gold fiducials (see Experimental Procedures) (Figures 2A and 2B). Subtomograms representing individual GroEL particles were extracted from the tomographic reconstructions and subjected to subvolume averaging to obtain an initial reconstruction at low resolution. The defocus for each tilt series at the untilted plane was determined using strip-based periodogram averaging (Figure 2C). Particle projections were extracted from the raw tilt series and defocus values assigned to each image as previously described. Initial image orientations were assigned according to the parameters of the tilt geometry and the orientations provided by subvolume averaging. The Fourier-based reconstruction was calculated and compared to the one obtained by subvolume averaging in terms of the FSC curve to a map derived from X-ray coordinates, showing successful CTF correction (Figure 2D).

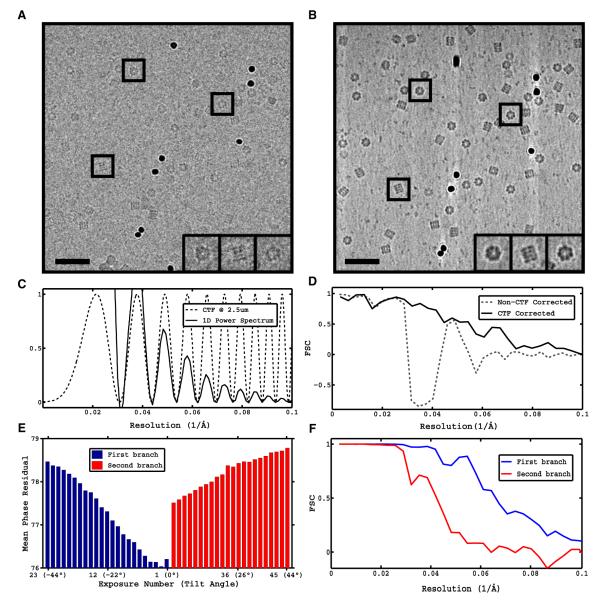
Figure 2. CTF Correction and Identification of Best Quality Images from Tilt Series of GroEL.

Tilt series of GroEL were collected and processed using conventional subvolume averaging (see Experimental Procedures) and the proposed reconstruction strategy.

(A) Zero-tilt exposure from representative tilt series at ~2.3 e−/Ų.

(B) Slice through corresponding tomographic reconstruction (~105 e⁻/Ų accumulated dose). Scale bars, 35 nm.

(C) Theoretical CTF curve at 2.5 μm defocus estimated from radially averaged, background-subtracted, 1D power spectrum obtained by periodogram averaging using tiles from the tilt series.

(D) FSC against X-ray model of GroEL of non-CTF corrected conventional subvolume averaging reconstruction from 10,000 GroEL particles and proposed CTF-corrected reconstruction by merging of projection sets.

(E and F) Difference in image quality between successive exposures in the tilt series and its impact on resolution of reconstructions. (E) Average phase residual per exposure in the tilt series plotted as a function of the tilt angle using a two-branch data collection scheme (0° to −45° and 2° to 45°). (F) FSC of reconstructions using first 11 exposures from first branch (0° to −20°) and first ten exposures from second branch (2° to 20°).

See also Figure S1.

We then measured the relative contribution of different parts of the tomographic data to the reconstruction, by analyzing the mean phase residual value per exposure plotted as a function of the tilt angle (Figure 2E). These results show the progressive degradation (increase) of the phase residual with each successive exposure (0°, ~45°) due to the cumulative effects of dose and the intrinsic problems of tilted projections. A transient improvement is observed at the start of the second branch of the tilt series (2°, 45°), reflecting the better quality of untilted projections and the irreversible effects of beam damage. Closer inspection of the first few exposures reveals that considerable degradation occurs after the 11th exposure (−20° tilt), and that particles extracted from second exposures are the most consistent with the 3D reconstruction. This finding is in-line with the observation that a small amount of preradiation “stabilizes” the sample, as shown in the analysis of single-particle movies (Brilot et al., 2012). To demonstrate the benefits of doing particle sorting based on phase residual values, we produced reconstructions using two subsets of images: the first 11 exposures in the first branch (−20°, 0°), and the first ten exposures in the second branch (2°, 20°) (Figure 2F). The subset with the lower phase-residual values produces a higher resolution reconstruction, confirming that the first few low-tilt exposures contain the best quality data of the tilt series, consistent with the reduced effect of beam damage and limited increase in effective ice thickness that reduces blurring due to charging. The cumulative dose used for this reconstruction is ~25 e⁻/Ų, comparable to the doses used in traditional single-particle cryo-EM on a single exposure.

To compare the performance of constrained refinement against traditional projection matching on this data set, we refined the reconstruction of GroEL obtained using only the first 11 exposures from the tilt series with three different refinement strategies. In the first, we kept the orientations provided by subvolume averaging fixed and iteratively refined only the x-y shifts of each particle projection, an approach reminiscent to (Zhang and Ren, 2012) but done on the entire set of particles. In the second strategy, we applied traditional projection matching and refined all five image parameters (three Euler angles and two shifts per image). In the third, we used constrained projection matching refinement as introduced in this work. For each case, we tracked three quantitative indicators of performance: the orientations assigned to particle projections represented on the asymmetric triangle, the average phase residual computed over all particle projections, and the FSC curves computed against a map derived from X-ray coordinates of GroEL (Figure 3). These experiments were designed to show the effects of enforcing the geometric constraints into the procedure for orientation determination of images extracted from tomographic tilt series, where the dose per image is one-tenth of the dose typically used in traditional single-particle cryo-EM.

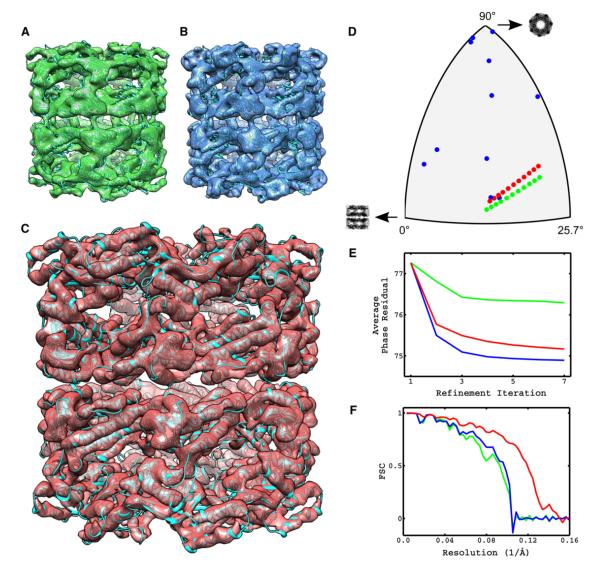
Figure 3. Constrained Refinement Minimizes Overfitting Effects and Produces Subnanometer Resolution Structures from Low-Dose Tomographic Tilt Series of GroEL.

Using particle projections extracted from the tilt series of GroEL, we compared the performance of orientation-fixed, traditional, and constrained projection-matching refinement in terms of agreement of assigned orientations with the tomographic constraints, value of the projection-matching objective function and resolution of reconstructions.

(A–C) Amplitude-corrected reconstructions obtained using orientation-fixed, traditional, and constrained projection-matching refinement, respectively.

(D) Comparison of orientations assigned to projections of the same single-particle by the three refinement strategies represented on the asymmetric triangle.

(E) Tracking of the projection matching objective function represented by Equation (1) for each of the three refinement strategies as a function of refinement iteration.

(F) FSC plots of reconstructions shown in (A)–(C) against X-ray model of GroEL. Color code in (D)–(F) is the same as in (A)–(C).

Tracking of the orientations assigned to projections of a given single-particle by the three refinement strategies allows us to verify their agreement with the tilt-geometry constraints. The use of a single tilt axis in cryo-ET implies that the orientations assigned to projections of a single-particle should be arranged along the “great circles” on the asymmetric triangle. This condition is clearly satisfied in the first strategy, because the orientations remain fixed and correspond to those provided by subvolume averaging. In contrast, unconstrained projection matching produces orientations that no longer satisfy the tomographic constraints indicating the presence of alignment errors due to insufficient contrast in images extracted from the tilt series. The constrained approach, however, is by design able to refine particle orientations while maintaining the arrangement of projection orientations consistent with the tilt geometry.

The average phase residual plots represent the value of the projection-matching objective function introduced in Equation (1) as a function of the refinement iteration. Presumably, smaller values of this quantity indicate a better alignment solution but they may also be indicative of overfitting (Stewart and Grigorieff, 2004). Monotonic decrease of the average phase residual is observed for all three refinement strategies as guaranteed by the optimization strategy, with the differences being in the amount of the decrease. The first strategy is the most restrictive in terms of degrees of freedom allowed in the optimization and shows the smallest reduction in average phase residual. Traditional or unconstrained refinement of orientations is the least restrictive strategy (the one with the most degrees of freedom), and correspondingly the one that achieves the lowest average phase residual. Constrained refinement lies in between these two extremes, consistent with its intermediate number of degrees of freedom. The FSC curves against the X-ray derived map, indicate a similar fall-off for the first two refinement strategies with constrained refinement achieving a significantly higher resolution. Collectively, these results demonstrate that the use of geometric constraints in the strategy for alignment of low-dose images extracted from the tilt series, helps prevent overfitting and leads to higher resolution reconstructions than those obtained with traditional projection matching.

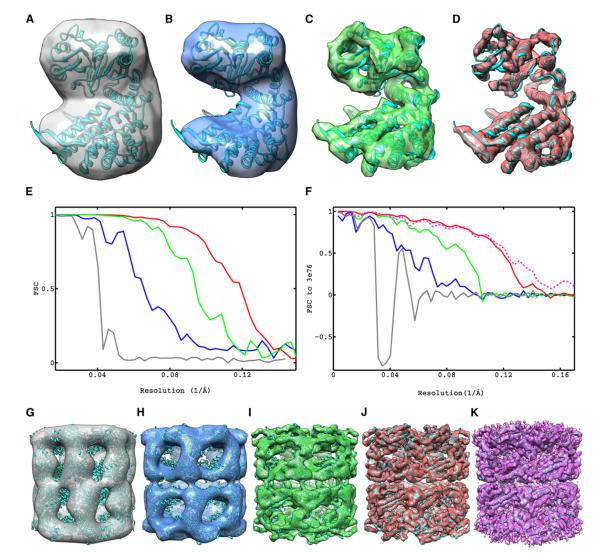
Starting from the reconstruction by subvolume averaging, we show the progressive improvement in resolution obtained from each step of the CSPT strategy (Figure 4). The first component is the strategy we adopt for reconstruction that directly uses the raw projection data, is fully CTF corrected, and uses only the first few low-tilt exposures from the tilt series. The second component is the refinement of image shifts using traditional projection matching while keeping the orientations provided by subvolume averaging fixed. The last component is the procedure for constrained refinement of particle orientations and geometric constraints. The overall improvement in resolution is from ~25 Å obtained with conventional subtomogram averaging to ~8 Å obtained with the proposed CSPT approach. This improvement was achieved by solely changing the refinement and reconstruction protocols while always using the same raw data, which highlights the ability of CSPT to successfully extract the high-resolution information from low-dose tomographic tilt series.

Figure 4. Progressive Improvement in Resolution Achieved by Each Component of Constrained Single-Particle Tomography and Comparison to Highest Resolution Map of GroEL Reported Using Cryo-EM.

Maps are represented as iso-surfaces with the fitted X-ray coordinates.

(A) Reconstruction by conventional subvolume averaging.

(B–D) Fourier-based CTF-corrected reconstructions using only first 11 exposures in the tilt series and alignments from subvolume averaging (B), after traditional projection-matching refinement of image shifts (C), and after constrained projection-matching refinement (D).

(E) FSC plots of maps in (A)–(D) obtained from the correlation of reconstructions between random halves of the image data set, indicating resolutions measured by the 0.5 cutoff criteria of 24.5, 15.3, 10.6, and 8.4 Å, respectively.

(F) FSC plots against a map derived from the X-ray model indicating resolutions measured by the 0.5 cutoff criteria of 34.1, 18.2, 10.8, and 8.5 Å for maps in (A)–(D) and 8.2 Å for map shown in (K).

(G–J) Maps of the entire complex corresponding to the subunits shown in (A)–(D).

(K) Map (4.2 Å₎ of GroEL (EMDB ID 5001) obtained by traditional single-particle cryo-EM (Ludtke et al., 2008), using 20,401 particles, 25–36 e⁻/Ų and 300 kV imaging (iso-surface shown at suggested contour level of 0.597).

DISCUSSION

The geometric information provided by tilt pair- or tilt series-based single-particle cryo-EM is critical to produce initial 3D models that are unambiguous, have the correct handedness, and where sample heterogeneity can be accounted for even when no reference structures are available (Sander et al., 2010;Kuybeda et al., 2012). Once an initial model is obtained, refinement by projection matching of single projection views of each molecule has been the modality of choice for high-resolution refinement because using all of the available dose to record one image results in higher image contrast. However, limitations of this refinement procedure such as inaccuracies in orientation determination, model bias, and overrefinement, inspired us to consider the use of multiple tilted projections not just for initial model building, but also for high-resolution refinement.

We have shown here that cryo-ET combined with subvolume averaging provides a suitable framework for processing multiple low-dose tilted projections. As such, it simplifies the various bookkeeping operations required for synchronized particle picking among multiple projections, provides a method for determining the parameters of the tilt geometry and a reliable way to estimate defocus of individual particle projections despite the low-contrast conditions imposed by the dose fractionation. To make this strategy compatible with high-resolution structure determination however, several changes had to be implemented both to the reconstruction and refinement protocols used in subvolume averaging in order to successfully extract the high-resolution information from images in the tilt series. Our strategy for reconstruction uses raw projection-images instead of subtomograms and implements a weighting scheme to minimize the effects of beam damage and shortcomings of imaging tilted specimens by only using the first few low-tilt exposures from the tilt series. For CTF correction we derive defocus values for each particle projection extracted from the tilt series and use reconstruction techniques used in traditional single-particle approaches. The proposed refinement strategy takes advantage of the geometric constraints imposed by tomography to iteratively refine particle orientations as well as the parameters of the tilt geometry using the intrinsic information present in the images, all as part of the same collaborative refinement loop.

We demonstrated the performance of CSPT using phantom data generated from the crystal structure of the RNA Polymerase II-TFIIB complex. For the experimentally derived data of GroEL, we showed that using the proposed framework it is possible to fractionate the electron doses typically used in traditional single-particle cryo-EM across a series of tilted projections, and still achieve subnanometer resolutions despite the challenges of dealing with lower contrast and tilted projections. This is a significant improvement over the resolutions that can currently be obtained by conventional subvolume averaging using the same tomographic data. Additionally, dose fractionation strategies like these have the potential to alleviate the detrimental effects of radiation damage and beam-induced specimen motion (Chen et al., 2008; Campbell et al., 2012).

To take advantage of CSPT most effectively, we anticipate that data collection schemes other than those currently used for standard cryo-ET may have to be considered. For example, increasing the spacing between successive tilts may be a good strategy to maximize the geometric information provided by the multiple exposures without sacrificing image contrast. Throughout this work we have assumed samples to be in solubilized form where complexes are studied in isolation. However, cryo-ET combined with subvolume averaging is the only method that can study structures of macromolecular complexes in situ when they are present in the native milieu of viruses and cells. The applicability of the methods described here to this important case constitutes an important direction for future work.

In summary, we showed that the effective use of multiple exposures at different tilt angles in single-particle cryo-EM constitutes a powerful tool for tackling the problem of structure determination of macromolecular complexes at subnanometer resolution. CSPT may help address questions of fundamental interest in 3D structure determination by cryo-EM, such as the following: (1) Is the contrast present in a single-exposure image enough to unambiguously determine particle orientations? (2) Is the additional geometric information obtained at the expense of image contrast and quality critical for the success of the alignment? and (3) How does the accuracy of particle alignment compare between strategies that use different number of exposures? Answers to these questions will provide clues into what strategies may be best suited to obtain the highest resolution structural information, especially from small, dynamic protein complexes with low levels of symmetry where, so far, traditional single-particle methods have had limited success.

EXPERIMENTAL PROCEDURES

Phantoms

X-ray coordinates of the RNA polymerase II-TFIIB complex (Protein Data Bank [PDB] ID 3K7A) were converted into density maps at 3 Å resolution using EMAN’s pdb2mrc (Ludtke et al., 1999). Multiple copies of the density maps in random orientations were combined into a single volume and projections of the resulting density obtained using xyzproj (Kremer et al., 1996) to simulate tomographic tilt series.

Data Collection and Processing of GroEL Tilt Series

GroEL specimens were imaged in a Titan Krios transmission electron microscope (FEI Company, Portland, OR) operated at 80 kV, with the specimen maintained at liquid nitrogen temperatures. Images were recorded on a 4K × 4K CCD camera (Gatan, Pleasanton, CA) under parallel illumination conditions, using full correction of defocus and x-y stage positions. Tilt series were imaged at a nominal magnification of 47,000× using four defocus groups of 2, 2.35, 2.5, and 3 μm, with a pixel size of 1.74Å. For each tilt series, 46 images were taken in 2° increments covering a ± 45° tilt range using 2.3 e⁻/Ų per image. Tilt series were automatically aligned using gold fiducials (Amat et al., 2008) and reconstructed using weighted back projection (Kremer et al., 1996). Ten thousand subvolumes containing individual GroEL particles were manually extracted from 145 tomograms and subjected to subvolume averaging to produce the initial reconstruction at low resolution (Bartesaghi et al., 2008).

CTF Estimation and Processing of Raw Particle Projections

Defocus values at the untilted plane for each tilt series were calculated using tomoctf (Fernández et al., 2006), including tiles 512 × 512 pixels in size within a 1,000 Å defocus range with respect to the tilt-axis plane. All traditional single-particle reconstructions and projection matching operations were done with FREALIGN (Grigorieff, 2007) imposing D7 symmetry. Subsequent to refinement, map amplitudes were weighted using a map generated from the X-ray coordinates PDB ID 3E76 as a reference. The asymmetric unit from these coordinates was fit into the density maps using the “fitting with symmetry” function in Chimera (Pettersen et al., 2004).