Efficiency of Study Designs in Diagnostic Randomized Clinical Trials

Abstract

From the patients’ management perspective, a good diagnostic test should contribute to both reflecting the true disease status and improving clinical outcomes. The diagnostic randomized clinical trial is designed to combine both diagnostic tests and therapeutic interventions. Evaluation of diagnostic tests are carried out with therapeutic outcomes as the primary endpoint, rather than test accuracy. We lay out the probability framework for evaluating such trials. Two commonly referred designs –the two-arm design and the paired design– are compared in a formal statistical hypothesis testing setup and the causal connection between the two tests is identified. The paired design is shown to be more efficient than the two-arm design. The efficiency gains vary depending on the discordant rates of test results. Sample size formulas are derived for both binary and continuous endpoints. Estimation of important quantities under the paired design is derived and simulation studies are also conducted to verify the theoretical results. The method is illustrated with an example of designing a randomized study on preoperative staging of bladder cancer.

1. INTRODUCTION

Most clinical studies of diagnostic tests are designed to assess the diagnostic and/or predictive performance of tests in particular clinical settings. However, the impact of a test on patient outcomes, such as morbidity, mortality, or health related quality of life is considerably harder to assess. Unlike therapeutic interventions, which can be linked directly to patient outcomes, a diagnostic modality produces information which is fed into subsequent decisions about disease management and treatment. As a result, the effects of a diagnostic modality on patient outcomes are generally mediated by subsequent therapeutic interventions.

The fundamental methodological difficulty of the mediated outcomes of diagnostic tests has led to the development of modeling approaches, such as decision analysis and micro-simulation [1]. These methods utilize results from clinical studies of diagnostic or predictive performance and combine them with information about the effectiveness of therapy and the natural course of the disease in order to estimate the impact of the use of diagnostic modalities. The literature on modeling methods and their applications is by now extensive.

An alternative but less utilized approach to the evaluation of patient outcomes of diagnostic tests is to use randomization. Indeed, with the exception of studies of the impact of modalities for early detection, randomized studies of diagnostic tests have been rare up to now. However, the growing availability and utilization of diagnostic tests, the recent advent of various types of biomarkers, and the limitations of modeling approaches, have all combined to create new interest in clinical studies of the patient outcomes of diagnostic tests.

The possibility of using randomized designs for diagnostic test evaluation and the efficiency limitations of such designs were discussed in a Lancet paper by Bossuyt and colleagues [2]. In subsequent work, Lijmer and Bossuyt examined several possible designs which incorporate randomization [3]. de Graaff and colleagues [4] compared a two-arm design and a paired design for the management of critical limb ischemia, where the reference standard is lacking. The acronym DRCT (Diagnostic Randomized Clinical Trial) was introduced to differentiate such designs from conventional RCTs.

The recent advent of biomarkers and the need to evaluate their utility and define their effective clinical role is also fueling interest in studies that combine diagnostic and therapeutic interventions. In their widely cited paper, Sargent and colleagues [5], discussed randomized designs for the study of a predictive marker and compared the sample size required for different study designs involving a predictive marker for survival outcomes. In practice, however, the utilization of such design is very limited, partly due to the lack of statistical justification. In a recent literature review paper, Vickers and colleagues [6] systematically reviewed 129 published studies of molecular biomarkers. They found that only a very small portion of those studies reported any measure of predictive accuracy and none of them experimentally evaluated the clinical value of the markers.

The major thrust of this paper is to lay out the probability framework for evaluating diagnostic randomized clinical trials. Two commonly referred designs are compared in a formal statistical hypothesis testing setup and the causal connection between the two tests is identified. We also provide sample size and power formulas for practitioners, which are not available in literatures, to the best of our knowledge. The sample size determination for the paired design is not trivial because it depends on the discordant rate, which is a function of the characteristics of the diagnostic tests. Unlike simple study design to compare interventions, the designs considered here combine both diagnostic tests and therapeutic interventions. Binary and continuous outcomes are two commonly seen types of clinical endpoints across clinical trials, including trials involving the comparison of tests. Without loss of generality, we illustrate our methodology with binary outcomes and assume that two alternative therapeutic interventions are available (The sample size formula for continuous outcomes are provided in the appendix). The first design is named as two-arm design in which patients are randomly assigned to one of the two tests and subsequent therapeutic interventions are based on the individual test results. The second design is named as paired design in the sense that patients undergo both tests. The therapeutic intervention is predetermined for cases in which the two tests agree but is decided by randomization for cases in which the two tests disagree. An essential feature of such design is that only patients with discordant tests results are randomized. An example of a trial in which patients with discordant test findings were randomized is the MINDACT trial [7, 8].

The paper is organized as follows. In section 2, we provide the formal description of the two designs, define the notation and derive sample size formulas for each of them. Point and interval estimators for the outcomes are presented in section 3. In section 4 we present the results of simulation studies comparing the sample size, power and estimations of the two designs. Section 5 presents an example of preoperative staging of bladder cancer to illustrate the proposed methodology. We summarize our conclusions and discuss the implementation of the two designs in section 6.

2. TWO DESIGNS FOR RANDOMIZED TEST COMPARISON

As noted above, we will examine two study designs intended to compare patient outcomes of two tests, A and B. We assume that two alternative therapeutic interventions, treatment I and II, are available and that the choice of therapy is determined by the test result as specified by the particular design. In many settings, treatment I may be a more intensive therapeutic intervention and treatment II may be a less intensive intervention or a placebo.

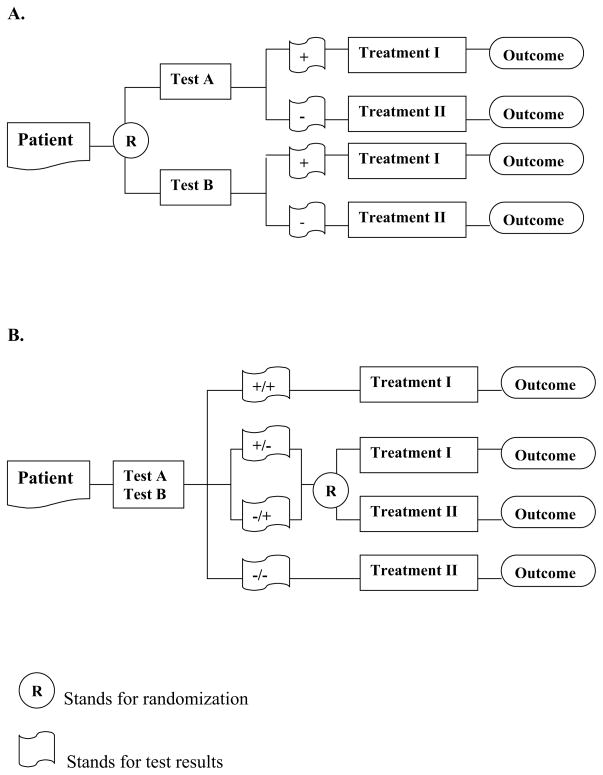
The first of the two designs we consider is a streamlined “two-arm” design, in which patients are randomized to test A or B and then undergo treatment I if the test result is positive and treatment II if the test result is negative (Figure 1A). The second design specifies that all patients undergo both tests. If the tests agree, the patient undergoes Treatment I if both test results are positive and Treatment II if both test results are negative. When the two tests disagree, treatment assignment is decided by randomization with equal probabilities for each discordant type (Figure 1B). As a result, half of the discordant cases are randomized to follow test A based strategy, and the other half follows test B based strategy.

Figure 1.

Study designs for comparing two test-based patient management strategies

To avoid the confusion from too many notations, we assume the primary outcome for comparison is binary in the main context and include the formulas for continuous outcomes in the appendix II. The outcome is denoted by Y with 1 for favorable outcome and 0 for unfavorable outcome. We also define a set of cure rate parameters to be the probability of a favorable clinical outcome given disease status and assigned treatment. As shown below, r₁₁ denotes the cure rate for treatment I assigned to true disease patients. We assume that the more aggressive treatment I should work better for true disease patients and the conservative treatment II should work better for disease-free patients. Therefore, practically, test-positive patients receive treatment I and test-negative patients receive treatment II. Mathematically, it implies that r₁₁ > r₂₁ and r₂₂ > r₁₂. A point worth noting in the flow of the two designs is that the treatment contributes to the patient’s outcome and the test result is used only to determine the treatment management. So, our goal is to compare two patient management strategies: one based on the results of test A and the other based on the results of test B.

The hypothesis of interest in the two-arm design can be written as $H_0:r_1^A=r_1^B$, where $r_1^A$ denotes the true rate of favorable outcomes for patients randomized to test A and $r_1^B$ denotes the corresponding rate for patients randomized to test B. For the paired design, the outcomes will be identical for (test-)concordant cases and will only differ in the discordant cases. Thus, the hypothesis of interest can be written as $H_0:r_2^A=r_2^B$, where $r_2^A$ denotes the rate of favorable outcomes in discordant cases who are randomized to follow test A based strategy and $r_2^B$ denotes the corresponding rate for those who follow test B based strategy.

For both designs the hypothesis of interest involves the comparison of two proportions based on independent samples. Following the notation in Meinert [9], we use α for type I error probability and β for type II error probability. Accordingly, z_α is the critical value for the standard normal distribution with upper tail probability of α and z_β is the critical value for the standard normal distribution with upper tail probability of β. For brevity, all the formulations in this paper are for one-sided test and they may be used for two-sided tests by replacing α by α/2 wherever it appears in the formulas. We also use λ = n_B/n_A as the sample size allocation parameter between the two arms. An equal allocation implies n_A = n_B with λ = 1 and an unequal allocation means λ ≠ 1. Therefore, the sample size formula for testing the equality of two binomial proportions p_a and p_b with equal allocation is given as:

$$n_A=n_B={\left[\sqrt{2\overline{p}(1-\overline{p})}{z}_{\alpha }+\sqrt{p_a(1-p_a)+p_b(1-p_b)}{z}_{\beta }\right]}^2/{(p_a-p_b)}^2$$ (1)

where p̄ = (p_a + p_b)/2. Similarly, for unequal allocation,

$$\begin{array}{l}{n}_A={\left[\sqrt{\overline{p}(1-\overline{p})(\lambda +1)/\lambda }{z}_{\alpha }+\sqrt{p_a(1-p_a)+p_b(1-p_b)/\lambda }{z}_{\beta }\right]}^2/{(p_a-p_b)}^2\\ n_B=\lambda n_A\end{array}$$

For brevity, In the following sections, we focus on the formulations for equal allocation only.

While both designs test a null hypothesis of the form H₀: R^A − R^B = 0, specifically, $H_0^{\mathit{two}-\mathit{arm}}:r_1^A-r_1^B=0$ and $H_0^{\mathit{paired}}:r_2^A-r_2^B=0$, the alternative hypotheses are different:

$$\begin{array}{l}{H}_A^{\mathit{Two}-\mathit{arm}}:r_1^A-r_1^B={\mathrm{\Delta }}_1\\ H_A^{\mathit{Paired}}:r_2^A-r_2^B={\mathrm{\Delta }}_2={\mathrm{\Delta }}_1/f\end{array}$$

Where f is the discordant rate. With sensitivities and specificities of the tests known, we can show the relationship Δ₂ = Δ₁/f later in this section.

2.1. Two-arm design – Sample Size

In the two-arm design, $r_1^A$ is the true response rate in patients randomized to arm A (to take test A) and likewise for $r_1^B$. Assuming the prevalence (p), and operating characteristics for tests A and B are known (sensitivities and specificities denoted by Se_A, Sp_A, Se_B, Sp_B). $r_1^A$ and $r_1^B$ are simply defined:

$$r_1^A=r_{11}{\mathit{pSe}}_A+r_{22}(1-p){Sp}_A+r_{12}(1-p)(1-{Sp}_A)+r_{21}p(1-{Se}_A)$$ (2)

$$r_1^B=r_{11}{\mathit{pSe}}_B+r_{22}(1-p){Sp}_B+r_{12}(1-p)(1-{Sp}_B)+r_{21}p(1-{Se}_B)$$ (3)

The difference in response rates is:

$${\mathrm{\Delta }}_1=r_1^A-r_1^B=(r_{21}-r_{11})p({Se}_B-{Se}_A)+(r_{22}-r_{12})(1-p)({Sp}_A-{Sp}_B)$$

The sample size formula (2) with $p_a=r_1^A$ and $p_b=r_1^B$ yields the required sample size in each arm to detect the response rate difference for pre-specified α and β.

2.2. Paired design – Sample Size

Under the paired design, each patient receives both tests and we randomize only the discordant patients. The derivation of the overall response rates is a bit more complicated because it depends on discordant rate that is a function of prevalence, sensitivities and specificities.

With known prevalence, sensitivities and specificities, we can cross tabulate test results for true disease patients and disease free patients respectively, as shown in tables 2A and 2B. Define θ⁺ = Pr(A⁺B⁻|D⁺) and it is easy to show that θ⁺ ∈[max(0, Se_A − Se_B), min(Se_A, 1 − Se_B)] since the cell counts are bounded by the marginal counts. Np(Se_B − Se_A + θ⁺) represents the subpopulation of true disease participants mis-classified only by test A, and Npθ⁺ is interpreted as the subpopulation of true disease participants mis-classified only by test B.

Table 2.

Cross Tabulation of Test Results

A. True Disease		Test B		total
		+	−
Test A	+	Np(SeA − θ+)	Npθ+	NpSeA
	−	Np(SeB − SeA + θ+)	Np(1 − SeB − θ+)	Np(1 − SeA)
		NpSeB	Np(1 − SeB)	Np

B. Disease Free		Test B		total
		+	−
Test A	+	N(1 − p)(1 − SpA − θ−)	N(1 − p)θ−	N(1 − p)(1 − SpA)
	−	N(1 − p)(SpA − SpB + θ−)	N(1 − p)(SpB − θ−)	N(1 − p)SpA
		N(1 − p)(1 − SpB)	N(1 − p)SpB	N(1 − p)

Similarly, we can derive θ⁻ = P (A⁺B⁻|D⁻) ∈ [max(0, Sp_B − Sp_A), min(Sp_B, 1 − Sp_A)]. The cell count of N (1 −p)θ⁻ is interpreted as the subpopulation of disease free participants mis-classified only by test A, and the cell count of N(1 − p)(Sp_A − Sp_B + θ⁻) is the subpopulation of disease free participant mis-classified only by test B.

The total number of participants with discordant test results is determined by summing up the off-diagonal cells in the above two tables, denoted by N^D. Grouping the cells together, we have

$$N^D=N[(1-p){\theta }^{-}+p{\theta }^{+}]+N[p({Se}_B-{Se}_A)]+N[(1-p){\theta }^{-}+p{\theta }^{+}]+N[(1-p)({Sp}_A-{Sp}_B)]$$

So the discordant rate is

$$f=\frac{N^D}{N}=2[(1-p){\theta }^{-}+p{\theta }^{+}]+[p({Se}_B-{Se}_A)+(1-p)({Sp}_A-{Sp}_B)]$$ (4)

In the discordant portion, half of the patients are randomized to follow test A and the other half are randomized to follow test B. So the response rate for A-based strategy is:

$$\begin{array}{l}{r}_2^A=[\frac{1}{2}{r}_{11}Np{\theta }^{+}+\frac{1}{2}{r}_{21}{N}_p({Se}_B-{Se}_A+{\theta }^{+})+\frac{1}{2}{r}_{12}N(1-p){\theta }^{-}+\frac{1}{2}{r}_{22}N(1-p)({Sp}_A-{Sp}_B+{\theta }^{-})]/\frac{N^D}{2}\\ =[r_{11}p({\theta }^{+})+r_{21}p({Se}_B-{Se}_A+{\theta }^{+})+r_{12}(1-p){\theta }^{-}+r_{22}(1-p)({Sp}_A-{Sp}_B+{\theta }^{-})]/f\end{array}$$ (5)

For B-based strategy:

$$\begin{array}{l}{r}_2^B=[\frac{1}{2}{r}_{21}Np{\theta }^{+}+\frac{1}{2}{r}_{11}{N}_p({Se}_B-{Se}_A+{\theta }^{+})+\frac{1}{2}{r}_{22}N(1-p){\theta }^{-}+\frac{1}{2}{r}_{12}N(1-p)({Sp}_A-{Sp}_B+{\theta }^{-})]/\frac{N^D}{2}\\ =[r_{21}p({\theta }^{+})+r_{11}p({Se}_B-{Se}_A+{\theta }^{+})+r_{22}(1-p){\theta }^{-}+r_{12}(1-p)({Sp}_A-{Sp}_B+{\theta }^{-})]/f\end{array}$$ (6)

The difference of response rates is

$$\begin{array}{l}{\mathrm{\Delta }}_2=r_2^A-r_2^B=[(r_{21}-r_{11})p({Se}_B-{Se}_A)+(r_{22}-r_{12})(1-p)({Sp}_A-{Sp}_B)]/f\\ ={\mathrm{\Delta }}_1/f\end{array}$$

Note that the difference in response rates is magnified by a factor of f when we consider only the discordant results.

The sample size formula evaluated with $p_a=r_2^A$ and $p_b=r_2^B$ yields N^D/2, the required number of discordant patients in each arm. Recall that $f=\frac{N^D}{N}$, so the required total (both concordant and discordant patients) sample size is therefore $N=\frac{N^D}{f}$.

2.3. A Causal Inference Perspective

In this subsection, we look at the causal implication of both designs using the potential outcome framework. The potential outcome framework was first proposed by Neyman [10], later formalized by Rubin [11], to evaluate the causal effect of the intervention. Under the classic potential outcome framework, each subject has a pair of potential outcomes depending on their assignment of interventions– one potential outcome if treated with the experimental intervention, another potential outcome if treated with other alternative or standard intervention. If both potential outcomes are equal, it indicates no difference in the effects between interventions.

In our setup, denote T be the treatment strategy indicator, i.e., T = 1 for patient management following test A results and T = 0 for patient management following test B results. For any final outcome of interest, Y, there is a pair of potential outcomes (Y ¹, Y ⁰) for T = 1 and T = 0. Ideally, the population average treatment effect between strategies is estimated as E(Y ¹ − Y ⁰), provided that both potential outcomes can be observed. In reality, only one of them can be observed for each subject at the same time. Therefore, randomization design is used to estimate the desired effect unbiasedly. Specifically, for the two designs we are comparing,

• two-arm design

  $$E(Y^1-Y^0)=E(Y^1)-E(Y^0)=E(Y\mid T=1)-E(Y\mid T=0)={\mathrm{\Delta }}_1$$

• paired design

  The population consists of two subpopulations: concordant and discordant subpopulation. In concordant subpopulation, Y ¹ = Y ⁰, since the two test results always agree. Therefore, the difference between the two treatment strategies is solely determined by their differences in the discordant subpopulation.

  $$\begin{array}{l}E(Y^1-Y^0)=E(Y^1-Y^0\mid \mathit{conc}.)\times P(\mathit{conc}.)+E(Y^1-Y^0\mid \mathit{disc}.)\times P(\mathit{disc}.)\\ =E(Y^1-Y^0\mid \mathit{disc}.)\times f=[E(Y\mid T=1,\mathit{disc}.)-E(Y\mid T=0,\mathit{disc}.)]\times f={\mathrm{\Delta }}_2\times f\end{array}$$

The above two equations yield the same relationship shown in section 2.2. From a causal inference perspective, the two-arm design is based the entire population, while the paired design is based on the discordant population. Both designs are valid for making inference regarding the treatment effect and the latter is more efficient since it takes advantage of extra test information to identify the differential subpopulation.

3. PARAMETER ESTIMATION

The formulas derived in the previous section can be used to compute the sample size needed to ensure adequate power to detect the postulated difference in response rates. In this section, we provide estimates for the individual response rate associated with each test and derive their standard errors. Recall that R^A and R^B are the rates of favorable clinical outcome due to treatments assigned by test A and B. Since the structures of the designs differ, we use subscripts to distinguish those estimators: $\widehat{r_1^A}$ for test A in the two-arm design and $\widehat{r_2^A}$ in the paired design. In all cases and in the interest of brevity, it suffices to derive the estimators for R^A and simply replace the notation of A with a B for formulas related to R^B.

3.1. Estimation in Two-arm design

In the two arm design, estimation is straightforward. Each patient receives treatment based on only one test, so $R^A=r_1^A$, which denotes the true rate of favorable outcomes in the treatment arm following test A. Under the usual Binomial assumptions, $Y_1^A~\mathit{Binomial}(N/2,r_1^A)$ where $Y_1^A$ is the count of patients with favorable outcomes in the arm. The standard estimator for R^A is just the sample proportion:

$$\widehat{r_1^A}=\frac{Y_1^A}{N/2}$$

with known properties:

$$\begin{array}{l}E(\widehat{r_1^A})=R^A=r_1^A\\ \mathit{Var}(\widehat{r_1^A})=\frac{R^A(1-R^A)}{N/2}\end{array}$$ (7)

3.2. Estimation in Paired Design

In the paired design, we previously defined $r_2^A,r_2^B$ to be the rate of favorable outcomes in the discordant portion. To find R^A in the paired design, we need to define the response in the concordant population and combine it with discordant part. To estimate the variance, we also need to consider the covariance structure between these two parts.

We partition the whole population into three groups with two test results, A⁺B⁺, A⁻B⁻ and discordant (including A⁺B⁻ and A⁻B⁺). Denote the corresponding sample size by N⁺, N⁻, N^D, and assume (N⁺, N^D, N⁻) ~ Multinomial(N; π⁺, f, π⁻), where π⁺ + f + π⁻= 1, where π⁺, π⁻ are the probabilities of concordant positives and concordant negatives. Randomizing the N^D patients into groups following test A and B evenly, the count of responses in each group conditional on the size of the group have the following distributions.

$$\begin{array}{l}{Y}^A\mid \frac{N^D}{2}~\mathit{Binomial}(\frac{N^D}{2},r_2^A)\\ Y^B\mid \frac{N^D}{2}~\mathit{Binomial}(\frac{N^D}{2},r_2^B)\\ Y^{+}\mid N^{+}~\mathit{Binomial}(N^{+},{\rho }^{+})\\ Y^{-}\mid N^{-}~\mathit{Binomial}(N^{-},{\rho }^{-})\end{array}$$

where ρ⁺ and ρ⁻are analogously the rates of favorable outcomes in the concordant portions. Their unconditional mean and variance are given as below (See Appendix for details in derivation):

$$\begin{array}{l}E(Y^A)=E\left(E(Y^A\mid \frac{N^D}{2})\right)=E\left(\frac{N^D{r}_2^A}{2}\right)=\frac{N{fr}_2^A}{2}\\ E(Y^{+})=E(E(Y^{+}\mid N^{+}))=E(N^{+}{\rho }^{+})=N{\pi }^{+}{\rho }^{+}\\ E(Y^{-})=E(E(Y^{-}\mid N^{-}))=E(N^{-}{\rho }^{-})=N{\pi }^{-}{\rho }^{-}\end{array}$$

Unconditional variances and covariances,

$$\begin{array}{l}\mathit{Var}(Y^A)=N\left[\frac{{fr}_2^A}{2}-\frac{f{(r_2^A)}^2}{4}-\frac{{({fr}_2^A)}^2}{4}\right]\\ \mathit{Var}(Y^{+})=N[{\pi }^{+}{\rho }^{+}-{({\pi }^{+}{\rho }^{+})}^2]\\ \mathit{Var}(Y^{-})=N[{\pi }^{-}{\rho }^{-}-{({\pi }^{-}{\rho }^{-})}^2]\\ \mathit{cov}(Y^{+},Y^{-})=-N{\rho }^{+}{\rho }^{-}{\pi }^{+}{\pi }^{-}\\ \mathit{cov}(Y^{+},2Y^A)=-N{\rho }^{+}{r}_2^A{\pi }^{+}f\\ \mathit{cov}(Y^{-},2Y^A)=-N{\rho }^{-}{r}_2^A{\pi }^{-}f\end{array}$$

Therefore, we can derive the estimator of R^A as sum of three components, correspondingly, concordant positives, concordant negatives and discordant patients. We substitute sample proportions for each parameter in estimation. The estimator can be considered as a weighted average of the three components by double counting the patients in discordant population since we do not have the information on half of the discordant patients who follow test B.

$$R^A={\pi }^{+}{\rho }^{+}+{\pi }^{-}{\rho }^{-}+{fr}_2^A$$ (8)

$$\begin{array}{l}\widehat{r_2^A}=\frac{Y^A}{N^D/2}\frac{N^D}{N}+\frac{Y^{+}}{N^{+}}\frac{N^{+}}{N}+\frac{Y^{-}}{N^{-}}\frac{N^{-}}{N}\\ =\frac{1}{N}(2Y^A+Y^{+}+Y^{-})\end{array}$$ (9)

R^B, $\widehat{r_2^B}$ have similar forms. We can show that the paired design estimators are unbiased with variance (See Appendix for details in derivation):

$$\mathit{Var}(\widehat{r_2^A})=\frac{R^A(1-R^A)}{N}+f\frac{r_2^A(1-r_2^A)}{N}$$ (10)

It is easy to show the consistency of the estimator as ${lim}_{N\to \infty }\mathit{Var}(\widehat{R_2^A})=0$. Comparing with (7), we observe that the efficiency gain of the paired design is high when the discordant rate, f, is low. This finding is confirmed by the simulation studies in the next section.

4. SIMULATION RESULTS

The simulation study presented in this section was conducted under the Multinomial and Binomial assumptions described above. In practice, the discordant rate, f, might not be known in advance. When the sensitivities and specificities are known, however, we can always specify the range of possible values for f because f is determined by (4) and θ⁺ and θ⁻ are bounded as shown in subsection 2.2. In this section, we simulate the data for five possible values of f to illustrate how the change of discordant rate would affect the sample size. In practice, if a reliable estimate of the frequency of discordant test results is available, it is advisable to use it. Otherwise, the maximal f should be used to ensure adequate sample size.

4.1. Algorithm

Given the sensitivities and specificities of the tests, the prevalence of disease, we can find the range of values for θ⁺ and θ ⁻ and determine the range of f since f is a monotonic linear function of θ⁺ and θ⁻. Taking five values evenly distributed in the range of θ⁺ and θ⁻, starting with the minimum and ending with the maximum, we compute five sample values of f over the its range. Each round of simulations follows the general steps as below:

• Sample a true disease status vector D as Binomial with Pr(D+) = p.

• Conditional on D, f, sensitivity, specificity and prevalence, simulate test results for tests A and B using a multinomial distribution as given in Table 2.

• Randomize the patients for each design. In the two-arm design, permute the assignment vector of N/2 ones and N/2 zeroes; in the paired design, permute the assignment vector of N^D/2 ones and N^D/2 zeroes for discordant population only.

• For each design, assign treatments according to the assignment vectors. For the paired design, concordant patients A⁺B⁺ and A⁻B⁻ are assigned to treatments I and II respectively.

• Finally, for each patient, a binary outcome of treatment is generated as Bernoulli with probability chosen from the corresponding cure rates in Table 1.

Table 1.

Cure Rates given Disease Status and Treatment

	D+	D−
Treatment I	r11	r12
Treatment II	r21	r22

For each set of operating characteristics, cure rates and each level of f, 1000 simulations have been run.

4.2. Sample Size Calculation and Power Simulation

We computed the required sample size under four different scenarios. The high accuracy test with perfect treatment (High-Accu. Perfect-Trt) scenario assumes that the diagnostic tests have high sensitivity and specificity and the patients respond perfectly to the right treatment decision; the high accuracy test with imperfect treatment (High-Accu. Imperfect-Trt) scenario assumes that the diagnostic tests have high sensitivity and specificity and half of the truly diseased patents respond favorably to the right treatment decision. The next two scenarios consider diagnostic tests with low sensitivity and specificity and patients responding perfectly to the right treatment decision. The difference is that the low accuracy test with perfect treatment and high prevalence (Low-Accu. Perfect-Trt High-Prev.) scenario assumes a high prevalence of 10%, the low accuracy test with perfect treatment and low prevalence (Low-Accu. Perfect-Trt Low-Prev.) scenario assumes a low prevalence of 5%. Table 3 lists all parameter values for four scenarios, the calculated range of f, as well as the true values for R^A,R^B and Δ₁.

Table 3.

Simulation Scenarios

Parameters	High-Accu. Perfect-Trt	High-Accu. Imperfect-Trt	Low-Accu. Perfect-Trt High-Prev.	Low-Accu. Imperfect-Trt Low-Prev.
Sensitivity (test a)	0.95	0.95	0.85	0.85
Specificity (test a)	0.80	0.80	0.70	0.70
Sensitivity (test b)	0.90	0.90	0.80	0.80
Specificity (test b)	0.75	0.75	0.65	0.65
Prevalence	0.1	0.1	0.1	0.05
Resp. rate of Trt. I on D+	1.0	0.5	1.0	1.0
Resp. rate of Trt. I on D−	0.2	0.2	0.2	0.2
Resp. rate of Trt. II on D+	0.2	0.2	0.2	0.2
Resp. rate of Trt. II on D−	1.0	1.0	1.0	1.0
Range of f	[0.05,0.42]	[0.05,0.42]	[0.05,0.62]	[0.05,0.635]
RA	0.852	0.8045	0.772	0.766
RB	0.812	0.767	0.732	0.726
Δ1	0.4	0.375	0.4	0.4

For the parameters above, the required number of patients in both arms in order to detect a specific alternative with power 0.80 for type I error of 0.05 are tabulated in Table 4. In all scenarios, the paired design require much less sample size than the two-arm design. We also see that the decrease in sample size is quite drastic for smaller f’s, the rate of discordant test results. In section 2, we showed the paired design magnifies the difference in responses by a factor of f. The pattern here suggests that the smaller the discordant rate, the more the difference is magnified and therefore the smaller sample size it demands. When treatment responses are less than ideal, the required sample size increases. In practice, however, the true discordant rate may be hard to estimate based on previous data. Then it is highly recommended to use a conservative sample size by assuming the highest discordant rate possible, which guarantees the desired power for type I error of 0.05.

Table 4.

Required sample sizes to test H₀ : R^A − R^B = 0 versus H_A : R^A − R^B = Δ

	Required sample size
	High-Accu. Perfect-Trt p = 0.10	High-Accu. Imperfect-Trt p = 0.10	Low-Accu. Perfect- Trt High-Prev. p = 0.10		Low-Accu. Perfect- Trt Low-Prev. p = 0.05
Two-arm	2742	3758	3658		3716
Paired			Paired		Paired
f = 0.05	180	220	f = 0.05	180	f = 0.05	180
f = 0.1425	656	760	f = 0.192	892	f = 0.196	912
f = 0.235	1098	1260	f = 0.335	1752	f = 0.342	1604
f = 0.3275	1536	1766	f = 0.477	2242	f = 0.489	2230
f = 0.42	1974	2262	f = 0.62	2916	f = 0.635	2988

Table 5 summarizes the estimated powers (the observed proportion of rejected tests). For illustration purpose, we just show the results under High-Accu. Perfect-Trt scenario. The simulated powers are right on target; the simulation errors here are no larger than 0.005, so the simulation appears to be well calibrated for both designs. We do not compute the power of the paired design when f = 0.05, because the expected sample size is 90 in each arm and the expected number of discordant patients is (90)f = 4.5, which is far too small to satisfy the normal approximation assumed for the sample size formulas.

Table 5.

Power and parameters estimation for the High-Accu. Perfect-Trt scenario with 1000 replications of simulated data

	f	SS	Est. Power	$\widehat{R^A}$	$\widehat{R^B}$	$s.e.(\widehat{R^A})$	$s.e.(\widehat{R^B})$
Two-Arm		2742	0.804	0.8523	0.8121	0.0096	0.0105
Paired	0.05	180	--†	0.8528	0.8132	0.0138	0.0156
	0.1425	656	0.802	0.8523	0.8120	0.0152	0.0169
	0.235	1098	0.808	0.8520	0.8120	0.0127	0.0139
	0.3275	1536	0.781	0.8519	0.8122	0.0114	0.0123
	0.42	1974	0.804	0.8523	0.8125	0.0106	0.0114

^† Note that the required sample size for f = 0.05 is too small to satisfy the requirements for the normal approximation, we do not compute the power for this specific scenario.

True parameter values are R^A = 0.852 and R^B = 0.812. $s.e.(\widehat{R^A})$ and $s.e.(\widehat{R^B})$ are the observed sample variances among 1000 replications.

4.3. Estimation

In each simulation, we compute the two-arm design estimators and the paired design estimators based the observed count of responses in each subpopulation. Results are also shown in Table 5. Recall that the true parameter values are R^A = 0.852 and R^B = 0.812.

The point estimators from the two-arm and paired design show very good agreement and both are very close to the true values, suggesting the estimation scheme for the paired design will be an adequate substitute for the two-arm design. We also notice that the variance of the estimators from the paired design is a bit bigger. This is due to fewer observations used in the paired design. The standard error of the estimator across the simulated samples also match well with theoretical results calculated by formula (10) (results not shown here).

Cautions should also be exercised in practice when the discordant rate is low. Because normal approximation to the binomial distribution is used in the testing, the classical rule of thumb of np(1 − p) should be checked to ensure that each arm of the discordant sample is large enough to apply the normal approximation.

5. EXAMPLE: PREOPERATIVE STAGING OF BLADDER CANCER

Randomized studies of the impact of tests on patient outcomes are not very common, with the possible exception of comparative studies of screening tests. However, there is increasing interest in comparative studies of tests outside the screening context [12–14]. In particular, this interest is fueled by the recent growth of Comparative Effectiveness Research. In this section, to illustrate the methodologic approaches, we choose an example in which a test is used for diagnosis and staging, given our familiarity with the specific medical context. In addition, we refer the reader to de Graaff’s work [4, 15] for a detailed discussion of the role of DRCT design to study tests used in critical limb ischemia, where a continuous outcome, bodily pain score (PBS) was evaluated.

Bladder cancer is the fourth most common cancer among males and the ninth most common among females. It is not known exactly how bladder cancer begins and the identified risk factors include smoking, occupational hazards, chronic bladder problems, etc. Commonly used diagnostic tests are urine test, cystoscopy, biopsy, CT, MRI and other imaging modalities. Imaging methods are used to determine if the cancer has spread to other organs. For non-metastatic bladder cancer, the standard treatment is surgical removal of the entire organ by radical cystectomy. However, this does not work well for the patients who already have tumor spread to the locoregional lymph nodes or occult distant metastases at the time of initial diagnosis. Recent studies indicate that the addition of neoadjuvant chemotherapy improves survival and cure fraction in patients with metastasis to the locoregional lymph node [16]. However, the potential disadvantage of the neoadjuvant chemotherapy may include unnecessary treatment in patients who may not respond to chemotherapy and a resulting delay in time to cystectomy [17]. So, accurate staging is pivotal in identifying patients that will respond to chemotherapy and in planning the optimal therapy. The conventional CT or MRI are not accurate enough for the therapeutic decisions. Recent studies have examined the diagnostic accuracy of newer imaging methods for the preoperative staging of bladder cancer, including enhanced MRI, PET, etc. [18,19] In particular, lymph node imaging is done before surgery in order to detect possible metastases and provide better guidance to the surgical intervention. Knowledge of the size, number, location and characterization of the nodes prior to surgery would increase the probability that malignant nodes would be removed and decrease the morbidity by avoiding removal of benign lymph nodes [20].

For illustrative purpose, suppose that researchers are interested in testing whether the enhanced MRI is superior to the conventional MRI, both followed by the appropriate therapeutic intervention, in terms of achieving better therapeutic outcomes. They want to investigate the prognostic value of the imaging beyond merely the accuracy of the test. To this end, we propose using the methods developed in the previous sections to design a randomized study among patients with urothelial cancer of the bladder. The two imaging modalities under evaluation are conventional MRI and Ferumoxtran-10-enhanced MRI. The participants undergo one or both of the two exams. Lymph nodes information is acquired from imaging and is used to determine whether extended lymphadenectomy and neoadjuvant chemotherapy may be appropriate. The primary outcome of interest is 5-year survival after treatment. As reported by Deserno et al. [18], the sensitivity and specificity for conventional MRI are 76% and 99%; corresponding values for enhanced MRI are 96% and 95%. We assume that if lymph node metastasis is present, the more aggressive treatment leads to 50% survival in 5 years and the conservative treatment leads to 20% survival. If there is no lymph node metastasis, the conservative treatment results in 85% survival and the more aggressive treatment results in 65% survival. The prevalence of metastasis is assumed to be 30% among the study population.

To test the null hypothesis of no difference in 5-year survival between the two imaging modalities and the following treatments, we set the type-I error at 0.05 and the power at 0.8. Under the above assumption, the enhanced MRI group is expected to have only a modest increase in 5-year survival by 1.24% over the conventional MRI group. A one-sided test is used and sample size formula is adjusted correspondingly. Table 5 summarizes the sample size required by the two designs to detect the difference of 1.24% in 5-year survival for the minimal and maximal level of discordant rate f.

In the paired design, the required sample size increases with the discordant rate. This is because that in the paired design, the true difference between the two patient management plan is magnified by the inverse of the discordant rate. So a smaller discordant rate is associated with a bigger difference to be detected, which, in turn, demands less sample. In practice, we may determine a range of possible values for the discordant portion given the test characteristics and the disease prevalence. A conservative approach would be to go with the maximum required sample size which corresponds to the scenario with the maximal discordant rate. In this example, the maximal sample size required is 6923, which is about one fifth of the sample size required by the traditional two-arm design.

Unlike the traditional design that determines the total sample size in one formula, the sample size determination for the paired design proceeds by first computing the sample size of the discordant pairs and subsequently dividing it by the discordant rate. To ensure adequate sample size for the discordant population, a practical solution is to derive the total sample size by inverting a Binomial one-sided confidence interval. Picking any reasonable confidence level (for example, 0.99 to be prudent), we can equate the lower bound of the one-sided interval to the required sample in the discordant population calculated in the first step, then solve it to find the total sample size. In this example, a total sample size of 6923 guarantees us to have 808 patients in the discordant population with 99% confidence for the discordant rate of 0.126.

6. DISCUSSION

At present, the assessment of the impact of diagnostic tests on patient outcomes is done primarily via modeling and secondarily via clinical and possibly randomized studies. With the exception of randomized studies of screening modalities, the methodology of clinical studies of the effect of tests on patient outcomes has not received much attention in the literature and the actual studies of this type have been rather few. However, this situation is changing rapidly in the era of personalized medicine. Diagnostic tests are increasingly used to guide therapy decisions at each step of the way, including decisions about withholding further treatment and/or switching to other available treatments without waiting for completion of the full course of therapy. In the language of biomarkers, there is wide interest in the evaluation of prognostic and predictive markers.

In this paper we study the efficiency of two of the simpler designs for comparing two diagnostic tests, the two-arm design in which randomization to one of the other test takes place at the outset, and the paired design in which both tests are performed on each patient and randomization is used to assign therapy in the discordant pairs. In both designs, the decisions of therapeutic procedures are made on the basis of test results. We discuss the estimation of the rate of favorable outcomes for each test and the comparison of rates between the two tests. We also discuss sample size considerations for each design and compare their efficiency in a simulation study. Our computations show that the paired design is more efficient than the two-arm design. This finding parallels the superiority of McNemar’s test, which also compares only the discordant portion.

In this paper we evaluate the feasibility of each design under different scenarios. We also use a clinical example to illustrate the sample size determination in a practical setting. Even though the sample size needed for the paired design is less than 20% of that required for the two-arm design, a study of 6,923 patients still seems prohibitively large for this particular clinical question. Such result is primarily due to the fact that the expected survival difference is so small, only 1.24%. The survival gain would be larger if the new treatment had much more favorable outcomes than the standard practice. Though the clinical implication might not be that significant for this example, we think it serves a good purpose of exemplifying the method.

A variety of other types of designs for diagnostic randomized clinical trials can be considered although not many of them have been used in practice [21]. We chose a streamlined version of the designs studied in this paper by assuming binary test results, two treatment strategies and binary/continuous patient outcomes. This version is potentially useful in many practical settings and the approach can also be generalized to more complex situations, for example, situations with more than two tests or with time-to-event type of outcomes.

Some difficulties may need to be overcome before DRCTs are used broadly. The practical feasibility of DRCTs depends on the possibility to base therapeutic strategy decisions on test results, without the need of definitive information on whether the test result is correct. As a consequence, the acceptability of such designs in practice would depend on how accurate the tests are thought to be. More elaborate designs could also be formulated to include, for example, verification of positive test findings, if that was feasible before making therapeutic decisions. Specifically for the paired design, randomization of patients with discordant results to one of the two therapies implicitly assumes there is still equipoise about which is the correct therapy approach after the two test results are known. Such equipoise would be feasible only for particular combinations of test performance characteristics and therapy effectiveness.

Our setup and results can be easily extended to predictive marker studies as a tool to evaluate the clinical value of the biomarkers. Sargent et al. [7] discussed clinical trial designs for predictive marker validation and compared the sample size required for different designs with only one predictive marker for survival outcomes. The predictive marker is a marker that predicts the differential efficacy of a particular therapy based on marker status and can aid in optimal therapy selection. By this definition, the diagnostic test is a special case of predictive markers, therefore, our methods can be used to compare two predictive markers in terms of treatment efficacy.

Table 6.

Sample size required to detect the outcome difference associated with conventional and enhanced MRI

			Sample Size
Two-arm Design			40412
Paired Design	f = 0.088 (minimum)	Discordant Total†	394 5008
	f = 0.126 (maximum)	Discordant Total†	808 6923

^†The total is calculated based on the lower bound of 99% Binomial confidence interval given the required discordant sample.

Table 7.

Mean Responses given Disease Status and Treatment

	D+	D−
Treatment I	y11	y12
Treatment II	y21	y22

Appendix I: Estimation in Paired Design

Following the notations and assumptions in section 3, we have

$$\begin{array}{l}{Y}^A\mid \frac{N^D}{2}~\mathit{Binomial}(\frac{N^D}{2},r_2^A)\\ Y^B\mid \frac{N^D}{2}~\mathit{Binomial}(\frac{N^D}{2},r_2^B)\\ Y^{+}\mid N^{+}~\mathit{Binomial}(N^{+},{\rho }^{+})\\ Y^{-}\mid N^{-}~\mathit{Binomial}(N^{-},{\rho }^{-})\end{array}$$

with unconditional expectations,

$$\begin{array}{l}E(Y^A)=E\left(E(Y^A\mid \frac{N^D}{2})\right)=E\left(\frac{N^D{r}_2^A}{2}\right)=\frac{N{fr}_2^A}{2}\\ E(Y^{+})=E(E(Y^{+}\mid N^{+}))=E(N^{+}{\rho }^{+})=N{\pi }^{+}{\rho }^{+}\\ E(Y^{-})=E(E(Y^{-}\mid N^{-}))=E(N^{-}{\rho }^{-})=N{\pi }^{-}{\rho }^{-}\end{array}$$

and unconditional variances,

$$\begin{array}{l}\mathit{Var}(Y^A)=E\left(\mathit{Var}(Y^A\mid \frac{N^D}{2})\right)+\mathit{Var}\left(E(Y^A\mid \frac{N^D}{2})\right)\\ =E\left(\frac{r_2^A(1-r_2^A)}{2}{N}^D\right)+\mathit{Var}\left(\frac{r_2^A{N}^D}{2}\right)\\ =\frac{1}{2}(r_2^A(1-r_2^A)Nf)+Nf(1-f){\left(\frac{r_2^A}{2}\right)}^2\\ =N\left[\frac{{fr}_2^A}{2}-\frac{f{(r_2^A)}^2}{4}-\frac{{({fr}_2^A)}^2}{4}\right]\\ \mathit{Var}(Y^{+})=\mathit{Var}(E(Y^{+}\mid N^{+}))+E(\mathit{Var}(Y^{+}\mid N^{+}))\\ =\mathit{Var}(N^{+}{\rho }^{+})+E(N^{+}{\rho }^{+}(1-{\rho }^{+})))\\ =N{\pi }^{+}(1-{\pi }^{+}){({\rho }^{+})}^2+N{\pi }^{+}{\rho }^{+}(1-{\rho }^{+})\\ =N[{\pi }^{+}{\rho }^{+}-{({\pi }^{+}{\rho }^{+})}^2]\\ \mathit{Var}(Y^{-})=N[{\pi }^{-}{\rho }^{-}-{({\pi }^{-}{\rho }^{-})}^2]\\ \mathit{cov}(Y^{+},Y^{-})=\mathit{cov}(E(Y^{+}\mid N^{+}),E(Y^{-}\mid N^{-}))+E(\mathit{Cov}(Y^{+},Y^{-}\mid N^{+},N^{-}))\end{array}$$

Since the outcomes are conditionally independent when N⁺, N⁻and N^D are known, the second term is zero.

$$\begin{array}{l}\mathit{Cov}(Y^{+},Y^{-})=\mathit{Cov}(N^{+}{\rho }^{+},N^{-}{\rho }^{-})\\ ={\rho }^{+}{\rho }^{-}\mathit{Cov}(N^{+},N^{-})\\ =-N{\rho }^{+}{\rho }^{-}{\pi }^{+}{\pi }^{-}\\ \mathit{Cov}(Y^{+},2Y^A)=2\mathit{Cov}\left(N^{+}{\rho }^{+},\frac{N^D}{2}{r}_2^A\right)\\ ={\rho }^{+}{r}_2^A\mathit{Cov}(N^{+},N^D)\\ =-N{\rho }^{+}{r}_2^A{\pi }^{+}f\\ \mathit{Cov}(Y^{-},2Y^A)=-N{\rho }^{-}{r}_2^A{\pi }^{-}f\end{array}$$

Therefore, we find our estimator of the overall response rate following test A as:

$$\begin{array}{l}\widehat{r_2^A}=\frac{Y^A}{N^D/2}\frac{N^D}{N}+\frac{Y^{+}}{N^{+}}\frac{N^{+}}{N}+\frac{Y^{-}}{N^{-}}\frac{N^{-}}{N}\\ =\frac{1}{N}(2Y^A+Y^{+}+Y^{-})\end{array}$$

which is unbiased,

$$\begin{array}{l}E(\widehat{r_2^A})=E\left(\frac{1}{N}(2Y^A+Y^{+}+Y^{-})\right)\\ =\frac{1}{N}(N{fr}_2^A+N{\pi }^{+}{\rho }^{+}+N{\pi }^{-}{\rho }^{-})\\ ={\pi }^{+}{\rho }^{+}+{\pi }^{-}{\rho }^{-}+{fr}_2^A=R^A\end{array}$$

with variance

$$\begin{array}{l}\mathit{Var}(\widehat{r_2^A})=\mathit{Var}\left(\frac{1}{N}(2Y^A+Y^{+}+Y^{-})\right)\\ =\frac{1}{N^2}(4\mathit{Var}{Y}^A+\mathit{Var}{Y}^{+}+\mathit{Var}{Y}^{-})-\frac{2}{N^2}(\mathit{Cov}(2Y^A,Y^{+})+\mathit{Cov}(2Y^A,Y^{-})+\mathit{Cov}(Y^{+},Y^{-}))\\ =\frac{1}{N}[{\pi }^{+}{\rho }^{+}-{({\pi }^{+}{\rho }^{+})}^2+{\pi }^{-}{\rho }^{-}-{({\pi }^{-}{\rho }^{-})}^2+2{fr}_2^A-f{(r_2^A)}^2-(f{(r_2^A)}^2]-\frac{2}{N}[{\rho }^{+}{\rho }^{-}{\pi }^{+}{\pi }^{-}+{\rho }^{+}{r}_2^A{\pi }^{+}f+{\rho }^{-}{r}_2^A{\pi }^{-}f]\end{array}$$

Noting that,

$$\begin{array}{l}{R}^A(1-R^A)=[r_2^{A}f+{\rho }^{+}{\pi }^{+}+{\rho }^{-}{\pi }^{-}][1-(r_2^{A}f+{\rho }^{+}{\pi }^{+}+{\rho }^{-}{\pi }^{-})]\\ ={\pi }^{+}{\rho }^{+}-{({\pi }^{+}{\rho }^{+})}^2+{\pi }^{-}{\rho }^{-}-{({\pi }^{-}{\rho }^{-})}^2+{fr}_2^A-{({fr}_2^A)}^2-2{\rho }^{+}{\rho }^{-}{\pi }^{+}{\pi }^{-}-2{\rho }^{+}{r}_2^A{\pi }^{+}f-2{\rho }^{-}{r}_2^A{\pi }^{-}f\end{array}$$

We can simplify the variance of the estimator to be

$$\mathit{Var}(\widehat{r_2^A})=\frac{R^A(1-R^A)}{N}+f\frac{r_2^A(1-r_2^A)}{N}$$

Appendix II: Sample Size Formulas for Continuous Outcomes

This appendix is to derive the sample size formulas for continuous outcomes. If there is a continuous outcome of primary interest, y, which is measured after the treatment, similar to table 1, we parameterize the mean changes of this outcome for different disease status and treatment combinations below:

Without loss of generality, we assume a positive change is beneficial. We further assume that for true disease patients, treatment I is better and for disease-free patients, treatment II is better. Then the above table implies, y₁₁ ≥ y₂₁ and y₂₂ ≥ y₁₂.

The primary hypothesis of interest is the mean comparison between the two treatment strategies. Then, we can write the hypothesis for the two-arm design as $H_0^{\mathit{Two}-\mathit{arm}}:y_1^A=y_1^B\text{vs}.H_A^{\mathit{Two}-\mathit{arm}}:y_1^A-y_1^B={\mathrm{\Delta }}_1$, where $y_1^A$ denotes the mean response for patients randomized to test A and $r_1^B$ denotes the mean response for patients randomized to test B. Similarly, we can write the hypothesis for the paired design as $H_0^{\mathit{Paired}}:y_2^A=y_2^B\text{vs}.H_A^{\mathit{Paired}}:y_2^A-y_2^B={\mathrm{\Delta }}_2$, where $y_2^A$ denotes the mean response for patients with discordant results who are randomized to test A based strategy and $r_2^B$ denotes the mean response for patients with discordant results who are randomized to test B based strategy. For comparison of two independent means, usually, normal approximation is used and a constant variance for all patients, σ², is assumed [7]. For brevity, we just show the formulations for one-sided tests and they may be used for tow-sided tests by replacing α by α/2 wherever it appears in the formulas.

For two-arm design, similar to section 2.1, the mean responses for the two arms are:

$$\begin{array}{l}{y}_1^A=y_{11}{\mathit{pSe}}_A+y_{22}(1-p){Sp}_A+y_{12}(1-p)(1-{Sp}_A)+y_{21}p(1-{Se}_A)\\ y_1^B=y_{11}{\mathit{pSe}}_B+y_{22}(1-p){Sp}_B+y_{12}(1-p)(1-{Sp}_B)+y_{21}p(1-{Se}_B)\end{array}$$

The difference in mean responses is:

$${\mathrm{\Delta }}_1=y_1^A-y_1^B=(y_{21}-y_{11})p({Se}_B-{Se}_A)+(y_{22}-y_{12})(1-p)({Sp}_A-{Sp}_B)$$

The sample size formula for equal allocation is given as:

$$n_A=n_B=\frac{2{(z_{\alpha }+z_{\beta })}^2{\sigma }^2}{{\mathrm{\Delta }}_1^2}$$

And the sample size formula for unequal allocation is given as:

$$\begin{array}{l}{n}_A=\frac{2{(z_{\alpha }+z_{\beta })}^2{\sigma }^2(\lambda +1)}{{\mathrm{\Delta }}_1^2\lambda }\\ n_B=\lambda n_A\end{array}$$

For paired-design, similar to section 2.2, the mean responses for the two arms are:

$$\begin{array}{l}{y}_2^A=[y_{11}p({\theta }^{+})+y_{21}p({Se}_B-{Se}_A+{\theta }^{+})+y_{12}(1-p){\theta }^{-}+y_{22}(1-p)({Sp}_A-{Sp}_B+{\theta }^{-})]/f\\ y_2^B=[y_{21}p({\theta }^{+})+y_{11}p({Se}_B-{Se}_A+{\theta }^{+})+y_{22}(1-p){\theta }^{-}+y_{12}(1-p)({Sp}_A-{Sp}_B+{\theta }^{-})]/f\end{array}$$

The difference of response means is

$$\begin{array}{l}{\mathrm{\Delta }}_2=y_2^A-y_2^B=[(y_{21}-y_{11})p({Se}_B-{Se}_A)+(y_{22}-y_{12})(1-p)({Sp}_A-{Sp}_B)]/f\\ ={\mathrm{\Delta }}_1/f\end{array}$$

The sample size formula for equal allocation is given as:

$$n_A=n_B=\frac{2{(z_{\alpha }+z_{\beta })}^2{\sigma }^2}{{\mathrm{\Delta }}_2^2}$$

And the sample size formula for unequal allocation is given as:

$$\begin{array}{l}{n}_A=\frac{2{(z_{\alpha }+z_{\beta })}^2{\sigma }^2(\lambda +1)}{{\mathrm{\Delta }}_2^2\lambda }\\ n_B=\lambda n_A\end{array}$$