Identification of parameters through which surface chemistry determines the lifetimes of hot electrons in small Au nanoparticles

Abstract

This paper describes measurements of the dynamics of hot electron cooling in photoexcited gold nanoparticles (Au NPs) with diameters of ∼3.5 nm, and passivated with either a hexadecylamine or hexadecanethiolate adlayer, using ultrafast transient absorption spectroscopy. Fits of these dynamics with temperature-dependent Mie theory reveal that both the electronic heat capacity and the electron–phonon coupling constant are larger for the thiolated NPs than for the aminated NPs, by 40% and 30%, respectively. Density functional theory calculations on ligand-functionalized Au slabs show that the increase in these quantities is due to an increased electronic density of states near the Fermi level upon ligand exchange from amines to thiolates. The lifetime of hot electrons, which have thermalized from the initial plasmon excitation, increases with increasing electronic heat capacity, but decreases with increasing electron–phonon coupling, so the effects of changing surface chemistry on these two quantities partially cancel to yield a hot electron lifetime of thiolated NPs that is only 20% longer than that of aminated NPs. This analysis also reveals that incorporation of a temperature-dependent electron–phonon coupling constant is necessary to adequately fit the dynamics of electron cooling.

This paper describes an observed dependence of two physical properties—the electronic heat capacity and the electron–phonon coupling magnitude—of small (diameter of ∼3.5 nm), completely absorptive plasmonic gold nanoparticles (Au NPs) on the surface chemistry of the NPs. The electronic heat capacity, quantified by the coefficient γ, is the amount of energy required to change the temperature of a population of electrons in the NP. The magnitude of the electron–phonon coupling, quantified by the coefficient g, is a measure of the rate of exchange of energy between the electrons and the lattice. Upon photoexcitation of the Au NPs at the absorption maximum of their plasmon resonance, the plasmonic electron oscillation in the NPs rapidly decoheres to form a thermally equilibrated population of hot electrons (1–8). Within the commonly used “two-temperature model (2TM),” the rate of subsequent cooling of these electrons is dictated by the initial electronic temperature of the particle and the efficiency of dissipation of electronic energy into available vibrational modes. These properties, in turn, depend on the electronic heat capacity of the system and the magnitude of electron–phonon coupling. Our observed dependence of the coefficients γ and g on the chemical structure of the organic adlayer therefore implies that electronic states that participate in the electron cooling process are not only those of the gold lattice, but also orbitals at the metal–organic interface—that is, the surface chemistry of the NPs influences the rate of hot electron cooling.

Interest in using metal and semiconductor NPs as optical and/or electronic components within energy conversion systems (9, 10) has inspired studies of energy dissipation and electron scattering at NP–ligand interfaces. Organic coatings play a crucial role in the chemical and electronic passivation of these particles, and therefore in the performance and stability of NP-based films under repeated photoexcitation and redox cycles (11). Photoexcitation into the plasmonic state of metal particles is a convenient means of changing the energy distribution of electrons to study energy dissipation. There are indications in the literature that the chemical environment of an Au NP impacts the lifetime of hot electrons (12–16); in these examples, however, the specific mechanism by which the surrounding matrix perturbs the electron dynamics, and the impact of this perturbation on the applicability of the current models for electron cooling—in particular, the 2TM—is not clear. Recently, Bauer and coworkers have described a phenomenological model in which the interface between the Au NP and an organic adlayer changes the rate at which plasmonic electrons equilibrate to form a thermal distribution by providing pathways for redistribution of the hot electrons’ kinetic energy. The authors adopt the name “ultrafast chemical interface scattering (UCIS)” for this mechanism, as it is consistent with chemistry-induced localized surface plasmon (LSP) damping that has long been observed in small NPs in the colloid field (17–20).

Here, we clarify the role of interfacial scattering in hot electron dynamics within high surface area-to-volume NPs and demonstrate the chemical tunability of these dynamics, by determining the relationship between the parameters that dictate the electron cooling process—namely, γ and g—and the density of states contributed by the organic adlayer at relevant energies. To measure γ, g, and the rate of hot electron cooling in the NPs as a function of surface chemistry, we exchanged datively bound alkylamines with covalently bound alkylthiolates on the surface of the NPs and performed ultrafast optical measurements of the time dependence of the electronic temperature of the NPs on both types of samples. We observed the following: (i) The electronic heat capacity coefficient γ is a factor of 1.4 ± 0.1 larger for the thiolated NPs than for the aminated NPs. The larger heat capacity translates into a smaller initial electron temperature for the thiolated NPs than for the aminated NPs for a given photoexcitation power. (ii) The electron–phonon coupling constant g is a factor of 1.3 ± 0.1 larger for the thiolated NPs than for the aminated Au NPs. (iii) The electron cooling process is a factor of 1.2 ± 0.07 faster for the aminated particles than for the thiolated particles; this difference in cooling rates for aminated and thiolated particles is smaller than the differences in either heat capacity or electron–phonon coupling because changes in these two parameters partially cancel each other: an increase in the electronic heat capacity decreases the cooling rate, whereas an increase in the electron–phonon coupling increases the cooling rate.

Density functional theory (DFT) calculations of aminated and thiolated Au slabs provide a physical mechanism for our experimental results: the thiolated NPs have a larger electronic heat capacity and electron–phonon coupling constant than the aminated NPs due to a higher density of electronic states (DOS) near the Fermi level of the system. Additional states at this energy are a result of mixing of the electronic states of thiolates with those of the Au core (21, 22).

An important conclusion from our data analysis is that the electron–phonon coupling coefficient g is dependent on the electronic temperature of the system. Temperature-dependent electron–phonon coupling is logical because g depends on the driving force for energy exchange between electron and vibrational populations, and has been observed in hot electron photoemission experiments (23–26), but has not been considered in experiments that measure hot electron cooling rates in metal NPs, because these experiments used low laser intensities that were assumed to create sufficiently small electronic temperatures to remain in a temperature-independent regime of the electron–phonon coupling. We find, however, that inclusion of a temperature dependence for g significantly improves the fits of all of the kinetic data, even those collected at low excitation power.

Results and Discussion

Description and Fitting of the Ground-State Absorption Spectra of Aminated and Thiolated Au NPs.

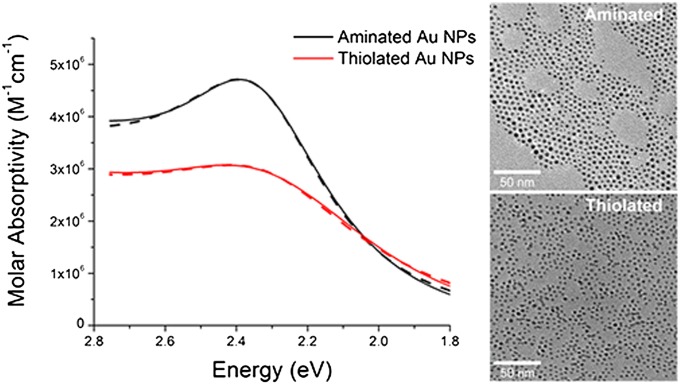
Fig. 1 (black solid line) shows the ground-state absorption spectrum of 0.7 µM solutions of hexadecylamine-coated Au NPs (diameter of 3.6 ± 0.7 nm) in toluene. We use small Au NPs because the absorptive contribution to the extinction cross-section of these particles is >1,000 larger than the scattering contribution (SI Text), so we can assume that all of the energy we put into the system is used to increase the electronic temperature. After exchange of the dative binding hexadecylamines on the Au NPs for more strongly chemisorbed hexadecanethiol, which adsorbs as a thiolate (27), the ground-state absorbance decreases in amplitude and increases in line width (Fig. 1, red solid line), a result that is consistent with previous reports (28–30). Within the theory of UCIS, an increased line width of the LSP absorbance after ligand exchange is expected due to dephasing of the plasmonic electrons as they transiently tunnel in and out of interfacial orbitals with metal and ligand character (17, 19, 20); however, this interfacial scattering processes is one of several possible contributions to the line width of the LSP (28). Inhomogeneous broadening due to polydispersity in size and shape is probably not a dominant factor in this line width. Inspection of transmission electron microscopy images (Fig. 1, Inset) reveals that the particles become more uniformly shaped upon exchange from amine to thiolate ligands, and the average diameter of the NPs is within experimental error for the two samples (3.6 ± 0.7 nm for the aminated particles, and 3.2 ± 0.6 nm for the thiolated particles; see histograms in the SI Text), with similar polydispersity. Although these diameters are not different from each other considering our measurement error, we believe that the slight etching of the NPs upon exchange from amines to thiolates accounts for the small decrease in integrated extinction coefficient of the LSP absorbance from 2.2 × 10⁵ (M⁻¹⋅cm⁻²⋅eV) for the aminated particles to 1.9 × 10⁵ (M⁻¹⋅cm⁻²⋅eV) for the thiolated particles (SI Text). Note that, in Fig. 1, although the LSP peak position appears to have shifted to higher energy upon exchange of amine ligands for thiolates, the peak has, in fact, shifted to lower energy (as expected), but the absorption at the wavelength of the LSP peak has a greater fractional contribution from the higher-energy Au d-sp interband transition once it is damped (SI Text).

Fig. 1.

(Left) Ground-state absorption spectra of 3.5-nm, 0.7 µM Au NPs passivated with hexadecanethiol (red) and hexadecylamine (black), and best fits with temperature-dependent Mie theory for both surface chemistries at 298 K, and with an exterior dielectric constant fixed to that of toluene. In the TA experiment, the pump beam excites the samples at 2.39 eV (520 nm). The increase in line width and decrease in magnitude of the LSP absorption is consistent with the literature for exchange to thiolate ligands. (Right) Transmission electron microscopy images of aminated Au NPs (3.6 ± 0.7 nm) and after ligand exchange with thiols (3.2 ± 0.6 nm). SI Text contains size histograms for both samples.

Fig. 1 also shows the best fit for the ground-state absorption spectra of the thiolated and aminated particles using Mie theory (dashed lines). In the Mie theory calculation of the fit function, we explicitly consider the dependence of the Au dielectric function on the electronic temperature using the model proposed by Scaffardi and Tocho (31), which is based on the work of Rosei et al. (32) and Inouye et al. (7). The surface chemistry-dependent parameters for fits of the ground-state spectra are two damping parameters for the intraband and d-sp interband transitions, respectively, and a scaling factor to account for changes in concentration of NPs (SI Text). The fixed parameters in these fits are the electronic temperature (T_e = 298 K), the dielectric constant of the medium (ɛ = 2.38), and the radii of the NPs listed above.

Determination of the Electronic Temperature of the Au NPs as a Function of Time.

Fig. 2 shows representative transient absorption (TA) spectra of 0.7 µM solutions of aminated and thiolated Au NP samples in toluene, at a series of time delays after photoexcitation: 1.5–4.5 ps, with 0.6-ps intervals. We acquired these sets of spectra for Au NPs with each surface chemistry at a series of laser powers, and thus at a series of expected photons absorbed per particle, 〈N〉. In choosing our laser powers, we accounted for the difference in absorption coefficients of the NPs at the excitation wavelength, 520 nm, for the two types of surface chemistry (Fig. 1).

Fig. 2.

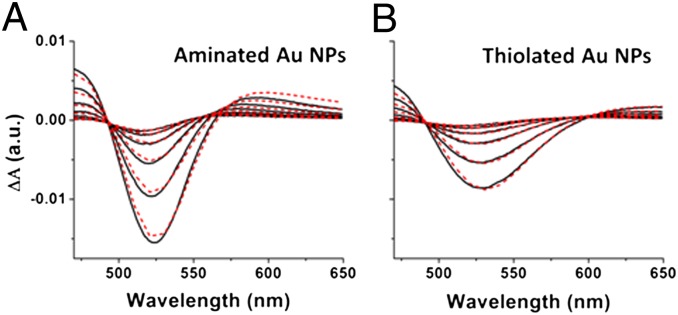
Representative transient absorption spectra of aminated (A) and thiolated (B) Au NP samples (expectation value 〈N〉 = 2 photons per particle), at a series of time delays after photoexcitation: 1.5–4.5 ps, with 0.6-ps intervals. The dashed red lines are the best fits to each differential spectrum (the difference between the plasmon absorbance at elevated electronic temperature and the plasmon absorbance at room temperature) with temperature-dependent Mie theory using fixed and floating parameters described in the text. From each fit, we extract the electronic temperature of the system at the corresponding time delay. SI Text contains additional TA spectra and fits.

As with the ground-state absorption, the bleach of the ground state within the TA spectrum is damped upon ligand exchange from amines to thiols. To translate the time dependence of the TA spectrum to the time dependence of the electronic temperature of the system, we use the parameters we obtained from fitting the ground-state spectrum of Au NPs with a particular surface chemistry in fitting the TA spectrum for NPs of that surface chemistry. Fitting of the TA spectrum over the spectral range of 470–650 nm (which includes the plasmon resonance centered at ∼520 nm) as a function of time with a temperature-dependent Mie theory is critical to monitoring the electronic temperature because recording the time evolution of the absorbance at a single wavelength does not account for the different absorption coefficients of aminated and thiolated NPs, or the fact that the LSP bleach minima shifts in wavelength as a function of temperature. The dashed red lines in Fig. 2 show that the temperature-dependent Mie theory model, which is detailed in the SI Text, fits very well to the experimental TA spectra using three fitting parameters per spectrum (the electronic temperature and two temperature-dependent damping constants).

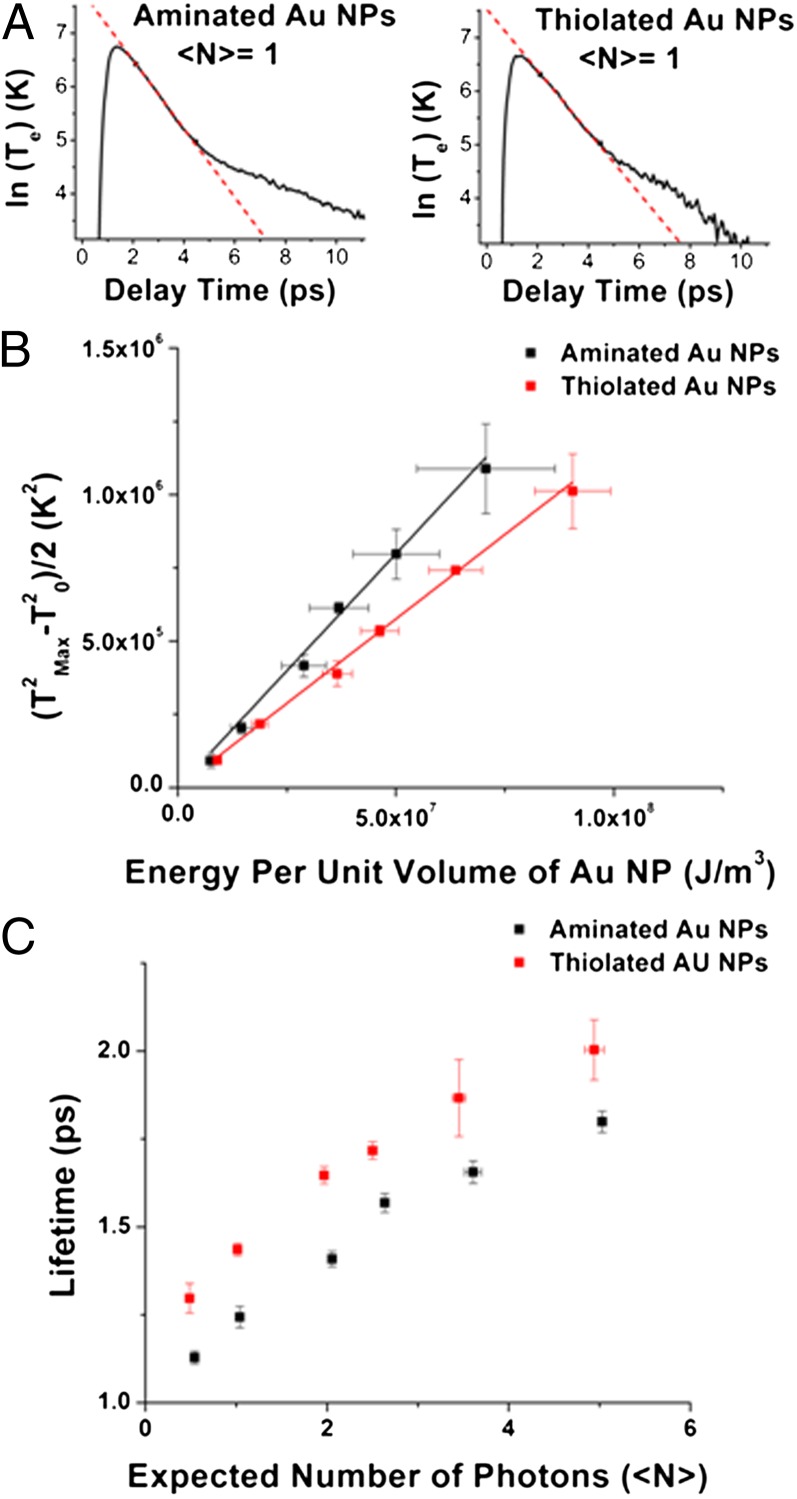
The fit function of each TA spectrum yields the electronic temperature, T_e, of the NPs as a function of time after photoexcitation, for NPs with each type of surface chemistry (Fig. 3A). Within these representative kinetic traces, the dynamics on the 300-fs timescale correspond to initial thermalization of the plasmon by electron–electron scattering (our TA instrument has an instrument response function of 200 fs, so we cannot accurately monitor electron–electron scattering processes). The dynamics on the 1- to 5-ps timescale correspond to the cooling of hot electrons through dissipation of energy into vibrational modes (the cooling process of interest). The dynamics on the tens-of-picoseconds timescale correspond to modulation of the plasmon resonance by dissipation of energy from local vibrational modes into the solvent bath.

Fig. 3.

Measurements of hot electron cooling parameters. (A) The electronic temperature of the thiolated (Right) and aminated (Left) Au NP-ligand systems, determined by fitting the TA spectra as a function of time (Fig. 2). The kinetic traces show an initial thermalization period (within the first 300 fs), followed by a period in which the hot electron gas equilibrates with available vibrations (1–5 ps), and a final period in which the lattice dissipates thermal energy to the solvent. The red lines are linear fits to the regime of interest, the cooling of the hot electron gas via electron–phonon coupling, assuming a first-order decay of the electronic temperature. (B) The square of the initial electronic temperature of the system (after thermalization of the plasmon) minus the square of the electronic temperature before photoexcitation, plotted against the energy of the laser excitation normalized by the unit volume of the Au NP. The slope of this plot is inversely proportional to the electronic heat capacity constant for the aminated (γ = 62 ± 2 J⋅m⁻³⋅K⁻²) and thiolated (γ = 87 ± 1 J⋅m⁻³⋅K⁻²) Au NPs. Note that the x-axis is U from Eq. 1 normalized by the volume of the Au NP. (C) The observed lifetime of hot electrons versus the average number of photons absorbed per NP, for the aminated (black) and thiolated (red) Au NPs. Expectation values were calculated with extinction coefficients of 4.71 × 10⁶ M⁻¹⋅cm⁻¹ for the aminated NPs and 3.07 × 10⁶ M⁻¹⋅cm⁻¹ for the thiolated NPs at 520 nm.

Thiolated Au NPs Have a Larger Electronic Heat Capacity than Aminated Au NPs.

The first piece of information we can extract from the kinetic traces in Fig. 3A is the electronic heat capacity of the system, γT_e, where γ is the electronic heat capacity coefficient, and T_e is the electronic temperature. The electronic heat capacity is related to the energy deposited in the electron population by the laser pulse (U) through , the initial electronic temperature of the system (immediately after thermalization from the plasmonic state) (Eq. 1). In Eq. 1, T₀ = 298 K is the temperature of the system before photoexcitation:

We estimate to be the maximum temperature in the T_e vs. time plots (Fig. 3A). Fig. 3B shows that, for a given value of U, which is determined from the absorbance of the sample and the energy density of the laser pulse (SI Text), is larger for the aminated Au NPs than for thiolated Au NPs. This result indicates that the electronic heat capacity constant γ, which is inversely proportional to the slope of the plot of (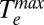² – T₀²)/2 vs. U in Fig. 3B, is larger for the thiolated Au NPs (γ = 87 ± 1 J⋅m⁻³⋅K⁻²) than for the aminated Au NPs (γ = 62 ± 2 J⋅m⁻³⋅K⁻²). This measurement shows the dependence of electronic heat capacity on the surface chemistry of a NP. We note that previous works on hot electron cooling in metal NPs (1, 3, 5, 6, 14, 33, 34) did not measure the electronic heat capacity of the NPs, but assumed it is equal to the electronic heat capacity of bulk Au (γ = 67.6 J⋅m⁻³⋅K⁻²). The linearity of the plot in Fig. 3B indicates that γ is temperature independent in the temperature range that we studied.

If we approximate the process of electron cooling via phonons as a first-order process, we can fit the kinetic traces in Fig. 3A on the 1- to 5-ps timescale with a line to extract the first-order lifetime, τ, of hot electrons as a function of 〈N〉 (=number of photons absorbed per particle). These fits are the red lines in Fig. 3A; Fig. 3C shows plots of τ vs. 〈N〉 extracted from the fits. The data point and error bar at each value of 〈N〉 correspond to the average and SD, respectively, of measurements on three separately prepared samples of Au NPs. The temperature dependence of the electronic heat capacity causes the hot electron lifetimes to depend on the initial electron temperature and 〈N〉 (5). The y-intercept of the plot in Fig. 3C is, within the first-order approximation, the “intrinsic” (zero-power) lifetime of the hot electrons in the Au NP, τ₀. The lifetimes of hot electrons are ∼20% longer for thiolated Au NPs than for aminated Au NPs at every value of 〈N〉, including 〈N〉 = 0. Within the 2TM, the hot electron lifetime (τ) should be proportional to γ, but the 20% increase in τ on going from aminated to thiolated particles is not commensurate with the ∼40% increase in γ on going from aminated to thiolated particles. We therefore explored the contribution of electron–phonon coupling, g, to the hot electron lifetimes in these systems.

Temperature-Dependent Electron–Phonon Coupling Counteracts the Effect of Electronic Heat Capacity in Hot Electron Cooling.

Within the first-order approximation of the 2TM, the intrinsic lifetime, τ₀, is proportional to γ/g. Having measured γ independently of this approximation, we could simply calculate g from the y-intercept of the lifetime plot in Fig. 3C and conclude that it partially compensates for the change in γ on going from aminated to thiolated NPs to result in a smaller-than-expected change in electron cooling lifetime. This approach is not valid in this case, however, because the first-order approximation for the 2TM leads to a specific quantitative relationship between the slope and the y-intercept of the lifetime plot in Fig. 3C that our data does not satisfy (SI Text). Furthermore, this approach does not allow for the temperature dependence for g that is suggested by separate experiments (23–26). We therefore use the general form of the 2TM, given by the differential Eqs. 2 and 3,

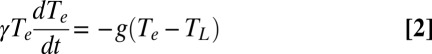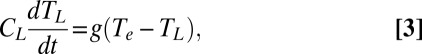to fit the dynamics of hot electron cooling obtained from fits of the TA spectra of the NPs. Eqs. 2 and 3 do not assume first order decay of electronic temperature. In these equations, T_L is the temperature of the lattice and C_L is the heat capacity of the lattice into which the electrons dissipate energy. In Eq. 3, we do not consider energy transfer from the Au phonons to the solvent bath because this process is 6–12 times slower than the electron–phonon thermalization and, therefore, has a negligible contribution to the hot electron cooling kinetics in the time window (1.5–4.5 ps) in which we perform the fits (SI Text).

For each Au NP system (thiolated or aminated), we perform a global fit of 18 kinetic traces of the electron cooling dynamics, T_e vs. time (six excitation powers, three replicates per pump power) using the system of differential Eqs. 2 and 3. The floating parameter in this fit function is g, which is shared across the fits of all 18 kinetic traces. This method produces a medium-quality fit to the experimental data using a constant value of g (SI Text). The quality of the fit can be greatly improved, however, by adding a first-order (linear) correction to g in ΔT = T_e – T_L (Eq. 4) as follows:

Fig. 4 shows the fits to the electron cooling dynamics using a temperature-dependent electron–phonon coupling constant. Semiempirical calculations in the literature suggest that the source of this temperature dependence is the increased probability of scattering of electrons far from the Fermi level with increasing electronic temperature (23–26). Table 1 compiles the values of the zero-temperature electron–phonon coupling constant, g₀, and the linear correction, g₁, determined for each Au NP system from these fits. Both g₀ and g₁ are larger for the thiolated Au NPs than the aminated Au NPs. The values of g₀ that we report here fall within the range of values reported in the literature [(1–4) × 10⁴ J⋅m⁻³⋅ps⁻¹⋅K⁻¹] (35, 36). Our value for g₀ matches particularly well to the value reported by Arbouet et al. (35) for similarly sized Au NPs, which we calculate to be 1.75 × 10⁴ J⋅m⁻³⋅ps⁻¹⋅K⁻¹ from their reported time constant for phonon-mediated electron cooling (1,150 fs), and the electronic heat capacity of bulk Au. We note that Arbouet et al. (35) reported a size dependence of the magnitude of electron–phonon coupling. We can, however, eliminate a change in size as the main source of the dependence of g on surface chemistry in our case because (i) the diameters of the aminated and thiolated NPs are not statistically different from one another, and (ii) even if we ignore the error bars on our estimation of diameter, the fit to Arbouet’s data predicts only a 6–7% increase in g on going from our aminated to thiolated NPs, whereas we observe a 30% increase.

Fig. 4.

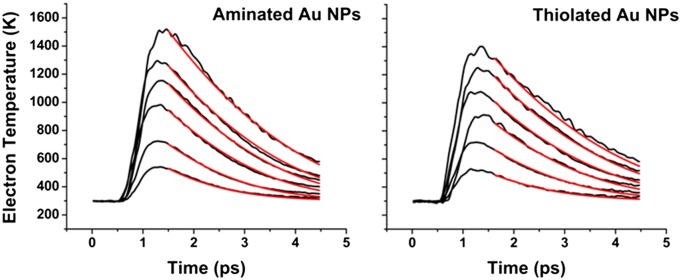
Plot of electronic temperature versus time for several values of 〈N〉 (0.5–5) for aminated Au NPs (Left) and thiolated Au NPs (Right). The red lines show the best fits of these traces to the general form of the 2TM (Eqs. 2 and 3) using g = g₀ + g₁(T_e – T_L). Table 1 lists the values of g₀ and g₁ extracted from these fits.

Table 1.

Electron–phonon coupling constants calculated from the fit functions in Fig. 4

Au NP sample	g0, J⋅m−3⋅ps−1⋅K−1	g1, J⋅m−3⋅ps−1⋅K−2
Aminated Au NPs	(2.20 ± 0.04) × 104	(12.0 ± 0.7)
Thiolated Au NPs	(2.78 ± 0.06) × 104	(17.4 ± 0.7)

The larger electronic heat capacity of thiolated Au NPs translates into a smaller driving force for energy exchange between electron and vibrational populations for a given initial electron temperature, and therefore a slower electron cooling process, for thiolated NPs than for aminated NPs. This effect is counteracted by the larger electron–phonon coupling for thiolated NPs than aminated NPs, because electron–phonon coupling increases the rate of energy transfer from electronic states to vibrational states. The increase in both g and γ upon exchanging amines for thiolates is not coincidental; both quantities are positively correlated with the electronic DOS near the Fermi level of the NP–ligand system.

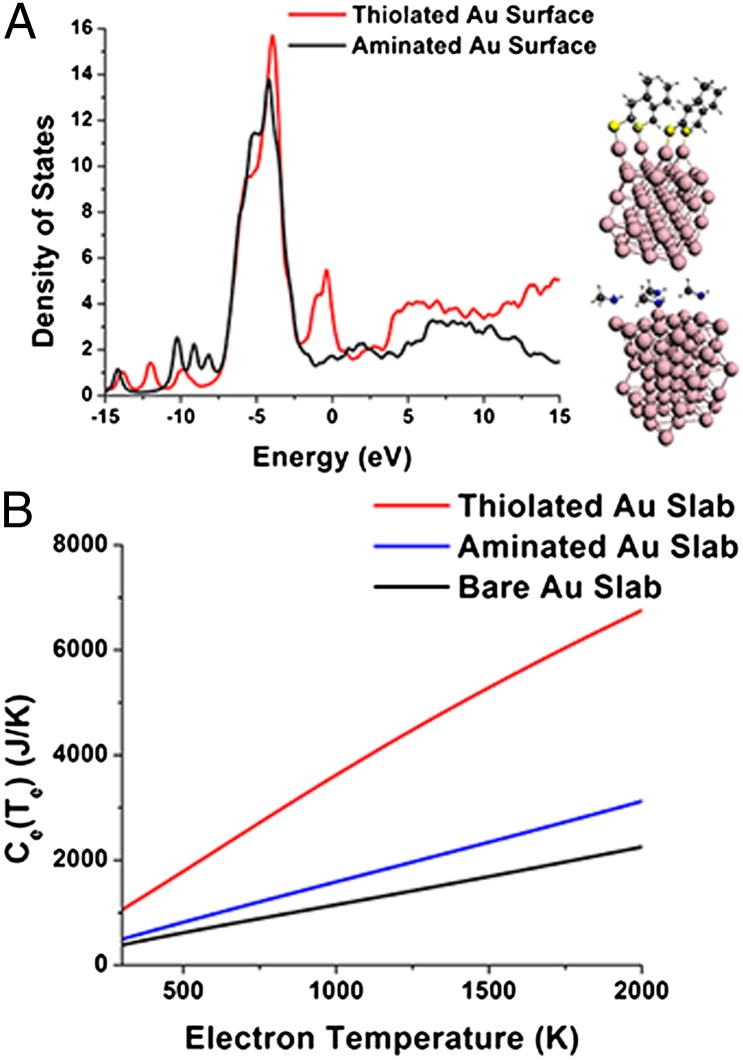
Fig. 5A shows the electronic DOS of Au slabs functionalized with thiols and amines calculated with DFT. To construct these systems, we passivated the (111) surface of a slab of gold with the bulk fcc lattice structure at four sites with either methylamine or ethylthiolate. Carbon and hydrogen atom positions were initially relaxed using molecular mechanics with the universal force field (UFF). Following relaxation of C and H positions, we relaxed the surfaces of the gold slab, along with the ligands, using DFT (GGA exchange-correlation functional, triple-zeta potential basis set with a single polarization function, and a 4f frozen core approximation for Au). There are twice as many electronic states within 1 eV of the Fermi level (set to 0 on the energy scale) for the thiolated Au slab than for the aminated Au slab. For the plot in Fig. 5A, we broadened the DOS stick spectra using a thermal broadening function with a width (σ) of 0.02 eV.

Fig. 5.

Calculations on Au–ligand model systems. (A) Density of electronic states as a function of energy for the Au slabs passivated with amines and thiolates (Right). Note that the aminated and thiolated clusters have different state density at the Fermi level (0 eV). Each surface atom on the Au slab is bound to a ligand, such that each cluster in the simulation has the same number of ligands. (B) Calculated electronic heat capacities for the ligated Au slabs in A reproduce the linear dependence of heat capacity on temperature predicted by Eq. 5, as well as a dependence of the electronic heat capacity on the electronic DOS at the Fermi level of the Au NP–ligand system.

Fig. 5B shows a calculation of the electronic heat capacity, C_e(T_e), for amine- and thiolate-passivated Au slabs using the electronic DOS determined by DFT, and the semiclassical expression for the electronic heat capacity, C_e(T_e) (Eq. 5) (36), as follows:

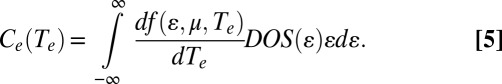In Eq. 5, the function f(ɛ,μ,T_e) is the Fermi–Dirac distribution as a function of energy (ɛ), chemical potential (μ), and electronic temperature (T_e). At low electronic temperatures, Eq. 5 reduces to the more intuitive Eq. 6 as follows:

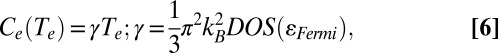where C_e(T_e) depends linearly on the electronic DOS. The results in Fig. 5B show that the heat capacity for thiolated NPs is about double that for the aminated NPs, as expected from Fig. 5A. This result, however, was reached for the slab model in Fig. 5A, where the ratio of ligand atoms to metal atoms is much larger than in the experiments. It is therefore not surprising that our experimentally measured increase in electronic heat capacity upon exchanging amines for thiolates (a factor of 1.4) is smaller than the predicted increase (a factor of 2). The zero-temperature electron–phonon coupling constant, g₀, also, in principle, increases with the electronic DOS (SI Text), but calculating g₀ from the DOS involves detailed knowledge of the energies of relevant phonon modes in the Au NPs, so we do not attempt that calculation here.

Conclusion

In summary, we have shown that thiolated Au NPs have a larger electronic heat capacity and a larger electron–phonon coupling than aminated Au NPs (Fig. 3B and Table 1). The hot electron cooling rate is positively correlated with electron–phonon coupling and negatively correlated with the electronic heat capacity, so their changes with surface chemistry partially cancel each other such that, within a first-order model for electron cooling, the hot electron lifetime of thiolated NPs is only ∼20% higher than that for aminated NPs (Fig. 3C).

Because the relationship between electron temperature and bleach intensity at a single wavelength is not conserved for the aminated and thiolated Au NPs, we use temperature-dependent Mie theory to fit the entire relevant portion of the TA spectrum as a function of time (Fig. 2) to obtain the electronic temperature of the system. This fitting procedure can be applied to NPs of arbitrary size and shape because it does not assume a particular relationship between electronic temperature and bleach amplitude.

The 2TM does adequately describe the electron cooling dynamics in these systems, despite the involvement of the ligands in determining the heat capacity and electron–phonon coupling, if we adapt the model to incorporate a temperature dependence to the electron–phonon coupling constant. The discovery of the temperature dependence of g was only possible because we fit the time dependence of the electronic temperature using the full differential Eqs. 2 and 3, rather than extracting the ratio of γ/g from the value of the hot electron lifetime in the zero-pump-power limit.

Surface chemistry-induced changes in the hot electron lifetimes are consistent with the general mechanism of ultrafast chemical interface scattering, where the electronic states of organic ligands are accessible to the electrons in the metal NP (37); the contributions of these states increase the electronic heat capacity (Fig. 5). If, in fact, the damping of the ground-state absorption spectrum of the thiolated NPs (Fig. 1), relative to the aminated NPs, is due to scattering of electrons across the inorganic/organic interface on the timescale of optical absorption, then it is reasonable that this scattering is fast enough to affect electron thermalization from the plasmonic state, and thereby increase the electronic heat capacity. This result suggests that, if our goal is to achieve a change in electron cooling time with a change in surface chemistry—as opposed to inducing canceling changes in both heat capacity and electron–phonon coupling, as we have done here—we need a ligand that has a smaller electronic coupling to the orbitals of the inorganic core than do thiolates. A weaker-coupling ligand (something intermediate between amines and thiolates) would enable scattering processes on a timescale slower than electron thermalization (but still faster than energy transfer to phonons) and therefore would increase the electron–phonon coupling without an accompanying increase in electronic heat capacity. An intermediate-coupling ligand would therefore cause a more dramatic increase in electron cooling rate upon ligand exchange from amines than do thiolates. Such an increase is desirable for fast optical switching applications. It is also interesting to consider controlling hot electron cooling in NPs through modification of surface chemistry in combination with modification of the crystal structure of the NP; crystallinity has been shown to influence the magnitude of electron–phonon coupling of silver nanoparticles (38).

Finally, the fact that the electronic heat capacity of the NP is strongly influenced by surface chemistry implies that hot electrons spend some time in orbitals of mixed Au–ligand character. Occupation of ligand orbitals by hot electrons, however transiently, is the first step to localization of initially plasmonic electrons onto proximate molecular redox centers, and the first step toward harvesting multiple electrons per photon within a photovoltaic or photocatalytic system.

Materials and Methods

Synthesis of Au NPs.

A solution of 8 g (34 mmol) of hexadecylamine (technical grade; Aldrich) and 15 mL of toluene (Aldrich) was stirred vigorously in a 100-mL round-bottom flask for 15 min, and then added to a solution of 0.66 g (1.7 mmol) of hydrogen tetrachloroaurate (III) trihydrate (≥99.9% trace metals basis; Aldrich) and 5 g (21 mmol) of hexadecylamine in 45 mL of toluene and stirred for an additional 10 min. With constant stirring, 6 mL of methanol was added to the solution, followed by 0.12 g (3.2 mmol) of sodium borohydride (Aldrich). Immediately after the addition of sodium borohydride, the solution turned a deep purple color, which is an indication of hexadecylamine-coated Au NPs formation. The particles were purified from the solvents and excess reagents by two cycles of methanol-induced precipitation, centrifugation (spun at 3,200 rpm with a Heraeus Instruments rotor #8179, 3 min), and resuspension in toluene.

Transient Absorption Measurements.

We split the 2.5-mJ output of a commercial amplified Ti-sapphire laser (Solstice; 1 kHz, 100 fs; Spectra Physics) and guided 95% to an optical parametric amplifier (TOPAS-C; Light Conversion) used to produce the pump wavelength for sample excitation, and 5% to a commercial TA spectrometer (Helios; Ultrafast Systems) for use as the probe. Within the spectrometer, a single-filament broadband continuum of wavelengths from 420 to 720 nm was generated in a sapphire plate. All samples were prepared with an absorbance of 0.3 ± 0.03 OD at the maximum of the LSP absorption feature. The output differential absorption spectrum (ΔA) was obtained through active background subtraction of the ground-state spectrum by chopping the pump at 500 Hz. The instrument response, given by the cross-correlation of the pump and probe, was measured by inducing the optical Kerr effect in a quartz microscope coverslip at the position of the sample, and it was found that the instrument response function of the system is 200 fs.

Fitting Procedures.

Ground-state and transient absorption spectra were fit using the quasistatic approximation for the absorption coefficient of a spherical particle of complex dielectric function ɛ(T_e) in an infinite medium of dielectric function ɛ_m (39, 40). The dielectric constant ɛ(T_e) was modeled with the model proposed by Scaffardi and Tocho (31), which is based on the work of Rosei et al. (32) and Inouye et al. (7). Details for the dielectric function are given in SI Text. We fitted the GS absorption spectrum by minimizing the difference between the experimental spectrum and the spectrum simulated for T_e = 298 K (these calculations were performed with a home-written program in MATLAB). We simulated the TA spectrum for a given delay time as the difference between the absorption spectrum for the electronic temperature of the excited Au NPs, T_e, and the absorbance spectrum for T_e = 298 K.

DFT Calculations.

All DFT calculations used the Amsterdam Density Functional (ADF) 2010.01 program (41, 42). A slab of gold having the bulk structure was passivated in four sites on the (111) surface with either methylamine or ethylthiolate (43, 44). C and H atom positions were initially relaxed using the UFF as implemented in the Avogadro 1.1.0 software (45). Following relaxation of the C and H positions, the surfaces of the gold slab and ligand atoms were relaxed using DFT. A BP86-D GGA exchange-correlation functional was used with a triple-zeta potential basis set having a single polarization function. A 4f frozen core approximation was used for gold, and scalar relativistic effects were incorporated using the zeroth-order regular approximation (46). In DOS plots, the system’s HOMO (Fermi level at 0 K) has been set as the zero of energy, and stick spectra were broadened using a thermal broadening function have a width (σ) of 0.02 eV.