Abstract
One of the oldest problems in linguistics is reconstructing the words that appeared in the protolanguages from which modern languages evolved. Identifying the forms of these ancient languages makes it possible to evaluate proposals about the nature of language change and to draw inferences about human history. Protolanguages are typically reconstructed using a painstaking manual process known as the comparative method. We present a family of probabilistic models of sound change as well as algorithms for performing inference in these models. The resulting system automatically and accurately reconstructs protolanguages from modern languages. We apply this system to 637 Austronesian languages, providing an accurate, large-scale automatic reconstruction of a set of protolanguages. Over 85% of the system’s reconstructions are within one character of the manual reconstruction provided by a linguist specializing in Austronesian languages. Being able to automatically reconstruct large numbers of languages provides a useful way to quantitatively explore hypotheses about the factors determining which sounds in a language are likely to change over time. We demonstrate this by showing that the reconstructed Austronesian protolanguages provide compelling support for a hypothesis about the relationship between the function of a sound and its probability of changing that was first proposed in 1955.
Keywords: ancestral, computational, diachronic
Reconstruction of the protolanguages from which modern languages are descended is a difficult problem, occupying historical linguists since the late 18th century. To solve this problem linguists have developed a labor-intensive manual procedure called the comparative method (1), drawing on information about the sounds and words that appear in many modern languages to hypothesize protolanguage reconstructions even when no written records are available, opening one of the few possible windows to prehistoric societies (2, 3). Reconstructions can help in understanding many aspects of our past, such as the technological level (2), migration patterns (4), and scripts (2, 5) of early societies. Comparing reconstructions across many languages can help reveal the nature of language change itself, identifying which aspects of language are most likely to change over time, a long-standing question in historical linguistics (6, 7).
In many cases, direct evidence of the form of protolanguages is not available. Fortunately, owing to the world’s considerable linguistic diversity, it is still possible to propose reconstructions by leveraging a large collection of extant languages descended from a single protolanguage. Words that appear in these modern languages can be organized into cognate sets that contain words suspected to have a shared ancestral form (Table 1). The key observation that makes reconstruction from these data possible is that languages seem to undergo a relatively limited set of regular sound changes, each applied to the entire vocabulary of a language at specific stages of its history (1). Still, several factors make reconstruction a hard problem. For example, sound changes are often context sensitive, and many are string insertions and deletions.
Table 1.
Sample of reconstructions produced by the system
 |
*Complete sets of reconstructions can be found in SI Appendix.
†Randomly selected by stratified sampling according to the Levenshtein edit distance Δ.
‡Levenshtein distance to a reference manual reconstruction, in this case the reconstruction of Blust (42).
§The colors encode cognate sets.
¶We use this symbol for encoding missing data.
In this paper, we present an automated system capable of large-scale reconstruction of protolanguages directly from words that appear in modern languages. This system is based on a probabilistic model of sound change at the level of phonemes, building on work on the reconstruction of ancestral sequences and alignment in computational biology (8–12). Several groups have recently explored how methods from computational biology can be applied to problems in historical linguistics, but such work has focused on identifying the relationships between languages (as might be expressed in a phylogeny) rather than reconstructing the languages themselves (13–18). Much of this type of work has been based on binary cognate or structural matrices (19, 20), which discard all information about the form that words take, simply indicating whether they are cognate. Such models did not have the goal of reconstructing protolanguages and consequently use a representation that lacks the resolution required to infer ancestral phonetic sequences. Using phonological representations allows us to perform reconstruction and does not require us to assume that cognate sets have been fully resolved as a preprocessing step. Representing the words at each point in a phylogeny and having a model of how they change give a way of comparing different hypothesized cognate sets and hence inferring cognate sets automatically.
The focus on problems other than reconstruction in previous computational approaches has meant that almost all existing protolanguage reconstructions have been done manually. However, to obtain more accurate reconstructions for older languages, large numbers of modern languages need to be analyzed. The Proto-Austronesian language, for instance, has over 1,200 descendant languages (21). All of these languages could potentially increase the quality of the reconstructions, but the number of possibilities increases considerably with each language, making it difficult to analyze a large number of languages simultaneously. The few previous systems for automated reconstruction of protolanguages or cognate inference (22–24) were unable to handle this increase in computational complexity, as they relied on deterministic models of sound change and exact but intractable algorithms for reconstruction.
Being able to reconstruct large numbers of languages also makes it possible to provide quantitative answers to questions about the factors that are involved in language change. We demonstrate the potential for automated reconstruction to lead to novel results in historical linguistics by investigating a specific hypothesized regularity in sound changes called functional load. The functional load hypothesis, introduced in 1955, asserts that sounds that play a more important role in distinguishing words are less likely to change over time (6). Our probabilistic reconstruction of hundreds of protolanguages in the Austronesian phylogeny provides a way to explore this question quantitatively, producing compelling evidence in favor of the functional load hypothesis.
Model
We use a probabilistic model of sound change and a Monte Carlo inference algorithm to reconstruct the lexicon and phonology of protolanguages given a collection of cognate sets from modern languages. As in other recent work in computational historical linguistics (13–18), we make the simplifying assumption that each word evolves along the branches of a tree of languages, reflecting the languages' phylogenetic relationships. The tree’s internal nodes are languages whose word forms are not observed, and the leaves are modern languages. The output of our system is a posterior probability distribution over derivations. Each derivation contains, for each cognate set, a reconstructed transcription of ancestral forms, as well as a list of sound changes describing the transformation from parent word to child word. This representation is rich enough to answer a wide range of queries that would normally be answered by carrying out the comparative method manually, such as which sound changes were most prominent along each branch of the tree.
We model the evolution of discrete sequences of phonemes, using a context-dependent probabilistic string transducer (8). Probabilistic string transducers efficiently encode a distribution over possible changes that a string might undergo as it changes through time. Transducers are sufficient to capture most types of regular sound changes (e.g., lenitions, epentheses, and elisions) and can be sensitive to the context in which a change takes place. Most types of changes not captured by transducers are not regular (1) and are therefore less informative (e.g., metatheses, reduplications, and haplologies). Unlike simple molecular InDel models used in computational biology such as the TKF91 model (25), the parameterization of our model is very expressive: Mutation probabilities are context sensitive, depending on the neighboring characters, and each branch has its own set of parameters. This context-sensitive and branch-specific parameterization plays a central role in our system, allowing explicit modeling of sound changes.
Formally, let τ be a phylogenetic tree of languages, where each language is linked to the languages that descended from it. In such a tree, the modern languages, whose word forms will be observed, are the leaves of τ. The most recent common ancestor of these modern languages is the root of τ. Internal nodes of the tree (including the root) are protolanguages with unobserved word forms. Let L denote all languages, modern and otherwise. All word forms are assumed to be strings in the International Phonetic Alphabet (IPA).
We assume that word forms evolve along the branches of the tree τ. However, it is usually not the case that a word belonging to each cognate set exists in each modern language—words are lost or replaced over time, meaning that words that appear in the root languages may not have cognate descendants in the languages at the leaves of the tree. For the moment, we assume there is a known list of C cognate sets. For each 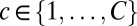 let
let 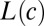 denote the subset of modern languages that have a word form in the cth cognate set. For each set
denote the subset of modern languages that have a word form in the cth cognate set. For each set 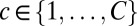 and each language
and each language 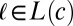 , we denote the modern word form by
, we denote the modern word form by 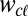 . For cognate set c, only the minimal subtree
. For cognate set c, only the minimal subtree 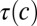 containing
containing 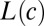 and the root is relevant to the reconstruction inference problem for that set.
and the root is relevant to the reconstruction inference problem for that set.
Our model of sound change is based on a generative process defined on this tree. From a high-level perspective, the generative process is quite simple. Let c be the index of the current cognate set, with topology 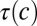 . First, a word is generated for the root of
. First, a word is generated for the root of 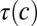 , using an (initially unknown) root language model (i.e., a probability distribution over strings). The words that appear at other nodes of the tree are generated incrementally, using a branch-specific distribution over changes in strings to generate each word from the word in the language that is its parent in
, using an (initially unknown) root language model (i.e., a probability distribution over strings). The words that appear at other nodes of the tree are generated incrementally, using a branch-specific distribution over changes in strings to generate each word from the word in the language that is its parent in 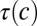 . Although this distribution differs across branches of the tree, making it possible to estimate the pattern of changes involved in the transition from one language to another, it remains the same for all cognate sets, expressing changes that apply stochastically to all words. The probabilities of substitution, insertion and deletion are also dependent on the context in which the change occurs. Further details of the distributions that were used and their parameterization appear in Materials and Methods.
. Although this distribution differs across branches of the tree, making it possible to estimate the pattern of changes involved in the transition from one language to another, it remains the same for all cognate sets, expressing changes that apply stochastically to all words. The probabilities of substitution, insertion and deletion are also dependent on the context in which the change occurs. Further details of the distributions that were used and their parameterization appear in Materials and Methods.
The flexibility of our model comes at the cost of having literally millions of parameters to set, creating challenges not found in most computational approaches to phylogenetics. Our inference algorithm learns these parameters automatically, using established principles from machine learning and statistics. Specifically, we use a variant of the expectation-maximization algorithm (26), which alternates between producing reconstructions on the basis of the current parameter estimates and updating the parameter estimates on the basis of those reconstructions. The reconstructions are inferred using an efficient Monte Carlo inference algorithm (27). The parameters are estimated by optimizing a cost function that penalizes complexity, allowing us to obtain robust estimates of large numbers of parameters. See SI Appendix, Section 1 for further details of the inference algorithm.
If cognate assignments are not available, our system can be applied just to lists of words in different languages. In this case it automatically infers the cognate assignments as well as the reconstructions. This setting requires only two modifications to the model. First, because cognates are not available, we index the words by their semantic meaning (or gloss) g, and there are thus G groups of words. The model is then defined as in the previous case, with words indexed as 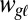 . Second, the generation process is augmented with a notion of innovation, wherein a word
. Second, the generation process is augmented with a notion of innovation, wherein a word 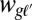 in some language
in some language 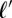 may instead be generated independently from its parent word
may instead be generated independently from its parent word 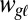 . In this instance, the word is generated from a language model as though it were a root string. In effect, the tree is “cut” at a language when innovation happens, and so the word begins anew. The probability of innovation in any given language is initially unknown and must be learned automatically along with the other branch-specific model parameters.
. In this instance, the word is generated from a language model as though it were a root string. In effect, the tree is “cut” at a language when innovation happens, and so the word begins anew. The probability of innovation in any given language is initially unknown and must be learned automatically along with the other branch-specific model parameters.
Results
Our results address three questions about the performance of our system. First, how well does it reconstruct protolanguages? Second, how well does it identify cognate sets? Finally, how can this approach be used to address outstanding questions in historical linguistics?
Protolanguage Reconstructions.
To test our system, we applied it to a large-scale database of Austronesian languages, the Austronesian Basic Vocabulary Database (ABVD) (28). We used a previously established phylogeny for these languages, the Ethnologue tree (29) (we also describe experiments with other trees in Fig. 1). For this first test of our system we also used the cognate sets provided in the database. The dataset contained 659 languages at the time of download (August 7, 2010), including a few languages outside the Austronesian family and some manually reconstructed protolanguages used for evaluation. The total data comprised 142,661 word forms and 7,708 cognate sets. The goal was to reconstruct the word in each protolanguage that corresponded to each cognate set and to infer the patterns of sound changes along each branch in the phylogeny. See SI Appendix, Section 2 for further details of our simulations.
Fig. 1.
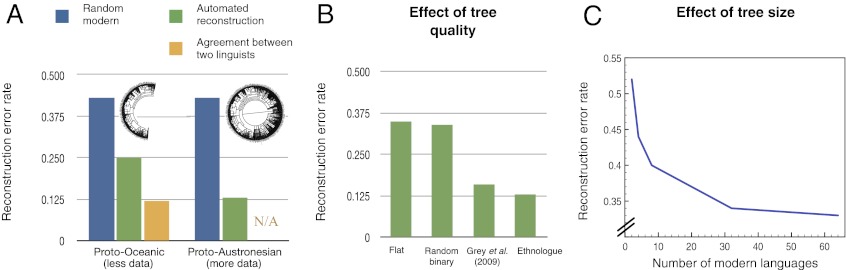
Quantitative validation of reconstructions and identification of some important factors influencing reconstruction quality. (A) Reconstruction error rates for a baseline (which consists of picking one modern word at random), our system, and the amount of disagreement between two linguist’s manual reconstructions. Reconstruction error rates are Levenshtein distances normalized by the mean word form length so that errors can be compared across languages. Agreement between linguists was computed on only Proto-Oceanic because the dataset used lacked multiple reconstructions for other protolanguages. (B) The effect of the topology on the quality of the reconstruction. On one hand, the difference between reconstruction error rates obtained from the system that ran on an uninformed topology (first and second) and rates obtained from the system that ran on an informed topology (third and fourth) is statistically significant. On the other hand, the corresponding difference between a flat tree and a random binary tree is not statistically significant, nor is the difference between using the consensus tree of ref. 41 and the Ethnologue tree (29). This suggests that our method has a certain robustness to moderate topology variations. (C) Reconstruction error rate as a function of the number of languages used to train our automatic reconstruction system. Note that the error is not expected to go down to zero, perfect reconstruction being generally unidentifiable. The results in A and B are directly comparable: In fact, the entry labeled “Ethnologue” in B corresponds to the green Proto-Austronesian entry in A. The results in A and B and those in C are not directly comparable because the evaluation in C is restricted to those cognates with at least one reflex in the smallest evaluation set (to make the curve comparable across the horizontal axis of C).
We used the Austronesian dataset to quantitatively evaluate the performance of our system by comparing withheld words from known languages with automatic reconstructions of those words. The Levenshtein distance between the held-out and reconstructed forms provides a measure of the number of errors in these reconstructions. We used this measure to show that using more languages helped reconstruction and also to assess the overall performance of our system. Specifically, we compared the system’s error rate on the ancestral reconstructions to a baseline and also to the amount of divergence between the reconstructions of two linguists (Fig. 1A). Given enough data, the system can achieve reconstruction error rates close to the level of disagreement between manual reconstructions. In particular, most reconstructions perfectly agree with manual reconstructions, and only a few contain big errors. Refer to Table 1 for examples of reconstructions. See SI Appendix, Section 3 for the full lists.
We also present in Fig. 1B the effect of the tree topology on reconstruction quality, reiterating the importance of using informative topologies for reconstruction. In Fig. 1C, we show that the accuracy of our method increases with the number of observed Oceanic languages, confirming that large-scale inference is desirable for automatic protolanguage reconstruction: Reconstruction improved statistically significantly with each increase except from 32 to 64 languages, where the average edit distance improvement was 0.05.
For comparison, we also evaluated previous automatic reconstruction methods. These previous methods do not scale to large datasets so we performed comparisons on smaller subsets of the Austronesian dataset. We show in SI Appendix, Section 2 that our method outperforms these baselines.
We analyze the output of our system in more depth in Fig. 2 A–C, which shows the system learned a variety of realistic sound changes across the Austronesian family (30). In Fig. 2D, we show the most frequent substitution errors in the Proto-Austronesian reconstruction experiments. See SI Appendix, Section 5 for details and similar plots for the most common incorrect insertions and deletions.
Fig. 2.
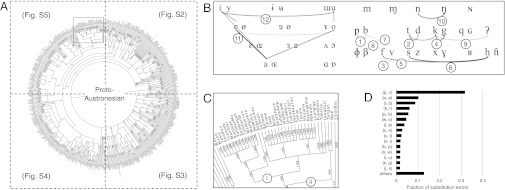
Analysis of the output of our system in more depth. (A) An Austronesian phylogenetic tree from ref. 29 used in our analyses. Each quadrant is available in a larger format in SI Appendix, Figs. S2–S5, along with a detailed table of sound changes (SI Appendix, Table S5). The numbers in parentheses attached to each branch correspond to rows in SI Appendix, Table S5. The colors and numbers in parentheses encode the most prominent sound change along each branch, as inferred automatically by our system in SI Appendix, Section 4. (B) The most supported sound changes across the phylogeny, with the width of links proportional to the support. Note that the standard organization of the IPA chart into columns and rows according to place, manner, height, and backness is only for visualization purposes: This information was not encoded in the model in this experiment, showing that the model can recover realistic cross-linguistic sound change trends. All of the arcs correspond to sound changes frequently used by historical linguists: sonorizations /p/ > /b/ (1) and /t/ > /d/ (2), voicing changes (3, 4), debuccalizations /f/ > /h/ (5) and /s/ > /h/ (6), spirantizations /b/ > /v/ (7) and /p/ > /f/ (8), changes of place of articulation (9, 10), and vowel changes in height (11) and backness (12) (1). Whereas this visualization depicts sound changes as undirected arcs, the sound changes are actually represented with directionality in our system. (C) Zooming in a portion of the Oceanic languages, where the Nuclear Polynesian family (i) and Polynesian family (ii) are visible. Several attested sound changes such as debuccalization to Maori and place of articulation change /t/ > /k/ to Hawaiian (30) are successfully localized by the system. (D) Most common substitution errors in the PAn reconstructions produced by our system. The first phoneme in each pair 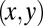 represents the reference phoneme, followed by the incorrectly hypothesized one. Most of these errors could be plausible disagreements among human experts. For example, the most dominant error (p, v) could arise over a disagreement over the phonemic inventory of Proto-Austronesian, whereas vowels are common sources of disagreement.
represents the reference phoneme, followed by the incorrectly hypothesized one. Most of these errors could be plausible disagreements among human experts. For example, the most dominant error (p, v) could arise over a disagreement over the phonemic inventory of Proto-Austronesian, whereas vowels are common sources of disagreement.
Cognate Recovery.
Previous reconstruction systems (22) required that cognate sets be provided to the system. However, the creation of these large cognate databases requires considerable annotation effort on the part of linguists and often requires that at least some reconstruction be done by hand. To demonstrate that our model can accurately infer cognate sets automatically, we used a version of our system that learns which words are cognate, starting only from raw word lists and their meanings. This system uses a faster but lower-fidelity model of sound change to infer correspondences. We then ran our reconstruction system on cognate sets that our cognate recovery system found. See SI Appendix, Section 1 for details.
This version of the system was run on all of the Oceanic languages in the ABVD, which comprise roughly half of the Austronesian languages. We then evaluated the pairwise precision (the fraction of cognate pairs identified by our system that are also in the set of labeled cognate pairs), pairwise recall (the fraction of labeled cognate pairs identified by our system), and pairwise F1 measure (defined as the harmonic mean of precision and recall) for the cognates found by our system against the known cognates that are encoded in the ABVD. We also report cluster purity, which is the fraction of words that are in a cluster whose known cognate group matches the cognate group of the cluster. See SI Appendix, Section 2.3 for a detailed description of the metrics.
Using these metrics, we found that our system achieved a precision of 0.844, recall of 0.621, F1 of 0.715, and cluster purity of 0.918. Thus, over 9 of 10 words are correctly grouped, and our system errs on the side of undergrouping words rather than clustering words that are not cognates. Because the null hypothesis in historical linguistics is to deem words to be unrelated unless proved otherwise, a slight undergrouping is the desired behavior.
Because we are ultimately interested in reconstruction, we then compared our reconstruction system’s ability to reconstruct words given these automatically determined cognates. Specifically, we took every cognate group found by our system (run on the Oceanic subclade) with at least two words in it. Then, we automatically reconstructed the Proto-Oceanic ancestor of those words, using our system. For evaluation, we then looked at the average Levenshtein distance from our reconstructions to the known reconstructions described in the previous sections. This time, however, we average per modern word rather than per cognate group, to provide a fairer comparison. (Results were not substantially different when averaging per cognate group.) Compared with reconstruction from manually labeled cognate sets, automatically identified cognates led to an increase in error rate of only 12.8% and with a significant reduction in the cost of curating linguistic databases. See SI Appendix, Fig. S1 for the fraction of words with each Levenshtein distance for these reconstructions.
Functional Load.
To demonstrate the utility of large-scale reconstruction of protolanguages, we used the output of our system to investigate an open question in historical linguistics. The functional load hypothesis (FLH), introduced 1955 (6), claims that the probability that a sound will change over time is related to the amount of information provided by a sound. Intuitively, if two phonemes appear only in words that are differentiated from one another by at least one other sound, then one can argue that no information is lost if those phonemes merge together, because no new ambiguous forms can be created by the merger.
A first step toward quantitatively testing the FLH was taken in 1967 (7). By defining a statistic that formalizes the amount of information lost when a language undergoes a certain sound change—on the basis of the proportion of words that are discriminated by each pair of phonemes—it became possible to evaluate the empirical support for the FLH. However, this initial investigation was based on just four languages and found little evidence to support the hypothesis. This conclusion was criticized by several authors (31, 32) on the basis of the small number of languages and sound changes considered, although they provided no positive counterevidence.
Using the output of our system, we collected sound change statistics from our reconstruction of 637 Austronesian languages, including the probability of a particular change as estimated by our system. These statistics provided the information needed to give a more comprehensive quantitative evaluation of the FLH, using a much larger sample than previous work (details in SI Appendix, Section 2.4). We show in Fig. 3 A and B that this analysis provides clear quantitative evidence in favor of the FLH. The revealed pattern would not be apparent had we not been able to reconstruct large numbers of protolanguages and supply probabilities of different kinds of change taking place for each pair of languages.
Fig. 3.
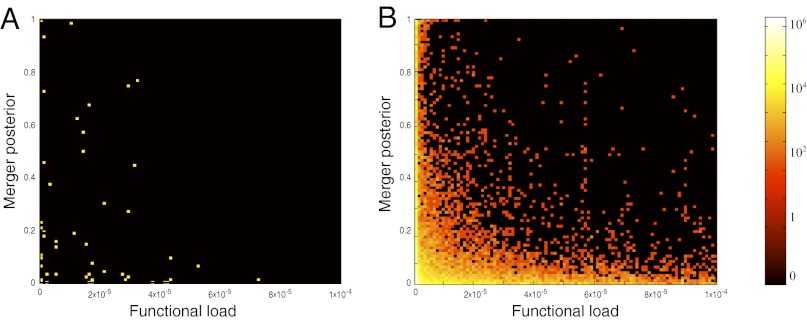
Increasing the number of languages we can reconstruct gives new ways to approach questions in historical linguistics, such as the effect of functional load on the probability of merging two sounds. The plots shown are heat maps where the color encodes the log of the number of sound changes that fall into a given two-dimensional bin. Each sound change x > y is encoded as a pair of numbers in the unit square,  , as explained in Materials and Methods. To convey the amount of noise one could expect from a study with the number of languages that King previously used (7), we first show in A the heat map visualization for four languages. Next, we show the same plot for 637 Austronesian languages in B. Only in this latter setup is structure clearly visible: Most of the points with high probability of merging can be seen to have comparatively low functional load, providing evidence in favor of the functional load hypothesis introduced in 1955. See SI Appendix, Section 2.4 for details.
, as explained in Materials and Methods. To convey the amount of noise one could expect from a study with the number of languages that King previously used (7), we first show in A the heat map visualization for four languages. Next, we show the same plot for 637 Austronesian languages in B. Only in this latter setup is structure clearly visible: Most of the points with high probability of merging can be seen to have comparatively low functional load, providing evidence in favor of the functional load hypothesis introduced in 1955. See SI Appendix, Section 2.4 for details.
Discussion
We have developed an automated system capable of large-scale reconstruction of protolanguage word forms, cognate sets, and sound change histories. The analysis of the properties of hundreds of ancient languages performed by this system goes far beyond the capabilities of any previous automated system and would require significant amounts of manual effort by linguists. Furthermore, the system is in no way restricted to applications like assessing the effects of functional load: It can be used as a tool to investigate a wide range of questions about the structure and dynamics of languages.
In developing an automated system for reconstructing ancient languages, it is by no means our goal to replace the careful reconstructions performed by linguists. It should be emphasized that the reconstruction mechanism used by our system ignores many of the phenomena normally used in manual reconstructions. We have mentioned limitations due to the transducer formalism but other limitations include the lack of explicit modeling of changes at the level of the phoneme inventories used by a language and the lack of morphological analysis. Challenges specific to the cognate inference task, for example difficulties with polymorphisms, are also discussed in more detail in SI Appendix. Another limitation of the current approach stems from the assumption that languages form a phylogenetic tree, an assumption violated by borrowing, dialect variation, and creole languages. However, we believe our system will be useful to linguists in several ways, particularly in contexts where there are large numbers of languages to be analyzed. Examples might include using the system to propose short lists of potential sound changes and correspondences across highly divergent word forms.
An exciting possible application of this work is to use the model described here to infer the phylogenetic relationships between languages jointly with reconstructions and cognate sets. This will remove a source of circularity present in most previous computational work in historical linguistics. Systems for inferring phylogenies such as ref. 13 generally assume that cognate sets are given as a fixed input, but cognacy as determined by linguists is in turn motivated by phylogenetic considerations. The phylogenetic tree hypothesized by the linguist is therefore affecting the tree built by systems using only these cognates. This problem can be avoided by inferring cognates at the same time as a phylogeny, something that should be possible using an extended version of our probabilistic model.
Our system is able to reconstruct the words that appear in ancient languages because it represents words as sequences of sounds and uses a rich probabilistic model of sound change. This is an important step forward from previous work applying computational ideas to historical linguistics. By leveraging the full sequence information available in the word forms in modern languages, we hope to see in historical linguistics a breakthrough similar to the advances in evolutionary biology prompted by the transition from morphological characters to molecular sequences in phylogenetic analysis.
Materials and Methods
This section provides a more detailed specification of our probabilistic model. See SI Appendix, Section 1.2 for additional content on the algorithm and simulations.
Distributions.
The conditional distributions over pairs of evolving strings are specified using a lexicalized stochastic string transducer (33).
Consider a language 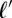 evolving to
evolving to  for cognate set c. Assume we have a word form
for cognate set c. Assume we have a word form 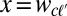 . The generative process for producing
. The generative process for producing 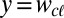 works as follows. First, we consider x to be composed of characters
works as follows. First, we consider x to be composed of characters 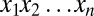 , with the first and last ones being a special boundary symbol
, with the first and last ones being a special boundary symbol 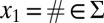 , which is never deleted, mutated, or created. The process generates
, which is never deleted, mutated, or created. The process generates 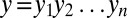 in n chunks
in n chunks 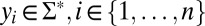 , one for each
, one for each 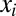 . The
. The 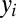 s may be a single character, multiple characters, or even empty. To generate
s may be a single character, multiple characters, or even empty. To generate 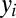 , we define a mutation Markov chain that incrementally adds zero or more characters to an initially empty
, we define a mutation Markov chain that incrementally adds zero or more characters to an initially empty 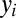 . First, we decide whether the current phoneme in the top word
. First, we decide whether the current phoneme in the top word 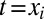 will be deleted, in which case
will be deleted, in which case 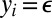 (the probabilities of the decisions taken in this process depend on a context to be specified shortly). If t is not deleted, we choose a single substitution character in the bottom word. We write
(the probabilities of the decisions taken in this process depend on a context to be specified shortly). If t is not deleted, we choose a single substitution character in the bottom word. We write  for this set of outcomes, where ζ is the special outcome indicating deletion. Importantly, the probabilities of this multinomial can depend on both the previous character generated so far (i.e., the rightmost character p of
for this set of outcomes, where ζ is the special outcome indicating deletion. Importantly, the probabilities of this multinomial can depend on both the previous character generated so far (i.e., the rightmost character p of 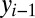 ) and the current character in the previous generation string (t), providing a way to make changes context sensitive. This multinomial decision acts as the initial distribution of the mutation Markov chain. We consider insertions only if a deletion was not selected in the first step. Here, we draw from a multinomial over
) and the current character in the previous generation string (t), providing a way to make changes context sensitive. This multinomial decision acts as the initial distribution of the mutation Markov chain. We consider insertions only if a deletion was not selected in the first step. Here, we draw from a multinomial over 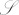 , where this time the special outcome ζ corresponds to stopping insertions, and the other elements of
, where this time the special outcome ζ corresponds to stopping insertions, and the other elements of 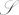 correspond to symbols that are appended to
correspond to symbols that are appended to 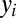 . In this case, the conditioning environment is
. In this case, the conditioning environment is 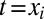 and the current rightmost symbol p in
and the current rightmost symbol p in 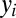 . Insertions continue until ζ is selected. We use
. Insertions continue until ζ is selected. We use 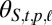 and
and 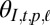 to denote the probabilities over the substitution and insertion decisions in the current branch
to denote the probabilities over the substitution and insertion decisions in the current branch 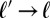 . A similar process generates the word at the root
. A similar process generates the word at the root  of a tree or when an innovation happens at some language
of a tree or when an innovation happens at some language  , treating this word as a single string
, treating this word as a single string 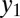 generated from a dummy ancestor
generated from a dummy ancestor 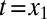 . In this case, only the insertion probabilities matter, and we separately parameterize these probabilities with
. In this case, only the insertion probabilities matter, and we separately parameterize these probabilities with 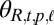 . There is no actual dependence on t at the root or innovative languages, but this formulation allows us to unify the parameterization, with each
. There is no actual dependence on t at the root or innovative languages, but this formulation allows us to unify the parameterization, with each 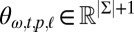 , where
, where 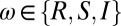 . During cognate inference, the decision to innovate is controlled by a simple Bernoulli random variable
. During cognate inference, the decision to innovate is controlled by a simple Bernoulli random variable 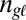 for each language in the tree. When known cognate groups are assumed,
for each language in the tree. When known cognate groups are assumed, 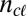 is set to 0 for all nonroot languages and to 1 for the root language. These Bernoulli distributions have parameters
is set to 0 for all nonroot languages and to 1 for the root language. These Bernoulli distributions have parameters 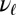 .
.
Mutation distributions confined in the family of transducers miss certain phylogenetic phenomena. For example, the process of reduplication (as in “bye-bye”, for example) is a well-studied mechanism to derive morphological and lexical forms that is not explicitly captured by transducers. The same situation arises in metatheses (e.g., Old English frist > English first). However, these changes are generally not regular and therefore less informative (1). Moreover, because we are using a probabilistic framework, these events can still be handled in our system, even though their costs will simply not be as discounted as they should be.
Note also that the generative process described in this section does not allow explicit dependencies to the next character in  . Relaxing this assumption can be done in principle by using weighted transducers, but at the cost of a more computationally expensive inference problem (caused by the transducer normalization computation) (34). A simpler approach is to use the next character in the parent
. Relaxing this assumption can be done in principle by using weighted transducers, but at the cost of a more computationally expensive inference problem (caused by the transducer normalization computation) (34). A simpler approach is to use the next character in the parent 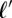 as a surrogate for the next character in
as a surrogate for the next character in  . Using the context in the parent word is also more aligned to the standard representation of sound change used in historical linguistics, where the context is defined on the parent as well.
. Using the context in the parent word is also more aligned to the standard representation of sound change used in historical linguistics, where the context is defined on the parent as well.
More generally, dependencies limited to a bounded context on the parent string can be incorporated in our formalism. By bounded, we mean that it should be possible to fix an integer k beforehand such that all of the modeled dependencies are within k characters to the string operation. The caveat is that the computational cost of inference grows exponentially in k. We leave open the question of handling computation in the face of unbounded dependencies such as those induced by harmony (35).
Parameterization.
Instead of directly estimating the transition probabilities of the mutation Markov chain (which could be done, in principle, by taking them to be the parameters of a collection of multinomial distributions) we express them as the output of a multinomial logistic regression model (36). This model specifies a distribution over transition probabilities by assigning weights to a set of features that describe properties of the sound changes involved. These features provide a more coherent representation of the transition probabilities, capturing regularities in sound changes that reflect the underlying linguistic structure.
We used the following feature templates: OPERATION, which identifies whether an operation in the mutation Markov chain is an insertion, a deletion, a substitution, a self-substitution (i.e., of the form x > y, 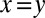 ), or the end of an insertion event; MARKEDNESS, which consists of language-specific n-gram indicator functions for all symbols in
), or the end of an insertion event; MARKEDNESS, which consists of language-specific n-gram indicator functions for all symbols in 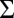 (during reconstruction, only unigram and bigram features are used for computational reasons; for cognate inference, only unigram features are used); FAITHFULNESS, which consists of indicators for mutation events of the form 1 [ x > y ], where
(during reconstruction, only unigram and bigram features are used for computational reasons; for cognate inference, only unigram features are used); FAITHFULNESS, which consists of indicators for mutation events of the form 1 [ x > y ], where 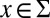 ,
, 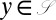 . Feature templates similar to these can be found, for instance, in the work of refs. 37 and 38, in the context of string-to-string transduction models used in computational linguistics. This approach to specifying the transition probabilities produces an interesting connection to stochastic optimality theory (39, 40), where a logistic regression model mediates markedness and faithfulness of the production of an output form from an underlying input form.
. Feature templates similar to these can be found, for instance, in the work of refs. 37 and 38, in the context of string-to-string transduction models used in computational linguistics. This approach to specifying the transition probabilities produces an interesting connection to stochastic optimality theory (39, 40), where a logistic regression model mediates markedness and faithfulness of the production of an output form from an underlying input form.
Data sparsity is a significant challenge in protolanguage reconstruction. Although the experiments we present here use an order of magnitude more languages than previous computational approaches, the increase in observed data also brings with it additional unknowns in the form of intermediate protolanguages. Because there is one set of parameters for each language, adding more data is not sufficient to increase the quality of the reconstruction; it is important to share parameters across different branches in the tree to benefit from having observations from more languages. We used the following technique to address this problem: We augment the parameterization to include the current language (or language at the bottom of the current branch) and use a single, global weight vector instead of a set of branch-specific weights. Generalization across branches is then achieved by using features that ignore  , whereas branch-specific features depend on
, whereas branch-specific features depend on  . Similarly, all of the features in OPERATION, MARKEDNESS, and FAITHFULNESS have universal and branch-specific versions.
. Similarly, all of the features in OPERATION, MARKEDNESS, and FAITHFULNESS have universal and branch-specific versions.
Using these features and parameter sharing, the logistic regression model defines the transition probabilities of the mutation process and the root language model to be
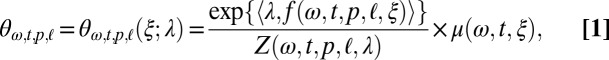 |
where  ,
, 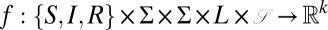 is the feature function (which indicates which features apply for each event),
is the feature function (which indicates which features apply for each event), 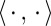 denotes inner product, and
denotes inner product, and 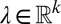 is a weight vector. Here, k is the dimensionality of the feature space of the logistic regression model. In the terminology of exponential families, Z and μ are the normalization function and the reference measure, respectively:
is a weight vector. Here, k is the dimensionality of the feature space of the logistic regression model. In the terminology of exponential families, Z and μ are the normalization function and the reference measure, respectively:
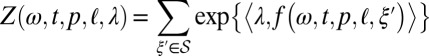 |
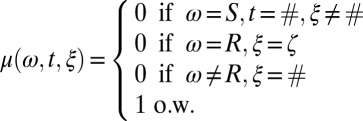 |
Here, μ is used to handle boundary conditions, ensuring that the resulting probability distribution is well defined.
During cognate inference, the innovation Bernoulli random variables 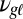 are similarly parameterized, using a logistic regression model with two kinds of features: a global innovation feature
are similarly parameterized, using a logistic regression model with two kinds of features: a global innovation feature 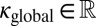 and a language-specific feature
and a language-specific feature 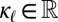 . The likelihood function for each
. The likelihood function for each 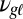 then takes the form
then takes the form
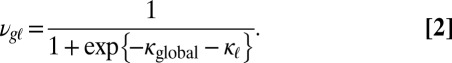 |
Supplementary Material
Acknowledgments
This work was supported by Grant IIS-1018733 from the National Science Foundation.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission. N.C. is a guest editor invited by the Editorial Board.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1204678110/-/DCSupplemental.
See Commentary on page 4159.
References
- 1.Hock HH. Principles of Historical Linguistics. The Hague, Netherlands: Mouton de Gruyter; 1991. [Google Scholar]
- 2.Ross M, Pawley A, Osmond M. The Lexicon of Proto Oceanic: The Culture and Environment of Ancestral Oceanic Society. Canberra, Australia: Pacific Linguistics; 1998. [Google Scholar]
- 3.Diamond J. Guns, Germs, and Steel: The Fates of Human Societies. New York: WW Norton; 1999. [Google Scholar]
- 4.Nichols J. 1999. Archaeology and Language: Correlating Archaeological and Linguistic Hypotheses, eds Blench R, Spriggs M (Routledge, London)
- 5.Ventris M, Chadwick J. Documents in Mycenaean Greek. Cambridge, UK: Cambridge Univ Press; 1973. [Google Scholar]
- 6.Martinet A. Économie des Changements Phonétiques [Economy of phonetic sound changes] Maisonneuve & Larose, Paris: 1955. [Google Scholar]
- 7.King R. Functional load and sound change. Language. 1967;43:831–852. [Google Scholar]
- 8.Holmes I, Bruno WJ. Evolutionary HMMs: A Bayesian approach to multiple alignment. Bioinformatics. 2001;17(9):803–820. doi: 10.1093/bioinformatics/17.9.803. [DOI] [PubMed] [Google Scholar]
- 9.Miklós I, Lunter GA, Holmes I. A “Long Indel” model for evolutionary sequence alignment. Mol Biol Evol. 2004;21(3):529–540. doi: 10.1093/molbev/msh043. [DOI] [PubMed] [Google Scholar]
- 10.Suchard MA, Redelings BD. BAli-Phy: Simultaneous Bayesian inference of alignment and phylogeny. Bioinformatics. 2006;22(16):2047–2048. doi: 10.1093/bioinformatics/btl175. [DOI] [PubMed] [Google Scholar]
- 11.Liberles DA, editor. Ancestral Sequence Reconstruction. Oxford, UK: Oxford Univ Press; 2007. [Google Scholar]
- 12.Paten B, et al. Genome-wide nucleotide-level mammalian ancestor reconstruction. Genome Res. 2008;18(11):1829–1843. doi: 10.1101/gr.076521.108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Gray RD, Jordan FM. Language trees support the express-train sequence of Austronesian expansion. Nature. 2000;405(6790):1052–1055. doi: 10.1038/35016575. [DOI] [PubMed] [Google Scholar]
- 14.Ringe D, Warnow T, Taylor A. Indo-European and computational cladistics. Trans Philol Soc. 2002;100:59–129. [Google Scholar]
- 15.Evans SN, Ringe D, Warnow T. Inference of Divergence Times as a Statistical Inverse Problem. 2004. McDonald Institute Monographs, eds Forster P, Renfrew C (McDonald Institute, Cambridge, UK) [Google Scholar]
- 16.Gray RD, Atkinson QD. Language-tree divergence times support the Anatolian theory of Indo-European origin. Nature. 2003;426(6965):435–439. doi: 10.1038/nature02029. [DOI] [PubMed] [Google Scholar]
- 17.Nakhleh L, Ringe D, Warnow T. Perfect phylogenetic networks: A new methodology for reconstructing the evolutionary history of natural languages. Language. 2005;81:382–420. [Google Scholar]
- 18.Bryant D. In: Phylogenetic Methods and the Prehistory of Languages. Forster P, Renfrew C, editors. Cambridge, UK: McDonald Institute for Archaeological Research; 2006. pp. 111–118. [Google Scholar]
- 19.Daumé H, III, Campbell L. A Bayesian model for discovering typological implications. Assoc Comput Linguist. 2007;45:65–72. [Google Scholar]
- 20.Dunn M, Levinson S, Lindstrom E, Reesink G, Terrill A. Structural phylogeny in historical linguistics: Methodological explorations applied in Island Melanesia. Language. 2008;84:710–759. [Google Scholar]
- 21.Lynch J, editor. Issues in Austronesian. Canberra, Australia: Pacific Linguistics; 2003. [Google Scholar]
- 22.Oakes M. Computer estimation of vocabulary in a protolanguage from word lists in four daughter languages. J Quant Linguist. 2000;7:233–244. [Google Scholar]
- 23.Kondrak G. 2002. Algorithms for Language Reconstruction. PhD thesis (Univ of Toronto, Toronto)
- 24.Ellison TM. Bayesian identification of cognates and correspondences. Assoc Comput Linguist. 2007;45:15–22. [Google Scholar]
- 25.Thorne JL, Kishino H, Felsenstein J. An evolutionary model for maximum likelihood alignment of DNA sequences. J Mol Evol. 1991;33(2):114–124. doi: 10.1007/BF02193625. [DOI] [PubMed] [Google Scholar]
- 26.Dempster AP, Laird NM, Rubin DB. Maximum likelihood from incomplete data via the EM algorithm. J R Stat Soc B. 1977;39:1–38. [Google Scholar]
- 27.Bouchard-Côté A, Jordan MI, Klein D. Efficient inference in phylogenetic InDel trees. Adv Neural Inf Process Syst. 2009;21:177–184. [Google Scholar]
- 28.Greenhill SJ, Blust R, Gray RD. The Austronesian basic vocabulary database: From bioinformatics to lexomics. Evol Bioinform Online. 2008;4:271–283. doi: 10.4137/ebo.s893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Lewis MP, editor. Ethnologue: Languages of the World. 16th Ed. Dallas, TX: SIL International; 2009. [Google Scholar]
- 30.Lyovin A. An Introduction to the Languages of the World. Oxford, UK: Oxford Univ Press; 1997. [Google Scholar]
- 31.Hockett CF. The quantification of functional load. Word. 1967;23:320–339. [Google Scholar]
- 32.Surendran D, Niyogi P. Competing Models of Linguistic Change. Evolution and Beyond. Amsterdam: Benjamins; 2006. [Google Scholar]
- 33.Varadarajan A, Bradley RK, Holmes IH. Tools for simulating evolution of aligned genomic regions with integrated parameter estimation. Genome Biol. 2008;9(10):R147. doi: 10.1186/gb-2008-9-10-r147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Mohri M. In: Handbook of Weighted Automata, Monographs in Theoretical Computer Science. Droste M, Kuich W, Vogler H, editors. Berlin: Springer; 2009. [Google Scholar]
- 35.Hansson GO. On the evolution of consonant harmony: The case of secondary articulation agreement. Phonology. 2007;24:77–120. [Google Scholar]
- 36.McCullagh P, Nelder JA. Generalized Linear Models. London: Chapman & Hall; 1989. [Google Scholar]
- 37.Dreyer M, Smith JR, Eisner J. Latent-variable modeling of string transductions with finite-state methods. Empirical Methods on Natural Language Processing. 2008;13:1080–1089. [Google Scholar]
- 38.Chen SF. Conditional and joint models for grapheme-to-phoneme conversion. Eurospeech. 2003;8:2033–2036. [Google Scholar]
- 39.Goldwater S, Johnson M. 2003. Learning OT constraint rankings using a maximum entropy model. Proceedings of the Workshop on Variation Within Optimality Theory eds Spenader J, Eriksson A, Dahl Ö (Stockholm University, Stockholm) pp 113–122.
- 40.Wilson C. Learning phonology with substantive bias: An experimental and computational study of velar palatalization. Cogn Sci. 2006;30(5):945–982. doi: 10.1207/s15516709cog0000_89. [DOI] [PubMed] [Google Scholar]
- 41.Gray RD, Drummond AJ, Greenhill SJ. Language phylogenies reveal expansion pulses and pauses in Pacific settlement. Science. 2009;323(5913):479–483. doi: 10.1126/science.1166858. [DOI] [PubMed] [Google Scholar]
- 42.Blust R. Subgrouping, circularity and extinction: Some issues in Austronesian comparative linguistics. Inst Linguist Acad Sinica. 1999;1:31–94. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.