Dynamical Casimir effect in a Josephson metamaterial

Abstract

The zero-point energy stored in the modes of an electromagnetic cavity has experimentally detectable effects, giving rise to an attractive interaction between the opposite walls, the static Casimir effect. A dynamical version of this effect was predicted to occur when the vacuum energy is changed either by moving the walls of the cavity or by changing the index of refraction, resulting in the conversion of vacuum fluctuations into real photons. Here, we demonstrate the dynamical Casimir effect using a Josephson metamaterial embedded in a microwave cavity at 5.4 GHz. We modulate the effective length of the cavity by flux-biasing the metamaterial based on superconducting quantum interference devices (SQUIDs), which results in variation of a few percentage points in the speed of light. We extract the full 4 × 4 covariance matrix of the emitted microwave radiation, demonstrating that photons at frequencies symmetrical with respect to half of the modulation frequency are generated in pairs. At large detunings of the cavity from half of the modulation frequency, we find power spectra that clearly show the theoretically predicted hallmark of the Casimir effect: a bimodal, “sparrow-tail” structure. The observed substantial photon flux cannot be assigned to parametric amplification of thermal fluctuations; its creation is a direct consequence of the noncommutativity structure of quantum field theory.

A fundamental theoretical result of modern quantum field theory is that the quantum vacuum is unstable (1–6) under certain external perturbations that otherwise produce no consequences in a classical treatment (7). As a result of this instability, virtual fluctuations populating the quantum vacuum are converted into real particles by the energy provided by the perturbation. For example, the application of intense electrical fields extracts electron-positron pairs from a vacuum (Schwinger effect), the bending of space-time in the intense gravitational field at event horizons is responsible for the evaporation of black holes (Hawking radiation), the acceleration of an observer in the Minkowski vacuum results in the detection of particles (Unruh effect), and sudden changes in the boundary conditions of electromagnetic field modes or in the speed of light (index of refraction) create photons [dynamical Casimir effect (DCE)] (8). The DCE is a particular case of parametric amplification of vacuum fluctuations (3, 4, 6). To date, preliminary evidence for the analog of Hawking radiation has been obtained (9), whereas in the case of the DCE, a very recent experiment has reported production of photons by the nonadiabatic change of a boundary condition (10). Many other theoretical estimations and proposals for observing this effect in a variety of physical systems exist in the literature (11–20).

In this paper, we demonstrate the DCE by modulating the background in which the field propagates (3). We periodically change the index of refraction (which appears as a parameter in the field Euler–Lagrange equations) of a medium that is cooled down to the quantum ground state. As a consequence, photons are generated from a vacuum. These photons have strong frequency correlations, and their power spectra display a bimodal, “sparrow-tail” structure when the cavity resonance is detuned away from half of the pump frequency. Notice that the standard techniques for generating frequency-correlated photons rely on nonlinear effects, using the Kerr nonlinearity of strongly pumped crystals (21, 22) or the equivalent nonlinearity provided by Josephson junctions (23–25). In contrast, the DCE is a purely dynamical effect, occurring in linear systems, and it is due to the mismatch between the field modes at different times when the vacuum is perturbed fast enough.

Experimental Setup

Our medium is a Josephson metamaterial consisting of an array of 250 superconductive quantum interference devices (SQUIDs), which form the signal line of a superconducting coplanar waveguide. This metamaterial is 4 mm in length (Fig. 1 A and B), and it is coupled to the external transmission line by a capacitor, resulting in the formation of a low-Q cavity (Q_res ∼100). The cavity (with parameters such as resonant frequency and external/internal decay rates that can be extracted from separate reflection measurements) produces a resonant enhancement of the DCE effect; thus, our system offers a significant amendment over the alternative realizations of DCE based on changing the boundary conditions in a transmission line (10), where spurious, uncontrolled resonances in the line play an essential role in the observability of the effect, as presented by Wilson et al. (10).

Fig. 1.

(A) Equivalent electrical and mechanical circuits. The modulation of the Josephson inductance in the metamaterial by a magnetic flux Φ_ext varies the wave length λ with respect to the cavity length, which is analogous to modulating the effective length d of the cavity by mechanical means. The coupling capacitor is equivalent to a semitransparent mirror. (B) Schematics of the measurement setup. The metamaterial sample is a 4-mm-long coplanar waveguide with 250 embedded SQUIDs, with each junction having a critical current of ∼10 μA. The modulation of the flux through the SQUIDs is realized through a lithographically fabricated spiral coil underneath the metamaterial. (C) Resonant frequency ω_res/2π vs. reduced magnetic flux Φ_ext/Φ₀ without the pump signal; the dc-operating point for DCE experiments is denoted by a green circle. (Inset) Display of the measured phase of the scattering parameter S₁₁ while sweeping frequency, which yields d arg(S₁₁)/dΦ_ext = d arg(S₁₁)/df × df/dΦ_ext . The steepness of the variation in the phase arg(S₁₁) governs the effective “movement of the mirrors.”

The samples were fabricated using a NbAlO_xNb trilayer process. The metamaterial cavity was cooled in a pulse tube-based dilution refrigerator down to 50 mK, corresponding to a thermal occupation number of at 5.4 GHz. To guarantee proper thermalization, all the lines to the sample were strongly attenuated, with more than 160 dB of attenuation in the flux-bias dc-feed line and about 70 dB in the microwave cables. The connection to the low-noise amplifier was isolated by two circulators in combination with high- and low-pass filters at the base temperature, providing attenuation on the order of 40 dB from the 4-K stage. The flux-tunable SQUIDs allow us to modulate the speed of light (v ≈ 0.5 c₀, with c₀ being the speed in a vacuum), and thus to change the effective electrical length of the cavity at drive (modulation) frequencies ω_d around 10 GHz over a relatively large spatial extent (up to 10 mm). This change in the electrical length is similar to that produced by a modulation of the boundary conditions (Fig. 1A).

Results and Discussion

We first established that the modulation of the electrical length of the cavity could be realized by an external magnetic field. Fig. 1C shows the variation of ω_res/2π with magnetic flux bias Φ. The inset displays the measured phase of the reflection coefficient S₁₁, which changes steeply as a function of frequency. The variation is a direct measure of how much the wavelength λ changes with the external flux. Changes in Φ_ext thus lead to variation of the electrical length of the system, which can equally well be established by modifying the physical length of the cavity by the movement of a mirror. As shown in the SI Text, the resonance quality factor enhances the characteristic effective length modulation of our system , where l denotes the inductance per unit length and δl denotes its change due to the modulation. Note that the entire device can be regarded as providing an effective boundary condition for the incoming (and reflected) waves in the transmission line connected to the cavity. Indeed, the input-output theory (21, 22) predicts that the field reflected by the cavity will acquire a phase that depends on the detuning with respect to the resonant frequency of the cavity. An observer somewhere along the transmission line far from the cavity would only see a change in the phase of the reflected field, which could have resulted equally well from the movement of a mirror reflecting the input field. From the point of view of this observer, the metamaterial plus cavity system is simply a phase-shifting device. The detailed arguments for this equivalence are outlined in SI Text.

Immediately, if a classical field is present in the cavity, the modulation of the electrical length should result in parametric amplification when the flux loop is pumped at ω_d = 2ω_res. Indeed, by feeding a signal at the input of the cavity, we have checked that our metamaterial works as a phase-sensitive parametric amplifier. We observe that the corresponding works on amplification in Josephson systems have used nonlinear Kerr effects (four-wave mixing); there, the frequency of the pump tone is close to the cavity resonance, and it is fed together with the signal at the input of the device (23–25). At a pump power P_d = −75 dBm (after the low-T attenuators), the gain reached 23 dB and the noise temperature at 5.5 GHz became T_n = 0.4 ± 0.2 K, as deduced from the increase in the signal/noise (S/N) ratio. Taking into account the losses in the circuitry of the S/N ratio measurement, this indicates that the metamaterial behaves as designed.

Generation of Casimir Photons

To demonstrate the generation of photons via the Casimir effect, we have used the setup shown in Fig. 1B, with the flux modulated at twice the resonant frequency ω_res/2π around a fixed dc-bias point. At a temperature of T = 50 mK, this setup with heavily filtered electrical leads ensures that the electromagnetic modes at the frequencies monitored in the experiment are in the vacuum (ground) state.

To develop an intuitive picture for the results presented below, we start by providing a simplified theoretical description of the Casimir effect in our system. Mathematically, the metamaterial is equivalent to a gravitational pendulum with a length proportional to the total Josephson energy. The mass of the pendulum is the analog of the electrical capacitance of the junction, and the angle with respect to the vertical is the analog of the superconducting phase difference. When the length is modulated at twice the natural frequency, initial oscillations or fluctuations of this angle become parametrically amplified. However, if the pendulum is at rest and not displaced with respect to the vertical, classical physics predicts that the modulation of the length of the pendulum will not produce any oscillation. However, the quantum-mechanical prediction is different: Due to the uncertainty principle, even in the ground state, the pendulum is not truly at rest and the quantum fluctuations will be parametrically converted into real, measurable oscillations of the superconducting phase. According to the ac-Josephson relation, oscillations of the phase will produce an oscillatory voltage that will propagate as real photons in the transmission line. Hence, the Josephson metamaterial acts as an antenna broadcasting information about the local vacuum.

A detailed mathematical analysis of the generation of photons by the DCE effect from the quantum vacuum in our system is presented in SI Text. To test these predictions, we first measured the noise power spectra using a drive at ω_d = 2ω_res (Fig. 2), which clearly demonstrates the generation of photons with frequencies around ω_res at different driving powers P_d. The increase in the noise level with P_d is saturated when a parametric oscillation sets in at P_d = −75 dBm. Below the threshold, the emitted power spectrum follows the theoretical predictions closely. For a lossless cavity, the DCE power spectrum (Eq. S36) is obtained as

Fig. 2.

(A) Color map of the output noise power (color scale in decibel units with k_B × 5 K as the reference level) measured across the resonant frequency ω_res/2π = 5.4 GHz while increasing the pump power P_d at ω_d = 10.8 GHz. At P_d > −75 dBm, the device becomes unstable against self-sustained oscillations. (B) Cross-correlations for in-phase (I) and quadrature (Q) amplitudes 〈I₊(t)I₋(t′)〉 and 〈Q₊(t)Q₋(t′)〉 between sidebands at ω_± = ω_d/2 ± ν vs. time delay t − t′ with the pump on. The IQ demodulators are at 5.398 GHz and 5.402 GHz. The used bandwidth is 200 kHz, and 10⁶ samples were collected. (C) Covariance matrix σ(A, B), measured at P_d in the stable low-gain region. The diagonal elements amount to quanta [where 0.5⋅DCE is marked in red and the vacuum part (1/4) is marked in green], whereas the nonzero off-diagonal elements describe the squeezing correlations of the system. This covariance matrix satisfies the nonseparability condition σ(x₊, x₊) − σ(x₊, x₋) < 1/4. (D) Covariances σ(x₊, x₋) (△) and σ(x₊, x₊) (+), and their ratio σ(x₊, x₋)/σ(x₊, x₊) (○) vs. modulation voltage V_d for the flux coil; the ratio and its fit are on the linear scale (Left), whereas the rest is on the logarithmic scale (decibels; Right). The dashed and dotted lines are theory predictions obtained using Eqs. S44–S52 supplemented with a 22% loss factor, most likely due to two-photon dissipation, which is not included in the theory. On the right scale, of a quantum corresponds to −6 dB (denoted by the green arrow). The parameter values used in the evaluation are listed in the legend for Fig. 3.

where 1/|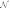(ν)|² is a factor producing parametric gain (Eq. S26), χ(ω) is the electrical susceptibility of the resonator with κ as the cavity decay rate introduced in Eq. S20, and α denotes the amplitude coupling to the flux drive defined in Eq. S14. The theoretical model can be extended to account for losses internal to the cavity (21, 23) by separating the total decay rate of the cavity into an internal cavity decay rate κ_I and external cavity decay rate κ_E (SI Text, Section IV).

Correlations Between Casimir Photons

Theory predicts that the Casimir photons are generated as correlated pairs having frequencies ω_± = ω_d/2 ± ν, with energy conservation satisfied by ω₊ + ω₋ = ω_d. To study the two-mode correlations (26) between the sidebands ω_± experimentally, we used two vector signal analyzers triggered simultaneously to collect in phase I and out of phase Q time-domain IQ-waveforms at ω_±. We calculate the correlations between the IQ data and eliminate the amplifier noise by a procedure described in SI Text. The resulting correlations, which we denote by 〈I₊I₋〉, 〈I₊Q₋〉, etc., turn out to be directly proportional to the correlations of the quadratures and of the outgoing fields in the two sidebands. For convenience, the homodyning reference phases θ₊ and θ₋ of the two analyzers and the phase of the pump field have been rotated so that 〈x_±y〉 = 〈y_±x〉 = 0. We have verified that all the measured quadrature correlations behave according to the theory under this rotation. Because this procedure is performed for every point at which we measure correlations, there is no need to write down the phases θ_± explicitly in the following. To denote the correlations in a compact form, we introduce the covariance matrix , where {,} denotes the anticommutator and A and B are any of the operators x_± or y_±. The experimental results for correlations are displayed in Fig. 2. The time dependence of 〈I₊I₋〉 and 〈Q₊Q₋〉 is displayed in Fig. 2B, and our results for the full covariance matrix are presented in Fig. 2C.

To compare the theoretical predictions for Casimir photon generation with our results, Fig. 2D displays the pumping power dependence of σ(x₊, x₋), σ(x₊, x₊) and their ratio, σ(x₊, x₋)/σ(x₊, x₊). Compared with the theory, σ(x₊, x₊) follows (Fig. 2D, dotted curve) closely and the covariance σ(x₊, x₋) agrees with the calculated two-mode correlations (Fig. 2D, dashed curve). The experimentally determined normalized squeezing correlator σ(x₊, x₋)/σ(x₊, x₊) also scales with the pumping drive amplitude V_d in agreement with the theory. The covariance matrix presented in Fig. 2C satisfies a nonseparability criterion for (entanglement) continuous variables (27, 28), σ(x₊, x₊) − σ(x₊, x₋) < 1/4. In our case, as calculated from the data in Fig. 2C, the difference was 0.18 ± 0.01 < 1/4. This corresponds to a logarithmic negativity E_N = 0.32 and to an entropy of formation E_F = 0.125 entangled bits. Nonseparability requires low loss operation and is not satisfied at higher pumping powers or higher losses (see Fig. S3).

Finally, we have measured what happens when the resonator is detuned from ω_d/2 while keeping P_d = constant. As seen in Fig. 3A, we observe a splitting of the noise spectrum into two peaks, which are in good agreement with our theoretical results depicted in Fig. 3B at T_E = 50 mK and T_I = 60 mK for the external (κ_E) and internal (κ_I) dissipation temperatures, respectively.

Fig. 3.

(A) Emitted noise as a function of ν = ω_res − ω_d/2 while tuning Δ = ω − ω_d/2 measured around ω_d/2 = 5.4 GHz at 50 mK. (B) Theoretical prediction from Eqs. S44–S48 evaluated using parameters α = 2π × 65 MHz, κ_E = 2π × 15 MHz (at 50 mK), and κ_I = 2π × 9.2 MHz (at 60 mK). In both A and B, the color scale for the noise power is cut at 0.3 dB in the vicinity of ω_d/2. (C) Theoretical prediction for a classical vacuum calculated at a single quantum of classical noise in the internal modes. (D) Slices with constant detuning Δ taken from B are compared with the theoretical predictions from Eqs. S44–S48; parameter values are the same as those listed above. The noise power is displayed in units of photons per hertz. This scaling is obtained by comparing the increase in measured noise power with the system noise temperature T_N = 5.5 K, which was obtained using the standard Y-method in the same cool-down. (Inset) Full, symmetrical noise pattern measured at a smaller pump power over the range −100 < Δ < 100 MHz and −100 < ν < 100 MHz.

Attempts to describe the measured spectra as resulting from extra classical noise sources would fail utterly to explain the structure displayed in Fig. 3A, which is demonstrated by a number of noise power considerations and systematic reliability checks (see Figs. S1 and S2) that are outlined in SI Text. As an example, in Fig. 3C, we show the effect of a single quantum of classical noise in the internal modes: The spectrum becomes strongly asymmetrical due to the asymmetrical T_I-dependence of the emitted cavity power in the “lower arm” in Fig. 3 A and B (Eqs. S44–S48). Thus, the symmetrical spectral pattern shown in Fig. 3A, with nearly equally strong peaks at ν ∼ Δ, can be considered as a clear signature of the DCE (6). This pattern provides direct evidence for the coupling of modes and (Eqs. S26 and S42) that leads to the Casimir photon generation. The experimental results at three different values of detuning are plotted and compared with the theoretical predictions in Fig. 3D. Based on these fits, or more precisely on the symmetry of the lower and upper peaks, we can be confident that the metamaterial temperature is not much different from the base temperature of the refrigerator.

Conclusions

To conclude, we have demonstrated experimentally the DCE in a Josephson metamaterial embedded into a low-quality-factor, coplanar cavity resonator. The DCE was produced by the modulation of the index of refraction of this material near its quantum ground state. We observe distinctive features in the noise power spectrum of the emitted radiation: When the cavity is pumped off-resonance, the spectrum splits into two well-resolved lines and their separation could be extended up to 800 MHz. In addition, we prove experimentally that the emitted radiation is strongly correlated and that it satisfies a nonseparability criterion. Our results pave the way for the EPR type of experiments with correlated microwave photon pairs and for quantum information processing with continuous variables (29, 30).

Materials and Methods

Josephson Metamaterial.

The system we are studying consists of an array of dc-SQUIDs, which form a metamaterial with externally tunable inductance per unit length. A dc-SQUID operating at currents well below the critical current behaves as a linear inductor with Josephson inductance

where E_J is the Josephson energy and Φ₀ = h/2e is the magnetic flux quantum. The Josephson energy, can be modulated by an external magnetic flux Φ_ext,

and, assuming that the junctions have approximately the same fabrication parameters, E_J1 = E_J2 = E_J, we get . If the current passing through the dc-SQUID elements is much smaller than the critical current of the junctions (which is the case in our experiment), the element behaves as a linear inductance of value L_J. Suppose the length of a single element is ɛ; then, the inductance per unit length of the metamaterial is l_u = L_J/ɛ. If the wavelength of the electromagnetic field is much larger than ɛ, we can treat our metamaterial as a continuum. Additional descriptive information is provided in SI Text.

DCE vs. Amplification of Classical Noise.

To rule out the possibility of a classical origin for our experimental observations, we have performed a careful out-of-equilibrium analysis of our setup. The most important question concerns the effect of temperature in the internal modes, which are not directly monitored in the experiment. It could be argued that pumping might increase the temperature of the internal modes out of equilibrium with respect to the external modes that remain at the bath temperature. The question is what would be the magnitude and contribution of this effect and its spectral signature. From analyzing the first term in Eq. S46, we see immediately that to obtain the same power levels as in the experiment, we would have to have an occupation on the order of one quanta in the internal modes, which is more than two orders of magnitude larger than occupation in the external modes. This would correspond to a temperature on the order of 200 mK, which would not remain unnoticed unless it were quite localized on the sample. To rule out this possibility, we have plotted in Fig. 3C the power spectrum with . What we see is that a strong asymmetry in the two branches appears. This is due to the preferential scattering of thermal photons in the cavity modes at ν = Δ. This spectrum clearly deviates from the symmetry between the two branches seen in the experiment. Sure enough, some nonthermalization of the internal modes is expected at low temperatures, and this produces a small asymmetry. In our experiment, this asymmetry corresponds to a difference of only about 10 mK in the temperature of the external and internal degrees of freedom. With this analysis and the additional checks described in SI Text, we can be confident that amplification of classical noise cannot account for these measurement results.

Field Theoretical Description.

The theoretical modeling of the experiment is done within the framework of the input-output theory. A detailed description of these results is presented in SI Text. The metamaterial forms a cavity with resonant frequency ω_res, which is capacitively coupled to a transmission line, giving a cavity decay rate κ. The modulation (driving) of the index of refraction of light inside the metamaterial translates into a modulation of the resonant frequency ω_res. As a result of the time dependence of the input modes, the output field modes a_out do not match with the same frequency modes of the input field a_in any longer, and they acquire a frequency-converted component. The following formula (Eq. S26) between the input and output modes is obtained:

where the frequency ν is measured with respect to half of the modulation (driving) frequency ω_d/2, α is the amplitude coupling to the driving field, χ(ω) = [κ/2 − i(ω − ω_res)⁻¹] is the cavity susceptibility, and . With vacuum as the input state, this connection formula yields the DCE power (Eq. 1), as well as the correlations of the quadratures in the output field. The expressions for the output noise powers due to thermal effects can be calculated using the same formalism. Finally, dissipation can be introduced by separating the decay rate of the cavity into the external part κ_E and the internal part κ_I, κ = κ_E + κ_I. The external decay rate is due to the coupling with the transmission line, which is monitored in the experiment, whereas the introduction of dissipation follows the standard procedure of assimilating it to the decay of the photons of the cavity, with rate κ_I, into an infinitely long transmission line.