Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2013 Mar 18;3:1475. doi: 10.1038/srep01475

Spiral microchannel with rectangular and trapezoidal cross-sections for size based particle separation

Guofeng Guan 1,2, Lidan Wu 3, Ali Asgar Bhagat 2,6, Zirui Li 2,4, Peter C Y Chen 1,2, Shuzhe Chao 1, Chong Jin Ong 1, Jongyoon Han 2,3,5,a
PMCID: PMC3600595  PMID: 23502529

Abstract

The paper reports a new method for three-dimensional observation of the location of focused particle streams along both the depth and width of the channel cross-section in spiral inertial microfluidic systems. The results confirm that particles are focused near the top and bottom walls of the microchannel cross-section, revealing clear insights on the focusing and separation mechanism. Based on this detailed understanding of the force balance, we introduce a novel spiral microchannel with a trapezoidal cross-section that generates stronger Dean vortices at the outer half of the channel. Experiments show that particles focusing in such device are sensitive to particle size and flow rate, and exhibits a sharp transition from the inner half to the outer half equilibrium positions at a size-dependent critical flow rate. As particle equilibration positions are well segregated based on different focusing mechanisms, a higher separation resolution is achieved over conventional spiral microchannels with rectangular cross-section.

Size-based microparticles separation is essential for many biomedical and chemical analysis assays1, with several lab-on-a-chip (LOC) separation methods developed in recent years2,3. Unlike active separation techniques that require external force field for functionality4,5, the size based passive microfluidic separation relies purely on the channel geometry and microfluidic phenomena6,7,8,9,10,11,12,13. The obvious advantage of passive separation techniques is the simplicity of fabrication and automation. However, these techniques suffer from limitations of low separation resolution and throughput. Three classes of methods that are capable of producing reasonably high (~106 particles/min) throughput are, the mechanical membrane filter (MF)14,15,16, the deterministic lateral displacement device (DLD)17, and inertial microfluidics (IM)18. Mechanical membrane filters, though capable of achieving the highest throughput among these methods (~109 cells/min), suffer from severe clogging issues, especially when dealing with complex particle/cell mixtures containing objects with diverse sizes and concentrations. In separating 10–35 μm cells with DLD, Green et al. reported a throughput of 105 cells/min19. In terms of resolution, DLD has been reported to be able to separate particles with a resolution of 0.1 μm with average particle diameter around 1 μm17, but the separation resolution deteriorates for flexible particles such as cells20. Inertial microfluidics (IM), with throughputs comparable to MF, have been applied in many practical applications21,22,23 recently. Kuntaegowdanahalli et al.24 showed that the Dean-coupled inertial migration in spiral microchannels could reach a throughput of ~106 cells/min to separate 8 μm cells from 15 μm cells with ~90% separation efficiency. Lee et al.25 reported a contraction-expansion array (CEA) microchannel, which utilized the inertial lift force to separate cancer cells from human whole blood. They achieved a throughput of 1.1 × 108 cells/min with cancer cell (~18 μm) recovery of 99.5% and blood cells (mostly RBCs, 6–8 μm discoid) rejection ratio of 92.8%. However, the dispersed band of 10 μm particles from the reported experiment indicates that the separation resolution at such high concentration might be limited when the size of cells are close to each other.

In a special case of inertial microfluidics, Seo et al.26 and Bhagat et al.27 introduced a spiral microchannel, which can introduce continuous and stable Dean vortices that apply drag force on microparticles leading to particle focusing along the channel inner walls. Kuntaegowdanahalli et al.24 further demonstrated that particles of varying diameters occupy distinct positions within the microchannel cross-section and can be separated and collected by designing a multiple outlet system. However, a major limitation of such a system is the decrease in separation resolution as the particle sizes get closer to one another. An approximate mathematical model for these channels was reported by Bhagat et al.27,28 based on empirical observations of the focusing position from the top view. The relationship between the focusing positions and various parameters such as the particle size and the flow rate has been studied by several groups, with the assumption that the particles focus near the center of the channel depth24,29,30,31,32, rather than forming two separate focusing lines18,33,34,35,36. However, there has been no direct experimental observation to support.

In this paper, we study the particle focusing mechanism in curved inertial microfluidic channels by observing three dimensional particle positions across the channel cross-section. A detailed numerical model is presented to explain the various forces acting on particles suspended in these spiral channels. These results have improved our understanding of such systems and resulted in the design of a new spiral microchannel with trapezoidal cross-section that generates strong Dean vortices at the outer half of channel. In this new design, larger particles can be focused near the inner microchannel wall while smaller particles are trapped within the Dean vortices near the outer wall of the channel at relatively high flow rates, facilitating high-resolution high-throughput size-based separations.

Results

Particle focusing positions in rectangular and trapezoidal cross-section spiral channels

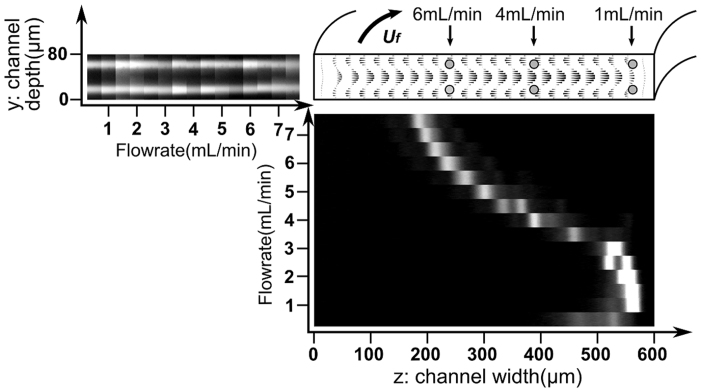
Figure 1 shows the focusing positions of 15.5 μm particles from the top and side view in a spiral channel with 80 μm × 600 μm (H × W) rectangular cross-section. As seen from the top view, the focusing position of the particle moves gradually from the inner wall towards outer wall with increasing flow. From the side view, two clear bands are observed along the depth direction, indicating two distinct focusing positions near the top and bottom walls. In contrast to the gradual change of focusing position along the width direction, the focusing position along the depth direction is largely independent of the flow rate, and remains fixed at 22.0 ± 1.1% of channel depth from the top and bottom walls for flow rates ranging from 0.5–7.5 mL/min. The result is in line with previous simulation37,38 and experiment21,39,40,41 work in straight rectangular or circular cross-section channel. From the simulated Dean flow profile, it is seen that the Dean flow changes its direction at 28 ± 0.5% of channel depth, indicating that the Dean drag force at the focusing position (depth) is always pointing to the inner wall. These results provide important insights into the focusing mechanism of particle moving in spiral channels. Detailed force balance will be discussed in the next section.

Figure 1. Balance of particles in a rectangular cross-section spiral microchannel.

Figure 1

Open in a new tab

The black cones within channel cross-section are the CFD simulation result of the Dean flow field at a flow rate of 3.5 mL/min in a channel with radius 7.5 mm. The figure also shows the vector plot of the Dean drag force on the particle since the force is proportional to the Dean velocity. The experimental images of 15.5 μm fluorescent beads distribution from the top view and side view are placed at the bottom and to the left side of the simulation profile. By combining the top- and side- view observations, the positions of 15.5 μm beads at typical flow rate are drawn as gray circles in the channel cross-section.

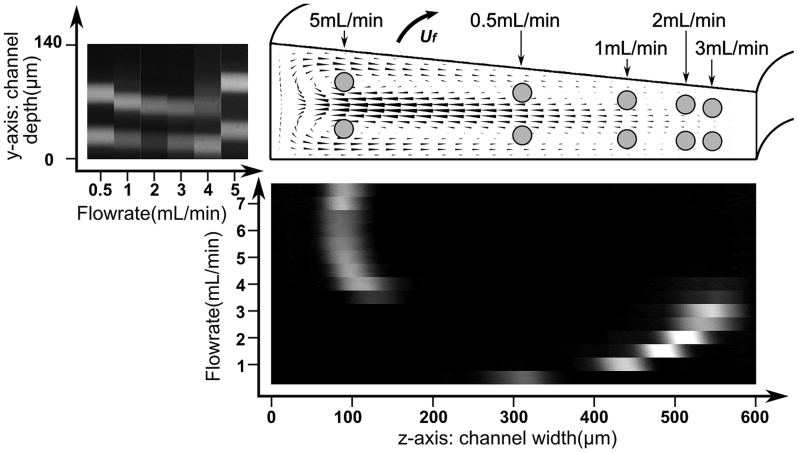
In a spiral channel with trapezoidal cross-section, the particle focusing behavior is different from that in a rectangular channel. In a trapezoidal channel, as shown in Figure 2, particles focus near the inner channel wall at low flow rate (similar to channels with rectangular cross-section), while beyond a certain threshold flow rate, they suddenly switch to an equilibrium position located at the outer half. Careful examination of the focusing positions in the top and side view reveals that particles are trapped exactly at the centers of the two Dean vortices formed at the outer half of the channel.

Figure 2. Balance of particles in a trapezoidal cross-section spiral microchannel with 80/140 μm inner/outer depth and 600 μm width.

Figure 2

Open in a new tab

The black cones within channel cross-section are CFD simulation result of the Dean flow velocity (also Dean drag force) at a flow rate of 3.5 mL/min in a channel with radius 7.5 mm. The experimental images of 26.25 μm fluorescent beads distribution from the top view and side view are placed at the bottom and the left side of the simulation. By combining the top and side view observations, the positions of 26.25 μm beads at typical flow rate are drawn in gray circles in the channel cross-section.

Along the depth direction, according to experimental measurements, particles are focused between 25.5–27.1% of the channel depth at flow rates of 0.5–3.0 mL/min. This result indicates that the distance between the focused particle and the channel wall in trapezoidal channel at the depth direction is larger than that in the rectangular channel.

Comparison of top view focusing

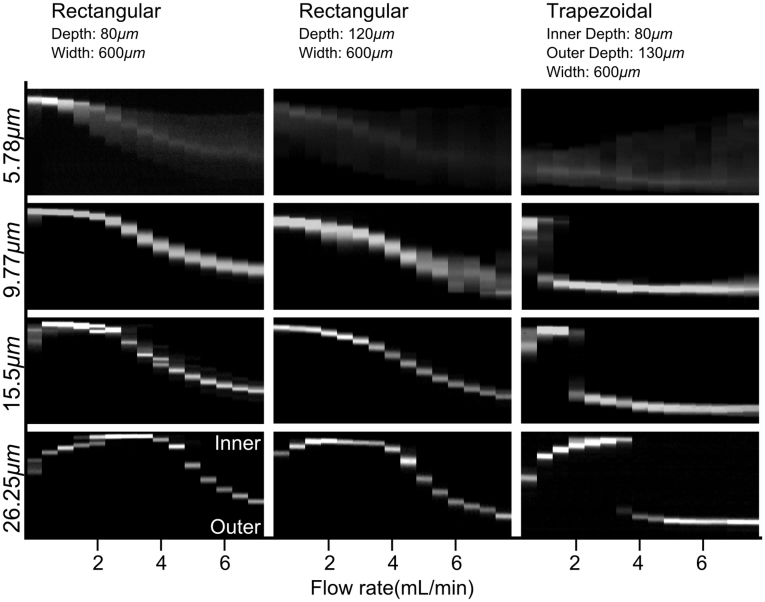
Figure 3 shows the flow rate dependence of the focusing position of fluorescent particles in a spiral channel with rectangular and trapezoidal cross-sections. The diameters of the particles are 5.78 μm, 9.77 μm, 15.5 μm, and 26.25 μm respectively. The cross-sections of the rectangular channel are 80 μm × 600 μm (H × W) and 120 μm × 600 μm (H × W) respectively. The width of trapezoidal channel is fixed at 600 μm, and the depths at the inner and outer side of the channel are 80 μm and 130 μm respectively. From the results shown in Figure 3, we learn that in the rectangular channels, particles are focused near the inner channel wall at low flow rate, and then the focusing position starts to gradually move towards the outer wall as the flow rate increases. At a given flow rate, particles of varying sizes occupy different positions within the channel cross-section. This phenomena was utilized by Kuntaegowdanahalli24 to demonstrate size-based separation with multi-outlets bifurcations at the end of the channel. However, since the difference in focusing positions between the particles is not significant, the resolution and throughput of separation of concentrated suspensions is limited42.

Figure 3. Top-view experimental observation of fluorescently labeled microparticles at the outlet of rectangular cross-section spiral microchannels with different channel depths and a trapezoidal cross-section spiral microchannel for increasing flow rates.

Figure 3

Open in a new tab

Measurements of the focusing position of particles with different sizes in trapezoidal channel demonstrates clearly distinct characteristics. As shown in Figure 3, for all the particles, there is a narrow flow rate range, i.e. a threshold, to ‘switch’ from inner side to the outer side of the channel as the flow rate increases. Below the threshold flow rate, particles are focused near the inner wall; while above the threshold, they are focused near the outer side of the channel. It is important to note that this threshold flow rate is a function of particle size. In particular, the 5.78 μm and 9.77 μm particles, which are smaller, shift to outer half of the channel at very low (≤1 ml/min) flow rate while the 15.5 μm and 26.25 μm remain focused near the inner wall at such low flow rate. Increasing the flow rate up to 3.5mL/min has negligible effect on the smaller particles (5.78 μm and 9.77 μm) once they are focused at the outer side. However, the 15.5 μm particles equilibrate at the outer side above 2.0 mL/min, while the 26.25 μm particles migrate at flow rates greater than 3.5 mL/min.

Separation resolution and throughput

For the separation of particles of two different sizes, the ideal scenario is for particles of different sizes to focus at positions as far as possible from each other. This will not only increase the separation resolution, but also allows one to process samples with higher particle concentrations by minimizing the interaction between particles of different sizes (e.g. high hematocrit cell solutions in the case of blood separation). The results in Figure 3 demonstrate that the trapezoidal cross-section channel can meet these requirements. Next, we conducted tests to show actual separations between particles of varying sizes.

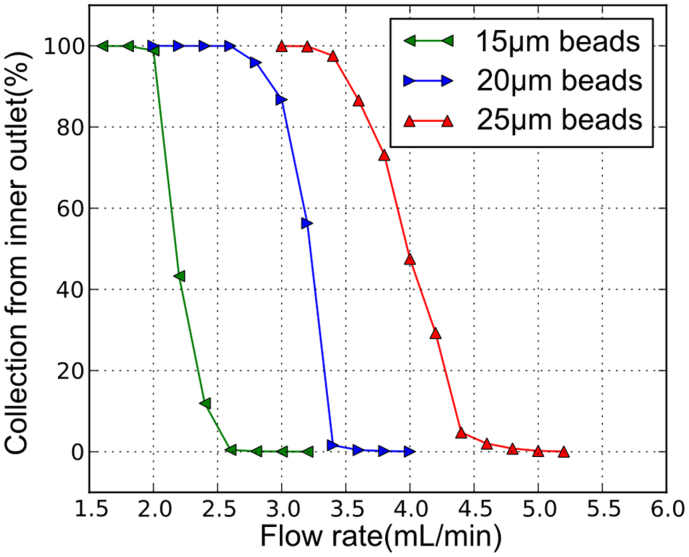
Figure 4 presents the collection of different standard NIST traceable particles (nominal diameter 15 μm, 20 μm and 25 μm, mean diameter 15.61 μm, 20.85 μm and 25.63 μm) diluted to 150–350 k/mL concentration and pumped through the spiral microchannel with trapezoidal cross-section. The outlet samples are collected and analyzed for particle recovery. The ratio of collected volumes from inner outlet and outer outlet is 1:4. The result shows that the required range of flow rate for the particles to migrate from the inner side to the outer half completely is between 2.0–2.6 mL/min for 15 μm beads, 2.6–3.4 mL/min for 20 μm beads and 3.4–4.8 mL/min for 25 μm beads. These data indicate that the flow rate threshold is sufficient to separate these three groups of particles respectively with high separation resolution.

Figure 4. Collection ratio of particles from the inner outlet of trapezoidal cross-section spiral channel (80/130 µm inner/outer depth, 600 μm width) at different flow rate for various particle size.

Figure 4

Open in a new tab

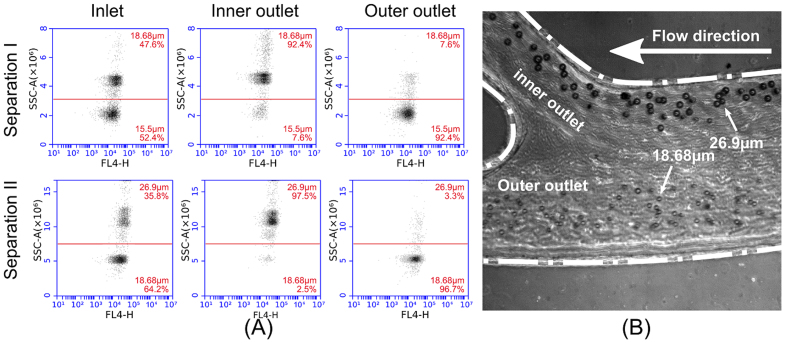
The high throughput separation capability of trapezoidal channels is presented in Figure 5 with fluorescently labeled particles which have different mean diameters. The scatter plots in Figure 5A clearly indicate two groups of particles and their separation efficiency. The separation result of 15.5 μm and 18.68 μm beads at 1.61 × 107/mL (1.87% volume concentration, equivalent to ‘hematocrit number’ in blood separation) throughput indicates over 92% separation efficiency. The separation result of 18.68 μm and 26.9 μm at an optimized flow rate of 3.4 mL/min shows that the purity of both outlets are over 96%, with a total throughput of 8.85 × 106/min, which is 1.33% volume concentration. A microscopic image demonstrating the separation between 18.68 μm and 26.9 μm particles is shown in Figure 5B. The high-speed image clearly indicates the separated particle streams near the opposite channel walls at the outlet.

Figure 5.

Figure 5

Open in a new tab

(A) Scatter plots captured using flow cytometer (Accuri C6, BD Biosciences, USA) showing the results of separations of particle mixtures in a trapezoidal cross-section channel (80/130 µm inner/outer depth, 600 µm width).(B) High speed microscopy image (Phantom V9.1, Vision Research Inc. USA, exposure time = 4 μs) captured at the outlet bifurcation clearly showing the separation of 18.68 μm and 26.9 μm particles at a flow rate of 3.4 mL/min (refer supplementary information for the video).

Cells are different from rigid particles in terms of the deformability and shape. Hur et al. have reported that the shape of particles does not have obvious influence on the focusing position in inertial microfluidics, but the hydraulic diameter of particles is the key factor43, while the deformability has an evident effect on the focusing position of particles/cells44, which makes the focused band of particles/cells slightly shift away from the channel wall as compared to that of rigid beads of the same size. If the device is employed in cell separation, the variation of cell deformability may affect the separation efficiency. But according to our recent study45, the trapezoidal spiral is capable of producing comparable separation between deformable leukocytes and red blood cells perhaps aided by the large distance between the inner focusing and outer trapping positions.

Discussion

For the analysis of the forces exerted on a particle in curved microchannel, we define a coordinate system (x, y, z) as shown in Figure 1 and Figure 2. The direction along the channel curve (main flow direction) is the x axis. The direction along the channel depth is the y axis, and the radial direction along the channel (the width direction), is the z axis.

Along the cross-section, the Dean induced drag force FDD and the inertial lift force FL are dominant among all of the forces subjected on the particles suspended in spiral channel (details of force analysis can be found in Supplementary material). The equilibrium position of a particle is thus dependent on the balance of these two forces.

The difference between the particle velocity along the y-z plane and the dean flow velocity in its proximity could generate a drag force on the particle that follows Stokes’ law (i.e. drag force being proportional to Dean velocity) as illustrated in Figure 1 and 2. This drag force FDD is entirely dependent on the Dean flow field. It is evident that the Dean flow pattern does not change significantly for flow rates increasing from 1.0 mL/min to 8.0 mL/min in our simulation model. At the mid-section of the channel cross-section along channel width (z-axis), the Dean flow velocity is always parallel to the z-axis and changes its direction along the channel depth as we move closer to the top and bottom walls (y-axis). Thus, except the inner/outer wall region, FDD is primarily acting parallel to z-axis. In the region between 28 ± 0.5% and 72 ± 0.5% of the channel depth, FDD points to the negative direction of z-axis, while at regions near the top/bottom wall, it follows along the positive direction of z-axis.

Small particles in a shear field experience a lift force FL that is perpendicular to the direction of the flow as a results of the inertial effects in the viscous flow around the particle. For the above designs of microfluidic channel, FL is dominant in most locations compared to FDD, except near the ‘minimal lift force’ regions. Although so far there has been no simulation result for the distribution of FL in low aspect ratio rectangular channel, FL always points toward the channel top or bottom wall within the center region of channel cross-section.

Near the channel wall, the lift force balance in straight channel has been numerically simulated46 and experimentally observed39,40 in previous studies. The direct observation of focusing position in the cross-section of square channel by Choi40 indicated that particles will balance close to the four channel walls, which is named as the “minimum lift force planes”. Bhagat et al.39, observed the distribution of fluorescent particles from both top and side views and showed that for rectangular straight channel, the four minimum lift force planes reduce into two minimum lift force planes along the longer side walls. Our results agree with their observation in the curved channel, in the sense that particles focused at the 22% and 78% of the channel depth along the top and bottom channel walls in a rectangular cross-section curved channel. Furthermore, according to their experimental data40, particles remain dispersed along the minimum lift force planes at low flow rates, and will focus to the centers of the minimum lift force planes as the flow rate increases. This experimental behavior in a straight rectangular channel, coupled with numerical calculation46, reveals that FL within the minimum lift force plane is still pushing particles toward the true equilibrium (center of the planes). While this force is weak at low flow rates, it leads to particles being dispersed along the planes39. With higher flow rates, FL increases more rapidly (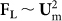Inline graphic, where Um is the mean velocity of main flow) and becomes significant, leading to particles being focused at the center of the minimum lift force planes.

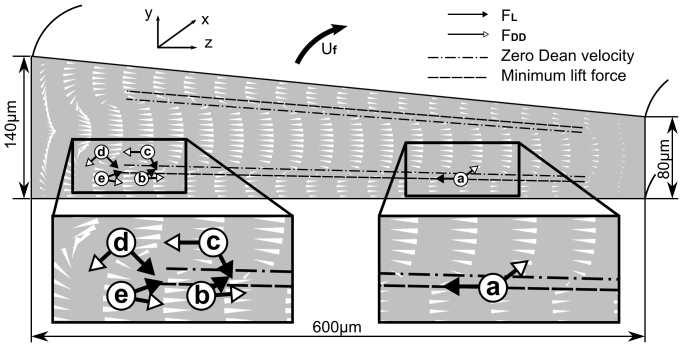
The behavior of particles in curved rectangular channel can similarly be explained. Because there is no FDD at y direction except near the side wall regions, the focusing position of all the particles in y axis is determined by FL, which focuses particles at 22% and 78% of the channel depth as in the straight rectangular channel. At these minimum lift force planes (22% and 78%), the Dean flow pushes the particles toward the inner wall until the particles start to experience weaker FDD (due to edge effect, around 10% of the width from the inner wall) and are balanced by weak FL within the minimum lift force planes. This (position a in Figure 6) is a stable equilibrium, since any departure (in y axis) would create much stronger FL, forcing the particle to return to the minimum lift force planes (position b and c in Figure 6). The focusing position here depends on the size of the particle(r), mainly through the FDD term(~r), pushing larger particles further into the inner side wall compared with the smaller ones. In this regime (below ~3 mL/min in Figure 4) higher flow rate will push the particles further toward the wall, due to increased FDD (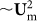Inline graphic).

Figure 6. Schematic illustrating the direction of forces acting on particles at typical positions in a rectangular cross-section spiral channel.

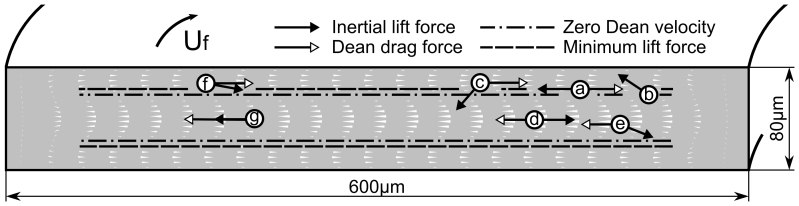
Figure 6

Open in a new tab

Particle (a) is at the minimum lift force line, which is a stable balance position. Particle (b) and (c) have a small offset from the minimum lift force line where the lift force will drive them to the equilibrium point. Although the lift and drag forces on particle (d) are in opposite directions at the center line of the depth and could potentially lead to force balancing, whose position is not a stable equilibrium point. And a small offset from the center line as illustrated by particle (e) would result in a significant deviation of the particle from the center line by the lift force. For particles at outer half of the channel, the two forces will always be acting in the same direction, as illustrated by Particle (f) and (g), and will prevent the force balancing or equilibration. White cones indicate the direction and relative magnitude of simulated Dean velocity as well as Dean drag.

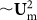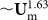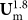When the flow rate increases (above ~3 mL/min in Figure 4), FL (Inline graphic) along z-axis increases faster than FDD (Inline graphic or Inline graphic), and the particle focusing position will start to move towards the outer wall. (Figure 3). For differently-sized particles, the magnitude of FL (FL ~ r3) grows faster with the flow rate than FDD for larger particles. This is the mechanism behind the second transition of focusing position (above ~3 mL/min) from the inner to the outer side of the channel. In this regime, the larger particles will undergo this transition more abruptly (more rapid increase in FL) than the smaller particles, as one can see in Figure 3. The significant implication is that the physical separation between the larger and the smaller particle streams becomes smaller, simply because the larger particle stream comes to the outer side more abruptly and overlaps with the smaller particle stream. As a result, separation resolution of the spiral inertial sorter with rectangular cross-section can be optimized at a certain flow rate, and cannot be further improved by changing flow rates only.

On the other hand, particles at the center line (particle d in Figure 6) could also be balanced at the inner half of channel, where FL (inward) and FDD (outward) are in opposite direction. However, this equilibrium, if it does exist, is not a stable one, since a small offset from the center line will result in significant particle position deviation (Particle e in Figure 6) towards the nearby minimum lift force plane. In the outer half of the channel, FL and FDD are generally in the same direction and therefore not possible to balance (particles f and g).

Notably, the above analysis does not consider the interaction between the particles and the flow field. In fact, it has been proposed that the presence of a particle could change the distribution of main flow dramatically47, and even induce lateral flow48. The change of the main flow can directly affect FL and FDD. Since the Dean flow is caused by the heterogeneity of the main flow, the distribution of Dean flow will also be modified by both the change of the main flow and the particle induced lateral flow, changing the magnitude of FDD in turn. Therefore, it would be difficult to give a quantitative analysis of these forces even when the simulation data of FL in straight channel is available. However, based on our simplified force analysis, one can still get a qualitative understanding of the force balancing within spiral inertial microfluidic channels, where the lift force is primarily balanced by the drag force.

In order to develop accurate computational models to predict particle behavior within the microfluidic channel, we are currently working on a customized 3-dimensional computational fluid dynamics model that considers the interaction between a freely movable object and the surrounding fluid. From the model, we then expect to extract accurate simulation results for the forces of interest, as well as the motion and trajectories of particles in a curved microfluidic channel with a given cross-section quantitatively.

In rectangular cross-section channels, particles focus at a certain positions (typically at the inner side of the curved channel) as a result of the balance between FDD and FL. If any force is changed, the balance is broken and the particle will shift to a new focusing position in the cross-section. The modification of the focusing position can be easily achieved by altering the geometry of the channel's cross-section. A trapezoidal channel with shallow inner and deep outer cross-section, for example, causes the main flow to shift towards the outer side of the channel cross-section. This generates a stronger Dean flow at the outer side and a weaker Dean flow at the inner side (Figure 7). Significant differences exists between the Dean flow field at the inner half of the rectangular and trapezoidal cross-section channels, with the latter having a Dean flow velocity with a significant component along the y-axis (i.e. the minimum lift force plane and the Dean flow field are not parallel with each other, as in the case of rectangular channels). It means that if particles are placed at corresponding minimum lift force planes in the trapezoidal cross-section channel, the particles will be subject to a component of FDD pointing to the channel center along y-axis direction. Thus particles will then balance further away (toward the center) from the minimum lift force planes in trapezoidal channels. This is supported by the experimental data showing that particles are focused at 25.5–27.1% of the local channel depth at flow rates ranging 0.5–3.0 mL/min, which is indeed very close to the “zero Dean flow plane” in the rectangular channel. Indeed there is no true ‘zero Dean flow plane' in the trapezoidal channel, except the Dean vortex centers on the outer side of the channel.

Figure 7. Schematic illustration of the forces acting on the particles at several typical positions in a trapezoidal cross-section microchannel.

Figure 7

Open in a new tab

Forces acting on particles at positions (a) indicate the imbalance at inner side at high flow rate. Forces acting on particles at positions (b), (c), (d) and (e) illustrate that these particles tend to be trapped near the Dean vortices center at different points. White cones indicate the direction and logarithmic magnitude of simulated Dean velocity as well as Dean drag.

Within the inner half of trapezoidal cross-section, the distribution of the Dean flow is similar to that in a rectangular cross-sectional channel, despite the lower magnitude, since the center of the Dean vortices are far away from the inner wall. At low flow rates, where the lift force is not high enough to push particles away from the inner side, the large particles will remain focused near the inner channel wall, as in the case of rectangular channels. With increasing flow rates, particles begin to move towards the outer wall due to the increase in FL along z-axis. FDD has two components here, a component along y-axis pointing toward the center of channel cross-section near “zero Dean flow plane”, termed as FDy and the corresponding component along z-axis, termed as FDz. From Figure 7 it can be seen that even at “zero Dean flow plane”, FDy remain non-zero and its magnitude is increasing from the inner side to the outer. This generally renders the balancing between FDD and FL more unstable, especially at higher flow rate. More specifically, as the particle in position a shows, the higher flow rate tend to push the focusing position toward the center of the channel, in where the Dean flow is stronger and therefore could strip the particles away from being trapped by the lift force.

Once the particle moves to the outer half of the channel near one of the vortex centers, the resultant force of FDD and FL will push the particle to an equilibration position close to the center of the vortex. The forces act on the particle near vortex centers are illustrated in Figure 7. The trapping is caused by a dynamic balance of these two forces, which rely on many parameters, such as the slant of channel, the flow rate, and the diameter of particle. For example, under the resultant force of FDD and FL, a particle at position b will tend to cross the minimum lift plane and migrate towards position c, where a strong FDD can then push the particle towards position d. Qualitatively, near the Dean core, particles on the minimum lift force plane (positions b, e) experience FDD that pushes them towards the Dean core, while the particles trapped near the Dean core (or zero FDz line, positions c, d) experience both FDD and FL that drive the particle back to minimum lift force planes.

The evolution of the trapezoidal cross-section spiral microchannel is based on the following two considerations. First, based on Di Carlo's study49, the hydraulic radius of the channel should be lesser than r/0.07, for inertial focusing of particles. Second, with this restriction of channel hydraulic radius, a channel with low aspect ratio can yield separation by focusing particles along the channel width as demonstrated by Kuntaegowdanahalli et al.24 Thus, the only parameter that can be changed to effect high resolution separation is to dynamically change the channel depth along the channel width, thus giving rise to a trapezoidal cross-sectional geometry.

A trapezoidal cross-section with a deeper inner wall compared to the outer wall will have strong vortices formed at the inner side, resulting in all the particles being trapped despite varying particle size and flow rate. Such geometry is not applicable for size based separation. We also fabricated microchannels with the top wall having a concave, convex or just a regular slanted top wall and studied their effect on particle focusing and trapping. The experimental comparisons of these three patterns is discussed in Supplementary Information.

For a trapezoidal cross-section spiral microchannel, there are several factors that affect the focusing position and separation efficiency, such as the width, inner and outer depth of channel cross-section, the radius of the spiral curvature, and the slant angle. As analyzed above, the slant of the channel affects the focusing behavior in two ways: (i) the threshold flow rate required to trap particles in the Dean vortices as a function of particle size and (ii) the location of the Dean vortex centers. A large slant angle will lead to strong Dean at the outer side and increase trapping capability of particle. Large slant angle can also decrease the threshold flow rate required to trap the particles of certain size within the Dean vortices. This understanding was further validated by the observation of particle bands in channels with different slant angles and three different channel cross-section geometries (data and discussion included in Supplementary material).

In this paper, for the first time, we show experimental results confirming the three dimensional particle focusing in spiral microchannels. The result indicates that particles form two bands along the depth symmetrically between the zero-lift force plane and the centers of the Dean vortices in spiral channels. Based on the experimental evidence and the numerical simulation of the Dean flow profile, a detailed explanation of the focusing mechanism is presented, taking into account of various forces acting on the particle. With this understanding of the particle focusing mechanism, a new trapezoidal cross-section spiral microchannel for particle separation was developed and analyzed. A multi-loop microchannel was employed to calibrate the focusing of different size standard microparticles of 5.78 μm, 9.77 μm, 15.5 μm, and 26.25 μm for flow rates ranging from 0.5-7.5 mL/min. The experimental results indicate that particles occupy an equilibrium position near the inner microchannel wall when particles are introduced under a lower flow rate. However, beyond a threshold flow rate (which is size-dependent) the equilibrium positions moved to the outer microchannel wall, suggested to be a Dean vortex trap. Taking advantage of this sudden transition, the trapezoidal cross-section spiral microchannel is capable of producing higher resolution separation of particles than conventional rectangular cross-section spiral. Separation of 15.5 μm and 18.68 μm beads at an ultra-high throughput of ~1.61 × 107/min with over 92% efficiency was achieved with this device. This, to our knowledge, is the highest throughput and efficiency among the current state of the art microfluidic particle separation methods. We believe that, with further optimization of the geometrical parameters, this separation technique will meet the requirements of high-throughput size based separations for many biomedical and other applications.

Methods

Device design and fabrication

Pressure-driven flows through a rectangular channel have a hyperbolic profile with the maximum velocity at the centroid of the cross section of the channel and zero velocity at wall surfaces. Particles suspended in such non-uniform flow fields experience appreciable inertial lift force resulting in their focusing at specific positions within the microchannel cross section. In a curved channel, the fluid experiences centrifugal acceleration directed radially outward giving rise to transverse flows characterized by two counter-rotating vortices, known as Dean vortices, at the top and bottom halves of the channel (Figure 8A). The behavior of particles in these channels has been characterized extensively in the past32.

Figure 8.

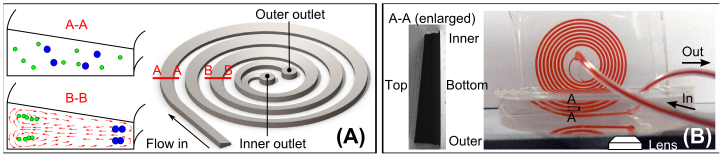
Figure 8

Open in a new tab

(A) Schematic of a trapezoidal cross-section spiral microchannel illustrating the principle of particle focusing and trapping within the Dean vortices.(B) An actual spiral microfluidic device for side view focusing position measurement. The microfluidic channel is filled with red dye for visualization. Samples are flowed from center loops to outer loops for the measurement.

Although inertial focusing within straight channels has been reported to require only 4 cm39, the Dean vortices generated in curvilinear microchannel applies additional force on the particles, requiring longer channel length for the suspended particles to migrate to their balancing position27. Considering this, all the microfluidic channels used in our experiments were designed to be 8-loops single-inlet-two-outlet spiral with radius increasing from 8 mm 24 mm to provide sufficient length for the particle migration. Since the dimensions of the channels are in sub-millimeter range, the master mold with the specific channel cross-sections for subsequent polydimethylsiloxane (PDMS) casting was milled in polymethyl methacrylate (PMMA). Due to the limitation of milling tool, the tolerance of the pattern is controlled to within 10 μm in the x-y direction and 2 μm in the z-direction with a surface roughness of Ra ~0.8 μm. The mold was carefully inspected and its dimensions were measured accurately before use. The microchannels were then made by casting Sylgard 184 silicone elastomer (PDMS) prepolymer mixed in a 10:1 ratio with the curing agent. After curing, the PDMS was peeled from the mold and plasma bonded to another 3 mm thick flat PDMS layer. Input and output ports were punched prior to bonding.

For the measurement of the vertical focusing positions, the device is cut along the periphery of the spiral channel with a ~2 mm gap between the channel and the edge of the PDMS part. The PDMS mold with the microchannel pattern is then placed vertically in a flat-bottomed petri-dish and a second cast of PDMS is poured to hold the chip vertically (Figure 8B). Tygon tubing is connected to the ports before the second cast to prevent PDMS from flowing into the channel. During the experiment, the device is placed on an inverted microscope and the image of the straight section is captured using fluorescent particles. Since PDMS is an elastic material the cross-section of channel would undergo pressure induced deformation due to high driving pressure. High speed images are taken near the outer reservoir where the pressure of channel is close to atmospheric pressure to minimize the influence of channel expansion. The device shown in Figure 8 is also used for size based particle separation. For separation experiments, the second cast is not required.

Fluid preparation

For the observation of particle focusing from the side view, a spiral channel with a low aspect ratio rectangular cross-section was fabricated. The microchannel is 600 μm wide and 80 μm deep, with the aspect ratio of 7.5 (width/depth). If the refractive index difference between the fluid and PDMS channel is large, the imaging of fluorescent particles within the channel through a thick piece of PDMS is challenging due to significant refraction at the interface. To overcome this, we mixed dimethyl sulfoxide (DMSO) with ethanol in a 1:1 volume ratio, which produces a mixture with refractive index of 1.42, density of 0.9805 g/ml and viscosity of 0.978 mPa·s at 298.15 K50. The refractive index of the mixture is similar to that of PDMS (1.43) and enhances imaging by elimination refraction based dispersion51. The solution was shown to dissolve the polystyrene (PS) particles (Bangs Laboratories, Inc. USA) and Tygon tubing after prolonged immersion of 1 week. However, for the short duration of the experiments, the fluid mixture has no effect on both the particles and the tubings, making it an ideal replacement to water for the experiments.

Numerical simulation

The Dean flow field of the fluid in curved channel is simulated using commercial computational fluid dynamics (CFD) software COMSOL 4.2a (Burlington, MA). Curved micro-channel sections with different cross sectional geometries are modeled as a 120° arc with radius of 7.5 mm. The parameters of the density and the dynamic viscosity of the fluid in the channel section are set to that of water. The equations of laminar flow used in this simulation are given by ρ(u·∇)u = ∇·[−pI + μ(∇u + (∇u)T)] + F and ρ∇·u = 0, where the symbols follow the default definition in COMSOL. The physical model is set to be incompressible and non-turbulent. The inlet boundary condition is set with the specified flow rate while the outlet is set to zero pressure with no viscous stress condition. At channel walls, no slip boundary condition is applied. Typical flow rate from 1.0 mL/min to 8.0 mL/min are simulated to get the full solution for fluid flow at the steady state. Components of the flow velocity within the cross-section, i.e. the secondary Dean flows, are extracted at the center of the arc.

Author Contributions

G.G., L.W., J.H. & A.A.B. designed research, G.G. performed experiments, Z.L. & G.G. contributed to the simulation model. All authors analyzed the data and contributed to the manuscript.

Supplementary Material

Supplementary Information

Supplementary information

srep01475-s1.pdf (573.7KB, pdf)
Supplementary Information

Particle separation video

Download video file (4.5MB, avi)

Acknowledgments

This research was supported by the National Research Foundation Singapore, through the Singapore MIT Alliance for Research and Technology (SMART) Centre's BioSyM IRG research programme. This work is also supported by the financial support by DARPA DLT (Dialysis-Like Therapeutics) program, under SSC Pacific grant N66001-11-1-4182. Any opinions, findings, and conclusions or recommendations expressed in this publication are those of the authors and do not necessarily reflect the views of the DARPA. Guofeng Guan would also like to acknowledge the financial support in the form of a Research Scholarship from the National University of Singapore.

References

  1. Pamme N. Continuous flow separations in microfluidic devices. Lab on a chip 7, 1644–59 (2007). [DOI] [PubMed] [Google Scholar]
  2. Bhagat A. A. S. et al. Microfluidics for cell separation. Medical & biological engineering & computing 48, 999–1014 (2010). [DOI] [PubMed] [Google Scholar]
  3. Gossett D. R. et al. Label-free cell separation and sorting in microfluidic systems. Analytical and bioanalytical chemistry 397, 3249–67 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Petersson F., Aberg L., Swärd-Nilsson A.-M. & Laurell T. Free flow acoustophoresis: microfluidic-based mode of particle and cell separation. Analytical chemistry 79, 5117–23 (2007). [DOI] [PubMed] [Google Scholar]
  5. Yung C. W., Fiering J., Mueller A. J. & Ingber D. E. Micromagnetic-microfluidic blood cleansing device. Lab on a chip 9, 1171–7 (2009). [DOI] [PubMed] [Google Scholar]
  6. Yamada M., Nakashima M. & Seki M. Pinched flow fractionation: continuous size separation of particles utilizing a laminar flow profile in a pinched microchannel. Analytical chemistry 76, 5465–71 (2004). [DOI] [PubMed] [Google Scholar]
  7. Yamada M. & Seki M. Hydrodynamic filtration for on-chip particle concentration and classification utilizing microfluidics. Lab on a chip 5, 1233–9 (2005). [DOI] [PubMed] [Google Scholar]
  8. Ji H. M. et al. Silicon-based microfilters for whole blood cell separation. Biomedical microdevices 10, 251–7 (2008). [DOI] [PubMed] [Google Scholar]
  9. Wu Z., Willing B., Bjerketorp J., Jansson J. K. & Hjort K. Soft inertial microfluidics for high throughput separation of bacteria from human blood cells. Lab on a chip 9, 1193–9 (2009). [DOI] [PubMed] [Google Scholar]
  10. Tan S. J. et al. Versatile label free biochip for the detection of circulating tumor cells from peripheral blood in cancer patients. Biosensors & bioelectronics 26, 1701–5 (2010). [DOI] [PubMed] [Google Scholar]
  11. Nam J., Lim H., Kim D., Jung H. & Shin S. Continuous separation of microparticles in a microfluidic channel via the elasto-inertial effect of non-Newtonian fluid. Lab on a chip 12, 1347–54 (2012). [DOI] [PubMed] [Google Scholar]
  12. McFaul S. M., Lin B. K. & Ma H. Cell separation based on size and deformability using microfluidic funnel ratchets. Lab on a chip 12, 2369–76 (2012). [DOI] [PubMed] [Google Scholar]
  13. Jain A. & Munn L. L. Biomimetic postcapillary expansions for enhancing rare blood cell separation on a microfluidic chip. Lab on a chip 11, 2941–7 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Zheng S. et al. Membrane microfilter device for selective capture, electrolysis and genomic analysis of human circulating tumor cells. Journal of chromatography. A 1162, 154–61 (2007). [DOI] [PubMed] [Google Scholar]
  15. Wei H. et al. Particle sorting using a porous membrane in a microfluidic device. Lab on a chip 11, 238–45 (2011). [DOI] [PubMed] [Google Scholar]
  16. Schirhagl R., Fuereder I., Hall E. W., Medeiros B. C. & Zare R. N. Microfluidic purification and analysis of hematopoietic stem cells from bone marrow. Lab on a chip 11, 3130–5 (2011). [DOI] [PubMed] [Google Scholar]
  17. Huang L. R., Cox E. C., Austin R. H. & Sturm J. C. Continuous particle separation through deterministic lateral displacement. Science 304, 987–90 (2004). [DOI] [PubMed] [Google Scholar]
  18. Di Carlo D. Inertial microfluidics. Lab on a chip 9, 3038–46 (2009). [DOI] [PubMed] [Google Scholar]
  19. Green J. V., Radisic M. & Murthy S. K. Deterministic lateral displacement as a means to enrich large cells for tissue engineering. Analytical chemistry 81, 9178–82 (2009). [DOI] [PubMed] [Google Scholar]
  20. Davis J. A. et al. Deterministic hydrodynamics: taking blood apart. Proceedings of the National Academy of Sciences 103, 14779–84 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Mach A. J. & Di Carlo D. Continuous scalable blood filtration device using inertial microfluidics. Biotechnology and bioengineering 107, 302–11 (2010). [DOI] [PubMed] [Google Scholar]
  22. Mach A. J., Kim J. H., Arshi A., Hur S. C. & Di Carlo D. Automated cellular sample preparation using a Centrifuge-on-a-Chip. Lab on a chip 11, 2827–34 (2011). [DOI] [PubMed] [Google Scholar]
  23. Lee M. G., Bae C. Y., Choi S., Cho H. & Park J. High-Throughput Inertial Separation Of Cancer Cells From Human Whole Blood In A Contraction-Expansion Array Microchannel. Proceedings of MicroTAS 2065–2067 (2011). [Google Scholar]
  24. Kuntaegowdanahalli S. S., Bhagat A. A. S., Kumar G. & Papautsky I. Inertial microfluidics for continuous particle separation in spiral microchannels. Lab on a chip 9, 2973–80 (2009). [DOI] [PubMed] [Google Scholar]
  25. Lee M. G., Choi S. & Park J.-K. Inertial separation in a contraction-expansion array microchannel. Journal of chromatography. A 1218, 4138–43 (2011). [DOI] [PubMed] [Google Scholar]
  26. Seo J., Lean M. H. & Kole A. Membraneless microseparation by asymmetry in curvilinear laminar flows. Journal of chromatography. A 1162, 126–31 (2007). [DOI] [PubMed] [Google Scholar]
  27. Bhagat A. A. S., Kuntaegowdanahalli S. S. & Papautsky I. Continuous particle separation in spiral microchannels using Dean flows and differential migration. Lab on a chip 8, 1906–14 (2008). [DOI] [PubMed] [Google Scholar]
  28. Bhagat A. A. S., Kuntaegowdanahalli S. S., Kaval N., Seliskar C. J. & Papautsky I. Inertial microfluidics for sheath-less high-throughput flow cytometry. Biomedical microdevices 12, 187–95 (2010). [DOI] [PubMed] [Google Scholar]
  29. Seo J., Lean M. H. & Kole A. Membrane-free microfiltration by asymmetric inertial migration. Applied Physics Letters 91, 033901 (2007). [Google Scholar]
  30. El Hasni A. et al. Focusing and Sorting of Particles in Spiral Microfluidic Channels. Procedia Engineering 25, 1197–1200 (2011). [Google Scholar]
  31. Nivedita N., Giridhar P. V., Kasper S. & Papautsky I. Sorting Human Prostate Epithelial (HPET) Cells In An Inertial Microfluidic Device. Proceedings of MicroTAS 1230–1232 (2011). [Google Scholar]
  32. Martel J. M. & Toner M. Inertial focusing dynamics in spiral microchannels. Physics of Fluids 24, 032001 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Ookawara S., Street D. & Ogawa K. Numerical study on development of particle concentration profiles in a curved microchannel. Chemical Engineering Science 61, 3714–3724 (2006). [Google Scholar]
  34. Ookawara S., Oozeki N., Ogawa K., Löb P. & Hessel V. Process intensification of particle separation by lift force in arc microchannel with bifurcation. Chemical Engineering and Processing: Process Intensification 49, 697–703 (2010). [Google Scholar]
  35. Russom A. et al. Differential inertial focusing of particles in curved low–aspect-ratio microchannels. New journal of physics 11, 75025 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Sun J. et al. Double spiral microchannel for label-free tumor cell separation and enrichment. Lab on a chip 12, 3952–60 (2012). [DOI] [PubMed] [Google Scholar]
  37. Yang B. H. et al. Migration of a sphere in tube flow. Journal of Fluid Mechanics 540, 109–131 (2005). [Google Scholar]
  38. Prohm C., Gierlak M. & Stark H. Inertial microfluidics with multi-particle collision dynamics. The European physical journal. E, Soft matter 35, 9757 (2012). [DOI] [PubMed] [Google Scholar]
  39. Bhagat A. A. S., Kuntaegowdanahalli S. S. & Papautsky I. Inertial microfluidics for continuous particle filtration and extraction. Micro fluidics and Nano fluidics 7, 217–226 (2008). [Google Scholar]
  40. Choi Y., Seo K. & Lee S. Lateral and cross-lateral focusing of spherical particles in a square microchannel. Lab on a chip 11, 460–5 (2011). [DOI] [PubMed] [Google Scholar]
  41. Tanaka T. et al. Inertial migration of cancer cells in blood flow in microchannels. Biomedical microdevices 14, 25–33 (2012). [DOI] [PubMed] [Google Scholar]
  42. Lee W. C. et al. High-throughput cell cycle synchronization using inertial forces in spiral microchannels. Lab on a chip 11, 1359–67 (2011). [DOI] [PubMed] [Google Scholar]
  43. Hur S. C., Choi S.-E., Kwon S. & Di Carlo D. Inertial focusing of non-spherical microparticles. Applied Physics Letters 99, 044101 (2011). [Google Scholar]
  44. Hur S. C., Henderson-MacLennan N. K., McCabe E. R. B. & Di Carlo D. Deformability-based cell classification and enrichment using inertial microfluidics. Lab on a Chip 11,912–920 (2011). [DOI] [PubMed] [Google Scholar]
  45. Wu L., Guan G., Hou H. W., Bhagat A. A. S. & Han J. Separation of leukocytes from blood using spiral channel with trapezoid cross-section. Analytical chemistry 84, 9324–31 (2012). [DOI] [PubMed] [Google Scholar]
  46. Di Carlo D., Edd J., Humphry K., Stone H. & Toner M. Particle Segregation and Dynamics in Confined Flows. Physical Review Letters 102, 1–4 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Joseph D. D., Ocando D. & Huang P. Y. Slip velocity and lift. Journal of Fluid Mechanics 454, 263–286 (2002). [Google Scholar]
  48. Amini H. & Sollier E. Intrinsic particle-induced lateral transport in microchannels. Proceedings of the National Academy of Sciences 109, 11593–8 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Di Carlo D., Irimia D., Tompkins R. G. & Toner M. Continuous inertial focusing, ordering, and separation of particles in microchannels. Proceedings of the National Academy of Sciences of the United States of America 104, 18892–7 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Nikam P. S. et al. Density and Viscosity of Mixtures of Dimethyl Sulfoxide + Methanol, +Ethanol, +Propan-1-ol, +Propan-2-ol, +Butan-1-ol, +2-Methylpropan-1-ol, and +2-Methylpropan-2-ol at 298.15 K and 303.15 K. Journal of Chemical & Engineering Data 2, 1028–1031 (1996). [Google Scholar]
  51. Cardenas-Valencia A. M., Dlutowski J., Fries D. & Langebrake L. Spectrometric determination of the refractive index of optical wave guiding materials used in lab-on-a-chip applications. Applied spectroscopy 60, 322–9 (2006). [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary information

srep01475-s1.pdf (573.7KB, pdf)
Supplementary Information

Particle separation video

Download video file (4.5MB, avi)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES