Case–sibling studies that acknowledge unstudied parents and permit the inclusion of unmatched individuals

Abstract

Background Family-based designs enable assessment of genetic associations without bias from population stratification. When parents are not readily available — especially for diseases with onset later in life — the case-sibling design, where each case is matched with one or more unaffected siblings, is useful. Analysis typically accounts for within-family dependencies by using conditional logistic regression (CLR).

Methods We consider an alternative to CLR that treats each case-sibling set as a nuclear family with both parents missing by design. One can carry out maximum likelihood analysis by using the Expectation-Maximization (EM) algorithm to account for missing parental genotypes. We compare conditional logistic regression and the missing-parents approach under several risk scenarios.

Results We show that the missing-parents approach improves power when some families have more than one unaffected sibling and that under weak assumptions the approach permits the incorporation of supplemental cases who have no sibling available and supplemental controls whose case sibling is unavailable (e.g., due to disability or death).

Conclusion The missing-parents approach offers both improved statistical efficiency and asymptotically unbiased estimation for genotype relative risks and genotype-by-exposure interaction parameters.

Introduction

Nuclear families can be used to study contributions of genetic variants to complex diseases. One can estimate genotype-relative risks by using cases and their parents and be protected against biases caused by population stratification^1–3 and self-selection. One can also use nuclear families to probe for maternally mediated genetic effects⁴ and parent-of-origin effects.³ Case-parent studies, however, are inappropriate for diseases with onset in later life when parents are selectively available.

For late-onset diseases, siblings can serve instead of parents. Case–sibling studies are typically analyzed through conditional logistic regression (CLR), using cases with at least one participating unaffected sibling. We describe an alternative approach that treats case-sibling data as nuclear family data with parents missing by design. This basic idea has been used for studying genetic main effects^5–10 and is implemented in some software.^9,10 However, it has remained uncertain whether the missing-parents approach is more efficient than traditional CLR. We assess the relative efficiency of the case–sibling and missing-parent approaches and propose that another advantage of the missing-parents approach is that it can allow both the inclusion of cases that lack a sibling control and sets of sibling controls that had a sibling case but cannot provide it, e.g. because of disability, death, or therapeutic abortion. We explore implications for power and unbiased estimation of including those unmatched subjects. We also extend the missing-parents approach to testing exposure effects and multiplicative gene-by-exposure interaction.

Methods

Determination of likelihoods

Suppose we ascertain sibships that consist of a single case subject with genotype G_C and a set of k control (unaffected) siblings with genotypes G_0i (i = 1, 2, … k) at a diallelic locus of interest. The variant under study could either be causative itself or be a marker in linkage disequilibrium with a causative variant. Further suppose that a logistic model describes the association of risk with genotype. (For a marker related to risk only through linkage disequilibrium with a causative variant, this model, although mis-specified in general, is correct under the null hypothesis, so that hypothesis testing is valid.) For scenarios without exposure effects or multiplicative gene-by-exposure interaction effects, the sibship’s contribution to the CLR likelihood is:

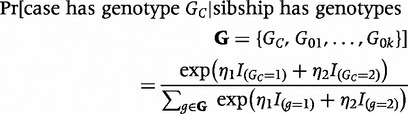(1)

Here, η_i represents the logarithm of the odds ratio for carriers of i copies of the variant allele (i.e. G_C = i) as compared with carriers of zero copies.

If, instead of data from control siblings, we had data from parents, we could fit either a log-linear model³ or, equivalently, a ‘pseudo-sibling’ model¹¹ that imposes Mendelian inheritance and considers all offspring that a given parental pair could have produced. Under the pseudo-sibling approach, the likelihood contribution from a nuclear family in which the mother’s genotype is G_M and father’s genotype G_F is:

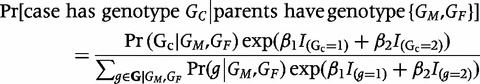(2)

Here, β_i represents the logarithm of the relative risk for carriers of i copies of the variant allele (i.e. G_C = i) as compared with the risk for carriers of zero copies, 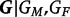denotes the set of possible offspring from parents with genotypes 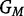and 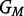, and the Mendelian genotype probabilities, Pr(g|G_M,G_F), are known. Inference on β₁ and β₂ using this likelihood is equivalent to that based on a log-linear Poisson model.³ For a rare disease, η_i in model 1 approximates β_i in model 2.

If, in addition to genotypes, exposure data are available, one can test for exposure effects and gene-by-exposure interaction (making the assumption that the genetic variant is causative when specifically testing gene-by-exposure interaction¹²). We used the approach proposed by Chatterjee et al.,¹³ which enhances power by enforcing within-family gene-by-exposure independence in the conditional likelihood. Let E_C denote the exposure of the case and E_0i (i = 1, 2, … k) denote the exposures of the control siblings. The likelihood contribution of a single sibship under the CLR model is:

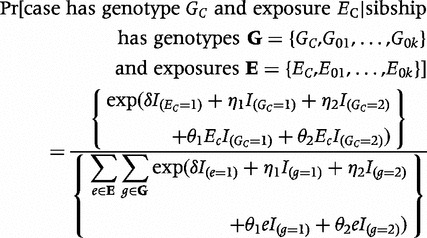(3)

Here, δ represents the logarithm of the odds ratio for the exposed as compared with the unexposed state, and θ₁, θ₂ represent odds-ratio–based multiplicative interaction parameters.

Imagine that we had genotypes from parents, genotype and exposure data from the case, and exposures (but no genotypes) from siblings (under a rare-disease assumption, genotypes of siblings provide no extra information once parental genotypes are known). We could then fit a pseudo-sibling model¹¹ that considers all possible offspring that a given pair of parents could have produced and all possible assignments of the observed exposures to those offspring. The likelihood contribution from a nuclear family under that pseudo-sibling model is:

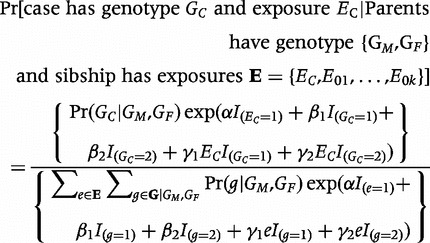(4)

Here, α represents the logarithm of the exposure relative risk and γ₁,γ₂ represent relative-risk-based interaction parameters. The derivation of this likelihood that includes unaffected control siblings requires a rare-disease assumption.⁸ For a rare disease, the parameters in model 3 correspond to the parameters in model 4.

The likelihood in model 4 differs from the pseudo-sibling likelihood described by Cordell et al.¹⁴ for examining multiplicative gene-by-exposure interactions with case–parents triads because it uses the exposures of unaffected siblings. This extra information allows estimation/testing of exposure effects, which cannot be done with case–parents triads alone. For case–parents triads, however, a log-linear model including multiplicative gene-by-exposure interactions¹⁵ provides a likelihood equivalent to the pseudo-sibling likelihood of Cordell et al.¹⁴ Consequently, under a rare-disease assumption, there is a log-linear model that provides a likelihood equivalent to the pseudo-sibling likelihood in model 4, provided exposure is categorical.

When parents are missing but unaffected siblings are genotyped, each family’s contribution to the observed-data pseudo-sibling log-likelihood is a weighted average of model 2 or of model 4 over possible families with parental genotypes compatible with those of the observed offspring genotypes. Even when all parents are missing by design, as in a case-sibling design, the family-based likelihood can be maximized by using the EM algorithm.¹⁶ Under such a design, a complete-data log-linear model, equivalent to the corresponding pseudo-sibling model, makes implementation of the EM algorithm¹⁷ straightforward.

Assumptions

We ascertain sibships known to have exactly one case sibling. Our analyses make the usual assumption for fine-matched case–control studies: given that a family has been sampled, we assume that any missing values of genotype and exposure (e.g. non-participation of siblings) are missing at random. For example, if the allele under study were causally related to survival (and hence participation) among cases, estimates of genetic effects would be biased. When the number of participants varies across families, the missing-parents approach, but not CLR, requires that the number of participating cases and control siblings, given that that family is sampled, provides no information about the unobserved parental genotypes. Without this assumption, inference could be biased when genetic population structure is present if, for example, allele frequency in subpopulations is related to the size of participating sibships from those subpopulations. For assessment of gene-by-environment interaction, both the missing-parents approach and the Chatterjee version of the CLR approach¹³ assume that genotype and exposure are independent within sibships. When exposure-related population stratification is present and interactions are assessed, both the missing-parents approach and CLR require either effective genomic control or that the single-nucleotide polymorphism (SNP) be itself causative and not in linkage disequilibrium with another causative SNP.¹² Under the assumptions made above, the missing-parents approach can validly incorporate data from unmatched subjects into the likelihood, whereas CLR typically cannot.

Missing-indicator approach

For data containing unmatched subjects, we compared the performance of the missing-parents approach with that of the missing-indicator method proposed by Huberman and Langholz.¹⁸ The missing-indicator method is a clever strategy that enables one to apply conditional logistic regression to analyze data that include matched pairs together with both some unmatched cases and some unmatched controls. Briefly, the analyzed data set is augmented by including pseudo-subjects that provide matched counterparts having opposite disease status for any unmatched actual subjects. Thus, for each unmatched case, the analyst constructs a pseudo-control, and for each unmatched set of control siblings the analyst constructs a pseudo-case. All covariates (genotype and exposure in our context) for these pseudo-subjects are set to zero, i.e. the referent coding. An indicator variable (0 for pseudo-subjects, 1 otherwise) is included as one of the covariates in the CLR model. This construction makes the contribution by the unmatched individuals to the conditional likelihood the same as their contribution to the likelihood for an unmatched analysis, thereby allowing the use of standard software for conditional logistic regression for analysis of all subjects together. One subtle problem with this approach was pointed out by Huberman and Langholz: the parameter being estimated is neither the stratum-specific sibling-based odds ratio nor the (typically somewhat attenuated) marginal population-based parameter. Under our proposed missing parents approach, the usual sibling-based odds ratio is estimated, so that the inference has a more straightforward parameter interpretation.

Type I error rate and power calculations

We studied type I error rate and power by calculating the non-centrality parameter (NCP) for the distribution of a chi-squared likelihood ratio test statistic (two-degree-of-freedom (df) tests for genetic or interaction effects, one-df tests for exposure effects). An NCP of 0 under the null hypothesis means that the test statistic approximately follows a central chi-squared distribution, which ensures the nominal type I error rate. Non-zero NCPs can be translated to statistical power as the tail probability for the corresponding non-central chi-squared distribution. The efficiency of the missing-parents approach relative to CLR is given by the ratio of their NCPs (which equals the reciprocal of the ratio of the sample sizes required to achieve any particular power). For one-df tests, the square root of that same ratio corresponds to the large sample ratio of the standard errors for the corresponding parameter estimates (i.e. the relative lengths of confidence intervals), so that relative efficiency also measures relative precision.

Calculation of the NCP begins by specifying a population structure including allele frequency and exposure prevalence, and a risk model. This information is used to calculate expected counts, i.e., the expected number of sibships with each possible configuration of genotypes and exposures. The relevant models are fitted by using the expected counts as data. The change in deviance (twice the maximized log likelihood) between the full and reduced models fitted to the expected counts gives the NCP for the corresponding likelihood ratio test.¹⁹ We fitted our models with LEM²⁰ software (LEM scripts available at http://www.niehs.nih.gov/research/resources/software/biostatistics/lem_scripts/index.cfm)

In calculating the expected counts, we assumed a rare disease and a log-linear model for risk. We considered a study of 300 sibships, each with one case sibling and one (or more) control sibling(s). To calculate the statistical power for any number of sibships, e.g. n, one can multiply our NCPs by n/300 and look up the corresponding tail probabilities for a non-central chi-squared distribution.

For tests of genetic effects, we considered a null scenario with (R₁, R₂) = (e^β₁, e^β₂) set at (1, 1). To explore robustness to genetic population stratification, we assumed a population with two subpopulations of equal size. The ratio of baseline disease risks (risk in population members with no copies of the allele under study) in the two subpopulations was 3:1, and the allele frequency in one population was p and in the other was 1 − p, with p ranging from 0.1 to 0.7. For tests of gene-by-exposure interaction, we assumed that the SNP was causative and simulated exposure-related population stratification¹²: both allele frequency and exposure frequency were p in one population and 1 − p in the other, with p ranging from 0.1 to 0.7. We considered an interaction-null scenario with (R₁, R₂) set at (1, 2), R_E = e^α set at 1.5 and (I₁, I₂) = (e^γ₁, e^γ₂) set at (1, 1).

When studying power, we assumed that the SNP under study was in Hardy–Weinberg equilibrium in the population (which is convenient for calculating expected counts but not needed for validity). For tests of genetic effects, the allele frequency ranged from 0.1 to 0.7. We examined three risk scenarios, with (R₁, R₂) set at (2, 2), (1, 3), and (1.5, 2.25), respectively. For tests of gene-by-exposure interactions, we allowed either the allele frequency or the exposure frequency to range from 0.1 to 0.7, with the other frequency set at 0.3. We modified our interaction-null scenario by setting (I₁, I₂) to (2, 2). For tests of exposure effects, we used the interaction-null scenario, assigned exposure status to siblings independently, and fitted a model with genetic and exposure effects only.

We evaluated the power gains provided by including supplemental singleton cases or supplemental sets of controls in the following scenarios: (i) 150 supplemental cases; (ii) 150 supplemental sets of controls (control siblings whose case sibling was unavailable; for a 1:k matched design, we added sets of k controls without a matched case); and (iii) 75 supplemental cases and 75 supplemental sets of controls. Both genotypes and exposures were ascertained for supplemental subjects.

Results

As with CLR, the missing-parents analysis maintained the correct type I error rates both for tests of genetic effect and for tests of gene-by-exposure interaction under population stratification with or without supplemental subjects. In all scenarios, the NCPs were 0, implying a correct type I error rate.

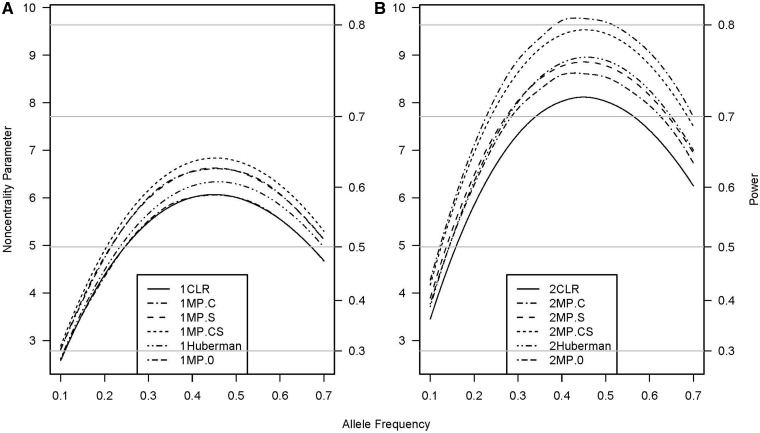
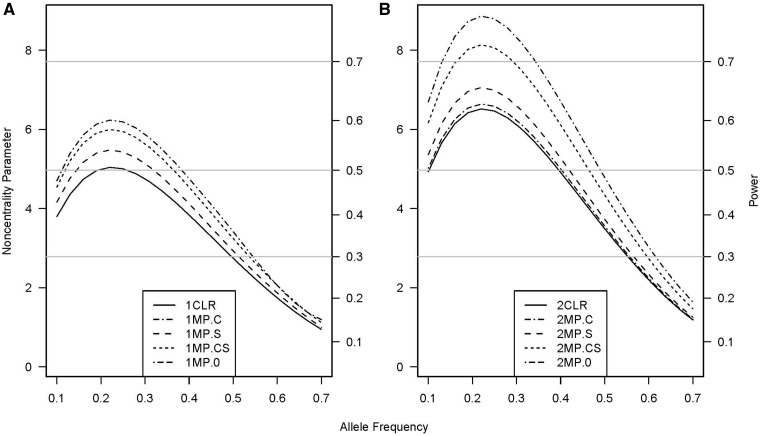
The power of the missing-parents approach and that of the sibship-based CLR were almost identical for both the genetic-effect test (Figure 1A and Supplementary figures S1A and S2A, available as Supplementary data at IJE online) and the interaction test (Figure 2A and Supplementary figure S3A, available as Supplementary data at IJE online) when each case had one matched control. The missing-parents approach showed a power advantage over CLR (i.e. the relative efficiency with the missing-parents approach always exceeded 1.0) when two or more control siblings were available, although the power advantage was higher for testing genetic effects (Figure 1B and Supplementary figures S1B and S2B, available as Supplementary data at IJE online) than for testing gene-by-exposure interactions (Figure 2B and Supplementary figure S3B, available as Supplementary data at IJE online). For tests of exposure effects without supplemental subjects, the CLR and missing-parents approaches provided the same power regardless of the number of unaffected siblings in each approach (data not shown).

Figure 1.

Non-centrality parameter and power for tests of genetic effects as a function of allele frequency. All designs used 300 sibships with one (panel A) or two control siblings (panel B); some designs included supplemental unmatched subjects. The relative risks are R₁ = 1.5 and R₂ = 2.25. Vertical axes: left, the chi-squared non-centrality parameter for a 2-df likelihood-ratio test; right, power at α = .05 (horizontal lines mark selected power levels). The 1 and 2 before the abbreviations represent 1 and 2 control siblings per case, respectively. Curves: solid (CLR), with or without supplemental subjects analyzed with conditional logistic regression (CLR does not use unmatched subjects and the power is therefore the same for scenarios with or without supplemental subjects); dash-dot (MP.C), 150 supplemental cases analyzed with the missing-parents approach; long-dash (MP.S), 150 supplemental sets of controls analyzed with the missing-parents approach; short-dash (MP.CS) (concealed under the dash-dot curve in panel A), 75 supplemental cases and 75 supplemental sets of controls analyzed with the missing-parents approach; dash-dot-dot (Huberman), 75 supplemental cases and 75 supplemental sets of controls analyzed with the missing-indicator method proposed by Huberman and Langholz¹⁸; and dash-dash-dot (MP.0), no supplemental subjects analyzed with the missing-parents approach (concealed under the solid curve in panel A)

Figure 2.

Non-centrality parameter and power for tests of multiplicative genetic-by-exposure interaction effects as a function of allele frequency. All designs used 300 sibships with one (panel A) or two control siblings (panel B); some designs included supplemental unmatched subjects. The risk parameters are: R₁ = 1, R₂ = 2, R_E = 1.5, I₂ = 2, and I₂ = 2. Exposure prevalence was 0.3. Vertical axes: left, the chi-squared non-centrality parameter for a 2-df likelihood-ratio test; right, power at α = 0.05 (horizontal lines mark selected power levels). The 1 and 2 before the abbreviations represent 1 and 2 control siblings per case, respectively. Curves: solid (CLR), with or without supplemental subjects analyzed with conditional logistic regression (CLR does not use unmatched subjects and the power is therefore the same for scenarios with or without supplemental subjects); dash-dot (MP.C), 150 supplemental cases analyzed with the missing-parents approach; long-dash (MP.S), 150 supplemental sets of controls analyzed with the missing-parents approach; short-dash (MP.CS), 75 supplemental cases and 75 supplemental sets of controls analyzed with the missing-parents approach; and dash-dash-dot (MP.0), no supplemental subjects analyzed with the missing-parents approach (concealed under the solid curve in panel A)

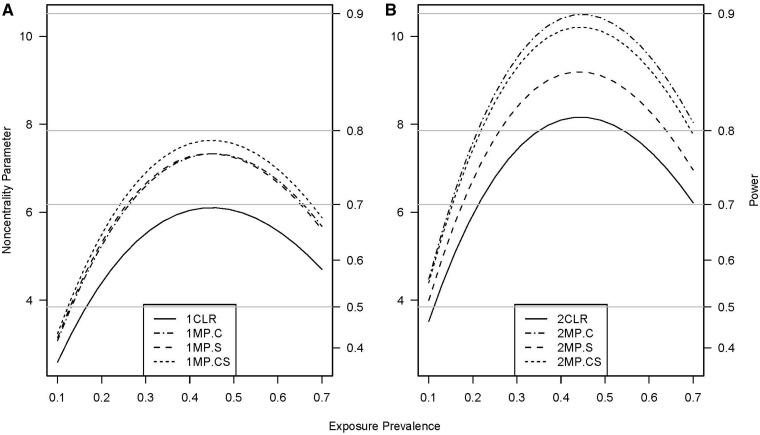
The ability of the missing-parents approach, unlike CLR, to make use of data from unmatched participants, and thereby incorporate a larger sample size, provides an increase in efficiency for assessing genetic, environmental, and interaction effects in a sibship-based design. With additional supplemental subjects included, the power of the missing-parents approach improves over that of the CLR approach for genetic-effects tests (Figure 1 and Supplementary figures S1 and S2, available as Supplementary data at IJE online), interaction tests (Figure 2 and Supplementary figure S3, available as Supplementary data at IJE online), and exposure-effect tests (Figure 3). With 150 supplemental singleton cases, the maximum relative efficiency for genetic effects was 122% and 134% for designs with one (Figure 1A) and two control siblings (Figure 1B), respectively. The corresponding maximum relative efficiency was 115% and 115% with 150 additional supplemental sets of controls, and 122% and 126% with 75 singleton cases and 75 sets of controls. The missing-parents approach was more powerful than the missing-indicator method, with maximum relative efficiency of 110% and 114% for designs with one and two control siblings, respectively. Additionally the missing-parents method can provide unbiased relative-risk estimates, whereas estimates under the missing-indicator method are known to be biased¹⁸ and were biased in our study (data not shown).

Figure 3.

Non-centrality parameter and power for tests of exposure effects as a function of exposure prevalence. All designs used 300 sibships one (panel A) or two control siblings (panel B); some designs included supplemental subjects. The risk scenario is: R₁ = 1, R₂ = 2, R_E = 1.5, I₂ = 1, and I₂ = 1. Allele frequency was 0.3. Vertical axes: left, the chi-squared non-centrality parameter for a 1-df likelihood-ratio test; right, power at α = 0.05 (horizontal lines mark common power levels). The 1 and 2 before the abbreviations of the designs in each figure represent 1 and 2 control siblings per case, respectively. Curves: solid (CLR), analyzed with conditional logistic regression (CLR does not use unmatched subjects and the power is therefore the same for scenarios with or without supplemental subjects); dash-dot (MP.C), 150 supplemental cases analyzed with the missing-parents approach; long-dash (MP.S), 150 supplemental sets of controls analyzed with the missing-parents approach; and short-dash(MP.CS), 75 supplemental cases and 75 supplemental sets of controls analyzed with the missing-parents approach. In panel (A), the dash-dot and long-dash curves coincide

For gene-by-exposure interactions, inclusion of 150 supplemental cases in scenarios with one (Figure 2A) or two (Figure 2B) control siblings markedly increased relative efficiency. The power advantage gained by the inclusion of 150 supplemental sets of controls was modest regardless of the number of control siblings per case. The power improvement by supplementing with 75 singleton cases and 75 sets of controls was between those for the design that included 150 supplemental cases and the design that included 150 supplemental sets of controls.

For exposure effects, the inclusion of supplemental subjects always increased power (Figure 3). When the matched design had one control sibling per case, the inclusion of 75 case singletons and 75 control singletons provided a greater power advantage than the inclusion of either 150 case singletons or 150 control singletons. When the matched design had two or more control siblings per case, the inclusion only of case singletons provided greater power than the inclusion only of sets of controls or of equal numbers of supplemental cases and sets of controls. The relative efficiency of including 150 supplemental sets of controls decreased as the number of matched controls per case increased.

Example: Association between rs680331 and oral clefts

To construct an illustrative example, we used data from a candidate-gene study of the birth defect of oral clefts.²¹ The original study recruited case-parents triads from two Scandinavian populations, those of Denmark and Norway, respectively, to investigate the association between SNPs in 375 candidate genes and oral clefts. We focus here on the association between rs680331 in the 3’ untranslated region (3’UTR) of the gene for interferon regulatory factor 6 (IRF6), a top hit in the original study,²¹ and oral clefts. For each of the 696 complete triad families, we generated genotypes for two hypothetical siblings, both unaffected, on the basis of the family’s observed parental genotypes by assuming Mendelian inheritance and a rare phenotype, thereby creating 696 sibships with one case and two controls. We randomly selected 522 (75%) of these sibships to serve as the core data. We also augmented this core data by including in turn 174 cases, or 174 control-sibling pairs, or 87 cases plus 87 unrelated control-sibling pairs. We analyzed the last scenario by using the missing-indicator approach and all four data sets with CLR and the missing-parents approach. Each of these data sets and approaches revealed an association of clefts with rs680331 (Table 1). In addition, the comparisons seen in our NCP calculations are largely recapitulated in this example: the missing-parents approach yielded a larger chi-squared statistic than did CLR with the core data, and the inclusion of unmatched subjects further enhanced the power and precision of this approach.

Table 1.

Association of SNP rs680331 with oral clefts in a Scandanavian sample^a

Sample	Analysis	R1 (95% CI)	R2 (95% CI)	χ2
522 complete triads	Log-linear	1.42 (1.12, 1.82)	1.70 (1.08, 2.70)	9.72
522 sibships	CLR	1.52 (1.12, 2.06)	2.00 (1.12, 3.59)	9.41
522 sibships	Missing-parents	1.52 (1.14, 2.03)	2.05 (1.17, 3.61)	10.40
522 sibships + 174 cases	Missing-parents	1.58 (1.20, 2.07)	1.97 (1.14, 3.39)	12.27
522 sibships + 174 control sibpairs	Missing-parents	1.50 (1.13, 1.99)	2.04 (1.17, 3.57)	10.16
522 sibships + 87 cases + 87 control sibpairs	Missing-parents	1.53 (1.16, 2.02)	2.07 (1.20, 3.55)	11.50
522 sibships + 87 cases + 87 control sibpairs	Missing-Indicator	1.45 (1.11, 1.90)	1.83 (1.11, 3.03)	9.69

^aThe additional cases and additional control sibpairs are unmatched. CI, confidence interval.

Discussion

In case–mother/control–mother studies,²² accounting for the actual family relationship markedly improves statistical power as compared with accounting for dependencies generically. We wanted to see whether it would be possible to analogously strengthen the analysis of case–sibling studies of a rare disease while retaining robustness to population structure by assuming Mendelianism in the population and maximizing the missing-parents likelihood via the expectation-maximization (EM) algorithm.¹⁶

Our power calculations showed that such a missing-parents analysis, although having the same power as CLR for disease-discordant sib pairs, does increase the power for testing for genetic effects when using two or more unaffected siblings and no supplemental subjects. By contrast, the increase in power from using two unaffected siblings instead of one was negligible for testing gene-by-exposure interaction, and there was no increase in power for testing exposure effects.

Although our power calculations assumed Hardy–Weinberg equilibrium, the missing-parents approach will show similar power advantages more generally because the method exploits two sources of added information unavailable to CLR: Mendelian inheritance and the possible inclusion of unmatched subjects. We show power for scenarios in which exposure-related population stratification is present in an online supplement (Supplementary figure S4, available as Supplementary data at IJE online).

The missing-parents approach also allows straightforward incorporation of unrelated singleton cases (for which a sibling may not be available) and sets of sibling controls into a case–sibling analysis while retaining unbiased estimation of genotype relative-risk and interaction parameters. The inclusion of supplemental subjects, with each providing genotype and exposure data, increases the power of this approach for all parameters of interest. Analysis that includes supplemental subjects retains robustness to bias from population stratification, under the assumption that among families in the sample, the occurrence of an unmatched case or of an unmatched set of unaffected siblings has no relationship to the unobserved parental genotypes. Ideally, as with other family-based analyses that use unrelated cases or controls (e.g. Epstein et al.²³), this assumption should be verified. Unfortunately, we see no powerful way to check this assumption formally with the data at hand and suggest reliance on informal checks instead. For example, one could compare relative risk estimates for analyses with and without the supplemental subjects, or compare the joint genotype/exposure distribution of unmatched cases and that of cases with siblings.

Occasionally, multiple control siblings are available with little added effort, such as when families affected by a condition have contributed deoxyribonucleic acid (DNA) to a biorepository. As the number of unaffected siblings per family grows, the relative efficiency of the missing-parents analysis will increase and approach what would have been achieved with a case-parents design.²⁴ In fact, under a rare-disease assumption and Mendelian inheritance, a case–parents design should be equivalent to a case–sibling study with infinitely many siblings, so that genotyping unaffected siblings confers benefit only when one or both parental genotypes are unknown.

When the number of participating siblings differs among families in a structured population, the missing-parents approach is unbiased only if the size of available sibships is non-informative about parental genotypes. To determine whether this is the case, one could conduct a missing-parents analysis allowing separate sets of parental mating-type parameters for sibships of different sizes. This approach, however, faces practical difficulties in model fitting as the number of mating-type parameters increases. Alternatively, one could fall back on CLR, which does not require that assumption.

The missing-data methods that we have described are well suited to the typical diverse array of family structures in a population. In practice, some families will contribute only an affected individual, others may have only an unaffected sibling (e.g. if the affected sibling did not survive), others may have the case and one or more unaffected siblings as well, and still others have one or both parents. Genotyping parents is often cost-effective, especially for conditions with an onset early in life. Parents offer both improvement in study efficiency and the opportunity to examine mechanisms such as effects of the maternal genotype that act before birth⁴ and parent-of-origin effects.²⁵ In families in which parents are genotyped, the genotyping of unaffected siblings adds no information about genetic effects, but knowing these siblings’ exposures contributes information about exposure and interaction effects.^12,26

The use of multiple unaffected siblings raises some issues related to linkage-induced correlations if one regards CLR, like the sib-transmission/disequilibrium test (sib-TDT),²⁷ as assessing association in the presence of possible linkage. In this context inference is strictly valid only for sibships with one case and one control, because when linkage is present, siblings with the same disease status will tend to share marker alleles, inducing dependency. Strictly speaking, such dependency invalidates both the missing-parents method and CLR. Various approaches that accommodate multiple affected and unaffected siblings are available.^8,28,29 In principle, as proposed by Siegmund et al.,³⁰ linkage-induced correlation can also be addressed by using a robust sandwich variance estimator in Wald tests of genetic effects. A re-sampling method could also be used.²⁹ The simulations of Siegmund et al. indicated, however, that the standard test performed adequately in most situations.³⁰

Alternately, most epidemiologists would probably consider the null hypothesis of interest to be no linkage and no association, i.e., a null hypothesis in which, conditional on the parents, the allele under consideration is completely unrelated to risk of the outcome. For that null hypothesis, either the missing-parents approach or CLR is valid with multiple siblings. However, after that null hypothesis has been rejected at a particular locus and one desires to estimate the relative risk of the non-null genotype and its standard error, those two methods do not yield strictly valid estimation if the association detected is due not to the SNP itself, but to its linkage with some unmeasured causative SNP. In such a situation, one of the alternative methods already mentioned could be used.

Both the case–sibling and the case–parents designs test and estimate gene-exposure interactions validly if the SNP under study is a disease-causing mutation that is not in linkage disequilibrium with another causative locus. If, instead, a marker in linkage disequilibrium with the risk-inducing variant is studied, an analysis of interaction effects that is robust to bias from exposure-related population stratification requires an approach that differs from the usual approaches.^12,26 A robust analysis of interaction, known as a sibling-augmented case-only (SACO) analysis, uses case and sibling exposures but only case genotypes.²⁶ Because it does not use parental or sibling genotypes, the SACO approach cannot be improved by enforcing Mendelian inheritance as the missing-parents approach does. On the other hand, testing genetic-effects and gene-by-exposure interactions jointly, as advocated by Kraft et al.,³¹ is robust even for marker SNPs without a SACO analysis, provided the corresponding null model (exposure effects only) is correctly specified.

The strategy that regards parental genotypes as missing when analyzing sibship data works well for single causative SNPs but becomes computationally daunting if applied to haplotype analyses of unphased multiple-marker data. In this latter case the chief problem is that phase ambiguity vastly increases the number of possible paired parental diplotypes that must be taken into account. Recently, Dudbridge et al.¹⁰ proposed an alternative to conditioning on parental diplotypes; this instead involves conditioning only on alleles transmitted into the sibship, greatly reducing the computational burden of such missing-data analyses while incurring little cost in power.

In conclusion, analyses of case–sibling studies that regard each sibship as a nuclear family with missing parental genotypes and use appropriate missing-data techniques to derive maximum-likelihood estimates for risk parameters offer power advantages for testing genetic-effects or gene-by-exposure interactions. These advantages accrue when some families have more than one unaffected sibling or when supplemental subjects can be included.

Supplementary Data

Supplementary Data are available at IJE online.

Funding

This research was supported by the Intramural Research Program of the NIH, National Institute of Environmental Health Sciences, under project numbers Z01 ES040007 and Z01 ES045002.