Dependency of image quality on system configuration parameters in a stationary digital breast tomosynthesis system

Abstract

Purpose: In principle, a stationary digital breast tomosynthesis (s-DBT) system has better image quality when compared to continuous motion DBT systems due to zero motion blur of the source. The authors have developed a s-DBT system by using a linear carbon nanotube x-ray source array. The purpose of the current study was to quantitatively evaluate the performance of the s-DBT system; and investigate the dependence of imaging quality on the system configuration parameters.

Methods: Physical phantoms were used to assess the image quality of each configuration including inplane resolution as measured by the modulation transfer function (MTF), inplane contrast as measured by the signal difference to noise ratio (SdNR), and depth resolution as measured by the z-axis artifact spread function. Five parameters were varied to create five groups of configurations: (1) total angular span; (2) total number of projection images; (3) distribution of exposure (mAs) across the projection images; (4) entrance dose; (5) detector pixel size.

Results: It was found that the z-axis depth resolution increased with the total angular span but was insensitive to the number of projection images, mAs distribution, entrance dose, and detector pixel size. The SdNR was not affected by the angular span or the number of projection images. A decrease in SdNR was observed when the mAs was not evenly distributed across the projection images. As expected, the SdNR increased with entrance dose and when larger pixel sizes were used. For a given detector pixel size, the inplane resolution was found to be insensitive to the total angular span, number of projection images, mAs distribution, and entrance dose. A 25% increase in the MTF was observed when the detector was operating in full resolution mode (70 μm pixel size) compared to 2 × 2 binned mode (140 μm pixel size).

Conclusions: The results suggest that the optimal imaging configuration for a s-DBT system is a large angular span, an intermittent number of projection views, and a uniform mAs distribution over all views. With the detector operating at full resolution, a stationary DBT system can achieve an inplane resolution of 5.1 cycles per mm, which is significantly better than continuous motion DBT systems.

INTRODUCTION

Breast cancer is the most common type of cancer found in women in the United States, with more than 200 000 new cases found each year.¹ When the cancer is diagnosed at an early stage, the five-year relative survival rate is between 83.9% and 98.4%. This number drops to 23.8% when the cancer is diagnosed at a stage at which it has already metastasized.¹ Screening mammography is the current gold standard for early detection of breast cancer.^{2, 3} However, 2D mammography imaging lacks depth information, which can cause underlying and overlying tissue to obstruct the view of lesions. This leads to high false positive and false negative rates.^{4, 5} Digital breast tomosynthesis (DBT) uses multiple low dose projection images distributed over an angular span to create a pseudo-3D reconstruction of the breast. This added depth information allows for otherwise obscured lesions to become visible.^{6, 7, 8, 9} Currently, only one DBT system is FDA approved for use in the United States.

Current DBT systems use a single x-ray source which is rotated over a limited angle arc. The x-ray source rotates in a continuous motion^{10, 11} or using a step-and-shoot motion.¹² In both methods, the motion of the x-ray source can have an adverse effect on tomosynthesis reconstruction quality and total imaging time.^{13, 14} The source motion results in a blurred focal spot. A blurred focal spot decreases the spatial resolution of the projection images which in turn reduces the spatial resolution of the reconstructed images. High spatial resolution is needed in mammography in order to resolve microcalcifications (MCs). MCs are important because the size and shape of them can indicate the likelihood that a particular lesion is benign or malignant. In both continuous motion and step-and-shoot DBT systems, the focal spot blurring effect can be reduced by decreasing the rotation speed and increasing the acquisition time.^{14, 15} However, a long acquisition time leads to patient motion which also degrades the image quality.¹⁶

We have developed a stationary digital breast tomosynthesis (s-DBT) system by retrofitting a linearly distributed carbon nanotube (CNT) x-ray source array onto a Hologic Selenia Dimensions DBT system.^{13, 17, 18, 19, 20} The system is capable of creating a full set of tomosynthesis projection images with no x-ray source motion and a potential acquisition time of less than 4 s when coupled with a high frame rate detector. Results have shown that the system resolution is increased from less than 3 cycles per mm with the Selenia Dimensions DBT system to more than 4 cycles per mm with the s-DBT system (1.08× magnification, 15 projection images, 15° angular span, 100 mAs). Accelerated lifetime measurements demonstrate an estimated x-ray tube lifetime of over 3 years in clinical service.¹³

Many variables must be taken into account when configuring a DBT system for optimal image quality. Factors such as the x-ray source, detector, reconstruction algorithm, image processing method, and imaging configuration must be tested and selected in order to realize the full potential of a system. A large number of previous studies have reported on the performance of rotating source DBT systems with respect to imaging configurations.^{14, 15, 21, 22, 23, 24, 25} Shaheen et al.¹⁴ conclude that a step-and-shoot system has higher contrast for imaging of MC clusters when compared to a continuous motion system. A number of studies have reported that an increase in the angular coverage of the projection images results in an improvement of z-axis resolution.^{15, 21, 22, 23, 24, 26} Chawla et al.²¹ report that increasing the dose level results in increased image quality. It has been reported that there is an optimal number of projection images for a fixed angular span, increasing the number of projection images above this number can reduce image quality.^{21, 23, 24, 25, 27}

The goal of the current study is to investigate how the reconstructed image quality is affected by imaging parameters in a s-DBT system. The parameters investigated include the total angular span, number of projection views, entrance dose, exposure (mAs) distribution across the projection images, and detector pixel size. Analysis was done on reconstructed images of physical phantoms using quantitative measures including signal difference to noise ratio (SdNR), z-axis artifact spread function (ASF), and the modulation transfer function (MTF).

METHODS

Using the s-DBT system, two phantoms were imaged using different configurations with different sets of imaging parameters. The resultant projection images were then reconstructed into a pseudo-3D volume and analysis was completed on the reconstructed slices. Reconstructed images are created using a backprojection filtering method developed by Real Time Tomography, LLC (Villanova, PA).²⁸ The value of the MTF was calculated from the reconstruction of a 50 μm wire phantom. The SdNR and ASF were calculated from the reconstructed images of a mammography accreditation phantom. An overall quality factor (QF) was determined from the three calculated values.

Stationary digital breast tomosynthesis system

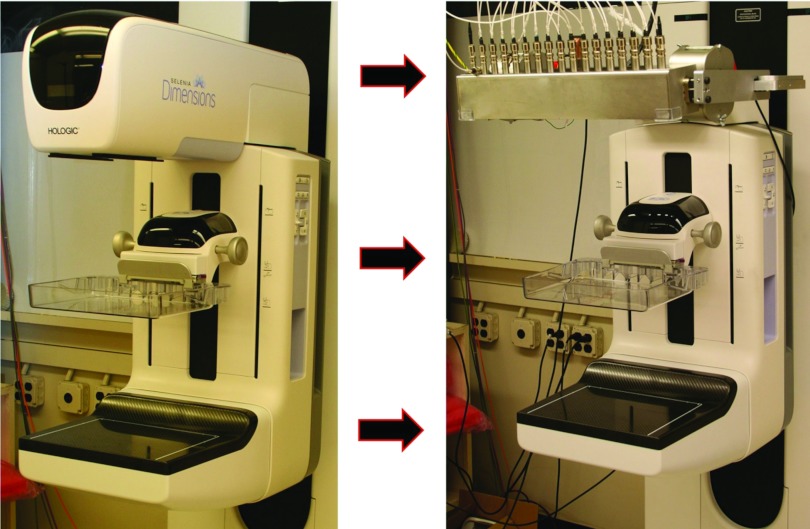
The s-DBT system consists of a linearly distributed CNT field emitting x-ray source array^{13, 17, 18, 19, 20} retrofitted on a Hologic Selenia Dimensions DBT system.¹¹ The CNT source array, manufactured by XinRay Systems, Inc. (Research Triangle Park, NC), consists of 31 x-ray generating focal spots distributed over a 336 mm straight line segment. The 31 sources are distributed with a 1° equal angular separation, 650 mm source to isocenter distance, and a 700 mm source to detector distance. The x-ray beam from each focal spot is independently controlled by the corresponding CNT field emission cathode. The tube is set up so that a constant kV is applied to the anode. The effective energy spectrum of each beam is determined by summing the constant anode voltage with the extraction voltage of the beam which is approximately −1400 V for the specific tube current used. Each energy spectrum closely mimics the Selenia Dimensions using a 1 mm thick aluminum window and a tungsten anode. The average focal spot size of each beam is 0.64 × 0.61 mm full-width at half maximum (FWHM).¹³ Images are acquired using the Selenia Dimensions workstation. The full resolution detector pixel size is 70 × 70 μm. The detector can be readout in full resolution (70 μm pixel size) or in 2 × 2 binning mode (140 μm pixel size). In 2 × 2 binned mode, the detector readout time is 180 ms. This time increases to 300 ms when the detector is in full resolution mode. The total acquisition time depends on the pulse width of the exposure. During typical operation the x-ray pulse width per projection view is 250 ms. With 15 projection images in an acquisition, the total acquisition time for binned mode is 6.45 s. For a full resolution dataset, this time increases to 8.25 s. Figure 1 shows the Selenia Dimensions before and after retrofitting of the linear CNT source array.

Figure 1.

(Left) Hologic Selenia Dimensions Digital Breast Tomosynthesis system with single rotating x-ray source, (right) stationary digital breast tomosynthesis system with integrated CNT x-ray source array (XinRay Systems, Inc. Research Triangle Park, NC). There are 31 x-ray generating focal spots; each x-ray beam can be electronically controlled to turn on/off instantaneously.

Configuration parameters

The quality of tomosynthesis reconstruction images can depend on many factors such as the total angular span of the projection images, the number of projection images, the entrance dose, distribution of the mAs, the detector resolution and sensitivity, and the reconstruction algorithm. Here, we concentrated on the variation of geometry parameters, entrance dose, and detector resolution. The reconstruction method that was used is outlined later (Sec. 2E).

Five groups of comparison studies were completed: (1) Comparison of 14° versus 28° angular span for a fixed total entrance dose uniformly distributed over 15 projection views; (2) comparison of 15 versus 29 projection views for a fixed total entrance dose uniformly distributed over an angular span of 28°; (3) for a fixed entrance dose, angular span of 28°, and 29 projection views we compare uniform versus nonuniform distributions of the mAs; (4) for a fixed angular span of 28° and 29 projection views, we varied the total entrance dose from 385 to 791 mR; (5) comparison of image quality for a detector operating in full resolution mode versus 2 × 2 binning mode. A summary of all configurations studied are listed in Table 1.

Table 1.

List of configurations and parameters that were analyzed. Five parameters were changed in order to create different configurations; number of projection views, total angular span, entrance dose, distribution of the mAs, and detector resolution. Some configurations are described by multiple groups and therefore appear multiple times in the table. Differences in entrance dose for equal mAs values can be attributed to different source to object distances for different x-ray sources. MMOC stands for more mAs on central projections. LMOC stands for less mAs on central projections.

Group	Number of projections	Total angular span	Angular spacing	Entrance dose (mR)	Detector resolution (μm)	Distribution of the mAs
1	15	14°	1°	727	140	Uniform
1	15	28°	2°	682	140	Uniform
2	15	28°	2°	682	140	Uniform
2	29	28°	1°	656	140	Uniform
3	29	28°	1°	656	140	Uniform
3	29	28°	1°	665	140	LMOC
3	29	28°	1°	675	140	MMOC
4	29	28°	1°	385	140	Uniform
4	29	28°	1°	523	140	Uniform
4	29	28°	1°	656	140	Uniform
4	29	28°	1°	791	140	Uniform
5	15	28°	2°	682	70	Uniform
5	15	28°	2°	682	140	Uniform

Entrance dose

The entrance dose was measured for each configuration using a dosimeter (Radcal Accu-Pro 9096) and ion chamber (Radcal 10 × 6-6 M Mammography Ion Chamber Sensor). The ion chamber was placed 2.8 mm from the chest wall in the center of the detector at the same height as the top of the phantoms (approximately 4 cm). A constant tube voltage of 31.4 kV was used for all configurations. The entrance dose for each configuration was measured three times. Each measurement was acquired in accumulated dose mode, meaning the dose from all projection views (oblique and perpendicular beams) were accumulated in the same measurement. The average of the three measurements was used as the entrance dose for the configuration. Variation of the dose between the measurements was found to be less than 1%.

Phantom imaging

Two phantoms were imaged for each configuration. A 50 μm tungsten wire phantom was used to determine the MTF of each configuration. The phantom was placed in the center of the detector near the focal line of the x-ray source. The wire was fixed to a metal frame and positioned parallel to the detector. A slight angle (approximately 3°) from perpendicular to the chest wall was applied to the wire to allow for oversampling of the line spread function (LSF). The same radiographic magnification factor of 1.12 (object-detector distance of 47.5 mm) was used for every configuration. An American College of Radiology (ACR) mammography accreditation phantom (CIRS Model 015) was imaged to assess the SdNR of masses and z-axis ASF sensitivity of MCs. The ACR phantom contains aluminum oxide (AL₂O₃) specks ranging from 0.54 to 0.16 mm in diameter, masses ranging from 2 to 0.25 mm in thickness, and nylon fibers that range from 1.56 to 0.4 mm in diameter. Figure 2 shows a schematic of the structures contained in the ACR phantom and a reconstructed volume slice of the ACR phantom using the s-DBT system.

Figure 2.

(Left) Schematic of simulated masses microcalcifications and fibers located in the ACR phantom. Analysis was conducted on the masses and microcalcifications. (Right) ACR phantom reconstructed slice acquired using the s-DBT system.

Image processing and reconstruction

For every projection image, a corresponding blank image was acquired. A blank image is an image where there is no object in the field of view of the detector. A different blank image was acquired for each mAs value. For each detector readout time, 15 dark images were acquired and averaged. All projection images were processed using Eq. 1, which corrects for detector and beam nonuniformity as well as gain offsets

$$\mathrm{Image}=\frac{\mathrm{Projection}-\mathrm{Dark}}{\mathrm{Blank}-\mathrm{Dark}}.$$ (1)

Image reconstruction was completed using a dynamic 3D reconstruction software package developed by Real Time Tomography, LLC (Villanova, PA). This software uses a backprojection filtering method.²⁸ The reconstructed images had a pixel size of 100 μm and a distance between slices of 0.5 mm, which is smaller than the 1 mm distance used in a typical breast tomosynthesis examination. The smaller slice distance was used in order to get better sampling of the z-axis ASF.

Modulation transfer function calculation

The size of the smallest object that a DBT system can detect is dependent on the inplane resolution. The value of the MTF is a good indication of the inplane resolution. Using the 50 μm tungsten wire phantom, the system MTF was calculated using a slant angle oversampling method.^{29, 30} Using the reconstructed slice at the focal plane of the wire, multiple LSFs were sampled. The LSFs were then formed into a single oversample LSF using the calculated angle of the wire. The resultant oversampled LSF was then fitted into a Gaussian function in order to remove noise. The Fourier transform of the fitted Gaussian function is the MTF. The resolution frequency at 10% MTF peak value was used as the quantitative measure of the inplane image resolution.

Signal difference to noise ratio calculation

The ability of a DBT system to detect masses in the breast is primarily determined by inplane contrast. Signal difference to noise ratio is a measure of the contrast with respect to the noise level. The SdNR was calculated on the largest mass, 2 mm in thickness, which is embedded in the ACR phantom. The largest mass was selected to ensure the object of interest was present in every reconstructed dataset. The foreground was selected to be the central region of the mass (approximately 2500 pixels in size) and the background was selected to be a ring-like region surrounding the mass (approximately 2700 pixels in size).

To determine the noise in the foreground and background, a moving average filter was applied across the original image and the resultant image was subtracted from the original. This step removes systematic variation of the background image that is not due to noise. The standard deviation was taken of the two regions in the subtracted image. The SdNR was calculated as

$$\mathrm{SdNR}=\frac{|{\mu }_{\mathrm{signal}}-{\mu }_{\mathrm{bkg}}|}{\sqrt{0.5\ast \left({\sigma }_{\mathrm{signal}}^2+{\sigma }_{\mathrm{bkg}}^2\right)}},$$ (2)

where “μ_signal” and “μ_bkg” are the average pixel intensity of the foreground and background, respectively, and “σ_signal” and “σ_bkg” are the corresponding standard deviations.¹⁴

Artifact spread function analysis

Due to the limited angle that tomosynthesis projections are taken, reconstructed slices at a particular focal plane can have “shadow” artifacts from objects that are at another depth. The ability of a particular DBT system to resolve objects in the z-axis (perpendicular to the detector) is a measure of the depth resolution. This is quantified by the z-axis artifact spread function.¹⁴ In this study, the ASF was calculated for the largest aluminum oxide specks (0.54 mm in diameter) in the ACR phantom. The largest specks were selected to ensure the object of interest was present in every reconstructed dataset. These specks are used to simulate MCs. There is a cluster of six 0.54 mm diameter specks in the phantom. ASF analysis was completed on all six specks in the cluster. Due to the small size of the MC it is difficult to determine the average pixel intensity value of the speck. We calculated the ASF by taking the maximum pixel value found in a small region of interest (ROI), where the speck of interest is located, through every reconstructed slice of the reconstruction space.¹⁴ The reconstructed slices are separated by 0.5 mm along the z-axis. As the distance from a slice to the object of interest's focal plane increases, the intensity of the ASF decreases. We use the FWHM of the ASF as a quantitative measure of the z-axis spatial resolution. The ASF at plane “z” is defined as

$$\mathrm{ASF}\left(\mathrm{z}\right)=\frac{|\max \left(\mathrm{signal}\left(\mathrm{z}\right)\right)-{\mu }_{\mathrm{bkg}}\left(\mathrm{z}\right)|}{{\mu }_{\mathrm{bkg}}\left(\mathrm{z}\right)},$$ (3)

where “max(signal(z))” is the maximum pixel value of the ROI for the slice located at “z,” and “μ_bkg(z)” is the average value of the background pixels of the ROI for the slice.¹⁴ Once the ASF was calculated the data were fitted to a Gaussian function plus a smooth background before the FWHM was determined.

Overall image quality factor

All three physical measurements: MTF, SdNR, and ASF are important in assessing the image quality of a reconstructed image set. The detection of MCs (high contrast objects) is primarily determined by the spatial resolution measured by the ASF and MTF, while the ability to detect masses (low contrast objects) is primarily determined by the SdNR. Sechopoulos and Ghetti²⁴ used an overall image QF that took into account the effect of contrast to noise ratio and ASF on image quality. Here, we define the relative overall image quality factor as

$$\mathrm{QF}=\frac{1}{3}\left(\frac{\mathrm{SdNR}}{{\mathrm{SdNR}}_0}+\frac{{\mathrm{ASF}}_0}{\mathrm{ASF}}+\frac{\mathrm{MTF}}{{\mathrm{MTF}}_0}\right),$$ (4)

where “SdNR” is the value determined from the signal difference to noise ratio calculation, and “ASF” is the FWHM of the artifact spread function, and “MTF” is the spatial resolution at 10% MTF peak value. MTF₀, SdNR₀, and ASF₀ refer to the corresponding values for the reference configuration of 28°, 15 projection views, 682 mR, and 140 μm detector pixel.

RESULTS

The SdNR and the FWHM of the ASF were calculated for each configuration from the reconstructed images of the ACR phantom. The value of the MTF at 10% was determined from the reconstructed images of the tungsten wire phantom. The values of the SdNR and MTF are averages of five measurements taken from the same datasets. Errors were not reported for the FWHM of the ASF and the QF due to insufficient statistical measurements. All the results acquired are summarized in Table 2.

Table 2.

Calculated results for SdNR, FHWM of the ASF, and MTF. Data are separated into the five groups of configurations that were outlined in Sec. 2B. The configuration with 29 projection views, a 28° angular span, and an even dose distribution resulted in the highest “quality factor” value for an exposure of 100 mAs. MMOC stands for more mAs on central projections. LMOC stands for less mAs on central projections.

Group	Number of projections	Total angular span	Entrance dose (mR)	Detector resolution (μm)	mAs distribution	SdNR	FWHM of ASF	MTF at 10%	QF
1	15	14°	727	140	Uniform	5.72 ± 0.21	7.80	4.14 ± 0.01	0.85
1	15	28°	682	140	Uniform	5.44 ± 0.20	4.08	4.20 ± 0.03	1.00
2	15	28°	682	140	Uniform	5.44 ± 0.20	4.08	4.20 ± 0.03	1.00
2	29	28°	656	140	Uniform	5.81 ± 0.16	4.10	4.25 ± 0.02	1.02
3	29	28°	656	140	Uniform	5.81 ± 0.16	4.10	4.25 ± 0.02	1.02
3	29	28°	665	140	LMOC	4.97 ± 0.20	4.03	4.23±0.01	0.98
3	29	28°	675	140	MMOC	5.04 ± 0.16	4.05	4.25 ± 0.01	0.98
4	29	28°	385	140	Uniform	4.32 ± 0.14	4.14	4.30 ± 0.01	0.93
4	29	28°	523	140	Uniform	4.87 ± 0.12	3.93	4.28 ± 0.02	0.98
4	29	28°	656	140	Uniform	5.81 ± 0.16	4.10	4.25 ± 0.02	1.02
4	29	28°	791	140	Uniform	6.06 ± 0.24	4.04	4.23 ± 0.02	1.04
5	15	28°	682	70	Uniform	2.97 ± 0.08	4.30	5.15 ± 0.05	0.91
5	15	28°	682	140	Uniform	5.44 ± 0.20	4.08	4.20 ± 0.03	1.00

Modulation transfer function

The spatial resolution at 10% MTF was used as a quantitative measure of the inplane resolution. Figure 3 shows an example of an oversampled LSF with Gaussian fitted data and the corresponding MTF.

Figure 3.

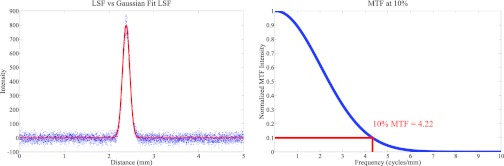
(Left) Plot of an oversampled LSF and the corresponding Gaussian fitted LSF which was used for MTF calculations. (Right) MTF of the LSF with the value at 10% highlighted. The MTF was found to be around 4.2 cycles per mm for a detector with a 140 μm pixel size (2 × 2 binning mode). Since there is no x-ray source motion in a s-DBT system, the MTF is found to be primarily dependent on the detector pixel size, and independent of other system parameters (see Fig. 8).

As can be seen in Table 2, there was no statistical difference in the value of the MTF at 10% for the first four groups of configurations. This is because the inplane resolution is predominately determined by the x-ray focal spot size and the detector pixel size. Since there is no focal spot blur in s-DBT for different configurations the MTF does not fluctuate.

Signal difference to noise ratio

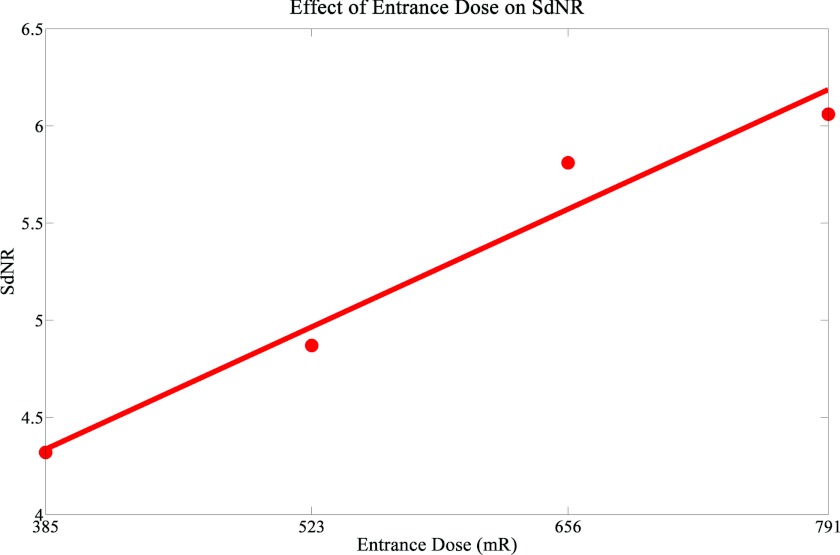
A magnified image of the 2 mm thick mass from the ACR phantom, which was used in the calculation of the SdNR, is shown in Fig. 4. Looking at Table 2, it can be seen that the SdNR did not greatly fluctuate when the angular span was increased (Group 1). This was expected since the only differences in photon counts was the slightly larger source to object distance for the wider angular span. When the number of projection images was increased, the SdNR did not change (Group 2). Group 3 had different mAs distributions with the same entrance dose. A lower SdNR was found in the configurations that had nonuniform distributions. This can be attributed to the lower photon counts on some of the projection images of the nonuniform mAs distributions. As expected, when the entrance dose was increased (Group 4) there was a corresponding increase in SdNR. Figure 5 shows a plot of the SdNR versus entrance dose. It can be concluded that in a s-DBT system the SdNR is primarily dependent on the entrance dose of a projection, not on other parameters.

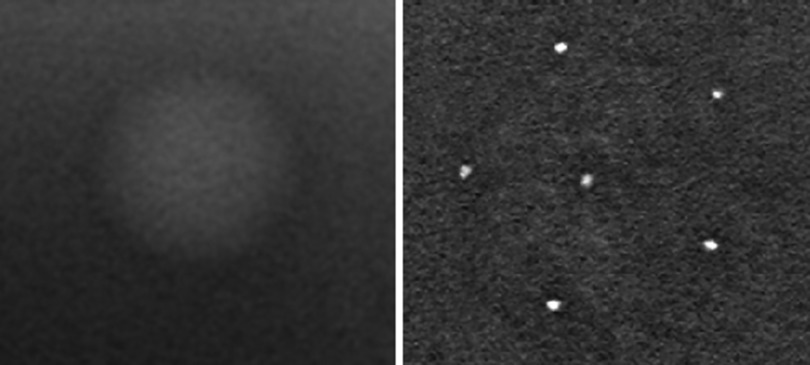
Figure 4.

(Left) Magnified view of 2 mm mass found in the ACR phantom. The SdNR of the mass and the surrounding background was calculated for each configuration. (Right) Magnified view of the 0.54 mm speck cluster found in the ACR phantom. ASF analysis was completed on all specks in the cluster for each configuration.

Figure 5.

The plot of the SdNR versus total entrance dose shows a linear increase of the SdNR with entrance dose within the dose range examined. A linear fit was applied to the dataset and plotted.

Artifact spread function along the z-axis

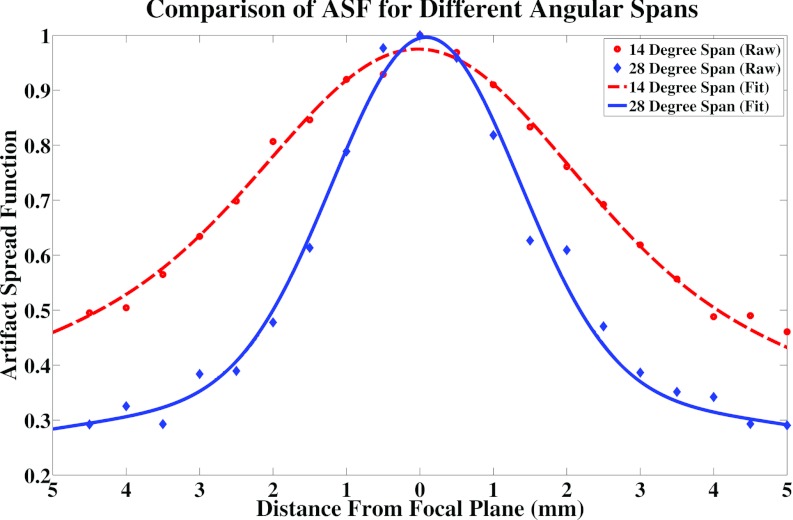
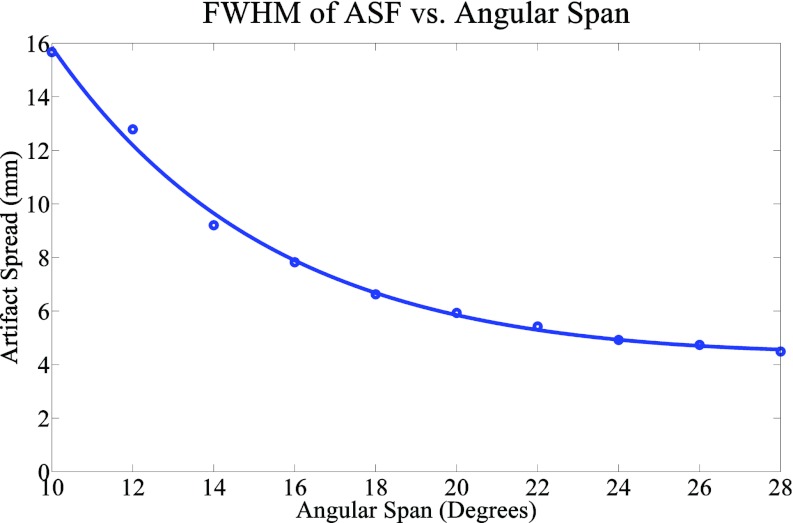
A magnified image of the cluster of six 0.54 mm specks found in the ACR phantom, which was used in the calculation of the artifact spread function along the z-axis, is shown in Fig. 4. All six specks were used for quantitative analysis of the ASF for all configurations. As can be seen in Table 2 and Fig. 6, there is a dramatic change in ASF width going from a 14° to a 28° angular span while keeping the number of projection views the same (Group 1). In order to further analyze the effect of angular span on the ASF, another group of images were used with an angular span ranging from 10° to 28°. In this group, the entrance dose per projection was kept constant but the number of projection views and total entrance dose decreased with the decrease in angular span. Figure 7 shows the ASF widths for this group. From this figure it can be seen that the width of the ASF decreases with increasing angular span of the projection images. The decrease can be attributed to the increased information which is collected in the projection space when the angular span is increased. Similar results have been found in previous studies.^{21, 24} For a fixed angular span, the ASF is found to be insensitive to the number of projection views, entrance dose, and mAs distribution (Groups 2–4).

Figure 6.

Plot of the ASF of an angular span of 14° versus an angular span of 28° with the same number of projection images and total entrance dose. Both the raw data and the fitted data are shown. The 14° span resulted in a much broader ASF due to the lack of information in the projection space.

Figure 7.

Results comparing the FWHM of the ASF and the total angular span of the projection images. A smooth fit was also applied to the data and plotted. A very noticeable trend can be seen which shows that an increased angular span results in a better artifact spread function.

Detector pixel size comparison

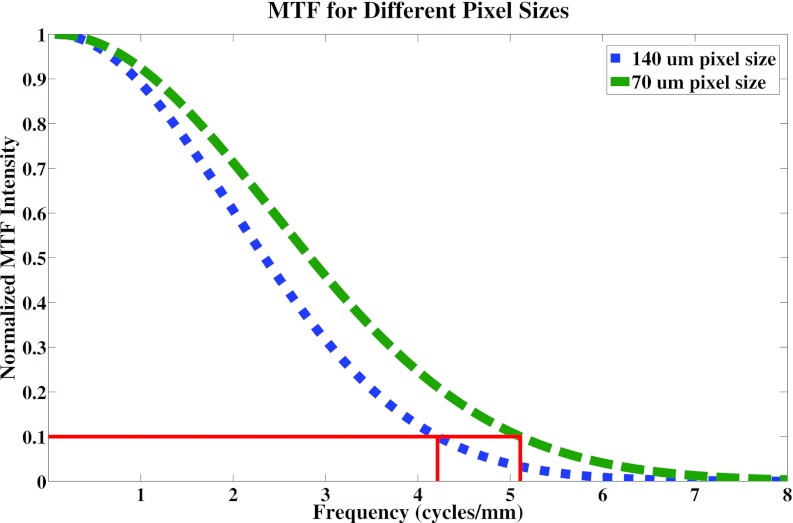
Decreasing the pixel size from 140 to 70 μm resulted in a 25% increase in the value of the MTF at 10%. Figure 8 is a plot of the MTFs for the two pixel sizes. The slight increase in the width of the ASF for the configuration with a 70 μm pixel size when compared to the 140 μm pixel size case is within the uncertainty of the calculation. Since the distance between slices is 0.5 mm, the error in calculation will be at least 1 mm.

Figure 8.

Plot of the MTFs for the 70 μm pixel size and the 140 μm pixel size. The value of the MTF at 10% was found to be approximately 25% better for the 70 μm pixel size (5.1 cycles per mm) when compared to the 140 μm case (4.2 cycles per mm).

The two configurations in Group 5 had the same total entrance dose but different detector pixel sizes. A decrease in SdNR was observed for the smaller pixel size configuration. Smaller pixels result in more pixels per area. Thus, the photon count per pixel is decreased resulting in the decrease of SdNR.

Overall image quality factor

The SdNR, MTF, and ASF are all important for assessing the image quality of a configuration. A composite image QF is used to assess the overall performance of a configuration to detect both MCs and masses. The different parameters tested have varying effects on the reconstructed image quality. An increase in entrance dose corresponds to an increase in SdNR. An increase in angular span creates a better artifact spread along the z-axis. A decrease in pixel size creates a better MTF and a worse SdNR. Of all configurations we investigated with 100 mAs exposure, it was found that the highest image QF was from the configuration with 29 projection images distributed uniformly over a 28° span and with binned detector pixels. However, the same configuration with 15 projections had a very similar QF. Using 29 projections instead of 15 projections will increase the total acquisition time by 2.52 s (due to additional readout time needed for more projection images). This increase in acquisition time could lead to a significant increase in patient motion during the acquisition, which will degrade the image quality.¹⁶ In clinical practice, the image quality may be optimal for the configuration with 15 projection views instead of 29.

DISCUSSION

The goal of this research was to determine (i) the effect of configuration parameters on image quality, and (ii) the configuration parameters which result in the overall best image quality using the s-DBT system. The inplane resolution, measured by the MTF, was found to primarily depend on the focal spot size of the x-ray source and the detector pixel size. It is insensitive to the number of projection views, projection view angular span, total entrance dose, and mAs distribution. The system inplane resolution of our s-DBT system is 4.2 cycles per mm for a detector with 140 μm pixels, and is 5.15 cycles per mm for one with 70 μm pixels. Because there is no x-ray source motion the system MTF in s-DBT is independent of acquisition time, total angular span, and the number of projection views. In contrast, rotating source DBT systems can have significant MTF degradation due to motion blur of the focal spot.¹³ Different configurations in DBT systems result in differing MTFs. For example, larger angular spans will require faster x-ray source motion if the total acquisition time and the number of projection images are held constant, resulting in lower MTF values.

A s-DBT system offers the flexibility of nonuniform distribution of the mAs among different projection views. It was found that a uniform distribution resulted in a higher quality factor than the nonuniform distributions that were tested. We conclude that there is no clear advantage of using nonuniform mAs distribution among different projection views.

As was expected, a higher entrance dose resulted in better image quality. However, the entrance dose used on a patient should be determined based on the thickness and composition of the breast being imaged. In DBT systems, the entrance dose is determined by the automatic exposure control (AEC) unit. Based on a low dose scout view, the AEC determines both the kVp and total mAs. In general, thin and fatty breasts require less dose in order to get similar image quality as thick and dense breasts. If the total dose is too low it may not be advantageous to distribute it over too many projection views. Thus, it may be advantageous to create a new AEC system for s-DBT which would allow optimization of the number of projection views and the angular span, in addition to the mAs and kVp. We will report on this study in future publications.

The number of projection images did not have a large effect on the overall image quality in our phantom study. However, in clinical practice this may not be the case due to differing acquisition times. The image acquisition time can be calculated from the equation

$${\mathrm{t}}_{\mathrm{acq}}=\mathrm{N}\ast \left({\mathrm{t}}_{\exp }+{\mathrm{t}}_{\mathrm{readout}}\right),$$ (5)

where “t_acq” is the total acquisition time, “N” is the number of projection images, “t_exp” is the exposure time per projection, and “t_readout” is the detector readout time per projection. Assuming that the total mAs stays the same for the 15 projection case as for the 29 projection case, the number of projection images will double and the exposure time per projection will half. Since the readout time of the detector is the same, the total acquisition time will increase by 14 times “t_readout.” Using the detector on the current Selenia Dimensions model (“t_readout” of 180 ms in 2 × 2 binned mode) the acquisition time for the 29 projections increases by 2.52 s. This is not desirable because the increase in acquisition time will lead to more patient motion, degrading the image quality.

Going from an angular span of 14° to 28° the FWHM of the ASF decreased approximately 50%. The increased z-axis resolution could be very beneficial when imaging patients by reducing tissue obstruction of the object of interest. Increased angular span becomes a problem for rotating source DBT systems due to the increased focal spot blur and/or acquisition time.

Changing from 2 × 2 binning to full resolution, in a s-DBT system, results in a 25% increase in the value of the MTF. This increase in spatial resolution comes at the cost of SdNR. The increased resolution could be beneficial when trying to image microcalcifications, but may not be desirable for detecting masses due to the loss in SdNR. It may be useful to present two sets of tomosynthesis reconstruction data, one optimized for MC detection using the full detector resolution projection data, and another for detecting masses using postacquisition binned projection data.

CONCLUSIONS

The optimal configuration of the carbon nanotube based stationary digital breast tomosynthesis system has been investigated. A configuration with a large angular span, an intermittent number of projection views, and an even mAs distribution resulted in the best overall image quality. Decreasing the pixel size from 140 to 70 μm resulted in a s-DBT system resolution of 5.15 cycles per mm, 60% better than continuous motion DBT systems (3 cycles per mm).¹³ All conclusions drawn in this paper are based on physical phantom models, whether these conclusions will carry over to clinical cases is yet to be determined.