Skip to main content
NCBI home page
CPT: Pharmacometrics & Systems Pharmacology logoLink to CPT: Pharmacometrics & Systems Pharmacology
. 2013 Feb 13;2(2):e26. doi: 10.1038/psp.2013.2

A Mathematical Model for the Rational Design of Chimeric Ligands in Selective Drug Therapies

V Doldán-Martelli 1, R Guantes 1, D G Míguez 1,*
PMCID: PMC3600755  PMID: 23887616

Abstract

Chimeric drugs with selective potential toward specific cell types constitute one of the most promising forefronts of modern Pharmacology. We present a mathematical model to test and optimize these synthetic constructs, as an alternative to conventional empirical design. We take as a case study a chimeric construct composed of epidermal growth factor (EGF) linked to different mutants of interferon (IFN). Our model quantitatively reproduces all the experimental results, illustrating how chimeras using mutants of IFN with reduced affinity exhibit enhanced selectivity against cell overexpressing EGF receptor. We also investigate how chimeric selectivity can be improved based on the balance between affinity rates, receptor abundance, activity of ligand subunits, and linker length between subunits. The simplicity and generality of the model facilitate a straightforward application to other chimeric constructs, providing a quantitative systematic design and optimization of these selective drugs against certain cell-based diseases, such as Alzheimer's and cancer.

Next-generation therapeutic drug development integrates tools from genomics, biotechnology, molecular modeling, and computational chemistry to reduce costs and time necessary to bring new drugs to market. This redesigned drug development pipeline incorporates quantitative approaches to overcome the challenge of better, more reliable, and more efficient treatments. In the context of cancer and other cell-based diseases, the ideal “perfect” drug can be envisaged as a compound that only affects diseased cells without harming the healthy surrounding cellular environment. These types of selective drugs are chimeric in nature, composed of a targeting element that discerns between undamaged and damaged cells, and an activity element that repairs or triggers apoptotic signals only in cells targeted by the targeting element. The most extensive family of chimeras are immunotoxins: cytotoxic agents comprising a modified toxin linked to a targeting domain derived from an antibody, a growth factor, a carbohydrate antigen, or a tumor-associated antigen.1 Examples of immunotoxins with good clinical performance are Ontak (the only agent approved to use for refractory cutaneous T-cell lymphomas by the US Food and Drug Administration),2 LMB-23 BL22,4 and IL13-PE.5

Another family of therapeutic chimeric proteins combines an antiproliferative agent, such as TRAIL, with an antibody fragment or a natural ligand as an specific cell surface tumor marker:6 scFv425:sTRAIL,7 scFvCD7:sTRAIL (specific for CD7),8 and scFvCD19:sTRAIL (targeting CD19-positive cells).9 Researchers also synthetized sFasL fusion proteins to target the T-cell leukemia–associated antigen CD710 or CD20.11 Type-1 interferons have also been fused with tumor-specific ligands, for instance, in antiCD20-interferon (antiCD20-IFN)12 or IFNα-2a-asparagine-glycine-arginine peptide13 in which the asparagine-glycine-arginine peptide targets the aminopeptidase N expressed in tumor vessels. IFNα-2a has also been combined with the epidermal growth factor (EGF) to target EGF receptors (EGFR)-overexpressing cells.14

The sequential mechanism of action of chimeric ligands (Figure 1) starts by a freely diffusing chimera (Figure 1a) that binds via one of its subunits to its complementary membrane receptor (Figure 1b,c). This first binding event maintains the other free subunit of the chimera in the vicinity of the membrane, facilitating the interaction with its corresponding receptor. The efficiency of the chimeric system depends on the balance between binding and unbinding rates of both ligand–receptor interactions, concentration of receptors for the targeting and activity elements, diffusion of both receptors on the membrane, and internalization of complexes, etc.

Figure 1.

Figure 1

Open in a new tab

Scheme of the chimeric ligand/receptor interaction. (a) The chimeric ligand is formed by two subunits (blue and green) connected by a protein linker of length “a.” Each subunit of the free ligand can bind to its corresponding receptor forming intermediate complexes (b) C1 and (c) C2. Vi is the effective reaction volume where the free ligand subunit is distributed (b–c) and hi corresponds to the height of receptor Ri (i = 1, 2) above cell surface. (d) Once both subunits of the ligand are bound to their corresponding receptors, complex C3 is formed, which gets internalized following the endocytotic constant 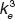Inline graphic.

Herein, we present a mathematical framework to design and enhance synthetic chimeric ligands. As a case study, we apply our model to different mutants of a IFNα-2a-EGF chimera developed in ref. 14, in which the EGF subunit targets cells overexpressing EGFR and the IFN subunit triggers apoptotic signals. These chimeras induced IFNα signaling in an EGFR-dependent manner in HeLa, and A431 cells, as well as in Daudi cells engineered to overexpress EGFR into the Daudi cell line (300× higher than the parental cell line). The Daudi cell line comes from a human Burkitt lymphoma and is susceptible to IFNα antiproliferative activity. Antiproliferative assays comparing Daudi and Daudi-EGFR cells showed that the inhibition of cell proliferation by chimeric proteins depended on the presence of EGFR on the cell surface.

The model allows us to understand the key aspects that determine the selective potential of the chimera and to optimize its design by testing variants with increased selectivity and efficiency. Our model quantitatively fits all experimental results, showing how different versions of the chimera exhibit enhanced selectivity (measured as the differential IFN activity of the chimera in Daudi-EGFR compared with Daudi cells). The model also allows us to test the dependence of the efficiency of the chimera on receptor abundance, length of the linker between both ligand subunits, and diffusion of membrane receptors. This general model can be easily tailored to other chimeric compounds to be used as a tool to understand the experimental observations as well as to optimize the design of potential chimeric constructs with improved selectivity.

Results

Activity of the chimera is enhanced in cells overexpressing EGFR

Figure 2 compares the dynamics of the different complexes Ci in Daudi (Figure 2a–c) vs. Daudi-EGFR cells (Figure 2d–f). After ligand stimulation at t = 0, the number of complexes increases initially to later drop due to internalization. The amount of IFN ligand–receptor complexes formed decreases when using IFN mutants with reduced affinity. In all cases, the maximum amount of IFN complexes formed is higher in Daudi-EGFR cells (Figure 2d–f) than in Daudi cells, with most of the IFN complexes also bound via the EGF subunit to EGFR (blue line). The dynamics of the EGF and IFN receptors (IFNR) is plotted in Supplementary Figure S1 online.

Figure 2.

Figure 2

Open in a new tab

The model predicts higher interferon (IFN) activation in EGFR overexpressing cells. Dynamics of formation of IFN complexes at L = 1 nmol/l in (a–c) Daudi and (d–f) Daudi-EGFR cells during 8 h. Black line corresponds to EGF complexes only bound via the EGF subunit (C1 variable in our model). Gray line corresponds to IFN complexes only bound via the IFN subunit (C2 variable). Blue line corresponds to complexes bound via both subunits of the chimera (C3 variable). (g–j) Bar diagram of the maximum number of IFN complexes (maximum of the sum of blue and gray lines in a–f) for monomer and chimeric ligands in ref. 14 (g–h) Daudi and (i–j) Daudi-EGFR cells. EGF, epidermal growth factor; EGFR, epidermal growth factor receptor; WT, wild-type.

Given that transcription of IFN-induced genes has been shown to correlate to IFNR occupancy,15 the maximum activity of the chimera can be monitored in terms of the maximum number of IFN complexes formed. Figure 2g–j plots the maximum amount of IFN complexes in monomer vs. chimeric configurations in both cell lines. The control cell line shows no difference in activity between monomer and chimeric ligand due to its low endogenous EGFR expression (Figure 2g,h). On the contrary, the chimeric ligand induces higher IFN complex formation in cells overexpressing EGFR, as compared with the monomer (Figure 2i,j). These results correlate with the measurements reported in ref. 14, at which the activity of the pathway is monitored in terms of pSTAT1 levels (a readout of IFN stimulation). Overall, the model shows how the efficiency of chimeric ligands is achieved: the formation of the IFN complex is enhanced by the presence of EGFR, which binds to the EGF subunit of the chimera while maintaining the IFN subunit close to the cell surface. This intermediate configuration increases the local concentration of IFN at the vicinity of the cell surface, facilitating the binding to IFNR. This mechanism increases the effective activity of IFN mutants with very low efficiency as monomers (K133A and R144A). With respect to chimeric configuration, these IFN variants outperform the wild type in terms of selectivity (see Selectivity is enhanced in chimeras with reduced IFN affinity section).

Selectivity is enhanced in chimeras with reduced IFN affinity

The efficacy of drugs in triggering apoptotic responses is often characterized in terms of percentage of viable cells in a population after treatment, in the form of dose–response curves.14 To correlate the model predictions with the experimental dose–response curves in ref. 14, we perform a calibration using values for the wild-type IFN monomer in both cell lines tested (see Methods section). This calibration translates the maximum number of IFN complexes formed into percentage of viable cells, and is used to calculate theoretical dose–response curves for the rest of monomer mutants and chimeric constructs, to be compared with their corresponding experimental curves. Other measurements of the chimeric activity, such as the sum of the number of IFN complexes formed until the maximum is reached, have also shown good correlation with experimental data (see Supplementary Figure S2 online).

Figure 3 shows the dose–response curves calculated for the two cell lines and the three different IFN mutants in monomeric and chimeric configurations. In Daudi cells (Figure 3a,c,e) the difference between chimera and monomer is negligible for all mutants. On the other hand, Daudi-EGFR cells (Figure 3b,d,f) present stronger response to chimeric ligand vs. monomer for all three IFN mutants. This difference increases when using mutants with reduced IFN affinity, resulting in a wider range of concentrations at which the monomer has a minimal effect whereas the chimera shows a strong effect in terms of percentage of viable cells.

Figure 3.

Figure 3

Open in a new tab

Theoretical dose–response curves predict highest selectivity for lowest affinity interferon mutants. Dose–response curves to compare cytotoxicity of the monomeric (green dotted lines) and chimeric (blue dotted lines) proteins in (a,c,e) Daudi and (b,d,f) Daudi-EGFR cell lines. (g–j) Bar diagram representing experimental and theoretical half maximal effective concentration (EC50) values for (g–h) monomer and (i–j) chimeric ligands (see Methods section). Numbers above each bar correspond to the EC50 (nmol/l) values for each condition. Note the different scale in the y-axis. EGFR, epidermal growth factor; WT, wild type.

Figure 3g–j plots the half maximal effective concentration (EC50) values of the ligand predicted by the model and the experimental data for each chimera in Daudi and Daudi-EGFR cells in ref. 14. The EC50 of the monomer (Figure 3g,h) increases as the affinity of the IFN mutants decreases, i.e., progressively higher ligand concentrations are required to trigger apoptosis in 50% of the cells. Of note, each IFN monomer mutant exhibits a higher EC50 in Daudi-EGFR cells as compared with the parental Daudi cell line, evidencing higher resistance of Daudi-EGFR cells to treatment with the IFN monomer. We hypothesize that this higher resistance is caused by the proliferative activity derived from EGFR overexpression.

EC50 values for the different chimeras are equivalent to their corresponding monomers when applied to Daudi cells, as expected (Figure 3g,i). On the contrary, EC50 values are lower for all chimeric mutants in Daudi-EGFR cells (compare Figure 3i with Figure 3j), meaning that low concentrations of the chimera can trigger stronger effect on these cells than on Daudi cells. This difference determines the selective power of chimeric constructs when applied to a population of cells, and when the activity element induces a stronger response in cells overexpressing the receptor of the targeting element. When overexpression of this receptor is a marker of disease, these chimeric constructs can trigger cytotoxic activity in unhealthy cells, leaving healthy cells unharmed. Therefore, comparison between Figure 3i,j shows that the mutant with the lowest IFN affinity (R144A) presents the highest selectivity, having a strong effect on unhealthy Daudi-EGFR cells whereas leaving healthy cells undamaged for a wide range of ligand concentrations.

Overall, the model quantitatively reproduces the experimental data for different monomers and chimeric constructs,14 and shows that the most selective chimera is the mutant with reduced affinity toward IFNR, again, consistent with the experiments.

Efficiency of the chimera depends on the balance between EGFR and IFNR expression

In the previous section, the model illustrates how the selectivity of chimeric constructs is achieved between cells expressing low and high levels of the targeting element receptor. However, in vivo cells do not express a disease marker in an on/off fashion but in a wide range of expression levels.16 To understand how the expression level of receptors influences the efficiency of the chimera, we calculate the maximum number of IFN complexes formed for different values of initial EGF and IFNR after stimulation with 1 nmol/l of chimeric ligand. Results are represented in Figure 4, in which each point in the graph corresponds to the maximum number of IFN complexes formed at certain values of IFNR and EGFR. Blue color represents harmless levels of IFN complex formed and red represents IFN complex levels high enough to trigger apoptosis in all cells of a population. IFNR and EGFR expression levels for Daudi (white circle) and Daudi-EGFR (white asterisk), in our experimental model system, are marked in all panels.

Figure 4.

Figure 4

Open in a new tab

Chimeric ligand activity depending on the number of EGF and interferon (IFN) receptor expression. Activity of the chimera measured as the maximum number of total IFN complexes, C2 + C3, in a color map as a function of initial amount of EGF and IFN receptors on the cell membrane. We varied the parameters R1 (0) and R2 (0) in Table 1 from 1 to 6,000 number of molecules. Ligand concentration L = 1 nmol/l. Color threshold has been selected to mark in red the number of IFN complexes that kills all the cells (0% cell viability). White symbols represent experimental values of EGF and IFN number receptors for Daudi (o) and Daudi-EGFR (*) cells, respectively. EGF, epidermal growth factor; EGFR, epidermal growth factor receptor; WT, wild-type.

For a constant ligand concentration, wild-type chimera activity (Figure 4a) does not depend on EGFR expression levels, respectively. This means that upon crossing a certain threshold in IFNR levels, all cells will die independently of the expression levels of our disease marker, EGFR. On the other hand, the R144A mutant chimera (Figure 4c) shows low activity in cells with low numbers of EGFR, but also reduced efficiency in cells with intermediate levels of EGFR expression, with the result that potentially harmful cells can be left undamaged. The mutant with intermediate affinity, K133A (Figure 4b), exhibits the best trade-off between selectivity and efficiency, with strong activity in cells expressing high and intermediate levels of EGFR (disease cells) and low activity in cells expressing low levels of EGFR (healthy cells).

Taken together, these results show that the expression levels of both targeting and activity receptor elements modulate the efficiency and selectivity of the chimera, and that different versions of the chimera can be designed and optimized in specific situations to achieve the best compromise between selective killing and efficiency.

Selectivity of the chimera depends on linker length and receptor diffusion

As discussed in the Methods section, formation of C3 complex via Eqs. 4 and 5 depends on two factors: first, both receptor types must become close enough on the cell surface. This process is controlled by diffusion and favored by longer chimera linkers a (see Eq. 7). In addition, the effective affinity constant Inline graphic (Eq. 9) decreases with linker length because the effective reaction volume increases for longer linkers. The global coupling rate in Inline graphic Eq. 6 is dominated by the slowest process: if diffusion of receptors is slow Inline graphic, and the reaction is said to be diffusion limited. On the other hand, for fast diffusive transport, Inline graphic, and the process becomes reaction limited. Between both regimes, there could be an intermediate optimal linker that maximizes the activity.

In ref. 14, the linker is formed by a chain of seven identical subunits of Gly4-Ser residues. The linker length a is estimated as the average end-to-end distance of a protein polymer containing N Kuhn segments (the Gly4-Ser subunits), using a worm-like chain model:17

graphic file with name psp20132e5.jpg

where N is the number of subunits, lc = N·aK and lp = aK/2 are the contour and persistent lengths, respectively. The Kuhn segment length, aK, is calculated as aK = 5·Cd, where Cd = 3.8 Å is the length of a residue.

To study the impact of receptor diffusion and linker length on the selectivity of chimeras, we calculated the difference in activity (measured as the maximum number of IFN complexes formed) between Daudi and Daudi-EGFR cells varying systematically the diffusion coefficient and the number of linker subunits. Figure 5 plots this differential activity in a color code as a function of linker length across a physiologically relevant range of diffusion coefficients for receptors in the membrane (D ε 10–11–10–9 cm2/s). Calculations corresponding to the experimental values are marked as asterisks. White lines mark a shallow maximum in differential activity as a function of linker length. For the wild-type chimera (Figure 5a), C3 formation is mainly diffusion limited, because the differential activity slightly increases with the linker length. For the K133A and R144A mutants (Figure 5b,c) the selectivity increases as expected, and C3 formation is mainly reaction limited, meaning that shorter linkers enhance the selective potential of the chimera. This presents a practical advantage because shorter linkers are easier to synthesize and longer chimeras are prone to cleavage in vivo.

Figure 5.

Figure 5

Open in a new tab

Chimeric ligand selectivity depends on receptor diffusion and linker length. Differential activity between Daudi and Daudi-EGFR cell lines (in a color code) as a function of receptor diffusion coefficient (D) and linker length (number of linker subunits) for the chimeras containing the (a) wild type, (b) K133A, and (c) R144A IFN ligands. The parameters corresponding to the experimental construct14 are marked with a black asterisk. White line represents maximum selectivity as a function of linker length for each value of the diffusion coefficient. The range in D where a maximum is observed separate the reaction limited regime (selectivity decreases as a function of linker length) from the diffusion limited regime (selectivity slightly increases as a function of linker length). Ligand concentration for each mutant is chosen at the half maximal effective concentration value of activity for the Daudi-EGFR cell line. EGFR, epidermal growth factor receptor.

Discussion

In this article, we present a theoretical model for chimeric ligands that allows us to study and optimize the selectivity of these types of constructs toward specific cell types. Some of these synthetic compounds have been developed as selective drugs,1,6,7,10,12 allowing high activity at very low drug concentration and therefore, reducing side effects. Our model provides an in silico tool to design and test the efficiency of new synthetic compounds, as well as to optimize the existing ones by testing variants with improved selective potential.

When tailored to the specific case of IFN-EGF chimera using parameter values from ref. 14, our model quantitatively reproduces the experimental results of the different chimeric constructs in terms of pathway activation (Figure 2g–j) and cytotoxic potential (Figure 3g–j).

We restricted our model to interactions occurring at the membrane level, calibrating downstream events using the experimental dose–response curve for the WT-IFN monomer (see Methods section). A detailed mathematical implementation of all downstream molecular interactions that ultimately trigger cytotoxic response will reduce the generality and simplicity of our model, so we consider this approach far from the scope of this contribution. In addition, internalization of C3 is computed as the sum of the internalization constants of both C1 and C2 complexes, assuming they are independent. However, the proximity of both complexes when in C3 configuration may induce dependence on the internalization of proximal active receptors linked to the same chimeric molecule.

Membrane diffusion of receptors and complexes is assumed uniform, so the well-known heterogeneity of the plasma membrane can impact diffusion of the components on the membrane. Moreover, the dimeric nature of both EGF and IFN complexes18,19 is not considered for the sake of generality. Instead, a simpler 1:1 ligand–receptor interaction scheme is considered. Given the accuracy of the 1:1 model reproducing the experimental results (Figure 3g–j), we hypothesize that receptor homodimerization is not playing a significant role in the dynamics of the system. In addition, the model does not include synthesis and degradation of free receptors, assuming a dynamic equilibrium that keeps a constant concentration of free receptors in unstimulated conditions.

The model also assumes that both subunits of the chimeric ligand are bound to receptors of the same cell. However, it is known that chimeras can act in a paracrine manner, crosslinking receptors of nearby cells.7 Finally, as previous studies suggested, EGF may have prosurvival signals, which are not considered in our model, and would counteract the cytotoxic activity of IFN.20 A detailed model including the effect of EGF stimulation on cell proliferation at cell population level is in progress.

Despite all simplifications and assumptions, the model accurately reproduces the experimental data14 for all compounds and both cell lines tested in a quantitative fashion. The present model provides a reliable and systematic tool to design chimeric ligands, allowing us to determine optimal configurations before synthesis and in vivo tests. All experimental data used here correspond to the IFN-EGF specific scenario, but the generality of the model ensures a straightforward customization to model other chimeric designs, using different combinations of activity and targeting elements to design selective compounds against specific cell types.

Methods

The chimeric ligand–receptor system can be considered as an extension of the monovalent ligand–receptor interaction model,21 assuming a sequential process with a single ligand able to interact with two different receptors following the scheme:

graphic file with name psp20132e6.jpg
graphic file with name psp20132e7.jpg
graphic file with name psp20132e8.jpg
graphic file with name psp20132e9.jpg

Eqs. 2 and 3 correspond to the individual binding of each subunit of the chimeric ligand L to its complementary receptor Ri to produce intermediate complexes Ci, where i = 1, 2 corresponds to each of the two targeted species (Figure 1b,c). These intermediate complexes are formed by one ligand subunit linked to its corresponding receptor whereas the other subunit is free and available to interact with its receptor via Eqs. 4 and 5 to generate the complex C3 (Figure 1d). This second binding event is modulated by two factors: the two-dimensional diffusion of the receptors at the cell membrane and the increase in local concentration close to the cell membrane due to the first binding event.22 The coupling rate constant Inline graphic is calculated as:21

graphic file with name psp20132e11.jpg

The diffusive rate constant, 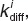Inline graphic is calculated using the model for binding of cell surface molecules to receptors from ref. 21, where the intermediate complexes C1 and C2 are considered as numbers of membrane molecules:

graphic file with name psp20132e13.jpg

Here D = D1 + D2 is the sum of diffusion coefficients on the cell membrane for both receptor species, and A is the typical cell surface area for mammalian cells.23 The parameter bi represents the average half-distance between receptors Ri on the cell surface, and is estimated as:

graphic file with name psp20132e14.jpg

The parameter a corresponds to the linker length between ligand subunits (Eq. 1). Normalization of Inline graphic by cell surface area A, Eq. 7, is necessary to express the diffusive rate constant in # molecules−1 min−1, the same units as Inline graphic, below. We remark that all molecular species, Ri, Ci, are given in molecule numbers.

On the other hand, Inline graphic, is the effective affinity constant recalculated for a two-dimensional binding process21 as follows:

graphic file with name psp20132e18.jpg

where Inline graphic is the corresponding three-dimensional rate affinity constant in Eqs. 2 and 3, Nav is Avogadro's number, and Vi is the effective reaction volume for the second binding event assumed as a spherical gasket above the cell surface where the free subunit gets distributed after the first binding event (see Figure 1b,c). This volume is calculated as Vi = A·(hi + a), where hi is the height of the extracellular domain of the receptor. 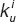Finally, the uncoupling rate Inline graphic in Eqs. 4 and 5 can be written as:

graphic file with name psp20132e21.jpg

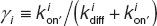Where Inline graphic the “capture probability” factor for receptor Ri, quantifying the probability that closely associated Ri and Cj (i, j = 1, 2) bind to become a C3 complex.21 ke represents the internalization constant of each of the different complexes after ligand binding, assuming Inline graphic, because internalization of the two complexes in C3 is considered to be independent. The set of reactions 2–5 is translated into the following differential equations:

graphic file with name psp20132e24.jpg
graphic file with name psp20132e25.jpg
graphic file with name psp20132e26.jpg
graphic file with name psp20132e27.jpg
graphic file with name psp20132e28.jpg

Note that, in contrast to other models of signal transduction by receptors,24 we consider extracellular ligand concentration as a constant in our equations. This choice is justified in Supplementary Text S1 online. To solve Eqs. 11–15 numerically, we developed an in-house MATLAB (MathWorks, Natick, MA) script (data not shown) using parameters for the chimeric system described.14 The system is composed by EGF as targeting element linked to different mutants of the IFNα-2a as the activity element. The activity of the chimera corresponds to the cytotoxic effect of the IFNα-2a subunit. This chimeric design is assumed to guide the antiproliferative and apoptotic effect25,26 of interferon toward cells overexpressing EGFR (upregulated in a number of tumoral cell lines).27 Mutants of IFN exhibiting different affinity toward the IFNR were tested in Daudi cells engineered to overexpress EGFR cells (~300× the levels of the Daudi control cell line). For our study, we selected the wild-type form of IFNα-2a and the mutant variants, K133A and R144A,28,29 with progressively less avidity toward IFNR. Parameter values are taken from experimental studies28,29,30,31,32,33,34,35 and are listed in Table 1. Within our modeling scheme, variable R1 represents EGFR, R2, IFNR, C1 and C2 represent EGF and IFN complexes alone (i.e., complexes formed by the receptor and one end of the chimera, with the other chimera subunit free to bind to its corresponding receptor). C3 corresponds to the chimera linked to EGFR and IFN at the same time. The initial number of EGFR and IFNR is written as R1 (0) and R2 (0), and the initial amount of complexes C1, C2, and C3 is equal to 0 (see Table 1).

Table 1. Kinetic parameters used in the chimeric model.

graphic file with name psp20132t1.jpg

Open in a new tab

To compare the theoretical predictions with experimental measurements, we established a correlation between cytotoxic effect of IFN and number of IFN complexes predicted. To do so, we compute the maximum value of IFN ligand–receptor complexes (i.e., C2 +C3 in the model) for the range of ligand concentrations experimentally used, resulting in the sigmoidal curves in Figure 6a,b. The prediction of maximum IFN complexes for each ligand concentration is correlated with its cytotoxic effect using the experimental dose–response curves for the wild-type IFN monomer ligand in ref. 14 for Daudi and Daudi-EGFR cells (both are sigmoidal curves reinterpreted in Figure 6c,d). The resulting calibration curves for both cell types are shown in Figure 6e,f, correlating the number of IFN complexes predicted with its activity in terms of percentage of viable cells. The calibration curve is then used to calculate the predicted cytotoxicity for other mutants of IFN monomer and all chimeric variants.

Figure 6.

Figure 6

Open in a new tab

Calibration curves for the IFN wild-type monomer in Daudi-EGFR and Daudi cell lines. (a,b) Model prediction of maximum IFNR activation for different ligand concentrations. (c,d) Experimental dose–response curves from ref. 14 fitted as sigmoidal curves. (e,f) Calibration curves to correlate predicted IFNR activation with experimental cytotoxic activity for a given ligand concentration. Parameters for the sigmoidal fitting of the calibration curves: (e) for Daudi cells are maximum value (Emax) =100, minimum value (E0) = 0, Inflection Point (IP) = 160.9, Slope (S) = −3.3 and (f) for Daudi-EGFR cells are Emax = 100, E0 = 0, IP = 814, S = −3.4. Sigmoidal fitting perfomed using an in-house MATLAB script. EGFR, epidermal growth factor receptor; IFN, interferon; IFNR, interferon receptor.

Supplementary Figure S2 online plots the dose–response curves and EC50 values calculating the IFN activity as the sum of the number of IFN complexes formed before the maximum (to be compared with Figure 3, calculated using the maximum value of IFN complexes). Both methods produce equivalent results in complete agreement with the experimental data.

The quantitative fit of the EC50 values for the different IFN monomers with the experimental data provides a good validation of the model, because changes in the affinity of the IFN ligand fully correlate with the experimental phenotype.

Author Contributions

V.D-.M., R.G., and D.G.M. wrote the manuscript, designed the model, performed the research, and analyzed the data.

Conflict of Interest

The authors declared no conflict of interest.

Study Highlights

graphic file with name psp20132i1.jpg

Acknowledgments

This work has been supported by the Ministry of Science and Technology of Spain via a Ramon Y Cajal Fellowship (Ref. RYC-2010-07450) and a Project from Plan National framework (Ref. BFU2011-30303), and a Marie Curie International Reintegration Grant from the EU (Ref. 248346-NMSSBLS). V.D.M. acknowledges financial support to the Universidad Autónoma de Madrid for a FPI-UAM fellowship. We thank the Instituto Nicolás Cabrera of the Universidad Autónoma de Madrid (Spain) and P. Cironi for helpful insights at the start of the project.

Supplementary Material

Supplementary Figure S1.
Click here for additional data file. (226.6KB, pdf)
Supplementary Figure S2.
Click here for additional data file. (603.2KB, pdf)
Supplementary Text S1.
Click here for additional data file. (57.8KB, zip)

References

  1. Kawakami K., Aggarwal B.B., &, Puri R.K. 1st edn., (CRC Press, Taylor & Francis, Boca Raton, FL, 2004); Cytotoxins and Immunotoxins for Cancer Therapy: Clinical Applications. [Google Scholar]
  2. Turturro F. Denileukin diftitox: a biotherapeutic paradigm shift in the treatment of lymphoid-derived disorders. Expert Rev. Anticancer Ther. 2007;7:11–17. doi: 10.1586/14737140.7.1.11. [DOI] [PubMed] [Google Scholar]
  3. Kreitman R.J.et al. Phase I trial of recombinant immunotoxin anti-Tac(Fv)-PE38 (LMB-2) in patients with hematologic malignancies J. Clin. Oncol. 181622–1636.2000 [DOI] [PubMed] [Google Scholar]
  4. Kreitman R.J.et al. Phase I trial of recombinant immunotoxin RFB4(dsFv)-PE38 (BL22) in patients with B-cell malignancies J. Clin. Oncol. 236719–6729.2005 [DOI] [PubMed] [Google Scholar]
  5. Kioi M., Husain S.R., Croteau D., Kunwar S., &, Puri R.K. Convection-enhanced delivery of interleukin-13 receptor-directed cytotoxin for malignant glioma therapy. Technol. Cancer Res. Treat. 2006;5:239–250. doi: 10.1177/153303460600500307. [DOI] [PubMed] [Google Scholar]
  6. Ruoslahti E., Bhatia S.N., &, Sailor M.J. Targeting of drugs and nanoparticles to tumors. J. Cell Biol. 2010;188:759–768. doi: 10.1083/jcb.200910104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Bremer E.et al. Simultaneous inhibition of epidermal growth factor receptor (EGFR) signaling and enhanced activation of tumor necrosis factor-related apoptosis-inducing ligand (TRAIL) receptor-mediated apoptosis induction by an scFv:sTRAIL fusion protein with specificity for human EGFR J. Biol. Chem. 28010025–10033.2005 [DOI] [PubMed] [Google Scholar]
  8. Bremer E.et al. Target cell-restricted apoptosis induction of acute leukemic T cells by a recombinant tumor necrosis factor-related apoptosis-inducing ligand fusion protein with specificity for human CD7 Cancer Res. 653380–3388.2005 [DOI] [PubMed] [Google Scholar]
  9. Stieglmaier J.et al. Selective induction of apoptosis in leukemic B-lymphoid cells by a CD19-specific TRAIL fusion protein Cancer Immunol. Immunother. 57233–246.2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Bremer E., ten Cate B., Samplonius D.F., de Leij L.F., &, Helfrich W. CD7-restricted activation of Fas-mediated apoptosis: a novel therapeutic approach for acute T-cell leukemia. Blood. 2006;107:2863–2870. doi: 10.1182/blood-2005-07-2929. [DOI] [PubMed] [Google Scholar]
  11. Bremer E.et al. Superior activity of fusion protein scFvRit:sFasL over cotreatment with rituximab and Fas agonists Cancer Res. 68597–604.2008 [DOI] [PubMed] [Google Scholar]
  12. Xuan C., Steward K.K., Timmerman J.M., &, Morrison S.L. Targeted delivery of interferon-alpha via fusion to anti-CD20 results in potent antitumor activity against B-cell lymphoma. Blood. 2010;115:2864–2871. doi: 10.1182/blood-2009-10-250555. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Zhang B., Gao B., Dong S., Zhang Y., &, Wu Y. Anti-tumor efficacy and pre-clinical immunogenicity of IFNa2a-NGR. Regul. Toxicol. Pharmacol. 2011;60:73–78. doi: 10.1016/j.yrtph.2011.02.007. [DOI] [PubMed] [Google Scholar]
  14. Cironi P., Swinburne I.A., &, Silver P.A. Enhancement of cell type specificity by quantitative modulation of a chimeric ligand. J. Biol. Chem. 2008;283:8469–8476. doi: 10.1074/jbc.M708502200. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Hannigan G., &, Williams B.R. Transcriptional regulation of interferon-responsive genes is closely linked to interferon receptor occupancy. EMBO J. 1986;5:1607–1613. doi: 10.1002/j.1460-2075.1986.tb04403.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Spencer S.L., &, Sorger P.K. Measuring and modeling apoptosis in single cells. Cell. 2011;144:926–939. doi: 10.1016/j.cell.2011.03.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. O'Brien E.P., Morrison G., Brooks B.R., &, Thirumalai D. How accurate are polymer models in the analysis of Förster resonance energy transfer experiments on proteins. J. Chem. Phys. 2009;130:124903. doi: 10.1063/1.3082151. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Yarden Y., &, Schlessinger J. Self-phosphorylation of epidermal growth factor receptor: evidence for a model of intermolecular allosteric activation. Biochemistry. 1987;26:1434–1442. doi: 10.1021/bi00379a034. [DOI] [PubMed] [Google Scholar]
  19. Uze G., Lutfalla G., &, Mogensen K.E. In Guidebook to Cytokines and Their Receptors (ed. Nicola, N.A.), 115–118 (Oxford UniversityPress, Oxford; New York; Tokyo, 1994)
  20. Caraglia M.et al. Interferon-alpha induces apoptosis in human KB cells through a stress-dependent mitogen activated protein kinase pathway that is antagonized by epidermal growth factor Cell Death Differ. 6773–780.1999 [DOI] [PubMed] [Google Scholar]
  21. Lauffenburger D.A., &, Linderman J. Oxford University Press, Huntington Beach, CA; 1996. Receptors: Models for Binding, Trafficking, and Signaling; pp. 130–180. [Google Scholar]
  22. Adam G., &, Delbruck M. Freeman, San Francisco, CA; 1968. Structural Chemistry in Molecular Biology; pp. 198–215. [Google Scholar]
  23. Zhao L., Kroenke C.D., Song J., Piwnica-Worms D., Ackerman J.J., &, Neil J.J. Intracellular water-specific MR of microbead-adherent cells: the HeLa cell intracellular water exchange lifetime. NMR Biomed. 2008;21:159–164. doi: 10.1002/nbm.1173. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Shankaran H., Resat H., &, Wiley H.S. Cell surface receptors for signal transduction and ligand transport: a design principles study. PLoS Comput. Biol. 2007;3:e101. doi: 10.1371/journal.pcbi.0030101. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Darnell J.E., Jr, Kerr I.M., &, Stark G.R. Jak-STAT pathways and transcriptional activation in response to IFNs and other extracellular signaling proteins. Science. 1994;264:1415–1421. doi: 10.1126/science.8197455. [DOI] [PubMed] [Google Scholar]
  26. Pestka S., Langer J.A., Zoon K.C., &, Samuel C.E. Interferons and their actions. Annu. Rev. Biochem. 1987;56:727–777. doi: 10.1146/annurev.bi.56.070187.003455. [DOI] [PubMed] [Google Scholar]
  27. Arteaga C.L. The epidermal growth factor receptor: from mutant oncogene in nonhuman cancers to therapeutic target in human neoplasia. J. Clin. Oncol. 2001;19:32S–40S. [PubMed] [Google Scholar]
  28. Dunne S.L., Bajzer Z., &, Vuk-Pavlovic S. Kinetics of receptor-mediated uptake and processing of interferon-alpha 2a and tumor necrosis factor-alpha by human tumor cells. Growth Factors. 1990;2:167–177. [PubMed] [Google Scholar]
  29. Piehler J., Roisman L.C., &, Schreiber G. New structural and functional aspects of the type I interferon-receptor interaction revealed by comprehensive mutational analysis of the binding interface. J. Biol. Chem. 2000;275:40425–40433. doi: 10.1074/jbc.M006854200. [DOI] [PubMed] [Google Scholar]
  30. Hendriks B.S., Orr G., Wells A., Wiley H.S., &, Lauffenburger D.A. Parsing ERK activation reveals quantitatively equivalent contributions from epidermal growth factor receptor and HER2 in human mammary epithelial cells. J. Biol. Chem. 2005;280:6157–6169. doi: 10.1074/jbc.M410491200. [DOI] [PubMed] [Google Scholar]
  31. Resat H., Ewald J.A., Dixon D.A., &, Wiley H.S. An integrated model of epidermal growth factor receptor trafficking and signal transduction. Biophys. J. 2003;85:730–743. doi: 10.1016/s0006-3495(03)74516-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Ogiso H.et al. Crystal structure of the complex of human epidermal growth factor and receptor extracellular domains Cell 110775–787.2002 [DOI] [PubMed] [Google Scholar]
  33. Garrett T.P.et al. Crystal structure of a truncated epidermal growth factor receptor extracellular domain bound to transforming growth factor alpha Cell 110763–773.2002 [DOI] [PubMed] [Google Scholar]
  34. Xiao Z., Zhang W., Yang Y., Xu L., &, Fang X. Single-molecule diffusion study of activated EGFR implicates its endocytic pathway. Biochem. Biophys. Res. Commun. 2008;369:730–734. doi: 10.1016/j.bbrc.2008.02.084. [DOI] [PubMed] [Google Scholar]
  35. Roisman L.C., Piehler J., Trosset J.Y., Scheraga H.A., &, Schreiber G. Structure of the interferon-receptor complex determined by distance constraints from double-mutant cycles and flexible docking. Proc. Natl. Acad. Sci. U.S.A. 2001;98:13231–13236. doi: 10.1073/pnas.221290398. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Figure S1.
Click here for additional data file. (226.6KB, pdf)
Supplementary Figure S2.
Click here for additional data file. (603.2KB, pdf)
Supplementary Text S1.
Click here for additional data file. (57.8KB, zip)

Articles from CPT: Pharmacometrics & Systems Pharmacology are provided here courtesy of Wiley

RESOURCES