Shear-induced Volume Decrease in MDCK Cells

Abstract

Using a microfluidic cell volume sensor we measured the change in the cell volume of Madin-Darby Canine Kidney (MDCK) cells induced by shear stress. An increase in shear stress from 0.2 to 2.0 dyn/cm² resulted in a volume decrease to a steady state volume ~ 20 – 30 % smaller than the initial resting cell volume. Independent experiments based on fluorescence quenching confirmed the volume reduction. This shear-induced cell shrinkage was irreversible on the time scale of the experiment (~ 30 min). Treatment of 0.1 μM Hg²⁺ significantly inhibited the volume decrease, suggesting that the shear-induced cell shrinkage is associated with water efflux through aquaporins. The volume decrease cannot be inhibited by 75 mM TEA, 100 μM DIDS, or 100 μM Gd³⁺ suggesting that volume reduction is not directly mediated by K⁺ and Cl⁻ channels that typically function during regulatory volume decrease (RVD), nor is it through cationic stretch-activated ion channels (SACs). The process also appears to be Ca²⁺ independent because it was insensitive to intracellular Ca²⁺ level. Since cell volume is determined by the intracellular water content, we postulate that the shear induced reductions in cell volume may arise from increased intracellular hydrostatic pressure as the cell is deformed under flow, which promotes the efflux of water. The increase in internal pressure in a deformable object under the flow is supported by the finite element mechanical model.

Introduction

Renal epithelial cells are exposed to a broad range of shear stresses due to the change in urinary flow under physiological and pathological conditions. Flow shear stress can affect the physiological behavior of renal tubule cells by altering ion channel activity [1, 2], organization of cytoskeleton [3–5], gene expression [6], or transcription factors [4]. Thus, sensing and responding to shear stress is an important function of epithelial cells.

Flow induced changes in ion transport have been observed with patch-clamp recording [1, 7]. Increases in shear stress cause Ca²⁺ influx in many cell types [8–11] and that activates a cascade of signal pathways affecting biochemical reactions and ion transport [12]. Flow-dependent Ca²⁺-activated K⁺ channels are postulated to account for the increase of K⁺ secretion under flow in the rabbit connecting tubule (CNT) [1] and cortical collecting ducts (CCD) [13, 14]. Shear stress might also activate stretch-activated ion channels (SACs) by creating gradients in membrane tension [15]. It has been recently reported that SACs are responsive to both shear stress and osmotic swelling [16, 17]. Since the influx or efflux of osmolytes from cells is accompanied by the water transport, effect of shear stress on membrane transport will cause the changes in cell volume. In addition, cell volume could also be changed by shear stress induced change in cell shape that promotes the efflux of water. Simple mechanics predicts that shear stress can introduce an increase in intracellular pressure due to cell deformation and that pressure will increase the efflux of water. These may result in changes in solute concentration and also in cytoplasmic stress with its biochemical consequences [18, 19].

Using the cell volume sensor based on an impedance measurement [20], we observed that cell volume decreases in response to increased flow shear stress. The change in the cell volume was only partly reversible within the experimental duration of ~ 1hr, suggesting that the cell structure had been altered during shear stress application. The shear-induced volume reduction was inhibited by Hg²⁺ suggesting the involvement of water efflux. Pharmacological blocking tests revealed that the volume changes did not utilize Ca²⁺-activated signaling pathways, K⁺ or Cl⁻ channels, Na⁺-H exchange or SACs. Finite element analysis results suggest that the decrease in cell volume by shear stress could be attributed to the compressive stress inside the cells that changes the cell shape and enhances water efflux.

Materials and Methods

Solution preparation

Hypotonic solution (168 mOsm) consisted of 75 mM NaCl, 5 mM KCl, 2 mM MgCl₂, 1 mM CaCl₂ with 10 mM HEPES at pH 7.4. Isotonic (320 mOsm) solution was prepared by adding mannitol to the hypotonic solution. This isotonic solution was lightly titrated with NaCl to have the same conductivity as the hypotonic solution. This titration step added less than 0.1 mM NaCl to the isotonic solution. The osmolarity was measured using an osmometer (Advanced Model 303, Advanced Instrument, Norwood, MA). Drug solutions of 10 mM of 4,4′-diisothiocyanatostilbene-2,2′-disulfonic acid (DIDS) and 100 mM amiloride solutions were prepared in DMSO and stored in the freezer. A 10 μM stock of HgCl₂ solution was prepared in isotonic solution and further diluted to 0.1 μM for experiments. Gadolinium chloride was prepared as a 10 mM stock solution in water. The solution of 5-(N,N-dimethyl)amiloride hydrochloride was prepared in isotonic saline and 75 mM tetraethylammonium (TEA) chloride solution was prepared in isotonic solution by replacing NaCl.

Cell culture

Microscope slides were cut to ~22 mm × 13 mm to fit on the sensor chip and cleaned as previously described [21]. MDCK cells (ATCC) were grown to confluence on the slide in a 35 mm Petri dish using Dulbecco’s Modified Eagle’s Medium (DMEM) containing 10% fetal bovine serum and 1% penicillin-streptomycin. It took 4–6 days to grow the cells to confluence. The cell passage number was between 5 and 35. Cells showed good adhesion on the glass surface without specialized coatings.

Measurement of cell volume change using cell volume sensor

The cell volume sensor was described in our previous paper [20]. It measures the real part of the (extracellular) impedance of a thin flow chamber of fixed volume containing the cells. An increase in cell volume appears as an increase in extracellular resistance. A slide with attached cells was inverted over the sensor so that cells faced the chamber. The sensing chamber was 1.5 mm wide, 2.5 mm long, and 18 or 24 μm thick and contained an evaporated four-electrode Pt array deposited on the surface by e-beam deposition. The chamber resistance was measured by supplying a constant current (100 Hz, 200 nA) to the outer pair of electrodes, while measuring the voltage between the inner pair with phase-lock detection [20]. Since the impedance of the cell membrane is high at these frequencies, the change of resistance represents the change of cell volume [20, 22]. The solution flow rate was controlled using a syringe pump (PHD 22/2200, Harvard Apparatus, Holliston, MA). The data was plotted as the ratio of cell volume change to the resting cell volume as previously described [20, 21, 23]. To measure the resistance of the empty chamber, after an experiment was finished the chamber was perfused with a detergent (1% Triton X-100) to permeabilize the cells and the chamber was then rinsed with isotonic solution. The resistance (or voltage) in the sensing chamber was then defined as V_empty. The ratio of the cell volume change to the resting volume at time t can be approximated as:

$$\frac{\mathrm{\Delta }CV}{{CV}_0}=\frac{V_t-V_0}{V_0-V_{\mathit{empty}}}$$ (1)

where, ΔCV is cell volume change, CV_o is resting cell volume, V_t is the voltage measured in the chamber at time t, and V_o is the initial voltage (chamber resistance with resting cells) in isotonic solution.

As a control, cells were fixed with 4 % paraformaldehyde for 10 min and treated with 0.1 % Triton X-100 solution for 5 min to remove the membranes. After the fixed cells were rinsed with isotonic solution, we examined whether there was any artifactual signal that could be interpreted as a change of cell volume with shear stress and found no significant change. We display raw data for this measurement because the fixed cells could not be removed from the sensing chamber to measure V_empty. To observe a change in the cell morphology, we recorded micrographs of the cells while collecting cell volume data using an upright microscope (Zeiss) equipped with a 10x objective and CCD camera.

Measurement of volume change using fluorescence concentration quenching [24]

To check out our method against published methods we also measured volume changes using fluorescence quenching. This method measures concentration-dependent quenching of intracellular calcein [24]. MDCK cells were grown to confluence and after rinsing with isotonic solution, they were incubated with isotonic solution containing 4 μM of calcein-AM (Invitrogen, Carlsbad, CA). To calibrate the sensitivity of the dye to cell volume changes, we exposed the cells to hypotonic and hypertonic solutions and monitored the fluorescence intensity. After we confirm that changes of cell volume caused the change of the fluorescence intensity, we examined the change in the cell volume under shear stress by using fluorescence. The relative fluorescence intensity was calculated using the following equation (Eqn. 2).

$$I_{\mathit{rel}}=\frac{(I_t-I_{Bk})-(I_o-I_{Bk})}{(I_o-I_{Bk})}$$ (2)

where I_rel is relative fluorescence intensity change, I_t is fluorescence intensity at time t, I_Bk is background fluorescence intensity, and I_o is fluorescence intensity at t=0.

Intracellular Ca²⁺ measurement

Cells were loaded with 6 μM Fluo-4 AM (Invitrogen, Carlsbad, CA) in isotonic solution for 30 min in an incubator. The cells were then rinsed with isotonic solution and incubated for another 10 min. The slide was mounted on the sensor and we collected fluorescence micrographs. Time-lapse experiments were recorded using AxioVision software (Zeiss).

Finite element analysis

We built a simple 2D model and calculated the intracellular stress distribution under flow using finite element analysis (ANSYS/CFX, ANSYS Inc.). The model consists of a flow chamber having the same dimensions as the sensor and a deformable elastic cell attached to the bottom of the chamber. The model had steady flow with non-slip boundary conditions and we used two-way coupling of fluid-structure interaction method. The fluid domain was calculated by ANSYS/CFX, and the deformable cell domain was analyzed by ANSYS. The flow domain and cell domain were coupled through continuity boundary condition for displacement, traction, and velocity at the fluid-cell interface.

Shear stress calculation

We used two microfluidic sensors with different channel heights of 18 and 24 μm. Unless otherwise noted, the experiments were conducted using a device with 24 μm channel height. Assuming confluent cells form a planar sheet, the wall shear stress τ was calculated using [25]:

$$\tau =\frac{6\mu Q}{{wd}^2}$$ (3)

here μ is viscosity, Q is volume flow rate, w is channel width, and d is channel height, respectively. Viscosity was assumed to be 1.0 × 10⁻³ Pa s.

Results

Shear stress induced decrease in cell volume

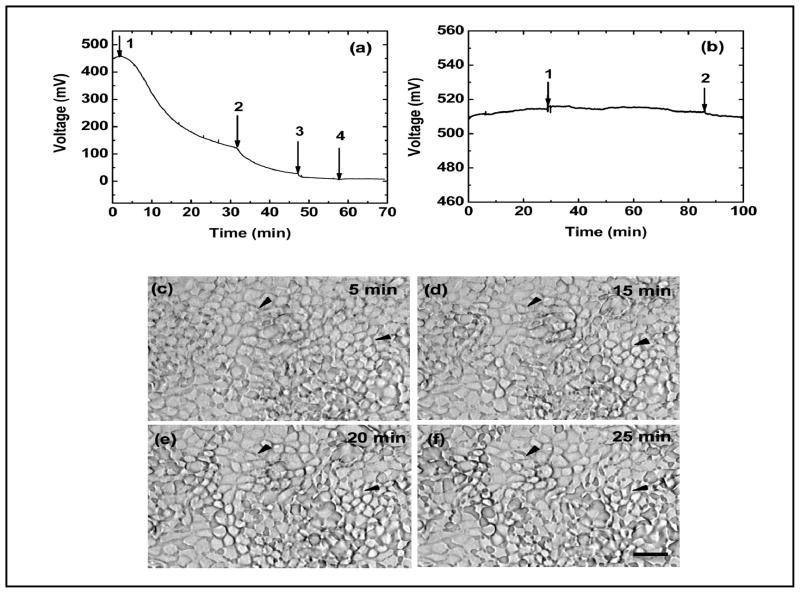
We initially measured the change of MDCK cell volume with stepwise increases in the flow rate using a sensor with an 18 μm high channel. The cells were first exposed to low shear at 0.1 μl/min (0.2 dyn/cm²) until the signal stabilized. We did not observe any noticeable Ca²⁺ response at this flow rate using the same chamber. We then increased the flow rate to 1, 5, 7.5, and 10 μl/min corresponding to shear stress of 2.0, 10, 15, and 20 dyn/cm², and followed the changes of cell volume (Fig. 1a). Fig. 1a shows that a stepwise increase in the flow rate (0.1 to 1 μl/min) caused the cells to rapidly shrink indicating a loss of intracellular water. A successive increase from 1 μl/min (2.0 dyn/cm²) to 10 μl/min (20 dyn/cm²) resulted in further decreases, eventually reaching a steady state volume approximately 30% smaller than the original volume.

Fig. 1.

(a) Resistance measurement of the sensor showing a change in the MDCK volume in response to shear flow. The arrows indicate an increase of flow rate from 0.1 μl/min (0.2 dyn/cm²) to 1: 1.0 μl/min (2.0 dyn/cm²); 2: 5.0 μl/min (10 dyn/cm²); 3: 7.5 μl/min (15 dyn/cm²); 4: 10.0 μl/min (20 dyn/cm²). The overall decrease of cell volume ranged from 10 to 30 % from steady state. (b) Fixed cells do not respond to shear stress. The arrows in (b) indicate change of shear stress from 0.2 to 2.0 and return to 0.2 dyn/cm², respectively. (c)–(f) Corresponding optical micrographs of cells obtained during the volume measurement in (a) at 5, 15, 20, and 25 min, respectively. There was no noticeable loss of cells from the chamber, but large changes in the cell morphology and widened intracellular gaps (two examples are indicated by black arrows). The scale bar is 10 μm.

The flow-dependent volume decrease is not an artifact due to the loss of cells from the sensing chamber. We collected optical micrographs every minute during the course of the measurement. Figures 1c–f are micrographs of the cells obtained at 5, 15, 20, and 25 min in Fig. 1a, showing that MDCK cells were not detached from the surface for shear of 0.2 – 2.0 dyn/cm². However, shear stress caused large changes in cell morphology at 2.0 dyn/cm², as indicated by the wide intercellular gaps (this was a widespread phenomenon, two examples were indicated by black arrows in Fig. 1c–f). This data supports the view that the decrease in mean cell volume arose from cell shrinkage, not the loss of cells.

We tested whether a change in flow rate (perfusion pressure) caused the chamber height to increase, which would be interpreted as a reduction in cell volume. There was no significant change in the signal in empty chambers containing fixed and permeabilized MDCK cells when the flow rate was increased (Fig. 1b).

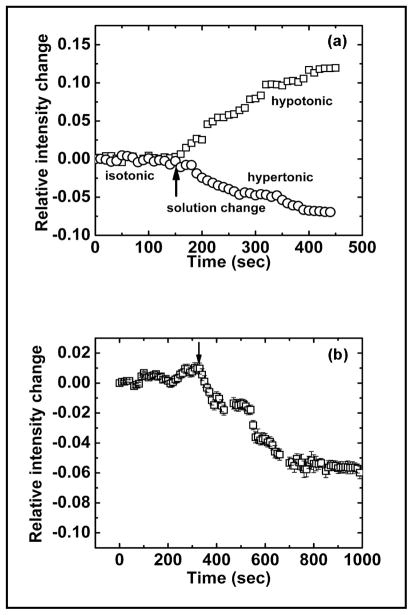
To confirm the effects of shear stress we double checked the data using the fluorescence quenching assay. We first examined whether the fluorescence was sensitive to anisotonic challenges. After stabilized in isotonic solution, the cells were exposed to 168 mOsm solution causing the cells to swell, while a 429 mOsm solution causing the cells to shrink. Figure 2a shows mean of relative fluorescence intensity from ten different locations, extracted from the time-lapse images. As shown in Fig. 2a, cell swelling increases the fluorescence intensity of calcein due to the reduced quenching and cell shrinkage decreased the intensity. We then applied shear stress to cells loaded with calcein and Fig. 2b shows the average intensity from ten different locations in a population of cells. The error bar indicates the standard deviation of ten measurements. When the shear stress increased from 0.7 to 7.0 dyn/cm², as indicated by the arrow, the fluorescence intensity significantly decreased showing that the shear stress caused cell shrinkage supporting our earlier sensor data.

Fig. 2.

Volume change measured with fluorescence quenching. (a) The change of cell volume in response to hypotonic and hypertonic perfusion. (b) The change of cell volume in response to shear stress. Both data sets were obtained from fluorescence micrographs of MDCK cells loaded with 4 μM calcein. The arrows in (a) indicates the solution change from isotonic (320 mOsm) to hypotonic (168 mOm) or hypertonic solution (429 mOsm). The arrow in (b) indicates the change of the shear stress from 0.7 to 7.0 dyn/cm². The plot in (b) is the average of relative intensity changes obtained from ten different locations in each of the micrographs. The error bar indicates the standard deviation.

Hg²⁺ inhibits the shear-induced volume shrinkage

To examine whether the volume decrease is a result of water transport via aquaporins (AQPs), we treated cells with 0.1 μM HgCl₂ and then measured the volume change under shear stress. Fig. 3 shows that Hg²⁺ significantly inhibited the shear-induced volume decrease. This suggests that the water transport via AQPs is involved with the cell shrinkage during shear stress. AQP2 and AQP3 are endogenously expressed in kidney epithelial cells [26] and low level of AQP2, 3 has been observed in wild type MDCK cells [27, 28]. Hg²⁺ blocks the water permeability of both AQP2 and 3, but lack the blocking effect on AQP4 [23, 29]. While cell shrinkage must be linked with loss of water regardless of mechanism, APQs can affect the kinetics of volume change. The slight increase in cell volume we saw at later times suggests that Hg²⁺, probably through non-specific effects, may have relaxed the stress in the cytoskeleton by inhibiting myosin, or increased the cell permeability to external salts such as NaCl [21, 30–32].

Fig. 3.

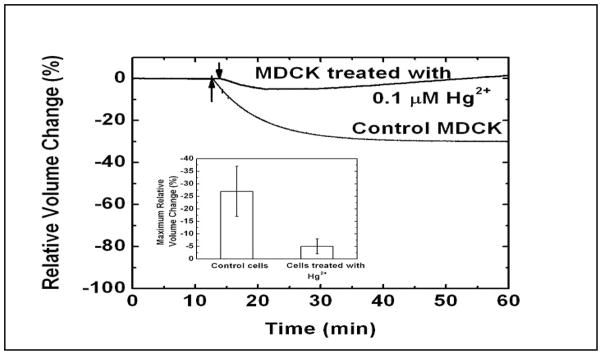
Volume response of cells to shear stress after mercurial treatment. The MDCK cells were treated with 0.1 μM HgCl₂ for 1 min followed by rinsing with isotonic solution. The volume change of the cells under shear stress was measured using the volume sensor. The arrows indicate the change of shear stress from 0.2 to 2.0 dyn/cm². The graph insert shows the maximum relative volume change of control cells (n=3) and cells treated with HgCl₂ (n=4). The error bar indicates the standard deviation. The cells treated with Hg²⁺ showed less cell volume reduction than the control cells suggesting that AQPs were involved.

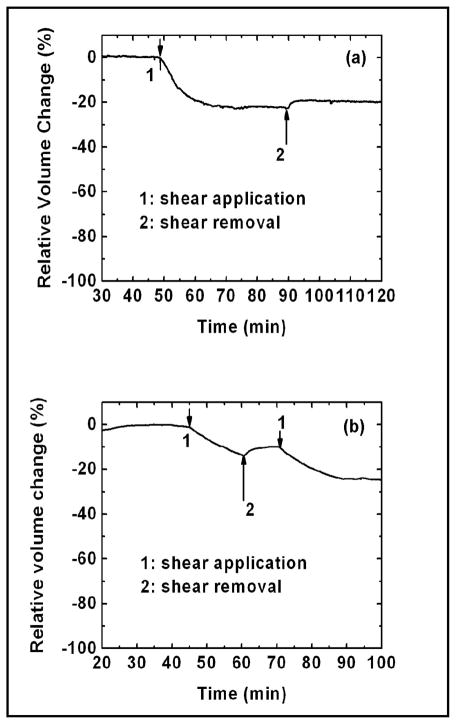
Slow recovery of flow-dependent shrunken cells

If water is the only molecule released from the cells by shear stress, cells might be expected to return to their initial volume when the shear stress is removed. However, if the cell anatomy changes, the local stress changes will correlate with osmotic pressure changes [18] and the recovery of cell volume may be delayed or never achieved. Similarly, changes in solute concentration during the change in shape would lead to a delayed recovery. Figure 4a shows a plot of relative cell volume over relatively a long period of time. The cell volume decreased by ~30% in response to an increase of shear stress from 0.2 to 2 dyn/cm² as indicated by arrow ‘1’ in Fig. 4(a). When the shear stress was removed (as indicated by the arrow ‘2’), the cell volume only partially recovered over the duration of the experiment. The removal of shear stress during the cell volume decrease partially recovered the cell volume (Fig. 4(b)).

Fig. 4.

Volume response to reversible steps in shear stress amplitude showing that the cellular response to shear stress is irreversible on a scale of 30 min. The arrows in (a) and (b) indicate the change of shear stress (1: from 0.2 to 2.0 dyn/cm² and 2: from 2.0 to 0.2 dyn/cm²). Removing high shear stress did not restore the reduced cell volume to the initial value (a).

The shear-induced volume decrease does not involve Ca²⁺ activated pathways

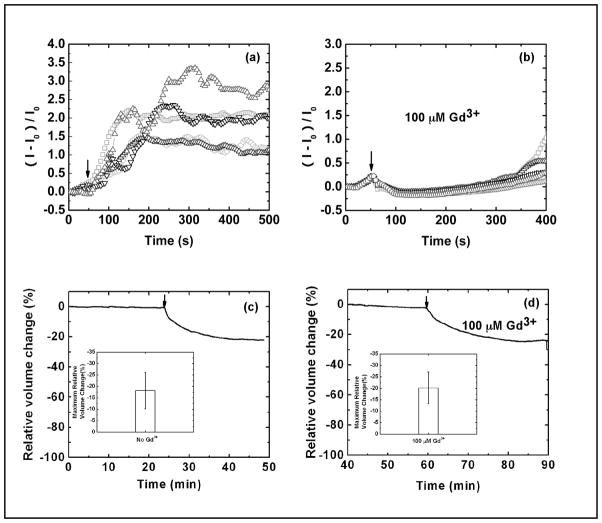
Using the Ca²⁺-sensitive dye, Fluo 4, we investigated the role of Ca²⁺ in the flow-dependent decrease in cell volume. A stepwise change of stress from 0.5 to 5.5 dyn/cm² caused a transient increase in Ca²⁺ (Fig. 5a) and a decrease in cell volume (Fig. 5c). We applied 100 μM Gd³⁺, a known inhibitor for non-selective stretch-activated-channels (SACs) [33, 34], to block the Ca²⁺ entry via SACs. Gd³⁺ completely blocked the shear-induced Ca²⁺ entry (Fig. 5b), but it did not affect the shear-induced cell shrinkage (Fig. 5d). These data suggest that the effect of shear stress on cell volume is not associated with Ca²⁺-activated signal pathways nor with SACs.

Fig. 5.

Effects of shear stress on intracellular Ca²⁺ and volume showing that the cell volume decrease under the shear stress is Ca²⁺ independent. (a) The Ca²⁺ increase in response to a stepwise rise of shear stress from 0.5 to 5.5 dyn/cm². (b) The flow-induced Ca²⁺ uptake is blocked by 100 μM Gd³⁺. Multiple regions in the chamber are measured and plotted in (a) and (b). (c) Cell volume response to an increase in isotonic shear stress from 0.2 to 2.0 dyn/cm². (d) Volume response to shear stress in the presence of 100 μM of Gd³⁺ showing Gd³⁺ does not inhibit the flow induced cell shrinkage. The arrow indicates the change of flow rate. The inserted graphs in (c) and (d) show the average of maximum relative cell volume change obtained from three independent experiments. The error bar indicates the standard deviation.

The role of ion channels in shear-induced shrinkage of cells

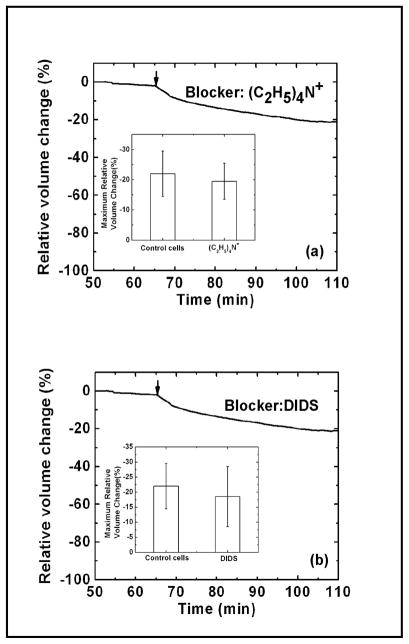
Although renal epithelium has a high intracellular K⁺, to maintain electroneutrality the efflux of K⁺ must be paralleled by the efflux of Cl⁻ or other anion so transport of KCl could occur via a pair of commonly available ion channels. Large-conductance K⁺ channels (maxi-K) have been detected in the apical membrane of MDCK cells [35, 36]. These channels can be activated by membrane depolarization, increases in intracellular Ca²⁺ concentration, or membrane stretch [13, 37–39]. To test the role of K⁺ channels we measured the volume response to shear stress in the presence of 75 mM tetraethylammonium (TEA), a known K⁺ channel blocker [40]. As shown in Fig. 6a, substituting NaCl with TEA (75 mM) did not eliminate the shear-induced shrinkage. This result suggests that K⁺ channels do not play a major role. A Cl⁻ channel blocker, 100 μM DIDS, also had no effect on shrinkage (Fig. 6b). In addition, neither amiloride, an ENaC inhibitor, nor dimethyl amiloride, a Na⁺-H⁺-exchange (NHE) inhibitor showed any effect (data not shown). Our data using pharmacologic blockers suggests that cell shape (cytoskeletal stress), not solute permeability, is the key player in shear-induced decrease in the cell volume.

Fig. 6.

Cell volume response to flow shear stress in the presence of 75 mM TEA (a) and 100 μM DIDS (b) showing that the cell volume decrease in response to shear stress is not likely to be mediated via K⁺ and Cl⁻ channels. The arrow indicates the change of shear stress from 0.2 to 2.0 dyn/cm². The inserted graphs in (a) and (b) show the average of maximum relative cell volume change obtained from three independent experiments in controls and in the presence of TEA and DIDS, respectively.

Numerical modeling of intracellular stress

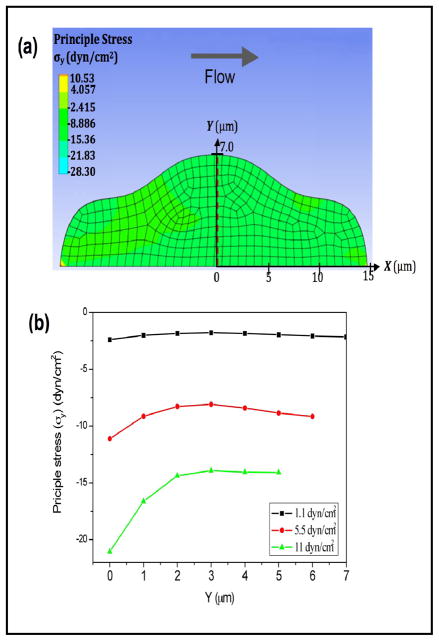
To estimate the influence of flow on intracellular pressure, we built a model of a cell in a flow chamber and calculated the distribution of internal stress using CFD software. The cell was defined as a deformable object with a Young’s modulus of 450 Pa [41]. As shown in Fig. 7a, a flow rate of 5 μl/min (5.5 dyn/cm²) produces a compression in the direction vertical to the bottom surface (Fig. 7b), indicating an increase in intracellular pressure. An increase in the flow rate enhances the intracellular compression (Fig. 7b). The simulation result suggests that flow induces a decrease in cell volume as a result of compressive stress that raises intracellular hydrostatic pressure.

Fig. 7.

(a) 2D simulation of the stress distribution in a deformable cell under shear stress (arrow) showing a compression in the transverse direction to flow. The cell modulus was 450 Pa; the flow rate was 5 μl/min (5.5 dyn/cm²). (b): Stress distribution along the y-direction (from basal to apical surface) at the center plane indicated by red dashed line in (a) at shear stresses of 1.1 (black), 5.5 (red) and 11 (green) dyn/cm2, showing an increase in compression with increased flow.

Discussion

We report for the first time that cells shrink when subjected to an increase in shear stress. Fluorescence quenching supports the results obtained by the volume sensor. Since cell volume is determined by water content, our results indicate that the shear stress must modulate the water content of the cell. It has been previously reported that AQP2 and 3 are endogenously expressed in kidney epithelium [26] and the water transport via AQP2 and 3 can be irreversibly blocked by Hg²⁺ [23, 29]. If the shear-induced cell shrinkage involves the water transport, the blocking of AQPs should inhibit the rate of relaxation of cell volume but cannot affect the endpoints since AQPs are catalysts, not sources of free energy. As shown in Fig. 3, 0.1 μM HgCl₂ blocked the volume decrease during the shear-stress application suggesting the shear-induced cell shrinkage involves the water transport and AQPs may contribute to the transport of water. The slight increase in volume at later times may have arisen from penetration of Hg²⁺ since Hg²⁺ is known to diffuse into cells under stretch causing excessive cell swelling [21].

While the volume decrease could be driven by the loss of solutes through flow-activated pathways, we could show that several common channels were not involved. Flow shear stress affects Ca²⁺-activated K⁺ channels known to be blocked by TEA or quinidine [36] and possibly SACs [16, 37, 42, 43]. The flow-induced volume decrease might result from the solute movement but there must be anionic and cationic channels active so that the net charge of transferred solutes is neutral [18, 43]. Previously, large-conductance K⁺ channels (maxi-K) have been identified in MDCK cells and known to be blocked by TEA or quinidine [36]. Our data shows that flow-induced volume decrease could not be blocked by K⁺ channel blocker (TEA) nor Cl⁻ channel blocker (DIDS) (Fig. 6), suggesting that maxi-K⁺ channel was not the major source for the volume decrease. Na⁺-H⁺ exchanger blockade did not prevent the cell shrinkage by shear stress (data not shown), eliminating the involvement of exchanger in shear-induced release of solutes.

SACs exhibit mechanosensitivity to both osmotic swelling and fluid shear stress [16, 17] and may contribute to RVD in some cell types [44, 45]. These channels are endogenously expressed in all cell types including renal epithelial cells, notably in the distal nephron and collecting ducts [17, 46, 47]. Since 100 μM Gd³⁺ was not able to inhibit the volume decrease by shear flow, while it did inhibit the regulatory volume decrease following osmotic stimuli [48], it is likely that MDCK cells do not use the same channels for mediating flow-induced volume change. Based on the lack of effect of ion channel blockers on shear-induced shrinkage (Fig. 6a,b) and the slow recovery of cell volume (Fig. 4a,b) we suspect that the shear stress effects on cell volume arise from flow-induced changes in cell shape or equivalently changes in cytoskeletal stress. This change in cell shape would significantly raise intracellular hydrostatic pressure resulting in an efflux of water. Our sensor measures changes in the volume of a population cells as defined by the volume enclosed by the plasma membrane. Modeling the cell as a deformable object, finite element calculations show that the internal compressive stresses rise as the cell is deformed. This indicates an increase in pressure within the cell. Given that the water flux across the membrane is driven by both osmotic and hydrostatic pressure, we suggest that the initial water efflux in response to the flow can be driven by internal pressure in parallel with solute transport. Changes in cell shape involve both passive and active changes in cytoskeletal structure. Because the changes in cross-linking take time to relax [49], the elimination of flow shear stress will not restore the shrunken cells to their initial volume in a short period of time as shown in Fig. 4a and 4b. Alternatively, but not exclusively, there may be some loss of intracellular solutes that are not contained in the perfusion solution so the cells could never return to their starting volume. In summary, flow shear causes cells, MDCKs in particular, to shrink and the shrunken cells do not recover over a period of 30 min after the removal of the flow. The volume change is the result of water transport across the membrane possibly driven by hydrostatic pressure.