Nonparametric Bayesian Dictionary Learning for Analysis of Noisy and Incomplete Images

Abstract

Nonparametric Bayesian methods are considered for recovery of imagery based upon compressive, incomplete, and/or noisy measurements. A truncated beta-Bernoulli process is employed to infer an appropriate dictionary for the data under test and also for image recovery. In the context of compressive sensing, significant improvements in image recovery are manifested using learned dictionaries, relative to using standard orthonormal image expansions. The compressive-measurement projections are also optimized for the learned dictionary. Additionally, we consider simpler (incomplete) measurements, defined by measuring a subset of image pixels, uniformly selected at random. Spatial interrelationships within imagery are exploited through use of the Dirichlet and probit stick-breaking processes. Several example results are presented, with comparisons to other methods in the literature.

I. Introduction

A. Sparseness and Dictionary Learning

Recently, there has been significant interest in sparse image representations, in the context of denoising and interpolation [1], [13], [24]–[26], [27], [28], [31], compressive sensing (CS) [5], [12], and classification [40]. All of these applications exploit the fact that images may be sparsely represented in an appropriate dictionary. Most of the denoising, interpolation, and CS literature assume “off-the-shelf” wavelet and DCT bases/dictionaries [21], but recent research has demonstrated the significant utility of learning an often overcomplete dictionary matched to the signals of interest (e.g., images) [1], [4], [12], [13], [24]–[26], [27], [28], [30], [31], [41].

Many of the existing methods for learning dictionaries are based on solving an optimization problem [1], [13], [24]–[26], [27], [28], in which one seeks to match the dictionary to the imagery of interest, while simultaneously encouraging a sparse representation. These methods have demonstrated state-of-the-art performance for denoising, superresolution, interpolation, and inpainting. However, many existing algorithms for implementing such ideas also have some restrictions. For example, one must often assume access to the noise/residual variance, the size of the dictionary is set a priori or fixed via cross-validation-type techniques, and a single (“point”) estimate is learned.

To mitigate the aforementioned limitations, dictionary learning has recently been cast as a factor-analysis problem, with the factor loading corresponding to the dictionary elements (atoms). Utilizing nonparametric Bayesian methods like the beta process (BP) [29], [37], [42] and the Indian buffet process (IBP) [18], [22], one may, for example, infer the number of factors (dictionary elements) needed to fit the data. Furthermore, one may place a prior on the noise or residual variance, with this inferred from the data [42]. An approximation to the full posterior may be manifested via Gibbs sampling, yielding an ensemble of dictionary representations. Recent research has demonstrated that an ensemble of representations can be better than a single expansion [14], with such an ensemble naturally manifested by statistical models of the type described here.

B. Exploiting Structure and Compressive Measurements

In image analysis, there is often additional information that may be exploited when learning dictionaries, with this well suited for Bayesian priors. For example, most natural images may be segmented, and it is probable that dictionary usage will be similar for regions within a particular segment class. To address this idea, we extend the model by employing a probit stick-breaking process (PSBP), with this generalization of the Dirichlet process (DP) stick-breaking representation [34]. Related clustering techniques have proven successful in image processing [26]. The model clusters the image patches, with each cluster corresponding to a segment type; the PSBP encourages proximate and similar patches to be included within the same segment type, thereby performing image segmentation and dictionary learning simultaneously.

The principal focus of this paper is on applying hierarchical Bayesian algorithms to new compressive measurement techniques that have been recently developed. Specifically, we consider dictionary learning in the context of CS [5], [9], in which the measurements correspond to projections of typical image pixels. We consider dictionary learning performed “offline” based on representative (training) images, with the learned dictionary applied within CS image recovery. We also consider the case for which the underlying dictionary is simultaneously learned with inversion (reconstruction), with this related to “blind” CS [17]. Finally, we design the CS projection matrix to be matched to the learned dictionary (when this is done offline), and demonstrate, as in [12], that in practice, this yields performance gains relative to conventional random CS projection matrices.

While CS is of interest for its potential to reduce the number of required measurements, it has the disadvantage of requiring the development of new classes of cameras. Such cameras are revolutionary and interesting [11], [35], but there have been decades of previous research performed on development of pixel-based cameras, and it would be desirable if such cameras could be modified simply to perform compressive measurements. We demonstrate that one may perform compressive measurements of natural images by simply sampling pixels measured by a conventional camera, with the pixels uniformly selected at random. This is closely related to recent research on matrix completion [6], [23], [33], but here, we move beyond simple low-rank assumptions associated with such previous research.

C. Contributions

This paper develops several hierarchical Bayesian models for learning dictionaries for analysis of imagery, with applications in denoising, interpolation, and CS. The inference is performed based on a Gibbs sampler, as is increasingly common in modern image processing [16]. Here, we demonstrate how generalizations of the beta-Bernoulli process allow one to infer the dictionary elements directly based on the underlying degraded image, without any a priori training data, while simultaneously inferring the noise statics and tolerating significant missingness in the imagery. This is achieved by exploiting the low-dimensional structure of most natural images, which implies that image patches may be represented in terms of a low-dimensional set of learned dictionary elements. Excellent results are realized in these applications, including for hyperspectral imagery, which has not been widely considered in these settings previously. We also demonstrate how the learned dictionary may be easily employed to define CS projection matrices that yield markedly improved image recovery, as compared with the much more typical random construction of such matrices.

The basic hierarchical Bayesian architecture developed here serves as a foundation that may be flexibly extended to incorporate additional prior information. As examples, we show here how dictionary learning may be readily coupled with clustering, through the use of a DP [15]. We also incorporate spatial information within the image via a PSBP [32], with these extensions yielding significant advantages for the CS application. The basic modeling architecture may also exploit additional information manifested in the form of general covariates, as considered in a recent paper [43].

The remainder of the paper is organized as follows: In Section II, we review the classes of problems being considered. The beta-Bernoulli process is discussed in Section III, with relationships made with previous work in this area, including those based on the IBP. The Dirichlet and PSBPs are discussed in Section IV, and several example results are presented in Section V. Conclusions and a discussion of future work are provided in Section VI, and details of the inference equations are summarized in the Appendix.

II. Problems Under Study

We consider data samples that may be expressed in the following form:

$${\mathit{x}}_i=\mathbf{D}{\mathit{w}}_i+{\mathit{\epsilon }}_i$$ (1)

where x_i ∈ ℝ^P, ε_i ∈ ℝ^P, and w_i ∈ ℝ^K. The columns of matrix D ∈ ℝ^P×K represent the K components of a dictionary with which x_i is expanded. For our problem, the x_i will correspond to B×B (overlapped) pixel patches in an image [1], [13], [24], [25], [27], [42]. The set of vectors{x_i}_i=1,N may be extracted from an image(s) of interest.

For the denoising problem, vectors ε_i may represent sensor noise, in addition to (ideally small) residual from representation of the underlying signal as Dw_i. To perform denoising, we place restrictions on vectors w_i, such that Dw_i by itself does not exactly represent x_i. A popular such restriction is that w_i should be sparse, motivated by the idea that any particular x_i may often be represented in terms of a small subset of representative dictionary elements, from the full dictionary defined by the columns of D. There are several methods that have been recently developed to impose such a sparse representation, including ℓ₁-based relaxation algorithms [24], [25], iterative algorithms [1], [13], and Bayesian methods [42]. One advantage of a Bayesian approach is that the noise/residual statistics may be nonstationary (with unknown noise statistics). Specifically, in addition to placing a sparseness-promoting prior on w_i, we may also impose a prior on the components of ε_i. From the estimated posterior density function on model parameters, each component of ε_i, corresponding to the ith B×B image patch, has its own variance. Given{x_i}_i=1,N, our goal may be to simultaneously infer D and {w_i}_i=1,N (and implicitly ε_i), and then, the denoised version of x_i is represented as Dw_i.

In many applications, the total number of pixels N · P may be large. However, it is well known that compression algorithms may be used on {x_i}_i=1,N after the measurements have been performed, to significantly reduce the quantity of data that need be stored or communicated. This compression indicates that while the data dimensionality N · P may be large, the underlying information content may be relatively low. This has motivated the field of CS [5], [9], [11], [35], in which the total number of measurements performed may be much less than N · P. Toward this end, researchers have proposed projection measurements of the following form:

$${\mathit{y}}_i=\mathbf{\sum }{\mathit{x}}_i$$ (2)

where Σ ∈ ℝ^n×P and y_i ∈ ℝⁿ, ideally with n ≪ P. The projection matrix Σ has traditionally been randomly constituted [5], [9], with a binary or real alphabet (and Σ may be also a function of the specific patch, and generalized as Σ_i). It is desirable that matrices Σ and D be as incoherent as possible.

The recovery of x_i from y_i is an ill-posed problem, unless restrictions are placed on x_i. We may exploit the same class of restrictions used in the denoising problem; specifically, the observed data satisfy y_i = Φw_i + ν_i, with Φ = ΣD and ν_i = Σε_i, and with sparse w_i. Note that the sparseness constraint implies that {w_i}_i=1,N (and hence, {x_i}_i=1,N) occupy distinct subspaces of ℝ^P, selected from the overall linear subspace defined by the columns of Φ.

In most applications of CS, D is assumed known, corresponding to an orthonormal basis (e.g., wavelets or a DCT) [5], [9], [21]. However, such bases are not necessarily well matched to natural imagery, and it is desirable to consider design of dictionaries D for this purpose [12]. One may even consider recovering {x_i}_i=1,N from {y_i}_i=1,N while simultaneously inferring D. Thus, we again have a dictionary-learning problem, which may be coupled with optimization of CS matrix Σ, such that it is matched to D (defined by a low coherence between the rows of Σ and columns of D [5], [9], [12], [21]).

III. Sparse Factor Analysis With the Beta-Bernoulli Process

When presenting example results, we will consider three problems. For denoising, it is assumed that we measure x_i = Dw_i + ε_i, where ε_i represents measurement noise and model error; for the compressive-sensing application, we observe y_i = Σ(Dw_i + ε_i) = Φw_i + ν_i, with Φ = ΣD and ν_i = Σε_i; and finally, for the interpolation problem, we observe Q_φ(Dw_i+ ε_i), where Q_φ(x_i) is a vector of elements from x_i contained within set φ. For all three problems, our objective is to infer underlying signal Dw_i, with w_i assumed sparse; we generally wish to simultaneously infer D and {w_i}_i=1,N. To address each of these problems, we consider a statistical model for x_i = Dw_i + ε_i, placing Bayesian priors on D, w_i, and ε_i; the way the model is used is slightly modified for each specific application. For example, when considering interpolation, only the observed Q_φ(x_i) are used within the model likelihood function.

A. Beta-Bernoulli Process for Active-Set Selection

Let binary vector z_i ∈ {0,1}^K denote which of the K columns of D are used for representation of x_i (active set); if a particular component of z_i is equal to one, then the corresponding column of D is used in the representation of x_i. Hence, for data {x_i}_i=1,N, there is an associated set of latent binary vectors {z_i}_i=1,N, and the beta-Bernoulli process provides a convenient prior for these vectors [29], [37], [42]. Specifically, consider the following model:

$${\mathit{z}}_i~\prod _{k=1}^K\text{Bernoulli}({\pi }_k),\mathit{\pi }~\prod _{k=1}^K\text{Beta}(a/K,b(K-1)/K)$$ (3)

where π_k is the kth component of π, and a and b are model parameters; the impact of these parameters on the model are discussed below. Note that the use of product notation in (3) is meant to denote that each component of z_i and π are independently drawn from distributions of the same form.

Considering limit K → ∞, and after integrating out π, the draws of {z_i}_i=1,N may be constituted as follows. For each z_i, draw c_i ~ Poisson(a/b + i − 1) and define $C_i={\sum }_{j=1}^i{c}_j$, with C₀ = 0. Let z_ik represent the kth component of z_i, and z_ik = 0 for k > C_i. For k = 1,…,C_i−1, z_ik ~ Bernoulli(n_ik/b + i−1), where $n_{ik}={\sum }_{j=1}^{i-1}{z}_{jk}$ (n_ik represents the total number of times the kth component of {z_j}_j=1,i−1 is one). For k = C_i−1 + 1,…,C_i, we set z_ik = 1. Note that as a/(b + i−1) becomes small, with increasing i, it is probable that c_i will be small. Hence, with increasing i, the number of new nonzero components of z_i diminishes. Furthermore, as a consequence of Bernoulli(n_ik/b+i−1), when a particular component of vectors {z_j}_j=1,i−1 is frequently one, it is more probable that it will be one for subsequent z_j, j≥i. When b = 1, this construction for {z_i}_i=1,N corresponds to the IBP [18].

Since z_i defines which columns of D are used to represent x_i, (3) imposes that it is probable that some columns of D are repeatedly used among set {x_i}_i=1,N, whereas other columns of D may be more specialized to particular x_i. As demonstrated below, this has been found to be a good model when {x_i}_i=1,N are patches of pixels extracted from natural images.

B. Full Hierarchical Model

The hierarchical form of the model may now be expressed as

$$\begin{array}{l}{\mathit{x}}_i=\mathbf{D}{\mathit{w}}_i+{\mathit{\epsilon }}_i\\ {\mathit{w}}_i={\mathit{z}}_i\odot {\mathit{s}}_i\\ {\mathit{d}}_k~\mathcal{N}(0,P^{-1}{\mathbf{I}}_P)\\ {\mathit{s}}_i~\mathcal{N}(0,{\gamma }_s^{-1}{\mathbf{I}}_K)\\ {\mathit{\epsilon }}_i~\mathcal{N}(0,{\gamma }_{\epsilon }^{-1}{\mathbf{I}}_P)\end{array}$$ (4)

where d_k represents the kth component (atom) of D, ⊙ represents the elementwise or Hadamard vector product, I_P (I_K) represents a P×P (K×K) identity matrix, and {z_i}_i=1,N are drawn as in (3). Conjugate hyperpriors γ_s ~ Gamma(c,d) and γ_ε ~ Gamma(e,f) are also imposed. The construction in (4), and with the prior in (3) for {z_i}_i=1,N, is henceforth referred to as the BP factor analysis (BPFA) model. This model was first developed in [22], with a focus on general factor analysis; here, we apply and extend this construction for image-processing applications.

Note that we impose independent Gaussian priors for d_k and s_i and ε_i for modeling convenience (conjugacy of consecutive terms in the hierarchical model). However, the inferred posterior for these terms is generally not independent or Gaussian. The independent priors essentially impose prior information about the marginals of the posterior of each component, whereas the inferred posterior accounts for statistical dependence as reflected in the data.

To make connections of this model to more typical optimization-based approaches [24], [25], note that the negative logarithm of the posterior density function is

$$\begin{array}{l}-logp(\mathbf{\Theta }\mid \mathcal{D},\mathcal{H})=\frac{{\gamma }_{\epsilon }}{2}\sum _{i=1}^N{\left|\right|{\mathit{x}}_i-\mathbf{D}({\mathit{s}}_i\odot {\mathit{z}}_i)\left|\right|}_2^2\\ +\frac{P}{2}\sum _{k=1}^K{\left|\right|{\mathit{d}}_k\left|\right|}_2^2+\frac{{\gamma }_s}{2}\sum _{i=1}^N{\left|\right|{\mathit{s}}_i\left|\right|}_2^2\\ -log{f}_{\text{Beta}-\text{Bern}}({\{{\mathit{z}}_i\}}_{i=1}^N;\mathcal{H})\\ -log\text{Gamma}({\gamma }_{\epsilon }\mid \mathcal{H})\\ -log\text{Gamma}({\gamma }_s\mid \mathcal{H})+\text{Const}.\end{array}$$ (5)

where Θ represents all unknown model parameters, 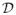= {x_i}_i=1,N, $f_{\text{Beta}-\text{Bern}}({\{{\mathit{z}}_i\}}_{i=1}^N;\mathcal{H})$ represents the beta-Bernoulli process prior in (3), and 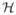represents model hyperparameters (i.e., a, b, c, d, e, and f). Therefore, the typical ℓ₂ constraints [24], [25] on the dictionary elements d_k and on the nonzero weights s_i correspond here to the Gaussian priors employed in (4). However, rather than employing an ℓ₁ (Laplacian prior) constraint [24], [25] to impose sparseness on w_i, we employ the beta-Bernoulli process and w_i = s_i ⊙ z_i. The beta-Bernoulli process imposes that binary z_i should be sparse and that there should be a relatively consistent (re)use of dictionary elements across the image, thereby also imposing self-similarity. Furthermore, and perhaps most importantly, we do not constitute a point estimate, as one would do if a single Θ was sought to minimize (5). 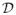We rather estimate the full posterior density p(Θ| 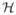), implemented via Gibbs sampling. A significant advantage of the hierarchical construction in (4) is that each Gibbs update equation is analytic, with detailed update equations provided in the Appendix. Note that consistent use of atoms is encouraged because the active sets are defined by binary vectors {z_i}_i=1,N, and these are all drawn from a shared probability vector π; this is distinct from drawing the active sets independent and identically distributed (i.i.d.) from a Laplacian prior. Furthermore, the beta-Bernoulli prior imposes that many components of w_i are exactly zero, whereas with a Laplacian prior, many components are small but not exactly zero (hence, the former is analogous to ℓ₀ regularization, with the latter closer to ℓ₁ regularization).

IV. Patch Clustering Via Dirichlet and PSBPs

A. Motivation

In the model previously discussed, each patch x_i had a unique usage of dictionary atoms, defined by binary vector z_i, which selects columns of D. One may wish to place further constraints on the model, thereby imposing a greater degree of statistical structure. For example, one may employ that the x_i cluster and that within each cluster of each of the associated x_i employ the same columns of D. This is motivated by the idea that a natural image may be clustered into different types of textures or general image structure. However, rather than imposing that all x_i within a given cluster use exactly the same columns of D, one may want to impose that all x_i within such a cluster share the same probability of dictionary usage, i.e., that all x_i within cluster c share the same probability of using columns of D, defined by π_c, rather than sharing a single π for all x_i (as in the original model above). Again, such clustering is motivated by the idea that natural images tend to segment into different textural or color forms. Below, we perform clustering in terms of vectors π_c, rather than explicit clustering of dictionary usage, which would entail cluster-dependent z_c; the “softer” nature of the former clustering structure is employed to retain model flexibility while still encouraging sharing of parameters within clusters.

A question when performing such clustering concerns the number of clusters needed, this motivating the use of nonparametric methods, like those considered in the next subsections. Additionally, since the aforementioned clustering is motivated by the segmentations characteristic of natural images, it is desirable to explicitly utilize the spatial location of each image patch, encouraging that patches x_i in a particular segment/cluster are spatially contiguous. This latter goal motivates use of a PSBP, as also detailed as follows.

B. DP

The DP [15] constitutes a popular means of performing non-parametric clustering. A random draw from a DP, i.e., G ~ DP(αG₀), with precision α ∈ ℝ⁺ and “base” measure G₀, may be constituted via the stick-breaking construction [34], i.e.,

$$G=\sum _{l=1}^{\infty }{\beta }_l{\delta }_{{\theta }_l^{\ast }},{\theta }_l^{\ast }~G_0$$ (6)

where ${\beta }_l=V_l{\prod }_{h=1}^{l-1}(1-V_h)$ and V_h ~ Beta(1, α). The β_l may be viewed as a sequence of fractional breaks from a “stick” of original length one, where the fraction of the stick broken off on break l is V_l. The ${\theta }_l^{\ast }$ are model parameters, associated with the lth data cluster. For our problem, it has proven effective to set $G_0={\prod }_{k=1}^K\text{Beta}(a/K,b(K-1)/K)$ analogous to (3), and hence, $G={\sum }_{l=1}^{\infty }{\beta }_l{\delta }_{{\mathit{\pi }}_l^{\ast }}·{\mathit{\pi }}_l^{\ast }$, drawn from G₀, corresponds to distinct probability vectors for using the K dictionary elements (columns of D). For sample i, we draw π_i ~ G, and a separate sparse binary vector z_i is drawn for each sample x_i, as ${\mathit{z}}_i~{\prod }_{k=1}^K\text{Bernoulli}({\pi }_{ik})$, with π_ik as the kth component of π_i. In practice, we truncate the infinite sum for the to G to N_L elements and impose V_NL = 1, such that ${\sum }_{l=1}^{N_L}{\beta }_l=1$. A (conjugate) gamma prior is placed on the DP parameter α.

We may view this DP construction as an “Indian buffet franchise, ” generalizing the Indian buffet analogy [18]. Specifically, there are N_L Indian buffet restaurants; each restaurant is composed of the same “menu” (columns of D) and is distinguished by different probabilities for selecting menu items. The “customers” {x_i}_i=1,N cluster based upon which restaurant they go to. The ${\{{\mathit{\pi }}_l^{\ast }\}}_{l=1,N_L}$ represent the probability of using each column of D in the respective N_L different buffets. The {x_i}_i=1,N cluster themselves among the different restaurants in a manner that is consistent with the characteristics of the data, with the model also simultaneously learning the dictionary/menu D. Note that we typically make truncation N_L large, and the posterior distribution infers the number of clusters actually needed to support the data, as represented by how many β_l are of significant value. The model in (4), with the above DP construction for {z_i}_i=1,N, is henceforth referred to as DP-BPFA.

C. PSBP

The DP yields a clustering of {x_i}_i=1,N, but it does not account for our knowledge of the location of each patch within the image. It is natural to expect that if x_i and x_i′ are proximate, then, they are likely to be constituted in terms of similar columns of D.¹ To impose this information, we employ the PSBP. A logistic stick-breaking process is discussed in detail in [32]. We employ the closely related probit version here because it may be easily implemented in a Gibbs sampler. We note that while the method in [32] is related to that discussed below, in [32], the concepts of learned dictionaries and beta-Bernoulli priors were not considered. Another related model, which employs a probit link function, is discussed in [7].

We augment the data as {x_i, r_i}_i=1,N, where x_i again represents pixel values from the ith image patch, and r_i ∈ ℝ² represents the 2-D location of each patch. We wish to impose that proximate patches are more likely to be composed of the same or similar columns of D. In the PSBP construction, all aspects of (4) are retained, except for the manner in which z_i are constituted. Rather than drawing a single K-dimensional vector of probabilities π, as in (3), we draw a library of such vectors, i.e.,

$${\mathit{\pi }}_l^{\ast }~\prod _{k=1}^K\text{Beta}(a/K,b(K-1)/K),l=1,\dots ,N_L$$ (7)

and each ${\mathit{\pi }}_l^{\ast }$ is associated with a particular segment in the image. One π_i is associated with location r_i and drawn

$${\mathit{\pi }}_i~\sum _{l=1}^{N_L}{\beta }_l({\mathit{r}}_i){\delta }_{{\mathit{\pi }}_l^{\ast }}$$ (8)

with ${\sum }_{l=1}^{N_L}{\beta }_l({\mathit{r}}_i)=1$ for all r_i, and ${\delta }_{{\mathit{\pi }}_l^{\ast }}$ represents a point measure concentrated at ${\mathit{\pi }}_l^{\ast }$. Once π_i is associated with a particular x_i, the corresponding binary vector z_i is drawn as in the first line of (3). Note that the distinction between DP and PSBP is that, in the former, mixture weights {β_l}_l=1,NL are independent of spatial position r, whereas the latter explicitly utilizes r within {β_l(r)}_l=1,NL (and below, we impose that β_l(r) smoothly changes with r).

The space-dependent weights are constructed as ${\beta }_l(\mathit{r})=V_l(\mathit{r}){\prod }_{h=1}^{l-1}[1-V_h(\mathit{r})]$, where 0 < V_l(r) < 1 constitute space-dependent probabilities. We set V_NL = 1, and for l ≤ N_L − 1, the V_l are space-dependent probit functions, i.e.,

$$V_l(\mathit{r})=\underset{-\infty }{\overset{g_l(\mathit{r})}{\int }}dx\mathcal{N}(x\mid 0,1),g_l(\mathit{r})={\zeta }_{l0}+\sum _{i=1}^N{\zeta }_{li}\mathcal{K}(\mathit{r},{\mathit{r}}_i;{\psi }_l)$$ (9)

where 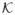(r, r_i; ψ_l) is a kernel characterized by parameter ψ_l and {ζ_li}_i=0,N is a sparse set of real numbers. To implement the sparseness on {ζ_li}_i=0,N, within prior ${\zeta }_{li}~\mathcal{N}(0,{\alpha }_{li}^{-1})$, and (conjugate) α_li ~ Gamma(a₀, b₀), with (a₀, b₀) set to favor most α_li being large (if α_li is large, draw $\mathcal{N}(0,{\alpha }_{li}^{-1})$ is likely to be near zero, such that most {ζ_li}_i=0,N are near zero). This sparseness-promoting construction is the same as that employed in the relevance vector machine (RVM) [39]. We here utilize radial basis function kernel 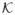(r, r_i; ψ_l) = exp[−||r_i&minus;r||₂/ψ_l].

Each g_l(r) is encouraged to only be defined by a small set of localized kernel functions, and via the probit link function ${\int }_{-\infty }^{g_l(\mathit{r})}dx\mathcal{N}(x\mid 0,1)$, the probability V_l(r) is characterized by localized segments over which the probability V_l(r) is contiguous and smoothly varying. The V_l(r) constitute a space-dependent stick-breaking process. Since V_NL = 1, ${\sum }_{l=1}^{N_L}{\beta }_l(\mathit{r})=1$ for all r.

The PSBP model is relatively simple to implement within a Gibbs sampler. For example, as indicated above, sparseness on ζ_li is imposed as in the RVM, and the probit link function is simply implemented within a Gibbs sampler (which is why it was selected, rather than a logistic link function). Finally, we define a finite set of possible kernel parameters {ψ_j}_j=1,Np, and a multinomial prior is placed on these parameters, with the multinomial probability vector drawn from a Dirichlet distribution [32] (each of the g_l(r) draws a kernel parameter from {ψ_j}_j=1,Np). The model in (4), with the PSBP construction for {z_i}_i=1,N, is henceforth referred to as PSBP-BPFA.

D. Discussion of Proposed Sparseness-Imposing Priors

The basic BPFA model is summarized in (4), and three related priors have been developed for sparse binary vectors {z_i}_i=1,N: 1) the basic truncated beta-Bernoulli process in (3); 2) a DP-based clustering of the underlying {π_i}_i=1,N; and 3) a PSBP clustering of {π_i}_i=1,N that exploits knowledge of the location of the image patches. For 2 and 3, x_i within a particular cluster have similar z_i, rather than exactly the same binary vector; we also considered the latter, but this worked less well in practice. As discussed further when presenting results, for denoising and interpolation, all three methods yield comparable performance. However, for CS, 2 and 3 yield marked improvements in image-recovery accuracy relative to 1. In anticipation of these results, we provide a further discussion of the three priors on {z_i}_i=1,N and on the three image-processing problems under consideration.

For the denoising and interpolation problems, we are provided with data {x_i}_i=1,N, albeit in the presence of noise and potentially with substantial missing pixels. However, for this problem, N may be made quite large since we may consider all possible (overlapping) B×B patches. A given pixel (apart from near the edges of the image) is present in B² different patches. Perhaps because we have such a large quantity of partially overlapping data, for denoising and interpolation, we have found that beta-Bernoulli process in (3) is sufficient for inferring the underlying relationships between the different data {x_i}_i=1,N and processing these data collaboratively. However, the beta-Bernoulli construction does not explicitly segment the image, and therefore, an advantage of the PSBP-BPFA construction is that it yields comparable denoising and interpolation performance as (3) while also simultaneously yielding an effective image segmentation.

For the CS problem, we measure y_i = Σx_i, and therefore, each of the n measurements associated with each image patch (Σ ∈ ℝ^n×P)loses the original pixels in x_i (the projection matrix Σ may also change with each patch, denoted by Σ_i). Therefore, for CS, one cannot consider all possible shifts of the patches as the patches are predefined and fixed in the CS measurement (in the denoising and interpolation problems, the patches are defined in the subsequent analysis). Therefore, for CS imposition of the clustering behavior, via DP or PSBP provides important information, yielding state-of-the-art CS-recovery results.

E. Possible Extensions

The “Indian buffet franchise” and PSBP constructions considered above and in the results below draw the K-dimensional probability vectors ${\mathit{\pi }}_l^{\ast }$ independently. This implies that within the prior, we impose no statistical correlation between the components of vectors ${\mathit{\pi }}_l^{\ast }$ and ${\mathit{\pi }}_{l^{\prime }}^{\ast }$, for l ≠ l′. It may be desirable to impose such structure, imposing that there is a “global” probability of using particular dictionary elements, and the different mixture components within the DP/PSBP constructions correspond to specific draws from global statistics of dictionary usage. This will encourage the idea that there may be some “popular” dictionary elements that are shared across different mixture components (i.e., popular across different buffets in the franchise). One can impose this additional structure via a hierarchical BP (HBP) construction [37], related to the hierarchical DP (HDP) [36]. Briefly, in an HBP construction, one may draw the ${\mathit{\pi }}_l^{\ast }$ via the hierarchical construction, i.e.,

$$\begin{array}{l}{\mathit{\pi }}_l^{\ast }~\prod _{k=1}^K\text{Beta}(c{\eta }_k,c(1-{\eta }_k)),\\ \mathit{\eta }~\prod _{k=1}^K\text{Beta}(a/K,b(K-1)/K)\end{array}$$ (10)

where η_k is the kth component of η. Vector η constitutes “global” probabilities of using each of the K dictionary elements (across the “franchise”), and ${\mathit{\pi }}_l^{\ast }$ defines the probability of dictionary usage for the lth buffet. This construction imposes statistical dependences among vectors { ${\mathit{\pi }}_l^{\ast }$}.

To simplify the presentation, in the following example results, we do not consider the HBP construction as good results have already been achieved with the (truncated) DP and PSBP models previously discussed. We note that in these analyses, the truncated versions of these models may actually help inference of statistical correlations among { ${\mathit{\pi }}_l^{\ast }$} within the posterior (since the set { ${\mathit{\pi }}_l^{\ast }$} is finite, and each vector ${\mathit{\pi }}_l^{\ast }$ is of finite length). If we actually considered the infinite limit on K and on the number of mixture components, inference of such statistical relationships within the posterior may be undermined because specialized dictionary elements may be constituted across the different franchises, rather than encouraging sharing of highly similar dictionary elements.

While we do not focus on the HBP construction here, a recent paper has employed the HBP construction in related dictionary learning for image-processing applications, yielding very encouraging results [43]. We therefore emphasize that the basic hierarchical Bayesian construction employed here is very flexible and may be extended in many ways to impose additional structure.

V. Example Results

A. Reproducible Research

The test results and the MATLAB code to reproduce them can be downloaded from http://www.ee.duke.edu/~mz1/Results/BPFAImage/.

B. Parameter Settings

For all BPFA, DP-BPFA, and PSBP-BPFA computations, the dictionary truncation level was set at K = 256 or K = 512 based on the size of the image. Not all K dictionary elements are used in the model; the truncated beta-Bernoulli process infers the subset of dictionary elements employed to represent the data {x_i}_i=1,N. The larger the image, the more distinct types of structure are anticipated and, therefore, the more dictionary elements are likely to be employed; however, very similar results are obtained with K = 512 in all examples, just with more dictionary elements are not employed for smaller images (therefore, to save computational resources, we set K = 256 for the smaller images). The number of DP and PSBP sticks was set at N_L = 20. The library of PSBP parameters is defined as in [32]; the PSBP kernel locations, i.e., {r_i}_i=1,N, were situated on a uniformly sampled grid in each image dimension, situated at every fourth pixel in each direction (the results are insensitive to many related definitions of {r_i}_i=1,N). The hyperparameters within the gamma distributions were set as c = d = e = f = 10⁻⁶, as is typically done in models of this type [39] (the same settings were used for the gamma prior for DP precision parameter α. The beta-distribution parameters are set as a = K and b = 1 if random initialization is used or a = K and b = N/8 if a singular value decomposition (SVD) based initialization is used. None of these parameters have been optimized or tuned. When performing inference, all parameters are randomly initialized (as a draw from the associated prior) or based on the SVD of the image under test. The Gibbs samplers for the BPFA, DP-BPFA, and PSBP-BPFA have been found to mix and quickly converge, producing satisfactory results with as few as 20 iterations. The inferred images represent the average from the collection samples. All software was written in nonoptimized MATLAB. On a Dell Precision T3500 computer with a 2.4-GHz central processing unit, for N = 148, 836 patches of size 8×8×3 with 20% of the RGB pixels observed at random, the BPFA required about 2 min per Gibbs iteration (the DP version was comparable), and PSBP-BPFA required about 3 min per iteration. For the 106-band hyperspectral imagery, which employed N = 428 578 patches of size 4×84×106 with 2% of the voxels observed uniformly at random, each Gibbs iteration required about 15 min.

C. Denoising

The BPFA denoising algorithm is compared with the original KSVD [13] and for both gray-scale and colored images. Newer denoising algorithms include block matching with 3-D filtering [8], the multiscale KSVD [28], and KSVD with the nonlocal mean constraints [26]. These algorithms assume that the noise variance is known, whereas the proposed model automatically infers, as part of the same model, the noise variance from the image under test. There are existing methods for estimation of the noise variance, as a preprocessing step, e.g., via wavelet shrinkage [10]. However, it was shown in [42] that the denoising accuracy of methods like that in [13] can be sensitive to small errors in the estimated variance, which are likely to occur in practice. Additionally, when doing joint denoising and image interpolation, as we consider below, methods like that in [10] may not be directly applied to estimate the noise variance, as there is a large fraction of missing data. Moreover, the BPFA, DP-BPFA, and PSBP-BPFA models infer a potentially nonstationary noise variance, with a broad prior on the variance imposed by the gamma distribution.

In the denoising examples, we consider the BPFA model in (3); similar results are obtained via the DP-BPFA and PSBP-BPFA models discussed in Section IV. To infer the final signal value at each pixel, we average the associated pixel contribution from each of the overlapping patches in which it is included (this is true for all results presented below in which overlapping patches were used).

In Table I, we consider images from [13]. The proposed BPFA performs very similarly to KSVD. As one representative example of the model’s ability to infer the noise variance, we consider the Lena image from Table I. The mean inferred noise standard deviations are 5.83, 10.59, 15.53, 20.48, 25.44, 50.46, and 100.54 for images contaminated by noise with the respective standard deviations of 5, 10, 15, 20, 25, 50, and 100. Each of these noise variances was automatically inferred using exactly the same model, with no changes to the gamma hyperparameters (whereas for the KSVD results, it was assumed that the noise variance was known exactly a priori).

TABLE I.

Gray-Scale Image Denoising PSNR Results, Comparing KSVD [13] and BPFA, Using Patch Size 8×8. The Top and Bottom Parts of Each Cell Are Results of KSVD and BPFA, Respectively

σ	C.man	House	Peppers	Lena	Barbara	Boats	F.print	Couple	Hill
5	37.87	39.37	37.78	38.60	38.08	37.22	36.65	37.31	37.02
	37.32	39.18	37.24	38.20	37.94	36.43	36.29	36.77	36.24
10	33.73	35.98	34.28	35.47	34.42	33.64	32.39	33.52	33.37
	33.40	36.29	34.31	35.62	34.63	33.70	32.42	33.63	33.31
15	31.42	34.32	32.22	33.70	32.37	31.73	30.06	31.45	31.47
	31.34	34.52	32.46	33.93	32.61	31.97	30.23	31.73	31.64
20	29.91	33.20	30.82	32.38	30.83	30.36	28.47	30.00	30.18
	30.03	33.25	31.10	32.65	31.10	30.70	28.72	30.34	30.47
25	28.85	32.15	29.73	31.32	29.60	29.28	27.26	28.90	29.18
	28.99	32.24	30.00	31.63	29.88	29.70	27.58	29.28	29.57
50	25.73	27.95	26.13	27.79	25.47	25.95	23.24	25.32	26.27
	25.67	28.49	26.46	28.29	26.03	26.50	24.14	25.94	26.81
100	21.69	23.71	21.75	24.46	21.89	22.81	18.30	22.60	23.98
	21.93	24.37	22.73	24.95	22.13	23.32	20.44	23.01	24.22

In Table II, we present similar results, for denoising RGB images; the KSVD comparisons come from [27]. An example denoising result is shown in Fig. 1. As another example of the BPFA’s ability to infer the underlying noise variance, for the castle image, the mean (automatically) inferred variances are 5.15, 10.18, 15.22, and 25.23 for images with additive noise with true respective standard deviations of 5, 10, 15, and 25. The sensitivity of the KSVD algorithm to a mismatch between the assumed and true noise variances is shown in [42, Fig. 1], and the insensitivity of BPFA to changes in the noise variance and to requiring knowledge of the noise variance is deemed an important advantage.

TABLE II.

RGB Image Denoising PSNR Results Comparing KSVD [27] and BPFA, Both Using a Patch Size of 7×7. The Top and Bottom Parts of Each Cell Show the Results of KSVD and BPFA, Respectively

σ	Castle	Mushroom	Train	Horses	Kangroo
5	40.37	39.93	39.76	40.09	39.00
	40.34	39.73	39.38	39.96	39.00
10	36.24	35.60	34.72	35.43	34.06
	36.28	35.70	34.48	35.48	34.21
15	33.98	33.18	31.70	32.76	31.30
	34.04	33.41	31.63	32.98	31.68
25	31.19	30.26	28.16	29.81	28.39
	31.24	30.62	28.28	30.11	28.86

Fig. 1.

(From left to right) The original horses image, the noisy horses image with the noise standard deviation of 25, the denoised image, and the inferred dictionary (from top left) with its elements ordered in the probability to be used. The low-probability dictionary elements are never used to represent {x_i}_i=1,N and are drawn from the prior, showing the ability of the model to learn the number of dictionary elements needed for the data.

It is also important to note that the gray-scale KSVD results in Table I were initialized using an overcomplete DCT dictionary, whereas the RGB KSVD results in Table II employed an extensive set of training imagery to learn dictionary D that was used to initialize the denoising computations. All BPFA, DP-BPFA, and PSBP-BPFA results employ no training data, with the dictionary initialized at random using draws from the prior or with the SVD of the data under test.

D. Image Interpolation

For the initial interpolation examples, we consider standard RGB images, with 80% of the RGB pixels uniformly missing at random (the data under test are shown in Fig. 2). Results are first presented for the Castle and Mushroom images, with comparisons between the BPFA model in (3) and the PSBP-BPFA model discussed in Section IV. The difference between the two is that the former is a “bag-of-patches” model, whereas the latter accounts for the spatial locations of the patches. Furthermore, the PSBP-BPFA simultaneously performs image recovery and segmentation. The results are shown in Fig. 3, presenting the mean reconstructed images and inferred segmentations. Each color in the inferred segmentation represents one PSBP mixture component, and the figure shows the last Gibbs iteration (to avoid issues with label switching between Gibbs iterations). While the BPFA does not directly yield a segmentation, its peak signal-to-noise ratio (PSNR) results are comparable to those inferred by PSBP-BPFA, as summarized in Table III.

Fig. 2.

Images with 80% of the RGB pixels missing at random. Although only 20% of the actual pixels are observed, in these figures, the missing pixels are estimated based upon averaging all observed neighboring pixels within a 5×5 spatial extent. (Left) Castle image (22.58-dB PSNR). (Right) Mushroom image (24.85 dB).

Fig. 3.

PSBP-BPFA analysis with 80% of the RGB pixels uniformly missing at random (see Fig. 2). The analysis is based on 8×8×3 image patches, considering all possible (overlapping) parches. For a given pixel, the results are the average based upon all patches in which it is contained. For each example: (left) recovered image based on an average of Gibbs collection samples and (right) each color representing one of the PSBP mixture components.

TABLE III.

Comparison of Interpolation of the Castle and Mushroom Images, Based Upon Observing 20% of the Pixels, Uniformly Selected at Random. Results Are Shown Using BPFA and PSBP-BPFA, and the Analysis Is Separately Performed Using 8×8×3 and 5×5×3 Image Patches

	Castle 8×8×3	Castle 5×5×3	Mushroom 8×8×3	Mushroom 5×5×3
BPFA	29.32	28.48	31.63	31.17
PSBP-BPFA	29.54	28.46	32.03	31.27

An important additional advantage of Bayesian models such as BPFA, DP-BPFA, and PSBP-BPFA is that they provide a measure of confidence in the accuracy of the inferred image. In Fig. 4, we plot the variance of the inferred error {ε_i}_i=1,N, computed via the Gibbs collection samples.

Fig. 4.

Expected variance of each pixel for the (Mushroom) data considered in Fig. 3.

To provide a more thorough examination of model performance, in Table IV, we present results for several well-studied gray-scale and RGB images, as a function of the fraction of pixels missing. All of these results are based upon BPFA, with DP-BPFA and PSBP-BPFA yielding similar results. Finally, in Table V, we perform interpolation and denoising simultaneously, again with no training data and without prior knowledge of the noise level (again, as previously discussed, it would be difficult to estimate the noise variance as a preprocessing step in this case using methods like that in [10] as, in this case, there is also a large number of missing pixels). An example result is shown in Fig. 5. To our knowledge, this is the first time that denoising and interpolation have been jointly performed while simultaneously inferring the noise statistics.

TABLE IV.

Top: BPFA Gray-Scale Image Interpolation PSNR Results, Using Patch Size 8×8. Bottom: BPFA RGB Image Interpolation PSNR Results, Using Patch Size 7×7

data ratio	C.man	House	Peppers	Lena	Barbara	Boats	F.print	Man	Couple	Hill
20%	24.11	30.12	25.92	31.00	24.80	27.81	26.03	28.24	27.72	29.33
30%	25.71	33.14	28.19	33.31	27.52	30.00	09.01	30.06	30.00	31.21
50%	28.90	38.02	32.58	36.94	33.17	33.78	33.53	33.29	35.56	34.23
80%	34.70	43.03	37.73	41.27	40.76	39.50	40.17	39.11	38.71	38.75

data ratio	Castle	Mushroom	Train	Horses	Kangroo
20%	29.12	31.56	24.59	29.99	29.59
30%	32.02	34.63	27.00	32.52	32.21
50%	36.45	38.88	32.00	37.27	37.34
80%	41.51	42.56	40.73	41.97	42.74

TABLE V.

Simultaneous Image Denoising and Interpolation PSNR Results for BPFA, Considering the Barbara256 Image and Using Patch Size 8×8

σ	10%	20%	30%	50%	100%
0	23.47	26.87	29.83	35.60	42.94
5	23.34	26.73	29.27	33.61	37.70
10	23.16	26.07	28.17	31.17	34.31
15	22.66	25.17	26.82	29.31	32.14
20	22.17	24.27	25.62	27.90	30.55
25	21.68	23.49	24.72	26.79	29.30

Fig. 5.

(From left to right) The original barbara256 image, the noisy and incomplete barbara256 image with the noise standard deviation of 15 and 70% of its pixels missing at random (displayed based upon imputing missing pixels as the average of all observed pixels in a 5×5 neighborhood), the restored image, and the inferred dictionary with its elements ordered in the probability to be used (from top left).

For all of the examples previously considered, for both gray-scale and RGB images, we also attempted a direct application of matrix completion based on the incomplete matrix X ∈ ℝ^P×N, with columns defined by the image patches (i.e., for N patches, with P pixels in each, the incomplete matrix is of size P×N, with the ith column defined by the pixels in x_i). We considered the algorithm in [20], using software from Prof. Candès’ web-site. For most of the examples previously considered, even after very careful tuning of the parameters, the algorithm diverged, suggesting that the low-rank assumptions were violated. For examples for which the algorithm did work, the PSNR values were typically 4 to 5 dB worse than those reported here for our model.

E. Interpolation of Hyperspectral Imagery

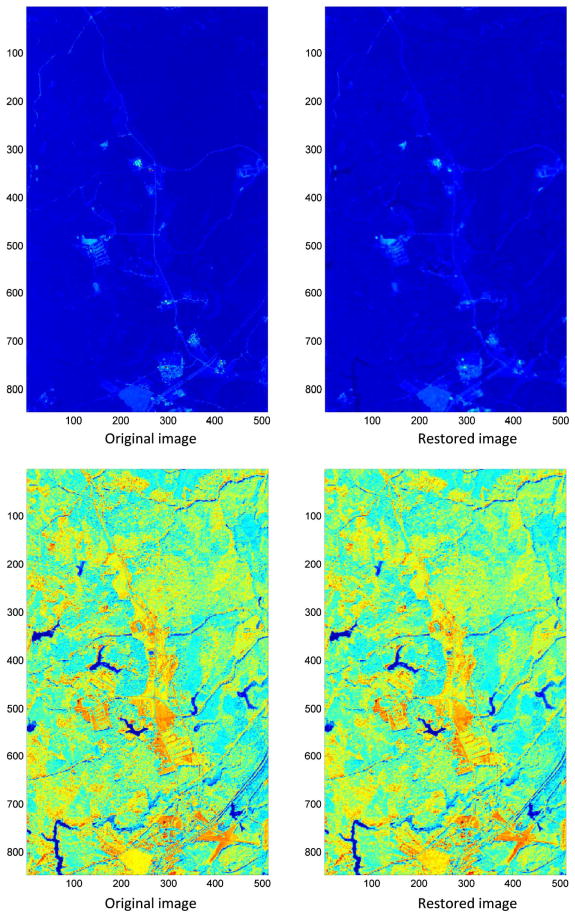
The basic BPFA, DP-BPFA, and PSBP-BPFA technology may be also applied to hyperspectral imagery, and it is here where these methods may have significant practical utility. Specifically, the amount of data that need be measured and read off a hyperspectral camera is often enormous. By selecting a small fraction of voxels for measurement and readout, uniformly selected at random, the quantity of data that need be handled is substantially reduced. Furthermore, one may simply modify existing hyperspectral cameras. We consider hyperspectral data with 106 spectral bands, from HyMAP scene A.P. Hill, VA, with permission from U.S. Army Topographic Engineering Center. Because of the significant statistical correlation across the multiple spectral bands, the fraction of data that need be read is further reduced, relative to gray-scale or RGB imagery. In this example, we considered 2% of the voxels, uniformly selected at random, and used image patches of size 4×4×106. Other than the increased data dimensionality, nothing in the model was changed.

In Fig. 6, we show example (mean) inferred images, at two (arbitrarily selected) spectral bands, as computed via BPFA. All 106 spectral bands are simultaneously analyzed. The average PSNR for the data cube (size 845×512×106) is 30.96 dB. While the PSNR value is of interest, for data of this type, the more important question concerns the ability to classify different materials based upon the hyperspectral data. In a separate forthcoming paper, we consider classification based on the full datacube, and based upon the BPFA-inferred datacube using 2% of the voxels, with encouraging results reported. We also tried the low-rank matrix completion algorithm from [20] for the hyperspectral data, and even after extensive parameter tuning, the algorithm diverged for all hyperspectral data considered.

Fig. 6.

Comparison of recovered band (average from Gibbs collection iterations) for hyperspectral imagery with 106 spectral bands. The interpolation is performed using 2% of the hyperspectral datacube, uniformly selected at random. The analysis employs 4×4×106 patches. All spectral bands are analyzed at once, and here, the data (recovered and original) are shown (arbitrarily) for bands (top) 1 and (bottom) 50. Results are computed using the BPFA model.

In Table VI, we summarize algorithm performance on another hyperspectral data set, composed of 210 spectral bands. We show the PSNR values as a function of percentage of observed data and as a function of the size of the image patch. Note that the 1×1 patches only exploit spectral information, whereas the other patch sizes exploit both spatial and spectral information.

TABLE VI.

BPFA Hyperspectral Image Interpolation PSNR Results. For This Example, the Test Image Is a 150×150 Urban Image With 210 Spectral Bands. Results Are Shown as a Function of the Percentage of Observed Voxels, for Different Sized Patches (e.g., the 4×4 Case Corresponds to 4×4×210 “Patches”)

Observed data (%)	1×1	2×2	3×3	4×4
2	15.34	21.09	22.72	23.46
5	17.98	23.58	25.30	25.88
10	20.41	25.27	26.36	26.68
20	22.22	26.50	27.02	27.16

F. CS

We consider a CS example in which the image is divided into 8×8 patches, with these constituting the underlying data {x_i}_i=1,N to be inferred. For each of the N blocks, a vector of CS measurements y_i= Σx_i is measured, where the number of projections per patch is n, and the total number of CS projections is n · N. In our first examples, the elements of Σ are randomly constructed, as draws from 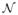(0,1); many other random projection classes may be considered [3] (and below, we also consider optimized projections Σ, matched to dictionary D). Each x_i is assumed represented in terms of dictionary x_i = Dw_i + ε_i, and three constructions for D were considered: 1) a DCT expansion; 2) learning of D using BPFA, using training images; and 3) using the BPFA to perform joint CS inversion and learning of D. For 2, the training data consisted of 4000 8×8 patches chosen at random from 100 images selected from the Microsoft database (http://research.microsoft.com/enus/projects/objectclassrecognition). The dictionary was set to K = 256, and the offline BP inferred a dictionary of size M = 237.

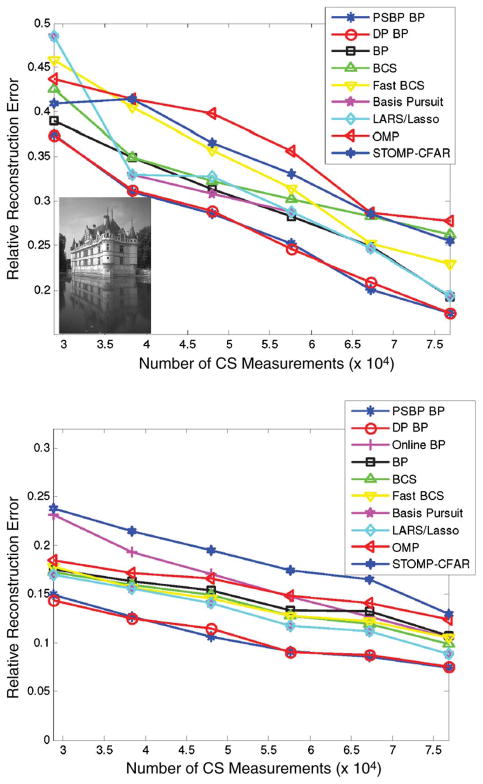
Representative CS reconstruction results are shown in Fig. 7 (left) based upon a DCT dictionary, for a gray-scale version of the “castle” image. The results in Fig. 7 (right) are based on a learned dictionary; except for the “online BP” results (where D and {w_i}_i=1,N are jointly learned), all of these results employ the same dictionary D learned offline, as previously mentioned, and the algorithms are distinguished by different ways of estimating {w_i}_i=1,N. A range of CS-inversion algorithms are considered from the literature, and several BPFA-based constructions are considered as well for CS inversion. The online BPFA results (with no training data) are quite competitive with those based on a dictionary learned offline.

Fig. 7.

(Left) CS results on gray-scale Castle image, based on DCT dictionary D. CS projection matrix Σ is randomly constituted, with elements drawn i.i.d. from 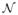(0,1). Results are shown using the DP-BPFA and PSBP-BPFA models in Section IV. Comparisons are also made with several CS inversion algorithms from the literature. (Right) Same as on the left but based on learned dictionary D, instead of DCT. The online BP results employ BPFA to learn D and do CS inversion jointly. All other results are based upon learned D with learning performed offline using distinct training images.

Note that results based on a learned dictionary are markedly better than those based on the DCT; similar results were achieved when the DCT was replaced by a wavelet representation. For the DCT-based results, note that the DP-BPFA and PSBP-BPFA CS inversion results are significantly better than those of all other CS inversion algorithms. The results reported here are consistent with tests we performed using over 100 images from the aforementioned Microsoft database, not reported here in detail for brevity.

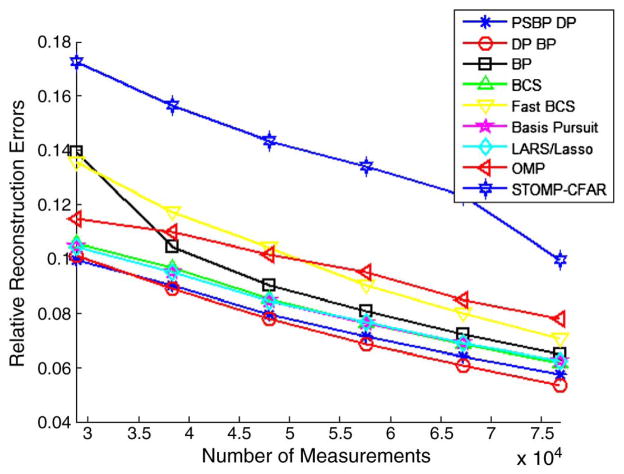
In all previous results, projection matrix Σ was randomly constituted. We now consider a simple means of matching Σ to a D learned offline, based upon representative training images. Assume a learned D ∈ ℝ^P×K, with K > P, which may be represented via SVD as D = UΛV^T; U ∈ ℝ^P×P and V ∈ ℝ^K×P are each composed of orthonormal columns, and Λ is a P×P diagonal matrix. The columns of U span the linear subspace of ℝ^P in which the columns of D reside. Furthermore, since the columns of D are generally not orthonormal, each column of D is “spread out” when expanded in the columns of U. Therefore, one expects that U and D are incoherent. Hence, a simple means of matching CS projections to the data is to define the rows of Σ in terms of randomly selected columns of U. This was done in Fig. 8 for the gray-scale “castle” image, using the same learned dictionary as considered in Fig. 7. It is observed that this procedure yields a marked improvement in CS recovery accuracy, for all CS inversion algorithms considered.

Fig. 8.

CS results on gray-scale Castle image, based on learned dictionary D (learning performed offline, using distinct training data). The projection matrix Σ is matched to D, based upon an SVD of D.

Concerning computational costs, all CS inversions were efficiently run on personal computers, with the specifics computational times dictated by the detailed MATLAB implementation and the machine run on. A rough ranking of the computational speeds, from fastest to slowest, is as follows: StOMP-CFAR, Fast BCS, OMP, BPFA, LARS/Lasso, Online BPFA, DP-BPFA, PSBP-BPFA, VB BCS, Basis Pursuit; in this list, algorithms BPFA through Basis Pursuits have approximately the same computational costs.

The improved performance of the CS inversion based upon the learned dictionaries is manifested as a consequence of the structure that is imposed on the underlying image while performing inversion. The early CS inversion algorithms, of the type considered in the above comparisons, imposed that the underlying image is sparsely represented in an appropriate basis (we showed results here based upon a DCT expansion of the 8×8 blocks over which CS inversion was performed, and similar results were manifested using a wavelet expansion). The imposition of such sparseness does not take into account the additional structure between the wavelet coefficients associated with natural images. Recently, researchers have utilized such structure to move beyond sparseness and achieve even better CS-inversion quality [2], [19]; in this paper, structural relationships and correlations between basis-function coefficients are accounted for. Additionally, there has been recent statistical research that has moved beyond sparsity and that are of interest in the context of CS inversion [38]. In the tests, we omit, for brevity, the algorithms in [2] and [19] yield performance that is comparable to the best results to the right in Fig. 7. Consequently, the imposition of structure in the form of learned dictionaries can be achieved using conventional basis expansions but with more sophisticated inversion techniques, that account for structure in imagery. Therefore, the main advantage of the learned dictionary in the context of CS is that it provides a very convenient means of defining projection matrices that are matched to natural imagery, as done in Fig. 8. Once those projection matrices are specified, the CS inversion may be employed based upon dictionaries as discussed here or based upon more traditional expansions (DCT or wavelets) and newer CS inversion methods [2], [19].

VI. Conclusion

The truncated beta-Bernoulli process has been employed to learn dictionaries matched to image patches {x_i}_i=1,N. The basic nonparametric Bayesian model is termed a BPFA framework, and extensions have been also considered. Specifically, the DP has been employed to cluster the {x_i}_i=1,N, encouraging similar dictionary-element usage within respective clusters. Furthermore, the PSBP has been used to impose that proximate patches are more likely to be similarly clustered (imposing that they are more probable to employ similar dictionary elements). All inference has been performed by a Gibbs sampler, with analytic update equations. The PBFA, DP-BPFA, and PSBP-BPFA have been applied to three problems in image processing: 1) denoising; 2) image interpolation based upon a subset of pixels selected uniformly at random; and 3) learning dictionaries for CS and also CS inversion. We have also considered jointly performing 1 and 2. Important advantages of the proposed methods are as follows. 1) A full posterior on model parameters are inferred, and therefore, “error bars” may be placed on the inverted images. 2) The noise variance need not be known; it is inferred within the analysis and may be non-stationary, and it may be inferred in the presence of significant missing pixels. 3) While training data may be used to initialize the dictionary learning, this is not needed, and the BPFA results are highly competitive even based upon random initializations. In the context of CS, the DP-BPFA and PSBP-BPFA results are state of the art, which is significantly better than existing published methods. Finally, based upon the learned dictionary, a simple method has been constituted for optimizing the CS projections.

The interpolation problem is related to CS, in that we exploit the fact that {x_i}_i=1,N reside on a low-dimensional subspace of ℝ^P, such that the total number of measurements is small relative to N · P (recall x_i ∈ ℝ^P). However, in CS, one employs projection measurements Σx_i, where Σ ∈ ℝ^n×P, ideally with n ≪ P. The interpolation problem corresponds to the special case in which the rows of Σ are randomly selected rows of the P×P identity matrix. This problem is closely related to the problem of matrix completion [6], [23], [33], where the incomplete matrix X ∈ ℝ^P×N has columns defined by {x_i}_i=1,N.

While the PSBP-BPFA successfully segmented the image while performing denoising and interpolation of missing pixels, we found that the PSNR performance of direct BPFA analysis performed very close to that of PSBP-BPFA in those applications. The use of PSBP-BPFA utilizes the spatial location of the image patches employed in the analysis, and therefore, it removes the exchangeability assumption associated with the simple BPFA (the location of the patches may be interchanged within the BPFA, without affecting the inference). However, since in the denoising and interpolation problems we have many overlapping patches, the extra information provided by PSBP-BPFA does not appear to be significant. By contrast, in the CS inversion problem, we do not have overlapping patches, and PSBP-BPFA provided significant performance gains relative to BPFA alone.

Biographies

Mingyuan Zhou received the B.Sc. degree in acoustics from Nanjing University, Nanjing, China, in 2005 and the M.Eng. degree in signal and information processing from the Chinese Academy of Sciences, Beijing, China, in 2008. He is currently working toward the Ph.D. degree with the Department of Electrical and Computer Engineering, Duke University, Durham, NC.

His current research interests include statistical machine learning and signal processing, with emphasis on dictionary learning, sparse coding, and image and video processing.

Haojun Chen received the M.S. and Ph.D. degrees in electrical and computer engineering from Duke University, Durham, NC, in 2009 and 2011, respectively.

His research interests include machine learning, data mining, signal processing, and image processing.

John Paisley received the B.S.E., M.S., and Ph.D. degrees from Duke University, Durham, NC, in 2004, 2007, and 2010.

He is currently a Postdoctoral Researcher with the Department of Computer Science, Princeton University, Princeton, NJ. His research interests include Bayesian nonparametrics and machine learning.

Lu Ren received the B.S. degree in electrical engineering from Xidian University, Xi’an, China, in 2002 and the Ph.D. degree in electrical and computer engineering from Duke University, Durham, NC, in 2010.

She is currently working with Yahoo! Lab as a Scientist. Her research interests include machine learning, data mining, and statistical modeling.

Lingbo Li received the B.Sc. degree in electronic information engineering with Xidian University, Xi’an, China, in 2008 and the M.Sc. degree in sensing and signals with Duke University, Durham, NC, in 2010. She is currently working toward the Ph.D. degree with the Department of Electrical and Computer Engineering, Duke University.

Her current research interests include statistical machine learning and signal processing, with emphasis on dictionary learning and topic modeling.

Zhengming Xing received the B.S. degree in telecommunications from the Civil Aviation University of China, Tianjin, China, in 2008 and the M.S. degree in electrical engineering from Duke University, Durham, NC, in 2010. He is currently working toward the Ph.D. degree in electrical and computer engineering with Duke University.

His research interests include statistical machine learning, hyperspectral image analysis, compressive sensing, and dictionary learning.

David Dunson is currently a Professor of statistical science with Duke University, Durham, NC. His recent projects have developed sparse latent factor models that scale to massive dimensions and improve performance in predicting disease and other phenotypes based on high-dimensional and longitudinal biomarkers. Related methods can be used for combining high-dimensional data from different sources and for massively dimensional variable selection. His research interests include the development and application of novel Bayesian statistical methods motivated by high-dimensional and complex data sets, with particular emphasis on nonparametric Bayesian methods that avoid assumptions, such as normality and linearity, and on latent factor models that allow dimensionality reduction in massively dimensional settings.

Dr. Dunson is a Fellow of the American Statistical Association and the Institute of Mathematical Statistics. He was a recipient of the 2007 Mortimer Spiegelman Award for the top public health statistician, the 2010 Myrto Lefkopoulou Distinguished Lectureship at Harvard University, and the 2010 COPSS Presidents’ Award for the top statistician under 41.

Guillermo Sapiro was born in Montevideo, Uruguay, on April 3, 1966. He received his B.Sc. (summa cum laude), M.Sc., and Ph.D. degrees from Technion Israel Institute of Technology, Hafia, Israel, in 1989, 1991, and 1993, respectively.

After his postdoctoral research with Massachusetts Institute of Technology, he became a member of the Technical Staff with the research facilities of HP Labs, Palo Alto, CA. He is currently with the Department of Electrical and Computer Engineering, University of Minnesota, where he holds the position of a Distinguished McKnight University Professor and the Vincentine Hermes-Luh Chair in electrical and computer engineering.

Lawrence Carin (F’01–SM’96) was born on March 25, 1963 in Washington, DC. He received the B.S., M.S., and Ph.D. degrees in electrical engineering from the University of Maryland, College Park, in 1985, 1986, and 1989, respectively.

In 1989, he joined the Department of Electrical Engineering, Polytechnic University, Brooklyn, Brooklyn, NY, as an Assistant Professor and, in 1994, became an Associate Professor. In September 1995, he joined the Department of Electrical Engineering, Duke University, Durham, NC. He is now the William H. Younger Professor of engineering with Duke University. He is a Cofounder with Signal Innovations Group, Inc., which is a small business where he serves as the Director of Technology. He is the author of over 200 peer-reviewed papers. His current research interests include signal processing, sensing, and machine learning.

Dr. Carin is a member of the Tau Beta Pi and Eta Kappa Nu Honor Societies.

Appendix. Gibbs Sampling Inference

The Gibbs sampling update equations are given below; we provide the update equations for the BPFA, and the DP and PSBP versions are relatively simple extensions. Below, Σ_i represents the projection matrix on the data, for image patch x_i. For the CS problem, Σ_i is typically fully populated, whereas for the interpolation problem, each row of Σ_i is all zeros, except for a single one corresponding to the specific pixel that is measured. The update equations are the conditional probability of each parameter, conditioned on all other parameters in the model.

Sample d_k:

$$p({\mathit{d}}_k\mid -)\propto \prod _{i=1}^N\mathcal{N}({\mathit{y}}_i;{\mathbf{\sum }}_i\mathbf{D}({\mathit{s}}_i\odot {\mathit{z}}_i),{\gamma }_{\epsilon }^{-1}{\mathbf{I}}_{{\left|\right|{\mathbf{\sum }}_i\left|\right|}_0})\times \mathcal{N}({\mathit{d}}_k;0,P^{-1}{\mathbf{I}}_P).$$

It can be shown that d_k can be drawn from a normal distribution as

$$p({\mathit{d}}_k\mid -)~\mathcal{N}({\mathit{\mu }}_{{\mathit{d}}_k},{\mathbf{\sum }}_{{\mathit{d}}_k})$$

with the covariance Σ_dk and mean μ_dk expressed as

$$\begin{array}{l}{\mathbf{\sum }}_{{\mathit{d}}_k}={\left(P\mathbf{I}+{\gamma }_{\epsilon }\sum _{i=1}^N{z}_{ik}^2{s}_{ik}^2{\mathbf{\sum }}_i^T{\mathbf{\sum }}_i\right)}^{-1}\\ {\mathit{\mu }}_{{\mathit{d}}_k}={\gamma }_{\epsilon }{\mathbf{\sum }}_{{\mathit{d}}_k}\sum _{i=1}^N{z}_{ik}{s}_{ik}{\stackrel{\sim }{\mathit{x}}}_i^{-k}\end{array}$$

where

$${\stackrel{\sim }{\mathit{x}}}_i^{-k}={\mathbf{\sum }}_i^T{\mathit{y}}_i-{\mathbf{\sum }}_i^T{\mathbf{\sum }}_i\mathbf{D}({\mathit{s}}_i\odot {\mathit{z}}_i)+{\mathbf{\sum }}_i^T{\mathbf{\sum }}_i{\mathit{d}}_k(s_{ik}\odot z_{ik}).$$

Sample z_k: = [z_1k, z_2k, ··· z_Nk]:

$$p(z_{ik}\mid -)\propto \mathcal{N}({\mathit{y}}_i;{\mathbf{\sum }}_i\mathbf{D}({\mathit{s}}_i\odot {\mathit{z}}_i),{\gamma }_{\epsilon }^{-1}{\mathbf{I}}_{{\left|\right|{\mathbf{\sum }}_i\left|\right|}_0})\text{Bernoulli}(z_{ik};{\pi }_k).$$

The posterior probability that z_ik = 1 is proportional to

$$p_1={\pi }_{k}exp\left[-\frac{{\gamma }_{\epsilon }}{2}\left(s_{ik}^2{\mathit{d}}_k^T{\mathbf{\sum }}_i^T{\mathbf{\sum }}_i{\mathit{d}}_k-2s_{ik}{\mathit{d}}_k^T{\stackrel{\sim }{\mathit{x}}}_i^{-k}\right)\right]$$

and the posterior probability that z_ik = 0 is proportional to

$$p_0=1-{\pi }_k.$$

Thus, z_ik can be drawn from a Bernoulli distribution as

$$z_{ik}~\text{Bernoulli}\left(\frac{p_1}{p_0+p_1}\right).$$ (11)

Sample s_k: = [s_1k, s_2k, ··· s_Nk]:

$$p(s_{ik}\mid -)\propto \mathcal{N}({\mathit{y}}_i;{\mathbf{\sum }}_i\mathbf{D}({\mathit{s}}_i\odot {\mathit{z}}_i),{\gamma }_{\epsilon }^{-1}{\mathbf{I}}_{{\left|\right|{\mathbf{\sum }}_i\left|\right|}_0})\mathcal{N}({\mathit{s}}_i;0,{\gamma }_s^{-1}{\mathbf{I}}_K).$$

It can be shown that s_ik can be drawn from a normal distribution, i.e.,

$$p(s_{ik}\mid -)~\mathcal{N}({\mu }_{s_{ik}},{\mathrm{\sum }}_{s_{ik}})$$ (12)

variance Σ_sik and mean μ_sik expressed as

$$\begin{array}{l}{\mathrm{\sum }}_{s_{ik}}={\left({\gamma }_s+{\gamma }_{\epsilon }{z}_{ik}^2{\mathit{d}}_k^T{\mathbf{\sum }}_i^T{\mathbf{\sum }}_i{\mathit{d}}_k\right)}^{-1}\\ {\mu }_{s_{ik}}={\gamma }_{\epsilon }{\mathrm{\sum }}_{s_{i,k}}{z}_{ik}{\mathit{d}}_k^T{\mathbf{\sum }}_i^T{\mathbf{\sum }}_i{\stackrel{\sim }{\mathit{x}}}_i^{-k}.\end{array}$$

Note that z_ik is equal to either 1 or 0, and Σ_sik and μ_sik can be further expressed as

$$\begin{array}{l}{\mathrm{\sum }}_{s_{ik}}=\{\begin{array}{ll}{({\gamma }_s+{\gamma }_{\epsilon }{\mathit{d}}_k^T{\mathbf{\sum }}_i^T{\mathbf{\sum }}_i{\mathit{d}}_k)}^{-1}\hfill & \text{if}{z}_{ik}=1\hfill \\ {\gamma }_s^{-1}\hfill & \text{if}{z}_{ik}=0\hfill \end{array}\\ {\mu }_{s_{ik}}=\{\begin{array}{ll}{\gamma }_{\epsilon }{\mathrm{\sum }}_{s_{ik}}{\mathit{d}}_k^T{\mathbf{\sum }}_i^T{\mathbf{\sum }}_i{\stackrel{\sim }{\mathit{x}}}_i^{-k}\hfill & \text{if}{z}_{ik}=1\hfill \\ 0\hfill & \text{if}{z}_{ik}=0.\hfill \end{array}\end{array}$$

Sample π_k:

$$p({\pi }_k\mid -)\propto \text{Beta}({\pi }_k;\text{a}/\text{K},\text{b}(\text{K}-1)/\text{K})\prod _{i=1}^N\text{Bernoulli}(Z_{ik};{\pi }_k).$$

It can be shown that π_k can be drawn from a Beta distribution as

$$p({\pi }_k\mid -)~\text{Beta}\left(\frac{a}{K}+\sum _{i=1}^N{z}_{ik}\frac{b(K-1)}{K}+N-\sum _{i=1}^N{z}_{ik}\right).$$

Sample γ_s:

$$p({\gamma }_s\mid -)\propto \mathrm{\Gamma }({\gamma }_s;c_0,d_0)\prod _{i=1}^N\mathcal{N}({\mathbf{s}}_i;0,{\gamma }_s^{-1}{\mathbf{I}}_K).$$

It can be shown that γ_s can be drawn from a Gamma distribution as

$$p({\gamma }_s\mid -)~\mathrm{\Gamma }\left(c_0+\frac{1}{2}KN,d_0+\frac{1}{2}\sum _{i=1}^N{\mathbf{s}}_i^T{\mathbf{s}}_i\right).$$

Sample γ_ε:

$$p({\gamma }_{\epsilon }\mid -)\propto \mathrm{\Gamma }({\gamma }_{\epsilon };e_0,f_0)\prod _{i=1}^N\mathcal{N}({\mathit{y}}_i;{\mathbf{\sum }}_i\mathbf{D}({\mathit{s}}_i\odot {\mathit{z}}_i),{\gamma }_{\epsilon }^{-1}{\mathbf{I}}_{{\left|\right|{\mathbf{\sum }}_i\left|\right|}_0}).$$ (13)

It can be shown that γ_ε can be drawn from a Gamma distribution as

$$p({\gamma }_{\epsilon }\mid -)~\mathrm{\Gamma }\left(e_0+\frac{1}{2}\sum _{i=1}^N{\left|\right|{\mathbf{\sum }}_i\left|\right|}_0,f_0+\frac{1}{2}\sum _{i=1}^N{\Vert {\mathbf{\sum }}_i^T{\mathit{y}}_i-{\mathbf{\sum }}_i^T{\mathbf{\sum }}_i\mathbf{D}({\mathit{s}}_i\odot {\mathit{z}}_i)\Vert }_{{\ell }_2}^2\right).$$ (14)

Note that ${\mathbf{\sum }}_i^T{\mathbf{\sum }}_i$ is a sparse identity matrix, Σ_dk is a diagonal matrix, and Z is a sparse matrix; it is easy to find that only basic arithmetical operations are needed, and many unnecessary calculations can be avoided, leading to fast computation and low memory requirement.