Local Dynamic Stability Associated with Load Carrying

Abstract

Objectives

Load carrying tasks are recognized as one of the primary occupational factors leading to slip and fall injuries. Nevertheless, the mechanisms associated with load carrying and walking stability remain illusive. The objective of the current study was to apply local dynamic stability measure in walking while carrying a load, and to investigate the possible adaptive gait stability changes.

Methods

Current study involved 25 young adults in a biomechanics research laboratory. One tri-axial accelerometer was used to measure three-dimensional low back acceleration during continuous treadmill walking. Local dynamic stability was quantified by the maximum Lyapunov exponent (maxLE) from a nonlinear dynamics approach.

Results

Long term maxLE was found to be significant higher under load condition than no-load condition in all three reference axes, indicating the declined local dynamic stability associated with load carrying.

Conclusion

Current study confirmed the sensitivity of local dynamic stability measure in load carrying situation. It was concluded that load carrying tasks were associated with declined local dynamic stability, which may result in increased risk of fall accident. This finding has implications in preventing fall accidents associated with occupational load carrying.

Introduction

In the workplace, slips, trips, and falls are a major concern, as they serve as a primary contributing factor for productivity and economic loss. The annual direct cost of disabling occupational injuries due to fall accidents is estimated to be 13.9 billion USD [1]. The combined fall categories (i.e., fall on the same level and fall to lower level) ranked no.1 in top causes of disabling workplace injuries, representing 25.3% of the total costs [1]. Over one-quarter of all fall-related injuries resulted in 31 days or more workdays being lost, costing the US economy nearly 10 billion USD/year [2].

As one of the primary occupational factors leading to slip and fall injuries, load carrying tasks are recognized as the first event or exposure resulting in over 30% (54,792 cases in 2001) of all non-fatal occupational slip and fall injuries with one or more days away from work [3-5]. Even though epidemiological findings clearly link risk of fall accidents to load carrying, the associated mechanisms and risk factors are still beyond current understanding.

Maintaining stability is a prerequisite for any walking activity including load carrying. It has also been suggested that compensatory gait behaviors are necessary when walking while carrying a load [6,7]. It was found that the craniovertebral angle significantly decreased during load carrying, suggesting that the head also plays a role to counterbalance load [8]. Changes in push-off force and maximum braking force were also evident during military load carrying [9]. Recently, a combination effect on gait variability was observed between whole body muscle fatigue and load carriage [10]. Further compensatory gait behavior may be associated with maximizing walking speed, optimizing the gait pattern for energy efficiency, or other criteria such as improving stability while carrying a load [11].

The ability to preserve multi-segment dynamic equilibrium (ankle, knee, hip, etc.) might be challenged by kinematic and control of perturbations (e.g., heel micro-slip) during walking as well as muscle recruitment pattern changes from carrying a load. Traditional measures of postural stability record postural sway changes while the subject performs quiet standing tasks [6]. Others try to measure the response while subjects try to sustain quiet stance in reaction to postural disturbances [12]. Nevertheless, standard postural stability measures offers limited insight into load carrying tasks. This is because, during a major portion of the gait cycle, the whole body center of mass is outside of the base of support, which is considered statically unstable [13].

Based on the nonlinear dynamic theory, local dynamic stability measure has recently been proposed as a more precise measurement of one's resistance to perturbations during walking activities. As opposed to traditional linear measures, local dynamic stability takes into account both temporal and spatial variability and has been used in various experimental conditions [14-17]. Nevertheless, very few studies have applied this technique in analyzing walking stability during load carrying. Recently a study was performed to investigate the possible interaction effect of physical load and cognitive load on local dynamic stability [18]. Carrying a higher load (i.e., 20 kg) was found to significantly impact the local dynamic stability regardless of the cognitive condition [18]. Nevertheless, there is still gap in knowledge regarding whether the load effect on local dynamic stability is short-term (ST) or long-term (LT), and whether this technique has the potential to be utilized beyond the laboratory constraints.

Therefore, the objective of the current study was to investigate the ST and LT local dynamic stability measures while carrying a load, and to explore the possibility of utilizing inertial sensors in performing local dynamic stability analysis. It was hypothesized that carrying a load will significantly reduce one's local dynamic stability.

Materials and Methods

Subject

Twenty-five young adults (7 females and 18 males) were involved in a laboratory study. Their anthropometric information was summarized as: age (mean = 22.9 years, standard deviation [SD] = 4.0 years), weight (mean = 79.2 kg, SD = 21.7 kg), and height (mean = 1.77 m, SD = 0.10 m). All subjects were free from musculo-skeletal injuries, as examined by the study physician. The study was approved by the local Institutional Review Board. Informed consent was obtained from all the subjects prior to any data collection.

Equipment and data collection

The data collection was conducted in a biomechanics research laboratory. An instrumented treadmill (Mercury 4.0; h/p/cosmos sports & medical gmbh, Nussdorf-Traunstein, Germany) was used to as the platform for continuous walking. A custom-made load vest (Fig. 1), in the shape of a double-pack, was used during load carrying. Composed of one front piece and one back piece, the load vest weighed about 12.7 kg. During the load condition, the vest was worn by the subjects. The vest was fastened to the subjects' trunk using velcro strips.

Fig. 1.

Illustration of experiment setup.

The subject carried one custom-made tri-axial accelerometer (MMA7260Q; Freescale Semiconductor Inc., Chandler, AZ, USA) on the low back region (close to L5/S1). Following the recommendations from International Society of Biomechanics [19], the accelerometer was oriented with X, Y, and Z axes representing anterior-poster (AP), medio-lateral (ML), and vertical (VT) directions, respectively. Operated at a range of ±2 g and a sampling rate of 100 Hz, the accelerometer transmitted data to a laptop via Bluetooth.

Procedures

Each subject was first allowed about 10 minutes to get used to the treadmill walking and the measurement instruments (i.e., accelerometer, and load vest). Each subject was also asked to wear laboratory clothing (e.g., sleeveless shirt, tight shorts, and athletic shoes of the same type). Individual normal walking velocity was obtained during over-ground walking. After static calibration [20], the accelerometer was before attached onto the subject.

Before the data collection, subjects were asked to stand in the anatomical position for 5 seconds for accelerometer tilt calibration [21]. Subjects were then instructed to walk on the treadmill as consistent as possible. Treadmill speed was adjusted to be consistent with that individual's over-ground velocity. After the subject's walking was stabilized, a two-minute data trial was acquired. Same procedure was followed in both load and no-load conditions. The order of load and no-load conditions was randomized for each subject.

Local dynamic stability

Local dynamic stability was quantified by the maximum Lyapunov exponent (maxLE) from a nonlinear dynamics approach. Computational details have been reported elsewhere [17,22-24]. For the sake of clarity, a brief description is provided: An experimental time series measurement (low back acceleration in current study) can be expanded into a state space with sufficient dimensions to describe the target dynamic system unambiguously [14]. A state space is a space defined by the independent coordinates (dimensions) required to unfold the target dynamic motion (locomotor control system in current study). The state space can be constructed from the discrete experimental data using the time-delayed coordinate method [25], with an appropriately chosen time delay [26] and embedding dimension [27].

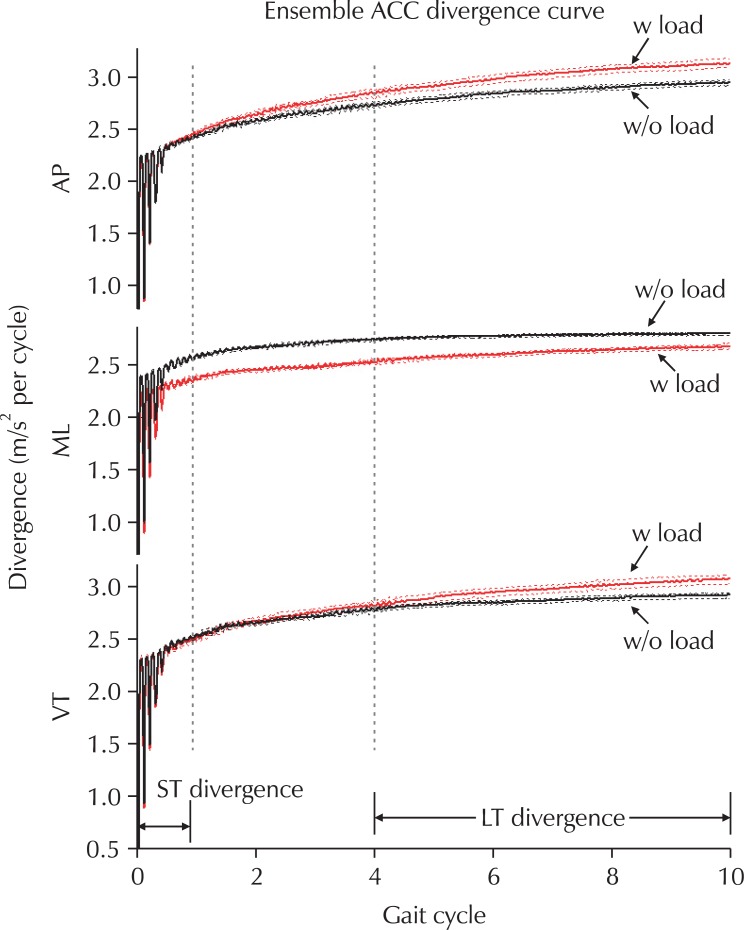
The influence of small perturbations to the dynamic system can be represented as neighboring trajectories deviating from the original trajectory in the state space. In the context of human walking, such perturbations can take the form of step-to-step variability and thus are referred to as local perturbations [14]. The Lyapunov exponents (i.e., characteristic exponents) of a trajectory measure the average rate of expansion or contraction of nearby trajectories. MaxLE can be computed by fitting the divergence curve within a specified range. In the current study, the slopes (maxLE) of the divergence curve during ST and LT ranges were measured (Fig. 2).

Fig. 2.

Ensemble divergence curve of state space reconstructed from acceleration signals for each axis. ST and LT maxLE were calculated for ST and LT divergence ranges, respectively. The dashed line around the ensemble average curve indicated ±3 standard error. ACC: accelerometer, w: with, w/o: without, AP: anterio-posterior, ML: mediolateral, VT: vertical, ST: short-term, LT: long-term.

Data analysis

Two data trials (i.e., one for load condition and one for no load condition) were collected for each subject. The accelerometer signals were compensated for initial tilt [21] and low-pass filtered (4th order, Butterworth, cut-off frequency = 20 Hz) before further processing.

For each data trial, heel contact (HC) events were determined from the accelerometer signal based on the method proposed by Zijlstra and Hof [28]. In summary, the AP acceleration was first low-pass filtered (4th order, Butterworth, cut-off frequency = 2 Hz). The peaks before the positive to negative change of sign of the filtered signal were then determined as HC. Gait cycles were further derived based on every other HC.

A series of 80 gait cycles were identified and extracted from each data trial for the purpose of local dynamic stability calculation. Such data series were re-sampled to 8,000 samples. This approach was adopted so that the between-subject comparison could be made on the same scale, yet without losing the temporal variability information [16]. A state space (time delay = 10, embedding dimension = 5) was reconstructed for each 8,000 sample data series in each of the three axes. ST local dynamic stabilities for each axis, as measured by ST maxLE, were calculated during the first 100 samples (approximately 0-1 gait cycle) [15]. Similarly, LT local dynamic stabilities for each axis, as measured by LT maxLE, were calculated during the 301 to 1,000 samples (approximately 4-10 gait cycles) [15]. In summary, six dynamic stability parameters (ST maxLE and LT maxLE for each of the three axes) were calculated from each data trial.

A custom-made MATLAB (ver 7.0, The MathWorks Inc., Natick, MA, USA) program was used for all the computation.

Statistical analysis

A one-way repeated-measure analysis of covariance (ANCOVA) was performed on ST maxLE and LT maxLE separately. Load condition, walking velocity, and axis, were considered as a within-subject factor, a covariate factor, and a blocking factor, respectively. To control the possible inflated type I error due to the multiple tests, a conservative significance level of p < 0.01 was adopted for all the tests. All the statistical analyses were performed in JMP 6.0 (SAS Institute Inc., Cary, NC, USA).

Results

The average walking velocity in current study was found to be 1.00 m/s (SD = 0.08 m/s). The ensemble divergence curves for both load and no-load conditions and for each axis are illustrated in Fig. 2. The divergence rate for the range of 0-1 gait cycle and 4-10 gait cycles were calculated as the ST maxLE and LT maxLE, respectively.

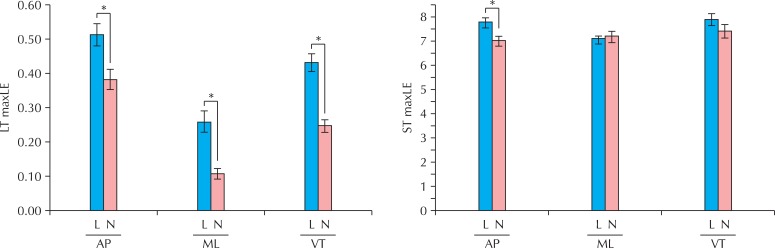
The ANCOVA tests indicated that there were significant differences in LT maxLE for all three axes under load condition, compared to no-load condition (Fig. 3). Specifically, the LT maxLE for AP axis was significantly higher (p = 0.0039) under load condition (mean = 0.51, SD = 0.15) than no-load condition (mean = 0.38, SD = 0.14), which indicated a reduced LT local dynamic stability during walking while carrying a load. Consistent load condition effect was also found in ML (p < 0.0001) and VT (p < 0.0001) axes, where load condition always resulted in a higher LT maxLE than no-load condition (Fig. 3).

Fig. 3.

Average LT maximum Lyapunov exponent (maxLE) and ST maxLE for different load conditions and axes. Error bar indicates 1 standard error. ^*Significant differences are indicated by connections. LT: long-term, ST: short-term, L: load, N: no-load, AP: anterio-posterior, ML: medio-lateral, VT: vertical.

However, the load condition effect was not obvious in ST maxLE (Fig. 3). For AP axis, SL maxLE was significantly higher (p = 0.0092) under load condition (mean = 7.78, SD = 1.00) than no-load condition (mean = 7.01, SD = 0.88). For both ML and VL axes, however, no significant differences were found between load and no-load conditions (Fig. 3). These results suggested that for ST maxLE, only the time series data in AP axis was sensitive to the load condition changes.

Discussion

The objective of the current study was to explore the feasibility of applying local dynamic stability measure in walking while carrying a load, and to investigate the possible adaptive gait stability changes. This research was expected to expand the body of knowledge on the dynamic stability aspect of load carrying, which would promote our understanding of the fall accidents associated with load carrying tasks.

As expected, carrying a load resulted in significantly increased LT maxLE (i.e., decreased LT local dynamic stability), suggesting a declined chaotic character of dynamic walking. Therefore, the sensitivity of the maxLE as a stability measure was supported. In addition, the current study provided the evidence of adaptive gait behavior changes associated with load carrying. Specifically, as indicated by the significant reduced LT maxLE, young adults demonstrated decreased local dynamic stability during walking while carrying a load.

The current study also contributes to the field of local dynamic stability by performing the analysis using the accelerometer signal along. Multiple standard laboratory data collection equipment has been used in the past, such as goniometer [14], motion analysis system [16,18], etc. As discussed in several reviews [29,30], the ambulatory sensors like accelerometer have supreme advantages for LT, unconstraint testing in more naturalistic environment. The method presented in the current study can be easily transferred into a filed research, without the laboratory constraints.

Limitations of the current study include fixed load configuration (fixed size and weight) and control for walking speed. All the participants reported they were able to walk normally with little discomfort. With fixed size and weight, the load may have variable effect on an individual's gait behavior. Future studies with configurable load condition may certainly offer better control of the load carrying effect. Nevertheless, it can be argued that load conditions with individual-specific weight and size may not reflect typical occupational scenarios or military load carrying. In the current study, the participants were instructed to walk at the consistent speed under both load conditions. This approach was adopted to control the speed effect on local dynamic stability [16,31]. In practice, however, the workers may naturally slow down during load carrying. Therefore, future research is warranted to look into the walking speed changes and their influences on local dynamic stability.

Admittedly, the load configuration (i.e., double-pack type of load vest) adopted in the current study may only represent limited load carrying tasks (e.g., fully equipped fire-fighters) in industrial settings. From a methodological perspective, however, current study provides the evidence that local dynamic stability is a viable stability measure, which can be readily applied into other types of load carrying research in the future.

In summary, current study confirmed the sensitivity of local dynamic stability measure in load carrying situation. It was concluded that load carrying tasks were associated with declined local dynamic stability, which may result in increased risk of fall accident. This finding has implications in preventing fall accidents associated with occupational load carrying.