Regional, kinetic [¹⁸F]FDG PET imaging of a unilateral Parkinsonian animal model

Abstract

Positron emission tomography (PET) imaging with the glucose analog 2-deoxy-2-[¹⁸F]fluoro-D-glucose ([¹⁸F] FDG) has demonstrated clinical utility for the monitoring of brain glucose metabolism alteration in progressive neurodegenerative diseases. We examined dynamic [¹⁸F]FDG PET imaging and kinetic modeling of atlas-based regions to evaluate regional changes in the cerebral metabolic rate of glucose in the widely-used 6-hydroxydopamine (6-OHDA) rat model of Parkinson’s disease. Following a bolus injection of 18.5 ± 1 MBq [¹⁸F]FDG and a 60-minute PET scan, image-derived input functions from the vena cava and left ventricle were used with three models, including Patlak graphical analysis, to estimate the influx constant and the metabolic rate in ten brain regions. We observed statistically significant changes in [¹⁸F]FDG uptake ipsilateral to the 6-OHDA injection in the basal ganglia, olfactory bulb, and amygdala regions; and these changes are of biological relevance to the disease. These experiments provide further validation for the use of [¹⁸F]FDG PET imaging in this model for drug discovery and development.

Introduction

Positron emission tomography (PET) imaging with the glucose analog 2-deoxy-2-[¹⁸F]fluoro-D-glucose ([¹⁸F]FDG) has demonstrated clinical utility for the monitoring of brain glucose metabolism in dementia [1-3], wherein [¹⁸F] FDG uptake is thought to reflect synaptic function and density [4]. Reduced basal glucose uptake has been observed with age and is believed to be associated with the generalized age-related decrease in cerebral functional capacity in rats [5], monkeys [6] and humans [7,8]. Further, marked decline in glucose metabolism and [¹⁸F]FDG uptake has been associated with pathology, specifically in progressive neurodegenerative diseases such as Alzheimer’s and Parkinson’s disease (AD and PD, respectively). In AD, [¹⁸F]FDG PET studies have consistently revealed that glucose metabolism is reduced in parietotemporal, frontal and posterior cingulated cortices, and these decreases are correlated with the severity of dementia [1,2]. In PD, regional metabolic reduction has been observed in the caudate nucleus and cingulate cortex in non-demented subjects [9,10], whereas conversion to PD with dementia involves additional subcortical and cortical changes [10,11].

A widely used experimental model of PD is the unilateral destruction of catecholaminergic neurons by intracerebral injection of 6-hydroxydopamine (6-OHDA) [12]. The pathology obtained following unilateral injection of 6-OHDA into the rat results in clinically relevant degeneration of dopaminergic neurons in the substantia nigra (SN). Recently, work by Casteels et al. has demonstrated that [¹⁸F]FDG PET imaging in the rat 6-OHDA model is feasible and indicates reductions in glucose metabolism [13]. Specifically, the authors note hemispheric hypometabolism ipsilateral to the 6-OHDA injection using SUV measures and a voxel-based approach. Since the SUV parameter is semi-quantitative [14,15], additional quantitative studies in the 6-OHDA model are required to corroborate these findings and enable further use of [¹⁸F]FDG PET for drug discovery and development studies.

In this work, we have revisited the 6-OHDA model with the primary aim of utilizing the unilateral disease presentation for hemispheric analysis of [¹⁸F]FDG uptake and kinetic modeling of the cerebral metabolic rate of glucose (CMR_glc) derived from Patlak [16-18] and other models. This analysis was performed on hemispheric brain regions obtained from a brain atlas automatically registered to the computer tomography (CT) scan; thereby, ipsi- and contralateral regions were compared among and between animals. The mathematics of the modeling, including defining the image-derived vascular input function (IDIF), is described in detail. IDIFs utilize the image data to determine the input to the kinetic modeling. While there exist several published, preclinical research methods on the use of an IDIF, there is as of now no accepted method [19-23]. For laboratories with advanced surgical capabilities, it may be that beta probes may provide the best option for high sensitivity and temporal resolution input function via continuous sampling of blood flowing through a femoral arteriovenous shunt [24-26]. These methods, however, are challenging in rodents, and investigation of IDIFs will remain of interest due to the relative ease of their implementation [27]. Ultimately, as in this work, it is necessary to qualify the use of the IDIF methods in the context of the research model and the experimental methods. Thus, the primary purpose this is work to characterize the use of dynamic [¹⁸F]FDG PET for drug discovery experiments in neurological conditionsand, secondarily, to provide a rigorous interrogation of the analysis methods.

Methods

Animal models

Experiments were conducted under protocols approved by Amgen’s Institutional Animal Care and Use Committee (IACUC) and in accordance with the National Institutes of Health Guide for Care and Use of Laboratory Animals in facilities accredited by the Association for the Assessment and Accreditation of Laboratory Animal Care (AALAC). All animals received from our vendor were acclimated to our facility, provided enrichment, and monitored for any post-operative complications.

Generation of the 6-OHDA animal model was performed by Taconic Farms (Germantown, NY). In a sterile surgical environment, the rat is anesthetized to the surgical plane and immobilized prone in a stereotaxic frame. A 2 cm midsagittal skin incision is made on the scalp to expose the skull, and a hole is drilled in the skull. For male Sprague Dawley (SD) rats (175-225 grams), the coordinates from Bregma are AP -4.3, ML +1.2, DV -8.3. An infusion cannula consisting of a sterilized length of 30 gauge stainless steel hypodermic tubing is advanced to the nigrostriatal pathway. A 2 μg/μl solution of 6-OHDA is infused at a rate of 1 μl/min for 4 minutes. Following infusion, the cannula remains in place for 5 minutes before slow withdrawal and closure of the incision using stainless steel wound clips. Due to potential influences of analgesia on lesion development, no post-operative analgesics were administered.

Confirmation of success and degeneration of dopaminergic neurons in the SN is evaluated by response to a subcutaneous injection of apomorphine (0.2 mg/kg) at 14 days post-lesion and at 21 days (0.05 mg/kg) post-lesion. The animal is placed in a rotometer and the rotational behavior (contralateral to the lesion side) is recorded for 6-consecutive, 5-minute periods (30 minutes total). Positive results are classified as multiple 5-minute periods with 6+ rotations per minute.

Animals confirmed to have established lesions by the rotational behavior assay were shipped to Amgen and acclimated to our facility for a minimum of three days. All animals were group housed on a filtered, forced air isolation rack, and maintained on sterile wood chip bedding in a quiet room on a 12 hour light-dark cycle, with food and water available ad libitum. For these studies, six male SD rats with unilateral 6-OHDA lesions were imaged. The lesion was further verified by autoradiography after the imaging experiment.

Autoradiography

In addition to the rotational behavior assay performed at Taconic, we confirmed the lesion by dopamine transporter autoradiography. After the imaging portion of the studies, to maximize the value of each animal included in the study, rats were sacrificed by CO₂ inhalation and then decapitated. Brains were quickly removed from the skull, placed in 2-methyl-butane (Sigma Aldrich, St. Louis, MO) and stored at -80°C until use. Sections (20 μm) were cut from frozen brain tissue at -20°C using a cryostat (Leica Microsystems, Wetzlar, Germany) and placed onto microscope slides, which were stored at -80°C. Slides were thawed at room temperature and then incubated with binding buffer (50 mM tris-hydroxymethyl-aminomethane and 120 mM sodium chloride, pH 7.4) containing 10 nM ³H-WIN 35,428 (βCFT) (Perkin Elmer, Boston, MA) for 120 minutes at 4°C. To assess non-specific binding, slides containing adjacent brain sections were incubated in the same solution with addition of 10 μM GRB12395 (Tocris, Ellisville, MO). Afterwords slides were washed three times in ice-cold binding buffer, dipped into distilled water to remove buffer salts, and dried under a stream of cold air. Emission of beta particles from the sections was counted for 24 hours using a Beta Imager 2000 (Biospace, Paris, France) and digitized using M3 Vision software (Biospace, Paris, France).

Image acquisition

[¹⁸F]FDG PET scans occurred 4-5 weeks following surgery. Before the imaging experiment animals were fasted overnight (<12 hrs) with free access to water. For these studies, six male SD rats with unilateral 6-OHDA lesions were imaged. [¹⁸F]FDG PET/CT experiments were performed using an Inveon PET/CT (Siemens Medical Solutions USA, Inc., Knoxville, TN, USA). For [¹⁸F]FDG PET imaging, animals were anesthetized primarily with 2-4% isoflurane delivered in 1-1.5 L/min oxygen and maintained with 1-2% isoflurane during the scan procedure. Further, temperature was maintained at 37°C with a heating pad, and respiration was monitored using a BioVet monitoring system (m2m Imaging Corp., Cleveland, Ohio). Tail vein catheters were inserted and pre-scan blood glucose levels were measured using a hand-held Alpha Trak glucometer (Abbott, Abbott Park, Illinois).

A CT scan was performed to provide both anatomical information as well as attenuation information for correction of the PET image. The CT parameters of interest include: two bed positions to ensure full body coverage; tube voltage and current of 80 keV and 500 μA; 175 projections over 220° (step-size of 1.26°); effective, isotropic pixel size of 83 μm; total scan duration of 4.3 minutes. Data were then reconstructed using a modified Feldkamp algorithm with a Shepp-Logan filter.

After CT image acquisition, a 60-minute dynamic PET image acquisition was started just before a bolus injection of 18.5 ± 1 MBq (500 ± 27 μCi) of [¹⁸F]FDG (PETNet, Culver City, CA) adjusted to a volume of not more than 5mL/kg with saline through the tail vein catheter. At the end of the experiment, post-scanning glucose levels were measured. Pre- and post-scanning glucose values were averaged for Patlak graphical analysis. Dynamic PET image reconstruction was performed using the Inveon system and scan data were transformed into sinograms, followed by Fourier rebinning. The PET image histograms consisted of 20×3, 6×5, 2×15, 2×60, 3×120, 4×300, and 3×600 second frames. Images were reconstructed iteratively using a 2-dimensional (2D) ordered subset-expectation maximization reconstruction algorithm (2D-OSEM) with a ramp filter with 0.5 of the Nyquist frequency as the cutoff, 4 iterations, and 128×128 array size. The energy window was set between 350 and 650 keV, and post-acquisition scatter correction was performed. Finally, image intensity was converted to absolute [¹⁸F]FDG concentration (μCi/mm³) using a calibration factor generated from an ¹⁸F phantom.

Analysis: image atlas registration

In separate studies, six T₁-weighted, high-spatial-resolution magnetic resonance imaging (MRI) scans of SD rats were registered and averaged to form a reference brain volume. Using an anatomical atlas [28], the brain images were manually segmented from each slice. Ten brain regions were chosen, including basal ganglia, cerebellum, olfactory, amygdaloid complex, cortex, hypothalamus, hippocampus, brain stem, corpus callosum, thalamus, and the entire brain. The image regions were assembled into the isotropic, digital atlas used in processing and analysis. Finally, the MRI-derived atlas was registered to a reference CT image of the rat skull.

The determination of brain regions in this study is performed by orienting the brain atlas with the skull from the CT acquired with the PET data. Specifically, the skeleton of the test CT skeleton (i.e., the six data sets collected in these experiments) is aligned coarsely to the reference skeleton using a mutual information-based 3D registration, incorporating translation and rotation [29,30]. A registration transform generated from this object is applied to all CT and PET data sets. The result is that the original data have been rotated and translated, and a final scaling or non-rigidly deformation can be applied.

Analysis: dynamic PET

Image analysis was performed using VivoQuant^TM (invicro, LLC, Boston, MA). Two quantities of interest were extracted from the dynamic image data to perform the analysis: (1) average FDG concentration in prescribed brain regions and (2) plasma concentration. As described in the previous section, a 3D rat brain atlas was registered with the respective PET and CT brain images to measure the average FDG concentrations within defined brain regions. Manually generated regions-of-interest (ROIs) from both the left ventricle (LV) and inferior vena cava (VC) provided the image-derived input functions (IDIFs) used to estimate plasma concentration.

The first IDIF was generated from the radio tracer signal in the VC, which was identified in the first few frames following injection of [¹⁸F]FDG. This ROI was then applied to each frame of the reconstruction to generate the vena cava derived input function, IDIF_VC.

The second IDIF was selected in the LV. List-mode data from the final 45 minutes of each acquisition were used to generate a static reconstruction, in which the myocardium was clearly distinguishable and digitally segmented using connected-threshold segmentation, which utilizes a threshold-bounded, region-growing algorithm available in the Insight Segmentation and Registration Toolkit (ITK, www.itk.org). The LV was identified and applied to all time frames of the dynamic acquisition to generate the IDIF_LV.

The irreversible two-compartment model employed in [¹⁸F]FDG PET studies is mathematically described as (Equations 1 and 2)

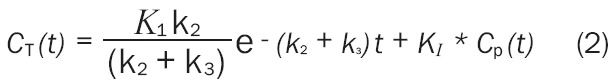where C_p(t), C₁(t), and C₂(t) represent radiotracer concentration in the plasma, reversible, and irreversible compartments, respectively. The rate constants of exchange are defined as: K₁, the plasma to intracellular exchange; k₂, the intracellular to plasma exchange; and k₃, the phosphorylation rate of [¹⁸F]FDG to [¹⁸F]FDG-6-PO₄ by hexokinase. In the irreversible compartment model, dephosphorylation of [¹⁸F]FDG-6-PO₄ (typically denoted by rate constant k₄) is assumed to be zero as it is biologically negligible in the brain [31,32].

Generally, only the sum of the concentrations in the reversible and irreversible regions may be measured via [¹⁸F]FDG PET imaging. This sum is indicated as C_T(t)=C₁(t)+C₂(t). An analytic solution to this equation is (Equation 3)

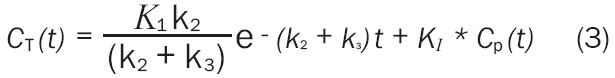and (Equation 4)

where K_I is the influx rate constant of [¹⁸F]FDG into the brain and for these studies was the primary parameter of interest.

Three methods were used to estimate the influx constant K_I. One estimation method is the analytical solution to Equation 3 to find best-fit estimates of K₁, k₂, and k₃, which are then used to calculate K_I. Hereafter, this method is referred to as the Computational model.

Under certain assumptions, two methods of estimating the influx constant given the concentration in the region of interest and the plasma curve are set forth by Patlak et al. [16-18]. First, if all reversible compartments are in equilibrium with plasma, only the accumulation of tracer in irreversible compartments is affecting the distribution. Thus, Equation 3 can be written (Equation 5)

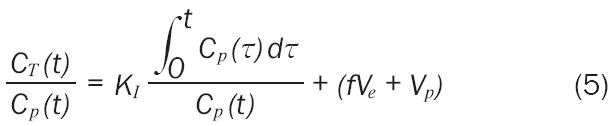where V_p represents the effective plasma volume, f is a factor between 0 and 1, and V_e represents the effective volume of the reversible compartment. After some time, the relationship between C_T(t)/C_p(t) and (Equation 10)

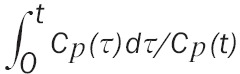becomes linear. Computing the slope of this line provides a second estimate of the influx constant [17]. This approach is commonly referred to as the graphical Patlak method or Patlak graphical analysis.

The third method employed in this work was also provided by Patlak [18]. At long times, when C_p(t) and C₁(t) are assumed to be zero, K_I can be estimated from (Equation 6)

where A(T) is the concentration of tracer in the region of interest at some time T >> 0. This method will be referred to as the Infinity model.

In summary, dynamic [¹⁸F]FDG PET images of the brain were segmented and analyzed by left and right hemispheres to assess the unilateral 6-OHDA lesion. Two IDIFs (IDIF_VC and IDIF_LV) were used, and the influx constant was estimated using all three methods: Patlak graphical, Computational, and Infinity models. From each modeling method, the cerebral metabolic rate of glucose, CMR_glc = C_pK_I/LC, was calculated from each K_I and the lumped constant, LC, was 0.67, which is the system default and is within the published range [33].

For statistical analysis we elected to utilize two methods. First, we assumed hemispheric symmetry enabling data analysis on the absolute CMR_glc values of the left versus right hemisphere as well as on ratio of the left-to-right CMR_glc: (Equation 7)

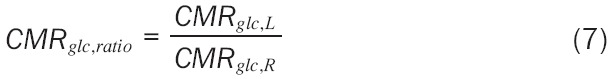where CMR_glc,L and CMR_glc,R are the CMR_glc of the left and right hemispheric regions, respectively. This metric assumes that no change in metabolism is a ratio of 1.0—that is CMR_glc,L = CMR_glc,R. Though it is acceptable to perform a one-sample t-test comparing CMR_glc,ratio to 1.0 (the null hypothesis), the classical one-sample test assumes standard deviation of 0.0 for the comparison group. To increase the statistical rigor of this analysis we assumed an equal variance, thus the modified t-statistic was defined as: (Equation 8)

Due to our modification of the t-statistic, calculation of p-values was made from the t-distribution table t_{(0.05, 5)} = 2.015. The second, statistical method used was a paired t-test of the left and right hemispheric data, which assumes dependent, matched pairs.

Finally, to compare with existing work [13] and to confirm that advantage of kinetic analysis, the SUV was calculated and statistically compared, where SUV is calculated as: (Equation 9)

Results

At the time of the 21 day post-lesion rotational behavior assay, the six animals weighted 280±19 g and averaged 190 rotations in the 30-minute test. Confirmation of the lesion was made at the end of the study by autoradiography, and a representative section is shown in Figure 1. The average pre-scanning glucose levels of 115±9 mg/dL and post-scanning glucose levels of 158±19 mg/dL. This increase in blood glucose is consistent with the effects of isoflurane anesthesia [34].

Figure 1.

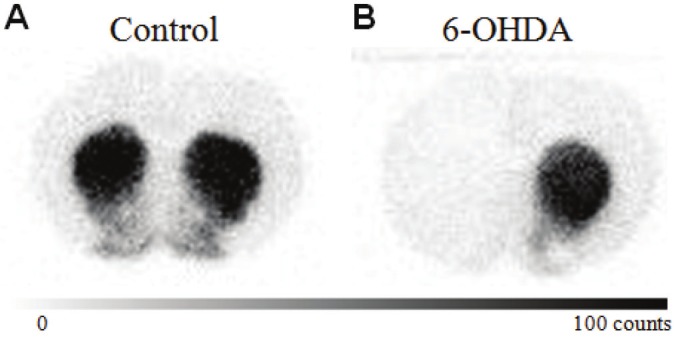
³H-WIN 35,428 (βCFT) autoradiography of normal (a) and 6-OHDA (b) brains. Note the lack of signal in the left hemisphere, ipsilateral to the 6-OHDA injection, consistent with nigral degeneration.

Average IDIF_VC and IDIF_LV curves from all six animals are shown in Figure 2A, with the data from the uptake of FDG in the entire brain and the linear region used in the Patlak graphical analysis shown in Figure 2B. Per the IDIF curves in Figure 2A, note the higher signal from the vena cava derived function but overall similarity in input form. To assess the variation across animals, we calculated the coefficient of variation (CV) for the interval of 13-150 seconds. The mean CV for the IDIF_VC was 28% and for the IDIF_LV was 19%. ExaminationIDIF_LV reveals no visual evidence of myocardial spillover, which is expected to manifest as rising signal. Further, both the LV and VC IDIFs are slightly declining in signal (-3.69×10^-5 mCi/ml and, -1.57×10^-4 mCi/ml respectively); thus, no myocardial spillover correction was applied.

Figure 2.

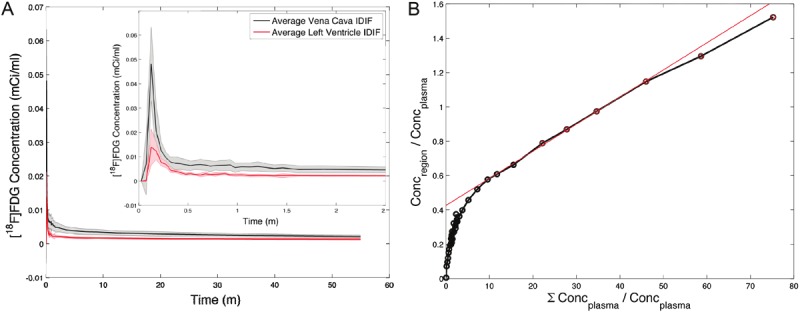
A: Average IDIF_VC (solid) and IDIF_LV (dotted) curves from all six animals with the coefficient of variation shown by the gray region. Only the first 2.5 minutes is show to enable visualization of the bolus. B: An example Patlak plot from this study (rat 2) taken over the entire brain region. The linear region (denoted by the red circles) and the fit (red line) are shown.

For visualization purposes, a single slice of a composite PET scan from all rats is shown in Figure 3. The image is shown with the contour of the atlas overlaid showing each brain region. The inset identifies each of the mapped regions. Note the visible hypo-intensity in the left basal ganglia as compared to the contralateral side.

Figure 3.

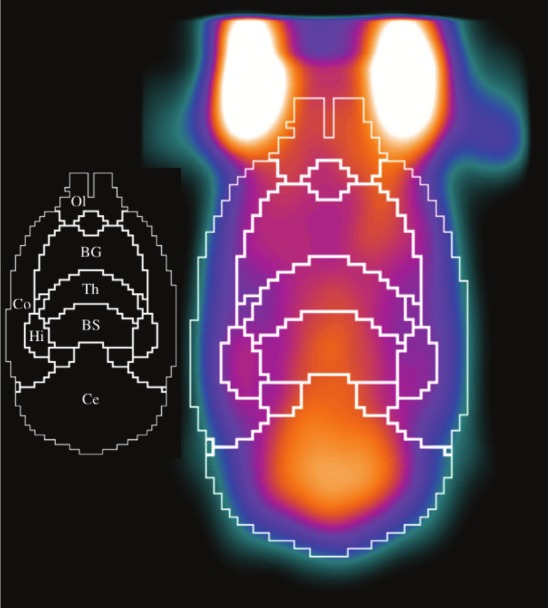
A single slice of composite PET scan from all rats, with the contour of the atlas overlaid. The inset identifies each of the mapped regions (Ol: Olfactory, BG: Basal Ganglia, Th: Thalamus, Co: Cortex, BS: Brain Stem, Hi: Hippocampus, Ce: Cerebellum). There is a visible hypo-intensity in the left basal ganglia as compared to the contralateral side. Note that not all analyzed regions are shown as this is a 2D slice to illustrate the mapping of the atlas to the PET image.

The absolute CMR_glc values calculated for the brain regions evaluated did not exhibit a statistically significant effect. This observation is explained by high CV values of 36%, 58%, and 20% for the IDIF_LV for the Patlak graphical, Computational, and Infinity models, respectively. For the IDIF_VC the CV measurements of the absolute CMR_glc values were 21%, 27%, 13% for the Patlak graphical, Computational, and Infinity models, respectively.

Published CMR_glc values for the rat brain under isoflurane conditions have been reported in the range of 0.37-0.66 μmol/min/g [35,36]. In this study, we found the Computational model to provide the poorest estimate of the CMR_glc values. For the entire brain, we computed 0.15±0.09 and 0.11±0.02 μmol/min/g, for the IDIF_LV and IDIF_VC, respectively. Alternatively, both Patlak methods yielded more realistic values of 0.34±0.14 and 0.31±0.07 μmol/min/g for the IDIF_LV with the graphical and Infinity method, respectively, and 0.19±0.02 and 0.16±0.02 μmol/min/g for the IDIF_VC with the graphical and Infinity method, respectively. The absolute values of the CMR_glc values varied between the IDIF_LV and IDIF_VC methods, primarily due to the difference in the influx constant, K_I, which was 1.7x higher in the IDIF_LV method. The selection of the LC value highly influences these results, and use of 0.55 brings the IDIF_LV derived CMR_glc valuesto 0.36-0.40 μmol/min/g, which is more in line with referenced values.

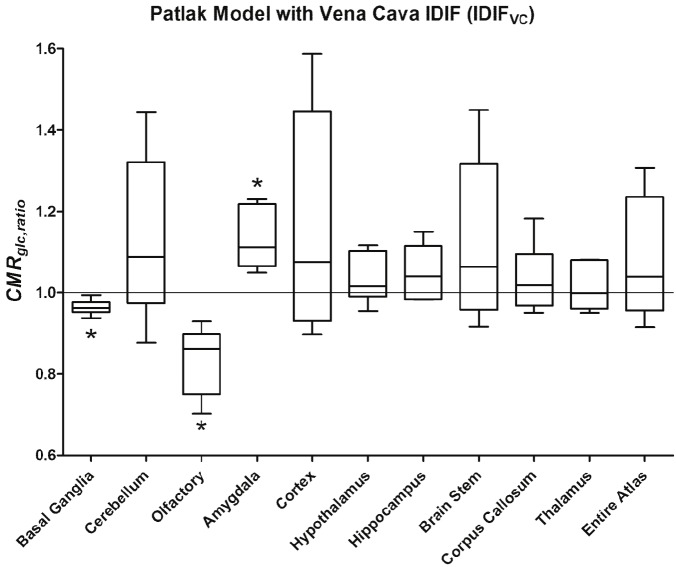
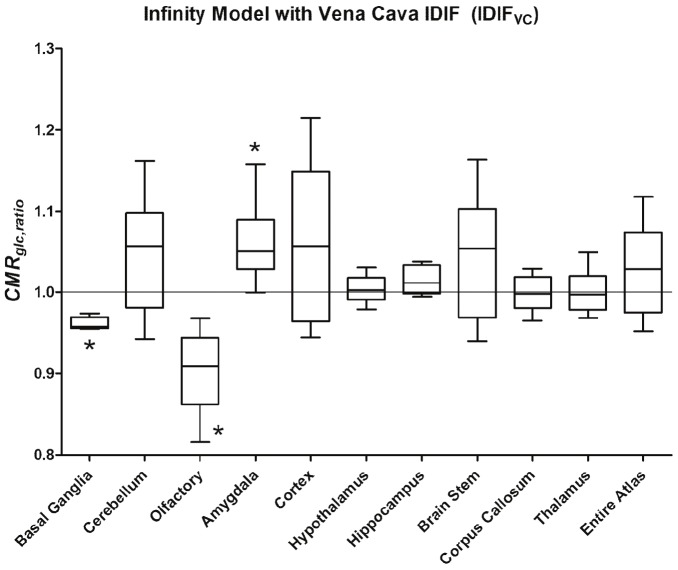
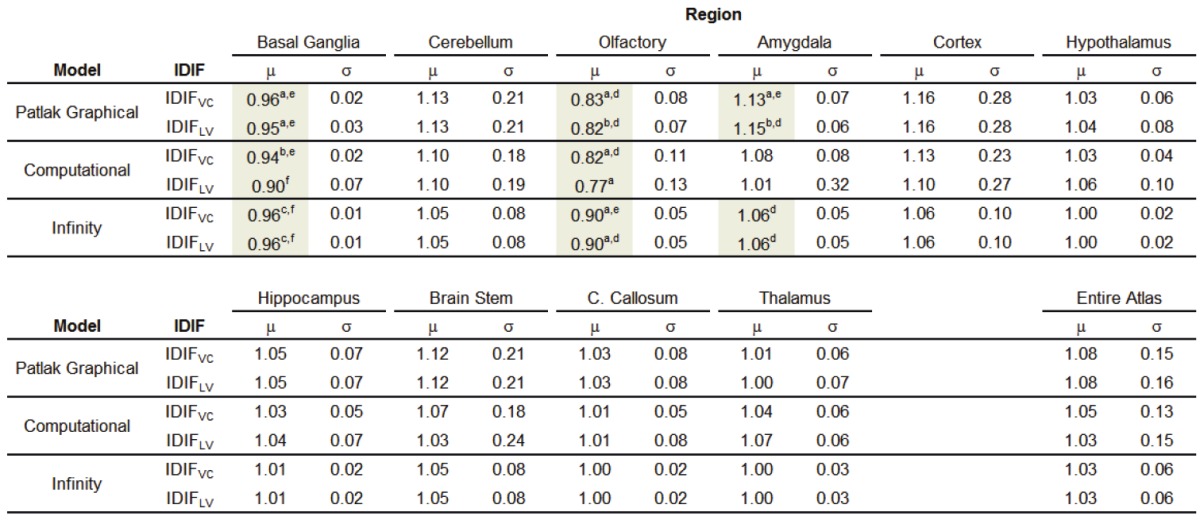
Rather than analyze the absolute values, the ratio of the cerebral metabolic rate of glucose, CMR_glc,ratio, was investigated to mitigate intraanimal differences in CMR_glc that could mask a biological effect. All means (μ), standard deviations (σ), and statistical analysis test results are shown in Table 1. Only the basal ganglia, olfactory bulb, and amygdala showed statistically significant differences in the ratio of the left to the right hemisphere, and that significance was dependent on the kinetic model. Specifically, for Patlak graphical analysis, the basal ganglia, olfactory bulb, and amygdala metabolism ratios were statistically different from unity (all p < 0.05). The Infinity and Computational models resulted in statistically significant differences in the basal ganglia and olfactory bulb, while the amygdala did not achieve the level of significance (p ~ 0.1), likely due to the noise and small sample size.

Table 1.

Hemispheric ratios (left-to-right) graphed in Figures 4 and 5. Highlighted cells and superscripts denote statistical significant and p-values, respectively, for both the modified one-way t-test and the paired t-test. Superscripts a, b, and c are from the modified one-way t-test, indicating p <^a0.05, ^b0.01, ^c0.001. Superscripts d, e, and f are from the paired t-test, indicating p <^d0.05, ^e0.01, ^f0.001

Modified one-way t-test p-value <^a0.05, ^b0.01, ^c0.001. Paired t-test p-value <^d0.05, ^e0.01, ^f0.001.

In Figure 4, the plot of the results for the Patlak graphical model and the vena cava input function, IDIF_VC, are shown with reach region analyzed represented in box-and-whisker format. Similarly, in Figure 5 is shown the results for the Infinity model and the IDIF_VC.

Figure 4.

Plot of the results of the Patlak graphical analysis with the input-function derived from the VC, IDIF_VC. Statistical significant decline in cerebral glucose metabolism was observed in the basal ganglia and olfactory bulb with a concomitant increase in the amygdala complex.

Figure 5.

Plot of the results of the Infinity model with the input-function derived from the VC, IDIF_VC. Statistical significant decline in cerebral glucose metabolism was observed in the basal ganglia and olfactory bulb with a concomitant increase in the amygdala complex.

Analysis of the SUV data, revealed limited statistically significant change in the left and right hemispheric regions. The olfactory bulb demonstrated a change of 15.8% (p = 0.008), and the cerebral cortex difference was 12.3% (p = 0.037). No other regions reached statistical significance.

Discussion

For the preclinical study of Parkinson’s disease and the development of new therapeutics, the 6-OHDA model is an accepted experimental model. The unilateral destruction of catecholaminergic neurons manifests a clinically-relevant pathology hallmarked by the degeneration of dopaminergic neurons in the substantia nigra (SN) [12,37]. To enhance the drug discovery process, it is desired that animal models recapitulate clinical pathophysiology as well as provide observable pharmacodynamic response. In that regard, noninvasive imaging is a method for the in vivo monitoring of disease and treatment, and this work aimed to further characterize the 6-OHDA model of PD coupled with cerebral glucose metabolism measurements by [¹⁸F]FDG PET.

To that end, we performed 60-minute dynamic [¹⁸F]FDG PET scans and extensive analysis of two image-derived input functions and three models to estimate the influx constant. This work is not intended to examine the full breadth of IDIF methods, rather to study the methods considered most common in rodent PET studies, in that regard IDIFs from the vena cava and left ventricle were studied by an analytical solution to the data (herein referred to as the Computation model) and by two variations of the Patlak graphical analysis [16-18]. These methods are tested with the intent of enabling future [¹⁸F]FDG PET in the rat 6-OHDA model for the development of new drug therapies. The results show a reduction in the cerebral metabolic rate of glucose (CMR_glc) in the basal ganglia and olfactory bulb with an increase in the amygdala regions. As detailed in Table 1, these regions demonstrated changes of 4-5%, 11-23%, and 6-13 %, respectively (with the range depending on the model).

Fully quantitative compartmental analysis requires blood sampling to obtain an input function [16], which can impose limitations on experimental design. For example, it precludes or at least complicates longitudinal studies, which may be of interest when studying animal models of neuro-degeneration, such as the 6-OHDA model. Therefore, to avoid the complications associated with blood sampling, it is generally accepted to use an IDIF. Though the results should be viewed in the specific context of rat brain imaging, our analysis revealed similar results utilizing IDIFs from manual volumes-of-interest draw within the vena cava or the left ventricle. Specifically, the mean CV for the first 2.5 minutes of the IDIF_VC was 28% and for the IDIF_LV was 19%. While the LV variation is lower, there was no difference in the subsequent modeling. Specifically, although the absolute values of CMR_glc did not yield statistically significant changes, the CMR_glc values derived from the IDIF_VC were of lower variance than the IDIF_LV. Our conclusion is that an IDIF derived from either the VC or LV is suitable.

As it pertains to the modeling and estimation of the influx rate constant, K_I, we assumed the gold standard to be the Patlak graphical model, as it is most commonly used in kinetic modeling. The model referred herein as the Infinity model carries the assumption that at 60 minutes the C_p(t) and C₁(t) are zero (i.e., C_p(60)=0 and C₁(60)=0). This method proved to be the least variable and thereby warrants additional consideration in future studies. Finally, the analytical solution to Equations 3 and 4 yielded results inconsistent with the other models and, thus, we recommend against using the Computational model for these studies.

The decrease in glucose metabolism in the basal ganglia observed in our study is in agreement with the findings by Casteels et al., demonstrating a relative decrease in the ipsilateral basal ganglia as compared to the contralateral side [13]. These observations are also in agreement with clinical studies demonstrating a hypometabolism in caudate nucleus in non-demented PD subjects [9,10] regardless of the status of L-Dopa therapy [9]. We, however, did not measure a change in basal ganglia by SUV analysis. Rather, SUV analysis in this study demonstrated a statistical difference in only the olfactory bulb and cortex. Moreover, when compared to control animals, the ipsilateral hypometabolism observed by Casteels et al. was not significant [13]. This most likely reflects an inter-individual variability in glucose uptake, which may also explain the conflicting data reported in earlier clinical [¹⁸F]FDG PET imaging studies of PD patients [38,39]. Contrary to the decrease in metabolic rate in the basal ganglia in both rat and human [¹⁸F]FDG PET imaging studies, preclinical studies using [¹⁴C]-2-deoxyglucose autoradiography in the 6-OHDA model found increases in glucose uptake in the ipsilateralglobuspallidus and habenula [40]. Since these striatal sub-regions are small with regard to the resolution of the PET scanner and partial volume effects cannot be excluded, we measured the entire basal ganglia. Thus, a decrease in the larger caudate-putamen may have masked a localized increase in the globuspallidus.

Changes in several cortical areas have been described in later clinical stages of PD and are associated with dementia [10,11,40]. Casteels et al. [13] find changes in additional brain regions including the cerebral cortex, which we only observed with the SUV analysis. These discrepancies could be due to the differences in time after surgery at which the rats were subjected to [¹⁸F]FDG PET, e.g. 4-5 weeks in our study, but 6-11 weeks in Casteels et al. [13]. With progressive deafferentiation of the striatum over time, additional brain structures with in a larger network are likely to be affected, such as cortical areas. Future longitudinal studies with the 6-OHDA model will further elucidate the effect of progressive dopaminergic deafferentiation on glucose metabolism in different brain areas.

In addition to the basal ganglia, we find a decrease in CMR_glc of 23% for the standard Patlak graphicalmodel and 11% for the Infinity model in the olfactory bulb. Unfortunately, Casteels et al. did not include this brain structure in their analysis [13]. The olfactory bulb is a relatively small structure in humans compared to rats, therefore no [¹⁸F]FDG PET imaging studies in PD patients are available to corroborate our data. However, histological post-mortem evidence suggests that the olfactory bulb is affected in PD [41] and decreases in olfactory function have been noted in PD patients [42,43] and animal models [44].

Olfactory dysfunction has been attributed to a decrease in the function of limbic cortical regions including the amygdala [45,46]. Unexpectedly, we detected a statistically significant increase in CMR_glc,ratio in the amygdala as measured with the Patlak graphical model and both the IDIF_VC and IDIF_LV (p = 0.018 and p = 0.004, respectively); however, this region was marginally insignificant in the Infinity model (p = 0.086 for both IDIFs). The explanation for the model differences could be related to the steady-state assumption implicit in the Infinity model reducing our sensitivity as well as our modification of the one-sample t-test that has altered the p-value from 0.03 to 0.086. The increase in metabolic rate in the amygdala could be hypothesized to reflect a compensatory mechanism at an early stage of striatal deafferentiation in the 6-OHDA model. Clearly, further studies will be required to understand the involvement of the amygdala in 6-OHDA induced metabolic changes in the rat brain. Finally, despite an observed a decline in hippocampus uptake (1-5%), the measurement does not reach the level of significance (p = 0.22 – 0.27). Power analysis reveals that a study with 16 animals per group should provide adequate samples to measure a change in the hippocampus.

The application of regional kinetic analysis in small animal PET imaging is complicated by the small cerebral structures in the rat brain, limited spatial resolution, and positron range (1-2 mm), and, taken together, these factors integrate to reduce the sensitivity to detect changes and call into question the specificity of the brain atlas to true brain regions. Further, it must be acknowledged that there are assumptions in this analysis regarding the lumped constant (LC): (1) that the LC is not altered by the 6-OHDA administration or the downstream biological consequences and (2) that the LC itself (0.67) is reasonable for this modeling. In either case, the result could be inaccurate estimation of the true CMR_glc; and, in practice, the interpretation of the CMR_glc values derived from [¹⁸F]FDG PET should be done in the context of the differing rates of transport and phosphorylation between glucose and 2-deoxy-2-(¹⁸F)fluoro-D-glucosethat the LC proportionality constant attempts to correct [47]. These assumptions included, the results of the study reflect the known biology of the 6-OHDA model and provide added confidence that well-executed preclinical [¹⁸F]FDG PET studies can be performed. Subsequent studies, especially those including drug intervention and correlation of imaging findings to accepted endpoints, may further the utility of regional, kinetic [¹⁸F]FDG PET for the evaluation of novel medicines for the treatment of Parkinson’s Disease.

Further, while probing reduction in glucose metabolism by [¹⁸F]FDG PET in neurological conditions is of clinical interest [1-4,9-11] and compliments our internal interest to better understand metabolic pathways and alterations in research models, changes in glucose metabolism are presumable downstream processes. In that regard, more proximal biology may be studied by ¹⁸F-dihydroxyphenylalanine ([¹⁸F]DOPA) PET. [¹⁸F]DOPA has been used to monitor the dopaminergic pathway, nigrostriatal dopaminergic presynaptic function, and Parkinson’s-related dopaminergic degeneration [48]. Future work related to the temporal and spatial correspondence of [¹⁸F]FDG and [¹⁸F] DOPA may yield further value for the study of the 6-OHDA model and drug treatment studies.

These experiments were intended to evaluate the cerebral metabolic rate of glucose in the accepted 6-OHDA model of Parkinson’s Disease. Despite the lack of spatial resolution in rat brain PET imaging, we found measurable reductions in glucose metabolism in disease-relevant brain regions when compared to the contralateral region as defined by a digital brain atlas. Further, we utilized this data to characterize the kinetic modeling methods that are commonly employed. Although direct blood sampling should remain the gold standard for assessing input functions, those measurements are not easily acquired in longitudinal experiments. These results demonstrate successful use of IDIFs from vena cava and left ventricle. We also characterized three models for the estimation of the influx constant, K_I, for which the standard Patlak graphical model identified regions of interest with high statistical certainty and the Infinity model (as termed herein) proved to be the least variable. Ultimately, the successful use of dynamic [¹⁸F] FDG PET and kinetic estimation in the 6-OHDA model may provide another metric to relate pharmacodynamic effect to drug efficacy in the discovery and development of new medicines.

Disclosures

MDS, CG, GHP, TK, DI, and SM are employees of Amgen, Inc. JH, JYH, KMO, MG are employees of inviCRO, LLC.

Dr. Silva has changed employment from Amgen, Inc. to inviCRO, LLC, and submission policies dictate referencing the institution where the work was conducted. Thereby, the second author, Dr. Glaus, is the corresponding author. This manuscript adheres to publication policies of both Amgen and inviCRO.