Sparse principal component analysis by choice of norm

Abstract

Recent years have seen the developments of several methods for sparse principal component analysis due to its importance in the analysis of high dimensional data. Despite the demonstration of their usefulness in practical applications, they are limited in terms of lack of orthogonality in the loadings (coefficients) of different principal components, the existence of correlation in the principal components, the expensive computation needed, and the lack of theoretical results such as consistency in high-dimensional situations. In this paper, we propose a new sparse principal component analysis method by introducing a new norm to replace the usual norm in traditional eigenvalue problems, and propose an efficient iterative algorithm to solve the optimization problems. With this method, we can efficiently obtain uncorrelated principal components or orthogonal loadings, and achieve the goal of explaining a high percentage of variations with sparse linear combinations. Due to the strict convexity of the new norm, we can prove the convergence of the iterative method and provide the detailed characterization of the limits. We also prove that the obtained principal component is consistent for a single component model in high dimensional situations. As illustration, we apply this method to real gene expression data with competitive results.

1. Introduction

Principal components analysis (PCA), as a popular feature extraction and dimension reduction tool, seeks the linear combinations of the original variables (principal components, PCs) such that the derived PCs capture maximal variance and guarantee minimal information loss. However, the classic PCA has major practical and theoretical drawbacks when it is applied to high-dimensional data. The classic PCA produces inconsistent estimates in high-dimensional situations (see Paul [11], Nadler [10] and Johnstone and Lu [7]). The loadings of PCs are typically non-zero. This often makes it difficult to interpret the PCs and identify important variables.

To address the drawbacks of classic PCA, various modified PCA methods have been proposed to form PCs where each PC is the linear combination of a small subset of the variables that can still explain high percentage of variance. SCoTLASS proposed in Jolliffe, Trendafilov and Uddin [8], a quite natural extension to classic PCA, maximizes the explained variances with l₁ constraints on the loadings, as well as orthogonal conditions on subsequent loadings. The nonconvexity of its objective function and feasible region leads to difficulties in computation, especially for higher order principal components. Trendafilov and Jolliffe [14] proposed a globally convergent algorithm to solve the optimization problem in the SCoTLASS based on the projected gradient approach. D’Aspremont, Bach and Ghaoui [4] suggested a semidefinite programming problem as a relaxation to the l₀-penalty for sparse covariance matrix. Amini and Wainwright [1] studied the asymptotic properties of the leading eigenvector of the covariance estimator obtained by D’Aspremont et al. [4]. The SPCA developed by Zou, Hastie and Tibshirani [16] formulates PCA as a regression-type optimization problem (SPCA), and then to obtain sparse loadings by imposing the lasso or elastic net penalty on the regression coefficients. Compared to SCotLASS, this method has more complicated objective function, but it is computationally efficient. The sparse PCs obtained from SPCA are neither orthogonal nor uncorrelated. Applications of SPCA to simulated and real examples indicated that different sparse PCs may be highly correlated, which makes it difficult in differentiating the variances explained by different PCs. To ease this difficulty, Zou and his colleagues proposed a new approach to computing the total variance explained by sparse PCs. However, without orthogonality or uncorrelation constraints, there are infinitely many sparse linear combinations which can achieve the same level of explained variances as the higher order PCs obtained by SPCA. Furthermore, the obtained PCs by SPCA appear to be sensitive to the choice of the number of PCs and all the sparsity parameters. Shen and Huang [13] proposed a sequential method (sPCA-rSVD) to find the sparse PCs via regularized singular value decomposition which extracts the PCs through solving low rank matrix approximation problems. Compared to SPCA, this method does not have the sensitivity problem as SPCA to the number of PCs and its higher order PCs are not affected by the sparsity parameters of the lower order PCs. But the nonorthogonality and correlation in PCs remain a problem. Based on their penalized matrix decomposition method, Witten, Tibshirani and Hastie [15] proposed an iterative method for obtaining sparse PCs, which yields an efficient algorithm to obtain the first PC of SCoTLASS. However, it is hard to study the convergence of this iterative method and to extend it to get orthogonal or uncorrelated higher order PCs. Johnstone and Lu [7] proposed a thresholding method and proved its consistency for a single component model in high dimensional situations. As pointed out by Cadima and Jolliffe [3], the thresholding approach can be potentially misleading in various respects.

In this paper, we propose a new criterion-based sequential sparse PCA method by replacing the l₂-norm in traditional eigenvalue problems with a new norm, which is a convex combination of l₁ and l₂ norms. Hence, the optimization problems in our methods are natural extensions of those in classic PCA and have relatively simple forms. We propose an efficient iterative algorithms to solve these optimization problems. Due to the strict convexity of the new norm, we can prove the convergence of this iterative algorithm and provide the detailed characterization of the limits. With this method, we can efficiently obtain un-correlated PCs or orthogonal loadings, and achieve the goal of explaining high percentage of variations with sparse loadings. Our method is almost as fast as SPCA and sPCA-rSVD for high-dimensional data such as gene expression data and single-nucleotide polymorphism (SNP) data. This new framework can be easily extended to other statistical techniques and methodologies involve solving eigenvalue problems (such as partial least square regression), generalized eigenvalue problems (such as linear discriminant analysis) and singular value decomposition problems (such as canonical correlation analysis), where the different components are required to be orthogonal or uncorrelated. They are our future research directions. We also prove that the obtained PC is consistent in the single component model proposed by Johnstone and Lu [7] when the ratio of the number of variables to the sample size goes to a nonnegative constant.

The paper is organized as follows. In Section 2, we describe our method, propose algorithms and provide the theoretical characterizations. We show the consistency result in Section 3, and conduct simulation studies and apply our method to the well-studied pitprop data set and a gene expression dataset in Section 4. The proofs of all theorems are given in Section 5. The proofs of some technical lemmas are given in the Appendix.

2. Sparse PCA by choice of norm

Let X be a n × p data matrix where n and p are the number of the observations and the number of the variables, respectively. Without loss of generality, assume the column means (sample means) of X are all 0. We will use Σ to denote the p × p sample covariance matrix $\frac{1}{n}{\mathbf{X}}^T\mathbf{X}$ throughout this paper except in Section 3 where the sample covariance matrix is denoted by Σ̂⁽ⁿ⁾ because we want to study the asymptotic property of our method as n → ∞. X^T is the transpose of the matrix X. For any v = (v₁, · · ·, v_p)^T ∈ ℝ^p and u = (u₁, · · ·, u_p)^T ∈ ℝ^p, let ${\left|\right|\mathbf{v}\left|\right|}_2={({\sum }_{i=1}^p{v}_i^2)}^{\frac{1}{2}}$ be the l₂-norm of v, 〈u, v〉 = u^Tv be the inner product between u and v, and ${\left|\right|\mathbf{v}\left|\right|}_1={\sum }_{i=1}^p\mid v_i\mid$ be the l₁-norm of v. If u and v are orthogonal under l₂-norm, that is, 〈u, v〉 = u^Tv = 0, we write u ⊥ v.

For any λ ∈ [0, 1], we define a “mixed norm” ||·||_λ in ℝ^p space by

$${\left|\right|\mathbf{v}\left|\right|}_{\lambda }={[(1-\lambda ){\left|\right|\mathbf{v}\left|\right|}_2^2+\lambda {\left|\right|\mathbf{v}\left|\right|}_1^2]}^{\frac{1}{2}},\forall \mathbf{v}\in {\mathbb{R}}^p.$$

If λ = 0, this norm reduces to the l₂ norm, and if λ = 1, it is the l₁ norm. Our definitions for the first and the higher order sparse PCs are given as follows.

Definition 1

The coefficient vector v₁ ∈ ℝ^p of the first sparse principal component is the solution to the following optimization problem,

$$\underset{\mathbf{v}\in {\mathbb{R}}^p,{\left|\right|\mathbf{v}\left|\right|}_2=1}{max}\frac{{\mathbf{v}}^T\mathbf{\sum }\mathbf{v}}{(1-{\lambda }_1){\left|\right|\mathbf{v}\left|\right|}_2^2+{\lambda }_1{\left|\right|\mathbf{v}\left|\right|}_1^2}=\underset{\mathbf{v}\in {\mathbb{R}}^p,{\left|\right|\mathbf{v}\left|\right|}_2=1}{max}\frac{{\mathbf{v}}^T\mathbf{\sum }\mathbf{v}}{{\left|\right|\mathbf{v}\left|\right|}_{{\lambda }_1}^2},$$ (2.1)

where 0 ≤ λ₁ ≤ 1 is the tuning parameter for the first sparse principal component.

λ₁ controls the sparsity of v₁. A larger λ₁ leads to sparser coefficients, but reduces the proportion of variations explained by the first PC. In practice, we need to choose an appropriate value of the tuning parameter to make a balance between sparsity and high percentage of explained variance. Because the objective function in (2.1) is homogeneous, that is, the objective function has the same values at v and av, where a is any nonzero real number, the optimization problem (2.1) is equivalent to the following problem,

$$\underset{\mathbf{u}\in {\mathbb{R}}^p}{max}{\mathbf{u}}^T\mathbf{\sum }\mathbf{u},\text{subject}\text{to}{\left|\right|\mathbf{u}\left|\right|}_{{\lambda }_1}\le 1.$$ (2.2)

The solutions to (2.1) and (2.2) differ only by a multiplicative constant. The solution to (2.2) always has the mixed norm equal to one, because Σ, the covariance matrix, is nonnegative definite, and hence u^T Σu is always nonnegative for any u. We will propose an efficient algorithm to solve (2.2). However, it is more convenient to consider the form (2.1) in studying the asymptotic consistency of our sparse PCs.

We now compare our method with SCoTLASS which solves the following problem,

$$\underset{\mathbf{u}\in {\mathbb{R}}^p}{max}{\mathbf{u}}^T\mathbf{\sum }\mathbf{u},\text{subject}\text{to}{\left|\right|\mathbf{u}\left|\right|}_2=1,{\left|\right|\mathbf{u}\left|\right|}_1\le t.$$ (2.3)

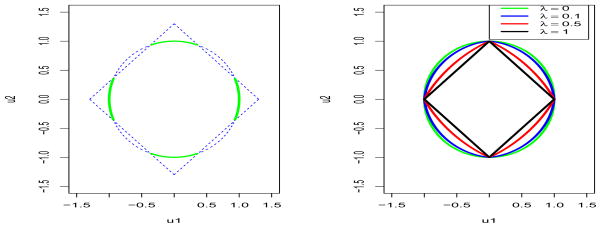
When $t\ge \sqrt{p}$, the l₁ constraint in (2.3) is not active. In this case, (2.3) is just the usual eigenvalue problem and equivalent to (2.2) with λ₁ = 0. When t < 1, the feasible region of (2.3) is empty. When $1\le t<\sqrt{p}$, the difference of the feasible regions between (2.2) and (2.3) is shown in Figure 1 for the two dimensional case. The left plot in Figure 1 shows the pattern of the feasible region for (2.3) with $1<t=1.3<\sqrt{2}$. The feasible region of (2.3) is the collection of the solid green lines and is nonconvex. The right plot in Figure 1 shows the feasible regions in (2.2) for different λ₁. The regions are strictly convex for 0 ≤ λ < 1, which plays a key role in the development of our method.

Figure 1.

Left: the feasible region ||u||₂ = 1, ||u||₁ ≤ t of SCoTLASS (where t = 1.3) is the collection of the solid green lines. Right: the feasible regions ||u||_λ ≤ 1 of our method for λ = 0, 0.1, 0.5 and 1 are the regions bounded by the lines with different colors.

The classic PCs possess two properties simultaneously: coefficient vectors of different PCs are orthogonal and different PCs are uncorrelated. However, for sparse PCA, at most one of the two properties can be possessed by principal components. Therefore, we consider two alternative definitions for higher order PCs. In the following definitions, v_k, k ≥ 1, denotes the coefficient vector of the k-th sparse PC.

Definition 2

Suppose that we have obtained v_j, 1 ≤ j ≤ k − 1, then v_k solves the following optimization problem,

$$\underset{\begin{array}{c}{\left|\right|\mathbf{v}\left|\right|}_2=1,\mathbf{v}\perp {\mathbf{v}}_j,\\ j=1,\cdots ,k-1\end{array}}{max}\frac{{\mathbf{v}}^T\mathbf{\sum }\mathbf{v}}{{\left|\right|\mathbf{v}\left|\right|}_{{\lambda }_k}^2},$$ (2.4)

where λ_k is the tuning parameter for v_k.

Definition 3

Suppose that we have obtained v_j, 1 ≤ j ≤ k − 1, then v_k solves the following optimization problem,

$$\underset{\begin{array}{c}{\left|\right|\mathbf{v}\left|\right|}_2=1,\mathbf{v}\perp \mathbf{\sum }{\mathbf{v}}_j,\\ j=1,\cdots ,k-1\end{array}}{max}\frac{{\mathbf{v}}^T\mathbf{\sum }\mathbf{v}}{{\left|\right|\mathbf{v}\left|\right|}_{{\lambda }_k}^2},$$ (2.5)

Under Definition 2, v_k, k ≥ 1, are orthogonal to each other and under Definition 3, different PCs are uncorrelated to each other. Our algorithm can be applied to both definitions. Different tuning parameters can be used for different PCs in our method. We first propose an algorithm to solve the problem (2.2) for the first PC.

Before we introduce our algorithm, in order to facilitate comparison among various sparse PCA methods, we summarize the criteria of the methods we can find as follows. It is definitely not a complete list.

• SCoTLASS (Jolliffe et al. [8] and Trendafilov and Jolliffe [14]): the coefficient vector for the k-th sparse principal component is the solution to

  $$\underset{\mathbf{u}\in {\mathbb{R}}^p}{max}{\mathbf{u}}^T\mathbf{\sum }\mathbf{u},\text{subject}\text{to}{\left|\right|\mathbf{u}\left|\right|}_2=1,{\left|\right|\mathbf{u}\left|\right|}_1\le t,\mathbf{u}\perp {\mathbf{u}}_j,1\le j\le k-1,$$

  where u_j is the coefficient vector for the j-th sparse principal component and t is tuning parameter.

• Semidefinite-programming relaxation (D’Aspremont et al. [4]): find the symmetric and nonnegative-definite matrix X which

  $$\text{maximize}Tr(\mathrm{\sum }X)\text{subject}\text{to}Tr(X)=1,\mathit{rank}(X)=1\sum _{i,j=1}^p\mid X_{ij}\mid \le k,$$

  where Tr(·) denotes the trace of a matrix and k is the tuning parameter. Then the estimate of the coefficient vector for the first principal component is the leading eigenvector of X.

• SPCA (Zou et al. [16]): solve the following regression-type problem,

  $$\underset{\mathbf{A},\mathbf{B}}{min}\left\{\sum _{i=1}^n{\left|\right|{\mathbf{x}}_i-{\mathbf{AB}}^T{\mathbf{x}}_i\left|\right|}_2^2+\lambda \sum _{j=1}^k{\left|\right|{\beta }_j\left|\right|}_2^2+\sum _{j=1}^k{\lambda }_{1,j}{\left|\right|{\beta }_j\left|\right|}_1\right\},\text{subject}\text{to}{\mathbf{A}}^T\mathbf{A}=\mathbf{I}$$

  where x₁, · · ·, x_n are the sample, A is a p × k matrix, B = (β₁, β₂, · · ·, β_k) is a p × k matrix and I is the identity matrix. Let (Â, B̂) be the solution to the above optimization problem. Then the columns of B̂, are the estimates of the coefficient vectors for the first k principal components.

• sPCA-rSVD (Shen and Huang [13]): solve the following problem,

  $$\underset{\mathbf{u},\mathbf{v},{\left|\right|\mathbf{u}\left|\right|}_2=1}{min}\left\{\sum _{i=1}^n\sum _{j=1}^p{({\mathbf{X}}_{ij}-u_i{v}_j)}^2+P_{\lambda }(\mathbf{v})\right\},$$

  where X is the data matrix, u = (u₁, · · ·, u_n)^T and v = (v₁, · · ·, v_p)^T, and P_λ(v) is the penalty term. Let (û, v̂) be the solution to the above optimization problem. The estimator of the coefficient vector for the first sparse principal component is v̂.

• In addition to the above criterion-based methods, there are thresholding methods such as the method proposed in Johnstone and Lu [7].

2.1. First sparse principal component

We propose the following iterative algorithm to solve (2.2).

Algorithm 2.1 (For solving (2.2))

1. Choose an initial vector u⁽⁰⁾ ∈ ℝ^p such that Σu⁽⁰⁾ ≠ 0.

2. Iteratively compute u⁽¹⁾, u⁽²⁾, · · ·, until convergence as follows: for any i ≥ 1, if we have obtained u⁽ⁱ⁻¹⁾, define w⁽ⁱ⁻¹⁾ = Σu⁽ⁱ⁻¹⁾, then u⁽ⁱ⁾ is the solution to

   $$\underset{\mathbf{u}\in {\mathbb{R}}^p}{max}{\left({\mathbf{w}}^{(i-1)}\right)}^T\mathbf{u},\mathit{subject}to{\left|\right|\mathbf{u}\left|\right|}_{{\lambda }_1}\le 1.$$ (2.6)

We first observe that if λ = 0, Algorithm 2.1 is the power iteration method for finding the largest eigenvalue of a symmetric matrix (see Section 5.3 in Quarteroni, Sacco and Saleri [12]). The power method is efficient to find the first eigenvector and has been applied to many real-life problems, such as calculating the page rank of documents in the search engine of Google. The convergence of the power method has been well studied. Algorithm 2.1 can be regarded as a generalized power method. The convergence of Algorithm 2.1 will be established at the end of this subsection. A second observation is that the key step of Algorithm 2.1 is the iteration step (2.6). Hence, in order to make Algorithm 2.1 fast, we will propose an efficient algorithm to solve the iteration step (2.6). The optimization problem (2.6) can be written in a general form: given a nonzero vector a ≠ 0, solve

$$\underset{\mathbf{u}\in {\mathbb{R}}^p}{max}{\mathbf{a}}^T\mathbf{u},\text{subject}\text{to}{\left|\right|\mathbf{u}\left|\right|}_{\lambda }\le 1,$$ (2.7)

where 0 ≤ λ < 1. The following theorem establishes the uniqueness of the solution to (2.7).

Theorem 2.1

For any 0 ≤ λ < 1, the space (ℝ^p, ||·||_λ) is a strictly convex Banach space, that is, its unit ball {u: ||u||_λ ≤ 1} is a strictly convex set. Moreover, the solution to (2.7) is unique and is a continuous function of a.

Remark

When λ = 1, the norm is just the l₁-norm, hence the feasible region is convex but not strongly convex. Therefore, in this case, the solution to (2.7) may not be unique.

Theorem 2.1 is important for studying the convergence and limits of Algorithm 2.1. A similar algorithm to Algorithm 2.1 has been proposed in Witten et al. [15] to solve the optimization problem (2.3) in SCoTLASS for the first PC. However, the feasible region in (2.3) is convex but not strictly convex, hence the solution to each iteration step may not be unique and thus it is not a function of a. Therefore, it is not easy to study the convergence and limits of the iterative algorithm and they did not propose the similar iterative algorithm for higher order PCs of SCoTLASS.

Note that (2.7) is a convex optimization problem. We first derive an explicit solution to a special case of (2.7) based on the Karush-Kuhn-Tucker (KKT) conditions in Theorem 2.2. Then the solutions to general cases of (2.7) can be easily derived. We introduce some notations. Let A^[λ] be the p × p matrix with diagonal elements equal to 1 and off-diagonal elements equal to λ. That is,

$${\mathbf{A}}^{[\lambda ]}=\left(\begin{array}{llll}1\hfill & \lambda \hfill & \cdots \hfill & \lambda \hfill \\ \lambda \hfill & 1\hfill & \cdots \hfill & \lambda \hfill \\ \cdots \hfill & \cdots \hfill & \cdots \hfill & \cdots \hfill \\ \lambda \hfill & \lambda \hfill & \cdots \hfill & 1\hfill \end{array}\right).$$

Suppose that I is a subset of {1, 2, · · ·, p} and the size of I is k. Let I^c be the complement of I. For any p × p matrix B, we use B_I to denote the k × k submatrix formed by the rows and columns which original indices are in I. For any u ∈ ℝ^p, we use u_I to denote the k-vector formed by the coordinates which original indices are in I.

Lemma 1

Let 0 ≤ λ < 1 and a = (a₁, · · ·, a_p)^T ≠ 0 with a₁ ≥ a₂ · · · ≥ a_p ≥ 0. Define the partial sums $S_i={\sum }_{j=1}^i{a}_j$, i = 1, · · ·, p. Then there exists a unique m ∈ {1, 2 · · ·, p} satisfying

$$a_{m+1}\le \frac{\lambda S_m}{(1-\lambda )+m\lambda }<a_m,$$ (2.8)

where we set a_p+1 = 0. Moreover, we have

$$\frac{\lambda S_i}{(1-\lambda )+i\lambda }<a_i,\forall i\le m\mathit{and}\frac{\lambda S_i}{(1-\lambda )+i\lambda }\ge a_i,\forall i>m.$$ (2.9)

Remark

For a special case where a₁ = a₂ = · · · = a_p > 0, it can be derived from the lemma that m = p.

Theorem 2.2

Let 0 ≤ λ < 1. Suppose that in (2.7), a = (a₁, · · ·, a_p)^T ≠ 0 with a₁ ≥ a₂ · · · ≥ a_p ≥ 0. Define the partial sums $S_i={\sum }_{j=1}^i{a}_j$, i = 1, · · ·, p. Then the unique solution ${\mathbf{u}}^{\ast }={(u_1^{\ast },\cdots ,u_p^{\ast })}^T$ to (2.7) satisfies

$$u_i^{\ast }=\{\begin{array}{rrr}\hfill \frac{1}{2\nu }\left[a_i-\frac{\lambda S_m}{(1-\lambda )+m\lambda }\right]& \hfill if& \hfill i\le m\\ \hfill 0& \hfill if& \hfill i>m\end{array},$$ (2.10)

where m, the number of nonzero coordinates of u^*, is the unique integer satisfying (2.8) and ν is a positive scale constant chosen to make ||u^*||_λ = 1. Furthermore, let I = {1, 2, · · ·, m} be the index set of nonzero coordinates of u^*, we have ${\mathbf{A}}_I^{[\lambda ]}{\mathbf{u}}_I^{\ast }={\mathbf{a}}_I/2\stackrel{\sim }{\nu }$, where ν̃ is a positive constant.

The solution to (2.7) for general cases can be easily obtained from Lemma 1 and Theorem 2.2.

Corollary 2.1

Let 0 ≤ λ < 1 and k₁, k₂, · · ·, k_p be a permutation of 1, 2, · · ·, p such that |a_k1| ≥ |a_k2| ≥ · · · ≥ |a_kp| is the sorted sequence of (a₁, · · ·, a_p) by their absolute values. Define the partial sums $S_i={\sum }_{j=1}^i\mid a_{k_j}\mid$, i = 1, · · ·, p, of the sorted sequence. Then there exists a unique m ∈ {1, 2 · · ·, p} satisfying

$$\mid a_{k_{m+1}}\mid \le \frac{\lambda S_m}{(1-\lambda )+m\lambda }<\mid a_{k_m}\mid ,$$ (2.11)

where we set |a_kp+1| = 0, and the unique solution ${\mathbf{u}}^{\ast }={(u_1^{\ast },\cdots ,u_p^{\ast })}^T$ of (2.7) satisfies

$$u_i^{\ast }=\{\begin{array}{rrr}\hfill \left[a_i-\mathbf{sgn}(a_i)\frac{\lambda S_m}{(1-\lambda )+m\lambda }\right]/2\nu & \hfill if& i\in I\hfill \\ \hfill 0& \hfill if& i\in I^c\hfill \end{array},$$ (2.12)

where sgn is the sign function, I = {k₁, · · ·, k_m} and ν is a positive constant chosen to make ||u^*||_λ = 1. Furthermore, let be the p × p diagonal matrix with the i-th diagonal element equal to the sign of a_i for all 1 ≤ i ≤ p, we have

$${\mathcal{E}}_I{\mathbf{A}}_I^{[\lambda ]}{\mathcal{E}}_I{\mathbf{u}}_I^{\ast }={\mathbf{a}}_I/2\stackrel{\sim }{\nu },$$ (2.13)

where ν̃ is a positive constant.

Now we propose the following algorithm to solve the optimization problem (2.7) in general cases based on Corollary 2.1.

Algorithm 2.2. (For solving (2.7))

1. Sort the coordinates a_i’s of a by their absolute values: |a_k1|≥ |a_k2|≥ · · · ≥ |a_kp|. Let b_i = |a_ki|, 1 ≤ i ≤ p.

2. Compute $S_i={\sum }_{j=1}^i{b}_j$ and find the unique m ∈ {1, 2 · · ·, p} satisfying

   $$b_{m+1}\le \frac{\lambda S_m}{(1-\lambda )+m\lambda }<b_m,$$

   where b_p+1 = 0.

3. Compute

   $$y_i=\{\begin{array}{rrr}\hfill b_i-\frac{\lambda S_m}{(1-\lambda )+m\lambda }& \hfill if& \hfill i\le m\\ \hfill 0& \hfill if& \hfill i>m\end{array},$$

4. Let û = (û₁, · · ·, û_p) with û_ki = sgn(a_ki)y_i for 1 ≤ i ≤ p. Then the solution is u^* = û/||û||_λ.

The following corollary is useful in our proof of consistency results.

Corollary 2.2

Suppose that a is the same as in Corollary 2.1 and ${\mathbf{u}}^{\ast }={(u_1^{\ast },\cdots ,u_p^{\ast })}^T$ is the solution to (2.7) and satisfies (2.12). Let δ > 0 satisfy δ/2ν < 1, where ν is the constant in (2.12). Then the solution to the following problem,

$$\underset{\mathbf{u}\in {\mathbb{R}}^p}{max}{(\mathbf{a}-\delta {\mathbf{u}}^{\ast })}^T\mathbf{u},\mathit{subject}to{\left|\right|\mathbf{u}\left|\right|}_{\stackrel{\sim }{\lambda }}\le 1,$$ (2.14)

is u^* multiplied by a positive constant, where $\stackrel{\sim }{\lambda }=\frac{\lambda }{\lambda +(1-\delta /2\nu )(1-\lambda )}$.

In the following, we study the convergence and limits of Algorithm 2.1. Let f_λ(a) denote the unique solution to (2.7). By Theorem 2.1, for a fixed λ, f_λ is a continuous function of a. Since λ is fixed in the following theorems, for simplicity, we omit the subscript λ of f_λ hereafter. As a function from ℝ^p\{0} to the unit sphere {u: ||u||_λ = 1} in (ℝ^p, ||·||_λ), f has the following property,

$$f(c\mathbf{a})=\mathbf{sgn}(c)f(\mathbf{a}),\forall 0\ne c\in \mathbb{R}.$$

Noting that u^(k+1) = f (Σu^(k)) in Algorithm 2.1, we define a subset of {u: ||u||_λ = 1},

$$\mathcal{L}=\{\mathbf{u}:{\left|\right|\mathbf{u}\left|\right|}_{\lambda }=1,\mathbf{u}=f(\mathbf{\sum }\mathbf{u})\}.$$ (2.15)

Then is the collection of all fixed points of the function f ∘ Σ. If the initial vector u⁽⁰⁾ in Algorithm 2.1 is a point in , we have u⁽⁰⁾ = u⁽¹⁾ = u⁽²⁾ = · · ·. In this case, Algorithm 2.1 converges to u⁽⁰⁾. Hence, any point in is a possible limit of Algorithm 2.1. We will prove that the iterative procedure in Algorithm 2.1 with any initial vector that satisfies Σu⁽⁰⁾ ≠ 0 will converge to one point in . The limit may depend on the initial vector. The following theorem provides a characterization of the points in .

Theorem 2.3

Assume that 0 ≤ λ < 1. Let u^* be a point in {u: ||u||_λ = 1}. Suppose that the number of nonzero coordinates of u^* is m and Σu^* = (c₁, c₂, · · ·, c_p)^T. Let |c_k1| ≥ |c_k2| ≥ · · · ≥ |c_kp| be the sorted sequence of c_i’s by their absolute values. Define a_i = |c_ki|, 1 ≤ i ≤ p. Then u^* ∈ if and only if

1. (a₁, a₂, · · ·, a_p) satisfy (2.8) in Lemma 1.

2. The index set I of nonzero coordinates of u^* is equal to {k₁, k₂, · · ·, k_m} and ${\mathbf{u}}_I^{\ast }$ is an eigenvector with nonzero eigenvalue of the following generalized eigenvalue problem

   $${\mathbf{\sum }}_I\mathbf{x}=\mu {\mathcal{E}}_I{\mathbf{A}}_I^{[\lambda ]}{\mathcal{E}}_I\mathbf{x},\mathbf{x}\in {\mathbb{R}}^m,$$ (2.16)

   where 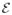is the diagonal matrix with the i-th diagonal element equal to the sign of $u_i^{\ast }$ for all 1 ≤ i ≤ p.

Now we study the convergence of the iteration in Algorithm 2.1 and its limits.

Theorem 2.4

Assume that 0 ≤ λ < 1. Suppose that for any subset J of {1, 2, · · ·, p}, and any p × p diagonal matrix with diagonal elements in {1, −1, 0} and the diagonal elements of nonzero, all the positive eigenvalues of the following generalized eigenvalue problem have multiplicities 1,

$${\mathbf{\sum }}_J\mathbf{x}=\mu {\mathcal{E}}_J{\mathbf{A}}_J^{[\lambda ]}{\mathcal{E}}_J\mathbf{x}.$$ (2.17)

Assume that for any u^* ∈ ,

$$\underset{i\notin I}{max}\mid c_i\mid \ne \frac{\lambda {\sum }_{j\in I}\mid c_j\mid }{(1-\lambda )+m\lambda },$$ (2.18)

where (c₁, c₂, · · ·, c_p)^T = Σu^*, I is the index set of nonzero coordinates of u^* and m is the size of I. Then the iteration in Algorithm 2.1 converges to a point in (the limit depends on the initial vector). Furthermore, only those u^* ∈ with ${\mathbf{u}}_I^{\ast }$ being the leading eigenvector of (2.16) are stable limits.

Remark

We say that a limit point is stable if there exists a neighborhood of this point such that once the iteration falls in the neighborhood, it will converge to the limit point.

From the proof of Theorem 2.4, for any unstable limit in , only an iteration sequence with all but finite points belonging to an affine subspace through that point with dimension strictly less than p can converge to it. Therefore, in practice, due to the rounding errors, the iteration sequence can only converge to stable limits. The solution to (2.2) is one of stable limits in . Although the stable limits may not be unique, due to the stringent conditions for stable limits in Theorem 2.3, there are only a few stable limits. Note that if u^* is a stable limit, so is −u^*. We do not differentiate the two limits. Our simulation studies and applications to real data suggest that when λ is small or the differences between the adjacent eigenvalues of covariance matrix are large, there is only one stable limit. For the cases with large λ and the close adjacent eigenvalues of covariance matrix, there can be two or three stable limits. For high dimensional data, a small λ is typically enough to achieve sparsity of the coefficients and high percentage of explained variance. In the case that there is more than one limit, if the initial vector is randomly chosen, our simulations suggest that with larger probability, the iteration converges to the solution to (2.2) than any other limit. These observations are also true for higher order sparse PCs.

2.2. Higher order sparse principal components

Now we propose a similar iterative algorithm for solving the optimization problem (2.4) or (2.5) for the higher order PCs. We will consider the following more general problem of which (2.4) and (2.5) are special cases:

$$\underset{{\left|\right|\mathbf{v}\left|\right|}_2=1,\mathbf{v}\perp \mathbf{M}}{max}\frac{{\mathbf{v}}^T\mathbf{\sum }\mathbf{v}}{{\left|\right|\mathbf{v}\left|\right|}_{\lambda }^2},$$ (2.19)

where M is a linear subspace of ℝ^p. M is the subspace spanned by {v₁, · · ·, v_k−1} for Definition 2, and M is spanned by {Σv₁, · · ·, Σv_k−1} for Definition 3. We propose the following algorithm to solve (2.19).

Algorithm 2.3. (For solving (2.19))

1. Choose an initial vector u⁽⁰⁾ ∈ ℝ^p such that Σu⁽⁰⁾ ∉ M.

2. Iteratively compute u⁽¹⁾, u⁽²⁾, · · ·, until convergence as follows: for any i ≥ 1, let w⁽ⁱ⁻¹⁾ = Σu⁽ⁱ⁻¹⁾, then u⁽ⁱ⁾ solves the following problem

   $$\underset{\mathbf{u}\in {\mathbb{R}}^p}{max}{\left({\mathbf{w}}^{(i-1)}\right)}^T\mathbf{u},\mathit{subject}to{\left|\right|\mathbf{u}\left|\right|}_{{\lambda }_k}\le 1,\mathbf{u}\perp \mathbf{M}.$$

The optimization problem in the second step of Algorithm 2.3 is a special case of the following problem: given a ∉ M,

$$\underset{\mathbf{u}\in {\mathbb{R}}^p}{max}{\mathbf{a}}^T\mathbf{u},\text{subject}\text{to}{\left|\right|\mathbf{u}\left|\right|}_{\lambda }\le 1,\mathbf{u}\perp \mathbf{M}.$$ (2.20)

For a general M, we cannot give an explicit solution to (2.20) as in Theorem 2.2. We will develop a method to solve (2.20) by relating the optimization problem (2.20) to the optimization problem (2.7) which has an explicit solution and can be solved quickly. Recall that f (a) is the solution to the optimization problem (2.7) and is a continuous function of a.

Theorem 2.5

Assume that a ∉ M. Let a_⊥ be the orthogonal projection of a onto the orthogonal complement of M. Let q be the dimension of M and {ψ₁, · · ·, ψ_q} be an orthonormal basis of M. Then there exists ${\mathbf{t}}^{\ast }=(t_1^{\ast },\cdots ,t_q^{\ast })\in {\mathbb{R}}^q$ such that $f({\mathbf{a}}_{\perp }+t_1^{\ast }{\mathit{\psi }}_1+\cdots +t_q^{\ast }{\mathit{\psi }}_q)\perp \mathbf{M}$. Moreover, $f({\mathbf{a}}_{\perp }+t_1^{\ast }{\mathit{\psi }}_1+\cdots +t_q^{\ast }{\mathit{\psi }}_q)$ is the unique solution to (2.20).

By Theorem 2.5, solving (2.20) is equivalent to finding t^* ∈ ℝ^q such that $f({\mathbf{a}}_{\perp }+t_1^{\ast }{\mathit{\psi }}_1+\cdots +t_q^{\ast }{\mathit{\psi }}_q)\perp \mathbf{M}$. For any t = (t₁, · · ·, t_q)^T ∈ ℝ^q, we define H(t) to be the squared norm of the orthogonal projection of f (a_⊥ + t₁ψ₁ + · · ·+ t_q ψ_q) onto M. Let Ψ = (ψ₁, …, ψ_q), where ψ_j = (ψ_1j, · · ·, ψ_pj)^T, 1 ≤ j ≤ q, are basis vectors, and x(t) = f (a_⊥ + t₁ψ₁ + · · · + t_q ψ_q) = f (a_⊥ + Ψt). Then

$$H(\mathbf{t})=\sum _{i=1}^q{\left({{\mathit{\psi }}_{\mathit{i}}}^{T}f({\mathbf{a}}_{\perp }+t_1{\mathit{\psi }}_1+\cdots +t_q{\mathit{\psi }}_q)\right)}^2=\mathbf{x}{(\mathbf{t})}^T\mathbf{\Psi }{\mathbf{\Psi }}^T\mathbf{x}(\mathbf{t}),$$ (2.21)

and H(t) is a continuous function of t. It follows from Theorem 2.5 that H(t^*) = 0 and t^* is also the minimum point of H(t). We will show that H(t) is a piecewise smooth function. Let

$$\mathbf{c}(\mathbf{t})={(c_1(\mathbf{t}),\cdots ,c_p(\mathbf{t}))}^T={\mathbf{a}}_{\perp }+\mathbf{\Psi }\mathbf{t},\forall \mathbf{t}={(t_1,\cdots ,t_q)}^T\in {\mathbb{R}}^q.$$ (2.22)

c_i(t)’s are linear functions of t. Let |c_k1(t)| ≥ |c_k2(t)| ≥ · · · ≥ |c_kq(t)| be the sorted sequence of {c₁(t), · · ·, c_p(t)} by their absolute values. Note that k_i, 1 ≤ i ≤ p, depends on t. Define the following subsets of ℝ^q,

$${\mathcal{J}}_m=\left\{\mathbf{t}\in {\mathbb{R}}^q:\mid c_{k_{m+1}}(\mathbf{t})\mid =\frac{\lambda {\sum }_{1\le i\le m}\mid c_{k_i}(\mathbf{t})\mid }{(1-\lambda )+m\lambda }\right\},1\le m\le p-1,$$ (2.23)

each of which is a union of faces of a finite number of polyhedrons.

Theorem 2.6

H(t) is smooth at any point $\mathbf{t}\notin {\cup }_{m=1}^{p-1}{\mathcal{J}}_m$. Suppose that

$$\mathbf{x}(\mathbf{t})={(x_1(\mathbf{t}),\cdots ,x_p(\mathbf{t}))}^T$$

is the solution to the following optimization problem

$$\underset{\mathbf{u}\in {\mathbb{R}}^p}{max}{({\mathbf{a}}_{\perp }+\mathbf{\Psi }\mathbf{t})}^T\mathbf{u},\mathit{subject}to{\left|\right|\mathbf{u}\left|\right|}_{\lambda }\le 1.$$ (2.24)

Then the first and the second partial derivatives of H(t) are

$$\begin{array}{l}\nabla H(\mathbf{t})=\frac{\mathbf{G}(\mathbf{t})-H(\mathbf{t})\mathbf{E}(\mathbf{t})}{\nu },\\ {\nabla }^{2}H(\mathbf{t})=\frac{4H(\mathbf{t})\mathbf{E}(\mathbf{t})\mathbf{E}{(\mathbf{t})}^T-2[\mathbf{E}(\mathbf{t})\mathbf{G}{(\mathbf{t})}^T+\mathbf{G}(\mathbf{t})\mathbf{E}{(\mathbf{t})}^T]+\mathbf{\Pi }(\mathbf{t})-H(\mathbf{t})\mathbf{F}(\mathbf{t})}{2{\nu }^2},\end{array}$$

where

$$\begin{array}{l}\mathbf{E}(\mathbf{t})=(1-\lambda )\mathbf{K}{(\mathbf{t})}^T\mathbf{x}(\mathbf{t})+\lambda {\left|\right|\mathbf{x}(\mathbf{t})\left|\right|}_1\mathbf{K}{(\mathbf{t})}^T\mathbf{N}(\mathbf{t})\mathbf{1},\mathbf{G}(\mathbf{t})=\mathbf{K}{(\mathbf{t})}^T\mathbf{\Psi }{\mathbf{\Psi }}^T\mathbf{x}(\mathbf{t}),\\ \mathbf{F}(\mathbf{t})=(1-\lambda )\mathbf{K}{(\mathbf{t})}^T\mathbf{K}(\mathbf{t})+\lambda \mathbf{K}{(\mathbf{t})}^T\mathbf{N}{(\mathbf{t})}^T\mathbf{1}{\mathbf{1}}^T\mathbf{N}(\mathbf{t})\mathbf{K}(\mathbf{t}),\\ \mathbf{\Pi }(\mathbf{t})=\mathbf{K}{(\mathbf{t})}^T\mathbf{\Psi }{\mathbf{\Psi }}^T\mathbf{K}(\mathbf{t}),\mathbf{K}(\mathbf{t})=\mathbf{N}(\mathbf{t})\left(\mathbf{I}-\frac{\lambda }{(1-\lambda )+m\lambda }\mathbf{1}{\mathbf{1}}^T\right)\mathbf{N}(\mathbf{t})\mathbf{\Psi },\end{array}$$

I is the p-dimensional identity matrix, 1 is the p vector with all coordinates equal to 1, and N(t) is the p-dimensional diagonal matrix with the i-th diagonal element equal to sgn(x_i(t)), 1 ≤ i ≤ p. 2ν is a scale constant which is the same as that in (2.12) with a and u^* replaced with a_⊥ + Ψt and x(t), respectively.

By Theorem 2.6, the first and the second partial derivatives of H(t) only involve c(t) and x(t) which can be obtained quickly from Algorithm 2.2. Hence, based on Theorems 2.5 and 2.6, we propose the following algorithm to solve (2.20) by using the Newton method. It is worth to point out that algorithms based on other numerical methods can also be proposed to get the zero point and minimum point t^* of H(t), which is equivalent to solving (2.20). Some of them do not use the second derivative of H(t).

Algorithm 2.4. (For solving (2.20))

1. Compute the projection matrix P = ΨΨ^T onto M.

2. Compute the orthogonal projection a_⊥ = (I − P)a of a onto the rthogonal complement space M^⊥ of M, where I is the identity matrix.

3. Set the initial value of t equal to zero.

4. Compute the solution x(t) to (2.24) using Algorithm 2.2.

5. Compute the first and the second partial derivatives, ∇H(t) and ∇²H(t), of H(t) using Theorem 2.6.

6. Compute Δt = −(∇²H(t))⁻¹ ∇H(t).

7. Update the value of t by setting t = t + Δt. Then go back to Step 4 and repeat the procedure until convergence.

In some cases, the second derivatives ∇²H(t) can be nearly singular. We can use the following formula

$$\mathrm{\Delta }\mathbf{t}=-{({\nabla }^{2}H(\mathbf{t})+\epsilon \mathbf{I})}^{-1}\nabla H(\mathbf{t}),$$

to calculate Δt in Step 6 of Algorithm 2.4, where ε is the sum of two times of the absolute value of the smallest eigenvalue of ∇²H(t) and a small number (for example, 0.001).

Now we will give the convergence results for Algorithm 2.3 which are very similar to those for the first PC. For any subspace M, define f ^M(a) to be the solution to (2.20). Then f ^M is a continuous function from ℝ^p\M to M^⊥∩{u: ||u||_λ = 1}, where M^⊥ is the orthogonal complement of M. Let

$${\mathcal{L}}^{\mathbf{M}}=\{\mathbf{u}:\mathbf{u}=f^{\mathbf{M}}(\mathbf{\sum }\mathbf{u})\}.$$ (2.25)

The following theorem involves some technical conditions which will be given in its proof.

Theorem 2.7

Assume that 0 ≤ λ < 1. Suppose that all u^* ∈ satisfy (5.47). Then the iteration in Algorithm 2.3 converges to one point in (the limit depends on the initial vector). Furthermore, only u^* ∈ with ${\mathbf{u}}_I^{\ast }$ being a leading eigenvector of problem (5.48) are stable limits, where I is the index set of nonzero coordinates of u^*.

2.3. Choice of the tuning parameters

The selection of tuning parameters is crucial for the performance of any penalized procedure. The main purpose of sparse PCA is twofold. On the one hand, we want to find principal components which can explain as much as possible variations in data sets. On the other hand, we want to make the coefficients of the principal components as sparse as possible. However, as the tuning parameters increases, sparsity increases, but variation explained decreases. We have to achieve a suitable tradeoff between these two goals. Hence we design the following criteria to choose appropriate tuning parameters. The criteria are similar to the AIC and BIC criteria for linear models. Since we have one tuning parameter for each component, we choose the tuning parameters sequentially from low-order components to high-order components.

For the first principal component, we choose λ₁ which maximize

$$C_1(\lambda )=(1-a)q_1(\lambda )+a\frac{k_1(\lambda )}{p},$$ (2.26)

where p is the dimension of the coefficients, q₁(λ) is the ratio of the explained variances by the first PCs when the tuning parameter is λ to the explained variances when it is zero (the classic PCA), k₁(λ) is the number of zeros in the coefficients of the first PC when the tuning parameter is λ. a ∈ (0, 1) is the weight which is chosen based on the purpose of the researchers, that is, the relative importance of sparsity and the explained variations. We choose a larger a if we need sparser principal components.

Suppose that we have chosen the tuning parameters for the first m − 1 components and obtained the first m − 1 principal components v₁, · · ·, v_m−1. Then the tuning parameter λ_m of the m-th principal component is chosen by maximizing

$$C_m(\lambda )=(1-a)q_m(\lambda ,{\mathbf{v}}_1,\cdots ,{\mathbf{v}}_{m-1})+a\frac{k_m(\lambda )}{p},$$ (2.27)

where a is the same as in (2.26) (that is, a is the same for all components), q_m(λ, v₁, · · ·, v_m−1) is the ratio of the explained variances by the m-th PCs when the tuning parameter is λ to the explained variances when it is zero (the m-th PC should be orthogonal to or uncorrelated with the first m − 1 components), k_m(λ) is the number of zeros in the coefficients of the m-th PCs when the tuning parameter is λ.

For the total number K of the principal components, we can choose K such that the total variations explained by the first K components is greater than a given large number, or the K + 1 component explain variance less than a given small number.

3. Consistency in high dimensions

In this section, we consider the single component model discussed in John-stone and Lu [7]. We will prove that the PC obtained by our method is consistent under this model when the ratio of the number of variables to the sample size goes to a nonnegative constant.

For each n ≥ 1, we assume that n i.i.d. random samples, ${\mathbf{x}}_i^{(n)}\in {\mathbb{R}}^{p_n}$, 1 ≤ i ≤ n, are drawn from the following model,

$${\mathbf{x}}_i^{(n)}=w_i^{(n)}{\mathit{\rho }}^{(n)}+\sigma {\mathbf{z}}_i^{(n)},i=1,\cdots ,n,$$ (3.1)

where ${\mathit{\rho }}^{(n)}={({\rho }_1^{(n)},\cdots ,{\rho }_{p_n}^{(n)})}^T\in {\mathbb{R}}^{p_n}$, the single component, is a nonrandom vector. { $w_i^{(n)}$, 1 ≤ i ≤ n, 1 ≤ n} is a set of i.i.d. standard normal variables and ${\mathbf{z}}_i^{(n)}={(z_{i1}^{(n)},\cdots ,z_{{ip}_n}^{(n)})}^T\in {\mathbb{R}}^{p_n}$ are the noise vectors with { $z_{ij}^{(n)}$: 1 ≤ j ≤ p_n, 1 ≤ i ≤ n} a set of i.i.d. standard normal variables. In this paper, for simplicity, we assume that the variance of noise, σ², does not depend on n. However, the main result can be easily extended to the cases where σ² depends on n and is bounded. In Johnstone and Lu [7], ||ρ⁽ⁿ⁾||₂ is assumed to converge to some positive constant. Without loss of generality, we will assume that ||ρ ⁽ⁿ⁾||₂ = 1 for simplicity. Our proof can be revised to give the consistency result for the case where the sequence, {||ρ⁽ⁿ⁾||₂: 1 ≤ n}, is bounded.

Our estimate ρ̂⁽ⁿ⁾ of the single component ρ⁽ⁿ⁾ is the solution to the following optimization problem,

$$\underset{\mathbf{v}\in {\mathbb{R}}^p,{\left|\right|\mathbf{v}\left|\right|}_2=1}{max}\frac{{\mathbf{v}}^T{\widehat{\mathbf{\sum }}}^{(n)}\mathbf{v}}{(1-{\lambda }^{(n)}){\left|\right|\mathbf{v}\left|\right|}_2^2+{\lambda }^{(n)}{\left|\right|\mathbf{v}\left|\right|}_1^2},$$ (3.2)

where ${\widehat{\mathbf{\sum }}}^{(n)}=\frac{1}{n}{\sum }_{i=1}^n{\mathbf{x}}_i^{(n)}{({\mathbf{x}}_i^{(n)})}^T$ and 0 ≤ λ⁽ⁿ⁾ < 1 is the tuning parameter. We will show that ||ρ̂⁽ⁿ⁾ − ρ⁽ⁿ⁾||₂ → 0 as n → ∞ under some conditions. An essential condition for consistency of the method in Johnstone and Lu [7] is the uniform “weak l_q decay” condition which is equivalent to the concentration of energy in a few coordinates. Suppose that

$$\mid {\mathit{\rho }}^{(n)}{\mid }_{(1)}\ge \mid {\mathit{\rho }}^{(n)}{\mid }_{(2)}\ge \cdots \ge \mid {\mathit{\rho }}^{(n)}{\mid }_{(p_n)}$$

are the ordered absolute values of the coordinates of ρ⁽ⁿ⁾. Then the uniform “weak l_q decay” condition is that for some 0 < q < 2 and C > 0,

$$\mid {\mathit{\rho }}^{(n)}{\mid }_{(\nu )}\le C{\nu }^{-1/q},\nu =1,\cdots ,p_n,n=1,2,\cdots ,$$ (3.3)

where C and q do not depend on n. In addition to this, we need another technical condition. For each n, we define the partial sum $S_i^{(n)}={\sum }_{\nu =1}^i\mid {\mathit{\rho }}^{(n)}{\mid }_{(\nu )}$, 1 ≤ i ≤ p_n. For notational reason, for all i > p_n, we define $S_i^{(n)}=S_{p_n}^{(n)}$. Then the technical condition is

$$\underset{m\to \infty }{limsup}\underset{n\ge 1}{sup}\frac{S_{2m}^{(n)}-S_m^{(n)}}{S_m^{(n)}}<1.$$ (3.4)

We conjecture that our method is consistent even without this condition. This condition implies that the sequences |ρ⁽ⁿ⁾|₍₁₎ ≥ |ρ⁽ⁿ⁾|₍₂₎ ≥ · · · have a uniform asymptotic decreasing rate. Note that if the condition (3.3) with 0 < q < 1 is satisfied, then (3.4) is automatically true with the limit equal to 0. However, if 1 ≤ q < 2, the condition (3.4) can not be derived from (3.3). Here is an example. Suppose that 1 ≤ q < 2, for each n, let p_n = 2n, $\mid {\mathit{\rho }}^{(n)}{\mid }_{(1)}=\sqrt{1-(2n-1){(2n)}^{-2/q}}$ and |ρ⁽ⁿ⁾|₍₂₎ = · · · = |ρ⁽ⁿ⁾|_(pn) = (2n)^−1/q, then the condition (3.3) is satisfied with C = 1. However, a simple calculation shows that the limit in (3.4) is 1 and hence the condition (3.4) is not true in this case. If |ρ⁽ⁿ⁾|_(ν) decrease with order ν^−1/q uniformly in the sense that

$$\underset{m\to \infty }{lim}\underset{n:p_n\ge m}{sup}\left|\frac{\mid {\mathit{\rho }}^{(n)}{\mid }_{(m)}}{m^{-1/q}}-c_n\right|=0,$$

where c_n, n ≥ 1, are positive numbers with inf_n c_n > 0, the condition (3.4) holds. Now we give the main consistency result in high dimension for our method.

Theorem 3.1

Suppose that ||ρ ⁽ⁿ⁾||₂ = 1 for all n ≥ 1 and satisfies the conditions (3.3) and (3.4). Assume that p_n is a nonrandom sequence such that p_n/n → c as n → ∞, where c is a real number. Suppose that c satisfies the following condition,

$$4\sigma \sqrt{c}+4{\sigma }^2\sqrt{c}+6{\sigma }^{2}c<1,$$ (3.5)

and there exists 0 < α < 1/3 such that

$$\underset{n\to \infty }{liminf}{\lambda }^{(n)}{n}^{\alpha }>0\mathit{and}\underset{n\to \infty }{lim}{\lambda }^{(n)}=0.$$ (3.6)

Then we have lim_n→∞||ρ̂⁽ⁿ⁾ − ρ ⁽ⁿ⁾||₂ = 0. Moreover, the number of nonzero coordinates of ρ̂⁽ⁿ⁾ is O_p(1/λ⁽ⁿ⁾).

4. Examples

4.1. Pitprops data

The pitprops data, with 180 observations and 13 measured variables, was first introduced by Jeffers [6]. It is a classic example showing the difficulty of interpreting PCs. To illustrate the performance of their sparse PCA methods, several authors have studied the pitprops data, such as Jolliffe et al. [8] (SCot-LASS), Zou et al. [16] (SPCA), and Shen and Huang [13] (sPCA-rSVD).

We first compare our method with SPCA and sPCA-rSVD. We apply our method to this data set and take (0.1, 0.1, 0.13, 0.12, 0.2, 0.2) as the values of λ for the first six PCs. The obtained sparse PC loadings are shown in Table 1. We use Definition 3 for higher order PCs. Then the six sparse PCs are uncorrelated and the explained variances by these PCs can be clearly distiguished. The percentages of the explained variances are listed in Table 1. They are close to the percentages achieved by the classical PCA: 32.4, 18.3, 14.4, 8.5, 7.0, 6.3, respectively. We can obtain sparser PCs by increasing the value of λ, but the percentages of explained variances will decrease.

Table 1.

Loadings of the first six PCs by our method on the pitprops data

Variables	PC1	PC2	PC3	PC4	PC5	PC6
topdiam	−0.471	0	0.197	0	0	0
length	−0.484	0	0.222	0	−0.045	0
moist	0	−0.684	0	0.060	0.261	0
testsg	0	−0.659	−0.072	0.063	0.189	−0.121
ovensg	0	0	−0.745	0	0	−0.455
ringtop	−0.134	0	−0.400	0	−0.137	0.345
ringbut	−0.383	0	−0.110	0	−0.139	0.299
bowmax	−0.254	0.137	0	−0.092	0	−0.679
bowdist	−0.383	0	0	0	−0.080	0
whorls	−0.410	0.163	0	0.035	0	0
clear	0	0	0	−0.978	−0.040	−0.091
knots	0	−0.229	0	0	−0.921	−0.318
diaknot	0	0	0.424	0.163	0	0
Variance(%)	0.301	0.156	0.132	0.078	0.065	0.046
Cum. var.(%)	0.301	0.457	0.589	0.666	0.731	0.778

The sparse PCs produced by SPCA and sPCA-rSVD are neither uncorrelated nor orthogonal. We calculate the correlation matrices of the first six sparse PCs obtained in Zou et al. [16] and Shen and Huang [13], respectively. The first matrix in the following is the correlation matrix for SPCA and the second one is for sPCA-rSVD:

$$\begin{array}{l}\left(\begin{array}{rrrrrr}\hfill 1& \hfill -0.17& \hfill -0.33& \hfill -0.00& \hfill -0.20& \hfill 0.08\\ \hfill -0.17& \hfill 1& \hfill 0.13& \hfill -0.14& \hfill -0.22& \hfill 0.08\\ \hfill -0.33& \hfill 0.13& \hfill 1& \hfill 0.10& \hfill 0.14& \hfill -0.40\\ \hfill -0.00& \hfill -0.14& \hfill 0.10& \hfill 1& \hfill 0.03& \hfill -0.01\\ \hfill -0.20& \hfill -0.22& \hfill 0.14& \hfill 0.03& \hfill 1& \hfill -0.18\\ \hfill 0.08& \hfill 0.08& \hfill -0.40& \hfill -0.01& \hfill -0.18& \hfill 1\end{array}\right),\\ \left(\begin{array}{rrrrrr}\hfill 1& \hfill 0.20& \hfill -0.46& \hfill -0.33& \hfill -0.20& \hfill -0.04\\ \hfill 0.20& \hfill 1& \hfill -0.11& \hfill 0.27& \hfill 0.13& \hfill 0.05\\ \hfill -0.46& \hfill -0.11& \hfill 1& \hfill 0.26& \hfill 0.16& \hfill -0.10\\ \hfill -0.33& \hfill 0.27& \hfill 0.26& \hfill 1& \hfill 0.20& \hfill 0.07\\ \hfill -0.20& \hfill 0.13& \hfill 0.16& \hfill 0.20& \hfill 1& \hfill -0.05\\ \hfill -0.04& \hfill 0.05& \hfill -0.10& \hfill 0.07& \hfill -0.05& \hfill 1\end{array}\right).\end{array}$$

We can see that some PCs in both methods are strongly correlated and there is no clear pattern in these correlation matrices. For example, in the second matrix, the third PC is strongly correlated to the first, but weakly correlated with the second and the sixth PCs.

We also compare our method with SCotLASS. In Table 2 (provided by one of the anonymous referees), the loadings of principal components produced by SCotLASS for the pitprops data are listed. The loading are orthogonal to each other and all have l₂ norms equal to one. However, the principal components are correlated. In order to make a fair comparison between our method and SCotLASS, we also produce principal components with orthonormal loadings. The loadings by our method with the tuning parameters equal to 0.1, 0.12, 0.12, 0.3, 0.3, 0.3 are listed in Table 3. One can see that two sets of principal components explain almost the same variances, however, the loadings by our method are sparser than those by SCotLASS.

Table 2.

Loadings of the first six PCs by SCotLASS on the pitprops data

Variables	PC1	PC2	PC3	PC4	PC5	PC6
topdiam	0.471	0	−0.081	0.001	0	0
length	0.484	0	−0.101	0.030	0	0
moist	0	−0.705	−0.013	0	0	0
testsg	0	−0.709	0	0	−0.001	0
ovensg	0	0	0.590	0	0	−0.762
ringtop	0.135	−0.026	0.358	0.009	0	0
ringbut	0.383	0	0.101	0	0	0
bowmax	0.254	0	0	−0.062	0	0
bowdist	0.383	0	0	0	0.051	0
whorls	0.410	0.009	0	0	−0.049	0
clear	0	0	0	0	0.997	0
knots	0	0	0	0.998	0	0
diaknot	0	0	−0.704	0	0	−0.638
Variance(%)	0.301	0.146	0.129	0.08	0.08	0.060
Cum. var.(%)	0.301	0.447	0.576	0.656	0.736	0.796

Table 3.

Orthonormal loadings of the first six PCs by our method on the pitprops data

Variables	PC1	PC2	PC3	PC4	PC5	PC6
topdiam	0.471	0	−0.16	0	0	0
length	0.484	0	−0.175	0	0	0
moist	0	−0.705	−0.013	0	0	0
testsg	0	−0.708	0	0	0	0
ovensg	0	0	0.542	0	0	−0.744
ringtop	0.134	−0.02	0.470	0	0	0
ringbut	0.383	0	0.253	0	0	0
bowmax	0.254	0	0	0	0	0
bowdist	0.383	0	0	0	0	0
whorls	0.410	0.007	0	0	0	0
clear	0	0	0	0	1	0
knots	0	0	0	1	0	0
diaknot	0	0	−0.604	0	0	−0.669
Variance(%)	0.301	0.146	0.146	0.077	0.077	0.061
Cum. var.(%)	0.301	0.447	0.593	0.671	0.748	0.809

Finally, we use the criteria (2.26) and (2.27) to choose the tuning parameters for the first six principal components, respectively. Suppose that sparsity and the variance explained are equally important. We choose a = 0.5 in (2.26) and (2.27). Then the tuning parameters chosen by these criteria are 0.10, 0.35, 0.05, 0.15, 0.30, 0.40. The corresponding loadings of the uncorrelated principal components and the proportions of variances explained are listed in Table 4. There are 44 zeros in the loadings and 78.2% variance is explained by the first six principal components.

Table 4.

loadings of the first six PCs corresponding to the tuning parameters chosen based on criteria (2.26) and (2.27)

Variables	PC1	PC2	PC3	PC4	PC5	PC6
topdiam	0.471	0	0.246	0	0	0
length	0.484	0	0.268	0	0	−0.266
moist	0	−0.717	0	0.089	0	0.330
testsg	0	−0.618	−0.106	0.088	0	0
ovensg	0	0	−0.576	0	−0.555	−0.396
ringtop	0.134	0	−0.450	0	0	0
ringbut	0.383	0	−0.262	0	0	0
bowmax	0.254	0	0	−0.064	0	0
bowdist	0.383	0	0.093	0	0	0
whorls	0.410	0.323	0	0	0.017	0
clear	0	0	0	−0.977	−0.126	−0.093
knots	0	0	0	0	0.476	−0.782
diaknot	0	0	0.494	0.157	−0.670	−0.208
Variance(%)	0.301	0.140	0.145	0.076	0.061	0.058
Cum. var.(%)	0.301	0.441	0.587	0.662	0.723	0.782

4.2. NCI cell line data

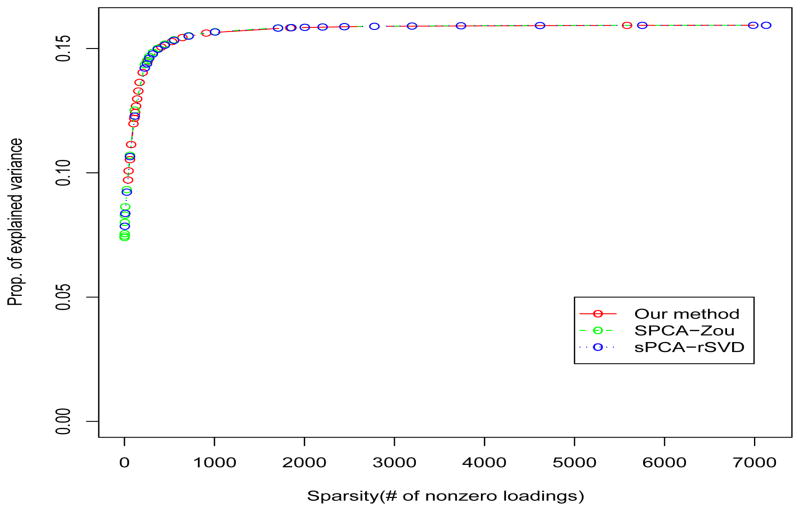
We apply the three methods to the NCI60 dataset which has n = 60 samples and p = 7129 genes (http://www-genome.wi.mit.edu/mpr/NCI60/). We list the percentages of explained variances and the number of nonzero loadings for different tuning parameters in our method in Table 5. We display, in Figure 2, the percentage of explained variances and the sparsity of the first PCs obtained from the three methods for different tuning parameters. The three curves are almost the same. Actually, the variables selected by the three methods are almost identical. For example, when the numbers of nonzero loadings are all 62 for the three methods, the variables selected by sPCA-rSVD and our method are exactly the same and differ from those selected from SPCA only by 4 variables.

Table 5.

Percentages of variations and the number of nonzero coefficients for different tuning parameters in NCI cell line data

λ	0	0.001	0.005	0.01
1st PC	15.9%(7129)	15.1%(411)	13.3%(155)	12%(101)
2nd PC	11.6% (7129)	10.2%(565)	8.4%(155)	7.8% (70)
3rd PC	7.9% (7129)	7.7% (579)	6.7%(216)	5.7%(149)
4th PC	5.6%(7129)	5.2% (437)	4.6%(142)	4.2% (86)
5th PC	4.9%(7129)	4.5%(522)	3.9% (164)	3.4%(110)
6th PC	4.2% (7129)	4.0%(403)	3.6%(123)	3.4%(79)

Figure 2.

Plot of percentages of explained variances versus the sparsity of the first PCs of the three methods for the NCI60 data.

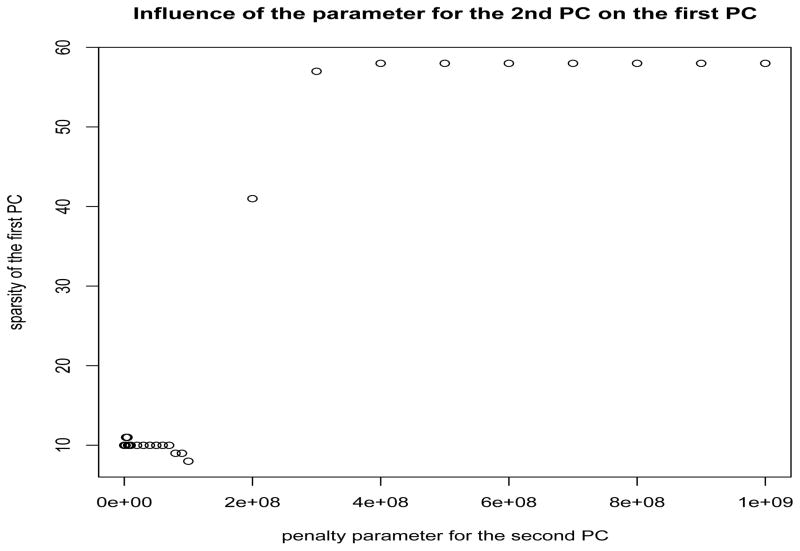
For higher order PCs, the three methods have quite different results. For SPCA, the first PC is strongly affected by the tuning parameter for the second PC, which is shown in Figure 3. It is hard to tune the parameters simultaneously for SPCA. The sPCA-rSVD and our method are sequential methods, that is, the tuning of parameters for higher order PCs does not affect the lower order PCs. To compare these two methods, we choose the tuning parameters for the first six PCs such that the numbers of nonzero loadings are the same for the two methods and equal to 101, 70, 149, 86, 110, 79, respectively. Our method provides uncorrelated PCs. But there exist strong correlations between some PCs obtained from sPCA-rSVD as shown in the following correlation matrix. Furthermore, in this case, the two methods selected different sets of variables. The numbers of common variables selected by the two methods are 101, 69, 137, 73, 33, 41 for the first six PCs, respectively.

Figure 3.

Influence of the parameter for the 2nd PC on the first PC in SPCA.

$$\left(\begin{array}{rrrrrr}\hfill 1& \hfill -0.037& \hfill 0.059& \hfill -0.37& \hfill -0.34& \hfill -0.016\\ \hfill -0.037& \hfill 1& \hfill 0.21& \hfill 0.016& \hfill -0.094& \hfill -0.22\\ \hfill 0.059& \hfill 0.21& \hfill 1& \hfill -0.051& \hfill -0.15& \hfill -0.084\\ \hfill -0.37& \hfill 0.016& \hfill -0.051& \hfill 1& \hfill 0.10& \hfill 0.027\\ \hfill -0.34& \hfill -0.094& \hfill -0.15& \hfill 0.10& \hfill 1& \hfill 0.013\\ \hfill -0.016& \hfill -0.22& \hfill -0.084& \hfill 0.027& \hfill 0.013& \hfill 1\end{array}\right)$$

5. Proofs

Proof of Theorem 2.1

We first show that ||·||_λ is a norm. It is easy to see that for any η ∈ ℝ and u ∈ ℝ^p, we have that ||ηu||_λ = |η|||u||_λ, ||u||_λ ≥ 0 and ||u||_λ = 0 if and only if u = 0. Hence, we only need to show the triangle inequality. For any u, v ∈ ℝ^p,

$$\begin{array}{l}{\left|\right|\mathbf{u}+\mathbf{v}\left|\right|}_{\lambda }^2=(1-\lambda ){\left|\right|\mathbf{u}+\mathbf{v}\left|\right|}_2^2+\lambda {\left|\right|\mathbf{u}+\mathbf{v}\left|\right|}_1^2\\ =(1-\lambda )\left(\sum _{i=1}^p{(u_i+v_i)}^2\right)+\lambda {\left(\sum _{i=1}^p\mid u_i+v_i\mid \right)}^2\\ \le (1-\lambda )\left(\sum _{i=1}^p{u}_i^2+\sum _{i=1}^p{v}_i^2+2\sum _{i=1}^p{u}_i{v}_i\right)+\lambda {\left(\sum _{i=1}^p\mid u_i\mid +\sum _{i=1}^p\mid v_i\mid \right)}^2\\ =(1-\lambda ){\left|\right|\mathbf{u}\left|\right|}_2^2+(1-\lambda ){\left|\right|\mathbf{v}\left|\right|}_2^2+2(1-\lambda )\sum _{i=1}^p{u}_i{v}_i+\lambda {\left|\right|\mathbf{u}\left|\right|}_1^2+\lambda {\left|\right|\mathbf{v}\left|\right|}_1^2+2\lambda {\left|\right|\mathbf{u}\left|\right|}_1{\left|\right|\mathbf{v}\left|\right|}_1\\ ={\left|\right|\mathbf{u}\left|\right|}_{\lambda }^2+{\left|\right|\mathbf{v}\left|\right|}_{\lambda }^2+2(1-\lambda )\sum _{i=1}^p{u}_i{v}_i+2\lambda {\left|\right|\mathbf{u}\left|\right|}_1{\left|\right|\mathbf{v}\left|\right|}_1\\ \le {\left|\right|\mathbf{u}\left|\right|}_{\lambda }^2+{\left|\right|\mathbf{v}\left|\right|}_{\lambda }^2+2\sqrt{\left((1-\lambda )\sum _{i=1}^p{u}_i^2+\lambda {\left|\right|\mathbf{u}\left|\right|}_1^2\right)\left((1-\lambda )\sum _{i=1}^p{v}_i^2+\lambda {\left|\right|\mathbf{v}\left|\right|}_1^2\right)}\\ ={\left|\right|\mathbf{u}\left|\right|}_{\lambda }^2+{\left|\right|\mathbf{v}\left|\right|}_{\lambda }^2+2{\left|\right|\mathbf{u}\left|\right|}_{\lambda }{\left|\right|\mathbf{v}\left|\right|}_{\lambda }={({\left|\right|\mathbf{u}\left|\right|}_{\lambda }+{\left|\right|\mathbf{v}\left|\right|}_{\lambda })}^2,\end{array}$$ (5.1)

where the equality in the inequality in the third line of (5.1) holds if and only if for each 1 ≤ i ≤ p, the coordinates u_i and v_i have the same signs if both of them are nonzero. The inequality in the second line from the last is due to Cauchy-Schwartz inequality and the equality holds if and only if v is a nonnegative scalar multiple of u or vice versa. Therefore, we have the triangle inequality,

$${\left|\right|\mathbf{u}+\mathbf{v}\left|\right|}_{\lambda }\le {\left|\right|\mathbf{u}\left|\right|}_{\lambda }+{\left|\right|\mathbf{v}\left|\right|}_{\lambda },$$ (5.2)

with equality if and only if v is a nonnegative scalar multiple of u or vice versa. The completeness of (ℝ^p, ||·||_λ) follows from the fact that ||u||₂ ≤ ||u||_λ ≤ ||u||₁ for any u ∈ ℝ^p. Hence, (ℝ^p, ||·||_λ) is a Banach space.

Now we show the unit ball of (ℝ^p, ||·||_λ) is a strictly convex set, that is, for any 0 < η < 1 and u ≠ v with ||u||_λ = ||v||_λ = 1, ||ηu + (1 − η)v||_λ < 1. Note that ||ηu + (1 − η)v||_λ ≤ η||u||_λ + (1 − η) ||v||_λ = 1 and the equality holds if and only if v is a nonnegative scalar multiple of u by the arguments in the last paragraph. Because ||u||_λ = ||v||_λ = 1 and u ≠ v, ||ηu + (1 − η)v||_λ = 1 if and only if u = v. Thus, we have ||ηu + (1 − η)v||_λ < 1.

(2.7) has at least one solution because its objective function is continuous and its feasible region is a compact set. Now suppose that we have two different solutions u₁ ≠ u₂ to (2.7). Then a^Tu₁ = a^Tu₂ = max_{||u||λ≤ 1} a^T u. It is obvious that ||u₁||_λ = ||u₂||_λ = 1. Let $\overline{\mathbf{u}}=\frac{{\mathbf{u}}_1+{\mathbf{u}}_2}{2}$. We have ||ū||_λ < 1 by the strict convexness. Hence,

$${\mathbf{a}}^T\left(\frac{\overline{\mathbf{u}}}{{\left|\right|\overline{\mathbf{u}}\left|\right|}_{\lambda }}\right)=\left(\frac{{\mathbf{a}}^T{\mathbf{u}}_1+{\mathbf{a}}^T{\mathbf{u}}_2}{2{\left|\right|\overline{\mathbf{u}}\left|\right|}_{\lambda }}\right)=\frac{1}{{\left|\right|\overline{\mathbf{u}}\left|\right|}_{\lambda }}\underset{{\left|\right|\mathbf{u}\left|\right|}_{\lambda }\le 1}{max}{\mathbf{a}}^T\mathbf{u}>\underset{{\left|\right|\mathbf{u}\left|\right|}_{\lambda }\le 1}{max}{\mathbf{a}}^T\mathbf{u}.$$

We have obtained a contradiction. Therefore, the sulotion to (2.7) is unique.

Let f (a) denote the unique solution to (2.7). Then f is a function from ℝ^p\{0} to {u: ||u||_λ = 1}. We show that f is a continuous function. Assume contrary, that is, there exist a point a ∈ ℝ^p\{0} such that f is discontinuous at a. By the compactness of {u: ||u||_λ = 1}, we can find a sequence {a_n, n ≥ 1} in ℝ^p\{0} such that a_n → a and f (a_n) → û ≠ f (a). By the definition of f, we have ${\mathbf{a}}_n^{T}f({\mathbf{a}}_n)\ge {\mathbf{a}}_n^{T}f(\mathbf{a})$. Let n → ∞, then we have a^T û ≥ a^T f (a) = max_{||u||λ≤ 1} a^T u. Therefore, both û and f (a) are solutions to (2.7), which contradicts to the uniqueness of the solution to (2.7). Thus f is a continuous function.

Proof of Lemma 1

Define

$$m=inf\left\{1\le i\le p:a_{i+1}\le \frac{\lambda S_i}{(1-\lambda )+i\lambda }\right\}.$$ (5.3)

Since we have set a_p+1 = 0, p belongs to the subset in the right hand side of (5.3). Hence, this subset is nonempty. By the definition (5.3), we have (define S₀ = 0 if m = 1)

$$a_m>\frac{\lambda S_{m-1}}{(1-\lambda )+(m-1)\lambda },\text{and}\text{hence},\lambda S_{m-1}<((1-\lambda )+(m-1)\lambda )a_m.$$

Therefore,

$$\frac{\lambda S_m}{(1-\lambda )+m\lambda }=\frac{\lambda S_{m-1}+\lambda a_m}{(1-\lambda )+m\lambda }<\frac{((1-\lambda )+(m-1)\lambda )a_m+\lambda a_m}{(1-\lambda )+m\lambda }=a_m,$$ (5.4)

and (2.8) follows from (5.3) and (5.4). By similar arguments as in (5.4), we can show that

$$\frac{\lambda S_{m+1}}{(1-\lambda )+(m+1)\lambda }\ge a_{m+1},\frac{\lambda S_{m+2}}{(1-\lambda )+(m+2)\lambda }\ge a_{m+2},\cdots .$$ (5.5)

By the definition (5.3), for any i < m, we have

$$\frac{\lambda S_i}{(1-\lambda )+i\lambda }<a_{i+1}\le a_i.$$ (5.6)

(5.4), (5.5) and (5.6) lead to (2.9). The uniqueness of m follows from (2.9) and the definition (5.3).

Proof of Theorem 2.2

Due to the conditions on a in this theorem, we have $u_i^{\ast }\ge 0$, for all 1 ≤ i ≤ p. Hence, u^* is also the unique solution to the following convex optimization problem,

$$\begin{array}{ll}\text{minimize}\hfill & -{\mathbf{a}}^T\mathbf{u},\hfill \\ \text{subject}\text{to}\hfill & (1-\lambda )\sum _{i=1}^p{u}_i^2+\lambda {(\sum _{i=1}^p{u}_i)}^2\le 1,u_i\ge 0,1\le i\le p.\hfill \end{array}$$ (5.7)

The condition $(1-\lambda ){\sum }_{i=1}^p{u}_i^2+\lambda {({\sum }_{i=1}^p{u}_i)}^2\le 1$ can be written as u^T A^[λ]u − 1 ≤ 0. Because (5.7) is a convex optimization problem, u^* is the solution to (5.7) if and only if it satisfies the following Karush-Kuhn-Tucker (KKT) conditions (see Section 5.5.3 of Boyd and Vandenberghe [2]),

$$\{\begin{array}{r}\hfill \frac{\partial }{\partial u_i}[-{\mathbf{a}}^T\mathbf{u}+\stackrel{\sim }{\nu }({\mathbf{u}}^T{\mathbf{A}}^{[\lambda ]}\mathbf{u}-1)-{\sum }_{i=1}^p{\mu }_i{u}_i]{\mid }_{\mathbf{u}={\mathbf{u}}^{\ast }}=0,1\le i\le p,\\ \hfill \stackrel{\sim }{\nu }({\mathbf{u}}^{\ast T}{\mathbf{A}}^{[\lambda ]}{\mathbf{u}}^{\ast }-1)=0,\\ \hfill \stackrel{\sim }{\nu }\ge 0,{\mu }_i{u}_i^{\ast }=0,{\mu }_i\ge 0,1\le i\le p,\end{array}$$ (5.8)

where μ = (μ₁, · · ·, μ_p)^T and ν̃ are unknown multipliers. From the equalities in the first line of (5.8), we obtain a set of linear equations

$${\mathbf{A}}^{[\lambda ]}{\mathbf{u}}^{\ast }=(\mathbf{a}+\mathit{\mu })/2\stackrel{\sim }{\nu }.$$ (5.9)

The solution to this set of linear equations is

$$u_i^{\ast }=[(\alpha +\beta )(a_i+{\mu }_i)-\beta (S_p+\mathrm{\Delta })]/2\stackrel{\sim }{\nu },1\le i\le p,$$ (5.10)

where $\mathrm{\Delta }={\sum }_{i=1}^p{\mu }_i$ and

$$\alpha =\frac{1+(p-2)\lambda }{1+(p-2)\lambda -(p-1){\lambda }^2},\beta =\frac{\lambda }{1+(p-2)\lambda -(p-1){\lambda }^2}.$$ (5.11)

Because ${\mu }_i{u}_i^{\ast }=0$ for all 1 ≤ i ≤ p, if $u_i^{\ast }>0$, then μ_i = 0 and if μ_i > 0, then $u_i^{\ast }=0$. Therefore, by (5.10), we have either $u_i^{\ast }=0$ or $u_i^{\ast }=[(\alpha +\beta )a_i-\beta (S_p+\mathrm{\Delta })]/2\stackrel{\sim }{\nu }>0$. Thus, we have $u_1^{\ast }\ge u_2^{\ast }\ge \cdots \ge u_p^{\ast }\ge 0$. Define

$$m=max\{i\in \{1,\cdots ,p\}:u_i^{\ast }>0\}.$$ (5.12)

We will show that m satisfies (2.8). Because $u_i^{\ast }>0$ and μ_i = 0 for all i ≤ m, and $u_i^{\ast }=0$ for all i > m, by (5.10),

$$0=\sum _{i=m+1}^p{u}_i^{\ast }=\sum _{i=m+1}^p[(\alpha +\beta )(a_i+{\mu }_i)-\beta (S_p+\mathrm{\Delta })]/2\stackrel{\sim }{\nu }=[(\alpha +\beta )(S_p-S_m+\mathrm{\Delta })-(p-m)\beta (S_p+\mathrm{\Delta })]/2\stackrel{\sim }{\nu },$$

from which we obtain

$$\mathrm{\Delta }=\frac{(p-m)\beta S_p-(\alpha +\beta )(S_p-S_m)}{\alpha -(p-m-1)\beta }.$$ (5.13)

It follows from (5.10), $u_m^{\ast }>0$ and μ_m = 0 that [(α + β)a_m − β(S_p + Δ)]/2ν̃ > 0, and hence by (5.13), $\frac{\lambda S_m}{(1-\lambda )+m\lambda }<a_m$. Similarly, from (5.10), $u_{m+1}^{\ast }=0$ andμ_m+1 ≥ 0, we can obtain $a_{m+1}\le \frac{\lambda S_m}{(1-\lambda )+m\lambda }$. Hence, m satisfies (2.8). The expressions of the solutions in (2.10) can be obtained from (5.10) with ν = ν̃/(α + β). Since I = {1, 2, · · ·, m}, $u_i^{\ast }>0$, μ_i = 0 for all i ∈ I and $u_i^{\ast }=0$ for all i ∈ I^c. By (5.9), we have ${\mathbf{A}}_I^{[\lambda ]}{\mathbf{u}}_I^{\ast }={\mathbf{a}}_I/2\stackrel{\sim }{\nu }$.

Proof of Corollary 2.2

Without loss of generality, we assume that a₁ ≥ a₂ ≥ · · · ≥ a_p ≥ 0. Let ã = (ã₁, · · ·, ã_p) = a − δu^* and S̃_i = ã₁ + · · · + ã_i. Then u^* satisfies (2.10) and

$${\stackrel{\sim }{a}}_i=\{\begin{array}{rrr}\hfill (1-\frac{\delta }{2\nu })a_i+\frac{\delta }{2\nu }\frac{\lambda S_m}{(1-\lambda )+m\lambda }& \hfill \text{if}& i\le m\hfill \\ \hfill a_i& \hfill \text{if}& i>m.\hfill \end{array}$$

Let ${\stackrel{\sim }{\mathbf{u}}}^{\ast }=({\stackrel{\sim }{u}}_1^{\ast },\cdots ,{\stackrel{\sim }{u}}_p^{\ast })$ be the solution to (2.14). A simple calculation shows that

$$\begin{array}{l}{\stackrel{\sim }{S}}_m=\left[1-\frac{\delta }{2\nu }\frac{1-\lambda }{(1-\lambda )+m\lambda }\right]S_m,\\ {\stackrel{\sim }{a}}_p\le \cdots \le {\stackrel{\sim }{a}}_{m+2}\le {\stackrel{\sim }{a}}_{m+1}\le \frac{\lambda S_m}{(1-\lambda )+m\lambda }=\frac{\stackrel{\sim }{\lambda }{\stackrel{\sim }{S}}_m}{(1-\stackrel{\sim }{\lambda })+m\stackrel{\sim }{\lambda }}<{\stackrel{\sim }{a}}_m\le \cdots \le {\stackrel{\sim }{a}}_1.\end{array}$$

Hence, by Theorem 2.2, ${\stackrel{\sim }{u}}_i^{\ast }=0=u_i^{\ast }$ for i > m and

$${\stackrel{\sim }{u}}_i^{\ast }=\frac{1}{2\stackrel{\sim }{\nu }}\left[{\stackrel{\sim }{a}}_i-\frac{\stackrel{\sim }{\lambda }{\stackrel{\sim }{S}}_m}{(1-\stackrel{\sim }{\lambda })+m\stackrel{\sim }{\lambda }}\right]=\frac{2\nu }{2\stackrel{\sim }{\nu }}(1-\frac{\delta }{2\nu })u_i^{\ast },$$

for i ≤ m, where ν̃ is a scale constant.

Proof of Theorem 2.3

Because u^* ∈ if and only if u^* is the solution to the optimization problem (2.7) with a replaced by Σu^*, this theorem follows from Corollary 2.1 and (2.16) can be derived from (2.13) by noticing that $u_i^{\ast }$ and c_i have the same sign for all i ∈ I.

Proof of Theorem 2.4

Recall that u⁽⁰⁾, u⁽¹⁾, u⁽²⁾, · · · is the iteration sequence in Algorithm 2.1.

Lemma 2

For any u with ||u||_λ = 1. Let u′ = f(Σu). Then we have u^TΣu ≤ u′^T Σu′, where equality holds if and only if u = u′. Hence, u^(k)T Σu^(k), k ≥ 1, is an increasing sequence.

Proof of Lemma 2

Because Σ is a nonnegative definite symmetric matrix, we can find a matrix B such that Σ = B^T B. By the definition of f and Cauchy-Schwarz inequality, we have

$$\begin{array}{l}{\mathbf{u}}^T\mathbf{\sum }\mathbf{u}={(\mathbf{\sum }\mathbf{u})}^T\mathbf{u}\le {(\mathbf{\sum }\mathbf{u})}^T{\mathbf{u}}^{\prime }={\mathbf{u}}^T\mathbf{\sum }{\mathbf{u}}^{\prime }={\mathbf{u}}^T{\mathbf{B}}^T{\mathbf{Bu}}^{\prime }\le {\left|\right|\mathbf{Bu}\left|\right|}_2{\left|\right|{\mathbf{Bu}}^{\prime }\left|\right|}_2\\ =\sqrt{{\mathbf{u}}^T{\mathbf{B}}^T\mathbf{Bu}}\sqrt{{{\mathbf{u}}^{\prime }}^T{\mathbf{B}}^T{\mathbf{Bu}}^{\prime }}=\sqrt{{\mathbf{u}}^T\mathbf{\sum }\mathbf{u}}\sqrt{{{\mathbf{u}}^{\prime }}^T\mathbf{\sum }{\mathbf{u}}^{\prime }}.\end{array}$$ (5.14)

Thus u^T Σu ≤ u′^T Σu′, where equality holds if and only if u = u′ because equality in the first inequality of (5.14) holds if and only if u = u′.

We first assume that ${\mathbf{u}}_I^{\ast }$ is the leading eigenvector of (2.16) where I is the index set of nonzero coordinates of u^*. We will find a neighborhood of u^* such that if u^(k) ∈ ∩ {u: ||u||_λ = 1} for some k ≥ 1, then the iteration will converge to u^*. Without loss of generality, we assume that

$$I=\{1,2,\cdots ,m\}\text{and}\text{all}\text{the}\text{coordinates}\text{of}{\mathbf{u}}^{\ast }\text{are}\text{nonnegative}.$$ (5.15)

We decompose the matrix Σ as follows

$$\mathbf{\sum }=\left[\begin{array}{cc}{\mathbf{\sum }}_I& \mathbf{\Lambda }\\ {\mathbf{\Lambda }}^T& {\mathbf{\sum }}_{I^c}\end{array}\right],$$ (5.16)

where I^c = {1, 2, · · ·, p}\I, Σ_I and Σ_I^c are m × m and (p − m) × (p − m) matrices, respectively, and Λ is a m × (p − m) matrix. It follows from (2.16) and (5.15), ${\mathbf{u}}_I^{\ast }$ is the leading eigenvector of the following generalized eigenvalue problem,

$${\mathbf{\sum }}_I\mathbf{x}=\mu {\mathbf{A}}_I^{[\lambda ]}\mathbf{x},\mathbf{x}\in {\mathbb{R}}^m.$$ (5.17)

Recall that A^[λ] is the p × p matrix with diagonal elements equal to 1 and off-diagonal elements equal to λ.

Lemma 3

Suppose that g, g′ ∈ ℝ^m are two eigenvectors of (5.17) corresponding to different eigenvalues. Then we have ${\mathbf{g}}^T{\mathbf{A}}_I^{[\lambda ]}{\mathbf{g}}^{\prime }=0$.

Proof of Lemma 3

Suppose that the eigenvalues corresponding to g and g′ are μ and μ′, respectively. Because

$${\mathbf{g}}^T{\mathbf{\sum }}_I{\mathbf{g}}^{\prime }={\mathbf{g}}^T({\mathbf{\sum }}_I{\mathbf{g}}^{\prime })={\mu }^{\prime }{\mathbf{g}}^T{\mathbf{A}}_I^{[\lambda ]}{\mathbf{g}}^{\prime }$$ (5.18)

and

$${\mathbf{g}}^T{\mathbf{\sum }}_I{\mathbf{g}}^{\prime }={({\mathbf{\sum }}_I\mathbf{g})}^T{\mathbf{g}}^{\prime }=\mu {\left({\mathbf{A}}_I^{[\lambda ]}\mathbf{g}\right)}^T{\mathbf{g}}^{\prime }=\mu {\mathbf{g}}^T{\mathbf{A}}_I^{[\lambda ]}{\mathbf{g}}^{\prime },$$ (5.19)

by subtracting (5.18) from (5.19), we obtain

$$\mathbf{0}=\mu {\mathbf{g}}^T{\mathbf{A}}_I^{[\lambda ]}{\mathbf{g}}^{\prime }-{\mu }^{\prime }{\mathbf{g}}^T{\mathbf{A}}_I^{[\lambda ]}{\mathbf{g}}^{\prime }=(\mu -{\mu }^{\prime }){\mathbf{g}}^T{\mathbf{A}}_I^{[\lambda ]}{\mathbf{g}}^{\prime }.$$

Since μ ≠ μ′, we have ${\mathbf{g}}^T{\mathbf{A}}_I^{[\lambda ]}{\mathbf{g}}^{\prime }=0$.

Suppose that μ₁ ≥ μ₂ ≥ · · · ≥ μ_m ≥ 0 are eigenvalues of (5.17) and the corresponding eigenvectors g₁, g₂, · · ·, g_m ∈ ℝ^m satisfying

$${\mathbf{g}}_i^T{\mathbf{A}}_I^{[\lambda ]}{\mathbf{g}}_i=1,1\le i\le m\text{and}{\mathbf{g}}_i^T{\mathbf{A}}_I^{[\lambda ]}{\mathbf{g}}_j=0,1\le i\ne j\le m.$$ (5.20)

Note that if μ_i ≠ μ_j, then by Lemma 3, the second equality in (5.20) is true. For μ_i = μ_j, we can apply the Gram-Schmidt orthogonalization procedure to choose the eigenvectors satisfying (5.20). Since ${\mathbf{u}}_I^{\ast }$ is the leading eigenvector of (5.17), by the condition (2) in Theorem 2.3, we have μ₁ ≠ 0. By the assumption of this theorem, the multiplicity of μ₁ is one, hence ${\mathbf{u}}_I^{\ast }$ is equal to g₁ multiplied by a constant. By (5.15), without loss of generality, we can assume that all coordinates of g₁ are positive. For 1 ≤ i ≤ m, define h_i to be the p-vector with the first m coordinates equal to g_i and the last p −m coordinates equal to zeros, that is,

$${\mathbf{h}}_i={({\mathbf{g}}_i^T,\mathbf{0})}^T,1\le i\le m.$$ (5.21)

Define h_m+j, 1 ≤ j ≤ p − m, to be the p-vectors with the m + j-th coordinate equal to 1 and other coordinates equal to 0. Then {h₁, · · ·, h_p} form a basis of ℝ^p and it follows from the following lemma that

$${\mathbf{u}}_I^{\ast }={\mathbf{g}}_1,{\mathbf{u}}^{\ast }={\mathbf{h}}_1.$$ (5.22)

Lemma 4

There exists δ₁ > 0 such that for any u = ηh₁ + ε₂h₂ + · · · + ε_mh_m with |1 − η| < δ₁ and $\sqrt{{\epsilon }_2^2+\cdots +{\epsilon }_m^2}<{\delta }_1$, we have

$${\left|\right|\mathbf{u}\left|\right|}_{\lambda }^2={\eta }^2+{\epsilon }_2^2+\cdots +{\epsilon }_m^2.$$ (5.23)

Hence, in this case, ||u||_λ = 1 if and only if ${\eta }^2=1-{\sum }_{i=2}^{p-m}{\epsilon }_i^2$.

Proof of Lemma 4

By the definition (5.21), the last p −m coordinates of u are zeros. The first m coordinates of h₁ are equal to coordinates of g₁ which are positive. Therefore, if η is close enough to 1 and ε₂, · · ·, ε_p−m are small enough, the first m coordinates of u are positive. Thus, by (5.20),

$$\begin{array}{l}{\left|\right|\mathbf{u}\left|\right|}_{\lambda }^2=(1-\lambda )\sum _{i=1}^m{u}_i^2+\lambda {(\sum _{i=1}^m{u}_i)}^2={\mathbf{u}}_I{\mathbf{A}}_I^{[\lambda ]}{\mathbf{u}}_I^T\\ ={\eta }^2{\mathbf{g}}_1^T{\mathbf{A}}_I^{[\lambda ]}{\mathbf{g}}_1+{\epsilon }_2^2{\mathbf{g}}_2^T{\mathbf{A}}_I^{[\lambda ]}{\mathbf{g}}_2+\cdots +{\epsilon }_m^2{\mathbf{g}}_m^T{\mathbf{A}}_I^{[\lambda ]}{\mathbf{g}}_m={\eta }^2+{\epsilon }_2^2+\cdots +{\epsilon }_m^2.\end{array}$$ (5.24)

Recall that Σu^* = c = (c₁, · · ·, c_p)^T. We sort the absolute values of c_i’s into an decreasing sequence |c_k1| ≥ |c_k2| ≥ · · · ≥ |c_kp| and define a_i = |c_ki|, 1 ≤ i ≤ p. Since u^* → , that is, u^* = f (Σu^*) = f (c), by Corollary 2.1 and (5.15), I = {k₁, k₂, · · ·, k_m} = {1, 2, · · ·, m}, that is, {k₁, k₂, · · ·, k_m} is a permutation of {1, 2, · · ·, m}, and $u_i^{\ast }$, 1 ≤ i ≤ m, has the same sign as c_i, that is

$$c_i>0,1\le i\le m.$$ (5.25)

Let $S_i={\sum }_{j=1}^i{a}_i$, 1 ≤ i ≤ p. By the condition (2.18),

$$a_{m+1}=\underset{i\notin I}{max}\mid c_i\mid \ne \frac{\lambda {\sum }_{i\in I}\mid c_i\mid }{(1-\lambda )+m\lambda }=\frac{\lambda S_m}{(1-\lambda )+m\lambda }.$$ (5.26)

It follows from (5.26) and the condition (2.11) in Corollary 2.1 that

$$a_{m+1}<\frac{\lambda S_m}{(1-\lambda )+m\lambda }<a_m.$$ (5.27)

Lemma 5

There exists a positive number δ₂ ≤ δ₁ (δ₁ is defined in Lemma 4) such that if there is a vector in the iteration sequence of Algorithm 2.1 belonging to the following subset of {u: ||u||_λ = 1},

$$\mathcal{A}=\{\mathbf{u}:\mathbf{u}=\eta {\mathbf{h}}_1+{\epsilon }_2{\mathbf{h}}_2+\cdots +{\epsilon }_m{\mathbf{h}}_m,{\eta }^2=1-\sum _{i=2}^m{\epsilon }_i^2,\sum _{i=2}^m{\epsilon }_i^2<{\delta }_2^2\},$$ (5.28)

then the iteration sequence converges to u^* = h₁.

Proof of Lemma 5

Without loss of generality, we assume that u⁽⁰⁾ ∈ . Suppose that

$${\mathbf{u}}^{(0)}=\eta {\mathbf{h}}_1+{\epsilon }_2{\mathbf{h}}_2+\cdots +{\epsilon }_m{\mathbf{h}}_m,{\eta }^2=1-\sum _{i=2}^m{\epsilon }_i^2.$$

Define ${(c_1^{\prime },\cdots ,c_p^{\prime })}^T=\mathbf{\sum }{\mathbf{u}}^{(0)}=\eta \mathbf{\sum }{\mathbf{h}}_1+{\epsilon }_2\mathbf{\sum }{\mathbf{h}}_2+\cdots +{\epsilon }_m\mathbf{\sum }{\mathbf{h}}_m$. Then as ${\sum }_{i=2}^m{\epsilon }_i^2\to 0$, by (5.22),

$${(c_1^{\prime },\cdots ,c_p^{\prime })}^T\to \mathbf{\sum }{\mathbf{h}}_1=\mathbf{\sum }{\mathbf{u}}^{\ast }={(c_1,\cdots ,c_p)}^T.$$ (5.29)

Hence, by (5.25), when ${\sum }_{i=2}^m{\epsilon }_i^2$ is small enough, we have

$$c_1^{\prime }>0,\cdots ,c_m^{\prime }>0.$$ (5.30)

Let $\mid c_{k_1^{\prime }}^{\prime }\mid \ge \mid c_{k_2^{\prime }}^{\prime }\mid \ge \cdots \ge \mid c_{k_p^{\prime }}^{\prime }\mid$ be the sorted sequence. Define $a_i^{\prime }=\mid c_{k_i^{\prime }}^{\prime }\mid$, 1 ≤ i ≤ p and $S_i^{\prime }={\sum }_{j=1}^i{a}_i^{\prime }$, 1 ≤ i ≤ p. Then, we have $a_j^{\prime }\to a_j$ and $S_j^{\prime }\to S_j$, 1 ≤ j ≤ p, as ${\sum }_{i=2}^m{\epsilon }_i^2\to 0$. Because by (5.27), max_{m+1≤ i ≤ p}|c_i| = max_i∉I |c_i| = a_m+1 < a_m = min_i∈I |c_i| = min_1≤i≤m |c_i|, when ${\sum }_{i=2}^m{\epsilon }_i^2$ is samll enough, we have ${max}_{m+1\le i\le p}\mid c_i^{\prime }\mid <{min}_{1\le i\le m}\mid c_i^{\prime }\mid$. Hence, { $a_1^{\prime },\cdots ,a_m^{\prime }$} is a permutation of { $\mid c_1^{\prime }\mid ,\cdots ,\mid c_m^{\prime }\mid$} and { $a_{m+1}^{\prime },\cdots ,a_p^{\prime }$} is a permutation of { $\mid c_{m+1}^{\prime }\mid ,\cdots ,\mid c_p^{\prime }\mid$}. In another word,

$$\{k_1^{\prime },\cdots ,k_m^{\prime }\}\text{is}\text{a}\text{permutation}\text{of}\{1,\cdots ,m\}.$$ (5.31)

and $a_{m+1}^{\prime }={min}_{m+1\le i\le p}\mid c_i^{\prime }\mid <{max}_{1\le i\le m}\mid c_i^{\prime }\mid =a_m^{\prime }$. Therefore, we can choose δ₂ ≤ δ₁ small enough such that (5.30), (5.31) and the following inequality (due to (5.27)) hold,

$$a_{m+1}^{\prime }<\frac{\lambda S_m^{\prime }}{(1-\lambda )+m\lambda }<a_m^{\prime }.$$ (5.32)

Now by (5.31), (5.32), and Corollary 2.1, the coordinates of u⁽¹⁾ with indices in $I^c=\{m+1,\cdots ,p\}=\{k_{m+1}^{\prime },\cdots ,k_p^{\prime }\}$ are zeros. It follows from (2.13) that

$${\mathbf{A}}_I^{[\lambda ]}{\mathbf{u}}_I^{(1)}=\frac{1}{\nu }{\mathbf{\sum }}_I{\mathbf{u}}_I^{(0)}=\frac{1}{\nu }(\eta {\mathbf{\sum }}_I{\mathbf{g}}_1+{\epsilon }_2{\mathbf{\sum }}_I{\mathbf{g}}_2+\cdots +{\epsilon }_m{\mathbf{\sum }}_I{\mathbf{g}}_m)=\frac{1}{\nu }(\eta u_1{\mathbf{A}}_I^{[\lambda ]}{\mathbf{g}}_1+{\epsilon }_2{\mu }_2{\mathbf{A}}_I^{[\lambda ]}{\mathbf{g}}_2+\cdots +{\epsilon }_m{\mu }_m{\mathbf{A}}_I^{[\lambda ]}{\mathbf{g}}_m),$$ (5.33)

where ν a positive scale constant chosen to make ||u⁽¹⁾||_λ = 1. Since ${\mathbf{A}}_I^{[\lambda ]}$ is invertible, we have ${\mathbf{u}}_I^{(1)}=\frac{1}{\nu }(\eta {\mu }_1{\mathbf{g}}_1+{\epsilon }_2{\mu }_2{\mathbf{g}}_2+\cdots +{\epsilon }_m{\mu }_m{\mathbf{g}}_m)$. Hence, ${\mathbf{u}}^{(1)}=\frac{1}{\nu }(\eta {\mu }_1{\mathbf{h}}_1+{\epsilon }_2{\mu }_2{\mathbf{h}}_2+\cdots +{\epsilon }_m{\mu }_m{\mathbf{h}}_m)$. By (5.30) and (5.33), ${\left|\right|{\mathbf{u}}^{(1)}\left|\right|}_{\lambda }^2={({\mathbf{u}}_I^{(1)})}^T{\mathbf{A}}_I^{(\lambda )}{\mathbf{u}}_I^{(1)}=\frac{1}{{\nu }^2}({\eta }^2{\mu }_1^2+{\epsilon }_2^2{\mu }_2^2+\cdots +{\epsilon }_m^2{\mu }_m^2)=1$. Hence, ${\nu }^2={\eta }^2{\mu }_1^2+{\epsilon }_2^2{\mu }_2^2+\cdots +{\epsilon }_m^2{\mu }_m^2$. we have

$${\mathbf{u}}^{(1)}={\eta }^{(1)}{\mathbf{h}}_1+{\epsilon }_2^{(1)}{\mathbf{h}}_2+\cdots +{\epsilon }_m^{(1)}{\mathbf{h}}_m,$$

where ${\eta }^{(1)}=\frac{\eta {\mu }_1}{\nu }$ and ${\epsilon }_i^{(1)}=\frac{{\epsilon }_i{\mu }_i}{\nu }$, 2 ≤ i ≤ m. By the assumptions of this theorem, the nonnegative eigenvalues have multiplicities 1, so μ₁ > μ₂ ≥ · · · ≥ μ_p. Then we have

$$\sum _{i=2}^m{({\epsilon }_i^{(1)})}^2=\frac{{\epsilon }_2^2{\mu }_2^2+\cdots +{\epsilon }_m^2{\mu }_m^2}{{\eta }^2{\mu }_1^2+{\epsilon }_2^2{\mu }_2^2+\cdots +{\epsilon }_m^2{\mu }_m^2}\le \frac{{\epsilon }_2^2{\mu }_1^2+\cdots +{\epsilon }_m^2{\mu }_1^2}{{\eta }^2{\mu }_1^2+{\epsilon }_2^2{\mu }_1^2+\cdots +{\epsilon }_m^2{\mu }_1^2}=\sum _{i=2}^m{\epsilon }_i^2<{\delta }_2.$$

Hence, u⁽¹⁾ ∈ . Similarly, all the iteration sequence

$${\mathbf{u}}^{(k)}={\eta }^{(k)}{\mathbf{h}}_1+{\epsilon }_2^{(k)}{\mathbf{h}}_2+\cdots +{\epsilon }_m^{(k)}{\mathbf{h}}_m\in \mathcal{A},k\ge 1,$$

where ${({\eta }^{(k)})}^2=1-{\sum }_{i=2}^m{({\epsilon }_i^{(k)})}^2$ and

$${({\epsilon }_i^{(k)})}^2=\frac{{\epsilon }_i^2{\mu }_i^{2k}}{{\eta }^2{\mu }_1^{2k}+{\epsilon }_2^2{\mu }_2^{2k}+\cdots +{\epsilon }_m^2{\mu }_m^{2k}}=\frac{{\epsilon }_i^2{\left(\frac{{\mu }_i}{{\mu }_1}\right)}^{2k}}{{\eta }^2+{\epsilon }_2^2{\left(\frac{{\mu }_2}{{\mu }_1}\right)}^{2k}+\cdots +{\epsilon }_m^2{\left(\frac{{\mu }_m}{{\mu }_1}\right)}^{2k}}\to 0\text{as}k\to \infty .$$

Therefore u^(k) ∈ h₁ as k → ∞.

Now define a neighborhood of u^* = h₁ as follows

$$\mathcal{N}=\{\mathbf{u}:\mathbf{u}=(1+{\omega }_1){\mathbf{h}}_1+{\omega }_2{\mathbf{h}}_2+\cdots +{\omega }_m{\mathbf{h}}_m+\cdots +{\omega }_p{\mathbf{h}}_p,{\omega }_1^2+\cdots +{\omega }_p^2<{\delta }_3^2\},$$ (5.34)

By a similar argument as that in the proof of Lemma 5, we can choose δ₃ small enough such that if u^(k) ∈ ∩ {u: ||u||_λ = 1} for some k ≥ 1, then u^(k+1) ∈ and the iteration will converge to u^* by Lemma 5.

Now we assume that ${\mathbf{u}}_I^{\ast }$ is not the leading eigenvector of the problem (2.16). Without loss of generality, we assume that ${\mathbf{u}}_I^{\ast }$ is the eigenvector corresponding to the second largest eigenvalue. For other cases, we have the similar results and proofs. We will adapt the same notations as above and still assume that the first m coordinates of u are positive and the last p −m coordinates are zeros. Hence, in this case, we have u^* = h₂ and ${\mathbf{u}}_I^{\ast }={\mathbf{g}}_2$. By the assumptions of this theorem, both μ₁ and μ₂ have multiplicities 1. Therefore, we have μ₁ > μ₂ > μ₃ ≥ · · ·. We define the following two subsets of {u: ||u||_λ = 1} around u^* = h₂,

$$\begin{array}{c}\mathcal{D}=\{\mathbf{u}:\mathbf{u}={\epsilon }_1{\mathbf{h}}_1+\eta {\mathbf{h}}_2+{\epsilon }_3{\mathbf{h}}_3+\cdots +{\epsilon }_m{\mathbf{h}}_m,{\eta }^2=1-{\epsilon }_1^2-\sum _{i=3}^m{\epsilon }_i^2,\\ {\epsilon }_1^2<\frac{2{\mu }_2}{{\mu }_1-{\mu }_2}{\delta }_4^2\text{and}{\epsilon }_3^2+\cdots +{\epsilon }_m^2<{\delta }_4^2\},\text{and}\\ \stackrel{\sim }{\mathcal{D}}=\{\mathbf{u}:\mathbf{u}={\epsilon }_1{\mathbf{h}}_1+\eta {\mathbf{h}}_2+{\epsilon }_3{\mathbf{h}}_3+\cdots +{\epsilon }_m{\mathbf{h}}_m,{\eta }^2=1-{\epsilon }_1^2-\sum _{i=3}^m{\epsilon }_i^2,\\ {\epsilon }_1^2<\frac{4{\mu }_1^2}{{\mu }_2({\mu }_1-{\mu }_2)}{\delta }_4^2\text{and}{\epsilon }_3^2+\cdots +{\epsilon }_m^2<{\delta }_4^2\}.\end{array}$$

The only difference between and is the ranges of ε₁. Note that ⊂

Lemma 6

For ${\delta }_4\le \frac{1}{2}$ small enough and any u ∈ , we have

$$f(\mathbf{\sum }\mathbf{u})=\frac{{\epsilon }_1{\mu }_1}{\nu }{\mathbf{h}}_1+\frac{\eta {\mu }_2}{\nu }{\mathbf{h}}_1+\cdots +\frac{{\epsilon }_m{\mu }_m}{\nu }{\mathbf{h}}_m,$$ (5.35)

where ${\nu }^2={\epsilon }_1^2{\mu }_1^2+{\eta }^2{\mu }_2^2+\cdots +{\epsilon }_m^2{\mu }_m^2$. Furthermore, f (Σu) ∈ .

Recall that f (Σu) is the solution to optimization problem (2.7) with a replaced with Σu.

Proof of Lemma 6

(5.35) can be derived by the same arguments as in the case that ${\mathbf{u}}_I^{\ast }$ is the leading eigenvector. Now we show that f (Σu) ∈ . Since

$$\begin{array}{r}{\left(\frac{{\epsilon }_3{\mu }_3}{\nu }\right)}^2+\cdots +{\left(\frac{{\epsilon }_m{\mu }_m}{\nu }\right)}^2=\frac{{\epsilon }_3^2{\mu }_3^2+\cdots +{\epsilon }_m^2{\mu }_m^2}{{\epsilon }_1^2{\mu }_1^2+{\eta }^2{\mu }_2^2+\cdots +{\epsilon }_m^2{\mu }_m^2}\\ \le \frac{({\epsilon }_3^2+\cdots +{\epsilon }_m^2){\mu }_2^2}{{\epsilon }_1^2{\mu }_1^2+{\eta }^2{\mu }_2^2+({\epsilon }_3^2+\cdots +{\epsilon }_m^2){\mu }_2^2}\le \frac{({\epsilon }_3^2+\cdots +{\epsilon }_m^2){\mu }_2^2}{({\epsilon }_1^2+{\eta }^2+{\epsilon }_3^2+\cdots +{\epsilon }_m^2){\mu }_2^2}\\ ={\epsilon }_3^2+\cdots +{\epsilon }_m^2<{\delta }_4,\end{array}$$

and

$$\begin{array}{r}{\left(\frac{{\epsilon }_1{\mu }_1}{\nu }\right)}^2=\frac{{\epsilon }_1^2{\mu }_1^2}{{\epsilon }_1^2{\mu }_1^2+{\eta }^2{\mu }_2^2+\cdots +{\epsilon }_m^2{\mu }_m^2}\le \frac{{\epsilon }_1^2{\mu }_1^2}{{\epsilon }_1^2{\mu }_1^2+{\eta }^2{\mu }_2^2}\\ =\frac{{\epsilon }_1^2{\mu }_1^2}{{\epsilon }_1^2{\mu }_1^2+(1-{\epsilon }_1^2-{\sum }_{i=3}^m{\epsilon }_i^2){\mu }_2^2}\le \frac{{\epsilon }_1^2{\mu }_1^2}{{\epsilon }_1^2({\mu }_1^2-{\mu }_2^2)+(1-{\delta }_4){\mu }_2^2}\le \frac{{\epsilon }_1^2{\mu }_1^2}{(1-{\delta }_4){\mu }_2^2}\\ \le \frac{2{\epsilon }_1^2{\mu }_1^2}{{\mu }_2^2}\le \frac{4{\mu }_1^2}{{\mu }_2({\mu }_1-{\mu }_2)}{\delta }_4^2,\end{array}$$

where the last inequality is due to the definition of . Thus f (Σu) ∈ .

Now without loss of generality, we assume that u⁽⁰⁾ ∈ . Let u⁽⁰⁾ = ε₁h₁ + ηh₂ + ε₃h₃ + · · · + ε_mh_m. If ε₁ = 0, by (5.35) in Lemma 6, the coefficient of h₁ in u⁽¹⁾ = f (Σu⁽⁰⁾) is also zero. This fact is true for all vectors in the iteration sequence. We can use the same arguments as in the case that ${\mathbf{u}}_I^{\ast }$ is the leading eigenvector to show that the iteration sequence converges to ${\mathbf{h}}_2={\mathbf{u}}_I^{\ast }$. However, if ε₁ ≠ 0, we have a different result.

Lemma 7

For any u ∈ \ , we have u^T Σu > (u^*)^T Σ(u^*).

Proof of Lemma 7

Let u = ε₁h₁ + ηh₂ + ε₃h₃ + · · · + ε_mh_m. Since u ∈ \ , we have

$${\epsilon }_3^2+\cdots +{\epsilon }_m^2<{\delta }_4^2,\text{and}\frac{2{\mu }_2}{{\mu }_1-{\mu }_2}{\delta }_4^2\le {\epsilon }_1^2<\frac{4{\mu }_1^2}{{\mu }_2({\mu }_1-{\mu }_2)}{\delta }_4^2.$$ (5.36)

Because the last p − m coordinates of u are zeros, we have

$$\begin{array}{l}{\mathbf{u}}^T\mathbf{\sum }\mathbf{u}={({\epsilon }_1{\mathbf{h}}_1+\eta {\mathbf{h}}_2+\cdots +{\epsilon }_m{\mathbf{h}}_m)}^T({\epsilon }_1\mathbf{\sum }{\mathbf{h}}_1+\eta \mathbf{\sum }{\mathbf{h}}_2+\cdots +{\epsilon }_m\mathbf{\sum }{\mathbf{h}}_m)\\ ={({\epsilon }_1{\mathbf{g}}_1+\eta {\mathbf{g}}_2+\cdots +{\epsilon }_m{\mathbf{g}}_m)}^T({\epsilon }_1{\mathbf{\sum }}_I{\mathbf{g}}_1+\eta {\mathbf{\sum }}_I{\mathbf{g}}_2+\cdots +{\epsilon }_m{\mathbf{\sum }}_I{\mathbf{g}}_m)\\ ={({\epsilon }_1{\mathbf{g}}_1+\eta {\mathbf{g}}_2+\cdots +{\epsilon }_{p-m}{\mathbf{g}}_m)}^T\left({\epsilon }_1{\mu }_1{\mathbf{A}}_I^{[\lambda ]}{\mathbf{g}}_1+\cdots +{\epsilon }_m{\mu }_m{\mathbf{A}}_I^{[\lambda ]}{\mathbf{g}}_m\right)\\ ={\epsilon }_1^2{\mu }_1+{\eta }^2{\mu }_2+{\epsilon }_3^2{\mu }_3+\cdots +{\epsilon }_m^2{\mu }_m\ge {\epsilon }_1^2{\mu }_1+{\eta }^2{\mu }_2\\ ={\epsilon }_1^2{\mu }_1+(1-{\epsilon }_1^2-\sum _{i=3}^m{\epsilon }_i^2){\mu }_2={\epsilon }_1^2({\mu }_1-{\mu }_2)+(1-\sum _{i=3}^m{\epsilon }_i^2){\mu }_2\\ >{\epsilon }_1^2({\mu }_1-{\mu }_2)+(1-{\delta }_4^2){\mu }_2\ge \frac{2{\mu }_2}{{\mu }_1-{\mu }_2}{\delta }_4^2({\mu }_1-{\mu }_2)+(1-{\delta }_4^2){\mu }_2=(1+{\delta }_4^2){\mu }_2\\ >{\mu }_2={({\mathbf{h}}_2)}^T\mathbf{\sum }({\mathbf{h}}_2)={({\mathbf{u}}^{\ast })}^T\mathbf{\sum }({\mathbf{u}}^{\ast }).\end{array}$$

Now if ε₁ ≠ 0, by (5.35), we can obtain that the coefficient of h₁ in u^(k) is ${\epsilon }_1{\mu }_1^k/\sqrt{{\epsilon }_1^2{\mu }_1^{2k}+{\eta }^2{\mu }_2^{2k}+\cdots +{\epsilon }_m^2{\mu }_m^{2k}}$ which is strictly increasing. Hence, when k is large enough, u^(k) will leave the subset . Suppose that k₀ is the index with u^(k₀) ∈ and u^(k₀+1) ∉ . Then by Lemmas 6 and 7, we have that u^(k₀+1) ∈ \ and (u^(k₀+1))^T Σu^(k₀+1> (u^*)^T Σ(u^*). Now by Lemma 2, {(u^(k))^T Σu^(k): k ≥ 1} is an increasing sequence, hence {u^(k): k ≥ 1} can not converge to u^*.

Now define a neighborhood of u^* = h₂ as follows

$$\mathcal{M}=\{\mathbf{u}:\mathbf{u}={\omega }_1{\mathbf{h}}_1+(1+{\omega }_2){\mathbf{h}}_2+\cdots +{\omega }_m{\mathbf{h}}_m+\cdots +{\omega }_p{\mathbf{h}}_p,{\omega }_1^2+\cdots +{\omega }_p^2<{\delta }_5^2\}.$$ (5.37)

By the same arguments as in the case that ${\mathbf{u}}_I^{\ast }$ is the leading eigenvector, we can show that when δ₅ small enough we have if u^(k) ∈ , then u^(k+1) ∈ . In this case, let u^(k) = ω₁h₁ + (1 + ω₂)h₂ + · · · + ω_mh_m + · · · + ω_ph_p. We will compute the coefficient of h₁ in u^(k+1). By the decomposition (5.16) of Σ and the following decompositions,

$${\mathbf{u}}^{(k)}=\left[\begin{array}{c}{\mathbf{u}}_I^{(k)}\\ {\mathbf{u}}_{I^c}^{(k)}\end{array}\right]\text{and}{\mathbf{u}}^{(k+1)}=\left[\begin{array}{c}{\mathbf{u}}_I^{(k+1)}\\ \mathbf{0}\end{array}\right],$$

where ${\mathbf{u}}_{I^c}^{(k)}={({\omega }_{m+1},\cdots ,{\omega }_p)}^T$.

$$\mathbf{\sum }{\mathbf{u}}^{(k)}=\left[\begin{array}{c}{\mathbf{\sum }}_I{\mathbf{u}}_I^{(k)}+\mathbf{\Lambda }{\mathbf{u}}_{I^c}^{(k)}\\ {\mathbf{\Lambda }}^T{\mathbf{u}}_I^{(k)}+{\mathbf{\sum }}_{I^c}{\mathbf{u}}_{I^c}^{(k)}\end{array}\right].$$

It follows from (2.13) that

$$\nu {\mathbf{A}}_I^{[\lambda ]}{\mathbf{u}}_I^{(k+1)}={\mathbf{\Lambda }}^T{\mathbf{u}}_{I^c}^{(k)}+{\mathbf{\sum }}_I{\mathbf{u}}_I^{(k)},$$

where ν is a positive scale constant. Then the coefficient of h₁ in u^(k+1) is equal to

$${\mathbf{g}}_1^T{\mathbf{A}}_I^{[\lambda ]}{\mathbf{u}}_I^{(k+1)}={\mathbf{g}}_1^T{\mathbf{\Lambda }}^T{\mathbf{u}}_{I^c}^{(k)}+{\mathbf{g}}_1^T{\mathbf{\sum }}_I{\mathbf{u}}_I^{(k)}={\mathbf{g}}_1^T{\mathbf{\Lambda }}^T{({\omega }_{m+1},\cdots ,{\omega }_p)}^T+{\omega }_1{\mu }_1.$$

Now define the following affine subspace passing through u^* = h₂ in ℝ^p with dimension strictly less than p,

$$\mathcal{S}=\{\mathbf{u}:\mathbf{u}={\omega }_1{\mathbf{h}}_1+(1+{\omega }_2){\mathbf{h}}_2+\cdots +{\omega }_m{\mathbf{h}}_m+\cdots +{\omega }_p{\mathbf{h}}_p,{\mathbf{g}}_1^T{\mathbf{\Lambda }}^T{({\omega }_{m+1},\cdots ,{\omega }_p)}^T+{\omega }_1{\mu }_1=0\}.$$ (5.38)

Then if u^(k) ∈ ∩ ∩ {{u: ||u||_λ = 1} for some k ≥ 1, then all u^(k+1), u^(k+2), · · ·, will belong to ∩ {{u: ||u||_λ = 1} and their coefficients of h₁ are all zeros. Hence, the iteration sequence converges to u^*. If u^(k) ∈ ∩ ∩ {{u: ||u||_λ = 1} for some k ≥ 1, all u^(k+1), u^(k+2), · · ·, will belong to ∩ {{u: ||u||_λ = 1}, but their coefficients of h₁ are all nonzero. The iteration sequence can not converge to u^*. Therefore, in this case, u^* is not a stable limit.

At last, we prove the iteration sequence converges. Because {u: ||u||_λ = 1} is a compact set, we can find a convergent subsequence {u_kj: k₁ < k₂ < · · ·} of the iteration sequence. Suppose that u_kj → u^* as j → ∞. We first show that u^* ∈ which is defined in (2.15). Because u_kj+1 = f (Σ_kj) and f is a continuous function, u_kj+1 → f (Σu^*). Let ū′ = f (Σu^*). Then we have ${\mathbf{u}}_{k_j}^T\mathbf{\sum }{\mathbf{u}}_{k_j}\to {\mathbf{u}}^{\ast T}\mathbf{\sum }{\mathbf{u}}^{\ast }$ and ${\mathbf{u}}_{k_j+1}^T\mathbf{\sum }{\mathbf{u}}_{k_j+1}\to {({\overline{\mathbf{u}}}^{\prime })}^T\mathbf{\sum }{\overline{\mathbf{u}}}^{\prime }$. By Lemma 2, { ${\mathbf{u}}_k^T\mathbf{\sum }{\mathbf{u}}_k:k\ge 1$} is an increasing sequence. Hence, u^*T Σu^* = (ū′)^T Σū′ and by Lemma 2, u^* = ū′, that is, u^* ∈ . Now if u^*_I is a leading vector of (2.16). Let be the neighborhood of u^* defined in (5.34). Then when k_j is large enough, u_kj ∈ . Hence, the iteration sequence converges to u^*. If u^*_I is not a leading vector. Let and be the subsets defined in (5.37) and (5.38). Since u_kj → u^*, we must have that when k_j is large enough, u_kj ∈ ∩ . Hence, the iteration sequence converges to u^*.

Proof of Theorem 2.5

Let Ψ = (ψ₁, …, ψ_q) be a p × q matrix, where the basis ψ_j = (ψ_1j, · · ·, ψ_pj)^T ∈ R^p, 1 ≤ j ≤ q. Then t₁ψ₁ + · · · + t_q ψ_q = Ψt, ∀t = (t₁, · · ·, t_q)^T ∈ ℝ^q. We first show that if for some t^* ∈ ℝ^p, f (a_⊥ + Ψt^*) ⊥ M, then f (a_⊥ + Ψt^*) is the solution to (2.20). Actually, for any u with u ⊥ M and ||u||_λ = 1, we have

$${\mathbf{a}}^T\mathbf{u}={\mathbf{a}}_{\perp }^T\mathbf{u}={({\mathbf{a}}_{\perp }+\mathbf{\Psi }{\mathbf{t}}^{\ast })}^T\mathbf{u}\le {({\mathbf{a}}_{\perp }+\mathbf{\Psi }{\mathbf{t}}^{\ast })}^{T}f({\mathbf{a}}_{\perp }+\mathbf{\Psi }{\mathbf{t}}^{\ast })={\mathbf{a}}^{T}f({\mathbf{a}}_{\perp }+\mathbf{\Psi }{\mathbf{t}}^{\ast }),$$

where the inequality follows from the definition of f. The uniqueness of the solution to (2.20) is due to the strict convexness of {u: ||u||_λ = 1}. For any t = (t₁, · · ·, t_q)^T ∈ ℝ^q, let the orthogonal projection of f (a_⊥ + Ψt) onto M have the basis expansion Ψs = s₁ψ₁ + · · · + s_q ψ_q, where s = (s₁, · · ·, s_q)^T ∈ ℝ^q is a function of t. Hence, we define s = Γ(t). Then Γ is a continous function from R^q to R^q because f is a continuous function. We only need to show that there exists t^* such that Γ(t^*) = 0. We first prove a technical lemma.

Lemma 8

If ${\left|\right|{\mathbf{a}}_{\perp }\left|\right|}_2<\frac{{\left|\right|\mathbf{t}\left|\right|}_2^2}{{\left|\right|\mathbf{\Psi }\mathbf{t}\left|\right|}_{\lambda }}$, we have t^TΓ(t) > 0. Moreover, if ||t||₂ → ∞, we have $\frac{{\left|\right|\mathbf{t}\left|\right|}_2^2}{{\left|\right|\mathbf{\Psi }\mathbf{t}\left|\right|}_{\lambda }}\to \infty$.

Proof of Lemma 8

We will proceed by contradiction. Assume that t^T Γ(t) ≤ 0. Let f (a_⊥ + Ψt) = ΨΓ(t) + u_⊥, where u_⊥ ⊥ M. Hence, ${\left|\right|{\mathbf{u}}_{\perp }\left|\right|}_2^2\le {\left|\right|f({\mathbf{a}}_{\perp }+\mathbf{\Psi }\mathbf{t})\left|\right|}_2^2\le {\left|\right|f({\mathbf{a}}_{\perp }+\mathbf{\Psi }\mathbf{t})\left|\right|}_{\lambda }^2=1$. Note that {ψ₁, · · ·, ψ_q} is an orthonormal basis. Then we have

$$\begin{array}{r}{({\mathbf{a}}_{\perp }+\mathbf{\Psi }\mathbf{t})}^{T}f({\mathbf{a}}_{\perp }+\mathbf{\Psi }\mathbf{t})={\mathbf{a}}_{\perp }^T{\mathbf{u}}_{\perp }+{\mathbf{t}}^T\mathrm{\Gamma }(\mathbf{t})\le {\mathbf{a}}_{\perp }^T{\mathbf{u}}_{\perp }\le {\left|\right|{\mathbf{a}}_{\perp }\left|\right|}_2{\left|\right|{\mathbf{u}}_{\perp }\left|\right|}_2\le {\left|\right|{\mathbf{a}}_{\perp }\left|\right|}_2\\ <\frac{{\left|\right|\mathbf{t}\left|\right|}_2^2}{{\left|\right|\mathbf{\Psi }\mathbf{t}\left|\right|}_{\lambda }}={(\mathbf{\Psi }\mathbf{t})}^T\frac{\mathbf{\Psi }\mathbf{t}}{{\left|\right|\mathbf{\Psi }\mathbf{t}\left|\right|}_{\lambda }}={({\mathbf{a}}_{\perp }+\mathbf{\Psi }\mathbf{t})}^T\frac{\mathbf{\Psi }\mathbf{t}}{{\left|\right|\mathbf{\Psi }\mathbf{t}\left|\right|}_{\lambda }}.\end{array}$$

It is a contradiction because, by the definition of f, (a_⊥ + Ψt)^T f (a_⊥ + Ψt) is the largest among all (a_⊥ + Ψt)^T u with ||u||_λ = 1. The last statement in this lemma follows from

$$\frac{{\left|\right|\mathbf{t}\left|\right|}_2^2}{{\left|\right|\mathbf{\Psi }\mathbf{t}\left|\right|}_{\lambda }}\ge \frac{{\left|\right|\mathbf{t}\left|\right|}_2^2}{{\sum }_{i=1}^q\mid t_i{\left|\right|\mid {\mathit{\psi }}_i\left|\right|}_{\lambda }}\ge \frac{{\left|\right|\mathbf{t}\left|\right|}_2^2}{\sqrt{{\sum }_{i=1}^q{t}_i^2}\sqrt{{\sum }_{i=1}^q{\left|\right|{\mathit{\psi }}_i\left|\right|}_{\lambda }^2}}=\frac{{\left|\right|\mathbf{t}\left|\right|}_2}{\sqrt{{\sum }_{i=1}^q{\left|\right|{\mathit{\psi }}_i\left|\right|}_{\lambda }^2}}.$$

Now if q = 1, t is the real number. By Lemma 8, we can choose t > 0 so large that tΓ(t) > 0 and (−t)Γ(−t) > 0. Hence, we have Γ(−t) < 0 < Γ(t). Because Γ is a continuous function, the intermediate value theorem implies that for some −t ≤ t^* ≤ t, Γ(t^*) = 0.

If q > 1, we need some basic results from topology. We first give a definition (see Section 51 in Munkres [9]). Suppose that ρ₀ and ρ₁ are continuous maps of from a space X into X, we say that ρ₀ is homotopic to ρ₁ if there is a continuous map F: X ×[0, 1] → X such that F (x, 0) = ρ₀(x) and F (x, 1) = ρ₁(x), ∀x ∈ X. If ρ₁ maps all points in X into a fixed point in X, we say that ρ₀ is null homotopic. It is well known that the identity map from the unit sphere S^q−1 of ℝ^q (with l₂-norm) onto S^q−1 is not null homotopic (see Exercise 4(a), after Section 55 in Munkres [9]). We will proceed by contradiction. Assume that Γ(t) ≠ 0 for all t ∈ ℝ^q. By Lemma 8, we can choose a large M > 0 such that if ||t̃||₂ = M, we have t̃^TΓ(t̃) > 0. Hence, for any t ∈ S^q−1, t^TΓ(M t) > 0. Now we define a continuous map F: S^q−1 × [0, 1] → S^q−1 as follows,

$$F(\mathbf{t},\theta )=\{\begin{array}{ccc}\frac{(1-2\theta )\mathbf{t}+2\theta \mathrm{\Gamma }(M\mathbf{t})}{{\left|\right|(1-2\theta )\mathbf{t}+2\theta \mathrm{\Gamma }(M\mathbf{t})\left|\right|}_2}& \text{if}& 0\le \theta \le \frac{1}{2},\\ \frac{\mathrm{\Gamma }(2(1-\theta )M\mathbf{t})}{{\left|\right|\mathrm{\Gamma }(2(1-\theta )M\mathbf{t})\left|\right|}_2}& \text{if}& \frac{1}{2}\le \theta \le 1,\end{array}$$

where (1 −2θ)t + 2θΓ(Mt) ≠ 0 for all $0\le \theta \le \frac{1}{2}$. It is easy to see that F(t, 0) is the identity map from S^q−1 to S^q−1 and F (t, 1) maps every t to Γ(0)/||Γ(0)||₂, which contradict to the fact that the identity map from S^q−1 onto S^q−1 is not null homotopic.

Proof of Theorem 2.6

Recall that Ψ = (ψ₁, …, ψ_q), where the basis ψ_j = (ψ_1j, · · ·, ψ_pj)^T ∈ R^p, 1 ≤ j ≤ q. Suppose that $\overline{\mathbf{t}}\notin {\cup }_{m=1}^{q-1}{\mathcal{J}}_m$. We will calculate the first and second order partial derivatives of H at point t̄. Let $S_i={\sum }_{j=1}^i\mid c_{k_j}(\overline{\mathbf{t}})\mid$, 1 ≤ i ≤ p, where c_i(t̄)’s are define in (2.22). Let m be the number of nonzero coordinates of f (a_⊥ + Ψt̄). Then by (2.11) in Corollary 2.1

$$\mid c_{k_{m+1}}(\overline{\mathbf{t}})\mid \le \frac{\lambda S_m}{(1-\lambda )+m\lambda }<\mid c_{k_m}(\overline{\mathbf{t}})\mid ,$$

and the set I of indices of nonzero coordinates of f (a_⊥ + Ψt̄) is equal to {k₁, · · ·, k_m}. By the definition of , we have the following strict inequalities,

$$\mid c_{k_{m+1}}(\overline{\mathbf{t}})\mid <\frac{\lambda S_m}{(1-\lambda )+m\lambda }<\mid c_{k_m}(\overline{\mathbf{t}})\mid ,$$ (5.39)

Let Δt = (Δt₁, Δ₂, · · ·, Δt_q) and $\mid c_{k_1^{\prime }}(\overline{\mathbf{t}}+\mathrm{\Delta }\mathbf{t})\mid \ge \cdots \ge \mid c_{k_p^{\prime }}(\overline{\mathbf{t}}+\mathrm{\Delta }\mathbf{t})\mid$ be the sorted sequence. Define $S_i^{\prime }={\sum }_{j=1}^i\mid c_{k_j^{\prime }}(\mathbf{t}+\mathrm{\Delta }\mathbf{t})\mid$, 1 ≤ i ≤ p. By similar arguments as in the proof of Lemma 5, it follows from (5.39) that when ||Δt||₂ is small enough, we have

$$\mid c_{k_{m+1}^{\prime }}(\overline{\mathbf{t}}+\mathrm{\Delta }\mathbf{t})\mid <\frac{\lambda S_m^{\prime }}{(1-\lambda )+m\lambda }<\mid c_{k_m^{\prime }}(\overline{\mathbf{t}}+\mathrm{\Delta }\mathbf{t}),$$ (5.40)

and $\{k_1^{\prime },\cdots ,k_m^{\prime }\}=\{k_1,\cdots ,k_m\}=I$. Recall that we have defined x(t) = (x₁(t), · · ·, x_q (t))^T = f (a_⊥ + Ψt̄). It follows from (5.40) and Corollary 2.1 that

$$\begin{array}{l}{x}_i(\overline{\mathbf{t}}+\mathrm{\Delta }\mathbf{t})=\{\begin{array}{ll}\hfill \frac{1}{2{\nu }^{\prime }}\left[c_i(\overline{\mathbf{t}}+\mathrm{\Delta }\mathbf{t})-\mathbf{sgn}(c_i(\overline{\mathbf{t}}+\mathrm{\Delta }\mathbf{t}))\frac{\lambda S_m^{\prime }}{(1-\lambda +m\lambda )}\right],& i\in I\hfill \\ \hfill 0,& i\in I^c\hfill \end{array},\\ x_i(\overline{\mathbf{t}})=\{\begin{array}{ll}\hfill \frac{1}{2\nu }\left[c_i(\overline{\mathbf{t}})-\mathbf{sgn}(c_i(\overline{\mathbf{t}}))\frac{\lambda S_m}{(1-\lambda )+m\lambda }\right],& i\in I\hfill \\ \hfill 0,& i\in I^c\hfill \end{array},\end{array}$$ (5.41)

where ν and ν′ are the scale constants. Since c_i(t̄ + Δt) = c_i(t̄) + (ΨΔt)_i, when ||Δt||₂ is small enough, we have sgn(c_i(t̄ + Δt)) = sgn(c_i(t̄)) ≠ 0 for i ∈ I. In this case,

$$\begin{array}{l}\mid c_i(\overline{\mathbf{t}}+\mathrm{\Delta }\mathbf{t})\mid =\mathbf{sgn}(c_i(\overline{\mathbf{t}}))c_i(\overline{\mathbf{t}}+\mathrm{\Delta }\mathbf{t})=\mathbf{sgn}(c_i(\overline{\mathbf{t}}))(c_i(\overline{\mathbf{t}})+{(\mathbf{\Psi }\mathrm{\Delta }\mathbf{t})}_i)\\ =\mid c_i(\overline{\mathbf{t}})\mid +\mathbf{sgn}(c_i(\overline{\mathbf{t}})){(\mathbf{\Psi }\mathrm{\Delta }\mathbf{t})}_i.\end{array}$$

Hence, for i ∈ I, we have

$$\begin{array}{l}{x}_i(\overline{\mathbf{t}}+\mathrm{\Delta }\mathbf{t})=\frac{1}{2{\nu }^{\prime }}\left[c_i(\overline{\mathbf{t}})+{(\mathbf{\Psi }\mathrm{\Delta }\mathbf{t})}_i-\mathbf{sgn}(c_i(\overline{\mathbf{t}}))\frac{\lambda {\sum }_{j\in I}(\mid c_j(\overline{\mathbf{t}})\mid +\mathbf{sgn}(c_j(\overline{\mathbf{t}})){(\mathbf{\Psi }\mathrm{\Delta }\mathbf{t})}_j)}{(1-\lambda )+m\lambda }\right]\\ =\frac{1}{2{\nu }^{\prime }}\left[2\nu x_i(\overline{\mathbf{t}})+{(\mathbf{\Psi }\mathrm{\Delta }\mathbf{t})}_i-\mathbf{sgn}(c_i(\overline{\mathbf{t}}))\frac{\lambda {\sum }_{j\in I}\mathbf{sgn}(c_j(\overline{\mathbf{t}})){(\mathbf{\Psi }\mathrm{\Delta }\mathbf{t})}_j}{(1-\lambda )+m\lambda }\right]\\ =\frac{1}{2{\nu }^{\prime }}\left[2\nu x_i(\overline{\mathbf{t}})+{(\mathbf{sgn}(x_i(\overline{\mathbf{t}})))}^2{(\mathbf{\Psi }\mathrm{\Delta }\mathbf{t})}_i-\mathbf{sgn}(x_i(\overline{\mathbf{t}}))\frac{\lambda {\sum }_{j\in I}\mathbf{sgn}(x_j(\overline{\mathbf{t}})){(\mathbf{\Psi }\mathrm{\Delta }\mathbf{t})}_j}{(1-\lambda )+m\lambda }\right]\\ =\frac{1}{2{\nu }^{\prime }}\left[2\nu x_i(\overline{\mathbf{t}})+{(\mathbf{sgn}(x_i(\overline{\mathbf{t}})))}^2{(\mathbf{\Psi }\mathrm{\Delta }\mathbf{t})}_i-\mathbf{sgn}(x_i(\overline{\mathbf{t}}))\frac{\lambda {\sum }_{j=1}^p\mathbf{sgn}(x_j(\overline{\mathbf{t}})){(\mathbf{\Psi }\mathrm{\Delta }\mathbf{t})}_j}{(1-\lambda )+m\lambda }\right],\end{array}$$ (5.42)

where the last two equalities follows from the facts that x_i(t̄) and c_i(t̄) have the same signs for i ∈ I and the signs of x_i(t̄) are zeros for all i ∈ I^c. Note that the last line in (5.42) is equal to x_i(t̄ + Δt) even if i ∈ I^c because both of them are equal to zero. Thus, we have

$$\mathbf{x}(\overline{\mathbf{t}}+\mathrm{\Delta }\mathbf{t})=\frac{1}{2{\nu }^{\prime }}[2\nu \mathbf{x}(\overline{\mathbf{t}})+\mathbf{K}(\overline{\mathbf{t}})\mathrm{\Delta }\mathbf{t}]$$ (5.43)

where the p × q matrix

$$\mathbf{K}(\overline{\mathbf{t}})=\mathbf{N}(\overline{\mathbf{t}})\left(\mathbf{I}-\frac{\lambda }{(1-\lambda )+m\lambda }\mathbf{1}{\mathbf{1}}^T\right)\mathbf{N}(\overline{\mathbf{t}})\mathbf{\Psi },$$ (5.44)

I is the p-dimensional identity matrix, 1 is the p vector with all coordinates equal to 1, and N(t̄) is the p-dimensional diagonal matrix with the i-th diagonal element equal to sgn(x_i(t̄)), 1 ≤ i ≤ p. Now by the definition of H, we have H(t̄) = x(t̄)^T ΨΨ^T x(t̄) and

$$\begin{array}{l}H(\overline{\mathbf{t}}+\mathrm{\Delta }\mathbf{t})=\mathbf{x}{(\overline{\mathbf{t}}+\mathbf{\Delta }\mathbf{t})}^T\mathbf{\Psi }{\mathbf{\Psi }}^T\mathbf{x}(\overline{\mathbf{t}}+\mathbf{\Delta }\mathbf{t})\\ =\frac{1}{{(2{\nu }^{\prime })}^2}({(2\nu )}^{2}H(\overline{\mathbf{t}})+4\nu \mathbf{G}{(\overline{\mathbf{t}})}^T\mathrm{\Delta }\mathbf{t}+\mathrm{\Delta }{\mathbf{t}}^T\mathbf{\Pi }(\overline{\mathbf{t}})\mathrm{\Delta }\mathbf{t}),\end{array}$$ (5.45)

where the q-vector G(t̄) = K(t̄)^T ΨΨ^T x(t̄) and the q × q matrix Π(t̄) = K(t̄)^T ΨΨ^T K(t̄). Now we compute (2ν′)². From (5.43), we have

$$\begin{array}{l}{(2{\nu }^{\prime })}^2={\left|\right|2\nu \mathbf{x}(\overline{\mathbf{t}})+\mathbf{K}(\overline{\mathbf{t}})\mathrm{\Delta }\mathbf{t}\left|\right|}_{\lambda }^2=(1-\lambda ){\left|\right|2\nu \mathbf{x}(\overline{\mathbf{t}})+\mathbf{K}(\overline{\mathbf{t}})\mathrm{\Delta }\mathbf{t}\left|\right|}_2^2+\lambda {\left(\sum _{i=1}^p\mid 2\nu x_i(\overline{\mathbf{t}})+{(\mathbf{K}(\overline{\mathbf{t}})\mathrm{\Delta }\mathbf{t})}_i\mid \right)}^2\\ =(1-\lambda )[{(2\nu )}^2{\left|\right|\mathbf{x}(\mathbf{t})\left|\right|}_2^2+4\nu \mathbf{x}{(\overline{\mathbf{t}})}^T\mathbf{K}(\overline{\mathbf{t}})\mathrm{\Delta }\mathbf{t}+\mathrm{\Delta }{\mathbf{t}}^T\mathbf{K}{(\overline{\mathbf{t}})}^T\mathbf{K}(\overline{\mathbf{t}})\mathrm{\Delta }\mathbf{t}]+\lambda {\left(\sum _{i=1}^{p}2\nu \mid x_i(\overline{\mathbf{t}})\mid +\sum _{i=1}^p\mathbf{sgn}(x_i(\overline{\mathbf{t}})){(\mathbf{K}(\overline{\mathbf{t}})\mathrm{\Delta }\mathbf{t})}_i\right)}^2\\ =(1-\lambda )[{(2\nu )}^2{\left|\right|\mathbf{x}(\overline{\mathbf{t}})\left|\right|}_2^2+4\nu \mathbf{x}{(\overline{\mathbf{t}})}^T\mathbf{K}(\overline{\mathbf{t}})\mathrm{\Delta }\mathbf{t}+\mathrm{\Delta }{\mathbf{t}}^T\mathbf{K}{(\overline{\mathbf{t}})}^T\mathbf{K}(\overline{\mathbf{t}})\mathrm{\Delta }\mathbf{t}]+\lambda [{(2\nu )}^2{\left|\right|\mathbf{x}(\overline{\mathbf{t}})\left|\right|}_1^2+4\nu {\left|\right|\mathbf{x}(\overline{\mathbf{t}})\left|\right|}_1{\mathbf{1}}^T\mathbf{N}(\overline{\mathbf{t}})\mathbf{K}(\overline{\mathbf{t}})\mathrm{\Delta }\mathbf{t}+\mathrm{\Delta }{\mathbf{t}}^T\mathbf{K}{(\overline{\mathbf{t}})}^T\mathbf{N}{(\overline{\mathbf{t}})}^T\mathbf{1}{\mathbf{1}}^T\mathbf{N}(\overline{\mathbf{t}})\mathbf{K}(\overline{\mathbf{t}})\mathrm{\Delta }\mathbf{t}]\\ ={(2\nu )}^2{\left|\right|\mathbf{x}(\overline{\mathbf{t}})\left|\right|}_{\lambda }^2+4\nu \mathbf{E}{(\overline{\mathbf{t}})}^T\mathrm{\Delta }\mathbf{t}+{(\mathrm{\Delta }\mathbf{t})}^T\mathbf{F}(\overline{\mathbf{t}})(\mathrm{\Delta }\mathbf{t}),\end{array}$$

where the q-vector E and the q × q matrix F are

$$\begin{array}{l}\mathbf{E}(\overline{\mathbf{t}})=(1-\lambda )\mathbf{K}{(\overline{\mathbf{t}})}^T\mathbf{x}(\overline{\mathbf{t}})+\lambda {\left|\right|\mathbf{x}(\overline{\mathbf{t}})\left|\right|}_1\mathbf{K}{(\overline{\mathbf{t}})}^T\mathbf{N}(\overline{\mathbf{t}})\mathbf{1},\\ \mathbf{F}(\overline{\mathbf{t}})=(1-\lambda )\mathbf{K}{(\overline{\mathbf{t}})}^T\mathbf{K}(\overline{\mathbf{t}})+\lambda \mathbf{K}{(\overline{\mathbf{t}})}^T\mathbf{N}{(\overline{\mathbf{t}})}^T\mathbf{1}{\mathbf{1}}^T\mathbf{N}(\overline{\mathbf{t}})\mathbf{K}(\overline{\mathbf{t}}).\end{array}$$

Since ||x(t̄)||_λ = 1,

$$\begin{array}{l}{\left(\frac{2\nu }{2{\nu }^{\prime }}\right)}^2={\left(1+\frac{2}{2\nu }{(\mathrm{\Delta }\mathbf{t})}^T\mathbf{E}(\overline{\mathbf{t}})+\frac{1}{{(2\nu )}^2}{(\mathrm{\Delta }\mathbf{t})}^T\mathbf{F}(\overline{\mathbf{t}})(\mathrm{\Delta }\mathbf{t})\right)}^{-1}\\ =1-\frac{2}{2\nu }{(\mathrm{\Delta }\mathbf{t})}^T\mathbf{E}(\overline{\mathbf{t}})-\frac{1}{{(2\nu )}^2}{(\mathrm{\Delta }\mathbf{t})}^T\mathbf{F}(\overline{\mathbf{t}})(\mathrm{\Delta }\mathbf{t})+\frac{4}{{(2\nu )}^2}{(\mathrm{\Delta }\mathbf{t})}^T\mathbf{E}(\overline{\mathbf{t}})\mathbf{E}{(\overline{\mathbf{t}})}^T(\mathrm{\Delta }\mathbf{t})+o({\left|\right|\mathrm{\Delta }\mathbf{t}\left|\right|}_2^2).\end{array}$$

Now by (5.45),

$$\begin{array}{l}H(\overline{\mathbf{t}}+\mathrm{\Delta }\mathbf{t})=\frac{{(2\nu )}^2}{{(2{\nu }^{\prime })}^2}\left[H(\overline{\mathbf{t}})+\frac{1}{\nu }{(\mathrm{\Delta }\mathbf{t})}^T\mathbf{G}(\overline{\mathbf{t}})+\frac{1}{{(2\nu )}^2}{(\mathrm{\Delta }\mathbf{t})}^T\mathbf{\Pi }(\overline{\mathbf{t}})\mathrm{\Delta }(\mathbf{t})\right]\\ =H(\overline{\mathbf{t}})+{(\mathrm{\Delta }\mathbf{t})}^T\left(\frac{\mathbf{G}(\overline{\mathbf{t}})-H(\overline{\mathbf{t}})\mathbf{E}(\overline{\mathbf{t}})}{\nu }\right)+{(\mathrm{\Delta }\mathbf{t})}^T\frac{4H(\overline{\mathbf{t}})\mathbf{E}(\overline{\mathbf{t}})\mathbf{E}{(\overline{\mathbf{t}})}^T-2[\mathbf{E}(\overline{\mathbf{t}})\mathbf{G}{(\overline{\mathbf{t}})}^T+\mathbf{G}(\overline{\mathbf{t}})\mathbf{E}{(\overline{\mathbf{t}})}^T]+\mathbf{\Pi }(\overline{\mathbf{t}})-H(\overline{\mathbf{t}})\mathbf{F}(\overline{\mathbf{t}})}{{(2\nu )}^2}\mathrm{\Delta }\mathbf{t}+o({\left|\right|\mathrm{\Delta }\mathbf{t}\left|\right|}_2^2).\end{array}$$

Hence we have

$$\begin{array}{l}\nabla H(\overline{\mathbf{t}})=\frac{\mathbf{G}(\overline{\mathbf{t}})-H(\overline{\mathbf{t}})\mathbf{E}(\overline{\mathbf{t}})}{\nu },\\ {\nabla }^{2}H(\overline{\mathbf{t}})=\frac{4H(\overline{\mathbf{t}})\mathbf{E}(\overline{\mathbf{t}})\mathbf{E}{(\overline{\mathbf{t}})}^T-2[\mathbf{E}(\overline{\mathbf{t}})\mathbf{G}{(\overline{\mathbf{t}})}^T+\mathbf{G}(\overline{\mathbf{t}})\mathbf{E}{(\overline{\mathbf{t}})}^T]+\mathbf{\Pi }(\overline{\mathbf{t}})-H(\overline{\mathbf{t}})\mathbf{F}(\overline{\mathbf{t}})}{2{\nu }^2}.\end{array}$$

Proof of Theorem 2.7

Recall that Ψ = (ψ₁, …, ψ_q) is the matrix of basis vectors of M, where q is the dimension of M. For any 1 ≤ j ≤ p, let e_j be the vector with q-th coordinate equal to 1 and other coordinates equal zeros. {e₁, · · ·, e_p} is a basis of ℝ^p. For any subset I of {1, · · ·, p}, we choose a subset J = J(I) of I^c such that {e_i: i ∈ J} ∪ {ψ_j: 1 ≤ j ≤ q} is a basis for the subspace spanned by {e_i: i ∈ I^c} ∪ {ψ_j: 1 ≤ j ≤ q}. For any u^* ∈ , let I be the index set of nonzero coordinates of u^*. Since u^* is the solution to

$$\underset{\mathbf{u}\in {\mathbb{R}}^p}{max}{(\mathbf{\sum }{\mathbf{u}}^{\ast })}^T\mathbf{u},\text{subject}\text{to}{\left|\right|\mathbf{u}\left|\right|}_{\lambda }\le 1,\mathbf{u}\perp \mathbf{M},$$

it is also the solution to

$$\begin{array}{c}\underset{\mathbf{u}\in {\mathbb{R}}^p}{min}-{(\mathbf{\sum }{\mathbf{u}}^{\ast })}^T\mathbf{u},\text{subject}\text{to}{\left|\right|\mathbf{u}\left|\right|}_{\lambda }\le 1,\mathbf{sgn}(u_i^{\ast })u_i\ge 0,i\in I;u_i=0,i\in I^c;\\ \text{and}{\mathit{\psi }}_j^T{\mathbf{u}}^{\ast }=0,1\le j\le q,\end{array}$$

which is equivalent to the problem

$$\begin{array}{c}\underset{\mathbf{u}\in {\mathbb{R}}^p}{min}-{(\mathbf{\sum }{\mathbf{u}}^{\ast })}^T\mathbf{u},\text{subject}\text{to}{\left|\right|\mathbf{u}\left|\right|}_{\lambda }\le 1,\mathbf{sgn}(u_i^{\ast })u_i\ge 0,i\in I;u_i=0,i\in J;\\ \text{and}{\mathit{\psi }}_j^T{\mathbf{u}}^{\ast }=0,1\le j\le q,\end{array}$$

By the Karush-Kuhn-Tucker condition, we have

$$2\stackrel{\sim }{\nu }\stackrel{\sim }{\mathcal{E}}{\mathbf{A}}^{[\lambda ]}\stackrel{\sim }{\mathcal{E}}{\mathbf{u}}^{\ast }=\mathbf{\sum }{\mathbf{u}}^{\ast }+\sum _{i\in J}{\mu }_i{\mathbf{e}}_i+\sum _{j=1}^q{\beta }_j{\mathit{\psi }}_j,$$ (5.46)

where ν̃ > 0, μ_i and β_j are multipliers and is the p-dimensional diagonal matrix with the i-th diagonal element equal to $\mathbf{sgn}(u_i^{\ast })$ if i ∈ I and 1 if i ∈ I ^c. We will assume that for all u^* ∈ ,

$${\mu }_i\ne 0\text{for}\text{all}i\in J,\text{and}{\beta }_j\ne 0\text{for}\text{all}1\le j\le q.$$ (5.47)

From (5.46), we have

$$2\stackrel{\sim }{\nu }{\stackrel{\sim }{\mathcal{E}}}_I{\mathbf{A}}_I^{[\lambda ]}{\stackrel{\sim }{\mathcal{E}}}_I{\mathbf{u}}_I^{\ast }={\mathbf{\sum }}_I{\mathbf{u}}_I^{\ast }+\sum _{j=1}^q{\beta }_j{({\mathit{\psi }}_j)}_I,$$

and thus

$${\mathbf{P}}_I^{\mathbf{M}}{\stackrel{\sim }{\mathcal{E}}}_I{\mathbf{A}}_I^{[\lambda ]}{\stackrel{\sim }{\mathcal{E}}}_I{\mathbf{P}}_I^{\mathbf{M}}{\mathbf{u}}_I^{\ast }=\frac{1}{2\stackrel{\sim }{\nu }}{\mathbf{P}}_I^{\mathbf{M}}{\mathbf{\sum }}_I{\mathbf{P}}_I^{\mathbf{M}}{\mathbf{u}}_I^{\ast }$$ (5.48)

where ${\mathbf{P}}_I^{\mathbf{M}}$ is the orthogonal projection matrix onto the orthogonal complement of the space spanned by (ψ_j)_I, 1 ≥ j ≥ q. Hence, ${\mathbf{u}}_I^{\ast }$ is an eigenvector of the generalized eigenvalue problem (5.48) corresponding nonzero eigenvaules. Now we can use the same arguments as in the proof of Theorem 2.4 to prove the convergence of Algorithm 2.3. Moreover, we can show that only u^* ∈ with ${\mathbf{u}}_I^{\ast }$ being a leading eigenvector of problem (5.48) are stable limits.

Proof of Theorem 3.1

Since $0<\alpha <\frac{1}{3}$, we can find a positive number β such that

$$\alpha <\beta <2\beta <1-\alpha .$$ (5.49)

Without loss of generality, we assume that for each n,

$${\rho }_1^{(n)}\ge {\rho }_2^{(n)}\ge \cdots \ge {\rho }_{p_n}^{(n)}\ge 0,$$ (5.50)

Then the uniform “weak l_q decay” condition (3.3) becomes

$${\rho }_{\nu }^{(n)}\le C{\nu }^{-1/q},\nu =1,\cdots ,p_n,n=1,2,\cdots .$$ (5.51)

and the partial sum $S_i^{(n)}={\sum }_{j=1}^i{\rho }_j^{(n)}$, 1 ≤ i ≤ p_n. Let ${\mathbf{w}}^{(n)}={(w_1^{(n)},\cdots ,w_p^{(n)})}^T,$, and ${\mathbf{Z}}^{(n)}=[{\mathbf{z}}_1^{(n)},\cdots ,{\mathbf{z}}_n^{(n)}]$ be the p_n × n noise matrix. Then the p_n × p_n sample covariance matrix is

$${\widehat{\mathbf{\sum }}}^{(n)}=\frac{{\left|\right|{\mathbf{w}}^{(n)}\left|\right|}_2^2}{n}{\mathit{\rho }}^{(n)}{({\mathit{\rho }}^{(n)})}^T+{\sigma }^2\mathbf{I}+{\mathit{\rho }}^{(n)}{({\mathbf{y}}^{(n)})}^T+{\mathbf{y}}^{(n)}{({\mathit{\rho }}^{(n)})}^T+{\sigma }^2\left(\frac{{\mathbf{\Pi }}^{(n)}}{n}-\mathbf{I}\right),$$ (5.52)

where I is the p_n-dimensional identity matrix, ${\mathbf{y}}^{(n)}=\frac{\sigma }{n}{\mathbf{Z}}^{(n)}{\mathbf{w}}^{(n)}$ is a p_n-dimensional random vector and Π⁽ⁿ⁾ = Z⁽ⁿ⁾(Z⁽ⁿ⁾)^T is a p_n × p_n random matrix and has a Wishart distribution with n degrees of freedom. By the condition (3.4), we can choose a positive integer m₀ (independent of n) and a real number 0 < τ < 1 such that for any m ≥ m₀,

$$\underset{n\ge 1}{sup}\frac{S_{2m}^{(n)}-S_m^{(n)}}{S_m^{(n)}}\le \tau .$$ (5.53)

Define

$${\widehat{\mu }}^{(n)}=\underset{\mathbf{v}\in {\mathbb{R}}^p,{\left|\right|\mathbf{v}\left|\right|}_2=1}{max}\frac{{\mathbf{v}}^T{\widehat{\mathbf{\sum }}}^{(n)}\mathbf{v}}{(1-{\lambda }^{(n)}){\left|\right|\mathbf{v}\left|\right|}_2^2+{\lambda }^{(n)}{\left|\right|\mathbf{v}\left|\right|}_1^2}=\frac{{({\widehat{\mathit{\rho }}}^{(n)})}^T{\widehat{\mathbf{\sum }}}^{(n)}{\widehat{\mathit{\rho }}}^{(n)}}{{\left|\right|{\widehat{\mathit{\rho }}}^{(n)}\left|\right|}_{{\lambda }^{(n)}}^2}.$$ (5.54)

We first provide several technical lemmas whose proofs are given in Appendix. Recall that for any two vectors u and v, we use 〈u, v〉 = u^T v to denote the inner product between u and v. By the condition (3.5), we have ${(2\sigma \sqrt{c})}^2<1-(4\sigma \sqrt{c}+4{\sigma }^2\sqrt{c}+2{\sigma }^{2}c)$ and $1-(2\sigma \sqrt{c}+2{\sigma }^2\sqrt{c}+{\sigma }^{2}c)>0$. Thus, we can find κ₁ > 0 and κ₂ > 0 small enough such that

$${({\kappa }_1+2\sigma \sqrt{c})}^2<1-[4\sigma \sqrt{c}+4{\sigma }^2\sqrt{c}+2{\sigma }^{2}c],$$ (5.55)

$$2{\kappa }_2{\sigma }^2<1-(2\sigma \sqrt{c}+2{\sigma }^2\sqrt{c}+{\sigma }^{2}c).$$ (5.56)

Lemma 9

Suppose that κ₁ and κ₂ satisfy (5.55) and (5.56), respectively, we have

$$\sum _{n=1}^{\infty }P\left(\left|\langle {\widehat{\mathit{\rho }}}^{(n)},{\mathit{\rho }}^{(n)}\rangle +\langle {\widehat{\mathit{\rho }}}^{(n)},{\mathbf{y}}^{(n)}\rangle \right|\le {\kappa }_1\right)<\infty ,$$ (5.57)

$$\sum _{n=1}^{\infty }P\left({\widehat{\mu }}^{(n)}\le (1+{\kappa }_2){\sigma }^2\right)<\infty ,\sum _{n=1}^{\infty }P\left({\left|\right|{\widehat{\mathit{\rho }}}^{(n)}\left|\right|}_1>\frac{\sqrt{3+{\sigma }^2}}{\sigma \sqrt{{\lambda }^{(n)}}}\right)<\infty .$$ (5.58)

Lemma 10

If μ̂ ⁽ⁿ⁾ > (1 + κ₂)σ² and λ⁽ⁿ⁾ ≤ κ₂/(1 + κ₂), then ρ̂⁽ⁿ⁾ is the solution to the following optimization problem multiplied by a constant,

$$\underset{\mathbf{u}\in {\mathbb{R}}^p}{max}{\left(\left({\widehat{\mathbf{\sum }}}^{(n)}-{\sigma }^2\mathbf{I}\right){\widehat{\mathit{\rho }}}^{(n)}\right)}^T\mathbf{u},\mathit{subject}to{\left|\right|\mathbf{u}\left|\right|}_{{\stackrel{\sim }{\lambda }}^{(n)}}\le 1,$$

where I is the identity matrix and ${\widehat{\lambda }}^{(n)}={\lambda }^{(n)}/\left(1-\frac{{\sigma }^2}{{\widehat{\mu }}^{(n)}}\right)$.

Let

$$\begin{array}{l}{\mathit{\xi }}^{(n)}={({\xi }_1^{(n)},\cdots ,{\xi }_{p_n}^{(n)})}^T\\ =\left({\widehat{\mathbf{\sum }}}^{(n)}-{\sigma }^2\mathbf{I}\right){\widehat{\mathit{\rho }}}^{(n)}-\left(\langle {\widehat{\mathit{\rho }}}^{(n)},{\mathit{\rho }}^{(n)}\rangle +\langle {\widehat{\mathit{\rho }}}^{(n)},{\mathbf{y}}^{(n)}\rangle \right){\mathit{\rho }}^{(n)}.\end{array}$$

Then we have the following lemma.

Lemma 11

If (5.58) holds for some positive κ₂, we have

$$\sum _{n=1}^{\infty }P\left(\underset{1\le i\le p_n}{max}\mid {\xi }_i^{(n)}\mid >n^{-\beta }\right)<\infty .$$ (5.59)

We choose and fix κ₁ > 0 and κ₂ > 0 such that (5.55) and (5.56) hold. Define ζ⁽ⁿ⁾ = ξ⁽ⁿ⁾/(〈ρ̂⁽ⁿ⁾, ρ⁽ⁿ⁾〉 + 〈ρ̂⁽ⁿ⁾, y⁽ⁿ⁾〉) and

$${\widehat{\mathit{a}}}^{(n)}={\mathit{\rho }}^{(n)}+{\mathit{\xi }}^{(n)}/\left(\langle {\widehat{\mathit{\rho }}}^{(n)},{\mathit{\rho }}^{(n)}\rangle +\langle {\widehat{\mathit{\rho }}}^{(n)},{\mathbf{y}}^{(n)}\rangle \right)={\mathit{\rho }}^{(n)}+{\mathit{\zeta }}^{(n)},$$

then

$$\left({\widehat{\mathbf{\sum }}}^{(n)}-{\sigma }^2\mathbf{I}\right){\widehat{\mathit{\rho }}}^{(n)}=\left(\langle {\widehat{\mathit{\rho }}}^{(n)},{\mathit{\rho }}^{(n)}\rangle +\langle {\widehat{\mathit{\rho }}}^{(n)},{\mathbf{y}}^{(n)}\rangle \right){\widehat{\mathit{a}}}^{(n)}.$$

It follows from (5.57) and (5.59) that

$$\sum _{n=1}^{\infty }P\left(\underset{1\le i\le p_n}{max}\left|{\zeta }_i^{(n)}\right|>\frac{n^{-\beta }}{{\kappa }_1}\right)<\infty ,$$ (5.60)

where ${\mathit{\zeta }}^{(n)}={({\zeta }_1^{(n)},\cdots ,{\zeta }_{p_n}^{(n)})}^T$. Define a sequence of measurable subsets of the probability space

$${\mathrm{\Omega }}^{(n)}=\left\{\left|\langle {\widehat{\mathit{\rho }}}^{(n)},{\mathit{\rho }}^{(n)}\rangle +\langle {\widehat{\mathit{\rho }}}^{(n)},{\mathbf{y}}^{(n)}\rangle \right|>{\kappa }_1\right\}\cap \left\{{\widehat{\mu }}^{(n)}>(1+{\kappa }_2){\sigma }^2\right\}\cap \left\{\underset{1\le i\le p_n}{max}\left|{\zeta }_i^{(n)}\right|\le \frac{n^{-\beta }}{{\kappa }_1}\right\}$$ (5.61)

It follows from Lemma 9 and (5.60) that

$$\sum _{n=1}^{\infty }P({({\mathrm{\Omega }}^{(n)})}^c)<\infty ,$$ (5.62)

where (Ω⁽ⁿ⁾)^c is the complement of Ω⁽ⁿ⁾. Hence by Borel-Cantelli Lemma, it holds almost surely that for all but finitely many n, the event Ω⁽ⁿ⁾ happens. Therefore, in the following, we will assume that the inequalities in the definition (5.61) of Ω⁽ⁿ⁾ hold for all n large enough. By Lemma 10, ρ̂⁽ⁿ⁾ is the solution to the following optimization problem multiplied by a constant,

$$\underset{\mathbf{u}\in {\mathbb{R}}^p}{max}{\left({\widehat{\mathit{a}}}^{(n)}\right)}^T\mathbf{u},\text{subject}\text{to}{\left|\right|\mathbf{u}\left|\right|}_{{\stackrel{\sim }{\lambda }}^{(n)}}\le 1.$$

Let |â⁽ⁿ⁾|₍₁₎ ≥ |â⁽ⁿ⁾|₍₂₎ ≥ · · · ≥ |â⁽ⁿ⁾|_(pn) be the sorted sequence of the co-ordinates ( ${\widehat{a}}_1^{(n)},\cdots ,{\widehat{a}}_{p_n}^{(n)}$) of â⁽ⁿ⁾ by their absolute values. Define the partial sums ${\widehat{S}}_i^{(n)}={\sum }_{j=1}^i\mid {\widehat{\mathit{a}}}^{(n)}{\mid }_{(j)}$, 1 ≤ i ≤ p_n. Since ${max}_{1\le i\le p_n}\mid {\zeta }_i^{(n)}\mid \le \frac{n^{-\beta }}{{\kappa }_1},\mid {\widehat{a}}_i^{(n)}\mid =\mid {\rho }_i^{(n)}+{\zeta }_i^{(n)}\mid \le {\rho }_i^{(n)}+\frac{n^{-\beta }}{{\kappa }_1}$, from which and (5.50) we can obtain that

$${\rho }_i^{(n)}-\frac{n^{-\beta }}{{\kappa }_1}\le \mid {\widehat{\mathit{a}}}^{(n)}{\mid }_{(i)}\le {\rho }_i^{(n)}+\frac{n^{-\beta }}{{\kappa }_1},\forall 1\le i\le p_n.$$ (5.63)

Let m̂⁽ⁿ⁾ be the number of nonzero coordinates of ρ̂⁽ⁿ⁾. We will give an upper bound for m̂⁽ⁿ⁾. Define

$$m^{(n)}=4\left(\lfloor \frac{1}{{\stackrel{\sim }{\lambda }}^{(n)}}max\{1,\frac{4\tau }{1-\tau }\}\rfloor +1\right).$$ (5.64)

where τ is the constant defined in (5.53), λ̃ ⁽ⁿ⁾ is defined in Lemma 10. For any real number x, ⌊x⌋ denotes the largest integer number smaller than x.

Lemma 12

With probability 1, m̂⁽ⁿ⁾ ≤ m⁽ⁿ⁾ when n is large enough.

By Corollary 2.1, we have

$${\widehat{\mathit{\rho }}}^{(n)}={\widehat{\mathit{b}}}^{(n)}/{\left|\right|{\widehat{\mathit{b}}}^{(n)}\left|\right|}_2,$$ (5.65)

where ${\widehat{\mathit{b}}}^{(n)}={({\widehat{b}}_1^{(n)},\cdots ,{\widehat{b}}_{p_n}^{(n)})}^T$ and

$${\widehat{b}}_i^{(n)}=\mathbf{sgn}({\widehat{a}}_i^{(n)}){\left(\mid {\widehat{a}}_i^{(n)}\mid -\frac{{\stackrel{\sim }{\lambda }}^{(n)}{\stackrel{\sim }{S}}_{{\widehat{m}}^{(n)}}^{(n)}}{(1-{\stackrel{\sim }{\lambda }}^{(n)})+{\widehat{m}}^{(n)}{\stackrel{\sim }{\lambda }}^{(n)}}\right)}_{+}.$$ (5.66)

(x)₊ denotes the function which is equal to zero if x < 0 and equal to x if x ≥ 0. We will show ${\left|\right|{\mathit{\rho }}^{(n)}-{\widehat{\mathit{b}}}^{(n)}\left|\right|}_2^2\to 0$ as n → ∞. Let

$$\begin{array}{l}{I}_0=\{1\le i\le p_n:{\widehat{b}}_i^{(n)}=0\},\\ I_1=\{1\le i\le p_n:{\widehat{b}}_i^{(n)}\ne 0,{\rho }_i^{(n)}\le \frac{n^{-\beta }}{{\kappa }_1}+\frac{{\stackrel{\sim }{\lambda }}^{(n)}{\widehat{S}}_{{\widehat{m}}^{(n)}}^{(n)}}{(1-{\stackrel{\sim }{\lambda }}^{(n)})+{\widehat{m}}^{(n)}{\stackrel{\sim }{\lambda }}^{(n)}}\},\\ I_2=\{1\le i\le p_n:{\widehat{b}}_i^{(n)}\ne 0,{\rho }_i^{(n)}>\frac{n^{\_\beta }}{{\kappa }_1}+\frac{{\stackrel{\sim }{\lambda }}^{(n)}{\widehat{S}}_{{\widehat{m}}^{(n)}}^{(n)}}{(1-{\stackrel{\sim }{\lambda }}^{(n)})+{\widehat{m}}^{(n)}{\stackrel{\sim }{\lambda }}^{(n)}}\}.\end{array}$$ (5.67)

Then I₀ ∪ I₁ ∪ I₂ = {1, 2, · · ·, p_n} and the number of elements in I₁ ∪ I₂ is m̂⁽ⁿ⁾. It can be seen that for any i ∈ I₀, we have

$${\rho }_i^{(n)}\le \frac{n^{-\beta }}{{\kappa }_1}+\mid {\widehat{a}}_i^{(n)}\mid \le \frac{n^{-\beta }}{{\kappa }_1}+\frac{{\stackrel{\sim }{\lambda }}^{(n)}{\widehat{S}}_{{\widehat{m}}^{(n)}}^{(n)}}{(1-{\stackrel{\sim }{\lambda }}^{(n)})+{\widehat{m}}^{(n)}{\stackrel{\sim }{\lambda }}^{(n)}},$$ (5.68)

for any i ∈ I₁,

$$\begin{array}{r}\mid {\rho }_i^{(n)}-{\widehat{b}}_i^{(n)}\mid \le \mid {\rho }_i^{(n)}\mid +\mid {\widehat{b}}_i^{(n)}\mid \le {\rho }_i^{(n)}+\mid {\widehat{a}}_i^{(n)}\mid +\frac{{\stackrel{\sim }{\lambda }}^{(n)}{\widehat{S}}_{{\widehat{m}}^{(n)}}^{(n)}}{(1-{\stackrel{\sim }{\lambda }}^{(n)})+{\widehat{m}}^{(n)}{\stackrel{\sim }{\lambda }}^{(n)}}\\ \le 2{\rho }_i^{(n)}+\frac{n^{-\beta }}{{\kappa }_1}+\frac{{\stackrel{\sim }{\lambda }}^{(n)}{\widehat{S}}_{{\widehat{m}}^{(n)}}^{(n)}}{(1-{\stackrel{\sim }{\lambda }}^{(n)})+{\widehat{m}}^{(n)}{\stackrel{\sim }{\lambda }}^{(n)}}\\ \le \frac{3n^{-\beta }}{{\kappa }_1}+\frac{3{\stackrel{\sim }{\lambda }}^{(n)}{S}_{{\widehat{m}}^{(n)}}^{(n)}}{(1-{\stackrel{\sim }{\lambda }}^{(n)})+{\widehat{m}}^{(n)}{\stackrel{\sim }{\lambda }}^{(n)}},\end{array}$$ (5.69)

and for any i ∈ I₂,

$$\mid {\rho }_i^{(n)}-{\widehat{b}}_i^{(n)}\mid \le \mid {\rho }_i^{(n)}-{\widehat{a}}_i^{(n)}\mid +\frac{{\stackrel{\sim }{\lambda }}^{(n)}{\widehat{S}}_{{\widehat{m}}^{(n)}}^{(n)}}{(1-{\stackrel{\sim }{\lambda }}^{(n)})+{\widehat{m}}^{(n)}{\stackrel{\sim }{\lambda }}^{(n)}}\le \frac{n^{-\beta }}{{\kappa }_1}+\frac{{\stackrel{\sim }{\lambda }}^{(n)}{\widehat{S}}_{{\widehat{m}}^{(n)}}^{(n)}}{(1-{\stackrel{\sim }{\lambda }}^{(n)})+{\widehat{m}}^{(n)}{\stackrel{\sim }{\lambda }}^{(n)}},$$ (5.70)

First we calculate

$$\begin{array}{l}{\left(\frac{{\stackrel{\sim }{\lambda }}^{(n)}{\widehat{S}}_{{\widehat{m}}^{(n)}}^{(n)}}{(1-{\stackrel{\sim }{\lambda }}^{(n)})+{\widehat{m}}^{(n)}{\stackrel{\sim }{\lambda }}^{(n)}}\right)}^2{\widehat{m}}^{(n)}\le {\left(\frac{{\stackrel{\sim }{\lambda }}^{(n)}{\widehat{S}}_{{\widehat{m}}^{(n)}}^{(n)}+{\widehat{\lambda }}^{(n)}{\widehat{m}}^{(n)}\frac{n^{-\beta }}{{\kappa }_1}}{(1-{\stackrel{\sim }{\lambda }}^{(n)})+{\widehat{m}}^{(n)}{\stackrel{\sim }{\lambda }}^{(n)}}\right)}^2{\widehat{m}}^{(n)}\\ \le {\left(\frac{{\stackrel{\sim }{\lambda }}^{(n)}{S}_{{\widehat{m}}^{(n)}}^{(n)}}{1-{\stackrel{\sim }{\lambda }}^{(n)}}+\frac{n^{-\beta }}{{\kappa }_1}\right)}^2{\widehat{m}}^{(n)}\le 2\frac{{({\stackrel{\sim }{\lambda }}^{(n)}{S}_{{\widehat{m}}^{(n)}}^{(n)})}^2{\widehat{m}}^{(n)}}{{(1-{\stackrel{\sim }{\lambda }}^{(n)})}^2}+2\frac{n^{-2\beta }{\widehat{m}}^{(n)}}{{\kappa }_1^2}\end{array}$$

By the condition (5.51), we have $S_{m^{(n)}}^{(n)}\le {\sum }_{\nu =1}^{m^{(n)}}C{\nu }^{-1/q}$

$$S_{m^{(n)}}^{(n)}=\{\begin{array}{lll}O({(m^{(n)})}^{1-1/q})\hfill & \text{if}\hfill & 1<q<2,\hfill \\ O(log(m^{(n)}))\hfill & \text{if}\hfill & q=1,\hfill \\ O(1)\hfill & \text{if}\hfill & 0<q<1.\hfill \end{array}$$

Hence, by Lemma 12, if 1 < q < 2,

$${({\stackrel{\sim }{\lambda }}^{(n)}{S}_{{\widehat{m}}^{(n)}}^{(n)})}^2{\widehat{m}}^{(n)}\le {({\stackrel{\sim }{\lambda }}^{(n)}{S}_{m^{(n)}}^{(n)})}^2{m}^{(n)}={({\stackrel{\sim }{\lambda }}^{(n)})}^{2}O\left({(m^{(n)})}^{3-2/q}\right)={({\stackrel{\sim }{\lambda }}^{(n)})}^{2}O\left({({\stackrel{\sim }{\lambda }}^{(n)})}^{-3+2/q}\right)=O\left({({\stackrel{\sim }{\lambda }}^{(n)})}^{-1+2/q}\right)\to 0,$$

Similarly, ${({\stackrel{\sim }{\lambda }}^{(n)}{S}_{{\widehat{m}}^{(n)}}^{(n)})}^2{\widehat{m}}^{(n)}\to 0$ for other two cases. Since n^−2βm̂⁽ⁿ⁾ ≤ n^−2βm ⁽ⁿ⁾ = O(n^−2β/λ̃⁽ⁿ⁾) = O(n^−2β+α) → 0 by (5.49),

$${\left(\frac{{\stackrel{\sim }{\lambda }}^{(n)}{\widehat{S}}_{{\widehat{m}}^{(n)}}^{(n)}}{(1-{\stackrel{\sim }{\lambda }}^{(n)})+{\widehat{m}}^{(n)}{\stackrel{\sim }{\lambda }}^{(n)}}\right)}^2{\widehat{m}}^{(n)}\to 0,$$ (5.71)

as n → ∞. By (5.68)–(5.70),

$${\left|\right|{\mathit{\rho }}^{(n)}-{\widehat{\mathit{b}}}^{(n)}\left|\right|}_2^2=\sum _{i\in I_0}{({\rho }_i^{(n)})}^2+\sum _{i\in I_1}{({\rho }_i^{(n)}-{\widehat{b}}_i^{(n)})}^2+\sum _{i\in I_2}{({\rho }_i^{(n)}-{\widehat{b}}_i^{(n)})}^2\le 8\sum _{i=1}^{p_n}{\left[{\rho }_i^{(n)}\wedge \left(\frac{n^{-\beta }}{{\kappa }_1}+\frac{{\stackrel{\sim }{\lambda }}^{(n)}{\widehat{S}}_{{\widehat{m}}^{(n)}}^{(n)}}{(1-{\stackrel{\sim }{\lambda }}^{(n)})+{\widehat{m}}^{(n)}{\stackrel{\sim }{\lambda }}^{(n)}}\right)\right]}^2$$ (5.72)

$$+9\sum _{i\in I_1}{\left[\frac{n^{-\beta }}{{\kappa }_1}+\frac{{\stackrel{\sim }{\lambda }}^{(n)}{\widehat{S}}_{{\widehat{m}}^{(n)}}^{(n)}}{(1-{\stackrel{\sim }{\lambda }}^{(n)})+{\widehat{m}}^{(n)}{\stackrel{\sim }{\lambda }}^{(n)}}\right]}^2.$$ (5.73)

It follows from (5.71) that

$$\sum _{i\in I_1}{\left[\frac{n^{-\beta }}{{\kappa }_1}+\frac{{\stackrel{\sim }{\lambda }}^{(n)}{\widehat{S}}_{{\widehat{m}}^{(n)}}^{(n)}}{(1-{\stackrel{\sim }{\lambda }}^{(n)})+{\widehat{m}}^{(n)}{\stackrel{\sim }{\lambda }}^{(n)}}\right]}^2\le {\left[\frac{n^{-\beta }}{{\kappa }_1}+\frac{{\stackrel{\sim }{\lambda }}^{(n)}{\widehat{S}}_{{\widehat{m}}^{(n)}}^{(n)}}{(1-{\stackrel{\sim }{\lambda }}^{(n)})+{\widehat{m}}^{(n)}{\stackrel{\sim }{\lambda }}^{(n)}}\right]}^2{\widehat{m}}^{(n)}\to 0.$$

Because each term in the sum (5.72) converges to zero as n → ∞ and the sequence dominated by {Ci^−1/q: i ≥ 1} which is square summable, by the Dominated Convergence Theorem, the sum (5.72) converges to zero. Hence, we have proved that ${\left|\right|{\mathit{\rho }}^{(n)}-{\widehat{\mathit{b}}}^{(n)}\left|\right|}_2^2\to 0$. Since ||ρ⁽ⁿ⁾||₂ = 1, ${\left|\right|{\widehat{\mathit{b}}}^{(n)}\left|\right|}_2^2\to 1$.

$${\left|\right|{\mathit{\rho }}^{(n)}-{\widehat{\mathit{\rho }}}^{(n)}\left|\right|}_2={\left|\right|{\mathit{\rho }}^{(n)}-\frac{{\widehat{\mathit{b}}}^{(n)}}{{\left|\right|{\widehat{\mathit{b}}}^{(n)}\left|\right|}_2}\left|\right|}_2\le {\left|\right|{\widehat{\mathit{b}}}^{(n)}-\frac{{\widehat{\mathit{b}}}^{(n)}}{{\left|\right|{\widehat{\mathit{b}}}^{(n)}\left|\right|}_2}\left|\right|}_2+{\left|\right|{\mathit{\rho }}^{(n)}-{\widehat{\mathit{b}}}^{(n)}\left|\right|}_2\to 0.$$

the right hand side goes to zero.

6. Appendix

We will use the following large deviation inequalities for chi-square distribution (see (A.2) and (A.3) in Johnstone and Lu [7]).

$$P\left(\left|\frac{{\chi }_{(n)}^2}{n}-1\right|>\epsilon \right)\le 2exp\{-3n{\epsilon }^2/16\},0\le \epsilon <\frac{1}{2}.$$ (6.1)

Proof of Lemma 9

By (5.55), we can pick $0<\epsilon <\frac{1}{2}$ small enough such that

$$(1-\epsilon )(1-{\epsilon }^2)-{\sigma }^2\epsilon -\frac{\epsilon (2-{\epsilon }^2)}{1-{\epsilon }^2}[3+2(1+\epsilon )\sigma +{\sigma }^2]-\frac{2-{\epsilon }^2}{1-\epsilon }[2\sigma \sqrt{c}+2{\sigma }^2\sqrt{c}+{\sigma }^{2}c]>{({\kappa }_1+(1+\epsilon )2\sigma (\sqrt{c}+\epsilon )+\epsilon )}^2$$ (6.2)

and

$$\begin{array}{l}1-{\epsilon }^2-3\epsilon -2(1+\epsilon )\epsilon \sigma -\epsilon {\sigma }^2-(1+\epsilon )(2\sigma \sqrt{c}+2{\sigma }^2\sqrt{c}+{\sigma }^{2}c)>(1+\epsilon )[({\kappa }_2+\epsilon ){\sigma }^2+(1-\epsilon ){\epsilon }^2],\end{array}$$ (6.3)

$$1+{\sigma }^2(1+\epsilon )+3\epsilon +2(1+\epsilon )\sigma \epsilon +(1+\epsilon )(2\sigma \sqrt{c}+2{\sigma }^2\sqrt{c}+{\sigma }^{2}c)<3+{\sigma }^2,$$ (6.4)

because the two sides of (6.2) and (6.3) converge to the two sides of (5.55) and (5.56), the left side of (6.4) goes to $1+[2\sigma \sqrt{c}+2{\sigma }^2\sqrt{c}+{\sigma }^{2}c]$ which is smaller than 3 by (5.56), as ε → 0. We choose an integer N > 0 (independent of n) such that ${\sum }_{\nu =N+1}^{\infty }{C}^2{\nu }^{-2/q}<{\epsilon }^2$. We define ${\mathit{\rho }}_{\epsilon }^{(n)}=({\rho }_1^{(n)},\cdots ,{\rho }_N^{(n)},0,\cdots ,0)$, then by the condition (5.51),

$$1\ge {\left|\right|{\mathit{\rho }}_{\epsilon }^{(n)}\left|\right|}_2^2=\langle {\mathit{\rho }}_{\epsilon }^{(n)},{\mathit{\rho }}^{(n)}\rangle \ge 1-{\epsilon }^2\text{for}\text{all}n.$$ (6.5)

Since ρ̂⁽ⁿ⁾ is the solution to (3.2), we have

$$\frac{{({\mathit{\rho }}_{\epsilon }^{(n)})}^T{\widehat{\mathbf{\sum }}}^{(n)}{\mathit{\rho }}_{\epsilon }^{(n)}}{{\left|\right|{\mathit{\rho }}_{\epsilon }^{(n)}\left|\right|}_{{\lambda }^{(n)}}^2}\le \frac{{({\widehat{\mathit{\rho }}}^{(n)})}^T{\widehat{\mathbf{\sum }}}^{(n)}{\widehat{\mathit{\rho }}}^{(n)}}{{\left|\right|{\widehat{\mathit{\rho }}}^{(n)}\left|\right|}_{{\lambda }^{(n)}}^2}\le \frac{{({\widehat{\mathit{\rho }}}^n)}^T{\widehat{\mathbf{\sum }}}^{(n)}{\widehat{\mathit{\rho }}}^{(n)}}{{\left|\right|{\widehat{\mathit{\rho }}}^{(n)}\left|\right|}_2^2}={({\widehat{\mathit{\rho }}}^{(n)})}^T{\widehat{\mathbf{\sum }}}^{(n)}{\widehat{\mathit{\rho }}}^{(n)}.$$ (6.6)

By a simple calculation, it follows from (5.52) that

$$\begin{array}{l}{({\widehat{\mathit{\rho }}}^{(n)})}^T{\widehat{\mathbf{\sum }}}^{(n)}{\widehat{\mathit{\rho }}}^{(n)}=\frac{{\left|\right|{\mathbf{w}}^{(n)}\left|\right|}_2^2}{n}{\langle {\widehat{\mathit{\rho }}}^{(n)},{\widehat{\mathit{\rho }}}^{(n)}\rangle }^2+{\sigma }^2{\left|\right|{\widehat{\mathit{\rho }}}^{(n)}\left|\right|}_2^2+2\langle {\widehat{\mathit{\rho }}}^{(n)},{\mathbf{y}}^{(n)}\rangle \langle {\widehat{\mathit{\rho }}}^{(n)},{\mathit{\rho }}^{(n)}\rangle +{\sigma }^2{({\widehat{\mathit{\rho }}}^{(n)})}^T\left(\frac{{\mathbf{\Pi }}^{(n)}}{n}-\mathbf{I}\right){\widehat{\mathit{\rho }}}^{(n)}\\ ={\langle {\widehat{\mathit{\rho }}}^{(n)},{\widehat{\mathit{\rho }}}^{(n)}\rangle }^2+{\sigma }^2+(\frac{{\left|\right|{\mathbf{w}}^{(n)}\left|\right|}_2^2}{n}-1){\langle {\widehat{\mathit{\rho }}}^{(n)},{\widehat{\mathit{\rho }}}^{(n)}\rangle }^2+2\langle {\widehat{\mathit{\rho }}}^{(n)},{\mathbf{y}}^{(n)}\rangle \langle {\widehat{\mathit{\rho }}}^{(n)},{\mathit{\rho }}^{(n)}\rangle +{\sigma }^2{({\widehat{\mathit{\rho }}}^{(n)})}^T\left(\frac{{\mathbf{\Pi }}^{(n)}}{n}-\mathbf{I}\right){\widehat{\mathit{\rho }}}^{(n)}\\ \le {\langle {\widehat{\mathit{\rho }}}^{(n)},{\mathit{\rho }}^{(n)}\rangle }^2+{\sigma }^2+\left|\frac{{\left|\right|{\mathbf{w}}^{(n)}\left|\right|}_2^2}{n}-1\right|+2{\left|\right|{\mathbf{y}}^{(n)}\left|\right|}_2+{\sigma }^2{\widehat{\gamma }}^{(n)},\end{array}$$ (6.7)

where γ̂⁽ⁿ⁾ is the largest eigenvalue of $\frac{1}{n}{\mathbf{\Pi }}^{(n)}-\mathbf{I}$. Similarly, by (6.5),

$$\begin{array}{l}{({\mathit{\rho }}_{\epsilon }^{(n)})}^T{\widehat{\mathbf{\sum }}}^{(n)}{\mathit{\rho }}_{\epsilon }^{(n)}\ge {\langle {\mathit{\rho }}_{\epsilon }^{(n)},{\mathit{\rho }}^{(n)}\rangle }^2+{\sigma }^2{\left|\right|{\mathit{\rho }}_{\epsilon }^{(n)}\left|\right|}_2^2-\left|\frac{{\left|\right|{\mathbf{w}}^{(n)}\left|\right|}_2^2}{n}-1\right|-2{\left|\right|{\mathbf{y}}^{(n)}\left|\right|}_2-{\sigma }^2{\widehat{\gamma }}^{(n)}\\ \ge {(1-{\epsilon }^2)}^2+(1-{\epsilon }^2){\sigma }^2-\left|\frac{{\left|\right|{\mathbf{w}}^{(n)}\left|\right|}_2^2}{n}-1\right|-2{\left|\right|{\mathbf{y}}^{(n)}\left|\right|}_2-{\sigma }^2{\widehat{\gamma }}^{(n)}.\end{array}$$ (6.8)

Now it follows from (6.6) − (6.8) that

$${\langle {\widehat{\mathit{\rho }}}^{(n)},{\mathit{\rho }}^{(n)}\rangle }^2\ge \frac{(1-{\epsilon }^2)(1+{\sigma }^2-{\epsilon }^2)}{{\left|\right|{\mathit{\rho }}_{\epsilon }^{(2)}\left|\right|}_{{\lambda }^{(n)}}^2}-{\sigma }^2-\left(1+\frac{1}{{\left|\right|{\mathit{\rho }}_{\epsilon }^{(n)}\left|\right|}_{{\lambda }^{(n)}}^2}\right)\left[\left|\frac{{\left|\right|{\mathbf{w}}^{(n)}\left|\right|}_2^2}{n}-1\right|+2{\left|\right|{\mathbf{y}}^{(n)}\left|\right|}_2+{\sigma }^2{\widehat{\gamma }}^{(n)}\right].$$ (6.9)

Since ${\left|\right|{\mathit{\rho }}_{\epsilon }^{(n)}\left|\right|}_{{\lambda }^{(n)}}^2\ge {\left|\right|{\mathit{\rho }}_{\epsilon }^{(n)}\left|\right|}_2^2\ge 1-{\epsilon }^2$ and ${\left|\right|{\mathit{\rho }}_{\epsilon }^{(n)}\left|\right|}_{{\lambda }^{(n)}}^2-{\left|\right|{\mathit{\rho }}_{\epsilon }^{(n)}\left|\right|}_2^2\to 0$ as n → 0, we have $1+\epsilon \ge {\left|\right|{\mathit{\rho }}_{\epsilon }^{(n)}\left|\right|}_{{\lambda }^{(n)}}^2\ge 1-{\epsilon }^2$when n is large enough. Therefore, it follows from (6.9) that when n is large enough,

$${\langle {\widehat{\mathit{\rho }}}^{(n)},{\mathit{\rho }}^{(n)}\rangle }^2\ge \frac{(1-{\epsilon }^2)(1+{\sigma }^2-{\epsilon }^2)}{1+\epsilon }-{\sigma }^2-\left(1+\frac{1}{1-{\epsilon }^2}\right)\left[\left|\frac{{\left|\right|{\mathbf{w}}^{(n)}\left|\right|}_2^2}{n}-1\right|+2{\left|\right|{\mathbf{y}}^{(n)}\left|\right|}_2+{\sigma }^2{\widehat{\gamma }}^{(n)}\right]=(1-\epsilon )(1-{\epsilon }^2)-{\sigma }^2\epsilon -\frac{2-{\epsilon }^2}{1-{\epsilon }^2}\left[\left|\frac{{\left|\right|{\mathbf{w}}^{(n)}\left|\right|}_2^2}{n}-1\right|+2{\left|\right|{\mathbf{y}}^{(n)}\left|\right|}_2+{\sigma }^2{\widehat{\gamma }}^{(n)}\right].$$ (6.10)

Since $\frac{p_n}{n}\to c$, we have $\sqrt{\frac{p_n}{n}}\le \sqrt{c}+\epsilon$ when n is large enough. If $\left|\frac{{\left|\right|{\mathbf{w}}^{(n)}\left|\right|}_2^2}{n}-1\right|\le \epsilon ,{\left|\right|{\mathbf{y}}^{(n)}\left|\right|}_2\le (1+\epsilon )\sigma \sqrt{\frac{p_n}{n}}+\epsilon$ and ${\widehat{\gamma }}^{(n)}\le (1+\epsilon ){(1+\sqrt{c})}^2-1$, then by (6.10) and (6.2), when n is large enough, we have

$$\begin{array}{l}{\langle {\widehat{\mathit{\rho }}}^{(n)},{\mathit{\rho }}^{(n)}\rangle }^2\ge (1-\epsilon )(1-{\epsilon }^2)-{\sigma }^2\epsilon -\frac{2-{\epsilon }^2}{1-{\epsilon }^2}\left[\epsilon +2(1+\epsilon )\sigma \sqrt{\frac{p_n}{n}}+2\epsilon +(1+\epsilon ){\sigma }^2{(1+\sqrt{c})}^2-{\sigma }^2\right]\\ \ge (1-\epsilon )(1-{\epsilon }^2)-{\sigma }^2\epsilon -\frac{2-{\epsilon }^2}{1-{\epsilon }^2}[3\epsilon +2(1+\epsilon )\sigma \epsilon +2(1+\epsilon )\sigma \sqrt{c}+(1+\epsilon ){\sigma }^2{(1+\sqrt{c})}^2-{\sigma }^2]\\ \ge (1-\epsilon )(1-{\epsilon }^2)-{\sigma }^2\epsilon -\frac{\epsilon (2-{\epsilon }^2)}{1-{\epsilon }^2}[3+2(1+\epsilon )\sigma +{\sigma }^2]-\frac{2-{\epsilon }^2}{1-\epsilon }[2\sigma \sqrt{c}+2{\sigma }^2\sqrt{c}+{\sigma }^{2}c]\\ >{({\kappa }_1+(1+\epsilon )2\sigma (\sqrt{c}+\epsilon )+\epsilon )}^2,\end{array}$$ (6.11)

moreover, by the definition (5.54) of μ̂ ⁽ⁿ⁾, (6.8) and (6.3),

$$\begin{array}{l}{\widehat{\mu }}^{(n)}\ge \frac{{({\mathit{\rho }}_{\epsilon }^{(n)})}^T{\widehat{\mathbf{\sum }}}^{(n)}{\mathit{\rho }}_{\epsilon }^{(n)}}{{\left|\right|{\mathit{\rho }}_{\epsilon }^{(n)}\left|\right|}_{{\lambda }^{(n)}}^2}\\ \ge \frac{1}{1+\epsilon }[(1-{\epsilon }^2)(1+{\sigma }^2-{\epsilon }^2)-3\epsilon -2(1+\epsilon )\sigma (\sqrt{c}+\epsilon )-(1+\epsilon ){\sigma }^2{(1+\sqrt{c})}^2+{\sigma }^2]\\ =(1-\epsilon )({\sigma }^2-{\epsilon }^2)+\frac{1}{1+\epsilon }[1-{\epsilon }^2-3\epsilon -2(1+\epsilon )\epsilon \sigma -\epsilon {\sigma }^2-(1+\epsilon )(2\sigma \sqrt{c}+2{\sigma }^2\sqrt{c}+{\sigma }^{2}c)]\\ >(1-\epsilon )({\sigma }^2-{\epsilon }^2)+({\kappa }_2+\epsilon ){\sigma }^2+(1-\epsilon ){\epsilon }^2>(1+{\kappa }_2){\sigma }^2,\end{array}$$ (6.12)

and by (6.6), (6.7), (6.12) and (6.4),

$$\begin{array}{l}{\lambda }^{(n)}{\left|\right|{\widehat{\mathit{\rho }}}^{(n)}\left|\right|}_1^2\le {\left|\right|{\widehat{\mathit{\rho }}}^{(n)}\left|\right|}_{{\lambda }^{(n)}}^2\le \frac{{({\widehat{\mathit{\rho }}}^{(n)})}^T{\widehat{\mathbf{\sum }}}^{(n)}{\widehat{\mathit{\rho }}}^{(n)}}{{({\mathit{\rho }}_{\epsilon }^{(n)})}^T{\widehat{\mathbf{\sum }}}^{(n)}{\mathit{\rho }}_{\epsilon }^{(n)}}{\left|\right|{\mathit{\rho }}_{\epsilon }^{(n)}\left|\right|}_{{\lambda }^{(n)}}^2\\ \le \frac{1}{(1+{\kappa }_2){\sigma }^2}{({\widehat{\mathit{\rho }}}^{(n)})}^T{\widehat{\mathbf{\sum }}}^{(n)}{\widehat{\mathit{\rho }}}^{(n)}\\ \le \frac{1}{{\sigma }^2}\left({\langle {\widehat{\mathit{\rho }}}^{(n)},{\mathit{\rho }}^{(n)}\rangle }^2+{\sigma }^2+\left|\frac{{\left|\right|{\mathbf{w}}^{(n)}\left|\right|}_2^2}{n}-1\right|+2{\left|\right|{\mathbf{y}}^{(n)}\left|\right|}_2+{\sigma }^2{\widehat{\gamma }}^{(n)}\right)\\ \le \frac{1}{{\sigma }^2}[1+{\sigma }^2(1+\epsilon )+3\epsilon +2(1+\epsilon )\sigma \epsilon +(1+\epsilon )(2\sigma \sqrt{c}+2{\sigma }^2\sqrt{c}+{\sigma }^{2}c)]\\ \le \frac{3+{\sigma }^2}{{\sigma }^2}.\end{array}$$ (6.13)

Hence, when n is large enough, by (6.11) − (6.13), we have

$$P\left({\langle {\widehat{\mathit{\rho }}}^{(n)},{\mathit{\rho }}^{(n)}\rangle }^2\le {({\kappa }_1+(1+\epsilon )2\sigma (\sqrt{c}+\epsilon )+\epsilon )}^2\right)\le P\left(\left|\frac{{\left|\right|{\mathbf{w}}^{(n)}\left|\right|}_2^2}{n}-1\right|>\epsilon \right)+P\left({\left|\right|{\mathbf{y}}^{(n)}\left|\right|}_2>(1+\epsilon )\sigma \sqrt{\frac{p_n}{n}}+\epsilon \right)+P\left({\widehat{\gamma }}^{(n)}>(1+\epsilon ){(1+\sqrt{c})}^2-1\right),$$ (6.14)

$$P\left({\widehat{\mu }}^{(n)}\le {\sigma }^2(1+{\kappa }_2)\right)\le P\left(\left|\frac{{\left|\right|{\mathbf{w}}^{(n)}\left|\right|}_2^2}{n}-1\right|>\epsilon \right)+P\left({\left|\right|{\mathbf{y}}^{(n)}\left|\right|}_2>(1+\epsilon )\sigma \sqrt{\frac{p_n}{n}}+\epsilon \right)+P\left({\widehat{\gamma }}^{(n)}>(1+\epsilon ){(1+\sqrt{c})}^2-1\right),$$ (6.15)

and

$$P\left({\left|\right|{\widehat{\mathit{\rho }}}^{(n)}\left|\right|}_1>\frac{\sqrt{3+{\sigma }^2}}{\sigma \sqrt{{\lambda }^{(n)}}}\right)\le P\left(\left|\frac{{\left|\right|{\mathbf{w}}^{(n)}\left|\right|}_2^2}{n}-1\right|>\epsilon \right)+P\left({\left|\right|{\mathbf{y}}^{(\mathbf{n})}\left|\right|}_2>(1+\epsilon )\sigma \sqrt{\frac{p_n}{n}}+\epsilon \right)+P\left({\widehat{\gamma }}^{(n)}>(1+\epsilon ){(1+\sqrt{c})}^2-1\right).$$ (6.16)

${\left|\right|{\mathbf{w}}^{(n)}\left|\right|}_2^2$ has ${\chi }_{(n)}^2$-distribution and ${\left|\right|{\mathbf{y}}^{(n)}\left|\right|}_2^2$ has the distribution ${\sigma }^2{n}^{-2}{\chi }_{(n)}^2{\chi }_{(p_n)}^2$ where ${\chi }_{(n)}^2$ and ${\chi }_{(p_n)}^2$ are independent (see (24) in Johnstone and Lu [7]). It follows from (6.1) that

$$\sum _{n=1}^{\infty }P\left(\left|\frac{{\left|\right|{\mathbf{w}}^{(n)}\left|\right|}_2^2}{n}-1\right|>\epsilon \right)<\infty .$$ (6.17)

Now we consider the term for ||y⁽ⁿ⁾ ||₂. If c > 0, then p_n → ∞ and thus

$$\begin{array}{l}\sum _{n=1}^{\infty }P\left({\left|\right|{\mathbf{y}}^{(n)}\left|\right|}_2>(1+\epsilon )\sigma \sqrt{\frac{p_n}{n}}+\epsilon \right)\le \sum _{n=1}^{\infty }P\left({\left|\right|{\mathbf{y}}^{(n)}\left|\right|}_2>(1+\epsilon )\sigma \sqrt{\frac{p_n}{n}}\right)\\ =\sum _{n=1}^{\infty }P\left(\frac{{\chi }_{(n)}^2}{n}\frac{{\chi }_{(p_n)}^2}{p_n}>{(1+\epsilon )}^2\right)\\ \le \sum _{n=1}^{\infty }\left[P\left(\frac{{\chi }_{(n)}^2}{n}>(1+\epsilon )\right)+P\left(\frac{{\chi }_{(p_n)}^2}{p_n}>(1+\epsilon )\right)\right]<\infty \end{array}$$ (6.18)

If c = 0, let $q_n=\lfloor \frac{{\epsilon }^{2}n}{{(1+\epsilon )}^2{\sigma }^2}\rfloor$, the largest integer less than or equal to $\frac{{\epsilon }^{2}n}{{(1+\epsilon )}^2{\sigma }^2}$.

$$\begin{array}{l}\sum _{n=1}^{\infty }P\left({\left|\right|{\mathbf{y}}^{(n)}\left|\right|}_2>(1+\epsilon )\sigma \sqrt{\frac{p_n}{n}}+\epsilon \right)\\ \le \sum _{n=1}^{\infty }P\left({\left|\right|{\mathbf{y}}^{(n)}\left|\right|}_2>\epsilon \right)=\sum _{n=1}^{\infty }P\left(\frac{{\chi }_{(n)}^2}{n}\frac{{\chi }_{(p_n)}^2}{p}>\frac{{\epsilon }^2}{{\sigma }^2}\right)\\ \le \sum _{n=1}^{\infty }\left[P\left(\frac{{\chi }_{(n)}^2}{n}>(1+\epsilon )\right)+P\left({\chi }_{(p_n)}^2>\frac{{\epsilon }^{2}n}{(1+\epsilon ){\sigma }^2}\right)\right]\\ \le \sum _{n=1}^{\infty }\left[P\left(\frac{{\chi }_{(n)}^2}{n}>(1+\epsilon )\right)+P\left(\frac{{\chi }_{(p_n)}^2+{\chi }_{(q_n-p_n)}^2}{q_n}>(1+\epsilon )\right)\right]<\infty ,\end{array}$$ (6.19)

where ${\chi }_{(q_n-p_n)}^2$ is independent of ${\chi }_{(p_n)}^2$. By (2) in Geman [5], because γ̂⁽ⁿ⁾ + 1 is the largest eigenvalue of Π⁽ⁿ⁾/n, we have

$$\sum _{n=1}^{\infty }P\left({\widehat{\gamma }}^{(n)}>(1+\epsilon ){(1+\sqrt{c})}^2-1\right)<\infty .$$ (6.20)

Hence, by (6.14)–(6.20),

$$\begin{array}{l}\sum _{n=1}^{\infty }P\left({\langle {\widehat{\mathit{\rho }}}^{(n)},{\mathit{\rho }}^{(n)}\rangle }^2\le {({\kappa }_1+(1+\epsilon )2\sigma (\sqrt{c}+\epsilon )+\epsilon )}^2\right)<\infty ,\\ \sum _{n=1}^{\infty }P\left({\widehat{\mu }}^{(n)}\le (1+{\kappa }_2){\sigma }^2\right)<\infty ,\sum _{n=1}^{\infty }P\left({\left|\right|{\widehat{\mathit{\rho }}}^{(n)}\left|\right|}_2>\frac{\sqrt{3+{\sigma }^2}}{\sigma \sqrt{{\lambda }^{n)}}}\right)<\infty .\\ P\left(\left|\langle {\widehat{\mathit{\rho }}}^{(n)},{\mathit{\rho }}^{(n)}\rangle +\langle {\widehat{\mathit{\rho }}}^{(n)},{\mathbf{y}}^{(n)}\rangle \right|\le {\kappa }_1\right)\le P\left(\left|\langle {\widehat{\mathit{\rho }}}^{(n)},{\mathit{\rho }}^{(n)}\rangle \right|\le {\kappa }_1+{\left|\right|{\mathbf{y}}^{(n)}\left|\right|}_2\right)\\ \le P\left(\left|\langle {\widehat{\mathit{\rho }}}^{(n)},{\mathit{\rho }}^{(n)}\rangle \right|\le {\kappa }_1+1+\epsilon )2\sigma \sqrt{\frac{p_n}{n}}+\epsilon \right)+P\left({\left|\right|{\mathbf{y}}^{(n)}\left|\right|}_2>(1+\epsilon )2\sigma \sqrt{\frac{p_n}{n}}+\epsilon \right)\\ \le P\left(\left|\langle {\widehat{\mathit{\rho }}}^{(n)},{\mathit{\rho }}^{(n)}\rangle \right|\le {\kappa }_1+1+\epsilon )2\sigma (\sqrt{c}+\epsilon )+\epsilon \right)+P\left({\left|\right|{\mathbf{y}}^{(n)}\left|\right|}_2>(1+\epsilon )2\sigma \sqrt{\frac{p_n}{n}}+\epsilon \right)<\infty .\end{array}$$

Proof of Lemma 10

First note that ρ̂⁽ⁿ⁾/||ρ̂⁽ⁿ⁾||_λ⁽ⁿ⁾ is the solution to the following optimization problem,

$$\underset{\mathbf{u}\in {\mathbb{R}}^P}{max}{\left({\widehat{\mathbf{\sum }}}^{(n)}{\widehat{\mathit{\rho }}}^{(n)}\right)}^T\mathbf{u},\text{subject}\text{to}{\left|\right|\mathbf{u}\left|\right|}_{{\lambda }^{(n)}}\le 1.$$

We will verify the conditions in Corollary 2.2. Then this lemma follows from Corollary 2.2. Let â ⁽ⁿ⁾ = Σ̂ ⁽ⁿ⁾ρ̂⁽ⁿ⁾. Without loss of generality, in this proof, we assume that ${\widehat{\rho }}_1^{(n)}\ge {\widehat{\rho }}_2^{(n)}\ge \cdots \ge {\widehat{\rho }}_m^{(n)}>0={\widehat{\rho }}_{m+1}^{(n)}=\cdots ={\widehat{\rho }}_{p_n}^{(n)}$. Let I = {1, 2, · · ·, m}. Then by Theorem 2.3, we have ${\widehat{\mathit{a}}}_I^{(n)}={\widehat{\mathbf{\sum }}}_I^{(n)}{\widehat{\mathit{\rho }}}_I^{(n)}={\widehat{\mu }}^{(n)}{\mathbf{A}}_I^{[{\lambda }^{(n)}]}{\widehat{\mathit{\rho }}}_I^{(n)}$, from which we can obtain that

$${\widehat{\rho }}_i^{(n)}=\{\begin{array}{lll}\hfill \left[{\widehat{a}}_i^{(n)}-\frac{{\lambda }^{(n)}{S}_m}{(1-\lambda )+m{\lambda }^{(n)}}\right]/{\widehat{\mu }}^{(n)}(1-{\lambda }^{(n)})& \text{if}\hfill & i\in I\hfill \\ \hfill 0& \text{if}\hfill & i\in I^c\hfill \end{array},$$

where ${\widehat{\mathit{a}}}^{(n)}={({\widehat{a}}_1^{(n)},\cdots ,{\widehat{a}}_{p_n}^{(n)})}^T$ and $S_m={\widehat{a}}_1^{(n)}+\cdots +{\widehat{a}}_m^{(n)}$. Under the conditions of this lemma, σ²/μ̂ ⁽ⁿ⁾(1 − λ ⁽ⁿ⁾) < 1, that is, the conditions of Corollary 2.2 are satisfied.

Proof of Lemma 11

By (5.52),

$$\begin{array}{l}{\mathit{\xi }}^{(n)}=\left({\widehat{\mathbf{\sum }}}^{(n)}-{\sigma }^2\mathbf{I}\right){\widehat{\mathit{\rho }}}^{(n)}-\left(\langle {\widehat{\mathit{\rho }}}^{(n)},{\mathit{\rho }}^{(n)}\rangle +\langle {\widehat{\mathit{\rho }}}^{(n)},{\mathbf{y}}^{(n)}\rangle \right){\mathit{\rho }}^{(n)}\\ =\left(\frac{{\left|\right|{\mathbf{w}}^{(n)}\left|\right|}_2^2}{n}-1\right)\langle {\widehat{\mathit{\rho }}}^{(n)},{\mathit{\rho }}^{(n)}\rangle {\mathit{\rho }}^{(n)}+\langle {\widehat{\mathit{\rho }}}^{(n)},{\mathit{\rho }}^{(n)}\rangle {\mathbf{y}}^{(n)}+{\sigma }^2\left(\frac{{\mathbf{\Pi }}^{(n)}}{n}-\mathbf{I}\right){\widehat{\mathit{\rho }}}^{(n)}.\end{array}$$

Hence,

$$\underset{1\le i\le p_n}{max}\mid {\xi }_i^{(n)}\mid \le \left|\frac{{\left|\right|{\mathbf{w}}^{(n)}\left|\right|}_2^2}{n}-1\right|+\underset{1\le i\le p_n}{max}\mid y_i\mid +\underset{1\le i\le p_n}{max}\left|{\left[{\sigma }^2\left(\frac{{\mathbf{\Pi }}^{(n)}}{n}-\mathbf{I}\right){\widehat{\mathit{\rho }}}^{(n)}\right]}_i\right|,$$

where y_i and ${\left[{\sigma }^2\left(\frac{{\mathbf{\Pi }}^{(n)}}{n}-\mathbf{I}\right){\widehat{\mathit{\rho }}}^{(n)}\right]}_i$ are the i-th coordinates of y⁽ⁿ⁾ and ${\sigma }^2\left(\frac{{\mathbf{\Pi }}^{(n)}}{n}-\mathbf{I}\right){\widehat{\mathit{\rho }}}^{(n)}$, respectively. First, we calculate

$$\begin{array}{l}P\left(\underset{1\le i\le p_n}{max}\left|{\left[{\sigma }^2\left(\frac{{\mathbf{\Pi }}^{(n)}}{n}-\mathbf{I}\right){\widehat{\mathit{\rho }}}^{(n)}\right]}_i\right|>\frac{n^{-\beta }}{3}\right)\\ =P\left(\underset{1\le i\le p_n}{max}\left|\frac{{\sigma }^2}{n}\sum _{j\ne i:1}^{p_n}\left(\sum _{k=1}^n{z}_{ki}^{(n)}{z}_{kj}^{(n)}\right){\widehat{\rho }}_j^{(n)}+{\sigma }^2\left(\sum _{k=1}^n\frac{{(z_{ki}^{(n)})}^2}{n}-1\right){\widehat{\rho }}_j^{(n)}\right|>\frac{n^{-\beta }}{3}\right)\\ \le P\left(\underset{1\le i\le p_n}{max}\left|\frac{{\sigma }^2}{n}\sum _{j\ne i:1}^{p_n}\left(\sum _{k=1}^n{z}_{ki}^{(n)}{z}_{kj}^{(n)}\right){\widehat{\rho }}_j^{(n)}\right|>\frac{n^{-\beta }}{6}\right)\\ +P\left(\underset{1\le i\le p_n}{max}\left|{\sigma }^2\left(\sum _{k=1}^n\frac{{(z_{ki}^{(n)})}^2}{n}-1\right){\widehat{\rho }}_j^{(n)}\right|>\frac{n^{-\beta }}{6}\right)\\ \le P\left(\underset{1\le i\le p_n}{max}\underset{1\le j\ne i\le p_n}{max}\left|\frac{{\sigma }^2}{n}\left(\sum _{k=1}^n{z}_{ki}^{(n)}{z}_{kj}^{(n)}\right)\right|{\left|\right|{\widehat{\mathit{\rho }}}^{(n)}\left|\right|}_1>\frac{n^{-\beta }}{6}\right)\\ +\sum _{i=1}^{p_n}P\left(\left|{\sigma }^2\left(\sum _{k=1}^n\frac{{(z_{ki}^{(n)})}^2}{n}-1\right)\right|>\frac{n^{-\beta }}{6}\right)\\ \le P(\underset{1\le i\le p_n}{max}\underset{1\le j\ne i\le p_n}{max}\left|\frac{{\sigma }^2}{n}\left(\sum _{k=1}^n{z}_{ki}^{(n)}{z}_{kj}^{(n)}\right)\right|{\left|\right|{\widehat{\mathit{\rho }}}^{(n)}\left|\right|}_1>\frac{n^{-\beta }}{6},{\left|\right|{\widehat{\mathit{\rho }}}^{(n)}\left|\right|}_1\\ \le \frac{\sqrt{3+{\sigma }^2}}{\sigma \sqrt{{\lambda }^{(n)}}})+P\left({\left|\right|{\widehat{\mathit{\rho }}}^{(n)}\left|\right|}_1>\frac{\sqrt{3+{\sigma }^2}}{\sigma \sqrt{{\lambda }^{(n)}}}\right)\\ +\sum _{i=1}^{p_n}P\left(\left|{\sigma }^2\left(\sum _{k=1}^n\frac{{(z_{ki}^{(n)})}^2}{n}-1\right)\right|>\frac{n^{-\beta }}{6}\right)\\ \le \sum _{i=1}^{p_n}\sum _{j\ne i}P\left(\left|\frac{{\sum }_{k=1}^n{z}_{ki}^{(n)}{z}_{kj}^{(n)}}{n}\right|>\frac{n^{-\beta }\sqrt{{\lambda }^{(n)}}}{6\sigma \sqrt{3+{\sigma }^2}}\right)\\ +P\left({\left|\right|{\widehat{\mathit{\rho }}}^n\left|\right|}_1>\frac{\sqrt{3+{\sigma }^2}}{\sigma \sqrt{{\lambda }^{(n)}}}\right)+p_{n}P\left(\left|\frac{{\chi }_{(n)}^2}{n}-1\right|>\frac{n^{-\beta }}{6{\sigma }^2}\right)\end{array}$$ (6.21)

Since

$$\frac{2{\sum }_{k=1}^n{z}_{ki}^{(n)}{z}_{kj}^{(n)}}{n}=\left[\frac{{\sum }_{k=1}^n{\left((z_{ki}^{(n)}+z_{kj}^{(n)})/\sqrt{2}\right)}^2}{n}-1\right]-\left[\frac{{\sum }_{k=1}^n{\left((z_{ki}^{(n)}-z_{kj}^{(n)})/\sqrt{2}\right)}^2}{n}-1\right],$$

where ${\sum }_{k=1}^n{\left((z_{ki}^{(n)}+z_{kj}^{(n)})/\sqrt{2}\right)}^2$ and ${\sum }_{k=1}^n{\left((z_{ki}^{(n)}-z_{kj}^{(n)})/\sqrt{2}\right)}^2$are two independent ${\chi }_{(n)}^2$ variables, the probability in (6.21) is less than or equal to

$$2p_n^{2}P\left(\left|\frac{{\chi }_{(n)}^2}{n}-1\right|\frac{n^{-\beta }\sqrt{{\lambda }^{(n)}}}{6\sigma \sqrt{3+{\sigma }^2}}\right)+P\left({\left|\right|{\widehat{\mathit{\rho }}}^{(n)}\left|\right|}_1>\frac{\sqrt{3+{\sigma }^2}}{\sigma \sqrt{{\lambda }^{(n)}}}\right)+p_{n}P\left(\left|\frac{{\chi }_{(n)}^2}{n}-1\right|>\frac{n^{-\beta }}{6{\sigma }^2}\right).$$

Since $n{(n^{-\beta }\sqrt{{\lambda }^{(n)}})}^2=O(n^{1-2\beta -\alpha })\to \infty$ by (5.49), it follows from (6.1) and (5.58) that

$$\sum _{n=1}^{\infty }P\left(\underset{1\le i\le p_n}{max}\left|{\left[{\sigma }^2\left(\frac{{\mathbf{\Pi }}^{(n)}}{n}-\mathbf{I}\right){\widehat{\mathit{\rho }}}^{(n)}\right]}_i\right|>\frac{n^{-\beta }}{3}\right)<\infty .$$ (6.22)

Second, because

$$\begin{array}{l}{y}_i=\frac{\sigma }{n}\sum _{k=1}^n{z}_{ki}^{(n)}{w}_k^{(n)}\\ =\frac{\sigma }{2}\left[\frac{{\sum }_{k=1}^n{\left((z_{ki}^{(n)}+w_k^{(n)})/\sqrt{2}\right)}^2}{n}-1\right]-\frac{\sigma }{2}\left[\frac{{\sum }_{k=1}^n{\left((z_{ki}^{(n)}-w_k^{(n)})/\sqrt{2}\right)}^2}{n}-1\right],\end{array}$$

where ${\sum }_{k=1}^n{\left((z_{ki}^{(n)}+z_{kj}^{(n)})/\sqrt{2}\right)}^2$ and ${\sum }_{k=1}^n{\left((z_{ki}^{(n)}-z_{kj}^{(n)})/\sqrt{2}\right)}^2$ are two independent ${\chi }_{(n)}^2$ variables, by the same argument, we have

$$\sum _{n=1}^{\infty }P\left(\underset{1\le i\le p_n}{max}\mid y_i\mid >\frac{n^{-\beta }}{3}\right)<\infty \text{and}\sum _{n=1}^{\infty }P\left(\left|\frac{{\left|\right|{\mathbf{w}}^{(n)}\left|\right|}_2^2}{n}-1\right|>\frac{n^{-\beta }}{3}\right)<\infty .$$ (6.23)

Then the lemma follows.

Proof of Lemma 12

Recall the partial sums

$$S_i^{(n)}=\sum _{j=1}^i{\rho }_j^{(n)},{\widehat{S}}_i^{(n)}=\sum _{j=1}^i\mid {\widehat{\mathit{a}}}^{(n)}{\mid }_{(j)},1\le i\le p_n.$$

By Theorem 2.2 and Lemma 1, we only need to show that

$$\mid {\widehat{\mathit{a}}}^{(n)}{\mid }_{(m^{(n)})}\le \frac{{\stackrel{\sim }{\lambda }}^{(n)}{\widehat{S}}_{m^{(n)}}^{(n)}}{(1-{\stackrel{\sim }{\lambda }}^{(n)})+m^{(n)}{\stackrel{\sim }{\lambda }}^{(n)}}.$$ (6.24)

Let $k=\frac{m^{(n)}}{4}$. Since m⁽ⁿ⁾ → ∞ as n → ∞, when n is large, we have k > m₀, where m₀ is defined in (5.53). Hence, the inequality (5.53) is true for k. From the definition (5.64) of m⁽ⁿ⁾, we can obtain that

$$4k{\stackrel{\sim }{\lambda }}^{(n)}\ge 1\text{and}k{\stackrel{\sim }{\lambda }}^{(n)}\frac{1-\tau }{\tau }\ge 1.$$ (6.25)

Then

$$\begin{array}{l}\frac{{\stackrel{\sim }{\lambda }}^{(n)}{S}_{m^{(n)}}^{(n)}}{(1-{\stackrel{\sim }{\lambda }}^{(n)})+m^{(n)}{\stackrel{\sim }{\lambda }}^{(n)}}-{\rho }^{m^{(n)}}=\frac{{\stackrel{\sim }{\lambda }}^{(n)}{S}_{4k}^{(n)}}{(1-{\stackrel{\sim }{\lambda }}^{(n)})+4k{\stackrel{\sim }{\lambda }}^{(n)}}-{\rho }_{4k}^{(n)}\\ =\frac{{\stackrel{\sim }{\lambda }}^{(n)}(S_{4k}^{(n)}-4k{\rho }_{4k}^{(n)})-(1-{\stackrel{\sim }{\lambda }}^{(n)}){\rho }_{4k}^{(n)}}{(1-{\stackrel{\sim }{\lambda }}^{(n)})+4k{\stackrel{\sim }{\lambda }}^{(n)}}\ge \frac{{\stackrel{\sim }{\lambda }}^{(n)}(S_{2k}^{(n)}-2k{\rho }_{4k}^{(n)})-(1-{\stackrel{\sim }{\lambda }}^{(n)}){\rho }_{4k}^{(n)}}{(1-{\stackrel{\sim }{\lambda }}^{(n)})+4k{\stackrel{\sim }{\lambda }}^{(n)}}\\ \ge \frac{{\stackrel{\sim }{\lambda }}^{(n)}\left(\frac{1}{\tau }(S_{4k}^{(n)}-S_{2k}^{(n)})-2k{\rho }_{4k}^{(n)}\right)-(1-{\stackrel{\sim }{\lambda }}^{(n)}){\rho }_{4k}^{(n)}}{(1-{\stackrel{\sim }{\lambda }}^{(n)})+4k{\stackrel{\sim }{\lambda }}^{(n)}}\\ \ge \frac{{\stackrel{\sim }{\lambda }}^{(n)}\left(\frac{1}{\tau }2k{\rho }_{4k}^{(n)}-2k{\rho }_{4k}^{(n)}\right)-(1-{\stackrel{\sim }{\lambda }}^{(n)}){\rho }_{4k}^{(n)}}{(1-{\stackrel{\sim }{\lambda }}^{(n)})+4k{\stackrel{\sim }{\lambda }}^{(n)}}=\frac{2k{\stackrel{\sim }{\lambda }}^{(n)}\frac{1-\tau }{\tau }-(1-{\stackrel{\sim }{\lambda }}^{(n)})}{(1-{\stackrel{\sim }{\lambda }}^{(n)})+4k{\stackrel{\sim }{\lambda }}^{(n)}}{\rho }_{4k}^{(n)}\\ \ge \frac{2k{\stackrel{\sim }{\lambda }}^{(n)}\frac{1-\tau }{\tau }-1}{1+4k{\stackrel{\sim }{\lambda }}^{(n)}}{\rho }_{4k}^{(n)}\ge \frac{2k{\stackrel{\sim }{\lambda }}^{(n)}\frac{1-\tau }{\tau }-k{\stackrel{\sim }{\lambda }}^{(n)}\frac{1-\tau }{\tau }}{4k{\stackrel{\sim }{\lambda }}^{(n)}+4k{\stackrel{\sim }{\lambda }}^{(n)}}{\rho }_{4k}^{(n)}=\frac{1-\tau }{8\tau }{\rho }_{m^{(n)}}^{(n)},\end{array}$$ (6.26)

where the inequality in the third line is due to (5.53) and the last inequality is due to (6.25). It follows from (5.63) that

$$S_{m^{(n)}}^{(n)}-m^{(n)}\frac{n^{-\beta }}{{\kappa }_1}\le {\widehat{S}}_{m^{(n)}}^{(n)}\le S_{m^{(n)}}^{(n)}+m^{(n)}\frac{n^{-\beta }}{{\kappa }_1}.$$ (6.27)

We will consider the following two cases separately. If $\frac{1-\tau }{8\tau }{\rho }_{m^{(n)}}^{(n)}\ge 2\frac{n^{-\beta }}{{\kappa }_1}$, by (6.26) and (6.27),

$$\begin{array}{l}\mid {\widehat{\mathit{a}}}^{(n)}{\mid }_{(m^{(n)})}\le {\rho }_{m^{(n)}}^{(n)}+\frac{n^{-\beta }}{{\kappa }_1}\le \frac{{\stackrel{\sim }{\lambda }}^{(n)}{S}_{m^{(n)}}^{(n)}}{(1-{\stackrel{\sim }{\lambda }}^{(n)})+m^{(n)}{\stackrel{\sim }{\lambda }}^{(n)}}-\frac{1-\tau }{8\tau }{\rho }_{m^{(n)}}^{(n)}+\frac{n^{-\beta }}{{\kappa }_1}\\ \le \frac{{\stackrel{\sim }{\lambda }}^{(n)}{\widehat{S}}_{m^{(n)}}^{(n)}+{\stackrel{\sim }{\lambda }}^{(n)}{m}^{(n)}\frac{n^{-\beta }}{{\kappa }_1}}{(1-{\stackrel{\sim }{\lambda }}^{(n)})+m^{(n)}{\stackrel{\sim }{\lambda }}^{(n)}}-\frac{1-\tau }{8\tau }{\rho }_{m^{(n)}}^{(n)}+\frac{n^{-\beta }}{{\kappa }_1}\\ \le \frac{{\stackrel{\sim }{\lambda }}^{(n)}{\widehat{S}}_{m^{(n)}}^{(n)}}{(1-{\stackrel{\sim }{\lambda }}^{(n)})+m^{(n)}{\stackrel{\sim }{\lambda }}^{(n)}}-\frac{1-\tau }{8\tau }{\rho }_{m^{(n)}}^{(n)}+2\frac{n^{-\beta }}{{\kappa }_1}\le \frac{{\stackrel{\sim }{\lambda }}^{(n)}{\widehat{S}}_{m^{(n)}}^{(n)}}{(1-{\stackrel{\sim }{\lambda }}^{(n)})+m^{(n)}{\stackrel{\sim }{\lambda }}^{(n)}}.\end{array}$$

If $\frac{1-\tau }{8\tau }{\rho }_{m^{(n)}}^{(n)}<2\frac{n^{-\beta }}{{\kappa }_1}$, let us compute

$$S_{m^{(n)}}^{(n)}=\sum _{j=1}^{m^{(n)}}{\rho }_j^{(n)}\ge \sqrt{\sum _{j=1}^{m^{(n)}}{({\rho }_j^{(n)})}^2}=\sqrt{1-\sum _{\nu =m^{(n)}+1}^{\infty }{({\rho }_{\nu }^{(n)})}^2}\ge \sqrt{1-\sum _{\nu =m^{(n)}+1}^{\infty }{C}^2{\nu }^{2/q}}\to 1,$$ (6.28)

where the last inequality follows from the condition (5.51). Hence,

$$\begin{array}{l}\frac{{\stackrel{\sim }{\lambda }}^{(n)}{\widehat{S}}_{m^{(n)}}^{(n)}}{(1-{\stackrel{\sim }{\lambda }}^{(n)})+m^{(n)}{\stackrel{\sim }{\lambda }}^{(n)}}-\mid {\widehat{\mathit{a}}}^{(n)}{\mid }_{(m^{(n)})}\ge \frac{{\stackrel{\sim }{\lambda }}^{(n)}{S}_{m^{(n)}}^{(n)}-{\stackrel{\sim }{\lambda }}^{(n)}{m}^{(n)}\frac{n^{-\beta }}{{\kappa }_1}}{(1-{\stackrel{\sim }{\lambda }}^{(n)})+m^{(n)}{\stackrel{\sim }{\lambda }}^{(n)}}-\mid {\widehat{\mathit{a}}}^{(n)}{\mid }_{(m^{(n)})}\\ \ge \frac{{\stackrel{\sim }{\lambda }}^{(n)}{S}_{m^{(n)}}^{(n)}}{1+m^{(n)}{\stackrel{\sim }{\lambda }}^{(n)}}-\frac{n^{-\beta }}{{\kappa }_1}-\mid {\widehat{\mathit{a}}}^{(n)}{\mid }_{(m^{(n)})}\ge \frac{{\stackrel{\sim }{\lambda }}^{(n)}{S}_{m^{(n)}}^{(n)}}{1+m^{(n)}{\stackrel{\sim }{\lambda }}^{(n)}}-{\rho }_{m^{(n)}}^{(n)}-2\frac{n^{-\beta }}{{\kappa }_1}\\ \ge \frac{{\stackrel{\sim }{\lambda }}^{(n)}{S}_{m^{(n)}}^{(n)}}{2m^{(n)}{\stackrel{\sim }{\lambda }}^{(n)}}-\frac{8\tau }{1-\tau }2\frac{n^{-\beta }}{{\kappa }_1}-2\frac{n^{-\beta }}{{\kappa }_1}=\frac{S_{m^{(n)}}^{(n)}}{m^{(n)}}-2\frac{1+7\tau }{1-\tau }\frac{n^{-\beta }}{{\kappa }_1},\end{array}$$

where the inequality in the last line is due to (6.25) and $\frac{1-\tau }{8\tau }{\rho }_{m^{(n)}}^{(n)}<2\frac{n^{-\beta }}{{\kappa }_1}$. By (6.28) and the definition (5.64) of m⁽ⁿ⁾, $\frac{{\widehat{S}}_{m^{(n)}}^{(n)}}{m^{(n)}}~\frac{1}{m^{(n)}}O(1)~{\stackrel{\sim }{\lambda }}^{(n)}~{\lambda }^{(n)}~O(n^{-\alpha })$ which is lager than $2\frac{1+7\tau }{1-\tau }\frac{n^{-\beta }}{{\kappa }_1}$ when n is large by (5.49). Therefore, we have proved (6.24).