Abstract
In Nature, directional surfaces on insect cuticle, animal fur, bird feathers, and plant leaves are comprised of dual micro-nanoscale features that tune roughness and surface energy. This feature article summarizes experimental and theoretical approaches for the design, synthesis and characterization of new bioinspired surfaces demonstrating unidirectional surface properties. The experimental approaches focus on bottom-up and top-down synthesis methods of unidirectional micro- and nanoscale films to explore and characterize their anomalous features. The theoretical component of the review focuses on computational tools to predict the physicochemical properties of unidirectional surfaces.
Keywords: Biomimetics, Polymeric Material, Superhydrophobic/philic Surfaces, Surface Modification, Nanostructures
1. Introduction
In the plant and animal kingdoms, directional textured surfaces with microscale and nanoscale features provide key functions for survival.[1] Directional surfaces enable butterflies to cast water from their wings, water striders to walk on water, and plants to trap pollen and insects. Directional textured surfaces on gecko, spider and lizard feet allow the animals to climb smooth and rough vertical walls, which requires that they controllably adhere to and detach from smooth and rough surfaces. The intestine and the lung are lined with microvilli that direct flow. All these natural surfaces derive their directional properties from asymmetric micro- or nano-structures such as ratchets or hairy forests, the asymmetric placement of such structures, or an emergent property due to a surface being coated with many copies of such structures. At the macroscopic scale, directionality manifests itself as anisotropic or unidirectional materials or processes. At the molecular scale, thermal Brownian motion and molecular polarity fuel spatial or dynamical symmetry breaking. A system exhibiting such directionality is often called a molecular ratchet.[2]
Inspired by natural directional surfaces, engineers have developed a myriad of synthetic surfaces with precisely tuned physicochemical properties to transport water droplets and soft materials, control liquid spreading, provide directional adhesion and exhibit directional friction. Due to the wide range of applications, there has been an increasing interest in studying the anisotropy of biological and synthetic materials. Reviews already exist for the large body of research on natural[3, 4] and engineered[5] superhydrophobic surfaces including the water repellent hairy exteriors of plant and animal species. Another review highlighted methods for synthesizing materials for dry adhesion that mimic the lizard or insect footpads.[5] This review focuses on anisotropic wet and dry adhesion properties of surfaces from experimental and theoretical perspectives. We first define anisotropy in section 2 and then characterize the myriad of directional biological surfaces in section 3. In section 4, we review fabrication methods for synthetic directional nanofilms. Finally, in section 5, we outline theoretical approaches for modeling wet and dry adhesion on materials demonstrating unidirectional surface properties.
2. Definition of Anisotropy in Materials Science
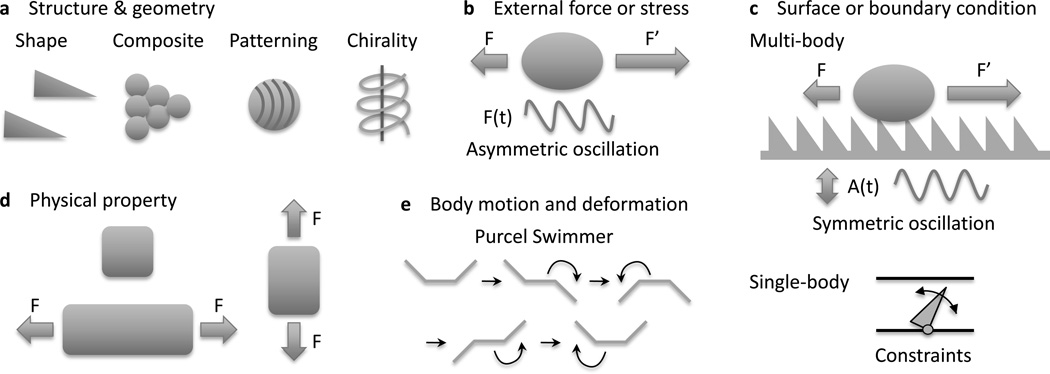
The physicochemical properties of materials often depend on direction. Most materials have anisotropic physical properties because of their asymmetric micro- and nanoscale features. To determine the anisotropy of a system, a host of factors must be considered: the asymmetry of the materials structure and geometry; the asymmetry of the external field or stress; the asymmetry of the surface or boundary conditions; the asymmetry of the physical property relating stress to strain; and the asymmetry of the resulting body motion or deformation. These are schematically shown in Figure 1. Here the stress and strain could be external (e.g. mechanical, optical, electrical, magnetic) or internal (e.g. self-oscillatory chemical reactions[6]). Examples include the walking of an asymmetric gel strip fueled by an oscillating chemical reaction (i.e. Belouzov[7]–Zhabotinsky[8]), and a polymer-magnetic composite swimmer actuated by a magnetic field.[9] Figure 1a illustrates types of material asymmetries, which could be due to structural or compositional variations. A recent review on nanomaterials assembly classified these variations in detail.[10] An example of such assembly are the anisotropic superstructures formed by uniformly amphiphile coated spherical nanoparticles to balance the energy gain between particle coalescence and the entropy of the distorting grafted polymers.[11] A schematic of field asymmetry is shown in Figure 1b. A particular example of field asymmetry is the anisotropic lateral vibration on a hydrophobic surface that induces unidirectional drop motion.[12] The influence of boundary conditions and geometry is illustrated in Figure 1c. The material itself may be isotropic, but its behavior may be anisotropic due to, for example, surface texture. Also, anisotropy may arise from multibody and single body interactions. In many cases, the asymmetric nature of a material is the result of a many-body emergent property. For example, a forest of carbon nanotubes[13] or a textured polymer nanofilm[14] will have different mechanical responses than the individual nanotubes or fibers. The most commonly known anisotropy of materials systems is sketched in Figure 1d: an anisotropic stretch or contraction can be created if the modulus has internal asymmetry. Lastly, strain asymmetry is illustrated in Figure 1e. An example is Purcell’s swimmer,[15] made of three slender rods, that performs an asymmetric stroke to translate at low speeds in viscous fluids.
Figure 1.
Sources of asymmetry in materials science. The asymmetry of (a) materials structure or geometry, (b) the external field or stress, (c) surface or boundary condition, (d) the physical property relating stress to strain, and (e) strain or deformation.
3. Examples of Directional Surfaces in Nature
Directional surfaces composed of asymmetric structures are widely used in Nature for wet and dry adhesion (Figure 2 and Table 1).[16] Some insects employ a special form of wet adhesion by secreting adhesive fluids through arrays of setae to adhere to smooth or rough substrates. The beetle uses such a technique to respond to a disturbance by activating a tarsal adhesion mechanism[17] which collectively bears approximately 60,000 directionally adhesive bristles (Figure 2a). While defending itself from a predator, the beetle presses a surface with all its bristles to withstand pulling forces of up to 60 times its body mass for up to 2 min.[17]
Figure 2.
Directional textured surfaces in nature. (a) Beetle (Hemisphaerota cyanea) tarsus consists of pads arranged in rows (left) and stuck together in clusters (middle, right). Scale bars, left to right, 200 µm, 40 µm, 10 µm. Source: Eisner and Aneshansley,[17] copyright (2000) National Academy of Sciences, U.S.A. (b) Tokay gecko (Gekko gecko) foot setae (left) and the finest terminal branches of a seta, called spatula (right). Scale bars 50 µm (left) and 1 µm (right). Source: Autumn et al.,[66] reprinted with permission from Macmillan Publishers: Nature, copyright 2000. (c) Wet-rebuilt silk of the cribellate spider (Uloborus walckenaerius), showing overall structure (top) with ESEM zooms of a spindle knot (bottom left) and joint (bottom right). Scale bars 50 µm (top) and 2 µm (bottom). Source: Zheng et al.,[23] reprinted with permission from Macmillan Publishers: Nature, copyright 2010. (d) The non-wetting leg of the water strider (Gerris remigis). Individual hairs are deflected by capillary forces as the drop advances against the grain (top). SEM images of the oriented microsetae (bottom left) and the nanoscale grooved structures on a seta (bottom right). Scale bars 100 µm (top), 40 µm (bottom left), 400 nm (bottom right). Top image reprinted from Prakash et al.,[24] copyright (2011), with permission from Elsevier. Bottom image from Gao and Jiang,[25] reprinted with permission from Macmillan Publishers: Nature, copyright 2004. (e) Overlapping microscales (top) on the wings of the butterfly (Morpho aega) are comprised of aligned nanostripes. Scale bars 100 mm (top) and 400 nm (bottom). Source: Zheng et al.,[28] reproduced by permission of The Royal Society of Chemistry. (f) Peristome surface of the Nepenthes pitcher plant has first and second order radial ridges. Scale bars 100 µm. Source: Bohn and Federle,[29] copyright (2004) National Academy of Sciences, U.S.A. (g) Micro-barbs on the surface of the grass species Hordeum murinum. Scale bar 50 µm. Source: Kulic et al.,[30] reprinted with permission of The Royal Society, copyright 2009.
Table 1.
Characterization of directional textured surfaces.
| Category | Figure examples |
|---|---|
| Structure | |
| hair/rod/groove | 2a,b,d,g; 3a–k; 4a–c,e–g |
| scales | 2e |
| surface contour | 2c,f; 3l; 4h |
| multi-scale | 2a,b,d,e; 3k |
| Directional property | |
| dry adhesion | 2b; 3i–k |
| lubricated adhesion | 2a; 4d |
| wet adhesion | 2c–f; 3a–h; 4a–c,e–f |
| mechanical force | 2g; 4g |
| flow streamlines | 3l |
| Usage | |
| water repellency | 2d,e; 3a–c,e,f; 4b,c |
| water spreading | 3d,g,h; 4a |
| transport | 2c–f; 3a–c,e,f,l; 4b–e,g,h |
| adhesion | 2a,b,g |
| Fabrication (engineered surfaces) | |
| template-free | 3e,f; 4b,c,e–g |
| template-assisted | 3j–l |
| lithographically patterned | 3a–d,g–i; 4a,h |
The hairy appendages of lizards, geckos and spiders have extremely fine endings[18] and finer adhesion structures to allow these creatures to climb both smooth and rough vertical surfaces via dry adhesion.[19, 20] The flexible hairs on such appendages bend and allow a much greater contact area with uneven surfaces compared to smooth appendages, a mechanism called “contact splitting”.[19, 20] The density of hairs on such appendages scales with body mass.[21] Insects, for example, have lower hair densities compared to lizards. Autumn et al.[18] reported the first direct measurements of the force on a single seta of a gecko toepad by using a two-dimensional micro-electro-mechanical system. The many fine terminal endings of a single seta as well as the particular seta orientation produce attachment forces 600 times that compared to a smooth piece of the underlying material. In addition, the seta’s directional structure (Figure 2b) allows the gecko toepad to be peeled from a substrate above a critical angle at a relatively low force compared with that of attachment. In many cases, a nanoscale thin film of adhesive fluid acts as a lubricating layer between the insect adhesive organs and the substrate.[22]
The ability of spider silk to collect water is an example of wet adhesion powered by a ratcheting mechanism (Figure 2c).[23] After wetting, a unique structure forms along a strand of spider silk. Periodic spindle-knots made of random nanofibrils are separated by joints made of aligned nanofibrils.[23] These directional structures create gradients in surface energy and Laplace pressure between the spindle-knots and joints, driving continuous condensation and directional water drop collection about the spindle-knots.[23]
The directional surfaces on the wings and legs of insects play dynamic roles for thrust generation and drag reduction.[24] The remarkable non-wetting property of water strider legs is derived from their hierarchical hairy surfaces comprised of numerous oriented needle-shaped microsetae with elaborate nanogrooves (Figure 2d).[25, 26] A coherent view of the form and function of the integument of water-walking insects and spiders was put forth in a recent review,[27] which demonstrated the influence of surface roughness on water repellency. Water repellency is a critical feature of water-walkers for avoiding entrapment at the interface, surviving the impact of raindrops and submerged breathing. Butterflies have superhydrophobic wings composed of overlapping strips with directed flexible nanotips (Figure 2e).[28] A dew or rain droplet may slip off the surface of the wing in the direction away from the body, but is prevented from moving toward the body by the nanotips.
Directional surfaces are also common in the plant world. Pitcher plants have directional leaves that capture, retain and digest insects. Insect attachment is prevented on the plant’s peristome by its anisotropic surface topography and by water lubrication (Figure 2f). [29] In another example, the anisotropic textured surfaces of grass awn naturally serve as motion rectifiers which convert non-equilibrium stresses from environmental sources such as variations in humidity into useful work (Figure 2g).[30] The ratchet efficiency is proportional to awn length and provides a selective environmental advantage to many plant species. Another example is the multi-length scale roughness that forms an anisotropic sliding surface on rice leaves.[31] Such natural surfaces have motivated the design and synthesis of a host of artificial directional surfaces.
4. Engineered Directional Surfaces: Form and Function
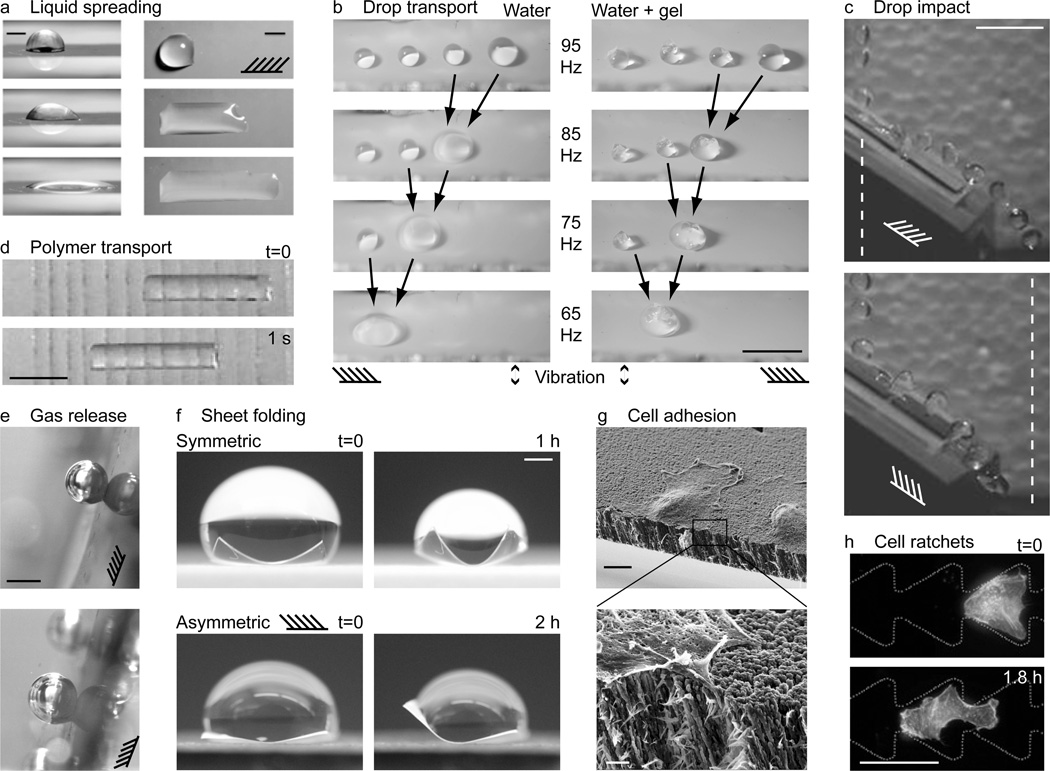
Inspired by the structure and utility of biological surfaces, various directional surfaces have been engineered with micro- and nanoscale features. Various microscale surfaces with lithographically patterned asymmetric line patterns, microposts and textured walls have been engineered for transporting drops (Figure 3a–c and Table 1). The force of retention on a drop is less in the drop’s direction of motion than in other directions. The source of this directional retention is related to contact angles and is discussed at length in the theory section (section 5). A number of groups have created substrates with microposts arranged in periodic asymmetric patterns to induce droplet transport when the surface was mechanically vibrated or droplets were forced by oscillatory electric fields (Figure 3a).[32, 33] Droplets have also been transported on microscale ratchet surfaces between parallel plates vibrated mechanically (Figure 3b).[34] The Leidenfrost effect,[35] in which a liquid or solid self propels on a hot surface, has also recently been employed to propel drops in a single direction on a hot ratchet surface (Figure 3c).[36] Lastly, surfaces patterned with asymmetric microstructures have controlled liquid spreading (Figure 3d). [37]
Figure 3.
Engineered textured directional surfaces with asymmetric or periodic structures. (a) Micropost array for directional drop transport. Zoomed image shows details of asymmetric positioning of posts. Scale bars 200 µm (left) and 100 µm (right). Reprinted with permission of Chung et al.[32] Copyright 2010, SPIE. (b) Wax microratchet surfaces for directional drop transport. Scale bar 1 mm. Reprinted with permission from Sandre et al.,[34] copyright (1999) by the American Physical Society. (c) Milliratchet surface for directional drop transport powered by the Leidenfrost effect. Scale bar 1 mm. Source: Lagubeau et al.,[36] reprinted with permission from Macmillan Publishers: Nature Physics, copyright 2011. (d) Shaped micropillar array for directional droplet spreading. Scale bars 200 µm (left) and 50 µm (right). Source: Jokinen et al.,[37] copyright (2009) John Wiley & Sons. (e) Nanofilm with tilted nanorods acting like nanoratchets for directional drop transport and adhesion. Scale bars 5 µm (left), 1 µm (middle, right). Source: Malvadkar et al.,[39] reprinted with permission from Macmillan Publishers: Nature Materials, copyright 2010. (f) Ion track textured surface with directional contact angle hysteresis. Scale bar 50 µm. Reprinted with permission from Spohr et al.[40] Copyright (2010) American Chemical Society. (g,h) Tilted nanohairs for directional wetting and drop spreading. Scale bars (g) 1 µm and (h) 10 µm. Sources: (g) Kim and Suh[41] – reproduced by permission of The Royal Society of Chemistry. (h) Chu et al.,[42] reprinted with permission from Macmillan Publishers: Nature Materials, copyright 2010. (i) Microratchet surface for directional dry adhesion. Scale bars 500 µm (left) and 20 µm (right). Source: Parness et al.,[43] reprinted with permission of The Royal Society, copyright 2009. (j) Tilted nanorods for directional dry adhesion. Scale bar 10 µm. Reprinted with permission from Lee et al.[44] Copyright 2008, American Institute of Physics. (k) Hierarchical texture (micro/nano) for directional dry adhesion. Scale bars 10 µm (left), 1 µm (right). Source: Jeong et al.,[45] copyright (2009) National Academy of Sciences, U.S.A. (l) Microchannel with ratchet-shaped walls for directional particle transport. Scale bar 2 µm. Reprinted with permission from Kettner et al.[47] Copyright (2009) by the American Physical Society.
A number of nanostructured surfaces have recently been developed with directional wet adhesion properties. The advantage of using nanostructures is the tenfold or more increase in droplet retention forces over microstructured surfaces. Recently, we reported an engineered nanofilm composed of an array of hydrophobic PPX nanorods (poly-chloro-p-xylylene, a.k.a, parylene[38]), which is both hydrophobic and exhibits anisotropic wet adhesion via a ratchet mechanism (Figure 3e).[39] Such a nanofilm provides a microscale smooth surface for transporting microliter droplets. Another hydrophobic surface exhibiting anisotropic wet adhesion comprised tilted nanostructures synthesized by ion track etching followed by a hydrophobic treatment (Figure 3f).[40]
Several groups have developed hydrophilic surfaces with nanoscale ratchets for controlled liquid spreading. Such surfaces could be used to channel fluids in microdevices for biosensing or liquid cooling applications. Replica molding and oblique electron beam irradiation were combined to create a surface with stooped polymer nanohairs to promote unidirectional spreading of a water droplet (Figure 3g).[41] Surfaces with tilted nanostructures may be designed to allow fluid to propagate in one direction while pinning it in all others (Figure 3h and Figure 4a).[42] Similar fabrication methods such as direct replica molding from a master with a slanted structure and nanofabrication (photolithography or molding) with post treatment such as e-beam exposure, thermal annealing and mechanical compression have been used to synthesize surfaces with tilted polymer nanorods for anisotropic wetting and directional dry adhesion.[5]
Figure 4.
Applications of directional surfaces. (a) Snapshots of a droplet spreading in one direction on a directional surface. Schematic indicates direction of nanorod tilt. Scale bars 1 mm. Source: Chu et al.,[42] reprinted with permission from Macmillan Publishers: Nature Materials, copyright 2010. (b) Drops and drops containing cargo being transported on directional surfaces forced with mechanical vibration. The forcing frequency was chosen close to the resonant frequency of the largest drop, and amplitude low enough so that smaller drops did not move. When two drops coalesced, their size increased and resonant frequency decreased. Thus, the forcing frequency was also reduced to keep the largest drop moving. Scale bar 5 mm. Reprinted with permission from Sekeroglu et al.[54] Copyright 2011, American Institute of Physics. (c) Drops impacting a directional surface with the grain (top) bounce further than those impacting against the grain (bottom). Dashed vertical lines demark the extent of the trajectory in the top image; schematics indicate the grain, i.e. nanorod direction. Scale bar 1 cm. Source: new unpublished work by the authors (see Experimental for details). (d) Soft gel transport on a PDMS surface with angled cuts aligned in the direction of motion. Snapshots shown 1 s apart. Scale bar 1 cm. Source: Mahadevan et al.,[55] copyright (2004) National Academy of Sciences, U.S.A. (e) Directional control of gas release. Gravity and buoyancy force point in (above) and against (below) the direction of nanorod tilt, as indicated by the schematic. Scale bar 1 mm. Source: new unpublished work by the authors (see Experimental for details). (f) Directional folding. Polymer sheets were folded by evaporating droplets. Folding was symmetric and asymmetric for sheets with isotropic and directional surfaces, respectively. Scale bar 4 mm. Source: new unpublished work by the authors (see Experimental for details). (g) Directional cell adhesion on a directional surface. Zoomed image indicates cell filopodia penetrating between the nanorods. Scale bars 10 µm (top) and 1 µm (bottom). Reprinted with permission from Christophis et al.[60] Copyright 2011, American Vacuum Society. (h) Channels with ratchet surfaces for cell transport. Scale bar 50 µm. Source: Mahmud et al.,[61] reprinted with permission from Macmillan Publishers: Nature Physics, copyright 2009.
Inspired by the gecko footpad, surfaces have been engineered for directional dry adhesion. Examples include microfabricated wedge-shaped adhesive arrays[43] (Figure 3i) and vertically aligned arrays of angled microfibers (Figure 3j).[44] The latter synthetic angled microfiber array was prepared by a rolling process at 50 °C, which was lower than the glass transition temperature of the polymer. Yet another example is a nanofilm with hierarchical patterns of high aspect ratio polyurethaneurea-vinyl (PUA) rods formed over a large area from an etched polySi substrate patterned with tilted nanoholes.(Figure 3k)[45] Our nanoPPX films also demonstrate directional dry adhesion.[46] By measuring the contact friction on these films, we found larger contact depths and higher friction coefficients for sliding in the direction of nanorod tilt compared to sliding against the tilt. In comparison, planar PPX films did not exhibit either frictional anisotropy or depth hysteresis.[46]
In addition to patterning planar surfaces, channels with asymmetric structures have also been engineered for directional transport applications. One of the first devices developed for transporting micron-sized particles employed a channel with ratchet-profile through which flow was periodically pumped (a single wavelength of such a channel is shown in Figure 3l).[47]
So far in this section we have focused on the structure of engineered directional surfaces. We now turn our attention to applications. The use of synthetic directional surfaces for dry adhesion applications has been reviewed earlier.[5] Here, we review applications of directional surfaces to soft materials (e.g. cells, gels) and liquids and augment the relatively few examples in the literature with new work from our group, including directional folding, friction and transport (Figure 4 and Table 1).
Microfluidic devices require smart surface coatings for flow control. So far, such control has been achieved using chemical patterns[48, 49] and topologically textured surfaces. The unidirectional surfaces described here may be patterned in microfluidic channels. The geometry of roughness elements, for example the tilt of nanorods, may be turned to achieve a particular fluidic resistance in continuous systems or contact line motion in drop-based (digital) systems. A preferential direction of transport may be achieved in a channel by aligning the unidirectional surface with the channel axis. Fluid droplets may either slide or roll on textured surfaces, depending on the viscosity, droplet size, wetting properties and forcing characteristics.[12, 50–52] Droplet motion may be powered by gravitational forces, alternating electric fields or mechanical vibration.[12, 50–52] Recent examples include unidirectional liquid spreading on nanofilms, where the liquid propagates in the tilt direction of hydrophilic nanoposts (Figure 4a),[42] and the unidirectional wetting behavior of hydrophobic nanofilms by a pin-release droplet ratchet mechanism (Figure 4b).[53] In the latter example, applying low-amplitude high frequency (~30–80 Hz) vibrations on the boundary induced droplet transport in the direction the asymmetric asperities. The maximum droplet translation speed was approximately 3.5 mm s−1 and depended on both the drop volume and vibration frequency, discussed in detail in section 5. By adjusting the vibration frequency, drops of different sizes could be selectively moved and merged.[54] Cargo such as microgels can be carried by such droplets (Figure 4b), which, combined with selective drop motion and merging, offers a pathway towards high throughput microgel assembly.[54]
Soft materials may also be transported on directional surfaces. One such example involves a gel cylinder riding atop a silicon rubber sheet (Figure 4d).[55] Angled parallel incisions were made in the rubber sheet, so that when vibrated, liquid seeped from the gel to form a thin lubricating layer between the gel and sheet. The asymmetric incisions opened only when the fluid between the gel and sheet sheared in one direction, resulting in an asymmetric coefficient of kinetic friction and the gel being transported along the sheet.[55]
A rich class of phenomena arises when a droplet impacts a textured surface. For particular impact speeds, drops may rebound from superhydrophobic surfaces without actually wetting the surface.[56] For a unidirectional surface, we expect that contact line motion and the rebound trajectory will depend not only on impact speed, but also the angle of attack. Preliminary experiments performed at our lab showed that when drops impacted an inclined directional nanorod surface in the direction of nanorod tilt, the horizontal extent of the trajectory was larger than when drop impact was against the nanorod direction (Figure 4c). In addition to the rebound trajectory, we suspect that the critical impalement speed, rebound angle and distorted drop shape will all depend on the orientation of droplet impact with respect to the asymmetric roughness features of the directional textured surface.
The directional release of gas bubbles may also be generated on anisotropic surfaces. We generated H2 bubbles by the catalytic release from alkaline aqueous solutions of sodium borohydride on cobalt functionalized directional PPX matrices. Cobalt catalysts were prepared on PPX nanofilm substrates via electroless plating with adsorbed pyridine ligand as an adhesion promoter.[57] The force of retention on gas bubbles was larger when the nanorods were pointing down than when pointing up (Figure 4e).
Capillary wrinkling and folding of thin sheets of soft material by droplets is another well documented phenomenon.[58] Two-dimensional soft polymer sheets will fold into three-dimensional structures as a function of the number and direction of folds.[59] Anisotropic textured surfaces could control the directionality of a folding sheet by creating an asymmetry in the contact angles along the contact line of the water drop folding the sheet. In new preliminary experiments, we showed that the anisotropy of the nanoPPX can guide sheet folding (Figure 4f). Folding was driven by water evaporation following droplet deposition; the shrinking contact line of the evaporating droplet pulled the edges inward to drive the folding. The orientation of the nanorods determined the direction of folding: when the nanorods tilt was to the right, the receding contact angle along the right edge was smaller than that on the left, making the component of force larger on the right edge than on all other edges. Hence, the thin film bent to the left (Figure 4f).
Bioadhesion properties have also been observed on synthetic directional nanofilms,[60] making them potentially useful for tissue engineering applications. In a previous study, we used fluidic shear stress to remove cells from a microfluidic channel whose substrate was coated with our nanoPPX film (Figure 4g).[60] Cells were removed with lower shear stresses when the flow was in the direction of nanorod tilt, compared to flow against the tilt. Lastly, ratchet-like channel geometries have been shown to rectify the random motions of motile cells and induce cell migration along a channel (Figure 4h).[61]
5. Modeling Adhesion, Wetting and Transport on Directional Surfaces
An integral part of understanding and designing directional surfaces involves modeling their behavior and interaction with fluids and solids. In this section we review an array of modeling approaches with a hierarchy of sophistication to model adhesion, wetting and transport on directional surfaces. The five sources of anisotropy outlined in section 2 and Figure 1 arise in theoretical models from asymmetries in the geometry or governing equations, such as conservation laws (i.e. mass, momentum, energy), kinematic relations and constitutive equations with boundary conditions.[62] The salient anisotropic mechanism must be included in theoretical models to achieve accurate predictions. For example, simulations of the microtextures within metallic thin films agree well with experimentally characterized microtextures when anisotropic interface properties are incorporated in the calculations, while agreement is poor when isotropic properties are used instead.[63] Similarly, at the nanoscale, fluctuations about the native conformation of proteins have been suitably reproduced using an anisotropic network model, which enables evaluation of the directional preferences of proteins.[64]
5.1. Modeling Dry Adhesion
Models for dry adhesion are based on contact mechanics balancing elastic and surface energies and include crack-like mechanisms to model separation.[65] Contaminants or roughness reduce the strength of dry adhesion, while hierarchical structures can be used to increase it.[19, 65] Modeling approaches range from analytic formulas to finite element method (FEM) simulations to calculate the contact mechanics in the presence of normal and shear loads between solids, viscoelastic material and biological matter.[18, 65–67] A recent example is the contact mechanics-based analytic model used to elucidate the robust and releasable adhesion of the gecko foot.[65]
When a thin layer of lubricating liquid exists between two solids, additional fluidic forces must be coupled to the solid mechanical model to describe contact and adhesion. For the example outlined in Figure 4d (i.e. a gel cylinder transported on a PDMS layer with angled incisions), an analytic model was developed to describe the oscillations in the gel and its net motion.[55]
5.2. Modeling Wetting, Adhesion, and Transport in Solid-Fluid Systems
The wetting of solid surfaces by fluid and the adhesion and transport of fluid on solid surfaces depends on both the topology of the solid surface and the chemical and material properties of the fluid and solid phases.[27, 68–70] In what follows, we provide a brief overview based on existing works[27, 69] of two important concepts related to wetting, adhesion and transport: contact angles and contact angle hysteresis. We then review theoretical tools for calculating and quantifying wetting, adhesion and transport in solid-fluid systems. Though such tools have been applied mainly to isotropic surfaces, they may be readily generalized to directional surfaces. As reviewed below, thus far three groups have put forth models of wetting and adhesion on directional surfaces.[39, 71, 72]
The contact angle θ is defined as the angle measured through the liquid between the meniscus (liquid-gas interface) and the substrate (liquid-solid interface) at the three-phase (solid-liquid-gas) contact line. The equilibrium contact angle between a drop and a flat smooth surface is given by Young’s relation,[73] cos θe = (γSG − γSL)/γ, where γ, γSL, and γSG, are the surface tensions of the gas-liquid, solid-liquid and solid-gas interfaces, respectively. In reality, a range of static contact angles, referred to as contact angle hysteresis, may be observed for a given solid-fluid combination,[74] θr ≤ θ ≤ θa, bounded above and below by the receding and advancing contact angles. Contact angle hysteresis is directly related to adhesion, because differences in contact angles around the drop perimeter can yield a net surface tension force that resists drop transport. The force of wet adhesion, also called the droplet retention force, is estimated by[75] Fr = kγR(cos θr − cos θa) where R is the radius of the drop and k is a coefficient depending on the shape of the contact line. Such a formula may be used to estimate the maximum force on a raindrop sticking to a window, where the advancing and receding contact angles θa and θr are the contact angles on the drop’s lower and upper edges, respectively. Contact angle hysteresis is due to contact lines pinning on microscopic irregularities on the surface;[76] consequently, the most effective way to reduce it is by removing such irregularities via polishing, or conversely by minimizing the interaction between the interface and solid by roughening or texturing the surface.
On chemically heterogeneous or rough surfaces, the microscopic contact angle θ will generally differ from the apparent angle θ* observed at a macroscopic scale. In cases where the fluid fully wets a rough surface, the apparent macroscopic contact angle θ* is given by Wenzel’s relation,[77] cosθ* = r cos θe where the roughness parameter r equals the real surface area per planar area of the surface. When air pockets are trapped between roughness elements and the liquid, θ* is given by the Cassie-Baxter[78] relation, cosθ*=1+ϕs(1+cos θe), where ϕs is the area solid fraction. The Cassie-Baxter formula reveals that as the area solid fraction vanishes, ϕs → 0, the contact angle θ* approaches 180°. For nanotextured surfaces, air pockets are trapped at the interface between water and nanoporous hydrophobic surfaces. Such air pockets may be generated when a hydrophobic surface is immersed in a liquid,[79] and may be quantified by X-ray scattering and contact angle measurements.[80] It has been shown that the layer of air at the solid-aqueous interfaces is less than 0.1 nm thick for several hydrophobic solids.[81]
5.2.1. Analytic Models of Contact Angle Hysteresis
An array of analytic models exist to predict contact angle hysteresis including simple averages of the intrinsic contact angles on a material surface and in the voids, to scaling models incorporating the shape of the meniscus. Extrand’s[82] geometrical scaling argument for the macroscopic advancing and receding contact angles, θa and θr, on a pillared substrate of a material with advancing angle over 90°, θa0 > π/2, gives θa = π and θr = λ θr0 + (1 − λ) π, where λ is the solid fraction, defined differently for different types of configurations. For example, for square arrays, λ = d/δ, where d is the post diameter and δ is the spacing. The contact angle hysteresis for a drop in a Cassie state on a pillared substrate has also been calculated[33] using a slice approach.[83] Other estimates have been made for the hysteresis on 2D substrates consisting of grooves with semi-circular surface undulations and on 3D substrates consisting of pillars made up of many spheres.[84]
The hysteresis on more complicated surfaces such as fiber layers with regular or random spacing may be estimated using the more general framework of de Gennes and colleagues.[68, 69, 85–87] In the limit of small contact angle, the hysteresis for a flat surface with single and distributed chemical defects has been derived.[85] The word “defect” refers to a perturbation in the wetting energy localized near a particular point. The pinning argument has been repeated for θ = π/2, i.e. a vertical meniscus on a flat surface passing a single chemical defect or a distribution of defects.[69] Similar results were found for the contact angle hysteresis due to weak random roughness.[86] The framework developed in these works may be used to determine the contact angle hysteresis of many textured surfaces, including directional surfaces.
Recently Reyssat & Quéré[87] generalized de Gennes’ spring-like model to the case of a drop in a Fakir (Cassie) state on square array of cylinders. Assuming the resistance was due entirely to the reced-ing contact line,[88] they calculated the force to depin the receding surface of the drop and found that the hysteresis scaled as the solid fraction ϕs times its log. Their model included a fitting parameter a quantifying the effects of contact line distortion: cos θr − cos θa = (aϕs/4)log(π/ϕs), where a = 2 (scaling) and a = 3.8 (data fit).[87]
We recently reported a simple ratchet model for the contact angle hysteresis to rationalize the directional wetting response observed in Figure 3e.[39] The model was based on the directional dependence of the advancing and receding contact angles, θa and θr, of a sessile droplet on the tilted pillared substrate.[39] We estimated θa and θr by generalizing Extrand[71, 82]’s approach for 2D ratchets and 3D vertical pillars. Following Extrand, we introduced the linear fraction of the receding or advancing contact lines on the pillars, λ. The contact angles θr and θa were approximated as weighted averages, in terms of λ, of the respective contact angles between the meniscus and pillar and 180° in air. Simple geometrical arguments then provided estimates of the contact angle between the receding or advancing meniscus and the pillared substrate in terms of the intrinsic contact angles θa0 and θr0 of the substrate material, the pillar tilt angle β, diameter d, spacing δ, and the linear fraction λ.
A large class of the directional textured surfaces considered in Figures 2 and 3 consist of asperities with long and thin features that bend when in contact with droplets.[39] The tips of these flexible asperities can pull back on the trailing surface of the drop as it passes, enhancing hysteresis. A future goal is to integrate the effects of such flexibility into analytic models of contact angle hysteresis to improve predictions of wetting, adhesion and transport.
5.2.2. Analytic models of drop transport on textured surfaces
The relation between drop speed and vibration frequency, amplitude, drop volume, and surface parameters may be rationalized theoretically.[12, 50–52] The power required to move a droplet at a speed U on a surface with retention force Fr scales as FrU plus the rate of energy dissipation in the vibrating and translating drop. The retention force on a moving droplet is somewhat less than that for a static droplet, but the static calculation, proportional to contact angle hysteresis, gives a reasonable upper bound. Steady droplet motion is achieved when the energy transferred to the droplet is balanced by dissipation (e.g. Figure 4b). For drops with length scales smaller than the capillary length lc = (γ/ρg)1/2, energy dissipation due to internal viscous motions is confined to a small dissipation zone near the region of contact with the substrate (elsewhere, the drop is in solid body motion), and scales as[51] µU2R4/(lc)3. The dissipative losses due to vibration may be estimated from Stokes 3rd problem[89] as µk(aω)2l2, where l ~ R2/lc is the radius of the contact region,[51] a and ω are the amplitude and angular frequency of vibration, and k = (ωρ/2µ)1/2. Drop speeds have been measured on isotropic textured surfaces for motion powered by gravity,[50, 51] anisotropic mechanical vibration[12] and on directional surfaces by mechanical vibration.[39, 54] Drop speed is highly dependent on the forcing frequency. For the same input energy, larger drop speeds are associated with the Rayleigh modes of the droplet.[12, 54] Estimates and scaling arguments of drop speed have been derived based on the simple estimates of contact angle hysteresis and dissipation listed above.[12, 50–52]
5.2.3. Finite element models of static drops on textured surfaces
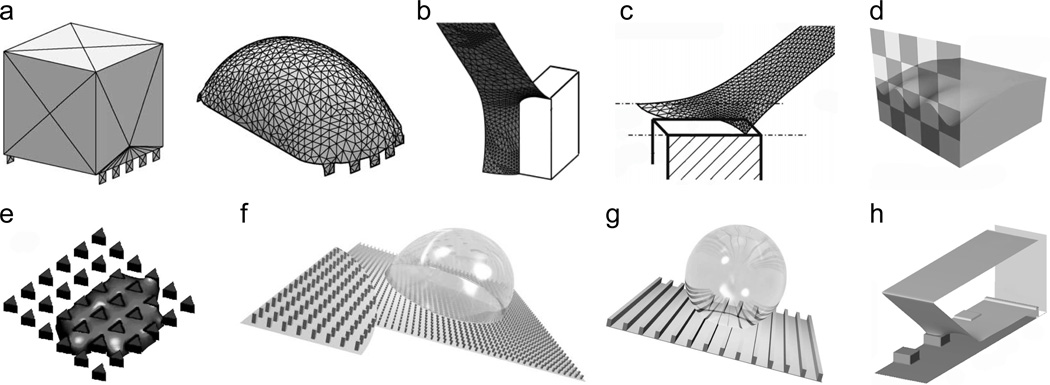
The simplest computational approach for modeling droplet behavior on textured surfaces involves finite element method (FEM) calculations of the static droplet meniscus and corresponding contact angle hysteresis. A popular public domain FEM package for such simulations is Surface Evolver,[90] which evolves a surface to achieve a state of minimal energy. The user creates an initial surface of vertices, edges and faces, and has broad control over the mesh refinement, surface evolution, energy functionals and convergence. The initial surface is iteratively evolved and refined until reaching a local energy minimum (Figure 5a). The package also includes basic programming constructs such as loops and conditional statements. Surface Evolver has been used to calculate free surface profiles on isotropic surfaces with chemical patterns,[48, 91, 92, 93] parallel grooves,[94] pillars[95, 96, 97] (Figure 5b,c) and inverted pillar surfaces.[98] Surface Evolver has also been used to calculate droplet profiles in electric fields.[99]
Figure 5.
Modeling wet adhesion on textured surfaces. (a) Initial and final Surface Evolver simulation profiles for a static drop on a pillared surface. Reprinted from Chen et al.,[94] copyright (2005), with permission from Elsevier. (b) Surface Evolver simulation of a portion of a droplet in a Wenzel state on a pillared surface. Reprinted with permission from Dorrer and Rühe.[97] Copyright (2008), American Chemical Society. (c) Surface Evolver simulation of a portion of a droplet in a Cassie state on a pillared surface. Reprinted with permission from Dorrer and Rühe.[95] Copyright (2007), American Chemical Society. (d) Surface Evolver simulation of a droplet advancing or receding on a checkerboard chemically patterned surface. Reprinted with permission from Kwon et al.[93] Copyright (2010), American Chemical Society. (e) Lattice Boltzmann simulation of directional spreading through an array of triangular pillars. Reprinted with permission of Blow et al.[106] Copyright 2009, Institute of Physics. (f,g) Lattice-Boltzmann simulations of drops sliding on pillared and grooved surfaces. Source: Hyväluoma et al.,[107] with kind permission of The European Physical Journal (EPJ). (h) Lattice Boltzmann simulation of a portion of a drop in a Cassie state receding on a pillared surface. Reprinted with permission from Mognetti and Yeomans.[111] Copyright (2010) American Chemical Society.
To calculate the contact angle between a sessile drop and a rough surface, the size of the computational domain may be significantly reduced when the roughness scale is much smaller than the drop radius and the capillary length (Figure 5b,c). In this regime, a good approximation is that the curvature of the liquid-gas interface near the roughness is effectively zero compared to the scale of the roughness. A zero curvature constraint may then be imposed within Surface Evolver to simulate the meniscus near the asperities. Note that zero curvature does not imply planar; a saddle shape in which the component curvatures in perpendicular directions cancel has zero curvature. Such saddle-like topology characterizes the meniscus geometry near the contact line of a drop on a rough surface. However, at the scale of the roughness, the far field condition (away from the roughness) is that the receding surface is in fact planar. In this regime, using such an approach allows the shape of the three-phase contact line and the local contact angle to be calculated to a good approximation with a computational domain that includes only the nearby free surface, and not the entire drop surface. Symmetries in the roughness configuration may also be used to further reduce the size of the computational domain.[95, 97]
The key to modeling adhesion and transport is to move beyond calculations of contact angles to the limiting cases of advancing and receding angles. In one of the few studies to report such a calculation, Kwon et al.[93] calculated the advancing and receding angles by gradually increasing or decreasing the volume of a drop, respectively, on a chemically patterned surface and averaging the contact angle along the contact line just prior to depinning events (Figure 5d). When the contact line moved, local contact angles were enforced by a phase field model coupled to the Surface Evolver calculations. The concept of coupling the phase field model to the FEM simulations not only maintained accurate contact angles during contact line motion, but also allowed the intrinsic advancing and receding angles of the material to be included in the simulations. Such an approach could be extended to model contact angle hysteresis for surfaces with hierarchical scales of roughness, such as those of the Lotus leaf.
The previous contact angle hysteresis models, both analytic and finite element, have all calculated the static meniscus. As noted above, the static calculations are useful to provide upper bounds on the wet adhesive property of a surface. However, accurately modeling dynamic situations such as a drop sliding along a surface or depinning events require full numerical treatment, discussed next.
5.2.3. Full numerical simulation of fluid flow and free surface on directional surfaces
An array of numerical approaches exists to generate full dynamical simulations of free surface flows in and over complex geometries. At the microscopic scale, molecular-dynamics (MD) simulations have modeled contact line dynamics and shed light on wetting hysteresis due to chemical defects and roughness.[100] At the mesoscale, phase field models employ a free energy field variable that acts as a marker for the different continuum phases.[101] Phase field models have been used to model a variety of dynamic multi-phase flow problems, including droplet hysteresis and contact line pinning and motion on chemically and structured heterogeneous surfaces.[101, 102] Phase field models have been implemented with both sharp and diffuse treatments of the interface to model drop, free surface and contact line phenomena.[103] A popular phase-field diffuse-interface approach is the Lattice Boltzmann method (LBM).[104] In LBM, a mean-field lattice-gas cellular automata model is implemented with a set of distribution functions to represent the average population of fluid particles.[105] Free surfaces are implemented using a free energy functional that is minimized in equilibrium.[105] The model can be extended to complex and multiphase fluids and complex geometries. Thus, LBM is ideal for simulating chemically patterned and rough surfaces. An array of dynamic wetting problems have been solved including the spreading of a fluid through a post array (Figure 5e),[106] droplets sliding on inclined pillared and grooved substrates (Figure 5f,g),[107] periodic droplet formation within chemically patterned microchannels,[108] anisotropic adhesion on ratcheted surfaces,[72] the impalement of a droplet on a superhydrophobic textured surface,[109] the advancing of a meniscus through microchannels patterned by posts[110] and receding contact lines on superhydrophobic surfaces (Figure 5h).[111] For static drops, FEM and LBM simulations produce comparable drop profiles.[92]
6. Conclusions
Inspired by directional surfaces in nature, engineers have employed recent innovations in microfabrication and materials synthesis to produce an array of synthetic directional surfaces with tunable anisotropic chemical, mechanical, physical, morphological and topological properties. Such directional surfaces may exhibit a host of emergent properties such as friction and wetting. These directional surfaces not only mimic biological surfaces, but also provide new avenues to discover surface phenomena beyond those in nature. In concert with innovative synthesis techniques, theoretical and computational tools link the structure to the behavior of directional surfaces. The next generation of directional surfaces will find use in syringes, hydropower turbines, micro- and nanoscale microfluidic devices for biomedical research, drag reducing and non-fouling ship hull coatings, self-cleaning solar-cell panels, high-efficiency thermal cooling systems for microchips and friction-control coatings for tires.
A future challenge is to engineer dynamic directional surfaces that change wetting and friction properties in real-time and enact such changes in response to external stimuli. In Nature, various stimuli response mechanisms exist to modify the surface shape or wetting properties. For example, water striders release surfactants to break through the free surface while laying eggs.[3] Certain insects generate emergency propulsion by releasing surface-active fluids to generate Marangoni stresses.[3] Many surface dwelling insects lift or pierce the free surface using retractable wetting claws at the ends of their hydrophobic legs.[112] Inspired by these natural systems, engineered surfaces exist that change their wetting and adhesion properties on command or in response to stimuli.[113] Such systems also employ surface clumping to lower the surface solid fraction and temperature gradients to induce surface tension gradients. Under the right conditions, cycling the stimulus may induce transport, offering a method to propel cargo or droplets in addition to mechanical vibration, acoustics and electrowetting. Marangoni flows induced by surfactant release could also be used to create fluid motion on a unidirectional surface. New theoretical tools must also be developed to link the structure and stimuli response mechanisms to the overall behavior of the directional surface and to better inform design criteria for optimal behavior.
7. Experimental
Asymmetric and Symmetric Folding
Oblique angle polymerization (OAP) produced an array of poly-chloro-p-xylylene (i.e., parylene or PPX) nanorods on a substrate.[39] We employed commercial systems to produce the vaporization and pyrolysis of a p-cyclophane precursor to generate a diradical vapor flux. The flux was directed at a controlled shallow angle onto silicon substrate, where surface diffusion combined with deposition geometry led to shadowing and selective growth of anisotropic structures during polymerization. The nanoPPX film (~20 µm thick) was peeled off the silicon surface as a self standing film. PDMS films were prepared using Sylgard® 184 Silicone Elastomer Base mixed at a 10:1 ratio with its associated curing agent. PDMS films were spin coated on a silicon substrate, cured and then lifted off the surface. Both films were placed on a hydrophobic surface with a contact angle of ~130° to prevent adhesion of the film to the substrate.
Directional bubbles
NanoPPX films were treated with 1M pyridine (aq) for ~48 h and rinsed in water for 4 min. The nanofilms were then immersed in a PdII-based colloidal dispersion for 45 min, and were then rinsed in water for 1 min followed by plating for 1 min in a Co bath. The Co bath was prepared as previously described.[57] NaBH4 solution in water was prepared using 2.5 wt% NaBH4 (0.677 M) and 1 wt% NaOH(aq) solution (0.261 M). Finally, cobalt coated nanoPPX film was dipped into the NaBH4 solution for H2 generation.
Drop impact
NanoPPX films were coated on silicon substrates and placed on a 45 degree inclined support. A water drop of 10 µl was release from a height of 10 cm to the center of the nanofilm. The drop impact was recorded using a high speed camera (Redlake MASD PCI Motionscope) at an acquisition rate of 1000 fps and at a resolution of 128×128 pixels.
Acknowledgements
We gratefully acknowledge financial support for this work from National Institutes of Health and the Pennsylvania State University. We thank Dr. Benjamin Hatton for helping with the high speed camera recordings for Figure 4c, and Prof. John Bush for useful discussions and comments.
Biographies

Prof. Melik Demirel is a tenured associate professor in engineering at Penn State, and has a decade of experience in directional nanomaterials. Prof. Demirel’s achievements have been recognized, in part, through his receipt of a Young Investigator Award-ONR, an Alexander von Humboldt Fellowship, an Institute for Complex Adaptive Matter Junior Fellowship and the Pearce Development Professorship. Prof. Demirel received a Ph.D. from Carnegie Mellon University and M.Sc and B.Sc degrees from Bogazici University in Turkey.

Dr. Matthew J. Hancock applies mechanics-based design, modeling and simulation tools to biomedical engineering, medicine, materials science and biology. He is currently a research fellow at Prof. Demirel’s laboratory studying fluid transport on directional surfaces. Previously, he was a research fellow at Harvard Medical School and an instructor in mathematics at MIT. He received bachelors and masters degrees in applied mathematics from the University of Waterloo, Canada, and a Ph.D. in environmental fluid mechanics from MIT.

Koray Sekeroglu is a Ph.D. candidate at Prof. Demirel’s laboratory. He is currently pursuing his degree on the fundamentals and physicochemical properties of directional polymeric films. He obtained his B.Sc in chemical engineering from the Izmir Institute of Technology in Turkey, where he subsequently worked as a research assistant.
References
- 1.Vogel S. Life's Devices: The Physical World of Animals and Plants. Princeton University Press; Princeton, USA: 1988. [Google Scholar]
- 2.Reimann P. Phys. Rep. 2002;361:57. [Google Scholar]
- 3.Bush JWM, Hu DL. Annu. Rev. Fluid Mech. 2006;38:339. [Google Scholar]
- 4.Hsu S-H, Woan K, Sigmund W. Mat. Sci. Eng. R. 2011;72:189. [Google Scholar]
- 5.Kwak MK, Jeong H-E, Kim T-I, Yoon H, Suh KY. Soft Matter. 2010;6:1849. [Google Scholar]
- 6.Epstein IR, Pojman JA. An Introduction to Nonlinear Chemical Dynamics: Oscillations, Waves, Patterns, and Chaos. New York: Oxford University Press; 1998. [Google Scholar]
- 7.Belousov BP. Collection of Short Papers on Radiation Medicine. 1959:145. [Google Scholar]
- 8.Zaikin AN, Zhabotinsky AM. Nature. 1970;225:535. doi: 10.1038/225535b0. [DOI] [PubMed] [Google Scholar]
- 9.Zimmermann K, Naletova VA, Zeidis I, Turkov VA, Kolev E, Lukashevich MV, Stepanov GV. J. Magn. Magn. Mater. 2007;311:450. [Google Scholar]
- 10.Glotzer SC, Solomon MJ. Nat. Mater. 2007;6:557. doi: 10.1038/nmat1949. [DOI] [PubMed] [Google Scholar]
- 11.Akcora P, Liu H, Kumar SK, Moll J, Li Y, Benicewicz BC, Schadler LS, Acehan D, Panagiotopoulos AZ, Pryamitsyn V, Ganesan V, Ilavsky J, Thiyagarajan P, Colby RH, Douglas JF. Nat. Mater. 2009;8:354. doi: 10.1038/nmat2404. [DOI] [PubMed] [Google Scholar]
- 12.Daniel S, Chaudhury MK, de Gennes P-G. Langmuir. 2005;21:4240. doi: 10.1021/la046886s. [DOI] [PubMed] [Google Scholar]
- 13.Ok JG, Tawfick SH, Juggernauth KA, Sun K, Zhang Y, Hart AJ. Adv. Funct. Mater. 2010;20:2470. [Google Scholar]
- 14.Boduroglu S, Cetinkaya M, Dressick WJ, Singh A, Demirel MC. Langmuir. 2007;23:11391. doi: 10.1021/la7025413. [DOI] [PubMed] [Google Scholar]; Demirel MC. Colloid Surface A. 2008;321:121. [Google Scholar]
- 15.Purcell EM. Am. J. Phys. 1977;45:3. [Google Scholar]
- 16.Federle W. J. Exp. Biol. 2006;209:2611. doi: 10.1242/jeb.02323. [DOI] [PubMed] [Google Scholar]
- 17.Eisner T. P. Natl. Acad. Sci. USA. 2000;97:11313. doi: 10.1073/pnas.190335397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Autumn K, Sitti M, Liang YA, Peattie AM, Hansen WR, Sponberg S, Kenny TW, Fearing R, Israelachvili JN, Full RJ. P. Natl. Acad. Sci. USA. 2002;99:12252. doi: 10.1073/pnas.192252799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Kamperman M, Kroner E, del Campo A, McMeeking RM, Arzt E. Advanced Engineering Materials. 2010;12:335. [Google Scholar]
- 20.Arzt E, Gorb S, Spolenak R. P. Natl. Acad. Sci. USA. 2003;100:10603. doi: 10.1073/pnas.1534701100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Arzt E, Gorb S, Spolenak R. P. Natl. Acad. Sci. USA. 2003;100:10603. doi: 10.1073/pnas.1534701100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Dirks J-H, Federle W. Soft Matter. 2011;7:11047. [Google Scholar]
- 23.Zheng Y, Bai H, Huang Z, Tian X, Nie F-Q, Zhao Y, Zhai J, Jiang L. Nature. 2010;463:640. doi: 10.1038/nature08729. [DOI] [PubMed] [Google Scholar]
- 24.Prakash M, Bush JWM. Int. J. Nonlin. Mech. 2011;46:607. [Google Scholar]
- 25.Gao X, Jiang L. Nature. 2004;432:36. doi: 10.1038/432036a. [DOI] [PubMed] [Google Scholar]
- 26.Feng XQ, Gao X, Wu Z, Jiang L, Zheng QS. Langmuir. 2007;23:4892. doi: 10.1021/la063039b. [DOI] [PubMed] [Google Scholar]
- 27.Bush JWM, Prakash M, Hu DL. Adv. Insect Physiol. 2007;34:117. [Google Scholar]
- 28.Zheng Y, Gao XF, Jiang L. Soft Matter. 2007;3:178. doi: 10.1039/b612667g. [DOI] [PubMed] [Google Scholar]
- 29.Bohn HF, Federle W. P. Natl. Acad. Sci. USA. 2004;101:14138. doi: 10.1073/pnas.0405885101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Kulic IM, Mani M, Mohrbach H, Thaokar R, Mahadevan L. P. R. Soc. B. 2009;276:2243. doi: 10.1098/rspb.2008.1685. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Wu D, Wang J-N, Wu S-Z, Chen Q-D, Zhao S, Zhang H, Sun H-B, Jiang L. Adv. Func. Mater. 2011;21:2927. [Google Scholar]; Gao J, Liu Y, Xu H, Wang Z, Zhang X. Langmuir. 2010;26:9673. doi: 10.1021/la100256b. [DOI] [PubMed] [Google Scholar]; Fraenkel G, Fallil F, Kumarasinghe KS. Entomologia Experimentalis et Applicata. 1981;29:147. [Google Scholar]
- 32.Chung Y-C, Hess G-Y, Yeh F-W, Han H-C, Chen C-Y, Lee C-J, Sheen H-J, Yang L-J. J. Micro/Nanolith. MEMS MOEMS. 2010;9:13035. [Google Scholar]
- 33.Shastry A, Case MJ, Böhringer KF. Langmuir. 2006;22:6161. doi: 10.1021/la0601657. [DOI] [PubMed] [Google Scholar]
- 34.Sandre O, Gorre-Talini L, Ajdari A, Prost J, Silberzan P. Phys. Rev. E. 1999;60:2964. doi: 10.1103/physreve.60.2964. [DOI] [PubMed] [Google Scholar]
- 35.Leidenfrost JG. De Aquae Communis Nonnullis Qualitatibus Tractatus. Duisburg: p. 1756. [Google Scholar]
- 36.Lagubeau G, Le Merrer M, Clanet C, Quéré D. Nat. Phys. 2011;7:395. [Google Scholar]
- 37.Jokinen V, Leinikka M, Franssila S. Adv. Mater. 2009;21:4835. doi: 10.1002/adma.200901171. [DOI] [PubMed] [Google Scholar]
- 38.Cetinkaya M, Malvadkar N, Demirel MC. Journal of Polymer Science Part B-Polymer Physics. 2008;46:640. [Google Scholar]; Demirel MC, Boduroglu S, Cetinkaya M, Lakhtakia A. Langmuir. 2007;23:5861. doi: 10.1021/la700538f. [DOI] [PubMed] [Google Scholar]
- 39.Malvadkar NA, Hancock MJ, Sekeroglu K, Dressick WJ, Demirel MC. Nat. Mater. 2010;9:1023. doi: 10.1038/nmat2864. [DOI] [PubMed] [Google Scholar]
- 40.Spohr R, Sharma G, Forsberg P, Karlsson M, Hallen A, Westerberg L. Langmuir. 2010;26:6790. doi: 10.1021/la904137t. [DOI] [PubMed] [Google Scholar]
- 41.Kim T-I, Suh KY. Soft Matter. 2009;5:4131. [Google Scholar]
- 42.Chu K-H, Xiao R, Wang EN. Nat. Mater. 2010;9:413. doi: 10.1038/nmat2726. [DOI] [PubMed] [Google Scholar]
- 43.Parness A, Soto D, Esparza N, Gravish N, Wilkinson M, Autumn K, Cutkosky M. J. Roy. Soc. Interface. 2009;6:1223. doi: 10.1098/rsif.2009.0048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Lee J, Fearing RS, Komvopoulos K. Appl. Phys. Lett. 2008;93:191910. [Google Scholar]
- 45.Jeong HE, Lee J-K, Kim HN, Moon SH, Suh KY. P. Natl. Acad. Sci. USA. 2009;106:5639. doi: 10.1073/pnas.0900323106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.So E, Demirel MC, Wahl KJ. J. Phys. D Appl. Phys. 2010;43:045403. [Google Scholar]
- 47.Kettner C, Reimann P, Hänggi P, Müller F. Phys. Rev. E. 2000;61:312. doi: 10.1103/physreve.61.312. [DOI] [PubMed] [Google Scholar]
- 48.Darhuber AA, Troian SM, Miller SM, Wagner S. J. Appl. Phys. 2000;87:7768. [Google Scholar]
- 49.Zhao B, Moore JS, Beebe DJ. Science. 2001;291:1023. doi: 10.1126/science.291.5506.1023. [DOI] [PubMed] [Google Scholar]
- 50.Lv C, Yang C, Hao P, He F, Zheng Q. Langmuir. 2010;26:8704. doi: 10.1021/la9044495. [DOI] [PubMed] [Google Scholar]
- 51.Mahadevan L, Pomeau Y. Phys. Fluids. 1999;11:2449. [Google Scholar]
- 52.Richard D, Quéré D. Europhys. Lett. 1999;48:286. [Google Scholar]
- 53.Malvadkar NA, Sekeroglu K, Dressick WJ, Demirel MC. Langmuir. 2010;26:4382. doi: 10.1021/la9034529. [DOI] [PubMed] [Google Scholar]
- 54.Sekeroglu K, Gurkan UA, Demirci U, Demirel MC. Appl. Phys. Lett. 2011;99:063703. doi: 10.1063/1.3625430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Mahadevan L, Daniel S, Chaudhury MK. P. Natl. Acad. Sci. USA. 2004;101:23. doi: 10.1073/pnas.2637051100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Bartolo D, Bouamrirene F, Verneuil É, Buguin A, Silberzan P, Moulinet S. Europhys. Lett. 2006;74:299. [Google Scholar]; Reyssat M, Pépin A, Marty F, Chen Y, Quéré D. Europhys. Lett. 2006;74:306. [Google Scholar]
- 57.Malvadkar N, Park S, Urquidi-MacDonald M, Wang H, Demirel MC. J. Power Sources. 2008;182:323. [Google Scholar]; Malvadkar NA, Sekeroglu K, Dressick WJ, Demirel MC. J. Power Sources. 2011;196:8553. [Google Scholar]
- 58.Huang J, Juszkiewicz M, de Jeu WH, Cerda E, Emrick T, Menon N, Russel TP. Science. 2007;317:650. doi: 10.1126/science.1144616. [DOI] [PubMed] [Google Scholar]; Py C, Reverdy P, Doppler L, Bico J, Roman B, Baroud CN. Phys. Fluids. 2007;19:91104. doi: 10.1103/PhysRevLett.98.156103. [DOI] [PubMed] [Google Scholar]
- 59.Py C, Reverdy P, Doppler L, Bico J, Roman B, Baroud CN. Phys. Rev. Lett. 2007;98:156103. doi: 10.1103/PhysRevLett.98.156103. [DOI] [PubMed] [Google Scholar]
- 60.Christophis C, Sekeroglu K, Demirel G, Thome I, Grunze M, Demirel MC, Rosenhahn A. Biointerphases. 2011;6:158. doi: 10.1116/1.3646093. [DOI] [PubMed] [Google Scholar]
- 61.Mahmud G, Campbell CJ, Bishop KJM, Komarova YA, Chaga O, Soh S, Huda S, Kandere-Grzybowska K, Grzybowski BA. Nat. Phys. 2009;5:606. [Google Scholar]
- 62.Newnham RE. Properties of Materials: Anisotropy, Symmetry, Structure. Oxford University Press; Oxford, UK: 2005. [Google Scholar]
- 63.Demirel MC, Kuprat AP, George DC, Rollett AD. Phys. Rev. Lett. 2003;90:016106. doi: 10.1103/PhysRevLett.90.016106. [DOI] [PubMed] [Google Scholar]; Kuprat A, George D, Straub G, Demirel MC. Comp. Mater. Sci. 2003;28:199. [Google Scholar]
- 64.Atilgan AR, Durell SR, Jernigan RL, Demirel MC, Keskin O, Bahar I. Biophys. J. 2001;80:505. doi: 10.1016/S0006-3495(01)76033-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Yao H, Gao H. J. Mech. Phys. Solids. 2006;54:1120. [Google Scholar]
- 66.Autumn K, Liang YA, Hsieh ST, Zesch W, Chan WP, Kenny TW, Fearing R, Full RJ. Nature. 2000;405:681. doi: 10.1038/35015073. [DOI] [PubMed] [Google Scholar]
- 67.Gao H, Yao H. P. Natl. Acad. Sci. USA. 2004;101:7851. doi: 10.1073/pnas.0400757101. [DOI] [PMC free article] [PubMed] [Google Scholar]; Gao H, Wang X, Yao H, Gorb S, Arzt E. Mech. Mater. 2005;37:275. [Google Scholar]; Persson BNJ. J. Chem. Phys. 2003;118:7614. [Google Scholar]; Spolenak R, Gorb S, Gao H, Arzt E. P. Roy. Soc. A - Math. Phy. 2005;461:305. [Google Scholar]; Huber G, Gorb SN, Spolenak R, Arzt E. Biol. Lett. 2005;1:2. doi: 10.1098/rsbl.2004.0254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.de Gennes P-G. Rev. Mod. Phys. 1985;57:827. [Google Scholar]
- 69.de Gennes P-G, Brochard-Wyart F, Quéré D. Capillarity and Wetting Phenomena: Drops, Bubbles, Pearls, Waves. Berlin: Springer; 2003. [Google Scholar]
- 70.Adamson AW. Physical Chemistry of Surfaces. New York: Wiley; 1982. [Google Scholar]; Dussan V EB. Ann. Rev. Fluid Mech. 1979;11:371. [Google Scholar]
- 71.Extrand CW. Langmuir. 2007;23:1867. doi: 10.1021/la0625289. [DOI] [PubMed] [Google Scholar]
- 72.Balazs AC, Yeomans JM. Soft Matter. 2010;6:703. [Google Scholar]
- 73.Young T. Phil. Trans. Roy. Soc. London A. 1805;95:65. [Google Scholar]
- 74.Johnson RE, Dettre RH. Vol. 43. Washington, DC: American Chemical Society; 1964. p. 112. [Google Scholar]; Dettre RH, Johnson RE. Vol. 43. Washington, DC: American Chemical Society; 1964. p. 136. [Google Scholar]; Dettre RH, Johnson RE. J. Phys. Chem. 1965;69:1507. [Google Scholar]
- 75.Dussan V EB, Chow RTP. J. Fluid Mech. 1983;137:1. [Google Scholar]; Extrand CW, Kumagai Y. J. Colloid Interf. Sci. 1995;170:515. [Google Scholar]
- 76.Nadkarni GD, Garoff S. Europhys. Lett. 1992;20:523. [Google Scholar]
- 77.Wenzel RN. Ind. Eng. Chem. 1936;28:988. [Google Scholar]
- 78.Cassie ABD, Baxter S. Trans. Faraday Soc. 1944;40:546. [Google Scholar]; Cassie ABD, Baxter S. Nature. 1945;155:21. [Google Scholar]
- 79.Krasowska M, Krastev R, Rogalski M, Malysa K. Langmuir. 2007;23:549. doi: 10.1021/la062320n. [DOI] [PubMed] [Google Scholar]
- 80.Checco A, Hofmann T, DiMasi E, Black CT, Ocko BM. Nano Lett. 2010;10:1354. doi: 10.1021/nl9042246. [DOI] [PubMed] [Google Scholar]
- 81.Mao M, Zhang J, Yoon RH, Ducker AW. Langmuir. 2004;20:1843. [Google Scholar]
- 82.Extrand CW. Langmuir. 2002;18:7991. [Google Scholar]
- 83.Brochard F. Langmuir. 1989;5:432. [Google Scholar]
- 84.Nosonovsky M. Langmuir. 2007;23:3157. doi: 10.1021/la062301d. [DOI] [PubMed] [Google Scholar]
- 85.Joanny JF, de Gennes PG. J. Chem. Phys. 1984;81:552. [Google Scholar]
- 86.Pomeau Y, Vannimenus J. J. Colloid Interf. Sci. 1985;104:477. [Google Scholar]
- 87.Reyssat M, Quéré D. J. Phys. Chem. B. 2009;113:3906. doi: 10.1021/jp8066876. [DOI] [PubMed] [Google Scholar]
- 88.Gao L, McCarthy TJ. Langmuir. 2006;22:2966. doi: 10.1021/la0532149. [DOI] [PubMed] [Google Scholar]; Dorrer C, Rühe J. Langmuir. 2006;22:7652. doi: 10.1021/la061452d. [DOI] [PubMed] [Google Scholar]
- 89.Acheson DJ. Elementary Fluid Dynamics. USA: Oxford University Press; 1990. [Google Scholar]
- 90.Brakke KA. Exp. Math. 1992;1:141. [Google Scholar]
- 91.Brandon S, Wachs A, Marmur A. J. Colloid Interf. Sci. 1997;191:110. doi: 10.1006/jcis.1997.4912. [DOI] [PubMed] [Google Scholar]; Gau H, Herminghaus S, Lenz P, Lipowsky R. Science. 1999;283:46. doi: 10.1126/science.283.5398.46. [DOI] [PubMed] [Google Scholar]; Darhuber AA, Troian SM, Davis JM, Miller SM, Wagner S. J. Appl. Phys. 2000;88:5119. [Google Scholar]; Brinkmann M, Lipowsky R. J. Appl. Phys. 2002;92:4296. [Google Scholar]; Brandon S, Haimovich N, Yeger E, Marmur A. J. Colloid Interf. Sci. 2003;263:237. doi: 10.1016/s0021-9797(03)00285-6. [DOI] [PubMed] [Google Scholar]
- 92.Ruiz-Cabello FJM, Kusumaatmaja H, Rodríguez-Valverde MA, Yeomans J, Cabrerizo-Vílchez MA. Langmuir. 2009;25:8357. doi: 10.1021/la900579s. [DOI] [PubMed] [Google Scholar]
- 93.Kwon Y, Choi S, Anantharaju N, Lee J, Panchagnula MV, Patankar NA. Langmuir. 2010;26:17528. doi: 10.1021/la102981e. [DOI] [PubMed] [Google Scholar]
- 94.Chen Y, He B, Lee J, Patankar NA. J. Colloid Interf. Sci. 2005;281:458. doi: 10.1016/j.jcis.2004.07.038. [DOI] [PubMed] [Google Scholar]
- 95.Dorrer C, Rühe J. Langmuir. 2007;23:3179. doi: 10.1021/la062596v. [DOI] [PubMed] [Google Scholar]
- 96.Dorrer C, Rühe J. Langmuir. 2007;23:3820. doi: 10.1021/la063130f. [DOI] [PubMed] [Google Scholar]; Moulinet S, Bartolo D. Eur. Phys. J. E. 2007;24:251. doi: 10.1140/epje/i2007-10235-y. [DOI] [PubMed] [Google Scholar]
- 97.Dorrer C, Rühe J. Langmuir. 2008;24:1959. doi: 10.1021/la7029938. [DOI] [PubMed] [Google Scholar]
- 98.Choi W, Tuteja A, Mabry JM, Cohen RE, McKinley GH. J. Colloid Interf. Sci. 2009;339:208. doi: 10.1016/j.jcis.2009.07.027. [DOI] [PubMed] [Google Scholar]
- 99.Bienia M, Quilliet C, Vallade M. Langmuir. 2003;19:9328. [Google Scholar]; Klingner A, Buehrle J, Mugele F. Langmuir. 2004;20:6770. doi: 10.1021/la036058j. [DOI] [PubMed] [Google Scholar]
- 100.Jin W, Koplik J, Banavar JR. Phys. Rev. Lett. 1997;78:1520. [Google Scholar]; Collet P, De Coninck J, Dunlop F, Regnard A. Phys. Rev. Lett. 1997;79:3704. doi: 10.1103/PhysRevLett.65.195. [DOI] [PubMed] [Google Scholar]; Lundgren M, Allan NL, Cosgrove T. Langmuir. 2006;23:1187. doi: 10.1021/la060712o. [DOI] [PubMed] [Google Scholar]
- 101.Luo K, Kuittu M-P, Tong C, Majaniemi S, Ala-Nissila T. The Journal of Chemical Physics. 2005;123:194702. doi: 10.1063/1.2102907. [DOI] [PubMed] [Google Scholar]; Vedantam S, Panchagnula MV. Phys. Rev. Lett. 2007;99:176102. doi: 10.1103/PhysRevLett.99.176102. [DOI] [PubMed] [Google Scholar]; Vedantam S, Panchagnula MV. J. Colloid Interface Sci. 2008;321:393. doi: 10.1016/j.jcis.2008.01.056. [DOI] [PubMed] [Google Scholar]
- 102.Do-Quang M, Amberg G. Math. Comput. Simulat. 2010;80:1664. [Google Scholar]; Do-Quang M, Amberg G. Phys. Fluids. 2009;21:022102. [Google Scholar]
- 103.Anderson DM, McFadden GB, Wheeler AA. Ann. Rev. Fluid Mech. 1998;30:139. [Google Scholar]; Jacqmin D. J. Fluid Mech. 2000;402:57. [Google Scholar]; Nguyen H-B, Chen J-C. Phys. Fluids. 2010;22:062102. [Google Scholar]; Scardovelli R, Zaleski S. Ann. Rev. Fluid Mech. 1999;31:567. [Google Scholar]; Das AK, Das PK. Langmuir. 2010;26:9547. doi: 10.1021/la100145e. [DOI] [PubMed] [Google Scholar]
- 104.Fakhari A, Rahimian MH. Physical Review E. 2010;81:036707. doi: 10.1103/PhysRevE.81.036707. [DOI] [PubMed] [Google Scholar]
- 105.Kusumaatmaja H, Yeomans JM. In: Hoekstra AG, Kroc J, Sloot PMA, editors. Berlin: Springer-Verlag; 2010. p. 241. [Google Scholar]
- 106.Blow ML, Kusumaatmaja H, Yeomans JM. J. Phys. 2013 Condens. Mat. 2009;21:464125. doi: 10.1088/0953-8984/21/46/464125. [DOI] [PubMed] [Google Scholar]
- 107.Hyväluoma J, Koponen A, Raiskinmäki P, Timonen J. Eur. Phys. J. E. 2007;23:289. doi: 10.1140/epje/i2007-10190-7. [DOI] [PubMed] [Google Scholar]
- 108.Kuksenok O, Jasnow D, Yeomans J, Balazs AC. Phys. Rev. Lett. 2003;91:108303. doi: 10.1103/PhysRevLett.91.108303. [DOI] [PubMed] [Google Scholar]
- 109.Kusumaatmaja H, Blow ML, Dupuis A, Yeomans JM. Europhys. Lett. 2008;81:36003. [Google Scholar]
- 110.Mognetti BM, Yeomans JM. Phys. Rev. E. 2009;80:056309. doi: 10.1103/PhysRevE.80.056309. [DOI] [PubMed] [Google Scholar]
- 111.Mognetti BM, Kusumaatmaja H, Yeomans JM. Faraday Discuss. 2010;146:153. doi: 10.1039/b926373j. [DOI] [PubMed] [Google Scholar]
- 112.Hu DL, Bush JWM. Nature. 2005;437:733. doi: 10.1038/nature03995. [DOI] [PubMed] [Google Scholar]
- 113.Dressick WJ, Kondracki LM, Chen M-S, Brandow SL, Matijević E, Calvert JM. Colloid Surface A. 1996;108:101. [Google Scholar]