Quantifying CFSE Label Decay in Flow Cytometry Data

Abstract

We developed a series of models for the label decay in cell proliferation assays when the intracellular dye carboxyfluorescein succinimidyl ester (CFSE) is used as a staining agent. Data collected from two healthy patients were used to validate the models and to compare the models with the Akiake Information Criteria. The distinguishing features of multiple decay rates in the data are readily characterized and explained via time dependent decay models such as the logistic and Gompertz models.

1 Introduction

The use of the intracellular dye carboxyfluorescein succinimidyl ester (CFSE) in proliferation assays has become an essential tool in mapping cellular division histories since its introduction in 1994 [17, 18, 19, 20, 23]–see also the recent surveys in [6, 12, 27]. The dye is first introduced into cell cultures in the minimally fluorescent form of carboxyfluorescein diacetate succinimidyl ester (CFDA-SE) which is able to freely diffuse across cell membranes and is readily taken up by cells. Once inside the cell, enzyme reactions with cellular esterases produce a stable fluorescent label within cells [23]. In vivo, measurable concentrations of the label remain within viable cells, regardless of type or activation, for several weeks, providing uniform labeling with little adverse effects on the cell’s intracellular machinery [6, 24, 27].

The importance of these techniques has led to a recent and intensive effort to develop and understand mathematical models for use in analysis of cell proliferation data [6, 12]. Among these are partial differential equation (PDE) structured population models which have been shown to accurately fit histogram data obtained from CFSE flow cytometry experiments [4, 5, 15, 16]. Recently one such model is the fragmentation equation which relates the structured population density n(t, x) to the rates of proliferation α(t, x) and death β(t, x) under the assumption of label decay with velocity $\frac{dx}{dt}=v(t,x)$ given by

$$\frac{\partial n(t,x)}{\partial t}+\frac{\partial [v(t,x)n(t,x)]}{\partial x}=-(\alpha (t,x)+\beta (t,x))n(t,x)+{\chi }_{[x_a,x^{\ast }]}4\alpha (t,2x-x_a)n(t,2x-x_a).$$ (1)

The structure variable x is the fluorescence intensity (FI) (in arbitrary units of intensity, UI) of the cells. Because this fluorescence intensity arises primarily from CFSE within the cell, we refer to this as a label structured population model (with label FI as opposed to age or size structure, etc. [22]). It is known that cells lose FI in time even in the absence of division as a result of the natural decay of CFSE and the turnover of intracellular proteins to which the fluorescent conjugates bind. The advection term in the equation above accounts for this phenomenon; it was shown in [4] that using a Gompertz [14] decay velocity yields an accurate description of the biphasic decay [21, 23, 28] of CFSE FI observed in data sets. The parameter x_a represents the natural autofluorescence intensity of cells in the absence of CFSE, assumed in (1) to be constant across the cell population.

A flow cytometer can be used to measure the fluorescence intensity (FI) of individual cells. The ability to make such measurements allows for the quantitative analysis of cell division, which has potential applications in areas ranging from cancer to immunosuppression therapies for transplant patients. Current mathematical models, such as those described above, allow one to estimate proliferation and death rates in terms of a CFSE FI structure variable as a surrogate for division number, so the manner in which CFSE naturally decays directly affects the cell turnover parameter estimates. Thus, the loss rate function, $\frac{dx}{dt}=v(t,x)$, is of vital importance to the PDE formulations such as (1) and subsequently developed models.

The goal of such a mathematical model is to provide biologists with simple yet intuitive and meaningful parameters with which a population of dividing cells can be described. In particular, information such as average rates of division and cell viability are essential to the analysis of the effects of changing experimental conditions (e.g., differences in donors, differences between diseased and healthy cells) on proliferative behavior. The motivation for the use of FI as a structure variable is that the serial dilution of CFSE by cell division creates a correlation between measured FI and the number of divisions a cell has undergone. Thus the proliferation and death rate functions α(t, x) and β(t, x), which are estimated in terms of the structure variable x as well as time, can be used to compute average division rates in terms of the number of divisions undergone [4]. While the model (1) is advantageous in being able to estimate average proliferation and death rates without any deconvolution [13] of the data into cell numbers, it cannot be used to accurately assess the number of cells in a particular generation. To better understand rates at the generation number cohort or division number cohort level, one should attempt to develop individual (cohort) dynamics to investigate the CFSE data.

Fortunately, a simple reformulation of (1) allows such an approach and permits both the accurate quantification of total cells per division number and the accurate estimation of proliferation and death rates in terms of division number in such a framework. Rather than modeling the population with a single differential equation, one can model each individual generation of cells with a single equation,

$$\frac{\partial n_i}{\partial t}+\frac{\partial [v(t,x)n_i(t,x)]}{\partial x}=-({\alpha }_i(t)+{\beta }_i(t))n_i(t,x)+R_i(t,x),$$ (2)

with the generations linked through the division mechanism R_i(t, x) as a source term (see [7, 12, 26]). Because each generation of cells is assigned to a particular compartment (indexed by i) with unique proliferation and death rates, it is not necessary to estimate these rates in terms of the structure variable x, so that peak overlap and label decay no longer affect the accuracy of the estimated rates.

It was hypothesized in [5, 16] that an exponential rate of loss

$$v_1(x)=-c(x-x_a),$$ (3)

is sufficient to model the label loss observed in the data, but later shown [4] that a Gompertz decay velocity

$$v_2(t,x)=-c(x-x_a)e^{-kt},$$ (4)

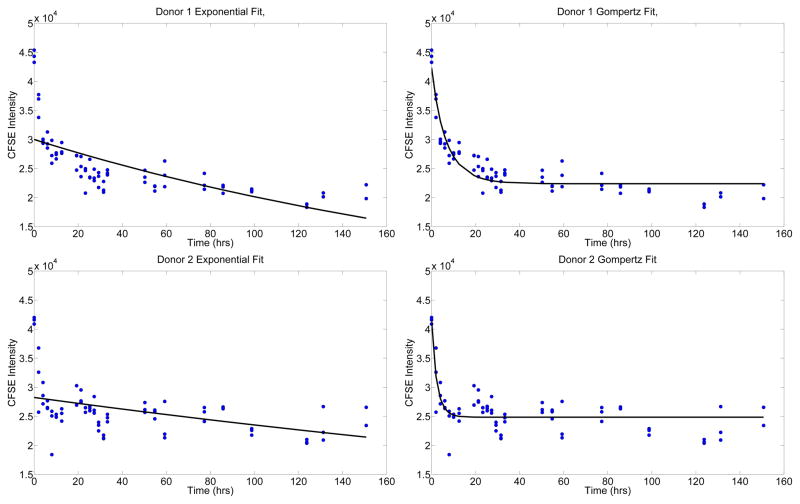
gave a significantly better fit to the flow cytometry data sets. (We remark that (4) is a generalization of (3), the latter being the limiting value (as k → 0) of the former.) It appears from the data fits in Figure 1 that the rate of exponential decay of label may itself decrease as a function of time. (This can be readily modeled by the Gompertz decay process.)

Figure 1.

Results of fitting the exponential model (3) and the Gompertz model (4) to the mean CFSE data. For both Donor 1 (top) and Donor 2 (bottom), we see that the Gompertz model is more capable of accurately replicating the observed data.

In order to investigate this assumption, a PBMC culture was taken from two donors and stained with CFSE following the standard procedure. However, these cells were not stimulated to divide. Because only viable cells are included when the cytometry data is gated, any decrease in mean FI in the population must be the result of natural CFSE FI decay. Over the course of 160 hours, cells from each donor were measured at 24 distinct time points in triplicate and the mean total FI of each sample was recorded. These data were used for the studies reported on here and are depicted in detail in [10].

We would like to determine the most appropriate functional forms which might be used in order to quantify the label loss observed in the data and that would also correspond to plausible biological assumptions. Through examination of the chemical properties and biological processes associated with CFDA-SE and its derivatives, namely CFSE, CF-R1, and CF-R2, we attempt to understand and model natural label decay in a cell treated with CFDA-SE. This allows us to test hypotheses regarding underlying mechanisms and formulate new assumptions about CFSE decay, future data, and the larger biological process of cell division. This also answers to a large extent the question raised in the recent overview [12, p.2695] regarding the need for basic understanding of label decay and appropriate forms for its mathematical representations in general proliferation assay models.

We first summarize our biological understanding of mechanisms related to CFSE labeling and subsequent loss in cells. Several biological models (increasing in simplicity) as formulated in [10] are given and findings with the corresponding mathematical models are discussed. In the final type of biological models tested, we consider decay represented by a single velocity term for total fluorescence loss and model these with exponential, logistic, and Gompertz decay mechanism fits-to-data, respectively.

2 Mechanistic Models of Growth and Decay

In the recent report [10], we examined and explained the characteristic features of several main types of differential equation representations that are frequently used to model growth and decay in dynamical systems of equations. The first is an exponential (also called Malthusian) growth and decay model ( $\frac{dx}{dt}=kx$) , for which a population is assumed to grow at a rate proportional to the size of the population at any given time [2, 3, 11, 14, 25]. The second is Michaelis-Menten kinetics [2, 25], which emulates enzyme mediated kinetics with velocity terms of the form $\frac{dx}{dt}=\frac{V_{\mathit{max}}x}{K_M+x}$. Finally, we use the Gompertz and logistic (also called Verhulst-Pearl) rate laws, which both involve time dependent growth/decay rates of the forms $\frac{dx}{dt}=\alpha x\text{ln}(\frac{K}{x})$ and $\frac{dx}{dt}=\alpha x(1-\frac{x}{K})$, respectively.

In order to better understand the process of label decay in cells treated with CFSE, we carried out a series of ordinary least squares (OLS) inverse problems (see [3]) for the different models of interest. Each of these models was evaluated according to its ability to provide fits to the experimental data. Although we have run the inverse problem on each model with every data set, we have only included here a summary of our results, referring the reader to [10] for further details. In this project, we assumed a constant variance statistical model [3] and thus focused on the ordinary least squares method.

3 Biological Models

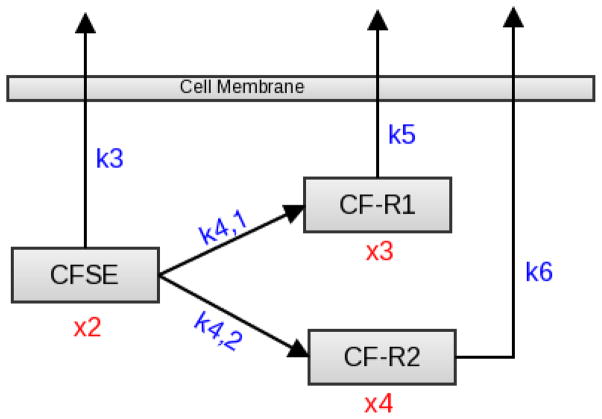
Due in part to the presence of two acetate esters in its structure, CFDA-SE has a high lipophilicity which allows it to passively diffuse across cell membranes [23], suggesting that both an inflow rate and an outflow rate should be accounted for. However, the data sets we are examining are the result of a particular procedure where, after initial exposure to CFDA-SE, the cell culture was flushed with water, eliminating any excess label [27]. Thus, the only source of CFDA-SE inflow would be re-entering CFDA-SE, which the data suggests is insignificant. Therefore, we considered it reasonable to assume that there is no continuing flow of CFDA-SE into the cell, but rather that all CFDA-SE is present inside the cell at the start of the procedure, as depicted in Figure 2.

Figure 2.

A schematic of the Basic Biological Model, with independent reaction rates from CFSE to CF-R1 and CF-R2.

Once inside the cell, CFDA-SE reacts with intracellular esterases, resulting in the formation of the highly fluorescent carboxyfluorescein succinimidyl ester (CFSE). At this point, our knowledge of the reaction is limited. Nonetheless, we know a great deal about the structure of the product, CFSE. The structure of CFSE lacks the two acetate esters present in CFDA-SE [23, 27, 29]. This absence decreases the lipophilicity of CFSE and renders it less membrane permeable. As before, this knowledge necessitates both inflow and outflow rates, but the data suggests that the mass of re-entering CFSE is insignificant in comparison to the mass of CFSE leaving the cell. Therefore, only the outflow of CFSE from the cell is assumed in our model. Additionally, the succinimidyl ester present in the structure of CFDA-SE is also present in CFSE. This succinimidyl moiety of CFSE is highly reactive with amino groups and can covalently couple 5-6-carboxyfluorescein (CF) to intracellular molecules [23]. Our knowledge of this reaction and its products is currently limited, but we are aware that two types of coupling can occur, yielding two types of products. One type of coupling occurs when CF is bound to a type of intracellular molecule, which we arbitrarily call R1-NH₂ that results in the conjugate CF-R1 which is unstable and quickly exits the cell or is degraded. The second type of coupling occurs when CF is bound to a type of long lived intracellular molecule, which we arbitrarily call R2-NH₂ that results in the conjugate CF-R2 that is stable and essentially membrane impermeable, maintaining a fluorescent label [23]. A initial schematic of this process within a cell is depicted in Figure 2 and is designated as the Basic Biological Model. The compartments x₁, x₂, x₃, x₄ represent concentrations of CFDA-SE, CFSE, CF-R1, CF-R2, respectively. In a subsequent model below we combined the compartments for CF-R1 and CF-R2 into a composite compartment x₅ representing the total concentration CF-R1 + CF-R2. Implementing the inverse problem processes in [3], we were able to calculate the parameters that produced the lowest cost functionals for the numerous models discussed below.

3.1 Basic Model: Exponential Decay

To begin with this basic biological model, we used law of mass action to obtain the system of equations

$$\begin{array}{l}\frac{{dx}_1}{dt}=-k_1{x}_1-k_2{x}_1\\ \frac{{dx}_2}{dt}=k_2{x}_1-k_3{x}_2-k_{4,1}{x}_2-k_{4,2}{x}_2\\ \frac{{dx}_3}{dt}=k_{4,1}{x}_2-k_5{x}_3\\ \frac{{dx}_4}{dt}=k_{4,2}{x}_2-k_6{x}_4,\end{array}$$ (5)

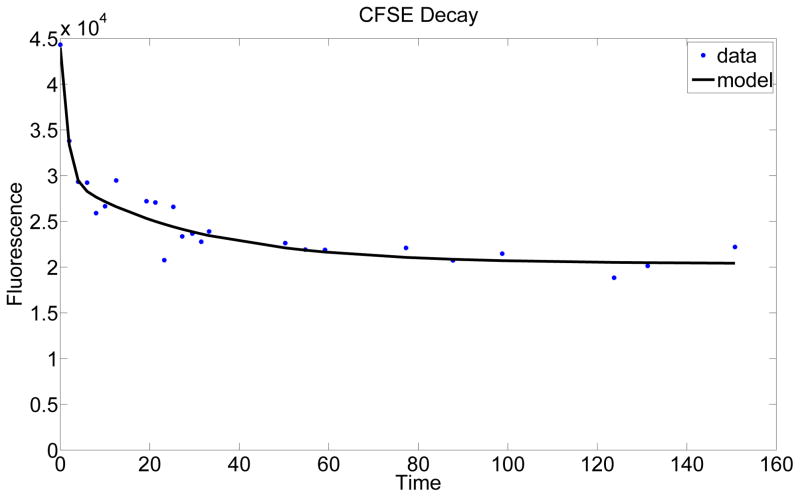
where k_4,1 and k_4,2 represent the rates of conversion to CF-R1 and CF-R2, respectively. The solution for the Basic Model versus the data set are presented in Figure 3. We obtained similar results with models using Michaelis-Menten kinetics for the conversion from x₁ to x₂ (which are thought to be enzyme regulated) as well as for subsequent models using bounded growth/decay Michaelis-Menten kinetics for all conversion rates.

Figure 3.

A plot of the solution to the Basic Biological Model against the first data set from Donor 1.

3.2 Biological Model R1

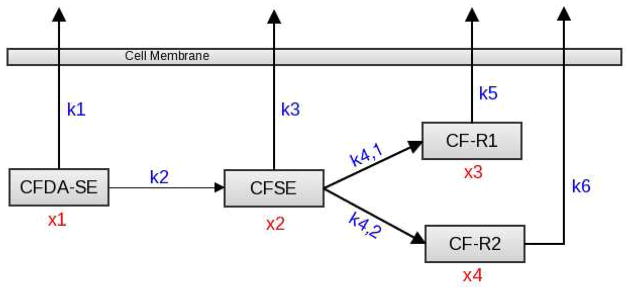
Upon further consideration, we embraced the hypothesis that CFDA-SE is converted to CFSE through the catalyzed hydrolysis of its acetyl esters by acetylesterase. It is generally accepted that intracellular esterases are responsible for the conversion of CFDA-SE to CFSE [23, 29]. These esterases are hydrolase enzymes that cleave the acetyl esters present in CFDA-SE into their parent carboxylic acid, acetate, and an alcohol [9]. The particular esterase which specializes in removing acetyl groups is called acetylesterase [1]. Further biological consideration [10] raised questions about the importance of the diffusion of CFDA-SE out of the cell, leading to the creation of a third biological model. Although we were comfortable with the assumption that there is no significant inflow of CFDA-SE into cells, previous models showed an efficient transfer of CFDA-SE to CFSE. This is consistent with the notion that catalyzed reactions occur quickly, so in the next model (denoted as the Biological Model R1 and depicted in Figure 4), all CFDA-SE was assumed to have already been converted to CFSE at t = 0 without any CF-R1 or CF-R2 yet present. Based on the assumption that CFDA-SE is immediately converted to CFSE, our original exponential system was altered to only depend on five rate parameters instead of seven, yielding a reduced system of equations. A three state mathematical model (x₂, x₃, x₄) for this biological model with exponential rates (or Michaelis-Menten rates) also produced reasonable fits-to-data similar to that depicted in Figure 3.

Figure 4.

A schematic of the Biological Model R1, assuming all CFDA-SE has already been converted to CFSE at t = 0.

3.3 Biological Models R2 and R3

Encouraged by our success in simplifying our model from four to three components, we decided to test simplification even further with several two-component systems. The first such system combines both of the CF-R1 and CF-R2 terms together as one single component. A schematic, depicted as the Biological Model R2, for this model is shown in Figure 5. Again a two state model with compartments (x₂, x₅) produced good fits to data with either exponential or Michaelis-Menten rates, comparable to those depicted in Figure 3.

Figure 5.

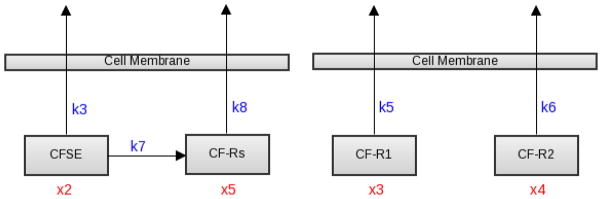
Left: A schematic of the Biological Model R2, in which the two CF-R1 and CF-R2 components combined as a single component; Right: Schematic of the Biological Model R3, which only accounts for the fluorescence loss given by CF-R1 and CF-R2.

For the Biological Model R3, there is only one loss function needed, and the differential equations can (as is the case for a number of our models) be solved analytically very easily. Accordingly, the equation for the fluorescence loss is given by

$$x(t)={cx}_0{e}^{-k_{5}t}+(1-c)x_0{e}^{-k_{6}t}$$ (6)

where the c term, 0 ≤ c ≤ 1, allows both components (x₃, x₄) to receive some of the initial fluorescence, denoted by x₀, with the loss rates of k₅, k₆, respectively. Simulation results for this model were similar to those for the Biological Model R2.

3.4 Simple Decay Models

In order to test ultimate simplification in our models, we carried out the inverse problem for the data sets using models with only one differential rate mechanism for label loss ( $\frac{dx}{dt}=v(t,x)$) instead of a system with multiple loss rates. These models only deal with the label loss, revealing the rate of change in the total fluorescence in the cell in the absence of cell division. We used exponential, logistic and Gompertz rates with sample results for exponential and Gompertz fits-to-data given in Figure 1. Results similar to those depicted in Figure 1 were found with the logistic model, giving fits-to-data virtually indistinguishable from those for the Gompertz model.

4 Results and Summary Remarks

In our efforts in [10], numerous different label loss models were investigated. Several questions related to model comparison were raised: How do we determine which of these models is the most efficient fit to the data? Is a model with fewer parameters and a larger cost function (poorer fit-to-data) better or worse than a model with more parameters and a lower cost function? How certain can one be that the model they deem to be the best is actually the best model? We used the Akaike Information Criterion (AIC) [8], which provides an approximately unbiased estimate of the Kullback-Leibler distance, or a measure of the distance between a model and the “truth” to analyze our findings. For details including our analysis of models, see [10].

After careful examination of related chemical processes and biological processes, twelve different mathematical models were formulated and analyzed for the rate of label decay in a cell treated with carboxyfluorescein diacetate succinimidyl ester (CDSA-SE). The first model, the Basic Biological Model, represents our best understanding of label staining, internal biochemistry and loss. It is important to note that CFDA-SE was disregarded after investigations of the Basic Biological Model; this was based on the assumption that CFDA-SE is converted to CFSE at a quickly catalyzed rate. The esterase reaction was hypothesized to specifically involve the enzyme acetylesterase, which binds to acetic ester and water, yielding alcohol and acetate as products. This knowledge led us to incorporate Michaelis-Menten kinetics to support the hypothesis that inflow of CFDA-SE and the rate of its conversion to CFSE can be ignored in model fitting to the data. Simple exponential, logistic and Gompertz decay rates were also used to model the decay of the total fluorescence. Although no specific model was the best fit for every data set, our AIC results suggest that any models which have multiple loss rate mechanisms are the models that most closely match the data. All of these models involve either multiple rates of label leaking/decay or a time-dependent rate for the decay of a single label quantity. These findings provide a reasonable explanation in support of the need for multiple or time variable decay rates involving CFSE labeling based on current best biological understanding of the labeling and loss processes.