The Welfare Effects of Medical Malpractice Liability

Abstract

We use variation in the generosity of local juries to identify the causal impact of medical malpractice liability on social welfare. Growth in malpractice payments contributed at most 5 percentage points to the 33% total real growth in medical expenditures from 1990-2003. On the other hand, malpractice leads to modest mortality reductions; the value of these more than likely exceeds the costs of malpractice liability. Therefore, reducing malpractice liability is unlikely to have a major impact on health care spending, and unlikely to be cost-effective over conventionally accepted values of a statistical life.

1. Introduction

Both physicians and the broader public identify the spiraling costs of malpractice insurance and lawsuits as a major problem facing the US health care system (cf, Blendon et al., 2002). Physician groups such as the American Medical Association have advocated federal limits on the damages that can be assessed in malpractice cases. Republican senators, governors, and presidents, have echoed this sentiment, and repeatedly pointed to rising malpractice costs as a major driver of growth in health care spending. Even many Democratic politicians who oppose limits on damages show little faith in the present tort liability system. For instance, President Obama has expressed opposition to damage caps, but he has also acknowledged the current liability environment as a major contributor to adverse outcomes for patients (Mullahy and Roberts, 2008), and expressed support, at least in principle, for reforming the tort system as it applies to health care.¹

The hardened political lines around malpractice reform belie major gaps in our understanding of the issue. This uncertainty caused the CBO (2006) and the GAO (1999) to conclude that the overall effects of malpractice exposure on total health spending and outcomes are simply not known. Some more recent effort post-dating these reports tackle the overall effects, but with some conflicting findings. As noted in two recent papers by Baicker and Chandra (2006; 2007), a strategy for causal inference is required, in order to elicit the policy implications of these relationships.

Fueling the political debate have been several apparently contradictory facts about malpractice. Opponents of malpractice reform often note that malpractice payments are a relatively small fraction – between 1 and 2 percent – of total expenditures on physician services. However, supporters of reform point to dramatic rises in malpractice costs (Mello et al., 2003). According to data from the National Practitioner Data Bank (NPDB), from 1991 to 2002 physicians’ real annual medical malpractice payments grew from $2.3 billion to $3.8 billion (65% growth).² Over the same time period, real health expenditures on physician services grew from $221 billion to $325 billion (47% growth).³ The total share of malpractice liability relative to expenditures also rose over this period; liability relative to expenditures on physician services displayed a general upward trend rising from a low of about 1.05% in 1991 to a high of over 1.3% in 2001. Moreover, previous research provides a mechanism for even modest malpractice payments to have a disproportionately large effect on total medical costs. Using data on elderly heart attack patients, Kessler and McClellan (2002a; 1996; 2002b) find that the threat of liability from medical malpractice causes doctors to practice “defensive medicine,” performing extraneous (and expensive) tests and medical procedures to ward off the possibility of a malpractice suit.

The identification of “defensive medicine” by Kessler and McClellan has been confirmed and deepened by a number of important studies. Several paper have identified a relationship between malpractice costs on the use of obstetric and pre-natal procedures (Corrigan et al., 1996; Dubay et al., 1999; Dubay et al., 2001; Tussing et al., 1994), more general medical practices (Bovbjerg et al., 1996), and the labor supply of physicians (Encinosa and Hellinger, 2005; Helland and Showalter, 2006; Kessler et al., 2005; Klick and Stratmann, 2007; Matsa, 2007). ⁴ Currie and MacLeod (2008) offer a more nuanced account of the impact of malpractice on physician behavior. While they find that tort reforms impact the behavior of obstetricians, they actually find that malpractice can deter some riskier procedures (e.g., caesarean sections).

More recent work has tried to establish the effect between malpractice pressure and aggregate health care costs. Avraham et al. (2010) find that tort reform is associated with declines in premiums for employer-provided health insurance premiums. Baicker and Chandra (2007) find evidence that malpractice pressure is associated with more diagnostic imaging. These papers, as well as a working paper version of this manuscript, helped shift the CBO’s thinking and they created an estimate of the potential cost savings from tort reform (CBO, 2009). However, there remains controversy about the overall size of the effects, as other work found no evidence that malpractice reforms had any effect on payments in Medicare (Sloan and Shadle, 2009).

While the mechanisms from malpractice to medical care have been studied, the overall welfare consequences of reducing malpractice costs have not received the same consideration, for two reasons. First, much of the causal research on defensive medicine has focused on particular kinds of patients, so as to homogenize the study population. For example, Kessler and McClellan caution that their studies were designed not to estimate the impact of malpractice risk on total medical spending, but rather the impacts on the treatment, costs, and outcomes of heart attack patients (Kessler and McClellan, 2002a; Kessler and McClellan, 1996, 2002b). Other researchers have focused on different subpopulations like expectant mothers (cf, Currie and MacLeod, 2008; Dubay et al., 1999). Unfortunately, the effects of malpractice are not always uniform and are difficult to generalize across the population (Congressional Budget Office, 2006).

Second, the dominant identification strategy to date has relied upon state-level tort reform. The empirical evidence supports tort reform’s validity in the frequently studied contexts of heart attack patients and expectant mothers (cf, Currie and MacLeod, 2008; Kessler and McClellan, 2002a). However, questions have been raised about validity in the study of overall medical costs and outcomes. Danzon (2000) argues that states with managed care may have been more likely to adopt tort reform measures, and that the cost savings attributed to tort reform could be a result of managed care itself.⁵ In the context of overall costs, the CBO finds empirical evidence consistent with this argument: reform states are more likely to have slower growth in total health care spending prior to the reform’s adoption (Congressional Budget Office, 2006).

In this paper, we attempt to quantify the social welfare effects of medical malpractice, and to do so with a new identification strategy. Our strategy relies on changes over time in the generosity of local juries. Using this approach, we find that malpractice risk increases medical spending in the aggregate, above and beyond its direct effects, but the total impact on overall medical costs is relatively modest. A ten percent reduction in malpractice costs would reduce total health care expenditures by, at most, 1.2 percent. During the malpractice “crisis” of the 1990s, we predict this would have added about 5 percent to real hospital expenditure growth, which exceeded 33% over this period. Using the same identification strategy, we find that, on the margin, 10 percent increases in malpractice costs reduce mortality by a modest amount, approximately 0.2%. Using values of a statistical life most commonly adopted by US regulators, the value of the mortality decline more than likely outweighs the increase in medical costs. On balance, reducing malpractice costs is more likely to harm than improve social welfare.

We proceed as follows. In Section 2, we present our framework for analysis. Section 3 describes how we measure the various components of medical costs and malpractice risk. Section 4 describes our data sources. Section 5 presents a number of tests that we perform to test the validity of our empirical strategy. Section 6 presents our results for costs, mortality, and overall welfare. Finally, we conclude with a discussion of directions for future research. Additional details about our data and methods are available in on online appendix.

2. Analytic Framework

2.1 A Framework for Welfare-Estimation

The standard approach to evaluating the welfare consequences of medical care is to estimate the social value of lives saved, and offset this against the cost of care (Cutler and McClellan, 2001; Murphy and Topel, 2006; Philipson and Jena, 2006). This abstracts from the value of morbidity reduction and the external benefits of care (e.g., the altruistic value of saving lives among the poor, or productivity spillovers from better health), but provides a concise summary of the most rigorously quantifiable components of health care value. Previous researchers have adopted a similar strategy on malpractice (Kessler and McClellan, 1996). The exclusion of other health benefits implies that our approach provides a conservative estimate for the value of malpractice liability.

In keeping with the literature, we conceive of social welfare (SW) as the value of health (H) to patients, net of medical spending (S); for completeness, we also net out the deadweight costs of transferring resources via the malpractice system. The effect of expected malpractice costs, E(M), on social welfare is given by:

$$\frac{\partial \mathit{SW}}{\partial E(M)}=\lambda \frac{\partial H}{\partial E(M)}-\frac{\partial S}{\partial E(M)}-\frac{\partial D}{\partial E(M)}$$

λ is the monetary value of health, and D is the deadweight loss of delivering malpractice benefits.

Given the controversy surrounding the monetary value of health, it is convenient to estimate welfare consequences by identifying λ*, the cost per unit of health produced by the malpractice system; this is defined as the value of λ at which $\frac{\partial \mathit{SW}}{\partial E(M)}=0$. For example, if health is measured by the number of lives saved, λ* represents the cost of saving a life through the malpractice system. More generally, if λ* exceeds conventional estimates of the willingness to pay for health, expected malpractice costs are lowering social welfare on the margin, and vice-versa. λ* can be written as:

$${\lambda }^{\ast }\equiv \frac{(\frac{\partial S}{\partial E(M)}+\frac{\partial D}{\partial E(M)})}{\frac{\partial H}{\partial E(M)}}$$ (1)

In the appendix we show that, relying on prior literature estimating that $\frac{\partial D}{\partial E(M)}=1$, this can be reduced to the simpler expression ${\lambda }^{\ast }=\frac{{\beta }_{1}S}{{\gamma }_{1}H}$, where β₁ and γ₁are the regression coefficients of spending and health, respectively, regressed against expected malpractice costs. Intuitively, the welfare parameter of interest is the ratio between the absolute cost impact of malpractice and its absolute longevity impact.

OLS estimation of β₁ and γ₁ can be biased by the behavioral responses of physicians. Greater treatment intensity will raise medical costs and lower malpractice costs. For example, if defensive medicine works, counties with high treatment intensity will have low malpractice costs; ordinary least squares would thus suggest that higher malpractice costs lead to lower medical costs, when in fact the opposite is occurring.

Our approach is to use the noneconomic component of jury awards as an instrument for expected malpractice costs. The underlying assumption here is that jurists determine pain and suffering awards independently of economic awards, conditional on other area and case characteristics. In the appendix we provide a theoretical framework that formally derives the assumptions that are necessary for this approach to be valid, and derive a number of testable implications. In what follows we outline the empirical model that we use to test the predicted relationships and assumptions, taking these derivations as given.

2.2 Econometric Framework and Testable Implications

We propose a two-stage estimation model where average noneconomic awards drive expected malpractice verdicts in the first stage, and expected malpractice verdicts drive medical expenditures or average mortality rates in the second stage. Our verdict data are available at the county-year level, so that is the level at which we implement our first stage. The first-stage regression equation can be expressed as a regression model of expected jury verdicts that accounts for variation across counties and over time as:

$$E(V_{\mathit{ct}})={\gamma }_0+{\gamma }_{1}E({\mathit{NE}}_{\mathit{ct}})+{\gamma }_3{\overline{X}}_{\mathit{ct}}+{\varphi }_c+{\delta }_t+{\eta }_{\mathit{ct}}$$

Where E(V_ct) is the expected value of malpractice verdicts in county c in year t, E(NE_ct) is the expected value of noneconomic damage awards in a county-year, X̄ represents a set of average, aggregate county characteristics (e.g., mean per-capita income), and ϕ_c and δ_t are county and year fixed-effects, respectively. Successfully using this as a first-stage regression equation requires excluding any covariates that would be endogenous in the second-stage cost and mortality equations in expression.

For E (NE_ct) to be a valid instrument, the following assumption must hold:

• A-1E*(NE_ct) ⊥ E*(E_ct): unexplained variation in non-economic awards is uncorrelated with unexplained variation in economic awards.

This assumption requires that the residual variation in noneconomic damages reflects jurors’ estimates for the value of pain and suffering; in the theory model we show that this is uncorrelated with other prices and market factors in our framework. This assumption leads to the testable hypothesis:

• H-1Residual variation in county-level non-economic awards is uncorrelated with residual variation in county-level economic awards.

The next key assumption is the standard instrumental variables assumption, where Y is some outcome of interest (medical expenditures or mortality):

• A-2. E*(NE_ct) ⊥ E(Y): residual non-economic damage awards are unrelated to medical costs, treatment intensity, and the patient outcomes influenced by intensity.

This assumption is in keeping with the theoretical prediction that pain and suffering awards are unrelated to measurable factors like medical costs and treatment intensity. It implies the testable hypothesis:

• H-2Higher medical costs do not lead to higher non-economic damage awards;

Finally, identification requires that our instrument be powerful and relevant. Since rational physicians and patients understand the components of verdicts, higher non-economic damages should cause individuals to update their expectations about malpractice costs.⁶ Greater malpractice risk has the first-order effect of raising malpractice costs. Moreover, greater malpractice risk generates higher malpractice cost, higher medical costs, and higher treatment intensity. These results imply the last two testable hypotheses:

• H-3Higher non-economic damage awards lead to higher medical costs and treatment intensity.
• H-4Higher non-economic damage awards lead to higher expected malpractice costs.

Performing the substitution E(V) = E(M), where M equals expected total malpractice cost (not just verdicts) produces the model for county c at time t:

$$\begin{array}{l}\ln S_{\mathit{ct}}={\beta }_0+{\beta }_{1}E(M)+{\beta }_2{\overline{X}}_{\mathit{ct}}+{\varphi }_c+{\delta }_t+{\nu }_{\mathit{ct}}\\ \ln H_{\mathit{ct}}={\gamma }_0+{\gamma }_{1}E(M)+{\gamma }_2{\overline{X}}_{\mathit{ct}}+{\varphi }_c+{\delta }_t+{\psi }_{\mathit{ct}}\\ E(M)={\alpha }_0+{\alpha }_{1}E({\mathit{NE}}_{\mathit{ct}})+{\alpha }_2{\overline{X}}_{\mathit{ct}}+{\varphi }_c+{\delta }_t+{\zeta }_{\mathit{ct}}\end{array}$$ (2)

Where S_ct measures county-year medical spending and H_ct measures county-year level health (mortality rates). For some specifications of medical spending, we run models at the hospital-, rather than county-level. These incorporate hospital, rather than county, fixed-effects.

3. Measurement

The framework developed earlier poses three challenges for empirical implementation: measuring expected malpractice costs, E(M); measuring health; and measuring medical costs.

3.1 Measuring Expected Malpractice Costs

Earlier, we assumed that expected malpractice costs are equal to the verdicts expected at trial. A stronger and empirically tractable version of this assumption is that lagged verdicts reflect current expectations about potential trial verdicts and predict expected malpractice costs, including settlements. If true, we can measure expected malpractice costs as a function of past verdicts in a county, according to:

$$E(M_{\mathit{ct}}\mid V_{c,t-1},V_{c,t-2},\dots )$$ (3)

where V_c,t−i represents jury verdicts in county c and time t − i. In the appendix we demonstrate the reliability of this strategy, and show that we can best identify the effect of malpractice by using moving averages of 3 years of lagged jury verdicts.

Based on this reasoning, we assume that moving averages of verdicts predict expected malpractice costs, or that E(M_ct) = bMA(V_c,t−i). This assumption yields our final set of estimating equations:

$$\begin{array}{l}\ln S_{\mathit{ct}}={\beta }_0+{\beta }_1\mathit{bMA}(V_{c,t-i})+{\beta }_2{\overline{X}}_{\mathit{ct}}+{\varphi }_c+{\delta }_t+{\nu }_{\mathit{ct}}\\ \ln H_{\mathit{ct}}={\gamma }_0+{\gamma }_1\mathit{bMA}(V_{c,t-i})+{\gamma }_2{\overline{X}}_{\mathit{ct}}+{\varphi }_c+{\delta }_t+{\psi }_{\mathit{ct}}\\ \mathit{MA}(V_{c,t-i})={\alpha }_0+{\alpha }_1\mathit{cMA}({\mathit{NE}}_{\mathit{ct}})+{\alpha }_2{\overline{X}}_{\mathit{ct}}+{\varphi }_c+{\delta }_t+{\zeta }_{\mathit{ct}}\end{array}$$ (4)

In spite of the measurement error in estimating expected malpractice verdicts and costs, we can consistently estimate the key welfare parameter, ${\lambda }^{\ast }=\frac{{\beta }_1(p\tau )}{{\gamma }_{1}H}=(\frac{{\beta }_{1}b(p\tau )}{{\gamma }_1\mathit{bH}})$, because the measurement error biases both the numerator and denominator proportionally. However, the estimation error is likely to cause the IV model to overstate the impact of malpractice on the individual outcome variables (proven in the appendix).

3.2 Measuring Health

We measure county-level health using information on mortality. This excludes any impacts of malpractice on morbidity or functional status, but has the advantage of focusing on a well-measured dimension of health. Assuming that malpractice has qualitatively similar effects on morbidity as on mortality, our estimated effects on health are too small and our estimate of λ* correspondingly too large. In other words, we understate the case for malpractice liability.

3.3 Measuring Medical Costs

We measure medical costs using data from Medicare and total hospital spending. These components together cover about two-thirds of the health care spending exposed to malpractice liability. The remainder consists of physician services paid for outside Medicare.

4. Data

4.1 Jury Verdicts

We use the RAND Jury Verdicts Database (JVDB) to recover verdicts data. The RAND JVDB contains information from 1985 to 1999 on jury verdicts occurring in all counties in the states of New York and California, as well as Cook County, IL (Chicago), Harris County, TX (Houston), King County, WA (Seattle) and the counties in the greater St. Louis, MO area (125 counties in all). These data cover 23.6% of the total US population, as of the 2000 Census.

Table 1 reports the geographic composition of the JVDB counties, ranked in decreasing order of population size. The Los Angeles metro area accounts for about 15% of the population covered by our sample, and the New York City metro area accounts for about the same. The cities outside New York and California represent about one-fifth of the data’s population weight.

Table 1.

Geographical composition of the counties in the JVDB sample.

County	2000 Population	Population Share
Los Angeles County, CA	9,519,338	14.6%
Cook County, IL	5,376,741	8.3%
Harris County, TX	3,400,578	5.2%
Orange County, CA	2,846,289	4.4%
San Diego County, CA	2,813,833	4.3%
Kings County, NY	2,465,326	3.8%
Queens County, NY	2,229,379	3.4%
King County, WA	1,737,034	2.7%
San Bernardino County, CA	1,709,434	2.6%
Santa Clara County, CA	1,682,585	2.6%
Riverside County, CA	1,545,387	2.4%
New York County, NY	1,537,195	2.4%
Alameda County, CA	1,443,741	2.2%
Suffolk County, NY	1,419,369	2.2%
St. Louis County, MO	1,846,486	2.8%
Nassau County, NY	1,334,544	2.1%
Bronx County, NY	1,332,650	2.0%
Sacramento County, CA	1,223,499	1.9%
Rest of California	11,054,004	17.0%
Rest of New York	8,494,928	13.1%

Notes: The population numbers for St. Louis County include the population of Jefferson County and St. Charles County.

The data in the JVDB are collected from court reporter publications, which provide trial attorneys with information on verdicts in local courts.⁷ The JVDB includes data on plaintiff win rates, average economic and noneconomic damage awards and type of injury for medical malpractice and other tort cases.

Table 2 shows the JVDB county-level averages for: total malpractice awards, malpractice awards per capita, average noneconomic damages awards per plaintiff win, and total jury verdict awards in all tort cases. The columns of the table present the current year’s average (year t), along with 3-year moving averages, defined as the mean across years t − 1, t − 2, and t − 3. On a per capita basis, the average county hands out $2.87 in malpractice awards. Larger counties tend to award more per capita: the population-weighted county average is $6.07. The average verdict in our sample involves a noneconomic award of $142,000, and an economic award of $328,000, where both means are higher on a population-weighted basis. Malpractice cases involve higher verdicts, due to higher noneconomic and economic damage awards.

Table 2.

Unweighted and Population-Weighted Means for Malpractice Variables.

	Single Year		3-Year Moving Average
	Unweighted	Weighted	Unweighted	Weighted
County-Level Means
Total Malpractice Awards (thousands)	2,949 (12,718)	16,837 (26,590)	2,772 (10,053)	16,613 (21,198)
Malpractice Awards Per Capita (dollars)	2.87 (18.06)	6.07 (14.57)	2.04 (7.96)	5.77 (8.87)
Verdict-Level Means
Average Noneconomic Award: All Cases (thousands)	142 (530)	312 (593)	105 (299)	292 (425)
Average Economic Award: All Cases (thousands)	328 (2,465)	634 (1,656)	200 (430)	585 (514)
Average Noneconomic Award: Malpractice Cases (thousands)	173 (803)	501 (1,120)	117 (484)	445 (740)
Average Economic Award: Malpractice Cases (thousands)	377 (2,691)	1,096 (2,646)	286 (885)	1,050 (1,446)
N	1,785		1,547

Notes: The table presents means (standard deviations in parentheses) of the average total jury awards in medical malpractice cases, average total malpractice awards per capita, average award for noneconomic damages in all tort cases with a plaintiff victory (defined as a nonzero damage award), and the total amount of awards in all tort cases. The unit of analysis is a county-year, or a verdict, as appropriate. Data come from the RAND JVDB, and include all counties in New York and California, as well as Cook County, IL (Chicago), King County, WA (Seattle), Harris County, TX (Houston) and all counties in the St. Louis, MO metropolitan area. The columns reporting lagged data represent the average of three years of lags. Data are available in the JVDB for 120 counties covering 15 years (1985-1999), but 2 years of data are lost to compute the 3-year moving average.

4.2 Hospital Costs and Utilization

Data on hospital spending, utilization, and facilities come from the American Hospital Association (AHA) database. Since 1946, the AHA has conducted an annual census of its member hospitals. We use data from the 1980 to 2003 survey years.

Hospital administrators are surveyed about their total facility expenditures over the most recent 12-month fiscal year, available resources at the end of that 12-month reporting period, and resource utilization during that period.⁸ Hospitals report information longitudinally. All costs, here and throughout the paper, are deflated over time using the overall Consumer Price Index.⁹

The upper panel of Table 3 summarizes the expenditure and utilization data from the AHA survey. Since our core regression models use the 1985-2003 data, we have restricted the summary statistics to cover these years. The table shows the weighted and unweighted statistics over the counties in our JVDB sample, as well as the corresponding numbers for all counties. The average person in our sample tends to live in a county with slightly higher expenditures and lower utilization than the average American, but these differences are typically around 5 percent.¹⁰

Table 3.

Unweighted and Population-Weighted Means of Medical Expenditures, Utilization, and County Characteristics.

	Counties in Sample		All Counties
	Unweighted	Weighted	Unweighted	Weighted
Hospital Level Expenditures
Hospital Facility Expenditures Per Bed (Thousands)	295 (233)	301 (231)	240 (220)	299 (252)
Hospital Facility Expenditures Per Bed Day	480 (306)	578 (318)	396 (299)	545 (359)
Total Days Per Hospital Bed	737 (796)	589 (560)	707 (821)	637 (697)
N	18,745		120,973
County Medicare Expenditures
Part A Expenditures Per Enrollee	2,220 (829)	2,512 (1,041)	2,226 (843)	2,385 (879)
Part B Expenditures Per Enrollee	1,413 (528)	1,518 (545)	1,431 (696)	1,510 (623)
County Demographics
Per Capita Income	21,325 (8,600)	25,782 (10,209)	17,769 (6,085)	22,745 (8,747)
Fraction Male	0.50 (0.02)	0.49 (0.01)	0.49 (0.02)	0.49 (0.01)
Fraction White	0.89 (0.10)	0.78 (0.11)	0.89 (0.15)	0.83 (0.14)
Fraction African-American	0.06 (0.07)	0.13 (0.10)	0.09 (0.14)	0.13 (0.13)
N	2,261		58,387
County Mortality Rates
Total Deaths Per 1,000 Population	8.03 (2.76)	7.62 (2.59)	7.43 (4.16)	6.72 (4.24)
Deaths Per 1,000 Age 20 to 64	3.26 (1.36)	3.39 1.40	3.02 (1.88)	2.84 (1.94)
Deaths Per 1,000 Age 65 and up	48.42 (11.75)	47.75 (11.93)	44.84 (22.48)	40.33 (23.36)
	1,473		10,199

Notes: The table presents means (standard deviations in parentheses) of the average cost of medical care and other demographic characteristics. The unit of analysis for the hospital data is a hospital-year, and for the county-level data it is a county-year. The counties “in sample” include all counties in New York and California, as well as Cook County, IL (Chicago), King County, WA (Seattle), Harris County, TX (Houston) and all counties in the St. Louis, MO metropolitan area. The “all counties” data include all counties in the U.S. for which data are available. For confidentiality reasons, starting in1989 all mortality data for counties below 100,000 individuals are collapsed into a single unit by state. All variables cover the time period from 1985 to 2003. All dollar amounts are reported in thousands of year 2000 dollars, adjusted by the Consumer Price Index (series CUUR0000SA0).

4.3 County-Level Medicare Costs

From the Centers for Medicare and Medicaid Services (CMS), we obtained county-level data on Medicare expenditures, from 1980 to 2003. Based on their administrative records, CMS reports total Medicare Part A and B enrollees residing in a county, and total Parts A and B expenditures for the residents of each county.¹¹ Due to inconsistencies over time in the reporting of Medicare HMO data, we use Medicare fee-for-service expenditures and enrollees, with a focus on aged (not disabled or end-stage renal disease) enrollees.

The Medicare data are summarized in the second panel of Table 3. Part A is the inpatient hospital insurance portion of Medicare that is free to all eligible Americans (over age 65 or disabled). Part B covers physician visits, outpatient procedures, and diagnostic imaging. Eligible individuals must pay a premium for Part B, but approximately 94 percent¹² of Part A beneficiaries enroll. Therefore, we focus on costs per enrollee, rather than enrollment itself.

4.4 County-Level Characteristics

Information on county-level demographics is taken from the Area Resource File (ARF). The ARF collects county-level per capita income from the Bureau of Economic Analysis (BEA) Local Area Income Tapes. The data on population are from the Census Bureau, which produces estimates for intercensal years based on a demographic model of its own. The vector X_ct includes time-varying county-level demographic characteristics: proportion male, proportion black, proportion white, income per capita and its square, and proportion of the population in 5-year age categories (one category for every five-year age interval between 0 and 85, and a single category for 85+). These demographic data are summarized in the third panel of Table 3.

In addition, we control for the time-varying characteristics of the county’s jury verdicts, based on the JVDB data, with a set of variables measuring the proportion of cases that fall into each of the following mutually exclusive and exhaustive categories: no injury, physical injury but no permanent disability, partial disability, permanent and total disability, death, or multiple plaintiffs in the suit. This accounts for changes in the severity of injuries, which might affect the size of awards. These covariates appear in both the first- and second-stage models.

4.5 County-Level Mortality Rates

We compute county-level mortality rates using the Multiple Cause-of-Death Mortality Data taken from the National Vital Statistics System of the National Center for Health Statistics (NCHS). The NCHS data provide detailed cause-of-death information on all deaths that occur in the United States. We aggregate to the county level, for every year between 1982 and 2003. Separate death rates, defined as the number of deaths per 1,000 people, are calculated for: total population, 20-64 year-olds, and 65+ year-olds. To protect individual privacy, county identifiers are suppressed for counties with less than 100,000 people, beginning in 1989. Rather than excluding these counties, we construct an aggregate “small California county” and “small New York county” by using weighted means for the other variables. The county level death rates are described in the bottom panel of Table 3.

5. Tests of Identification

Above we noted four testable hypotheses that will be rejected if the key empirical assumptions fail to hold.

• H-1Residual variation in county-level non-economic awards is uncorrelated with residual variation in county-level economic awards;
• H-2Higher medical costs do not lead to higher non-economic damage awards;
• H-3Higher non-economic damage awards lead to higher medical costs;
• H-4Higher non-economic damage awards lead to higher malpractice costs.

The first two hypotheses test different aspects of instrument validity; the second two test its power and relevance.

5.1 Non-Economic and Economic Damage Awards

We first test Hypothesis 1, that residual variation in noneconomic awards is uncorrelated with residual variation in economic awards in malpractice. Specifically, we regress average noneconomic awards per plaintiff win at the county-year level against county and year fixed effects, the distribution of injuries and other county characteristics. We then run the same regression using average economic awards per capita as the dependent variable. We then compute the covariance between the residuals for both regression models. Residuals are computed for both the current year damages and the three-year moving averages. The point-estimate for correlation between the residuals is approximately 0.341 for the current year awards and 0.066 for the moving average; neither is statistically significant at the 10% level.¹³ Since unobserved variation in injury severity cuts against our hypothesis, this test is particularly strong.

5.2 Non-Economic Damages and Medical Outcomes

The theory predicts that medical costs and outcomes should not drive non-economic damage awards (Hypothesis 2), but that non-economic damage awards should increase medical costs, increase treatment intensity, and influence patient outcomes associated with greater intensity (Hypothesis 3).

As the first test of Hypothesis 2, we find that plaintiffs’ claimed medical losses are highly correlated with economic damage awards, but entirely uncorrelated with noneconomic damage awards. Table 3 presents the results of this test for the 2,328 malpractice cases that involved a plaintiff win in our sample. The first two columns of the table illustrate the estimated impact of claimed medical losses on the compensatory economic award granted by the jury, with and without non-medical losses, respectively. The second two columns provide similar estimates for the noneconomic award. An additional dollar of claimed medical and non-medical losses is associated with about a $0.34 and $0.22 higher economic awards, respectively (medical and non-medical damages are jointly significant, but only medical losses are statistically significant on their own). However, there is virtually no impact of claimed medical losses on noneconomic awards. The point estimates are smaller by at least an order of magnitude, and they are not statistically significant (individually or jointly).

Next, we show that past medical costs do not affect contemporaneous or current noneconomic damage awards (Hypothesis 2), but past noneconomic damages do affect current medical spending and intensity (Hypothesis 3). This suggests that causality runs from the instrument to medical spending, and not in the opposite (and invalid) direction.

To implement this pair of tests, we ran reduced-form versions of the instrumental variables model in equations 4, where health expenditures and mortality outcomes are regressed on the (lagged values of the) instrument, state and year fixed-effects, and all the exogenous covariates X. In addition to the reduced-forms, we ran analogous models regressing current health expenditures and outcomes on future values of the instrument, as a falsification test. Table 4 presents the results for four different expenditure measures as dependent variables, one dependent variable measuring inpatient utilization, and three dependent variables measuring mortality.

Table 4.

The Relationship between Claimed Economic Losses and Jury Awards in Medical Malpractice Cases.

	(1) Jury Award: Economic	(2) Jury Award: Economic	(3) Jury Award: Noneconomic	(4) Jury Award: Noneconomic
Claimed Economic Losses: Medical	0.337** (0.147)	0.380*** (0.141)	0.0002 (0.048)	0.005 (0.050)
Claimed Economic Losses: Non-medical	0.216 (0.208)		0.025 (0.066)
R-squared	0.29	0.29	0.09	0.09

Notes: Table presents the coefficients from OLS regression of different components of the compensatory jury award (economic and noneconomic) against claimed economic losses (medical and non-medical). The unit of observation is a verdict of a malpractice case with a plaintiff “win” (i.e., a nonzero dollar amount awarded to the plaintiff). Each regression has 2,328 observations. Regressions include county-, year-, and injury type fixed-effects. Standard errors clustered by county. A ** or *** represents statistical significance at the 5% or 1% level, respectively.

There are 16 regressions testing the causal link from lagged noneconomic damages to current medical spending (i.e., the 4 right-most columns); 11 yield significant effects at the 10% level. On the other hand, only one of the 20 regressions testing the opposite effect — of current health care spending on the current year or leads of noneconomic damages —is significant. This result is not an artifact of differences in power, since the regressions have narrower confidence intervals when we test for the reverse causality running from medical spending to noneconomic damages. Also note that the current year regressions have the most power, but fail to find any significant relationship. This is an important argument against the possibility that juries use current growth in medical spending as a reason to raise awards, or that an unobserved third factor simultaneously drives verdicts and medical spending.¹⁴

For utilization, we find little evidence of reverse causality, but also no reduced-form effects. This is consistent with our later findings that malpractice has little estimated impact on inpatient utilization.

Our findings with respect to mortality also support the validity and relevance of the instrument in estimating mortality effects. Of the 12 regressions comparing the impact of past noneconomic awards on current mortality rates, 6 imply a negative and statistically significant relationship at the 10% level or better. Conversely, none of the current or future noneconomic damage award coefficients are significant at conventional levels.

5.3 Non-Economic Damages and Expected Malpractice Costs

Finally, the theory implies that higher non-economic damage awards lead to higher expected malpractice costs (Hypothesis 4). If true, non-economic damages provide meaningful first-stage variation.

At a minimum, there should be a strong first-stage relationship, which is illustrated in Table 5. The instrument is the average noneconomic damage award, per plaintiff win, granted by juries in the county. The included endogenous variable is the total value of malpractice awards, per county resident. The first-stage model is always run at the county-level. For all the models with lagged noneconomic damages as the instrument, first-stage power meets the “rule of thumb” suggesting a Wald statistic of 10.0 or better.

Table 5.

Medical Costs, Health, and Noneconomic Damage Awards: Causality Tests of the Instrument.

	Timing of noneconomic award variable
	Moving average of leading values				Current Year (t)	Moving average of lagged values
	t+4, t+5, t+6	t+3, t+4, t+5	t+2, t+3, t+4	t+1, t+2, t+3		t-1, t-2, t-3	t-2, t-3, t-4	t-3, t-4, t-5	t-4, t-5, t-6
Hospital Cost Estimates
Dependent Variable: Hospital Facility Expenditures Per Bed
Noneconomic Award (Hundreds of Thousands)	-183.970 (365.466)	643.497 (555.175)	768.325* (424.522)	309.522 (439.570)	83.116 (157.477)	1,198.059*** (432.643)	2,393.893*** (554.984)	2,486.269*** (505.182)	943.709 (654.647)
Dependent Variable: Hospital Facility Expenditures Per Bed Day
Noneconomic Award (Hundreds of Thousands)	-0.119 (1.163)	0.571 (0.950)	0.738 (1.084)	-0.346 (0.783)	0.059 (0.433)	1.161 (1.084)	5.242*** (1.403)	4.661*** (1.297)	2.191 (1.438)
County Medicare Estimates
Dependent Variable: Medicare Part A Expenditures Per Enrollee
Noneconomic Award (Hundreds of Thousands)	2.778 (4.767)	0.821 (4.811)	4.774 (5.283)	6.143 (7.370)	1.578 (2.050)	21.940** (8.786)	31.916*** (11.537)	24.734** (10.853)	24.308* (12.920)
Dependent Variable: Medicare Part B Expenditures Per Enrollee
Noneconomic Award (Hundreds of Thousands)	1.063 (1.985)	1.559 (2.539)	2.471 (2.586)	3.144 (2.968)	1.492 (1.178)	10.320** (4.143)	7.789* (4.572)	5.117 (4.851)	5.195 (5.317)
Hospital Utilization Estimates
Dependent Variable: Hospital Days Per Bed
Noneconomic Award (Hundreds of Thousands)	-1.332 (2.250)	0.024 (3.069)	1.779 (2.233)	0.232 (1.427)	-0.300 (0.559)	0.188 (1.857)	-4.290 (3.501)	-4.026 (2.694)	-3.932 (2.472)
Mortality Estimates
Dependent Variable: Total Deaths Per 1,000 Population
Noneconomic Award (Hundreds of Thousands)	-0.021 (0.015)	-0.017 (0.017)	-0.015 (0.016)	-0.015 (0.014)	-0.004 (0.003)	-0.019* (0.010)	-0.014** (0.007)	-0.012* (0.007)	-0.006 (0.005)
Dependent Variable: Deaths Per 1,000 Age 20 to 64
Noneconomic Award (Hundreds of Thousands)	-0.013 (0.010)	-0.011 (0.010)	-0.011 (0.010)	-0.011 (0.009)	-0.003 (0.002)	-0.015** (0.006)	-0.011** (0.004)	-0.009 (0.007)	-0.007 (0.007)
Dependent Variable: Deaths Per 1,000 Age 65 and up
Noneconomic Award (Hundreds of Thousands)	-0.091 (0.065)	-0.060 (0.074)	-0.043 (0.066)	-0.038 (0.054)	-0.015 (0.014)	-0.064 (0.043)	-0.060* (0.033)	-0.049* (0.027)	-0.010 (0.025)

Note: Table shows the reduced-form estimates of average noneconomic damage awards on hospital and Medicare expenditures and on county mortality rates. Each coefficient is from a separate regression, with each column representing a different lag or lead for the noneconomic damages. The unit of analysis for the top panel is a hospital-year, while for the bottom panel it is a county-year. County population is used as a weight in all regressions. Other explanatory variables include hospital or county fixed-effects, year fixed-effects, as well as a quadratic for personal income per capita, the percent of the population that is male, white, African American, of Hispanic ethnicity, and that falls into 5-year age ranges. Robust standard errors allowing clustering at the county level are reported in parentheses. A *, **, or *** represents statistical significance at the 10, 5, or 1% level, respectively.

Next, we present several pieces of evidence that noneconomic awards cause agents to update their expectations about malpractice costs. The earlier finding that noneconomic awards affect medical costs are at least consistent with the idea that physicians update their belief. In addition, we verified that noneconomic awards are positively associated with both the insurance premia charged by malpractice insurers and with the probability of being sued (see appendix).

5.4 Impact of Tort Reform

The occurrence of tort reform generates a final potential validity issue to address. If in fact tort reform is driven by overall medical expenditures, and if tort reform affects noneconomic damages in our data, the instrument could be compromised. However, there are relatively few reforms adopted in our sampled states during the time period of study. California has the strictest reforms in our sample, and perhaps in the country, but these were adopted in 1979. ¹⁵ Missouri adopted a damage cap at the very beginning of our sample (1986), but excluding the initial year has no impact on our results. Illinois adopted reform in 1987, but it was ruled unconstitutional that same year. Other observed reforms likely had little effect on damage awards. For example, Texas adopted a cap on punitive damages in 1995, but punitive damages are rare in medical malpractice cases, and should have little effect on expected payments (Eisenberg et al., 1997).

6. Results

6.1 OLS Relationships

An instrumental variables approach is needed because, according to theory, treatment intensity simultaneously raises medical costs and reduces malpractice costs. To underscore the point, Table 6 presents for comparison OLS regression estimates of the relationship between expected malpractice costs (current and lagged) and medical costs and mortality rates. These regressions also include the full complement of covariates and fixed-effects discussed above. The OLS estimates imply that malpractice costs have either no effect or negative effects on hospital costs, in spite of ample evidence documenting a mechanism that works in the other direction. Similarly, the OLS results suggest that malpractice costs are associated with higher mortality rates. Both sets of results run counter to the theory, but may suffer from the endogeneity problem identified earlier.

Table 6.

First-Stage Regression Relationship between Malpractice Award Dollars Per Capita and Average Noneconomic Damage Awards Per Plaintiff Victory.

	Timing of malpractice award and average noneconomic damages variables
	Current Year (t)	Three-Year Moving Average of Lagged Values
		t-1, t-2, t-3	t-2, t-3, t-4	t-3, t-4, t-5	t-4, t-5, t-6
Malpractice Award Dollars Per Capita	1.150** (0.579)	0.631*** (0.169)	0.620*** (0.173)	0.581*** (0.161)	0.517*** (0.153)
Wald Statistic	3.954**	13.885***	12.775***	13.028***	11.335***
R2	0.519	0.747	0.733	0.731	0.737
N	1,785	1,547	1,547	1,547	1,547

Notes: The table reports the estimated effect of average noneconomic damage awards in all tort cases with a nonzero award to the plaintiff on total malpractice awards per capita. Each coefficient is from a separate regression, with each column representing a different lag for the dependent variable and the instrument. The unit of analysis is a county-year. The time periods for each regression are restricted by data availability; regressions for the current year period cover 1985-1999, the regression for lags 1 through 3 cover 1988-2000, the regressions for lags 2 through 4 cover 1989-2001, the regressions for lags 3 through 5 cover 1990 to 2002, and the regressions for lags 4 through 6 cover 1991 through 2003. County population is used as a weight in all regressions. Other explanatory variables include county and year fixed-effects, as well as county personal income per capita, the percent of the population that is male, white, African American, and that falls into 5-year age ranges. Robust standard errors allowing clustering at the county level are reported in parentheses. A *, **, or *** represents statistical significance at the 10, 5, or 1% level, respectively.

6.2 Causal Effects of Malpractice on Costs

6.2.1 Hospital Costs

We estimate our model of medical costs at the hospital level. Since our first-stage equation for malpractice costs is estimated at the county-level, this requires a two-sample IV approach (Angrist and Krueger, 1992). We estimate the first-stage equation, use the predicted values for malpractice in the second-stage, and calculate the standard errors via a bootstrap procedure. ¹⁶

The resulting instrumental variables estimates are given in Table 7. We model costs per bed, costs per bed-day, and days per bed (in the bottom panel).¹⁷ These represent three different measures of treatment intensity. Separate estimates are provided for the current measure of malpractice as well as each set of moving averages.

Table 7.

OLS Regression of Health Care Costs on Malpractice Costs.

	Timing of Malpractice Awards Per Capita:
	Current Year	Three-Year Moving Average: Lags 1, 2 and 3 Years
Hospital Cost Estimates
Dependent Variable: Hospital facility expenditures per bed
Malpractice Awards Per Capita	-117.459 (143.050)	-197.162 (197.106)
Elasticity	-0.0026	-0.0039
Dependent Variable: Hospital facility expenditures per bed-day
Malpractice Awards Per Capita	-0.296* (0.150)	-0.355 (0.564)
Elasticity	-0.0031	-0.0035
Total Deaths per 1,000 Population
Malpractice Awards Per Capita	0.005** (0.002)	0.013* (0.007)
Elasticity	0.0037	0.0092
Deaths per 1,000 Age 20 to 64
Malpractice Awards Per Capita	0.003* (0.001)	0.005 (0.004)
Elasticity	0.0042	0.0075
Deaths per 1,000 Age 65 and up
Malpractice Awards Per Capita	0.019*** (0.007)	0.050* (0.027)
Elasticity	0.0023	0.0059

Notes: The table reports the estimated effect of per capita malpractice jury award dollars on medical expenditures. Each coefficient is from a separate regression, and each column represents a different lag for the malpractice variable. The unit of analysis is a hospital-year. County population is used as a weight in all regressions. Other explanatory variables include hospital and year fixed-effects, a quadratic for per capita income, the percent of the population that is male, white, African-American, and that falls into 5-year age ranges. Elasticities are evaluated at the mean values of the dependent and independent variables. Robust standard errors allowing clustering at the county level are reported in parentheses.

^***A *** represents statistical significance at the 1% level.

Hospital costs account for the majority — approximately 60% — of total spending on hospitals, physicians, and clinical services, which represent the segment of the health care market exposed to malpractice risk. While the OLS models showed little relationship between malpractice and hospital costs, the IV models suggest that malpractice risk raises cost per bed-day and overall spending. There is no significant effect on total hospital quantity, although separate specifications revealed that malpractice significantly reduces total inpatient days and admissions. The overall elasticity of the hospital cost measures with respect to lagged malpractice cost ranges from approximately 0.02 to 0.08. While the elasticity for hospital costs never exceeds 0.1, it is considerably higher than the share of malpractice in medical costs, which is around 0.01 or 0.02. As a result, it must be the case that health care providers are changing their behavior in response to rising expected malpractice costs; a simple mechanical increase in costs with no behavioral change would not generate such a large effect.

6.2.2 Medicare Costs

The middle panels of Table 7 studies the relationship between malpractice costs and Medicare costs per enrollee. Medicare costs are a significant portion of total health expenditures, accounting for 30% of hospital costs and 20% of spending on physicians and clinical services (2000 National Health Expenditures data). The IV estimates suggest that malpractice risk raises Medicare Part A expenditures per enrollee, but has a somewhat smaller impact on Part B spending, which consists of outpatient and physician services spending. The elasticity for Part A spending ranges from 0.08 to 0.12. The elasticity for Part B is around 0.03 to 0.06. The evidence suggests a substantial indirect effect of malpractice — approximately 5-8% — on Part A spending.

The modest size of the Part B elasticities is consistent with earlier research finding small overall effects of malpractice on Medicare Part B, in spite of considerable impacts on specific diagnostic and imaging procedures (Baicker and Chandra, 2007).

6.2.3 Overall Effect on Costs

The estimates above help us calculate an estimated effect on total costs. The analysis of Medicare spending and total hospital spending covers approximately 66% of total US health care spending on hospitals, physicians, and clinical services, which is the segment of health care spending exposed to malpractice risk.¹⁸ Moreover, the uncovered portion is physician spending paid for outside Medicare. Our analysis suggests that physician costs are less responsive to malpractice risk, as confirmed by other research (Baicker and Chandra, 2007). Therefore, it seems plausible to assume that the effects of malpractice on physician costs are no higher than our estimates for hospital costs.

While our elasticities are not that sensitive to model choice, we use the t − 3 through t − 5 moving average models for this calculation, since those displayed the highest first-stage Wald statistic and are likely to display the best coverage rates as a result (Staiger and Stock, 1997). The estimated elasticity of malpractice on daily hospital expenditures is 0.078. Between 1991 and 2002, medical expenditures grew by 34%, while malpractice payments grew by 65%. Our point estimate would imply that, over this period, the growth in malpractice payments added 5.1% to the growth in medical expenditures. This represents about 15% of the total growth.

In absolute terms, this is rather a modest effect, but disproportionate to the very small share of malpractice in total medical spending. Doubling malpractice risk has a direct 2% impact on spending at most, but the total effect could be as high as 8%. Therefore, doctors do change their behavior in response to malpractice risk, even though the latter is not a major driver of overall health care costs.

The modest but persistent and significant effect sizes we estimate are robust to other specifications. In the appendix we show that the effect is robust to the inclusion of HMO penetration variables and controls for local variation in the number of attorneys per capita. Areas with more attorneys are likely more litigious on average and have higher expected malpractice liability costs, and could be correlated with other factors driving health care costs (e.g., if they were also systematically correlated with medical technology growth or other cost drivers). The findings in the appendix demonstrate that no such correlation is driving our results.

6.3 Malpractice Growth and Changes in Mortality

Faced with the threat of malpractice liability, physicians may undertake actions that limit risk to patients. As such, part or all of their behavioral response may improve outcomes for patients. We use our identification strategy to estimate the impact of malpractice on total county-level mortality rates.

One identification concern unique to the mortality estimates is the possibility that noneconomic damages influence mortality through channels other than malpractice. For example, lower payoffs to litigation may encourage people to avoid taking risks, since adverse outcomes are less well compensated. ¹⁹ We tested this and found that noneconomic damages significantly reduce non-accidental deaths, but have little to no impact on accidental deaths (see appendix). There and elsewhere, limiting our analysis to non-accidental deaths has no quantitative impact on our results.

We estimate the effect of malpractice risk on the total mortality rate, and deaths among individuals 20 to 64 or 65 and older. We do not disaggregate by specific causes of death because these data fields are generally considered unreliable on mortality statistics. The death rate is calculated as the number of deaths per 1,000 members of the county population.

The results appear in Table 9. The elasticities for total death rates with respect to malpractice costs are approximately 0.02. This implies that doubling malpractice costs lowers the total death rate by 2 percent. The age-specific breakdowns suggest these effects are stronger for the non-elderly, although this could be due to greater statistical noise in the estimates for the elderly.

Table 9.

The Impact of Malpractice on County Level Mortality.

	Timing of noneconomic damage awards and malpractice awards
	Current Year (t)	Moving average of lagged values
		t-1, t-2, t-3	t-2, t-3, t-4	t-3, t-4,t-5	t-4, t-5, t-6
		Total Deaths Per 1,000 Population
Malpractice Awards Per Capita	-0.005 (0.004)	-0.035* (0.018)	-0.026* (0.014)	-0.023** (0.010)	-0.012 (0.009)
Elasticity	-0.0036	-0.0258	-0.0192	-0.0171	-0.0094
		Deaths Per 1,000 Age 20 to 64
Malpractice Awards Per Capita	-0.004 (0.003)	-0.028** (0.011)	-0.021** (0.009)	-0.019 (0.012)	-0.017 (0.015)
Elasticity	-0.0060	-0.0457	-0.0351	-0.0328	-0.0299
		Deaths Per 1,000 Age 65 and up
Malpractice Awards Per Capita	-0.016 (0.017)	-0.112 (0.080)	-0.099 (0.063)	-0.079* (0.040)	-0.015 (0.050)
Elasticity	-0.0019	-0.0131	-0.0117	-0.0095	-0.0018

Notes: The table reports the estimated effect of per capita malpractice jury award dollars on aggregate mortality rates. Malpractice awards are instrumented by the average noneconomic awards in medical malpractice verdicts with a plaintiff win. Each coefficient is from a separate regression, and each column represents a different lag for the malpractice variable. The unit of analysis is a county-year. County population is used as a weight in all regressions. Other explanatory variables include county and year fixed-effects, a quadratic for per capita income, the percent of the population that is male, white, African-American, and that falls into 5-year age ranges. Elasticities are evaluated at the mean values of the dependent and independent variables. Robust standard errors allowing clustering at the county level are reported in parentheses. A *, **, or *** represents statistical significance at the 10, 5, or 1% level, respectively.

Overall, the results of Table 9 provide evidence that exposure to malpractice costs leads to modest reductions in mortality. The estimates are not uniformly precise, but consistently negative and significant, at least for total deaths. Still, it is hard to draw policy inferences from these results alone, because the confidence intervals often span ranges with inconsistent implications for net social benefit.

6.4 The Welfare Consequences of Changes in Malpractice Cost

As we argued earlier, the policy-relevant output is the cost per life saved by the malpractice system, as defined by λ* in equation 1. The statistical uncertainty around our estimates implies that we ought to examine the distribution of this parameter, not just its point-estimate. Comparing this distribution to conventional values for a statistical life yields a conclusion about the likely welfare consequences of a given policy change.

Our approach resembles the method of “cost-effectiveness acceptability curves” (cf, Fenwick et al., 2004; Lothgren and Zethraeus, 2000), which calculates the empirical distribution of the “dollars per life lost” parameter via a bootstrap methodology (whose technical underpinnings are discussed in the appendix). This distribution then implies a probability for whether or not malpractice cost-reduction is cost-effective, conditional on a value of life. ²⁰ For example, suppose we adopt the view that the value of a statistical life is $6m. Suppose further that the “dollars saved per life lost” parameter exceeds $6m about 40% of the time. In this case, lowering malpractice costs at the margin has a 40% probability of improving net social welfare.²¹

To estimate the distribution of λ*, or dollars spent per life saved, we use a bootstrap approach that jointly estimates the variance in the estimates of costs and mortality. We use the same bootstrap technique described earlier (see footnote 16), except here we use 1,000 replications, in order to gain more precision for the estimation of probabilities. We separately calculate distributions for the total population, and for the Medicare population.

To illustrate, we explicitly lay out the bootstrap algorithm for the Medicare analysis:

1. Randomly draw a county, and include all observations (years) from that county;

2. Repeat step 1, sampling with replacement, until the bootstrap sample of counties is complete;

3. Using the bootstrap sample constructed in steps 1 and 2, estimate the model in equations (4) using total Medicare spending per elderly beneficiary as the outcome. This yields an estimate for (β₁ (pτ))^Medicare, the effect of malpractice on Medicare costs.

4. With the same bootstrap sample used in step 3, estimate the model in 4 separately using county-level death rates for the over 65 population as the outcome. This provides an estimate of (γ₁ H)^Medicare, the effect of malpractice costs on Medicare mortality.

5. Using estimates of total nationwide deaths to measure H, and costs in the year 2000 to measure pτ,²² dollars per life gained in the Medicare population is given by:

   $${\lambda }^{\ast M}=\frac{{\beta }_1{(\mathrm{p}\tau )}^{\mathrm{Medicare}}}{{({\gamma }_{1}H)}^{\mathit{Medicare}}}$$ (5)

A similar procedure is used to estimate dollars per life in the overall population. We first estimate the model in equations 4 using total hospital costs per bed-day²³ aggregated to the county level²⁴ to derive the impact of malpractice costs on hospital costs. Estimating the model using total county-level mortality as the outcome then yields its impact on deaths. (We must assume that our hospital cost elasticity is not substantially different from the elasticity for other medical costs.²⁵) These are then combined with year 2000 data on total nationwide medical spending and total deaths, to estimate:²⁶

$${\lambda }^{\ast T}=\frac{{\beta }_1{(\mathrm{p}\tau )}^{\mathrm{Total}}}{{({\gamma }_{1}H)}^{\mathit{Total}}}$$ (6)

We conducted 1,000 bootstrap replications. For completeness, we repeated this procedure for all the various lag specifications reported in Table 7 and Table 9. Here, we present results using the t − 3 through t − 5 moving average specification, as this yielded the most powerful first-stage.²⁷

Figure 1 depicts the empirical cumulative distribution function for the estimated dollars per life saved.²⁸ For each dollar value, the Figure reveals the probability that dollars per life saved lies above that value, and thus the probability that malpractice cost-reduction is cost-effective. The figure can be interpreted as a “menu” of policy implications for malpractice cost-reduction, conditional on choices for the value of a statistical life.

Figure 1. The Welfare Impact of Reducing Malpractice Costs.

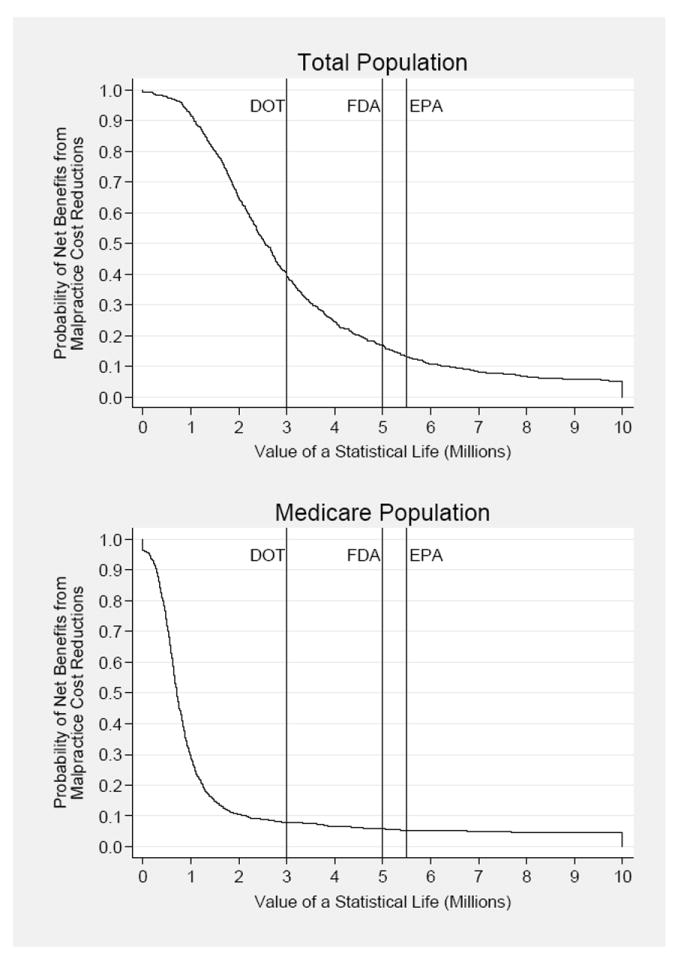
Notes: The curves depict the empirical probabilities that the estimated dollars saved per life lost exceed the given value of a statistical life. The empirical probabilities are based on 1000 bootstrap replications of the IV models in equations 2, which yield elasticities of malpractice cost on county-level mortality, and separately on medical costs. The results illustrated here use the three year moving average of malpractice costs lagged 3, 4 and 5 years. Vertical lines correspond to values of statistical life (in year 2000 dollars) used by the following federal government regulatory agencies: Department of Transportation (DOT), Food and Drug Administration (FDA), and Environmental Protection Agency (EPA).

In the Medicare population, tort reform is more likely than not to be cost-effective for values of a statistical life lower than $900,000. There is a stronger case for tort reform in the overall population, but it is much shakier than reliance on the borderline significance of the point estimates would suggest. Reductions in malpractice costs are more likely to be cost-ineffective for values at or above $2.5m.

Using the figure to assess the desirability of reducing malpractice costs requires clarity on the exact value of a statistical life. In a prominent literature review, Viscusi and Aldy locate the value of a statistical life within the range of $5.5m to $7.5m (Viscusi and Aldy, 2003). In their study on the social value of life-extension, Murphy and Topel (2006) advocate $6.3m as a weighted average applicable to those aged 25 and 55. Others have dissented markedly. Ashenfelter and Greenstone (2004) use the impact of speed limit increases on mortality to conclude that the value of a statistical life is bounded above by $1.5m. Malpractice cost reduction has a better than even chance of being cost-effective for values lower than $2m, but is a poor bet for the values cited by Viscusi and Aldy, or used by Murphy and Topel. In general, a nearly five-fold difference in this value makes it hard to draw unambiguous policy conclusions.

One way through the controversy is to follow the actual thresholds employed by US regulators. The US Environmental Protection Agency typically makes decisions based on a value of at least $5.2m (U.S. Environmental Protection Agency, 2002), while the Department of Transportation (along with the Federal Aviation Administration) most often uses $3m (U.S. Department of Transportation, 2002). Perhaps most directly relevant is the $5m number often used by the Food and Drug Administration (FDA) to assess health risks.²⁹ All these thresholds would imply that, on the margin, malpractice reform is more likely to be cost-ineffective. The FDA threshold implies that malpractice reform is more than 80% likely to be cost-ineffective. Therefore, any policymaker wishing to defend tort reform would need to depart from these accepted US regulatory practices, and advocate a lower value of statistical life than conventionally used, in order to justify their case.³⁰

7. Conclusions

The impact of liability for medical malpractice on the cost of medical care has been one of the highest profile issues in debates over the U.S. health care system for many years. Malpractice payments have grown enormously over the past 20 years, but this has likely had a modest impact on the cost of health care in the US. It may have other significant effects, such as decreasing the supply of physicians or changing the nature of treatment. Our findings, however, suggest that limiting malpractice liability is no panacea for rising health care costs.

Moreover, while the mortality benefits of malpractice may be quite modest, these seem more likely than not to justify its direct and indirect health care costs. Therefore, we conclude that — for values of statistical life traditionally employed by US regulators —reducing malpractice costs is not likely to be a worthwhile policy goal in itself. As emphasized by Currie and MacLeod (2008), however, specific policies must be evaluated on a case-by-case basis, as they can have unexpected effects on physicians’ expected liability and incentives. In addition, there may be policies that reduce malpractice costs but have other social benefits; we do not rule those out, but note that the case for their adoption rests on their auxiliary effects. Moreover, policies that make the malpractice system more efficient by lowering overhead costs without reducing the expected liability of physicians from providing negligent care would still be welfare enhancing. This is a nontrivial qualification given the findings of high overhead costs of each dollar of malpractice liability that is delivered to injured patients (Studdert, Mello et al. 2006).

At a minimum, our analysis reveals the tenuousness of the case for tort reform, but it is important to note its limitations. First, we account only for impacts of tort reform on medical costs and mortality, excluding its impacts (if any) on morbidity, physician utility, and patient satisfaction. These quantities are extremely difficult to measure objectively. In addition, we do not account for the adjustment costs (e.g., on the utilization of the health care system) that would be induced by any large-scale reform project. The size and even direction of these excluded effects is not clear. Finally, even if we ignore these limitations and accept the estimates at face value, the probabilistic nature of our analysis means we cannot rule with certainty for or against tort reform over the range of conventionally accepted values of life.

Putting our results together with earlier work suggests that malpractice may have substantial impacts on the care and costs of specific patient subgroups — like heart attack patients — but much more modest impacts on the average patient, and on health care spending as a whole. Future research should endeavor to determine whether tort reform can be targeted toward these subgroups in a cost-effective manner.

Another important avenue for future work is to evaluate whether malpractice has effects on more fine-grained measures of health outcomes— such as morbidity or disability — or on the nature of health care delivery. Medical costs and mortality are likely to be the first-order costs and benefits of changes to the malpractice system, but the auxiliary effects may be quite significant. If, for example, malpractice risk has had limited impacts on costs but appreciable positive impacts on average outcomes other than mortality, the malpractice “crisis” may be anything but. If, on the other hand, it has negative impacts on outcomes, the major costs of malpractice may be in health rather than in dollars.

Table 8.

The Impact of Malpractice on Hospital Costs and County Medicare Costs.

	Timing of noneconomic damage awards and malpractice awards
	Current Year (t)	Moving average of lagged values
		t-1, t-2, t-3	t-2, t-3, t-4	t-3, t-4, t-5	t-4, t-5, t-6
Hospital and County Medicare Cost Estimates
Dependent Variable: Hospital Facility Expenditures Per Bed
Malpractice Awards Per Capita	72.252 (202.170)	1,897.295* (1,077.975)	3,863.612*** (1,316.800)	4,282.672*** (1,403.649)	1,826.520 (2,176.261)
Elasticity	0.002	0.037	0.072	0.076	0.030
Dependent Variable: Hospital Facility Expenditures Per Bed Day
Malpractice Awards Per Capita	0.051 (0.402)	1.838 (2.184)	8.461*** (3.375)	8.030*** (3.177)	4.241 (4.384)
Elasticity	0.001	0.018	0.083	0.078	0.040
Dependent Variable: Medicare Part A Expenditures Per Enrollee
Malpractice Awards Per Capita	1.371 (1.939)	34.744** (15.316)	51.511*** (13.534)	42.605*** (15.102)	47.047* (24.127)
Elasticity	0.0036	0.0806	0.1162	0.0933	0.0989
Dependent Variable: Medicare Part B Expenditures Per Enrollee
Malpractice Awards Per Capita	1.297 (1.255)	16.343** (7.399)	12.571* (7.125)	8.815 (7.939)	10.055 (9.962)
Elasticity	0.0057	0.0632	0.0470	0.0320	0.0348
Hospital Utilization Estimates
Dependent Variable: Total Hospital Days Per Bed
Malpractice Awards Per Capita	-0.261 (0.654)	0.297 (4.855)	-6.924 (7.500)	-6.936 (5.757)	-7.609 (6.755)
Elasticity	-0.003	0.003	-0.068	-0.066	-0.070

Notes: The table reports the estimated effect of per capita malpractice jury award dollars on medical expenditures. In the IV models, malpractice awards are instrumented by the average noneconomic awards in all tort cases with a plaintiff win. Each coefficient is from a separate regression, and each column represents a different lag for the malpractice variable. The unit of analysis is a hospital-year for the hospital spending regressions, and a county-year for the county Medicare regressions. County population is used as a weight in all regressions. Other explanatory variables include hospital and year fixed-effects, a quadratic for per capita income, the percent of the population that is male, white, African-American, and that falls into 5-year age ranges. Elasticities are evaluated at the mean values of the dependent and independent variables. Robust standard errors allowing clustering at the county level are reported in parentheses. For the hospital level regressions, these standard errors are calculated using 500 bootstrap replications with bootstrap resampling done at the county level. A *, **, or *** represents statistical significance at the 10, 5, or 1% level, respectively.

Research highlights.

• We study the causal impact of medical malpractice liability on social welfare.

• Growth in malpractice payments contributed up to 15% of growth in medical costs from 1990-2003.

• The threat of malpractice liability also led to modest mortality reductions during this period.

• Reducing liability may not be cost-effective given conventional value of life estimates.

Appendix

In our paper we derived a number of theoretical and empirical findings to justify the validity and robustness of our approach. In the interest of preserving space and the readability of the manuscript, we present them here in the appendix. Each set of results is provided in the order in which its material is relevant in the manuscript.

1. Theoretical Framework

One question about our approach is whether noneconomic damages will be a valid instrument—both in the sense of whether it will have an effect on expectations and whether it is plausibly exogenous to provider behavior. Here we provide a theoretical framework that ties provider behavior to expected malpractice costs, expected malpractice costs to jury verdicts, and jury behavior to expected medical costs. We then formally derive the assumptions that are necessary for our assumptions to be valid, and describe how each of them is testable empirically.

1.1 Physician Behavior and the Malpractice Environment

A representative physician stands in for a competitive market. She decides how many patients to see, and how intensively to treat them. Patients possess fixed characteristics, X, which vary across physicians but not within them. Treatment intensity, τ, involves a marginal cost of c, and a unit price of p.¹ Intensity includes the number of diagnostic tests performed, the number of possible conditions addressed, and all other resource-consuming interventions. Greater treatment intensity may improve or worsen patient health outcomes.

The physician will pay an uncertain malpractice cost, M for each patient he sees. This includes: the actual compensation paid, in the form of settlements or jury verdicts; the deadweight costs of delivering these benefits, such as attorneys’ fees and court costs; and any nonpecuniary costs associated with defending against a malpractice claim, such as time spent or loss of reputation.

Crucially, however, the physician’s chosen treatment intensity may influence her expected malpractice costs. In principle, this could go in either direction. More surgeries could expose a physician to greater risk of committing errors, but more tests could insulate physicians against errors of omission. Our derivation focuses on the latter possibility, or that doctors practice “defensive medicine” on the margin. It is straightforward to develop the converse case in which treatment intensity raises malpractice costs.

It should be understood that our simple model reflects a wide variety of possible mechanisms. Greater treatment intensity could reduce the likelihood of a real medical error, but it could also reduce a patient’s likelihood of filing suit in the event of (or even in the absence of) an error, perhaps because the patient believes the physician did all that was possible. Finally, treatment intensity could also reduce the health harm suffered by a patient in the event of an error. The model includes all these channels through which costly interventions reduce expected malpractice liability.²

Formally, malpractice cost, M(R, τ, X), depends on: a local risk, R, that reflects local litigiousness, tort reforms, and other factors, so that E(M_R) > 0; and on the physician’s chosen treatment intensity, τ. As mentioned earlier, we assume that treatment intensity wards off lawsuits, so that E(M_τ) < 0. We also assume that physicians in riskier areas have greater incentives to reduce risk, in the sense that E(M_τR) < 0. To abstract from the roles of patients and insurers, we assume physicians internalize the resource costs of treatment. Therefore, physician expected profits are given by pτN − cτN − E(M(R, τ, X))N. The optimal level of treatment intensity is given by:

$$p-E(M_{\tau }(R,\tau ,X))=c$$

When R rises, so does the optimal treatment intensity, τ*.³ This raises the marginal social cost of treating each patient, cτ, and may also affect patient health outcomes by altering treatment intensity τ. As a result, growth in malpractice risk leads to higher medical costs. In equilibrium, it also leads to higher expected malpractice costs, as the physician’s behavioral response will be second-order.

1.2 A Framework for Welfare-Estimation

We define social welfare (SW) as the value of health (H) to patients, net of medical costs (cτ); for completeness, we also net out the deadweight costs of transferring resources via the malpractice system. The effect of expected malpractice costs, E(M), on social welfare is given by:

$$\frac{\partial \mathit{SW}}{\partial E(M)}=\lambda \frac{\partial H}{\partial E(M)}-c\frac{\partial \tau }{\partial E(M)}-\frac{\partial D}{\partial E(M)}$$

λ is the monetary value of health, and D is the deadweight loss of delivering malpractice benefits.

Given the controversy surrounding the monetary value of health, it is convenient to estimate welfare consequences by identifying λ*, the cost per unit of health produced by the malpractice system; this is defined as the value of λ at which $\frac{\partial \mathit{SW}}{\partial E(M)}=0$. For example, if health is measured by the number of lives saved, λ* represents the cost of saving a life through the malpractice system. More generally, if λ* exceeds conventional estimates of the willingness to pay for health, expected malpractice costs are lowering social welfare on the margin, and vice-versa. λ* can be written as:

$${\lambda }^{\ast }\equiv \frac{(c\frac{\partial \tau }{\partial E(M)}+\frac{\partial D}{\partial E(M)})}{\frac{\partial H}{\partial E(M)}}$$ (1)

The components of λ* can be recovered by estimating:

$$\begin{array}{ccc}\ln p_{\mathit{ct}}{\tau }_{\mathit{ct}}& =& {\beta }_0+{\beta }_{1}E(M)+{\beta }_2{\overline{X}}_{\mathit{ct}}+{\varphi }_c+{\delta }_t+{\nu }_{\mathit{ct}}\\ \ln H_{\mathit{ct}}& =& {\gamma }_0+{\gamma }_{1}E(M)+{\gamma }_2{\overline{X}}_{\mathit{ct}}+{\varphi }_c+{\delta }_t+{\psi }_{\mathit{ct}}\end{array}$$ (2)

Observe that $\frac{\partial H}{\partial E(M)}\equiv {\gamma }_{1}H$, and $c\frac{\partial \tau }{\partial E(M)}\equiv {\beta }_1(\mathit{p\tau })-1$.⁴ In addition, we rely on prior literature estimating that $\frac{\partial D}{\partial E(M)}=1$, or that it costs $1 of real resources (in lawyer time, for instance) to transfer $1 of malpractice liability to patients (through litigation or settlement) (Kakalik and Pace, 1986; Studdert et al., 2006). Taken together, these results imply that ${\lambda }^{\ast }=\frac{{\beta }_1(\mathit{p\tau })}{{\gamma }_{1}H}$. Intuitively, the welfare parameter of interest is the ratio between the absolute cost impact of malpractice and its absolute longevity impact.

OLS estimation of the medical cost equation in 2 is biased by the behavioral responses of physicians. Greater treatment intensity will raise medical costs and lower malpractice costs. This induces a correlation between the error term, ν, and the dependent variable, pτ. For example, if defensive medicine works, counties with high treatment intensity will have low malpractice costs; ordinary least squares would thus suggest that higher malpractice costs lead to lower medical costs, when in fact the opposite is occurring.

1.3 The Determination of Malpractice Costs

To solve this estimation problem, we specify a model of malpractice costs that results in a first-stage estimating equation for expected malpractice cost.

1.3.1 Malpractice Costs and Verdicts

We take the simple theoretical view that expected malpractice costs are always equal to the expected verdict (E(V)) a jury would hand down if a trial were to take place; this assumes settlements are reached in the shadow of possible litigation.⁵ While convenient for the theoretical exposition, the assumption of equality between expected verdicts and settlements is stricter than we need for the empirical analysis, which requires only that within-area changes in verdicts are strongly correlated with within-area changes in settlements, an assumption we test against the data.

A harmed patient can expect to receive a verdict equal to the jury’s estimation of his monetized utility loss. To align with the jury’s estimation problem, a harmed patient’s utility depends on “replaceable” goods, R, and “irreplaceable” goods, I. Replaceable goods – like property, wealth, or earnings – can be perfectly replaced in the market, but the loss of irreplaceable goods – like freedom from pain, presence of a loved one, or freedom from anxiety – can be only imperfectly compensated. These two concepts correspond to the economic damages and non-economic damages component of a jury verdict, respectively.

When a patient loses replaceable and irreplaceable goods, his total utility loss is given by:

$$U(R_1,I_1,X)-U(R_0,I_0,X)$$

Taking a first-order Taylor expansion, his monetized loss can be approximated as:

$$R_1-R_0+\frac{U_I(R_0,I_0,X)}{U_R(R_0,I_0,X)}(I_1-I_0)$$

A rational jury must estimate this loss. In general, they have reliable information about R₁ − R₀, because this component involves measurable losses of goods that are priced in the market. They also have information about I₁ − I₀: for example, the death of a spouse likely leads to a larger loss than the discomfort of a spouse. However, they face Knightian uncertainty when estimating the plaintiff’s shadow price of irreplaceable goods, $\frac{U_I(R_0,I_0)}{U_R(R_0,I_0)}$. Even qualitative relationships are theoretically uncertain, initial wealth R₀ could either increase or decrease this price, depending on whether replaceable goods are substitutable or complementary with irreplaceable goods. Fundamentally, the price of replaceable goods is constant across plaintiffs, but the shadow price of irreplaceable goods may vary considerably. This motivates our assumption that jurors cannot form systematic estimates for the shadow price of irreplaceable goods.

This assumption is consistent with the empirical finding that jurors revert to introspection and rules of thumb when estimating the value of pain and suffering loss, and that these estimates tend to fluctuate substantially. Apart from the actual extent of the injury, I₁ − I₀, the primary determinants of pain and suffering awards are jurors’ own internal monetary evaluations of an injury. Other factors, such as jurors’ perceptions of how liable the defendant actually is, or the pre-existing characteristics of the plaintiff (e.g., race or income) have been found less relevant (McCaffery et al., 1995; Wissler et al., 1997). At the same time, jurors report great difficulty in monetizing pain and suffering losses (Wissler et al., 1997). Perhaps as a result, the experimental literature on jury behavior has found that jurors very frequently rely on heuristics or unsystematic rules of thumb such as “anchoring bias” (Marti and Wissler, 2000; Robbennolt and Studebaker, 1999; Sunstein, 1997).

1.3.2 Juror Beliefs

We assume that juries deliver unbiased estimates of the replaceable goods loss and even the magnitude of the irreplaceable goods loss (I₁ − I₀), but rely on unsystematic methods – such as rules of thumb and introspection -- for estimating the shadow price of irreplaceable goods, π.

The expected value of the verdict then follows:

$$E(V\mid \pi )=E(R_1-R_0)+\pi \ast (I_1-I_0)$$ (3)

In the absence of formal rules for estimating π, we assume that jurors rely on a variety of unobserved idiosyncratic rules, including the observable behavior of earlier juries in their area. We focus on these “neighborhood peer effects” for two major reasons. First, there is a strong pattern of local trends in the data: jurors in some regions seem to award consistently higher non-economic damages at a point in time and thus suggest geographically specific beliefs; and that these “judicial hell-holes” (a phrase coined by defense lawyers) emerge and fade away at particular points in time, as would be expected if there is also some individual idiosyncratic component to beliefs. For example, from 2002 to 2005, there were 6 new entrants into the “top ten” most generous jurisdictions.⁶ Second, a plausible mechanism explains the influence of local verdicts: potential jurors are more likely to be exposed to media coverage of verdicts in their particular area (Garber and Bower, 2000), and exposure to media coverage influences the verdicts that jurors render (MacCoun, 2005).

In sum, economic damages will vary systematically with medical prices, wages, and other market prices for replaceable goods. However, controlling for the size of a plaintiff’s loss – e.g., death, permanent disability, etc – non-economic damage awards will contain an unsystematic component that reflects idiosyncratic local assessments of the shadow price of irreplaceable goods. This model generates testable implications that can be used to validate, and provides the necessary empirical framework for, a first-stage model of malpractice costs.

Finally, note that this simple model abstracts from more complex aspects of litigation such as the decision to settle a case or proceed to trial. While these dynamics are of great interest, our model rests most immediately on the assumption that higher noneconomic verdicts today increase physician expectations about future expected malpractice costs. Settlement behavior is not likely to reverse this relationship theoretically. In the manuscript we present several direct empirical tests that support this hypothesis.

2. Testing the Relationship between Past Jury Verdicts and Current Settlements

In our empirical strategy we use jury verdict dollars per capita as our primary measure of malpractice pressure, under the theory that changes in verdict amounts will drive expected malpractice costs of providers. We assess the reliability of this strategy using the 1990-2005 National Practitioner Data Bank (NPDB), which reports both malpractice jury verdicts and total malpractice settlements paid, but only at the state level. For state s at time t, we estimate:

$$M{P}_{\mathit{st}}={\phi }_0+{\sum }_{i=1}^6{\phi }_i{V}_{s,t-i}+{\omega }_{\mathit{st}}$$ (4)

This regression tests past jury verdicts as predictors of current malpractice payments MP_st, which include both settlements and verdicts. The payment and verdicts variables are calculated on a per capita basis.⁷

The results of this regression appear in Appendix Table 1, which reports models using 5 different specifications, differing in the included lags. Column 1 reports a regression of MP_st on V_s,t−1 through V_s,t−6, and the corresponding regression of MP_st on the moving average of V_s,t−1 through V_s,t−6. Similarly, column 2 repeats this for lags V_s,t−1 through V_s,t−3, and so forth.

On their own, past malpractice verdicts explain a significant amount of the variation in current malpractice payments. Six lags explain 74% of variation in payments, while the first three lags alone explain 72%. Even historical lags have good explanatory power: lags 4 through 6 explain about 66% of the variation in current malpractice payments. This suggests that malpractice verdicts are defensible, if imperfect, proxies for total payments.

Second, for all models, we cannot reject the possibility that the coefficients on all the lags are equal. As a result, we cannot reject the simplest measurement strategy of using moving averages of jury verdicts as proxies for total malpractice costs. The regressions at the bottom of the table explicitly test the relationship between moving averages of verdicts, and current malpractice payments. In terms of R-squared, almost nothing is lost by moving from the specification with individual lags to one with a combined, equal-weighted moving average. This motivates our use of moving averages in our empirical implementation.

3. Econometric Identification

3.1 Consistency of Elasticity Estimates

Assume that assumptions (A-1), (A-2) and (H-1) to (H-4) in the text all hold. Under these assumptions, the instrumental variables model yields a consistent estimate of β₁b. The true elasticity of medical costs with respect to expected malpractice is given by:

$$\mathit{plim}\left(\frac{{\widehat{\beta }}_1{\overline{M}}_{\mathit{ct}}}{p_{\mathit{ct}}{\tau }_{\mathit{ct}}}\right)=\frac{{\beta }_{1}E{(M)}_{\mathit{ct}}}{E(p_{\mathit{ct}}{\tau }_{\mathit{ct}})}$$ (5)

We have a proxy for E(M)_ct, defined as MA(V)_ct. If our proxy is an unbiased predictor, E(M)_ct = bE(MA(V)_ct). However, our estimator for the elasticity of medical costs with respect to malpractice still converges to the same value as in equation 5:⁸

$$\mathit{plim}\left(\frac{{\widehat{\beta }}_1\widehat{b}\overline{\mathit{MA}{(V)}_{\mathit{ct}}}}{\overline{p_{\mathit{ct}}{\tau }_{\mathit{ct}}}}\right)=\frac{{\beta }_1\mathit{bE}(\mathit{MA}{(V)}_{\mathit{ct}})}{E(p_{\mathit{ct}}{\tau }_{\mathit{ct}})}=\frac{{\beta }_{1}E{(M)}_{\mathit{ct}}}{E(p_{\mathit{ct}}{\tau }_{\mathit{ct}})}$$ (6)

The argument for the mortality elasticity proceeds identically (or γ₁ b).

3.2 Estimating Upper Bounds on Elasticities

To simplify the algebra for the balance of this appendix, consider the residualized instrumental variables regression of Y* on the single regressor V* using the residualized instrument J* and residual e. Suppose that assumption (A-1) holds, but assumption (A-2) does not. In particular, suppose that cov(J*, e) ≥ 0. In words, growth in noneconomic damages leads to a higher forecast for expected malpractice costs, holding malpractice verdicts constant. The instrumental variable estimate has the following asymptotic value:

$$\mathit{plim}{({\beta }_{1}b)}_{\mathit{IV}}=\frac{\mathit{cov}(Y^{\ast },J^{\ast })}{\mathit{cov}(V^{\ast },J^{\ast })}=\frac{\mathit{cov}({\beta }_{1}b{V}^{\ast }+{\beta }_{1}e+\epsilon ,J^{\ast })}{\mathit{cov}(V^{\ast },J^{\ast })}={\beta }_{1}b\left[\frac{\mathit{cov}\left(V^{\ast }+\frac{e}{b}+\frac{\epsilon }{{\beta }_{1}b},J^{\ast }\right)}{\mathit{cov}(V^{\ast },J^{\ast })}\right]={\beta }_{1}b\left[1+\frac{\mathit{cov}\left(\frac{e}{b},J^{\ast }\right)}{\mathit{cov}(V^{\ast },J^{\ast })}\right]$$

So long as the proxy is positively related to expected malpractice costs (b > 0), this expression implies that |plim((β₁b)_IV)| ≥ |β₁b|. It then follows that the instrumental variables estimate yields an elasticity estimate that exceeds the true elasticity. This result holds analogously for mortality.

3.3 Estimating Welfare Parameters

Continue to suppose that assumption (A-1) holds, but that assumption (A-2) need not, and maintain the notation from the previous section. The object of interest is dollars of malpractice cost per life saved, or $\frac{{\beta }_1}{{\gamma }_1}$ (with the coefficients β₁ and γ₁ coming from the cost and mortality models, respectively.

Our estimator for this ratio will be $\frac{{({\beta }_{1}b)}_{\mathit{IV}}}{{\left({\gamma }_{1}b\right)}_{\mathit{IV}}}$. This converges to the following:

$$\mathit{plim}\left(\frac{{({\beta }_{1}b)}_{\mathit{IV}}}{{({\gamma }_{1}b)}_{\mathit{IV}}}\right)=\frac{{\beta }_{1}b\left[\frac{\mathit{cov}\left(\frac{e}{b},J^{\ast }\right)}{\mathit{cov}(V^{\ast },J^{\ast })}\right]}{{\gamma }_{1}b\left[\frac{\mathit{cov}\left(\frac{e}{b},J^{\ast }\right)}{\mathit{cov}(V^{\ast },J^{\ast })}\right]}=\frac{{\beta }_1}{{\gamma }_1}$$

This proves the required result.

4. Analysis of National-Representativeness

The JVDB covers about one-quarter of the US population, but it over-represents large counties in the US. To verify that this has no undue influence on our key findings, we replicated our welfare analysis using statistical methods to account for the over-representation (Little and Rubin, 1987).

We begin by taking the full set of counties for a single year (2000) and generating a binary variable indicating which counties are in our analytic sample. We then use a logistic regression to predict the probability of being included in our sample: the dependent variable is the indicator for sample inclusion, and the independent variables are population, and county demographic characteristics (age distribution, income, and race). We then use the inverse of these predicted probabilities to generate sampling weights. These weights are larger on average for the smaller counties in our sample, giving them additional weight in the analysis.

The sampling weights do not enter directly into our analysis. Rather, we use them to conduct weighted bootstrap draws. That is, we conduct 1,000 bootstrap replications of counties, just as before, but the probability of inclusion in each replication sample is proportional to the sampling weight. The resulting bootstrapped sample is adjusted to be nationally representative, based on the predicted probability of a county being in the sample.

Based on the bootstrapped samples, we estimate the cost and mortality effects of malpractice and use the full set of bootstrap replications to generate the cost-effectiveness acceptability curves. The results of the weighted bootstrap analysis are illustrated in Appendix Figure 1. The figure is nearly identical to before, indicating that our sample is highly representative. From the figure it appears that malpractice reform is likely to be cost-effective at values of life around $1 million or less, though perhaps not for the Medicare population. For the values of life used by U.S. regulatory agencies, however, malpractice reform appears more likely than not to reduce welfare.

5. HMO Penetration

Danzon (2000) has argued that HMO penetration can serve as a third factor that creates a spurious link between malpractice risk and medical costs. She argues that HMO’s work to reduce both medical and malpractice costs. Kessler and McClellan (2002) confirm this, and find that HMO penetration weakens the estimated effect of tort reform on costs. To assess the impact of this effect on our estimates, we included measures of HMO penetration in our models.

The HMO data on number of enrollees in a county come from two sources. The 1990-1994 data come from publications of the Group Health Association of America, whereas the 1995-2003 data come from Interstudy. With both data sources, penetration is defined as the number of enrollees per people in the county. See Baker (2000) for an example of these data used in past work.

Appendix Table 2 presents the results when HMO penetration estimates are included. Inclusion of the HMO data has few impacts on our estimates, which remain quantitatively stable and similar to those presented in the text. If anything, the impact of malpractice appears stronger when the data on HMO penetration is included. This suggests that the impact of HMO penetration operates through the adoption of tort reform and not through impacts on pain and suffering damage awards.

6. Geographic Variation in the Number of Attorneys

One factor that we do not control for in our primary analysis is the possibility that malpractice and medical costs are driven by confounding variation in the litigiousness of different areas. More litigious areas will naturally be associated with higher expected malpractice liability costs. If those areas have systematically higher medical costs—if, for example, they also had more rapid adoption of new medical technology—then we might spuriously attribute medical cost growth causally to growth in malpractice.

We use the number of attorneys per capita to proxy for local variation in litigiousness and re-estimate our primary regressions to verify that it does not affect our results. One limitation to this approach is that the number of attorneys per capita is potentially endogenous, if attorneys are drawn to an area because of higher jury generosity in malpractice cases. We also only have data on the number of attorneys through 2002, so we estimate these results with one less year of data. For these reasons we use attorneys as a robustness check and verify that our central results are unchanged.

The results are presented in Appendix Table 6 and strongly support the validity of our approach even controlling for local variation in litigiousness. The main cost results are all positive and significant, with comparable but slightly higher elasticities than in the main results. The findings for days per bed are also similar, with some modest evidence of a negative but statistically weak effect. Overall these results suggest that our main findings are likely not driven by unobserved variation in litigiousness across areas.

7. Noneconomic Awards and Malpractice Premiums

Our use of pain and suffering awards in jury cases is based on the theory that these act as shocks to expectations about future malpractice costs. Here we examine empirically whether changes in noneconomic damages are correlated with future changes in insurance premiums. Appendix Table 3 provides the estimated effect of lagged noneconomic damage awards on current malpractice premiums. The data on premiums come from the Medical Liability Monitor (MLM), an annual publication that surveys malpractice insurers about premium levels in each state. The MLM do not publish average rates, rather they publish rates for three specialties: internal medicine, obstetrics and general surgery. We run regressions at the insurer level, and the aggregated county-level. The average county-level premium is calculated as the mean across companies reporting in a county-year; the results are essentially the same if the weighted average of specialties within a county-year is used as the dependent variable (where the weights are based on the fraction of physicians in each specialty as computed from the ARF). At the insurer level, we report results with fixed effects for county, year, and specialty, along with results that include fixed-effects for insurers.

These regressions indicate a positive relationship between lagged noneconomic damages and premiums, but no significant relationship between current damages and current premiums. This suggests that causality runs from damages to premiums, rather than in the opposite direction. For the lags, the coefficients range from $650 to $1200 increase in annual premiums for every hundred thousand dollar increase in average noneconomic damages per plaintiff victory. The coefficients are significant in 7 of the 12 specifications, and near significance in the others. For the 5 insignificant estimates, the associated p-values are: 0.121, 0.124, 0.126, 0.159, and 0.165.

8. Noneconomic Damages and the Probability of Lawsuits

The IV strategy in the paper isolates a relevant local average treatment effect if noneconomic damages affect the probability of lawsuits, and thus uninsurable costs for providers. To test this assumption, we use California closed-claim data from a large malpractice insurer covering approximately 20% of the California market. These data include the number and type of claims for all policyholders from 1991 to 2000, as well as the county in which each physician was rated and practiced. The data include information on 12,382 physicians for an average of about 11 years per physician located in 54 counties in California.

Appendix Table 4 presents the results from our regression analysis testing whether or not the probability of lawsuits faced by physicians vary with a county’s average noneconomic damage awards. We estimate separate linear probability models for two dependent variables: an indicator for whether a physician faced any claim in a given year, and an indicator for whether a physician faced a claim in a given year that incurred a positive defense cost. Physicians are required to report any event in which they think there is a chance someone might sue, but about 25% of the time these are resolved with no cost (i.e., the claim is simply dropped or never pursued). In our data, the probability of a claim in a given year is 17%, whereas the probability that the claim incurs some defense cost is about 13%.⁹ The table reports results with and without physician fixed-effects. The other demographic variables described in the text are also included in the regressions.

The probability that a physician is sued is increasing in the average noneconomic damage awards in tort cases. A $100K increase in noneconomic damages is associated with a 0.4 to 0.7 percentage point increase in the probability of a claim in a given year, for an elasticity of 0.069 to 0.138. The coefficients and elasticities change little when the physician fixed effects are introduced, though the standard errors do increase (enough so that the impact on all claims is not significant).

9. Accidental and Non-Accidental Deaths

In Appendix Table 4 we present reduced form results for the effect of noneconomic damages on accidental and non-accidental deaths. The results for non-accidental deaths are consistent with the results for all deaths displayed in the manuscript. There is a slight inconsistency with accidental deaths; the correlation is positive in most cases and significant for one of the lags. Nevertheless, the share of accidental deaths is too small for it to have any impact on our overall findings.

10. Bootstrapped Cost-Effectiveness Acceptability Curves

In this appendix, we demonstrate and justify the conditions under which the bootstrapped distribution of “dollars per life saved” is a valid approximation to the true distribution. Define ε^C as the estimator of the elasticity of malpractice with respect to medical costs, and ε^M as the stimator of the elasticity with respect to mortality. Define ${\epsilon }_0^C$ and ${\epsilon }_0^M$ as their respective probability limits. In calculating dollars per life saved, we take the ratio of two elasticities, $\frac{{\mathit{\epsilon }}^C}{{\mathit{\epsilon }}^M}$. Note, however, that all our policy conclusions are exactly symmetric if we take the inverse ratio, $\frac{{\epsilon }^M}{{\epsilon }^C}$. Therefore, without loss of generality, we will show that this ratio’s distribution can be bootstrapped.

A sufficient condition for this result is that ${\epsilon }_0^C$ is bounded away from zero. If this is true, then the function $\frac{{\epsilon }^M}{{\epsilon }^C}$ is differentiable at $\frac{{\epsilon }_0^M}{{\epsilon }_0^C}$. In addition, provided that the underlying IV models are valid, both these estimators are scalar multiples of $\sqrt{n}$-consistent, asymptotically normal estimators. This fact coupled with the differentiability assumption implies — via the Delta Method — that $\frac{{\epsilon }^M}{{\epsilon }^C}$ is asymptotically normal. Since the ratio of elasticities is asymptotically linear, the bootstrap provides a valid approximation of its distribution (Abadie and Imbens, 2006; Mammen, 1992).

The key condition is that ${\epsilon }_0^C$ is bounded away from zero, which flows from the economics of the problem. Recall that the direct effect of malpractice on medical costs is equal to the share of malpractice costs in medical costs, s > 0. Moreover, the indirect effects must be nonnegative, since providers will weakly spend resources (not save them) in order to avoid risks that are imposed upon them. Risk-neutral providers will spend zero, but risk-averse providers will spend positive resources. Therefore, theory predicts that ${\epsilon }_0^C\ge s>0$, or that the cost elasticity is bounded away from zero.

Finally, note that the policy implications of the bootstrap procedure will be invalid only if ${\epsilon }_0^C={\epsilon }_0^M=0$, or that malpractice has no true effect on costs or mortality. If both these conditions held, the malpractice regime would have no costs and no benefits, rendering all policy reforms welfare-neutral.¹⁰ Following this polar case to its logical conclusion, our policy recommendations would be welfare-neutral, rendering them at least weakly welfare-enhancing, even considering the possibility of invalidity for the bootstrap procedure.

Empirically, the bootstrap estimates yield hypothesis test results similar to those of the asymptotic IV analysis, as shown in Appendix Table 7.¹¹ For the sake of comparison, the table reports p-values for one-tailed hypothesis tests assessing whether the coefficients have the theoretically predicted sign — positive effect of malpractice on costs, and negative effect of malpractice on mortality.¹² The bootstrapped p-values are reasonably close to the asymptotic p-values. Some departures are observed in the case with 1, 2, and 3 lags, where the asymptotic estimates seem to lead to over-rejection.¹³

Finally, our results are fairly similar for our different lag specifications, and fairly similar across states with and without noneconomic damage caps. Appendix Figure 2 plots the empirical distribution of dollars per life lost for all major lag specifications used in the paper. Appendix Figure 3 plots the empirical distribution for the parameter that is estimated using only the uncapped state of New York.

Appendix Table 1.

Past Malpractice Verdicts as a Measure of Expected Malpractice Costs.

Dependent Variable: Current Total Malpractice Payments Per Capita at year t
	(1)	(2)	(3)	(4)	(5)
Individual Lagged Malpractice Verdicts Per Capita
Coefficients
Year t-1	3.143*** (1.203)	5.261*** (1.090)
Year t-2	3.752*** (1.055)	5.216*** (1.003)	6.132*** (1.147)
Year t-3	3.261*** (1.235)	5.145*** (1.179)	5.398*** (1.150)	6.167*** (1.236)
Year t-4	1.277 (1.153)		3.764*** (1.176)	3.571*** (1.294)	4.201*** (1.324)
Year t-5	2.102 (1.546)			5.746*** (1.646)	5.063*** (1.611)
Year t-6	3.934*** (1.395)				7.485*** (1.562)
Testing for equality of coefficients
F-statistic	0.7482	0.0019	0.8278	0.7917	1.0682
p-value	0.5877	0.9981	0.4375	0.4536	0.3444
Regression statistics
R2	0.7436	0.7229	0.6998	0.6726	0.6605
Moving Average of Lagged Verdicts Per Capita
Coefficients
Average of Lagged Trial Verdicts	17.300*** (1.288)	15.623*** (1.081)	15.354*** (1.164)	15.391*** (1.310)	16.343*** (1.433)
Regression statistics
R2	0.7375	0.7229	0.6957	0.6682	0.6550
N	508	661	610	559	508

Notes: The table illustrates the predicted relationship from regressions of per capita malpractice payments (from verdicts at trial and settlements) in the current year as the dependent variable against lagged values of per capita payments from trial verdicts as the independent variable. Each column represents a separate regression, including the indicated lags. The coefficients for the moving averages also come from separate regressions, with each moving average defined as the average of the lags included in the top part of the table in the same column. Data come from the National Practitioner Data Bank (NPDB) from years 1990-2005, aggregated to the state-year level. Robust standard errors are in parentheses.

^***A *** indicates statistical significance at the 1% level.

Appendix Table 2.

HMO Penetration and the Effects of Malpractice.

	Current Year	Lagged: 1, 2 and 3 Years	Lagged: 2, 3 and 4 Years	Lagged: 3, 4 and 5 Years	Lagged: 4, 5 and 6 Years
IV Estimates
Hospital Cost Estimates
Dependent Variable: Hospital Facility Expenditures Per Bed
Malpractice Awards Per Capita	31.576 (182.665)	2,023.300* (1,174.366)	4,164.870*** (1,433.954)	4,340.461*** (1,361.019)	1,833.339 (2,121.661)
Elasticity	0.001	0.040	0.079	0.077	0.030
Dependent Variable: Hospital Facility Expenditures Per Bed Day
Malpractice Awards Per Capita	0.308 (0.411)	-0.509 (2.710)	8.755*** (2.981)	8.276*** (3.043)	4.577 (4.301)
Elasticity	0.003	-0.005	0.088	0.080	0.043
County Medicare Estimates
Dependent Variable: Medicare Part A Expenditures Per Enrollee
Malpractice Awards Per Capita	1.874 (1.746)	22.450** (10.377)	45.901*** (13.252)	43.848*** (13.346)	48.507** (22.806)
Elasticity	0.0048	0.0513	0.1037	0.0961	0.1019
Dependent Variable: Medicare Part B Expenditures Per Enrollee
Malpractice Awards Per Capita	0.892 (1.039)	10.550* (6.055)	8.201 (6.765)	9.325 (7.303)	11.068 (9.150)
Elasticity	0.0038	0.0402	0.0307	0.0339	0.0383
Hospital Utilization Estimates
Dependent Variable: Total Hospital Days Per Bed
Malpractice Awards Per Capita	-0.510 (0.785)	3.396 (5.515)	-7.854 (7.596)	-7.327 (5.537)	-8.429 (6.352)
Elasticity	-0.005	0.035	-0.079	-0.070	-0.078

Notes: The table reports the estimated IV effects of per capita malpractice jury award dollars on medical expenditures. Each coefficient is from a separate regression, and each column represents a different lag for the malpractice variable. The unit of analysis is a hospital-year for the hospital-level regressions or a county year for the county-level regression. County population is used as a weight in all regressions. Other explanatory variables include hospital or county fixed-effects, year fixed-effects, a quadratic for per capita income, the percent of the population that is male, white, African-American, and that falls into 5-year age ranges. Elasticities are evaluated at the mean values of the dependent and independent variables. Robust standard errors allowing clustering at the county level are reported in parentheses. For the hospital level regressions, these standard errors are calculated using 500 bootstrap replications with bootstrap resampling done at the county level. A *, **, or *** represents statistical significance at the 10, 5, or 1% level, respectively.

Appendix Table 3.

Noneconomic Awards and Malpractice Premiums.

	Current Year	Lagged: 1, 2 and 3 Years	Lagged: 2, 3 and 4 Years	Lagged: 3, 4 and 5 Years	Lagged: 4, 5 and 6 Years
		Insurer Level Regressions
		Dependent Variable: Annual Malpractice Premium
Noneconomic Award (Hundreds of Thousands)	12.748 (65.794)	681.614** (336.628)	584.905 (386.884)	768.075* (425.067)	1,192.766* (641.043)
R2	0.83	0.83	0.82	0.82	0.81
Fixed effects:		County, Year, Specialty
Noneconomic Award (Hundreds of Thousands)	34.814 (47.207)	556.848 (368.333)	626.990 (444.700)	764.533* (448.321)	1,074.783* (600.943)
R2	0.84	0.84	0.83	0.84	0.83
Fixed effects:		Insurer, County, Year, Specialty

Notes: Table reports the regressions of annual malpractice premiums against different lags of the average noneconomic damage awards in tort cases. Premium data come from the Medical Liability Monitor (MLM), and are measured at the county-county-year level for three specialties: internal medicine, general surgery, and OBGYN. Standard errors adjusted to reflect clustering by county are reported in parentheses.

Appendix Table 4.

The Impact of Average Noneconomic Damage Awards in a County on the Probability of Facing a Malpractice Suit.

	Any Claim		Claim with Defense Costs
Noneconomic Award (Hundreds of Thousands)	0.005 (0.003)*	0.005 (0.003)*	0.007 (0.003)**	0.006 (0.003)**
Elasticity	0.055	0.068	0.093	0.111
Physician fixed effects:	No	Yes	No	Yes

Notes: The table reports the estimated effect of average noneconomic jury award dollars in tort cases on the probability of being sued. Sample includes claims reported against insured physicians in California who purchase their policies from a single large insurance company from 1991-2000. The model is estimated as a linear probability model with an indicator variable indicating a lawsuit reported against a physician in a year as the dependent variable. The coefficient is reported for the moving average of noneconomic damage awards in plaintiff wins in tort cases lagged 1, 2 and 3 years. The unit of analysis is a physician-year. County population is used as a weight in all regressions. Other explanatory variables include indicators for physician specialty, physician age, year fixed-effects, a quadratic for per capita income, the percent of the population that is male, white, African-American, and that falls into 5-year age ranges. Elasticities are evaluated at the mean values of the dependent and independent variables. Robust standard errors allowing clustering at the physician level are reported in parentheses. A *, **, or *** represents statistical significance at the 10, 5, or 1% level, respectively.

Appendix Table 5.

Noneconomic Damage Awards and Alternative Mortality Measures

	Lead: 4, 5 and 6 Years	Lead: 3, 4 and 5 Years	Lead: 2, 3 and 4 Years	Lead: 1, 2 and 3 Years	Current Year	Lagged: 1, 2 and 3 Years	Lagged: 2, 3 and 4 Years	Lagged: 3, 4 and 5 Years	Lagged: 4, 5 and 6 Years
Dependent Variable: Accidental Deaths Per 1,000 Population
Noneconomic Award (Hundreds of Thousands)	0.0002 (0.0007)	0.0005 (0.0005)	0.0004 (0.0006)	0.0000 (0.0006)	-0.0002 (0.0002)	0.0017** (0.0008)	0.0019 (0.0012)	0.0003 (0.0007)	0.0002 (0.0005)
Dependent Variable: Non-Accidental Deaths Per 1,000 Population
Noneconomic Award (Hundreds of Thousands)	-0.022 (0.015)	-0.018 (0.017)	-0.015 (0.016)	-0.015 (0.013)	-0.004 (0.003)	-0.021** (0.010)	-0.016** (0.007)	-0.012* (0.007)	-0.006 (0.005)
N	739	801	801	801	925	801	801	802	803

Note: Table shows the reduced-form estimates of average noneconomic damage awards on county level mortality. Each coefficient is from a separate regression, with each column representing a different lag or lead for the noneconomic damages. The unit of analysis is a county-year. County population is used as a weight in all regressions. Other explanatory variables include county and year fixed-effects, a quadratic for per capita income, the percent of the population that is male, white, African-American, and that falls into 5-year age ranges. Robust standard errors allowing clustering at the county level are reported in parentheses. A *, **, or *** represents statistical significance at the 10, 5, or 1% level, respectively.

Appendix Table 6.

Attorneys per Capita and the Effects of Malpractice.

	Current Year	Lagged: 1, 2 and 3 Years	Lagged: 2, 3 and 4 Years	Lagged: 3, 4 and 5 Years	Lagged: 4, 5 and 6 Years
IV Estimates
Hospital Cost Estimates
Dependent Variable: Hospital Facility Expenditures Per Bed
Malpractice Awards Per Capita	55.919 (452.611)	2,680.799** (1,168.733)	4,698.495*** (1,598.773)	4,111.168*** (1,457.976)	1,673.662 (2,446.596)
Elasticity	0.0012	0.0532	0.0877	0.0729	0.0278
Dependent Variable: Hospital Facility Expenditures Per Bed Day
Malpractice Awards Per Capita	0.359 (1.044)	1.575 (2.566)	10.399*** (2.747)	7.705*** (2.031)	5.536 (4.319)
Elasticity	0.0039	0.0160	0.1019	0.0745	0.0521
County Medicare Estimates
Dependent Variable: Medicare Part A Expenditures Per Enrollee
Malpractice Awards Per Capita	0.889 (1.101)	31.560** (15.644)	54.421*** (17.216)	43.269** (17.357)	44.862* (26.214)
Elasticity	0.0023	0.0730	0.1228	0.0948	0.0943
Dependent Variable: Medicare Part B Expenditures Per Enrollee
Malpractice Awards Per Capita	0.521 (0.804)	14.727* (7.568)	12.627 (7.838)	7.856 (8.390)	8.464 (10.726)
Elasticity	0.0022	0.0567	0.0472	0.0285	0.0293
Hospital Utilization Estimates
Dependent Variable: Total Hospital Days Per Bed
Malpractice Awards Per Capita	-0.919 (1.936)	3.134 (4.959)	-8.566 (6.590)	-6.637* (3.534)	-11.092* (6.357)
Elasticity	-0.0102	0.0321	-0.0837	-0.0635	-0.1025

Notes: The table reports the estimated IV effects of per capita malpractice jury award dollars on medical expenditures. Each coefficient is from a separate regression, and each column represents a different lag for the malpractice variable. The unit of analysis is a hospital-year for the hospital-level regressions or a county year for the county-level regression. County population is used as a weight in all regressions. Other explanatory variables include hospital or county fixed-effects, year fixed-effects, a quadratic for per capita income, the percent of the population that is male, white, African-American, and that falls into 5-year age ranges. Elasticities are evaluated at the mean values of the dependent and independent variables. Robust standard errors allowing clustering at the county level are reported in parentheses. For the hospital level regressions, these standard errors are calculated using 500 bootstrap replications with bootstrap resampling done at the county level. A *, **, or *** represents statistical significance at the 10, 5, or 1% level, respectively.

Appendix Table 7.

Distribution of Estimated Effects of Malpractice on Mortality and Cost.

Hospital Expenditures
		Lagged:
		1, 2, 3	2, 3, 4	3, 4, 5	4, 5, 6
IV Model	Coeff.	1.359	5.134	6.894	5.677
	Std.Er.	(1.532)	(2.103)	(2.338)	(2.881)
	Elasticity	0.0169	0.0621	0.0818	0.0645
	Pr(b<0)	0.188	0.007	0.002	0.025
Bootstrap	Pr(b<0)	0.313	0.008	0.008	0.051
Total Medicare Expenditures
		Lagged:
		1, 2, 3	2, 3, 4	3, 4, 5	4, 5, 6
IV Model	Coeff.	48.604	63.041	48.122	53.912
	Std.Er.	(24.619)	(21.388)	(22.511)	(33.659)
	Elasticity	0.0705	0.0887	0.0658	0.0705
	Pr(b<0)	0.024	0.002	0.016	0.055
Bootstrap	Pr(b<0)	0.014	0.007	0.039	0.046
Total Mortality
		Lagged:
		1, 2, 3	2, 3, 4	3, 4, 5	4, 5, 6
IV Model	Coeff.	-0.035	-0.026	-0.023	-0.012
	Std.Er.	(0.018)	(0.014)	(0.010)	(0.009)
	Elasticity	-0.0258	-0.0192	-0.0171	-0.0094
	Pr(b>0)	0.026	0.032	0.011	0.091
Bootstrap	Pr(b>0)	0.152	0.144	0.011	0.033
Mortality Over Age 65
		Lagged:
		1, 2, 3	2, 3, 4	3, 4, 5	4, 5, 6
IV Model	Coeff.	-0.112	-0.099	-0.079	-0.015
	Std.Er.	(0.080)	(0.063)	(0.040)	(0.050)
	Elasticity	-0.0131	-0.0117	-0.0095	-0.0018
	Pr(b>0)	0.081	0.058	0.024	0.382
Bootstrap	Pr(b>0)	0.272	0.188	0.039	0.373

Notes: Table illustrates, for consistent sampling schemes, properties of IV and bootstrap estimates for effects of malpractice on medical costs and mortality. For comparison, the tables report p-values for one-tailed tests of whether coefficients are greater than or less than zero.

Appendix Figure 1. The welfare effects of reducing malpractice costs, correcting for over-sampling of large counties.

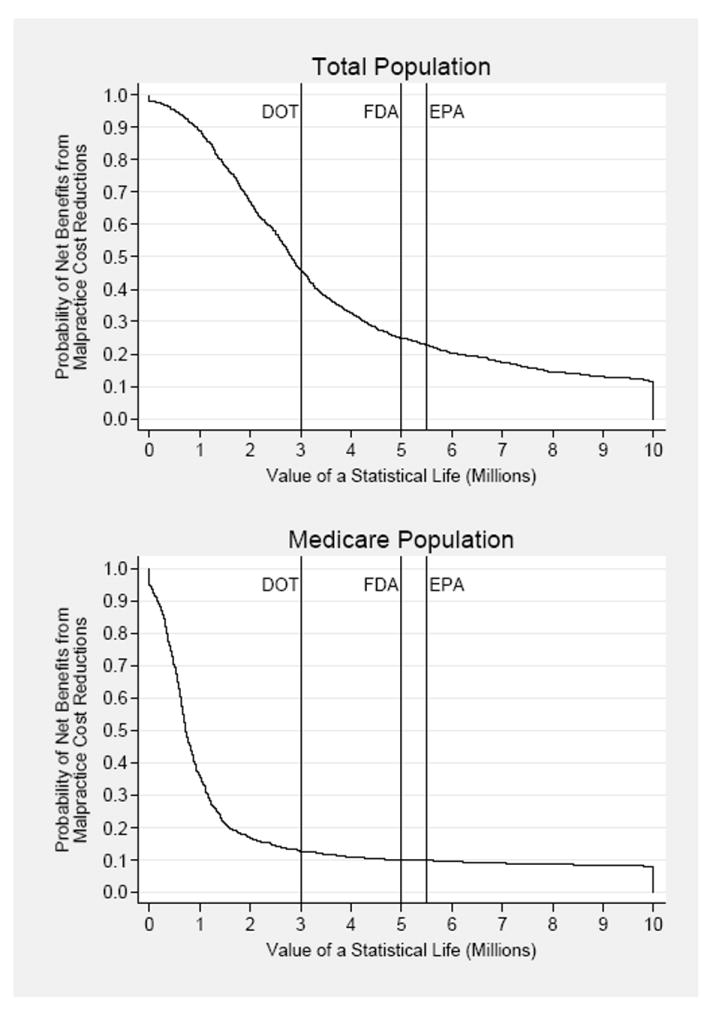
Notes: The curves depict the empirical probabilities that the estimated dollars saved per life lost exceed the given value of a statistical life. These are constructed identically as in the manuscript, except that in this the bootstrap is weighted with sampling weights that reflect the undersampling of small counties in our data. The weights function in such a way that the probability of inclusion in the bootstrap is proportional to the sampling weight (which is higher for the undersampled counties).

Appendix Figure 2. The Welfare Effects of Reducing Malpractice Costs Using the Full Set of Lags.

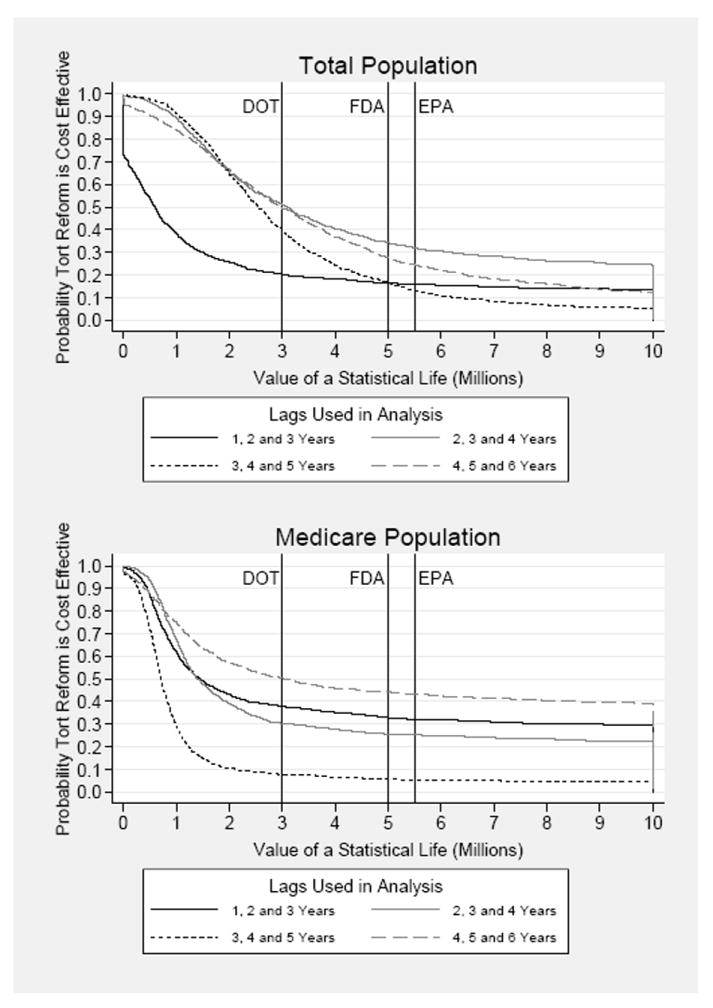
Notes: The curves depict the empirical probabilities that the estimated dollars saved per life lost exceed the given value of a statistical life. These are constructed identically as in the manuscript, except that in this figure, we include the full set of lags for our analysis (as shown in the legend).

Appendix Figure 3. The Welfare Effects of Reducing Malpractice Costs without Noneconomic Damage Caps.

Notes: The curves depict the empirical probabilities that the estimated dollars saved per life lost exceed the given value of a statistical life. These are constructed identically as in the manuscript, except that in this figure, we estimate the model to identify an effect net of the influence of California, which had a cap on noneconomic damages in place during our study period.