Detecting Rare Variant Effects Using Extreme Phenotype Sampling in Sequencing Association Studies

Abstract

In the increasing number of sequencing studies aimed at identifying rare variants associated with complex traits, the power of the test can be improved by guided sampling procedures. We confirm both analytically and numerically that sampling individuals with extreme phenotypes can enrich the presence of causal rare variants and can therefore lead to an increase in power compared to random sampling. While application of traditional rare variant association tests to these extreme phenotype samples requires dichotomizing the continuous phenotypes before analysis, the dichotomization procedure can decrease the power by reducing the information in the phenotypes. To avoid this, we propose a novel statistical method based on optimal SKAT (SKAT-O) that allows us to test for rare variant effects using continuous phenotypes in the analysis of extreme phenotype samples. The increase in power of this method is demonstrated through simulation of a wide range of scenarios as well as in the triglyceride data of the Dallas Heart Study.

Introduction

With the increase in the number of sequencing studies[Biesecker, et al. 2011], there is a newfound access to samples with low frequency (MAF 1–5%) and rare (MAF <1%) genetic variants. In the search for genetic components of complex traits, discovered common variants (MAF > 5%) from genome-wide association studies explain only a small proportion of the total heritability of these traits[Ioannidis, et al. 2009; Maher 2008; Manolio, et al. 2009]. As a result, attention has turned to low frequency and rare variants instead expecting that they could play an important role in uncovering gene-phenotype relationships[Cirulli and Goldstein 2010; Ji, et al. 2008; Nejentsev, et al. 2009; Ng, et al. 2008; Ramser, et al. 2008]. Unfortunately, rare variants are difficult to detect in even reasonably large samples. This problem can be alleviated through the development of powerful study designs. To this effort, numerous association studies have chosen to sample subjects with extreme phenotypes in the hope of increasing power to detect causal SNPs[Clement, et al. 1995; Gu, et al. 1997; Hu, et al. 2009; Khor and Goh 2010; Li and Leal 2008; Liang, et al. 2000; Price, et al. 2008; Risch and Zhang 1995]. There have also been numerous developments in methodology to detect QTLs under these extreme phenotype sampling (EPS) study designs[Chen, et al. 2005; Huang and Lin 2007; Li, et al. 2011; Slatkin 1999; Wallace, et al. 2006]. A fundamental assumption that motivates these EPS methods is that rare causal variants are more likely found in the extremes of the quantitative trait. In this paper, we support the use of this practice by showing both analytically and numerically that EPS increases the presence of rare causal variants in a variety of settings. As a result, we show that EPS is more powerful for detecting for rare variant effects than random sampling.

Various methods have been proposed to tackle the challenge of association testing for rare variants. Burden tests such as the Combined Multivariate and Collapsing method (CMC)[Li and Leal 2008], Cohort Allelic Sums Test (CAST)[Morgenthaler and Thilly 2007] and the Weighted Sum Test (WST)[Madsen and Browning 2009] combine information from all rare variants within a target region such as an exon or gene by collapsing them into a single genetic variable, which is tested for association with the phenotypes of interest. Numerous rare variants testing methods have been developed using the same strategies [Bansal, et al. 2010; Basu and Pan 2011; Lee, et al. 2012a; Morris and Zeggini 2010; Price, et al. 2010]. A limitation of all burden tests is that they could lose significant amount of power in the presence of variants with different association directions and a large fraction of non-causal variants in the region. Alternatively the Sequence Kernel Association Test (SKAT)[Wu, et al. 2011] aggregates evidence of individual variant effects across the region using a kernel function and uses a computationally efficient mixed model variance component test to test for association. SKAT can naturally adjust covariates and has robust power in the presence of variants with different association directions and a large proportion of null variants. It is also a generalization of several non burden tests such as C-alpha test[Neale, et al. 2011], the SSU test[Pan 2009], and the haplotype association test[Tzeng and Zhang 2007]. Recently the optimal SKAT (SKAT-O)[Lee, et al. 2012b] has been proposed to unify the burden test and SKAT to a single framework and to construct the optimal test within the framework.

Moreover, limited statistical methods have been developed for studying rare variant effects when extreme phenotypes are sampled. In a typical EPS study, the two extremes are treated as two different groups representing a dichotomous phenotype. For example, Hu et al.[Hu, et al. 2009] used the contrast between subjects with high HDL-C levels against those with low HDL-C levels to identify an association with the ABCA1 gene. If the same method of extreme sampling were to instead retain the continuous phenotype values, the gain in information could provide greater power to detect gene-phenotype associations. For common variants, Huang and Lin[Huang and Lin 2007] proposed testing for associations between extreme continuous phenotypes and variants using the maximum likelihood method assuming a truncated normal distribution for extreme phenotype. Recently, this approach was adapted by Li et al. [Li, et al. 2011] to accommodate testing for multiple rare variant effects with the burden CMC approach. As a burden test, this approach is powerful when most variants in a region are causal and the effects of causal variants are in the same direction. However, it loses power in the presence of variants with different association directions or a large number of non-causal variants in a region.

In this paper, we first confirm both analytically and empirically that EPS substantially increases the chance to observe rare causal variants and hence increases their observed frequencies in finite study samples. Using this result, we demonstrate that EPS provides a more powerful design strategy for testing rare variant effects compared to random sampling. We next develop a new more powerful statistical method for testing for rare variant effects in EPS. Specifically, we extend SKAT and the optimal SKAT (SKAT-O) to EPS by analyzing extreme phenotypes as continuous variables within a likelihood framework. We show that the proposed tests perform well in a wide range of situations and outperform burden tests. We further show that analysis using continuous extreme phenotypes (CEP) improves power for detecting rare variant effects compared to using dichotomized extreme phenotypes (DEP). We illustrate the finite sample performance of proposed methods by conducting extensive simulations and application to analysis of triglyceride levels from the Dallas Heart Study.[Victor, et al. 2004]

Material and Methods

Goals and notation

The goal is to find an optimum sampling strategy when resources are limited and to develop powerful association test methods to detect phenotype-genotype associations. We evaluate the effectiveness of extreme phenotype sampling (EPS) compared to random phenotype sampling.

We first confirm analytically that extreme phenotype sampling enriches causal rare variants by increasing their MAFs (Supplementary Materials Section 1). We consider the cases with a single causal variant and multiple causal variants and calculate the MAF in extreme phenotype sampling as a function of the population MAF, the threshold used to select extreme phenotypes, and the effect sizes of genotypes.

We next evaluate the two different methods that utilize EPS phenotypes in different ways: the method that retains continuous phenotypes and the method that dichotomizes them into cases and controls. We consider the case with a sample of n individuals who have been sequenced in a genomic region of interest containing p genetic variants. The i-th individual has covariate information over m covariates X_i=(X_i1,…, X_im)', genotypes of the p variants in the region G_i=(G_i1,…,G_ip)', and a continuous phenotype y_i. The genotype G_ij represents the number of copies of the minor allele of the j-th variant that the i-th individual has.

Model

To test for an association between the variants and continuous phenotype while controlling for covariates, consider a linear model

$$y_i={\alpha }_0+\mathit{\alpha }\text{'}{\mathit{X}}_i+\mathit{\beta }\text{'}{\mathit{G}}_i+{\epsilon }_i$$

where ε_i ~ N(0, σ²). Here α0 is an intercept term, α = [α₁, α₂,…, α_m]' is a vector of regression coefficients for the m covariates, and β = [β₁, β₂,…, β_p]' is a vector of regression coefficients for the p genetic variants. The null hypothesis of H₀: β=0 corresponds to no genetic effect on the trait. Since a p-DF likelihood ratio test has little power to detect causal variants particularly in the presence of a large number of rare variants, the gene-phenotype relationship is instead tested for by region-based tests such as burden tests and non-burden tests, e.g., SKAT. An adaptation of the CMC[Li and Leal 2008] burden test is used that collapses genotype information by counting the number of variants in the region before applying logistic regression to the collapsed statistic. We call this test DEP-Burden.

Association tests under the extreme phenotype sampling design

Since both SKAT and burden tests are capable of handling dichotomous phenotypes in the case-control setting, they can be applied to test for associations after using EPS. Dichotomizing the high phenotypic extremes as cases and the lower phenotypic extremes as controls is a natural extension of each test’s functionality. However, applying SKAT and SKAT-O to continuous phenotype data obtained from EPS requires further development, since the extreme continuous phenotypes do not follow Gaussian distribution due to the phenotypic selection. Suppose we select n samples with either y_i > c₁ or y_i < c₂, and denote the selected y_i as $y_i^{*}$. Then under the null hypothesis $y_i^{*}$ follows truncated Gaussian distribution with a density function

$$f(y_i^{*})=\frac{\varphi (X_i\alpha ,{\sigma }^2)}{\mathrm{\Phi }(c_2,{\sigma }^2)+1-\mathrm{\Phi }(c_1,{\sigma }^2)}$$

where ϕ(μ, σ²) and Φ(μ, σ²) are density and distribution functions of Gaussian distribution with mean μ and variance σ².

To increase test power and decrease the test DF, we assume β_j follows an arbitrary distribution with mean 0 and variance φw_j². We note that H₀: β=0 is equivalent to H₀: φ=0. The score test statistic of φ=0 is

$$Q_s={\displaystyle \sum _{j=1}^p{w}_j^2{\left(\sum _{i=1}^n{G}_{ij}(y_1^{*}-{\widehat{\mu }}_i)\right)}^2}$$

where µ̂_j is an estimated mean of $y_i^{*}$ under the null hypothesis. We show that Q_S asymptotically follows a mixture of chi-square distribution (Supplementary Materials Section 2), and p-values can be obtained by the matching the moments or inverting the characteristic function[Davies 1980].

Recently Lee et al. (2012)[Lee, et al. 2012b] proposed an optimal unified approach, which unifies SKAT and burden test to adaptively select best test structure. Suppose Q_B is the score test statistics of the weighted burden test:

$$Q_B={(\sum _{i=1}^n(y_i^{*}-{\widehat{\mu }}_i)\sum _{j=1}^p{w}_j{G}_{ij})}^2$$

and then the test statistic of unified test is

$$Q_{\rho }=(1-\rho )Q_s+\rho Q_B,$$

where ρ (0≤ρ≤1) is a parameter to determine whether test is close to SKAT (ρ=0) or burden tests (ρ=1). It is based on a recent generalization of SKAT which allows the correlation among variants effects β’s. Under this setting, they proposed the optimal SKAT, called SKAT-O. This test is defined by selecting the ρ that minimizes the p-value of the SKAT-O test statistic,

$$T=\underset{0\le \rho \le 1}{\text{min}}{p}_{\rho }$$

where p_ρ is a p-value with given ρ. The test statistic T can be obtained by simple grid search across a range of ρ: set a grid 0 = ρ₁ < ρ₂ < … < ρ_b =1, then T=min(p_ρ1,…,,p_ρb). In simulation studies and real data analysis, we used the equal sized grid of 11 points (from 0 to 1) to obtain T. From the fact that the Q_ρ can be decomposed to the shared random variables, asymptotic p-value of T can be obtained through computationally efficient one-dimensional numerical integration (Supplementary Materials Section 3). We use this extreme phenotype optimal SKAT in our simulation studies and data analysis.

When the sample size is small, SKAT family methods (including SKAT and SKAT-O) can produce conservative results with both binary and extreme continuous phenotypes. To resolve this issue, Lee et al. (2012a, 2012b)[Lee, et al. 2012a; Lee, et al. 2012b] have proposed a method to adjust asymptotic null distribution by estimating small sample moments when the trait is dichotomous. We employ a similar approach (details in Supplementary Materials Section 4). For all simulation studies and real data analysis we used small sample adjustment for SKAT methods given the small to moderate sample sizes we considered. We used SKAT-O for continuous extreme phenotype SKAT (CEP-SKAT-O) and dichotomous extreme phenotype SKAT (DEP-SKAT-O), and for random sample continuous phenotypes (RS-SKAT-O). It should be noted that for larger sample sizes, the small sample adjustment is not necessary. Through simulations we found sample sizes lower than n=500 to benefit from the small sample adjustment, with sample sizes as low as n=1000 to not benefit from the adjustment.

Type 1 error simulations

We first generated haplotype data by the forward simulator, SFS_CODE[Hernandez 2008], which offers the ability to incorporate purifying selection on deleterious variants and thus provides better model to simulate variants in exomes. Data were simulated according to the European demographic model with a population bottleneck followed by exponential growth. We simulated 32,000 haplotypes each 100,000 base pairs wide as our population base. To achieve a simulated sample over a 3kb exon, a random 3kb region is selected (containing 41 variants on average) and each individual genotype is formed by combining at random two haplotypes over that region. Phenotypes for the i-th individual in a sample were produced from the generated genotype and covariate data according to

$${\mathrm{Y}}_{\mathrm{i}}=0.5{\mathrm{X}}_{\mathrm{i}1}+0.5{\mathrm{X}}_{\mathrm{i}2}+{\mathrm{\epsilon }}_{\mathrm{i}}$$

Where the covariate X_i1 is 1 with probability 0.5 and 0 otherwise, and the covariate X_i2 and the residual ε_i are both instances of a standard normal random variable.

Using the simulated genotype and phenotype data for the N individuals, a random sample of size n is selected. For random sampling of continuous traits, SKAT-O with the default w_j=Beta(1,25) weight is used to test for an association between the continuous phenotype and genotype after controlling for both covariates, producing a p-value (RS-SKAT-O). In order to test for the association between variants and phenotype under EPS using the standard dichotomizing method, we treat the highest (n/2) extremes as cases and lowest (n/2) extremes as controls. The dichotomized phenotypes are used by both DEP-SKAT-O and DEP-Burden. This same extreme phenotype sample is used to compare with the tests that retain the continuous phenotype (CEP-SKAT-O and CEP-Burden). A p-value for the CEP-SKAT-O test and the CEP-Burden burden test are produced from these continuous phenotype values and the corresponding genotype and covariate data. The proportion of p-values below a specified α-level provides an estimate for the Type 1 error at that α significance level.

Power Simulations

Power comparisons between the various sampling methods were performed using simulated genotype data as was used in the Type 1 error simulation setting. After generating the genotypes for N individuals, 20% of the variants with MAF < 0.03 are selected to be causal variants. Different percentages of causal variants were also considered. Phenotypes are then generated for the N individuals according to:

$$\mathrm{y}=0.5{\mathrm{X}}_1+0.5{\mathrm{X}}_2+{\mathrm{\beta }}_1{\mathrm{G}}_1+{\mathrm{\beta }}_2{\mathrm{G}}_2+\dots +{\mathrm{\beta }}_p{\mathrm{G}}_p+\mathrm{\epsilon }$$

The covariate X₁ is generated as a Bernoulli random variable with p=0.5. The covariate X₂ and the added noise ε are generated independently from a standard normal distribution. Non-causal variants are assigned β_j=0, and the causal variants are generated according to:

$$\left|{\mathrm{\beta }}_j\right|=-a{\text{log}}_{10}({\text{MAF}}_{\mathrm{j}})$$

Here, a>0 is a parameter that specifies the strength of variant-phenotype associations, hence the strength of heritability. Large values of a lead to stronger effects of causal variants on phenotype and cause rare variants to become more enriched in the phenotypic extremes. In one simulation setting an increase in a from 0.3 to 0.4 increases the heritability of the phenotype from 0.034 to 0.042. The heritability also increases with the number of causal variants. To obtain an estimate of the heritability, the proportion of the variance in phenotype explained by the genotypes of causal variants is estimated assuming no LD between variants.

Power estimates are obtained for various (extreme phenotype) sample sizes (n=500, 1000, and 2000), percentages in each phenotypic extreme sampled (10% and 25%), percentages of causal variants with a positive effect (80%, 100%), and percentages of causal variants with MAF < 0.03 (20%, 40%, and 60%).

Results

Extreme sampling enriches rare causal variants

Our analytical calculations (See Material and Methods and Supplementary Materials Section 1) confirm that rare causal variants can be enriched in phenotypic extremes. The degree of enrichment increases when more extreme phenotypes are sampled and a higher percentage of causal variants are present in a region. To empirically validate this finding, randomly selected 3kb exonic regions were simulated using the population genetic simulation model with European demographic history (see Material and Methods). For each 3kb region, causal variants were randomly selected to be 100%, 70%, 40% and 0% of sufficiently rare variants (MAF < 0.03) and the j-th causal variant was given the effect size β_j as a function of its MAF. Note that these causal variant percentages differ from those in the power simulations so as to further accentuate the effect of causal variant percentage on the inflation of MAF due to EPS. Also for the power simulations, causal variant percentages of 10% and 20% were used instead. Phenotypes are then generated from a linear model with heritability of genetic variants being 2.6%, 1.3%, and 0%.

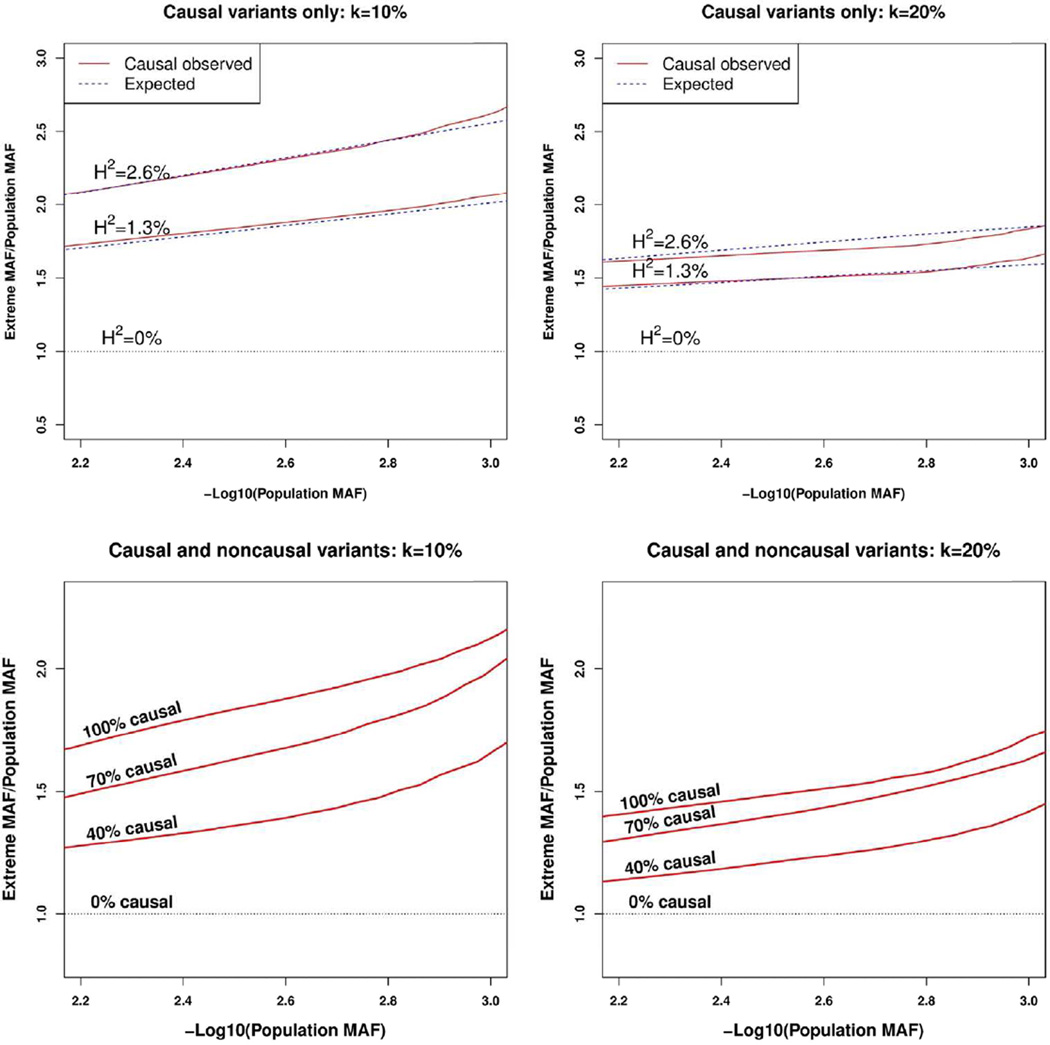
Because the causal variants are known in the simulation setting, the expected MAF of a causal variant using EPS can be computed analytically (see Supplementary Materials Section 1). The expected MAFs of causal variants using EPS matched closely with the sample MAFs of causal variants using EPS (Figure 1). The MAFs of simulated causal variants after EPS had an overall increased frequency over the respective population MAFs. This trend decreases as samples are restricted to less extreme phenotypes and heritability is lower. No enrichment is found when there is no causal variant. When both the causal and non-causal variants in a region are considered simultaneously, the median MAF using EPS is much less inflated than when only causal variants are examined.

Figure 1. Enrichment of causal rare variants in phenotypic extremes.

Estimated folds increase of the observed MAFs of causal variants in phenotypic extremes over population MAFs. The red lines represent the smoothed observed fold increases. The dotted lines represent the theoretical fold increase. For each causal variant, population MAF was computed using the full simulated population while extreme phenotype MAF was computed after sampling the tails. See Supplemental Materials for derivation of theoretical expected MAF for extreme phenotypes. The top two figures consider the case where all variants are causal by sampling k=10% and 20% high/low extremes. For each case, three situations were considered by heritability of causal variants: H2=2.6%, 1.3%, and 0% (no causal variant). Higher heritability gives more enrichment of rare variants. The bottom two figures consider the case where different fractions of variants in a region are causal (100%, 70%, 40% and 0%) by sampling k=10% and 20% high/low extremes. Presence of non-causal variants in a region lower the degree of enrichment of rare variants.

Sampling methods for comparison

Motivated by the enrichment of causal rare variants in phenotypic extremes, we expect to find that EPS methods can increase power to detect rare causal variants over random sampling methods. We extend the SKAT family methods to test for region-level rare variant effects when continuous phenotypes obtained from EPS are used in analysis. In simulation and data analysis, we only use the extreme phenotype optimal SKAT (SKAT-O), which accounts for extreme phenotype sampling and unifies the burden test and SKAT to a single framework and by constructing the optimal test within the framework. Using the simulated genotype data over 3kb regions the phenotypes were generated using the additive linear model (see Material and Methods). Given the same sample size, we compare the power of three tests designed for detecting rare variant effects using EPS. We first consider a burden test, DEP-Burden, that uses dichotomized extreme phenotypes along with collapsed information over genotypes by simply counting the number of rare variants with MAF<3% in the gene before applying logistic regression to the collapsed statistic. We also apply this same collapsed statistic to continuous extreme phenotypes as done in Li et al.[Li, et al. 2011] and call this test CEP-Burden. Next we consider dichotomized extreme phenotype SKAT-O (DEP-SKAT-O), which applies optimal SKAT (SKAT-O) to dichotomized extreme phenotypes while applying small sample adjustments when sample sizes are small[Lee, et al. 2012a]. Finally we consider continuous extreme phenotype SKAT (CEP-SKAT-O), which does not dichotomize and instead extends linear regression optimal SKAT over the continuous extreme phenotypes (see Material and Methods) by using a truncated normal distribution. We also applied the small sample adjustment to CEP-SKAT-O to obtain the correct type I error rates when sample sizes are small. To demonstrate the benefits of EPS compared to random sampling, we included in the comparison a fourth method using random sampling SKAT-O (RS-SKAT-O), which applies optimal SKAT to the continuous phenotypes of a random sample. We assume the same sample size when comparing different methods so their powers are comparable. The power of each competing method is estimated as the proportion of p-values less than α=10⁻⁶ in an effort to imitate genome-wide association studies.

The type 1 error rates for CEP-SKAT-O were accurate at α=0.01 and α=0.05 and slightly inflated at genome-wide significance levels α=10^–6(see Supplementary Table 1). When all causal variants had the same direction of effect, CEP-SKAT-O and CEP-Burden had the greatest power with a substantial lead over every other method (Figure 2). When causal variants had effects in opposite directions all tests lost power uniformly due to less enrichment of rare variants, but CEP-SKAT-O became the most powerful by a large margin (Figure 3). In this case DEP-Burden had the least power. The power of the three methods employing SKAT-O (CEP-SKAT-O, DEP-SKAT-O, and RS-SKAT-O) is much more robust to changes in the proportion of causal variants that have a positive effect than the burden test’s power is. This is because SKAT-O allows for each individual variant to affect phenotype in different directions and also allows for no effect. On the other hand, burden tests assume all the causal variants share the same direction of effect and that all the variants in a region are causal, and so the power of the burden tests greatly diminishes when causal variants are allowed effects in opposite directions or many causal variants are allowed no effect.

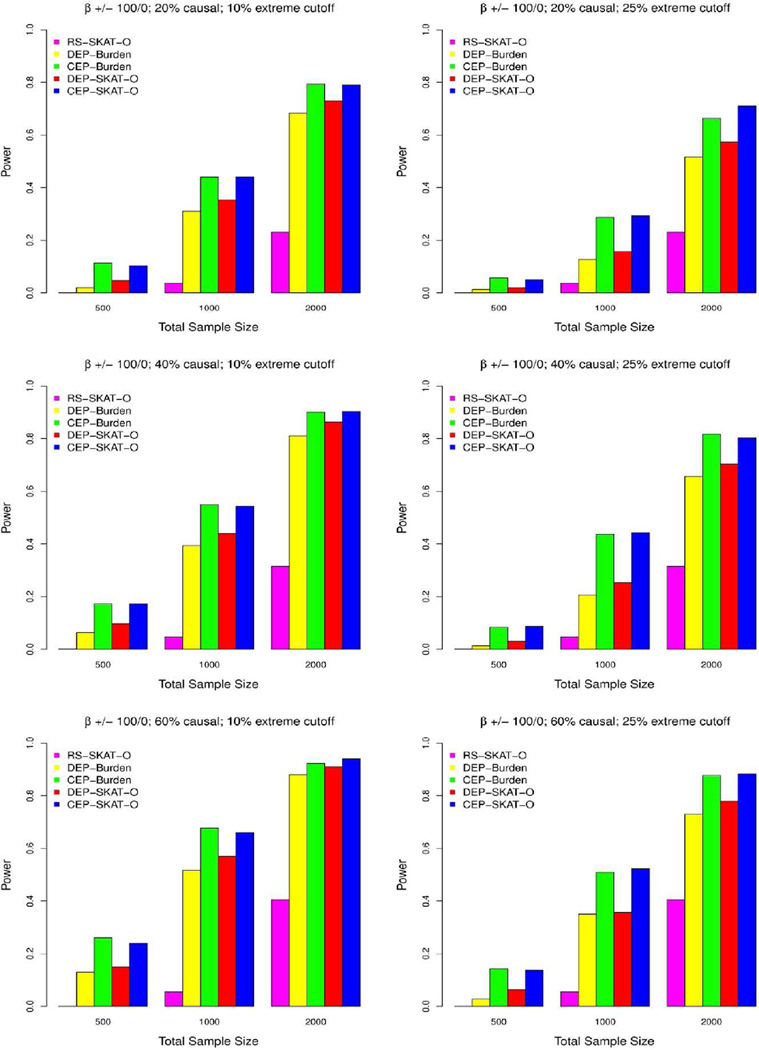
Figure 2. Power comparisons when all causal variants have the same effect direction.

Simulated power comparisons between four rare variants association tests with all causal variants having a positive effect on phenotype. The five tests are random sample optimal SKAT (RS-SKAT-O), dichotomized extreme phenotype burden test (DEP-Burden), continuous extreme phenotype burden test (CEP-Burden), dichotomized extreme phenotype optimal SKAT (DEP-SKAT-O), and continuous extreme phenotype optimal SKAT (CEP-SKAT-O). The left panel considers the situation where 10% high/low extremes are sampled with the three rows corresponding to 20% (0.6% heritability), 40% (1.2% heritability) and 60% (1.8% heritability) variants in a 3kb region being causal. Three total sample sizes are considered: n=500, 1000, 2000. The right panel considers the situation where 25% high/low extremes are sampled. Exonic regions are simulated with effect sizes for each causal variant equal to β=−0.2log10MAF. Power is estimated by the proportion of tests that detect an association at the α=10−6 level.

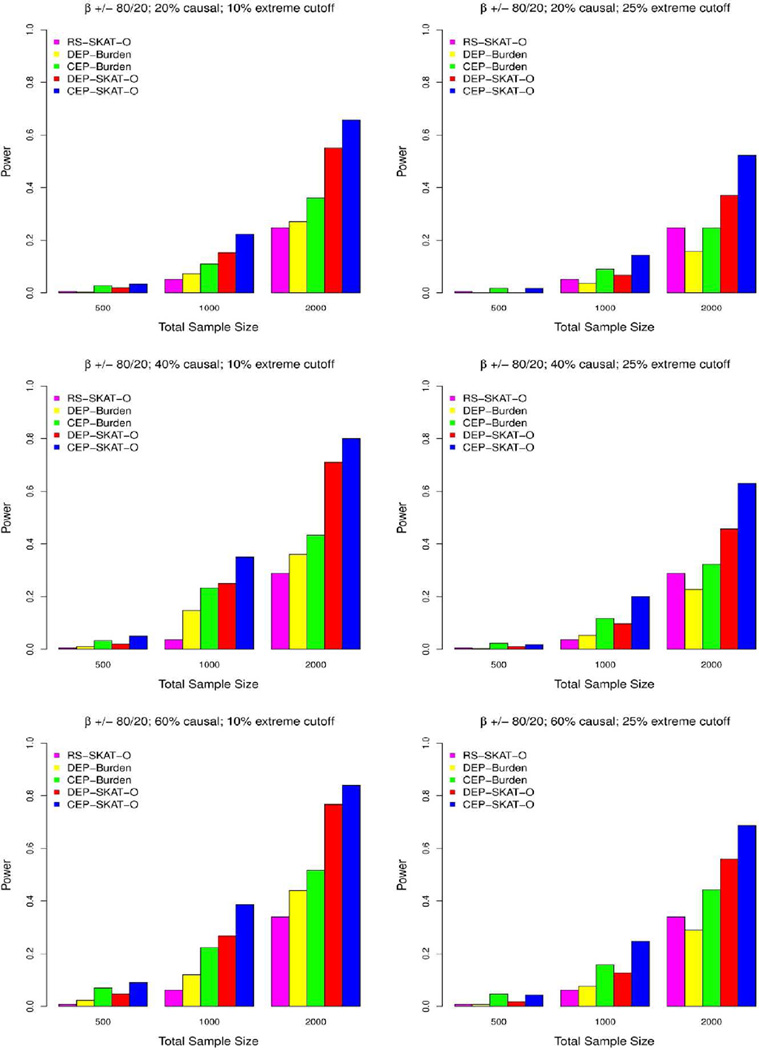
Figure 3. Power comparisons when causal variants have opposite effect directions.

Simulated power comparisons between four rare variants association tests with 80% of rare causal variants selected to have a positive effect on phenotype while the remaining 20% have a negative effect. The five tests are random sample SKAT (RS-SKAT-O), dichotomized extreme phenotype burden test (DEP-Burden), continuous extreme phenotype burden test (CEP-Burden), dichotomized extreme phenotype optimal SKAT (DEP-SKAT-O), and continuous extreme phenotype optimal SKAT (CEP-SKAT-O). The left panel considers the situation where 10% high/low extremes are sampled with the three rows corresponding to 20% (0.6% heritability), 40% (1.2% heritability) and 60% (1.8% heritability) variants in a 3kb region being causal. Three total sample sizes are considered: n=500, 1000, 2000. The right panel considers the situation where 25% high/low extremes are sampled. Exonic regions are simulated with effect sizes for each causal variant equal to |β|=−0.2log10MAF with the effect being negated 20% of the time. Power is estimated by the proportion of tests that detect an association at the α=10−6 level.

When all causal variants having the same direction of effect and as the percent of rare variants that were causal increased, the power gap between DEP-Burden and DEP-SKAT-O reduces, an observation that is also true for the relationship between CEP-Burden and CEP-SKAT-O (Figure 2). This is because CEP-SKAT-O includes CEP-Burden as a special case and behaves like CEP-Burden automatically when most variants are causal with effects in the same direction. To see this, we found that in simulations the estimated ρ decreased by a factor of 0.36 on average when changing from the case of having all positive causal variant effects to the case of having causal variant effects in opposite directions.

Methods utilizing extreme sampling benefit as the cutoff for extreme phenotypes increases. In particular, as the percent of the tails sampled from the distribution of phenotype decreases from 25% to 10%, all EPS tests show incremental increases in power given the same sample size due to higher enrichment of rare variants. Relative power comparisons remain unchanged after decreasing the heritability of the phenotype and after increasing the exon length to 5kb or 10kb (regions of these lengths contain 69 variants and 138 variants on average, respectively). Also, simulations were also performed where the β was selected to be a constant rather than being a decreasing function of the MAF but the relative power of the methods remained the same (Supplementary Figure 2). Regardless of the setting, CEP-SKAT-O was consistently robust and had the greatest overall power to detect gene-phenotype associations over the other methods.

Application to the Dallas Heart Study data

In the Dallas Heart Study [Victor, et al. 2004], 3476 individuals were sequenced over the genes ANGPTL3 (MIM 604774), ANGPTL4 (MIM 605910), and ANGPTL5 (MIM 607666). A total of 93 variants are present over these genes, and the variants in all three genes were tested simultaneously for an association with log-transformed serum triglyceride levels (logTG). Analysis for each of three genes separately is also considered (see Supplementary Materials Section 6). Ethnicity and sex were adjusted for in the analysis. To demonstrate rare variant association test methods for extreme phenotype sampling (EPS), a total of 1,389 individuals with the highest 20% and lowest 20% of logTG levels in each age-gender stratum were selected as the ESP sample. The continuous values were used in CEP-SKAT-O while dichotomized values were used for DEP-SKAT-O and DEP-Burden. Random samples of equivalent size were selected for the RS-SKAT-O method for comparison purposes.

To compare the effects of the different cutoffs of tails, we considered to sample individuals from wider tails (30% and 40%). Since wider tails had more samples, to make p-values comparable, we randomly sub-sampled 1,389 individuals among individuals in wider tails in order to have the same sample size as compared to a 20% cut off. In these cases, median p-values calculated from multiple random samples were obtained (Table 1). The p-values for all EPS methods are sensitive to the extreme phenotype cutoff. CEP-SKAT-O outperforms the other methods when there is sufficient information about the continuous trait distribution. It performs similarly to DEP-SKAT-O where there is limited information in the data, e.g., when the cutoff is low or when there are a small number of rare variants in a gene (Supplementary Materials Section 6). When extremes were sampled from wider tails (30% and 40%) all of the tests tended to lose significance, demonstrating the strength of EPS. We also computed p-values with different cutoffs and unequal sample sizes (Supplementary Figure 1), and CEP-SKAT-O outperformed other competing methods overall.

Table I.

Analysis results of the Dallas Heart Study triglyceride data

n=1389	CEP-SKAT-O	DEP-SKAT-O	RS-SKAT-O	CEP-Burden	DEP-Burden
20%	5.0×10−5	3.0×10−5	1.3×10−2	1.2×10−4	7.2×10−5
30%	1.0×10−3	1.9×10−3	1.3×10−2	2.2×10−3	2.8×10−3
40%	8.9×10−3	1.2×10−2	1.3×10−2	3.4×10−3	1.9×10−2

Analysis results of the Dallas Heart Study sequence data using various test methods and sampling schemes. A total of 3,476 subjects were sequenced. A total 1,389 individuals were selected with highest and lowest 20% logTG levels in each age-gender spectrum from the total 3,476 sequenced subjects. For sampling with higher cutoffs (30% and 40%), 1389 individuals were randomly sub-sampled among the individuals belongs to larger tails to make powers comparable. In these cases, median p-values are presented in the table from 1000 sampling iterations. Since the sample size was large, the small sample adjustment was not applied. The five tests are continuous extreme phenotype SKAT (CEP-SKAT-O), dichotomous extreme phenotype SKAT (DEP-SKAT-O), continuous extreme phenotype burden test (CEP-Burden), dichotomous extreme phenotype burden test (DEP-Burden), and random sample SKAT (RSSKAT-O).

Power Estimation

In the planning of new sequencing studies, it is important to be able to estimate the power to detect causal variants under various study designs. We provide such power and sample size calculations for extreme phenotype sampling designs using CEP-SKAT-O. We use analytical formulas to obtain the distribution of our statistic by allowing users to specifying desirable parameters of interest (see Supplementary Materials Section 5). The parameters that can be specified by the user include sample size, the percent of causal variants, the length of the genomic region, the effect size of the causal variants, the proportion of causal variants that have a positive effect, and the proportion of the tails that are sampled in EPS. We find that power is increased as sample size increases, as the proportion of causal variants increases, as the effect size increases, when causal variants have their effect in the same direction, and when we are more selective by sampling individuals with more extreme phenotypes. The power is also dependent on the genomic region as the distribution of the number of genetic variants, the MAF distribution, and the LD structure vary over the genome, so for genome-wide studies power estimations are averaged over many randomly selected regions of equivalent size.

To evaluate the accuracy of these analytic power estimations, we show a side by side comparison with empirical power simulations (Figure 4 and Supplementary Figure 3). In this setting we consider 3kb regions with 20% of variants being causal with all effects in the same direction. We see that the estimated power with our analytic calculations matches the empirical power over a wide range of sample sizes.

Figure 4. Comparison of theoretical and empirical powers.

Estimated power of CEP-SKAT for testing 3kb regions with 20% of variants being causal with all effects in the same direction and the casual variants have effects to |β|=−0.2log10MAF. Theoretical power was calculated as described in section 5 of the Supplementary material, and empirical power was estimated by simulation using 300 replicates. No covariates were considered in either the theoretical or empirical power calculations. Furthermore empirical power was computed using CEP-SKAT without small sample adjustments.

Discussion

We confirm in this paper through analytical calculations and simulation studies that sampling phenotypic extremes of a population can enrich rare causal variants. As a consequence, we show that sampling from phenotypic extremes profit over analogous random sampling methods by showing a sizable gain in power when the same size is used. In particular, analysis using dichotomized extreme phenotype (DEP-SKAT-O) is shown to be more powerful than that using random sampling with continuous phenotypes (RS-SKAT-O) in almost all scenarios. We develop a new method, continuous extreme phenotype optimal SKAT (CEP-SKAT-O), which improves upon DEP-SKAT-O by retaining continuous phenotype information rather than dichotomizing, includes the continuous extreme phenotype burden test as a special case, and results in a significant increase in sensitivity to causal variants. We find that CEP-SKAT-O has the overall greatest power in a wide variety of settings over DEP-SKAT-O, RS-SKAT-O, and comparable collapsing methods.

In the realm of region based association testing methodology, there already exist many methods capable of handling continuous phenotypes when a normal distribution is assumed. However in the case of extreme sampling, phenotype follows a truncated normal distribution instead, and so current methods cannot be directly applied without dichotomizing. The advantage of CEP-SKAT-O is that it adapts SKAT-O, a method that applies multiple linear regression of a phenotype on all genotypes in a region, to be able to handle phenotypes coming from a truncated normal. This adaptation allows for the usual continuous phenotype analysis without forcing the usual loss of phenotype information that occurs due to dichotomizing.

CEP-SKAT-O assumes that subjects are sampled from the extremes of a normally distributed phenotype, which in some circumstances may be inappropriate, and hence the test results can be biased when the normality of the underlying trait is violated. Dichotomizing phenotypes using DEP-SKAT-O is robust to departure from normality, although it is subject to some power loss when normality assumption is true. For candidate gene studies, permutation can be used to estimate the null distribution of the CEP-SKAT-O test statistic when the underlying trait does not follow a normal distribution. However, this is computationally difficult for GWAS where genome-wide significance levels are very stringent and a large number of genes are tested. We have found the maximum likelihood estimator of σ² seems to be sensitive to the distribution of the underlying trait. It is of future research interest to develop an alternative estimator of σ² that is more robust to deviations from normality.

In several ongoing exome sequencing studies conducted in the NHLBI Exome Sequencing Project https://esp.gs.washington.edu/drupal/, subjects were sampled using extremes of multiple phenotypes, future research is needed to develop methods for analyzing this more complex sampling setting. When subjects with extreme phenotypes are sampled for sequencing, covariate confounding effects need to be accounted for at the design phase to ensure representative samples. One strategy is to use stratified sampling, i.e. sample extreme phenotypes within key covariate stratum. For example, a phenotype distribution is likely to be gender-specific. It is desirable to sample extreme phenotypes within each gender stratum. The residual covariate confounding effects can be adjusted for at the analysis stage.