Abstract
A Bayesian framework is presented for modeling Effects of climate change on pollen indices such as annual birch pollen count, maximum daily birch pollen count, start date of birch pollen season and the date of maximum daily birch pollen count. Annual mean CO2 concentration, mean spring temperature and the corresponding pollen index of prior year were found to be statistically significant accounting for Effects of climate change on four pollen indices. Results suggest that annual productions and peak values from 2020 to 2100 under different scenarios will be 1.3-8.0 and 1.1-7.3 times higher respectively than the mean values for 2000, and start and peak dates will occur around two to four weeks earlier. These results have been partly confirmed by the available historical data. As a demonstration, the emission profiles in future years were generated by incorporating the predicted pollen indices into an existing emission model.
Keywords: Climate change, Birch, Pollen, Bayesian analysis
1. Introduction
Climate change exerts important Effects on annual cumulative airborne pollen count, maximum daily pollen count, start date of pollen season and the date of maximum daily pollen count (Fitter and Fitter, 2002; Damialis et al., 2007; Alizoti et al., 2010). These pollen indices hereafter referred as annual production, peak value, start date and peak date, are closely associated with allergic airway diseases (AAD) (Blando et al., 2012) and genetic manipulation of plants (Martin et al., 2010). These four pollen indices are further classified as pollen quantity indices (annual production and peak value) and pollen timing indices (start and peak dates). An increasing number of individuals su ering from seasonal AAD caused by pollen (Singh et al., 2010a), and the corresponding increased healthcare and financial costs have been reported in many industrialized countries (Lamb et al., 2006).
Modeling efforts have been made to understand the exacerbation of AAD and genetic contamination caused by increased pollen levels (Sofiev et al., 2006). These models are either based on simple regression of phenological and aerobiological observations (Jato, 2007), or utilize physical principles of transport and meteorology (Siljamo et al., 2008; Martin et al., 2009). Pollen concentration estimations generated by most of these models are qualitative or semi-quantitative (Schueler and Schlnzen, 2006; Sofiev et al., 2006) due to the scarcity of emissions information.
A major challenge for the physics-based models to construct exact pollen spatial and temporal distribution is establishing an accurate emissions module that incorporates the influence of multiple climatic factors. different methods have been utilized to try to tackle this issue. Kawashima and Takahashi (1999) and Schueler and Schlnzen (2006) adopted regression equations of phenological observations as emission modules to simulate pollen transport and distribution from cedar and oak, respectively. Starting from the measured pollen count, Lagrangian algorithms were used by Aylor (2005) and Pasken and Pietrowicz (2005) to simulate pollen transport and distribution from maize, and oak, respectively. Mechanistic models based on the formulation of Helbig et al. (2004) were developed by Efstathiou et al. (2011) and linked to the Community Multiscale Air Quality model in order to simulate the transport and distribution of birch and ragweed pollen. The above mentioned methods do not account for the long term influence of multiple climatic factors in the emission module.
In this work, Bayesian models are employed to describe climatic change Effects on annual production, peak value, start date and peak date of birch (Betula) pollen. The modeling process consists of four steps: variable selection, parameterization, evaluation and prediction. Probabilities of each sub-model, and probabilities of inclusion of each variable in full model were calculated and analyzed. Then Bayesian parameterizations of these selected models were conducted with published data (Rasmussen, 2002). The parameterized models were evaluated using data from Yli-Panula et al. (2009), Frei and Gassner (2008) and two pollen stations in the US, and used to predict plausible global mean trends of pollen indices of future years based on the climatic data reported in the Intergovernmental Panel on Climate Change (IPCC) assessment report (IPCC, 2007a,c). The intrinsic interannual variations of pollen indices were also examined and used to simulate the fluctuations around the mean trends. Finally, a case study demonstrates using the results of Bayesian modeling for generating the future spatiotemporal emission profiles of birch pollen in the Northeastern US. The statistical calculation and simulation were carried out in R and visualizations were implemented in Matlab and ArcGis.
2. Methods
2.1. Model
We assumed that observed pollen indices are normally distributed variables which fluctuate around mean trends depending on the combination of multiple random climate/meteorology factors, and that pollens of the same genus (Betula) have similar responses to climate/meteorology changes. The ordinary norm linear regression model (Marin and Robert, 2007a) is presented in equation 1,
| (1) |
where Y = (y1, …, yn)T is a vector of pollen indices, the five year overlapping mean of either annual production (pollen/m3) or peak value (pollen/m3) or start date (day) or peak date (day). With day 1 being January 1st, the start date is defined when the cumulative pollen count reached a certain percentage of the annual production (e.g. 2.5%) (Rasmussen, 2002) and peak date is reached when the daily maximum count is registered. X is the n × k matrix of explanatory variables in which each column vector xi corresponds to values of a climatic factor in n years and k is the number of variables. In is the n × n identity matrix. β and σ2 are the unknown vector of coefficient and variance, respectively.
Equation 2 is the likelihood function of the Bayesian model.
| (2) |
Zellner’s informative G-priors (Zellner, 1971) are assumed for β and σ2 as shown in equation 3,
| (3) |
where and c are further assumed to be 0k+1 and 100 respectively so that parameterizations are mainly dependent on the explanatory matrix X. In this study c = 100, the prior gets a weight corresponding to 1% of the sample.
2.2. Variable selection
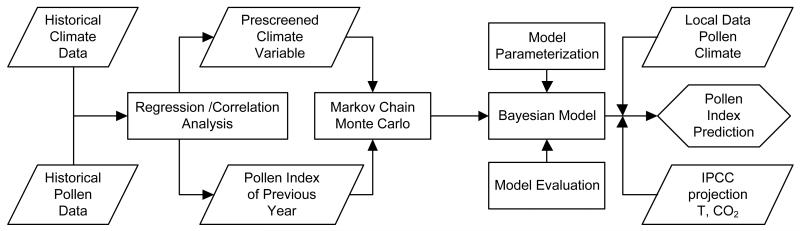
Figure 1 shematically depicts the Bayesian modeling framework. Multiple climatic factors were first prescreened by regressing each individual pollen index against each individual climatic factor of a given month for historical data of twenty years. Climatic factors in two periods influence the pollen indices (Masaka and Maguchi, 2001): (1) initiation of flower primordial during the burst period in spring and early summer of the current year; and (2) development of flower inflorescences in autumn and winter of the previous year. In this study, monthly climatic factors for CO2, temperature, precipitation, cloud coverage, and sunshine hours in June to December of previous year and January to May of current year were taken into account in the prescreening stage. First, multiple monthly climatic factors were consecutively screened starting from the smallest P value and the largest R2; then monthly climatic factors in consecutive months were lumped together to form nine preselected variables for each pollen index.
Figure 1.
Overall flow of Bayesian modeling framework. Multiple monthly climatic factors from June of previous year to May of current year were first screened using simple linear regression and correlation analysis. The prescreened climatic factors and pollen indices were then further selected using method of Markov Chain Monte Carlo based on Bayesian statistics. Finally, the selected Bayesian models were parameterized and evaluated using different datasets, and utilized to predict future pollen indices based on IPCC projection.
The preselected climatic variables were further selected and assessed by calculating the probability of each sub-model and the probability of inclusion of each variable in the full model.
Calculation of sub-model probability is obtained through equation 4,
| (4) |
where binary indicator vector γ∈Γ = {0, 1}k, γi=1 means variable xi is included in the model while γi=0 means xi not included in the model; βγ, Xγ, qγ are sub-vectors, sub-matrix and number of variables in the sub-model, respectively.
A Gibbs sampling algorithm, as shown in the following, was used to calculate inclusion probabilities. It is a Markov chain, and after a large number of iterations, its output can be used to approximate the posterior probabilities P (γi = 1|Y, X) based on the Monte Carlo method in the form of equation 5,
| (5) |
where T is the number of total iterations, and T0 is the “burn-in” period, such that the first T0 values are eliminated to guarantee convergence. In this work, T was set to be 20,000 and T0 to be 10,000.
| Initialization: draw γ0 from the uniform distribution on Γ: |
|---|
| (1). draw according to , |
| (2). draw according to , |
| … … … … … … … |
| (k). draw according to , |
2.3. Parameterization
The corresponding Bayesian estimator of expectations of β and σ2 are presented in equations 6 and 7:
| (6) |
| (7) |
where is the maximum likelihood estimator obtained by maximizing the likelihood function shown in equation 2.
P values were calculated based on F-statistics. The highest posterior density regions (HPD) in Bayesian statistics are the sections of the parameter space where the parameters most likely take values. HPD of β were calculated to characterize the regions of most probable variations of predicted pollen indices. A Bayes factor (Marin and Robert, 2007b) was constructed through null hypothesis H0: βi = 0.
2.4. Prediction
The future vector based on the posterior and future explanatory matrix has a Gaussian distribution (Marin and Robert, 2007a) and its expectation can be predicted by equation 8:
| (8) |
The pollen indices for base year (2000) were obtained by averaging over the corresponding five year overlapping means of pollen indices from Basel (Switzerland), Turku (Finland), and New Jersey and North Dakota (US). These locations span different climate zones, geographical regions and forest vegetations in the northern hemisphere. Birch pollen levels from these locations are su ciently representative to generate and analyze future plausible pollen indices and their mean trends.
The intrinsic inter-annual variation of the pollen index has been observed by many researchers (Silvertown, 1980). According to Masaka and Maguchi (2001), the mast and sparse years occur alternately due to evolution stress. As for the intrinsic inter-annual variation of pollen indices in the current study, the data from Yli-Panula et al. (2009) were first normalized using their mean values, and then fit using equation 9,
| (9) |
where YNP (i) is the normalized pollen index in year i, and parameters P1, P2, P3 and P4 are to be determined. The first and fourth terms describe the mean trends of the pollen index. The second and third terms in equation 9 characterize the intrinsic inter-annual variation of pollen indices and are used to simulate the fluctuations around the mean trends obtained through equation 8.
2.5. Application
As an example, the predicted annual pollen production under B1 scenario was incorporated into the mechanistic emission model described in Efstathiou et al. (2011) to generate future sptiotemporal emission profiles of birch pollen in the Northeastern US based on future meteorology profiles predicted by the Weather Research Forecasting model and obtained from the North American Regional Climate Change Assessment Program (NARCCAP) (Mearns et al., 2011). The simulations were performed on the Ozone Transport Commission modeling domain with spatial resolution of 12km, for the month of April from 2002 and 2040. The connection between annual emission flux and observed airborne annual pollen count were reported in Jato (2007).
2.6. Data source
Variable selections and parameterizations were based on pollen data in Copenhagen, Denmark (Rasmussen, 2002); the corresponding monthly mean temperature, total precipitation, sunshine hours, and mean cloud coverage were obtained from the website of Denmark’s Meteorology Institute (Cappelen, 2009). Since we could not obtain the data of monthly mean CO2 concentration in Copenhagen from 1978 to 2000, we instead used the data of CO2 concentrations from the nearby and representative monitor stations in Poland, Norway and Portugal of Europe, and Mauna Loa (Hawaii) of US. Because CO2 is a long-lived greenhouse gas (GHG) and well mixed in the atmosphere, measurements made at such sites as Mauna Loa, which is the first and longest established in situ continuous CO2 station (Keeling et al., 2009), provide an integrated picture of large parts of the Earth, including continents and city point sources (IPCC, 2007b).
Evaluation of the selected model was conducted using pollen data from Turku (Yli-Panula et al., 2009), Basel (Frei and Gassner, 2008), and New Jersy and North Dakota, respectively. For New Jersy and North Dakota, the pollen data originate from stations of the American Academy of Allergy Asthma and Immunology; the spring temperatures and CO2 levels originate from the climate and meteorology databases of the closest US stations on the website of the National Oceanic and Atmospheric Administration. Mean spring temperature in Basel was obtained from the website of the Federal O ce of Meteorology and Climatology. Since we could not obtain the dataset for mean spring temperature in Turku, we used instead the annual mean temperature reported by Yli-Panula et al. (2009). For Turku, the corresponding CO2 concentrations came from monitor stations in Finland, Norway, Portugal and Mauna Loa. For Basel, the corresponding CO2 concentrations came from monitor stations in Hungary, Poland, Norway, Portugal and Mauna Loa.
Prediction of future pollen indices was performed using the global annual mean temperature and global annual mean CO2 concentration projections in the IPCC 2007 report (IPCC, 2007a,c).
3. Results and Discussion
3.1. Variable selection
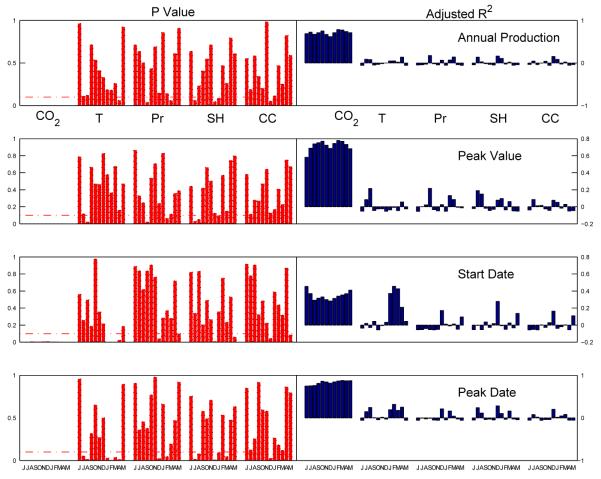
The results for prescreening climatic factors are summarized in Figure 2. It is indicated that CO2 concentrations throughout the year are important for the four pollen indices, and have a positive relationship with quantity indices and a negative relationship with timing indices. This corresponds to the fact that increased CO2 levels will favor evolutional and productive plant growths. These results are consistent with the observations from Ziska et al. (2003), which concluded that ragweed grew faster, flowered earlier, and produced significantly greater pollen at urban locations (high CO2 concentration) than at rural locations (low CO2 concentration). Wolf et al. (2010) also reported that elevated CO2 concentrations led to increased spore production of A.alternata, a ubiquitous allergenic fungus.
Figure 2.
P values and adjusted R2 for the relationships between pollen indices and monthly CO2 level, mean temperature(T), precipitation(Pr), sunshine hours(SH) and cloud coverage(CC) in June to December of previous year and January to May of current year; dashed line corresponds to P value equal to 0.1.
Spring temperatures in January, February and March of current year are crucial climatic factors for timing indices, while less important for quantity indices, according to both p values and adjusted R2. Overall, spring temperature of current year has a negative relationship with the four pollen indices. Similar results of temperature Effects have been reported by Singh et al. (2010b) through experiments of Cowpea and Prasad et al. (2006) through observation of Sorghum bicolor (L.) Moench.
Correlation analysis indicated that each pollen index of current year was closely correlated with the corresponding pollen index of previous year. In order to incorporate the Effects of climatic factors of the previous year into the Bayesian model, the corresponding pollen index of previous year was also added as a variable in the Bayesian model.
Based on the discussion above, climatic factors for Bayesian models were preselected as following. For quantity indices, xi1 is the corresponding pollen index of previous year (pollen/m3), xi2 the temperature in April of current year (°C), xi3 the mean temperature in July and August of previous year, xi4 the annual mean CO2 concentration of current year (ppm), xi5 the total precipitation in February and March of current year (mm), xi6 the total precipitation in September of previous year (mm), xi7 the mean cloud coverage in December of previous year and January of current year (%), xi8 the total sunshine hours in January of current year and December of previous year (hour), and xi9 the sunshine hours in July of previous year (hour). While for timing indices, xi1 is the corresponding pollen index of previous year, xi2 the mean spring temperature in January, February and March of current year, xi3 the annual mean CO2 concentration of current year, xi4 the total precipitation in March of current year, xi5 the total precipitation in December of previous year, xi6 the mean cloud coverage in March of current year, xi7 the mean cloud coverage in December of previous year, xi8 the sunshine hours in March of current year, and xi9 the sunshine hours in December of previous year. The first index i in a variable xij indicates the year, and the second index j identifies the corresponding variable in Tables 1 and 2, with 0 meaning intercept.
Table 1.
Ten most likely sub-models under Zellner’s informative G-Prior. A sub-model is defined asa linear combination of the climatic variables indicated by a group of numbers in column t1(γ). Higher randomness of the corresponding pollen index can be described bya sub-model with a higher posterior probability.
| Annual Production |
Peak Value |
Start Date |
Peak Date |
||||
|---|---|---|---|---|---|---|---|
| t1(γ) | Π(γ|Y,X) | t1(γ) | Π(γ|Y,X) | t1(γ) | Π(γ|Y,X) | t1(γ) | Π(γ|Y,X) |
| 0,4,6,7 | 0.17 | 0,1,6,8 | 0.17 | 0,1 | 0.17 | 0,3 | 0.11 |
| 0,4,6 | 0.16 | 0,1,6 | 0.12 | 0,2 | 0.09 | 0,1 | 0.11 |
| 0,4,6,8 | 0.06 | 0,1,6,7 | 0.07 | 0,3 | 0.06 | 0,5 | 0.06 |
| 0,4,5,6 | 0.04 | 0,1,4,6 | 0.06 | 0,9 | 0.05 | 0,2 | 0.06 |
| 0,1,6,8 | 0.04 | 0,4,6 | 0.05 | 0,5 | 0.05 | 0,9 | 0.06 |
| 0,3,4,6,7 | 0.03 | 0,1,4,6,7 | 0.04 | 0,7 | 0.04 | 0,8 | 0.05 |
| 0,2,4,6,7 | 0.02 | 0,1,4,6,8 | 0.04 | 0,8 | 0.04 | 0,7 | 0.05 |
| 0,1,6 | 0.02 | 0,1,2,6,8 | 0.03 | 0,4 | 0.03 | 0,6 | 0.05 |
| 0,4,5,6,7 | 0.02 | 0,4,6,7 | 0.02 | 0,6 | 0.03 | 0,4 | 0.05 |
| 0,2,4,6 | 0.02 | 0,1,2,6 | 0.02 | 0,1,2 | 0.02 | 0,2,3 | 0.01 |
Table 2.
Probability of inclusion () of each climatic variable in the full model under Zellner’s informative G-Prior. The full model incorporates all climatic variables anda constant intercept. A climatic variable witha higher posterior probability of inclusion tends to explain more variation in the corresponding pollen index.
| Annual Production | Peak Value | Start Date | Peak Date | |
|---|---|---|---|---|
| γ 1 | 0.25 | 0.86 | 0.36 | 0.22 |
| γ 2 | 0.12 | 0.13 | 0.24 | 0.15 |
| γ 3 | 0.14 | 0.10 | 0.15 | 0.25 |
| γ 4 | 0.84 | 0.36 | 0.14 | 0.13 |
| γ 5 | 0.15 | 0.09 | 0.16 | 0.16 |
| γ 6 | 0.90 | 0.96 | 0.12 | 0.13 |
| γ 7 | 0.40 | 0.24 | 0.13 | 0.14 |
| γ 8 | 0.24 | 0.38 | 0.13 | 0.15 |
| γ 9 | 0.10 | 0.12 | 0.15 | 0.16 |
Table 1 lists the probabilities of the top 10 sub-models. A sub-model is defined as a linear combination of the variables indicated by a group of numbers in column t1(γ) of Table 1. Probability of inclusion of each variable in the full model is presented in Table 2. As shown in these tables, quantity indices can be fairly well described using two or three variables, among which the annual mean CO2 concentration (4), corresponding pollen index of previous year (1) and monthly mean precipitation in September of previous year (6) are the dominant variables. The corresponding pollen index of previous year (1), mean spring temperature in January, February and March of current year (2), and mean annual CO2 concentration (3) are good candidates to be used as variables to model timing indices. Any single variable from these candidates seems adequate for characterizing the Effects of climatic change on timing indices.
Climatic factors like monthly mean precipitation, total sunshine hours and mean cloud coverage contributed su ciently to a given pollen index based on the values of sub-model probabilities and inclusion probabilities. However these types of data are generally not publicly available for most of the times and locations. Particularly, they are difficult to be projected via current climatic models, making the predictions of future pollen indices based on such data impossible. Furthermore, variables for describing annual production were assumed to be consistent with those describing peak value. Similarly, variables describing start date were assumed to be consistent with those describing peak date. Taking statistical values and data availability into consideration, and also accounting for consistency of model structure for both pollen quantity and timing, the corresponding pollen index of the previous year and the annual mean CO2 concentration were selected as the final variables for the Bayesian models of pollen quantity; the corresponding pollen index of the previous year and the mean spring temperature in January, February and March of the current year were selected for the Bayesian models of pollen timing.
3.2. Parameterization
The posterior means and variances of parameters are listed in Table 3. All estimated parameters are statistically significant according to the listed P values. The statistical significance of four models has been dramatically improved by selecting and combining crucial climatic factors. However, many of the values of Bayes factors are in favor of the null hypothesis H0 according to Jeffery’s scale of evidence (Marin and Robert, 2007b).
Table 3.
Posterior mean and variance, and Bayes factors of pollen idices under Zellner’s informative G-prior
| Annual Production |
Peak Value |
||||||
|---|---|---|---|---|---|---|---|
| E(βi|Y,X) | V(βi|Y,X) | E(βi|Y,X) | V (βi|Y,X) | ||||
| β ap0 | −24,665 | 3.22×108 | −0.63 | β pv0 | −3,395 | 5.40×106 | −0.56 |
| β ap1 | 77 | 2,940 | −0.60 | β pv1 | 10 | 47 | −0.54 |
| β ap2 | 0.39 | 0.09 | −0.67 | β pv2 | 0.57 | 0.05 | 0.14 |
|
| |||||||
| 0.72 | 0.81 | ||||||
| P value | 1.40×10−5 | P value | 7.58×10−7 | ||||
|
| |||||||
| Start Date |
Peak Date |
||||||
| E(βi|Y,X) | V (βi|Y,X) | E(βi|Y,X) | V (βi|Y,X) | ||||
|
| |||||||
| β sd0 | 32 | 5,163 | −0.96 | β pd0 | 25 | 8,506 | −0.99 |
| β sd1 | −0.50 | 2.51 | −0.98 | β pd1 | −0.26 | 1.94 | −0.99 |
| β sd2 | 0.71 | 0.38 | −0.71 | β pd2 | 0.79 | 0.54 | −0.75 |
|
| |||||||
| 0.82 | 0.86 | ||||||
| P value | 4.99×10−7 | P value | 5.70×10−8 | ||||
The parameters of intrinsic inter-annual variability are listed in Table 4. The plausible values of the four pollen indices were obtained by multiplying the mean trend estimations with the sum of fluctuated term and unity as shown in equations 10 to 13, where yap(i), ypv(i), ysd(i) and ypd(i) are respectively the annual production, peak value, start date and peak date in year i.
| (10) |
| (11) |
| (12) |
| (13) |
Table 4.
Parameters of intrinsic inter-annual variability based on Yli-Panula’s data
| P 1 | P 2 | P 3 | P 4 | |
|---|---|---|---|---|
| Annual Production | 0.0541 | −0.1137 | 3.465 | −106.3 |
| Peak Value | 0.0465 | −0.1149 | 3.462 | −91.42 |
| Start Date | −0.0047 | −0.0115 | 1.571 | 10.39 |
| Peak Date | −0.0046 | 0.0049 | 1.570 | 10.07 |
β0 can be explained as the base level of the pollen indices with units of pollen/m3 or day; β1 has a unit of pollen/ppm or day/°C describing the CO2 concentration or the temperature effect on pollen quantity or timing; β2 is dimensionless and accounts for the comprehensive influence of pollen indices of the previous year on pollen indices of current year.
For inter-annual variation, P2 is responsible for the amplitude of the inter-annual variation of the pollen indices; and P3 may suggest the periods of the variations of pollen indices. This can be shown through dividing 2π by P3. For annual production and peak value, the quotients approximate 2; while for start and peak dates, they approximate 4. This suggests that the annual production and peak values fluctuate intrinsically every other year, and the start and peak dates change periodically every four years. Although few reports were made about the intrinsic fluctuation of start and peak dates, the inter-annual variation of birch pollen production was indeed studied by many researchers (Masaka and Maguchi, 2001) and is in good agreement with the period in the current study.
3.3. Evaluation
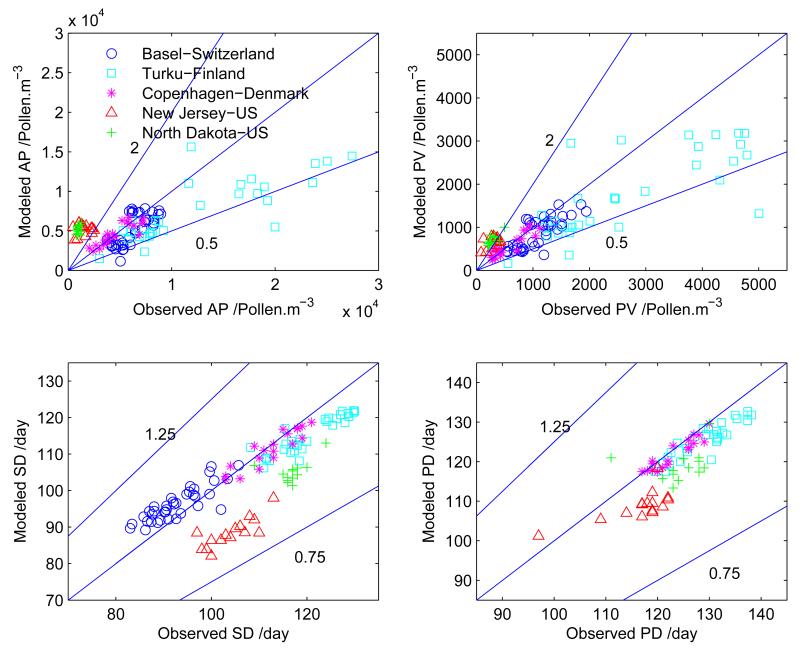
Modeling results are compared with corresponding observed values in Figure 3 for five different locations. Three diagonal lines have been plotted in each panel: the middle line has a slope of unity, the upper line has a slope of 2 or 1.25, and the lower line has a slope of 0.5 or 0.75. It is illustrated that the phenologically observed values of the four pollen indices can be well matched by the modeling values. Most of the points of annual productions and peak values either from Turku or Basel fall into the range between diagonal lines 0.5 and 2; and those of start and peak dates from five locations fit into the space between diagonal lines 0.75 and 1.25. The estimated pollen indices in the US stations can capture the trends, but the deviations are larger compared with the estimates for European locations because of the non-local parameterizations of the models.
Figure 3.
Comparison of pollen indices [annual production(AP); peak value(PV); start date(SD); and peak date(PD)] between the phenological observations and mean model estimations for five different locations. Three diagonal lines have been plotted in each panel: the middle line has a slope of unity, the upper line has a slope of 2 or 1.25, and the lower line has a slope of 0.5 or 0.75.
Root mean square error (RMSE) and RMSE relative to mean value of pollen index were calculated to quantify the deviation between the observations and estimations. Results listed in Table 5 indicate that relative RMSEs (RRMSE) approximate 30%, 50% and 20% for estimates of annual productions and peak values in Basel, Turku, and Copenhagen, respectively. RRMSEs of estimates of start and peak dates for three European locations are between 1.5% and 5.1%, which are much lower than those for annual production and peak value. For the US stations, the RRMSE of annual production and peak value range from 123.8% to 370.7%, and RRMSE of start and peak dates vary between 6.1% and 15.2%.
Table 5.
Root mean square error (RMSE) and relative RMSE (RRMSE) of estimations of Bayesian model
| Annual Production |
Peak Value |
Start Date |
Peak Date |
|||||
|---|---|---|---|---|---|---|---|---|
| RMSE (pollen.m−3) |
RRMSE (%) |
RMSE (pollen.m−3) |
RRMSE (%) |
RMSE (day) |
RRMSE (%) |
RMSE (day) |
RRMSE (%) |
|
| Basel | 1,701 | 27.7 | 326 | 30.0 | 5 | 5.0 | - | - |
| Turku | 6,586 | 54.0 | 1,312 | 49.2 | 6 | 5.1 | 4 | 3.4 |
| Copenhagen | 786 | 17.8 | 116 | 20.7 | 3 | 2.2 | 2 | 1.5 |
| New Jersey | 3,825 | 266.9 | 388 | 137.8 | 16 | 15.2 | 9 | 7.7 |
| North Dakota | 4,170 | 370.7 | 427 | 123.8 | 12 | 10.4 | 8 | 6.1 |
The deviations between estimations and observations are most likely due to the following: (1) For estimates of pollen indices in Basel, Turku, and New Jersey and North Dakota, the Bayesian models were not parameterized with the local pollen and climate data; (2) The spring temperature and especially the annual mean CO2 concentrations used in evaluations were not derived from the exact sites where the four pollen stations are located; (3) Because of the data availability of multiple climate factors, the Bayesian models used were not the optimum ones; and (4) The Bayesian models used to predict mean trends did not incorporate the information on inter-annual variation.
3.4. Prediction
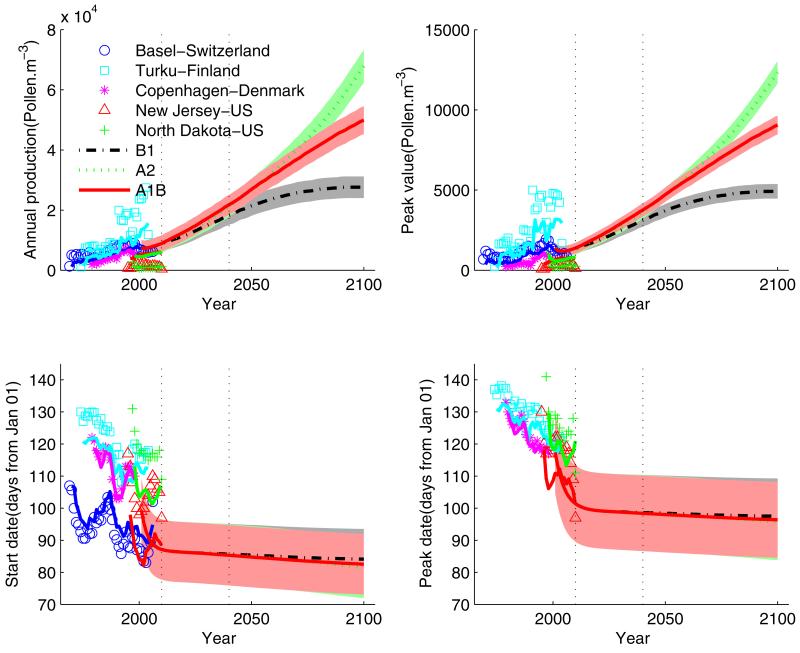
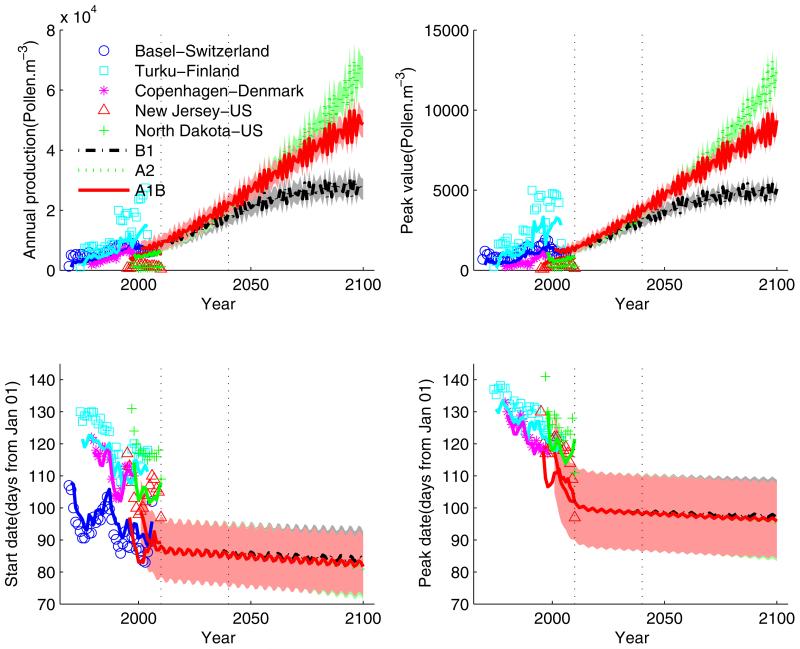
The historical estimates and future predictions of mean trends of the pollen indices under three representative IPCC scenarios B1, A2 and A1B, are presented on left and right, respectively, of Figure 4 using heavy lines. The top 5% HPD regions of future predictions were also calculated and are shown as a shaded area around the mean trends. Vertical dotted lines at 2010 identify the historical data and future predictions. Alternative development pathways are assumed in different IPCC scenarios which cover a wide range of demographic, economic and technological driving forces and resulting GHG emissions (IPCC, 2007d). Scenario B1 assumes future development will be globally and environmentally oriented with projection of CO2 level being 600 ppm in year 2100; and A2 assumes regionally and economically oriented development with projection of CO2 level being 850 ppm; while A1B features with rapid economic growth and a balanced emphasis on all energy sources, and with projection of CO2 level being 800 ppm.
Figure 4.
Predictions of mean trends of pollen indices based on the global annual mean temperatures and global annual mean CO2 concentrations projected by the IPCC under three representative scenarios. Heavy lines are the mean trends and the corresponding shaded areas are top 5% HPD regions. Also shown on the left are time series of historical pollen indices and their corresponding mean trends calculated by the model.
Overall, the mean trends of historical pollen indices can be reasonably captured by the mean model estimates with the exceptions of pollen indices in two US stations where start and peak dates were systematically underestimated, and annual production and peak value were overestimated. Simple comparisons between global mean pollen indices in future years and the corresponding mean values in 2000 are summarized in Table 6. Under scenario B1, the global means of annual production and peak value in 2020 to 2040 will be 1.3-2.2 and 1.1-1.9 times as many as the mean values of 2000, respectively; while the start and peak dates will be 19 days and 23 days earlier, respectively. Under scenario A2, the annual production and peak values will be 1.4-2.5 and 1.2-2.2 times higher, respectively; while the start and peak dates will be also 19 days and 23 days earlier, respectively. Pollen indices under scenario A1B are similar to those of A2.
Table 6.
Comparison of mean pollen indices between future years and the base year 2000. The ratios to or differences from base year were put in the parentheses
| Scenario | 2000 | 2020 | 2040 | 2060 | 2080 | 2100 | |
|---|---|---|---|---|---|---|---|
| Annual Production (pollen.m−3) |
B1 | 8,455 | 11,413(1.3) | 18,286(2.2) | 23,872(2.8) | 26,913(3.2) | 27,621(3.3) |
| A2 | 8,455 | 12,019(1.4) | 21,047(2.5) | 33,005(3.9) | 47,779(5.7) | 67,831(8.0) | |
| A1B | 8,455 | 12,673(1.5) | 21,735(2.6) | 31,950(3.8) | 41,518(4.9) | 49,889(5.9) | |
|
| |||||||
| Peak Value (pollen.m−3) |
B1 | 1,684 | 1,844(1.1) | 3,121(1.9) | 4,187(2.5) | 4,768(3.2) | 4,918(3.3) |
| A2 | 1,684 | 1,951(1.2) | 3,622(2.2) | 5,851(3.5) | 8,601(5.1) | 12,334(7.3) | |
| A1B | 1,684 | 2,067(1.2) | 3,758(2.2) | 5,671(3.4) | 7,468(4.4) | 9,056(5.4) | |
|
| |||||||
| Start Date (days from January 1st) |
B1 | 105 | 86(−19) | 86(−19) | 85(−20) | 84(−21) | 84(−21) |
| A2 | 105 | 86(−19) | 86(−19) | 84(−21) | 83(−22) | 81(−24) | |
| A1B | 105 | 86(−19) | 85(−20) | 84(−21) | 83(−22) | 83(−22) | |
|
| |||||||
| Peak Date (days froma January 1st) |
B1 | 122 | 99(−23) | 99(−23) | 98(−24) | 98(−24) | 97(−25) |
| A2 | 122 | 99(−23) | 99(−23) | 98(−24) | 97(−25) | 96(−26) | |
| A1B | 122 | 99(−23) | 98(−24) | 98(−24) | 97(−25) | 96(−26) | |
These ratios and differences are within the ranges reported in the literature (Post et al., 2009). The start and peak dates in 2000 were observed 14 days and 17 days earlier, respectively, than in 1977 (Rasmussen, 2002). Extreme observation has also been reported in Turku by Yli-Panula et al. (2009) showing that the annual production of birch pollen in 1993 was 70,445 pollen/m3 which was 119.4 times greater than that recorded in 1994.
Figure 5 shows the predictions of the four pollen indices obtained by incorporating the information on intrinsic inter-annual variation. Comparison between estimated pollen indices and historical observations indicate that the variations of pollen indices can be reasonably characterized by the estimates. Similar trends and phenomena as those shown in Figure 4 can also be observed in Figure 5. Calculations of RMSE and RRMSE showed that the incorporation of intrinsic inter-annual variation improves the modeling results for the pollen indices in Turku, while it has no obvious influence on pollen indices in Basel, Copenhagen, New Jersey, and North Dakota.
Figure 5.
Predictions of pollen indices based on the global annual mean temperature and global annual mean CO2 concentrations projected by the IPCC under three representative scenarios. The intrinsic inter-annual variation was used to simulate the fluctuations of pollen indices around the mean trends. Heavy lines are the predicted pollen indices and the corresponding shaded areas are top 5% HPD regions. Also shown on the left are time series of historical pollen indices and their corresponding estimates.
Parameterization and incorporation of intrinsic inter-annual variability based on more precise local information and introducing other significant climate factors in the Bayesian model will further increase the precision and accuracy of the results. Note that the predictions were based on the statistical relationship established using historical pollen and climatic data of 20 years, and the IPCC projected CO2 levels and temperatures. The predictions after 2040 (second vertical dotted line) are expected to contain substantial uncertainties. Biological limitations and physics should be taken into consideration in terms of interpreting and using the predictions from Bayesian models.
3.5. Application
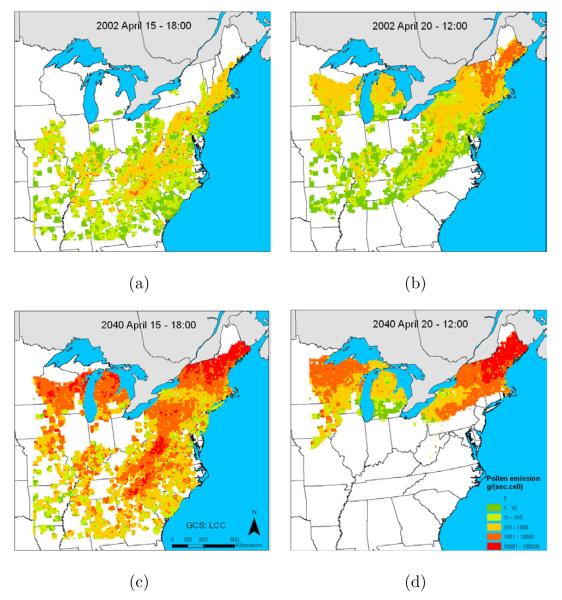
Figure 6 shows four snapshots of the spatial emission profiles at 18:00 April 15 and 12:00 April 20 of 2002 and 2040. Emission fluxes of birch pollen in April of 2040 will increase dramatically due to the rising CO2 and temperature projected by IPCC. Also shown is that spatial emission patterns at the same hour and day of 2002 and 2040 are similar, and that the emissions seem to start earlier in the northern part of the modeling domain. The shift in emission timing is caused mainly by the early flowering of birch under the scenario of increasing concentrations of CO2 and rising temperature. These future emission profiles can be coupled with future meteorology and land use/land cover profiles to generate detailed sptiotemporal distributions of pollen levels, and thus provide useful information for the management and prevention of AAD in future years.
Figure 6.
Comparisons of emission fluxes of birch pollen between April of 2002 and 2040.
4. Conclusions
A Bayesian framework has been presented for modeling Effects of climate change on annual production, peak value, start date, and peak date of birch pollen. The corresponding pollen index of the previous year, and the annual mean CO2 concentration were selected as the most significant variables to model annual production and peak value; the corresponding pollen index of the previous year and the mean spring temperature in January, February and March of current year were selected to model the start and peak dates.
Predictions of these models under three representative scenarios of the IPCC (2007d) report indicate that annual productions and peak values of birch pollen will increase dramatically, while the start and peak dates of the birch pollen season will occur earlier in future years. Outputs of the Bayesian models can be used to generate detailed spatiotemporal emission profiles of pollen in future years.
Highlights (for review).
A Bayesian framework is presented to model climate change effect on birch pollen
Airborne pollen levels are estimated based on observed and projected climate factors
Pollen emission fluxes are generated using the output from Bayesian model
Pollen season tend to start earlier with rising airborne pollen levels in the future
Acknowledgements
This research was funded in part by USEPA under STAR Grant EPA-RD-83454701-0 to Rutgers University and UMDNJ, and by the NIEHS sponsored UMDNJ Center for Environmental Exposures and Disease at EOHSI (P30ES005022). We also wish to thank NARCCAP for providing the future meteorology data.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Alizoti PG, Kilimis K, Gallios P. Temporal and spatial variation of flowering among Pinus nigra Arn. clones under changing climatic conditions. Forest Ecology and Management. 2010;259:786–797. [Google Scholar]
- Aylor DE. Quantifying maize pollen movement in a maize canopy. Agricultural and Forest Meteorology. 2005;131:247–256. [Google Scholar]
- Blando J, Bielory L, Nguyen V, Diaz R, Jeng HA. Anthropogenic climate change and allergic diseases. Atmosphere. 2012;3:200–212. [Google Scholar]
- Cappelen J. Dmi annual climate data collection 1873-2008, the faroe islands and greenland - with graphics and danish summary. 2009 http://www.dmi.dk/dmi/tr09-04_data.zip.
- Damialis A, Halley JM, Gioulekas D, Vokou D. Long-term trends in atmospheric pollen levels in the city of Thessaloniki, Greece. Atmospheric Environment. 2007;41:7011–7021. [Google Scholar]
- Efstathiou C, Isukapalli S, Georgopoulos P. A mechanistic modeling system for estimating large-scale emissions and transport of pollen and co-allergens. Atmospheric Environment. 2011;45:2260–2276. doi: 10.1016/j.atmosenv.2010.12.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fitter AH, Fitter RSR. Rapid Changes in Flowering Time in British Plants. Science. 2002;296:1689–1691. doi: 10.1126/science.1071617. [DOI] [PubMed] [Google Scholar]
- Frei T, Gassner E. Climate change and its impact on birch pollen quantities and the start of the pollen season an example from Switzerland for the period 19692006. International Journal of Biometeorology. 2008;52:667–674. doi: 10.1007/s00484-008-0159-2. [DOI] [PubMed] [Google Scholar]
- Helbig N, Vogel B, Vogel H, Fiedler F. Numerical modelling of pollen dispersion on the regional scale. Aerobiologia. 2004;20:3–19. [Google Scholar]
- IPCC . Technical Report. Cambridge; United Kingdom and New York, NY, USA: 2007a. Summary for Policymakers. [Google Scholar]
- IPCC . Technical Report. Cambridge; United Kingdom and New York, NY, USA: 2007b. Chapter 2 Changes in Atmospheric Constituents and in Radiative Forcing. [Google Scholar]
- IPCC . Technical Report. Cambridge; United Kingdom and New York, NY, USA: 2007c. Chapter 10 Global Climate Projections. [Google Scholar]
- IPCC . Synthesis Report. Technical Report; Geneva, Switzerland: 2007d. [Google Scholar]
- Jato V, Rodrgues-Rajo JFAJM. Use of phenological and pollen-production data for interpreting atmospheric birch pollen curves. Annals of Agricultural and Environmental Medicine. 2007;14:271–280. [PubMed] [Google Scholar]
- Kawashima S, Takahashi Y. An improved simulation of mesoscale dispersion of airborne cedar pollen using a flowering-time map. Grana. 1999;38:316–324. [Google Scholar]
- Keeling R, Piper S, Bollenbacher A, Walker J. Atmospheric carbon dioxide record from mauna loa. Carbon Dioxide Information Analysis Center, Oak Ridge National Laboratory, U.S. Department of Energy, Oak Ridge, Tenn.; U.S.A.: 2009. doi: 10.3334/CDIAC/atg.035. [Google Scholar]
- Lamb CE, Ratner PH, Johnson CE, Ambegaonkar AJ, Joshi AV, Day D, Sampson N, Eng B. Economic impact of workplace productivity losses due to allergic rhinitis compared with select medical conditions in the United States from an employer perspective. Current Medical Research and Opinion. 2006;22:1203–1210. doi: 10.1185/030079906X112552. [DOI] [PubMed] [Google Scholar]
- Marin JM, Robert CP. Regression and variable selection, in: Bayesian Core: A Practical Approach to Computational Bayesian Statistics. Springer Texts in Statistics; Springer New York: 2007a. pp. 47–84. [Google Scholar]
- Marin JM, Robert CP. Bayesian Core: A Practical Approach to Computational Bayesian Statistics. Springer Texts in Statistics; Springer New York: 2007b. Normal models; pp. 15–46. [Google Scholar]
- Martin MD, Chamecki M, Brush GS. Anthesis synchronization and floral morphology determine diurnal patterns of ragweed pollen dispersal. Agricultural and Forest Meteorology. 2010;150:1307–1317. [Google Scholar]
- Martin MD, Chamecki M, Brush GS, Meneveau C, Parlange MB. Pollen clumping and wind dispersal in an invasive angiosperm. Am. J. Bot. 2009;96:1703–1711. doi: 10.3732/ajb.0800407. [DOI] [PubMed] [Google Scholar]
- Masaka K, Maguchi S. Modelling the Masting Behaviour of Betula platyphylla var. japonica using the Resource Budget Model. Annals of Botany. 2001;88:1049–1055. [Google Scholar]
- Mearns L, Leung R, Correia J, Qian Y. The north american regional climate change assessment program dataset. National Center for Atmospheric Research Earth System Grid data portal; 2011. http://www.narccap.ucar.edu/data/index.html. [Google Scholar]
- Pasken R, Pietrowicz JA. Using dispersion and mesoscale meteorological models to forecast pollen concentrations. Atmospheric Environment. 2005;39:7689–7701. [Google Scholar]
- Post E, Forchhammer MC, Bret-Harte MS, Callaghan TV, Christensen TR, Elberling B, Fox AD, Gilg O, Hik DS, Hye TT, Ims RA, Jeppesen E, Klein DR, Madsen J, McGuire AD, Rysgaard S, Schindler DE, Stirling I, Tamstorf MP, Tyler NJ, van der Wal R, Welker J, Wookey PA, Schmidt NM, Aastrup P. Ecological dynamics across the arctic associated with recent climate change. Science. 2009;325:1355–1358. doi: 10.1126/science.1173113. [DOI] [PubMed] [Google Scholar]
- Prasad PVV, Boote KJ, Allen LH. Adverse high temperature effects on pollen viability, seed-set, seed yield and harvest index of grain-sorghum Sorghum bi-color (L.) Moench are more severe at elevated carbon dioxide due to higher tissue temperatures. Agricultural and Forest Meteorology. 2006;139:237–251. [Google Scholar]
- Rasmussen A. The effects of climate change on the birch pollen season in Denmark. Aerobiologia. 2002;18:253–265. [Google Scholar]
- Schueler S, Schlnzen K. Modeling of oak pollen dispersal on the landscape level with a mesoscale atmospheric model. Environmental Modeling and Assessment. 2006;11:179–194. [Google Scholar]
- Siljamo P, Sofiev M, Severova E, Ranta H, Kukkonen J, Polevova S, Kubin E, Minin A. Sources, impact and exchange of early-spring birch pollen in the Moscow region and Finland. Aerobiologia. 2008;24:211–230. [Google Scholar]
- Silvertown JW. The evolutionary ecology of mast seeding in trees. Biological Journal of the Linnean Society. 1980;14:235–250. [Google Scholar]
- Singh K, Axelrod S, Bielory L. The epidemiology of ocular and nasal allergy in the united states, 1988-1994. Journal of Allergy and Clinical Immunology. 2010a;126:778–783.e6. doi: 10.1016/j.jaci.2010.06.050. [DOI] [PubMed] [Google Scholar]
- Singh SK, Kakani VG, Surabhi GK, Reddy KR. Cowpea (Vigna unguiculata L. Walp.) genotypes response to multiple abiotic stresses. Journal of Photochemistry and Photobiology B-Biology. 2010b;100:135–146. doi: 10.1016/j.jphotobiol.2010.05.013. [DOI] [PubMed] [Google Scholar]
- Sofiev M, Siljamo P, Ranta H, Rantio-Lehtimki A. Towards numerical forecasting of long-range air transport of birch pollen: theoretical considerations and a feasibility study. International Journal of Biometeorology. 2006;50:392–402. doi: 10.1007/s00484-006-0027-x. [DOI] [PubMed] [Google Scholar]
- Wolf J, O’Neill NR, Rogers CA, Muilenberg ML, Ziska LH. Elevated Atmospheric Carbon Dioxide Concentrations Amplify Alternaria alternata Sporulation and Total Antigen Production. Environ Health Perspect. 2010;118:1223–1228. doi: 10.1289/ehp.0901867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yli-Panula E, Fekedulegn DB, Green BJ, Ranta H. Analysis of Airborne Betula Pollen in Finland; a 31-Year Perspective. International Journal of Environmental Research and Public Health. 2009;6:1706–1723. doi: 10.3390/ijerph6061706. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zellner A. An introduction to bayesian inference in econometrics. New York, USA: 1971. [Google Scholar]
- Ziska LH, Gebhard DE, Frenz DA, Faulkner S, Singer BD, Straka JG. Cities as harbingers of climate change: Common ragweed, urbanization, and public health. Journal of Allergy and Clinical Immunology. 2003;111:290–295. doi: 10.1067/mai.2003.53. [DOI] [PubMed] [Google Scholar]