Internationally Comparable Health Indices

Abstract

One of the most intractable problems in international health research is the lack of comparability of health measures across countries or cultures. We develop a cross-country measurement model for health in which functional limitations, self-reports of health, and a physical measure are interrelated to construct health indices. To establish comparability across countries, we define the measurement scales by the physical measure while other parameters vary by country to reflect cultural and linguistic differences in response patterns. We find significant cross-country variation in response styles of health reports along with variability in genuine health that is related to differences in national income. Our health indices achieve satisfactory reliability of about 80% and their gradients by age, income, and wealth for the most part show the expected patterns. Moreover, the health indices correlate much more strongly with income and net worth than self reported health measures.

1 Introduction

One of the most intractable problems in international research on health is the comparability (or incomparability) of health measures across countries or cultures. The conventional approach to evaluating health within and across nations relies heavily on using measures of subjective health assessment such as self-reports of health status and health conditions. Arguably, these measures are conditioned by cultural or social norms, differences in thresholds for medical diagnosis and access to health care resources, so that comparisons of health across different populations may be difficult or impossible with such gauges. In response to this issue, research on modeling comparable health measures has focused on finding objective measurement tools that provide consistent evaluations of health within and across nations.

The ability to compare health across countries is a prerequisite for understanding the role of national policies and institutions in influencing behavior. Health plays a substantial role in many economic models, including models of labor force participation, retirement, or savings decisions. Omitting health for a lack of comparable health measures may produce biased estimates of model parameters if health is correlated with the variables of interest. Although economic models differ greatly in what categorization and specific pecuniary factors they use, the reality is that economic incentives (e.g., disability benefits) are often conditioned on health. In a cross-national study of economic behavior, the use of comparable health measures helps to provide unbiased assessment of behavior and predict the effects of policy changes. Based on comparable measures of health, we can evaluate effectiveness of different policy initiatives, assess health interventions across countries, and set priorities for intervention.

The analysis of inequalities in health within and across nations points at another dimension of research that needs comparable health measures. Health inequalities, which are generally traced to inequalities in income, education and other socioeconomic categories, persist in all countries but there are cross-national differences in their level, rate of change and strength of association (Carlson, 1998; Kopp et al., 2000; Kunst et al., 2005; Macinko et al., 2003; van Doorslaer et al., 1997).

Efforts to develop comparable, composite measures of population health have a long history. This has resulted in a palette of measures, including Disability-Adjusted Life Year (DALY; World Bank, 1993), Disability-Adjusted Life Expectancy (DALE; see, e.g., Murray et al., 2002), the Health and Activity Limitation Index (HALex), also known as the Years of Healthy Life (YHL; Erickson, 1998; Sondik, 2002; Stewart et al., 2005), and the Centers for Disease Control and Prevention Health-Related Quality-of-Life 14-Item Measure (CDC HRQOL-14, “Healthy Days Measure”; http://www.cdc.gov/hrqol/hrqol14_measure.htm).

Recent innovations in the design and data collection of some household surveys make it possible to construct internationally comparable health measures using a more objective and accurate evaluation of health than self-perceived health. These advances include collecting information on physical measures like grip strength and walking speed in cross-national multidisciplinary studies such as the U.S. Health and Retirement Study (HRS), the English Longitudinal Study of Ageing (ELSA), and the Survey of Health, Ageing and Retirement in Europe (SHARE). Interviewers take physical measures of health using the same protocol across all countries. Such assessments are therefore less likely to be subject to biases affecting self-reports of health, and may overcome the measurement issues of cultural differences in how people evaluate their health. The importance of using objective measures of health was stressed by Bound (1991) and Burkhauser and Cawley (2006).

Another recent innovation is the use of vignette questions, in which hypothetical persons are rated on the same scale as respondents rate themselves. These can then be used to anchor the scales of the self-reported data and thus allow cross-country comparisons. See Kapteyn et al. (2007) for an application of this methodology to comparing work disability in the U.S. and The Netherlands.

The primary objective of this paper is to construct internationally comparable measures of individual health, based on a health measurement model that includes self-reported health measures as well as an objective health indicator (grip strength). The objective measure addresses the scaling issues inherent in cross-national comparability of subjective health questions. As shown by Lindeboom and van Doorslaer (2004), self-reports may differ across nations because of differences in reporting patterns that are unrelated to health. They regress self-reports of health status on another supposedly more objective measure of health. Jürges (2007) takes the same approach, but includes a larger number of health measures as explanatory variables. Between-population differences in the resulting coefficients are then interpreted as reflections of differing reporting patterns in health reports across countries. Similar ideas define our approach, but we differ in the operationalization from Lindeboom and van Doorslaer. We treat our objective measure not as an infallible measure of health, but as an imperfect indicator that can still be subject to measurement error (but not to differences in reporting patterns, unlike the self-reported measures). We also use more indicators of health than Lindeboom and van Doorslaer, and different ones than Jürges. Incorporating vignette questions in our approach is possible in principle, but complicates the analyses. Moreover, we do not need these for identification. Therefore we do not use these.

Section 2 describes the data, while section 3 presents our model for health and describes how we use it to construct a health index. Section 4 then presents the empirical results and section 5 concludes.

2 Data on Health

We use information collected in the first wave of the Survey of Health, Ageing and Retirement in Europe (SHARE), which is a multidisciplinary cross-national longitudinal survey of continental Europeans over the age of 50 and their spouses. The baseline SHARE study includes data on 12 countries providing a balanced representation of the different European regions from Scandinavia (Denmark and Sweden) through Central Europe (Austria, France, Germany, Switzerland, Belgium, The Netherlands) to the Mediterranean (Spain, Italy, Greece, and Israel). Designed after the role models of HRS and ELSA, SHARE combines information on health (e.g., self-reported health, physical and cognitive functioning, health behaviors, health care utilization and expenditure), psychological conditions (e.g., mental health, well-being, life satisfaction), socio-economic status (e.g., work activity, job characteristics, income, wealth and consumption, housing, education), and social support (e.g., social networks, volunteer activities).

The SHARE Wave 1, Release 2.0.1 sample includes 31,115 respondents, with the majority interviewed in 2004 and some respondents in 2005–2006. The survey has been administered by means of computer assisted personal interviewing (CAPI). The sampling plan follows a complex probabilistic multistage design to produce estimates representative of the non-institutionalized population aged 50 and above in each country. The study also interviews spouses younger than 50. The response rate varies by country but on average is 62% for households and 85% for individuals within participating households. A detailed description of the SHARE data and methodology is published elsewhere (Börsch-Supan et al., 2005; Börsch-Supan and Jürges, 2005). The data are available to registered users from the SHARE website (http://www.share-project.org).

We removed all observations with missing individual sampling weights. These are mostly persons younger than 50 years of age and a few persons with missing age and/or gender. We did not remove cases with missing data on other variables. Specifically, there are 129 cases that lack all dependent variables for the health model. These have no influence on the estimation of the parameters of the health model, but it will turn out that we can still compute a value of the health index for them, based on the information from the covariates. The resulting analytic sample contains 29,835 observations.

There are 686 cases with missing height and/or weight, including a few cases with unlikely values (height < 110 cm or weight < 10 kg). How we accommodate such missing covariates in the model will be described in section 3. SHARE uses multiple imputations (5) for various missing variables including household income, assets, and education.¹ A textbook usage of the multiple imputations would imply that we would have to repeat all our analyses five times and then combine the estimates (e.g., Rubin, 1987). Because these variables play only a minor role in our analyses, we decided that the statistical advantage of such an approach were outweighed by its additional complications and opted for a simpler approach by using only a single value for each observation. We use the means of the five imputations as our income and asset variables, because these are arguably more precise estimates than any of the five imputations by itself. We treat zero mean incomes as missing (negative incomes do not occur). For education we use the first imputation, but there are only 83 observations for which education had to be imputed. We have classified “other” education as missing.

Health Measures

SHARE contains extensive modules on physical health, combining information on subjective health assessment (based on the U.S. categorization on the five-point scale from “poor” to “excellent” and the European categorization on the five-point scale from “very bad” to “very good”), indicators of doctor-diagnosed chronic conditions (heart disease, high blood cholesterol, hypertension, stroke, diabetes, lung disease, asthma, arthritis/rheumatism, osteoporosis, cancer, ulcer, Parkinson's disease, cataracts, hip fracture), a battery of functional limitations from more severe limitations with activities of daily living (ADL) to less disabling problems with instrumental activities of daily living (IADL) and mobility, arm function, and fine motor function limitations. In addition, SHARE has a limited number of physical measures, including self-reported body weight and height, interviewer-measured walking speed (for respondents aged 76 and older and those who had indicated having difficulty with walking 100m) and grip strength (for all respondents).

Grip strength is a core physical measure of health that potentially enables cross-national comparability of health estimates and avoids some of the endogeneity problems inherent in more subjective health measures like self-rated health. It also helps to overcome the measurement issues related to biases that arise from subjectivity of health conditions due to cultural differences across and within countries, differential physician contacts or cross-national differences in the criteria for thresholds of medical diagnosis. Predictive validity of grip strength for assessing health was established in studies that found grip strength to be a better predictor of future medical problems than self-reported health (Christensen et al., 2000; Rantanen et al., 1999, 2000; Al Snih et al., 2002).

We have selected 25 indicators to measure health and functional ability in SHARE, including reports of limitations with 10 activities of mobility, arm function and fine motor function, 6 ADLs, 7 IADLs, self-reported health, and grip strength. We have combined the two mobility limitations with climbing stairs into one ordinal variable, with values 1 = no difficulty with climbing stairs, 2 = difficulty with climbing several flights of stairs, but not with one flight of stairs, and 3 = difficulty with climbing one flight of stairs. As mentioned above, self-reported health is also ordinal, with five categories; we use the version with the U.S. categorization, which is more symmetrically distributed than the version with the European categorization. Grip strength is continuous, and all the other health indicators we use are binary.

Covariates

We use a set of standard socio-demographic covariates in modeling physical health and functional ability. These include a third degree age polynomial, educational achievement (secondary and tertiary education, primary or no education is the reference category), household size, and living with a spouse or partner.

Our model includes household net worth (PPP adjusted) to reflect opportunities for more investment in health with higher amounts of economic resources. As the functional form, we use the inverse hyperbolic sine of net worth rather than the log to account for a non-negligible fraction of households with negative net worth. The inverse hyperbolic sine function is defined as $\mathrm{IHS}\left(x\right)\equiv \text{log}(x+\sqrt{1+x^2})$. For positive numbers not close to zero, it is virtually indistinguishable from a logarithmic function, IHS(x) ≈ log(2x). IHS(x) is antisymmetric: IHS(x) = –IHS(–x).

We also include a measure of relative body weight to account for the well-documented effects of excessive body weight or obesity on physical health and functioning. Individuals are classified by relative weight based on their body mass index (BMI), calculated from self-reported weight and height (weight in kilograms divided by the square of height in meters). We use the evidence-based clinical guidelines for the classification of overweight and obesity in adults to stratify the study respondents into five weight classes: underweight (BMI < 18.5), normal weight (BMI: 18.5–25), overweight (BMI: 25–30), obesity class I (BMI: 30–35), and obesity classes II and III (BMI: 35+). The sample size for extreme obesity or class III (BMI ≥ 40) is too small to enable meaningful analysis separate from class II.

In the model specification, we have linearly transformed some explanatory variables to obtain better scaling and less multicollinearity. A more detailed account of the variable construction is available upon request.

3 Health Measurement Model

The model structure is a special case of the LISCOMP model that integrates factor analysis and regression models but also has the ability to handle categorical dependent variables. See Muthén and Satorra (1995) or Wansbeek and Meijer (2000, section 11.4) for an extensive discussion of the LISCOMP model. A somewhat stylized path diagram of the model, showing its overall structure, is presented in Figure 1. From this figure, we see that the model is an extension of a MIMIC model (Jöreskog and Goldberger, 1975), with multiple indicators of health (dependent variables) and multiple “causes” (explanatory variables), although we explain below that we do not necessarily assume causality for the latter.

Figure 1.

Stylized path diagram of the health measurement model

Our model closely resembles the health measurement sub-model of Börsch-Supan et al. (1996) and Soldo et al. (2006), although we add a continuous physical measure (grip strength), which allows us to make cross-country comparisons while allowing different response styles for the self-reported variables. The work of Bound et al. (1999) and Jürges (2007) is also related, in the sense that they attempt to address differences in response styles. However, in their models, self-reported general health status is the only dependent variable, and health measures that we consider dependent variables that are subject to measurement error or to cross-country differences unrelated to health status (e.g., functional limitations) are included as explanatory variables in their models, with the assumption that they are not subject to cross-country reporting differences.

The dependent variables in our model are a combination of continuous (grip strength), binary (most mobility, arm function, and fine motor function limitations, ADLs, and IADLs), and ordinal (climbing stairs, self-reported health) variables. They are collected in the vector y_cn, where c denotes the country and n the individual. All our analyses are separate for males and females, but we suppress the gender subscript to economize on the notation. Note that this implies that we will not be able to compare health of males with health of females, but this is inevitable, as we are not prepared to make assumptions about equal response patterns for males and females.

We use i to denote the variable number. Limited dependent outcome variables must be treated differently from continuous outcome variables. As with standard limited dependent variables regression models (Maddala, 1983), we assume that the binary and ordinal variables in y_cn are reflections of underlying continuous latent response variables $y_{cni}^{\ast }$. For grip strength, $y_{cni}=y_{cni}^{\ast }$. For the binary and ordinal dependent variables, the relationships between y_cni and $y_{cni}^{\ast }$ are step functions with steps at given or estimated thresholds as in binary and ordinal probit models: y_cni = j corresponds with ${\alpha }_{ci,j-1}<y_{cni}^{\ast }\le {\alpha }_{ci,j}$. Here, the αs are the threshold parameters, with α_ci,0 = –∞ and α_ci,Ji = +∞, where J_i is the number of categories of variable i (3 for climbing stairs, 5 for self-reported health, and 2 for all other self-reported measures). By allowing the thresholds to vary across countries, we allow for different response styles in different countries.

We assume that the latent response variables depend on unobserved (latent) true health η_cn:

$$y_{cni}^{\ast }={\tau }_{ci}+{\lambda }_{ci}{\eta }_{cn}+{\epsilon }_{cni},$$ (1)

where τ_ci is an intercept, λ_ci is a coefficient (factor loading), and ε_cni is a residual, which we refer to as the measurement error. If $y_{cni}^{\ast }$ is continuous and observable, and if τ_ci = 0 and λ_ci = 1, then (1) is a traditional measurement error model, which explains our usage of this term. We assume that the measurement errors of different equations are independent, so that the dependent variables are conditionally independent given true health, and (1) is a factor analysis model with one factor. In the factor analysis literature, the dependent variables are called indicators of the latent variables, and we adopt this terminology as well. The variances of the measurement errors are collected in the diagonal covariance matrix Ω_c. Again, the various parameters are allowed to vary across countries to accommodate country-specific response styles.

In the equation for grip strength, we use an extension of (1). As grip strength tends to be associated with size irrespective of health, we allow for a direct effect of body height and weight on grip strength. Our preliminary exploration suggested that a second-degree polynomial captures this relation well. Hence, the grip strength equation becomes

$$y_{cn,\mathrm{GS}}^{\ast }={\tau }_{\mathrm{GS}}+{\lambda }_{\mathrm{GS}}{\eta }_{cn}+{\beta }^{\prime }{p}_{cn}+{\epsilon }_{cn,\mathrm{GS}},$$ (2)

where p_cn includes height, weight, their squares, and the product of height and weight. As indicated in the notation, we assume that τ_GS, λ_GS, and β are the same across countries (but not across genders, as mentioned above). This crucial assumption ensures cross-country comparability of health.

We interpret (1) and (2) as causal structural relations with the exception of the added polynomial in height and weight for grip strength, which has a reduced form interpretation. Our model development relies on an important assumption that the latent response variables depend structurally on health.

The explanatory variables (including the constant) are collected in the vector x_cn, which is used in the model of true health η_cn:

$${\eta }_{cn}={\gamma }_c^{\prime }{x}_{cn}+{\zeta }_{cn},$$ (3)

where ζ_cn is a random error (disturbance) and γ_c is a vector of regression coefficients. We define ψ_c ≡ Var(ζ_cn). The parameters γ_c and ψ_c are also allowed to vary across countries. The reason for this is that some of the variables in x_cn may not be defined consistently across countries, for example, because educational systems are difficult to compare. Furthermore, different institutional settings in different countries (e.g., health care systems) may imply different relationships between the explanatory variables and health.

In line with the standard LISCOMP model and probit models, we assume that the equation errors and measurement errors are normally distributed. Results for this type of model tend to be insensitive to this distributional assumption. However, with our estimation method, it is fairly straightforward to use other distributional assumptions for the errors, which can be used for sensitivity analyses in assessing the extent that the results are driven by the normality assumption. We leave such analyses for future research.

In contrast to (1), our interpretation of (3) is relatively agnostic. In particular, it makes little sense to view it as a structural health production function because such a function should have a strong dynamic component with current health depending on past investments in health over a longer period of time and not just a few contemporaneous covariates. Instead, (3) has the flavor of a reduced form model, although net worth cannot be assumed to be exogenous. Therefore, our term for this equation is a “predictive equation”. More precisely, (3) is formally interpreted as

$$({\eta }_{cn}\mid x_{cn})\sim \mathcal{N}({\gamma }_c^{\prime }{x}_{cn},{\psi }_c).$$

Thus, it is an assumption about a conditional distribution without being causal or structural. In addition, we assume that conditional on true health, the indicators are stochastically independent of the covariates. Again, an exception is grip strength, which is allowed to depend on height and weight directly.

Identification, normalizations, and cross-country comparability

In models with latent variables, many restrictions on the parameters are typically needed to obtain an identified model. Our model is no exception. Each latent variable, including the latent response variables $y_{cn}^{\ast }$, must be assigned a location and scale. We use the probit convention of fixing the scales of latent response variables by normalizing the variances of the errors in the matrix Ω_c to 1 and fixing their locations by normalizing the thresholds to 0 for the binary outcomes and normalizing the intercept to 0 for the ordinal ones. For grip strength no such normalizations are necessary, because the location and scale of $y_{cni}^{\ast }$ are determined by the identity $y_{cni}=y_{cni}^{\ast }$.

The location and scale of η_cn can be assigned in different ways. For our purposes, the most convenient and useful normalization is to assign a reference variable from the list of indicators. The factor loading relating the reference indicator to η_cn is normalized to 1 and the intercept (or one of the thresholds in case of an ordinal variable) of this reference indicator is normalized to 0.

The arbitrariness of the locations and scales of the latent variables affects the extent to which parameters and derived statistics such as the marginal distributions of the latent variables or the constructed health indices can be compared across countries. For example, if the threshold for reporting a certain type of difficulty is higher in one country for the same true health, but the thresholds are normalized to the same value for this variable, the difference in parameters incorrectly appears to reflect a difference in true health. The same is true of different factor loadings: if a certain activity is more sensitive to health in one country, the factor loadings are different. If they are normalized to be the same, this shows up as a difference in health distributions. As indicated above, we assume that grip strength does not suffer from such problems of cross-country differences and therefore we use grip strength as our reference indicator. This should make the location and scale of health comparable across countries. Note in particular that the normalizations of the thresholds of binary indicators and intercepts of ordinal indicators, and the variances of these variables, do not affect cross-country comparability of health. They only serve to identify location and scale of $y_{cni}^{\ast }$.

All other parameters are allowed to differ across countries to account for cultural variation in response patterns, differences in educational and health systems, and other cross-country attributes that may give rise to country-specific parameters.

In our specification, grip strength is the only indicator for which we assume cross-country equality of parameters; all other indicators are allowed to have country-specific response styles. If we had additional objective measures, or would be willing to assume country-independent response styles for one or more of the other indicators in our model, we could constrain the parameters of these to be the same across countries as well. As usual with restrictions on parameters, this would lead to more precise estimates, and in particular, this would lead to less sampling variation in the anchoring of the parameters of the different countries to the same scale, and thus to more precise cross-country comparisons. Also, because these restrictions are not necessary for identification, we would be able to test the assumption of equal response styles in these variables (maintaining the assumption of equal response styles for grip strength). In the SHARE data, walking speed would be a candidate indicator to add, but as mentioned above, this is only measured for a small and selective group of respondents, so we concluded that adding this would not be useful for our purposes. An alternative would be to add the anchoring vignettes for self-reported health, but as indicated earlier, we have chosen not to include these because of the additional complications of incorporating these.

Estimation and Model Fit

LISCOMP models are typically estimated in multiple steps (Muthén and Satorra, 1995; Wansbeek and Meijer, 2000, section 11.4). First, univariate unrestricted linear regressions, binary probits, and/or ordinal probits (whatever appropriate) are estimated with the elements of y as dependent variables and x as explanatory variables. This gives a set of regression coefficients that can be collected into a reduced-form regression coefficient matrix $\widehat{\Pi }$ and a set of estimated threshold parameters for the ordinal dependent variables. Second, a set of bivariate regressions (again respecting the measurement level of the dependent variables) is estimated in which regression coefficients and thresholds are fixed to their first-step values. This gives an estimate $\widehat{\Sigma }$ of the covariance matrix of the errors in the reduced-form regressions. Third, the parameters of interest are estimated through a minimum distance method where the elements of $\widehat{\Pi }$ and $\widehat{\Sigma }$ take the role of sample statistics collected in the vector $\widehat{\sigma }$. The model specifies how their population values depend on the parameters of interest: σ = σ(θ). The estimate of θ is then obtained by minimizing a quadratic form ${(\widehat{\sigma }-\sigma \left(\theta \right))}^{\prime }W(\widehat{\sigma }-\sigma \left(\theta \right))$ where W is a weight matrix.

This estimation method gives consistent estimators and tends to be fast and computationally convenient. However, the first step breaks down in our highly skewed data. Many binary dependent variables and some explanatory variables have very low frequencies of positive answers, leading to empty cells in some 2×2 cross-tables of dependent with explanatory variables. The corresponding reduced-form coefficients are infinite.

To overcome this technical problem, we have derived the full information joint loglikelihood function and programmed it in Stata. An explicit expression is given in the appendix. We use Maximum Simulated Likelihood with 100 Halton draws (Train, 2003) to solve the numerical integrals involved. The likelihood deals with missing values on the dependent variables using the missing at random (MAR; Rubin, 1976; Little and Schenker, 1995) assumption, also called selection on observables (Fitzgerald et al., 1998), which allows for systematic patterns of missingness that depend on the values of non-missing variables. This is important because there are such patterns in the data. Most saliently, grip strength is often missing for individuals who are in bad health, as judged by other indicators. Simulation studies have found that MAR-based methods tend to work well, even if the MAR assumption is violated (e.g., Muthén et al., 1987; Jamshidian and Bentler, 1999). An alternative to employing the MAR assumption would be to allow the selection mechanism to depend on unobservables, in particular the values of the missing variables themselves. However, this requires modeling of this mechanism and such methods are very sensitive to minor misspecifications and thus may make things worse (Little and Schenker, 1995; Jamshidian and Bentler, 1999). Missing covariates are generally more problematic than missing dependent variables, because we do not want to make assumptions about the conditional distributions of the covariates. A common practical solution, which we adopt here, is to set the value of a missing covariate to an arbitrary fixed value (zero) and add a dummy variable for “missingness”.

Almost all parameters in the model are either fixed to 0 or 1, or are country-specific free parameters. Hence, it is computationally preferable to estimate the parameters separately for each country. However, the coefficients of the height-weight polynomial in the grip strength equation are assumed to be equal across countries. Given these cross-country restrictions on the parameters, estimation should ideally be done jointly for all countries, which is computationally prohibitive. Therefore, we take a two-step approach. In the first step, we insert the “predictive” health equation (3) into the grip strength equation of (2) and estimate the resulting reduced-form parameters jointly for all countries. Then we subtract the estimated height-weight polynomial from grip strength. (We also subtract the grand mean of the resulting residual and divide by 10 to obtain better scaling.) In the second step, we use the residual grip strength as an ordinary indicator. Because there are no joint parameters left, the remaining model is estimated separately for each country.

The fit of the model with the latent health dimension (the target model) is compared to the fit of the null model. The null model is the analog of the constant-only model in linear regression. In our case, the null model is the model without the latent variable η, and thus without λ, γ, ψ, and x. This model is also called the independence model, because it implies that all indicators are independently distributed of each other and of the covariates. The fit of the target model compared to the null model is then assessed by the value of a pseudo-R² measure, defined as 1 – Ľ₍₁₎/L₍₀₎ where Ľ₍₁₎ is the maximized simulated log-pseudolikelihood for the target model with one health dimension and L₍₀₎ is the maximized log-pseudolikelihood for the null model. Because of the absence of a latent variable, the latter does not involve simulation.

The target model can also be formally tested against the null model, using the Scaled LR test statistic (Asparouhov and Muthén, 2005, section 7), which is a generalization of a likelihood ratio test statistic to log-pseudolikelihoods, which we use here because we use sampling weights. The Scaled LR test serves the same purpose as the F-test in linear regression models. Other model fit criteria that we consider are the AIC and BIC information criteria as implemented in Stata.

Distribution of Health and Definition of the Health Index

Given the assumed model structure and parameter estimates, we can compute the unconditional mean and variance of health for each country-gender combination where the x variables are treated as random variables. Specifically, we first compute estimates of ${\mu }_{\eta ,cn}\equiv {\mathrm{E}}_{\zeta }({\eta }_{cn}\mid x_{cn})={\gamma }_c^{\prime }{x}_{cn}$ and ${\sigma }_{\eta ,cn}^2\equiv {\text{Var}}_{\zeta }({\eta }_{cn}\mid x_{cn})={\psi }_c$ and then aggregate them into estimates of the unconditional mean ${\mu }_{\eta ,c}\equiv {\mathrm{E}}_x\left({\mu }_{\eta ,cn}\right)={\gamma }_c^{\prime }\mathrm{E}\left(x_{cn}\right)$ and the unconditional variance ${\sigma }_{\eta ,c}^2\equiv {\mathrm{E}}_x\left({\sigma }_{\eta ,cn}^2\right)+{\text{Var}}_x\left({\mu }_{\eta ,cn}\right)={\psi }_c+{\gamma }_c^{\prime }\text{Cov}\left(x_{cn}\right){\gamma }_c$. Here, E(x_cn) and Cov(x_cn) are estimated by the (country-gender specific) sample mean and covariance matrix of x_cn (taking the sampling weights into account), and the maximum simulated likelihood estimates of ψ_c and γ_c are used.

We then construct a health index that is the conditional expectation of unknown true health, conditional on all observed variables:

$${\widehat{\eta }}_{cn}\equiv \mathrm{E}({\eta }_{cn}\mid y_{cn},x_{cn};\text{parameter estimates}).$$

Apart from being an intuitively appealing estimate of true health, it follows from generic properties of expectations that the conditional expectation minimizes the mean squared error and thus is the best estimate in this sense. The appendix discusses computation of ${\widehat{\eta }}_{cn}$ in more detail.

A measure of the precision with which ${\widehat{\eta }}_{cn}$ estimates η_cn is the conditional variance of η_cn, Var(η_cn | y_cn, x_cn), which is (asymptotically, i.e., abstracting from parameter uncertainty) equal to the mean squared error of ${\widehat{\eta }}_{cn}$. Just like the conditional expectation, this can be computed in a relatively straightforward way. More details are given in the appendix.

The reliability of the health index is the squared correlation between the health index and true health, or, equivalently, the R² of the hypothetical regression of η_cn on ${\widehat{\eta }}_{cn}$. A convenient expression is $1-\text{Var}({\eta }_{cn}\mid y_{cn},x_{cn})∕{\sigma }_{\eta ,c}^2$. Note that, based on the model assumptions and estimates, we are able to estimate the precision and reliability of the health index even though true health is unobserved.

4 Results

Table 1 summarizes the distribution of health indicators across countries and gender. We report four measures of subjective health assessment in SHARE: any limitation with (1) Mobility, arm function, and fine motor function, (2) ADL, and (3) IADL, and (4) self-reported fair or poor general health. The distribution of the data on self-reported health is particularly illustrative of the large cross-country differences embedded in self-reports. For example, the percentage of men who rate their health status as poor or fair is more than three times as large in Germany as in Sweden, whereas approximately the same proportion of men in both countries reports having some chronic health condition (about 70%, not reported in the table). Another example is the male population of Denmark whose life expectancy is on average one year less than of French men, but who are 20% less likely than the French to rate their health as poor/fair.

Table 1.

Sample distributions of the health measures

	Sample size	At least one limitation (%)			Fair/poor SRH (%)	Grip (kg)
Country		Mobility	ADL	IADL		Mean	s.d.
Male
Austria	777	44.1	7.8	11.8	28.2	46.1	9.8
Belgium	1,696	39.6	9.4	13.4	25.0	44.0	10.2
Denmark	757	34.2	9.9	11.7	24.6	46.7	10.5
France	1,365	38.3	12.8	13.0	32.7	42.4	10.7
Germany	1,364	47.5	8.5	11.1	37.1	46.0	10.9
Greece	1,235	44.4	6.5	11.3	25.2	41.2	11.1
Israel	1,135	40.9	11.8	18.5	38.0	39.4	11.7
Italy	1,125	43.8	10.1	9.6	34.6	39.7	11.1
The Netherlands	1,344	31.7	6.4	10.5	25.6	45.5	10.4
Spain	984	43.1	10.2	16.9	34.9	37.4	10.5
Sweden	1,406	35.5	8.0	11.5	11.1	44.9	10.0
Switzerland	448	28.4	4.5	4.7	13.8	44.3	9.5
Total	13,636	42.2	9.6	12.0	32.4	42.6	11.2
Female
Austria	1,072	58.3	10.6	22.0	31.5	28.9	7.8
Belgium	1,921	58.1	16.2	24.2	29.5	26.2	7.1
Denmark	857	50.3	11.0	21.9	26.3	26.9	7.3
France	1,671	59.0	12.5	21.5	35.8	25.5	7.0
Germany	1,566	61.7	12.0	18.7	42.6	28.3	7.8
Greece	1,424	64.6	11.4	25.9	37.3	24.9	6.9
Israel	1,349	56.7	13.0	29.7	38.7	23.4	7.5
Italy	1,382	60.2	13.9	20.6	47.8	23.3	7.2
The Netherlands	1,515	51.5	10.7	21.6	29.7	27.7	7.6
Spain	1,357	64.9	15.1	30.1	49.4	22.3	7.6
Sweden	1,588	55.5	12.7	22.5	15.6	26.4	7.3
Switzerland	497	46.4	8.7	11.8	18.5	27.2	7.2
Total	16,199	60.0	12.8	21.9	40.2	25.6	7.8

Note. Weighted results, except for sample sizes. Due to item nonresponse, sample sizes vary across columns. Mobility = mobility, arm, and fine motor function; ADL = activities of daily living, IADL = instrumental activities of daily living, SRH = self-reported health, Grip = grip strength.

The last two columns of Table 1 present the mean value and standard deviation of grip strength measurements by country and gender. The cross-national variation in grip strength is much smaller than the observed differences in self-reports of health. The difference between the highest and the lowest average national measurements is about 25% for both men and women. In all countries, the average grip strength of women is about two-thirds of the average level for men.

Table 2 presents the pseudo-R² measures of the estimated health measurement models. This shows that the latent variable explains a sizeable amount of the variation in the data, but more experience with the pseudo-R² in this type of model is needed to be able to judge whether the values reported here are “good”. The Scaled LR test statistic is always extremely large and significant (p = 0.0000 in all cases), and the information criteria AIC and BIC are much smaller for this model than for the null model. We do not present detailed results here, but they are available upon request.

Table 2.

Pseudo-R² values for the health model with one latent variable

Country	Male	Female
Austria	0.23	0.24
Belgium	0.21	0.26
Denmark	0.26	0.25
France	0.26	0.26
Germany	0.23	0.25
Greece	0.26	0.26
Israel	0.31	0.35
Italy	0.25	0.30
The Netherlands	0.18	0.29
Spain	0.28	0.29
Sweden	0.28	0.27
Switzerland	0.17	0.20

The model contains a large number of parameters. Rather than presenting all individual parameter estimates, Tables 3–5 give the ranges of the estimates and their t-statistics for the intercepts (τ_ci), threshold parameters (α_cij), and measurement error standard deviation $\left(\sqrt{{\Omega }_{c,ii}}\right)$, factor loadings (λ_ci), and predictive health equation (γ_c and $\sqrt{{\psi }_c}$).

Table 3.

Estimation results for intercepts, thresholds, and measurement error s.d.

	Male				Female
	Estimates		t-values		Estimates		t-values
Indicator	Min	Max	Min	Max	Min	Max	Min	Max
Intercepts (τc,i)
Walk 100m	–4.121	–1.630	–12.0	–5.8	–3.204	–1.429	–16.9	–6.1
Sit 2hrs	–2.713	–1.160	–22.6	–7.5	–2.467	–0.917	–26.8	–7.2
Get up from chair	–2.371	–0.593	–16.8	–3.0	–2.659	–0.443	–19.1	–5.1
Stoop	–2.143	–0.333	–13.1	–1.5	–2.159	0.066	–10.6	0.6
Reach	–3.567	–1.297	–22.8	–7.0	–2.518	–1.033	–27.4	–8.4
Pull	–3.765	–1.441	–15.2	–4.7	–3.027	–0.733	–16.6	–5.9
Lift 5kg	–3.558	–0.958	–16.8	–2.8	–1.639	–0.339	–13.5	–3.2
Pick up coin	–4.717	–1.608	–16.3	–5.5	–3.313	–1.592	–24.5	–8.2
Dress	–4.670	–1.593	–15.0	–5.6	–5.355	–1.838	–18.0	–5.2
Walk room	–9.584	–2.942	–9.4	–2.6	–7.166	–2.382	–9.4	–5.1
Bath	–9.618	–3.063	–10.5	–2.5	–8.020	–2.082	–17.1	–4.4
Eat	–6.869	–2.730	–12.6	–4.1	–5.365	–2.337	–12.3	–2.2
Get out of bed	–6.024	–2.213	–10.4	–3.6	–6.539	–2.177	–13.1	–5.6
Use toilet	–12.308	–2.333	–13.4	–3.0	–9.455	–2.761	–10.2	–4.2
Use map	–4.631	–1.614	–17.3	–6.2	–2.386	–1.082	–23.0	–7.3
Prepare hot meal	–6.326	–1.889	–10.5	–3.3	–7.646	–3.139	–9.7	–2.3
Shop for groceries	–13.922	–3.037	–8.5	–2.4	–6.996	–2.242	–11.1	–4.4
Phone calls	–8.978	–2.291	–17.9	–4.0	–5.041	–2.875	–11.8	–3.3
Take medication	–13.212	–2.721	–11.1	–2.8	–6.074	–3.016	–10.4	–1.3
Work around house	–7.509	–1.606	–10.8	–4.3	–4.550	–1.078	–13.2	–6.4
Manage money	–6.150	–2.411	–14.4	–4.3	–4.196	–2.016	–15.2	–6.1
Thresholds (αc,ij)
Climbing stairs (1)	0.050	2.262	0.2	12.0	–0.252	1.437	–2.2	13.0
Climbing stairs (2)	1.405	3.648	4.5	17.7	0.921	2.943	7.3	21.4
Self-reported health (1)	–2.891	–0.694	–21.9	–4.7	–3.296	–0.403	–26.9	–1.6
Self-reported health (2)	–1.516	0.015	–13.4	0.2	–2.026	0.149	–17.7	0.7
Self-reported health (3)	0.042	1.528	0.2	20.4	–0.257	1.442	–2.5	21.4
Self-reported health (4)	1.482	2.562	6.6	23.3	1.387	2.495	8.1	28.3
$Measurementerrors.d.\left(\sqrt{{\Omega }_{c,ii}}\right)$
Grip strength residual	0.687	0.945	18.7	44.4	0.545	0.659	19.0	43.2

Note: Intercepts for climbing stairs and self-reported health are normalized to 0 because the thresholds have this role. Intercept for grip strength is normalized to 0 to identify the mean of the latent variable.

Table 5.

“Predictive” health equation

	Male				Female
	Estimates		t-values		Estimates		t-values
Predictor	Min	Max	Min	Max	Min	Max	Min	Max
(Age – 65)/10	–0.431	–0.104	–8.2	–3.4	–0.211	–0.069	–9.7	–3.2
[(Age – 65)/10]2	–0.072	0.063	–2.4	2.6	–0.032	0.040	–2.4	1.2
[(Age – 65)/10]3	–0.045	0.034	–2.4	2.6	–0.024	0.007	–2.9	0.9
Secondary educ.	0.035	0.185	0.6	4.1	–0.001	0.176	0.0	4.1
Tertiary educ.	0.085	0.266	1.1	5.4	–0.003	0.318	–0.1	6.6
Household size	–0.093	0.053	–3.4	2.0	–0.081	0.054	–3.9	2.0
Living w/spouse	–0.038	0.187	–1.0	1.9	–0.055	0.162	–1.6	3.4
IHS networth	–0.003	0.019	–0.7	4.5	0.006	0.017	1.7	5.8
Underweight	–1.221	0.169	–5.5	1.1	–0.290	0.023	–3.7	0.4
Overweight	–0.075	0.029	–1.4	0.6	–0.150	–0.043	–5.5	–1.2
Obese Class I	–0.295	–0.081	–4.0	–1.7	–0.290	–0.153	–7.4	–2.8
Obese Class II and III	–0.563	–0.065	–4.4	–0.6	–0.567	–0.181	–8.2	–2.0
Missing educ.	–0.225	0.234	–2.6	2.1	–0.440	0.277	–3.3	3.5
Missing BMI	–0.905	0.482	–2.5	4.1	–0.296	0.112	–4.1	1.1
Constant	–0.544	0.049	–4.9	0.6	–0.220	0.273	–4.3	5.4
Residual s.d.	0.274	0.611	6.3	17.1	0.235	0.375	6.3	23.3

The values of the intercepts (Table 3) are difficult to interpret, but given the unit residual variances associated with the standard probit specifications and generally larger ranges of the estimates and large t-values, we conclude that there is considerable cross-country variation in reporting that is not due to genuine health differences. Also, the generally large negative values (combined with the values of the factor loadings and the distribution of latent health) reflect the small number of difficulties that is typically reported, and thus the high threshold for reporting a difficulty (the intercept can also be interpreted as the negative of a threshold with the intercept being zero). The cross-country differences between the threshold parameters for the ordinal indicators (climbing stairs and self-reported health) are large and comparable to the results for the intercepts. Closer scrutiny of the original estimation results indicates that the cross-country differences in the differences between adjacent thresholds are much smaller, which suggests that differential reporting behavior may only be due to a uniform shift. The estimated standard deviations for the grip strength equation are similar across countries.

The factor loadings (Table 4) have the expected negative sign to suggest that better underlying health gives fewer functional limitations and better self-reported health. Almost all factor loadings are statistically significant, most of them very strongly. Still, we observe substantial differences across countries and gender in these results.

Table 4.

Factor loadings (λ)

	Male				Female
	Estimates		t-values		Estimates		t-values
Indicator	Min	Max	Min	Max	Min	Max	Min	Max
Mobility, arm, and fine motor function limitations
Walk 100m	–4.572	–1.591	–8.8	–4.5	–4.838	–2.952	–11.6	–4.0
Sit 2hrs	–2.355	–0.961	–7.3	–3.6	–2.402	–1.282	–9.4	–3.8
Get up from chair	–3.120	–1.329	–8.7	–4.1	–4.139	–2.106	–12.5	–5.3
Climbing stairs	–5.251	–1.839	–11.5	–5.4	–4.522	–3.035	–14.3	–5.3
Stoop	–3.597	–1.779	–10.3	–4.3	–4.300	–2.682	–13.9	–3.2
Reach	–3.003	–1.272	–7.5	–3.7	–3.351	–1.597	–10.7	–4.0
Pull	–5.469	–1.710	–8.9	–3.5	–4.169	–2.574	–13.7	–3.8
Lift 5kg	–5.762	–1.828	–9.3	–4.4	–3.643	–2.079	–13.8	–3.3
Pick up coin	–3.490	–1.534	–6.6	–3.1	–2.965	–1.393	–8.3	–3.3
ADLs
Dress	–4.223	–2.040	–8.5	–3.1	–5.858	–2.731	–10.3	–3.8
Walk room	–11.836	–3.172	–5.8	–2.2	–8.955	–2.815	–6.4	–3.5
Bath	–12.223	–4.004	–6.6	–2.2	–10.215	–3.633	–11.3	–3.9
Eat	–5.072	–1.989	–5.4	–3.0	–6.391	–2.162	–6.6	–1.5
Get out of bed	–4.851	–2.262	–6.4	–2.4	–6.399	–2.405	–7.9	–3.1
Use toilet	–7.429	–1.050	–5.3	–2.1	–8.865	–3.044	–6.5	–2.7
IADLs
Use map	–3.693	–1.794	–8.3	–3.4	–3.012	–1.545	–11.0	–3.9
Prepare hot meal	–4.342	–2.333	–6.6	–2.0	–10.828	–4.241	–6.9	–1.8
Shop for groceries	–12.631	–3.398	–6.3	–2.4	–11.679	–4.698	–9.1	–3.7
Phone calls	–5.172	–1.760	–5.4	–2.3	–5.041	–2.499	–6.5	–2.2
Take medication	–9.448	–1.419	–5.3	–2.4	–7.605	–2.466	–6.3	–1.1
Work around house	–6.313	–2.834	–7.8	–3.2	–7.436	–3.739	–10.8	–5.1
Manage money	–5.827	–2.110	–6.5	–2.7	–4.234	–2.993	–8.9	–3.2
Self-reported health	–3.525	–0.932	–11.5	–4.7	–3.146	–2.018	–15.6	–4.6
Grip strength resid.	1	1	n.a.	n.a.	1	1	n.a.	n.a.

As an indication of whether countries’ response patterns are systematic across indicators, we have computed the correlations between the intercepts, thresholds, and loadings parameters, using the country as the unit of observation. After changing the signs of the threshold parameters, to make them comparable with intercepts, all correlations among intercepts and thresholds (except one small negative one) are positive, strongly indicating consistent response patterns across indicators. The sizes of the correlations are generally large, with an average of 0.66 for males and 0.63 for females. The picture is slightly less clear-cut for the loadings. Still, most correlations are positive (93% for males, 83% for females), but there are more negative ones, and the sizes of the correlations are smaller as well (0.46 on average for males, 0.28 for females). The correlations between intercepts or thresholds on the one hand and loadings on the other hand vary considerably, with 41% positive for males and 79% positive for females, and averages of –0.07 and 0.24, respectively. Thus, the cross-country variation in the response patterns tends to be systematic, but this is not uniformly so.

Table 5 shows the estimation results from the “predictive” equation for the latent health variable η. This has some expected patterns: higher education and higher wealth are associated with better health and being overweight or obese is related with poor health. The coefficients of age and its higher powers are difficult to interpret, although the linear part clearly points at the expected negative relationship between health and age. Plots of the cubic polynomial and pointwise confidence bands around them show that this negative slope generally holds for the complete polynomial, but there are some exceptions at the highest ages. At these ages, however, the confidence bands are very wide.

The results in Table 6 show substantial cross-country differences in average true health (μ_η,c, as defined above). The differences between the countries with the highest and lowest mean health exceed the within-country standard deviation. The patterns in average health resemble income patterns: average health is worse in Southern European countries (Spain, Italy, Greece) and better in Central and Northern Europe with more affluent countries (Germany, Switzerland, Austria, Denmark and The Netherlands for males).

Table 6.

Estimated distribution of latent (true) health η

Country	Male		Female
	mean	s.d.	mean	s.d.
Austria	0.22	0.31	0.21	0.40
Belgium	0.08	0.47	0.02	0.41
Denmark	0.27	0.53	0.04	0.40
France	–0.04	0.55	–0.02	0.40
Germany	0.21	0.56	0.17	0.39
Greece	–0.19	0.53	–0.13	0.31
Israel	–0.39	0.74	–0.31	0.48
Italy	–0.29	0.63	–0.25	0.42
The Netherlands	0.15	0.46	0.05	0.43
Spain	–0.41	0.57	–0.32	0.47
Sweden	0.04	0.55	–0.04	0.41
Switzerland	0.15	0.51	0.13	0.40

Note. Weighted results.

The sample means of the health index track the estimated means of true health quite closely. The sample standard deviations of the health index are somewhat smaller than the standard deviations of true health. This is always the case when a conditional mean is used as the best estimate of a random variable.

Table 7 shows the precision of estimates for individual true health. It presents the R² of the “predictive” health equation derived from the estimates, which is a measure of how well health is estimated from the explanatory variables and the model parameters, and the reliability of the health index, which is the squared correlation between the health index and true health. Although the covariates clearly provide some information about true health, the resulting R²s are too low to use the index functions (i.e., ${\widehat{\mu }}_{\eta ,cn}={\widehat{\gamma }}_c^{\prime }{x}_{cn}$) as a health index. In contrast, our proposed health index achieves a satisfactory reliability of about 0.80.

Table 7.

Squared correlation (R², reliability) between health measure and true latent health

Country	Male		Female
	Covariates only	Health index	Covariates only	Health index
Austria	0.22	0.78	0.35	0.84
Belgium	0.17	0.76	0.35	0.85
Denmark	0.29	0.78	0.32	0.83
France	0.30	0.79	0.39	0.83
Germany	0.32	0.81	0.42	0.86
Greece	0.29	0.79	0.43	0.85
Israel	0.32	0.81	0.38	0.88
Italy	0.30	0.79	0.36	0.86
The Netherlands	0.19	0.73	0.32	0.83
Spain	0.22	0.81	0.40	0.88
Sweden	0.34	0.78	0.41	0.84
Switzerland	0.38	0.74	0.29	0.80

Note. Derived from parameter estimates; weighted results.

The difference between the covariates-only index function and the health index is that the former is the conditional mean of true health conditional on only the covariates (x_cn), whereas the latter is the conditional mean of true health conditional on both the covariates and the health indicators (y_cn). The much higher reliability of the health index shows that the health indicators contain much additional information about true health beyond the information available in the covariates. In particular, the indicators contain information about the residual ζ_cn. One of the reasons for the large magnitude of the difference is that we use many health indicators. If each contributes a small amount of additional information then the combined amount of information is large. To shed some light on this, we have also computed the reliability of a potential index that uses only the grip strength residual in addition to the covariates. That is, it is defined as E(η_cn | x_cn, grip strength). The reliability of this index can be expressed as $1-(1-R_c^2){\Omega }_{c,\mathrm{GS}}∕({\Omega }_{c,\mathrm{GS}}+{\psi }_c)$, where $R_c^2$ is the R² from Table 7. This reliability is about 0.50 for most country-gender combinations and the increase in reliability from the covariates-only index is about 0.15. Hence, the information present in grip strength explains some of the difference between the reliabilities of the health index and the covariates-only index, but the other indicators jointly contribute a larger part. It would be possible to compute the additional contribution of each indicator in this way, but for the binary and ordinal indicators, this is more involved, because it requires running the simulated likelihood program for each combination of interest. Note also that the additional contribution of an indicator depends on the order in which the various indicators are added.

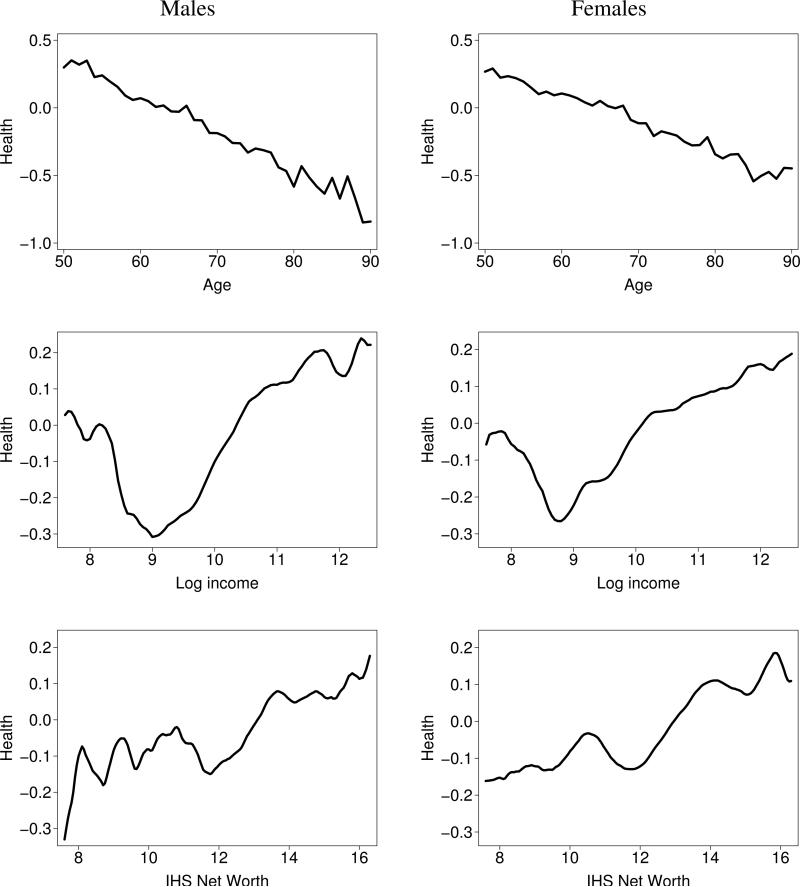
The top panels of Figure 2 plot age and the mean of the health index, aggregated across countries with weights proportional to population size. Health deteriorates linearly over the age range studied.

Figure 2.

Mean health index by age, income, and net worth; males and females (aggregated across countries; weighted)

The middle and bottom panels of Figure 2 plot the average of the health index versus log household income (PPP adjusted, Euros) and the inverse hyperbolic sine of household net worth (ditto) for males and females, using weighted nonparametric regression. This shows the well-known health-SES gradient: health is better for the more affluent group. However, at very low income levels (roughly below €8,000/year), the relationship becomes more erratic. There are a number of observations with even lower income and wealth levels and these relationships are even more erratic (not shown). Presumably this can be attributed to significant measurement errors at these levels.

As a further indication of the added value of the health index, we have run within-country, within-gender, bivariate linear regressions with either the health index or self-reported health as the dependent variable and either income or net worth as the explanatory variable. With only two exceptions (Austria and Italy for females with income as explanatory variable), the R²s of these regressions were higher with the health index than with self-reported health, often substantially so. For example, for the Danish females, the R² with income as explanatory variable is 0.0412 with self-reported health as dependent variable, but 0.0824 with the health index as dependent variable, twice as large. To address potential nonlinearities, we have repeated this exercise using nonparametric bivariate regressions, with similar results. Complementing these within-country regressions, we have also run the between-country (linear) regressions of average health status (health index or self-reported health) on average income or net worth. The R²s of these regressions with the average health index as the dependent variable and income as explanatory variable are 0.58 for males and 0.43 for females, whereas these numbers are considerably smaller with average self-reported health as explanatory variable: 0.16 for males and 0.30 for females. The R²s with net worth as explanatory variable are much smaller, with in one case a higher value for self-reported health: 0.049 for males, versus 0.017 with the health index; for females these numbers are 0.014 with self-reported health and 0.015 with the health index. Summarizing, the regressions show that in the overwhelming majority of cases, the health index produces more pronounced health-SES gradients than with self-reported health, but there are a few minor exceptions.

5 Discussion

In this paper we have estimated a measurement model of latent health. The key indicators of health are mobility, arm function, and fine motor function limitations, ADLs, IADLs, self-reported health, and grip strength. The latter also depends on a second-degree polynomial in body height and weight. The health model contains a “predictive” health equation, in which latent health is regressed on a standard set of socio-demographic covariates. The model is a special case of the LISCOMP model with a linear structure in the latent domain and threshold relations between latent response variables and categorical indicators. All analyses have been done with the SHARE wave 1 data.

In order to assure cross-country comparability of health, the coefficient of latent health in the grip strength equation was normalized to 1, and the intercept in this equation was normalized to 0. Using this objective indicator for normalization led to a specification that makes the latent health construct in the model comparable across countries.

The model fit seems satisfactory, with pseudo-R² values generally between 0.20 and 0.30. Scaled LR tests are highly significant and AIC and BIC statistics also support the fit of the model. However, more experience with the pseudo-R² in this type of model and comparison with competing models are necessary to be able to make firmer statements about model fit.

The results show that there are considerable differences in the self-reported health indicators that reflect country-specific reporting styles rather than differences in genuine health. However, we also observe cross-country variability in genuine health. Differences in average health status across countries are related to differences in average income across countries.

Using the estimation results of our model, we computed a health index for each observation. This health index is the best possible estimate (in the mean squared error sense) of the latent health variable in the model. The reliabilities of the constructed health indices are satisfactory at approximately 80%. Using the health indices, we find that the health gradients by age, income, and wealth show the expected patterns, with the exception of some erratic patterns at the very bottom of the income distribution.

Further research is needed to improve the measurement of health and assess its use in economic modeling. Various sensitivity analyses, using different specifications of the “predictive” health equation and different distributional assumptions, are expected to give more insight into the robustness of the results to possible misspecification and in particular whether this affects the properties of the health index noticeably.

We have done some preliminary experimentation with including the health index in simple models of retirement status. These results show that the health index is strongly related to retirement status. Moreover, using the health index leads to better model fit overall (judged by AIC and/or BIC) than using other health summary measures (simple aggregates of subsets of the indicators used here but also of chronic conditions or health symptoms) alone or in combination. However, in some country-gender combinations, the health index is outperformed by a combination of two or more other health measures. This indicates that an extension of the health model with more than one health dimension, which better reflects the multidimensional nature of health, may be important in retirement modeling. A detailed account of these results is beyond the scope of the current paper.

Appendix

Loglikelihood

For deriving the loglikelihood function, it is convenient to define ${\delta }_c\equiv \sqrt{{\psi }_c}$ and z_cn = ζ_cn/δ_c. Given the assumptions in the model, z_cn is standard normally distributed and independent of x_cn. Then (3) becomes ${\eta }_{cn}={\gamma }_c^{\prime }{x}_{cn}+{\delta }_c{z}_{cn}$. The likelihood contribution of individual n in country c is

$${\mathcal{L}}_{cn}=f_{y\mid x}(y_{cn}\mid x_{cn})={\int }_{-\infty }^{+\infty }{f}_{y\mid z,x}(y_{cn}\mid z_{cn},x_{cn})\varphi \left(z_{cn}\right)\mathrm{d}{z}_{cn}={\mathrm{E}}_z\left[f_{y\mid z,x}(y_{cn}\mid z_{cn},x_{cn})\right],$$ (4)

where f is used as a generic symbol to denote a probability density or probability mass function, and ϕ(·) is the standard normal density function. For notational convenience, we suppress the dependence of the likelihood and its components on the parameters.

The assumption of independence of the measurement errors implies that f_y|z,x(y_cn | z_cn, x_cn) factors into a product of univariate conditional densities and mass functions. Following the literature on maximum simulated likelihood (e.g., Train, 2003), we approximate the integral in (4) by drawing a sample {ž_cn,1, . . . , ž_cn,R} of standard normally distributed random numbers and replace the mean by the sample average over these draws. The resulting simulated likelihood contribution is

$${\check{\mathcal{L}}}_{cn}=\frac{1}{R}\sum _{r=1}^R\left[\prod _i{f}_{y_i\mid z,x}(y_{cni}\mid {\check{z}}_{cn,r},x_{cn})\right],$$ (5)

and the simulated log-pseudolikelihood for the whole sample is

$$\check{L}=\sum _c\sum _n{w}_{cn}\text{log}{\check{\mathcal{L}}}_{cn},$$

where w_cn is the sampling weight. This is the function that has to be maximized with respect to the parameters. As indicated in the text, we have first partialed the height-weight polynomial out of the grip strength equation, so that all remaining free parameters are country-specific. Hence, maximizing Ľ can be done by maximizing ${\check{L}}_c\equiv {\sum }_n{w}_{cn}\text{log}{\check{\mathcal{L}}}_{cn}$ for each country separately, which greatly alleviates the computational burden.

Let ${\check{\eta }}_{cn,r}\equiv {\gamma }_c^{\prime }{x}_{cn}+{\delta }_c{\check{z}}_{cn,r}$. Then the conditional densities and mass functions in (5) are relatively standard (binary or ordinal) probit and regression likelihoods: For a binary indicator,

$$f_{y_i\mid z,x}(y_{cni}\mid {\check{z}}_{cn,r},x_{cn})=\{\begin{array}{cc}\Phi ({\tau }_{ci}+{\lambda }_{ci}{\check{\eta }}_{cn,r})\hfill & \text{if}{y}_{cni}=1;\hfill \\ 1-\Phi ({\tau }_{ci}+{\lambda }_{ci}{\check{\eta }}_{cn,r})\hfill & \text{if}{y}_{cni}=0,\hfill \end{array}\phantom{\}}$$

where Φ(·) is the standard normal distribution function. For an ordinal indicator (self-reported health, climbing stairs),

$$f_{y_i\mid z,x}(y_{cni}\mid {\check{z}}_{cn,r},x_{cn})=\{\begin{array}{cc}\Phi ({\alpha }_{ci1}-{\lambda }_{ci}{\check{\eta }}_{cn,r})\hfill & \text{if}{y}_{cni}=1;\hfill \\ \Phi ({\alpha }_{ci,j}-{\lambda }_{ci}{\check{\eta }}_{cn,r})-\Phi ({\alpha }_{ci,j-1}-{\lambda }_{ci}{\check{\eta }}_{cn,r})\hfill & \text{if}1<y_{cni}<J_i;\hfill \\ 1-\Phi ({\alpha }_{ci,J_i-1}-{\lambda }_{ci}{\check{\eta }}_{cn,r})\hfill & \text{if}{y}_{cni}=J_i;\hfill \end{array}\phantom{\}}$$

where J_i is the number of categories of variable i and the category codes are assumed to be the integers 1, . . . , J_i. Finally, for a continuous indicator (the grip strength residual),

$$f_{y_i\mid z,x}(y_{cni}\mid {\check{z}}_{cn,r},x_{cn})=\frac{1}{{\rho }_{ci}}\varphi \left(\frac{y_{cni}-{\tau }_{ci}-{\lambda }_{ci}{\check{\eta }}_{cn,r}}{{\rho }_{ci}}\right),$$

where ${\rho }_{ci}=\sqrt{{\Omega }_{c,ii}}$ and, as a result of the normalizations, τ_ci = 0 and λ_ci = 1. If a variable is missing, f_yi|z,x(y_cni | ž_cn,r, x_cn) = 1 is used, which leads to correct inference under the missing at random (MAR) assumption, as discusssed in the text.

To increase accuracy without unduly increasing the computation time, we use Halton sequences, which is a more systematic (nonrandom) method to generate draws in a way that reduces variance and thus increases precision. Train (2003, pp. 224–238) gives a detailed description. A function generating Halton sequences is supplied with Stata (Drukker and Gates, 2006). Based on earlier experience, some experimentation, and the remarks in Train (2003, p. 231), we assumed that R = 100 Halton draws should be sufficient. However, we experimented (for Germany) with R = 1000 and R = 5000. The differences between 100 and 1000 draws are noticeable but relatively small. The differences between 1000 and 5000 draws are negligible. More importantly, none of these differences leads to substantively different conclusions, and the resulting health indices are very highly correlated (0.999). Therefore, the results here have all been obtained using 100 draws, with the exception for Germany, where we use the results with 1000 draws.

An expression for the health index and its precision

As mentioned in the text, the health index is defined as ${\widehat{\eta }}_{cn}=\mathrm{E}({\eta }_{cn}\mid y_{cn},x_{cn})$. To obtain a convenient expression for this, we write this first as

$${\widehat{\eta }}_{cn}={\gamma }_c^{\prime }{x}_{cn}+{\delta }_c\mathrm{E}(z_{cn}\mid y_{cn},x_{cn}).$$

Its precision can be measured by its conditional variance, which is also the mean squared prediction error:

$$\text{Var}({\eta }_{cn}\mid y_{cn},x_{cn})={\delta }_c^2\text{Var}(z_{cn}\mid y_{cn},x_{cn})={\delta }_c^2\left\{\mathrm{E}(z_{cn}^2\mid y_{cn},x_{cn})-{\left[\mathrm{E}(z_{cn}\mid y_{cn},x_{cn})\right]}^2\right\}.$$

The conditional density of z_cn is

$$f_{z\mid y,x}(z_{cn}\mid y_{cn},x_{cn})=\frac{f_{y\mid z,x}(y_{cn}\mid z_{cn},x_{cn})f_z\left(z_{cn}\right)}{f_{y\mid x}(y_{cn}\mid x_{cn})}=\frac{f_{y\mid z,x}(y_{cn}\mid z_{cn},x_{cn})\varphi \left(z_{cn}\right)}{{\mathcal{L}}_{cn}},$$

and ${\mathcal{L}}_{cn}$ was defined in (4). It follows that

$$\begin{array}{cc}\hfill \mathrm{E}(z_{cn}\mid y_{cn},x_{cn})& =\frac{1}{{\mathcal{L}}_{cn}}{\int }_{-\infty }^{+\infty }{z}_{cn}{f}_{y\mid z,x}(y_{cn}\mid z_{cn},x_{cn})\varphi \left(z_{cn}\right)\mathrm{d}{z}_{cn}\hfill \\ \hfill & =\frac{1}{{\mathcal{L}}_{cn}}{\mathrm{E}}_z\left[z_{cn}{f}_{y\mid z,x}(y_{cn}\mid z_{cn},x_{cn})\right]\hfill \end{array}$$

and

$$\mathrm{E}(z_{cn}^2\mid y_{cn},x_{cn})=\frac{1}{{\mathcal{L}}_{cn}}{\mathrm{E}}_z\left[z_{cn}^2{f}_{y\mid z,x}(y_{cn}\mid z_{cn},x_{cn})\right].$$

Note that in these expressions, E_z denotes the expectation over the marginal distribution of z_cn, i.e., the standard normal distribution. The expectations in these expressions have the same form as (4), and so can be computed in the same way, by inserting ž_cn,r and ${\check{z}}_{cn,r}^2$, respectively, between the summation and product symbols in (5). Of course, in practice, we compute these expressions with the parameters replaced by their estimates from the model estimation.