Abstract
We introduce an electromechanical model for human cardiac tissue which couples a biophysical model of cardiac excitation (Tusscher, Noble, Noble, Panfilov, 2006) and tension development (adjusted Niederer, Hunter, Smith, 2006 model) with a discrete elastic mass-lattice model. The equations for the excitation processes are solved with a finite difference approach, and the equations of the mass-lattice model are solved using Verlet integration. This allows the coupled problem to be solved with high numerical resolution. Passive mechanical properties of the mass-lattice model are described by a generalized Hooke's law for finite deformations (Seth material). Active mechanical contraction is initiated by changes of the intracellular calcium concentration, which is a variable of the electrical model. Mechanical deformation feeds back on the electrophysiology via stretch-activated ion channels whose conductivity is controlled by the local stretch of the medium. We apply the model to study how stretch-activated currents affect the action potential shape, restitution properties, and dynamics of spiral waves, under constant stretch, and dynamic stretch caused by active mechanical contraction. We find that stretch conditions substantially affect these properties via stretch-activated currents. In constantly stretched medium, we observe a substantial decrease in conduction velocity, and an increase of action potential duration; whereas, with dynamic stretch, action potential duration is increased only slightly, and the conduction velocity restitution curve becomes biphasic. Moreover, in constantly stretched medium, we find an increase of the core size and period of a spiral wave, but no change in rotation dynamics; in contrast, in the dynamically stretching medium, we observe spiral drift. Our results may be important to understand how altered stretch conditions affect the heart's functioning.
Introduction
The heartbeat is governed by electrical waves of excitation that periodically propagate through the cardiac muscle and initiate its contraction. Abnormal electrical excitation of the heart may result in cardiac arrhythmias disturbing the heart's pumping function. Heart failure due to cardiac arrhythmias is a major cause of death in the industrialized world [1]. It is known that dangerous types of arrhythmias are caused by spiral waves of electrical excitation in the cardiac muscle [2]–[4].
Electrical waves of excitation are affected by the deformation of the heart via the mechano-electrical feedback phenomenon. It has been shown that the rapid stretching of cardiac tissue (mechanical stimulation) has a significant effect on the heart's functioning, for example, due to the initiation of electrical waves [5], [6]. Important examples are “commotio cordis” [7], [8], the phenomenon that an impact on the chest can cause arrhythmia; and the “precordial thump”, the phenomenon that an impact on the chest of a patient may stop an arrhythmic heart condition [9]. Both phenomena are believed to be a result of an abrupt deformation of the heart, and the main effect of deformation on the electrical activity is considered to be transmitted via so-called stretch-activated ion channels. These channels produce depolarizing inward current as a response to stretch of the tissue [5]. The study of mechano-electrical feedback is an important direction of research in current cardiac electrophysiology [10].
A valuable method to study mechano-electrical feedback is mathematical modeling allowing to study the coupled mechanical and electrical activity of the heart, which is a difficult problem in experimental research. Generic electromechanical models for heart tissue are successfully applied, for instance, to investigate the effect of mechano-electrical feedback on pacemaking and spiral wave activity [11]–[15] and to find mechanisms for the onset of spiral waves [16], [17]. Yet, these generic models are limited to studies on a qualitative level, and more detailed models for cardiac tissue need to be developed. First steps in that direction have been made by coupling continuous mechanical models to biophysical models of cardiac excitation and contraction [18], [19]. However, continuum mechanics is computationally demanding and makes it difficult to achieve high spatial and temporal resolution of the coupled electrical and mechanical processes. In this paper, we introduce an electromechanical model for human cardiac tissue which couples detailed biophysical models for cardiac excitation and contraction to a discrete mechanical model. We use an ionic model of excitation for human cardiac cells (Tusscher, Noble, Noble, Panfilov 2006 model) [20], [21] and a biophysical model for excitation-contraction coupling (adjusted Niederer, Hunter, Smith, 2006 model) [22], [23]. Our method applies a generic model for cardiac elasticity, an ideal crystal lattice of mass points connected with springs. The mass-lattice model describes a material which was introduced by Seth 1935 to discuss problems of finite strain [24]. The Seth material relation is an extension of the generalized Hooke's law to finite elasticity. To solve the mechanical equations we apply the Verlet integration [25] (explicit, finite difference backwards integration scheme), a method which is widely used in molecular dynamics simulations. The Verlet integration has first been used to solve mass-lattice models in cardiac elasticity by Mohr [26]. We applied this discrete mechanical description before in a model to study reaction-diffusion-mechanics systems [15], and use it here to set up an electromechanical model for cardiac tissue. An advantage of this method is its computational efficiency which allows to solve the coupled electromechanical equations with high spatiotemporal resolution.
To demonstrate the value of the discrete electromechanical model we apply it to study effects of deformation on basic properties of cardiac tissue, such as the action potential shape, restitution properties, and the dynamics of spiral waves. In this study we consider two mechanical conditions. The first one is a constantly stretched medium, a simple assumption which was widely used in initial studies on mechano-electric feedback [27], [28], and mimics conditions such as dilated cardiomyopathies [27]. As a second condition, we assume a deforming medium which resembles deformation occurring as a result of cardiac contraction. We find that these stretch conditions have very different effects on the studied characteristics of excitation, and discuss the underlying mechanisms. The results of our application study may be important to understand how situations of increased mechanical load in the cardiac muscle alter the qualitative effect of stretch-activated currents.
Methods
Model for Cardiac Excitation
We use the 2006 version of the Tusscher Noble Noble Panfilov model for human epicardial myocytes (TP06) [20], [21]. The model is given as the following reaction-diffusion equation for the transmembrane potential 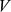
| (1) |
with the membrane capacitance density 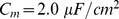 , the diffusivity
, the diffusivity 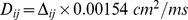 , and the transmembrane ion current
, and the transmembrane ion current
| (2) |
where 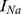 is fast Na
is fast Na current,
current, 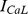 is L-type Ca
is L-type Ca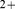 current, and the K
current, and the K currents are
currents are 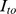 (transient outward),
(transient outward), 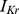 (rapid delayed rectifier),
(rapid delayed rectifier), 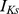 (slow delayed rectifier), and
(slow delayed rectifier), and 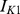 (inward rectifier). Furthermore,
(inward rectifier). Furthermore, 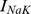 is the Na
is the Na /K
/K pump current,
pump current, 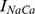 is the Na
is the Na /Ca
/Ca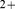 exchanger current,
exchanger current, 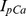 ,
, 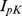 are plateau Ca
are plateau Ca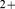 and K
and K currents, and
currents, and 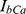 ,
, 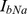 are background Ca
are background Ca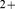 and Na
and Na currents. The voltage dependency of ion channels is modeled [29] by gating variables with dynamics of the form
currents. The voltage dependency of ion channels is modeled [29] by gating variables with dynamics of the form
| (3) |
where 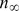 describes the voltage-dependent steady state activation, and
describes the voltage-dependent steady state activation, and  the voltage-dependent characteristic time for a respective gating variable. The TP06 model also describes Ca
the voltage-dependent characteristic time for a respective gating variable. The TP06 model also describes Ca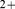 dynamics of intracellular compartments of the sarcoplasmatic reticulum. A list of parameters and equations for these currents is given in [20].
dynamics of intracellular compartments of the sarcoplasmatic reticulum. A list of parameters and equations for these currents is given in [20].
In our model we add a stretch-activated depolarizing current 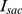 which will be introduced in the section “Mechano-Electrical Feedback”.
which will be introduced in the section “Mechano-Electrical Feedback”.
We will now describe the coupling of the electrical excitation process of the cardiomyocytes to their tension development.
Model for Excitation-Contraction Coupling
We model myocyte excitation-contraction coupling in our model with a numerically improved version of the Niederer, Hunter, Smith (NHS) model [22], [23] adjusted to human cardiac tissue. The NHS model describes active tension in a sarcomere as a function of intracellular calcium concentration [Ca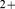 ]
] , sarcomere length, and the rate of sarcomere length change, determinants which have been shown to substantially affect the active tension development (see [22] and references within).
, sarcomere length, and the rate of sarcomere length change, determinants which have been shown to substantially affect the active tension development (see [22] and references within).
The NHS model takes the dynamics of sarcomere length into account. We follow previous studies [12], [15]–[17] and define as a pseudo normalized sarcomere length.
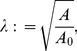 |
(4) |
where the 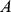 is the surface area of a smallest area element in the model (see section “Mass-Lattice Model”), and
is the surface area of a smallest area element in the model (see section “Mass-Lattice Model”), and 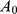 is the surface area of such a smallest area element in undeformed state.
is the surface area of such a smallest area element in undeformed state.
Adjustments for Human Ventricular Cells
We followed changes on the original version of the NHS model [22], which was originally set up using experimental data of rat and guinea pig hearts, that have been made in the work [18] to model human ventricular myocytes. These changes were explained in [18] by experimentally observed relaxation rates due to higher body temperatures [30]. The changes are a speeding up of myocyte relaxation rates to 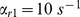 ,
, 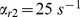 , and adjusting the contractile tension by setting parameters T
, and adjusting the contractile tension by setting parameters T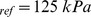 (maximum contractile tension at resting length of sarcomere) and pCa
(maximum contractile tension at resting length of sarcomere) and pCa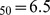 (p[Ca
(p[Ca ]
] at half maximal contractile tension).
at half maximal contractile tension).
Active Tension in Myocytes
The NHS model describes the tension  development in cross bridges as.
development in cross bridges as.
| (5) |
| (6) |
where 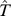 is the length and velocity independent tension, (
is the length and velocity independent tension, (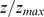 ) is the fraction of available actin sites in a sarcomere
) is the fraction of available actin sites in a sarcomere  to the maximal available actin sites
to the maximal available actin sites 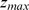 at a particular sarcomere length. Variable
at a particular sarcomere length. Variable  provides the coupling of the electrical and mechanical system and is found during integration of the NHS model where it is directly related to [Ca
provides the coupling of the electrical and mechanical system and is found during integration of the NHS model where it is directly related to [Ca ]
] , which is given by the electrical equations of the TP06 model. Scaling functions
, which is given by the electrical equations of the TP06 model. Scaling functions  and
and 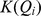 describe the sarcomere length and velocity dependencies of the total tension [22]. In particular, the function
describe the sarcomere length and velocity dependencies of the total tension [22]. In particular, the function  models the influence of the dynamics of the cross bridge cycle and thin filaments in a sarcomere, and function
models the influence of the dynamics of the cross bridge cycle and thin filaments in a sarcomere, and function 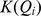 accounts for the velocity dependency of tension development via a fading memory model.
accounts for the velocity dependency of tension development via a fading memory model.
It has been shown that in strongly coupled electromechanical models for cardiac tissue, in which the equations for excitation processes and mechanical processes are jointly solved, computational difficulties may occur due to the velocity and length-dependency of a sarcomere [23]. To solve this problem, Niederer and Smith proposed the “update method” [23], where the functions 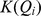 and
and  are continuously calculated within the mechanical iteration algorithm to calculate the total tension
are continuously calculated within the mechanical iteration algorithm to calculate the total tension  via Eq.(5). In this paper, we apply the NHS model, adjusted for human cardiac tissue, together with the “update method”. For a detailed model description and parameters, see [22], [23].
via Eq.(5). In this paper, we apply the NHS model, adjusted for human cardiac tissue, together with the “update method”. For a detailed model description and parameters, see [22], [23].
We will now describe the passive elastic properties of the medium.
Mass-Lattice Model
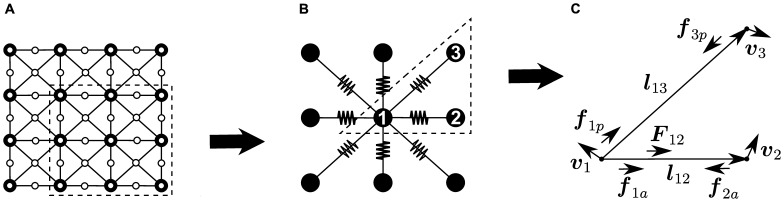
We use the mass-lattice framework introduced in [15]. The two-dimensional lattice consists of material points connected by springs (Figure 1A). In this square lattice each mass point is connected to  (if not at the boundary) direct neighboring mass points with springs that follow Hooke's law (Figure 1B). The equations of the model are.
(if not at the boundary) direct neighboring mass points with springs that follow Hooke's law (Figure 1B). The equations of the model are.
| (7) |
| (8) |
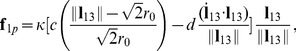 |
(9) |
| (10) |
Figure 1. Coupled mechanical and electrical mesh.
(A) Coupled mechanical and electrical mesh. The mass points are indicated as large black dots. The finite difference points to solve Eq.(1) are indicated as small white dots. The lattice springs are indicated as black lines. (B) Unit cell of the two-dimensional lattice. Mass point 1 and its four horizontal and vertical nearest neighbors and four diagonal next-nearest neighbors are connected with direct active and diagonal passive springs. Lattice springs are indicated by zigzagging lines (fat lines for active and thin lines for passive springs). Dotted contours indicate insets for the associated subfigures. (C) Vectors used in Eqs.(7)-(10) for calculating lattice interactions. Figure taken from [15].
Figure 1C illustrates main forces and the displacements of active and passive lattice springs connecting the mass point 1 to the mass points 2 and 3. Each mass point is connected to its  diagonal neighbors with “passive springs” (passive elastic properties), and to its
diagonal neighbors with “passive springs” (passive elastic properties), and to its  vertical and
vertical and  horizontal neighbors with “active springs” (passive and active forces). Eq.(7) describes the excitation-contraction coupling of two neighboring mass points
horizontal neighbors with “active springs” (passive and active forces). Eq.(7) describes the excitation-contraction coupling of two neighboring mass points  and
and  connected with an active spring, where
connected with an active spring, where 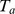 is active tension from Eq.(5), and
is active tension from Eq.(5), and 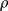 is the mass point surface density (see section “Numerical Methods”). Eqs.(8),(9) describe forces
is the mass point surface density (see section “Numerical Methods”). Eqs.(8),(9) describe forces  mediated through an active spring to mass points
mediated through an active spring to mass points 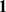 and
and 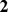 , and forces
, and forces  mediated through a passive spring to mass points
mediated through a passive spring to mass points 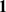 and
and  . In Eqs.(8),(9) the spring vectors are given by mass point's positions as
. In Eqs.(8),(9) the spring vectors are given by mass point's positions as 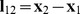 and
and 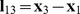 ,
, 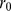 is the resting length of an active spring and
is the resting length of an active spring and 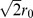 the resting length of a passive spring,
the resting length of a passive spring, 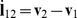 and
and 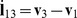 are the time derivatives of the respective spring vectors
are the time derivatives of the respective spring vectors 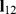 ,
, 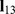 . Parameter
. Parameter  is the stiffness constant, and
is the stiffness constant, and 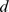 is the damping parameter. Parameter
is the damping parameter. Parameter 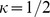 is the stiffness ratio between active and passive springs which causes the lattice to be macroscopically isotropic [31] for small deformations, and can be described by the generalized Hooke's law.
is the stiffness ratio between active and passive springs which causes the lattice to be macroscopically isotropic [31] for small deformations, and can be described by the generalized Hooke's law.
| (11) |
with the small strain tensor 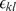 , Cauchy's stress tensor
, Cauchy's stress tensor 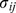 , linear elasticity tensor
, linear elasticity tensor 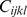 , Kronecker delta
, Kronecker delta 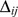 , and Lamé coefficients
, and Lamé coefficients 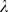 and
and 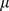 . Krivtsov showed in [32] that the lattice can be approximated by the Seth material relation [24] for non-linear deformations which is given by Eq.(11) when the Almansi's finite strain tensor is used instead of the small strain tensor. Young's elastic modulus of cardiac tissue has been measured in an atomic force microscopy study
. Krivtsov showed in [32] that the lattice can be approximated by the Seth material relation [24] for non-linear deformations which is given by Eq.(11) when the Almansi's finite strain tensor is used instead of the small strain tensor. Young's elastic modulus of cardiac tissue has been measured in an atomic force microscopy study 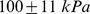 [33]. However, cardiac tissue provides a nonlinear elastic behavior for larger deformations, and we found that setting Young's elastic modulus to
[33]. However, cardiac tissue provides a nonlinear elastic behavior for larger deformations, and we found that setting Young's elastic modulus to 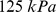 in our model results in maximal deformations of springs of
in our model results in maximal deformations of springs of 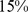 , similar to contracting cardiac cells. Thus we set the spring stiffness
, similar to contracting cardiac cells. Thus we set the spring stiffness  accordingly to
accordingly to 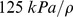 (see section “Numerical Methods”). As we assume elastostatics
(see section “Numerical Methods”). As we assume elastostatics  and
and 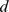 have no physical relevance and should be set to optimize computations. Following [15], we set
have no physical relevance and should be set to optimize computations. Following [15], we set  to the identical numerical value of
to the identical numerical value of  (
(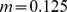 for
for 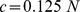 compare section “Numerical Methods”), and set
compare section “Numerical Methods”), and set 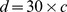 to achieve stable and efficient computations (see section “Model Validation”).
to achieve stable and efficient computations (see section “Model Validation”).
In section “Model for Excitation-Contraction Coupling” we defined a pseudo normalized sarcomere length 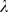 in terms of the surface area of a smallest area element
in terms of the surface area of a smallest area element 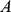 in the lattice (see Eq.(4)), which is a quadrilateral formed by 4 direct neighboring mass points connected with active springs (see Figure 1A). Parameter
in the lattice (see Eq.(4)), which is a quadrilateral formed by 4 direct neighboring mass points connected with active springs (see Figure 1A). Parameter 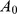 is the surface area of such a smallest area element in the undeformed model,
is the surface area of such a smallest area element in the undeformed model, 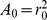 (see Figure 1A).
(see Figure 1A).
We will now describe how we model mechano-electrical feedback via stretch-activated currents.
Mechano-Electrical Feedback
The deformation of a cardiomyocyte affects its excitation processes. It has been shown in studies of excised cardiac tissue and the whole heart that a direct electrophysiological influence of the deformation of cardiac tissue is a depolarizing stretch-activated current 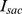 (compare Eq.(2)) through stretch-activated ion channels [5]. Experimental studies have shown that these channels are activated instantaneously with mechanical stretch and follow a linear current-voltage relationship [34], [35]. Linear, time-independent models have been proposed for
(compare Eq.(2)) through stretch-activated ion channels [5]. Experimental studies have shown that these channels are activated instantaneously with mechanical stretch and follow a linear current-voltage relationship [34], [35]. Linear, time-independent models have been proposed for 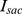 [27], [28], and have been used in other electromechanical models [12], [14], [18]. Following these previous studies we use.
[27], [28], and have been used in other electromechanical models [12], [14], [18]. Following these previous studies we use.
| (12) |
where 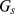 is the maximal conductance, and
is the maximal conductance, and 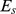 is the reversal potential of the stretch activated channels. For
is the reversal potential of the stretch activated channels. For 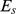 values around
values around 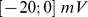 have been reported [36], [37], and we set
have been reported [36], [37], and we set 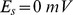 . It has been shown that
. It has been shown that 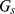 is within
is within  to
to 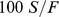 [5], [38], and in this paper we vary
[5], [38], and in this paper we vary 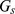 in this range to study the influence of
in this range to study the influence of 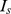 on several properties. Parameter
on several properties. Parameter 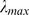 is the maximal pseudo normalized sarcomere length which we set to
is the maximal pseudo normalized sarcomere length which we set to 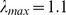 as in [18].
as in [18].
Numerical Methods
We solved the model applying an explicit Euler method for the TP06 and NHS models, and Verlet integration [25] for the mechanical model. After each Euler computation of the electrical system a new [Ca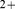 ]
] is obtained, and a length and velocity independent tension
is obtained, and a length and velocity independent tension 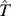 is computed via Eq.(6).
is computed via Eq.(6). 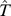 is then passed to the mechanics model, where the mechanical equations are solved, using Verlet integration time step
is then passed to the mechanics model, where the mechanical equations are solved, using Verlet integration time step 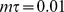 , until the sum of forces on each mass point is smaller than threshold
, until the sum of forces on each mass point is smaller than threshold 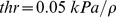 . The Verlet computation of the position of a mass point
. The Verlet computation of the position of a mass point  for integration time
for integration time 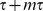 is
is
where 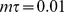 is the Verlet integration time step and
is the Verlet integration time step and  is the integration time. For the very first time step, we use
is the integration time. For the very first time step, we use
The acceleration of a mass point 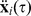 is given by Eq.10. At each time step the velocities of the mass points are calculated by
is given by Eq.10. At each time step the velocities of the mass points are calculated by
During the mechanical iteration algorithm the length and velocity dependent tension scaling functions 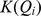 and
and  of the total tension
of the total tension 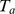 which is computed via Eq.(5) are updated together with the mesh configuration using the “update-method” [23]. We found that numerical difficulties can occur in situations when the damping force in a spring exceeds the Hooke's force, for example in an active spring (see section “Mass-Lattice Model”).
which is computed via Eq.(5) are updated together with the mesh configuration using the “update-method” [23]. We found that numerical difficulties can occur in situations when the damping force in a spring exceeds the Hooke's force, for example in an active spring (see section “Mass-Lattice Model”).
| (13) |
which in turn causes slow convergence of the iterative algorithm requiring in some cases thousands of iterations before convergence. However, we found that good convergence can be achieved by setting the absolute damping force to 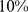 of the Hooke's spring force (for springs for which condition of Eq.(13) is true). With this, we observe a significant improvement - typically the mechanical system converges within
of the Hooke's spring force (for springs for which condition of Eq.(13) is true). With this, we observe a significant improvement - typically the mechanical system converges within 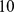 –
–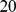 iterations. In this paper the “update method” is applied within the Verlet routine on discrete nodes, whereas in the original work [23] the method is used within the Newton algorithm to solve equations of continuum mechanics. Moreover, here the actual sarcomere length was not used for the mechano-electrical feedback calculation, but a pseudo normalized sarcomere length
iterations. In this paper the “update method” is applied within the Verlet routine on discrete nodes, whereas in the original work [23] the method is used within the Newton algorithm to solve equations of continuum mechanics. Moreover, here the actual sarcomere length was not used for the mechano-electrical feedback calculation, but a pseudo normalized sarcomere length 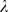 from Eq.(4). For simulations we used an Euler integration space step from
from Eq.(4). For simulations we used an Euler integration space step from 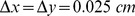 to
to 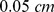 and Euler integration time step of
and Euler integration time step of 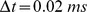 . We computed a quadratic grid of up to
. We computed a quadratic grid of up to 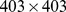 finite difference points (and up to
finite difference points (and up to 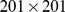 mass points) using no-flux boundary conditions modeling a thin quadratic layer of
mass points) using no-flux boundary conditions modeling a thin quadratic layer of 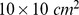 cardiac tissue. The spring stiffness
cardiac tissue. The spring stiffness  and mechanical threshold
and mechanical threshold 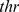 are functions of the mass point density. Mass point density
are functions of the mass point density. Mass point density 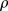 is function of the coarseness of the mass-lattice model, here we set the resting length of an active spring to be as long as two finite difference integration steps
is function of the coarseness of the mass-lattice model, here we set the resting length of an active spring to be as long as two finite difference integration steps 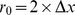 (see Figure 1A), thus the mass point density is
(see Figure 1A), thus the mass point density is
where the factor 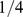 is the ratio of mesh coarseness (#mechanical points/#electrical points) in the model. For an Euler space step of
is the ratio of mesh coarseness (#mechanical points/#electrical points) in the model. For an Euler space step of 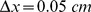 , the mass point density is
, the mass point density is 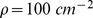 , spring stiffness is
, spring stiffness is 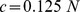 , and the mechanical threshold is
, and the mechanical threshold is 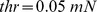 . The boundaries of the medium were fixed in space modeling isometric contraction to mimic isovolumic phases in the cardiac cycle, a common assumption which was used in similar electromechanical studies [12], [14]–[16].
. The boundaries of the medium were fixed in space modeling isometric contraction to mimic isovolumic phases in the cardiac cycle, a common assumption which was used in similar electromechanical studies [12], [14]–[16].
Model Validation
The numerical coupling and integration of the Euler and the Verlet scheme require the choice of several parameters. We will first discuss the integration parameters and then parameters for the coupling of the numerical grids to assure efficient and stable computations.
Integration Parameters
It has been shown that the TP06 model together with the improved NHS model coupled with a whole heart continuum mechanics model can be stably integrated with the Euler method using integration parameters 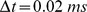 and
and 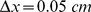 [18]. We use Euler integration steps of
[18]. We use Euler integration steps of 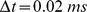 and
and 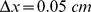 as in [15] for most computations, and use a stricter setting
as in [15] for most computations, and use a stricter setting 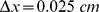 for simulations on spiral wave dynamics. To validate the usage of larger space step
for simulations on spiral wave dynamics. To validate the usage of larger space step 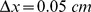 we performed simulations of our main results on potential shape, and restitution properties using
we performed simulations of our main results on potential shape, and restitution properties using 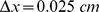 . In these simulations we found that our setting of Euler integration parameters yields consistent results. We update the mechanical configuration after each Euler step, and achieve stable and accurate integration of the coupled electromechanical model. For solving the mechanical Eqs.(8)-(10) we use a Verlet integration time step of
. In these simulations we found that our setting of Euler integration parameters yields consistent results. We update the mechanical configuration after each Euler step, and achieve stable and accurate integration of the coupled electromechanical model. For solving the mechanical Eqs.(8)-(10) we use a Verlet integration time step of 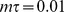 (as in [15]). We find that this setting allows efficient and stable computations of new configurations of the mechanical grid for this paper's simulations.
(as in [15]). We find that this setting allows efficient and stable computations of new configurations of the mechanical grid for this paper's simulations.
Damping-Stiffness-Ratio
The system of coupled, damped, driven, mechanical oscillators described by Eqs.(8)-(10) has been shown in [15] to allow fast stable convergence of the lattice mass points to their new configuration in a similar application as in this paper. In this work we found that setting the damping-stiffness ratio 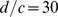 (dimensionless) as in [15] yields stable and efficient computations of mechanical mesh configurations in most situations. However, we found that in some situations (e.g. under external stimulation) we get numerical difficulties when Eq.(13) is true even for smaller values of the damping-stiffness ratio
(dimensionless) as in [15] yields stable and efficient computations of mechanical mesh configurations in most situations. However, we found that in some situations (e.g. under external stimulation) we get numerical difficulties when Eq.(13) is true even for smaller values of the damping-stiffness ratio 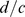 (e.g.
(e.g. 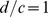 ). Thus, we apply
). Thus, we apply 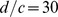 together with the stability criterion outlined in the section “Numerical Methods” for all this paper's simulations.
together with the stability criterion outlined in the section “Numerical Methods” for all this paper's simulations.
Electrical and Mechanical Grids
In [15] we applied a method to validate the mesh coupling of the finite difference mesh and the mechanical mesh via an error norm defined by residues of mass point trajectories. This method allowed us to find accurate coupling parameters. We found in these validation experiments that the usage of a coarser finite difference mesh compared to the mechanical mesh as shown in Figure 1A allows accurate computations. This is, because changes in tension and strain are typically distributed more smoothly in space than electrical variables. For example, the upstroke of an electrical excitation wave has a length of the order of one to two millimeters, whereas the mechanical tension changes over a range of few centimeters. In this paper, we performed simulations to test how a change in resolution of the mechanical mesh compared to the electrical system affects the main results of the paper, and we found that our parameter setting yields consistent results. We also found in [15] that our mechanics model converges better with a frequent update rate, and therefore we also choose here to update the mechanical mesh after each time the electrical system was solved (every 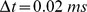 ). We performed a convergence study to determine a suitable value for the threshold of convergence for the mechanical problem for numerical step sizes. For this we halved and quartered the value for
). We performed a convergence study to determine a suitable value for the threshold of convergence for the mechanical problem for numerical step sizes. For this we halved and quartered the value for 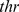 , and found qualitatively same results (influence of stretch on action potential, restitution properties, spiral wave dynamics). Thus we set
, and found qualitatively same results (influence of stretch on action potential, restitution properties, spiral wave dynamics). Thus we set 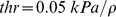 , e.g. for
, e.g. for 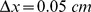 ,
, 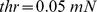 , and for
, and for 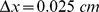 ,
, 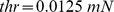 .
.
Mesh Initial Conditions
The main determinant of cardiac contraction is the [Ca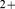 ]
] transient, and it is necessary to set initial conditions of the TP06 model so that it describes a steady state Ca
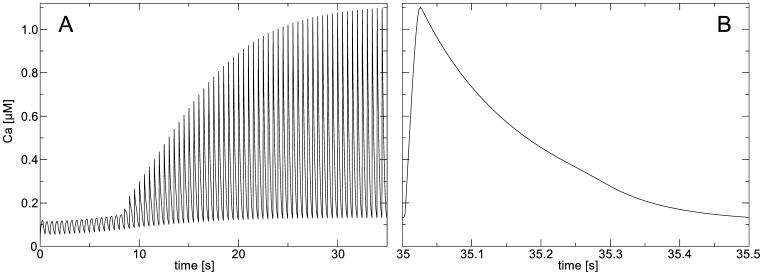
transient, and it is necessary to set initial conditions of the TP06 model so that it describes a steady state Ca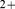 dynamics of a working cardiac cell. We found that one should carefully approach this problem as establishing of such a steady state can take a substantial period of time. To demonstrate this, we performed a numerical experiment on a single, non-deforming cell in which we stimulated it with a frequency of
dynamics of a working cardiac cell. We found that one should carefully approach this problem as establishing of such a steady state can take a substantial period of time. To demonstrate this, we performed a numerical experiment on a single, non-deforming cell in which we stimulated it with a frequency of 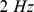 by setting
by setting 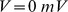 for one time step
for one time step 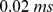 . We see in Figure 2A that it requires a long time to reach steady state dynamics for [Ca
. We see in Figure 2A that it requires a long time to reach steady state dynamics for [Ca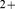 ]
] . Figure 2B illustrates the [Ca
. Figure 2B illustrates the [Ca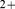 ]
] transient after
transient after 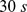 of applying the stimulation protocol. According to this simulation we adjusted initial conditions of the TP06 model: [Ca
of applying the stimulation protocol. According to this simulation we adjusted initial conditions of the TP06 model: [Ca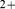 ]
]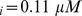 ; [CaSR]
; [CaSR]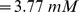 ; CaSS
; CaSS 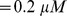 . Note that these calcium concentrations were taken at peak values of [Ca
. Note that these calcium concentrations were taken at peak values of [Ca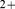 ]
] , and that in following numerical experiments we performed additional initialization procedures.
, and that in following numerical experiments we performed additional initialization procedures.
Figure 2. Mesh initialization (A) [Ca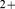
 ] transient during pacing experiment.
] transient during pacing experiment.
[Ca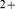 ]
] is shown for a single non-deforming cell undergoing
is shown for a single non-deforming cell undergoing 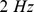 pacing. (B) Steady state [Ca
pacing. (B) Steady state [Ca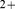
 ] transient. [Ca
] transient. [Ca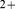 ]
] is shown for a single non-deforming cell after
is shown for a single non-deforming cell after 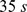 of
of 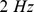 pacing.
pacing.
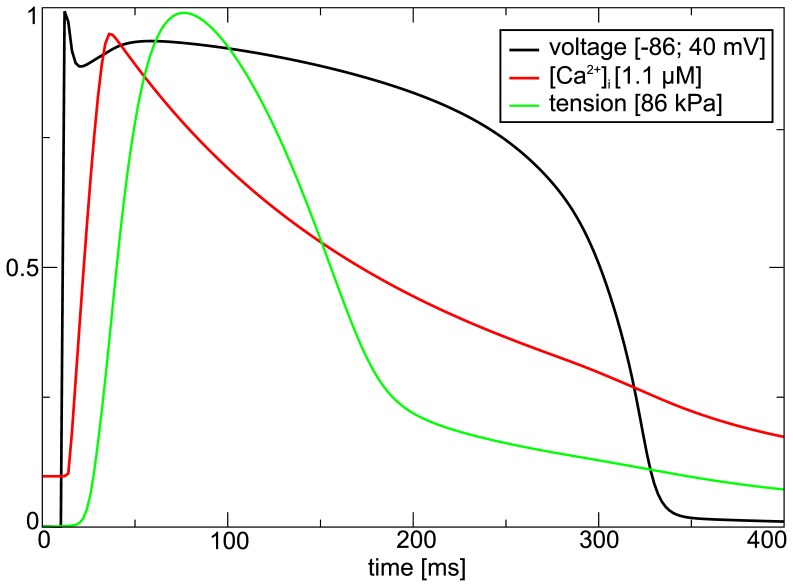
Figure 3 shows an electromechanical pulse of a single fiber during isometric contraction. One can see that as in experimental records [39] the tension is slightly delayed from the [Ca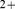 ]
] transient, the fiber produces a maximal contractile tension of
transient, the fiber produces a maximal contractile tension of 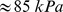 approximately after
approximately after 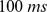 after the upstroke of the action potential.
after the upstroke of the action potential.
Figure 3. Electromechanical activity of an isolated fiber.
A pulse is initialized at time 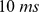 by setting voltage to
by setting voltage to 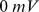 for
for 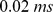 . Fiber was kept at its resting length during the simulation.
. Fiber was kept at its resting length during the simulation.
Results
We applied our discrete electromechanical model to study the effects of stretch-activated currents and stretch conditions on action potential duration (APD) and conduction velocity (CV) restitution, and spiral wave dynamics. The results of these studies are shown in this section.
We consider two mechanical conditions, a constantly stretched medium, and a contracting medium. The condition of sustained stretch in the medium has been assumed previously, for example, in a model to study how dilated cardiomyopathies may affect defibrillation efficacy [27], and in a model to study the effect of mechano-electrical feedback on the action potential of ventricular cells [28]. However, under normal physiological conditions cells are not constantly stretched, but contract during most of the action potential. It is interesting to note, that as an experimental condition, constantly applied mechanical load is often applied to study effects of mechano-electrical feedback, for example, in cardiac cell cultures [40] or animal models [41]. Therefore, we perform studies both, in a constantly stretched medium, and in a contracting medium to investigate the effects of different mechanical conditions.
Action Potential Shape and Restitution Properties
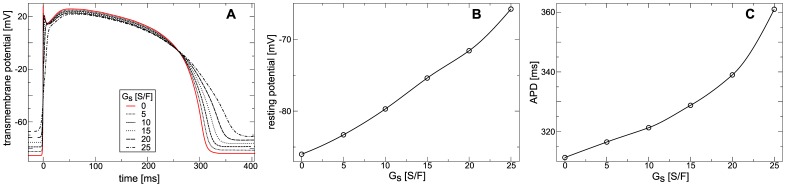
Constant stretch
We used a  medium which we assumed stretched to
medium which we assumed stretched to 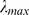 . From Eq.(12) we see that in this situation every cell in the medium experiences
. From Eq.(12) we see that in this situation every cell in the medium experiences 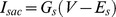 , thus we apply
, thus we apply 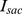 to every cell without actually deforming the medium. We initiated a train of traveling plain waves with a period of
to every cell without actually deforming the medium. We initiated a train of traveling plain waves with a period of 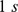 to study the influence of
to study the influence of 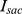 on characteristics of the action potential for
on characteristics of the action potential for 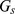 from
from  to
to 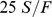 . In Figure 4A we show the shape of the action potential of the cell in the center of the medium for different
. In Figure 4A we show the shape of the action potential of the cell in the center of the medium for different 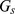 after
after 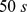 application of the stimulation protocol. From Figure 4A we see that increasing
application of the stimulation protocol. From Figure 4A we see that increasing 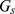 causes an increase in the resting potential in the medium and increase in APD. In particular, Figure 4B shows that increase of
causes an increase in the resting potential in the medium and increase in APD. In particular, Figure 4B shows that increase of 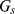 from
from  to
to 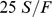 increases the resting potential by
increases the resting potential by 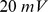 (from
(from 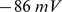 to
to 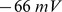 ). Figure 4C shows that increasing
). Figure 4C shows that increasing 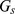 from
from  to
to 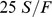 increases APD from
increases APD from 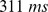 to
to 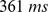 . This effect occurs as a larger
. This effect occurs as a larger 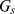 causes a stronger depolarizing
causes a stronger depolarizing  . As a result of stronger
. As a result of stronger 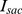 the resting potential increases, and during an action potential
the resting potential increases, and during an action potential 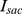 counteracts repolarizing currents elongating the APD.
counteracts repolarizing currents elongating the APD.
Figure 4. Effect of stretch-activated currents on the action potential in constantly stretched medium.
(A) Action potential vs
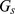 . (B) Resting membrane potential vs
. (B) Resting membrane potential vs
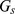 . (C) APD vs
. (C) APD vs
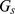 . Traveling plain waves were periodically (
. Traveling plain waves were periodically (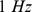 ) induced in a medium held at (
) induced in a medium held at (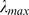 ) for different
) for different 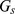 . Action potentials were measured after
. Action potentials were measured after 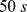 . Resting potential was measured in the medium without external stimulations. APD was measured at
. Resting potential was measured in the medium without external stimulations. APD was measured at 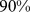 recovery.
recovery.
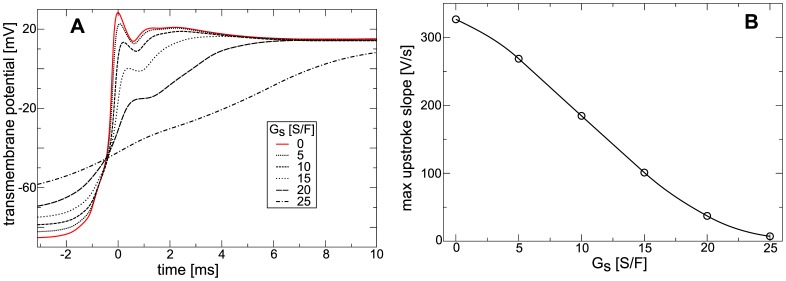
The effect of 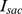 on the upstroke of the action potential in the constantly stretched medium is illustrated in Figure 5. We see in Figure 5A that the upstroke peak and slope decreases with increasing
on the upstroke of the action potential in the constantly stretched medium is illustrated in Figure 5. We see in Figure 5A that the upstroke peak and slope decreases with increasing 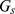 , and that for
, and that for 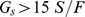 no typical sodium driven upstroke takes place. In Figure 5B the upstroke slope is shown as a function of
no typical sodium driven upstroke takes place. In Figure 5B the upstroke slope is shown as a function of 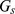 . We see that for
. We see that for 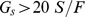 the upstroke slope drops to values under
the upstroke slope drops to values under 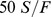 which is much lower than the sodium driven upstroke in the TP06 model without deformation. This effect of
which is much lower than the sodium driven upstroke in the TP06 model without deformation. This effect of 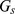 on the upstroke can be explained by a depletion of fast sodium channels via the accommodation phenomenon, a decrease of opening probability of fast sodium channels due to sub-threshold depolarization [29]. In a previous study [28], which also assumed a constantly stretched medium, similar effects of
on the upstroke can be explained by a depletion of fast sodium channels via the accommodation phenomenon, a decrease of opening probability of fast sodium channels due to sub-threshold depolarization [29]. In a previous study [28], which also assumed a constantly stretched medium, similar effects of 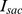 on the APD, upstroke and resting potential were found. Moreover, it was shown previously in Langendorff-perfused rabbit hearts that sustained volume load causes increased resting potential and decreased the slope of the action potential upstroke [41].
on the APD, upstroke and resting potential were found. Moreover, it was shown previously in Langendorff-perfused rabbit hearts that sustained volume load causes increased resting potential and decreased the slope of the action potential upstroke [41].
Figure 5. Effect of constant stretch on the action potential upstroke.
(A) Upstroke of action potential vs
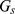 . (B) Maximal upstroke slope vs
. (B) Maximal upstroke slope vs
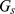 . Protocol was as in Figure? 4.
. Protocol was as in Figure? 4.
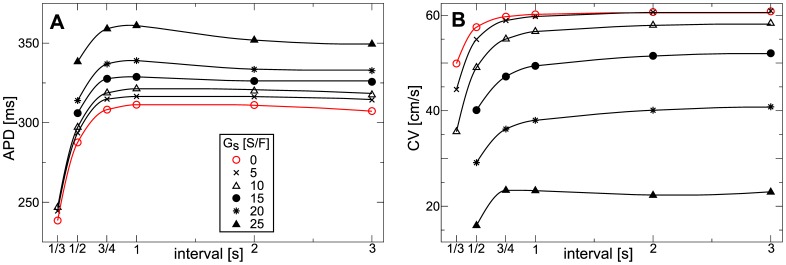
To measure restitution properties in the constantly stretched medium we applied the same setup as above, but varied the stimulation period from 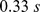 to
to 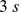 . We measured CV from the difference in front arrival times between two points, one at the center, and the other
. We measured CV from the difference in front arrival times between two points, one at the center, and the other 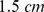 further in propagation direction. Figure 6 illustrates the APD and CV restitution. We see from Figure 6A that increasing
further in propagation direction. Figure 6 illustrates the APD and CV restitution. We see from Figure 6A that increasing 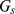 increases the APD. For
increases the APD. For 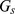 between
between  and
and 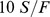 the slope of the APD restitution curve is not affected much, and APD grows continuously for longer stimulation periods to a plateau. For
the slope of the APD restitution curve is not affected much, and APD grows continuously for longer stimulation periods to a plateau. For 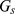 between
between 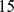 and
and 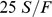 and a stimulation period longer than
and a stimulation period longer than 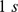 we see that an increasing, slightly negative slope of the APD restitution curve is caused. From Figure 6B we see, that increasing
we see that an increasing, slightly negative slope of the APD restitution curve is caused. From Figure 6B we see, that increasing 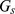 causes decreasing CV. For stimulation intervals shorter than
causes decreasing CV. For stimulation intervals shorter than 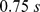 we observe that increasing
we observe that increasing 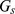 causes a higher steepness of the CV restitution curve. Restitution curves for
causes a higher steepness of the CV restitution curve. Restitution curves for 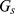 between
between  and
and 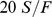 are monotonically increasing for longer stimulation intervals; yet, for
are monotonically increasing for longer stimulation intervals; yet, for 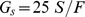 we see a biphasic shape with a local maximum of around
we see a biphasic shape with a local maximum of around 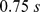 , and slightly negative slope of the CV restitution curve for longer stimulation interval. We also see that the minimal period of excitation increases with increase of
, and slightly negative slope of the CV restitution curve for longer stimulation interval. We also see that the minimal period of excitation increases with increase of 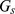 from about
from about 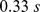 for
for 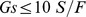 to about
to about 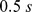 for
for 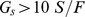 . In a previous study [27], where also constant stretch was assumed in the medium, increasing
. In a previous study [27], where also constant stretch was assumed in the medium, increasing 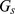 also caused longer APD and decreased CV.
also caused longer APD and decreased CV.
Figure 6. Dependence of restitution on stretch-activated currents in constantly stretched medium.
(A) APD restitution vs
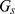 . (B) CV restitution vs
. (B) CV restitution vs
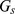 . Same parameters were used as in Figure? 4.
. Same parameters were used as in Figure? 4.
Contracting Medium
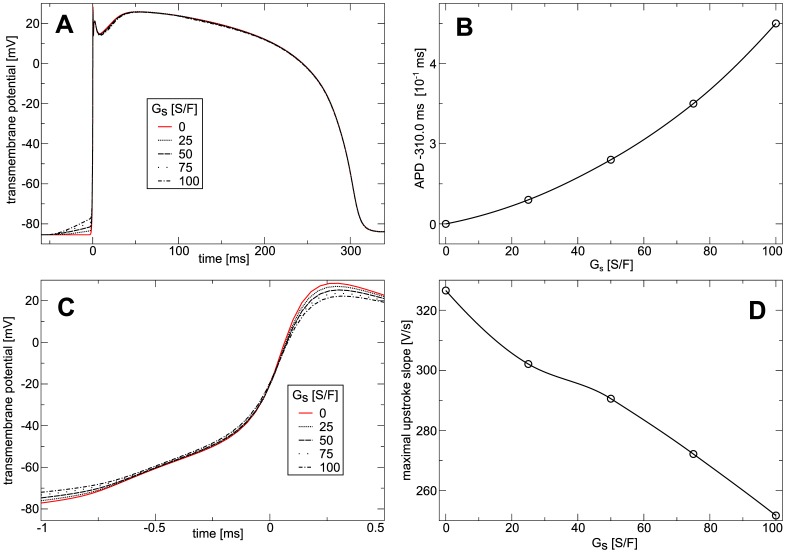
For the simulations in a contracting medium we applied the same system size, stimulation protocol, and parameter setting as for the constantly stretched medium; however, the medium is deforming due to excitation-contraction waves, and the boundaries are fixed space (see section “Numerical Methods”). In Figure 7A we show how the shape of the action potential is affected by 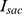 . We see that increasing
. We see that increasing 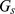 in from
in from  to
to 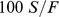 causes no substantial increase in the resting potential and in APD. Another effect of increasing
causes no substantial increase in the resting potential and in APD. Another effect of increasing 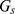 is a linear increase in the transmembrane potential starting
is a linear increase in the transmembrane potential starting 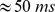 prior the upstroke. For example, for
prior the upstroke. For example, for 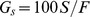 the transmembrane potential increases to
the transmembrane potential increases to 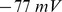 , which is well under the threshold of excitation, that is at
, which is well under the threshold of excitation, that is at 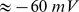 . In Figure 7B we illustrate the effect of
. In Figure 7B we illustrate the effect of 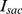 on APD. One can see that increasing
on APD. One can see that increasing 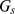 from
from  to
to 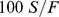 increases APD by
increases APD by 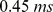 . This effect of
. This effect of 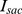 on APD is small in the studied parameter range compared to the constantly stretched medium, where increasing
on APD is small in the studied parameter range compared to the constantly stretched medium, where increasing 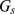 from
from  to
to 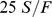 resulted in increase of APD by
resulted in increase of APD by 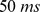 .
.
Figure 7. Effect of stretch-activated currents on the action potential in contracting medium.
(A) Action potential vs
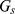 . (B) APD vs
. (B) APD vs
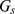 . (C) Upstroke of action potential vs
. (C) Upstroke of action potential vs
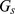 . (D) Maximal upstroke slope vs
. (D) Maximal upstroke slope vs
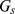 . Traveling plain waves were periodically (
. Traveling plain waves were periodically (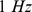 ) induced for different
) induced for different 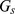 . Action potentials were measured after
. Action potentials were measured after 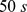 . Resting potential was measured in the medium without external stimulations. APD was measured at
. Resting potential was measured in the medium without external stimulations. APD was measured at  recovery.
recovery.
In Figure 7C we illustrate the effect of 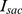 on the action potential upstroke in the deforming medium. We can see that the upstroke peak decreases for increasing
on the action potential upstroke in the deforming medium. We can see that the upstroke peak decreases for increasing 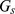 ; from
; from 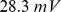 (for
(for 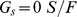 ) to
) to 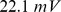 (for
(for 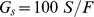 ). This decrease in upstroke peak is small compared to the constantly stretched medium, where an increase of
). This decrease in upstroke peak is small compared to the constantly stretched medium, where an increase of 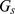 from
from 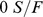 to
to 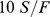 caused a decrease of the upstroke amplitude by
caused a decrease of the upstroke amplitude by 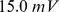 (compare Figure 5A). Furthermore, in Figure 7D we illustrate the maximal upstroke slope against
(compare Figure 5A). Furthermore, in Figure 7D we illustrate the maximal upstroke slope against 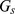 . The maximal upstroke slope decreases for increasing
. The maximal upstroke slope decreases for increasing 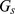 . The effect of
. The effect of 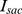 is small compared to the constantly stretched medium. In particular, increasing
is small compared to the constantly stretched medium. In particular, increasing 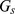 from
from  to
to 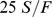 in the contracting medium decreases the upstroke slope from
in the contracting medium decreases the upstroke slope from 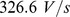 to
to 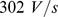 , whereas in the constantly stretched medium an increase of
, whereas in the constantly stretched medium an increase of 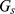 from
from 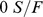 to
to  causes a decrease to
causes a decrease to 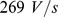 .
.
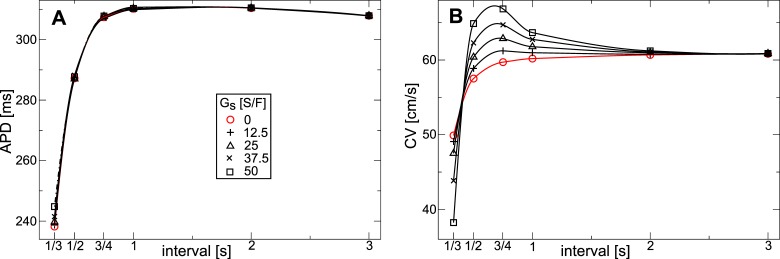
Figure 8A illustrates the effect of 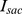 on the APD restitution in the contracting medium. From Figure 8A we see a small effect of
on the APD restitution in the contracting medium. From Figure 8A we see a small effect of 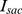 on the APD. Only for a stimulation period shorter than
on the APD. Only for a stimulation period shorter than 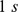 we see a small decrease in steepness of the restitution curve with increasing
we see a small decrease in steepness of the restitution curve with increasing 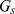 .
.
Figure 8. Dependence of restitution on stretch-activated currents in contracting medium.
(A) APD restitution vs
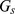 . (B) CV restitution vs
. (B) CV restitution vs
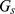 . Same parameters were used as in Figure? 6.
. Same parameters were used as in Figure? 6.
Figure 8B illustrates the effect of 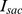 on CV restitution in the contracting medium. We see, that for a stimulation period longer than
on CV restitution in the contracting medium. We see, that for a stimulation period longer than 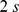 stretch activated currents have only little effect on CV. This is because for a slow stimulation period the effects of deformation caused by a preceding wave progressively decrease. For stimulation periods shorter than
stretch activated currents have only little effect on CV. This is because for a slow stimulation period the effects of deformation caused by a preceding wave progressively decrease. For stimulation periods shorter than 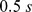 , a steep positive CV restitution is present for all measured values of
, a steep positive CV restitution is present for all measured values of 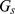 , and the slope of the CV curve increases when
, and the slope of the CV curve increases when 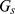 is larger. For stimulation periods between
is larger. For stimulation periods between 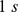 and
and 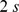 we see that contraction results in negative CV restitution slopes: a higher periodic stimulation causes higher wave velocities. Note that CV depends on the position it is measured, as the medium before the wave is depolarized by
we see that contraction results in negative CV restitution slopes: a higher periodic stimulation causes higher wave velocities. Note that CV depends on the position it is measured, as the medium before the wave is depolarized by 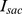 . Here we used an average CV to illustrate the abnormal CV restitution.
. Here we used an average CV to illustrate the abnormal CV restitution.
Effect of Mechanical Conditions
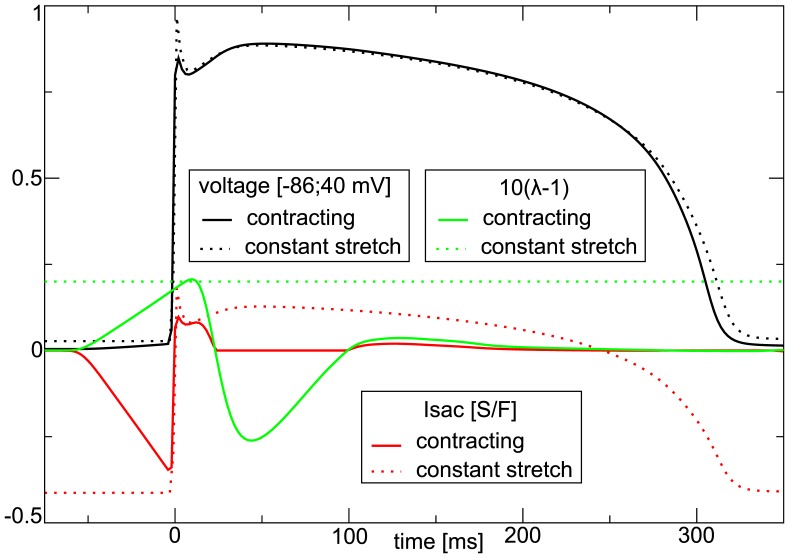
Let us now compare the results for a constantly stretched and contracting medium. We found, that under both, dynamical and static stretch conditions, increasing 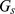 causes an elongation of the APD; however, in the deforming medium the effect is much smaller than in the constantly stretched medium (compare Figures 6A, and 4 with Figures 7B, and 8A). Furthermore, the results of the CV restitution in the constantly stretched and the contracting medium are significantly different. We can explain these differences by substantially different time courses of stretch in a constantly stretched and in contracting tissue. Figure 9 illustrates the shape of action potential, stretch activated current, and deformation of the medium for a single cell which is subject to a constant stretch (similar to Figure 4), and for a cell in a contracting medium, in which we measured the APD restitution shown in Figure 8. In both setups the cell was paced at
causes an elongation of the APD; however, in the deforming medium the effect is much smaller than in the constantly stretched medium (compare Figures 6A, and 4 with Figures 7B, and 8A). Furthermore, the results of the CV restitution in the constantly stretched and the contracting medium are significantly different. We can explain these differences by substantially different time courses of stretch in a constantly stretched and in contracting tissue. Figure 9 illustrates the shape of action potential, stretch activated current, and deformation of the medium for a single cell which is subject to a constant stretch (similar to Figure 4), and for a cell in a contracting medium, in which we measured the APD restitution shown in Figure 8. In both setups the cell was paced at 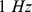 . We see that
. We see that 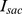 in a constantly stretched cell is active during the entire action potential, and
in a constantly stretched cell is active during the entire action potential, and 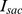 has a substantial negative value (inward current) at the waveback, which results in APD prolongation. On the contrary, for a cell in the contracting medium
has a substantial negative value (inward current) at the waveback, which results in APD prolongation. On the contrary, for a cell in the contracting medium 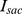 is absent at the waveback. This is because at this phase of the action potential the cell is contracting, and thus no stretch activated current is produced. As a result of that difference, the APD for a cell in the deforming tissue is only slightly longer than that of a cell in a non-deforming tissue. Some elongation of the APD at increased
is absent at the waveback. This is because at this phase of the action potential the cell is contracting, and thus no stretch activated current is produced. As a result of that difference, the APD for a cell in the deforming tissue is only slightly longer than that of a cell in a non-deforming tissue. Some elongation of the APD at increased 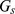 can be explained with the negative current prior/during the upstroke of the action potential which slightly decreases the sodium current via the accommodation phenomenon. The linear increase of transmembrane potential shown in Figure 7 is also present in Figure 9, and we can see that it is caused by a linear increase of stretch and thus
can be explained with the negative current prior/during the upstroke of the action potential which slightly decreases the sodium current via the accommodation phenomenon. The linear increase of transmembrane potential shown in Figure 7 is also present in Figure 9, and we can see that it is caused by a linear increase of stretch and thus 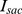 which sets in
which sets in 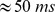 prior the upstroke. Overall, in the deforming medium the cell is affected by
prior the upstroke. Overall, in the deforming medium the cell is affected by 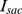 only from
only from 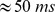 before the upstroke until
before the upstroke until 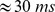 after the upstroke, while during constant stretch
after the upstroke, while during constant stretch 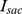 is always present. This explains why the effect of
is always present. This explains why the effect of 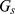 on the APD is much smaller in the contracting medium compared to the constantly stretched medium. Note the change in sign of
on the APD is much smaller in the contracting medium compared to the constantly stretched medium. Note the change in sign of 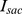 when the transmembrane potential reaches the reversal potential of the stretch activated channels
when the transmembrane potential reaches the reversal potential of the stretch activated channels 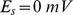 (compare Eq.(12)). Thus
(compare Eq.(12)). Thus 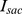 has a depolarizing effect on cardiac cells prior an action potential, and can have a repolarizing effect during the action potential. From Figure 9 we can also understand the different results on the CV restitution curves for the constantly stretched and the contracting medium. In the constantly stretched medium decrease of velocity is due to the constantly depolarizing
has a depolarizing effect on cardiac cells prior an action potential, and can have a repolarizing effect during the action potential. From Figure 9 we can also understand the different results on the CV restitution curves for the constantly stretched and the contracting medium. In the constantly stretched medium decrease of velocity is due to the constantly depolarizing 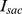 causing accommodation, whereas in the contracting medium, a depolarization of the medium
causing accommodation, whereas in the contracting medium, a depolarization of the medium 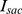 sets in only about
sets in only about 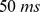 prior to the upstroke (compare Figure 4), so that no significant accommodation takes place, and causes a preexcitation of the medium prior the traveling wave. As a result, for intermediate stimulation periods, an increase in
prior to the upstroke (compare Figure 4), so that no significant accommodation takes place, and causes a preexcitation of the medium prior the traveling wave. As a result, for intermediate stimulation periods, an increase in  causes an increase of CV.
causes an increase of CV.
Figure 9. Effect of stretch conditions on stretch-activated currents and action potential shape.
Continuous lines show variables for cell in the medium, dotted lines show variables for constantly stretched cell. The constantly stretched cell was constantly held at 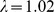 , and paced at
, and paced at 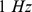 to steady state dynamics. The other cell was in a contracting medium in the same setup as in Figure? 6, and also paced at
to steady state dynamics. The other cell was in a contracting medium in the same setup as in Figure? 6, and also paced at 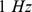 to steady state dynamics.
to steady state dynamics.  .
.
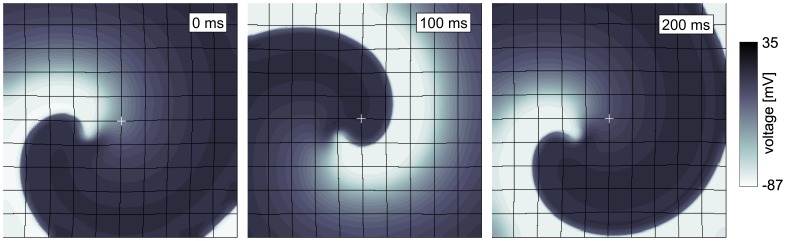
Spiral Wave Dynamics
We studied effects of deformation on spiral wave dynamics in our model. We initiated a spiral wave with an S1–S2 protocol in the medium, and then simulated spiral rotation for 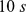 to avoid artifacts from the spiral initiation protocol. During this initial phase
to avoid artifacts from the spiral initiation protocol. During this initial phase 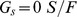 . The values of all variables are then recorded, and used as initial conditions for the following simulations. We set
. The values of all variables are then recorded, and used as initial conditions for the following simulations. We set 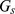 to various values, in contracting and constantly stretched medium, and studied how this affects the dynamics of the rotating spiral wave. We studied spiral wave dynamics for
to various values, in contracting and constantly stretched medium, and studied how this affects the dynamics of the rotating spiral wave. We studied spiral wave dynamics for 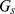 between
between  and
and 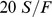 . Figure 10 illustrates the simulation experiment, it shows spiral rotation in the model for
. Figure 10 illustrates the simulation experiment, it shows spiral rotation in the model for 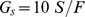 in the contracting medium.
in the contracting medium.
Figure 10. Illustration of spiral wave dynamics in contracting medium.
Time after stretch activated current 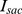 was activated is shown top right of each subfigure.
was activated is shown top right of each subfigure.  .
.
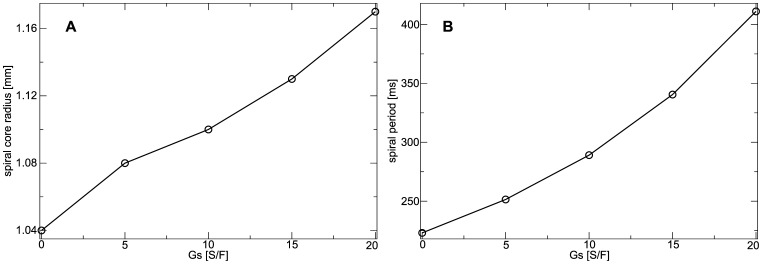
We found that in the constantly stretched medium (assumed to be stretched to 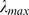 ) the spiral tip follows a static circular core (data not shown). Figure 11A illustrates how
) the spiral tip follows a static circular core (data not shown). Figure 11A illustrates how 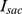 affects the spiral core radius. We found that the size of the spiral wave core increases with increasing
affects the spiral core radius. We found that the size of the spiral wave core increases with increasing 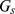 (
(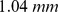 for
for 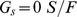 , and
, and 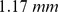 for
for 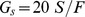 ). In Figure 11B it is illustrated how the spiral period is affected by
). In Figure 11B it is illustrated how the spiral period is affected by 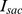 in the constantly stretched medium. We find, that the spiral period increases for increasing
in the constantly stretched medium. We find, that the spiral period increases for increasing 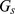 . An increase of
. An increase of 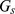 from
from 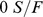 to
to 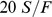 causes an increase of spiral period from
causes an increase of spiral period from 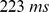 to
to 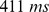 . This increase in the period can be explained by elongation of APD under constant stretch conditions (Figure 9).
. This increase in the period can be explained by elongation of APD under constant stretch conditions (Figure 9).
Figure 11. Dependence of spiral wave dynamics on stretch-activated currents in constantly stretched medium.
(B) Spiral core radius as a function of  . (C) Spiral wave period as function of
. (C) Spiral wave period as function of 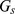 .
.
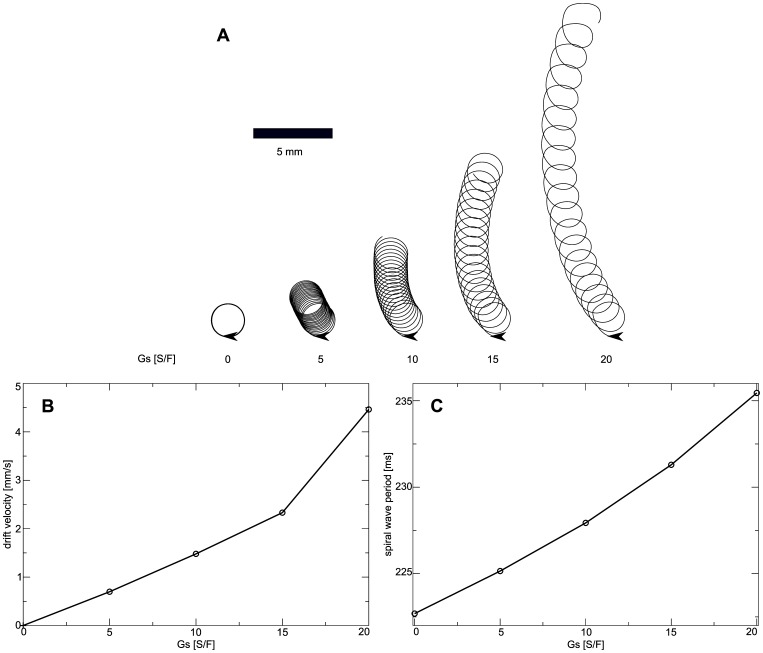
Figure 12A illustrates how the spiral wave rotation is affected by 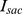 in the contracting medium. We see that in absence of
in the contracting medium. We see that in absence of 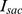 the spiral rotates around a circular core. However, for increasing
the spiral rotates around a circular core. However, for increasing 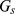 the spiral starts to drift, and drift velocity increases with an increase of
the spiral starts to drift, and drift velocity increases with an increase of 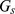 . All spiral tip trajectories in Figure 12A show drift for the same time interval (
. All spiral tip trajectories in Figure 12A show drift for the same time interval (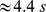 ), and we see that the distance traveled by the spiral tip increases substantially with an increase of
), and we see that the distance traveled by the spiral tip increases substantially with an increase of 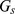 . We use the traveled distance of the spiral tip to estimate the velocity of spiral wave drift. Figure 12B shows the velocity of spiral wave drift as a function of
. We use the traveled distance of the spiral tip to estimate the velocity of spiral wave drift. Figure 12B shows the velocity of spiral wave drift as a function of 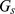 . We see an approximately linear increase in drift velocity with increase of
. We see an approximately linear increase in drift velocity with increase of 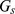 . Figure 12C illustrates the effect of
. Figure 12C illustrates the effect of 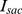 on spiral wave period. We see that increasing
on spiral wave period. We see that increasing 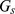 increases the spiral wave period: an increase of
increases the spiral wave period: an increase of 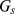 from
from 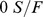 to
to 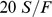 causes an increase of spiral period from
causes an increase of spiral period from 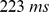 to
to 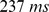 . This effect can be explained by the accommodation phenomenon.
. This effect can be explained by the accommodation phenomenon. 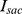 decreases the availability of sodium channels which results in a decrease of excitability which is known to increase the period of a spiral wave. However, as the effect of
decreases the availability of sodium channels which results in a decrease of excitability which is known to increase the period of a spiral wave. However, as the effect of 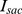 on APD is minimal (see Figure 8A) the increase of the period is also less substantial compared to the constantly stretched medium. Moreover, a decrease in excitability of a medium is known to increases the radius of a spiral core [42]. We calculated the size of the core of drifting spirals by correcting the spiral tip position data for the drift of the core, and indeed found some increase of the core radius with increasing
on APD is minimal (see Figure 8A) the increase of the period is also less substantial compared to the constantly stretched medium. Moreover, a decrease in excitability of a medium is known to increases the radius of a spiral core [42]. We calculated the size of the core of drifting spirals by correcting the spiral tip position data for the drift of the core, and indeed found some increase of the core radius with increasing 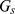 (
(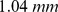 for
for 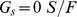 , and
, and 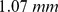 for
for 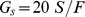 ); however, the effect is small.
); however, the effect is small.
Figure 12. Dependence of spiral wave dynamics on stretch-activated currents in contracting medium.
(A) Spiral tip trajectories are shown for different values of 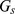 . Each tip trajectory illustrates drift for
. Each tip trajectory illustrates drift for 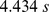 . Starting points and drift directions are illustrated with arrows. (B) Spiral wave drift velocity as function of
. Starting points and drift directions are illustrated with arrows. (B) Spiral wave drift velocity as function of 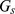 . Drift velocity is estimated from the tip trajectories using the distance of the spiral core position. (C) Spiral wave period as function of
. Drift velocity is estimated from the tip trajectories using the distance of the spiral core position. (C) Spiral wave period as function of 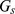 . Spiral period was measured from the last spiral rotation.
. Spiral period was measured from the last spiral rotation.
Our results on spiral wave drift in contracting tissue are qualitatively similar to that observed in [14], where a low dimensional model of cardiac tissue was applied, and the spiral drift was discussed as a so-called resonant drift mechanism [43]. Resonant-drift can be induced by a periodical variation of the medium properties such as its excitability synchronously with the spiral wave period [44]. In our model a rotating spiral wave itself periodically affects the excitability of the medium. We can understand this from Figure 10, where we can see that the fraction of the excited surface area (and thus the fraction of contracting medium) to the total surface area of the medium changes in synchrony with the spiral rotation, in turn affecting the mediums excitability properties. Therefore, we believe that in our simulations and in [14] the underlying mechanism of spiral drift is the resonant drift.
Discussion
We introduced a discrete electromechanical model of the human heart which couples a biophysical model of cardiac excitation [20], [21] and tension development [22], [23] with a discrete elastic mass-lattice model. We demonstrated the value of the model in an application study. We used our new model to investigate how stretch conditions and stretch-activated currents affect the heart's functioning. For this we studied how stretch-activated currents affect action potential shape, restitution properties, and spiral wave activity in a medium which we assumed constantly stretched, and a contracting medium with isometric boundary conditions. We found that stretch conditions significantly influence these properties by activating stretch-activated ion channels. In the freely deforming medium we find that the primary effects are accommodation, and preexcitation of the medium. In the constantly stretched medium we find a much stronger accommodation effect, no effect of preexcitation, and substantial elongation of the APD caused by depolarizing 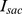 during the recovery phase of the action potential. We found that spiral wave drift is caused in the deforming medium, whereas in the constantly stretched medium rotation dynamics is not affected, but spiral period and core size is increased.
during the recovery phase of the action potential. We found that spiral wave drift is caused in the deforming medium, whereas in the constantly stretched medium rotation dynamics is not affected, but spiral period and core size is increased.
It has been shown that the dynamics of spiral waves in the heart manifests itself in the type of cardiac arrhythmia, for example, a drifting spiral wave can induce a polymorphic ventricular tachycardia which is a known precursor for ventricular fibrillation [45]. Our results show that in addition to heterogeneity induced spiral wave drift [46]–[48] there is a drift due to mechano-electrical feedback which can also affect the type of cardiac arrhythmia.
Our results on restitution properties suggest that in dynamic stretch-conditions 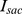 causes abnormal CV restitution due to a preexcitation in the medium. It has been shown that abnormal CV restitution can cause alternans and initiation of spiral waves [49], [50], and also important phenomena on spiral wave dynamics such as discordant alternans can be caused by abnormal CV restitution [51], [52]. We expect that this mechanism of mechanically caused abnormal CV-restitution is important to understand the onset of arrhythmias due to emergent dynamic inhomogeneities.
causes abnormal CV restitution due to a preexcitation in the medium. It has been shown that abnormal CV restitution can cause alternans and initiation of spiral waves [49], [50], and also important phenomena on spiral wave dynamics such as discordant alternans can be caused by abnormal CV restitution [51], [52]. We expect that this mechanism of mechanically caused abnormal CV-restitution is important to understand the onset of arrhythmias due to emergent dynamic inhomogeneities.
The computation time of our mechanical model scales linearly against the number of mechanical nodes, which allows to solve the model with a higher mechanical node density and thus high spatial resolution of 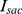 [16]. Furthermore, this computational efficiency of the discrete mechanical model allows us to update the its configuration after each electrical step (
[16]. Furthermore, this computational efficiency of the discrete mechanical model allows us to update the its configuration after each electrical step (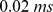 ). Continuous mechanical studies on cardiac function normally solve mechanics following several electrical steps, because its more demanding numerical schemes, for example in [18] the mechanical configuration was solved following
). Continuous mechanical studies on cardiac function normally solve mechanics following several electrical steps, because its more demanding numerical schemes, for example in [18] the mechanical configuration was solved following 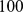 electrical steps.
electrical steps.
The passive elasticity of the heart is most commonly described by hyperelastic constitutive relations in finite element formulations of continuum mechanics, for example, the Guccione material relation in [18]. A drawback of the mass-lattice framework of the new model is its difficulty to reproduce passive mechanical properties of biological tissue with a discrete mechanical model, for example volume conservation or specific passive mechanical properties such as hyperelasticity. In contrast, these properties can be directly described in constitutive relations in continuum mechanics. The discrete electromechanical model could be extended to describe hyperelastic material relations, for example using the approach developed by Fritz et al. in [53], where a mass-spring model is in fact adapted to a hyperelastic material relation to describe cardiac mechanics. Moreover, also volume conservation and anisotropy of heart tissue can be introduced to discrete mechanical models [54], [55].
As another next step, the discrete electromechanical model can be extended to three-dimensional simulations to study the effect of mechano-electrical feedback on the dynamics of scroll waves.
Our modeling framework can potentially be used to estimate effects of mechanical or electrical components in experimental studies of wave propagation in the heart. However, it needs to be adjusted to the specific tissue type and mechanical properties of the experimental system. It can be done by changing the parameters on our model based on direct measurements.
We set up the new electromechanical model using a standard form for the stretch-activated currents 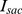 in Eq.(12). This allows us to compare the new results to results previously achieved with electromechanical models using a continuous mechanical description, for instance results on spiral wave drift in [14]. Experimental studies showed that
in Eq.(12). This allows us to compare the new results to results previously achieved with electromechanical models using a continuous mechanical description, for instance results on spiral wave drift in [14]. Experimental studies showed that 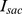 depends also on additional factors, for example, the stretch rate [56]. Our model can easily be adjusted to other formulations of
depends also on additional factors, for example, the stretch rate [56]. Our model can easily be adjusted to other formulations of 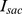 , for example, to the formulation of Jie et al. [19] which considers a stretch rate dependency. It can be interesting to compare the effect of different formulations of
, for example, to the formulation of Jie et al. [19] which considers a stretch rate dependency. It can be interesting to compare the effect of different formulations of 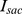 on the dynamics of wave propagation.
on the dynamics of wave propagation.
The effect of deformation of the medium on the metric tensor are neglected in the model, as we assume that the main resistivity between cells is constituted by gap junctions. We used this assumption also in [15], where we found that the change of the metric tensor did not affect qualitative results our study on mechanically caused pacemaking activity in a low-dimensional model.
Acknowledgments
The authors are grateful to Dr. Rikkert H. Keldermann, Dr. Martyn Nash, Dr. Kirsten ten Tusscher, and Ivan Kazbanov for valuable discussions. We thank Jan Kees van Amerongen for excellent technical support.
Funding Statement
LDW is funded by the Netherlands Organization for Scientific Research (http://www.nwo.nl) (NWO Grant No. 613.000.604) of the research Council for Physical Sciences (EW). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Pool R (1990) Heart like a wheel. Science 247: 1294–1295. [DOI] [PubMed] [Google Scholar]
- 2. Winfree AT (1989) Electrical instability in cardiac muscle: Phase singularities and rotors. J Theor Biol 138: 353–405. [DOI] [PubMed] [Google Scholar]
- 3. Davidenko J, Pertsov A, Salomonsz R, Baxter W, Jalife J (1992) Stationary and drifting spiral waves of excitation in isolated cardiac muscle. Nature 355: 349–351. [DOI] [PubMed] [Google Scholar]
- 4. Pertsov A, Davidenko J, Salomontsz R, BaxterW, Jalife J (1993) Spiral waves of excitation underlie reentrant activity in isolated cardiac muscle. Circ Res 72: 631–650. [DOI] [PubMed] [Google Scholar]
- 5. Kohl P, Hunter P, Noble D (1999) Stretch-induced changes in heart rate and rhythm: Clinical observations, experiments and mathematical models. Prog Biophys Molec Biol 71: 91–138. [DOI] [PubMed] [Google Scholar]
- 6. Wang Z, Taylor LK, Denney WD, Hansen DE (1994) Initiation of ventricular extrasystoles by myocardial stretch in chronically dilated and failing canine left ventricle. Circulation 90: 2022–2031. [DOI] [PubMed] [Google Scholar]
- 7. Kohl P, Nesbitt A, Cooper P, Lei M (2001) Sudden cardiac death by commotio cordis: role of mechano-electric feedback. Cardiovasc Res 50: 280–289. [DOI] [PubMed] [Google Scholar]
- 8. Lab M (1982) Contraction-excitation feedback in myocardium. Physiological basis and clinical relevance. Circ Res 50: 757–766. [DOI] [PubMed] [Google Scholar]
- 9. Cave DM, Gazmuri RJ, Otto CW, Nadkarni VM, Cheng A, et al. (2010) Part 7: CPR techniques and devices 2010 american heart association guidelines for cardiopulmonary resuscitation and emergency cardiovascular care. Circulation 122: S720–S728. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Kohl P, Ravens U (2003) editors (2003) Mechano-Electric Feedback and Cardiac Arrhythmias, Prog. Biophys. Molec. Biol., Elsevier Ltd, volume 82(1–3): 1–266. [DOI] [PubMed] [Google Scholar]
- 11. Nash M, Panfilov A (2004) Electromechanical model of excitable tissue to study reentrant cardiac arrhythmias. Prog Biophys Mol Biol 85: 501–522. [DOI] [PubMed] [Google Scholar]
- 12. Panfilov A, Keldermann R, Nash M (2005) Self-organized pacemakers in a coupled reactiondiffusion-mechanics system. Phys Rev Lett 95(25): 258104. [DOI] [PubMed] [Google Scholar]
- 13. Keldermann RH, Nash MP, Panfilov AV (2007) Pacemakers in a reaction-diffusion mechanics system. Journal of Statistical Physics 128: 375–392. [Google Scholar]
- 14. Panfilov A, Keldermann R, Nash M (2007) Drift and breakup of spiral waves in reaction-diffusionmechanics systems. Proc Natl Acad Sci USA 104: 7922–7926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Weise LD, Nash MP, Panfilov AV (2011) A discrete model to study reaction-diffusion-mechanics systems. PLoS ONE 6(7): e21934. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Weise LD, Panfilov AV (2011) New mechanism of spiral wave initiation in a reaction-diffusionmechanics system. PLoS ONE 6(11): e27264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Weise LD, Panfilov AV (2012) Emergence of spiral wave activity in a mechanically heterogeneous reaction-diffusion-mechanics system. Phys Rev Lett 108: 228104. [DOI] [PubMed] [Google Scholar]
- 18. Keldermann RH, Nash MP, Gelderblom H, Wang VY, Panfilov AV (2010) Electromechanical wavebreak in a model of the human left ventricle. Am J Physiol Heart Circ Physiol 299: H134–143. [DOI] [PubMed] [Google Scholar]
- 19. Jie X, Gurev V, Trayanova N (2010) Mechanisms of mechanically induced spontaneous arrhythmias in acute regional ischemia. Circ Res 106: 185–192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Ten Tusscher K, Panfilov A (2006) Alternans and spiral breakup in a human ventricular tissue model. Am J Physiol Heart Circ Physiol 291: H1088–100. [DOI] [PubMed] [Google Scholar]
- 21. Ten Tusscher K, Noble D, Noble P, Panfilov A (2004) A model for human ventricular tissue. Am J Physiol Heart Circ Physiol 286: H1573–H1589. [DOI] [PubMed] [Google Scholar]
- 22. Niederer S, Hunter P, Smith N (2006) A quantitative analysis of cardiac myocyte relaxation: a simulation study. Biophys J 90: 1697–1722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Niederer S, Smith N (2008) An improved numerical method for strong coupling of excitation and contraction models in the heart. Prog Biophys Mol Biol 96: 90–111. [DOI] [PubMed] [Google Scholar]
- 24. Seth B (1935) Finite strain in elastic problems. Phil Trans R Soc Lond A 234: 231–264. [Google Scholar]
- 25. Verlet L (1967) Computer “experiments” on classical fluids. i. thermodynamical properties of lennard-jones molecules. Phys Rev 159: 98. [Google Scholar]
- 26.Mohr M (2006) A hybrid deformation model of ventricular myocardium. Karlsruhe: PhD thesis, Fridericiana University.
- 27. Trayanova N, Li W, Eason J, Kohl P (2004) Effect of stretch activated channels on defibrillation efficacy. Heart Rhythm 1: 67–77. [DOI] [PubMed] [Google Scholar]
- 28. Vetter F, McCulloch A (2001) Mechanoelectric feedback in a model of the passively inflated left ventricle. Ann Biomed Eng 29: 414–426. [DOI] [PubMed] [Google Scholar]
- 29. Hodgkin A, Huxley A (1952) A quantitative description of membrane current and its application to conduction and excitation in nerve. J Physiol 117: 500–544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. de Tombe PP, Stienen GJM (2007) Impact of temperature on cross-bridge cycling kinetics in rat myocardium. The Journal of Physiology 584: 591–600. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Schargott M, Popov V, Heß M (2007) Macroscopic isotropy of two- and three-dimensional elastic lattice models. Tribology International 40: 937–941. [Google Scholar]
- 32. Krivtsov A (1999) Constitutive equations of the nonlinear crystal lattice. Z angew Math Mech 79: 419–420. [Google Scholar]
- 33. Mathur AB, Collinsworth AM, Reichert WM, Kraus WE, Truskey GA (2001) Endothelial, cardiac muscle and skeletal muscle exhibit different viscous and elastic properties as determined by atomic force microscopy. Journal of biomechanics 34: 1545–1553. [DOI] [PubMed] [Google Scholar]
- 34. Hu H, Sachs F (1997) Stretch-activated ion channels in the heart. J Mol Cell Cardiol 29: 1511–1523. [DOI] [PubMed] [Google Scholar]
- 35. Zhang Y, Youm J, Sung H, Lee S, Ryu S, et al. (2000) Stretch-activated and background nonselective cation channels in rat atrial myocytes. J Physiol 523: 607–619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Kohl P, Hunter P, Noble D (1999) Stretch-induced changes in heart rate and rhythm: clinical observations, experiments and mathematical models. Progress in Biophysics and Molecular Biology 71: 91–138. [DOI] [PubMed] [Google Scholar]
- 37. Skouibine K, Trayanova N, Moore P (2000) A numerically efficient model for simulation of defibrillation in an active bidomain sheet of myocardium. Math Biosci 166: 85–100. [DOI] [PubMed] [Google Scholar]
- 38. Kohl P, Day K, Noble D (1998) Cellular mechanisms of cardiac mechano-electric feedback in a mathematical model. Can J Cardiol 14: 111–119. [PubMed] [Google Scholar]
- 39. Vahl CF, Timek T, Bonz A, Fuchs H, Dillman R, et al. (1998) Length dependence of calciumand force-transients in normal and failing human myocardium. Journal of molecular and cellular cardiology 30: 957–966. [DOI] [PubMed] [Google Scholar]
- 40. Zhang Y, Sekar RB, McCulloch AD, Tung L (2008) Cell cultures as models of cardiac mechanoelectric feedback. Progress in Biophysics and Molecular Biology 97: 367–382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Franz M, Cima R, Wang D, Profitt D, Kurz R (1992) Electrophysiological effects of myocardial stretch and mechanical determinants of stretch-activated arrhythmias. Circulation 86: 968–978. [DOI] [PubMed] [Google Scholar]
- 42.Panfilov AV (2009) Theory of reentry. In: Zipes DP, Jalife J, editors, Cardiac electrophysiology. From cell to bedside, 5th edition. New York: Elsevier, 329–337.
- 43. Agladze K, Davydov V, Mikhailov A (1987) An observation of resonance of spiral waves in distributed excitable medium. JETP Lett 45: 767–769. [Google Scholar]
- 44. Grill S, Zykov V, Müller S (1995) Feedback-controlled dynamics of meandering spiral waves. Phys Rev Lett 75: 3368–3371. [DOI] [PubMed] [Google Scholar]
- 45. Gray RA, Jalife J, Panfilov A, Baxter WT, Cabo C, et al. (1995) Nonstationary vortexlike re-entrant activity as a mechanism of polymorphic ventricular tachycardia in the isolated rabbit heart. Circulation 91: 2454–2469. [DOI] [PubMed] [Google Scholar]
- 46. Ten Tusscher K, Panfilov A (2003) Reentry in heterogeneous cardiac tissue described by the Luo-Rudy ventricular action potential model. Am J Physiol Heart Circ Physiol 284: H542–H548. [DOI] [PubMed] [Google Scholar]
- 47. Panfilov A, Holden A (1990) Vortices in a system of two coupled excitable fibers. Phys Lett A 147: 463–466. [Google Scholar]
- 48. Rudenko AN, Panfilov AV (1983) Drift and interaction of vortices in two-dimensional heterogeneous active medium. Studia Biophysica 98: 183–188. [Google Scholar]
- 49. de Lange E, Kucera JP (2010) Alternans resonance and propagation block during supernormal conduction in cardiac tissue with decreased [K+]o. Biophysical Journal 98: 1129–1138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50. de Lange E, Kucera JP, Qu Z (2011) Supernormal excitability causes alternans, block, wavebreak and reentry in cardiac tissue. Biophysical Journal 100: 435a. [Google Scholar]
- 51. Echebarria B, Rder G, Engel H, Davidsen J, Br M (2011) Supernormal conduction in cardiac tissue promotes concordant alternans and action potential bunching. Physical Review E 83: 040902. [DOI] [PubMed] [Google Scholar]
- 52. Kwon O, Kim TY, Lee KJ (2010) Period-2 spiral waves supported by nonmonotonic wave dispersion. Physical review E, Statistical, nonlinear, and soft matter physics 82: 046213. [DOI] [PubMed] [Google Scholar]
- 53.Fritz T, Jarrousse O, Dössel O (2009) Adapting a mass-spring system to energy density function describing myocardial mechanics. In: Vander Sloten J, Verdonck P, Nyssen M, J H, editors, 4th European Conference of the International Federation for Medical and Biological Engineering. Berlin, Heidelberg: Springer, 2003–2006.
- 54.Bourguignon D, Cani MP (2000) Controlling anisotropy in mass-spring systems. In: Eurographics Workshop on Computer Animation and Simulation (EGCAS). Springer-Verlag, Springer Computer Science, 113–123. URL http://www-evasion.imag.fr/Publications/2000/BC00. Proceedings of the 11th Eurographics Workshop, Interlaken, Switzerland, August 21–22, 2000.
- 55. Mohr M, Seemann G, Sachse F, Dössel O (2003) Modeling of myocardial deformation with an extended spring mass system. Biomedical Engineering 48(1): 6–7. [Google Scholar]
- 56. Nishimura S, Kawai Y, Nakajima T, Hosoya Y, Fujita H, et al. (2006) Membrane potential of rat ventricular myocytes responds to axial stretch in phase, amplitude and speed-dependent manners. Cardiovascular research 72: 403–411. [DOI] [PubMed] [Google Scholar]