MRI of Fast-Relaxing Spins

Abstract

MR imaging of extremely fast-relaxing spins is currently a topic of much interest due to recent technical innovations and groundbreaking studies demonstrating its utility in biomedical research applications. From a technical perspective, this article examines the different classes of pulse sequences currently available to image spins with ultra-short transverse relaxation times (T₂ and T₂*), with particular attention focused on the newest member of the class, sweep imaging with Fourier transformation (SWIFT).

1. INTRODUCTION

In many tissues a significant fraction of the water protons cannot easily be visualized using conventional MRI methods due to an ultra-short (<1 ms) transverse relaxation time. For example, in hard tissues such as cortical bone and teeth the linewidth of the water resonance is homogeneously broadened due to restricted molecular tumbling and dipole-dipole interactions; thus, the T₂ of these spins is ultra-short. In connective tissues such as tendon, the motion of water molecules is often highly anisotropic and consequently these water molecules have an ultra-short T₂ that depends on tissue orientation relative to the static field, B₀. In other tissues like lung, microscopic field inhomogeneity from interfaces between regions with different magnetic susceptibility (e.g., alveolar versus lung parenchyma) cause heterogeneous broadening of the water resonance; thus, the T₂* of these spins is ultra-short.

The inability to preserve signals from spins having ultra-short T₂ or T₂* with conventional MRI sequences has limited biomedical applications to involve mainly soft tissues, both in research and in the clinic. Due to technical constraints, in conventional MRI the excitation and acquisition events are separated by an echo time (TE) that cannot easily be less than ~1 ms. As a result, it is challenging to detect ultra-short-lived signals. During the past two decades, pulse sequences that acquire the free-induction decay (FID) instead of a gradient- or spin-echo signal have been shown to offer improved capabilities for imaging spins with ultra-short T₂ or T₂*. Early FID-based sequences were based on conventional MRI sequences and accomplish spin excitation with constant-frequency RF pulses. Some limitations of these techniques include finite acquisition delay (i.e., the time between excitation and detection) due to the finite pulse length and the sinc-shaped excitation profile that is produced when using a conventional square pulse for excitation. To date, the translation of FID-based MRI methods into routine preclinical and clinical use has been slowed by the need for specialized hardware (e.g., fast switching between transmit and receive modes) and the technical challenges associated with reconstructing images from FID projections. Despite increased technical demands, interest in FID-based imaging methods has steadily increased in recent years, due in large part to the many pioneering works by Graeme Bydder and others who have demonstrated the utility of FID-based sequences to capture important short-lived signals in tissues (for reviews, see [1, 2]).

We recently introduced a radically different excitation and acquisition scheme to accomplish FID-based imaging. The method, called Sweep imaging with Fourier transformation (SWIFT) [3], exploits frequency-modulated (FM) excitation and a simultaneous acquisition strategy to capture signals arising from spins having almost any T₂ or T₂*. Images of spins with T₂ and T₂* values as short as ~50 μs have been demonstrated and even shorter times should be possible in the future. SWIFT provides yet another way of thinking about how best to preserve fast-decaying signals with FID-based MRI. This article provides a perspective on the strengths and limitations of the pulse sequences for imaging spins with ultra-short T₂ and T₂*, with particular emphasis on the newest member of the class, SWIFT.

2. SEQUENCES TO VISUALIZE SPINS WITH ULTRA-SHORT T₂ or T₂*

An early approach to 2D Fourier imaging of ultra-short-T₂ spins exploited coherent averaging methods derived from solid state NMR spectroscopy. In one early demonstration of this, the MREV-8 line-narrowing sequence was used to reduce the effective size of the dipolar coupling during the evolution and detection periods of a spin-echo sequence which included phase- and frequency-encoding gradients for imaging [4]. In that work, a sequence of pulses was also used to “store” magnetization to minimize signal decay while the gradients were being switched. Although such approaches have succeeded in imaging materials and rigid tissues, they are not widely used in living subjects due to the high RF power demanded by line narrowing sequences and the possibility of tissue heating.

In the case of fibrous tissues such as ligaments and tendons, other Fourier imaging methods with spin- or stimulated-echo sequences have been much more successful. Water populations associated with tendons and ligaments have short and anisotropic T₂ values because the interaction of water molecules with collagen fibers induces to a motional anisotropy [5]. As a result, the intramolecular dipolar interaction Hamiltonian for these water populations does not average to zero. The splitting of the water proton signal due to the residual dipolar coupling is difficult to observe directly because it is masked by the large signal from the isotropic water. To solve this problem, spin- and stimulated-echo sequences that contain a double quantum filter (DQF) have been used to separate the signals from anisotropic versus isotropic water protons in the tissue [6, 7]. By this approach, only water molecules that interact with an ordered macromolecule contribute to the DQF NMR signal. Recent work has suggested an important clinical role for DQF MRI in monitoring the healing process in injured tendons [8].

The simplest pulse sequence to image fast-decaying spins, regardless of origin of their ultra-short T₂, is essentially that used in the early days of MRI by Lauterbur [9]. In the presence of a field gradient, the spins were excited with a short radiofrequency (RF) pulse and then immediately the FID was acquired. After Fourier transformation, a single projection (or view) of the object was obtained. The multiple views required to reconstruct an image were acquired using different orientations of the gradient vector G. This type of pulse sequence is nowadays generally known as radial projection imaging or simply radial MRI. By acquiring the FID rather than a gradient or spin echo, such sequences allow the shortest time between signal creation and signal acquisition. Lauterbur's classic sequence, and more recent variants thereof, provide close to optimal performance for imaging ultra-short T₂ or T₂*. Improvements in scanner performance over the years, in particular, the precision of executing sequence events and faster transmit/receive (T/R) electronics, have helped to make such techniques more robust, and consequently, have spurred a steady increase in their use.

Pulse sequences that evolved from Lauterbur's original technique are known by various names and acronyms, some of which are: BLAST [10], RUFIS [11], WASPI [12], FID-projection imaging [13], ZTE [14], and UTE [12, 15, 16]. However, one fundamental feature distinguishes the two most common sub-classes of these sequences. Specifically, these differ by whether the gradient is turned on or off during the application of the RF pulse.

BLAST, RUFIS, WASPI, FID-projection imaging, and ZTE best resemble Lauterbur's projection imaging experiment in that the gradient is turned on and stable when the RF pulse is applied. In this manner, loss of short-lived signals can be minimized since gradient switching is avoided. The latter is an important distinction, particularly when imaging larger objects like the human body since the rise time of the gradients of most clinical MRI scanners is not faster than 100 - 200 μs. As such, the acquisition delay is limited only by T/R switching times and potentially the coil ring-down time.

In UTE, on the other hand, the gradient is ramped on after the pulse has been applied, and data sampling usually begins while the gradient is ramping on to minimize the loss of the short-lived signals. By applying the RF pulse before the gradient is turned on, broadband excitation is no longer necessary. However, high peak RF power is still generally used to keep the pulse length short for minimizing signal decay during excitation.

A related technique is the single-point imaging (SPI) method [17-19]. In SPI, as in Lauterbur's sequence, the RF pulse is applied in the presence of a gradient (G), but instead of acquiring the whole FID, only a single phase-encoded data point is acquired. Phase-encoding in SPI has the advantage of avoiding image blur from resonance offsets arising, for example, from chemical shift and magnetic susceptibility differences. The latter problem can be a significant challenge for the frequency-encoded techniques discussed herein. Thus, SPI and variants thereof could be preferred approaches to image materials and other non-living solid objects. Unfortunately, the SPI acquisition scheme (i.e., one data point acquired per phase-encode step) usually requires a scan time that is too long for in vivo applications. A recently introduced pulse sequence called PETRA is an interesting hybrid of ZTE and SPI which solves the problem of the missing first FID data point(s) in ZTE [20].

With the exception of UTE, the sequences described above have limitations related to the finite length (T_p) of the constant-frequency RF pulse used for excitation, since it must be short to achieve uniform excitation in the presence of the gradient that's used for spatial encoding. In other words, the excitation bandwidth of the pulse (b_w) must be at least as large as the acquisition bandwidth (sw) which is given by γG × L, where L is maximum dimension of the object being imaged. With a square pulse, the excitation bandwidth is approximately T_p^-1 (FWHM), and to attain sufficiently large b_w, the need for high peak RF power increases significantly. Due to limitations on peak power, the flip angle is often constrained to a small, sub-optimal value, and this can result in reduced signal-to-noise ratio (SNR), particularly for spins with short longitudinal relaxation times (T₁ << 1 s). The necessity to achieve high peak RF power to flip spins rapidly has generally limited the utility of these methods to investigations of small objects using small RF coils. In addition, the excitation profile produced by a square pulse is sinc-shaped. Hence, at locations other than the center of the projections, the flip angle varies radially. This problem intensifies as the repetition time decreases (TR << T₁). In this case, the magnetization profile depends on flip angle, TR, and T₁, and this can lead to image artifacts and loss of specificity of tissue contrast.

In an effort to overcome these limitations, we proposed the SWIFT technique. SWIFT is also a projection imaging sequence, and it also possesses features of some classic NMR sequences. Specifically, SWIFT employs an FM pulse to excite spins, and in this manner, it resembles the earliest NMR spectroscopy method, continuous-wave (CW) NMR. Of course, CW NMR is highly inefficient as compared to pulsed FT NMR [21, 22], and as a result, CW NMR is rarely used these days. On the other hand, not long after the development of pulsed FT NMR, an efficient FM technique for spectroscopy was introduced known as rapid scan correlation [23]. Like CW NMR, rapid scan correlation was originally developed for NMR spectroscopy and is rarely used nowadays. But SWIFT, in a sense, represents the rebirth of this classic technique in MRI. As in CW NMR and rapid scan correlation, in SWIFT the different spin frequencies (isochromats) in the bandwidth of interest are excited sequentially in time using a frequency sweep. This sequential excitation has the advantage of reducing the need for short T_p and high peak RF power to achieve a given flip angle. The frequency sweep can be produced by modulating either the static field (B₀) or the frequency of RF irradiation. With SWIFT MRI, the signal acquired with a given setting of G is processed to yield a single projection of the object. To generate a three-dimensional (3D) image, the frequency sweeps are repeated, each time with a different gradient orientation. Other ways in which SWIFT differs from rapid scan correlation include: 1) the signal is considered in the time domain, like in pulsed NMR, 2) the sweep rate is much higher, 3) the sequence need not be restricted to using a linear frequency sweep (i.e., chirp), and 4) signal acquisition can continue after the pulse duration. These features add flexibility to the SWIFT sequence.

To date, most FM pulses that have been used in SWIFT were based on continuous FM functions that operate by means of a rapid passage. Rapid passage can be accomplished with any FM pulse having the property that we called offset-independent adiabaticity (OIA) [24]. Examples of OIA pulses include chirp [25], the original hyperbolic secant (HS) pulse [26], stretched versions of the HS pulse known as HSn pulses [24], and WURST [27]. Such rapid passage pulses can be used to excite spins when satisfying the condition

$$\mid \mathrm{d}\left({\omega }_{RF}\right)∕\mathrm{d}t\mid >>{\left(T_2\right)}^{-2},$$ (1)

where ω_RF is the time-dependent pulse frequency [22]. In classical terminology, the manner in which the rapid passage is executed can be distinguished based on the applicable condition:

$$\mid \mathrm{d}\left({\omega }_{\mathrm{RF}}\right)∕\mathrm{d}t\mid <<{\left({\omega }_1\left(t\right)\right)}^2$$ (2)

or

$$\mid \mathrm{d}\left({\omega }_{\mathrm{RF}}\right)∕\mathrm{d}t\mid >>{\left({\omega }_1\left(t\right)\right)}^2,$$ (3)

where ω₁ is the amplitude of the RF field in frequency units, ω₁(t) ≡ γB₁(t). The conditions expressed by the inequalities of equations (2) and (3) are known as the adiabatic region and the linear region, respectively [22]. There can be significant benefits to exciting spins with FM pulses operating in the linear region. For example, rapid passage performed in the linear region can be used to excite a broad bandwidth using only low peak RF amplitude, because the bandwidth is set by the sweep range, not the peak power. In conventional MRI, such pulses are not widely exploited for broadband excitation because the phase of the resultant transverse magnetization (M_xy) is a quadratic function of resonance offset. This quadratic phase dependence can be problematic and will lead to signal loss in some cases (e.g., when used for slice selection in conventional MRI sequences). On the other hand, the quadratric phase is not a problem when signal is acquired simultaneously as in SWIFT. In SWIFT, the rapid passage operating in the linear region creates a highly linear spin response for flip angles up to 90° [28] and the quadratic phase of the resultant M_xy is removed with a cross-correlation method identical to that used to recover phase information in stochastic NMR spectroscopy [29, 30]. Accordingly, the spin system response can be treated as a linear system, in which case the response r(t) to an input function x(t) is the convolution process given by

$$r\left(t\right)=h\left(t\right)\otimes x\left(t\right),$$ (4)

where h(t) is the unit impulse response (i.e., the FID), and H(ω) is the unit frequency response function (i.e., a projection of the object in the frequency domain). These functions are related to one another by direct FT [21, 31]. According to Fourier theory, the convolution in the time domain is a complex multiplication in the frequency co-domain:

$$F\left\{r\left(t\right)\right\}=R\left(\omega \right)=H\left(\omega \right)X\left(\omega \right)$$ (5)

where X(ω) is the FT of the input function x(t), which in our case is the pulse expressed as

$$x\left(t\right)={\omega }_1\left(t\right)\exp \left\{-i{\int }_0^t({\omega }_{\mathrm{RF}}\left(\tau \right)-{\omega }_{\mathrm{c}})d\tau \right\},$$ (6)

where ω_c is the center frequency in the sweep range. A projection of the object is obtained by correlation, which is straightforward to perform in the frequency domain with complex conjugate multiplication by the pulse function [32],

$$H\left(\omega \right)=\frac{R\left(\omega \right)X^{\ast }\left(\omega \right)}{{\mid X\left(\omega \right)\mid }^2},$$ (7)

where |X(ω)| is the modulus of X(ω). With certain types of rapid passage such as the HS and HSn class of pulses [24, 26, 33], b_w is determined by the range of the frequency sweep and the excitation profile is highly uniform within the sweep range; as a result, |X(ω)| is approximately constant in the baseband.

To this point in the discussion, we have not addressed the obvious question of how SWIFT can excite spins while simultaneously detecting their signals. Obviously, with traditional pulsed techniques that rely on high power (constant-frequency) RF pulses, attempts to acquire signal while transmitting the pulse will fail, not only due to hardware constraints, but also because large amounts of transmitted signal and noise will leak into the receiver channel and this will severely degrade data quality. On the other hand, with OIA pulses, RF energy is distributed incrementally in time across the baseband. In this manner, a uniform flip angle across a large bandwidth can be excited with a long pulse having substantially reduced peak RF power. Hence, the actual isolation needed between transmit and receive channels is only ~40 dB, which we previously showed can be provided by a simple quadrature hybrid [34]. Other options include magnetic field modulation in the slow sweep condition together with phase-sensitive detection and lock-in amplifier, as has been demonstrated for CW NMR imaging of materials [35]. In addition, a sideband modulation technique adapted to a modern scanner using a digital receiver has been proposed recently [36, 37]. Despite these accomplishments, at the present time it appears further engineering developments are needed before continuous acquisition during RF transmission will be sufficiently practical and robust. Therefore, most SWIFT experiments to date have been performed in a time-shared mode. In this implementation, N gaps are inserted in the FM pulse and signal acquisition takes place in these gaps. Gapping unfortunately compromises SNR as compared to continuous (non-gapped) acquisition because $\mathrm{SNR}\propto \sqrt{1-({\tau }_{\mathrm{p}}+t_{\mathrm{d}})b_{\mathrm{w}}}$, where t_d is the “dead time” occurring after the pulse element (τ_p) and the start of signal acquisition in the gap. This “dead time” is needed because the decaying residual transmitter signal is higher than the thermal noise background, which prevents acquisition. In addition, time is needed for switching between transmit and receive modes and to allow for coil ringing. Accordingly, it is apparent that such time-shared implementation of SWIFT is sub-optimal. For example, finite t_d makes it difficult to achieve very high excitation bandwidth. Furthermore, t_d consumes valuable acquisition time in the gaps, resulting in less than optimal SNR. These technical issues highlight the importance of future hardware developments for bringing continuous acquisition in SWIFT into routine use.

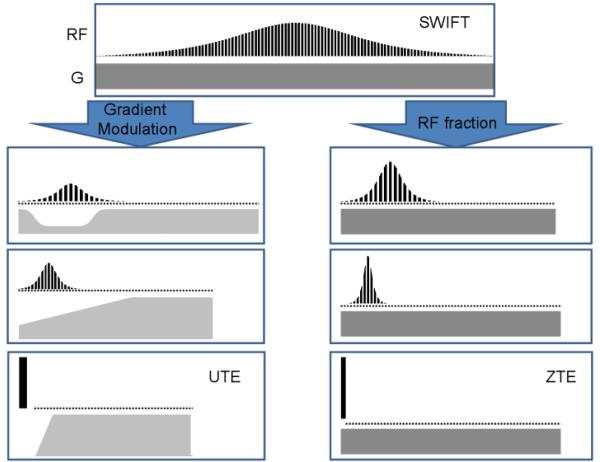
A final point can be made about SWIFT's connection with the other FID-based methods that utilize constant-frequency pulses. As described above, with an FM pulse the excitation bandwidth b_w is determined by range of frequencies swept during T_p, and the flip angle θ increases approximately linearly with peak RF amplitude for values of θ < 90° [28]. Thus, for given frequency-sweep range and flip angle, it is possible to reduce T_p, although at the expense of increasing RF amplitude. When T_p is decreased while keeping b_w fixed, the FM pulse increasingly becomes more like an equivalent hard pulse. In the limit that the FM pulse becomes a delta pulse, there is no difference between the FM pulse and the constant-frequency pulse. Likewise, in this limit, there is no difference between SWIFT and the other FID-based sequences that apply a constant-frequency pulse in the presence of the gradient (e.g., ZTE). However, SWIFT permits intermediate versions between these two extreme cases, as illustrated in the right panel of Fig. 1. Alternatively, methods have been developed to permit modulating the gradient during an FM pulse, while keeping the excitation constant in space [38]. These pulses, which we call gradient-modulated offset-independent adiabatic (GOIA) pulses, can also be used in SWIFT. In this case, when the gradient amplitude starts at zero and increases during the pulse, the SWIFT sequence begins to resemble the UTE sequence, as illustrated in the left panel of Fig. 1. This illustrates how SWIFT represents a bridge between these different FID-based methods.

Figure 1.

An illustration showing SWIFT's linkage with UTE and ZTE methods. SWIFT resembles ZTE when the FM pulse (or RF fraction) decreases until no dwell times occur during the pulse (right panel). SWIFT resembles UTE when using gradient-modulated FM pulses and the pulse length decreases until no dwell times occur during the pulse (left panel). As such, SWIFT provides a bridge between these different techniques.

Finally, it is interesting to contemplate whether other types of RF pulses besides rapid passage might meet the needs or even enhance the performance of SWIFT. Delay periods (gaps) can be inserted into conventional (constant-frequency) pulses to allow sampling inside the pulse [39], but this approach would appear to offer no advantage for FID-based MRI because without a frequency modulation the RF amplitude needs to increase proportionately to keep the same bandwidth. Other types of pulses that could work in SWIFT include those that excite magnetization in discrete bands in a sequential manner, such as the so-called polychromatic pulses [40]. Indeed, a similar type of polychromatic pulse containing gaps, called a Frank sequence, has been successfully employed in an FID-based sequence similar to SWIFT [41, 42]. Although these approaches are interesting and further improvements are likely, at the present time they do not appear to offer performance advantages (e.g., reduced SAR, flatness of excitation profile) over rapid passage implemented with a smooth frequency sweep.

3. THE GOOD AND BAD OF RADIAL PROJECTION IMAGING

Of course, there are intrinsic limits to the achievable spatial resolution when imaging spins with ultra-short T₂. In frequency-encoded MRI, a diffuse spherical blurring occurs when the intrinsic line-width of fast relaxing spins exceeds the voxel size expressed in frequency units.

When frequency encoding is used, image blur also arises from frequency offsets. That is, a constant frequency offset of internal magnetic origin, such as from chemical shift or magnetic susceptibility change, is additive to the spatially-dependent frequency produced by the gradient. In Cartesian sampling, a frequency offset leads to a spatial shift only in the time-invariant frequency-encoded direction. In radial MRI, the shift occurs in all radially-sampled views. The blur is a consequence of these shifts (or equivalently, the phase evolution) that occurs radially outward from the center of k-space in concentric spherical shells. Fortunately, all signals are preserved over the blurred distribution, and a number of methods utilizing algorithmic or acquisition strategies to minimize non-Cartesian off-resonance artifacts are available [43-46]. Future implementations of these and/or other new approaches are expected to obviate much of the blur in radial MRI.

Recently, phase and frequency contrast obtained with GRE sequences has become a topic of much interest. The phase component of the collected complex image data has been shown to contain information beyond that found in the magnitude image alone. In GRE imaging of brain, for example, phase contrast originates from small frequency shifts on the order of a few Hertz [47] due to magnetic susceptibility differences [48], microstructure [49], and chemical exchange [50]. In addition, orientation dependence of the phase contrast has been demonstrated [51]. In GRE imaging, phase contrast originates from the phase shift experienced by off-resonance spins during the TE period which can be as long as tens of milliseconds. SWIFT does not have an echo time, yet it has been shown to provide excellent phase contrast [52, 53]. Likewise, phase contrast is possible with other radial sequences, including UTE [54]. Although there is no TE and thus no phase shift at the center of the radially-sampled k-space, phase evolution takes place during the acquisition of each radial spoke. Hence, as the acquisition time increases, the phase accumulates in the FID as a consequence of frequency offsets. In GRE imaging, even relatively small B₀ fluctuations can cause phase wrapping, requiring post-processing that entails phase unwrapping [48] and possibly B₀ correction [55]. On the other hand, each radial spoke is inherently high-pass filtered and thus is relatively unaffected by low frequency B₀-variations like bulk magnetic susceptibility effects. One way to increase phase contrast in radial MRI is to decrease the acquisition bandwidth, sw. Further investigation is needed before clear conclusions can be drawn about the relative merits of producing phase contrast with standard Cartesian GRE versus radial acquisition of FIDs.

In addition to their ability to make more tissues visible to MRI, radial MRI sequences offer a means to preserve frequency-shifted signals in the vicinity of magnetic nanoparticles (e.g., super paramagnetic iron-oxide nanoparticles (SPIONs)) and magnetic objects (e.g., metallic implants from orthopedic surgeries). Regarding the former, SPIONs are increasingly being developed and exploited for biomedical applications. Normally, the presence of iron-oxide nanoparticles is manifested as signal voids in MR images due to the ultra-short T₂ they create; but with FID-based methods, such nanoparticles can give rise to positive contrast (bright spots). The latter occurs because the water protons surrounding the SPIONs have shortened T₁ values and/or the image-domain signal “piles up” due to the off-resonance effect described above [53, 56, 57]. These features promise to provide improved ability to track and quantify targeted contrast agents and molecular therapies, as well as to follow magnetically-labeled molecules and cells. Due to these and other future developments, FID-based MRI sequences are expected to play increased roles in the ever-expanding fields of molecular imaging and nanotechnology.

4. CONCLUDING REMARKS

The first images obtained by Lauterbur approximately 4 decades ago were based on FID acquisitions using radial sampling of k-space. Yet, soon after the invention of MRI, the vast majority of efforts in MRI technical development became focused on gradient- and spin-echo methodologies using k-space sampling on a Cartesian grid. During the past two decades, however, a revival of FID-based radial MRI has been taking place, due in large part to many groundbreaking studies demonstrating the utility of these sequences to capture important short-lived signals.

The most recent newcomer to the class of FID-based MRI sequences, SWIFT, appears to offer additional opportunities and capabilities for biomedical MRI. These arise mainly from SWIFT's unique way of acquiring spatially-encoded signals simultaneously (or nearly simultaneously) with a frequency sweep. However, some technical challenges remain for SWIFT to attain optimal performance; these include 1) improved switching times, 2) enhanced isolation between transmitter and receiver channels, and 3) reconstruction algorithms to minimize blur and other artifacts related to radial imaging. Fortunately, much of the technology already exists to tackle these problems. Despite its recent development and unique technical demands, SWIFT has already demonstrated its ability produce high quality images of water protons having almost any T₂ or T₂*, from the very long (tens of seconds) to the ultra-short (tens of microseconds).

For the past four decades, MRI technology has also focused mainly on methodologies that are based on the principles of pulsed FT NMR which uses constant-frequency RF pulses. Now, the classic frequency-swept NMR methods are making a small comeback in SWIFT. Given that SWIFT is very different from conventional MRI, and that it appeared on the scene only recently, it is interesting to imagine what roles and capabilities might evolve for SWIFT in the future. To achieve maximum efficiency in terms of RF power and SNR, it is postulated that MRI sequences of the future will increasingly use simultaneous signal detection during frequency-swept excitation, like that used in SWIFT.

• We analyze FID-based MRI sequences from a technical perspective

• Frequency-modulation reduces the need for high peak power in FID-based imaging

• Ultra-short T2 imaging sequences are expanding MRI capabilities